Numerical Turbulent Flow Analysis through a Rotational Heat Recovery System
Abstract
:1. Introduction
- -
- The global carbon footprint mitigation of numerous human activities [1].
- -
2. Materials and Methods
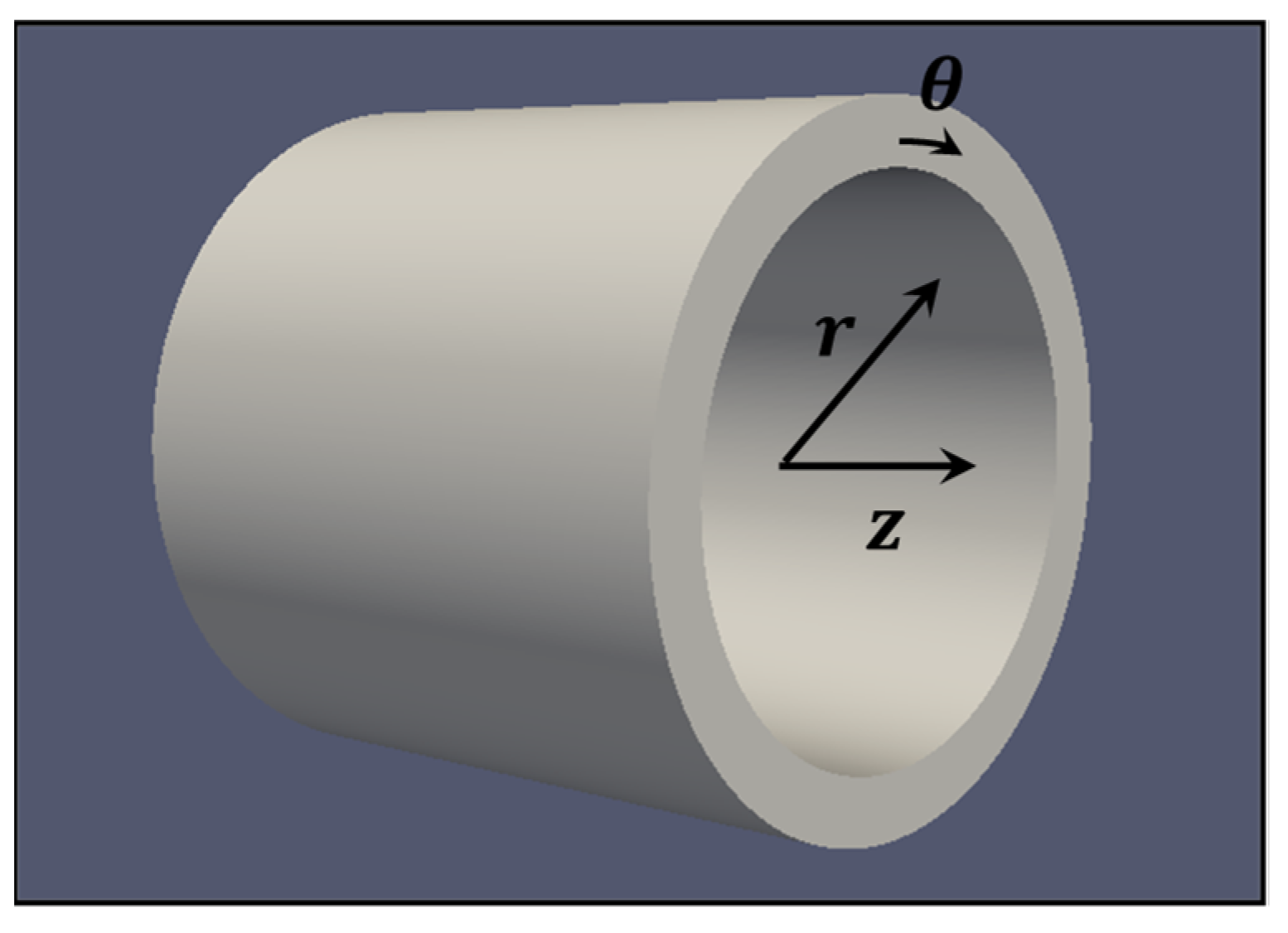
2.1. Numerical Strategy
- -
- A derived RANS approach based on a second-order model, taking into account the curve wall effect [22];
- -
2.2. Meshes Parameters
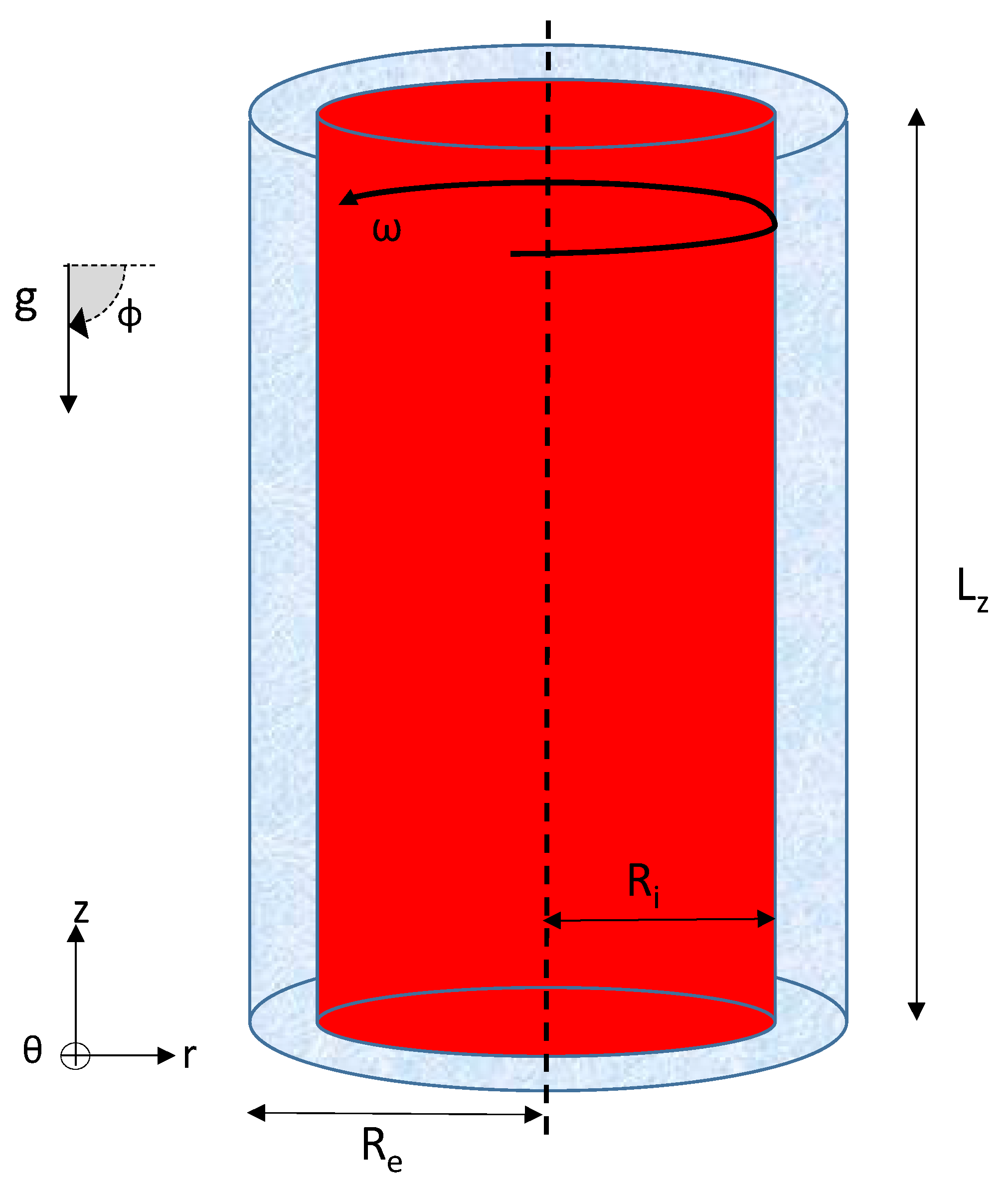
2.3. Boundary Conditions
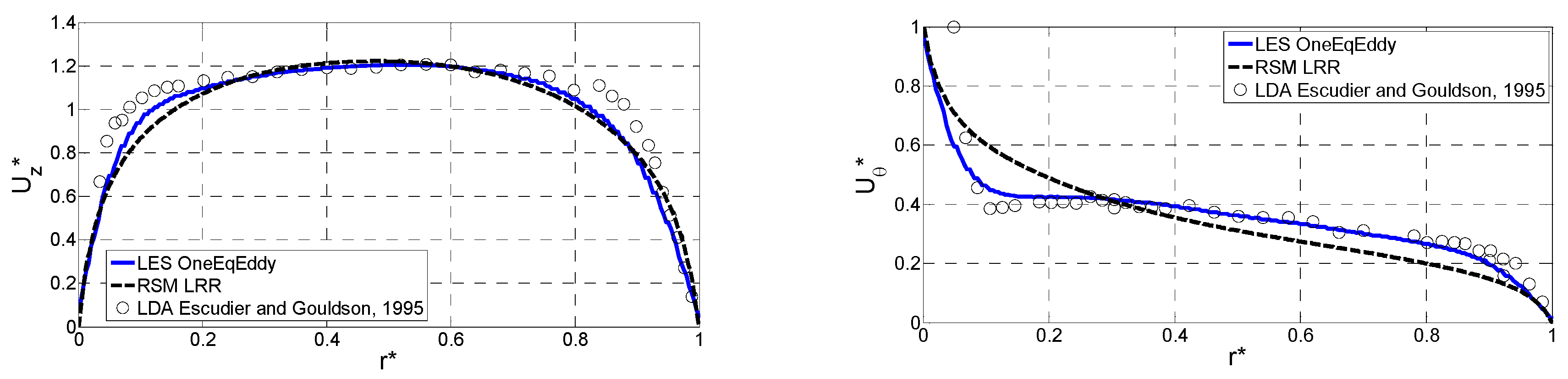
3. Numerical Validation
4. Results and Discussion
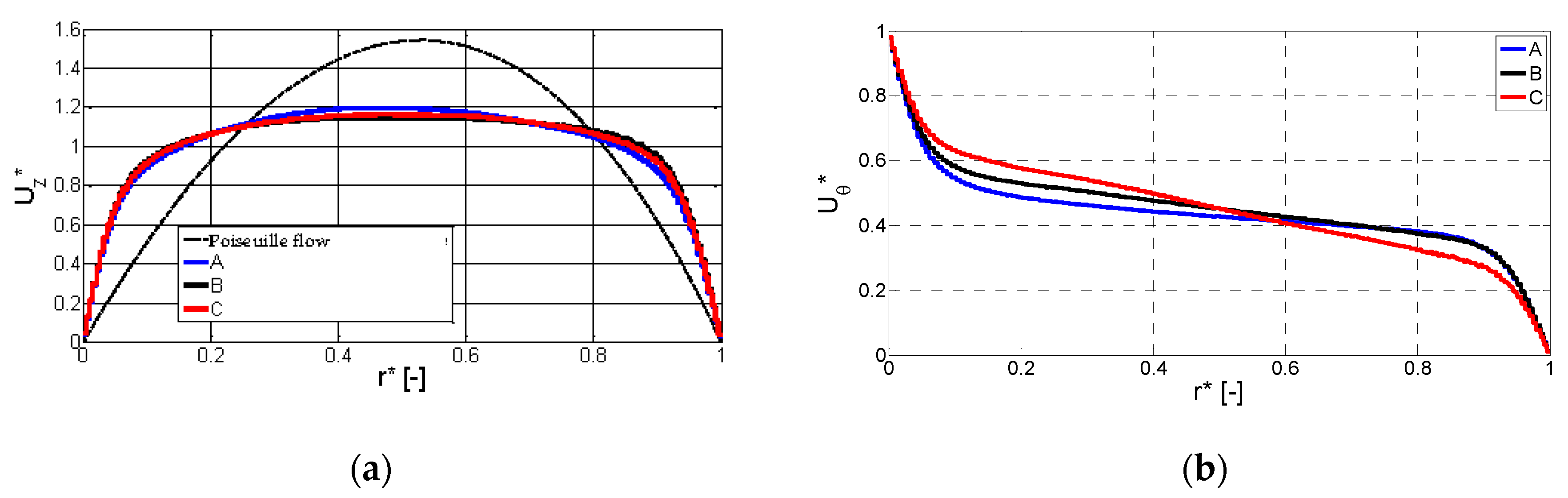
4.1. Mean Flow Fields
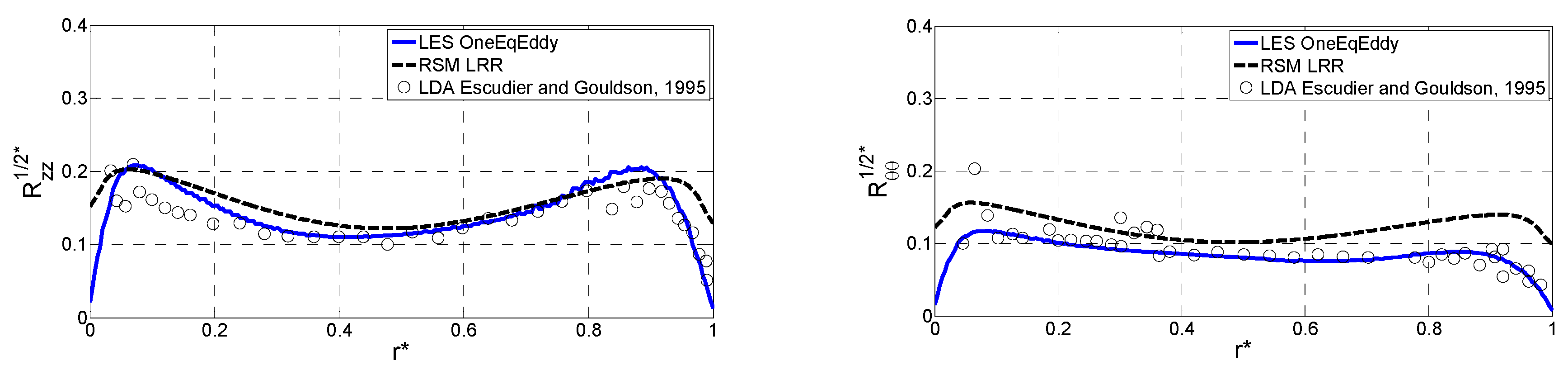
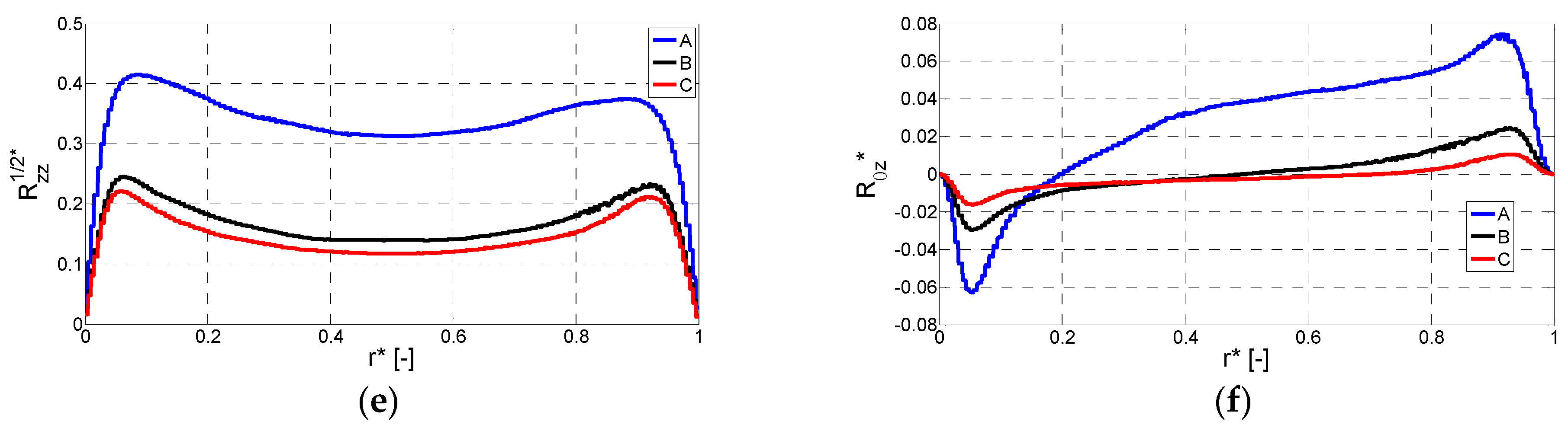
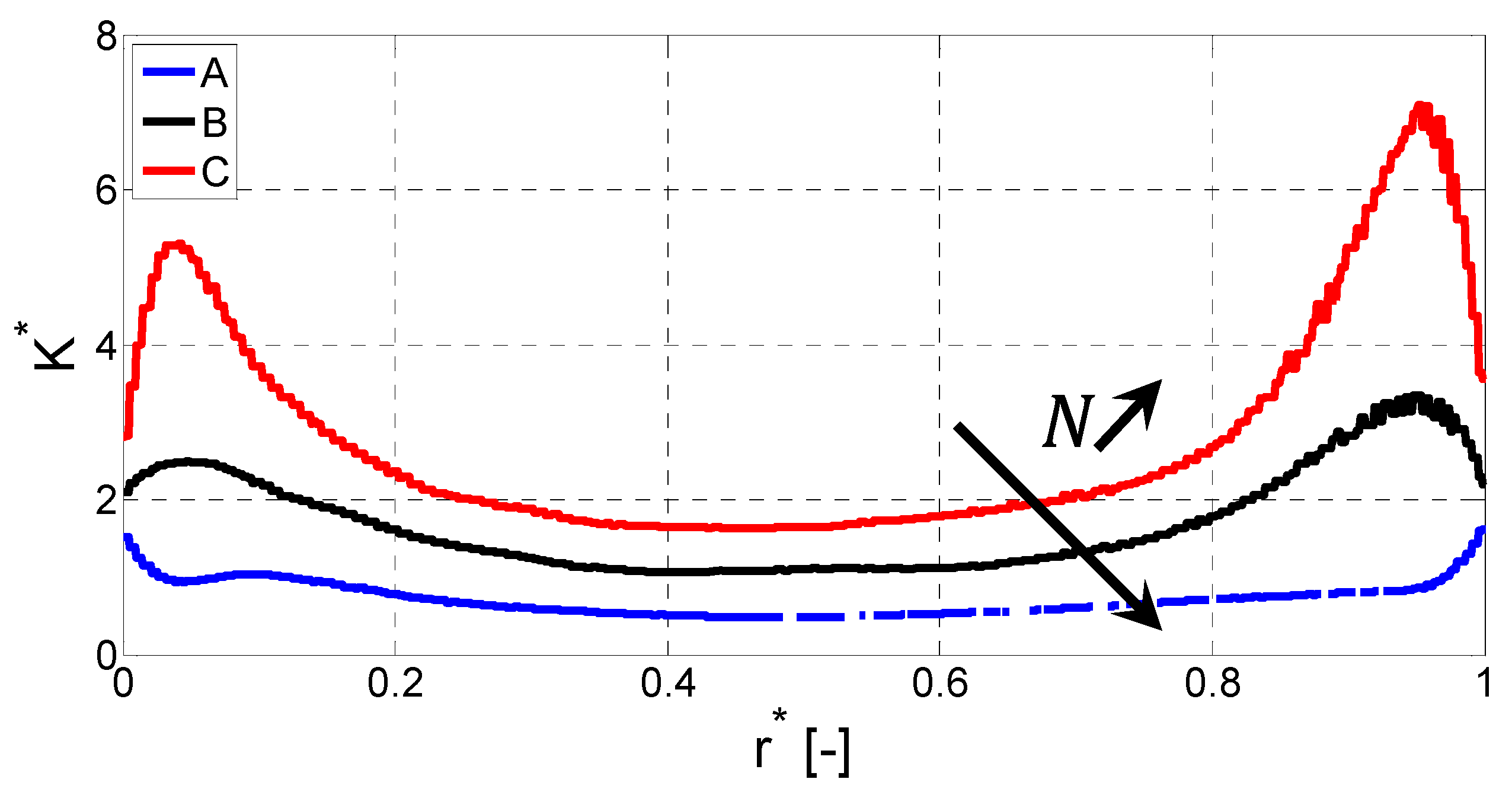
4.2. Reynolds Stress Tensor
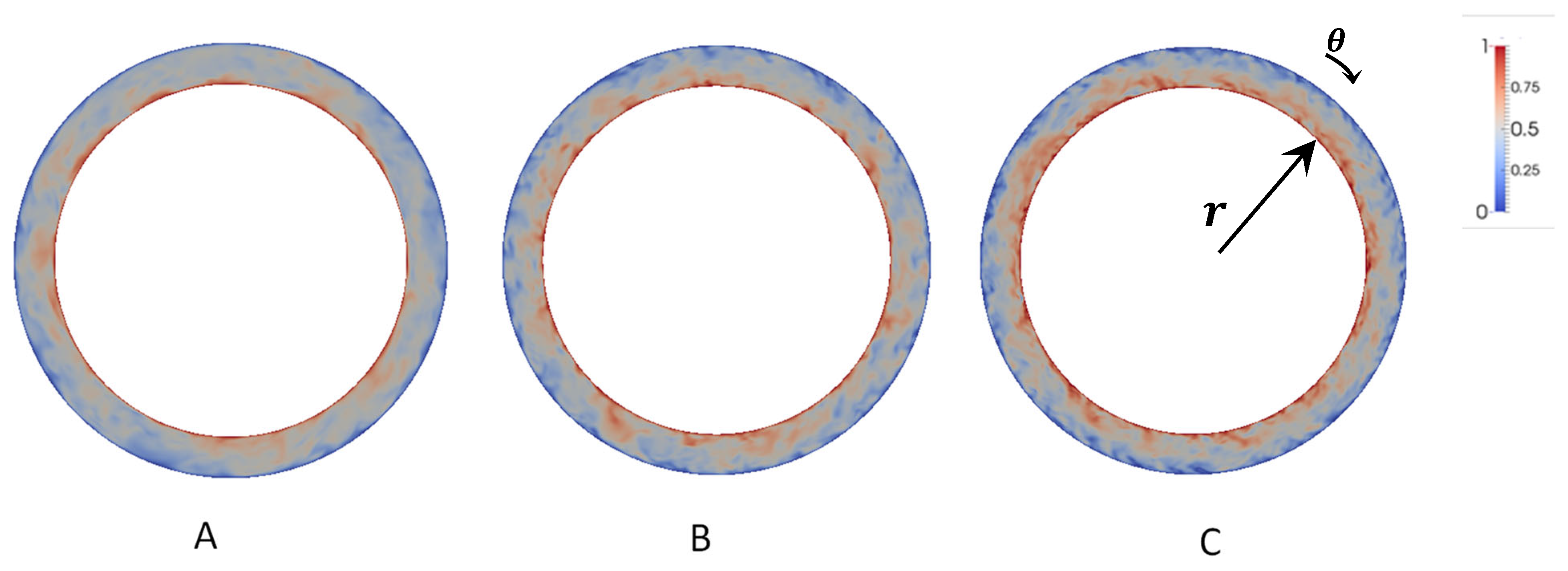
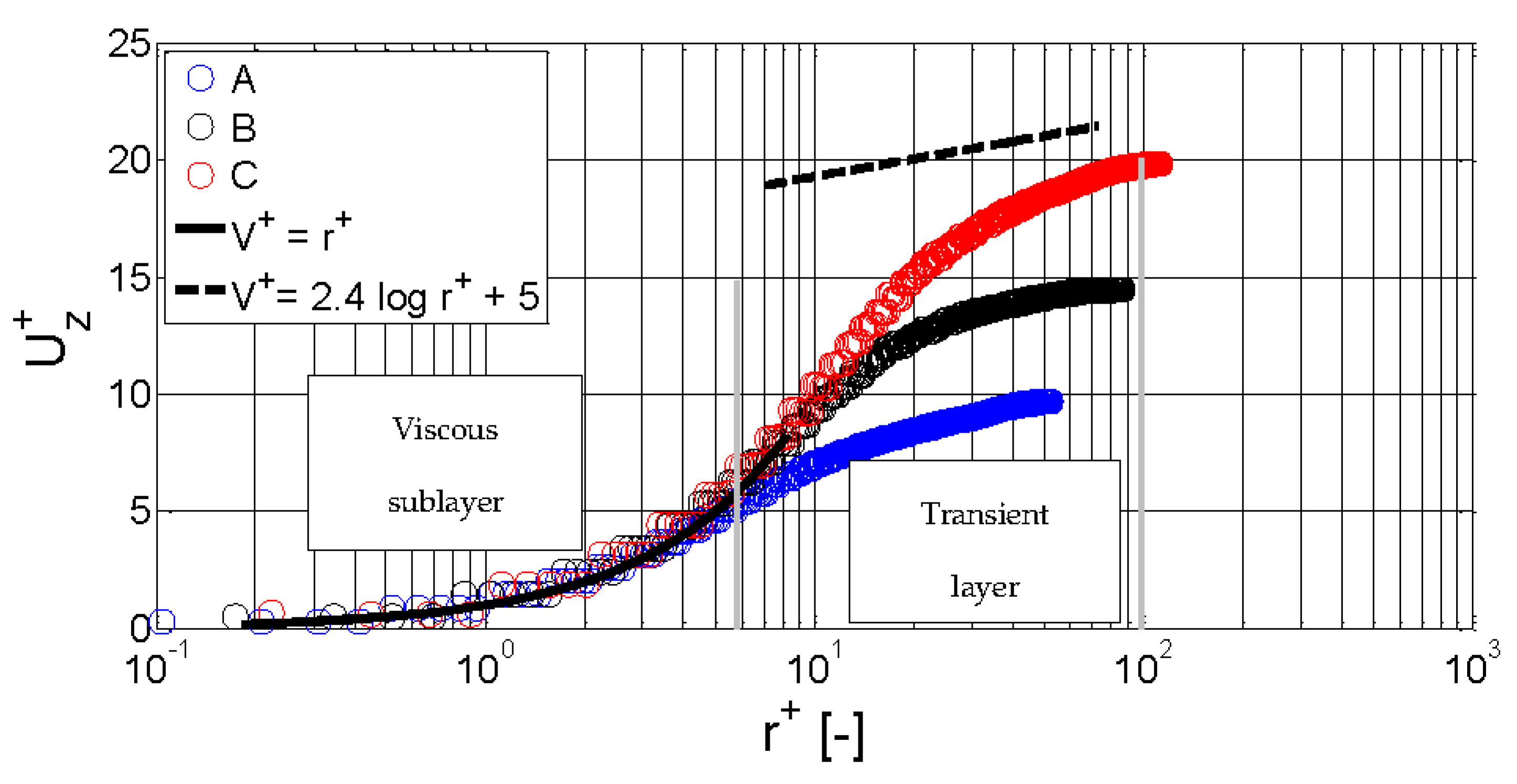
4.3. Boundary Layer Properties
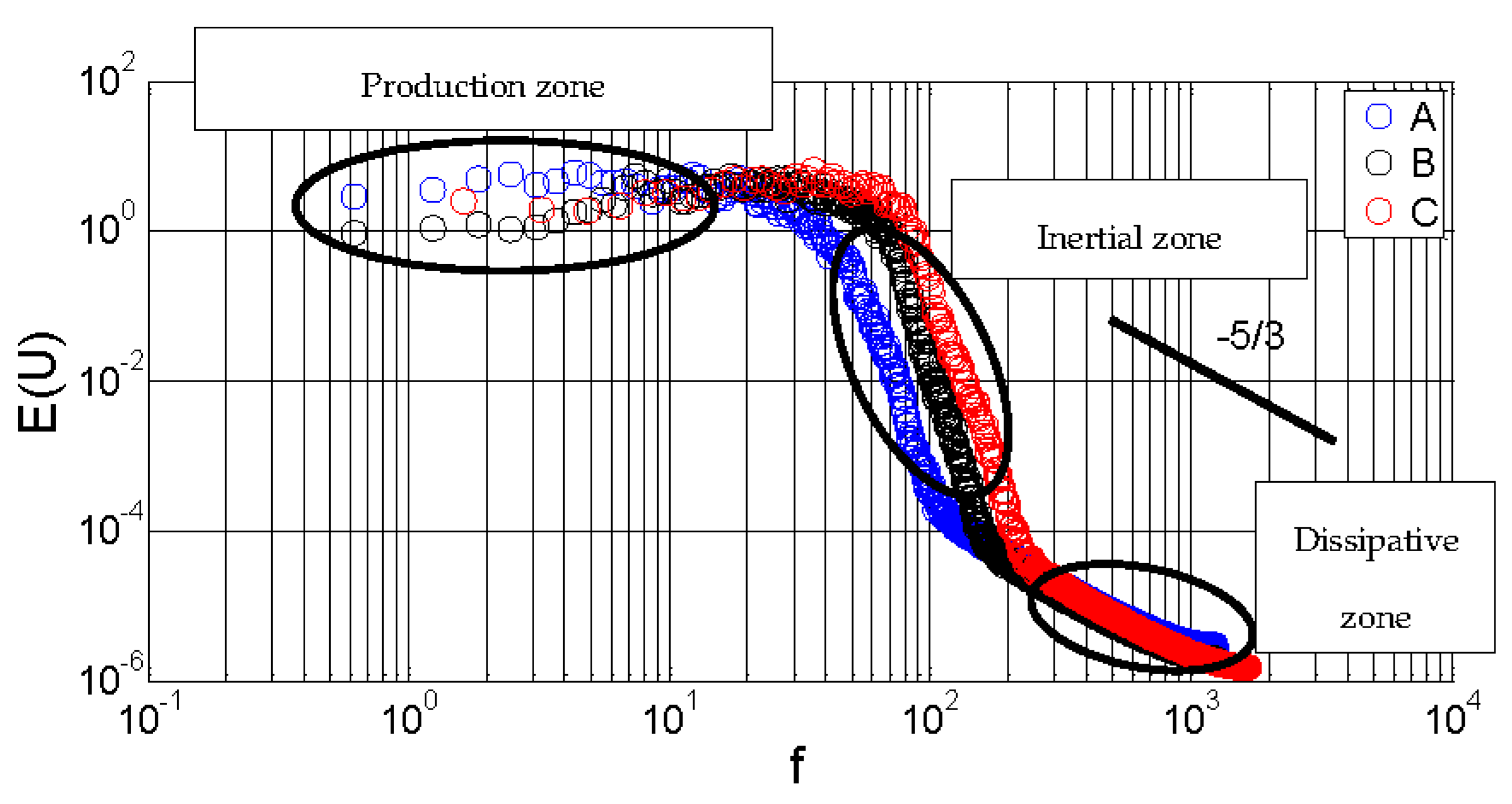
4.4. Energy Cascade in the Near-Wall Region
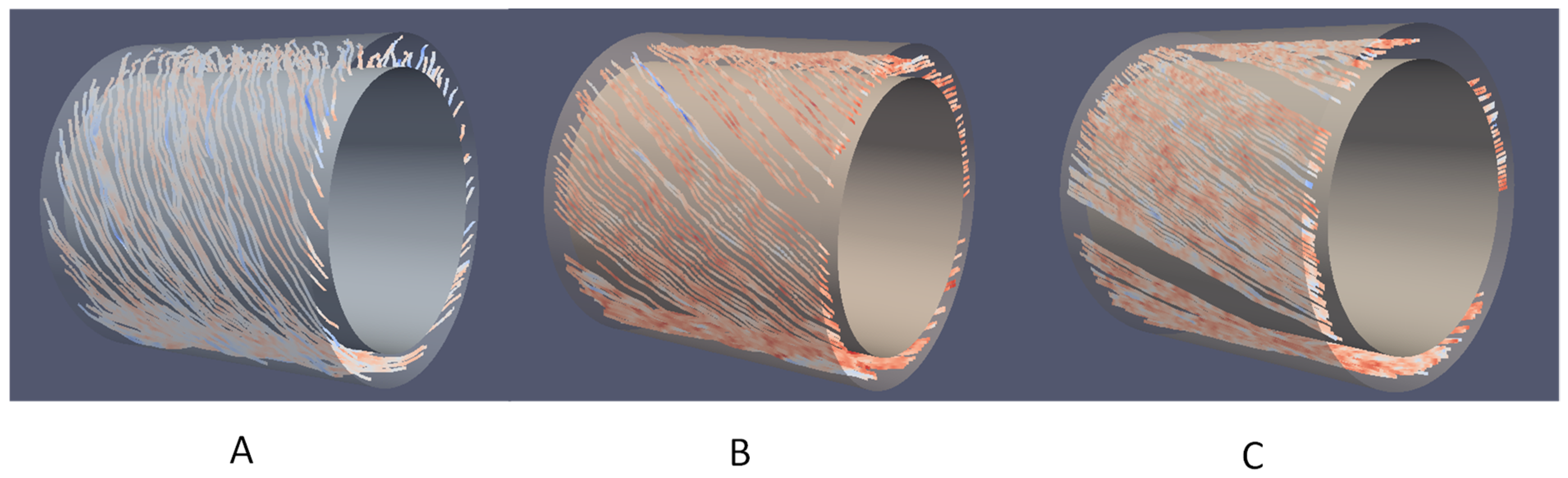
4.5. Turbulent Structures
4.5.1. Q-Criteria
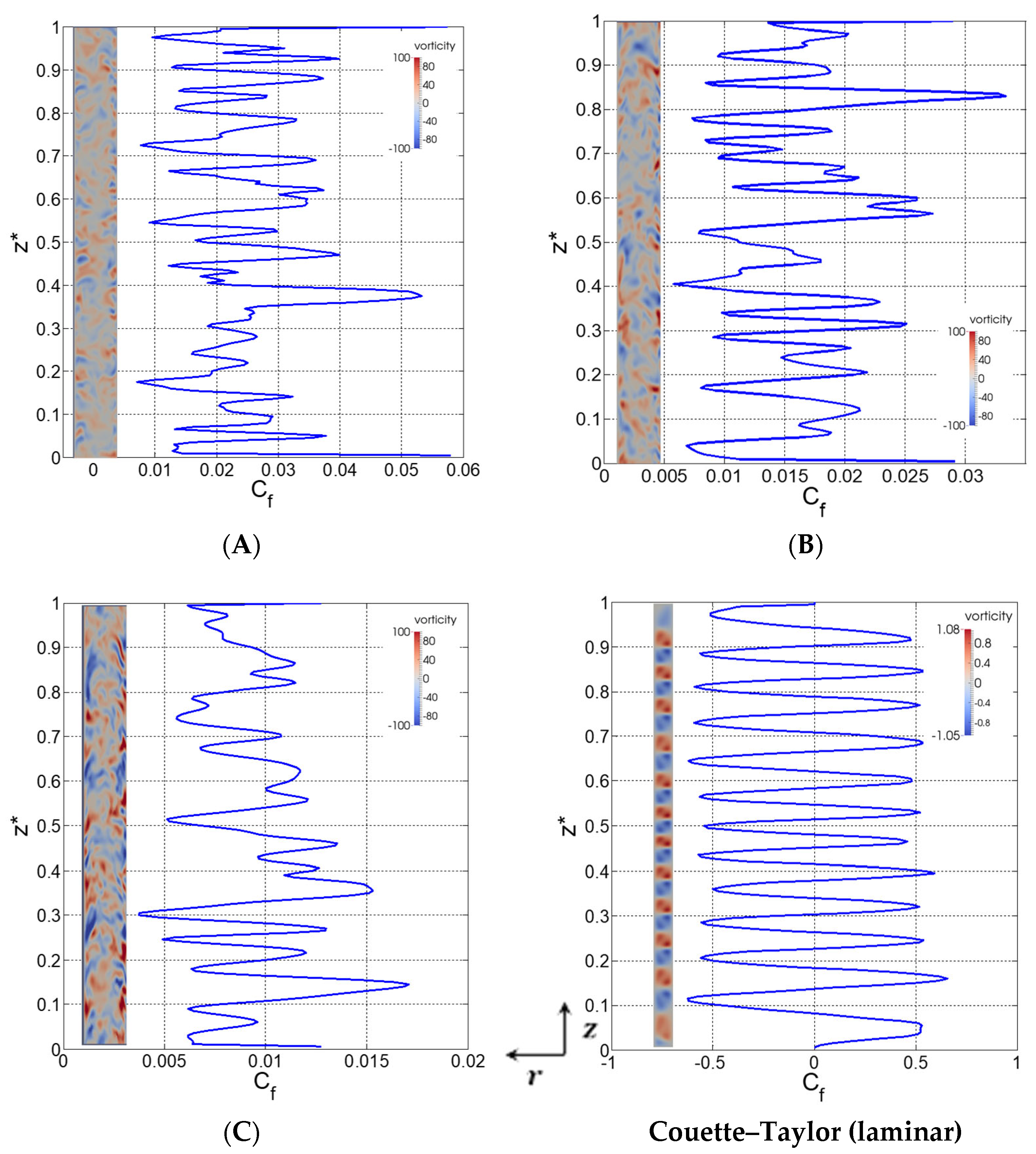
4.5.2. Vorticity
5. Conclusions
- Streamwise components of the velocity exhibit a Blasius “type“ flow profile, while the spanwise components are characterized by three different regions; the inner boundary layer, the central region, and the external boundary layer.
- The distribution of the Reynolds stress tensor is composed of two main normal components in the streamwise and the spanwise directions, the radial one being slightly less important. The crossed components are negligible compared to the normal ones. Whatever the components, the more elevated values are located in the near-wall location where the turbulence fluctuating rates are the more pronounced.
- The fluctuating rate of the turbulence is much more important in the axial direction than the two other directions for the RB and RC cases, while in the RA case, its contribution is similar to the two others.
- A wall model solving the overall boundary layer is used in the LES algorithm resulting in the logarithmic profiles. The wall law is verified in the viscous sublayer, while the profile in the transient region does not fit with the von Kármán constants established for pipe flow. The thickness of the boundary layer is reduced as the rotational velocity of the inner cylinder is raised compared to the axial flow rate.
- Spectral analysis was applied to the fluctuating streamwise velocity in the near-wall region. Turbulence spectra are observed in the frequency domain with three distinct areas of production, inertia, and dissipative zones. The inertia zone is characterized by a strong anisotropy far from the −5/3 slope.
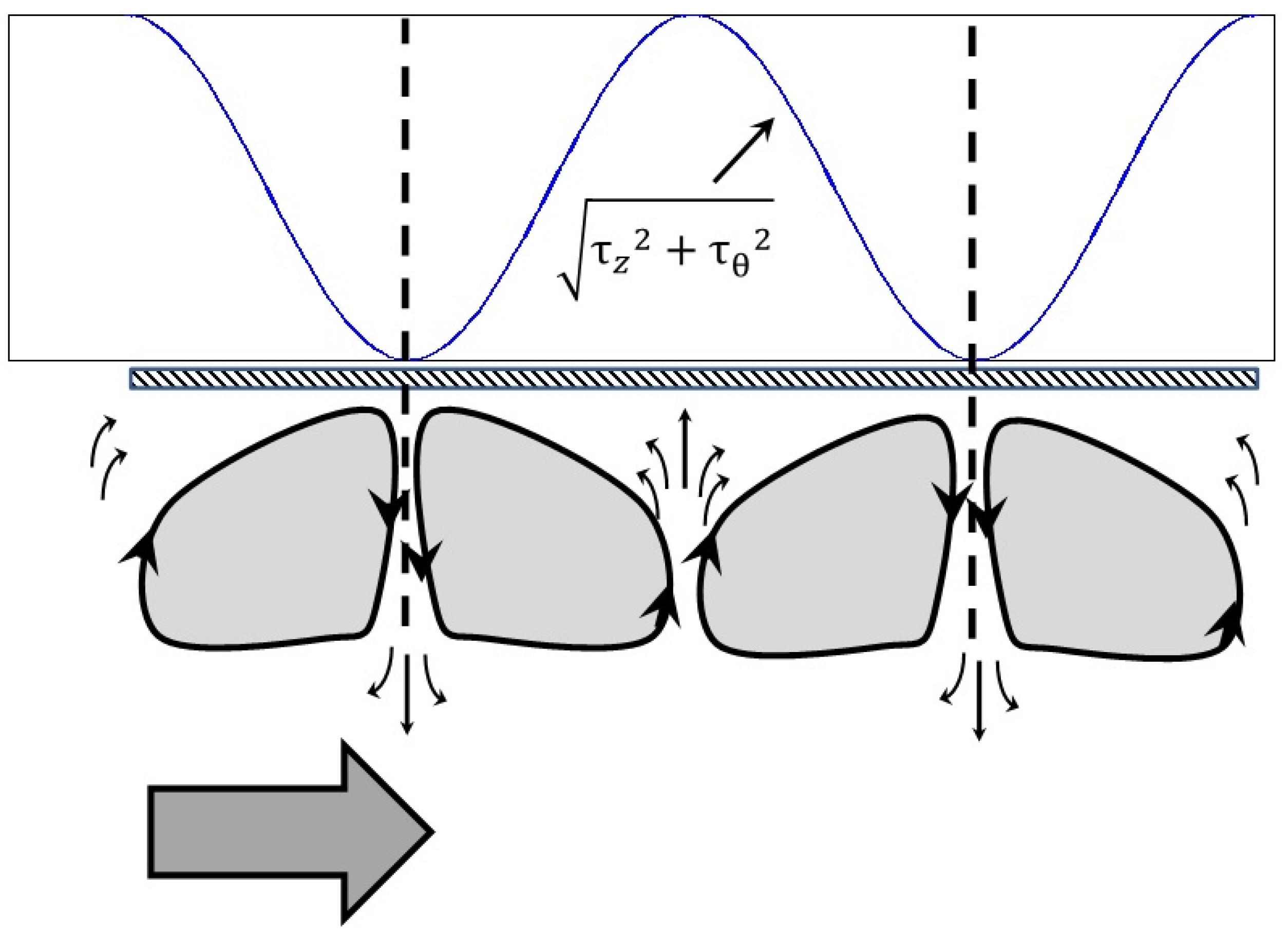
- The turbulence scales were considered by using the Q-criterion and the vorticity in the near-wall region. The flow anisotropy is confirmed by the helix shape of the vortex flow structures. The angle of tilt of the structures is progressively reduced as the axial flow rates are raised at the inner and outer cylinders.
- The skin-friction coefficients were assessed, showing a large amplitude imputed to the vortex flow organization. A comparison with Couette–Taylor flow results is provided, which explains the nature of the amplitude linked to the ejection of the fluid between the vortex cells toward the bulk region. The averaged and fluctuating values of the skin-friction are reduced as the axial flow rates increase; damping the counter-rotating vortex effect.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Viklund, S.B.; Johansson, M.T. Technologies for utilization of industrial excess heat: Potentials for energy recovery and CO2 emission reduction. Energy Convers. Manag. 2014, 77, 369–379. [Google Scholar] [CrossRef]
- Kongtragool, B.; Wongwises, S. A review of solar-powered Stirling engines and low temperature differential Stirling engines. Renew. Sustain. Energy Rev. 2003, 7, 131–154. [Google Scholar] [CrossRef]
- Gonzales, A.; Riba, J.R.; Puig, R.; Navarro, P. Review of micro and small-scale technologies to produce electricity and heat from Mediterranean forest’ wood chips. Renew. Sustain. Energy Rev. 2015, 43, 143–155. [Google Scholar] [CrossRef]
- Nakhchi, M.E.; Hatami, M.; Rahmati, M. Experimental evaluation of performance intensification of double-pipe heat exchangers with rotary elliptical inserts. Chem. Eng. Process.-Process Intensif. 2021, 169, 108615. [Google Scholar] [CrossRef]
- Mungyeko Bisulandu, B.-J.R.; Huchet, F. Rotary kiln process: An overview of physical mechanisms, models and applications. Appl. Therm. Eng. 2022. Submitted. [Google Scholar]
- Swann, P.B.; Russel, H.; Jahn, I.H. Taylor-Couette-Poiseuille flow heat transfer in a high Taylor number test rig. J. Glob. Power Propuls. Soc. 2021, 5, 126–147. [Google Scholar] [CrossRef]
- Sögüt, Z.; Oktay, Z.; Karakoç, H. Mathematical modeling of heat recovery from a rotary kiln. Appl. Therm. Eng. 2010, 30, 817–825. [Google Scholar] [CrossRef]
- Engin, T.; Ari, V. Energy auditing and recovery for dry type cement rotary kiln systems-A case study. Energy Conserv. Manag. 2005, 46, 551–562. [Google Scholar] [CrossRef]
- Mujumdar, A.; Ranade, A. Modeling of Rotary Cement Kiln: Applications to Reduction in Energy Consumption. Ind. Eng. Chem. Res. 2006, 45, 2315–2330. [Google Scholar] [CrossRef]
- Caputo, A.C.; Pelegagge, P.M.; Salini, P. Performance modeling of radiant heat recovery exchangers for rotary kilns. Appl. Therm. Eng. 2011, 31, 2578–2589. [Google Scholar] [CrossRef]
- Mastorakos, E.; Massias, A.; Tsakiroglou, C.D.; Goussi, D.A.; Burganos, V.N.; Payatakes, A.C. CFD prediction for cement kilns including flame modelling heat transfer and clinker chemistry. Appl. Math. Model. 1999, 23, 55–76. [Google Scholar] [CrossRef]
- Huchet, F.; Piton, M.; Del Barrio, A.; Le Corre, O.; Cazacliu, B. Air-cooling heat exchanger applied to external rotary kiln wall in forced and natural draft. Energy Convers. Manag. 2017, 154, 517–525. [Google Scholar] [CrossRef]
- Leguen, L.; Huchet, F.; Dumoulin, J.; Baudru, Y.; Tamagny, P. Convective heat transfer analysis in aggregates rotary drum reactor. Appl. Therm. Eng. 2013, 54, 131–139. [Google Scholar] [CrossRef]
- Le Guen, L.; Huchet, F. Thermal imaging as a tool for process modelling: Application to a flight rotary kiln. Quant. InfraRed Thermogr. J. 2020, 17, 79–95. [Google Scholar] [CrossRef]
- Taylor, G.I. Stability of viscous liquid contained between two rotating cylinders. Philos. Trans. R. Soc. Lond. 1923, 223, 289–343. [Google Scholar]
- Nguyen, D.B.; Monico, R.O.; Chen, G. A Visualization Framework for Multi-scale Coherent Structures in Taylor-Couette Turbulence. IEEE Trans. Vis. Comput. Graph. 2021, 27, 902–912. [Google Scholar] [CrossRef] [PubMed]
- Razzak, A.; Akter, S.; Hannan, M.A. The influence of wavy vortex in reducing wall shear stress. IOP Conf. Ser. Mater. Sci. Eng. 2020, 788, 012093. [Google Scholar] [CrossRef]
- Mehrez, I.; Gheith, R.; Aloui, F.; Nasrallah, S.B. Theoretical and numerical study of Couette-Taylor flow with an axial flow using lattice Boltzmann method. Int. J. Numer. Meth. Fluids 2019, 90, 427–441. [Google Scholar] [CrossRef]
- Nourri, J.M.; Whitelaw, J.H. Flow of Newtonian and non-Newtonian fluids in a concentric annulus with rotation of inner cylinder. J. Fluid Eng. 1994, 116, 821–827. [Google Scholar] [CrossRef]
- Escudier, M.P.; Gouldson, I.W. Concentric annular flow with centerbody rotation of a Newtonian and a shear-thinning liquid. Int. J. Heat Fluid Flow 1995, 16, 156–162. [Google Scholar] [CrossRef]
- Naser, A. Prediction of Newtonian and non-Newtonian flow through concentric annulus with centerbody rotation. In Proceedings of the 1st International Conference on CFD in Mineral and Metal Processing and Power Generation, Melbourne, Australia, 13–15 December 1996. [Google Scholar]
- Poncet, S.; Haddadi, S.; Viazzo, S. Numerical modeling of fluid flow and heat transfer in a narrow Taylor-Couette-Poiseuille system. Int. J. Heat Fluid Flow 2011, 32, 128–144. [Google Scholar] [CrossRef]
- Chung, S.Y.; et Sung, H.J. Large-eddy simulation of turbulent flow in concentric annulus with rotation of an inner cylinder. Int. J. Heat Fluid Flow 2005, 26, 191–203. [Google Scholar] [CrossRef]
- Poncet, S.; Viazzo, S.; Oguic, R. Large eddy simulation of Taylor-Couette-Poiseuille flows in a narrow-gap system. Phys. Fluids 2014, 26, 105108. [Google Scholar] [CrossRef]
- Havlica, J.; Kramolis, D.; Huchet, F. A revisit of the electro-diffusional theory for wall shear stress measurements. Int. J. Heat Mass Transf. 2021, 165, 120610. [Google Scholar] [CrossRef]
- Chung, S.Y.; Rhee, G.H.; Sung, H.J. Direct numerical simulation of turbulent concentric annular pipe flow. Part. 1: Flow field. Int. J. Heat Fluid Flow 2002, 23, 426–440. [Google Scholar] [CrossRef]
- Hadziabdic, M.; Hanjalic, K.; Mullyadzhanov, R. LES of turbulent flow in a concentric annulus with rotating outer wall. Int. J. Heat Fluid Flow 2013, 43, 74–84. [Google Scholar] [CrossRef]
- Lee, M.J.; Kim, J.; Moin, P. Structure of turbulence at high shear rate. J. Fluid Mech. 1990, 216, 561–583. [Google Scholar] [CrossRef]
- Singh, H.; Suazo, C.A.; Liné, A. Log law of the wall revisited in Taylor-Couette flows at intermediate Reynolds numbers. Phys. Rev. E 2016, 94, 053120. [Google Scholar] [CrossRef]
- Belkadi, H.; Laghouati, Y.; Sobolik, V.; Oualli, H.; Bouabdallah, A. Axial Flow Effect on the Stability of Circular Couette Flow. J. Appl. Fluid Mech. 2022, 15, 271–281. [Google Scholar]
- Huchet, F.; Legentilhomme, P.; Legrand, J.; Montillet, A.; Comiti, J. Unsteady flows in milli- and microsystems: Analysis of wall shear rate fluctuations. Exp. Fluids 2011, 51, 597–610. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 1962, 13, 82–85. [Google Scholar] [CrossRef]
- Hinze, J.O. Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE J. 1955, 1, 289–295. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, Streams, and Convergence Zones in Turbulent Flows; Center for Turbulence Research Report CTR-S88; NASA: Washington, DC, USA, 1988; p. 193.




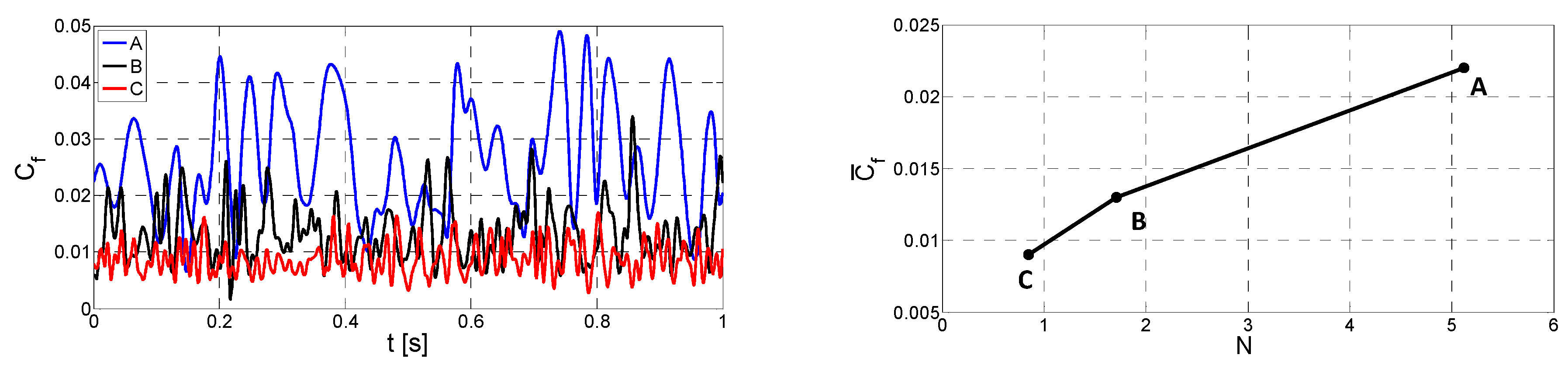
| A | B | C | |
|---|---|---|---|
| [tr.min−1] |  50 50  | ||
 7488 7488  | |||
| [m3.h−1] | 31.4 | 94.3 | 188.6 |
| 1462 | 4388 | 8776 | |
| 5.12 | 1.71 | 0.85 | |
| [23] | [24] | A | B | C | |
|---|---|---|---|---|---|
| η | 0.50 | 0.89 | 0.809 | 0.809 | 0.809 |
| 0.21–0.86 | 1.49–6.71 | 5.12 | 1.71 | 0.85 | |
| 0.27–0.35 | 0.47–0.86 | 1.23 | 1.24 | 1.24 | |
| 8.01–10.40 | 94.76–44.45 | 12.13 | 12.15 | 12.18 | |
| 13.86–15.80 | 96.05–45.27 | 15.21 | 14.98 | 15.01 | |
| 9.93–22.95 | 26.95–48.82 | 14.95 | 15.28 | 15.32 | |
| (65, 64, 128) | (65, 144, 130)–(91, 128, 182) | (123, 672, 200) | (123, 672, 200) | (123, 672, 200) | |
| (s) | - | - | |||
| - | - | 0.20 | 0.21 | 0.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piton, M.; Huchet, F.; Cazacliu, B.; Le Corre, O. Numerical Turbulent Flow Analysis through a Rotational Heat Recovery System. Energies 2022, 15, 6792. https://doi.org/10.3390/en15186792
Piton M, Huchet F, Cazacliu B, Le Corre O. Numerical Turbulent Flow Analysis through a Rotational Heat Recovery System. Energies. 2022; 15(18):6792. https://doi.org/10.3390/en15186792
Chicago/Turabian StylePiton, Maxime, Florian Huchet, Bogdan Cazacliu, and Olivier Le Corre. 2022. "Numerical Turbulent Flow Analysis through a Rotational Heat Recovery System" Energies 15, no. 18: 6792. https://doi.org/10.3390/en15186792
APA StylePiton, M., Huchet, F., Cazacliu, B., & Le Corre, O. (2022). Numerical Turbulent Flow Analysis through a Rotational Heat Recovery System. Energies, 15(18), 6792. https://doi.org/10.3390/en15186792








