Taguchi Techniques as an Effective Simulation-Based Strategy in the Design of Numerical Simulations to Assess Contact Stress in Gerotor Pumps
Abstract
:1. Introduction
2. Trochoidal Gear Set Background
2.1. Gear Sets under Study
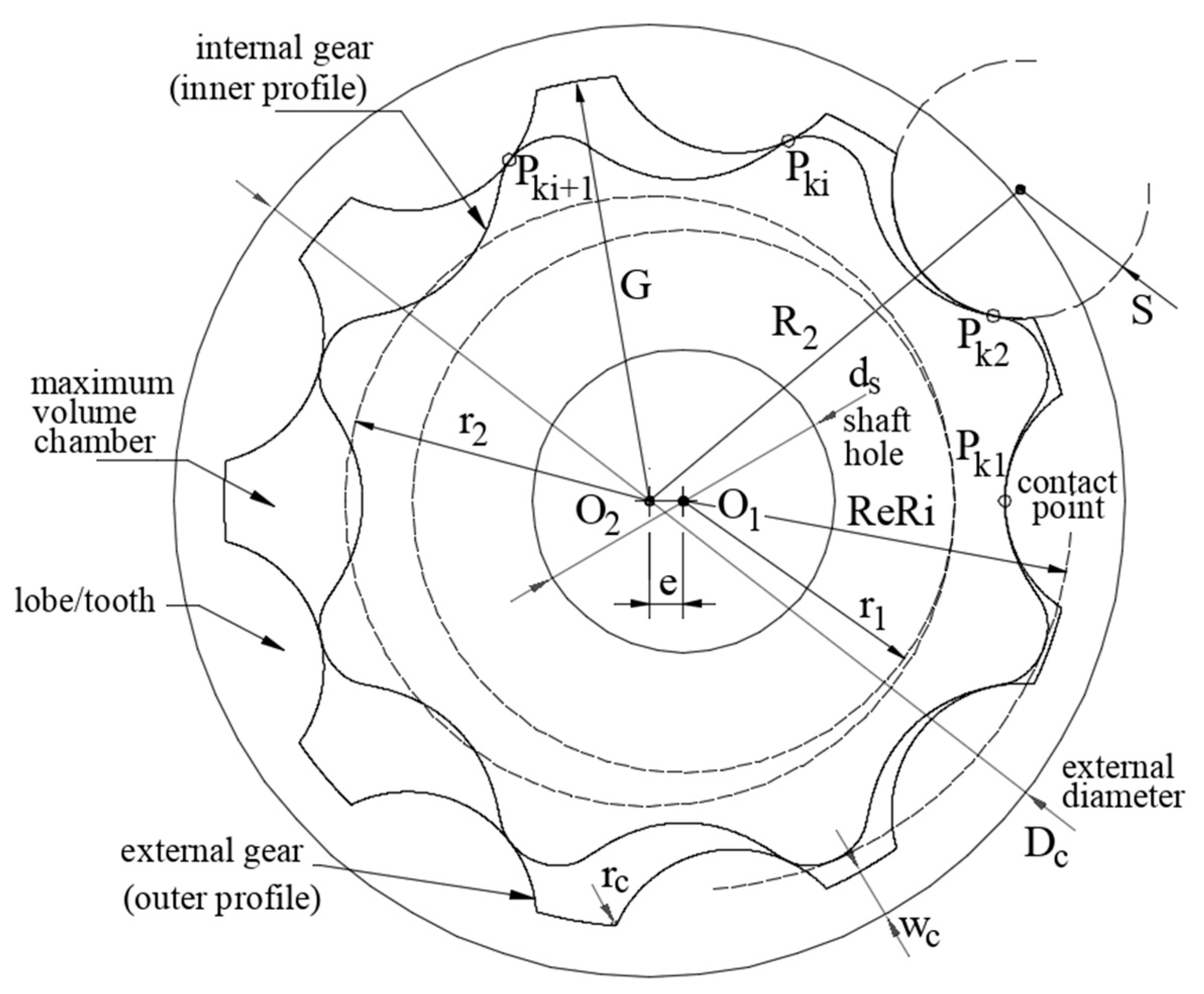
2.2. Nomenclature and Notation
2.3. Geometry Generation
3. Verification of Contact Stress Numerical Simulation
3.1. Numerical Model Definition
3.1.1. Geometry and Material Properties
3.1.2. Loads, Contacts, and Boundary Conditions
3.1.3. Elements and Mesh
3.1.4. Analysis
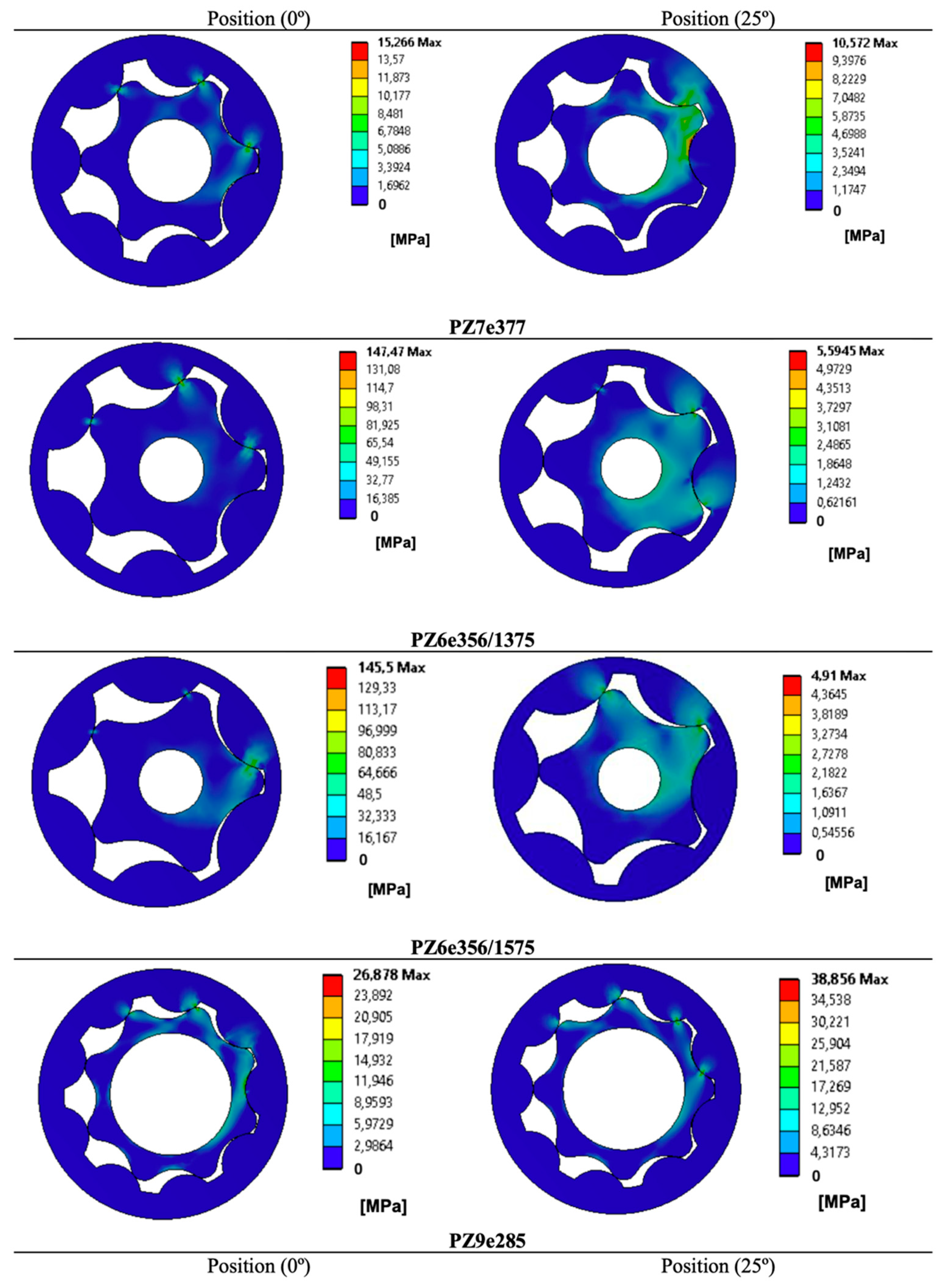
3.2. Simulation Results: Validation and Discussion
- Maximum volume chamber position corresponding to PZ7e377(25°), PZ6e356/1375(0°), PZ6e356/1575(0°), and PZ9e285(0°). The location of the contact point at maximum stress is Pk2 for all gear sets, according to researchers’ and authors’ results. (Note: PZ7e377(25°) gear set in reference [17] does not provide an exact value but it can be gathered from the graphical figures);
- Minimum volume chamber position corresponding to PZ7e377(0°), PZ6e356/1375(25°), PZ6e356/1575(25°), PZ9e285(25°), and MZ9e885(25°). The location of the contact point at maximum stress are Pk and Pki + 1 for all results, researchers’ and author’s, respectively. The exceptions are PZ7e377(0°) and MZ9e885(25°).
4. The Taguchi Approach to a Gerotor Pump
4.1. The Volumetric Capacity Target and the Dimensional Constraints of the Gerotor Pump
- The PZ9e285 gear set is the chosen prototypical gerotor because it is well-known by the authors regarding, among others, its fluid dynamic performance [54];
- The material properties remain unchangeable in all the experiments: Young’s module, density, and Poisson’s coefficient of the PZ9e285 gear set (refer to Table 2);
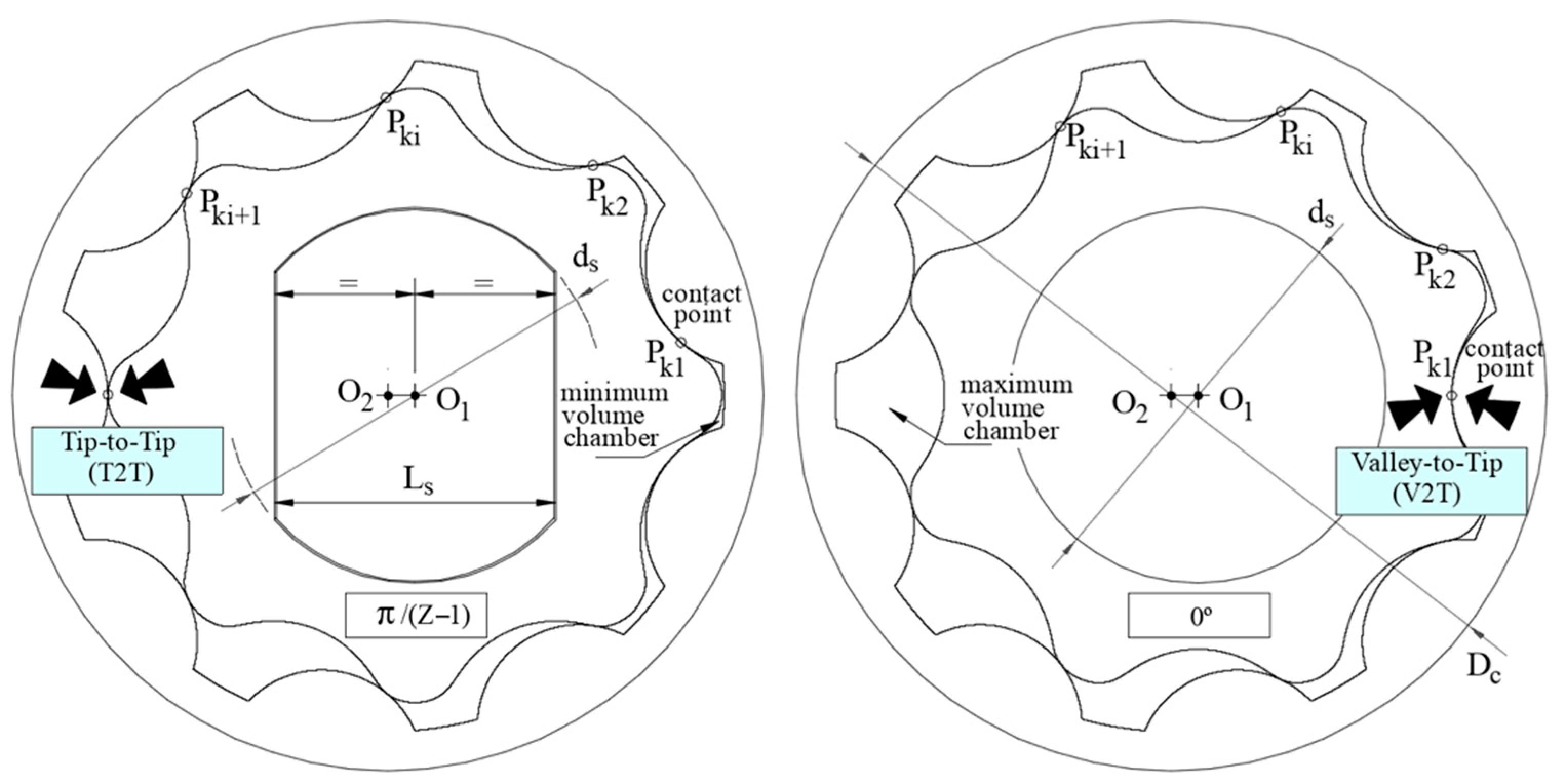
- Two specific angular positions as working functions will be under the study: Tip-to-Tip (T2T) and Valley-to-Tip (V2T), both depicted in Figure 6. The V2T corresponds to the maximum volume chamber and the T2T corresponds to the minimum volume chamber. This labeling presumes to enhance the comprehension of the contact points’ action;
4.2. The Taguchi Method: The Designed Experiments
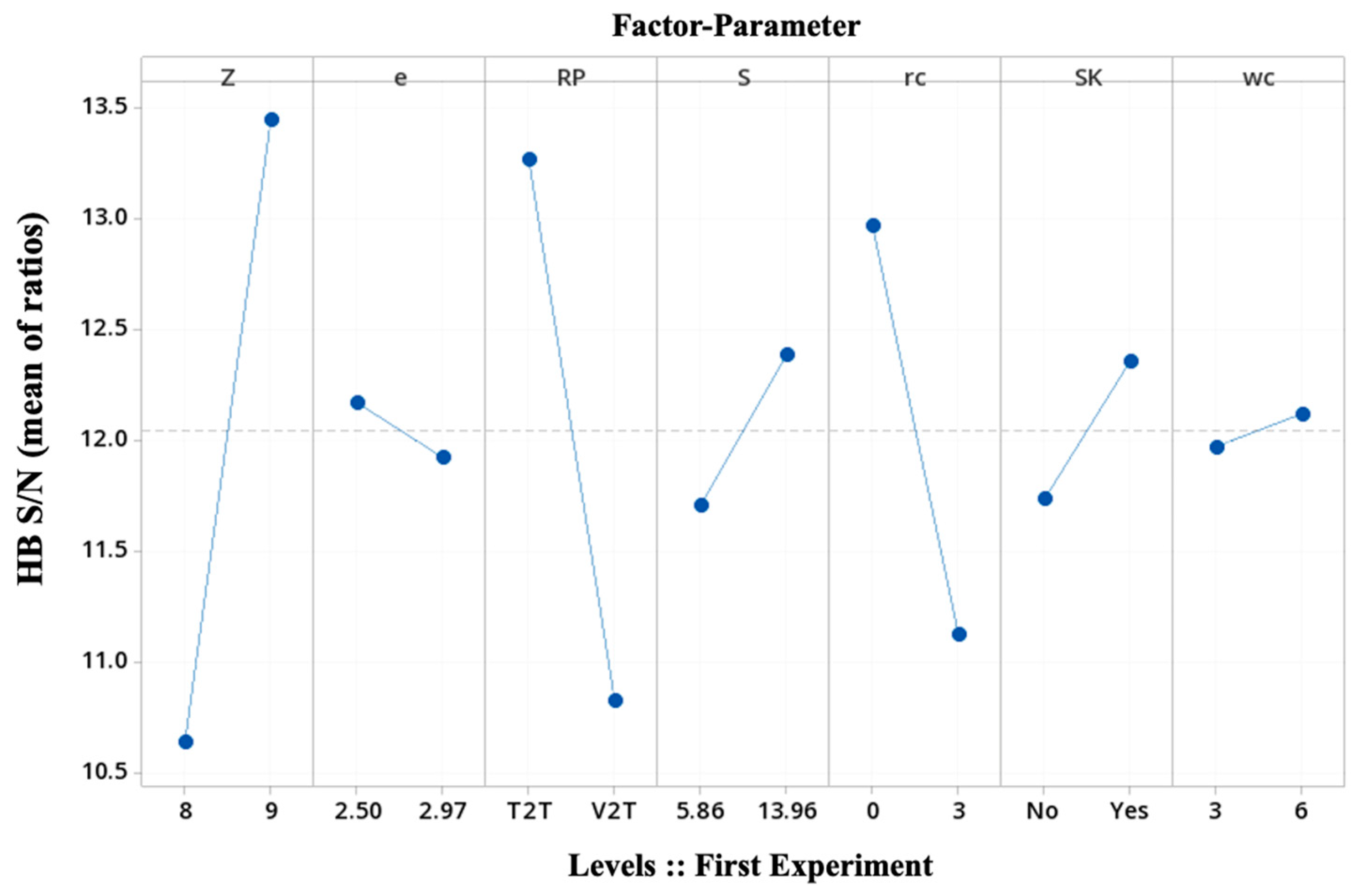
- The number of control factors. The number of parameters is chosen based on the trochoidal gear profile (Z, e, S), external gear (rc, wc), and working function (reference position RP, shaft keyway SK);
- The number of levels. The levels of each parameter are chosen to be significant in the study, from the benchmark gerotor, the literature, the previously presented FEM validation, and the authors’ know-how. In addition, all level combinations have to accomplish the feasible geometry of a trochoidal gear set practicable to be generated with GeroLAB, which has become a challenging task. The number of levels is selected as the Taguchi approach is going forward, from two-levels to a mixed-level design;
- The noise factors. The mechanical operating conditions of the gear pump are described by three factors: material temperature (θ), torque (T), and material friction coefficient (µ), which can be tuned by surface modification methods [56,57]. The designed experiments can use these operating conditions as the input of FEM conditions as prescribed by an outer array only for noise factors (T, µ and θ);
- Improve the quality of contact stress assessment. The goal of the experiments is to maximize the safety factor (SF) as the response of the signal-to-noise ratio (S/N) set to Higher-is-Better (HB) where:where n = the number of tests in a trial (number of repetitions regardless of noise levels) and yi = each observed value (data points). In all cases, the target is to maximize the HB S/N ratio. The development of a family of matrices based on orthogonal arrays (OA) and the signal-to-noise (S/N) definition as an indicator of the ratio of the mean to the standard deviation are great contributions of the Taguchi method. As a result, they will be used to evaluate and discuss the results of each Taguchi experiment:
- Statistical treatment. In all experiments, the significance (alpha) level was set as 0.05, and means and standard deviation were calculated for all volumetric capacities. The p-value inferior to alpha concludes that there is a statistically significant association between the response characteristic and the term. The p-value between the significance levels of 0.05 and 0.1 can be used for evaluating terms, and it can be considered with practical significance. A higher p-value will conclude that there were no statistically significant differences observed.
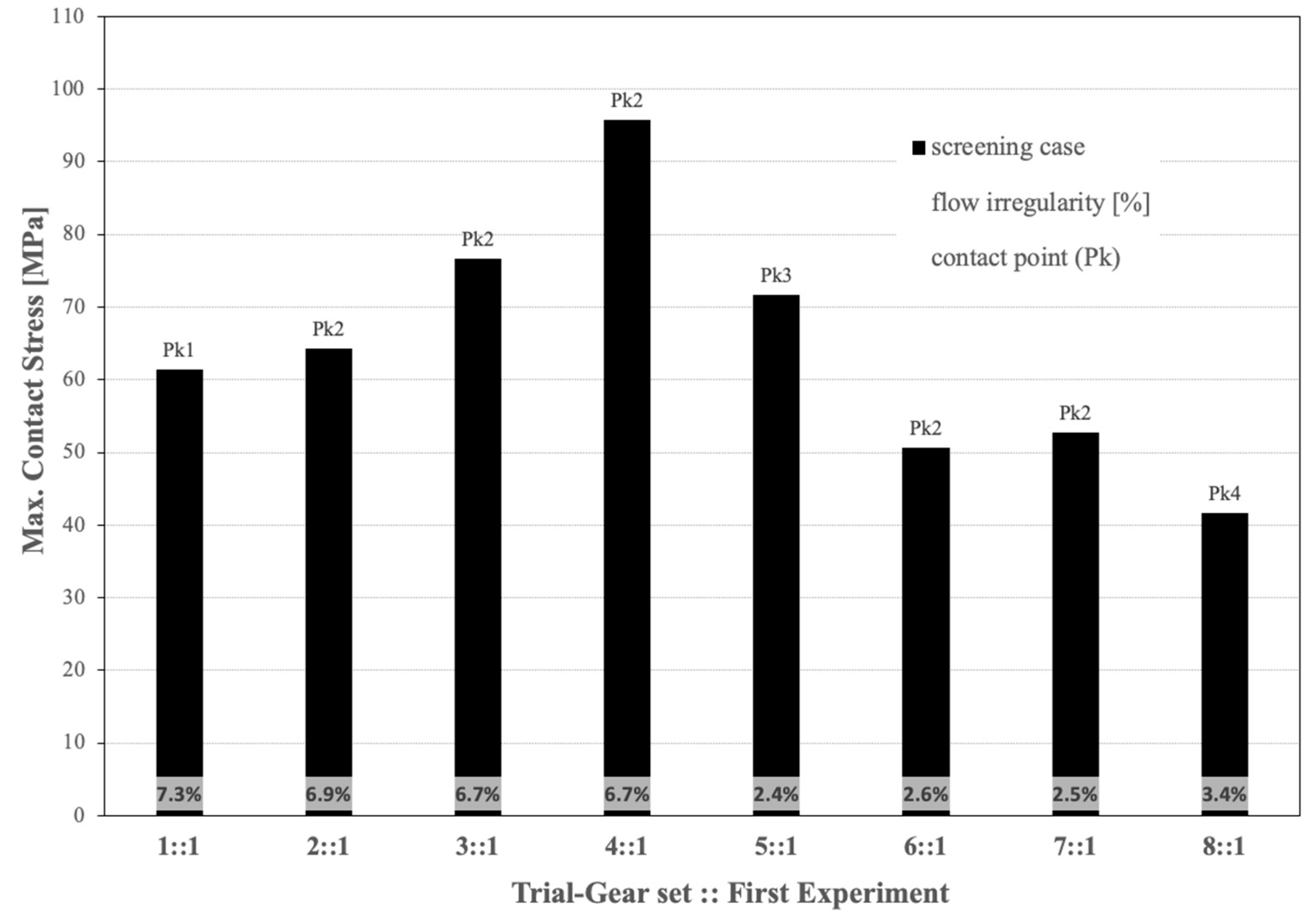
4.3. First Taguchi Experiment: The Screening Case
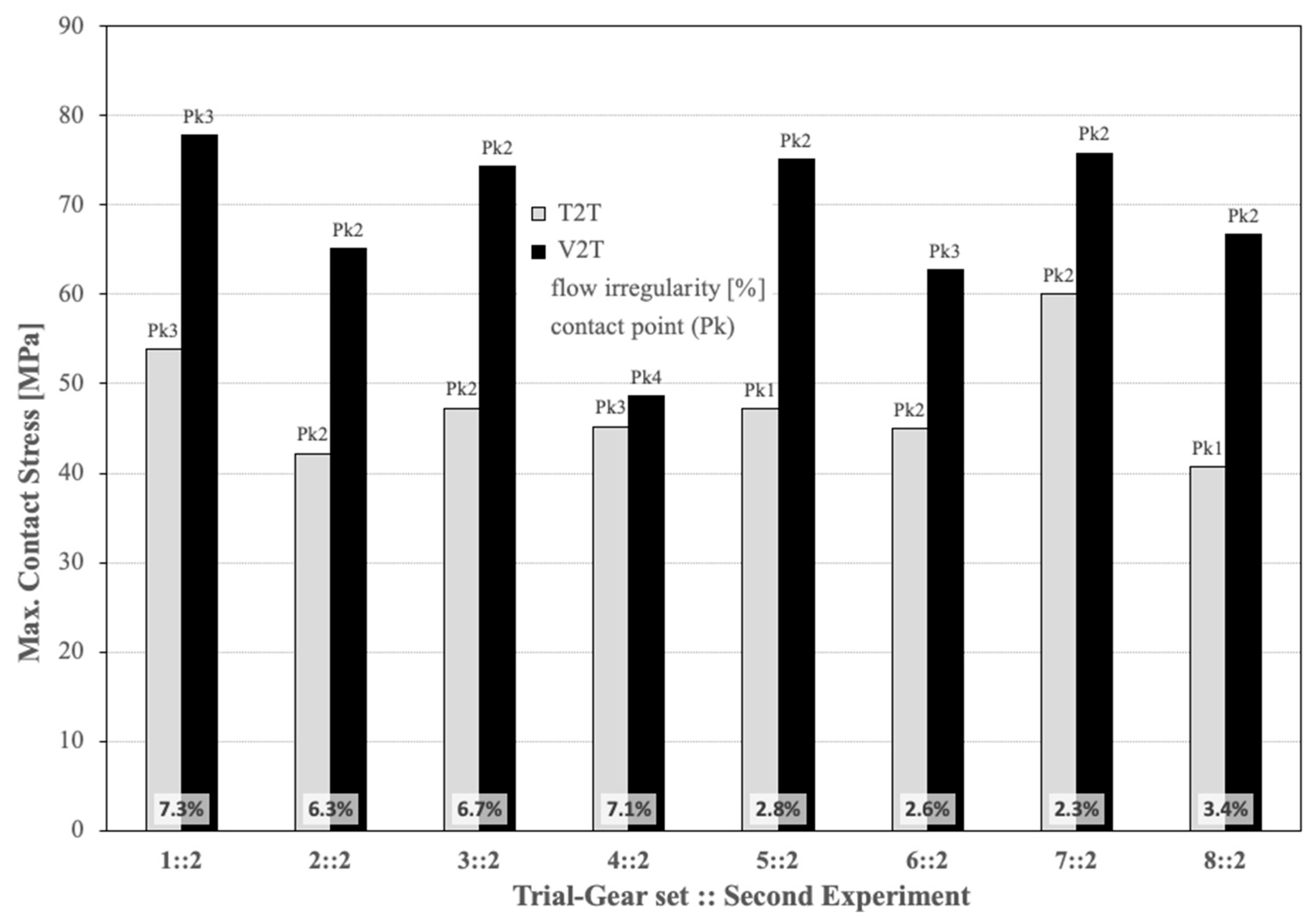
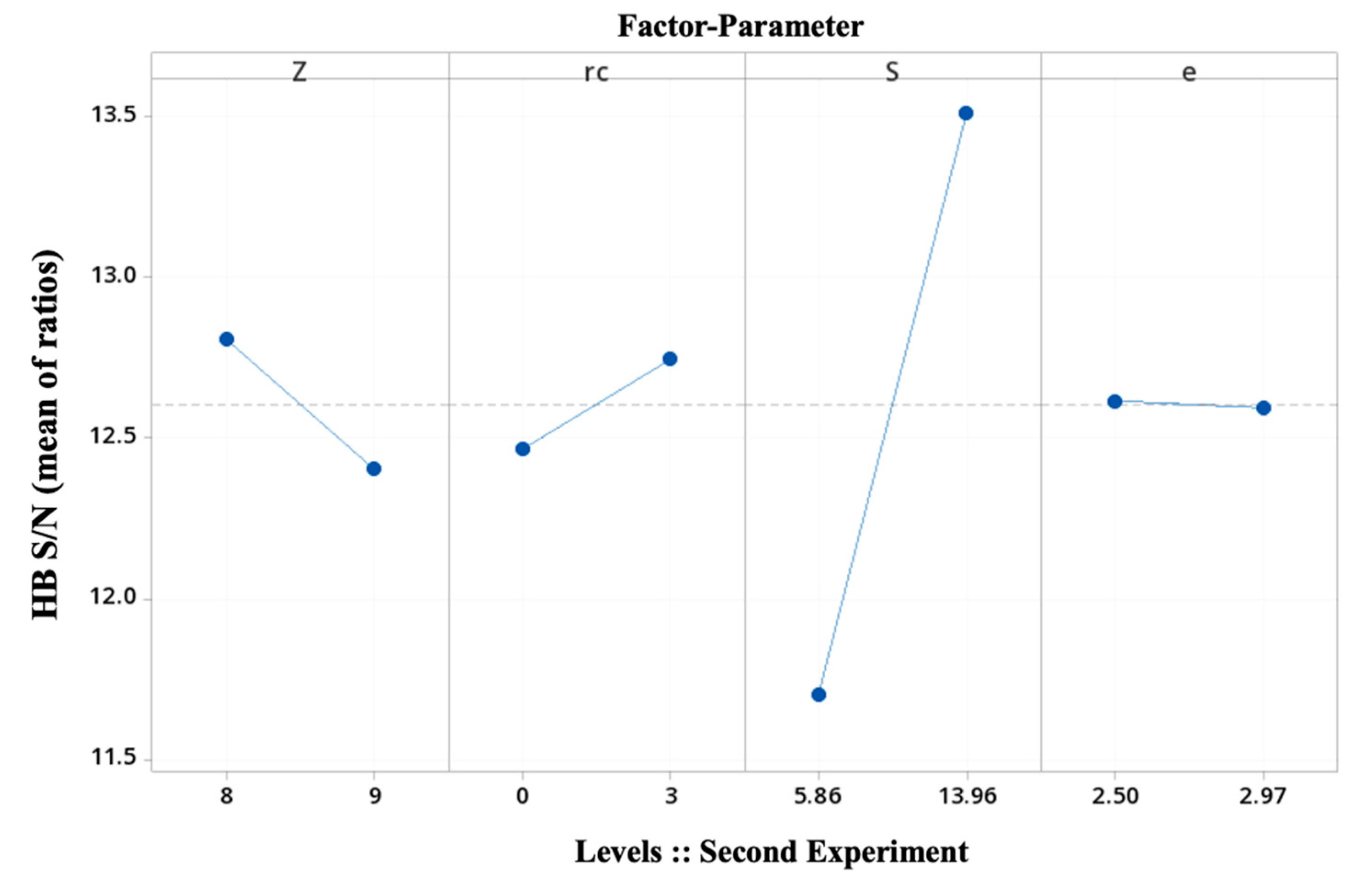
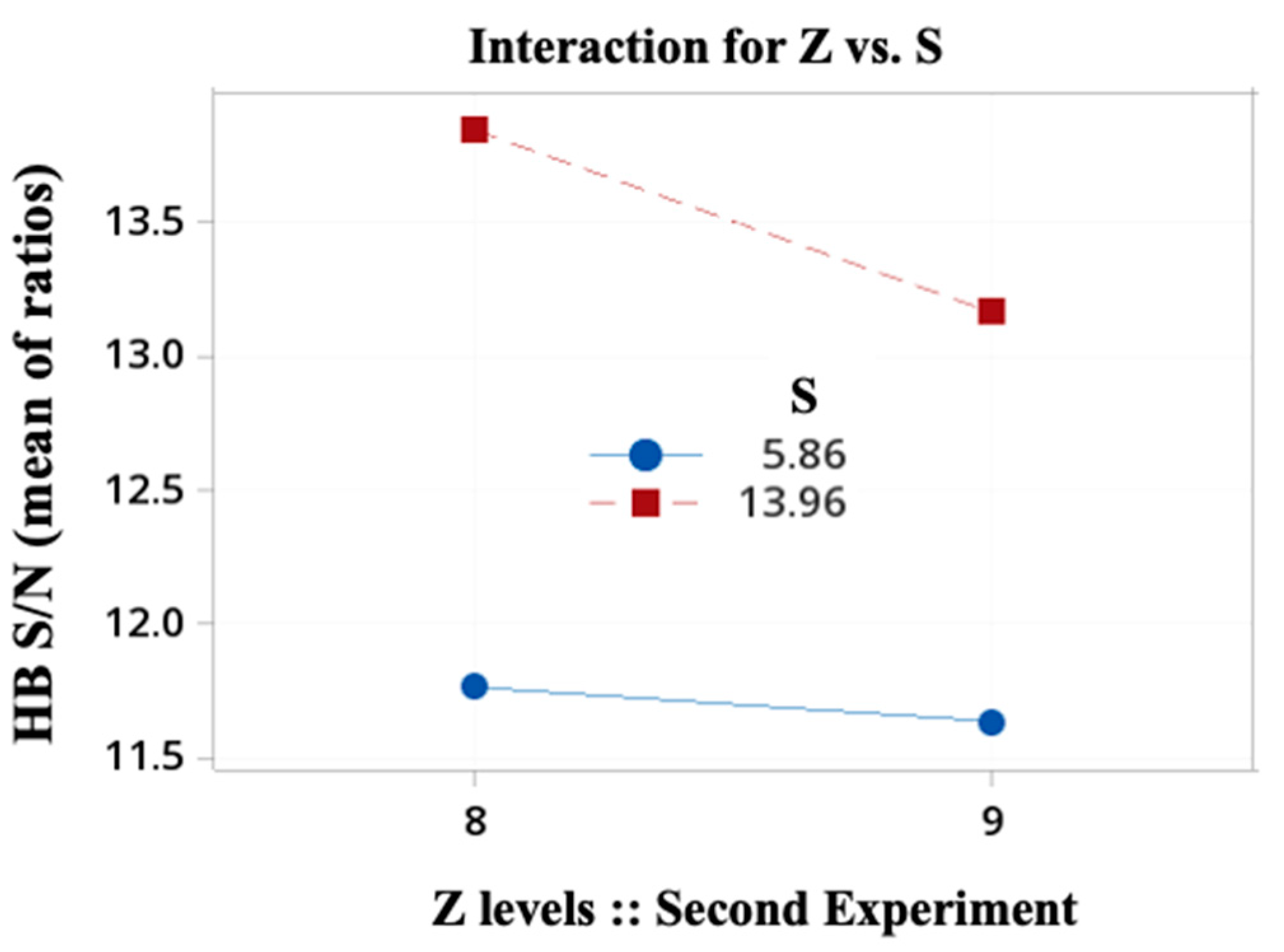
4.4. Second Taguchi Experiment: The Two-Levels-Four-Geometric-Basic-Parameters Case and One Noise Factor
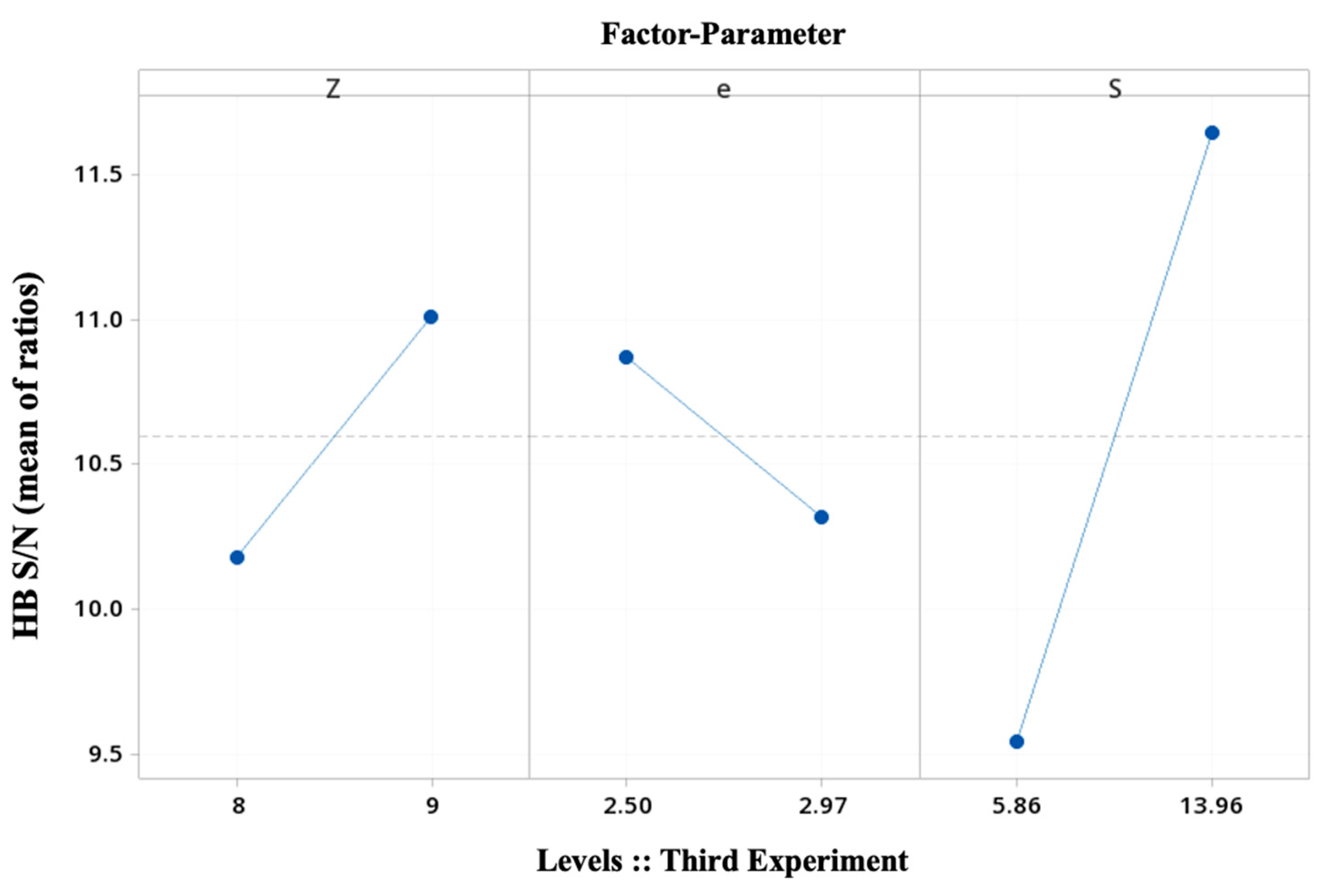
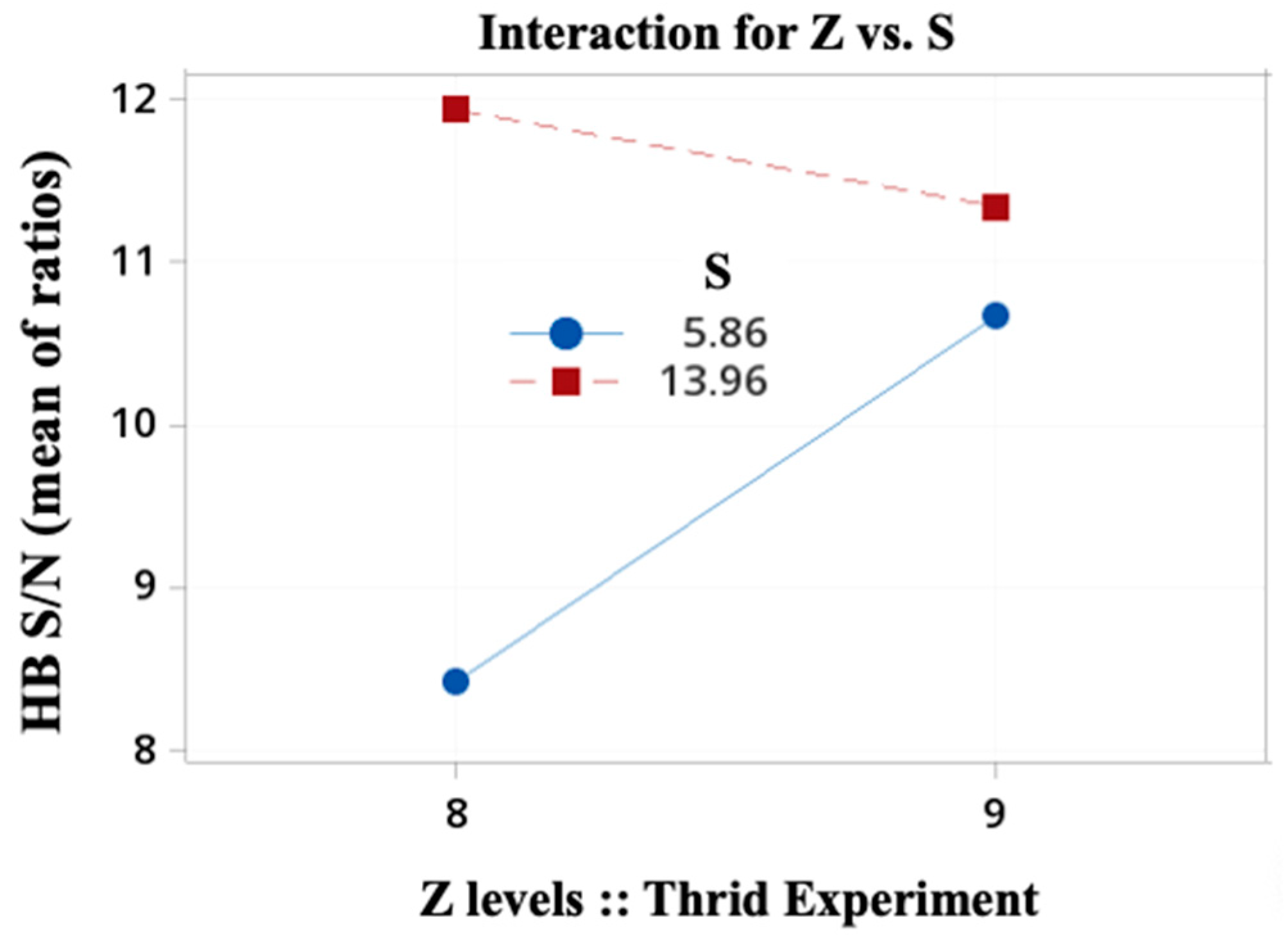
4.5. Third Taguchi Experiment: The Two-Levels-Three-Geometric-Basic-Parameters Case and Three Noise Factors
4.6. Fourth Taguchi Experiment: The Mixed-Level-Design-Case with Three Noise Factors
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| cv | Volumetric capacity/displacement |
| cv,H | Volumetric capacity/displacement per gear thickness |
| DeRi | External diameter of internal gear (DeRi = 2·ReRi) |
| ds | Shaft hole, internal diameter located in the inner gear |
| Dc | External diameter of external gear |
| e | Eccentricity (centre distance) |
| G | Radius of circle to complete external gear |
| H | Gear thickness |
| Ls | Shaft keyway length |
| O1 | Inner/internal gear centre |
| O2 | Outer/external gear centre |
| Pk | Contact point |
| rc | Cutting radius |
| r1 | Inner pitch circle |
| r2 | Outer pitch circle |
| R2 | Distance O2Ps |
| S | Arc radius of the external gear tooth |
| T | Torque |
| wc | Wall width of the external gear |
| Z, (Z − 1) | Number external (internal) teeth |
| λ | Tooth profile height correction coefficient (λ = r2/R2) |
| μ | Friction coefficient |
| θ | Temperature |
| υ | Equidistant index (υ = S·Z/R2) |
References
- Rundo, M. Models for flow rate simulation in gear pumps: A review. Energies 2017, 10, 1261. [Google Scholar] [CrossRef]
- Pareja-Corcho, J.; Moreno, A.; Simoes, B.; Pedrera-Busselo, A.; San-Jose, E.; Ruiz-Salguero, O.; Posada, J. A Virtual Prototype for Fast Design and Visualization of Gerotor Pumps. Appl. Sci. 2021, 11, 1190. [Google Scholar] [CrossRef]
- Kawamata, H.; Kuroda, S.; Tanaka, S.; Oshima, M. Improvement of Practical Electric Consumption by Drag Reducing under Cross Wind; SAE Technical Paper 2016-01-1626; SAE International: Warrendale, PA, USA, 2016; pp. 1–10. [Google Scholar] [CrossRef]
- Colbourne, J.R. Reduction of contact stress in internal gear pumps. J. Eng. Ind. 1976, 98, 1296–1300. [Google Scholar] [CrossRef]
- Roy, D. Mechanics and FEM estimation of deformation, gaps and stresses generated in star-ring active contacts of GEROTOR units during operation. J. Br. Soc. Mech. Sci. Eng. 2021, 43, 429. [Google Scholar] [CrossRef]
- Roy, D.; Maiti, R.; Das, P.K. Mechanics and FEM estimation of gaps generated in star-ring active contacts of ORBIT motor during operation. Int. J. Mech. Mater. Des. 2020, 16, 69–89. [Google Scholar] [CrossRef]
- Sliwinski, P. The methodology of design of satellite working mechanism of positive displacement machine. Sci. Rep. 2022, 12, 1–22. [Google Scholar] [CrossRef]
- Gamez-Montero, P.J.; Codina, E.; Castilla, R. A Review of Gerotor Technology in Hydraulic Machines. Energies 2019, 12, 2423. [Google Scholar] [CrossRef]
- Ivanović, L.; Devedžić, G.; Ćuković, S.; Mirić, N. Modeling of the Meshing of Trochoidal Profiles with Clearances. J. Mech. Des. 2012, 134, 041003. [Google Scholar] [CrossRef]
- Ivanović, L.; Josifović, D.; Ilić, A. Modelling of trochoidal gearing at the gerotor pump. Mech. Mach. Sci. 2013, 13, 553–562. [Google Scholar] [CrossRef]
- Ivanović, L.; Ilić, A.; Miloradović, D.; Josifović, D. Modelling and simulation of the load in the epicyclic rotary pump with trochoidal gear profiles. IOP Conf. Ser. Mater. Sci. Eng. 2018, 393, 1–9. [Google Scholar] [CrossRef]
- Ivanović, L.; Devedžić, G.; Mirić, N.; Ćuković, S. Analysis of forces and moments in gerotor pumps. Proc. Inst. Mech. Eng. C 2010, 224, 2257–2269. [Google Scholar] [CrossRef]
- Ivanović, L. Reduction of the maximum contact stresses by changing geometric parameters of the trochoidal gearing teeth profile. Meccanica 2016, 51, 2243–2257. [Google Scholar] [CrossRef]
- Ivanović, L.; Rakić, B.; Stojanović, B.; Matejić, M. Comparative analysis of analytical and numerical calculations of contact stresses at rotational elements of gerotor pumps. Appl. Eng. Lett. 2016, 1, 1–7. [Google Scholar]
- Ivanović, L.; Mackić, T.; Stojanović, B. Analysis of the instantaneous friction coefficient of the trochoidal gear pair. J. Balk. Tribol. Assoc. 2016, 22, 281–293. [Google Scholar]
- Ivanović, L.; Matejić, M. Improving gerotor pump performance through design, modelling and simulation. Int. J. Fluid Power 2021, 21, 327–346. [Google Scholar] [CrossRef]
- Biernacki, K.; Stryczek, J. Analysis of stress and deformation in plastic gears used in gerotor pumps. J. Strain Anal. Eng. Des. 2010, 45, 465–479. [Google Scholar] [CrossRef]
- Biernacki, K. Selection of the optimum tooth profile for plastic cycloidal gears. Proc. Inst. Mech. Eng. C 2014, 228, 3395–3404. [Google Scholar] [CrossRef]
- Stryczek, J.; Bednarczyk, S.; Biernacki, K. Strength analysis of the polyoxymethylene cycloidal gears of the gerotor pump. Arch. Civ. Mech. Eng. 2014, 14, 647–660. [Google Scholar] [CrossRef]
- Stryczek, J.; Bednarczyk, S.; Biernacki, K. Gerotor pump with POM gears: Design, production technology, research. Arch. Civ. Mech. Eng. 2014, 14, 391–397. [Google Scholar] [CrossRef]
- Biernacki, K. Analysis of the material and design modifications influence on strength of the cycloidal gear system. Int. J. Adv. Manuf. Technol. 2015, 16, 537–546. [Google Scholar] [CrossRef]
- Biernacki, K. New concept of power transmission for gerotor hydraulic machines. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 4873–4883. [Google Scholar] [CrossRef]
- Biernacki, K. New construction of cycloidal gear unit made of plastics. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 800–811. [Google Scholar] [CrossRef]
- Robison, A.; Vacca, A. Multi-objective optimization of circular-toothed gerotors for kinematics and wear by genetic algorithm. Mech. Mach. Theory 2018, 128, 150–168. [Google Scholar] [CrossRef]
- Robison, A.; Vacca, A. Performance comparison of epitrochoidal, hypotrochoidal, and cycloidal gerotor gear profiles. Mech. Mach. Theory 2021, 158, 104228. [Google Scholar] [CrossRef]
- De Martin, A.; Jacazio, G.; Sorli, M. Optimization of Gerotor Pumps with Asymmetric Profiles through an Evolutionary Strategy Algorithm. Machines 2019, 7, 17. [Google Scholar] [CrossRef]
- Tessari, F.; Galluzzi, R.; Amati, N. Efficiency-driven design methodology of gerotor hydraulic units. J. Mech. Des. 2020, 142, 063501. [Google Scholar] [CrossRef]
- Puliti, M.; Tessari, F.; Galluzzi, R.; Tonoli, A.; Amati, N. Design methodology of gerotor hydraulic machines for mechatronic applications. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, IMECE2021, Virtual, Online, 5 November 2021. [Google Scholar]
- Phadke, M.S. Quality Engineering Using Robust Design; Prentice Hall International: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Antony, J. Taguchi or classical design of experiments: A perspective from a practitioner. Sens. Rev. 2006, 26, 227–230. [Google Scholar] [CrossRef]
- Taguchi, G. Introduction to Quality Engineering: Designing Quality into Products and Processes; Asian Productivity Organization: Tokyo, Japan, 1986. [Google Scholar]
- Unal, R.; Dean, E.B. Taguchi approach to design optimization for quality and cost: An overview. In Proceedings of the 1991 Annual Conference of the International Society of Parametric Analysts, Hampton, VA, USA, 1 January 1991. [Google Scholar]
- Ross, R. Taguchi Techniques for Quality Engineering, 2nd ed.; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Antony, J.; Jiju Antony, F. Teaching the Taguchi method to industrial engineers. Work Study 2001, 50, 141–149. [Google Scholar] [CrossRef]
- Jung, S.-Y.; Bae, J.-H.; Kim, M.-S.; Kim, C. Development of a new gerotor for oil pumps with multiple profiles. Int. J. Precis. Eng. Manuf. 2011, 12, 835–841. [Google Scholar] [CrossRef]
- Ivanović, L.T.; Veličković, S.N.; Stojanović, B.Ž.; Kandeva, M.; Jakimovska, K. The selection of optimal parameters of gerotor pump by application of factorial experimental design. FME Trans. 2017, 45, 159–164. [Google Scholar] [CrossRef]
- Ivanović, L.; Stojanović, B.; Blagojević, J.; Bogdanović, G.; Marinković, A. Analysis of the flow rate and the volumetric efficiency of the trochoidal pump by application of Taguchi method. Teh. Vjesn. 2017, 24, 265–270. [Google Scholar] [CrossRef] [Green Version]
- Lazić, L.; Milinković, S. Reducing software defects removal cost via design of experiments using Taguchi approach. Software Qual. J. 2015, 23, 267–295. [Google Scholar] [CrossRef]
- Vosniakos, G.C.; Kalattas, A.; Siasos, A. Optimal process planning for helical bevel gears using Taguchi design of simulated machining experiments. Proc. IMechE Part B J Eng. Manuf. 2018, 232, 2627–2640. [Google Scholar] [CrossRef]
- Choudhury, K.; Mandol, S.; Dan, P.K. Optimization of Operations in Epicyclic Gear Train Modelled Through Computer Aided Design. Asia-Pac. J. Manag. Res. Innov. 2014, 10, 323–335. [Google Scholar] [CrossRef]
- Stryczek, J.; Stryczek, P. Synthetic approach to the design, manufacturing and examination of gerotor and orbital hydraulic machines. Energies 2021, 14, 624. [Google Scholar] [CrossRef]
- Gamez-Montero, P.J.; Castilla, R.; Khamashta, M.; Codina, E. Contact problems of a trochoidal-gear pump. Int. J. Mech. Sci. 2006, 48, 14711480. [Google Scholar] [CrossRef]
- Gamez-Montero, P.J.; Castilla, R.; Mujal, R.; Khamashta, M.; Codina, E. GEROLAB package system: Innovative tool to design a trochoidal-gear pump. J. Mech. Des. 2009, 131, 074502. [Google Scholar] [CrossRef]
- GeroLAB Package System. Available online: http://www.gerolab.es (accessed on 1 February 2022).
- Ram Kumar, A.C.; Mohammed Raffic, N.; Ganesh Babu, K.; Selvakumar, S. Static structural analysis of spur gear using ANSYS 15.0 and material selection by COPRAS, MOORA techniques. Mater. Today Proc. 2021, 47, 25–36. [Google Scholar] [CrossRef]
- Karthick, L.; Shanmugasundaram, A.; Jagadish, C.A.; Prabhu, T.; Vidya Prakash, S. Numerical analysis of Modified tooth in Spur Gear for increasing the performance using fool proofing technology. Mater. Today Proc. 2021, 47, 5862–5868. [Google Scholar] [CrossRef]
- Benaïcha, Y.; Perret-Liaudet, J.; Beley, J.D.; Rigaud, E.; Thouverez, F. On a flexible multibody modelling approach using FE-based contact formulation for describing gear transmission error. Mech. Mach. Theory 2022, 167, 104505. [Google Scholar] [CrossRef]
- Rao, P.S. Contact Stress and Shear Stress Analysis of Spur Gear Using ANSYS and Theoretical. Int. J. Mod. Stud. Mech. Eng. 2016, 2, 9–14. [Google Scholar] [CrossRef]
- Lahtivirta, J.; Lehtovaara, A. Modelling of spur gear contact using a local adaptive finite element mesh. Tribologia 2016, 34, 41–55. [Google Scholar]
- Lisle, T.J.; Shaw, B.A.; Frazer, R.C. External spur gear root bending stress: A comparison of ISO 6336:2006, AGMA 2101-D04, ANSYS finite element analysis and strain gauge techniques. Mech. Mach. Theory 2017, 111, 1–9. [Google Scholar] [CrossRef]
- Puneeth, M.L.; Mallesh, G. Static contact behavior of asymmetric spur gear. Mater. Today Proc. 2021, 47, 3095–3104. [Google Scholar] [CrossRef]
- Munoz, G.A. Lecture 7: Mesh Quality & Advanced Topics; ANSYS Inc.: Canonsburg, PA, USA, 2015; p. 37. Available online: https://www.academia.edu/16970000/MESH_QUALITY_AND_ADVENCED_TOPICS_ANSYS_WORKBENCH_16_0 (accessed on 1 February 2022).
- Sliwinski, P. Determination of the Theoretical and Actual Working Volume of a Hydraulic Motor—Part II (The Method Based on the Characteristics of Effective Absorbency of the Motor). Energies 2021, 14, 1648. [Google Scholar] [CrossRef]
- Garcia-Vilchez, M.; Gamez-Montero, P.J.; Codina, E.; Castilla, R.; Raush, G.; Freire, J.; Rio, C. Computational fluid dynamics and particle image velocimetry assisted design tools for a new generation of trochoidal gear pumps. Adv. Mech. Eng. 2015, 7, 1–14. [Google Scholar] [CrossRef]
- Gamez-Montero, P.J.; Castilla, R.; Codina, E. Methodology based on best practice rules to design a new-born trochoidal gear pump. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 1057–1068. [Google Scholar] [CrossRef]
- Skowrońska, J.; Kosucki, A.; Stawiński, Ł. Overview of Materials Used for the Basic Elements of Hydraulic Actuators and Sealing Systems and Their Surfaces Modification Methods. Materials 2021, 14, 1422. [Google Scholar] [CrossRef]
- Student, M.; Hvozdetskyi, V.; Stupnytskyi, T.; Student, O.; Maruschak, P.; Prentkovskis, O.; Skačkauskas, P. Mechanical Properties of Arc Coatings Sprayed with Cored Wires with Different Charge Compositions. Coatings 2022, 12, 925. [Google Scholar] [CrossRef]




| Gear Set | Researchers’ Work | Analysis–Environment | Observation |
|---|---|---|---|
| PZ7e377 | Biernacki [23] | FEM–ABAQUS | The keyway is removed |
| PZ6e356/1375 PZ6e356/1575 | Ivanović et al. [14] | FEM–CATIA/FEMAP | λ’ = 1/λ = 1.375 λ’ = 1/λ = 1.575 |
| PZ9e285 | Gamez-Montero et al. [42] | FEM–GiD/COMET | The shaft hole is included |
| MZ9e855 | Photoelasticity model | Scaled 3:1 of PZ9e285 |
| Input Gear Set Variable/ Parameter | PZ7e377 | PZ6e356/1375 PZ6e356/1575 | PZ9e285 | MZ9e885 |
|---|---|---|---|---|
| GeroLAB | 3:1 (PZ9e285) | |||
| Z [-] | 7 | 6 | 9 | |
| e [mm] | 3.77 | 3.56 | 2.85 | |
| S [mm] | 11.11 | 9.79 (/1375) 14.06 (/1575) | 10.85 | |
| DeRi [mm] | 53.24 | 46.28 | 65.45 | |
| G [mm] | 30.50 | 26.94 | 35.80 | |
| rc [mm] | 0 | 0 | 0 | |
| H [mm] | 10.40 | 16.46 | 9.25 | |
| Geometrical | 3:1 (PZ9e285) | |||
| wc [mm] | 7.0 | 4.1 | 4.2 | |
| Dc (O2) [mm] | 75 | 62 | 80 | |
| ds (O1) [mm] | 25 | 16 | 44 | |
| Material properties | POM * | Steel | Sintered metallic powder | Epoxy |
| Young’s module [GPa] | 3 | 200 | 115 | 3 |
| Density [kg/m3] | 1410 | - | 6800 | 1160 |
| Poisson’s coefficient [-] | 0.43 | 0.30 | 0.25 | 0.35 |
| Friction coefficient, m [-] | 0.40 | 0.40 | 0.40 | 0.30 |
| Torque, T [N·m] | 7.16 | 0.621 (/1375) 0.632 (/1575) | 18.75 | 37.5 |
| Parameter | Value | Significance/Target |
|---|---|---|
| cv,H = cv/H [cc/(rev·mm)] | 1 | Volumetric capacity/Flow rate |
| Dc [mm] | 80 | Housing/Dimensional constraint |
| ds [mm] | 40 | Internal diameter located in the inner gear to accommodate the shaft/Through-shaft application |
| H [mm] | 9.25 | Casing/Dimensional constraint |
| 8 gear sets in common | |||||||
| Vol. capacity target: Dimensional constraints: FEM conditions: | = 1 cc·rev−1·mm−1 (0.093), mean (standard deviation) Dc = 80 mm; ds = 40 mm; H = 9.25 mm T = 18.75 N·m; µ = 0.4; θ = 20° | ||||||
| L8 OA inner array | |||||||
| (control factors) | A | B | C | D | E | F | G |
| Factor parameter (column) Trial gear set::Taguchi experiment (row) | Z | e [mm] | Reference position (RP) (Figure 6) | S [mm] | rc [mm] | Shaft keyway (SK) (Figure 6) | wc [mm] |
| 1::1 | 8 | 2.50 | T2T | 5.86 | 0.0 | No | 3.0 |
| 2::1 | 8 | 2.50 | T2T | 13.96 | 3.0 | Yes | 6.0 |
| 3::1 | 8 | 2.97 | V2T | 5.86 | 0.0 | Yes | 6.0 |
| 4::1 | 8 | 2.97 | V2T | 13.96 | 3.0 | No | 3.0 |
| 5::1 | 9 | 2.50 | V2T | 5.86 | 3.0 | No | 6.0 |
| 6::1 | 9 | 2.50 | V2T | 13.96 | 0.0 | Yes | 3.0 |
| 7::1 | 9 | 2.97 | T2T | 5.86 | 3.0 | Yes | 3.0 |
| 8::1 | 9 | 2.97 | T2T | 13.96 | 0.0 | No | 6.0 |
| 8 gear sets in common | |||||||
| Vol. capacity target: Dimensional constraints: FEM conditions: | = 0.997 cc·rev−1·mm−1 (0.023), mean (standard deviation) Dc = 80 mm; ds = 40 mm; H = 9.25 mm; (SK = yes) T = 18.75 N·m; µ = 0.4; θ = 20° | ||||||
| L8 OA inner array (control factors) | A | B | D | G | L1 OA outer array (noise factor) | N1 | N2 |
| Factor parameter (column) Trial gear set::Taguchi experiment (row) | Z | rc [mm] | S [mm] | e [mm] | Reference position (Figure 6) (column) | T2T | V2T |
| 1::2 | 8 | 0.0 | 5.86 | 2.50 | |||
| 2::2 | 8 | 0.0 | 13.96 | 2.97 | |||
| 3::2 | 8 | 3.0 | 5.86 | 2.97 | |||
| 4::2 | 8 | 3.0 | 13.96 | 2.50 | |||
| 5::2 | 9 | 0.0 | 5.86 | 2.97 | |||
| 6::2 | 9 | 0.0 | 13.96 | 2.50 | |||
| 7::2 | 9 | 3.0 | 5.86 | 2.50 | |||
| 8::2 | 9 | 3.0 | 13.96 | 2.97 | |||
| 8 gear sets in common | ||||||||
| Vol. capacity target: Dimensional constraints: FEM conditions: | = 0.997 cc·rev−1·mm−1 (0.023), mean (standard deviation) Dc = 80 mm; ds = 40 mm; H = 9.25 mm; (SK = yes) Noise factors | |||||||
| L8 OA inner array (control factors) | A | B | D | L4 OA outer array (noise factors) | N1 | N2 | N3 | N4 |
| Factor parameter (column) Trial gear set::Taguchi experiment (row) | Z | e [mm] | S [mm] | T [N·m] μ [-] θ [°C] (column) | 15.0 0.01 20 | 22.5 0.50 20 | 22.5 0.01 40 | 15.0 0.50 40 |
| 1::3 | 8 | 2.50 | 5.86 | |||||
| 2::3 | 8 | 2.50 | 13.96 | |||||
| 3::3 | 8 | 2.97 | 5.86 | |||||
| 4::3 | 8 | 2.97 | 13.96 | |||||
| 5::3 | 9 | 2.50 | 5.86 | |||||
| 6::3 | 9 | 2.50 | 13.96 | |||||
| 7::3 | 9 | 2.97 | 5.86 | |||||
| 8::3 | 9 | 2.97 | 13.96 | |||||
| 18 gear sets in common | |||||||||
| Vol. capacity target: Dimensional constraints: FEM conditions: | = 0.996 cc·rev−1·mm−1 (0.041), mean (standard deviation) Dc = 80 mm; ds = 40 mm; H = 9.25 mm; (SK = yes) Noise factors | ||||||||
| L18 OA inner array (control factors) | A | B | C | D | L2 OA outer array (noise facts) | N1 | N2 | N3 | N4 |
| Factor parameter (column) Trial gear set::Taguchi experiment (row) | Reference position (RP) (Figure 6) | Z | S [mm] | e [mm] | T [N·m] μ [-] θ [°C] (column) | 15.0 0.0 ** 20 | 22.5 0.4 20 | 22.5 0.0 ** 40 | 15.0 0.4 40 |
| 1::4 | V2T | 7 | 5.8 | 2.61 | |||||
| 2::4 | V2T | 7 | 8.0 | 2.77 | |||||
| 3::4 | V2T | 7 | 10.4 | 2.93 | |||||
| 4::4 | V2T | 9 | 5.8 | 2.61 | |||||
| 5::4 | V2T | 9 | 8.0 | 2.77 | |||||
| 6::4 | V2T | 9 | 10.4 | 2.93 | |||||
| 7::4 | V2T | 11 | 5.8 | 2.77 | |||||
| 8::4 | V2T | 11 | 8.0 | 2.93 | |||||
| 9::4 | V2T | 11 | 10.4 | 2.61 | |||||
| 10::4 | T2T | 7 | 5.8 | 2.93 | |||||
| 11::4 | T2T | 7 | 8.0 | 2.61 | |||||
| 12::4 | T2T | 7 | 10.4 | 2.77 | |||||
| 13::4 | T2T | 9 | 5.8 | 2.77 | |||||
| 14::4 | T2T | 9 | 8.0 | 2.93 | |||||
| 15::4 | T2T | 9 | 10.4 | 2.61 | |||||
| 16::4 | T2T | 11 | 5.8 | 2.93 | |||||
| 17::4 | T2T | 11 | 8.0 | 2.61 | |||||
| 18::4 | T2T | 11 | 10.4 | 2.77 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gamez-Montero, P.J.; Bernat-Maso, E. Taguchi Techniques as an Effective Simulation-Based Strategy in the Design of Numerical Simulations to Assess Contact Stress in Gerotor Pumps. Energies 2022, 15, 7138. https://doi.org/10.3390/en15197138
Gamez-Montero PJ, Bernat-Maso E. Taguchi Techniques as an Effective Simulation-Based Strategy in the Design of Numerical Simulations to Assess Contact Stress in Gerotor Pumps. Energies. 2022; 15(19):7138. https://doi.org/10.3390/en15197138
Chicago/Turabian StyleGamez-Montero, Pedro Javier, and Ernest Bernat-Maso. 2022. "Taguchi Techniques as an Effective Simulation-Based Strategy in the Design of Numerical Simulations to Assess Contact Stress in Gerotor Pumps" Energies 15, no. 19: 7138. https://doi.org/10.3390/en15197138
APA StyleGamez-Montero, P. J., & Bernat-Maso, E. (2022). Taguchi Techniques as an Effective Simulation-Based Strategy in the Design of Numerical Simulations to Assess Contact Stress in Gerotor Pumps. Energies, 15(19), 7138. https://doi.org/10.3390/en15197138








