Small-Signal Stability Research of Grid-Connected Virtual Synchronous Generators
Abstract
:1. Introduction
2. VSG Control Strategy
2.1. VSG Topology
2.2. VSG Algorithm
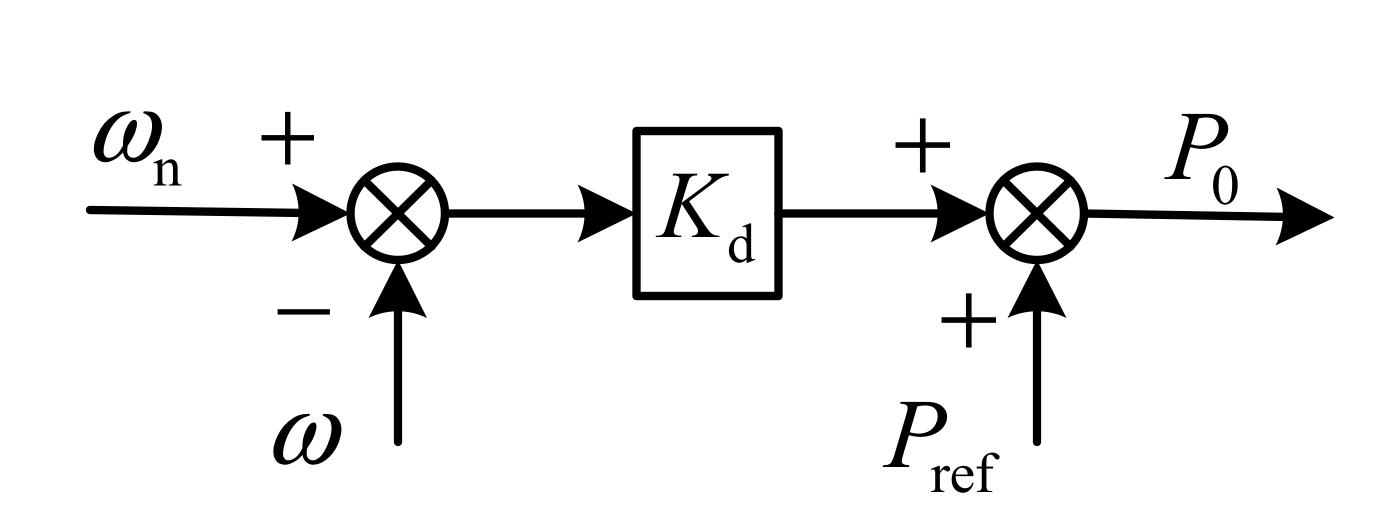
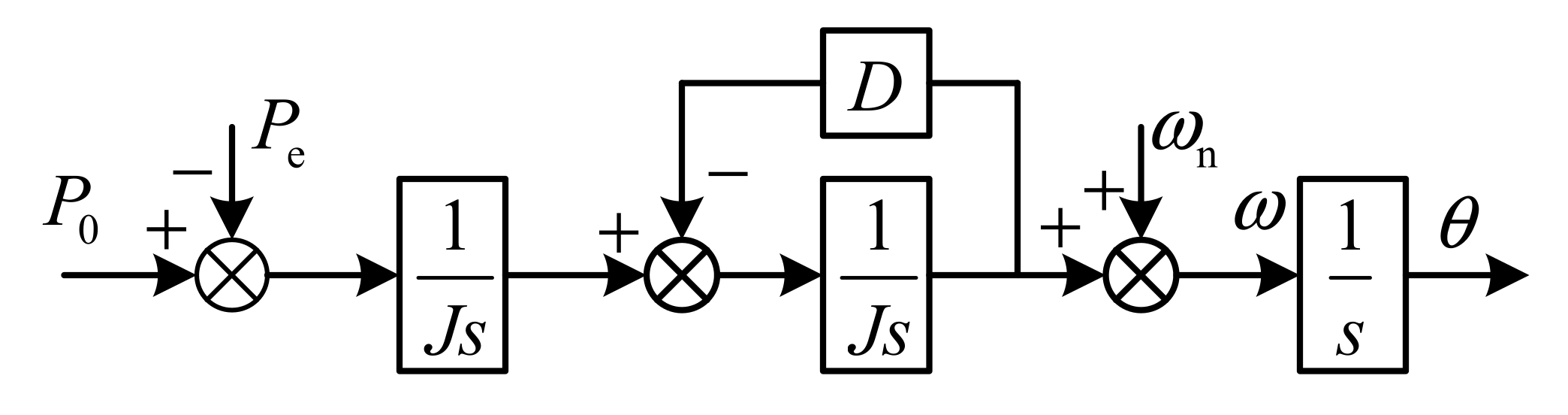
2.2.1. Virtual Power Frequency Controller
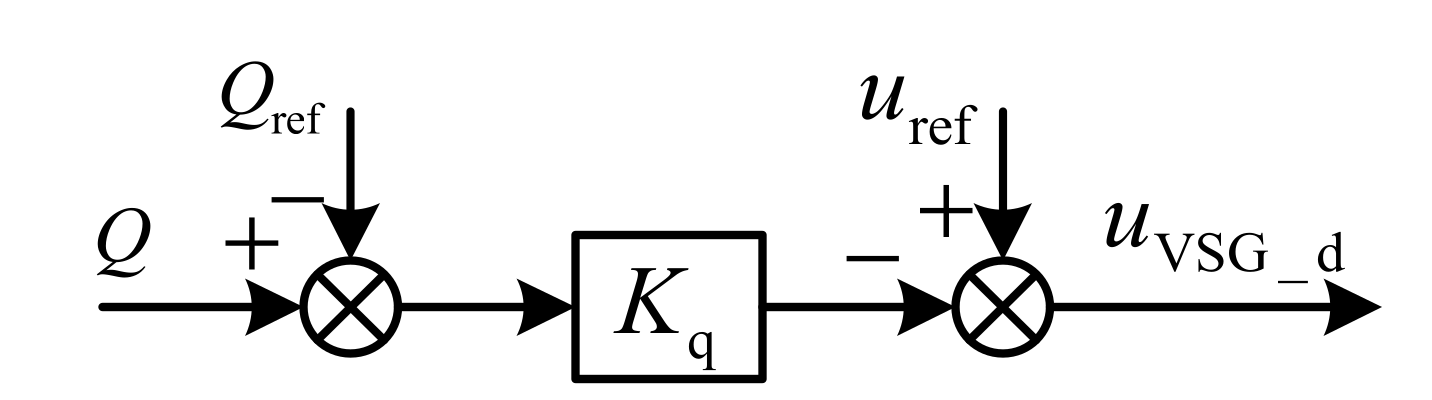
2.2.2. Virtual Excitation Controller
3. Small-Signal Model of Single-VSG Grid-Connected System
3.1. Small-Signal Model of Filter and Connecting Line
3.2. Small-Signal Models of Power Calculation and VSG Control Algorithm
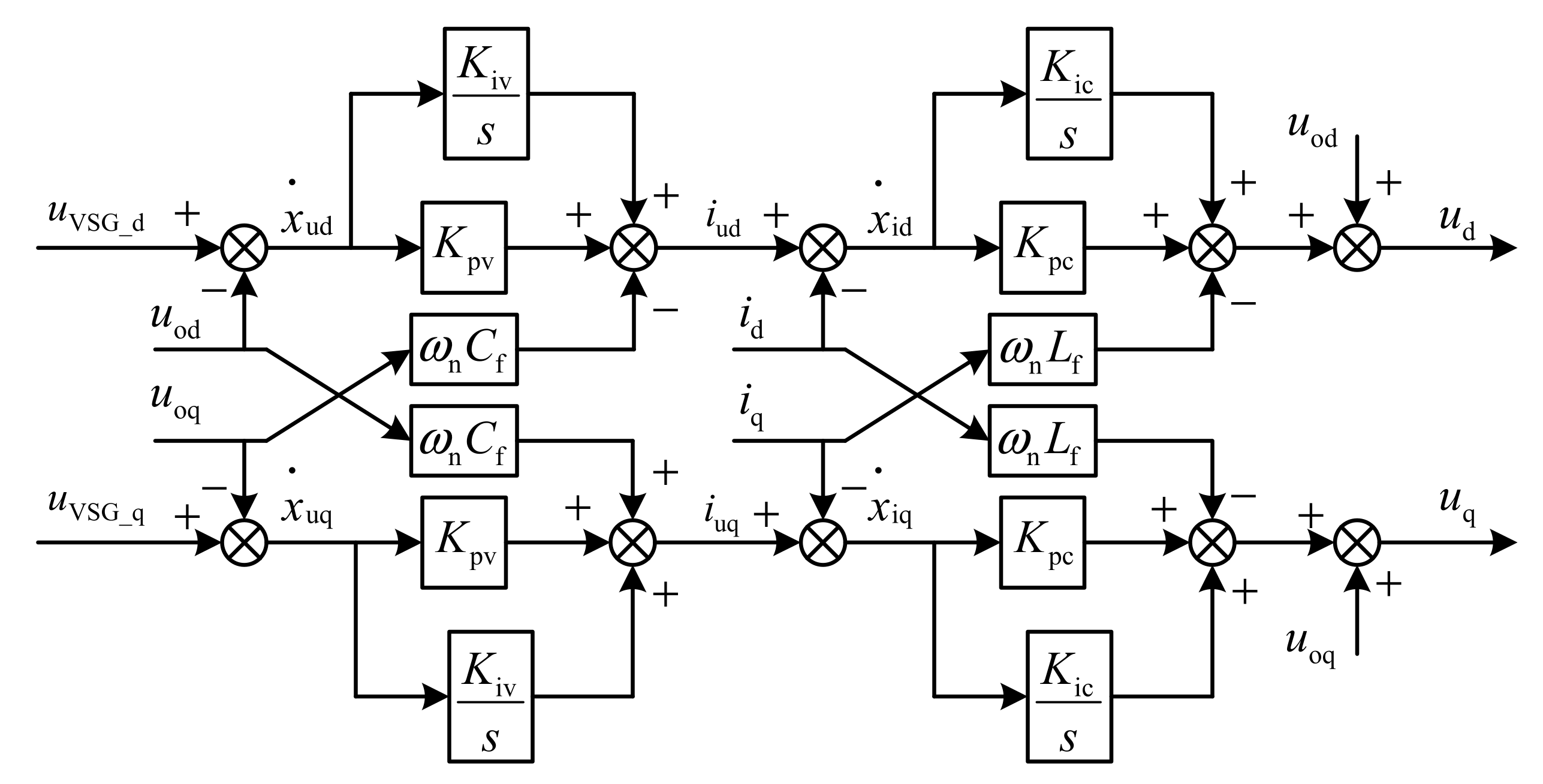
3.3. Small-Signal Model of Voltage and Current Closed Loops
3.4. Small-Signal Model of Power Grid
4. Small-Signal Model of Multi-VSG Grid-Connected System
5. Stability Analysis Based on Eigenvalues
5.1. Stability Analysis of Single-VSG Grid-Connected System
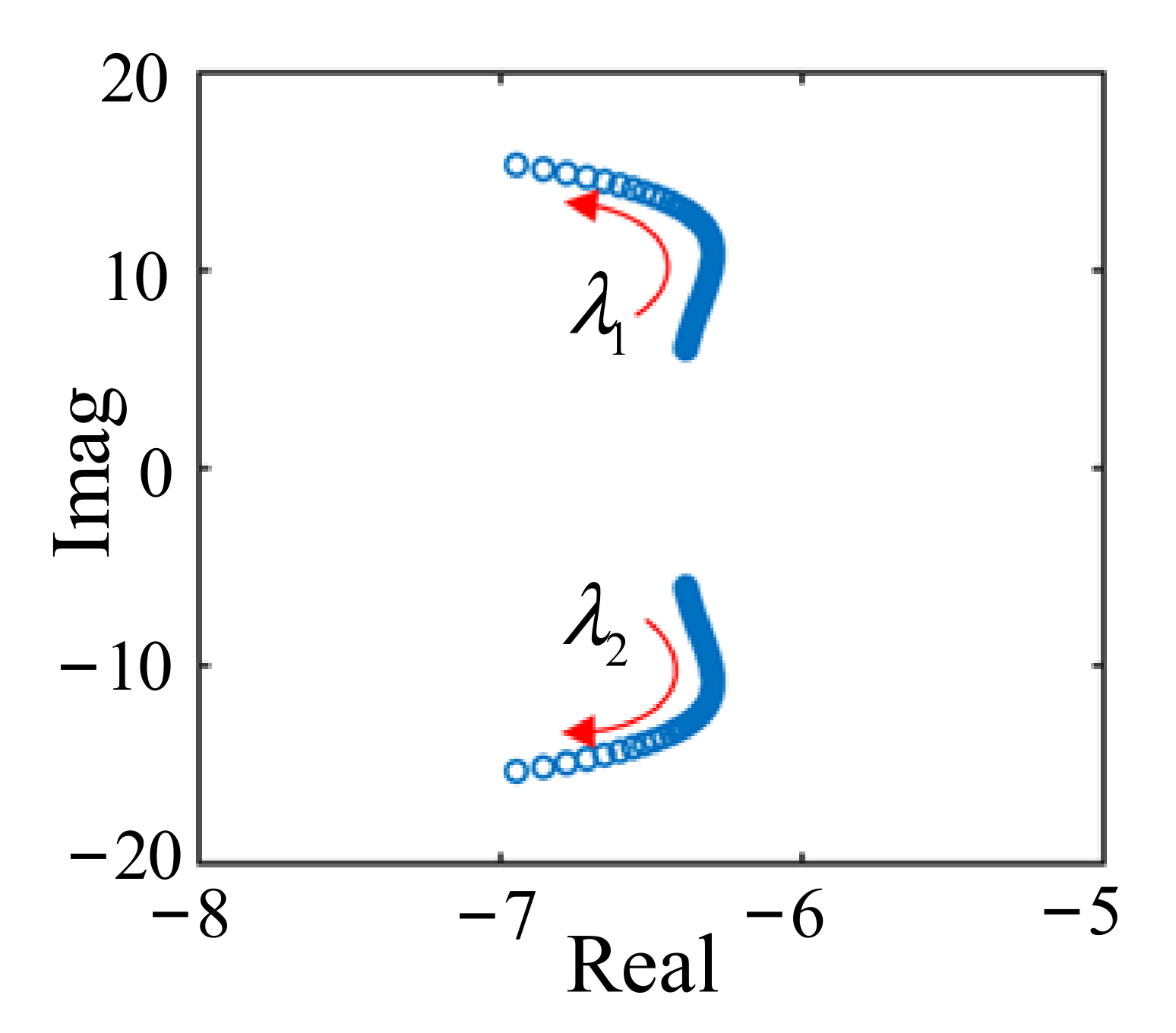
5.1.1. Oscillation Mode Analysis of Single-VSG System
5.1.2. Influence of Active Power Loop Control Parameters on Eigenvalues
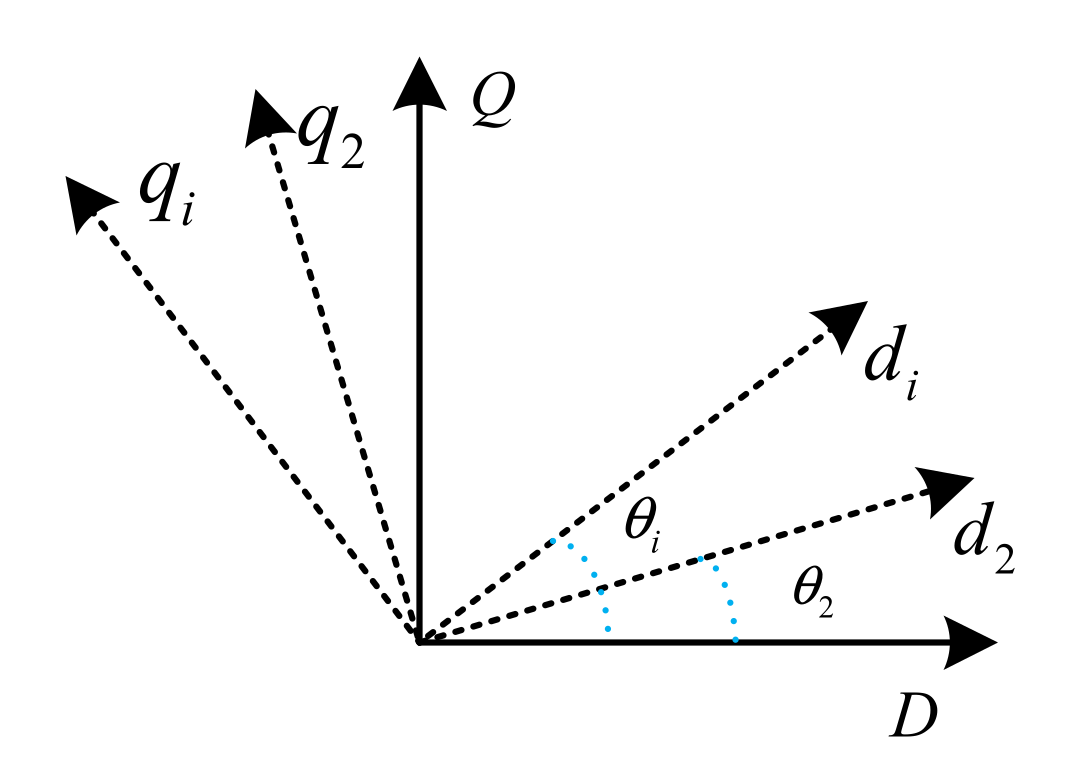
5.1.3. Influence of Resistance Inductance Ratio of Connecting Line on Eigenvalues
5.2. Stability Analysis of Multi-VSG System
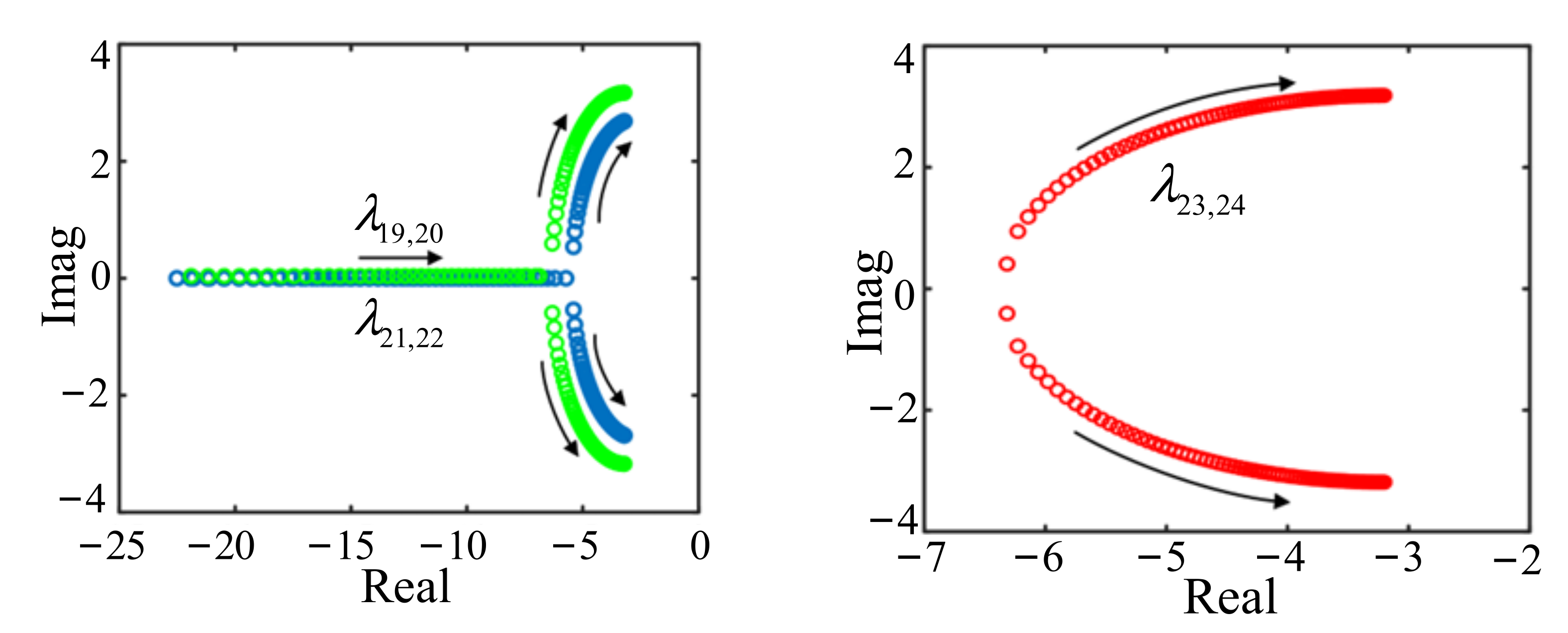
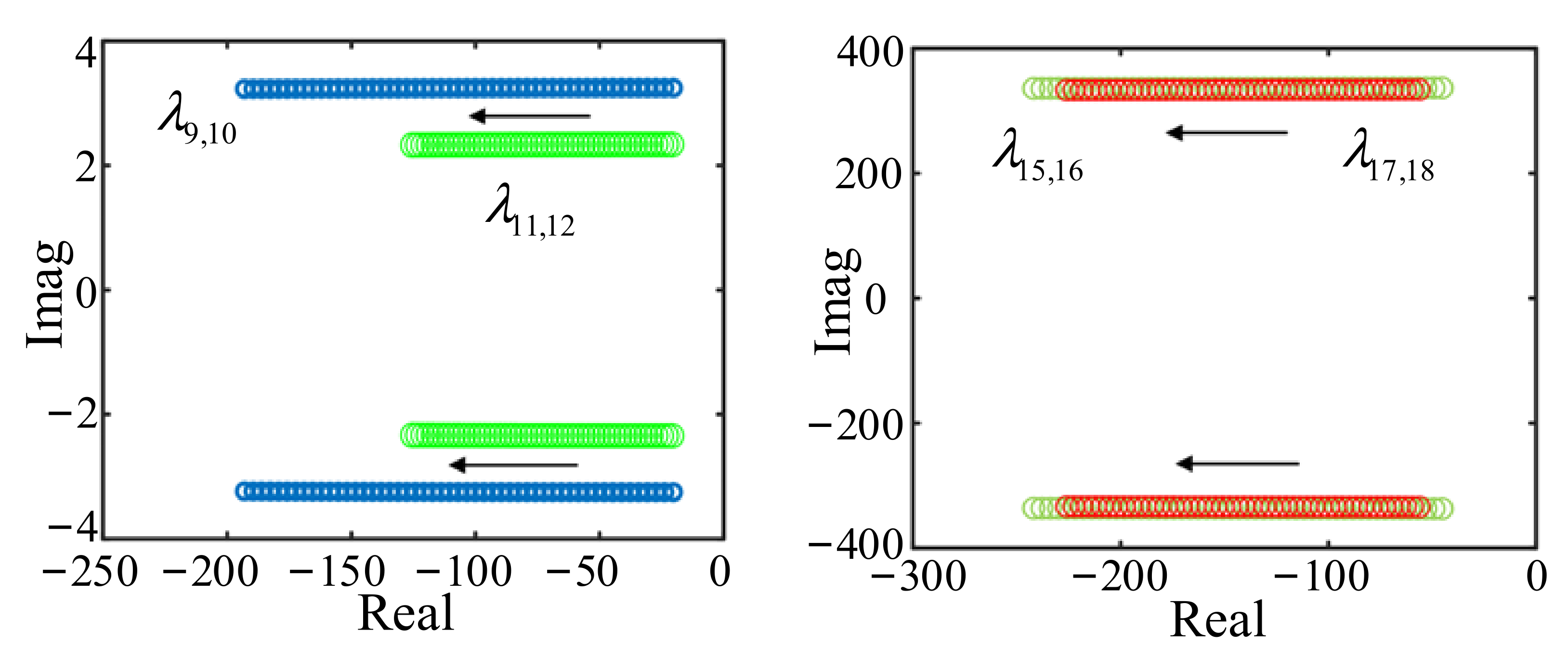
5.2.1. Oscillation Mode Analysis of Multi-VSG System
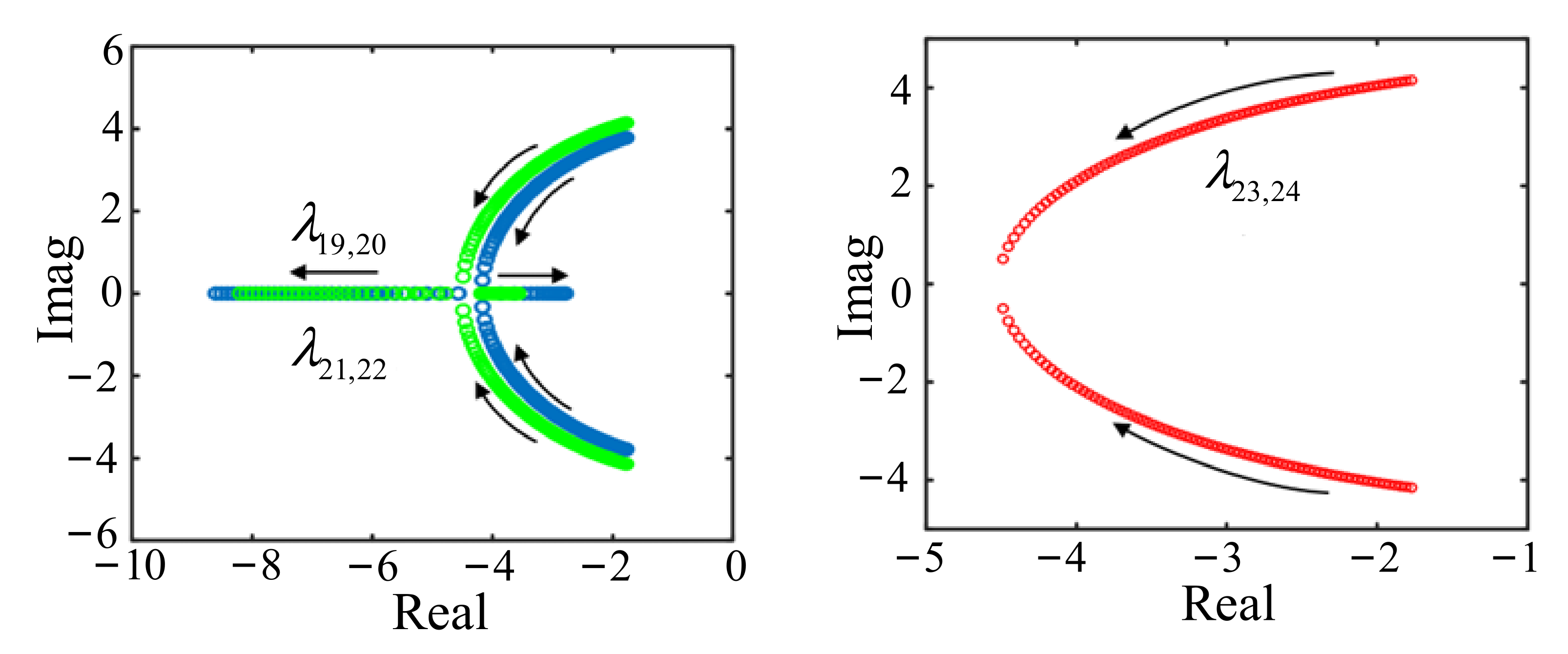
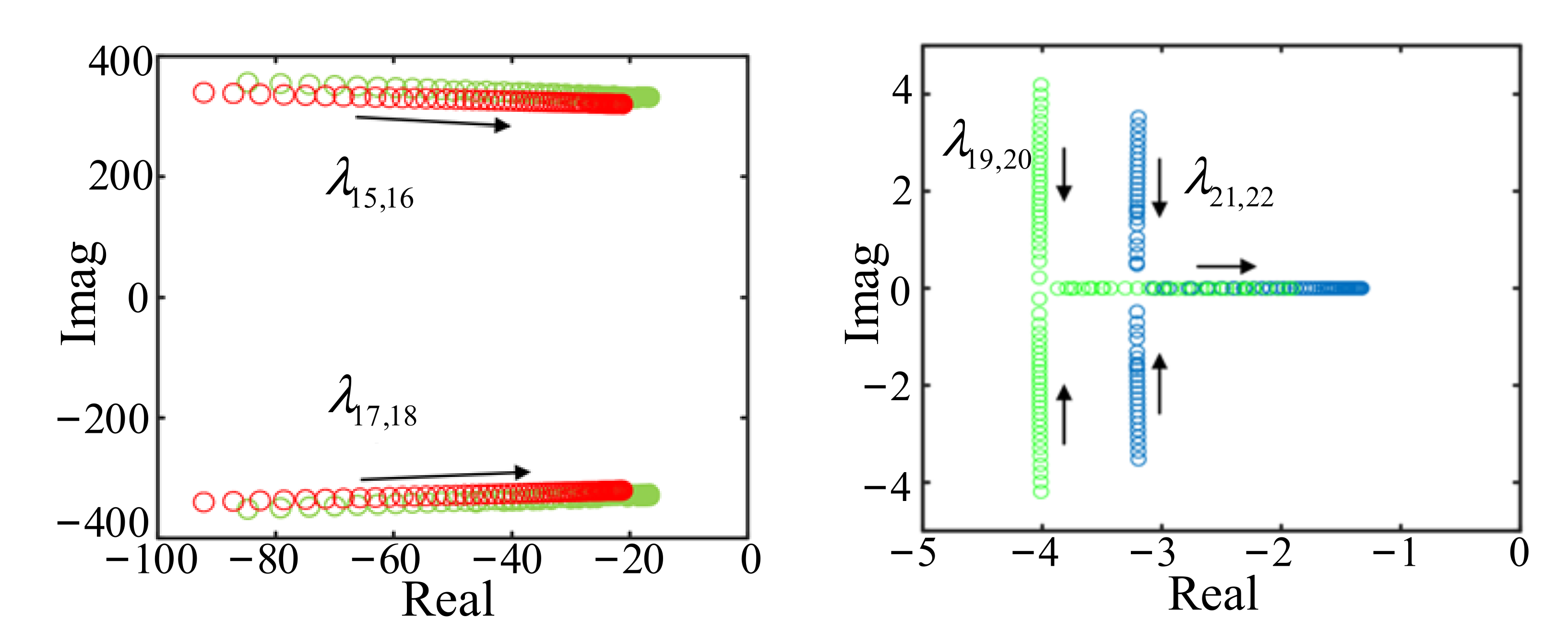
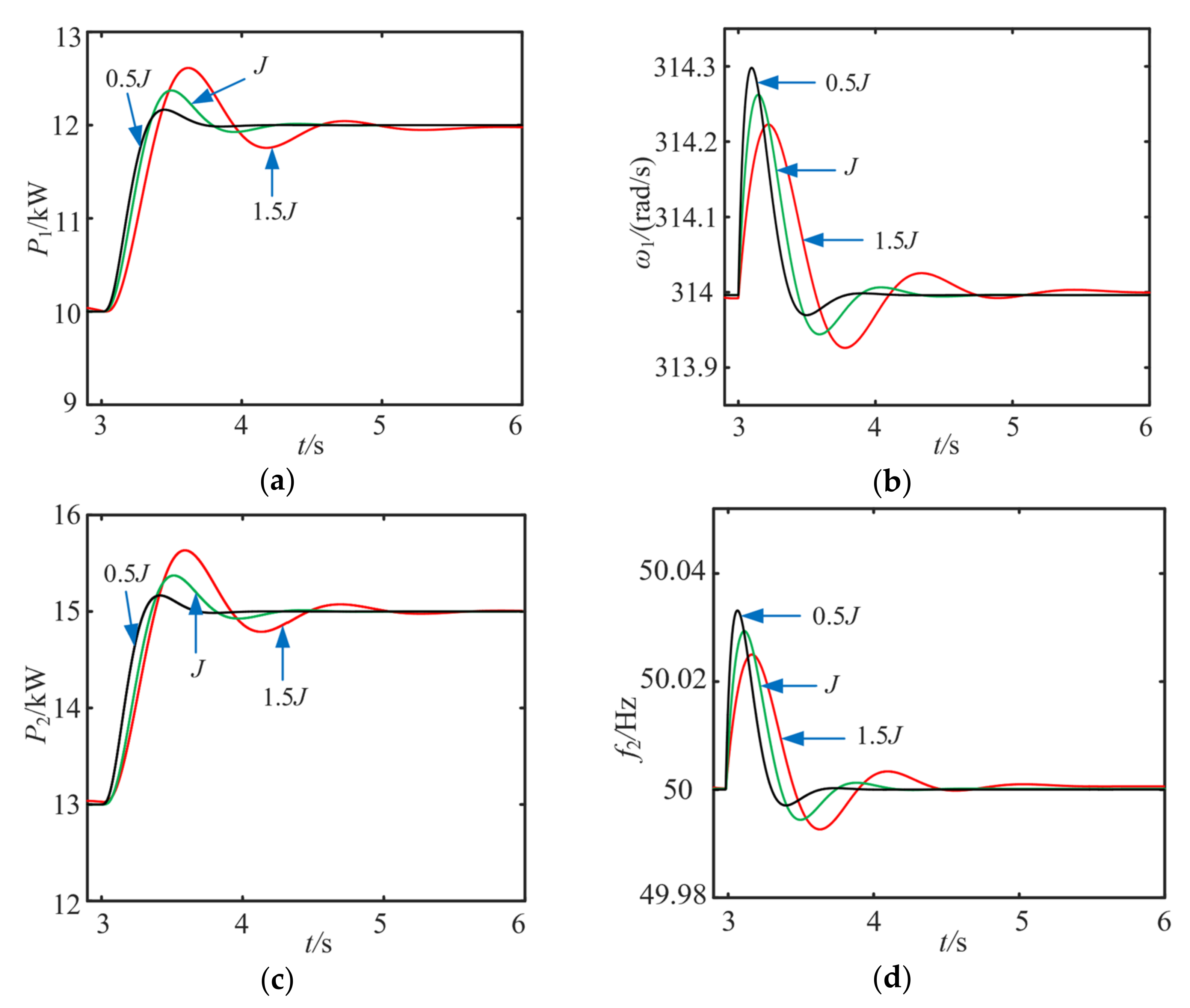
5.2.2. Influence of Virtual Inertia on Eigenvalues
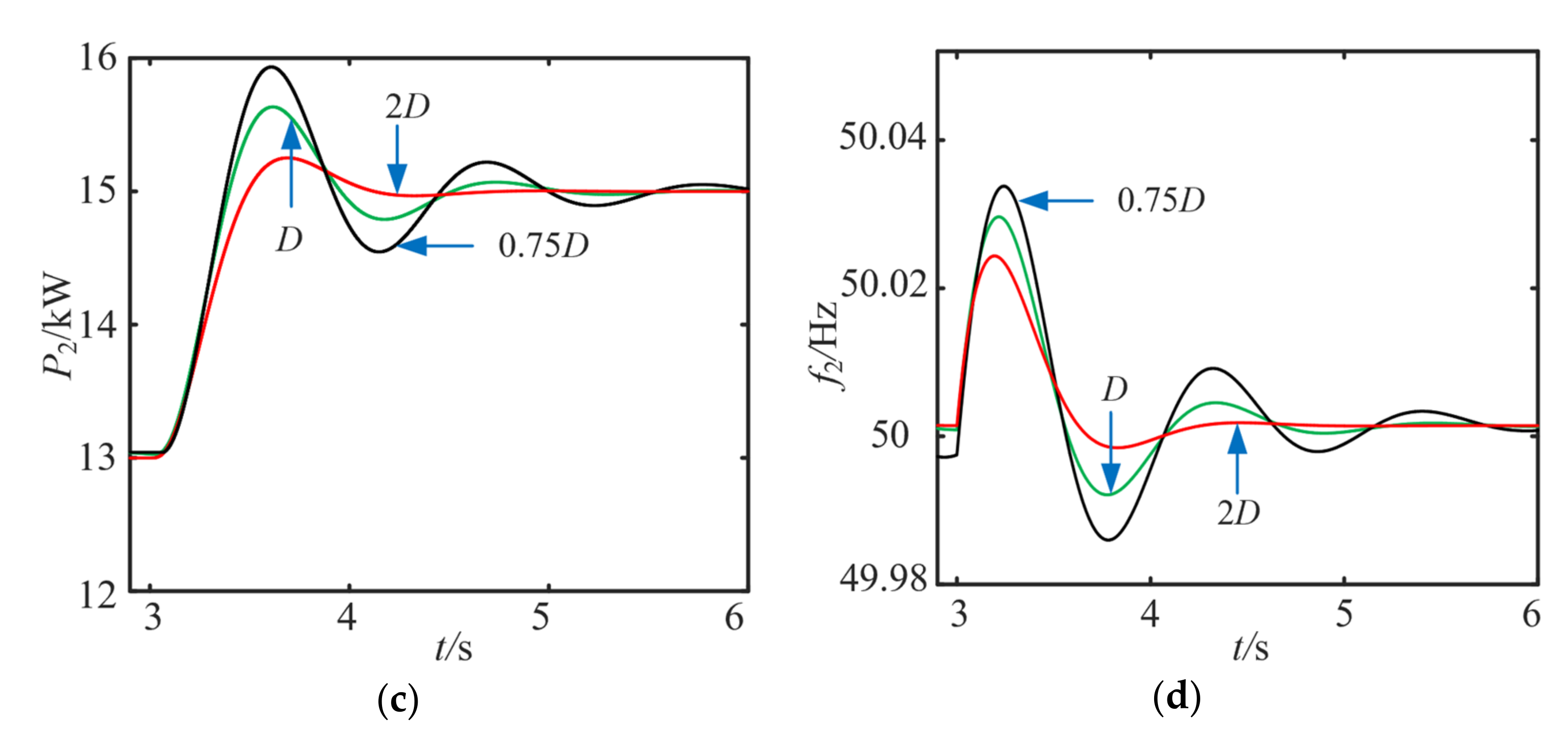
5.2.3. Influence of Damping Coefficient on Eigenvalues
5.2.4. Influence of Line Resistance on Eigenvalues
5.2.5. Influence of Line Inductance on Eigenvalues
6. Time Domain Simulation Verification and Result Discussion
6.1. Simulation of Single-VSG Grid-Connected System
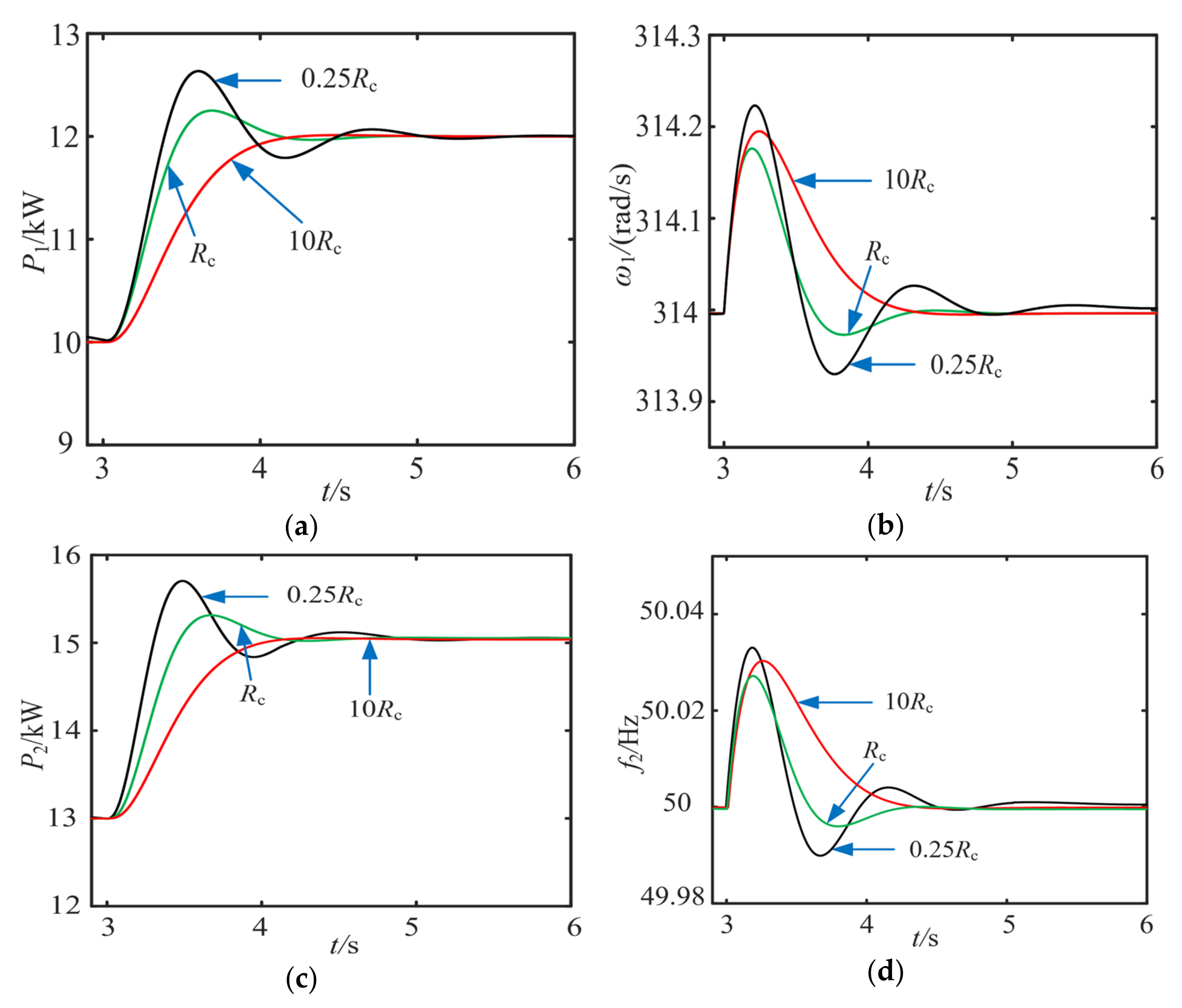
6.2. Simulation of Multi-VSG Grid-Connected System
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Du, W.J.; Fu, Q.; Wang, H.F. Damping torque analysis of DC voltage stability of an MTDC network for the wind power delivery. IEEE Trans. Power Deliv. 2020, 35, 324–338. [Google Scholar] [CrossRef]
- Liu, C.L.; Li, D.Z.; Wang, L.C.; Li, L.; Wang, K. Strong robustness and high accuracy remaining useful life prediction on supercapacitors. APL Mater. 2022, 10, 061106. [Google Scholar] [CrossRef]
- Yi, Z.X.; Zhao, K.; Sun, J.R.; Wang, L.; Wang, K.; Ma, Y. Prediction of the remaining useful life of supercapacitors. J. Power Sources 2022, 2022, 7620382. [Google Scholar] [CrossRef]
- Li, D.Z.; Li, S.; Zhang, S.; Sun, J.; Wang, L.; Wang, K. Aging state prediction for supercapacitors based on heuristic kalman filter optimization extreme learning machine. Energy 2022, 250, 123773. [Google Scholar] [CrossRef]
- Zarifakis, M.; Coffey, W.T.; Kalmykov, Y.P. Active damping of power oscillations following frequency changes in low inertia power systems. IEEE Trans. Power Syst. 2019, 34, 4984–4992. [Google Scholar] [CrossRef]
- Wu, W.H.; Chen, Y.D.; Zhou, L.M.; Luo, A.; Zhou, X.P.; He, Z.X.; Yang, L.; Xie, Z.W.; Liu, J.M.; Zhang, M.M. Sequence impedance modeling and stability comparative analysis of voltage-controlled VSGs and current-controlled VSGs. IEEE Trans. Ind. Electron. 2019, 66, 6460–6472. [Google Scholar] [CrossRef]
- Khajehoddin, S.A.; Karimi-Ghartemani, M.; Ebrahimi, M. Grid-supporting inverters with improved dynamics. IEEE Trans. Ind. Electron. 2019, 65, 3655–3667. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Bevrani, H.; Ise, T. Enhanced virtual synchronous generator control for parallel inverters in microgrids. IEEE Trans. Smart Grid 2017, 8, 2268–2277. [Google Scholar] [CrossRef]
- Xu, Y.; Nian, H.; Hu, B. Impedance modeling and stability analysis of VSG controlled type-IV wind turbine system. IEEE Trans. Energy Convers. 2021, 36, 3438–3448. [Google Scholar] [CrossRef]
- Baruwa, M.; Fazeli, M. Impact of virtual synchronous machines on low-frequency oscillations in power systems. IEEE Trans. Power Syst. 2021, 36, 1934–1946. [Google Scholar] [CrossRef]
- Shuai, Z.K.; Shen, C.; Liu, X.; Li, Z.; Shen, Z.J. Transient angle stability of virtual synchronous generators using lyapunov’s direct method. IEEE Trans. Smart Grid 2019, 10, 4648–4661. [Google Scholar] [CrossRef]
- Xiong, X.L.; Wu, C.; Blaabjerg, F. Effects of virtual resistance on transient stability of virtual synchronous generators under grid voltage sag. IEEE Trans. Ind. Electron. 2022, 69, 4754–4764. [Google Scholar] [CrossRef]
- Liu, H.; Sun, D.W.; Song, P.; Cheng, X.; Zhao, F.; Tian, Y. Influence of virtual synchronous generators on low frequency oscillations. CSEE J. Power Energy Syst. 2022, 8, 1029–1038. [Google Scholar]
- Wang, G.Y.; Fu, L.J.; Hu, Q.; Ma, F.; Liu, C.; Lin, Y. Low frequency oscillation analysis of VSG grid-connected system. In Proceedings of the 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 26–29 March 2021; pp. 631–637. [Google Scholar]
- Qin, B.S.; Xu, Y.H.; Yuan, C.; Jia, J. A unified method of frequency oscillation characteristic analysis for multi-VSG grid-connected system. IEEE Trans. Power Deliv. 2022, 37, 279–289. [Google Scholar] [CrossRef]
- Alipoor, J.; Miura, Y.; Ise, T. Stability assessment and optimization methods for microgrid with multiple VSG units. IEEE Trans. Smart Grid 2018, 9, 1462–1471. [Google Scholar] [CrossRef]
- Choopani, M.; Hosseinian, S.H.; Vahidi, B. New transient stability and LVRT improvement of multi-VSG grids using the frequency of the center of inertia. IEEE Trans. Power Syst. 2020, 35, 527–538. [Google Scholar] [CrossRef]
- Fu, S.Q.; Sun, Y.; Li, L.; Liu, Z.; Han, H.; Su, M. Power oscillation suppression of multi-VSG grid via decentralized mutual damping control. IEEE Trans. Ind. Electron. 2022, 69, 10202–10214. [Google Scholar] [CrossRef]
- Shi, M.X.; Chen, X.; Zhou, J.Y.; Chen, Y.; Wen, J.Y.; He, H. Frequency restoration and oscillation damping of distributed VSGs in microgrid with low bandwidth communication. IEEE Trans. Smart Grid 2021, 12, 1011–1021. [Google Scholar] [CrossRef]
- Hu, Y.; Bu, S.Q.; Zhang, X.; Chung, C.Y.; Cai, H. Connection between damping torque analysis and energy flow analysis in damping performance evaluation for electromechanical oscillations in power systems. J. Mod. Power Syst. Clean Energy 2022, 10, 19–28. [Google Scholar] [CrossRef]





| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rf/Ω | 0.2 | Lc/mH | 1.8 |
| Lf/mH | 3.2 | Pref/kW | 10 |
| Cf/μF | 100 | Qref/var | 0 |
| Rc/Ω | 0.1 | J/kg·m2 | 10 |
| D/N·m·s·rad−1 | 70 | Kd | 30 |
| Kq | 0.0005 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Id/A | 21.27 | Iod/A | 1.8 |
| Iq/A | 11.66 | Ioq/A | 10 |
| Uod/V | 311.3 | ω0/rad·s−1 | 314.2 |
| Uoq/V | 4.401 |
| Eigenvalue | Real Part | Imaginary Part | Oscillation Frequency/Hz | Damping Ratio | Dominant Related State Variables |
|---|---|---|---|---|---|
| λ1–2 | −3.15 | ±6.89 | 1.09 | 0.42 | id, iq, xud, xuq |
| λ3–4 | −30.21 | ±22.38 | 3.56 | 0.80 | id, iq, xid, xiq |
| λ5–6 | −6.84 | ±39.03 | 6.21 | 0.17 | ω, δg, |
| λ7–8 | −418.3 | ±349.98 | 55.73 | 0.77 | iod, ioq |
| λ9–10 | −217.04 | ±4797.2 | 763.89 | 0.045 | id, iq, uod, uoq |
| λ11–12 | −1000 | ±5525.8 | 879.90 | 0.18 | id, iq, uod, uoq |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rf1,2/Ω | 0.2 | Pref1/kW | 10 |
| Lf1,2/mH | 3.2 | J1,2 | 10 |
| Cf1,2/μF | 100 | D1,2 | 70 |
| Rc1,2/Ω | 0.1 | Kd1,2 | 30 |
| Lc1,2/mH | 1.8 | Kq1,2 | 0.0005 |
| Pref2/kW | 13 | Kpv | 2 |
| Kiv | 50 | Kpc | 7 |
| Kic | 75 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Id1/A | 21.24 | Id2/A | 27.64 |
| Uod1/V | 311.70 | Uod2/V | 311.90 |
| Iod1/A | 21.38 | Iod2/A | 27.78 |
| Iq1/A | 13.36 | Iq2/A | 14.05 |
| Uoq1/V | 4.41 | Uoq2/V | 4.41 |
| Ioq1/A | 3.43 | Ioq2/A | 4.12 |
| Eigenvalue | Real Part | Imaginary Part | Oscillation Frequency/Hz | Damping Ratio | Dominant Related State Variables |
|---|---|---|---|---|---|
| λ1–2 | −55129.01 | ±319.24 | 50.03 | 0.99 | iodq1, iodq2 |
| λ3–4 | −1268.41 | ±4247.55 | 676.36 | 0.29 | uodq1, uodq2, idq1, idq2 |
| λ5–6 | −937.89 | ±1537.41 | 244.81 | 0.52 | uodq1, uodq2, iodq1, iodq2 |
| λ7–8 | −41.48 | ±848.78 | 135.16 | 0.05 | uodq1, uodq2, iodq1, iodq2 |
| λ9–10 | −33.72 | ±3247.69 | 517.15 | 0.01 | uodq1, uodq2, idq1, idq2 |
| λ11–12 | −29.00 | ±2340.81 | 372.74 | 0.02 | uodq1, uodq2, idq1, idq2 |
| λ13–14 | −122.46 | ±542.93 | 86.45 | 0.22 | iodq1, iodq2 |
| λ15–16 | −69.26 | ±331.68 | 52.81 | 0.21 | iodq1, iodq2, idq1 |
| λ17–18 | −60.38 | ±336.65 | 53.6 | 0.18 | iodq1, iodq2, idq2 |
| λ19–20 | −4.03 | ±1.12 | 0.18 | 0.96 | ω1, ω2 |
| λ21–22 | −3.2 | ±3.17 | 0.50 | 0.71 | θ2, ω1, ω2, δg |
| λ23–24 | −4.39 | ±2.17 | 0.35 | 0.89 | θ2, ω1, ω2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, S.; Zhu, Y.; Dong, L.; Na, G.; Hao, Y.; Zhang, G.; Zhang, W.; Cheng, S.; Yang, J.; Sui, Y. Small-Signal Stability Research of Grid-Connected Virtual Synchronous Generators. Energies 2022, 15, 7158. https://doi.org/10.3390/en15197158
Lu S, Zhu Y, Dong L, Na G, Hao Y, Zhang G, Zhang W, Cheng S, Yang J, Sui Y. Small-Signal Stability Research of Grid-Connected Virtual Synchronous Generators. Energies. 2022; 15(19):7158. https://doi.org/10.3390/en15197158
Chicago/Turabian StyleLu, Shengyang, Yu Zhu, Lihu Dong, Guangyu Na, Yan Hao, Guanfeng Zhang, Wuyang Zhang, Shanshan Cheng, Junyou Yang, and Yuqiu Sui. 2022. "Small-Signal Stability Research of Grid-Connected Virtual Synchronous Generators" Energies 15, no. 19: 7158. https://doi.org/10.3390/en15197158
APA StyleLu, S., Zhu, Y., Dong, L., Na, G., Hao, Y., Zhang, G., Zhang, W., Cheng, S., Yang, J., & Sui, Y. (2022). Small-Signal Stability Research of Grid-Connected Virtual Synchronous Generators. Energies, 15(19), 7158. https://doi.org/10.3390/en15197158





