Multi-Step Ahead Natural Gas Consumption Forecasting Based on a Hybrid Model: Case Studies in The Netherlands and the United Kingdom
Abstract
:1. Introduction
1.1. Background
1.2. Related Work
2. XGBoost and Its Nonlinear Auto-Regressive Formulation
2.1. Extreme Gradient Boosting
2.2. Data Division Method and Forecasting Method
3. The Overall Computational Steps
3.1. Structure of the Optimization Problem
3.2. Salp Swarm Algorithm
3.2.1. Leaders’ Position Update
3.2.2. Folsmallers’ Position Update
3.3. Hyperparameter Optimization of XGBoost by SSA
4. Application
4.1. Experimental Settings
4.2. Information of the Medels and Algorithms for Comparison
- Random Forest (RF). Two American statisticians, Leo Breiman and Adele Culter, first proposed RF in 2001. It is an ensemble learning algorithm that combines classification and regression trees [52]. The RF algorithm mainly consists of the following three steps: (a) First, through the method of simple random sampling with replacement, n samples are randomly selected from the sample set; (b) Arbitrarily choose k features from all features, and use these features and the samples from to build a decision tree; (c) Repeat the above steps continuously until multiple decision trees are generated to form a RF.
- Light Gradient Boosting Machine (LightGBM). LightGBM is a distributed gradient boosting framework based on the decision tree algorithm [53]. Its essence is an integrated learning algorithm that promotes weak learners to strong learners. Specifically, it combines many tree models with smaller accuracy. In each iteration, the loss function is made smaller and smaller by moving to the negative gradient direction of the loss function, and finally, a better tree is obtained. Compared with the traditional GBDT model, LightGBM has several very prominent advantages: smaller memory consumption, faster training speed, higher accuracy, and fast processing of massive data.
- Particle swarm optimization (PSO). Particle swarm optimization is a swarm intelligence algorithm designed to simulate the predation behavior of birds. It was first proposed by American scientists Eberhart and Kennedy [39] in 1995. Particle swarm optimization mimics the behavior of groups of insects, birds, fish, etc., which cooperatively search for food. Each group member continually changes its search patterns by learning from their own and other members’ experiences.
- Grey wolf optimization (GWO). The GWO is an algorithm with a simple structure small number of parameters and is easy to implement. Since it was first proposed by Mirjalili et al. in 2014 [43], it has been rapidly and widely used in parameter optimization and image classification. Since the algorithm is inspired by the predation behavior of the grey wolf, it is named the grey wolf optimization algorithm.
- Harris hawk optimization (HHO). HHO is an intelligent optimization algorithm simulating the predation behavior of the Harris Eagle, which was proposed by Heidari et al. in 2019 [46]. The HHO algorithm comprises three stages: search, search and development conversion, and development. The algorithm has excellent global search ability and requires the adjustment of few parameters.
- Multi-Verse Optimizer (MVO), The MVO algorithm is inspired by the motion behavior of multiverse populations under the combined action of white holes, black holes, and wormholes. Seyedali Mirjalili first proposed the algorithm in 2016 [48]. In the MVO algorithm, the main performance parameters are the wormhole existence probability and the wormhole travel distance rate. The parameters are relatively few, and the low-dimensional numerical experiments show fairly excellent performance.
- Whale optimization algorithm (WOA). Mirjalili, a researcher at Griffith University in Australia, proposed a novel swarm intelligence optimization algorithm called Whale optimization algorithm in 2016 [50]. The algorithm is a novel swarm optimization algorithm imitating the hunting behavior of humpback whales. Its advantages are simple operation, few parameters, and the fact it does not easy fall into local optimum.
4.3. Data Description
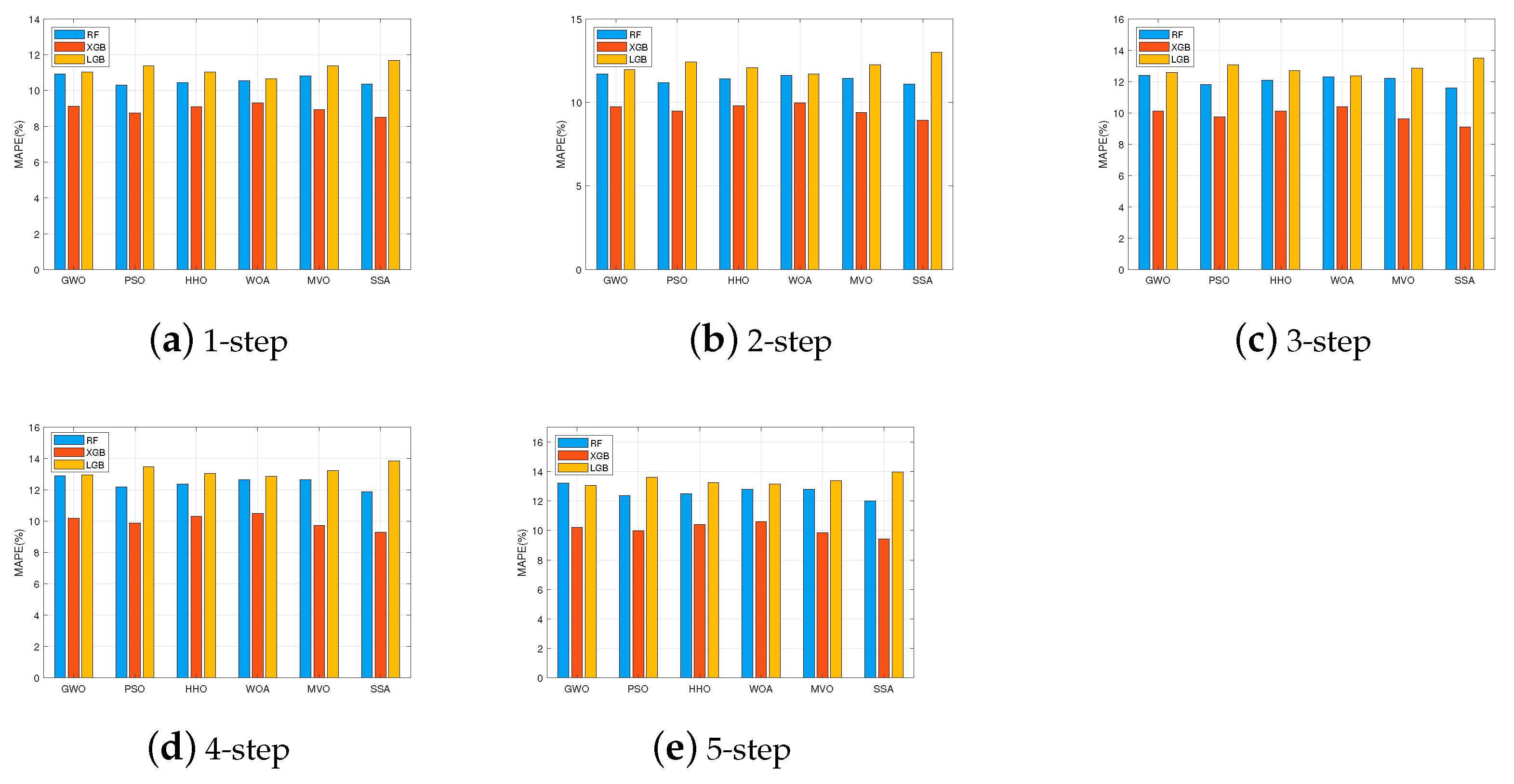
4.4. Forecasting Results
4.5. Discussions
4.5.1. Boosting Effect of the Same Algorithm for Different Models
4.5.2. Optimization Effect of Different Algorithms on XGBoost
4.5.3. Sensitive Analysis of Time Lags and Forecasting Steps of the Proposed Method
4.5.4. The Effect of Different Time Scales on the Forecasting Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network | MLP | Multilayer perceptron |
| ARMA | Autoregressive moving average model | MLR | Multiple linear regression |
| CFNHGBM(1,1,k) | The consistent fractional nonhomogeneous grey Bernoulli model | MVO | Multi-verse optimizer |
| CG | Conjugate gradient algorithm | MVO-LGB | LGB optimized by MVO |
| CMARS | Conic multivariate adaptive regression spline | MVO-RF | RF optimized by MVO |
| DFGM(1,1,) | Discrete fractional grey models with time power terms | MVO-XGBoost | XGBoost optimized by MVO |
| DGMNF(1,1) | A novel discrete grey model considering nonlinearity and fluctuation | NN | Neural network |
| EIA | Energy Information Administration | NG | Natural gas |
| FM-MLP | Forecasting monitoring multi-layered perceptron | NGC | Natural gas consumption |
| FPDGM(1,1) | Fractional accumulation polynomial discrete grey prediction model | PCA | Principal component analysis |
| GBDT | Gradient Boosting Decision Tree | PFSM(1,1) | Fractional cumulative inhomogeneous discrete grey seasonal model for PSO optimization |
| GB | gradient boosting | PSO | Particle swarm optimization |
| GB-PCA | A block-wise gradient boosting model using features from PCA | PSO-LGB | LightGBM optimized by PSO |
| GDP | Gross domestic product | PSO-RF | RF optimized by PSO |
| GPRM | A grey prediction with rolling mechanism | PSO-XGBoost | XGBoost optimized by PSO |
| GRA | grey-related analysis | RF | Random Forest |
| GRA-LSSVM | Least squares support vector machine model based on grey relational analysis | SecPSO | The second-order particle swarm |
| GWO | grey wolf optimization | SSA | Salp swarm algorithm |
| GWO-LGB | LightGBM optimized by GWO | SSA-LGB | LightGBM optimized by SSA |
| GWO-RF | RF optimized by GWO | SSA-RF | RF optimized by SSA |
| GWO-XGBoost | XGBoost optimized by GWO | SSA-XGBoost | XGBoost optimized by SSA |
| HHO | Harris hawks optimization | SVM | Support vector machine model |
| HHO-LGB | LightGBM optimized by HHO | Support vector regression model | |
| HHO-RF | RF optimized by HHO | TDPGM(1,1) | A novel time-delayed polynomial grey prediction model |
| HHO-XGBoost | XGBoost optimized by HHO | UK | United Kingdom |
| ISSA | Improved singular spectrum analysis | U.S. | United States |
| ISSA-LSTM | Combining ISSA with LSTM, a novel hybrid model. | WASecPSO | Weighted adaptive second-order PSO algorithm |
| LightGBM | Light gradient boosting machine | WOA | The whale optimization algorithm |
| LMD | A combinatorial model with local mean decomposition | WOA-LGB | LGB optimized by WOA |
| LR | Linear regression | WOA-RF | RF optimized by WOA |
| LSSVM | Least squares support vector machine | WOA-XGBoost | XGBoost optimized by WOA |
| LSTM | Long short-term memory | WTD | Wavelet threshold denoising |
| MAPE | Mean absolute percentage error | XGBoost | Extreme gradient boosting |
References
- Fuller, R.; Landrigan, P.J.; Balakrishnan, K.; Bathan, G.; Bose-O’Reilly, S.; Brauer, M.; Caravanos, J.; Chiles, T.; Cohen, A.; Corra, L.; et al. Pollution and health: A progress update. Lancet Planet. Health 2022, 6, e535–e547. [Google Scholar] [CrossRef]
- Liu, L.Q.; Liu, C.X.; Wang, J.S. Deliberating on renewable and sustainable energy policies in china. Renew. Sustain. Energy Rev. 2013, 17, 191–198. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, H.; Zhou, Q.; Wu, J.; Qin, S. Chinas natural gas production and consumption analysis based on the multicycle hubbert model and rolling grey model. Renew. Sustain. Energy Rev. 2016, 53, 1149–1167. [Google Scholar] [CrossRef]
- Karanam, V. The Need to Enact Federal, Environmental-Friendly Incentives to Facilitate Infrastructure Growth of Electric Automobiles. Bachelor’s Thesis, College of Community Innovation and Education, Orlando, FL, USA, 2022. [Google Scholar]
- Vivoda, V. LNG export diversification and demand security: A comparative study of major exporters. Energy Policy 2022, 170, 113218. [Google Scholar] [CrossRef]
- Beauchampet, I.; Walsh, B. Energy citizenship in the netherlands: The complexities of public engagement in a large-scale energy transition. Energy Res. Soc. Sci. 2021, 76, 102056. [Google Scholar] [CrossRef]
- Di Bella, G.; Flanagan, M.J.; Foda, K.; Maslova, S.; Pienkowski, A.; Stuermer, M.; Toscani, F.G. Natural Gas in Europe: The Potential Impact of Disruptions to Supply. IMF Work. Pap. 2022, 2022, 145. [Google Scholar] [CrossRef]
- Liu, C.; Wu, W.; Xie, W.; Zhang, T.; Zhang, J. Forecasting natural gas consumption of china by using a novel fractional grey model with time power term. Energy Rep. 2021, 7, 788–797. [Google Scholar] [CrossRef]
- Boran, F.E. Forecasting natural gas consumption in turkey using grey prediction. Energy Sources Part B Econ. Plan. Policy 2015, 10, 208–213. [Google Scholar] [CrossRef]
- Ma, X.; Liu, Z. Application of a novel time-delayed polynomial grey model to predict the natural gas consumption in China. J. Comput. Appl. Math. 2017, 324, 17–24. [Google Scholar] [CrossRef]
- Xiong, P.; Li, K.; Shu, H.; Wang, J. Forecast of natural gas consumption in the asia-pacific region using a fractional-order incomplete gamma grey model. Energy 2021, 237, 121533. [Google Scholar] [CrossRef]
- Ma, X.; Mei, X.; Wu, W.; Wu, X.; Zeng, B. A novel fractional time delayed grey model with grey wolf optimizer and its applications in forecasting the natural gas and coal consumption in chongqing china. Energy 2019, 178, 487–507. [Google Scholar] [CrossRef]
- Li, N.; Wang, J.; Wu, L.; Bentley, Y. Predicting monthly natural gas production in china using a novel grey seasonal model with particle swarm optimization. Energy 2021, 215, 119118. [Google Scholar] [CrossRef]
- Zhang, J.; Qin, Y.; Duo, H. The development trend of chinas natural gas consumption: A forecasting viewpoint based on grey forecasting model. Energy Rep. 2021, 7, 4308–4324. [Google Scholar] [CrossRef]
- Zhou, W.; Wu, X.; Ding, S.; Pan, J. Application of a novel discrete grey model for forecasting natural gas consumption: A case study of jiangsu province in china. Energy 2020, 200, 117443. [Google Scholar] [CrossRef]
- Zheng, C.; Wu, W.; Xie, W.; Li, Q. A mfo-based conformable fractional nonhomogeneous grey bernoulli model for natural gas production and consumption forecasting. Appl. Soft Comput. 2021, 99, 106891. [Google Scholar] [CrossRef]
- Ding, S. A novel self-adapting intelligent grey model for forecasting china’s natural-gas demand. Energy 2018, 162, 393–407. [Google Scholar] [CrossRef]
- Sharma, V.; Cali, Ü.; Sardana, B.; Kuzlu, M.; Banga, D.; Pipattanasomporn, M. Data-driven short term natural gas demand forecasting with machine learning techniques. J. Pet. Sci. Eng. 2021, 206, 108979. [Google Scholar] [CrossRef]
- Rodger, J.A. A fuzzy nearest neighbor neural network statistical model for predicting demand for natural gas and energy cost savings in public buildings. Expert Syst. Appl. 2014, 41, 1813–1829. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Y.; Wu, Z.; Fu, H.; Shi, Y.; Guo, H. Scenario analysis of natural gas consumption in china based on wavelet neural network optimized by particle swarm optimization algorithm. Energies 2018, 11, 825. [Google Scholar] [CrossRef] [Green Version]
- Beyca, O.F.; Ervural, B.C.; Tatoglu, E.; Ozuyar, P.G.; Zaim, S. Using machine learning tools for forecasting natural gas consumption in the province of istanbul. Energy Econ. 2019, 80, 937–949. [Google Scholar] [CrossRef]
- Wu, Y.-H.; Shen, H. Grey-related least squares support vector machine optimization model and its application in predicting natural gas consumption demand. J. Comput. Appl. Math. 2018, 338, 212–220. [Google Scholar] [CrossRef]
- Qiao, W.; Liu, W.; Liu, E. A combination model based on wavelet transform for predicting the difference between monthly natural gas production and consumption of us. Energy 2021, 235, 121216. [Google Scholar] [CrossRef]
- Laib, O.; Khadir, M.T.; Mihaylova, L. Toward efficient energy systems based on natural gas consumption prediction with lstm recurrent neural networks. Energy 2019, 177, 530–542. [Google Scholar] [CrossRef]
- Peng, S.; Chen, R.; Yu, B.; Xiang, M.; Lin, X.; Liu, E. Daily natural gas load forecasting based on the combination of long short term memory, local mean decomposition, and wavelet threshold denoising algorithm. J. Nat. Gas Sci. Eng. 2021, 95, 104175. [Google Scholar] [CrossRef]
- Wei, N.; Li, C.; Peng, X.; Li, Y.; Zeng, F. Daily natural gas consumption forecasting via the application of a novel hybrid model. Appl. Energy 2019, 250, 358–368. [Google Scholar] [CrossRef]
- Ervural, B.C.; Beyca, O.F.; Zaim, S. Model estimation of arma using genetic algorithms: A case study of forecasting natural gas consumption. Procedia-Soc. Behav. Sci. 2016, 235, 537–545. [Google Scholar] [CrossRef]
- Duan, H.; Tang, X.; Ren, K.; Ding, Y. Medium-and long-term development path of natural gas consumption in china: Based on a multi-model comparison framework. Nat. Gas Ind. B 2021, 8, 344–352. [Google Scholar] [CrossRef]
- Özmen, A.; Yılmaz, Y.; Weber, G. Natural gas consumption forecast with mars and cmars models for residential users. Energy Econ. 2018, 70, 357–381. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Xiang, X.; Ma, X.; Ma, M.; Wu, W.; Yu, L. Research and application of novel euler polynomial-driven grey model for short-term pm10 forecasting. Grey Syst. Theory Appl. 2020, 11. [Google Scholar] [CrossRef]
- Cheng, H.; Tan, P.; Gao, J.; Scripps, J. Multistep-ahead time series prediction. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Berlin/Heidelberg, Germany, 2006; pp. 765–774. [Google Scholar]
- Song, Y.; Li, H.; Xu, P.; Liu, D. A method of intrusion detection based on woa-xgboost algorithm. Discret. Dyn. Nat. Soc. 2022, 2022, 5245622. [Google Scholar] [CrossRef]
- Abbasi, A.; Firouzi, B.; Sendur, P. On the application of harris hawks optimization (hho) algorithm to the design of microchannel heat sinks. Eng. Comput. 2021, 37, 1409–1428. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Andersen, V.; Nival, P. A model of the population dynamics of salps in coastal waters of the ligurian sea. J. Plankton Res. 1986, 8, 1091–1110. [Google Scholar] [CrossRef]
- Zhou, J.; Dai, Y.; Huang, S.; Armaghani, D.J.; Qiu, Y. Proposing several hybrid SSA—Machine learning techniques for estimating rock cuttability by conical pick with relieved cutting modes. Acta Geotech. 2022, 1–16. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Citeseer: University Park, PA, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Fang, J.; Wang, H.; Yang, F.; Yin, K.; Lin, X.; Zhang, M. A failure prediction method of power distribution network based on PSO and XGBoost. Aust. J. Electr. Electron. Eng. 2022, 1–8. [Google Scholar] [CrossRef]
- Grichi, Y.; Dao, T.-M.; Beauregard, Y. A new approach for optimal obsolescence forecasting based on the random forest (rf) technique and meta-heuristic particle swarm optimization (pso). In Proceedings of the International Conference on Industrial Engineering and Operations Management, Paris, France, 26–27 July 2018. [Google Scholar]
- Liu, J.; Yang, D.; Lian, M.; Li, M. Research on intrusion detection based on particle swarm optimization in iot. IEEE Access 2021, 9, 38254–38268. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Duan, Y.; Mao, Y.; Guo, Y.; Wang, X.; Gao, S. COVID-19 Propagation Prediction Model Using Improved Grey Wolf Optimization Algorithms in Combination with XGBoost and Bagging-Integrated Learning. Math. Probl. Eng. 2022, 2022, 1314459. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, L.; Wu, Y. Research on transformer fault diagnosis based on gwo-rf algorithm. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 1952, p. 032054. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Yang, F.; Guo, X. Research on rehabilitation effect prediction for patients with SCI based on machine learning. World Neurosurg. 2022, 158, e662–e674. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, S.; Qiu, Y. Optimization of random forest through the use of MVO, GWO and MFO in evaluating the stability of underground entry-type excavations. Tunn. Undergr. Space Technol. 2022, 124, 104494. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Liu, D.; Fan, Z.; Fu, Q.; Li, M.; Faiz, M.A.; Ali, S.; Li, T.; Zhang, L.; Khan, M.I. Random forest regression evaluation model of regional flood disaster resilience based on the whale optimization algorithm. J. Clean. Prod. 2020, 250, 119468. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T. Lightgbm: A highly efficient gradient boosting decision tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]





















| Model Type | Reference | Model | Conclusions |
|---|---|---|---|
| grey model | [8] | DFGM(1,1,) | It is expected that China’s NGC will maintain an upward trend, reaching 439.14 billion cubic meters in 2025. |
| [9] | GPRM | GPRM method has high forecasting accuracy and applicability in the presence of limited data. | |
| [10] | TDPGM(1,1) | The annual NGC will exceed 5000 ( m) by 2020. | |
| [11] | A fractional-order incomplete gamma grey model | The model has excellent predictive performance in predicting NGC and can be generalized to more energy forecasting problems. | |
| [12] | Fractional time delayed grey model optimized by GWO | Compared with some traditional grey models, the new model has better forecasting performance and generalization. | |
| [13] | PFSM(1,1) | This model is suitable for data with significant seasonal variation. | |
| [14] | FPDGM(1,1) | The novel model has better predictive performance than the other models in all cases. | |
| [15] | DGMNF(1,1) | The forecasting results obtained by the new model are more accurate and reliable than other models, and the forecasting error is smaller. | |
| [16] | CFNHGBM(1,1,k) | The novel model outperforms other competitors. | |
| [17] | A novel self-adapting intelligent grey model | By 2020, China’s NG demand will exceed 340 billion m. | |
| Machine learning model | [18] | GB, GB-PCA, ANN-CG-PCA | The forecasting accuracy of the combined model is better than that of the individual models, and the MAPE of the combined model is about 15% smaller than that of the individual models. |
| [19] | ANN | The system can be used to monitor the necessary gas flow and predict demand changes due to internal and external temperature, which can effectively reduce costs. | |
| [20] | |||
| [21] | MLR, SVR, ANN | The forecasting performance of SVR is much better than that of ANN, and it has a smaller forecasting error in NGC forecasting, and can provide more reliable and accurate results. | |
| [22] | GRA-LSSVM | The proposed model has a better generalization ability, and compared with the PSO algorithm and the SecPSO algorithm, the GRA-LSSVM model optimized by WASecPSO has higher forecasting accuracy. | |
| Deep learning model | [23] | A hybrid model based on wavelet transform | Wavelet transform can effectively improve the forecasting accuracy of the model, and the forecasting accuracy of the hybrid model exceeds that of other AI models. |
| [24] | MLP, LSTM | A two-stage FM-MLP method is proposed. | |
| [25] | LMD-WTD-LSTM | When the forecasting time length is 20 days, this method has the best forecasting performance among the five methods, and its MAPE is 11.63%. | |
| [26] | ISSA-LSTM | ISSA-LSTM is the best performing model among all the forecasting models. In its forecasts in the four cities of London, Melbourne, Karditsa, and Hong Kong, the obtained MAPE values are 4.68%, 5.72%, 5.76%, and 14.10%, respectively. | |
| Time series | [27] | An integrated genetic-ARMA approach | The proposed hybrid model has more stable forecasting performance, outperforming the classic ARMA model in terms of MAPE. |
| Other model | [28] | Integrated assessment models | China’s total primary energy consumption in 2060 will be smaller than in 2019 and NGC will account for approximately 6% of China’s total primary energy consumption in 2060 |
| [29] | MARS, CMARS | MARS and CMRS outperform NN and LR in all evaluation metrics. |
| Algorithm | Model | Hybrid Mode |
|---|---|---|
| SSA [36] | XGBoost | SSA-XGBoost |
| Random Forest | SSA-RF [38] | |
| LightGBM (LGB) | SSA-LGB | |
| PSO [39] | XGBoost | PSO-XGBoost [40] |
| Random Forest | PSO-RF [41] | |
| LightGBM | PSO-LGB [42] | |
| GWO [43] | XGBoost | GWO-XGBoost [44] |
| Random Forest | GWO-RF [45] | |
| LightGBM | GWO-LGB | |
| HHO [46] | XGBoost | HHO-XGBoost |
| Random Forest | HHO-RF [47] | |
| LightGBM | HHO-LGB | |
| MVO [48] | XGBoost | MVO-XGBoost |
| Random Forest | MVO-RF [49] | |
| LightGBM | MVO-LGB | |
| WOA [50] | XGBoost | WOA-XGBoost [34] |
| Random Forest | WOA-RF [51] | |
| LightGBM | WOA-LGB |
| Metrics | Equation | Remark |
|---|---|---|
| MAPE | The smaller, the better | |
| RMSE | The smaller, the better |
| Dataset | Interval | Mean | Maximum | Minimum | Standard Deviation | Numbers | Units |
|---|---|---|---|---|---|---|---|
| NGC (UK) | Quarterly | 146,035.137 | 257,790.410 | 51,914.490 | 63,678.848 | 93 | Gigawatt–hour |
| NGC (Netherlands) | Monthly | 3682.230 | 7079.000 | 1696.000 | 1223.898 | 472 | million m |
| Indices | XGBoost | Random Forest | LightGBM | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-Step | 2-Step | 3-Step | 4-Step | 5-Step | 1-Step | 2-Step | 3-Step | 4-Step | 5-Step | 1-Step | 2-Step | 3-Step | 4-Step | 5-Step | ||||
| SSA | 14.124 | 4.428 | 4.453 | 4.304 | 4.298 | 9.726 | 9.750 | 10.757 | 11.476 | 11.894 | 6.389 | 6.184 | 6.280 | 5.723 | 5.492 | |||
| PSO | 5.355 | 5.414 | 5.081 | 4.809 | 4.592 | 7.529 | 7.368 | 6.727 | 6.343 | 5.988 | 7.551 | 7.453 | 7.687 | 7.263 | 7.263 | |||
| GWO | 6.102 | 6.310 | 6.699 | 6.886 | 6.728 | 6.032 | 7.698 | 9.089 | 9.380 | 10.071 | 7.196 | 7.050 | 7.117 | 6.510 | 6.517 | |||
| WOA | 6.740 | 6.479 | 6.175 | 5.508 | 5.349 | 9.573 | 11.518 | 13.638 | 15.049 | 15.191 | 6.980 | 6.925 | 7.351 | 7.038 | 7.042 | |||
| HHO | 5.907 | 6.114 | 5.857 | 5.497 | 5.290 | 8.867 | 9.703 | 10.497 | 10.602 | 10.879 | 6.902 | 6.734 | 6.864 | 6.324 | 6.124 | |||
| MVO | 5.673 | 5.645 | 5.528 | 5.401 | 5.362 | 9.096 | 9.604 | 9.485 | 10.001 | 10.460 | 7.201 | 7.053 | 7.120 | 6.511 | 6.512 | |||
| SSA | 5.839 | 5.809 | 5.791 | 5.515 | 5.300 | 7.020 | 6.528 | 6.329 | 6.102 | 5.855 | 9.749 | 10.273 | 10.415 | 10.119 | 9.977 | |||
| PSO | 5.798 | 6.106 | 6.831 | 7.355 | 7.619 | 8.428 | 8.668 | 9.324 | 9.497 | 9.666 | 9.960 | 10.472 | 10.643 | 10.335 | 10.204 | |||
| GWO | 6.380 | 6.591 | 7.250 | 7.474 | 7.787 | 12.457 | 13.163 | 13.652 | 13.694 | 13.847 | 9.767 | 10.292 | 10.437 | 10.141 | 9.999 | |||
| WOA | 7.397 | 7.630 | 7.764 | 7.698 | 7.618 | 9.424 | 9.632 | 9.754 | 9.283 | 8.961 | 7.995 | 8.751 | 8.960 | 8.612 | 8.566 | |||
| HHO | 6.087 | 6.168 | 6.251 | 6.264 | 6.215 | 10.011 | 9.695 | 9.867 | 9.594 | 9.729 | 9.729 | 10.236 | 10.327 | 10.009 | 9.864 | |||
| MVO | 6.928 | 7.117 | 6.920 | 6.616 | 6.442 | 8.378 | 8.486 | 8.599 | 8.705 | 8.908 | 9.755 | 10.279 | 10.422 | 10.126 | 9.984 | |||
| SSA | 4.490 | 4.734 | 5.182 | 5.287 | 5.188 | 8.009 | 7.755 | 7.767 | 7.489 | 7.328 | 15.684 | 15.966 | 16.248 | 16.315 | 16.657 | |||
| PSO | 7.150 | 6.938 | 7.366 | 7.666 | 7.835 | 7.147 | 7.212 | 7.493 | 7.421 | 7.458 | 15.684 | 15.966 | 16.248 | 16.315 | 16.657 | |||
| GWO | 6.736 | 6.724 | 6.877 | 7.152 | 7.375 | 7.390 | 7.798 | 7.936 | 7.585 | 7.418 | 15.681 | 15.964 | 16.246 | 16.311 | 16.652 | |||
| WOA | 6.731 | 6.477 | 6.594 | 6.577 | 6.786 | 6.888 | 6.947 | 7.848 | 7.977 | 8.152 | 15.684 | 15.966 | 16.248 | 16.315 | 16.657 | |||
| HHO | 6.072 | 6.542 | 6.780 | 6.864 | 7.070 | 10.649 | 10.477 | 10.847 | 10.481 | 10.456 | 15.518 | 15.872 | 16.118 | 15.987 | 16.172 | |||
| MVO | 5.490 | 5.606 | 5.852 | 5.929 | 5.981 | 8.045 | 8.043 | 8.045 | 8.070 | 7.783 | 15.650 | 16.043 | 16.337 | 16.314 | 16.564 | |||
| Indices | XGBoost | Random Forest | LightGBM | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-Step | 2-Step | 3-Step | 4-Step | 5-Step | 1-Step | 2-Step | 3-Step | 4-Step | 5-Step | 1-Step | 2-Step | 3-Step | 4-Step | 5-Step | ||||
| SSA | 8.889 | 9.528 | 9.966 | 10.445 | 10.693 | 11.290 | 12.557 | 13.414 | 13.894 | 14.003 | 13.605 | 15.782 | 16.697 | 17.521 | 17.880 | |||
| PSO | 9.483 | 10.247 | 10.595 | 10.765 | 10.980 | 10.990 | 12.239 | 13.229 | 13.821 | 14.100 | 12.733 | 14.154 | 15.291 | 16.136 | 16.519 | |||
| GWO | 10.052 | 10.974 | 11.619 | 11.898 | 12.050 | 11.227 | 12.319 | 13.568 | 14.737 | 15.569 | 12.820 | 14.294 | 15.519 | 16.395 | 16.848 | |||
| WOA | 10.157 | 11.057 | 11.559 | 11.713 | 11.945 | 11.526 | 12.984 | 14.076 | 14.639 | 14.852 | 11.646 | 13.209 | 14.435 | 15.533 | 16.265 | |||
| HHO | 9.656 | 10.650 | 11.120 | 11.444 | 11.549 | 10.816 | 12.195 | 13.339 | 13.927 | 14.157 | 12.563 | 14.026 | 15.127 | 15.819 | 16.318 | |||
| MVO | 9.366 | 10.233 | 10.631 | 10.826 | 11.149 | 11.939 | 12.329 | 13.629 | 14.468 | 14.703 | 9.366 | 10.233 | 10.631 | 10.826 | 11.149 | |||
| SSA | 9.365 | 10.058 | 10.136 | 10.235 | 10.326 | 11.272 | 11.975 | 12.487 | 12.734 | 12.906 | 12.085 | 13.298 | 13.679 | 13.897 | 13.866 | |||
| PSO | 9.663 | 10.600 | 10.945 | 11.026 | 11.105 | 11.319 | 12.347 | 13.048 | 13.415 | 13.637 | 11.943 | 13.185 | 13.785 | 14.140 | 14.135 | |||
| GWO | 9.687 | 10.438 | 10.817 | 10.775 | 10.637 | 12.292 | 13.222 | 13.773 | 13.985 | 14.125 | 11.466 | 12.514 | 13.002 | 13.185 | 13.067 | |||
| WOA | 10.024 | 10.892 | 11.226 | 11.277 | 11.326 | 11.111 | 12.415 | 13.088 | 13.410 | 13.610 | 10.835 | 11.974 | 12.579 | 12.923 | 13.106 | |||
| HHO | 10.019 | 10.949 | 11.375 | 11.547 | 11.669 | 11.621 | 12.766 | 13.384 | 13.571 | 13.577 | 10.850 | 12.112 | 12.864 | 13.250 | 13.410 | |||
| MVO | 9.552 | 10.100 | 10.334 | 10.392 | 10.374 | 11.430 | 12.612 | 13.429 | 13.745 | 13.886 | 9.552 | 10.100 | 10.334 | 10.392 | 10.374 | |||
| SSA | 7.238 | 7.175 | 7.211 | 7.248 | 7.307 | 8.507 | 8.755 | 8.916 | 9.047 | 9.101 | 9.317 | 9.952 | 10.153 | 10.154 | 10.188 | |||
| PSO | 7.117 | 7.565 | 7.712 | 7.871 | 7.908 | 8.599 | 8.966 | 9.182 | 9.304 | 9.374 | 9.477 | 9.963 | 10.118 | 10.158 | 10.148 | |||
| GWO | 7.609 | 7.846 | 7.872 | 7.879 | 7.935 | 9.271 | 9.597 | 9.811 | 9.974 | 10.000 | 8.777 | 9.040 | 9.196 | 9.297 | 9.278 | |||
| WOA | 7.722 | 7.969 | 8.348 | 8.525 | 8.532 | 8.970 | 9.485 | 9.741 | 9.883 | 9.898 | 9.486 | 9.956 | 10.052 | 10.165 | 10.110 | |||
| HHO | 7.583 | 7.765 | 7.871 | 7.937 | 7.996 | 8.857 | 9.247 | 9.496 | 9.656 | 9.729 | 9.662 | 10.118 | 10.121 | 10.116 | 10.003 | |||
| MVO | 7.909 | 7.853 | 7.922 | 7.995 | 8.014 | 9.035 | 9.351 | 9.551 | 9.759 | 9.836 | 7.909 | 7.853 | 7.922 | 7.995 | 8.014 | |||
| Indices | XGBoost | Random Forest | LightGBM | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-Step | 2-Step | 3-Step | 4-Step | 5-Step | 1-Step | 2-Step | 3-Step | 4-Step | 5-Step | 1-Step | 2-Step | 3-Step | 4-Step | 5-Step | ||||
| = 6 | SSA | 7083.789 | 7284.455 | 7360.300 | 7397.350 | 7625.696 | 11,224.130 | 10,725.460 | 12,734.978 | 14,494.509 | 15,601.880 | 9130.401 | 8297.729 | 8132.263 | 7825.397 | 7720.972 | ||
| PSO | 7697.141 | 7677.178 | 7379.942 | 7294.624 | 7278.992 | 12,259.029 | 11,750.404 | 11,103.528 | 10,886.963 | 10,557.026 | 10,049.930 | 9488.347 | 9467.416 | 9325.154 | 9472.552 | |||
| GWO | 8676.628 | 8805.201 | 8986.479 | 9205.312 | 8921.273 | 10,619.739 | 12,073.005 | 12,891.806 | 13,235.472 | 15,042.777 | 9849.726 | 9167.982 | 9060.385 | 8792.475 | 9404.556 | |||
| WOA | 12,758.536 | 10,620.400 | 9585.015 | 8832.159 | 9084.639 | 22,079.333 | 25,402.291 | 27,561.550 | 29,142.259 | 28,812.118 | 8774.836 | 8307.744 | 8472.084 | 8394.022 | 8518.347 | |||
| HHO | 8257.153 | 10,896.835 | 11,838.193 | 12,340.044 | 13,144.967 | 10,944.117 | 11486.998 | 12403.300 | 12,759.115 | 13,076.733 | 9513.738 | 8768.511 | 8650.105 | 8384.835 | 8318.968 | |||
| MVO | 10,667.405 | 10,626.755 | 9712.374 | 9297.356 | 9600.802 | 11,110.344 | 11,430.623 | 11,080.077 | 11,936.990 | 12,432.405 | 9870.943 | 9186.526 | 9078.698 | 8808.895 | 9413.312 | |||
| = 9 | SSA | 7365.363 | 7028.222 | 6955.842 | 6905.631 | 6727.568 | 12,405.341 | 15,353.614 | 16,598.810 | 16,810.806 | 16,476.152 | 13,307.409 | 13,521.694 | 13,707.760 | 13,881.910 | 14,007.213 | ||
| PSO | 12,801.210 | 13,169.912 | 13,894.771 | 14,508.964 | 14,837.154 | 11,696.771 | 11,844.595 | 12,250.961 | 12,589.016 | 12,784.163 | 13,340.530 | 13,525.821 | 13,718.938 | 13,881.420 | 14,018.135 | |||
| GWO | 10,107.088 | 10,325.109 | 10,860.832 | 11,271.831 | 11,819.062 | 24,427.493 | 25,134.852 | 25,866.764 | 26,620.196 | 27,366.568 | 13,316.945 | 13,533.257 | 13,720.707 | 13,895.577 | 14,019.931 | |||
| WOA | 11,756.110 | 11,999.820 | 12,274.938 | 12,575.960 | 12,688.952 | 10,208.066 | 10,170.301 | 10,240.144 | 10,148.747 | 9890.040 | 10,213.108 | 10,747.026 | 10,982.412 | 11,076.597 | 11,284.956 | |||
| HHO | 8503.489 | 8498.406 | 8755.758 | 9022.435 | 9012.168 | 11,593.676 | 11,088.775 | 11,133.853 | 11,124.317 | 11,365.227 | 13,122.186 | 13,342.096 | 13,490.780 | 13,642.937 | 13,772.342 | |||
| MVO | 13,149.165 | 13,448.241 | 13,482.311 | 13,670.174 | 13,938.481 | 11,991.064 | 11,988.071 | 12,168.603 | 12,449.394 | 12,785.796 | 13,310.375 | 13,525.289 | 13,711.784 | 13,886.158 | 14,011.166 | |||
| = 12 | SSA | 8379.824 | 8621.319 | 8902.975 | 9156.637 | 8951.197 | 11,384.764 | 10,343.044 | 10,099.481 | 10,007.199 | 9918.844 | 30,666.753 | 31,186.128 | 31,952.261 | 32,858.987 | 35,050.104 | ||
| PSO | 16,009.912 | 15,760.478 | 16,094.090 | 16,413.965 | 16670.100 | 9697.053 | 9716.762 | 9935.180 | 10,124.934 | 10,312.847 | 30,666.757 | 31,186.132 | 31,952.265 | 32,858.991 | 35,050.108 | |||
| GWO | 13932.088 | 14115.732 | 14451.148 | 14859.809 | 15245.074 | 8995.554 | 9254.092 | 9414.683 | 9450.739 | 9505.770 | 30,654.423 | 31,174.299 | 31,940.251 | 32,846.564 | 35,038.724 | |||
| WOA | 9890.686 | 9565.611 | 9614.929 | 9758.711 | 10,058.354 | 15,973.339 | 16,225.195 | 16,731.542 | 17,185.036 | 17,673.006 | 30,666.736 | 31,186.112 | 31,952.245 | 32,858.970 | 35,050.089 | |||
| HHO | 12,460.225 | 12,891.544 | 13,278.332 | 13,685.566 | 14,288.333 | 11,864.541 | 11,211.504 | 11,193.034 | 11,045.136 | 11,083.211 | 29,638.496 | 30,214.224 | 30,988.834 | 31,862.582 | 34,091.278 | |||
| MVO | 12,045.233 | 12,294.365 | 12,637.379 | 13,012.692 | 13,337.793 | 17,104.638 | 17,226.866 | 17,563.214 | 18,024.568 | 17,815.142 | 30,137.679 | 30,755.022 | 31,546.292 | 32,447.906 | 34,541.608 | |||
| Indices | XGBoost | Random Forest | LightGBM | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-Step | 2-Step | 3-Step | 4-Step | 5-Step | 1-Step | 2-Step | 3-Step | 4-Step | 5-Step | 1-Step | 2-Step | 3-Step | 4-Step | 5-Step | ||||
| SSA | 356.238 | 381.175 | 401.012 | 417.665 | 430.288 | 472.075 | 532.859 | 576.005 | 599.399 | 597.645 | 546.790 | 667.395 | 716.870 | 760.507 | 773.509 | |||
| PSO | 373.979 | 400.275 | 420.036 | 427.138 | 433.865 | 471.816 | 524.954 | 567.269 | 594.772 | 598.810 | 524.414 | 616.136 | 675.307 | 717.661 | 730.802 | |||
| GWO | 407.599 | 442.148 | 467.035 | 483.877 | 488.219 | 493.738 | 537.951 | 594.793 | 645.197 | 668.219 | 535.987 | 623.412 | 678.135 | 715.468 | 732.752 | |||
| WOA | 408.537 | 442.148 | 467.193 | 477.913 | 481.535 | 493.536 | 560.126 | 604.106 | 628.672 | 633.016 | 498.255 | 575.298 | 620.185 | 668.858 | 698.847 | |||
| HHO | 406.515 | 435.701 | 458.468 | 471.961 | 470.648 | 461.945 | 524.314 | 575.269 | 602.803 | 608.983 | 540.492 | 621.025 | 672.508 | 707.921 | 728.220 | |||
| MVO | 388.870 | 418.748 | 435.887 | 444.497 | 451.226 | 509.677 | 536.868 | 581.791 | 614.797 | 628.032 | 524.460 | 616.209 | 675.389 | 717.747 | 730.876 | |||
| SSA | 384.360 | 408.778 | 418.485 | 425.234 | 425.147 | 479.534 | 508.496 | 532.474 | 546.459 | 554.607 | 511.036 | 563.624 | 583.815 | 593.139 | 591.898 | |||
| PSO | 403.497 | 432.150 | 446.117 | 450.034 | 448.399 | 482.550 | 533.534 | 561.512 | 577.765 | 586.517 | 496.293 | 554.076 | 580.429 | 599.770 | 602.119 | |||
| GWO | 384.848 | 406.469 | 428.627 | 429.633 | 425.440 | 535.503 | 571.591 | 589.594 | 593.953 | 597.448 | 485.978 | 525.657 | 545.414 | 556.849 | 553.014 | |||
| WOA | 412.235 | 442.998 | 459.982 | 464.254 | 463.782 | 450.004 | 511.061 | 546.656 | 560.572 | 566.189 | 483.814 | 535.551 | 563.002 | 578.734 | 586.113 | |||
| HHO | 428.424 | 456.915 | 474.113 | 479.481 | 480.546 | 476.351 | 527.784 | 559.621 | 569.669 | 569.772 | 480.889 | 531.030 | 560.691 | 578.016 | 585.106 | |||
| MVO | 389.824 | 409.517 | 420.104 | 422.943 | 419.757 | 471.128 | 527.959 | 566.788 | 581.958 | 588.160 | 516.489 | 558.465 | 585.009 | 600.780 | 600.495 | |||
| SSA | 311.836 | 313.310 | 316.684 | 320.091 | 323.343 | 359.217 | 367.487 | 378.066 | 384.599 | 388.549 | 401.884 | 426.376 | 436.110 | 441.555 | 445.513 | |||
| PSO | 308.835 | 329.864 | 335.774 | 341.866 | 342.365 | 376.505 | 389.588 | 400.976 | 408.514 | 411.706 | 407.908 | 430.400 | 433.532 | 439.031 | 442.448 | |||
| GWO | 331.762 | 343.138 | 344.481 | 345.524 | 347.518 | 398.146 | 415.099 | 423.329 | 430.700 | 431.755 | 399.393 | 415.227 | 420.986 | 425.814 | 425.697 | |||
| WOA | 340.117 | 343.945 | 361.685 | 370.629 | 371.046 | 388.525 | 412.406 | 423.497 | 430.657 | 431.623 | 422.878 | 444.544 | 449.673 | 454.801 | 452.427 | |||
| HHO | 327.979 | 332.795 | 337.025 | 340.658 | 342.889 | 385.326 | 395.703 | 407.409 | 414.682 | 418.466 | 421.483 | 437.880 | 440.650 | 442.834 | 442.810 | |||
| MVO | 335.774 | 338.018 | 341.628 | 345.156 | 346.876 | 378.489 | 394.041 | 405.139 | 415.111 | 418.640 | 424.321 | 435.284 | 439.702 | 444.536 | 441.716 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Ma, X.; Zhang, H.; Zhang, G.; Zhang, P. Multi-Step Ahead Natural Gas Consumption Forecasting Based on a Hybrid Model: Case Studies in The Netherlands and the United Kingdom. Energies 2022, 15, 7437. https://doi.org/10.3390/en15197437
Zhang L, Ma X, Zhang H, Zhang G, Zhang P. Multi-Step Ahead Natural Gas Consumption Forecasting Based on a Hybrid Model: Case Studies in The Netherlands and the United Kingdom. Energies. 2022; 15(19):7437. https://doi.org/10.3390/en15197437
Chicago/Turabian StyleZhang, Longfeng, Xin Ma, Hui Zhang, Gaoxun Zhang, and Peng Zhang. 2022. "Multi-Step Ahead Natural Gas Consumption Forecasting Based on a Hybrid Model: Case Studies in The Netherlands and the United Kingdom" Energies 15, no. 19: 7437. https://doi.org/10.3390/en15197437
APA StyleZhang, L., Ma, X., Zhang, H., Zhang, G., & Zhang, P. (2022). Multi-Step Ahead Natural Gas Consumption Forecasting Based on a Hybrid Model: Case Studies in The Netherlands and the United Kingdom. Energies, 15(19), 7437. https://doi.org/10.3390/en15197437







