Control Strategy and Parameter Optimization Based on Grid Side Current Dynamic Change Rate for Doubly-Fed Wind Turbine High Voltage Ride Through

Abstract

High voltage ride through (HVRT) control strategies for doubly-fed induction wind turbines (DFIG) have mostly focused on the rotor side converter, while the reactive power compensation capability of the grid side converter and the impact of grid side converter current transients have often been ignored on the DC bus voltage and reactive power. Therefore, a control strategy based on grid side current dynamic change characteristics is proposed, which resets the reference values of the grid side active and reactive currents for wind turbine HVRT to ensure partial absorption of reactive power on the grid side. Secondly, the key parameter in the proposed control strategy is optimization to get the most suitable DC bus voltage value with the grey wolf algorithm. Finally, the grid-integrated wind turbine simulation model is built on the MATLAB/SIMULINK and RT-Lab platforms. The simulation test results show that the proposed HVRT control strategy and its parameter optimization method are effective, DFIG can achieve HVRT when the wind turbine voltage rises to 1.3 pu.

1. Introduction

With a high proportion of wind turbines connected to the grid on a large scale, grid faults occur from time to time. Unlike the scenario where a system short circuit fault triggers a low voltage ride through problem, the current HVRT problem for wind power mainly occurs in the large-scale wind power base DC feeder scenario. When a phase change failure or lockout occurs in the DC inverter station, excess reactive power generated by filter capacitors and reactive power compensation devices can lead to transient overvoltage at the AC bus at the feeder, putting the turbine at risk of high voltage off grid [1,2]. DFIGs are the most common type of wind turbine used for power generation. The safe and stable operation of the grid places more stringent requirements on its power generation technology and fault ride through capability [3]. Low voltage ride through technology is relatively new, the technology is more mature, and national standards are more detailed. However, HVRT control technology started later, and national standards still need to be supplemented, so DFIG HVRT control technology requires more effort to be invested in research.

The existing control methods for DFIG HVRT are mainly involved in adding hardware circuits and improving the control strategy. The addition of hardware circuits [4,5,6,7,8] can improve the HVRT capability significantly, but it requires additional investment; improved control strategies have also received attention and research by many scholars at home and abroad [9,10,11,12,13,14,15,16,17,18,19]. The results can be divided into the following categories.

The first type is to replace the controller: In refs. [9,10], it is proposed to replace the traditional PI controller with a more advanced controller, and use its own antidisturbance capability and stability to improve the ride through capability; the second type is to modify the compensation amount. The literature [11,12] analyzes the effect of voltage dips on the stator magnetic chain, and again, based on the design of the current inner loop compensation amount, the decay of the transient DC component of the stator magnetic chain is accelerated. In refs. [13,14], a control strategy is proposed to eliminate the effect of dynamic changes in the stator magnetic chain on the system by modifying the amount of power outer-loop or current inner-loop compensation, which ultimately reduces the rotor side current and DC bus voltage. Refs. [15,16] proposes adding the feedforward component to the rotor side power outer loop, while modifying the grid side DC bus voltage reference to limit the rotor overcurrent and DC bus overvoltage. The third type is the design reference value. This type of control strategy is to set the rotor side and grid side current reference values so as to improve the HVRT capability of the DFIG. Ref. [17] adopts the idea of limit division, where the instantaneous value of the stator magnetic chain is directly involved in the stator voltage calculation, forming a dynamic reference value design for the d-axis current to solve the transient fluctuation and time at the occurrence and end of the fault; In the literature [18,19], a HVRT technique considering reactive power support is proposed, which allows the DFIG to absorb inductive reactive power from the grid by configuring the active and reactive power on the rotor side and the grid side when a fault occurs, and can suppress the DC bus overvoltage at the same time. In ref. [20], a rotor side and grid side active power coordination control method is proposed.

Although the above literature can improve the high voltage ride through capability, it does not sufficiently utilize the reactive power support capability of the grid side converter and is not effective in suppressing the DC bus overvoltage peaks. To address this issue, this paper investigates a HVRT control strategy that takes into account dynamic changes in the grid side current. Firstly, the causes of the DC bus voltage rise are analyzed, the transient process of the grid side reactive current is derived in accordance with the analysis, and the reactive support during the ride through is considered. Accordingly, the reference values of the active and reactive currents on the grid side are modified. Furthermore, the grid side and rotor side control strategies are investigated. Then, the grid side and rotor side control strategies are studied. Additionally, the ability of the HVRT control strategy studied in this paper to limit the DC bus overvoltage and control the DFIG to absorb inductive reactive power from the grid is tested by simulation experiments to provide a reference for the study of DFIG fault ride-through technology and to provide a basis for the analysis of DC bus voltage transient characteristics.

2. Analysis of the Reactive Current Limit of DFIG

2.1. Stator side Reactive Current Limit Analysis

In order to ensure that the DFIG is justified in injecting reactive currents into the grid during HVRT, an analytical derivation of the stator side and grid side converter output reactive current limits is required.

The DFIG system and power flow is shown in Figure 1.

According to the system power flow diagram, the following is obtained:

$$\{\begin{array}{l}{P}_z=P_s+P_g\\ Q_z=Q_s+Q_g\end{array}$$

(1)

Ignoring the DFIG stator and rotor copper consumption and core losses, the active power satisfies the following:

$$\{\begin{array}{l}{P}_s=\frac{P_z}{1-s}\\ P_g=-\frac{s{P}_z}{1-s}\end{array}$$

(2)

Stator side active and reactive power after dq decomposition.

$$\{\begin{array}{l}{P}_s=-\frac{3}{2}\frac{U_s{L}_m}{L_s}{i}_{rd}\\ Q_s=-\frac{3}{2}{U}_s(\frac{{\psi }_s}{L_s}-\frac{L_m}{L_{\mathrm{s}}}{i}_{rq})\end{array}$$

(3)

Derive the rotor dq current from Equation (3).

$$\{\begin{array}{l}{i}_{rd}=-\frac{2}{3}\frac{P_s{L}_s}{L_m{U}_s}\\ i_{rq}=-\frac{L_s}{L_m}{i}_{sq}-\frac{U_s}{{\omega }_s{L}_m}\end{array}$$

(4)

The expression for the rotor-current amplitude is as follows:

$$I_r=\sqrt{\frac{2}{3}{\left(\frac{P_z{L}_s}{L_m{U}_s(1-s)}\right)}^2{\left(\frac{L_s}{L_m}{i}_{sq}+\frac{U_s}{{\omega }_s{L}_m}\right)}^2}$$

(5)

When the rotor current is taken as the maximum magnitude I_rmax, the expression for the maximum reactive current output on the stator side can be deduced as follows:

$$I_{sq\max }=\sqrt{{\left(\frac{L_m}{L_s}{I}_{r\max }\right)}^2-\frac{4}{9}{\left[\frac{P_z}{U_s(1-s)}\right]}^2}-\frac{U_s}{{\omega }_s{L}_s}$$

(6)

Analysis by Equation (6): It can be concluded that the stator output reactive power limit decreases with the strengthening of the voltage lifting degree under a certain DFIG output active current. When the voltage at the machine end is raised to 1.1 pu, the maximum reactive current output from the stator reaches 0.683 pu.

2.2. Grid Side Reactive Current Limit Analysis

The grid side current can be calculated from the dq-axis current components as follows:

$$I_g=\sqrt{i_{gd}^2+i_{gq}^2}$$

(7)

The maximum reactive current limit can be derived from the active capacity on the grid side.

$$I_{gq\max }=\sqrt{I_{g\max }^2-{\left[\frac{s{P}_z}{U_s(1-s)}\right]}^2}$$

(8)

The variation law of the output reactive current limit of the grid side converter of the doubly-fed generator versus the grid voltage and the total active current output of the unit to the grid can be obtained.

Analysis by Equation (8): The variation law of the output reactive current limit of the grid side converter of the doubly-fed generator versus the grid voltage and the total active current output of the unit to the grid can be obtained. When the DFIG output active power is certain, the reactive current limit on the grid side decreases with the strengthening degree of voltage lifting. When the voltage at the machine end is raised to 1.1 pu, the maximum reactive current output on the grid side reaches 0.2 pu.

By analyzing the DFIG output reactive current limits, output limits are set for later studies on grid side and stator side reactive current reference values.

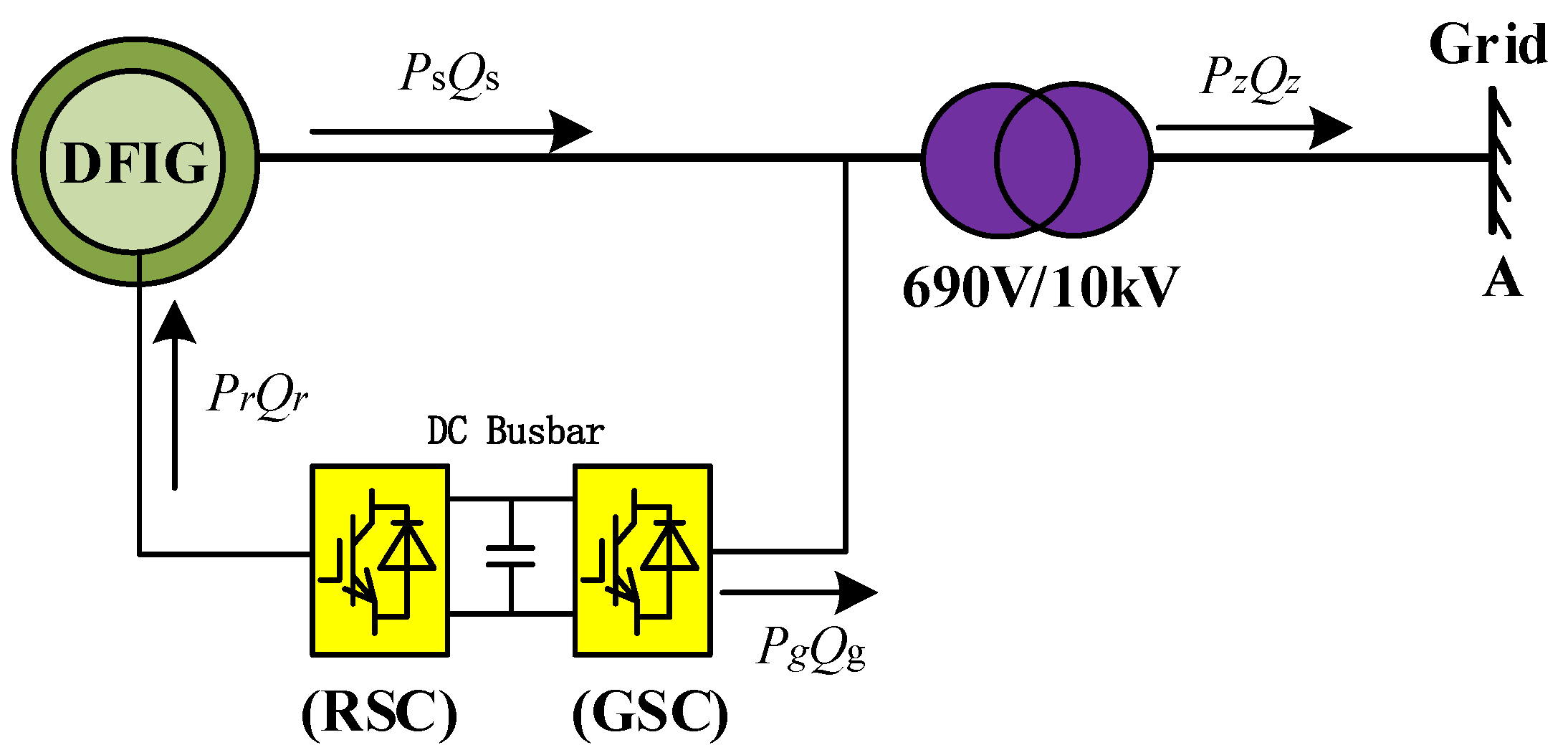
3. Analysis of the DC Bus Overvoltage Limiting Mechanism

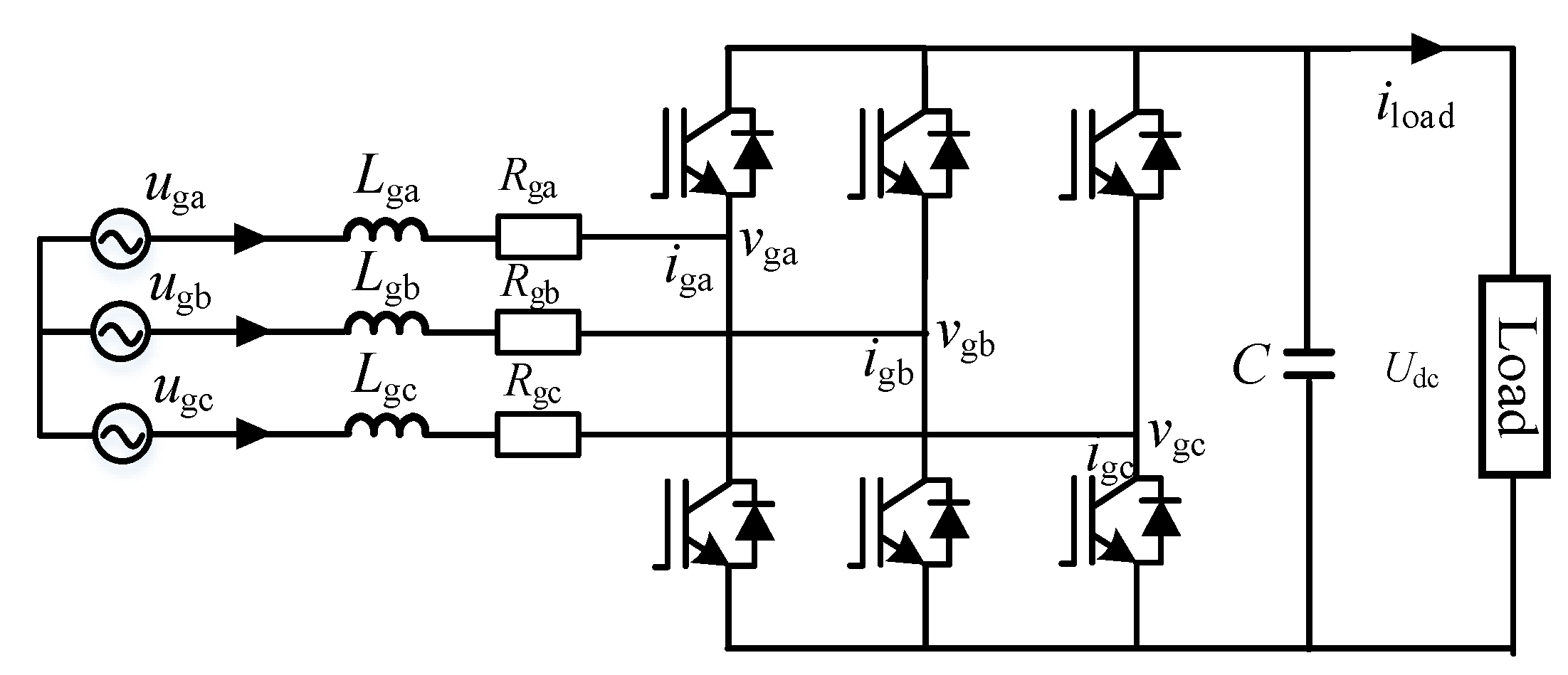
3.1. Voltage Limitation of the DC Bus with the Grid side Converter

The grid side converter in DFIG usually uses a three-phase voltage PWM rectifier as shown in Figure 2, which is characterized by a bidirectional power flow, adjustable power factor and operation at a single power factor, and adjustable DC voltage. u_ga, u_gb, and u_gc are the grid voltages and the value at steady state is 690 v.

The mathematical model of the GSC in a three-phase stationary coordinate system is as follows:

$$\{\begin{array}{l}{u}_{\mathrm{ga}}-i_{\mathrm{ga}}{R}_{\mathrm{ga}}-L_{\mathrm{ga}}\frac{\mathrm{d}{i}_{\mathrm{ga}}}{\mathrm{d}t}-S_{\mathrm{ga}}{U}_{\mathrm{dc}}=u_{\mathrm{gb}}-i_{\mathrm{gb}}{R}_{\mathrm{gb}}-L_{\mathrm{gb}}\frac{\mathrm{d}{i}_{\mathrm{gb}}}{\mathrm{d}t}-S_{\mathrm{gb}}{U}_{\mathrm{dc}}\\ u_{\mathrm{gb}}-i_{\mathrm{gb}}{R}_{\mathrm{gb}}-L_{\mathrm{gb}}\frac{\mathrm{d}{i}_{\mathrm{gb}}}{\mathrm{d}t}-S_{\mathrm{gb}}{U}_{\mathrm{dc}}=u_{\mathrm{gc}}-i_{\mathrm{gc}}{R}_{\mathrm{gc}}-L_{\mathrm{gc}}\frac{\mathrm{d}{i}_{\mathrm{gc}}}{\mathrm{d}t}-S_{\mathrm{gc}}{U}_{\mathrm{dc}}\\ \mathrm{C}\frac{\mathrm{d}{U}_{\mathrm{dc}}}{\mathrm{d}t}=S_{\mathrm{ga}}{i}_{\mathrm{ga}}+S_{\mathrm{gb}}{i}_{\mathrm{gb}}+S_{\mathrm{gc}}{i}_{\mathrm{gc}}-i_{\mathrm{load}}\end{array}$$

(9)

S_ga, S_gb, and S_gc stand for the switching functions of the bridge arms of each phase, respectively, and are equal to one when the upper bridge arm is on and zero when the lower bridge arm is on. v_ga, v_gb, and v_gc are voltage on the AC side of the converter; i_ga, i_gb, and i_gc stand for three-phase input current; U_dc is the DC busbar voltage;i_load is load current; L_ga, L_gb, and L_gc stand for the inlet reactor inductance; R_ga, R_gb, and R_gc stand for the line resistance.

According to the requirements for the HVRT process in the technical specifications for wind farm access to the power system [20], the turbine can be removed when the voltage at the DFIG machine exceeds 1.3 pu.

In the synchronous rotation coordinate system, when grid voltage orientation is used $u_{\mathrm{g}d}=u_{\mathrm{g}}$, $u_{\mathrm{g}q}=0$. The GSC AC side voltage can be expressed as follows:

$$\{\begin{array}{l}{v}_{\mathrm{g}d}=-L_{\mathrm{g}}\frac{\mathrm{d}{i}_{\mathrm{g}d}}{\mathrm{d}t}-R_{\mathrm{g}}{i}_{\mathrm{g}d}+{\omega }_1{L}_{\mathrm{g}}{i}_{\mathrm{g}q}+u_{\mathrm{g}d}\\ v_{\mathrm{g}q}=-L_{\mathrm{g}}\frac{\mathrm{d}{i}_{\mathrm{g}q}}{\mathrm{d}t}-R_{\mathrm{g}}{i}_{\mathrm{g}q}-{\omega }_1{L}_{\mathrm{g}}{i}_{\mathrm{g}d}\end{array}$$

(10)

Ignore the voltage drop across R_g. At this point the GSC AC side voltage can be reduced as follows:

$$\{\begin{array}{l}{v}_{\mathrm{g}d}=-L_{\mathrm{g}}\frac{\mathrm{d}{i}_{\mathrm{g}d}}{\mathrm{d}t}+{\omega }_1{L}_{\mathrm{g}}{i}_{\mathrm{g}q}+u_{\mathrm{g}}\\ v_{\mathrm{g}q}=-L_g\frac{\mathrm{d}{i}_{\mathrm{g}q}}{\mathrm{d}t}-{\omega }_1{L}_{\mathrm{g}}{i}_{\mathrm{g}d}\end{array}$$

(11)

According to voltage space vector modulation theory, the modulation ratio m has the following limits:

$$m=\frac{2\sqrt{v_{\mathrm{g}d}^2+v_{\mathrm{g}q}^2}}{U_{\mathrm{dc}}}\le \frac{2}{\sqrt{3}}$$

(12)

Further simplification of Equation (12).

$$U_{\mathrm{dc}}\ge \sqrt{3}\sqrt{v_{\mathrm{g}d}^2+v_{\mathrm{g}q}^2}$$

(13)

Bringing Equation (11) into Equation (13), we obtain the DC bus voltage limitation condition.

$$U_{\mathrm{dc}}\ge \sqrt{3}\sqrt{{(-L_{\mathrm{g}}\frac{\mathrm{d}{i}_{\mathrm{g}d}}{\mathrm{d}t}+{\omega }_1{L}_{\mathrm{g}}{i}_{\mathrm{g}q}+u_{\mathrm{g}})}^2+{(L_{\mathrm{g}}\frac{\mathrm{d}{i}_{\mathrm{g}q}}{\mathrm{d}t}+{\omega }_1{L}_{\mathrm{g}}{i}_{\mathrm{g}d})}^2}$$

(14)

From Equation (14), it can be seen that the DC bus voltage is limited by the grid voltage, the grid side inductance, the active and reactive currents, and their change rates. When the system is in a steady state, the reactive current as well as the variation of the current are zero and can be neglected.

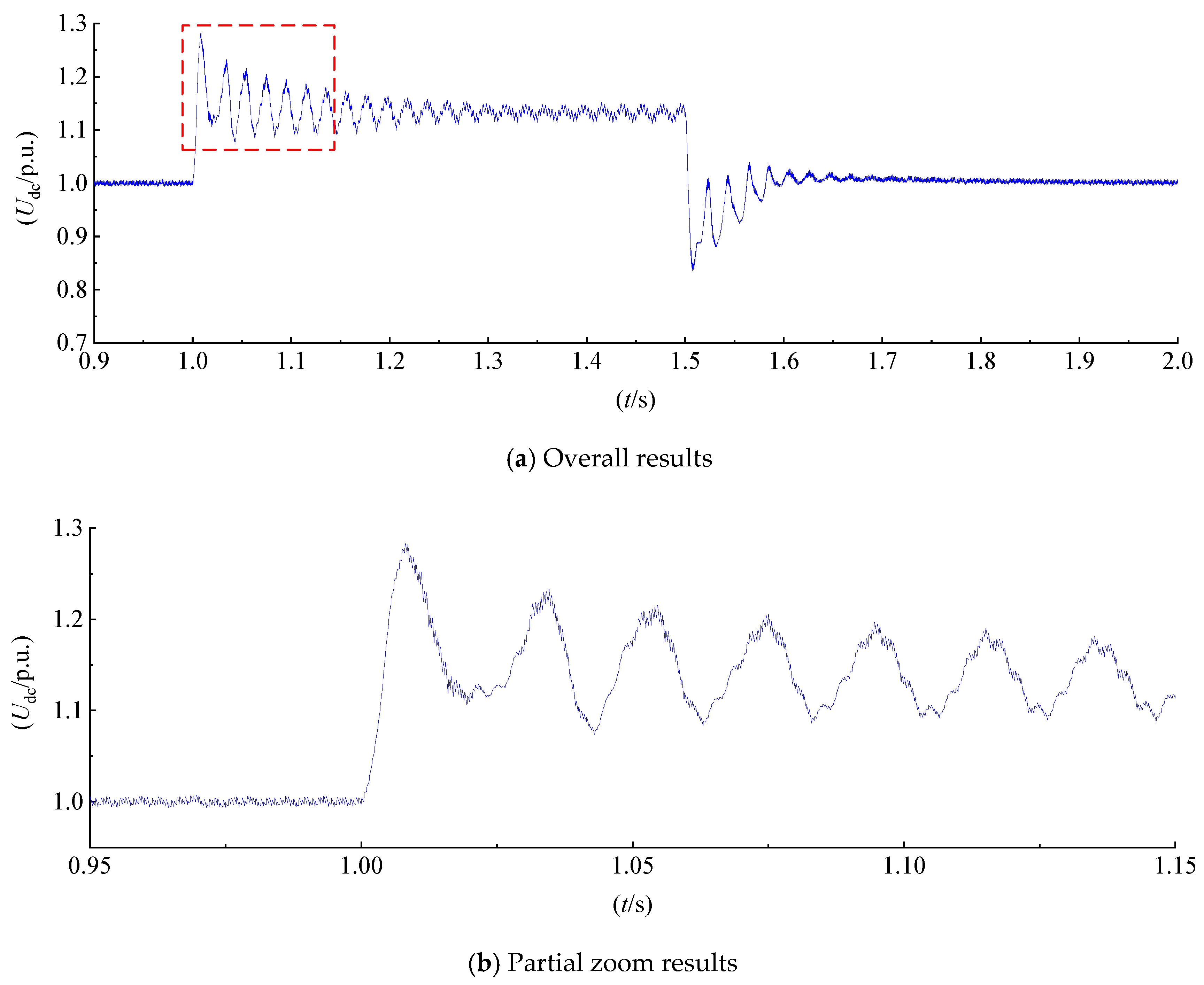
3.2. DC Bus Overvoltage Full Process Analysis

When the voltage at the end of the machine suddenly rises instantaneously, the rate of change in the current produces a transient amplitude that leads to an increase in the DC bus voltage. Therefore, the DC bus limiting condition can be divided into a transient process at the moment of voltage surge (hereinafter referred to as Process I) and a transient equation during overvoltage (hereinafter referred to as Process II).

In the equation, t₀ indicates the moment when the fault starts, t₁ indicates the moment when the transient process ends, and t₂ indicates the moment when the voltage rise ends.

Since the active current has a small effect on the DC bus voltage, the ${\omega }_1{L}_{\mathrm{g}}{i}_{\mathrm{g}d}$ can be ignored. However, due to the large transient fluctuation of active current at the moment of voltage surge, the rate of change of active current $-L_{\mathrm{g}}\frac{\mathrm{d}{i}_{\mathrm{g}d}}{\mathrm{d}t}$ cannot be ignored. To simplify Equation (14), the following is obtained:

$$U_{\mathrm{dc}}\ge \sqrt{3}\sqrt{{(-L_{\mathrm{g}}\frac{\mathrm{d}{i}_{\mathrm{g}d}}{\mathrm{d}t}+{\omega }_1{L}_{\mathrm{g}}{i}_{\mathrm{g}q}+u_{\mathrm{g}})}^2+{(L_{\mathrm{g}}\frac{\mathrm{d}{i}_{\mathrm{g}q}}{\mathrm{d}t})}^2}$$

(15)

Figure 3 shows the waveform of the DFIG DC bus voltage transient response at 1 s when the voltage rises to 1.3 pu and the fault ends at 1.5 s with the conventional control strategy.

The DC bus voltage response shown in Figure 3 is divided into three stages: (1) When the system is in the voltage unsurge steady state. When the dc bus voltage value is 1 pu, only a single power factor control is required. (2) In Process I, the peak DC bus voltage rises from 1 pu to 1.279 pu. At this time, if the single power factor control strategy is still in use, the continuous overvoltage will cause serious damage to the DC bus capacitors. (3) In Process II, the DC bus voltage reaches 1.11 pu, which is still higher than 1.1 pu. Therefore, a new grid side control strategy needs to be studied to make the DC bus voltage lower than 1.1 pu in all three operation stages to ensure the safe operation of the GSC converter.

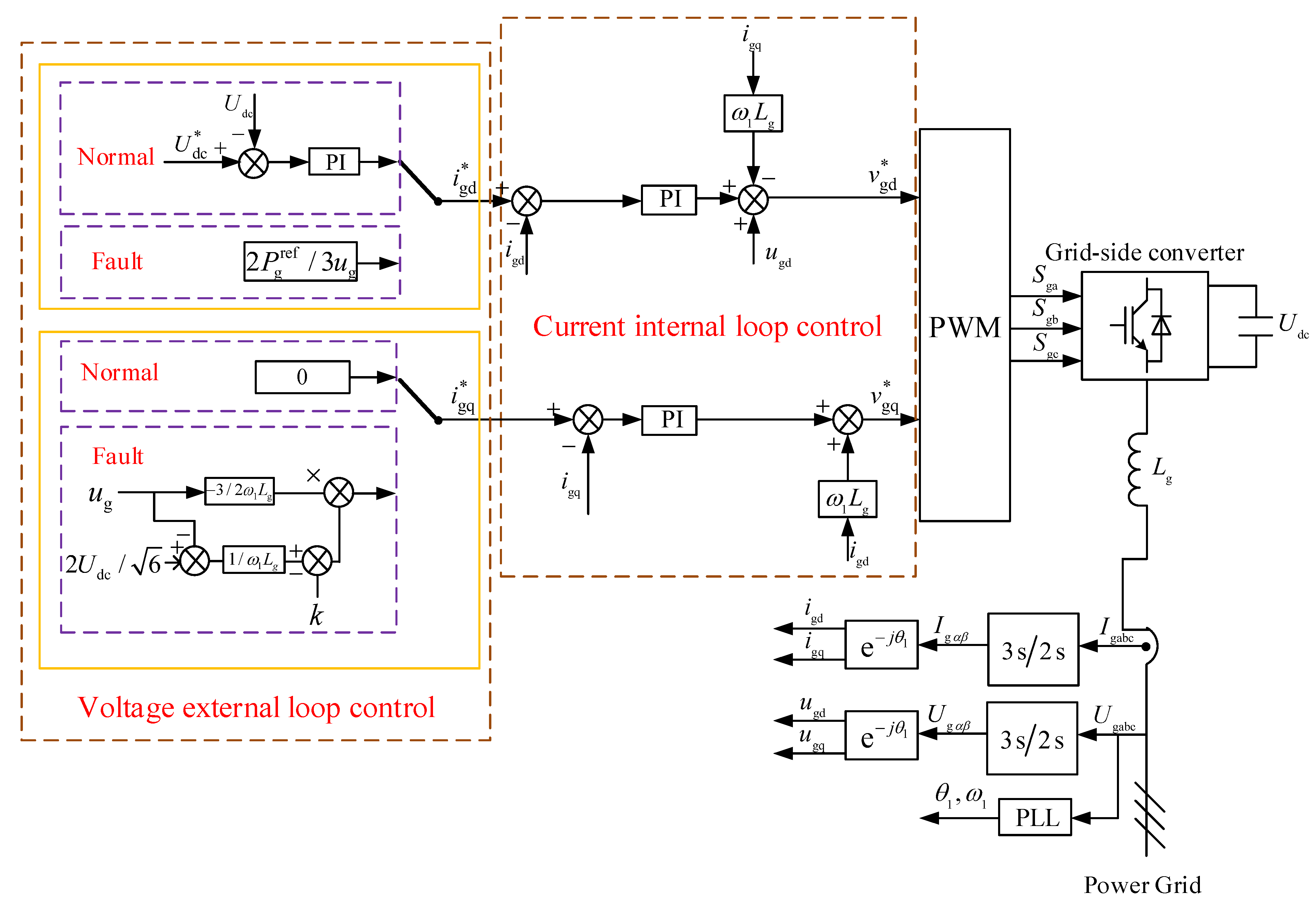
4. HVRT Control Strategy Based on Grid Side Current Variation

4.1. Grid Side d-Axis Control

By analyzing the DC bus voltage limiting condition in Equation (15), it contains both active and reactive current rates of change, and the reactive power support control strategy ignores the current rate of change, resulting in a DC bus voltage that is still higher than 1.1 pu. In order to reduce the impact of the current variation rate on the DC bus voltage and control the grid side converter’s absorption of inductive reactive power from the grid, the d-axis of the grid side converter is designed to reduce the active current rate of change, and the q-axis is designed to reduce the reactive current rate of change.

The DC bus voltage of the back-to-back converter depends on the difference between the active power at both ends. The relationship between the DC bus voltage and power is nonlinear, so feedforward linearization is usually used so that the energy stored in the capacitor $W_{dc}=u_{dc}^2$. The DC bus can be equated to an approximate linearized system as follows:

$$\frac{1}{2}C\frac{\mathrm{d}{W}_{\mathrm{dc}}}{\mathrm{d}t}=P_{\mathrm{g}}-P_{\mathrm{r}}$$

(16)

When the voltage at the machine end rises suddenly, the difference between the active power on the net side and the rotor side fluctuates to the extent that it causes a transient rise in the DC bus voltage. Therefore, the active power on the net side is designed to change in line with the active power on the rotor side.

$$P_{\mathrm{g}}=\frac{3}{2}{u}_{\mathrm{g}}{i}_{\mathrm{g}d}$$

(17)

The reference value of active current is designed according to Equation (18) as follows:

$$i_{\mathrm{g}d}^{\mathrm{ref}}=\frac{2}{3}\frac{P_{\mathrm{g}}^{\mathrm{ref}}}{u_{\mathrm{g}}}$$

(18)

To keep the net-side active power in line with the rotor side active power variation, $P_{\mathrm{g}}^{\mathrm{ref}}=P_{\mathrm{r}}$.

4.2. Grid Side q-Axis Control

By designing the d-axis control logic of the grid side converter, the active current variation rate can be reduced; then the DC bus voltage limiting condition can be reduced to the following:

$$U_{\mathrm{dc}}\ge \sqrt{3}\sqrt{{({\omega }_1{L}_{\mathrm{g}}{i}_{\mathrm{g}q}+u_{\mathrm{g}})}^2+{(L_{\mathrm{g}}\frac{\mathrm{d}{i}_{\mathrm{g}q}}{\mathrm{d}t})}^2}$$

(19)

The maximum value of reactive current is as follows:

$$i_{\mathrm{g}q\max }=\frac{2/\sqrt{6}{U}_{\mathrm{dc}}-u_{\mathrm{g}}}{{\omega }_1{L}_{\mathrm{g}}}-k{e}^{-{\omega }_{1}t}$$

(20)

The analysis of Equation (20) shows that the value of the transient reactive current consists of two parts, the steady state part, which is mainly influenced by the voltage at the end of the machine, and the transient part, which is a time-dependent and decreasing quantity related to the synchronous speed. However, the reactive current calculation with time t is very complex and difficult to implement in simulations and practical applications, part $k{e}^{-\omega t}$ needs to be simplified. Due to the large oscillations of the reactive current on the grid side and the short duration of the amplitude above 1.1 pu and the fact that $k{e}^{-\omega t}$ partly changed a little, can be ignored; secondly, in order to effectively limit the maximum value of the reactive current, it is necessary to take its extreme value, so this part is reduced to k.

The reference value of q-axis reactive current is as follows:

$$i_{\mathrm{g}q}^{\mathrm{ref}}=\frac{2/\sqrt{6}{U}_{\mathrm{dc}}-u_{\mathrm{g}}}{{\omega }_1{L}_{\mathrm{g}}}-k$$

(21)

Equations (18) and (21), obtained by analysis, form the reference value for the grid side current during HVRT.

When the DFIG is operating normally, the network side uses conventional voltage and power external loop control to keep the DC bus voltage stable, and no reactive power support is required. When external factors cause the voltage at the end of the machine to rise, a current reference input is used, and the control block diagram is shown in Figure 4.

4.3. Rotor Side Control

According to GB/T 19963.1-2021 Technical Specification for Wind Farm Access to Power Systems [21], when a sudden three-phase voltage rise occurs at the wind turbine parallel grid, the turbine needs to output dynamic reactive current to the grid and satisfy the following equation.

$$i_{\mathrm{TC}}=1.5(U_{\mathrm{T}}-1.1)I_{\mathrm{N}} 1.1\mathrm{p}.\mathrm{u}.\le U_{\mathrm{T}}\le 1.3\mathrm{p}.\mathrm{u}.$$

(22)

As part of the reactive current is already output from the grid on the grid side (as shown in Equation (21)), the rotor side needs to control the remaining part of the reactive current output from the grid by the stator.

$$i_{\mathrm{s}q}=1.5(U_{\mathrm{s}}-1.1)I_{\mathrm{N}}-i_{\mathrm{g}q}$$

(23)

In the equation, i_sq is the stator reactive current, and U_s is the stator voltage.

In the above equations, the grid voltage is equal to the stator voltage. The following relationship exists between the q-axis stator current and the rotor current.

$$i_{\mathrm{r}q}=-\frac{L_{\mathrm{s}}{i}_{\mathrm{s}q}}{L_{\mathrm{m}}}-\frac{U_{\mathrm{s}}}{{\omega }_1{L}_{\mathrm{m}}}$$

(24)

L_s and L_m in Equation (24) are the stator inductance and the mutual inductance between the stator and rotor.

According to Equations (23) and (24), the rotor side reactive current reference value is described as follows:

$$i_{\mathrm{r}q}^{ref}=-\frac{L_{\mathrm{s}}}{L_{\mathrm{m}}}\left[1.5\left(U_{\mathrm{s}}-1.1\right)I_{\mathrm{N}}-i_{\mathrm{g}q}\right]-\frac{U_{\mathrm{s}}}{{\omega }_1{L}_{\mathrm{m}}}$$

(25)

Thus, Equations (18), (21), and (25) form the design of the grid side and rotor side current reference values under voltage dips.

5. Parameter Optimization for HVRT Control Strategy

Analysis by Equation (21): The value of k in this equation is related to the degree of voltage rise and the initial value of the transient process. It is assumed that the DC bus voltage can be controlled at 1.1 pu for a given degree of voltage lift. Since there is a limit to the reactive current on the grid side, there is also a limit to the choice of k.

A range of values for k was obtained from the analysis, as shown in

Table 1. Range of k values for different voltage rises.

Us	1.15	1.2
k range	−0.3861, −0.1861	−0.4678, −0.2678
Us	1.25	1.3
k range	−0.5431, −0.3431	−0.6185, −0.4185

. However, the value range is still too large, the process of taking the value still requires several attempts, and the value of k will affect the DC bus voltage amplitude. In practice, there is an inconvenience, so the algorithm needs to be selected to find the optimal calculation of the k value.

5.1. Grey Wolf Advantage Search Algorithm

The commonly used algorithms for this type of problem of parameter optimization are particle swarm optimization and grey wolf optimizer (GWO), ant colony algorithm, and glowworm swarm optimization. Among them, GWO has the characteristics of fewer regulation parameters and strong convergence [22]. Here is a brief introduction.

GWO [23] is a typical biologically inspired algorithm proposed by Mirjalili et al. in 2014 that simulates hierarchical stratification of grey wolf packs, and pack predation [24]. The head wolf is $\alpha$, the secondary wolves are $\beta ,\delta$, others are $\omega$.

When a wolf pack goes out to hunt, the alpha wolf takes the lead and the directions, and the secondary wolves serve in assistance, and the rest listen to the first three wolves, and the hunting process can be divided into three processes: encirclement, capture and attack.

(1)

Encirclement: a mathematical model of the process of encirclement of prey by a wolf pack is established.

$$\overrightarrow{D}=\left|\overrightarrow{C}\cdot \overrightarrow{X_p}(j)-\overrightarrow{X}(j)\right|$$

(26)

$$\overrightarrow{X}(j+1)=\overrightarrow{X_p}(j)-\overrightarrow{A}\cdot \overrightarrow{D}$$

(27)

$$\overrightarrow{A}=2\overrightarrow{a}\cdot \overrightarrow{r_1}-\overrightarrow{a}$$

(28)

$$\overrightarrow{C}=2\cdot \overrightarrow{r_2}$$

(29)

In the equation, $\overrightarrow{D}$ is the distance vector; j is the number of iterations;$\overrightarrow{X_p}$ is the prey position vector; $\overrightarrow{C}$ and $\overrightarrow{A}$ are the coefficient vectors; $\overrightarrow{r_1},\overrightarrow{r_2}\in [0,1]$ are the random amount; $a$ as a control from 2 to 0.

(2)

Capture: further capture of prey by the wolf pack, led jointly by three wolves, with constant updates of individual grey wolf positions, is mathematically modeled as follows:

$$\{\begin{array}{l}\overrightarrow{D_{\alpha }}=\left|\overrightarrow{C_1}\cdot \overrightarrow{X_{\alpha }}-\overrightarrow{X}\right|\\ \overrightarrow{D_{\beta }}=\left|\overrightarrow{C_2}\cdot \overrightarrow{X_{\beta }}-\overrightarrow{X}\right|\\ \overrightarrow{D_{\delta }}=\left|\overrightarrow{C_3}\cdot \overrightarrow{X_{\delta }}-\overrightarrow{X}\right|\end{array}$$

(30)

$$\{\begin{array}{l}\overrightarrow{X_1}=\overrightarrow{X_{\alpha }}-\overrightarrow{A_1}\cdot \overrightarrow{D_{\alpha }}\\ \overrightarrow{X_2}=\overrightarrow{X_{\beta }}-\overrightarrow{A_2}\cdot \overrightarrow{D_{\beta }}\\ \overrightarrow{X_3}=\overrightarrow{X_{\delta }}-\overrightarrow{A_3}\cdot \overrightarrow{D_{\delta }}\end{array}$$

(31)

$$\overrightarrow{X}(j+1)=\frac{\overrightarrow{X_1}+\overrightarrow{X_2}+\overrightarrow{X_3}}{3}$$

(32)

Equation (30) defines the forward distance of an individual pack wolf. Equation (31) defines the forward direction of an individual pack wolf and Equation (32) defines the updated position of an individual pack wolf.

(3)

Attack: Eventually the wolves attack the prey. If $\left|A\right|>1$, the wolves focus on the attack and the algorithm performs local optimization. If $\left|A\right|\le 1$, the wolves disperse, and global optimization is performed.

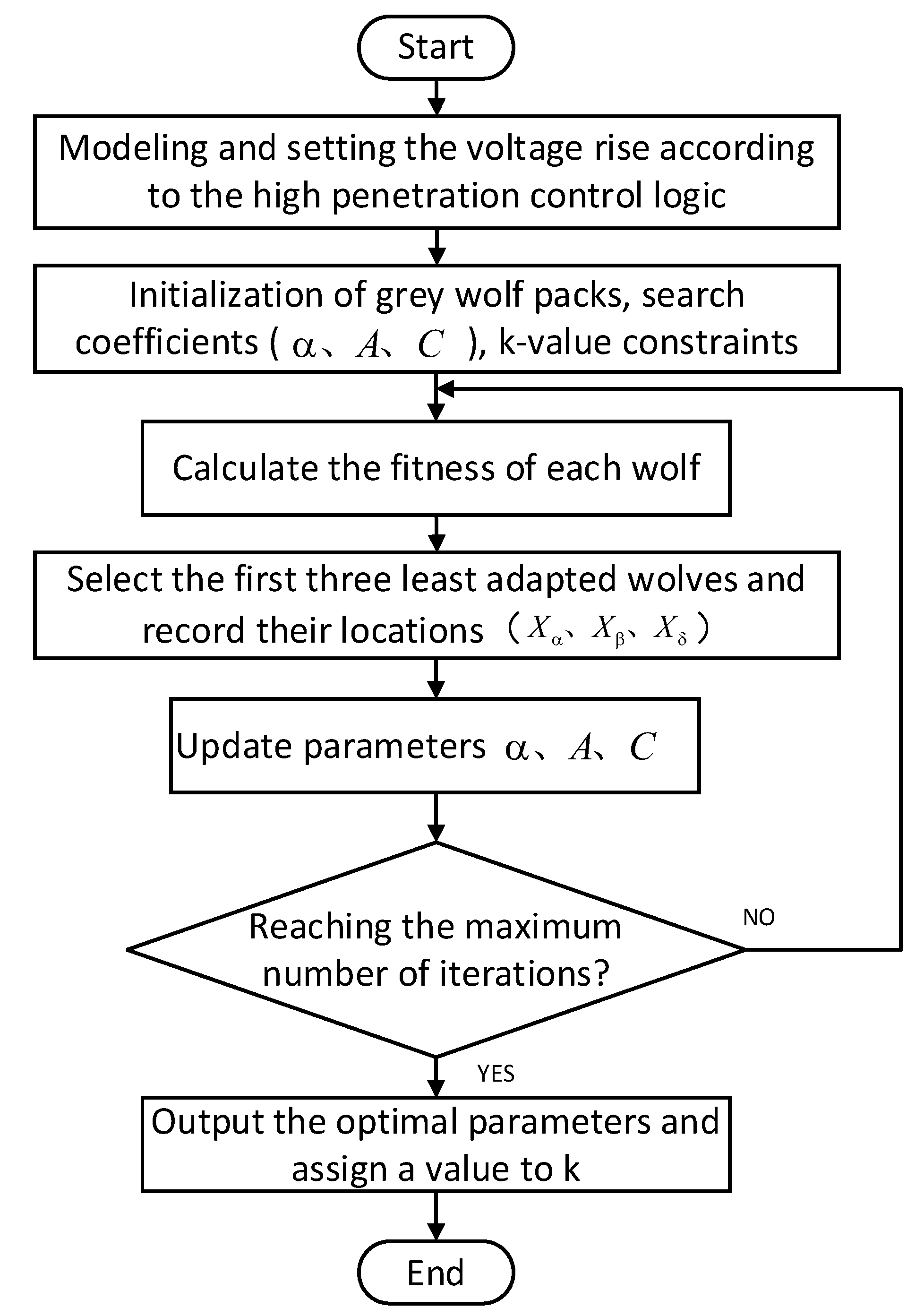
5.2. Application of the Grey Wolf Algorithm

The range of k values is used as an optimization range and is continuously assigned to the DFIG model. To ensure that the transient voltage fluctuations of the DC bus during the fault ride through are minimized, the objective function is set, the maximum value of the voltage during the fault is calculated and saved as $U_{dc\_\max }$, and the objective function is optimally solved by using the grey wolf algorithm to finally obtain a unique k value, as follows:

(1)

Set up the DFIG HVRT model, establish the control logic in accordance with the previous section, and set the degree of voltage lift at the machine end.

(2)

Set up the assignment module in the grid side control logic, take values within the k constraint range as constant input and store the DC bus voltage maximum value as $U_{dc\_\max }$ during the fault, and optimally solve the objective function.

Target function:

$$f=\min (U_{dc\_\max }-1)$$

(33)

(3)

Initialize the parameters of the grey wolf algorithm: pack size N, solution dimension d, maximum number of iterations J_max, individual position, etc.

(4)

Use Equation (33) to calculate the fitness of individual grey wolves and rank them in order, defining the top three as $\alpha ,\beta ,\delta$ and save their locations as $X_{\alpha },X_{\beta },X_{\delta }$

(5)

Update individual wolf pack locations and parameters $\alpha ,A,C$.

(6)

The first three wolves are updated according to the fitness ranking, and an iterative search is continuously performed until the maximum number of iterations is reached, the iteration is cut off, and the optimal fitness function value is output.

The optimal search process of the grey wolf algorithm in the net-side q-axis control strategy studied in this paper is shown in Figure 5.

6. Simulation Testing and Analysis

6.1. System for Simulation Testing

In order to test the function and performance of the HVRT control strategy proposed in this paper considering the dynamic changes in the grid side current, simulations were carried out in MATLAB/Simulink to verify the DFIG simulation schematic shown in Figure 1 and the main parameters of the DFIG are shown in

Table 2. Main parameters of DFIG.

Parameter Name	Numerical Value
Power Rating	3 MW
Rated voltage at machine end	690 V
Nominal DC bus voltage	1200 V
Rated frequency	50 Hz
polar logarithm	3
Stator resistance	0.013 pu
Stator leakage resistance	0.239 pu
Rotor leakage resistance	0.213 pu
Rotor resistance	0.024 pu
Stator-rotor mutual inductance	3.99 pu

.

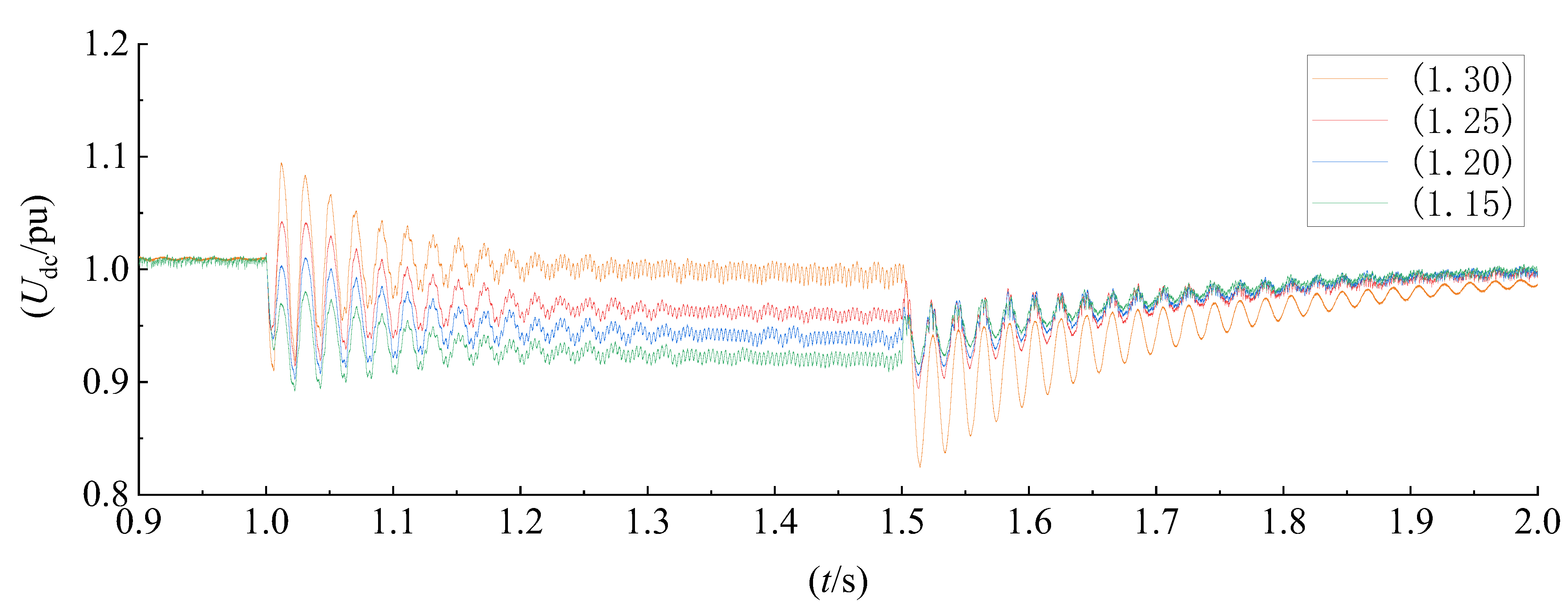
6.2. Simulation Test of HVRT Control Method under Different Voltage Rise Conditions

Setting the DFIG voltage up to 1.3 pu, the grey wolf algorithm can get the k value to take −0.6169, and the DC bus voltage peak reaches 1.090 pu at minimum.

Table 3. DC bus voltage poles at different k values.

k	−0.6185	−0.6169	−0.6035	−0.5885	−0.5735
Udc_max	1.0922	1.090	1.0949	1.0992	1.106
k	−0.5585	−0.5435	−0.5285	−0.5135	−0.4985
Udc_max	1.1095	1.1136	1.1182	1.1233	1.1256
k	−0.4835	−0.4685	−0.4535	−0.4385	−0.4185
Udc_max	1.1323	1.1364	1.141	1.1407	1.1428

shows the comparison results of the DC bus voltage extreme value for different k values.

Analysis of Table 3 shows that the grey wolf algorithm is capable of efficiently and accurately seeking the k value in the most severe cases of voltage rise, ensuring that the peak DC bus voltage is below 1.1 pu.

Setting the wind turbine voltage to rise to 1.3 pu from 1.15 pu, we get the DC bus voltage as shown in Figure 6:

The results for the optimum k value and DC bus voltage for different degrees of voltage lift are shown in

Table 4. Results for optimal k values and DC bus voltages for different voltage rises.

Us	1.15	1.20	1.25	1.30
k	−0.3861	−0.4652	−0.5407	−0.6169
Udc_max	1.026	1.034	1.068	1.090

.

By analyzing Table 4, it can be seen that the grey wolf algorithm can adapt to different levels of voltage lift and efficiently solve for the global optimum of k values.

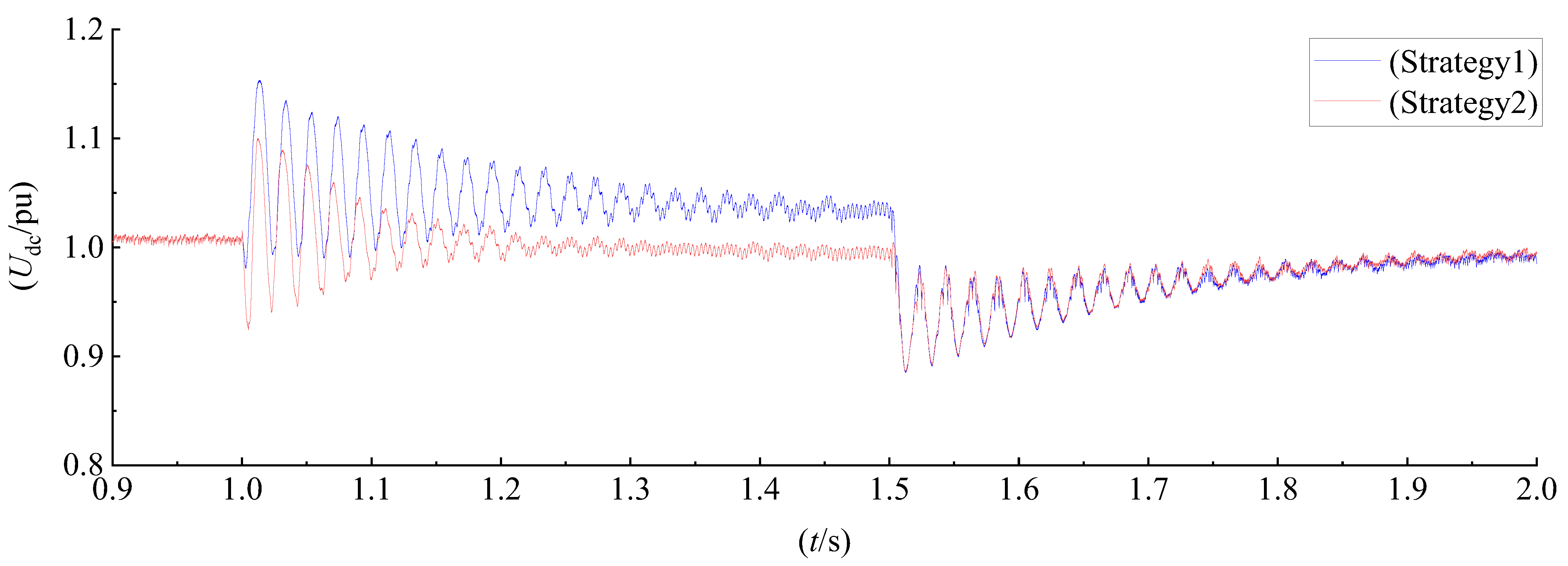
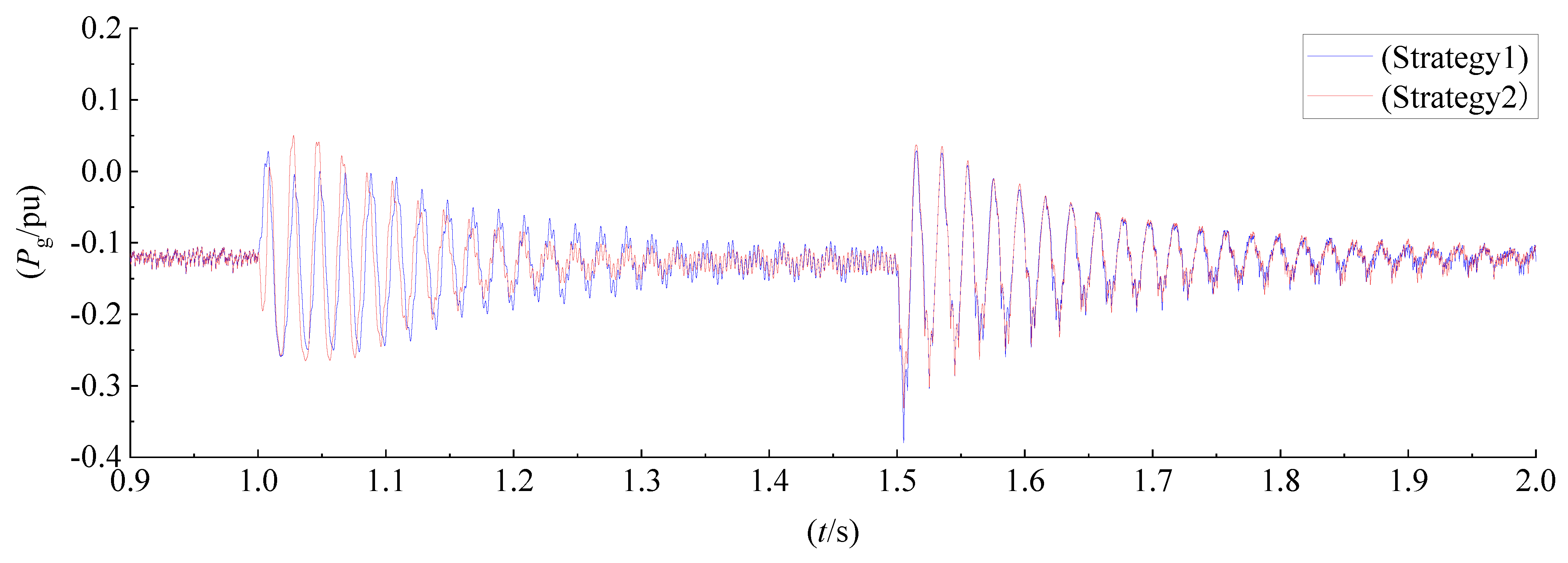
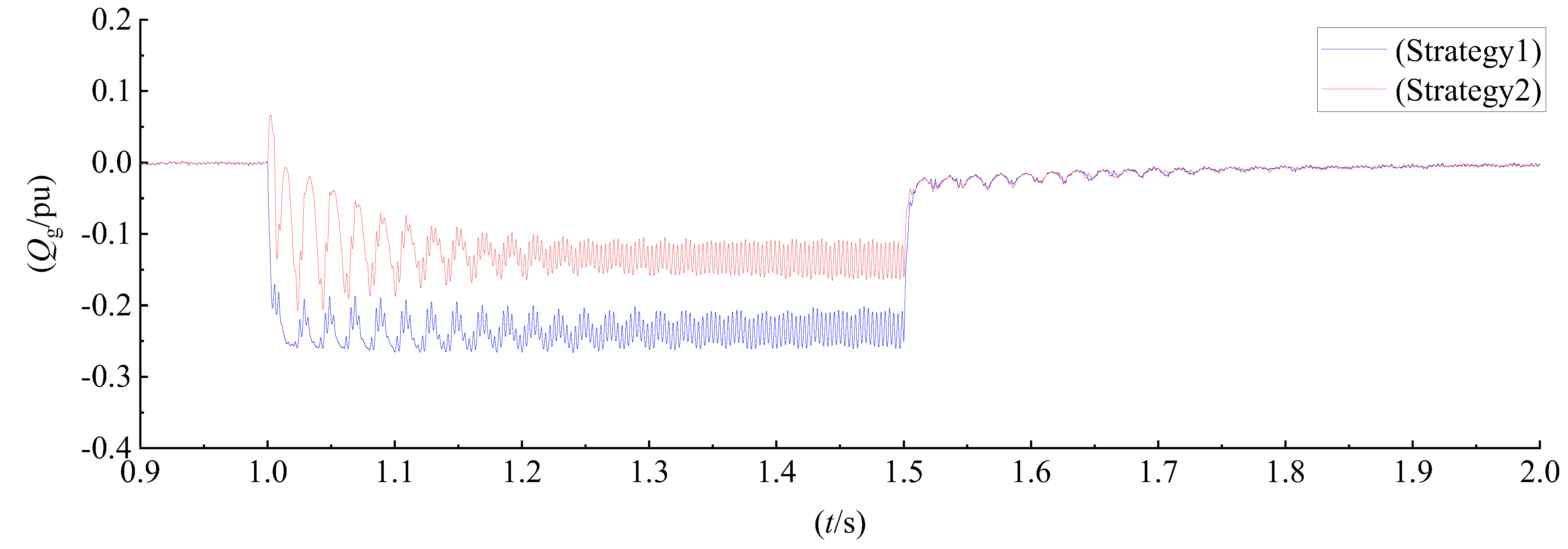
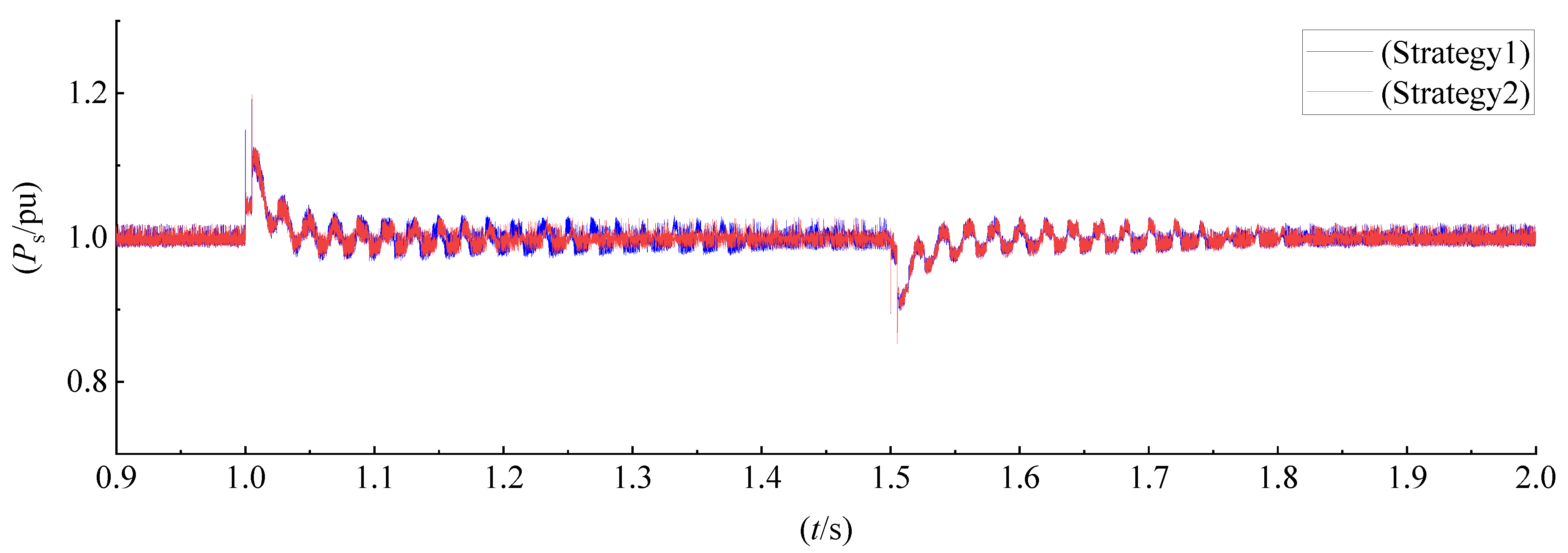
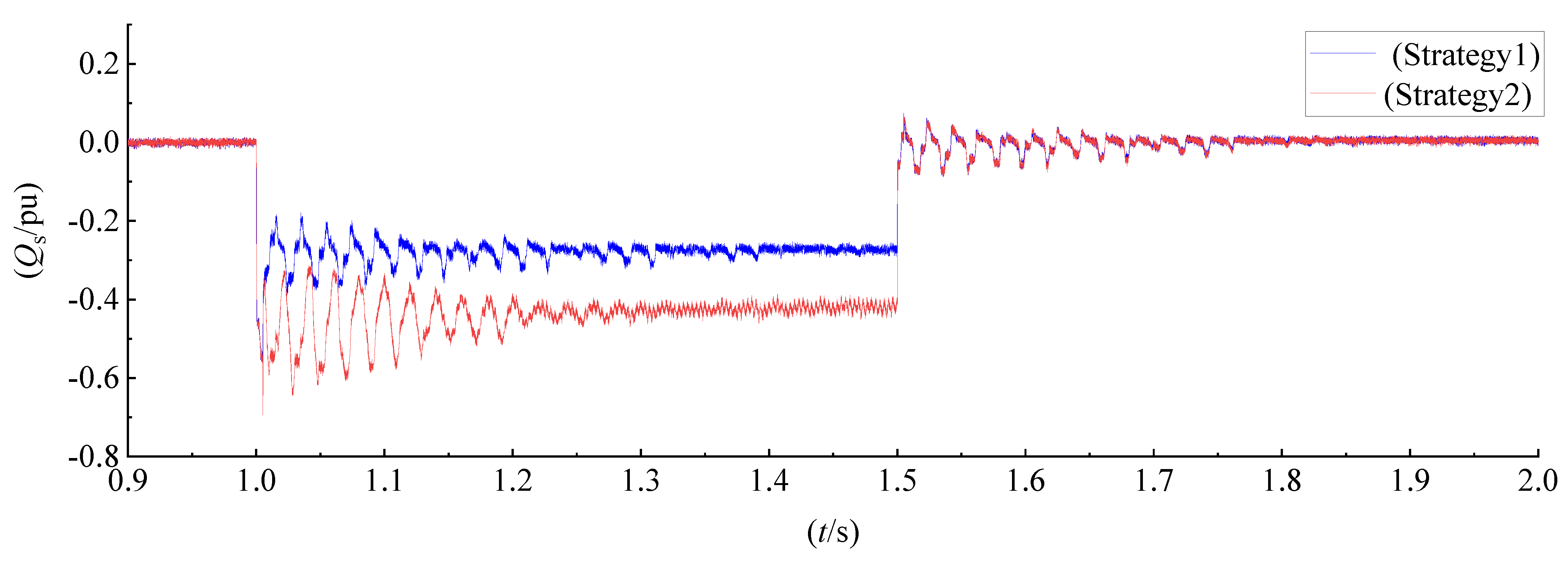
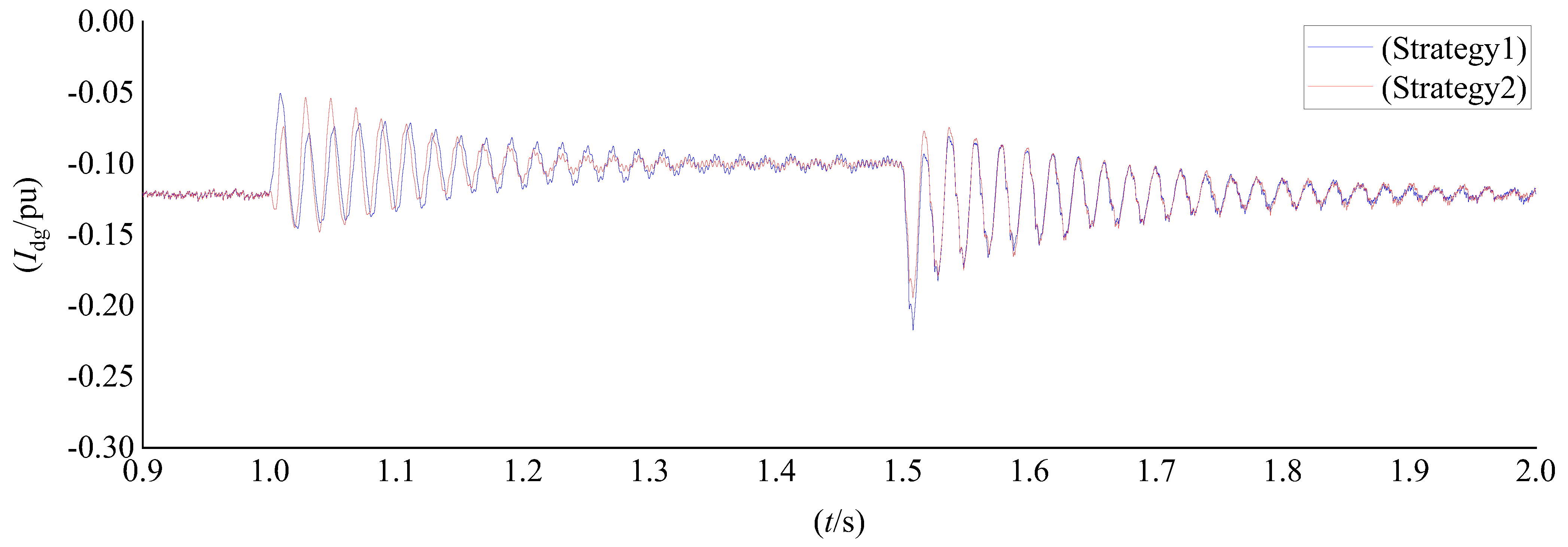
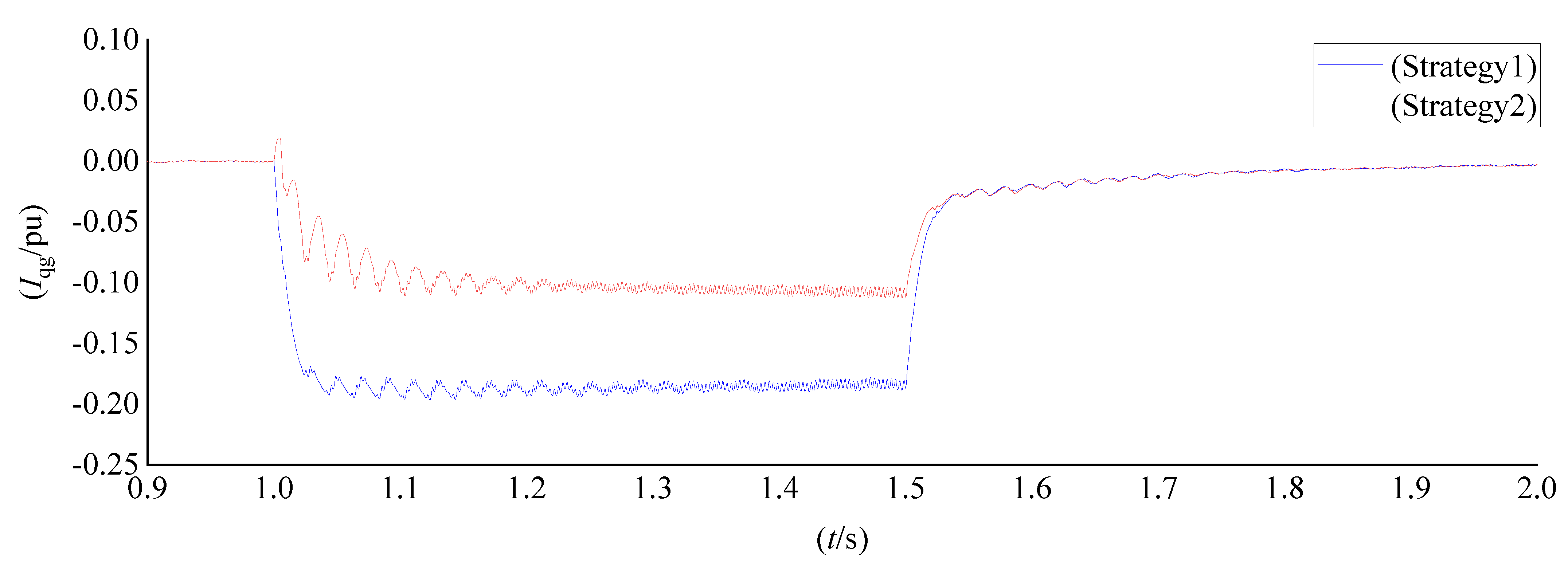
6.3. HVRT Control Methods Comparative Simulation

Simulation of the control strategy considering dynamic reactive power support (Strategy 1) and the control strategy considering dynamic changes in grid side current (Strategy 2) are proposed in this paper, with the voltage at the machine end undergoing a sudden rise at 1 s to 1.3 times, the nominal value (duration 500 ms). The simulation results are shown in Figure 7,Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13.

Figure 7 shows the DC bus voltage. It can be seen that the peak DC bus voltage of Strategy 1 reaches 1.15 pu at the moment when the end-of-machine voltage rises, and lasts longer than 1.1 pu for 170 ms, which may lead to damage to the DC capacitor and the grid side converter. This control strategy has a long oscillation time, which is not conducive to the stable operation of the system; compared with Strategy 1, the DC bus voltage is 1.090 pu at the moment of voltage rise at the machine end, which is well limited to below 1.1 pu, and enters transient Process II after 200 ms oscillation, which is well limited to 1 pu. Strategy 2 can better limit the voltage of the two transient processes than Strategy 1. At the same time, the time of waveform oscillation is better reduced, which is more conducive to system stability.

Figure 8 and Figure 9 show the output power of the DFIG grid side converter. Through the analysis, it can be obtained that the inductive reactive power absorbed from the grid is similar to Strategy 1 and Strategy 2, with the former being 0.25 pu and the latter being 0.15 pu during the voltage rise at the machine end; compared with the active power, Strategy 2 can approach stability faster after a short period of oscillation.

Figure 10 and Figure 11 show the DFIG stator side output power. Strategy 1 reaches 0.26 pu after a transient amplitude fluctuation at the moment of voltage lift at the machine end; Strategy 2 can control the DFIG to absorb 0.43 pu of inductive reactive power from the grid to help the grid recover the voltage. The active power waveforms of both are similar, and both stabilize after a short fluctuation after the voltage lift and recovery.

Figure 12 and Figure 13 show the DFIG grid side converter output current waveforms. At the moment of voltage rise at the machine end, Strategy 2 and Strategy 1 are designed in this paper. Their reactive current values are 0.1 pu and 0.19 pu, respectively. Strategy 2 sacrifices part of the reactive margin to help limit the DC bus overvoltage. The data analyses above are all smaller than the grid side reactive power limits analyzed in Chapter 1 and are consistent with the design and analysis of the grid side active and reactive current reference values in Section 3.

Through the above analysis, it can be seen that the control strategy designed in this paper, compared with the control strategy considering dynamic reactive power support, can better limit the peak value of DC bus voltage at the moment of and during the voltage rise at the machine, and better suppress the transient amplitude fluctuation of voltage, current, and power at the moment of voltage rise. The coordinated operation of the grid side and rotor side converters not only ensures that the DFIG does not operate off-grid during the voltage rise, but also absorbs inductive reactive power from the grid, which is conducive to grid voltage recovery and safe operation.

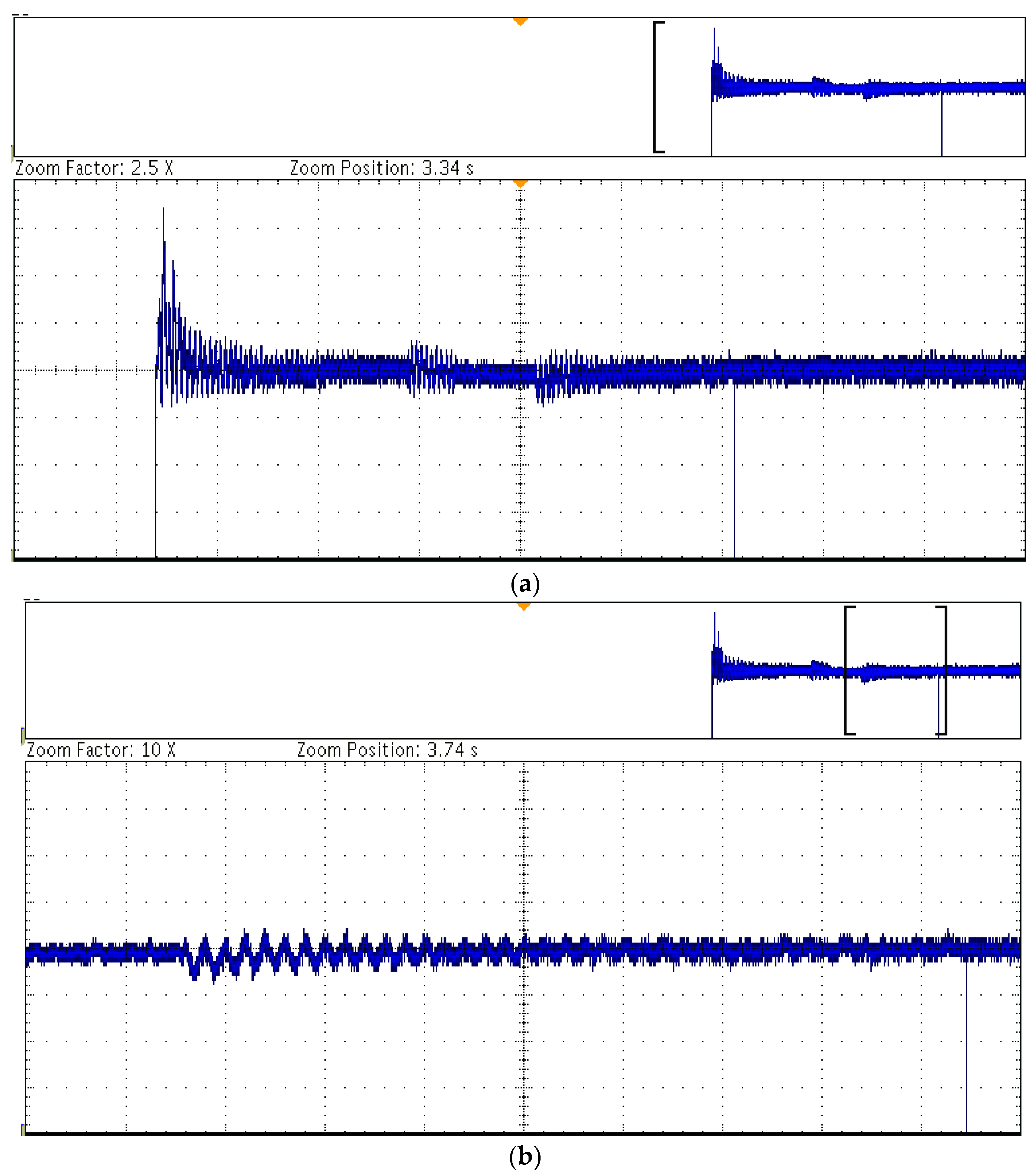
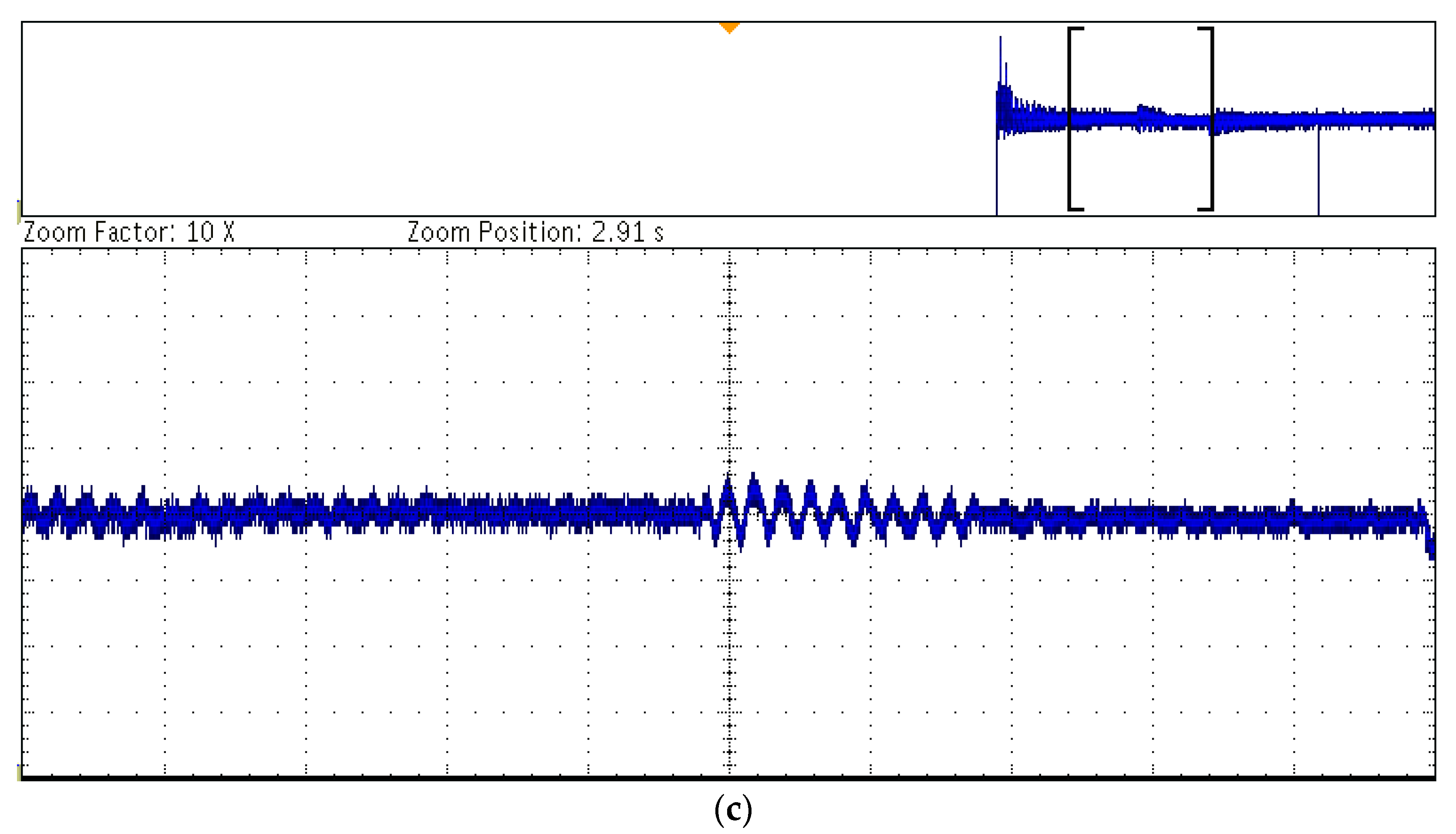
6.4. Performance Analysis of the Control Method Based on the RT−Lab Simulation Platform

To further verify the strong applicability of the control strategy studied in this paper, the model was built on RT−Lab. The simulation platform is shown in Figure 14.

The DC bus voltage is used as the output and further analyzed as shown in Figure 15a–c.

Though the whole process of real time simulation can be obtained, this research’s control strategy can limit the DC bus voltage in the moment of voltage lift below 1.1 pu, and the high wear process oscillation amplitude is small, conducive to DFIG stable operation.

7. Conclusions

In this paper, the causes of the DC bus voltage rise were analyzed, and the overvoltage limiting mechanism was analyzed. On this basis, the control strategy was investigated. The simulation analysis verified the correctness of the theoretical analysis and the effectiveness of the control strategy, and the following conclusions were drawn.

(1)

In the DFIG HVRT process, the grid side and stator output reactive current limit is influenced by the initial value of active power and the degree of voltage lift, so a current limiting section is required when designing the reactive current reference. Additionally, the rate of change in the grid side current will have a large impact on the DC bus voltage.

(2)

This paper proposes a method for reducing the rate of change in active and reactive currents to limit overvoltage at the DC bus point and investigates a HVRT control strategy that takes into account the dynamic changes in grid side currents.

(3)

Analysis of busbar overvoltage lift limiting conditions, on the basis of which active and reactive current reference values are set, can effectively reduce DC busbar overvoltage. At the same time, the DFIG can be controlled to absorb inductive reactive power from the grid according to different degrees of voltage rise.

(4)

The key parameter k in the grid side current reference value has a certain influence on the DC bus voltage. By introducing the gray wolf search algorithm, a convenient and accurate global optimum search for the key parameters can be carried out.

This paper provides a reference for the study of fault ride through technology for doubly fed induction wind turbines, and also provides some reference values for the analysis of grid side fault currents.