The Development of a Cross-Border Energy Trade Cooperation Model of Interconnected Virtual Power Plants Using Bilateral Contracts ^†

Abstract

By coordinating the operation of regionally interconnected virtual power plants (VPPs), the growing penetration problem of renewable energy sources (RESs) into the power system can be addressed. This study presents an interactive trading cooperation model of regionally interconnected VPPs using bilateral contracts. The proposed model maximizes overall electricity market social welfare (SW) (i.e., maximization of consumer benefits while minimizing energy costs). The focus of the proposed approach is to design and develop a parallel energy exchange cooperation model of interconnected VPPs, ensuring the operational efficiency and reliability of interconnected power systems over the planning horizon. Given that adjacent VPPs may have differences in their energy generation and usage patterns, a scenario tree method is used to model the uncertainties associated with solar irradiation and load demand. A case study of two interconnected VPPs is used, the operational scenario is designed, and the corresponding computational model is developed. The results highlight that the proposed approach gives VPPs the option to utilize their internal network’s maximum capacity. As a result, there will be less reliance on the main grid for interconnected VPPs, and an improvement in key performance indicators, including the cost of the VPPs systems and renewable power variations.

1. Introduction

VPPs are small-scale, electrical power-trading entities capable of accommodating a wide range of small generators, including photovoltaics (PVs) systems, wind turbines (WTs), energy storage systems (ESSs), demand response (DR) programs, and different types of energy consumers, as shown in Figure 1. A VPP is viewed as a viable trading platform that will increase the utilization of distributed energy resources (DERs) and also benefiting end users. [1,2,3,4,5]. However, a number of critical challenges must be dealt with to ensure the safe operation and reliability of the power systems at a local level. One of these challenges is the misalignment of DER’s supply and load (demands), driven by DER’s uncertainty. Consequently, designing a mutual economic trading model is a key that will ensure the maximization of the operational performance of interconnected VPPs by fulfilling supply and demand requirements [6,7,8,9]. There are different types of approaches that can be applied to address this kind of problem. One preferred solution is where nearby VPPs may trade energy directly through designated energy networks, hereafter referred to as flow gates. A flow gate is a network of direct power lines that connects nearby VPPs and lets them exchange and trade surplus energy through bilateral contracts. The power loss owing to the proximity of these VPPs will also be minimized.

The main idea proposed in light of the following considerations is as follows: (1) VPPs are used for diverse objectives and may differ greatly in terms of their design architecture, energy types, and loads within them, just as their day-to-day power patterns of energy generation and consumption may likewise also vary; (2) this imbalance between energy generation and consumption typically results in “complementarities” between their peak and valley demand times. As a result, the complementary characteristics of both VPPs can be exploited to compensate for each other’s short-term energy shortfall. For instance, residential locations with rooftop solar energy will experience a daytime energy excess and a night-time energy peak. If their sites are close to each other, it would be advantageous for both neighborhoods if the excess energy from the rooftop solar supply could be distributed to places with a lack of energy. Moreover, the main grid will benefit from it as surplus power can be injected into the regional distribution system, improving grid reliability. The effort of this study is therefore concentrated on a novel framework to build electrical connections and energy trading between VPPs, as opposed to the existing VPP control approaches. Furthermore, a novel paradigm is presented in this work that makes use of direct energy consumption to reduce the impact of DER generation variability on the reliability and stability of the power system.

To the best of the author’s knowledge, no literature exists that investigates mutual economic trading operational mechanisms of interconnected VPPs within the energy market environment. This work considers cross-border energy cooperation using bilateral contracts between adjacent VPPs. A new approach of mutual energy cooperation between interconnected VPPs in grid-connected mode within the market environment is presented, aiming to maximize the mutual economic benefits of interconnected VPPs. It will also mitigate the volatile nature of variable renewable energy (VRE) sources, which is one of the primary contributions of the research paper. A scenario tree method is used to model the uncertainties associated with solar irradiation and load demand.

1.1. Literature Review

Some recent studies in the literature have focused on the interaction of multiple power systems with distribution systems [10,11,12,13,14,15,16,17,18,19,20]. The majority of these research works advocated for a cost-cutting strategy. The authors of [10] have presented a control mechanism for managing the operation of interconnected VPPs in a market environment. The aim was to minimize the overall operating costs of interconnected VPPs by formulating the problem as a two-stage stochastic optimization problem. The authors of [8] have presented an inter-regional cooperation model to maximize the economic benefits for participating members. The authors of [11,12] have proposed a two-stage operational mechanism for grid-connected MGs in a distribution system. The aim was to minimize power losses, enhance voltage profiles, and maximize variable energy usage. To fully harness the nondispatchable potential and capacity of dispersed generators, the authors of [13], have developed a collaboration model between interconnected MGs in the presence of energy storage devices. This keeps operational costs to a minimum. The authors of [14] have presented an energy management framework for sharing energy between numerous MGs, while taking into consideration the security constraints. The authors have presented a distributed energy management mechanism for interconnected MGs in [15]. It was intended to coordinate the power planning of various aspects of the MGs while adhering to the operational limits of the power networks. The authors in [16] proposed a centralized control mechanism for smart cooperative microgrids that facilitate power interchanges between neighbors, with the aim of maximizing the aggregate benefit of all microgrid operators. The authors in [17] investigated the commercial performance of heterogeneous interconnected microgrids using a stochastic decision model. The authors of [18] have presented a data-driven decision mechanism to evaluate the electricity exchange in the context of renewables uncertainty for a housing network. However, because of the large amount of data training required and the extended training period, it is inappropriate for the short-term operational scheduling of MGs. The authors of [19], presented a scenario-based approach to cope with variations in the collective operation of multiple-house networks. However, in order to achieve precise probability distributions of the uncertainties, stochastic operation techniques require a large number of scenarios, which might increase computational complexity and cost. According to reference [20], each microgrid attempted to achieve the lowest possible operation cost by collaborating with other microgrids while retaining a record of the power reference supplied by the DNO. However, this strategy is challenging to implement because microgrid operators have no interest in adhering to the DNO’s schedule.

Many contemporary studies, in contrast to our work, have not considered the energy trade cooperation characteristics of regionally interconnected VPPs. Therefore, there is a lack of a coordinated mechanism of cross-border interaction and cooperation of interconnected VPPs. From the energy trade cooperation perspective, the direct power exchange mechanism between interconnected VPPs is investigated with the aim to understand how the trading model would perform in a real-world environment. A comparison of the proposed model with the existing literature is presented in

Table 1. Comparison of the proposed method with existing literature.

References	Renewable Energy	Model	Uncertainty Modeling	Power Market	SW
[10]	Yes	Bidding strategy	No	Yes	Yes
[8]	Yes	Cooperative model	Yes	Yes	No
[11,12,13]	Yes	Optimal dispatch	Yes	No	No
[14,15]	Yes	Energy management	No	No	No
[16]	Yes	Cooperative model	No	No	No
[17]	Yes	Economic dispatch	Yes	No	No
[18]	Yes	Ancillary service	No	No	No
[19,20]	Yes	Economic dispatch	Yes	Yes	No
This paper	Yes	Regional cooperation	Yes	Yes	Yes

.

1.2. Contributions and Study Layout

The main contributions of this work in relation to the literature reviewed are succinctly stated as follows:

• A cross-border energy trade cooperation model of regionally interconnected VPPs is designed and developed within the energy market environment, maximizing SW.
• The power exchange between two VPPs in the grid-connected mode is studied using the energy-flow gates.
• A case study is performed on interconnected VPPs to demonstrate the effectiveness and fairness of the proposed approach by thoroughly assessing the simulation results.

The rest of the paper is organized as follows: Section 2 presents the methodology, the uncertainty modeling approach, an explanation of the proposed model and method with assumptions, a solution approach, the objective function and an explanation of the VPP electricity market structure. A case study model with required data, simulation results and discussion is presented in Section 3. Finally, meaningful conclusions are made in Section 4.

2. Methodology

The main aim of this study is to design and develop an energy trade cooperation model of regionally interconnected VPPs, maximizing the SW of the interacting VPPs. This work presents a new strategy for the cross-border energy trade cooperation models of regionally interconnected VPPs within the market environment, subject to equality and inequality constraints. Modeling the uncertainties associated with solar irradiation and load demand is done using the scenario tree method. The method analyzes the impact of the proposed mechanism in regard to energy cooperation maximizing the economic benefits of the participating members over the planning horizon.

The uncertainties related to load demand and solar irradiation are modeled using the scenario tree method, in which each scenario represents a probable realization of an unknown parameter. [21]. To generate scenarios, the probability density function (PDF) is implemented for each block of load demand and solar irradiation.

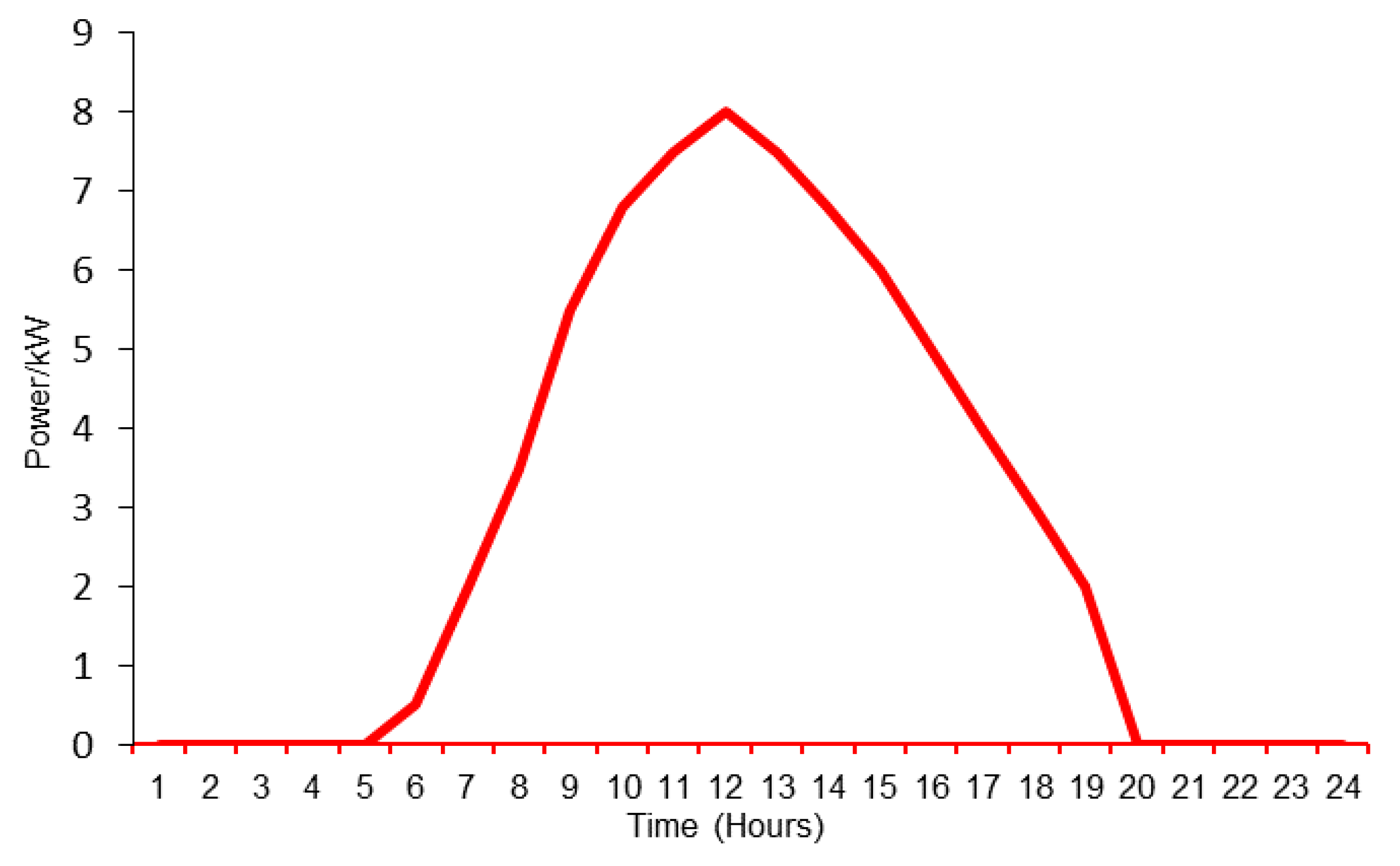
2.1. Modeling of Solar Irradiance

The solar irradiance given by Equation (1) is modeled using beta PDF (1).

$$PDF(S)=\left\{\begin{array}{l}\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )+\Gamma (\beta )}\times {{\displaystyle s}}^{\alpha -1}\times {{\displaystyle (1-s)}}^{\beta -1}, 0\le s\le 1,0\le \alpha ,\beta \\ 0 else\end{array}\right\}$$

(1)

In Equation (1), S is the representation of the solar irradiance in (kW/m²). What follows are the Equations used for determining the Beta PDF parameters, such as (α and β) [22,23,24,25].

$$\beta =(1-\mu )\times \left(\frac{\mu \times (1-\mu )}{{{\displaystyle \sigma }}^2}-1\right)$$

(2)

$$\alpha =\frac{\mu \times \beta }{1-\mu }$$

(3)

where σ and µ represent the standard deviation and the mean value. The main factors used to determine the power generation of a PV module are ambient temperature and solar irradiation, which are given by Equations (4) and (5).

$${{\displaystyle P}}_{PV}={{\displaystyle P}}_{STC}\left\{\frac{G}{100}\left[1+\delta \left({{\displaystyle T}}_{cell}-25\right)\right]\right\}$$

(4)

$${{\displaystyle T}}_{cell}={{\displaystyle T}}_{amb}+\left(\frac{NOCT-20}{800}\right)G$$

(5)

where P_PV and P_STC refer to the power in megawatts (MW) under standard test conditions and, correspondingly, the kilowatt represents the output power of the PV module. δ is the representation of the power temperature coefficient in (%/°C). The ambient temperature in °C is represented by T_amb. The cell temperature in °C is represented by T_cell, and NOCT stands for nominal operating cell temperature conditions in °C. Where G represents solar irradiance in (W/m²) [26,27,28].

2.2. Load Demand Uncertainty Modeling

PDF function is applied to model the load demand of each bus. Equation (6) provides the PDF of the normal distribution, with an unknown load of l [20,29,30,31].

$$PDF(l)=\frac{1}{{{\displaystyle \sigma }}_l\sqrt{2\pi }}\times \exp \left[-\left(\frac{\left(l-{{\displaystyle \mu }}_l\right)\stackrel{2}{}}{2{{\displaystyle \sigma }}_l^2}\right)\right]$$

(6)

where σƖ and μ_Ɩ represent the standard deviation and the mean value [21,22,26].

2.2.1. Explanation of the Proposed Method and Model

Figure 2 shows the designed structure of a mutual energy trade cooperation model of interconnected VPPs using energy-flow gates (power lines). The energy-flow gates function as the energy exchange points between regionally interconnected VPPs. It makes the interconnected VPPs a backup for each other in case of a supply deficit. Both interacting VPPs are also wired to the grid. According to the proposed approach, If the “VPP1” has an additional energy compared to its internal consumption, then the flow gates can be utilized to trade the excess power locally with the “VPP2”, which is experiencing an energy supply deficit using predetermined bilateral contracts and reciprocally. Our proposed approach has the following advantages: (1) owing to the proximity of the interconnected VPPs, losses in transmission can be minimized; (2) instantaneous surpluses or deficits of energy can be managed via local regionally interconnected VPPs; (3) importing renewable energy from a region with excess wind and solar energy capability can avoid the need to curtail renewable sources that cannot be managed locally; and (4) the volatile nature of VRE sources can be relieved. Consequently, the installed capacity of the power system would therefore be reduced, while improving the reliability of power system.

This work aims to procure the best energy cooperation mechanism of regionally interconnected VPPs, maximizing SW while mitigating the volatile impact of variable renewable energy sources. Therefore, the following decisions are made by solving the scheduling problem as shown in Figure 3.

(A)

Whether to trade energy with adjacent VPPs and how much energy can be sold and purchased during each period of time, t.

(B)

Whether to trade energy with the main grid and how much energy can be sold/purchased during each period of time, t.

(C)

Whether the ESS should be charged or discharged, and how much power can be charged or discharged during each period of time, t.

2.2.2. Model Assumptions

The following are the main assumptions considered in this research work:

• For economic reasons, the VPP role is considered to be centralized as a smart energy services provider.
• For the sake of simplicity, we only focused on the economic benefits of the VPP, while leaving the technical aspects of the electrical grid for future work.
• The VPP is made up of renewable energy resources, load demand, and energy storage systems.
• The VPP operators aggregate all of its coalition members’ energy offers and bids services in blocks for each hour.
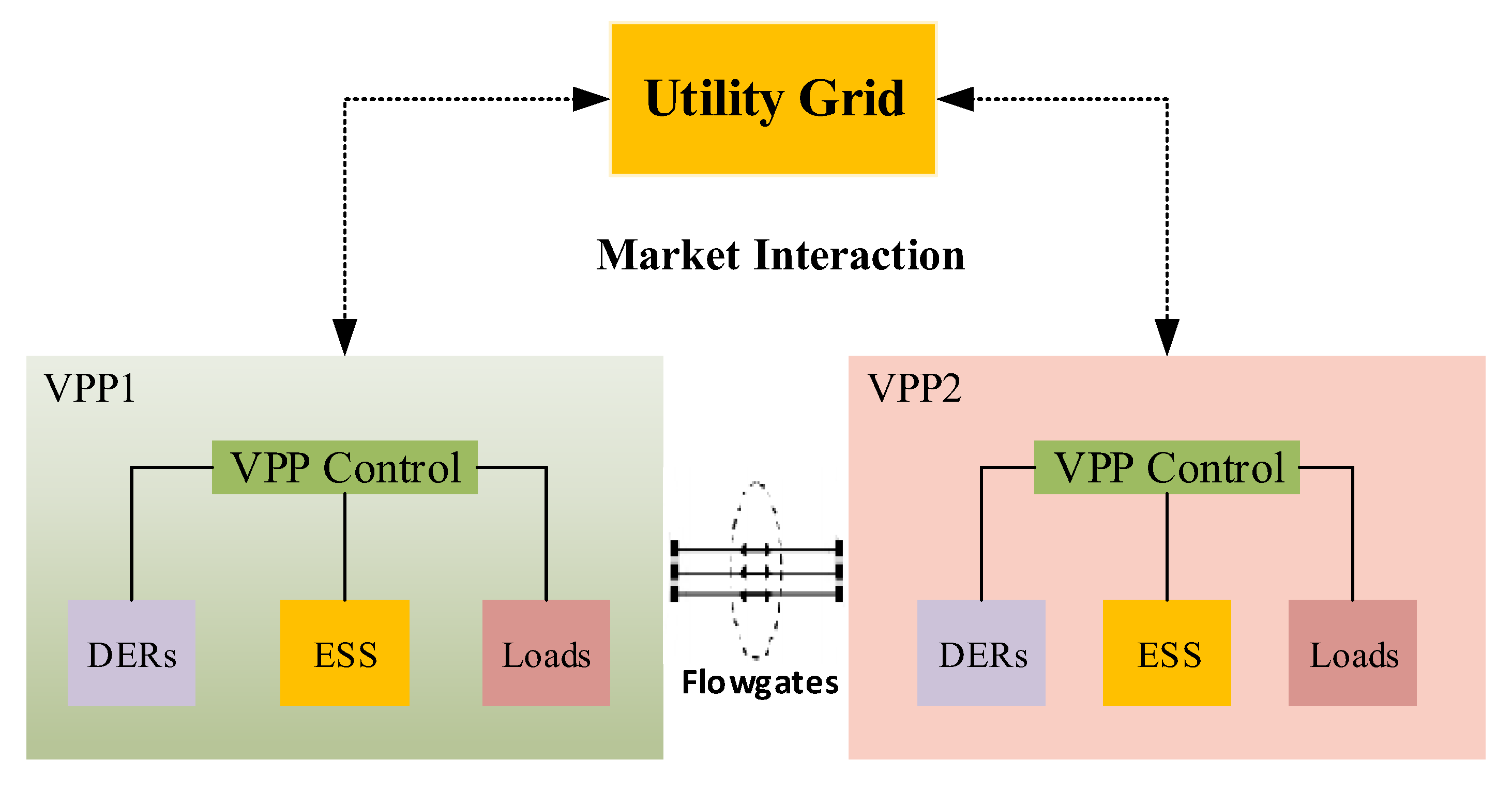
• The VPP under study is considered to be connected directly to another VPP in its neighborhood, permitting them to cooperate through bilateral contracts in the case of an energy supply deficit.

2.2.3. Solution Approach

The steps in the suggested decision-making approach, which aims to maximize the VPP’s social welfare, are as follows:

Step 1: The VPP invites bids and offers from distributed generators and neighboring VPPs for their partaking in the local energy market

Step 2: Each qualifying participant declares their resource capacity’s strength.

Step 3: The VPP analyzes historical data to estimate the performance of eligible participants who signed a contract with the VPP operators.

Step 4: The midpoint of energy pricing and DER generation will be calculated using historical data of DER generation and market price for the following 24 h.

Step5: The VPP solves the suggested decision-making problem by maximizing the social welfare of its participating members.

Step 6: The finding of the decision-making problem is communicated to both parties the energy suppliers and the buyers through the VPP operators.

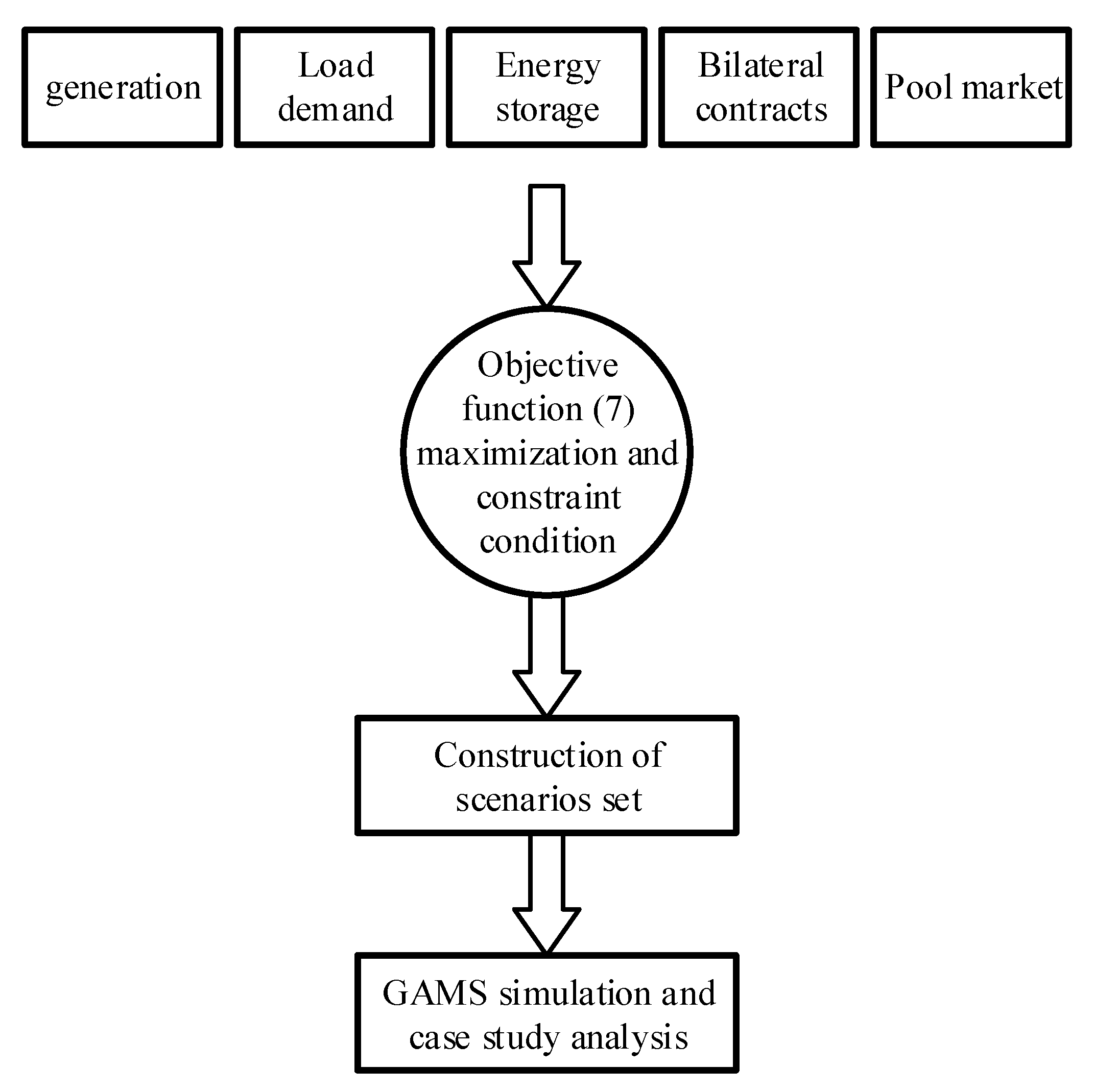
2.2.4. Objective Function

The following is the mathematical formulation of the proposed VPP model that jointly optimizes end-user benefits, while minimizing the cost of energy generation over the short-term planning horizon.

$$Maximize SW={\displaystyle \sum _{t=1}^T}\left[\begin{array}{l}{{\displaystyle P}}_{t,w}^{DEM}\cdot {{\displaystyle Cost}}_{t,w}^{DEM}+{\displaystyle \sum _{K\in Grid}}{{\displaystyle P}}_{k,t,w}^{GRID}\cdot {{\displaystyle Cost}}_{k,t,w}^{GRID}-{\displaystyle \sum _{u\in SG}}{{\displaystyle P}}_{u,t,w}^{PV}\cdot {{\displaystyle Cost}}_{u,t,w}^{PV}\\ +{\displaystyle \sum _{k\in NTP}}\left(\left({{\displaystyle VPP}}_{k,t,w}^{EXPORT}.{{\displaystyle Cost}}_{k,t,w}^{EXPORT}\right)-\left({{\displaystyle VPP}}_{k,t,w}^{IMPORT}.{{\displaystyle Cost}}_{k,t,w}^{IMPORT}\right)\right)\\ +{\displaystyle \sum _{b\in B}}\left(\left({{\displaystyle P}}_{b,t,w}^{DISCH}.{{\displaystyle Cost}}_{b,t,w}^{DISCH}\right){{\displaystyle U}}_t^{DISCH}-\left({{\displaystyle P}}_{b,t,w}^{CHAR}.{{\displaystyle Cost}}_{b,t,w}^{CHAR}\right){{\displaystyle U}}_t^{CHAR}\right)\end{array}\right]$$

(7)

where SW stands for social welfare maximization of the proposed model. ${{\displaystyle P}}_{t,w}^{DEM}$ represents the power demand of the internal consumers and ${{\displaystyle Cost}}_{t,w}^{DEM}$ is the price that is charged to the VPP’s internal consumers. ${{\displaystyle P}}_{k,t,w}^{GRID}$ represents active power sold (bought) to (from) the utility grid, and ${{\displaystyle Cost}}_{k,t,w}^{GRID}$ is the cost associated with utility. ${{\displaystyle P}}_{u,t,w}^{PV}$ denotes power generation of PVs, and ${{\displaystyle Cost}}_{u,t,w}^{PV}$ is the cost of PVs generators. ${{\displaystyle VPP}}_{k,t,w}^{IMPORT}$/${{\displaystyle VPP}}_{k,t,w}^{EXPORT}$ represent the import/export of active power through GSP k, and ${{\displaystyle Cost}}_{k,t,w}^{IMPORT}$/${{\displaystyle Cost}}_{k,t,w}^{EXPORT}$ refer to import/export cost of the VPP through GSP k. ${{\displaystyle P}}_{b,t,w}^{CHAR}$/${{\displaystyle P}}_{b,t,w}^{DISCH}$ denote charge/discharge of the energy storage unit, and ${{\displaystyle Cost}}_{b,t,w}^{CHAR}$/${{\displaystyle Cost}}_{b,t,w}^{DISCH}$ represent the cost of charging/discharging of the energy storage unit. ${{\displaystyle U}}_t^{CHAR}$/${{\displaystyle U}}_t^{DISCH}$ are binary variables, representing charging/discharging of the energy storage unit.

Constraints

Constraints (8) and (9) represent the minimum and maximum installed capacity of PV generators.

$$0\le {{\displaystyle P}}_{u,t,w}^{PV.MIN}$$

(8)

$${{\displaystyle P}}_{u,t,w}^{PV.MIN}\le {{\displaystyle P}}_{u,t,w}^{PV.MAX}$$

(9)

The hourly power exchanges between the VPPs and the electricity market via GSPs are limited by the interconnection capacity, and the hourly consumer demand is shown by Constraint (10).

$$-\zeta k.{{\displaystyle P}}_k^{EXCHANGE.MAX}\le {{\displaystyle P}}_{(k,t,w)}^{Grid}\le {{\displaystyle P}}_k^{EXCHANGE.MAX}$$

(10)

Constraints (11) and (12) represent the minimum and maximum power sold and/or purchased via neighboring transaction points.

$$0\le {{\displaystyle P}}_{k,f,b}^{SOLD}\le {{\displaystyle P}}_{k,f,b}^{SOLD.MAX}$$

(11)

$$0\le {{\displaystyle P}}_{k,f,b}^{BOUGHT}\le {{\displaystyle P}}_{k,f,b}^{BOUGHT.MAX}$$

(12)

Constraints (13) and (14) refer to the power sold and/or purchased for each contract is equal to the amount of power specified in each block.

$${{\displaystyle P}}_{k,f}^{SOLD}={\displaystyle \sum _b{{\displaystyle P}}_{k,f,b}^{SOLD}}$$

(13)

$${{\displaystyle P}}_{k,f}^{BOUGHT}={\displaystyle \sum _b{{\displaystyle P}}_{k,f,b}^{BOUGHT}}$$

(14)

The maximum capacity of power sold/purchased in each contractual arrangement is expressed by Constraints (15) and (16).

$${{\displaystyle P}}_{k,f}^{SOLD}\le {{\displaystyle P}}_f \cdot {{\displaystyle \eta }}_{k,f}^{SOLD}$$

(15)

$${{\displaystyle P}}_{k,f}^{BOUGHT}\le {{\displaystyle P}}_f \cdot {{\displaystyle \eta }}_{k,f}^{BOUGHT}$$

(16)

Constraint (17) refers to the state of charge of the battery. The minimum and maximum state of charge and discharge of unit b at time t are represented by Constraints (18) and (19). The minimum and maximum storage capacity of unit b at time t is represented by Constraint (20). Charging/discharging of the energy storage unit b at the same time period is not allowed, as stated by Equation (21).

$${{\displaystyle P}}_{b,t}^{CHAR}={{\displaystyle P}}_{b(t-1)}^{CHAR}+{{\displaystyle P}}_{b,t}^{CHAR}\times {{\displaystyle \eta }}_b^{CHAR}-\frac{{{\displaystyle P}}_{b,t}^{DISCH}}{{{\displaystyle \eta }}_b^{DISCH}}$$

(17)

$$0\le {{\displaystyle P}}_{b,t,w}^{CHAR}\le {{\displaystyle P}}_{b,t}^{CHAR.MAX} .{{\displaystyle U}}_t^{CHAR}$$

(18)

$$0\le {{\displaystyle P}}_{b,t,w}^{DISCH}\le {{\displaystyle P}}_{b.t}^{DISCH.MAX} .{{\displaystyle U}}_t^{DISCH}$$

(19)

$${{\displaystyle P}}_{b,t}^{ENERGY STORED.MIN}\le {{\displaystyle P}}_{(b,t)}^{ENERGY STORED}\le {{\displaystyle P}}_{b,t}^{ENERGY STORED.MAX}$$

(20)

$${{\displaystyle U}}_t^{CHAR}+{{\displaystyle U}}_t^{DISCH}\le 1$$

(21)

Constraint (22) represents the power exchange between regionally interconnected VPPs via NTPs at time t. The import/export between regionally interconnected VPPs is constrained by Equations (23) and (24).

$${{\displaystyle VPP}}_{(k,t)}^{EXCHANGE}={{\displaystyle VPP}}_{k,t,w}^{EXPORT}\cdot {{\displaystyle U}}_t^{EXPORT}-{{\displaystyle VPP}}_{k,t,w}^{IMPORT}\cdot {{\displaystyle U}}_t^{IMPORT}$$

(22)

$$0\le {{\displaystyle VPP}}_{k,t,w}^{EXPORT}\cdot {{\displaystyle U}}_t^{EXPORT}$$

(23)

$$0\le {{\displaystyle VPP}}_{k,t,w}^{IMPORT}\cdot {{\displaystyle U}}_t^{IMPORT}$$

(24)

Considering the VPP’s commitments to buy and sell power through bilateral contracts and load demand within the VPPs setting, the VPPs electrical energy balance in each period of time is represented as (24).

$${\displaystyle \sum _{u=SG}{{\displaystyle P}}_{u,t,w}^{PV}}-{\displaystyle \sum _{k\in NTP}{\displaystyle \sum _f{{\displaystyle P}}_{k,t,f}^{BOUGHT}}}-{\displaystyle \sum _{k\in Grid}{{\displaystyle P}}_{k,t,w}^{GRID}}+{\displaystyle \sum _{b\in B}{{\displaystyle P}}_{b,t,w}^{DISCH}}\ge {{\displaystyle P}}_{t,w}^{DEM}+{\displaystyle \sum _{k\in NTP}{\displaystyle \sum _f{{\displaystyle P}}_{k,t,f}^{SOLD}}}+{\displaystyle \sum _{b\in B}{{\displaystyle P}}_{b,t,w}^{CHAR}}$$

(25)

2.2.5. VPP Electricity Market Model

The VPP electricity market model is presented in Figure 4. The VPP market operator (VPP-MO) is a smart energy services provider that allows end-user participation in the electricity market, regulates operational facilities, and purchases active power through bilateral or pool contracts. Every hour, distributed generators (DGs) and flexible loads (FLs) submit their offers and bid prices for active power in the form of blocks to the virtual power plant market (VPPM). The VPP-MO then combines offers and bid prices in order to maximize the overall social welfare (SW). In the proposed energy market design, the VPP-MO has two key tasks: first, it receives VPPM demand bids, before makes a collective bid to the wholesale power market. Second, it will obtain distributed generators and flexible load schedules from the wholesale power market one day ahead of time, based on market prices.

The VPP-MO would receive bids from the VPPM, and the VPP-MO would then notify them of the amount of electricity that will be allocated. The quantity of power traded with the distribution grid is allocated by the VPP-MO, therefore it is known to the VPP-MO ahead of time, minimizing the VPPM’s uncertainty. Once the power transfer with the distribution grid is known, as well as the VPPM schedule for the next 24 h, the VPPM would be able to deal with the energy market scheduling problem to better schedule its distributed generators and flexible loads. For the purpose of clarity, the design of the proposed VPP electricity market is highlighted in Figure 4.

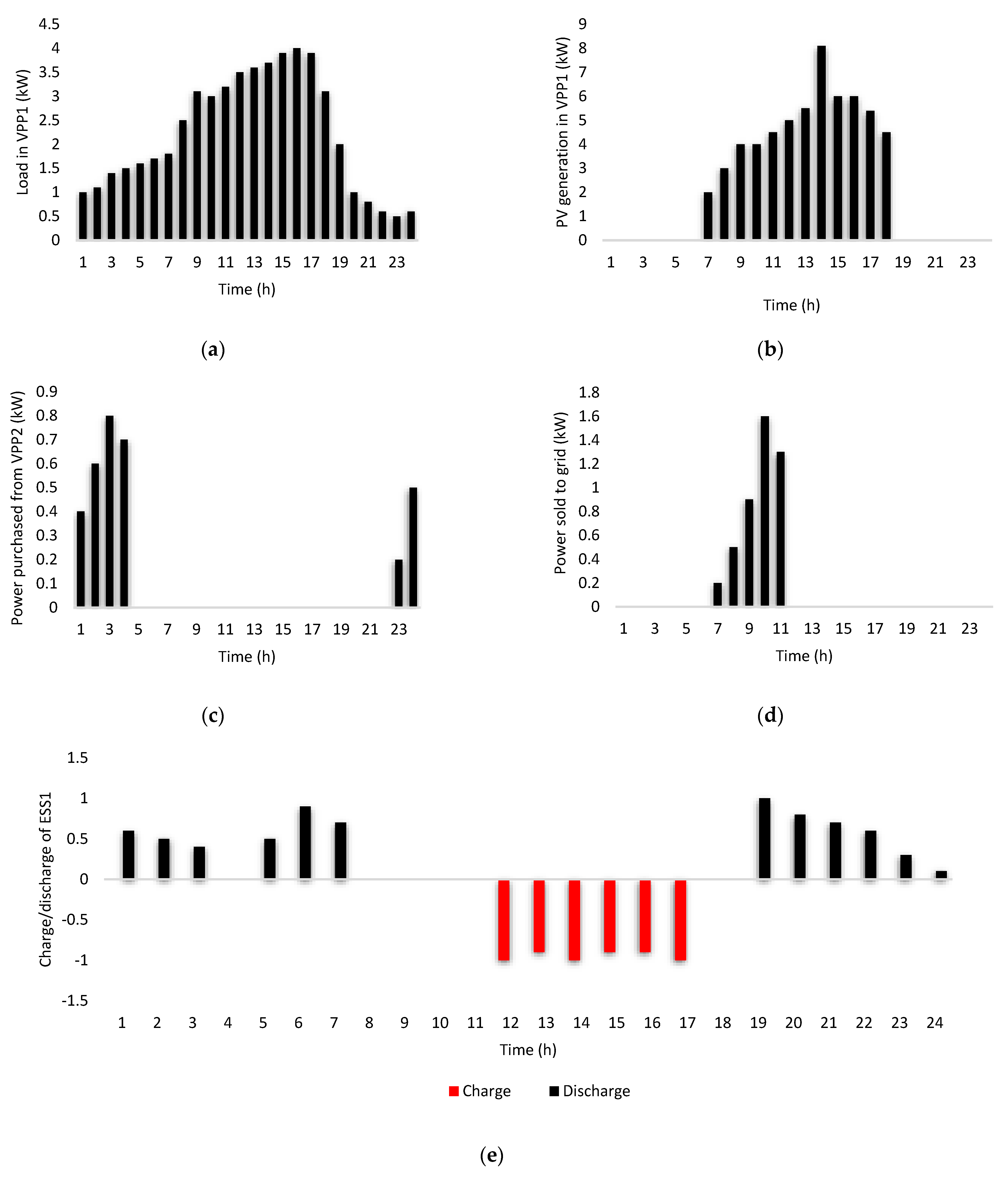
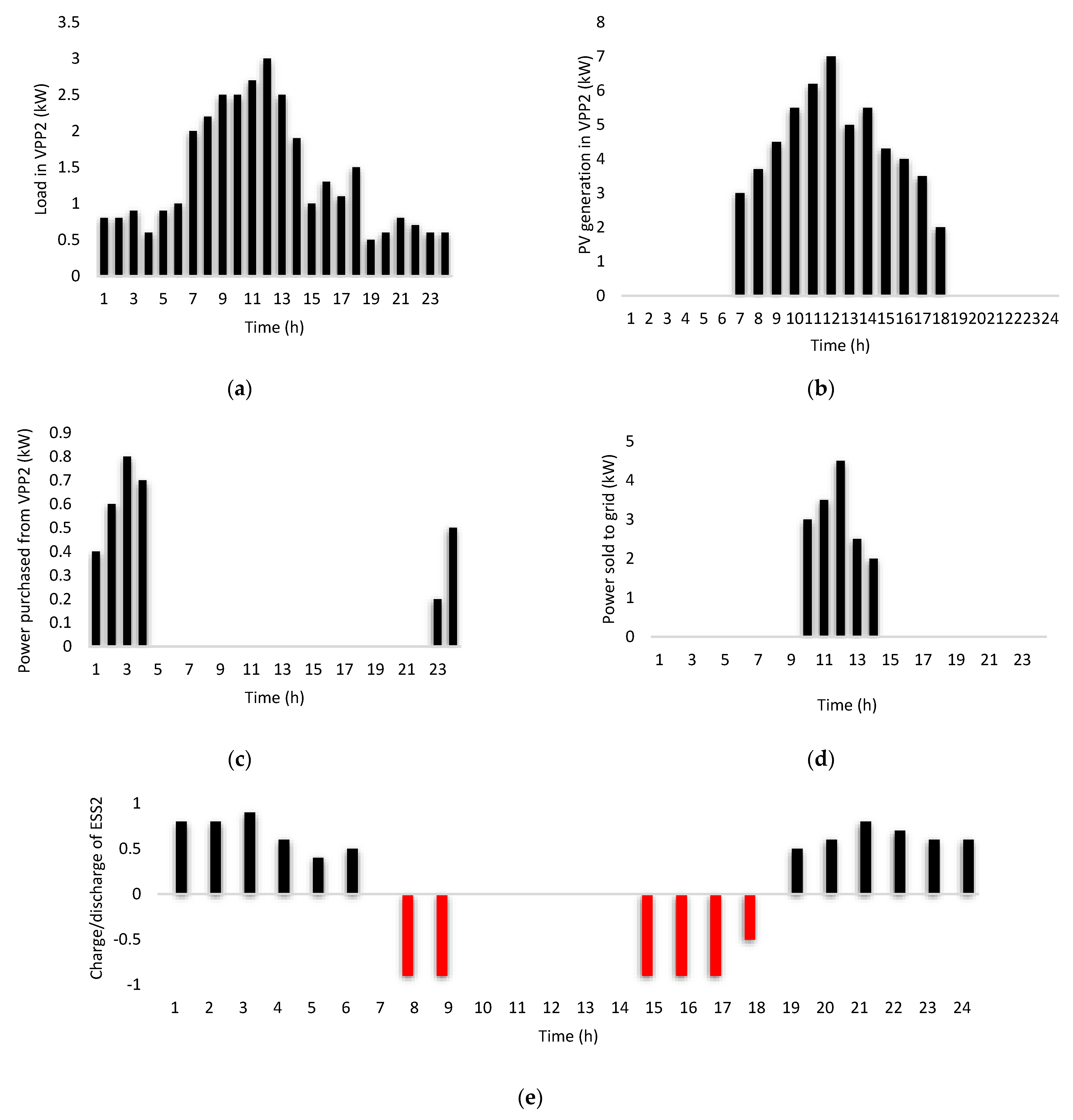
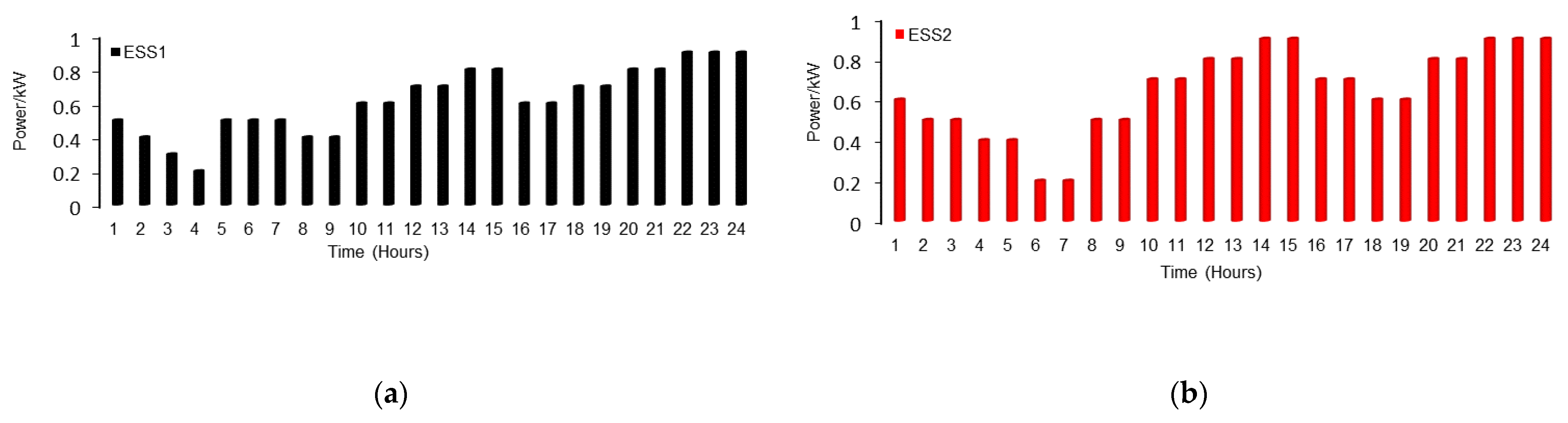
3. Case Study, Simulation Results and Discussion

To validate the correctness of the proposed model, a case study of interconnected VPPs in grid-connected mode is presented. The main focus of the proposed approach is to study the collaboration and interaction of regionally interconnected VPPs using energy-flow gates. A case study approach is carried out with the objective of maximizing mutual economic benefits of interactive VPPs, while minimizing the uncertain nature of VRE sources. The resulting model is coded and simulated in GAMS [32,33,34,35,36]. The proposed approach is trialed and evaluated in a citizen community, consisting of two diverse interconnected VPPs. Both VPPs are made up of electrical loads, PV units, and energy storage systems. The number of scenarios has been limited to 24 for the sake of computational burden relaxation and improving the speed and accuracy of addressing the problem.

The hourly load profiles of regionally interconnected VPPs are provided by Figure 5a,b. The generation profile of PV generator is shown in Figure 6. The generator deviation of the PV unit is fixed at 0.5 kW. All DGs are assumed to generate active power at the unity power factor, with no reactive power being requested or produced. Power exchanges are limited to 50 kW.

Table 2. Parameters of ESS.

Index for ESS	ESS Capacity/kWh	Charging & Discharging Limits/kW	Charging & Discharging Efficiencies	Initial Values of SOC
ESS1	10	3 3	0.95 0.94	0.50
ESS2	11	3 3	0.95 0.94	0.60

provides energy storage system parameters values and

Table 3. Electricity tariffs (unit: $/kWh).

Time Periods Purchasing Price Selling Price Exchange Price in (h) from the Grid ($) to the Grid ($) the VPPS ($)
Peak (11,12,13 14,19,20,21,22)	1.32	1.00	1.16
Shoulder (9,10,15 16,17,18,23,24)	0.82	0.58	0.72
Valley (1,2,3,4 5,6,7,8)	0.33	0.20	0.26

provides the time of use tariff.

The key to regionally interconnected VPPs cooperation is to take advantage of the diverse characteristics of aggregated resources at different locations. The cooperation and contribution characteristics of both VPPs are highlighted in Figure 7 and Figure 8.

According to Figure 7a, the hourly load demand of the VPP1 is higher than its internal renewable generation and is shown in Figure 7b during certain hours (i.e., 1, 2, 3, 4, 23, and 24). Therefore, it cannot fulfil its internal electrical load demand. As a result, VPP1 buys a total of 2.8 kWp of electricity regionally from VPP2, as is shown in Figure 7c, using energy-flow gates at a cheaper cost to satisfy its internal load demand. Figure 7d also shows that, in some set periods (i.e., 7, 8, 9, 10, and 11), the internal generation of the VPP1 exceeds its load demand; therefore, it feeds surplus power back into the utility grid and earns economic benefits in return. It is also apparent from Figure 7e that when energy demand exceeds energy generation, as shown in certain hours (i.e., 1, 2, 3, 4, 5, 6, 19, 20, 21, 22, 23, and 24), the ESS1 is scheduled to dispatch the stored energy to meet its internal load requirement. While the ESS1 is charging during hours 12, 13, 14, 15, 16, 17, and 18 due to more generation and less demand for electricity, this mitigates the dependency of VPP1 on the utility grid, while also lowering its overall energy cost. Therefore, this approach makes a contribution to the stability of the power grid at a local level.

According to Figure 8a, VPP2 has a higher load demand than its internal PV generation, as shown in Figure 8b during certain hours (i.e., 5, 6, 21, and 22), and it cannot satisfy its own load demand. Therefore, it buys a total of 2.3 kWp of energy regionally from VPP1 via energy-flow gates, as shown in Figure 8c, at a cheaper cost to fulfil its load requirements. It is also evident from Figure 8d that, during certain set hours (i.e., 10, 11, 12, 13, 14), the VPP2 sells the surplus power back to the utility grid and earns economic rewards. Figure 8e shows that the ESS2 is scheduled to supply the energy stored to fulfil domestic load requirements during certain hours (i.e., 1, 2, 3, 4, 5, 6,1 9, 20, 21, 22, 23, and 24), while it charges during hours 8, 9, 15, 16, 17, and 18. As a result, the energy procurement of the VPP2 from the utility grid mitigates demand and also overall energy cost of the VPP2. Hence, this strategy makes a contribution to the stability of the power system.

The state of charge (SOC) profiles of ESS1 and ESS2 are highlighted by Figure 9a,b. Both (ESS1 and ESS2) are set to discharge during certain hours (i.e., 1, 2, 3, 4, 5, 6, 19, 20, 21, 22, 23, and 24), and charge during certain hours (i.e., 8, 9, 12, 13, 14, 15, 16, 17, and 18) to fulfil their respective load satisfaction duty or attain the needed SOC levels. Regardless of their initial SOC levels, both ESSs can reach the required SOC level specified by their respective users. This confirms that the proposed approach is capable of scheduling ESSs to fulfil their consumers load demand requirements at an acceptable level.

Based on simulation and numerical studies, it can be inferred that energy exchange of regionally interconnected VPPs in grid-connected mode and the utilization of energy storage systems can make local coordination of renewable energy resources easier under the VPP setting, thereby reducing reliance and costly energy purchase from the utility grid during peak-hours, lowering overall energy cost and maximizing end-user’s satisfaction and benefits. This makes contributions to the reliability and stability of the power grid.

4. Conclusions

In this paper, a new and flexible interactive mechanism of regionally interconnected VPPs is designed and developed that operates collaboratively in a grid-connected mode. The VPP electricity market mechanism is designed and developed. The proposed approach utilized energy-flow gates to facilitate a direct energy trade between regionally interconnected VPPs. The optimal dispatch of PV and the ESS of both VPPs operating in a grid-connected mode is carried out with the objective of maximizing the overall electricity market social welfare in a way which is subject to system constraints. After a comprehensive investigation of the case study, the following conclusions are drawn.

• The strategy is advantageous as it supports local energy generation and consumption while simultaneously improving interconnected VPP’s commercial benefits and easing peak load demand on the grid.
• The supply reliability and efficiency can be improved in the event of reduced generation at one VPP. The power can be dispatched at a lower cost by another VPP on a local level.
• This method allows the cross-border import and export of renewable generation using energy-flow gates. The volatile nature of renewable energy can be diversified in interconnected VPPs.
• The ESS accomplishes a very considerable level of performance in terms of flattening the load curve.
• The implementation of the cross-border cooperative model allows local market systems to dispatch energy between interconnected VPPs at the lowest possible cost, leading to lower total costs for end-users (on both sides) and also less reliance on the main grid for interconnected VPPs. Hence, the proposed strategy could be executed in real-world applications to assist VPPs decision makers in determining the best possible collaborative operation of two or more neighboring VPPs in grid-connected mode.

However, there are some limitations that will need to be further addressed in our subsequent work, including the cost of ESS and the technical aspects of VPP. We will concentrate on these elements in our upcoming work.