Single Phase T-Type Multilevel Inverters for Renewable Energy Systems, Topology, Modulation, and Control Techniques: A Review
Abstract
:1. Introduction
2. Similarity between Neutral Point Clamped (NPC)
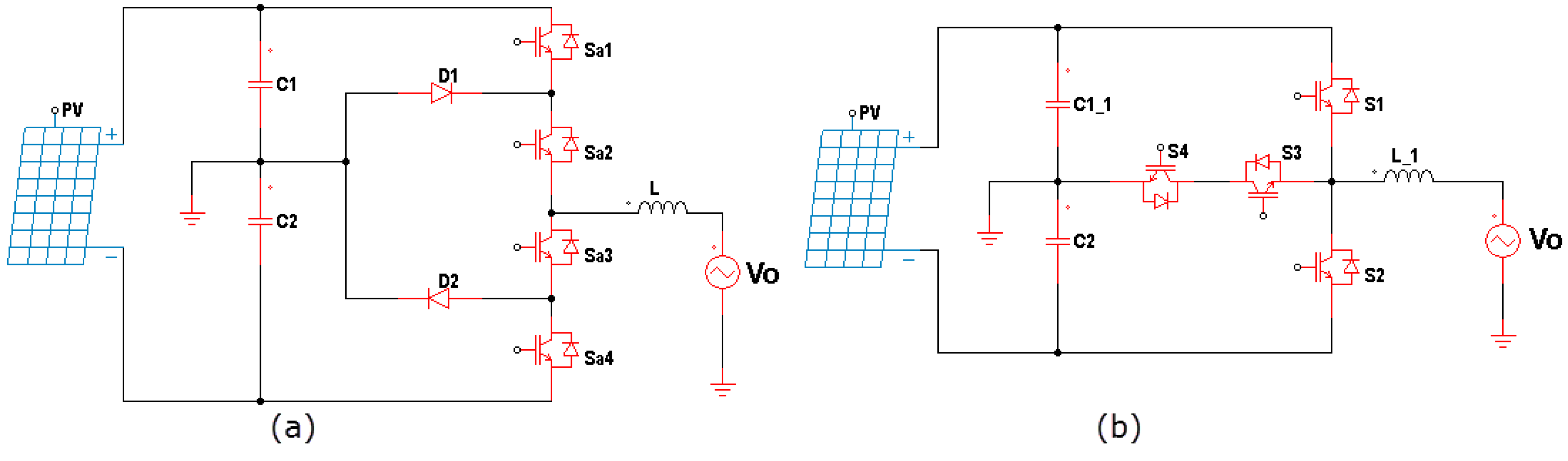
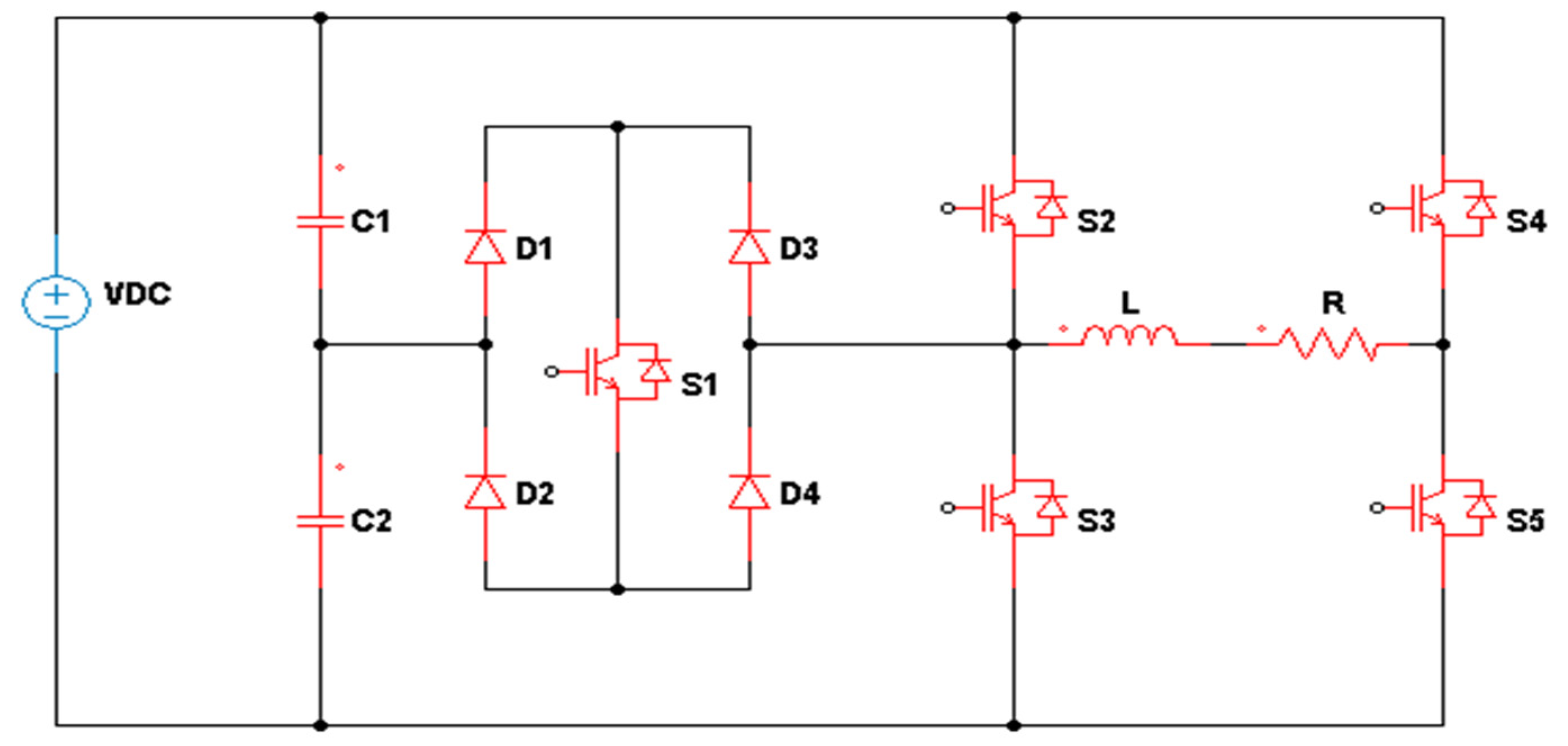
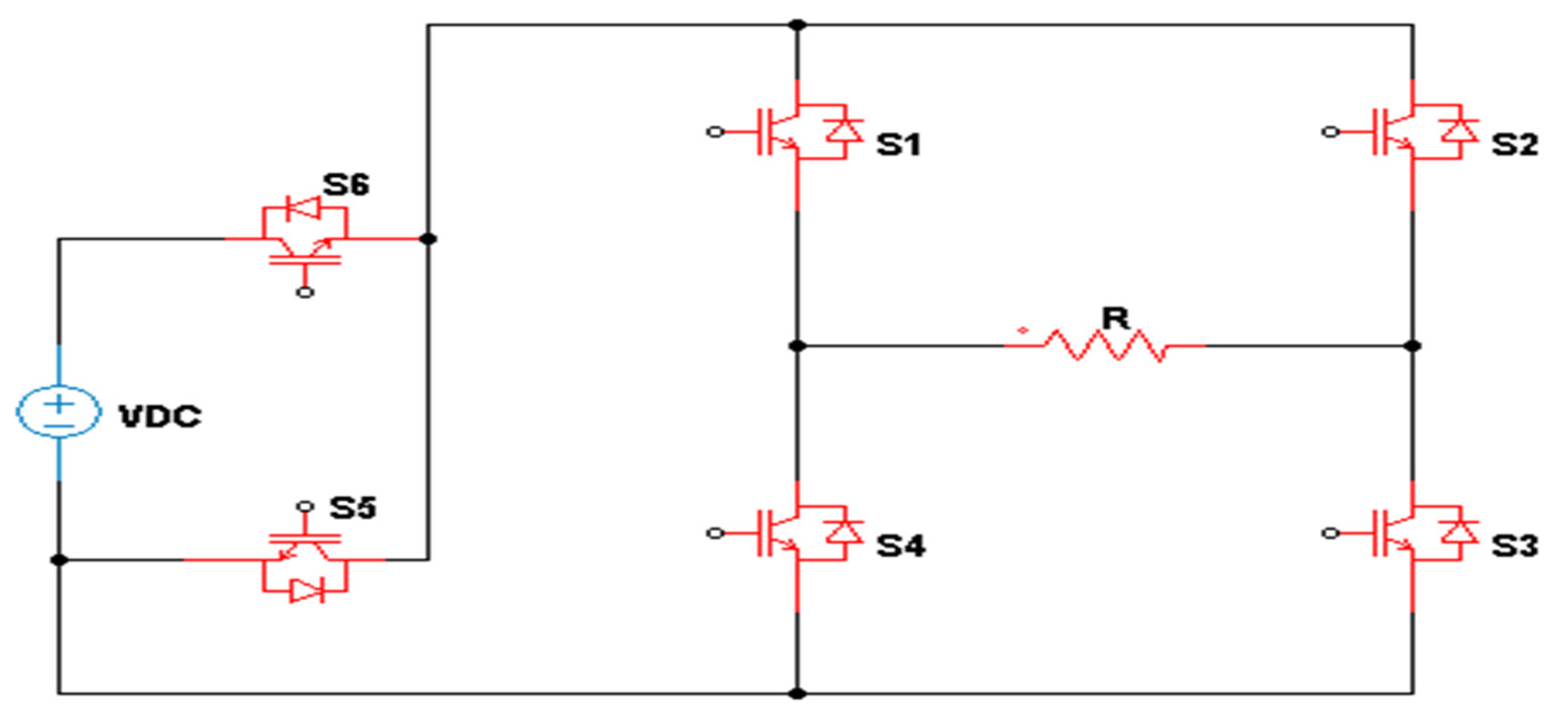
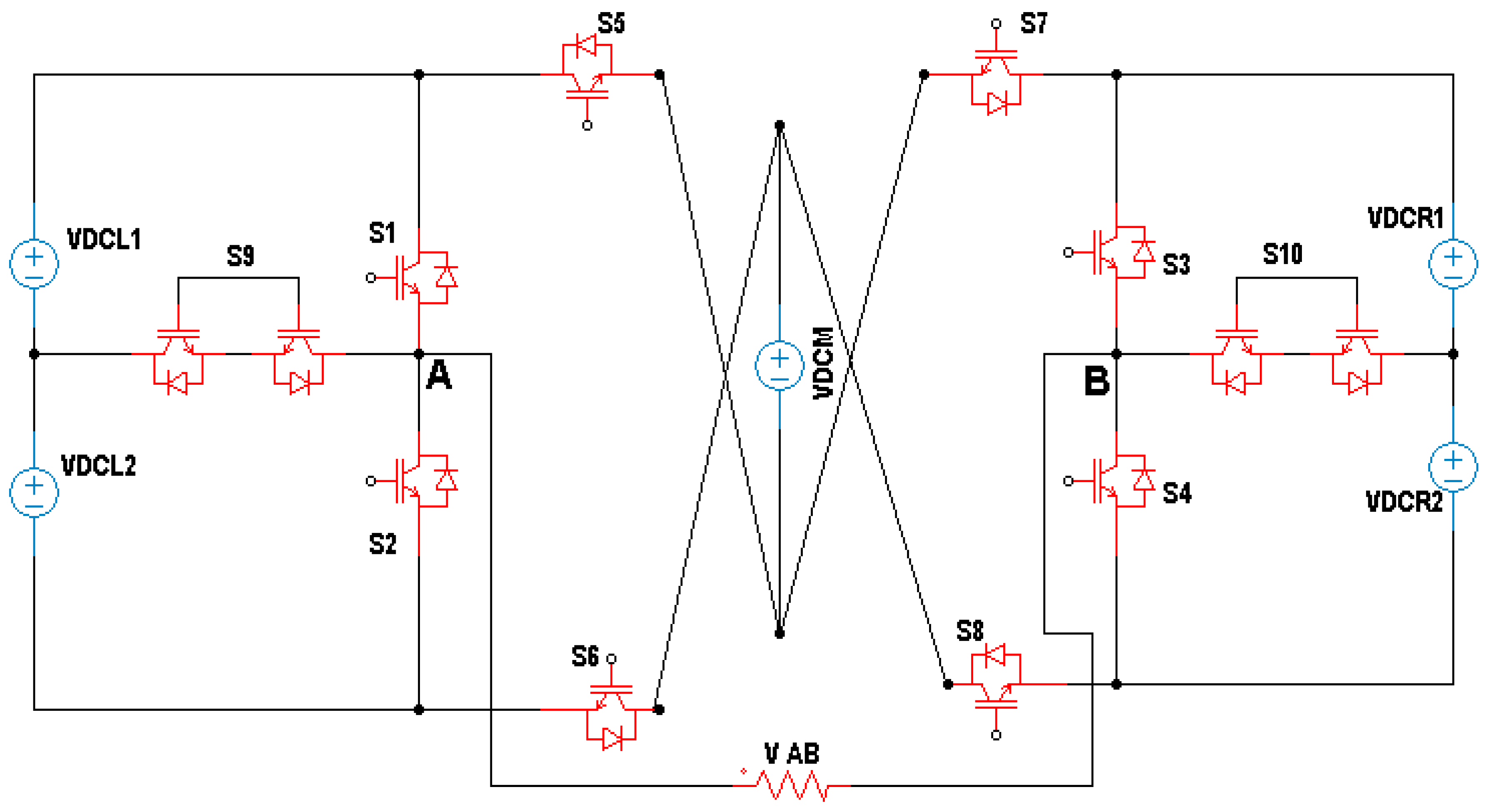
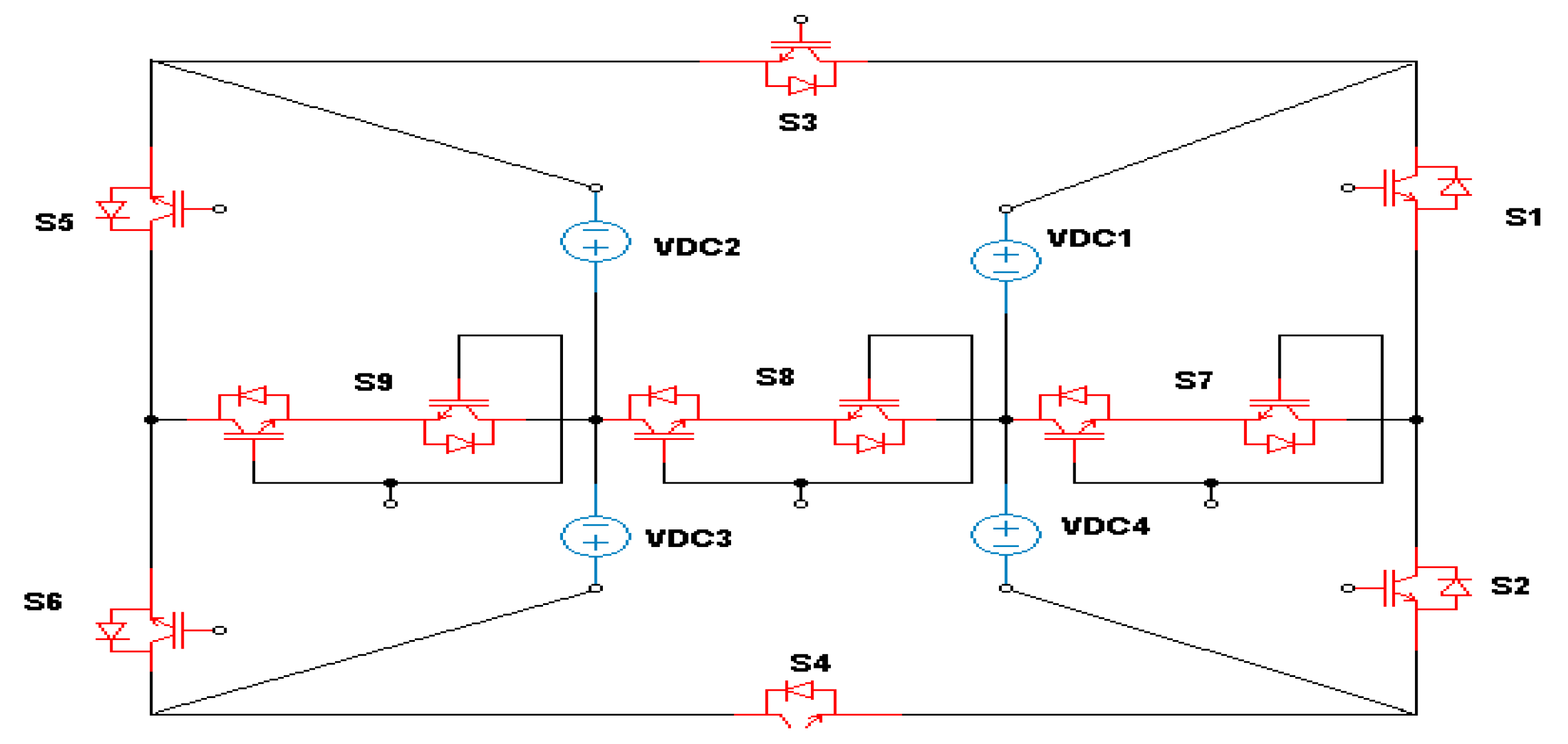
3. Topologies of T-Type MLIs
3.1. Simple Designs
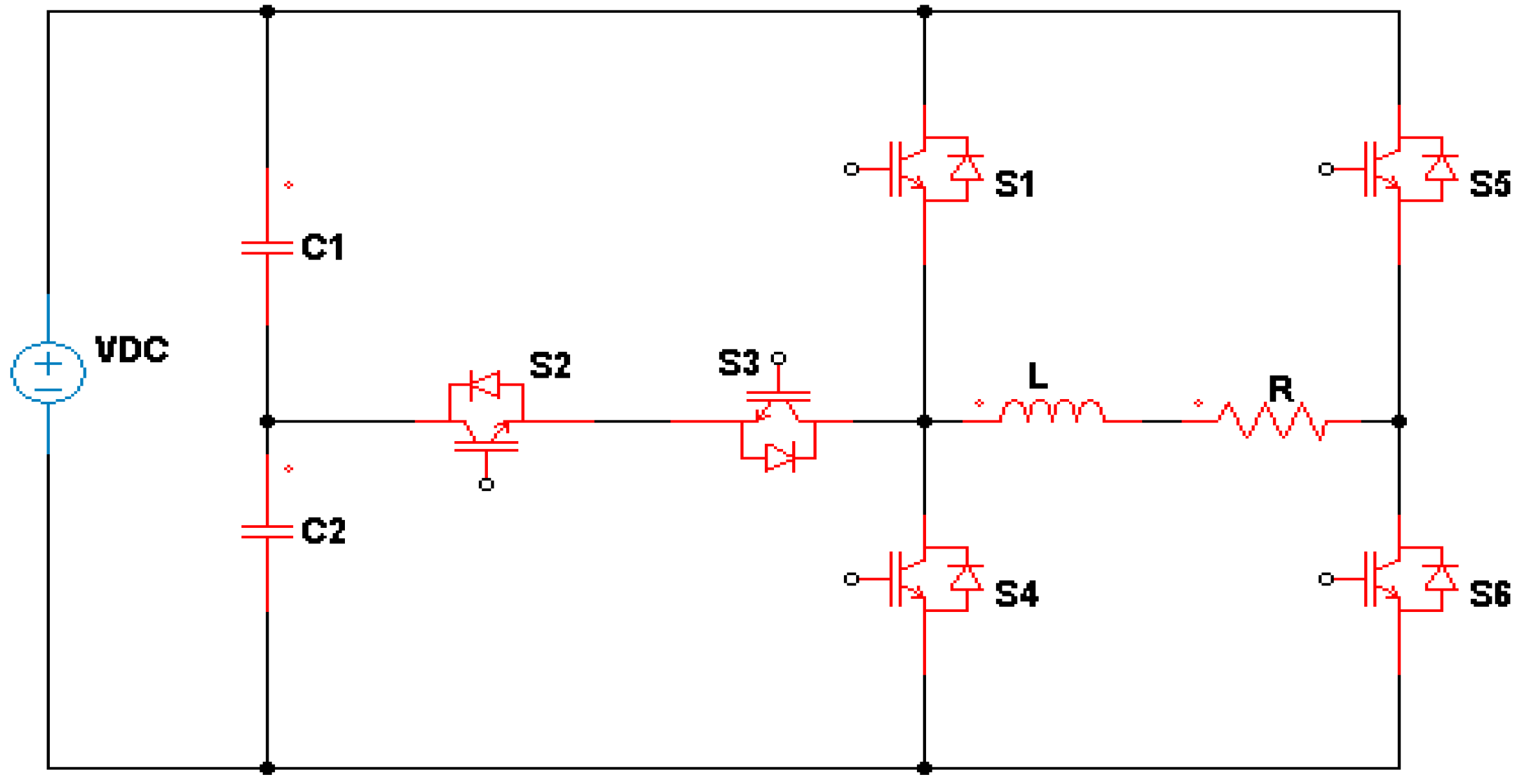
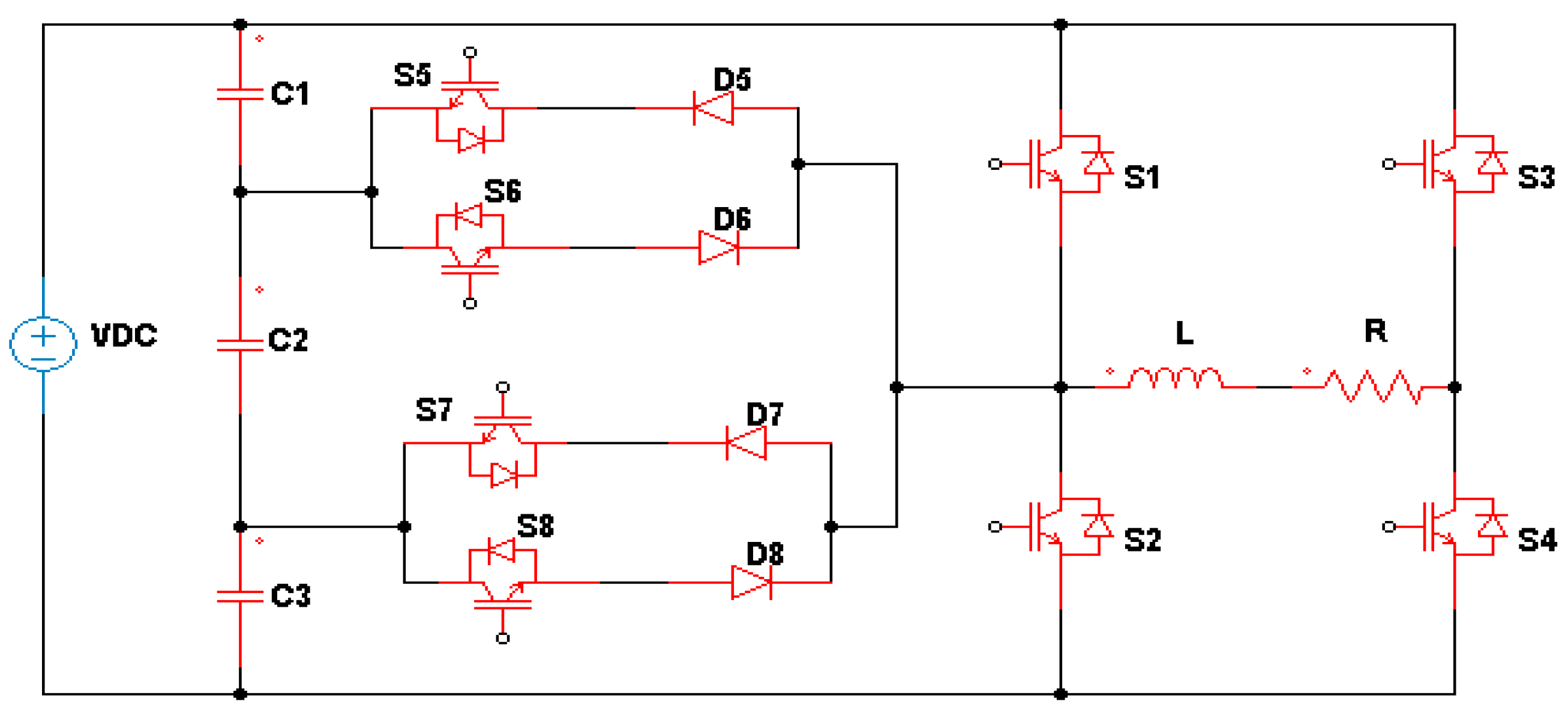
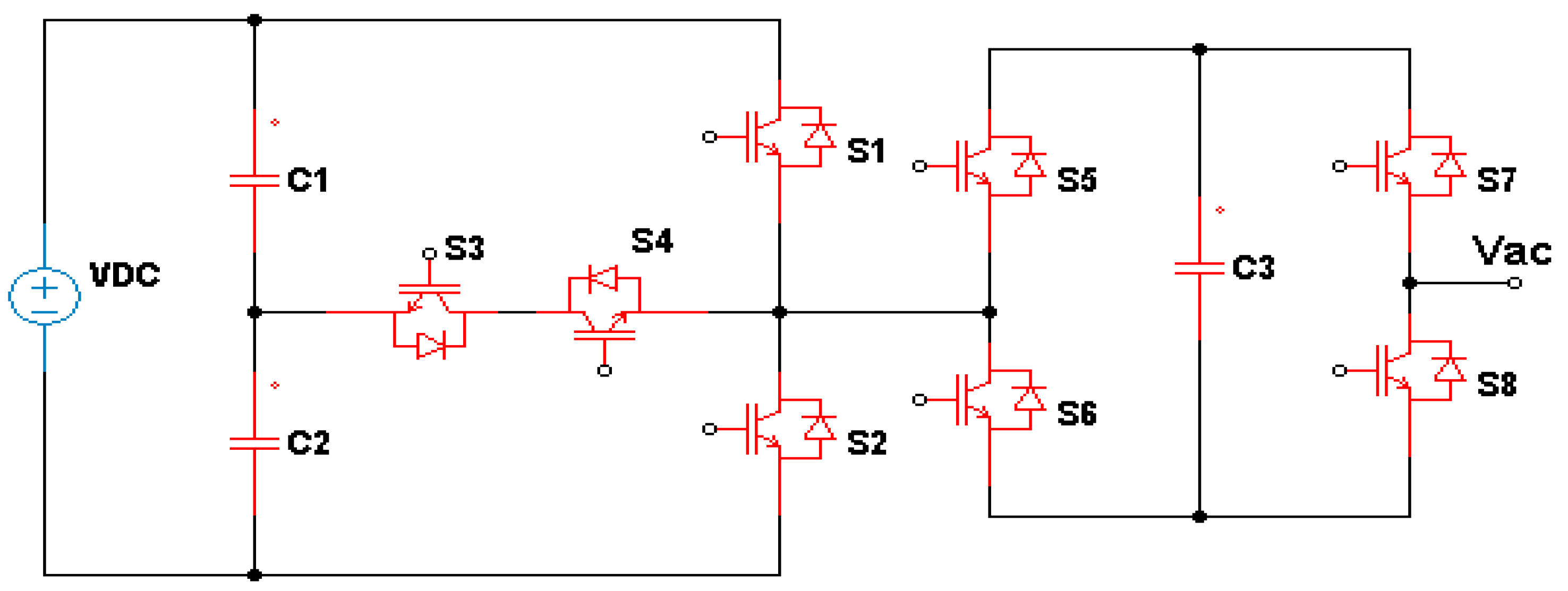
3.2. Complex Designs
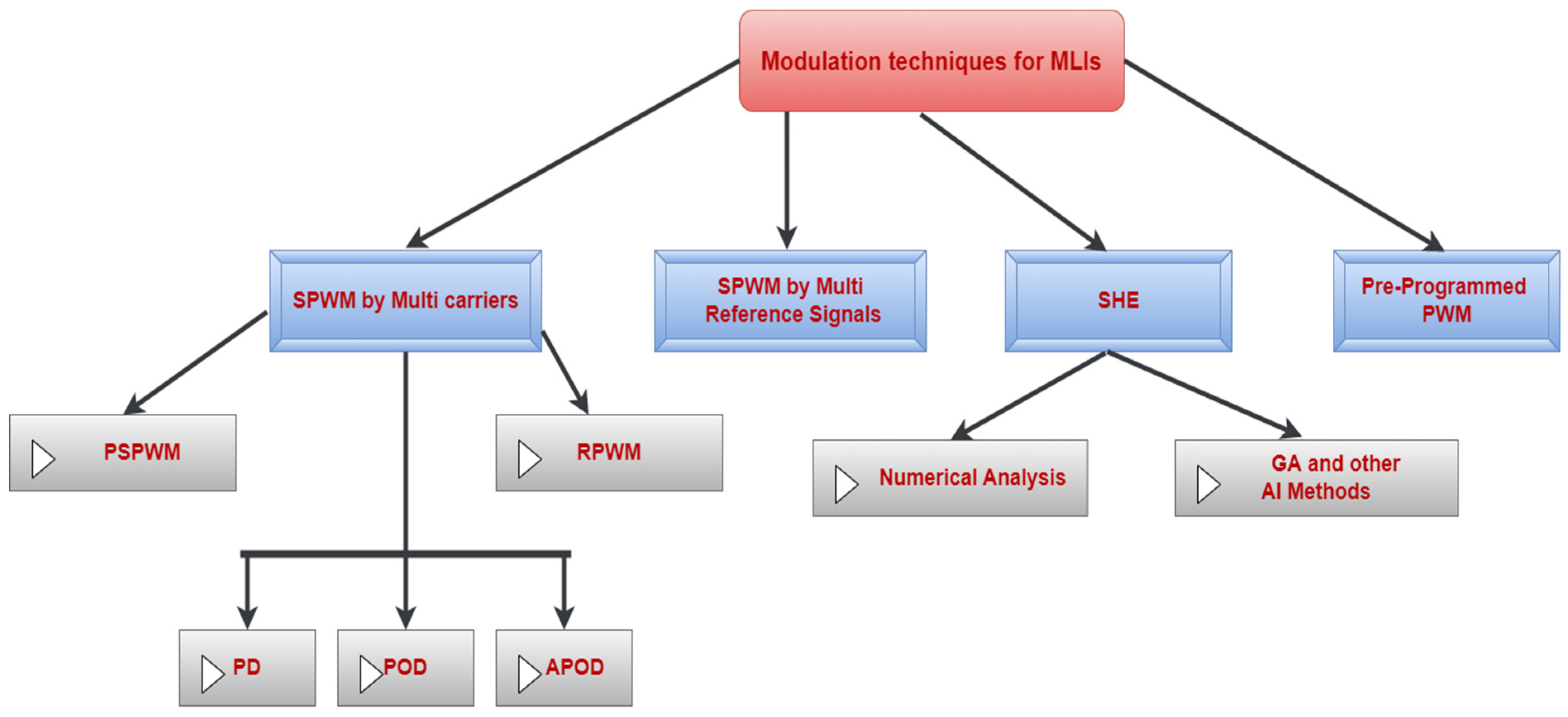
4. Modulation Techniques
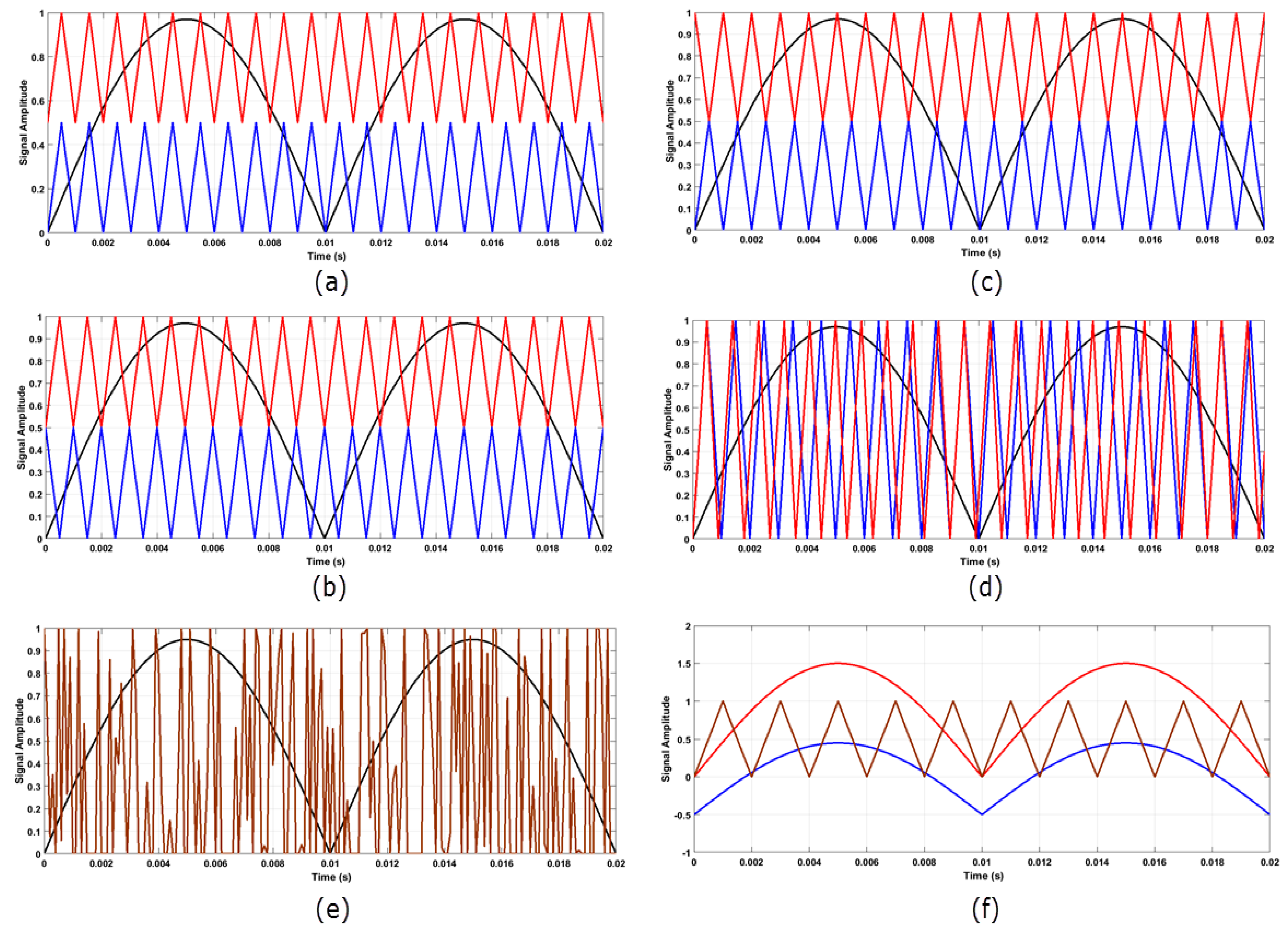
4.1. SPWM by Multi-Carriers
4.1.1. PD, POD, and APOD
4.1.2. PSPWM
4.1.3. RPWM
4.2. SPWM by Multi Reference Signals
4.3. Selective Harmonics Elimination (SHE)
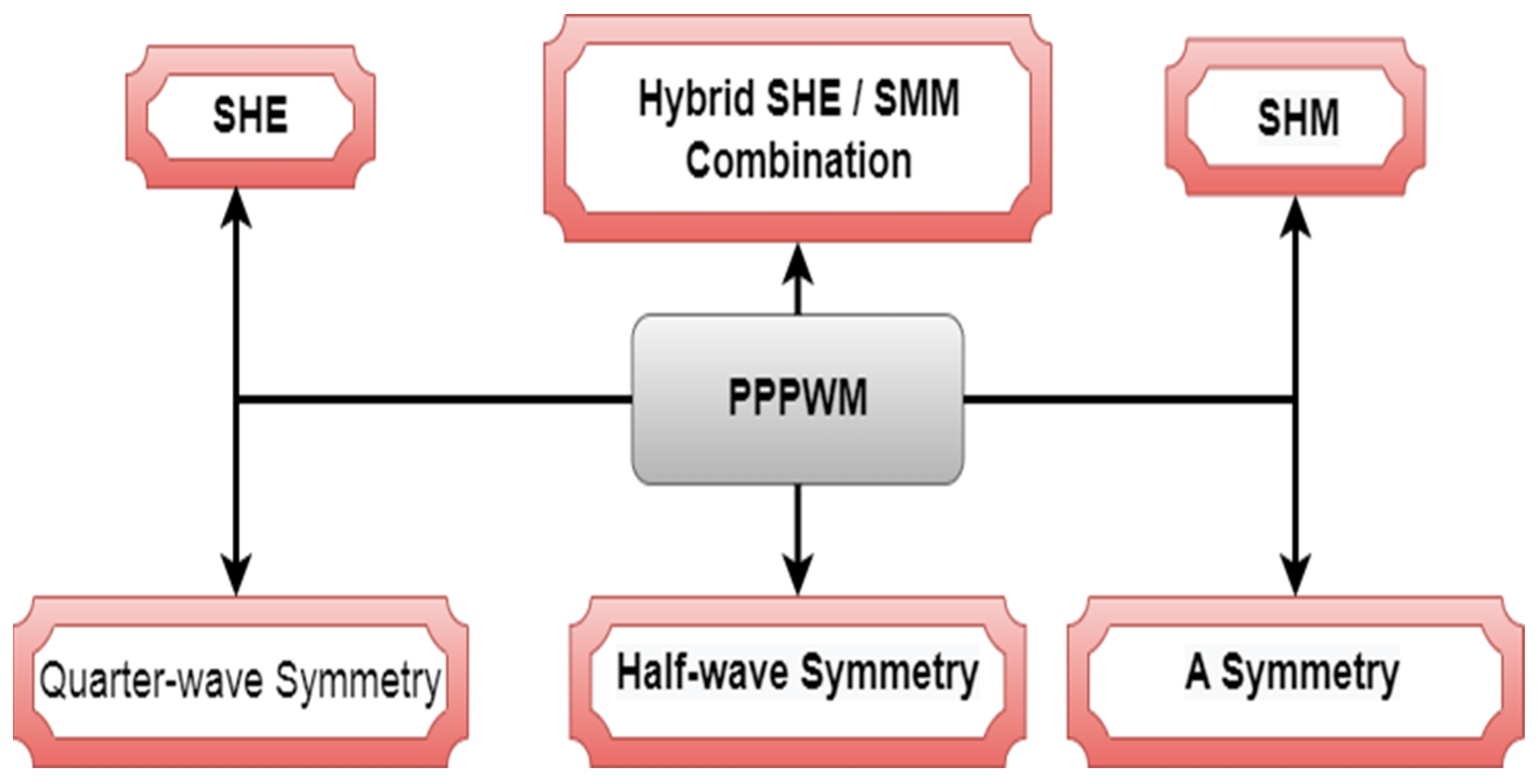
4.4. Pre-Programmed PPPWM
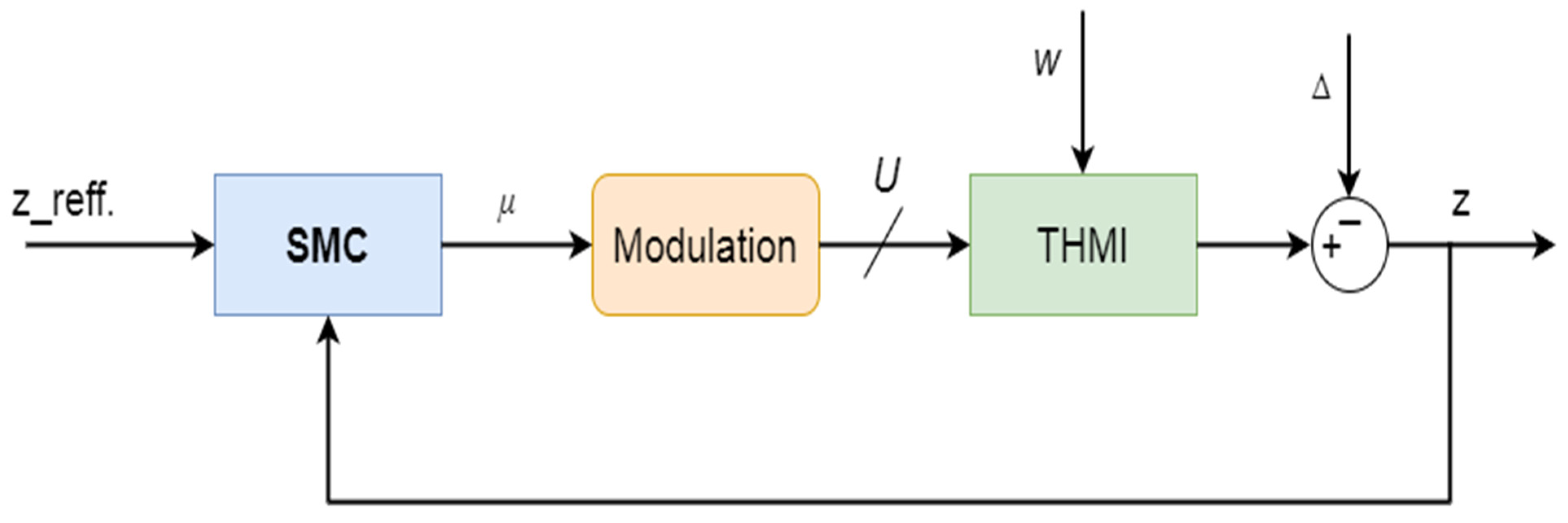
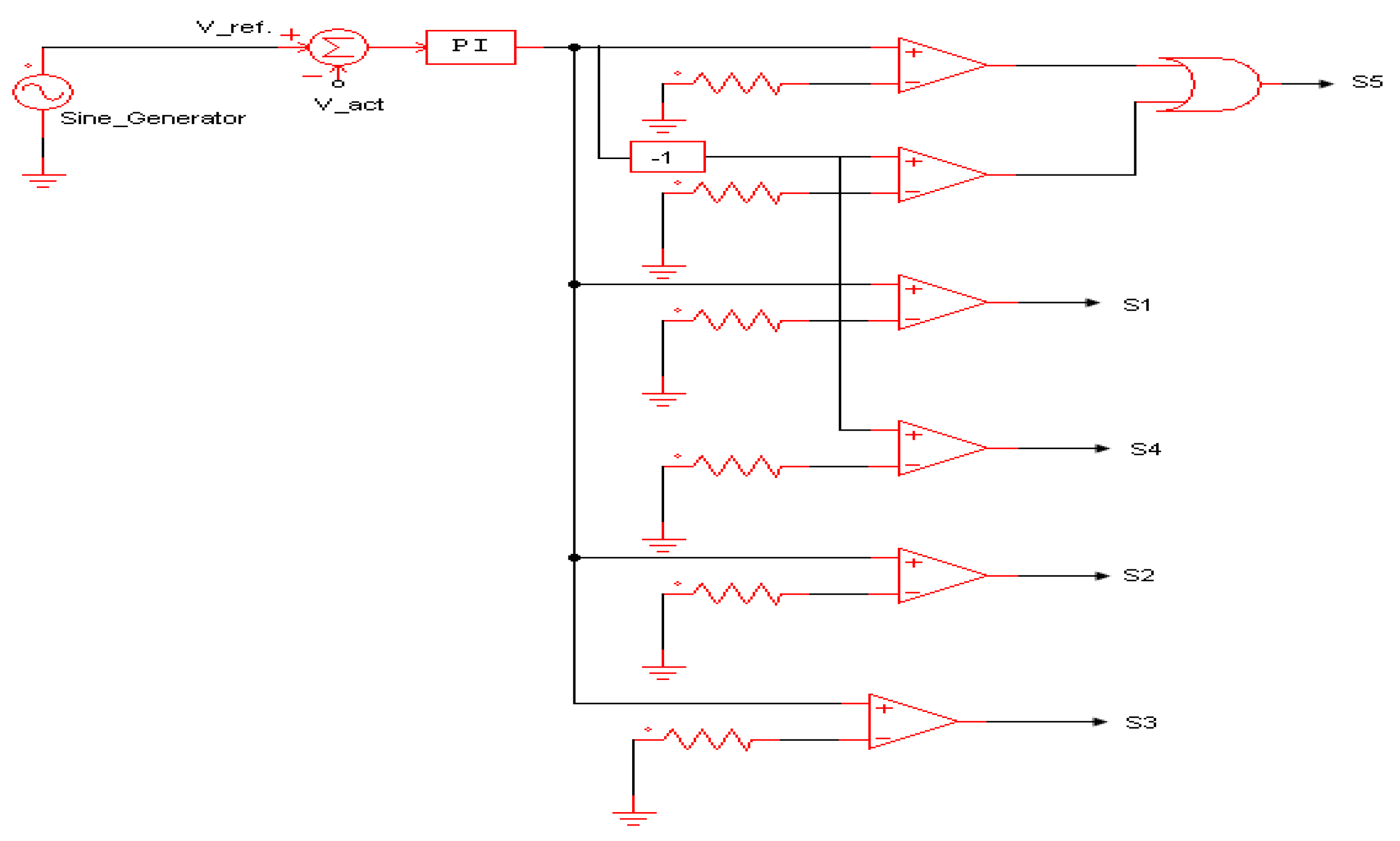
5. Output Voltage Control
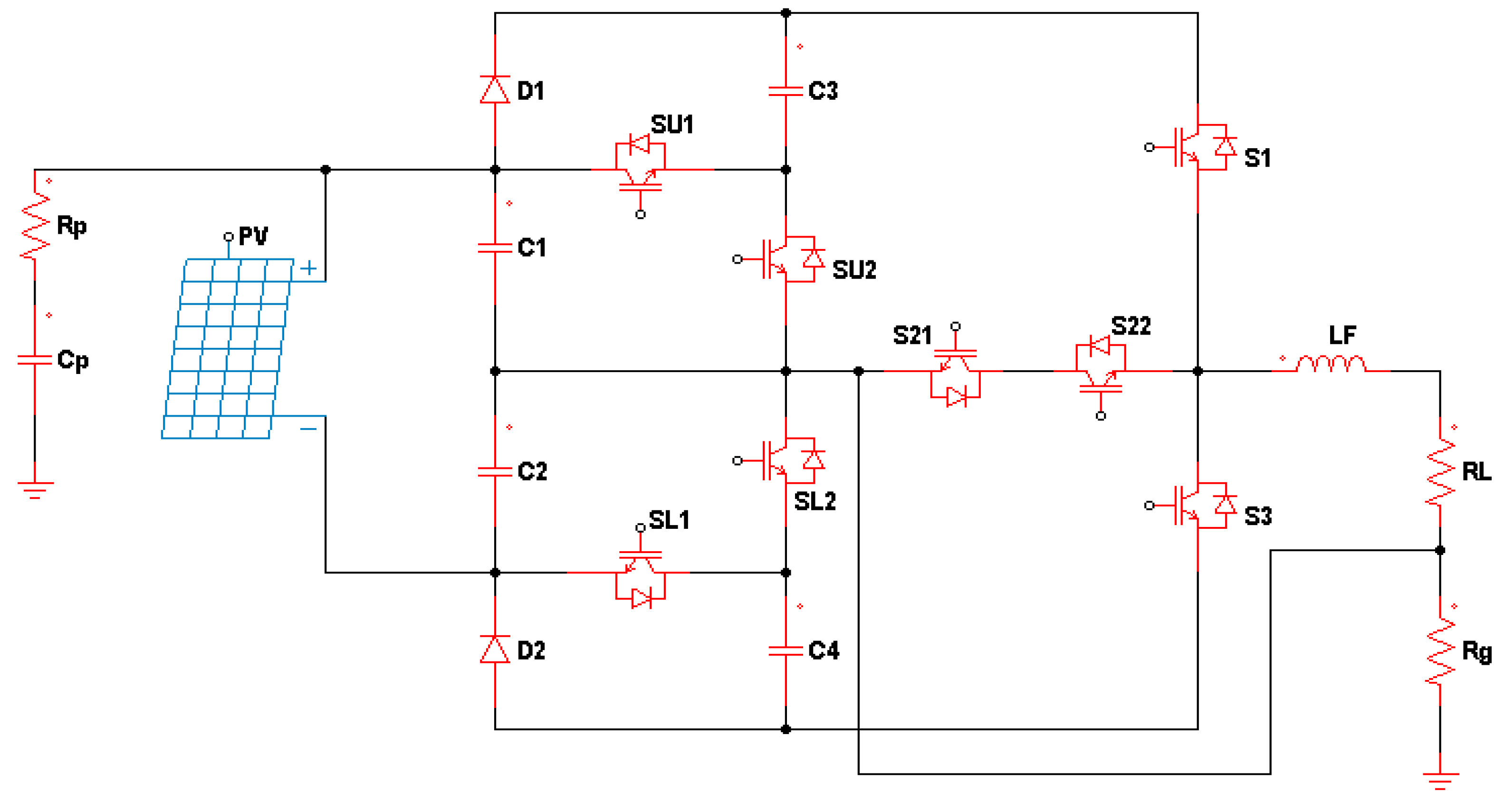
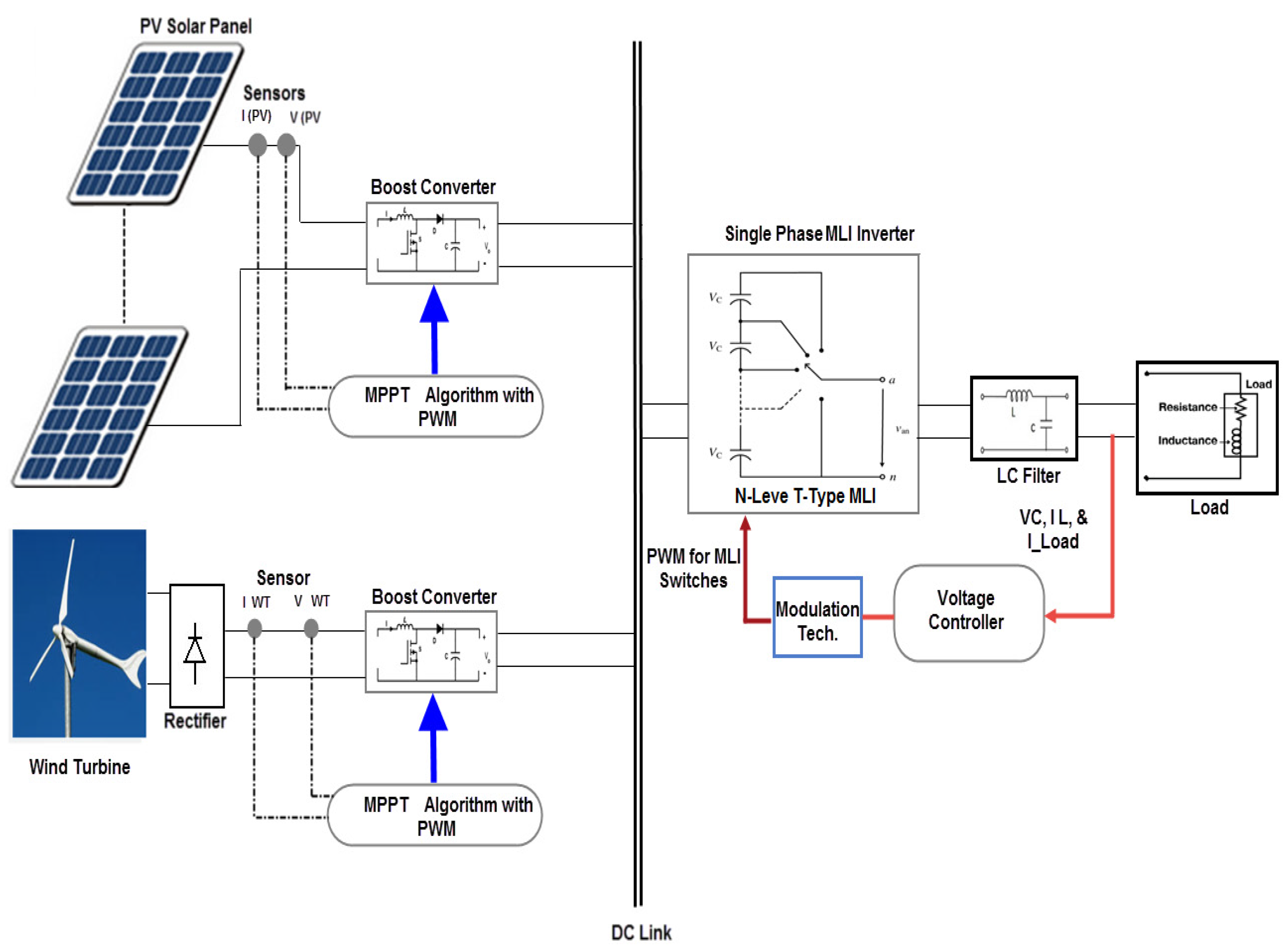
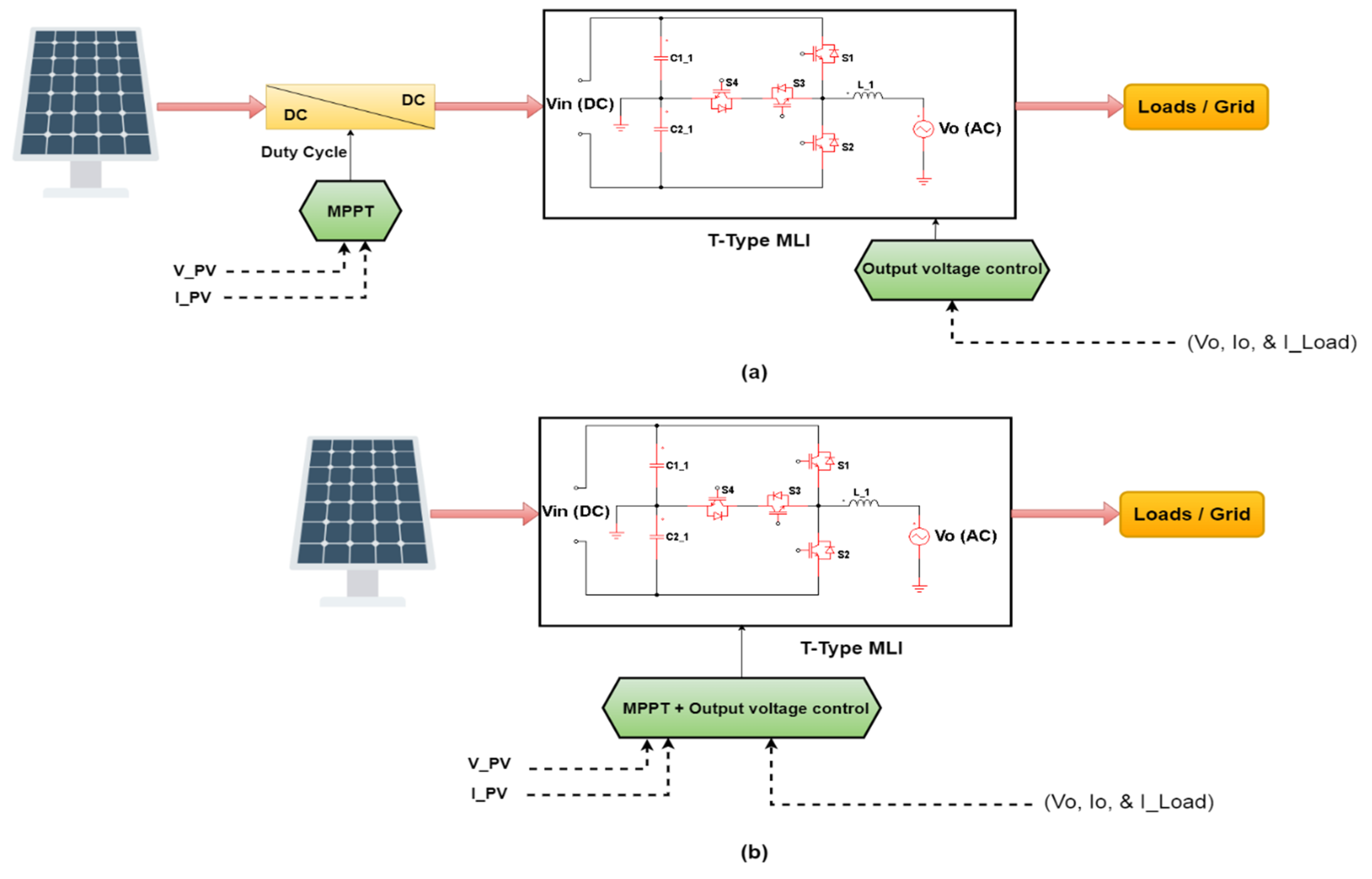
6. Connecting T-MLIs to RES
7. Output Voltage Filter Design
8. Challenges of Using T-MLIs
- The main challenge of using T-MLI is in selecting their voltage-balancing capacitors on the DC link side. With an increasing number of output voltage levels, it is difficult to have the same voltage for all capacitors. In the case of unbalanced voltage levels of DC link capacitors, the output voltages will not be similar at all levels, which may lead to increased harmonics;
- DC link capacitors should be of the type that is charged on both sides since the current can flow in either direction by changing the voltage from a positive value to one that is negative. Using unidirectional charging of capacitors or DC capacitors should be avoided since negative charging may overheat the capacitors and cause them to explode;
- Selecting a proper voltage controller to regulate output voltage is important since, in most cases, these MLIs are supplied from a RES through DC/DC converters employing MPPT methods. Due to the variable nature of RES voltage, the DC link voltage should be sufficiently high, i.e., more than 1.5 times the rated DC link value. If the inverter provides 220 V AC, its DC link voltage is 311 V so, the DC link voltage should be 1.5 times this value. This is to allow flexible voltage control to regulate the output voltage level;
- To increase the efficiency of a T-MLI, fewer switching devices should be used, which reflects the proper design topology of an MLI. Also, each switching device must be selected for low and properties;
- The reliability of power converters is highly dependent on the reliable operation of semiconductor components. For each MLI topology, the switching device voltage and current stresses should be tested and analyzed during switching transients under different load conditions. Peak device current, peak device voltage, peak rate of change of device current , and peak rate of change of device voltage during turn-on and turn-off transients are measured over a wide range of operating conditions. To reduce the heavy , it is helpful to design a damping circuit suitable for this purpose;
- Since these MLIs are practically implemented to reduce their size, microcontrollers can be inserted into their circuitry to perform modulation techniques and regulate output voltage without depending on ICs and sub-circuits that could, in turn, increase losses and hence increase device temperature, as well as increase its size. For higher numbers of levels and at high switching frequencies, the MLIs will suffer from several thermal issues due to switching losses. Also, during normal operation, MLIs are subject to many variations in electrical loadings, which, through the Joule effect, create cyclic thermal stresses within the assembly. Thermally induced failure modes are the main causes of power inverter reliability issues. Due to the fact that the module contains a stack of various materials, cyclic thermal variations may drive mechanical strains, which are reduced by the mechanical cohesion of the assembly. Through the aging of the switching modules, these thermal effects may cause failure to it. The analysis of the thermal cycling frequency for the IGBT switching modules of the specific MLI topology can extend the time to failure by providing adequate cooling to the IGBT power modules [131,132,133]. Thus, the design of a good cooling and ventilation system is required where thermal cycling and ripples of temperature in low-frequency applications should be taken into consideration in the practical implementation of T-type MLIs.
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Thakre, K.; Mohanty, K.B.; Kommukuri, V.S.; Chatterjee, A.; Nigam, P.; Gupta, S.K. Modified cascaded multilevel inverter for renewable energy systems with less number of unidirectional switches. Energy Rep. 2022, 8, 5296–5304. [Google Scholar] [CrossRef]
- Obrecht, M.; Denac, M. Technologyforecast of sustainable energy development prospects. Futures 2016, 84, 12–22. [Google Scholar] [CrossRef]
- Emrani, A.; Berrada, A.; Arechkik, A.; Bakhouya, M. Improved techno-economic optimization of an off-grid hybrid solar/wind/gravity energy storage system based on performance indicators. J. Energy Storage 2022, 49, 104163. [Google Scholar] [CrossRef]
- Abu-Rub, H.; Malinowski, M.; Al-Haddad, K. Power Electronics for Renewable Energy Systems, Transportation and Industrial Applications; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Suntio, T.; Messo, T. Power Electronics in Renewable Energy Systems. Energies 2019, 12, 1852. [Google Scholar] [CrossRef] [Green Version]
- Ikonen, M.; Laakkonen, O.; Kettunen, M. Two-Level and Three-Level Converter Comparison. In Wind Power Application; Citeseer: Princeton, NJ, USA, 2005. [Google Scholar]
- Srinivasan, G.K.; Rivera, M.; Loganathan, V.; Ravikumar, D.; Mohan, B. Trends and Challenges in Multi-Level Inverter with Reduced Switches. Electronics 2021, 10, 368. [Google Scholar] [CrossRef]
- Qin, H.; Xie, S.; Xun, Q.; Zhang, F.; Xu, Z.; Wang, L. An optimized parameter design method of SiC/Si hybrid switch considering turn-off current spike. Energy Rep. 2022, 8 (Suppl. S13), 789–797. [Google Scholar] [CrossRef]
- Li, L.L.; Liu, Z.F.; Tseng, M.L.; Zhou, L.; Qi, F.D. Prediction of IGBT power module remaining lifetime using the aging state approach. Microelectron. Reliab. 2019, 102, 113476. [Google Scholar] [CrossRef]
- Khomfoi, S.; Tolbert, L.M. Chapter 13-Multilevel Power Converters. In Power Electronics Handbook, 4th ed.; Rashid, M.H., Ed.; Butterworth-Heinemann: Oxford, UK, 2018; pp. 385–416. [Google Scholar]
- Mali, R.; Adam, N.; Satpaise, A.; Vaidya, A.P. Performance Comparison of Two Level Inverter with Classical Multilevel Inverter Topologies. In Proceedings of the 2019 IEEE International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 20–22 February 2019; pp. 1–7. [Google Scholar]
- Jaouad, N.C.; Chaikhy, H.; Belhora, F.; Hajjaji, A. Comparison between two levels and multi-level (NPC and Cascade) inverters. Mater. Today Proc. 2022, 66, 162–180. [Google Scholar] [CrossRef]
- Venkataramanaiah, J.; Suresh, Y.; Panda, A.K. A review on symmetric, asymmetric, hybrid and single DC sources based multilevel inverter topologies. Renew. Sustain. Energy Rev. 2017, 76, 788–812. [Google Scholar] [CrossRef]
- Dhanamjayulu, C.; Sanjeevikumar, P.; Muyeen, S.M. A structural overview on transformer and transformer-less multilevel inverters for renewable energy applications. Energy Rep. 2022, 8, 10299–10333. [Google Scholar] [CrossRef]
- Ngo, B.B.; Nguyen, M.K.; Kim, J.H.; Zare, F. Single-phase multilevel inverter based on switched-capacitor structure. IET Power Electron. 2018, 11, 1858–1865. [Google Scholar] [CrossRef]
- Vo, D.-V.; Nguyen, M.-K.; Do, D.-T.; Choi, Y.-O. A Single-Phase Nine-Level Boost Inverter. Energies 2019, 12, 394. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, M.F.; Ahmad, A.H.; Humod, A.T. New Switching Technique for The Modified Cascade Five Levels Inverter. ARPN J. Eng. Appl. Sci. 2018, 13, 4346–4350. [Google Scholar]
- Han, D.; Peng, F.Z.; Dwari, S. Advanced PWM Techniques for Multi-level Inverters with a Multi-level Active CM Noise Filter. IEEE J. Emerg. Sel. Top. Power Electron. 2021. [Google Scholar] [CrossRef]
- Farias, F.; Abdulla, W. A method for selecting a proper modulation technique for the parametric acoustic array. IOP Conf. Ser. J. Phys. 2018, 1075, 012035. [Google Scholar] [CrossRef]
- António-Ferreira, A.; Collados-Rodríguez, C.; Gomis-Bellmunt, O. Modulation techniques applied to medium voltage modular multilevel converters for renewable energy integration: A review. Electr. Power Syst. Res. 2018, 155, 21–39. [Google Scholar] [CrossRef] [Green Version]
- Rashid, M.H. Power Electronics Circuits, Devices, and Applications, 3rd ed.; Pearson Education Inc.: New York, NY, USA, 2007; pp. 248–270. [Google Scholar]
- Bimbhra, P.S. Power Electronics, 4th ed.; Khanna Publishers: Bangalore, India, 2010; pp. 455–456. [Google Scholar]
- Schweizer, M.; Kolar, J.W. Design and Implementation of a Highly Efficient Three-Level TType Converter for Low-Voltage Applications. IEEE Trans. Power Electron. 2013, 28, 899–907. [Google Scholar] [CrossRef]
- “Three-Phase T-Type Inverter”, PLECS DEMO MODEL, Last updated in PLECS 4.6.1. Available online: https://www.plexim.com/sites/default/files/demo_models_categorized/plecs/three_phase_t_type_inverter.pdf (accessed on 15 September 2022).
- Zhou, L.; Gao, F.; Yang, T. Neutral-point-clamped circuits of single-phase PV inverters: Generalized principle and implementation. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 442–449. [Google Scholar]
- Nabae, A.; Takahashi, I.; Akagi, H. A New Neutral-Point-Clamped PWM Inverter. IEEE Trans. Ind. Appl. 1981, IA-17, 518–523. [Google Scholar] [CrossRef]
- Faraji, F.; Hajirayat, A.; Birjandi, A.A.M.; Al-Haddad, K. Single-stage single-phase three-level neutral-point-clamped transformerless grid-connected photovoltaic inverters: Topology review. Renew. Sustain. Energy Rev. 2017, 80, 197–214. [Google Scholar] [CrossRef]
- Sinha, G.; Lipo, T.A. A new modulation strategy for improved DC bus utilization in hard and soft switched multilevel inverters. In Proceedings of the IECON’97 23rd International Conference on Industrial Electronics, Control, and Instrumentation (Cat. No.97CH36066), New Orleans, LA, USA, 14 November 1997; Volume 2, pp. 670–675. [Google Scholar] [CrossRef]
- Alepuz, S.; Busquets- Monge, S.; Nicolás-Apruzzese, J.; Filbà-Martínez, À.; Bordonau, J.; Yuan, X.; Kouro, S. A Survey on Capacitor Voltage Control in Neutral-Point-Clamped Multilevel Converters. Electronics 2022, 11, 527. [Google Scholar] [CrossRef]
- Gurpinar, E.; Castellazzi, A. Single-Phase T-Type Inverter Performance Benchmark Using Si IGBTs, SiC MOSFETs, and GaN HEMTs. IEEE Trans. Power Electron. 2016, 31, 7148–7160. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, J.; Wu, X. A single phase T-type inverter operating in boundary conduction mode. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar]
- Mohammed, M.F.; Ahmad, A.H.; Humod, A.T. Design and Simulation of a New Seven Levels Inverter for Renewable Energy Sources. J. Eng. Appl. Sci. 2018, 13, 6866–6872. [Google Scholar]
- Mohammed, M.F.; Ahmad, A.H.; Humod, A.T. Harmonics reduction of a five-level inverter by unbalanced carriers and over-modulation techniques. Int. J. Eng. Technol. 2018, 7, 1059–1063. [Google Scholar] [CrossRef]
- Yu, H.; Chen, B.; Yao, W.; Lu, Z. Hybrid Seven-Level Converter Based on T-Type Converter and H-Bridge Cascaded Under SPWM and SVM. IEEE Trans. Power Electron. 2018, 33, 689–702. [Google Scholar] [CrossRef]
- Jacob, J.T.; Kirubakaran, D. A Hybrid T-Type Multilevel Inverter with A Novel Modulation Strategy for Isolated Supply Electric Systems. J. Eng. Sci. Technol. 2019, 14, 1614–1638. [Google Scholar]
- Ceglia, G.; Guzman, V.; Sanchez, C.; Ibanez, F.; Walter, J.; Gimenez, M.I. A New Simplified Multilevel Inverter Topology for DC–AC Conversion. IEEE Trans. Power Electron. 2006, 21, 1311–1319. [Google Scholar] [CrossRef]
- Bhaskar, M.S.; Almakhles, D.; Padmanaban, S.; Ionel, D.M.; Blaabjerg, F.; He, J.; Kumar, A.R. Investigation of a Transistor Clamped T-Type Multilevel H-Bridge Inverter With Inverted Double Reference Single Carrier PWM Technique for Renewable Energy Applications. IEEE Access 2020, 8, 161787–161804. [Google Scholar] [CrossRef]
- Rahim, N.A.; Chaniago, K.C.; Selvarage, J. A modified H Bridge Multilevel Inverter for Photovoltaic System. IEICE Elecronic Express 2010, 7, 751–758. [Google Scholar] [CrossRef] [Green Version]
- Sudheer, D.S.; Reddy, S.; Kumar, J.S.; Ayyapparaju, C.B.; Reddy, M.S. A Single-Phase Inverter Topology with Seven-Level Output based on T-type Structure. In Proceedings of the 2021 6th International Conference for Convergence in Technology (I2CT), Maharashtra, India, 2–4 April 2021; pp. 1–4. [Google Scholar]
- Mustafa, I.N.C.I. Performance Analysis of T-type Inverter Based on Improved Hysteresis Current Controller. Balk. J. Electr. Comput. Eng. 2019, 7, 147–155. [Google Scholar]
- Karthik, K.I.N.; Srinivasa Rao, S. Five-Level Inverter Using POD PWM Technique. In Proceedings of the International Conference on Electrical, Electronics, Signals, Communication and Optimization (EESCO), Visakhapatnam, India, 24–25 January 2015; pp. 1–6. [Google Scholar]
- Sunddararaj, S.P.; Rangarajan, S.S.; Subashini, N.; Subramaniam, U.; Collins, E.R.; Senjyu, T. A novel T-Type Multilevel Inverter for Electric Vehicle and Grid-connected applications. In Proceedings of the 2021 7th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 11–13 February 2021; pp. 166–170. [Google Scholar]
- Dhara, S.; Hota, A.; Jain, S.; Agarwal, V. A Novel Single-Phase T-Type PV Inverter with Improved DC Utilization. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–5. [Google Scholar]
- Ouchatti, A.; Majdoul, R.; Moutabir, A.; Taouni, A.; Touati, A. Modified T-type topology of three-phase multi-level inverter for photovoltaic systems. Int. J. Electr. Comput. Eng. 2022, 12, 262–268. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, Y.; Li, G.; Chen, T.; Wang, K.; Liang, J. A Generalized Multilevel Inverter Based on T-Type Switched Capacitor Module with Reduced Devices. Energies 2020, 13, 4406. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.A.; Sarbanzadeh, M.; Sarebanzadeh, E.; Rivera, M.; Munoz, J. Reduced modified T-type topology for cascaded multilevel inverters. In Proceedings of the 2018 IEEE International Conference on Automation/XXIII Congress of the Chilean Association of Automatic Control (ICA-ACCA), Concepcion, Chile, 17–19 October 2018; pp. 1–6. [Google Scholar]
- Meraj, S.T.; Yahaya, N.Z.; Hasan, K.; Masaoud, A. A hybrid T-type (HT-type) multilevel inverter with reduced components. Ain Shams Eng. J. 2021, 12, 1959–1971. [Google Scholar] [CrossRef]
- Khenar, M.; Taghvaie, A.; Adabi, J. Multi-level inverter with combined T-type and cross-connected modules. IET Power Electron. 2018, 11, 1407–1415. [Google Scholar] [CrossRef]
- Samadaei, E.; Sheikholeslami, A.; Gholamian, S.A.; Adabi, J. A Square T-Type (ST-Type) Module for Asymmetrical Multilevel Inverters. IEEE Trans. Power Electron. 2018, 33, 987–996. [Google Scholar] [CrossRef]
- Chandwani, H.B.; Matnani, M.K. A review of modulation techniques for hybrid multilevel inverter. In Proceedings of the 2012 1st International Conference on Emerging Technology Trends in Electronics, Communication & Networking, Surat, India, 19–21 December 2012; pp. 1–7. [Google Scholar]
- Balamurugan, C.R.; Natarajan, S.P.; Bensraj, R.; Shanthi, B. A Review on Modulation Strategies of Multi Level Inverter. Indones. J. Electr. Eng. Comput. Sci. 2016, 3, 681–705. [Google Scholar] [CrossRef]
- Hasan, N.S.; Rosmin, N.; Osman, D.A.A.; Musta’amal, A.H. Reviews on multilevel converter and modulation techniques. Enewable Sustain. Energy Rev. 2017, 80, 163–174. [Google Scholar] [CrossRef]
- Kumar, M.S.; Ramani, K. Comparative Review of Modulation Techniques for Harmonic Minimization in Multilevel Inverter. Int. J. Electr. Comput. Eng. 2014, 8, 1938–1945. [Google Scholar]
- Poorfakhraei, A.; Narimani, M.; Emadi, A. A Review of Modulation and Control Techniques for Multilevel Inverters in Traction Applications. IEEE Access 2021, 9, 24187–24204. [Google Scholar] [CrossRef]
- Rodriguez, J.; Lai, J.-S.; Peng, F.Z. Multilevel inverters: A survey of topologies, controls, and applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef] [Green Version]
- McGrath, B.P.; Holmes, D.G. Multicarrier PWM Strategies for Multilevel Inverters. IEEE Trans. Ind. Electron. 2002, 49, 858–867. [Google Scholar] [CrossRef]
- Rathore, S.; Kirar, M.K.; Bhardwaj, S.K. Simulation of cascaded h- bridge multilevel inverter using pd, pod, apod techniques. Electr. Comput. Eng. Int. J. 2015, 4, 27–41. [Google Scholar] [CrossRef]
- Suresh, S.R.K. Analysis of pd, pod, apod, co and vf pwm techniques for cascaded inverter. South Asian J. Eng. Technol. 2016, 2, 46–55. [Google Scholar]
- Aghdam, M.G.H.; Fathi, S.H.; Gharehpetian, G.B. Analysis of multi-carrier PWM methods for asymmetric multi-level inverter. In Proceedings of the 2008 3rd IEEE Conference on Industrial Electronics and Applications ICIEA, Singapore, 3–5 June 2008; pp. 2057–2062. [Google Scholar]
- İnci, M. Performance Evaluation of Multi-carrier PWM Techniques: PD, POD and APOD. Int. J. Appl. Math. Electron. Comput. 2019, 7, 38–43. [Google Scholar] [CrossRef]
- Kumar, K.V.; Thulasiram, I. Comparison Of APOD And POD Control Techniques For A Cascaded H-Bridge Multi Level Inverter. Int. J. Eng. Res. Technol. 2013, 2, 1–5. [Google Scholar]
- Venkatakrishna, A.; Somanatham, R.; Reddy, M.S. Phase Shifted and Level Shifted PWM Based Cascaded Multilevel Inverter Fed Induction Motor Drive. Int. J. Curr. Eng. Technol. 2014, 4, 350–354. [Google Scholar]
- Xiao, M.; Xu, Q.; Ouyang, H. An Improved Modulation Strategy Combining Phase Shifted PWM and Phase Disposition PWM for Cascaded H-Bridge Inverters. Energies 2017, 10, 1327. [Google Scholar] [CrossRef] [Green Version]
- Radan, A.; Shahirinia, A.H.; Falahi, M. Evaluation of carrier-based PWM methods for multi-level inverters. In Proceedings of the IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 389–394. [Google Scholar]
- Cheng, Q.; Wang, C.; Wang, J. Analysis on Displacement Angle of Phase-Shifted Carrier PWM for Modular Multilevel Converter. Energies 2020, 13, 6743. [Google Scholar] [CrossRef]
- Mardaneh, M.; Hashemi, Z. A random switching method for PWM cascaded H-bridge multi-level inverter. In Proceedings of the 2012 IEEE International Conference on Circuits and Systems (ICCAS), Kuala Lumpur, Malaysia, 3–4 October 2012; pp. 76–79. [Google Scholar]
- George, D.S.; Shiny, G. Random pulsewidth modulation technique for a 4-level inverter. Int. J. Adv. Res. Eng. Technol. 2015, 6, 24–33. [Google Scholar]
- Jadeja, R.; Ved, A.; Chauhan, S. An Investigation on the Performance of Random PWM Controlled Converters. Eng. Technol. Appl. Sci. Res. 2015, 5, 876–884. [Google Scholar] [CrossRef]
- Rahim, N.A.; Selvaraj, J. A novel multi-string five-level PWM inverter for photovoltaic application. In Proceedings of the 2011 IEEE International Electric Machines & Drives Conference (IEMDC), Niagara Falls, ON, Canada, 15–18 May 2011; pp. 510–514. [Google Scholar]
- Vemuganti, H.P.; Sreenivasarao, D.; Kumar, G.S. Improved pulse-width modulation scheme for T-type multilevel inverter. IET Power Electron. 2017, 10, 968–976. [Google Scholar] [CrossRef]
- Fakhry, M.G.; Massoud, A.; Ahmed, S. Quasi seven-level operation of multilevel converters with selective harmonic elimination. In Proceedings of the 26th International Conference on Microelectronics (ICM), Doha, Qatar, 14–17 December 2014. [Google Scholar]
- Konstantinou, G.; Ciobotaru, M.; Agelidis, V. Selective harmonic elimination pulse width modulation of modular multilevel converters. IET Power Electron. 2013, 6, 96–107. [Google Scholar] [CrossRef]
- Guzman, J.I.; Melin, P.E.; Espinoza, J.R.; Moran, L.A.; Baier, C.R.; Munoz, J.A.; Guinez, G.A. Digital implementation of selective harmonic elimination techniques in modular current source rectifiers. IEEE Trans. Ind. Inform. 2013, 9, 1167–1177. [Google Scholar] [CrossRef]
- Gabour, N.E.H.; Boudissa, E.G.; Bounekhla, M.H. Optimal HSE-PWM based on genetic algorithm for seven levels diode clamped multilevel inverter. Period. Eng. Nat. Sci. 2020, 8, 859–869. [Google Scholar]
- Yang, K.; Yuan, Z.; Yuan, R.; Yu, W.; Yuan, J.; Wang, J. A Groebner Bases Theory-Based Method for Selective Harmonic Elimination. IEEE Trans. Power Electron. 2015, 30, 6581–6592. [Google Scholar] [CrossRef]
- Salas, V.; Olías, E. An analysis of the technical exigencies and CE marking relative to low voltage (less than 5 kW) photovoltaic inverters marketed in Spain. Renew. Sustain. Energy Rev. 2009, 13, 1635–1640. [Google Scholar] [CrossRef]
- Abdelaziz, E.A.; Saidur, R.; Mekhilef, S. A review on energy saving strategies in industrial sector. Renew. Sustain. Energy Rev. 2011, 15, 150–168. [Google Scholar] [CrossRef]
- Meral, M.E.; Diner, F. A review of the factors affecting operation and efficiency of photovoltaic based electricity generation systems. Renew. Sustain. Energy Rev. 2011, 15, 2176–2184. [Google Scholar] [CrossRef]
- Sallama, A.; Abbod, M.; Khan, S.M. Applying sequential particle swarm optimization algorithm to improve power generation quality. Int. J. Eng. Technol. Innov. 2014, 4, 223–233. [Google Scholar]
- Rasheed, M.; Omar, R.; Sulaiman, M.; Halim, W.A.; Majeda, M.M.A.A. Artificial Intelligence Technique to Real-Time Based on Selective Harmonic Elimination in Modified Multilevel Inverter. J. Eng. Appl. Sci. 2019, 14, 9692–9700. [Google Scholar] [CrossRef] [Green Version]
- Rasheed, M.; Alakkad, M.M.A.; Omar, R.; Sulaiman, M.; Halim, W.A. Enhance the accuracy of control algorithm for multilevel inverter based on artificial neural network. J. Electr. Eng. Comput. Sci. 2020, 20, 1148–1158. [Google Scholar] [CrossRef]
- Dahidah, M.S.A.; Konstantinou, G.; Agelidis, V.G. A review of multilevel selective harmonic elimination PWM: Formulations, solving algorithms, implementation and applications. IEEE Trans. Power Electron. 2015, 30, 4091–4106. [Google Scholar] [CrossRef]
- Konstantinou, G.; Agelidis, V.G. Bipolar Switching Waveform: Novel Solution Sets to the Selective Harmonic Elimination Problem. In Proceedings of the IEEE International Conference on Industrial Technology, Via del Mar, Chile, 14–17 March 2010. [Google Scholar]
- Agelidis, V.G.; Balouktsis, A.; Balouktsis, I. On applying a minimization technique to the harmonic elimination PWM control:The bipolar waveform. IEEE Trans. Power Electron. 2004, 2, 41–44. [Google Scholar]
- Konstantinou, G.; Agelidis, V.G. On re-examining symmetry of two-level selective harmonic elimination PWM: Novel formulations, solutions and performance evaluation. Electr. Power Syst. Res. 2014, 108, 185–197. [Google Scholar] [CrossRef]
- Agelidis, V.G.; Balouktsis, A.; Balouktsis, I.; Cossar, C. Multiple sets of solutions for harmonic elimination PWM bipolar waveforms: Analysis and experimental verification. IEEE Trans. Power Electron. 2006, 21, 415–421. [Google Scholar] [CrossRef] [Green Version]
- Dahidah, M.S.A.; Konstantinou, G.; Flourentzou, N.; Agelidis, V.G. On comparing the symmetrical and non-symmetrical selective harmonic elimination pulse-width modulation technique for two-level three-phase voltage source converters. IET Power Electron. 2010, 3, 829–842. [Google Scholar] [CrossRef]
- El-Bakry, M. Selective Harmonics Minimization for Multilevel Inverters. In Proceedings of the IEEE International Conference on Computer and Electrical Engineering, Dubai, United Arab Emirates, 28–30 December 2009. [Google Scholar]
- Sahali, Y.; Fellah, M.K. Application of the Optimal Minimization of The THD Technique to The Multilevel Symmetrical Inverters and Study of Its Performance in Comparison with the Selective Harmonic Elimination Technique. In Proceedings of the IEEE International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Taormina, Italy, 23–26 May 2006. [Google Scholar]
- Naderi, Y.; Hosseini, S.H.; Mahari, A.; Naderi, R. A New Strategy for Harmonic Minimization Based on Triple Switching of Multilevel Converters. In Proceedings of the Iranian Conference on Electrical Engineering, Mashhad, Iran, 1–6 December 2013. [Google Scholar]
- Liu, Y.; Hong, H.; Huang, A.Q. Real-time calculation of switching angles minimizing THD for multilevel inverters with step modulation. IEEE Trans. Ind. Electron. 2009, 56, 285–293. [Google Scholar] [CrossRef]
- Liu, Y.; Hong, H.; Huang, A.Q. Real-time algorithm for minimizing THD in multilevel inverters with unequal or varying voltage steps under staircase modulation. IEEE Trans. Ind. Electron. 2009, 56, 2249–2258. [Google Scholar] [CrossRef]
- Ahmad, S.; Khan, I.; Iqbal, A.; Rahman, S. A Novel Pulse Width Amplitude Modulation for Elimination of Multiple Harmonics In Asymmetrical Multilevel Inverter. In Proceedings of the 2021 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 2–5 February 2021; pp. 1–6. [Google Scholar]
- Jing, T.; Maklakov, A.; Radionov, A.; Gasiyarov, V.; Liang, Y. Formulations, Solving Algorithms, Existing Problems and Future Challenges of Pre-Programmed PWM Techniques for High-Power AFE Converters: A Comprehensive Review. Energies 2022, 15, 1696. [Google Scholar] [CrossRef]
- Qasim, M.A.; Velkin, V.I. Maximum Power Point Tracking Techniques for Micro-Grid Hybrid Wind and Solar Energy Systems—A Review. Int. J. Energy Convers. (IRECON) 2020, 8, 223–234. [Google Scholar] [CrossRef]
- Qasim, M.A.; TAlwan, N.; PraveenKumar, S.; Velkin, V.I.; Agyekum, E.B. A New Maximum Power Point Tracking Technique for Thermoelectric Generator Modules. Inventions 2021, 6, 88. [Google Scholar] [CrossRef]
- Köse, F.; Aksoy, M.H.; Özgören, M.B. Experimental Investigation of Solar/Wind Hybrid System for Irrigation in Konya, Turkey. Therm. Sci. 2019, 23, 4129–4139. [Google Scholar] [CrossRef]
- Qasim, M.A. PWM effect on MPPT for hybrid PV solar and wind turbine generating systems at various loading conditions. Period. Eng. Nat. Sci. 2021, 9, 581–592. [Google Scholar] [CrossRef]
- Mohammed, M.F.; Ahmad, A.H.; Humod, A.T. Design of isolated IGBT driving and control circuits for an interleaved boost converter. Eng. Appl. Sci. Res. 2021, 48, 48–55. [Google Scholar]
- Sivagamasundari, M.S.; Mary, P.M. Real Time Implementation of PI and PID Controlled Cascaded H-Bridge Eleven Level Inverter using SPWM. J. Microelectron. Electron. Compon. Mater. 2016, 46, 65–73. [Google Scholar]
- Shtessel, Y. Christopher Edwards, Leonid Fridman, and Arie Levant. In Sliding Mode Control and Observation; Springer Science+Business Media: New York, NY, USA, 2014. [Google Scholar]
- Tan, S.C.; Lai, Y.M.; Tse, C.K. Sliding Mode Control of Switching Power Converters Techniques and Implementation; Taylor & Francis Group: Abingdon, UK, 2012. [Google Scholar]
- Vivert, M.; Patino, D.; Diez, R. Variation of a sliding mode control applied to a trinary hybrid multilevel inverter. In Proceedings of the 2017 IEEE 3rd Colombian Conference on Automatic Control (CCAC), Cartagena, Colombia, 18–20 October 2017; pp. 1–6. [Google Scholar]
- Chenchireddy, K.; Jegathesan, V. Multilevel Inverter Topologies with Sliding Mode Control: A Review. Int. J. Adv. Sci. Technol. 2020, 29, 8449–8460. [Google Scholar]
- Santoso, D.; Pratomo, L.H. The Voltage Control in Single-Phase Five-Level Inverter for a Stand-Alone Power Supply Application. J. Robot. Control. 2021, 2, 421–428. [Google Scholar]
- Alabbasi, R.H.; Salih, S.M. Control of cascade multilevel inverter using fuzzy logic technique. In Proceedings of the 2nd International Symposium on Power Electronics for Distributed Generation Systems, Hefei, China, 16–18 June 2010; pp. 96–101. [Google Scholar]
- Srinivasan, B.; Gotivada, N.R. Mathematical Modelling of Fuzzy Controlled Multilevel Inverter for Unified Power Quality Conditioner. J. Algebraic Stat. 2022, 13, 1562–1568. [Google Scholar]
- Rashag, H.F. Optimization of Three Level Inverter based on Fuzzy Logic Control to Improve the System Performance. Int. J. Appl. Eng. Res. 2018, 13, 1982–1987. [Google Scholar]
- Suresh, D.; Singh, S.P. Type-2 Fuzzy Logic Controlled Three-level Shunt Active Power Filter for Power Quality Improvement. Electr. Power Compon. Syst. 2016, 44, 873–882. [Google Scholar] [CrossRef]
- Hagh, M.T.; Taghizadeh, H.; Razi, K. Optimum control of multilevel inverters using Artificial Neural Networks. In Proceedings of the 2008 IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 2336–2341. [Google Scholar]
- Padmasuresh, L.; Muthukumar, P. Genetic algorithm based 15 level multilevel inverter with SHE PWM. Int. J. Eng. Technol. 2018, 7, 893–897. [Google Scholar]
- Barkat, S.; Berkouk, E.M.; Boucherit, M.S. Particle swarm optimization for harmonic elimination in multilevel inverters. Electron. Eng. 2009, 91, 221–228. [Google Scholar] [CrossRef]
- Qasim, M.A.; Velkin, V.I.; Shcheklein, S.E. Experimental and Implementation of a 15 × 10 TEG Array of a Thermoelectric Power Generation System Using Two-Pass Flow of a Tap Water Pipeline Based on Renewable Energy. Appl. Sci. 2022, 12, 7948. [Google Scholar] [CrossRef]
- Qasim, M.A.; Velkin, V.I.; Shcheklein, S.E. The Experimental Investigation of a New Panel Design for Thermoelectric Power Generation to Maximize Output Power Using Solar Radiation. Energies 2022, 15, 3124. [Google Scholar] [CrossRef]
- Qasim, M.A.; Velkin, V.I.; Hassan, A.K. Seebeck Generators and Their Performance in Generating Electricity. J. Oper. Autom. Power Eng. 2022, 10, 200–205. [Google Scholar] [CrossRef]
- Nandhini Gayathri, M. A DC–DC Converter for Green Energy Applications. In DC—DC Converters for Future Renewable Energy Systems. Energy Systems in Electrical Engineering; Priyadarshi, N., Bhoi, A.K., Bansal, R.C., Kalam, A., Eds.; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Khoramikia, H.; Heydari, M.; Dehghan, S.M. A New Three-Port Non-Isolated DC-DC Converter for Renewable Energy Sources Application. In Proceedings of the Electrical Engineering (ICEE), Iranian Conference on, Mashhad, Iran, 8–10 May 2018; pp. 1101–1106. [Google Scholar] [CrossRef]
- Mansour, A.S.; Amer, A.H.H.; El-Kholy, E.E.; Zaky, M.S. High gain DC/DC converter with continuous input current for renewable energy applications. Sci. Rep. 2022, 12, 12138. [Google Scholar] [CrossRef]
- Sivakumar, S.; Sathik, M.J.; Manoj, P.S.; Sundararajan, G. An assessment on performance of DC–DC converters for renewable energy applications. Renew. Sustain. Energy Rev. 2016, 58, 1475–1485. [Google Scholar] [CrossRef]
- Prabaharan, N.; Palanisamy, K. A Single Phase Grid Connected Hybrid Multilevel Inverter for Interfacing Photo-voltaic System. Energy Procedia 2016, 103, 250–255. [Google Scholar] [CrossRef]
- Janardhan, K.; Mittal, A.; Ojha, A. Performance investigation of stand-alone solar photovoltaic system with single phase micro multilevel inverter. Energy Rep. 2020, 6, 2044–2055. [Google Scholar] [CrossRef]
- Shimi, S.L.; Thakur, T.; Kumar, J.; Chatterji, S.; Karanjkar, D. MPPT based solar powered cascade multilevel inverter. In Proceedings of the 2013 Annual International Conference on Emerging Research Areas and 2013 International Conference on Microelectronics, Communications and Renewable Energy, Kanjirapally, India, 4–6 June 2013; pp. 1–5. [Google Scholar]
- Thiagarajan, M.; Pavunraj, P. Multilevel Inverter For PV System Employing MPPT Technique. Int. J. Eng. Res. Technol. 2012, 1, 1–6. [Google Scholar]
- Santhiya, R.; Senthilnathan, A.; Kumar Chinnaiyan, V.; Nithya Priya, R. Grid Connected Multilevel Inverter and MPPT for Photovoltaic System. In Power Electronics and Renewable Energy Systems; Lecture Notes in Electrical Engineering; Kamalakannan, C., Suresh, L., Dash, S., Panigrahi, B., Eds.; Springer: New Delhi, India, 2015; Volume 326. [Google Scholar] [CrossRef]
- Princy, K.; Gowri, M.S. A Multilevel Inverter For PV System Using Adaptive MPPT Control With Reduced Harmonics. Int. Res. J. Eng. Technol. 2016, 3, 2679–2684. [Google Scholar]
- Chi, Z.; Dragicevic, T.; Vasquez, J.; Guerrero, J. Resonance damping techniques for grid-connected voltage source converters with LCL filters—A review. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Cavtat, Croatia, 13–16 May 2014; pp. 169–176. [Google Scholar]
- Wu, W.; Huang, M.; Blaajberg, F. Efficiency comparison between the LLCL and LCL-filters based single-phase grid-tied inverters. Arch. Electr. Eng. 2014, 63, 1674–1689. [Google Scholar] [CrossRef] [Green Version]
- Qureshi, M.R.; Mahar, M.A.; Larik, A. Harmonic Analysis and Design of LC Filter for a Seven-level Asymmetric Cascaded Half Bridge Multilevel Inverter. Int. J. Electr. Eng. Emerg. Technol. 2020, 3, 52–58. [Google Scholar]
- Ramteke, R.G.; Patil, U.V. Design and comparative study of filters for multilevel inverter for grid interface. In Proceedings of the 2014 International Conference on Power, Automation and Communication (INPAC), Amravati, India, 6–8 October 2014; pp. 39–44. [Google Scholar]
- Jayaraman, M.; VT, S. Power Quality Improvement in a Cascaded Multilevel Inverter Interfaced Grid Connected System Using a Modified Inductive–Capacitive–Inductive Filter with Reduced Power Loss and Improved Harmonic Attenuation. Energies 2017, 10, 1834. [Google Scholar] [CrossRef] [Green Version]
- Wani, F.; Shipurkar, U.; Dong, J.; Polinder, H. Thermal Cycling in Converter IGBT Modules with Different Cooling Systems in Pitch- and Active Stall-Controlled Tidal Turbines. Energies 2021, 14, 6457. [Google Scholar] [CrossRef]
- Pellecuer, G.; Huselstein, J.J.; Martiré, T.; Forest, F.; Chrysochoos, A.; Arnould, O. Impact of Thermal Cycling Frequency on IGBT Power Module Lifetime. In Proceedings of the International Exhiition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, PCIM Europe, Nuremberg, Germany, 10–12 May 2022; pp. 1–8. [Google Scholar]
- Górecki, P. Electrothermal Averaged Model of a Diode–IGBT Switch for a Fast Analysis of DC–DC Converters. IEEE Trans. Power Electron. 2022, 37, 13003–13013. [Google Scholar] [CrossRef]



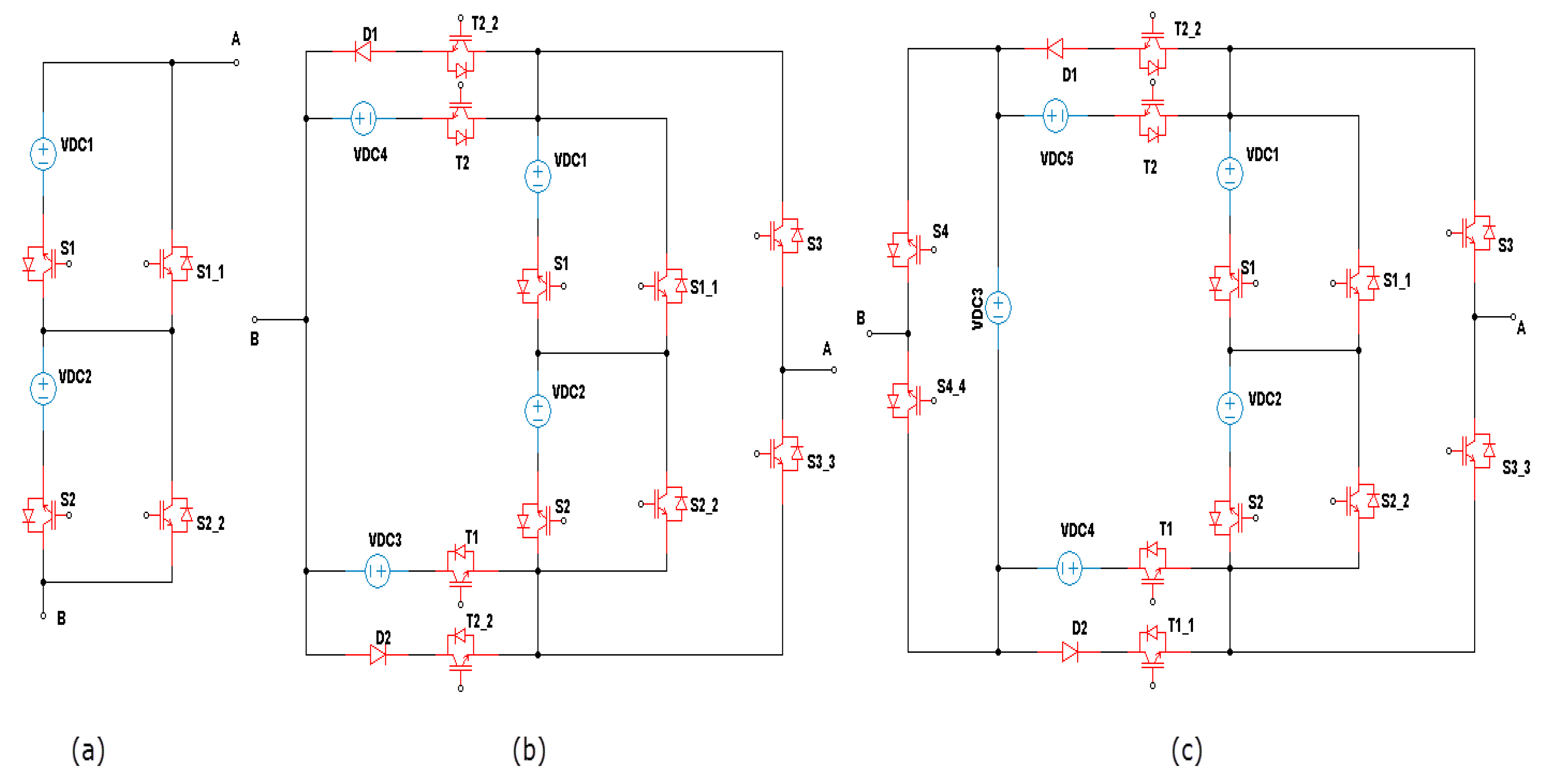

| Level of the Output Voltage | S1 | S2 | S3 | T1 | T1_1 | T2 | T2_2 |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| Ref. No. | Number of Switching Devices | Number of Voltage Sources | Number of DC-Link Capacitors | Switching Modules | Blocking Diodes |
|---|---|---|---|---|---|
| [31] | 1 | No | No | ||
| [32] | 1 | No | Yes | ||
| [34] | 1 | No | No | ||
| [36] | 1 | Yes | Yes | ||
| [41] | No | No | No | ||
| [42] | 8 for five-level | 1 | 2 | No | Yes |
| [43] | 8 for five-level | 4 for five-level | No | Yes | Yes |
| [45] | 10 for nine-level | 1 | 4 for nine-level | No | No |
| [46] | 12 for fifteen-level | 4 for fifteen-level | No | No | Yes |
| [47] | 12 for eleven-level | 4 for eleven-level | No | No | No |
| [49] | 12 for seventeen-level | 4 for seventeen-level | No | Yes | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, M.F.; Qasim, M.A. Single Phase T-Type Multilevel Inverters for Renewable Energy Systems, Topology, Modulation, and Control Techniques: A Review. Energies 2022, 15, 8720. https://doi.org/10.3390/en15228720
Mohammed MF, Qasim MA. Single Phase T-Type Multilevel Inverters for Renewable Energy Systems, Topology, Modulation, and Control Techniques: A Review. Energies. 2022; 15(22):8720. https://doi.org/10.3390/en15228720
Chicago/Turabian StyleMohammed, Mustafa F., and Mohammed A. Qasim. 2022. "Single Phase T-Type Multilevel Inverters for Renewable Energy Systems, Topology, Modulation, and Control Techniques: A Review" Energies 15, no. 22: 8720. https://doi.org/10.3390/en15228720
APA StyleMohammed, M. F., & Qasim, M. A. (2022). Single Phase T-Type Multilevel Inverters for Renewable Energy Systems, Topology, Modulation, and Control Techniques: A Review. Energies, 15(22), 8720. https://doi.org/10.3390/en15228720






