Distributed Secondary Control for Battery Management in a DC Microgrid
Abstract
1. Introduction
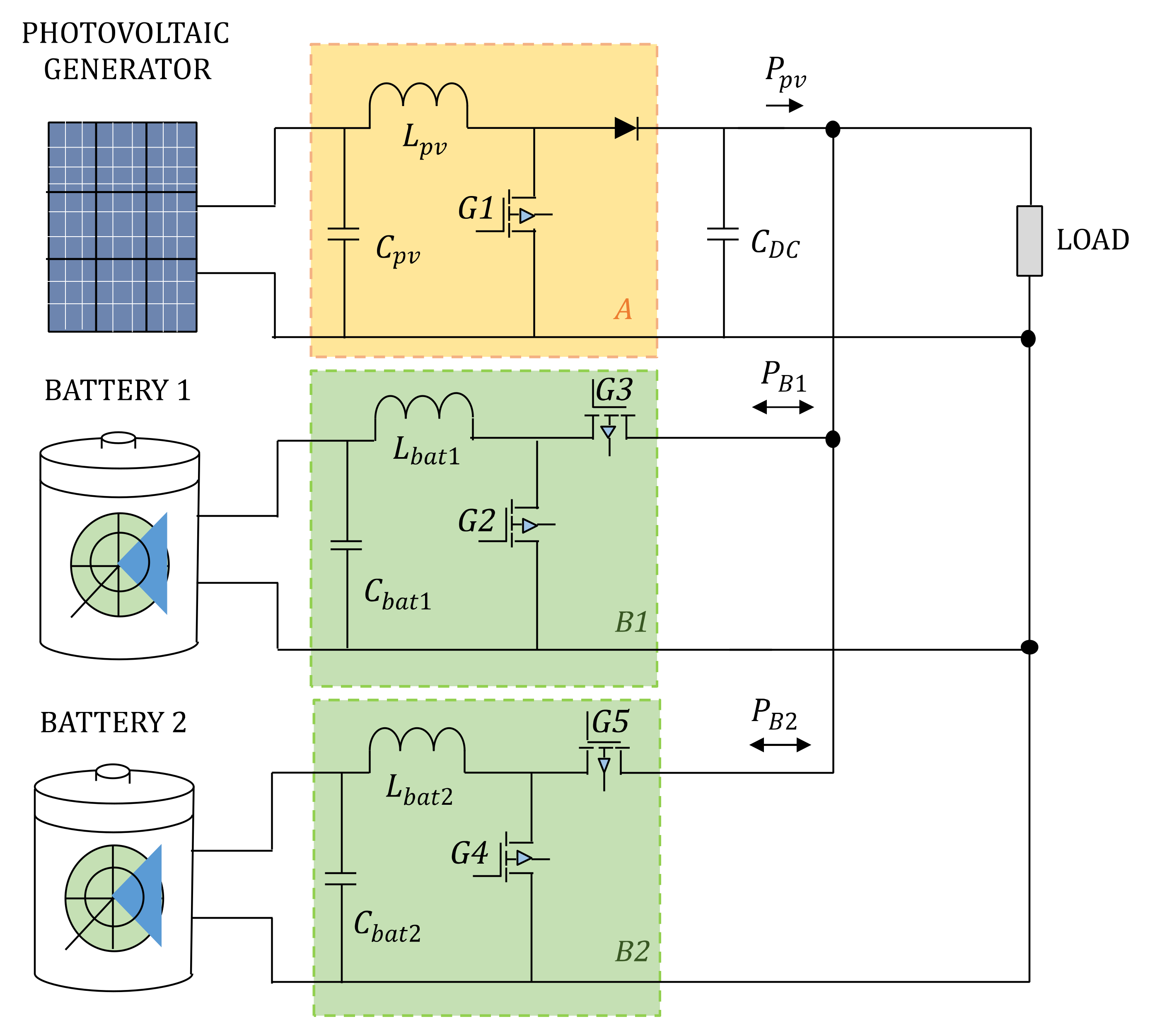
2. System Description
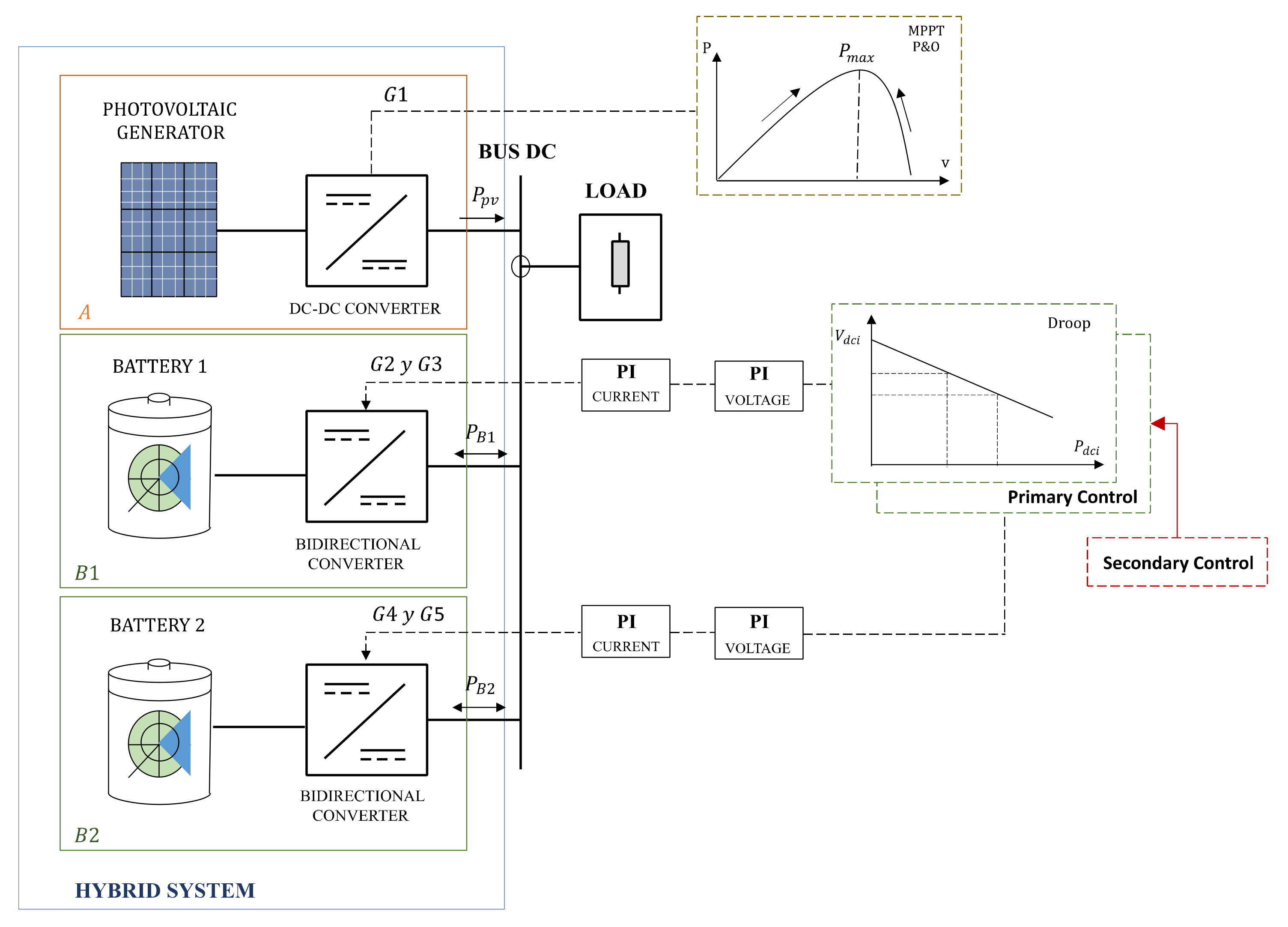
3. Design of System Control Strategies
3.1. Design of Local Controllers
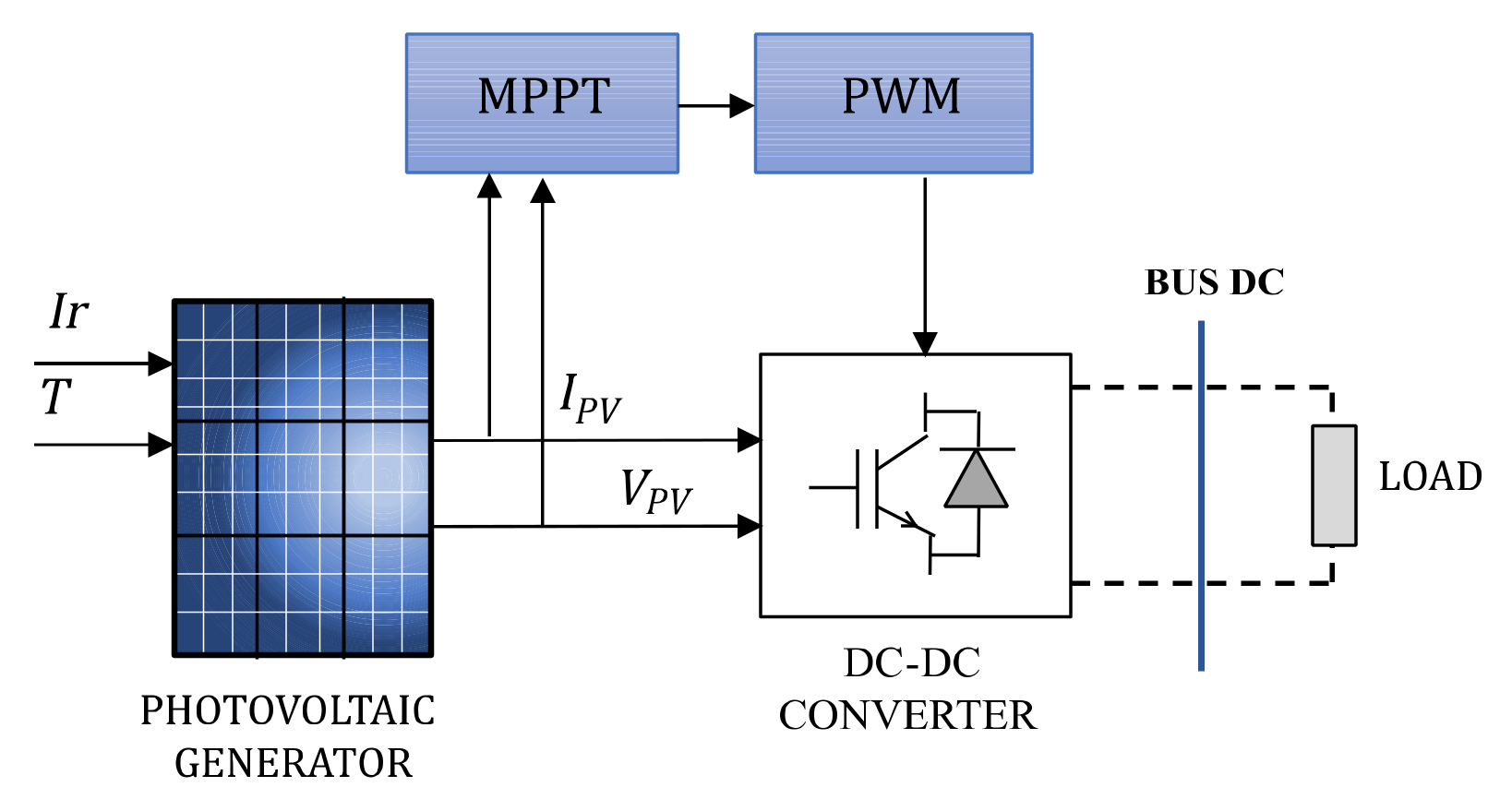
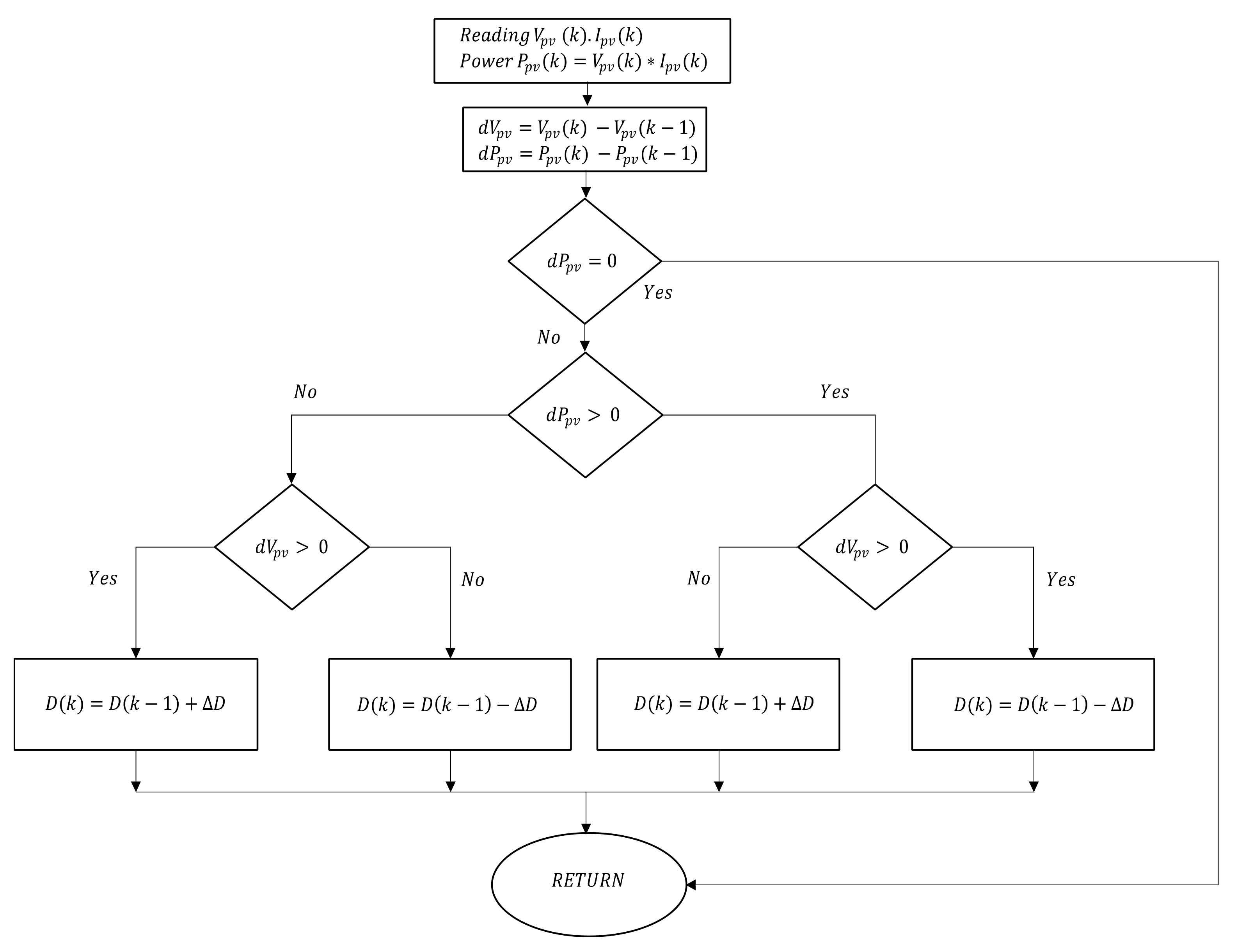
3.1.1. Design of an MPPT Control Strategy for the Photovoltaic Panel
3.1.2. Design of a Local Control Strategy for the Storage System
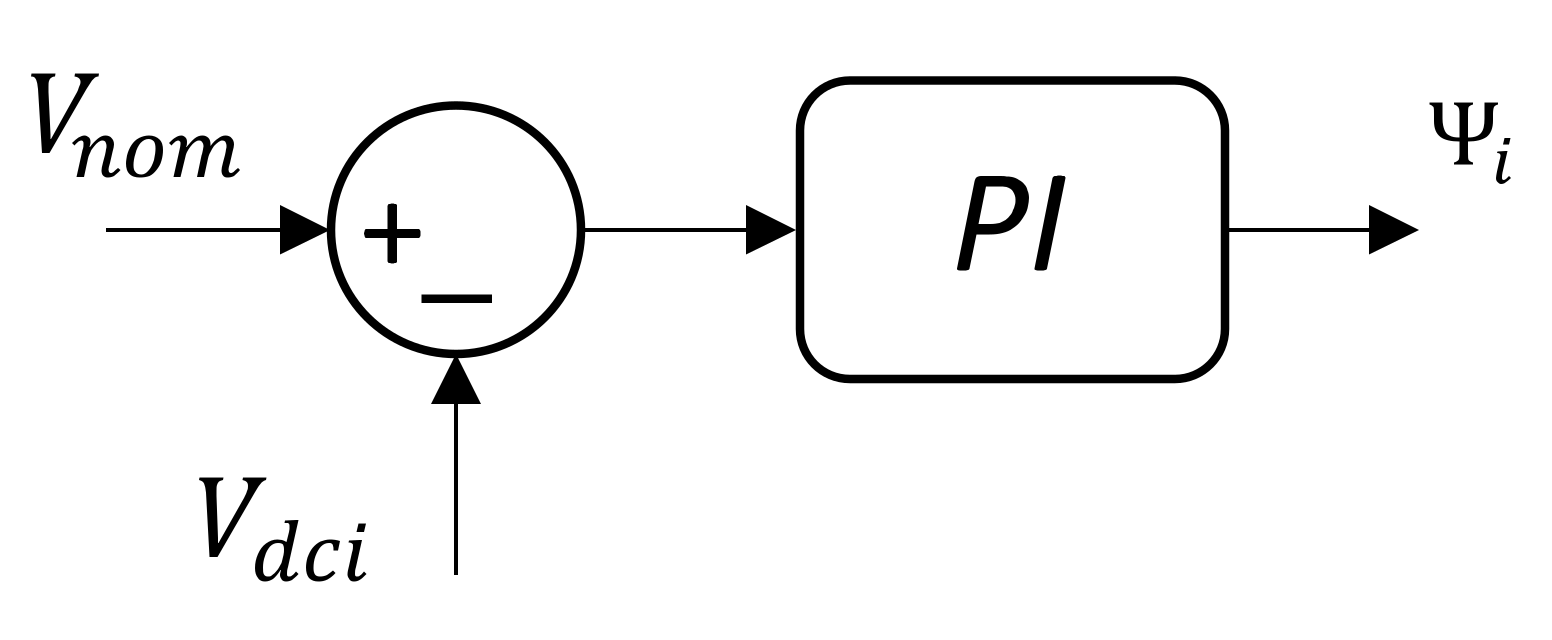
3.2. Droop (V-P) Controller Design in Batteries
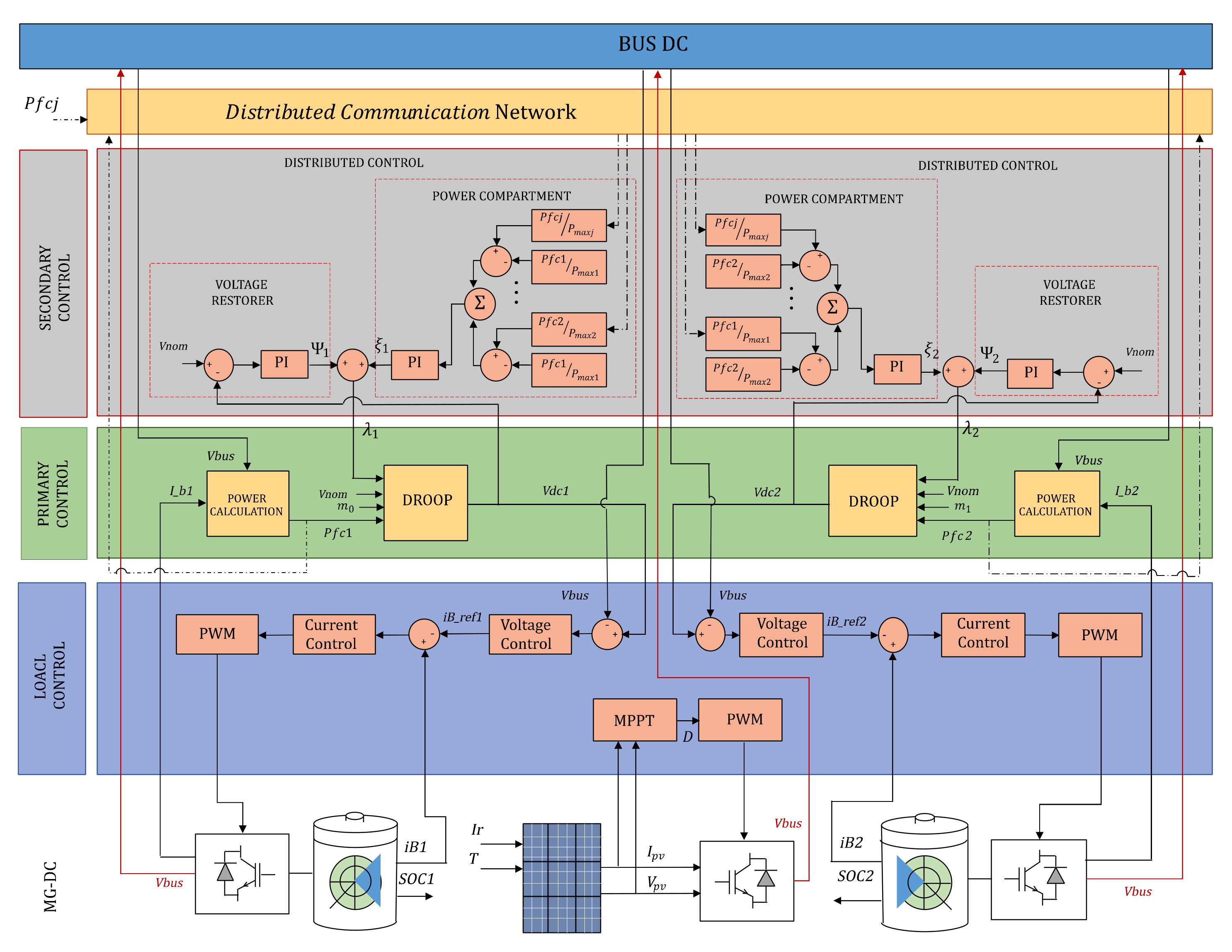
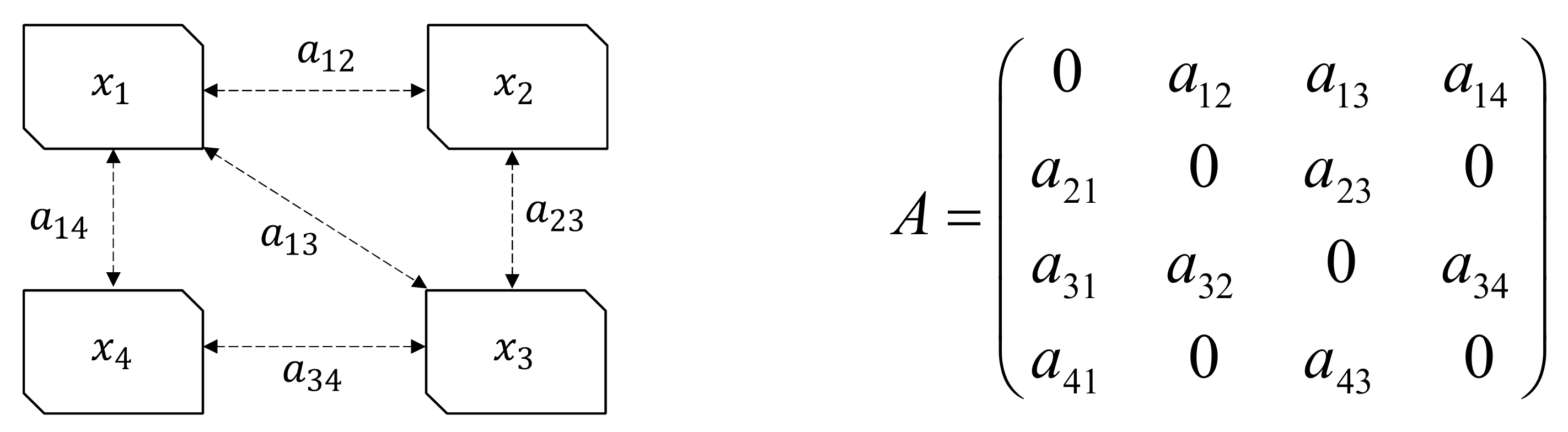
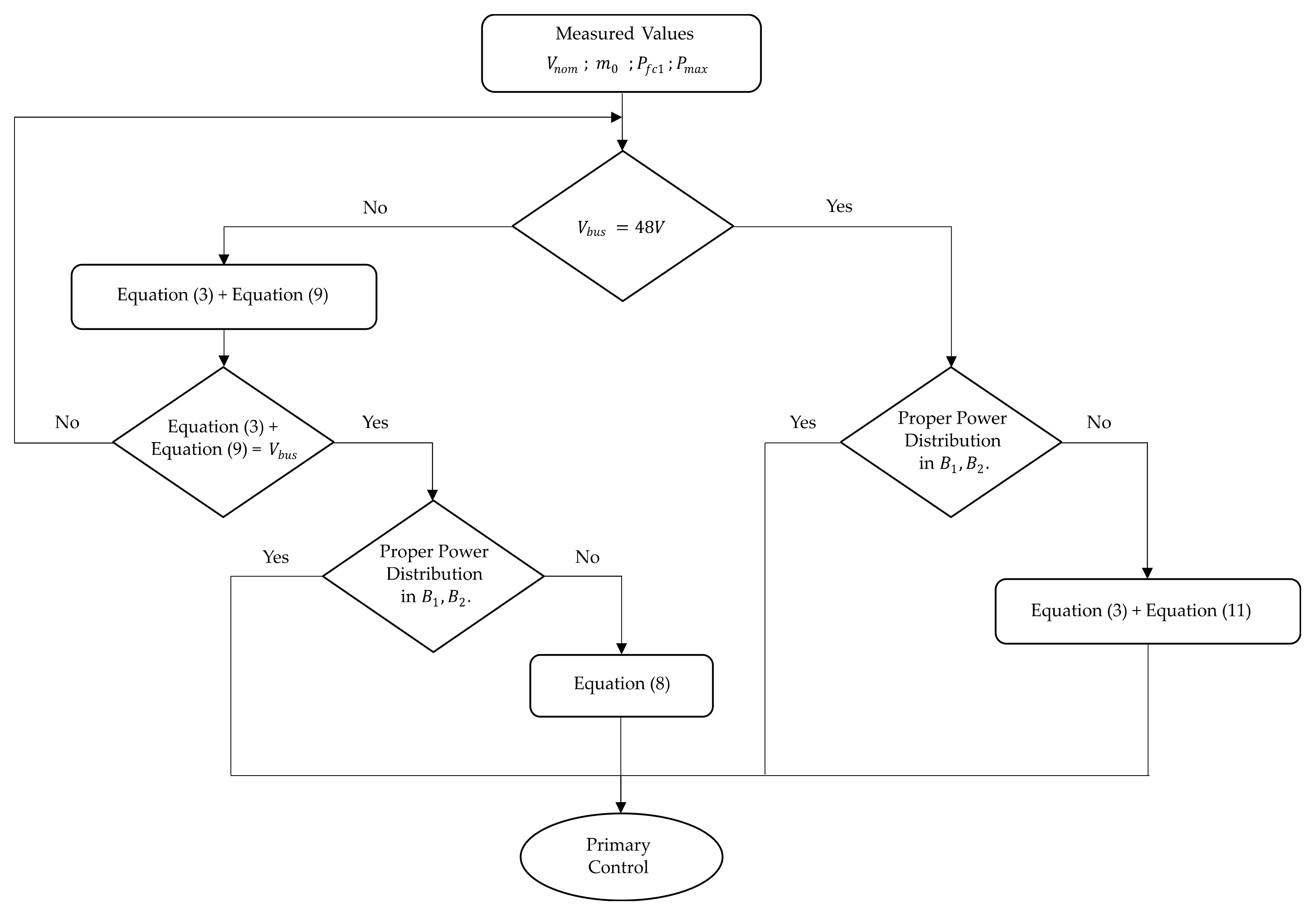
4. Distributed Secondary Controller for Efficient Battery Management
Distributed Control Design
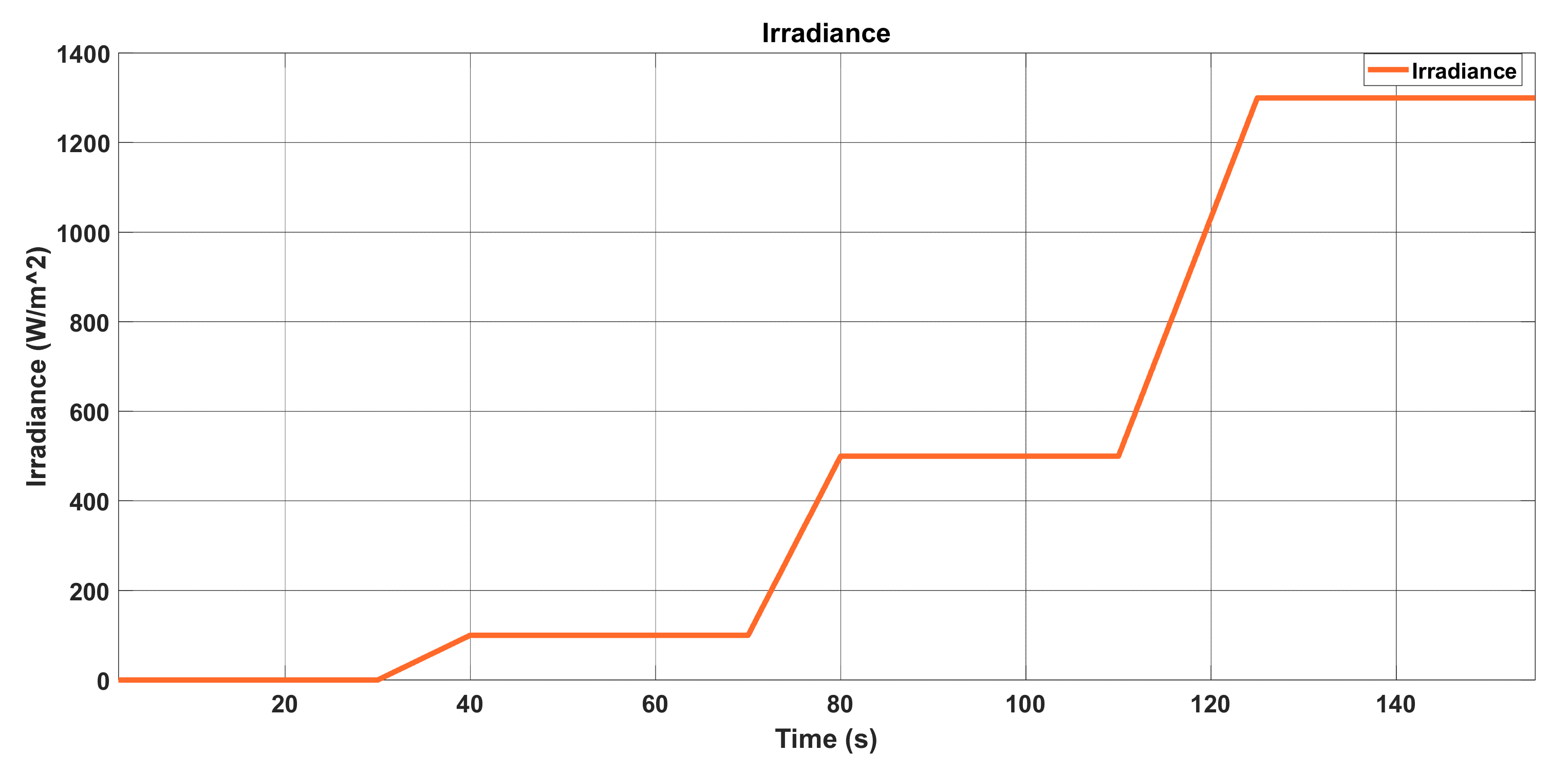
5. Results
5.1. Power Balance
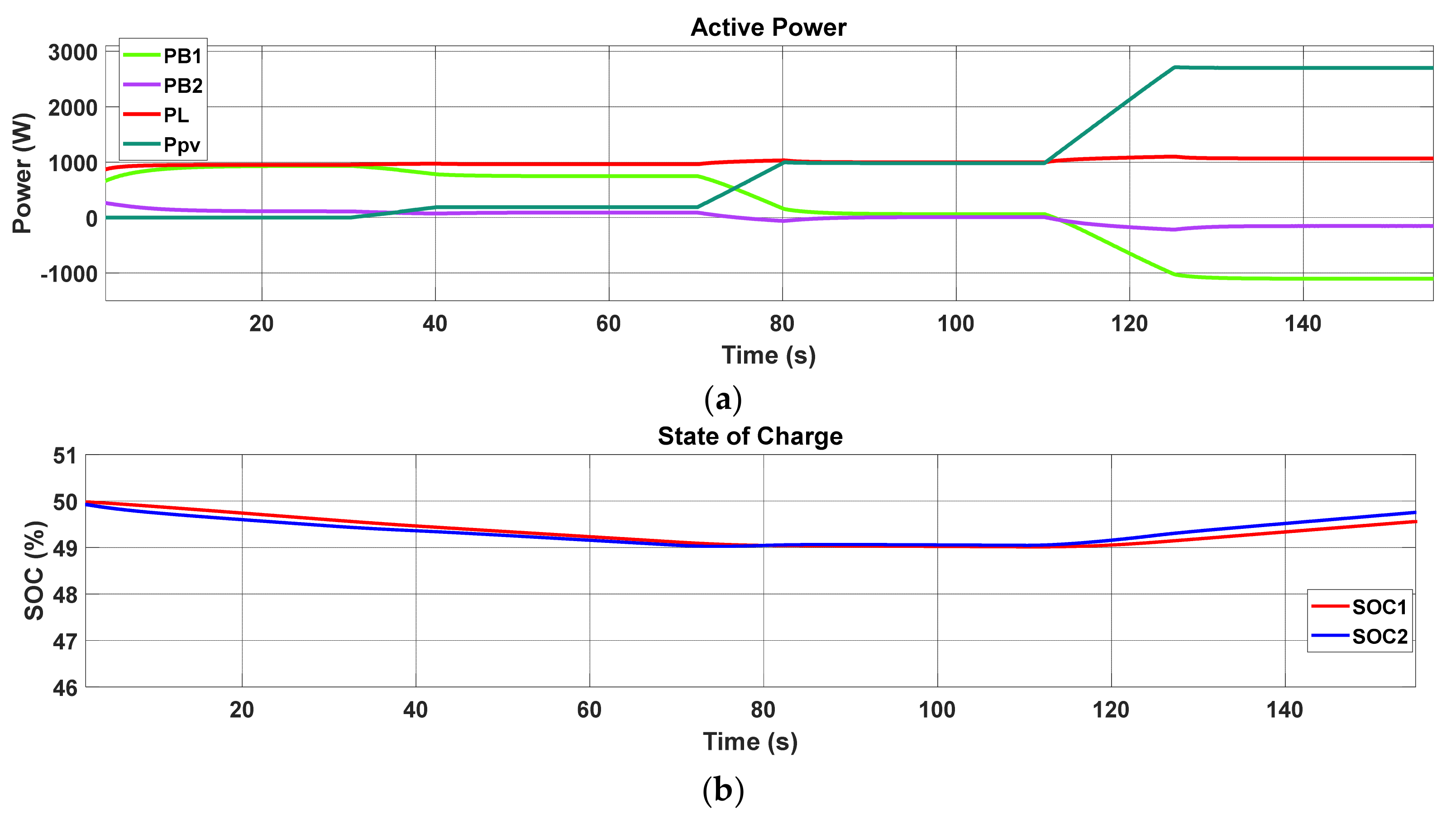
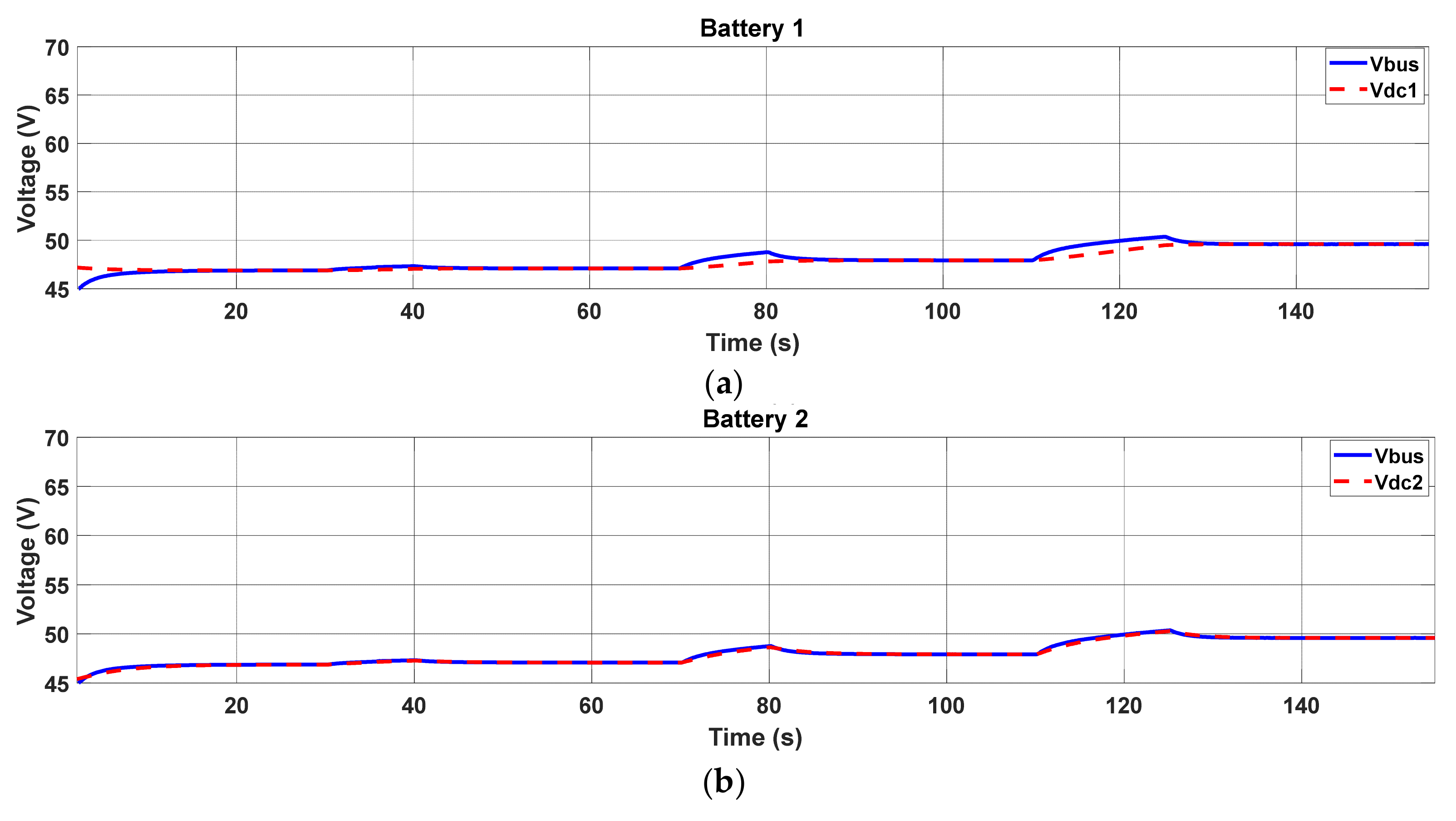
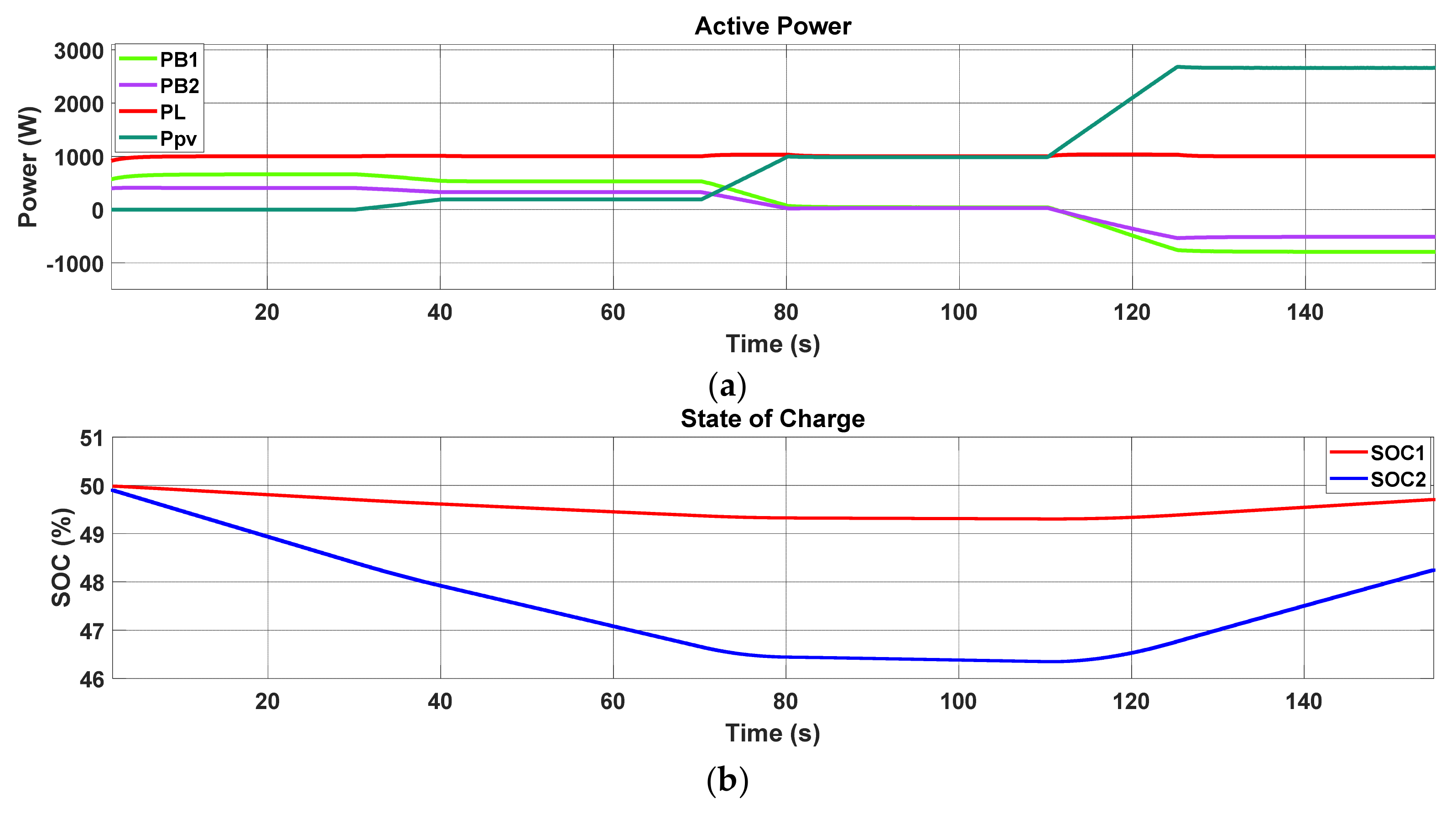
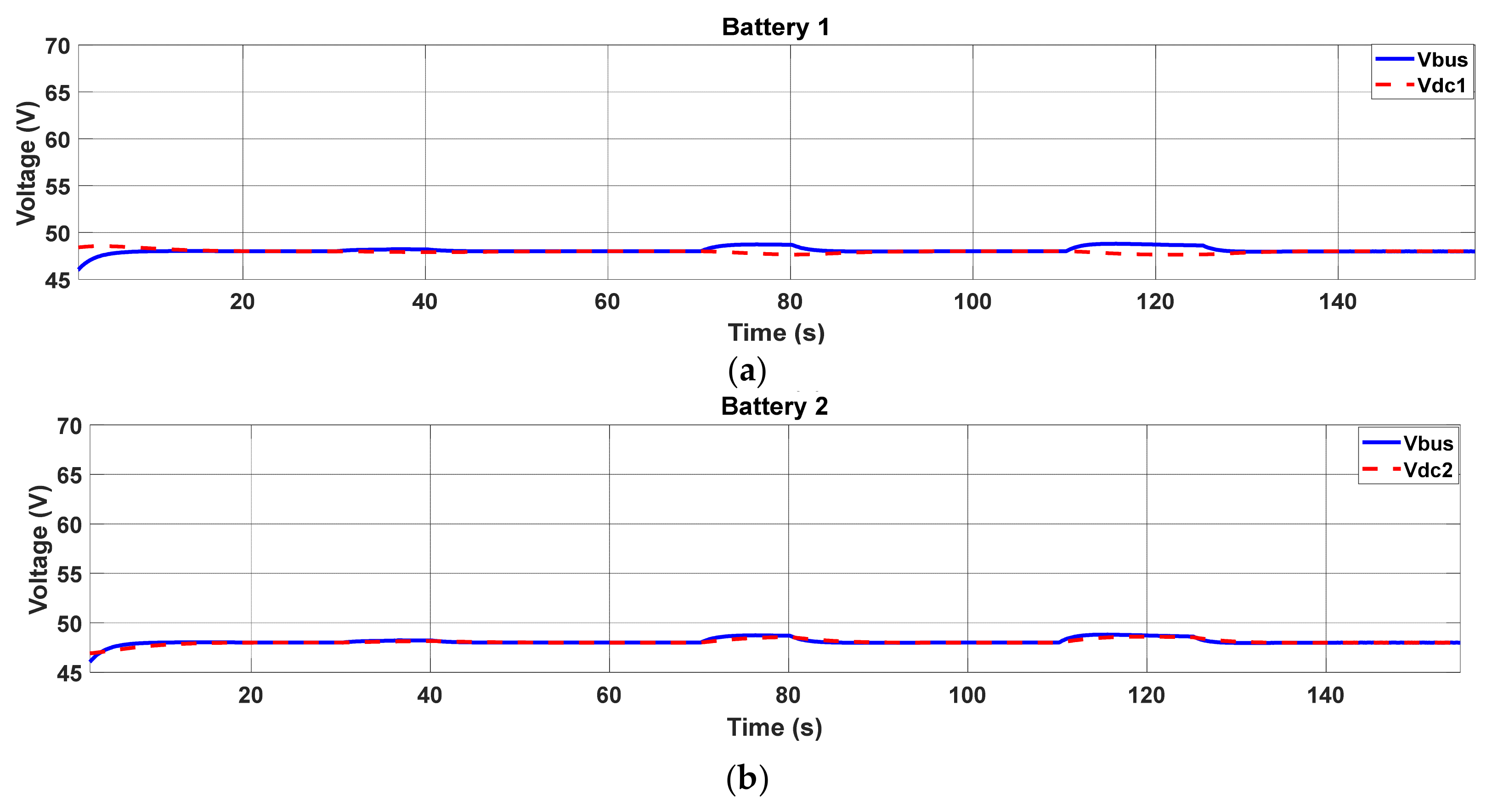
5.2. Primary Control (Local Control and Conventional Droop Control)
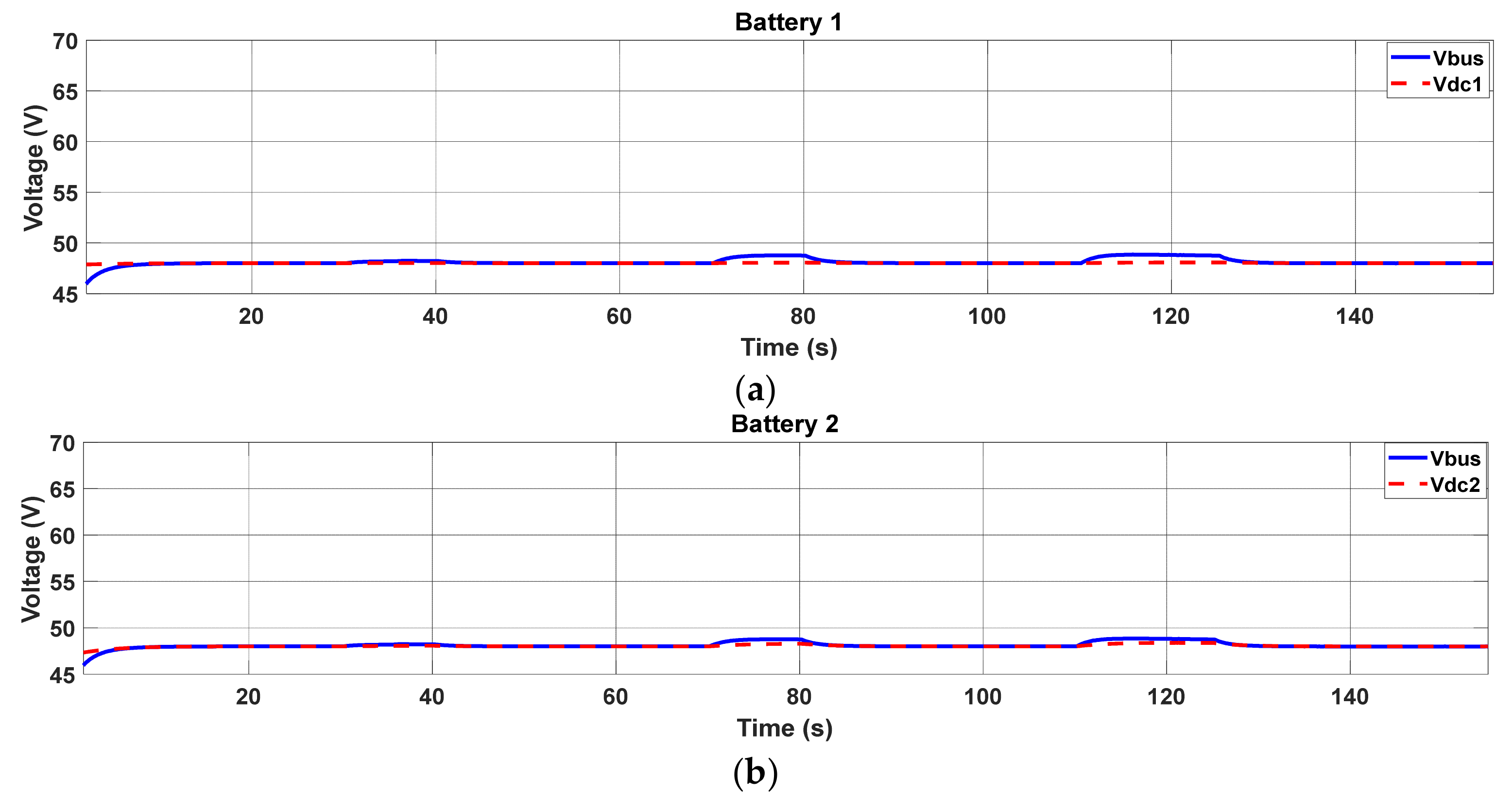
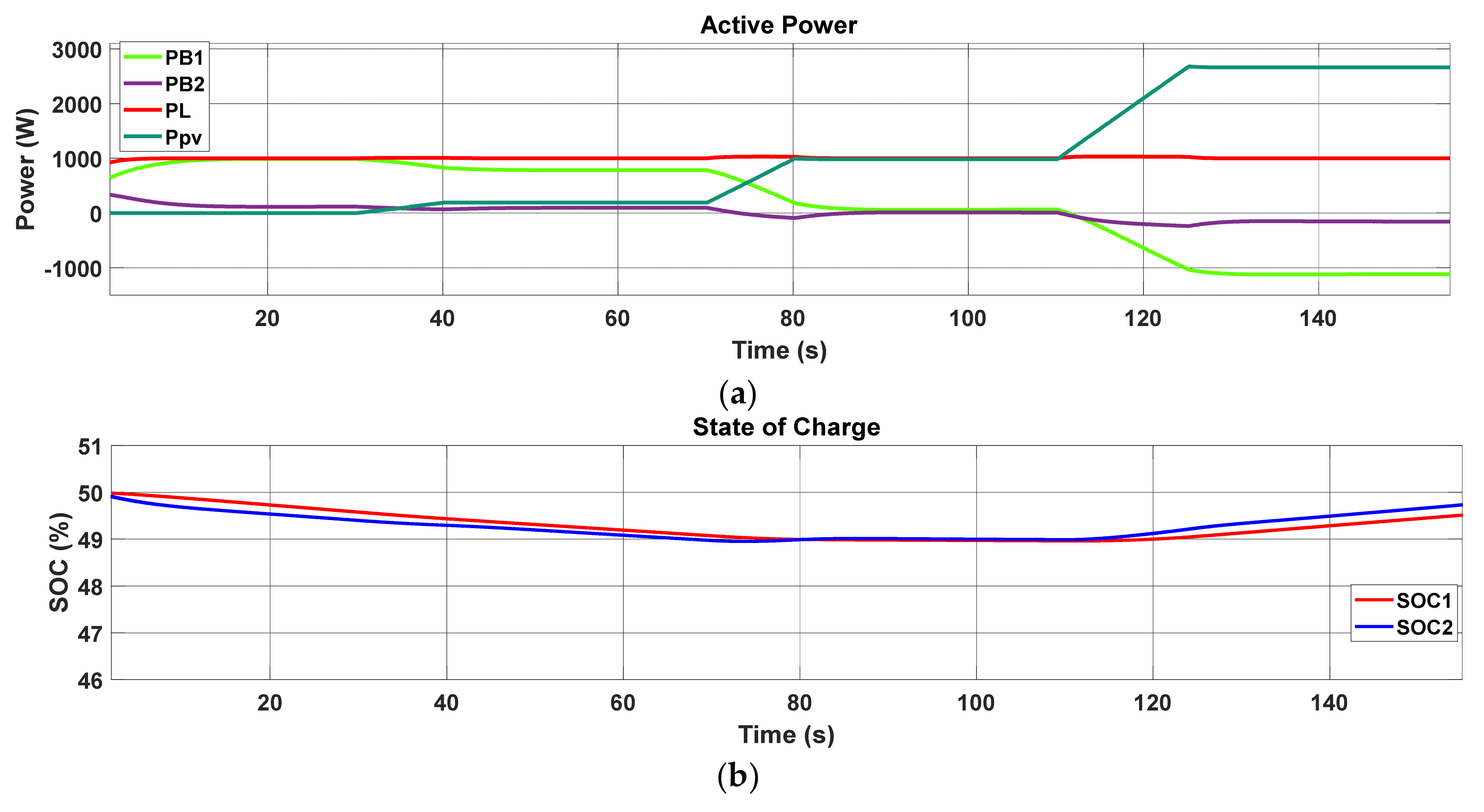
5.3. Distributed Secondary Control
5.4. Distributed Control Based on a Consensus Algorithm
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Adjacency matrix | |
| Elements of the adjacency matrix ( is the local node and is the neighboring node) | |
| Nominal Capacity | |
| Batteries Capacitor | |
| DC Capacitor | |
| PV Capacitor | |
| Duty cycle | |
| Current duty cycle | |
| Previous duty cycle | |
| Set of edges of the communication links | |
| Graph of the communication links | |
| Converter gates | |
| Storage unit | |
| Reference current output of the PI control | |
| Battery current | |
| Max. power array current | |
| Photovoltaic current | |
| Array current panel | |
| Integral gain | |
| Proportional gain | |
| Joint gain of proportional gain and integral gain for voltage regulator | |
| Joint gain of proportional and integral gain for the consensus-based algorithm | |
| Batteries inductance | |
| Inductance at PV | |
| Droop coefficient | |
| Set of vertices | |
| Battery power | |
| Power obtained at the output of the filter | |
| Power demanded to supply the MG-DC load | |
| Represents the maximum power in the battery | |
| Photovoltaic power | |
| Photovoltaic power in a previous instant | |
| Nominal voltage batteries | |
| Reference voltage on the DC bus | |
| Output of the droop controller | |
| Acceptable minimum voltage | |
| Voltage nominal Load | |
| Nominal value of the microgrid | |
| Array tension panel | |
| Photovoltaic voltage | |
| Photovoltaic voltage in a previous instant | |
| Represents the battery in a communication link | |
| Perturbation around the duty cycle | |
| Variation in the maximum acceptable voltage | |
| PI controller is implemented to restore the voltage with a traditional approach | |
| PI controller based on consensus theory | |
| Joint value of regulatory action and a consensus algorithm | |
| Distributed energy storage units | |
| Distributed generation | |
| Energy management system | |
| Energy storage system | |
| Fractional order proportional integral derivative | |
| AC microgrid | |
| DC microgrid | |
| MPPT | Maximum power point tracking |
| OD | Optimal dispatch |
| PID | Control proportional integral derivative |
| PV | Photovoltaic |
| PWM | Pulse width modulation |
| P & O | Perturb and observe |
| RES | Renewable energy sources |
| SOC | State of charge |
| SP | Set point |
| TS | Takagi–Sugeno |
References
- Cervantes Leopoldo, X.G. La Generación Distribuida y las Fuentes Renovables de energía en el Ecuador Distributed Generation and Renewable Sources of energy in Ecuador Geração Distribuída e Fontes Renováveis de Energia no Equador. Dom. Cien. 2021, 7, 884–895. [Google Scholar]
- Ullah, Z.; Elkadeem, M.; Kotb, K.M.; Taha, I.B.; Wang, S. Multi-criteria decision-making model for optimal planning of on/off grid hybrid solar, wind, hydro, biomass clean electricity supply. Renew Energy 2021, 179, 885–910. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, P.; Gu, J.; Schmidt, F.; Li, W. Measures to improve energy demand flexibility in buildings for demand response (DR): A review. Energy Build. 2018, 177, 125–139. [Google Scholar] [CrossRef]
- Carrión, D.; Ortiz, L. Generación distribuida a partir de bicicletas estáticas y sistemas híbridos. Ingenius 2013, 44–48. [Google Scholar] [CrossRef][Green Version]
- Pata, U.K. Linking renewable energy, globalization, agriculture, CO2 emissions and ecological footprint in BRIC countries: A sustainability perspective. Renew. Energy 2021, 173, 197–208. [Google Scholar] [CrossRef]
- Chen, C.; Pinar, M.; Stengos, T. Determinants of renewable energy consumption: Importance of democratic institutions. Renew. Energy 2021, 179, 75–83. [Google Scholar] [CrossRef]
- Rodriguez, M.; Espin, V.; Arcos-Aviles, D.; Martinez, W. Energy management system for an isolated microgrid based on Fuzzy logic control and meta-heuristic algorithms. In Proceedings of the 2022 IEEE 31st International Symposium on Industrial Electronics (ISIE), Anchorage, AK, USA, 1–3 June 2022. [Google Scholar]
- Yépez, H.; Yépez, D. Control de Modo Deslizante Para Microrredes: Una Revisión. Investig. Tecnológica IST Cent. Técnico 2020, 2, 14. [Google Scholar]
- Arcos-Aviles, D.; Pascual, J.; Guinjoan, F.; Marroyo, L.; Sanchis, P.; Marietta, M.P. Low complexity energy management strategy for grid profile smoothing of a residential grid-connected microgrid using generation and demand forecasting. Appl. Energy 2017, 205, 69–84. [Google Scholar] [CrossRef]
- Dulce Mera, F.A. Modelamiento y Control de Una Microrred en Modo Isla. Master’s Thesis, Universidad de los Andes, Bogotá, Colombia, June 2015. [Google Scholar]
- Rodriguez, M.; Arcos-Aviles, D.; Llanos, J.; Salazar, A.; Guinjoan, F.; Motoasca, E.; Martinez, W. Fuzzy-based energy management system for isolated microgrids using generation and demand forecast. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications, EPE 2021 ECCE Europe, Ghent, Belgium, 6–10 September 2021; pp. 1–10. [Google Scholar]
- Arcos-Aviles, D.; Pascual, J.; Marroyo, L.; Sanchis, P.; Guinjoan, F. Fuzzy Logic-Based Energy Management System Design for Residential Grid-Connected Microgrids. IEEE Trans. Smart Grid 2016, 9, 530–543. [Google Scholar] [CrossRef]
- Espina, E.; Llanos, J.; Burgos-Mellado, C.; Cardenas-Dobson, R.; Martinez-Gomez, M.; Saez, D. Distributed Control Strategies for Microgrids: An Overview. IEEE Access 2020, 8, 193412–193448. [Google Scholar] [CrossRef]
- Garcés, A. Small-signal stability analysis of DC microgrids considering electric vehicles. Rev. Fac. Ing. 2018, 2018, 1–7. [Google Scholar] [CrossRef]
- Bayrak, G.; Ghaderi, D. An improved step-up converter with a developed real-time fuzzy-based MPPT controller for PV-based residential applications. Int. Trans. Electr. Energy Syst. 2019, 29, e12140. [Google Scholar] [CrossRef]
- Rao, C.; Hajjiah, A.; El-Meligy, M.A.; Sharaf, M.; Soliman, A.T.; Mohamed, M.A. A Novel High-Gain Soft-Switching DC-DC Converter with Improved P&O MPPT for Photovoltaic Applications. IEEE Access 2021, 9, 58790–58806. [Google Scholar] [CrossRef]
- Das, M.; Agarwal, V. Novel High-Performance Stand-Alone Solar PV System with High-Gain High-Efficiency DC–DC Converter Power Stages. IEEE Trans. Ind. Appl. 2015, 51, 4718–4728. [Google Scholar] [CrossRef]
- Abdel-Rahim, O.; Wang, H. Aswan University a New High Gain DC-DC Converter with Model-Predictive-Control Based MPPT Technique for Photovoltaic Systems. CPSS Trans. Power Electron. Appl. 2020, 5, 191–200. [Google Scholar] [CrossRef]
- Romero Andrade, G.D. Optimización del Proceso de Carga y Descarga de Bancos de Baterías en Sistemas de Generación Fotovoltaica. Bachelor’s Thesis, Universidad Politécnica Salesiana, Quito, Ecuador, August 2018. [Google Scholar]
- Rezk, H.; Nassef, A.M.; Abdelkareem, M.A.; Alami, A.H.; Fathy, A. Comparison among various energy management strategies for reducing hydrogen consumption in a hybrid fuel cell/supercapacitor/battery system. Int. J. Hydrogen Energy 2019, 46, 6110–6126. [Google Scholar] [CrossRef]
- Al Alahmadi, A.A.; Belkhier, Y.; Ullah, N.; Abeida, H.; Soliman, M.S.; Khraisat, Y.S.H.; Alharbi, Y.M. Hybrid Wind/PV/Battery Energy Management-Based Intelligent Non-Integer Control for Smart DC-Microgrid of Smart University. IEEE Access 2021, 9, 98948–98961. [Google Scholar] [CrossRef]
- Belal, E.K.; Yehia, D.M.; Azmy, A.M. Adaptive droop control for balancing SOC of distributed batteries in DC microgrids. IET Gener. Transm. Distrib. 2019, 13, 4667–4676. [Google Scholar] [CrossRef]
- Baharizadeh, M.; Golsorkhi, M.S.; Shahparasti, M.; Savaghebi, M. A Two-Layer Control Scheme Based on P—V Droop Characteristic for Accurate Power Sharing and Voltage Regulation in DC Microgrids. IEEE Trans. Smart Grid 2021, 12, 2776–2787. [Google Scholar] [CrossRef]
- Xing, L.; Xu, Q.; Guo, F.; Wu, Z.-G.; Liu, M. Distributed Secondary Control for DC Microgrid With Event-Triggered Signal Transmissions. IEEE Trans. Sustain. Energy 2021, 12, 1801–1810. [Google Scholar] [CrossRef]
- Xing, L.; Mishra, Y.; Guo, F.; Lin, P.; Yang, Y.; Ledwich, G.; Tian, Y.-C. Distributed Secondary Control for Current Sharing and Voltage Restoration in DC Microgrid. IEEE Trans. Smart Grid 2019, 11, 2487–2497. [Google Scholar] [CrossRef]
- Lu, X.; Sun, K.; Guerrero, J.M.; Vasquez, J.C.; Huang, L. State-of-Charge Balance Using Adaptive Droop Control for Distributed Energy Storage Systems in DC Microgrid Applications. IEEE Trans. Ind. Electron. 2013, 61, 2804–2815. [Google Scholar] [CrossRef]
- Xu, D.; Xu, A.; Yang, C.; Shi, P. A Novel Double-Quadrant SoC Consistent Adaptive Droop Control in DC Microgrids. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 2034–2038. [Google Scholar] [CrossRef]
- Papadimitriou, C.N.; Zountouridou, E.I.; Hatziargyriou, N.D. Review of hierarchical control in DC microgrids. Electr. Power Syst. Res. 2015, 122, 159–167. [Google Scholar] [CrossRef]
- Dahale, S.; Das, A.; Pindoriya, N.M.; Rajendran, S. An overview of DC-DC converter topologies and controls in DC microgrid. In Proceedings of the 2017 7th International Conference on Power Systems, ICPS 2017, Pune, India, 21–23 December 2017; pp. 410–415. [Google Scholar] [CrossRef]
- Hichem, L.; Leila, M.; Amar, O. Comparative Study of Perturb-and-Observe and Fuzzy Logic MPPT for Stand-Alone PV System; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; Volume 361. [Google Scholar] [CrossRef]
- Islam, F.R.; Prakash, K.; Mamun, K.A.; Lallu, A.; Mudliar, R. Design a Optimum MPPT Controller for Solar Energy System. Indones. J. Electr. Eng. Comput. Sci. 2016, 2, 545. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W.; Shafiee, Q.; Dörfler, F.; Vasquez, J.C.; Guerrero, J.M.; Bullo, F. Secondary Frequency and Voltage Control of Islanded Microgrids via Distributed Averaging. IEEE Trans. Ind. Electron. 2015, 62, 7025–7038. [Google Scholar] [CrossRef]
- Llanos, J.; Gomez, J.; Saez, D.; Olivares, D.; Simpson-porco, J. Economic Dispatch by Secondary Distributed Control in Microgrids Economic Dispatch by Secondary Distributed Control in Microgrids Acknowledgments Keywords. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 3–5 September 2019. [Google Scholar] [CrossRef]
- Burgos-Mellado, C.; Donoso, F.; Llanos, J.; Martinez-Gomez, M.; Morales-Paredes, H.K.; Torres, M. Consensus-Based Distributed Control for Improving the Sharing of Unbalanced Currents in Three-Phase Three-Wire Isolated Microgrids. In Proceedings of the 2021 6th IEEE Workshop on the Electronic Grid (eGRID), New Orleans, LA, USA, 8–10 November 2021. [Google Scholar]
- Burgos-Mellado, C.; Llanos, J.J.; Cardenas, R.; Saez, D.; Olivares, D.E.; Sumner, M.; Costabeber, A. Distributed Control Strategy Based on a Consensus Algorithm and on the Conservative Power Theory for Imbalance and Harmonic Sharing in 4-Wire Microgrids. IEEE Trans. Smart Grid 2019, 11, 1604–1619. [Google Scholar] [CrossRef]
- Gomez, J.S.; Llanos, J.; Espina, E.; Burgos-Mellado, C.; Rodriguez, J. Cooperative Power Conditioners for Microgrids in Mining. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Ghent, Belgium, 6–10 September 2021. [Google Scholar] [CrossRef]
- Llanos, J.; Olivares, D.E.; Simpson-Porco, J.W.; Kazerani, M.; Saez, D. A Novel Distributed Control Strategy for Optimal Dispatch of Isolated Microgrids Considering Congestion. IEEE Trans. Smart Grid 2019, 10, 6595–6606. [Google Scholar] [CrossRef]
- Llanos Proaño, J.D.R. Design and Evaluation of Distributed Controllers for Optimal Dispatch and Congestion Management of Microgrids. Ph.D. Thesis, Universidad de Chile, Santiago de Chile, Chile, December 2020. [Google Scholar]


| Description | Parameter | Battery 1 | Battery 2 |
|---|---|---|---|
| Nominal Voltage | 36 | 36 | |
| Nominal Capacity | 50 | 6.5 | |
| Initial Charge State | SOC (%) | 50% | 50% |
| Description | Parameter | Value |
|---|---|---|
| Array tension panel | 36.3 V | |
| Array current panel | 7.84 A | |
| Max. Power array tension | 29 V | |
| Max. Power array current | 7.35 A |
| Description | Parameter | Value | |
|---|---|---|---|
| Inductance at PV | |||
| Battery Inductance 1 | |||
| Battery Inductance 2 | |||
| PV Capacitor | |||
| DC Capacitor | |||
| Capacitor Battery 1 | |||
| Capacitor Battery 2 | |||
| Load | Voltage nominal | 48 | |
| Active power | 1000 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moya, A.P.; Pazmiño, P.J.; Llanos, J.R.; Ortiz-Villalba, D.; Burgos, C. Distributed Secondary Control for Battery Management in a DC Microgrid. Energies 2022, 15, 8769. https://doi.org/10.3390/en15228769
Moya AP, Pazmiño PJ, Llanos JR, Ortiz-Villalba D, Burgos C. Distributed Secondary Control for Battery Management in a DC Microgrid. Energies. 2022; 15(22):8769. https://doi.org/10.3390/en15228769
Chicago/Turabian StyleMoya, Alexander Paul, Polo Josue Pazmiño, Jacqueline Rosario Llanos, Diego Ortiz-Villalba, and Claudio Burgos. 2022. "Distributed Secondary Control for Battery Management in a DC Microgrid" Energies 15, no. 22: 8769. https://doi.org/10.3390/en15228769
APA StyleMoya, A. P., Pazmiño, P. J., Llanos, J. R., Ortiz-Villalba, D., & Burgos, C. (2022). Distributed Secondary Control for Battery Management in a DC Microgrid. Energies, 15(22), 8769. https://doi.org/10.3390/en15228769







