Modeling, Experimental Analysis, and Optimized Control of an Ocean Wave Energy Conversion System in the Yellow Sea near Lianyungang Port
Abstract
:1. Introduction
2. Motion Model of Double-Buoy OWECS
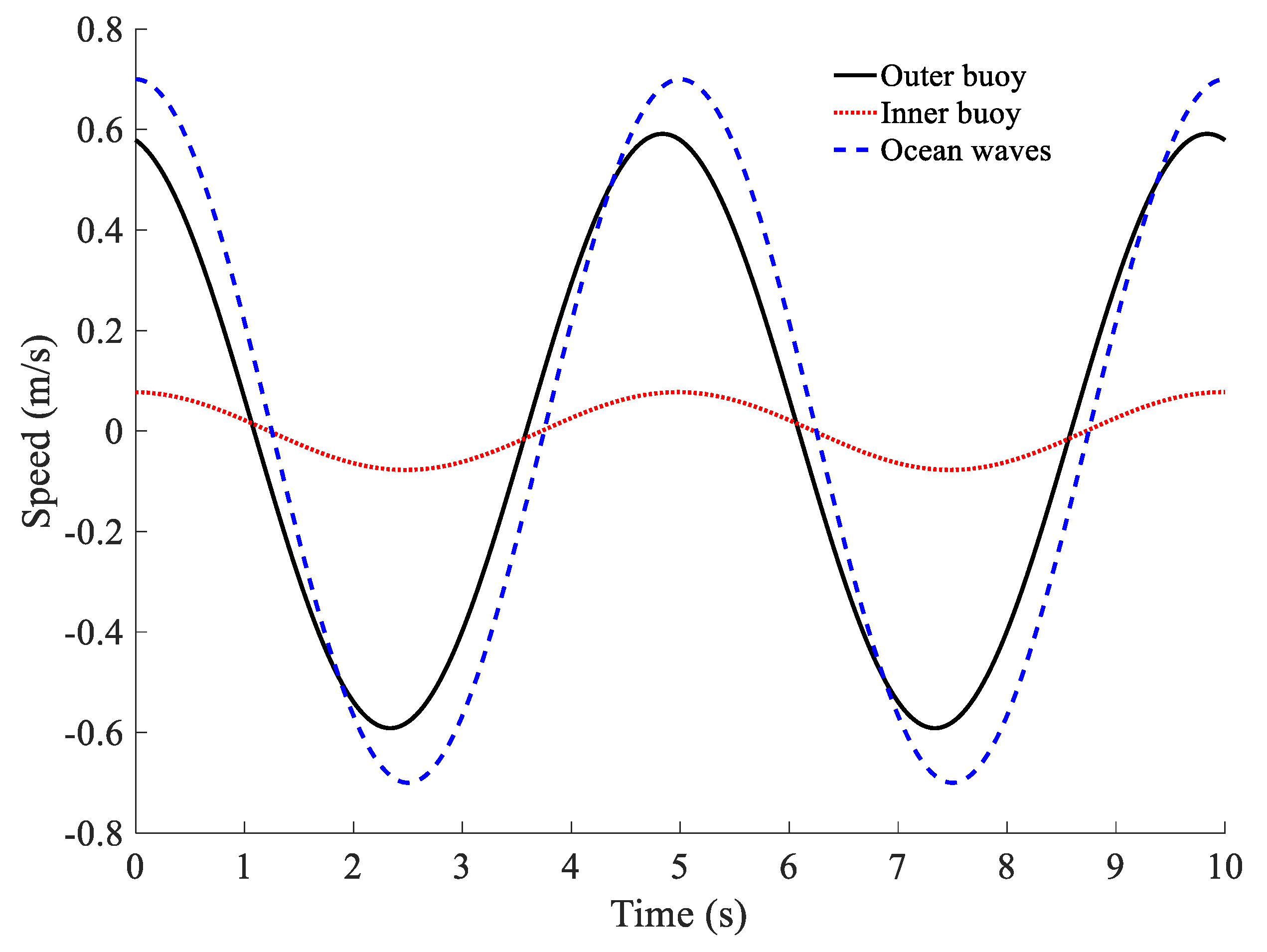
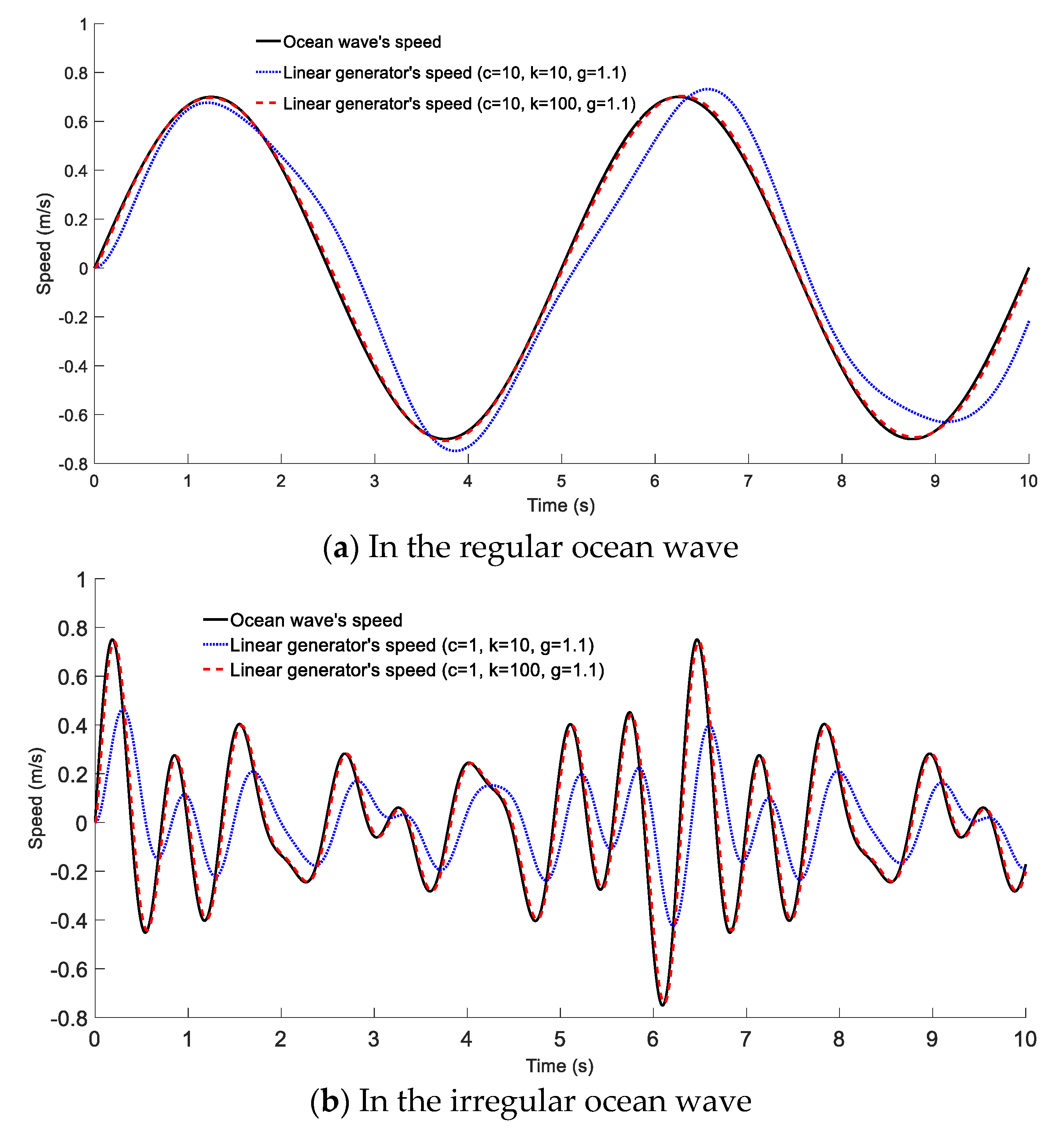
2.1. Vertical Direction Speed of Buoy
2.2. Analysis of Energy Conversion Efficiency
3. Experimental Results
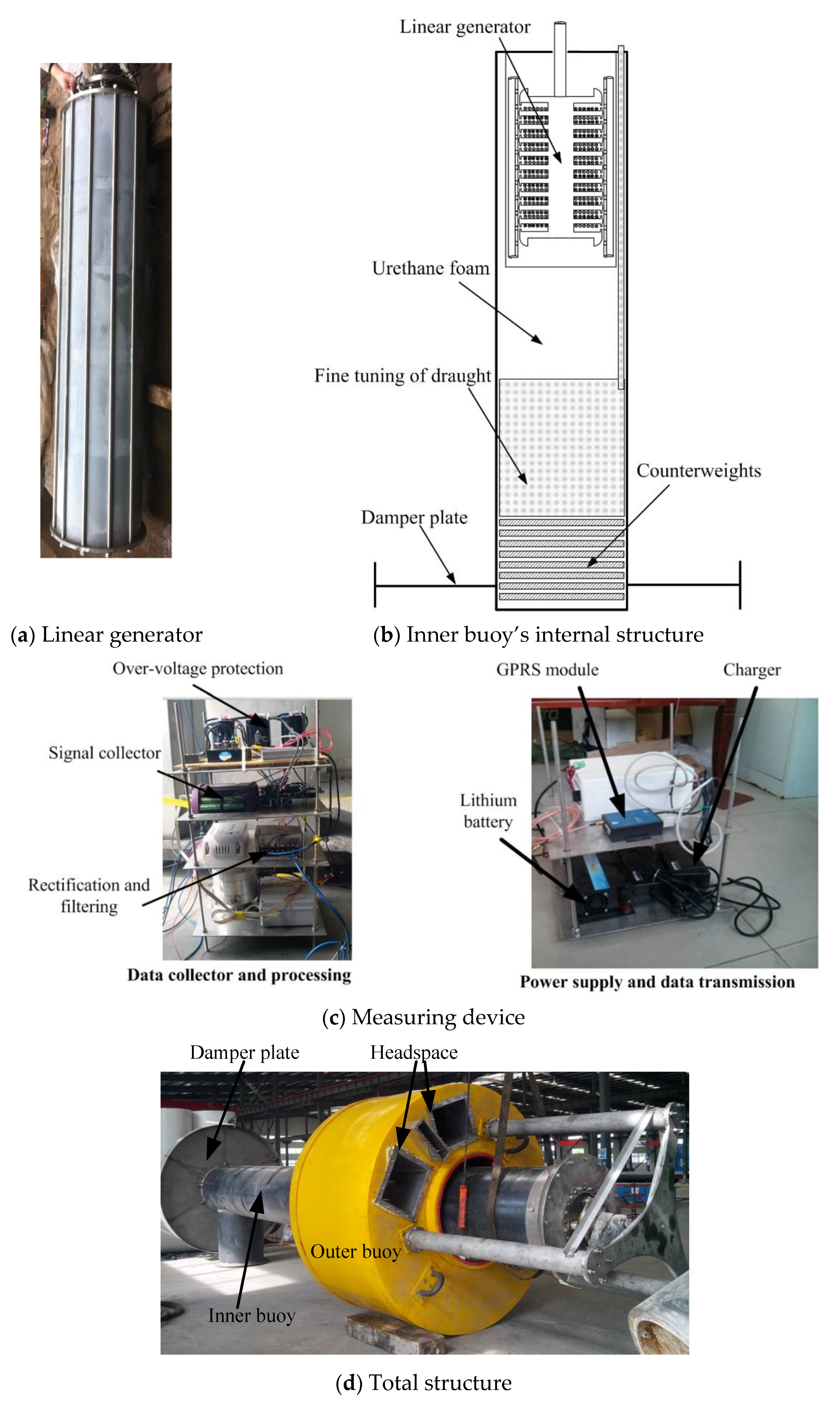
3.1. The Specific Structure of Double-Buoy OWECS
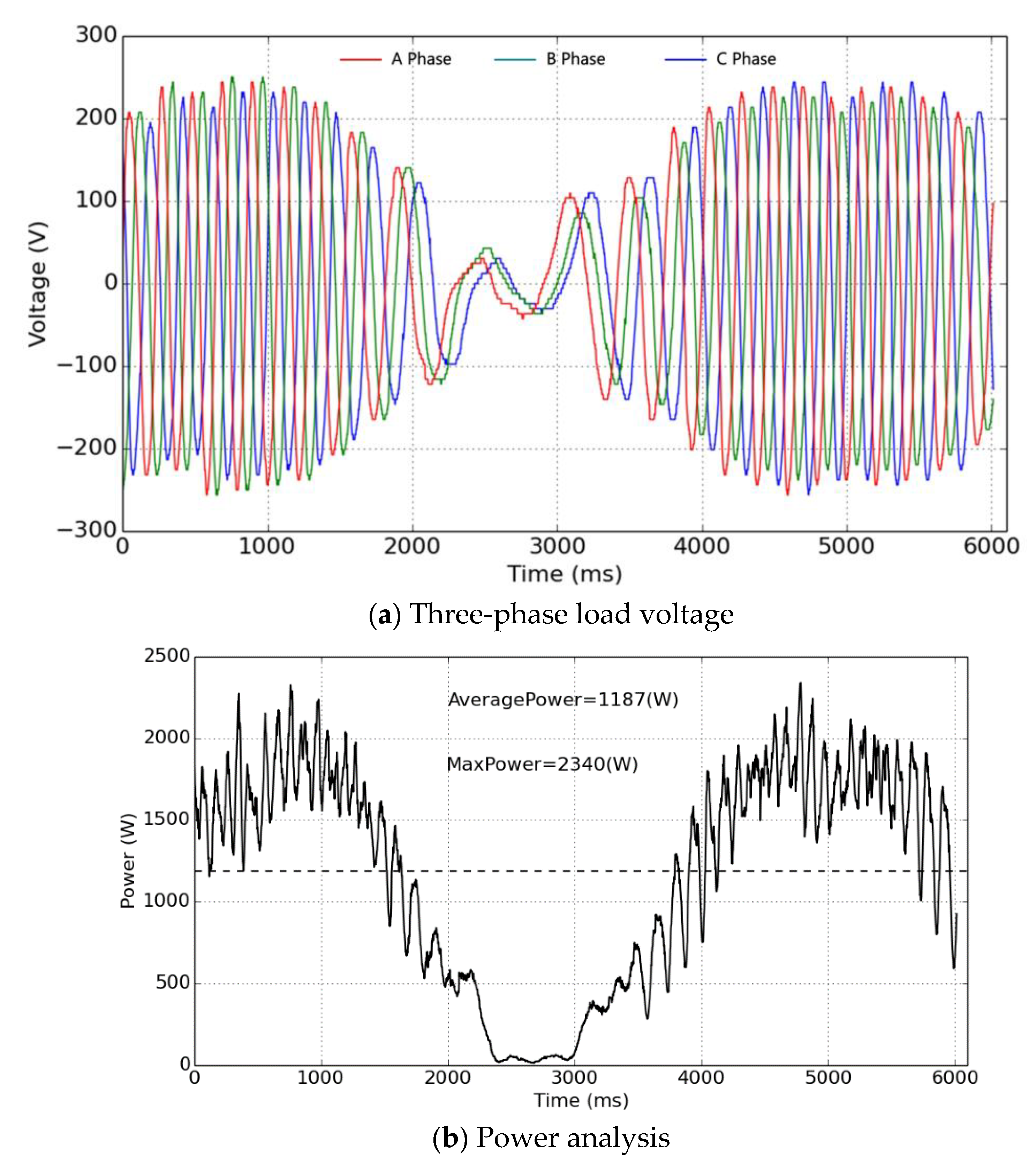
3.2. Output Voltage and Power Analysis
4. Efficiency Improvement of Double-Buoy OWECS
4.1. The Relationship between Load Force and q-Axis Current of Linear Generator
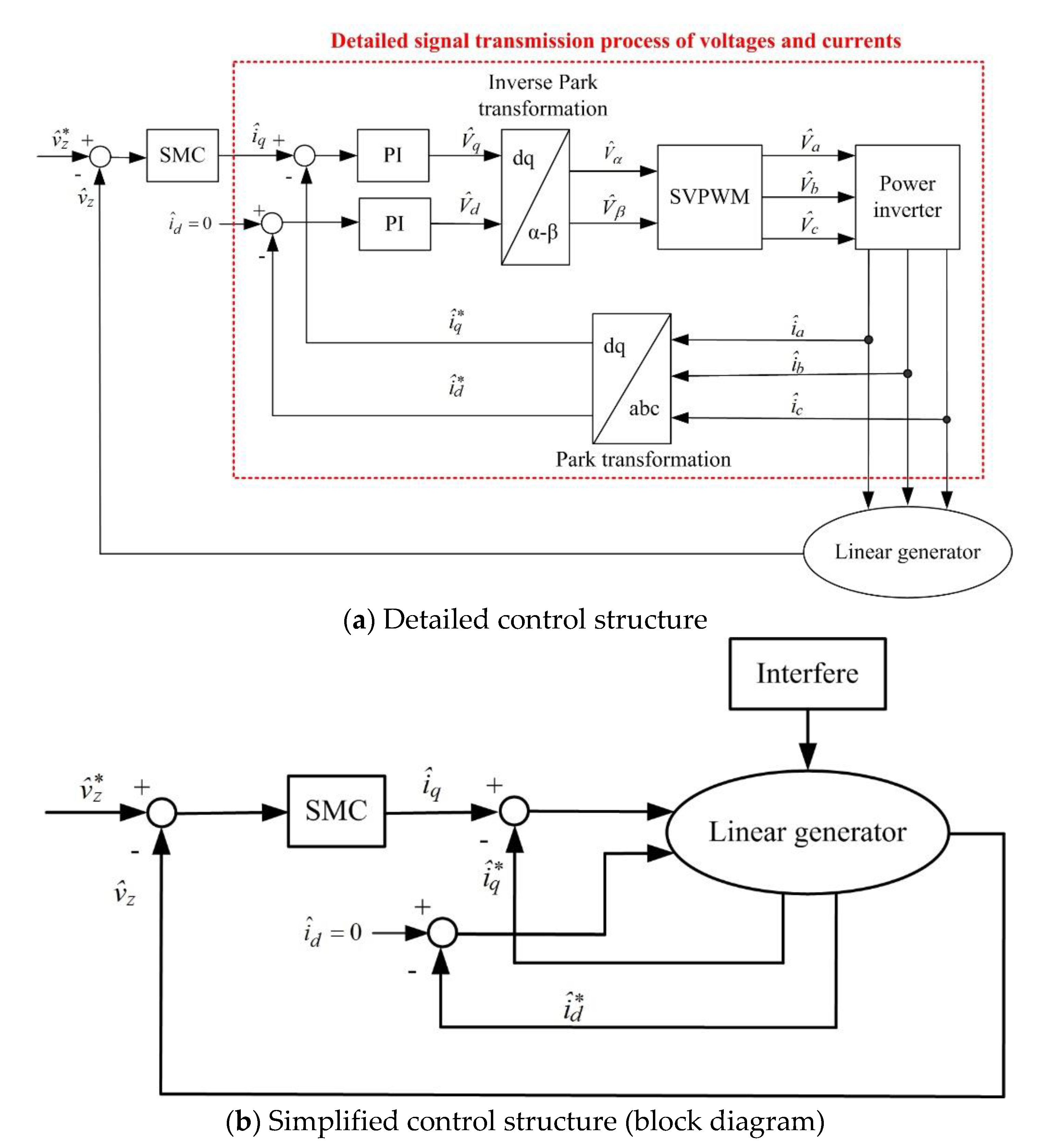
4.2. Optimized Control of Double-Buoy OWECS
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mustapa, M.A.; Yaakob, O.B.; Ahmed, Y.M.; Rheem, C.K.; Koh, K.K.; Adnan, F.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energy Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
- Brodersen, K.M.; Bywater, E.A.; Lanter, A.M.; Schennum, H.H.; Furia, K.N.; Sheth, M.K.; Kiefer, N.S.; Cafferty, B.K.; Rao, A.K.; Garcia, J.M.; et al. Direct-drive ocean wave-powered batch reverse osmosis. Desalination 2022, 523, 115393. [Google Scholar] [CrossRef]
- Fischer, A.; Silva, J.S.; Beluco, A. Feasibility limits for a hybrid system with ocean wave and ocean current power plants in southern coast of brazil. Comput. Water Energy Environ. Eng. 2021, 10, 104581. [Google Scholar] [CrossRef]
- Viet, N.V.; Wang, Q.; Carpinteri, A. Development of an ocean wave energy harvester with a built-in frequency conversion function. Int. J. Energy Res. 2018, 42, 684–695. [Google Scholar] [CrossRef]
- Edwards, E.C.; Yue, K.P. Optimisation of the geometry of axisymmetric point-absorber wave energy converters. J. Fluid Mech. 2022, 933, 1–17. [Google Scholar] [CrossRef]
- Qin, H.; Tan, S.; Xia, Z.; Zhu, Y. An analysis of international patents on ocean wave energy. Libr. Inf. Stud. 2012, 4, 45–53. [Google Scholar]
- Cheng, Y.; Fu, L.; Dai, S.; Collu, M.; Cui, L.; Yuan, Z.; Incecik, A. Experimental and numerical analysis of a hybrid WEC-breakwater system combining an oscillating water column and an oscillating buoy. Renew. Sustain. Energy Rev. 2022, 169, 112909. [Google Scholar] [CrossRef]
- Cheng, Y.; Fu, L.; Dai, S.; Collu, M.; Ji, C.; Yuan, Z.; Incecik, A. Experimental and numerical investigation of WEC-type floating breakwaters: A single-pontoon oscillating buoy and a dual-pontoon oscillating water column. Coast. Eng. 2022, 177, 104188. [Google Scholar] [CrossRef]
- Jia, C.; Cao, H.; Pan, H.; Ahmed, A.; Jiang, Z.; Azam, A.; Zhang, Z.; Pan, Y. A wave energy converter based on a zero-pressure-angle mechanism for self-powered applications in near-zero energy sea crossing bridges. Smart Mater. Struct. 2022, 31, 095006. [Google Scholar] [CrossRef]
- Baghbani Kordmahale, S.; Do, J.; Chang, K.A.; Kameoka, J. A hybrid structure of piezoelectric fibers and soft materials as a smart floatable open-water wave energy converter. Micromachines 2021, 12, 1269. [Google Scholar] [CrossRef] [PubMed]
- Zou, S.; Abdelkhalik, O. Modeling of a variable-geometry wave energy converter. IEEE J. Ocean. Eng. 2021, 46, 879–890. [Google Scholar] [CrossRef]
- Park, J.S.; Gu, B.G.; Kim, J.R.; Cho, I.H.; Jeong, I.; Lee, J. Active phase control for maximum power point tracking of linear wave generator. IEEE Trans. Power Electron. 2017, 32, 7651–7662. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems; Cambridge University Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Farrok, O.; Islam, M.R.; Sheikh, M.R.; Guo, Y.; Zhu, J.; Xu, W. A novel superconducting magnet excited linear generator for wave energy conversion system. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef] [Green Version]
- García-Tabarés, L.; Lafoz, M.; Blanco, M.; Torres, J.; Obradors, D.; Nájera, J.; Navarro, G.; García, F.; Sánchez, A. New type of linear switched reluctance generator for wave energy applications. IEEE Trans. Appl. Supercond. 2020, 30, 19642959. [Google Scholar]
- Xia, T.; Yu, H.; Guo, R.; Liu, X. Research on the field-modulated tubular linear generator with quasi-halbach magnetization for ocean wave energy conversion. IEEE Trans. Appl. Supercond. 2018, 28, 17610493. [Google Scholar] [CrossRef]
- Viet, N.V.; Xie, X.D.; Liew, K.M.; Banthia, N.; Wang, Q. Energy harvesting from ocean waves by a floating energy harvester. Energy 2016, 112, 1219–1226. [Google Scholar] [CrossRef]
- Masoumi, M.; Wang, Y. Repulsive magnetic levitation-based ocean wave energy harvester with variable resonance: Modeling, simulation and experiment. J. Sound Vib. 2016, 381, 192–205. [Google Scholar] [CrossRef] [Green Version]
- Xie, D.M.; Chen, Y.P.; Zhang, C.K. On wave distribution of the East China Sea. Port Waterw. Eng. 2012, 11, 14–21. [Google Scholar]
- Masamichi, I.; Shinji, D. PMSM Model Discretization in Consideration of Park Transformation for Current Control System. In Proceedings of the International Power Electronics Conference, Niigata, Japan, 20–24 May 2018. [Google Scholar]
- Liu, K.; Hou, C.; Hua, W. A Novel Inertia Identification Method and Its Application in PI Controllers of PMSM Drives. IEEE Access 2016, 7, 13445–13454. [Google Scholar] [CrossRef]
- Wang, P.; Xu, Y.; Ding, R.; Liu, W.; Shu, S.; Yang, X. Multi-Kernel Neural Network Sliding Mode Control for Permanent Magnet Linear Synchronous Motors. IEEE Access 2021, 9, 57385–57392. [Google Scholar] [CrossRef]
- Liu, J. Sliding Mode Control Design and MATLAB Simulation: The Basic Theory and design Method; Tsinghua University Press: Beijing, China, 2015. [Google Scholar]
- Wei, Y.; Sun, L.; Chen, Z. An improved sliding mode control method to increase the speed stability of permanent magnet synchronous motors. Energies 2022, 15, 15176313. [Google Scholar] [CrossRef]






| Outer Diameter | 2.4 m | |
|---|---|---|
| Inner diameter | 1.0 m | |
| Outer buoy | Height | 1.8 m |
| Draft () | 0.771 m | |
| Outer diameter | 0.83 m | |
| Inner buoy | Height | 7.9 m |
| Draft () | 6.059 m |
| Wave Amplitude (m) | Wave Period (s) | Power (kW) | Efficiency | ||
|---|---|---|---|---|---|
| Ocean Wave (Kinetic Energy) | Outer Buoy | Inner Buoy | |||
| 0.7 | 3 | 10.7275 | 3.4206 | 0.5225 | 27.02% |
| 0.7 | 5 | 17.879 | 7.0680 | 0.5615 | 36.39% |
| 0.7 | 7 | 25.0305 | 6.3139 | 0.5258 | 23.12% |
| 0.7 | 8 | 28.6065 | 5.9704 | 0.5189 | 19.06% |
| Season | ||
|---|---|---|
| Spring | 5–5.5 s | 1.1424–1.2566 rad/s |
| Summer | 5.5–6 s | 1.0472–1.1424 rad/s |
| Autumn | 5–5.5 s | 1.1424–1.2566 rad/s |
| Winter | 5–5.5 s | 1.1424–1.2566 rad/s |
| Wave Amplitude (m) | Wave Period (s) | Power (kW) | Efficiency | |
|---|---|---|---|---|
| Ocean Wave (Kinetic Energy) | Linear Generator | |||
| 0.7 | 5.5 | 19.667 | 1.176 | 5.98% |
| 0.75 | 8.5 | 34.8915 | 1.187 | 3.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Li, X.; Cui, Y.; Hong, L. Modeling, Experimental Analysis, and Optimized Control of an Ocean Wave Energy Conversion System in the Yellow Sea near Lianyungang Port. Energies 2022, 15, 8788. https://doi.org/10.3390/en15238788
Chen Z, Li X, Cui Y, Hong L. Modeling, Experimental Analysis, and Optimized Control of an Ocean Wave Energy Conversion System in the Yellow Sea near Lianyungang Port. Energies. 2022; 15(23):8788. https://doi.org/10.3390/en15238788
Chicago/Turabian StyleChen, Zhongxian, Xu Li, Yingjie Cui, and Liwei Hong. 2022. "Modeling, Experimental Analysis, and Optimized Control of an Ocean Wave Energy Conversion System in the Yellow Sea near Lianyungang Port" Energies 15, no. 23: 8788. https://doi.org/10.3390/en15238788






