The Effect of Nodalization Schemes on the Stability Characteristics of a Three Heated Channels under Supercritical Flow Condition

Abstract

The present analysis is aimed at conducting node sensitivity analysis on the thermal–hydraulic performance of supercritical fluid in a three parallel channel configuration system. The heated channel was divided into different nodes and is examined under wide-ranging operating conditions. Firstly, the heated channel was divided into two nodes, like the two-phase flow system. In the second case, based on the correlation between the fluid properties, the heated channel was divided into three regions: heavy, mixture, and supercritical fluids. Finally, the channel was divided into N-nodes. Post the nodalization analysis, a non-linear analysis of three parallel channels was carried out under varied heat flux conditions. The analytical approximation functions were developed to capture the fluid flow dynamics. These functions were used to capture each node’s density, enthalpy, and velocity profiles under a wide range of operating conditions. The different flow instability (density wave oscillations and static) characteristics were observed at low pseudo- and relatively high subcooling numbers. In the density wave oscillations regime, out-of-phase oscillations and limit cycles are observed. A co-dimension parametric analysis with numerical simulations was carried out to confirm the obtained non-linear characteristics. Such analysis for parallel channel systems under supercritical working fluid flow conditions is missing in the literature which is limited to only linear stability analysis. This analysis can help to improve heat and mass transfer for designing efficient heated channel systems.

1. Introduction

Energy demand has been rapidly increasing with population, industrialization, and urbanization demands. Therefore, green and renewable energy is being adopted on a large scale. However, safety and high efficiency are a big hurdle for mass utilization of several energy systems such as biomass, geothermal and nuclear energy. Therefore, research has repeatedly recognized the potential of supercritical fluids to operate energy systems at high temperatures and system pressures. Saeed [1,2,3] carried out a detailed analysis on the geometrical design and optimization of thermal–hydraulic performance of a supercritical Brayton cycle. They studied different components and proposed straight and zigzag channel systems to significantly improve the overall thermal hydraulic performance. Moreover, the supercritical fluid (SCF) is adopted as a working fluid in advanced generation VI supercritical nuclear reactors [4]. Although SCF undergoes no phase change, it exhibits drastic changes in fluid properties (sharp downfall and peaks) near the pseudocritical temperature. Such drastic variations in fluid properties cause flow instabilities and sudden changes in operating conditions [5,6,7,8,9].

Recently, flow instability has gained massive attention from researchers since large magnitudes and continuous flow fluctuations can cause mechanical vibrations, disrupt control systems, and cause operational issues. Therefore, flow instabilities are widely studied experimentally [10,11,12,13] as well as numerically [14,15,16,17,18,19]. The discussion reveals that the real dynamics of the above-discussed systems are complex and complicated. Hence, considerable computational and human efforts are required to study the system’s complete stability characteristics (linear and non-linear). The above discussion shows that in several fluid flow systems, mainly solar thermal and nuclear reactors, heated channels capture and maximize the heat transfer. However, channel-to-channel interaction, flow, and heat distribution also complicate the real dynamics of these systems. This necessitates the development of reduced-order models (ROMs), which can deliver qualitative features of complex dynamics while keeping computational effort and complexity at a reasonable level [20,21,22]. Therefore, to replicate the real dynamics, several researchers adopted a reduced-order modeling approach along with appropriate approximation functions and, as a geometry reduction, single heated channels and configurations with a few parallel channel’s geometries have been studied. In this context, Zuber [23] first demonstrated the flow instability characteristics of a supercritical pressure system through single heated channel geometry. They used analogous formulations and assumptions which are commonly used in two-phase flow systems. They considered density as a function of enthalpy and divided the heated channel into two fluid regions as liquid-like (light fluid) and gas-like (heavy or supercritical fluid). In order to maintain continuity, they used equations of state such as van der Waals or fact gas equation. Later, Antoni [24] introduced a two-phase or heavy–light fluid mixture region to capture the fluid behavior more accurately near the pseudocritical temperature and significantly improve the two-node model. In this context, Zhao [9] also proposed a new model by using IAPWS-IF 97 region data in a pressure–temperature plane to divide a single heated channel into three regions, as shown in Figure 1; heavy fluid (HF), mixture fluid (light and heavy fluid; HLF), and light fluid (LF) based on temperature calculation. The simulation carried out using this approach shows the DWOs and Ledinegg instability. Zhang et al. [25] extended this study and stated that the partition method based on the temperature is unsuitable as fluid property behavior changes with the system pressure. Therefore, to study the DWO phenomena of SCFs (water) in a heated channel, he proposed a new partition method using a specific value of the coefficient of volume expansion by dividing the heated channel into three regions. However, they have not reported the occurrence of Ledinegg instability in their system. In this continuation, several authors also used the n-node nodalization scheme based on the different interpretation of equation of states to divide the heated channel into n-number of nodes [26,27,28,29,30].

The channel-to-channel interaction, increasing number of channels, flow, and heat distribution significantly influence the non-linear dynamics of parallel channel systems. However, flow instabilities in multiple parallel channel systems are not widely studied, specifically for non-linear analysis. This influence mainly causes in-phase and out-of-phase oscillations. Therefore, such non-linear characteristics challenge system safety and must be examined carefully. Zhang et al. [31] conducted an experimental study on the instability of supercritical water flow inside two parallel channels. It has been observed that two types of self-sustained oscillations occur at different temperatures. When the fluid temperature is near the pseudocritical temperature, fluid experiences significant disturbances in the fluid properties and causes pressure drop, which leads to large in-phase oscillations, whereas it has been observed that at in certain conditions, 180-degree out-of-phase oscillations with a small period are formed. As mentioned above, in several dynamical systems, a bundle of channels is used, and channel-to-channel interaction significantly affects the non-linear dynamics of the system.

Several researchers increased the number of channels to study the more realistic system dynamics in this context. Recently, Lee et al. [32] adopted the Zhang et al. [25] three-region methodology to develop a model for three parallel channels with polynomial functions of density and enthalpy. They show the non-linear dynamics in close agreement to the experimental data. These studies are not limited to numerical analysis; several researchers have also conducted experiments to verify several linear and non-linear dynamics of the system [7,10,33,34].

Rai [19,35,36] has studied and reviewed flow instabilities for supercritical natural circulation systems. They observed the static and dynamic stability characteristics for supercritical natural circulation loops and carried out the sensitivity analysis of geometric and operating parameters. Hou [37] has used a parallel channel system to study flow instability through the time and frequency domain methods. The mass flow rate heated channel has been examined under different heat flux conditions.

In this work, a nodalized reduced ordered model approach for a single channel [5,34,36,38] has been extended to develop a ROM for a parallel channel system under supercritical fluid (water and carbon dioxide) flow conditions and compared with the literature. The developed ROM has been simulated in bifurcation tools, MATCONT6p11 (numerical continuation software) [39]. The channels system has been examined under different applied heat flux distribution conditions. The stability boundary has been obtained with several bifurcation characteristics showing several non-linear characteristics. They have used the coefficient of volume expansion $\left(\alpha =\rho {\left(\frac{\partial \left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\rho $}\right.\right)}{\partial T}\right)}_P\right)$ to define each region’s threshold.

The different nodalization schemes are portrayed in Figure 1. From a thorough literature survey, it was observed that the models for supercritical fluid systems are limited to the linear stability analysis and only capture the oscillations and Ledinegg instability characteristics. An immense research gap has been observed in the absence of non-linear analysis. Herein, the bifurcation theory provides an interface between physical and mathematical interpretations of the non-linear analysis. Moreover, the recent advances in non-linear dynamics and bifurcation theory allow an analysis of local as well as global stability bifurcation analysis in a wide parametric space. Therefore, in the present study, a different nodalization method has been used to study the thermal–hydraulic behavior of the three parallel channel system through non-linear stability analysis under varied heat flux conditions.

2. Numerical Modeling and Analysis

In the present work, a three parallel heated channels system has been used, as shown in Figure 2, and the design and operating parameters are mentioned in Appendix A (

Table A1. The parametric values for the supercritical pressure channel system.

Property	Value	Unit
System pressure	25	MPa
$P_c^{*}$	22.064	MPa
$L_H^{*}$	4.2672	m
$D_H^{*}$	0.0034	m
$T_{pc}^{*}$	373.95	$\mathrm{K}$
${\rho }_{pc}^{*}$	317.03	$\mathrm{kg}/{\mathrm{m}}^3$
$h_{pc}^{*}$	2152.54	$\mathrm{kJ}/\mathrm{kg}$
${\beta }_{pc}^{*}$	0.129	$1/\mathrm{K}$
$C_{p, pc}^{*}$	76.445	$\mathrm{kJ}/\mathrm{kg}-\mathrm{K}$
$w_o^{*}$	1	m/s

). The thermal–hydraulic phenomena have been captured using 1-D Navier–Stokes equations. The non-dimensional parameters and some appropriate assumptions have been used to simplify the analysis.

• The flow is homogenous in nature.
• The inlet conditions remain constant to maintain the initial conditions.
• The heat flux distribution is uniform in the axial direction.
• The isobaric conditions are used to capture real thermodynamics properties of fluids.

Based on a previous study, steady state solution at each node has been obtained through NIST [40] steam table data, whereas analytical functions for density, enthalpy, and velocity [30,41] have been used to predict the transit fluid behavior as follows:

$${\rho }_{i,j}\left(t\right)=\frac{1}{\frac{1}{{\rho }_{i,j-1}\left(t\right)}+b_{i,j}\left(t\right)\left(z_{i,j}\left(t\right)-z_{i,j-1}\left(t\right)\right)}$$

(1)

$$h_{i,j}\left(t\right)=h_{i,j-1}\left(t\right)+a_{i,j}\left(t\right)\left(z_{i,j}\left(t\right)-z_{i,j-1}\left(t\right)\right)$$

(2)

$$w_{i,j}\left(t\right)=w_{i,j-1}\left(t\right)+D_{i,j} N_{tpc} \left(z_{i,j}\left(t\right)-z_{i,j-1}\left(t\right)\right)$$

(3)

$$\frac{\partial \rho }{\partial t}+\frac{\partial \rho w}{\partial z}=0$$

(4)

$$\frac{\partial \rho w}{\partial t}+\frac{\partial \rho w^2}{\partial z}+\frac{\partial p}{\partial z}=-\frac{\rho }{Fr}-\left[\Lambda +K_{in}{\delta }_d\left(z\right)+K_{exit}{\delta }_d\left(z-1\right)\right]\rho w^2$$

(5)

$$\frac{\partial \rho h}{\partial t}+\frac{\partial \rho wh}{\partial z}=N_{tpc}^{\prime } f_q\left(z\right)$$

(6)

$$\rho =\rho \left(h, P\right)$$

(7)

Here, i = number of nodes, j = number of channels, $a_{i,j}, b_{i,j}$ are phase variables, and $D_{i,j}$ are constant terms and have been calculated using mass balance and energy equations (Equations (4) and (6)). More details can be found in a previous study [41,42,43]. The weighted residual approach has been used with these approximation functions to transform the partial differential equations into ordinary differential equations. In the next section, different nodalization approaches are studied to observe the non-linear thermal–hydraulic characteristics of a three-heated channel system.

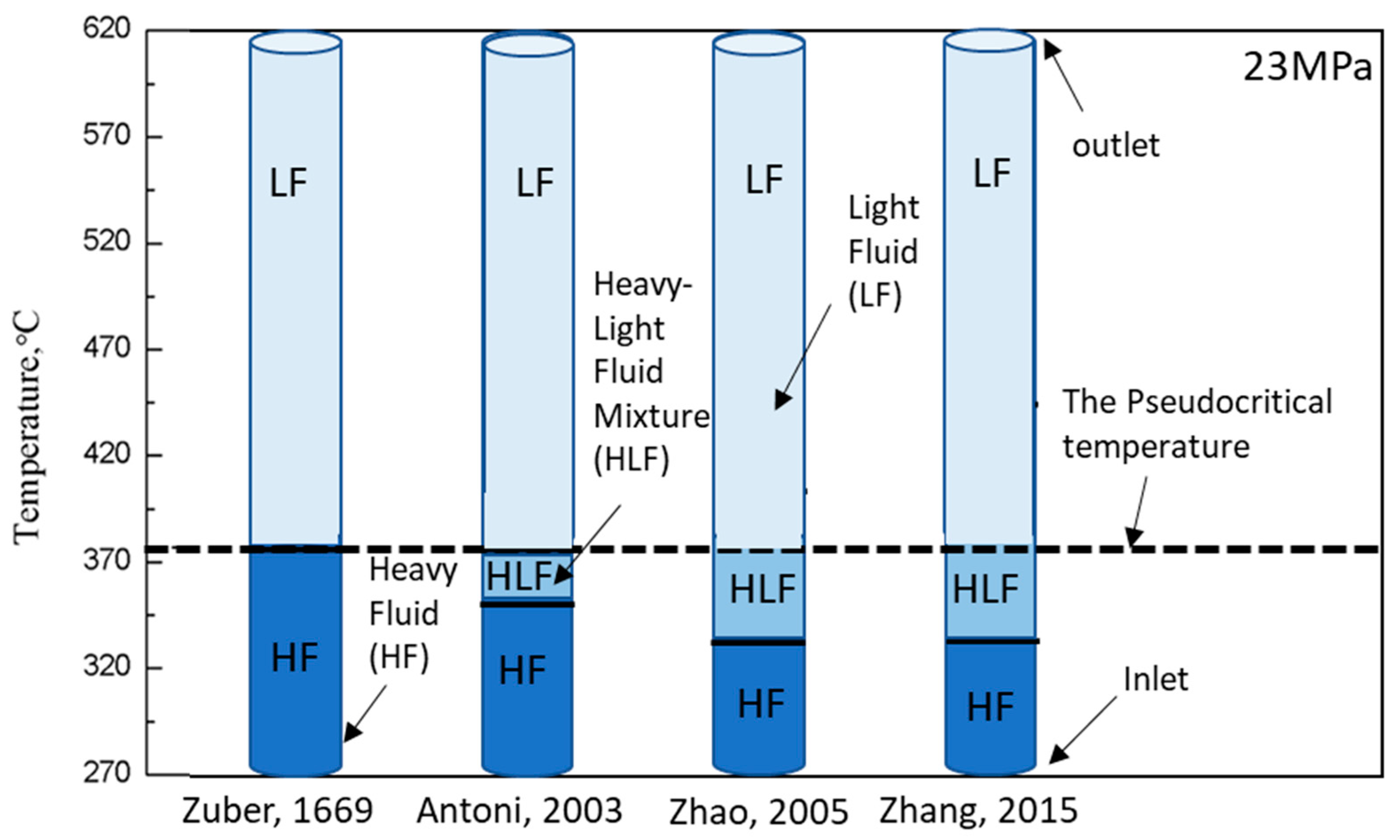
2.1. Case I: Two-Node Nodalization Scheme

The two-phase flow methodology has been widely adopted, but since there is no phase change in supercritical fluid properties, pseudocritical point $\left({\left(\frac{\partial C_p}{\partial T}\right)}_P=0\right)$ has been considered as a reference point. Based on this, Ambrosini [44] proposed new dimensionless parameters. In comparison to subcooling and phase change number, they introduced pseudo-subcooling and trans-pseudocritical or pseudo-phase change numbers for the supercritical fluid. Hence, a two-node scheme has been used to nodalize the heated channels, as shown in Figure 3. The assumptions mentioned above and approximation functions are used to transform the ODEs as follows:

To obtain the ODE phase variable $a_{i,j}$, the energy balance equation (Equation (6)) has been integrated by applying a weighted residual method on each node with limits, heavy region z = 0 to z = $z_{pc}\left(t\right)$, and supercritical region z = $pc\left(t\right)$ to z =$z_{exit}\left(t\right)$ as

$${{\displaystyle \int }}_{z_{i,j-1}\left(t\right)}^{z_{i,j}\left(t\right)}\left(M h_{i,j}\left(t\right) – R\right) {\Psi }_k\left(z\right) dz=0$$

(8)

Here, M = $\left(\frac{\partial }{\partial t}+\frac{\partial w}{\partial z}\right){\rho }_{i,j}\left(t\right)$ and R = $N_{tpc}^{\prime }$. The PDEs are transformed into ODEs in terms of $a_{i,j}$ as

$$\frac{d{a}_{i,j}\left(t\right)}{dt}={\chi }_{i,j}\left(\overrightarrow{X}, P\right)$$

(9)

Analogously, for the phase variable $b_{i,j}$, a mass conservation equation has been integrated over the node and obtained the ODEs $b_{i,j}$ as,

$$\frac{d{b}_{i,j}\left(t\right)}{dt}={{\rm Y}}_{i,j}\left(\overrightarrow{X}, P\right)$$

(10)

Now, to obtain the time-dependent ODEs for inlet velocity, all pressure drop components are calculated by integrating the momentum conservation equation over each node as follows:

$${{\displaystyle \int }}_{z_{i-1}\left(t\right)}^{z_i\left(t\right)}\Delta P_{i,j}dz={{\displaystyle \int }}_{z_{i-1}\left(t\right)}^{z_i\left(t\right)}{\left(\Delta P_{acc}+C\frac{d{w}_{in}\left(t\right)}{dt}+\Delta P_{fri}+\Delta P_{grav}\right)}_{i,j}dz$$

(11)

$$\Delta P_{k_{in},j}={\left(K_{in} {\rho }_{in} w_{in}^2\right)}_j$$

(12)

$$\Delta P_{k_{exit},j}={\left(K_{exit} {\rho }_{exit} w_{exit}^2\right)}_j$$

(13)

Further, adding all these pressure drop components (Equations (11)–(13)) and equating to the applied external pressure drops across the heated channel as

$${{\displaystyle \sum }}_{i=1,j=1}^{i=n, j=m}\Delta P_{i,j}+\Delta P_{k_{in}}+\Delta P_{k_{exit}}=\Delta P_{j,ext}$$

(14)

Additionally, the boundary conditions for the three-channel system have been used as follows:

• All heated channels are linked through a common lower and upper plenum. Therefore, an applied external pressure drop is the same as follows:

  $$\Delta P_{1,ext}=\Delta P_{2,ext}=\Delta P_{3,ext}\dots =\Delta P_{ext}$$

  (15)
• The sum of the mass flow rate in each channel is equal to the total mass flow rate, so

  $$w_{total}=w_{1,in}+w_{2,in}+w_{3,in}\dots +w_{N,in}$$

  (16)

Using the abovementioned BCs along with Equations (15) and (16) to represent the final equation for the inlet velocity of the fluid of each channel as

$$\frac{d{w}_{j,in}\left(t\right)}{dt}=f_{i,j}\left(\overrightarrow{X},\overrightarrow{P}\right); \mathrm{here} j=1,2$$

(17)

$$\frac{d{w}_{3in}\left(t\right)}{dt}=\frac{d{w}_{total}}{dt}-\left(\frac{d{w}_{1,in}\left(t\right)}{dt}+\frac{d{w}_{2,in}\left(t\right)}{dt}\right)$$

(18)

On the right-hand side of the above-developed equations, ${\chi }_{i,j}\left(\overrightarrow{X}, P\right)$,${{\rm Y}}_{i,j}\left(\overrightarrow{X}, P\right)$,$f_{i,j}\left(\overrightarrow{X}, P\right)$, ${\left(\Delta P_{acc},\Delta P_{grav},\Delta P_{fri}\right)}_{i,j},$ and $\Delta P_{exit}$ are marginally complex terms, mentioned in Appendix A. In this section, three channels are divided into two regions, based on the two-node nodalization scheme. The total of 13 (2 equations from each node and one from momentum) non-linear coupled ODEs are developed to study the thermal–hydraulic phenomena of supercritical fluid through a stability analysis. These developed ROM models have been numerically simulated using the bifurcation tool (MATCONT [39]). As shown in Figure 4, a stability threshold has been drawn for uniform and non-uniform heat flux conditions on each channel in a wide range of selective parameter planes.

It can be seen from Figure 4 that, under uniform heat flux, all three channels have equal applied heat flux; a double Hopf bifurcation point has been observed, which exists in the system when two pairs of eigenvalues are zero or purely imaginary. This confirms the presence of two fixed-point solutions, whereas no GH point has been observed, implying that the whole dynamic is supercritical in nature, meaning only stable limit cycles occurred in an unstable region. This phenomenon was also confirmed through the presence of a negative first Lyapunov coefficient value. On the other hand, when all three channels have different applied heat flux (non-uniform heat flux) conditions, heat transfer characteristics were significantly affected, and no double Hopf bifurcation point or GH point has been observed.

2.2. Case II: Three-Node Nodalization Scheme

The Zhang [25] three-region partition method has been used to nodalize the heated channels in this section. As mentioned above, they proposed the mathematical correlation between temperature and system pressure (Pa) to define each node threshold as follows:

$$T_{A }(℃)=309.50661+1.26935\left(P {10}^{-6}\right)+0.01174 \left(P {10}^{-6}\right)$$

(19)

$$T_B (℃)=279.44318+8.5502\left(P {10}^{-6}\right)-0.07014\left(P {10}^{-6}\right)$$

(20)

Based on the above correlation, heavy fluid has been considered from inlet temperature $\left(280 ℃\right)$ to $T_A=349 ℃$ for the supercritical water at system pressure (25 MPa), whereas for mixture fluid, the inlet temperature has been considered up to $T_B=449 ℃$. The heated channel has been nodalized into three nodes as shown in Figure 5.

Similar to the previous section, the conservation equation and approximation function have been used to develop the time-dependent ODEs for three nodes. Therefore, now, instead of 4 equations, 6 ODEs for each channel means a total of 19 ODEs have been developed to perform the numerical analysis, instead of the 13 ODEs used in the previous two-mode approach.

It has been observed from Figure 6 that, under uniform heat flux conditions, no GH point is observed. However, under non-uniform heat flux, systems are more critical and non-linear. Therefore, two GH points have been observed. This phenomenon confirms that under uniform heat flux, complete dynamics are supercritical, although it changes from supercritical to subcritical or vice versa once under non-uniform heat flux. Moreover, as an interaction between dynamic and static instability, one Bogdanov–Takens (BT) bifurcation point has been observed under high uniform heat flux conditions. At the high subcooling number, Ledinegg instability has been observed; similar phenomena have also been observed in other research [26,41].

2.3. Case III: N-Node Nodalization Scheme

In this section, based on previous studies [30], the heated channel is nodalized into N-nodes, as shown in Figure 7. To nodalize the channel, variation in enthalpy change was formulated in such a way that the nodalization scheme will behave like auto-adaptive schemes and, as it is adjusted, the node will size automatically (a similar idea has been used for two-phase flows in [28,45,46]).

Figure 7 shows that, under uniform heat flux conditions, multiple GH points, as well as multiple BT points, have been observed. This indicates that in addition to change of system dynamics between supercritical to subcritical (and vice versa), it also changes between dynamic to static instability, and vice versa in a wide parametric space. On the other hand, at non-uniform heat flux conditions, non-linearity and sensitivity increase with the ratio of heat flux across each channel. They also disturb the heat transfer characteristics and subcooled fluid in each channel. Therefore, other higher order bifurcation points have been observed along the stability boundary, as shown in Figure 8.

In order to validate and compare each nodalization scheme in Figure 9, only each nodalization scheme has been compared as these schemes are already validated with the different numerical models, as well as with experimental studies in previously reported works [9,24,25,30]. It has been observed that as the number of nodes increases, the stability boundary becomes broader, representing and covering a wider parametric range.

3. Non-Linear Analysis

To perform the non-linear dynamics, bifurcation theory along with MATCONT [39] bifurcation tools have been used to perform the numerical analysis. Along with the stability threshold, different non-linear dynamics in terms of bifurcation characteristic points have been observed. The generalized Hopf (GH) bifurcation point is the first type of bifurcation characteristic detected in the system. It is associated with the dynamic stability, when self-sustained (density and pressure drop) oscillation along with a limit cycle has been exhibited in the system. The GH bifurcation point originates or terminates the stable and unstable limit cycles, which are well known as a supercritical and subcritical Hopf bifurcation, respectively. To confirm these characteristics, mathematical coefficients and numerical simulations at different operating conditions have been performed, as shown in Figure 10.

Based on the applied external perturbation on the system, growing and constant high amplitude oscillations have been observed near to the unstable side of the stability boundary. This phenomenon shows that a high amplitude stable limit cycle has been observed on the unstable side as it is an attractor for all the trajectories at high amplitude cycles. This phenomenon has been recognized as a supercritical Hopf bifurcation, whereas on the other side of the stability boundary for small perturbation, decaying oscillations have been observed. Meanwhile, sudden growing oscillations occur when the system experiences relatively large perturbation during initial conditions. This indicates that the unstable limit cycle has occurred on the stable side of the boundary. These unstable limit cycles act like a repellant for all trajectories. This phenomenon is known as subcritical Hopf bifurcation and is considered more dangerous for normal operating conditions.

The Bogdanov–Takens (BT) bifurcation point has also been detected in the system as shown in Figure 11. According to the bifurcation theory [47,48], this is a co-dimension two bifurcation that is associated to static instability. This is characterized by the existence of two complex eigenvalues with opposite signs and the same real parts. Therefore, the system experiences a sudden jump from one equilibrium to another equilibrium, where the nature of equilibrium could vary between stable and unstable. The limit point (LP) is also another type of bifurcation point found in the system. It is also a co-dimension two bifurcation, which appears in the system when it has all negative real eigenvalues. Therefore, non-oscillatory solutions have been observed at the LP boundary. More details of such non-linear phenomena can be found in the literature for different energy systems [15,47,48,49,50].

4. Conclusions

The present analysis demonstrates and compares different nodalization schemes to study the non-linear thermal–hydraulic characteristics in a three-channel system. The study modeled and investigated different nodalized schemes to distinguish fluid phases in the heated channels under different heat flux conditions. The results show dynamic and static instability along with several non-linear characteristics. Preliminarily, the heated channel has been divided into two nodes to mimic a two-phase flow system, where a complete supercritical phenomenon has been observed under uniform heat flux conditions, with a double Hopf bifurcation point and no Generalized Hopf bifurcation (GH) point. Secondly, the heated channel has been divided into three regions as heavy, mixture, and supercritical fluids. Herein, no GH point has been observed under uniform heat flux conditions, whereas at a high subcooling number, a Bogdanov–Takens bifurcation (BT) point has been observed, which indicates the occurrence of Ledinegg instability. Further, alternating limit cycles between supercritical and subcritical regions and vice versa have been detected under non-uniform heat flux conditions. Finally, in the case of an N-node system, changes between dynamic to static instability, and vice versa, have also been observed in a wide parametric space, in addition to system dynamics between supercritical and subcritical. Additionally, with an increase in the ratio of heat flux across each channel, the non-linearity in the system increases, and higher bifurcation points such as limit point have been observed. The present analysis can be instrumental in understanding the safety and design principles for parallel channel energy systems for different applications.