Optimal Design of Three-Dimensional Circular-to-Rectangular Transition Nozzle Based on Data Dimensionality Reduction
Abstract
:1. Introduction
2. Model Description and Performance Parameter Definition
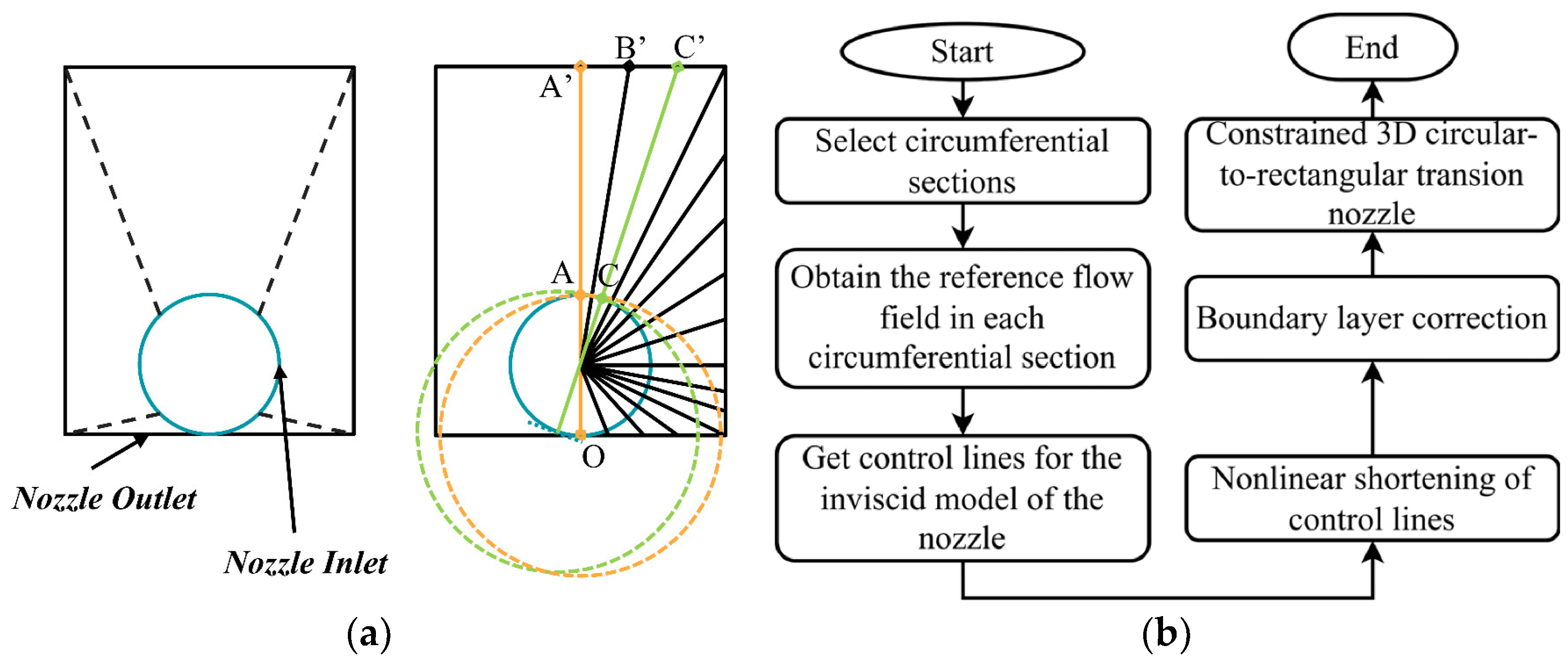
2.1. Geometric Shape of 3D Circular-to-Rectangular Transition Nozzle
2.2. Definition of Performance Parameters
3. Numerical Simulation and Validation of the Method
3.1. Governing Equations
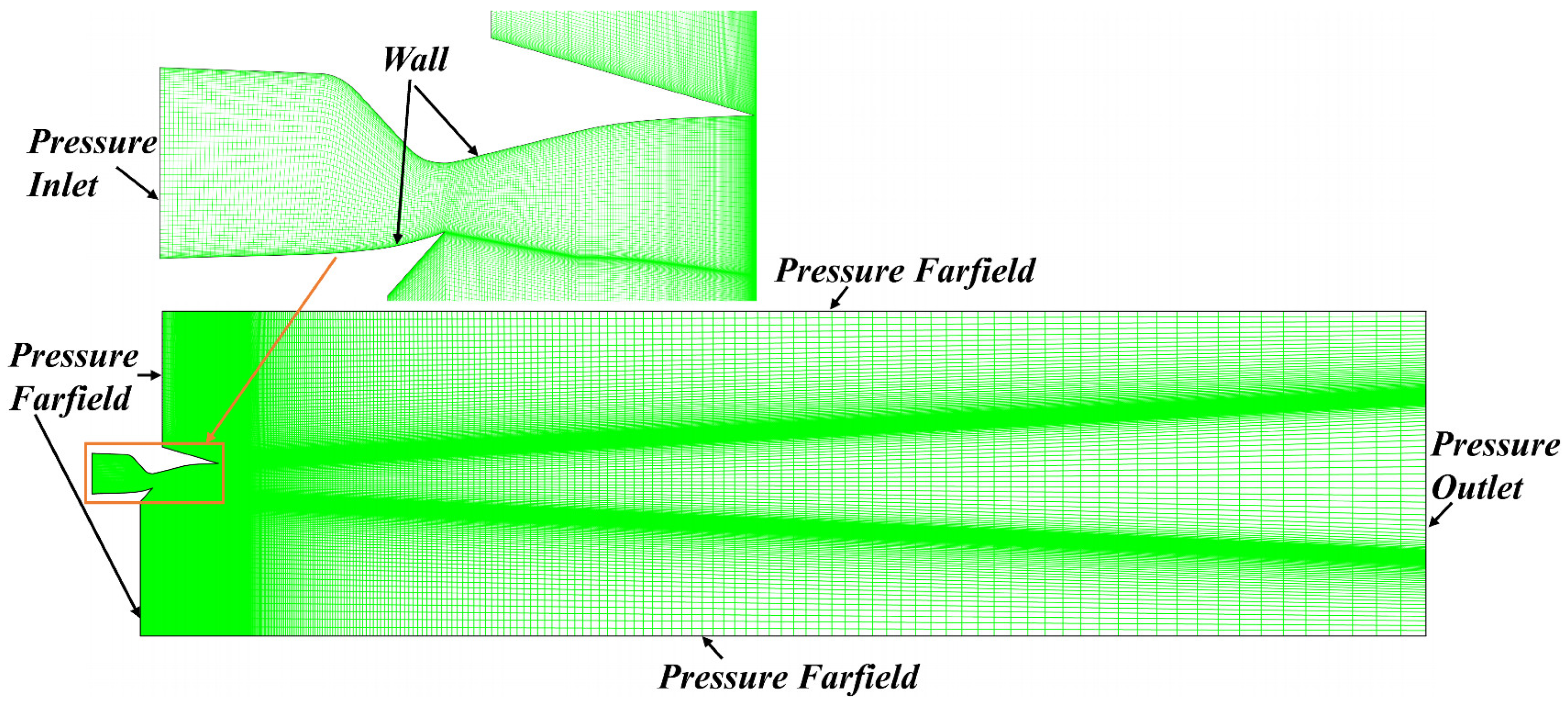
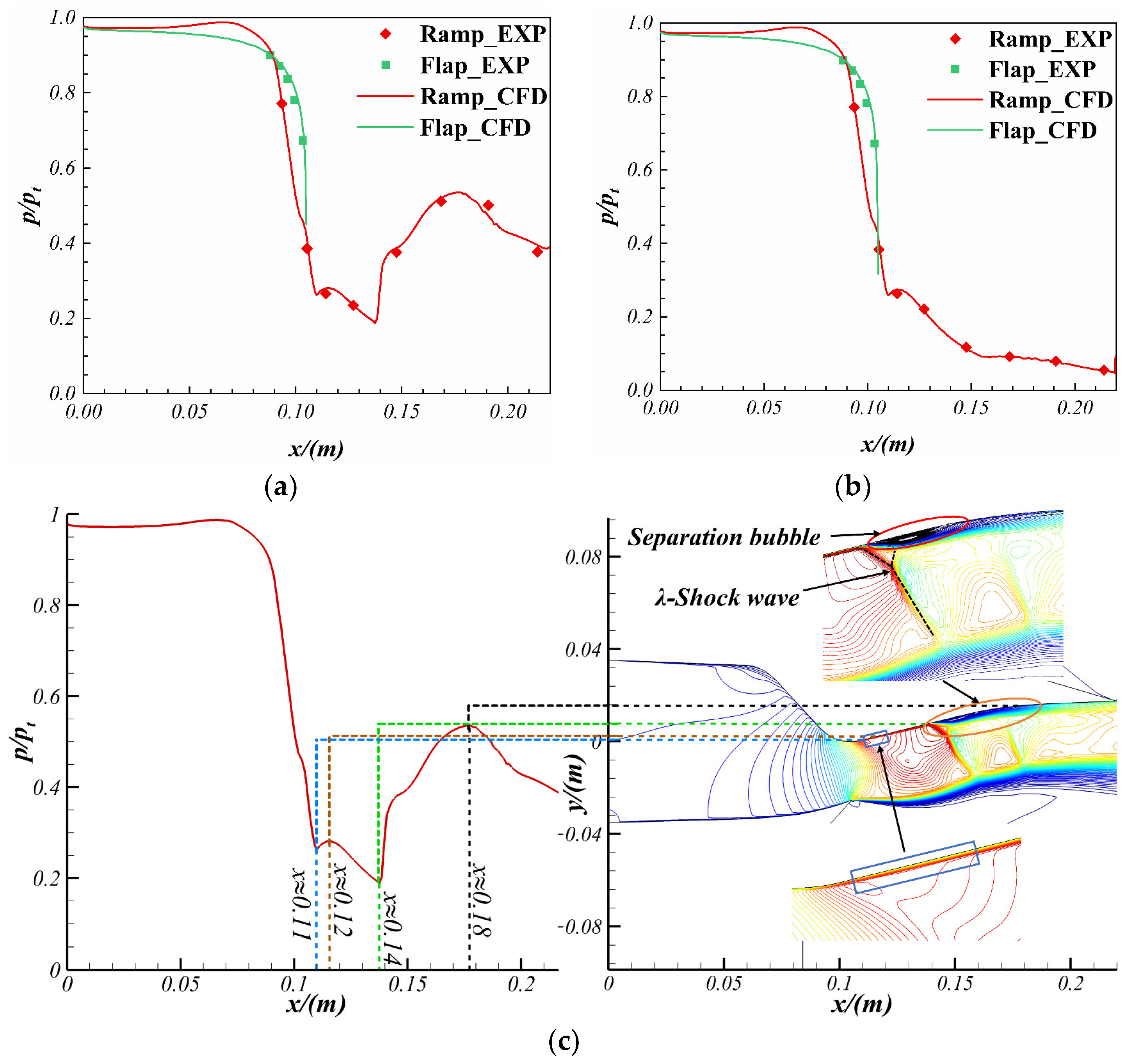
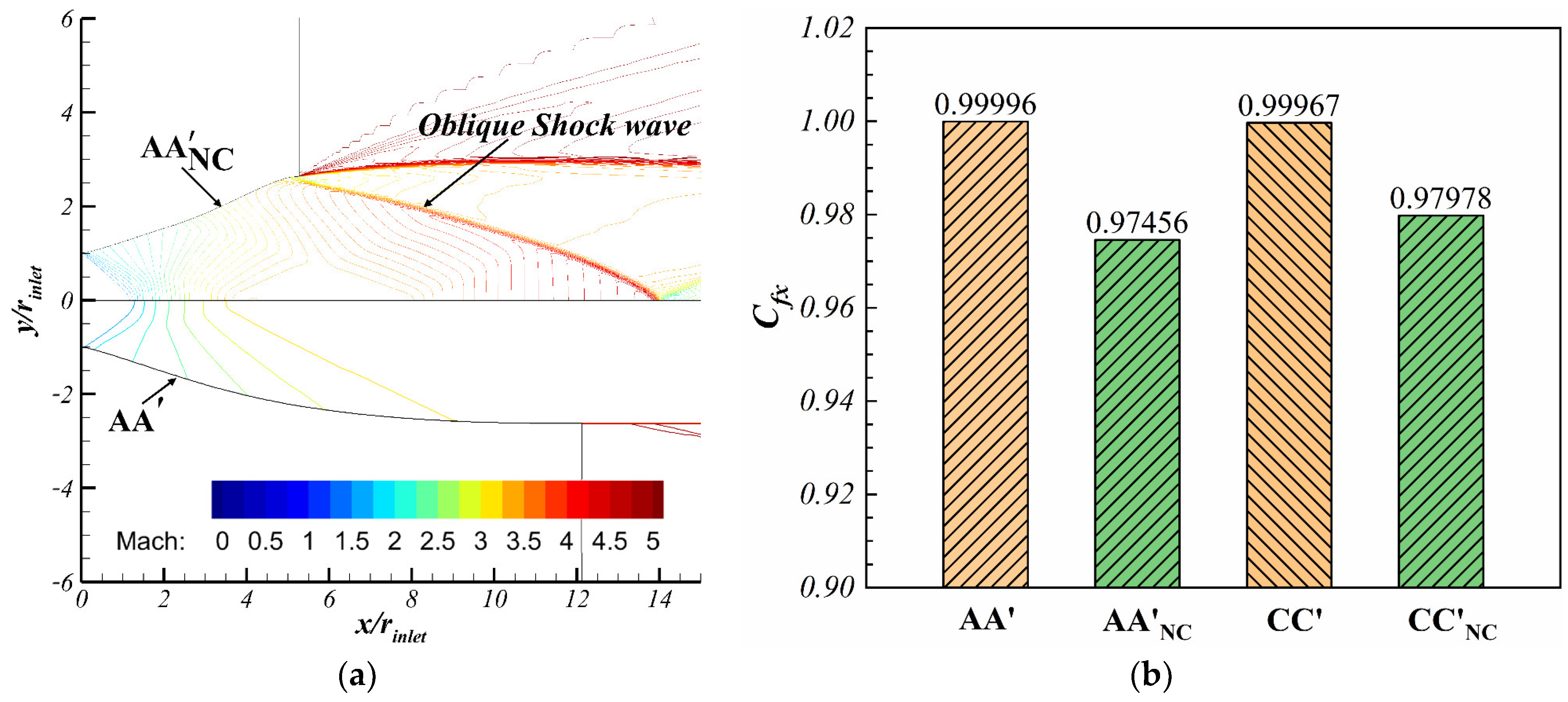
3.2. Validation of the Numerical Simulation Method
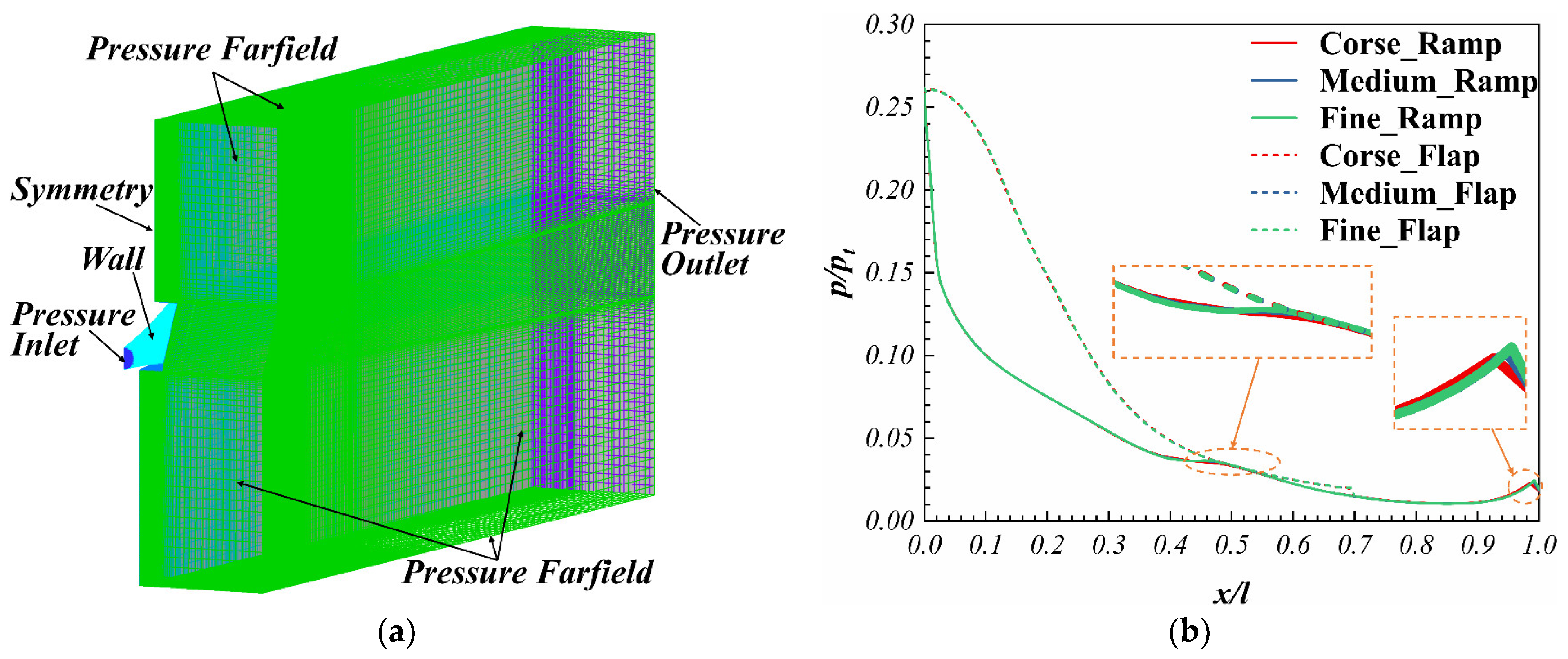
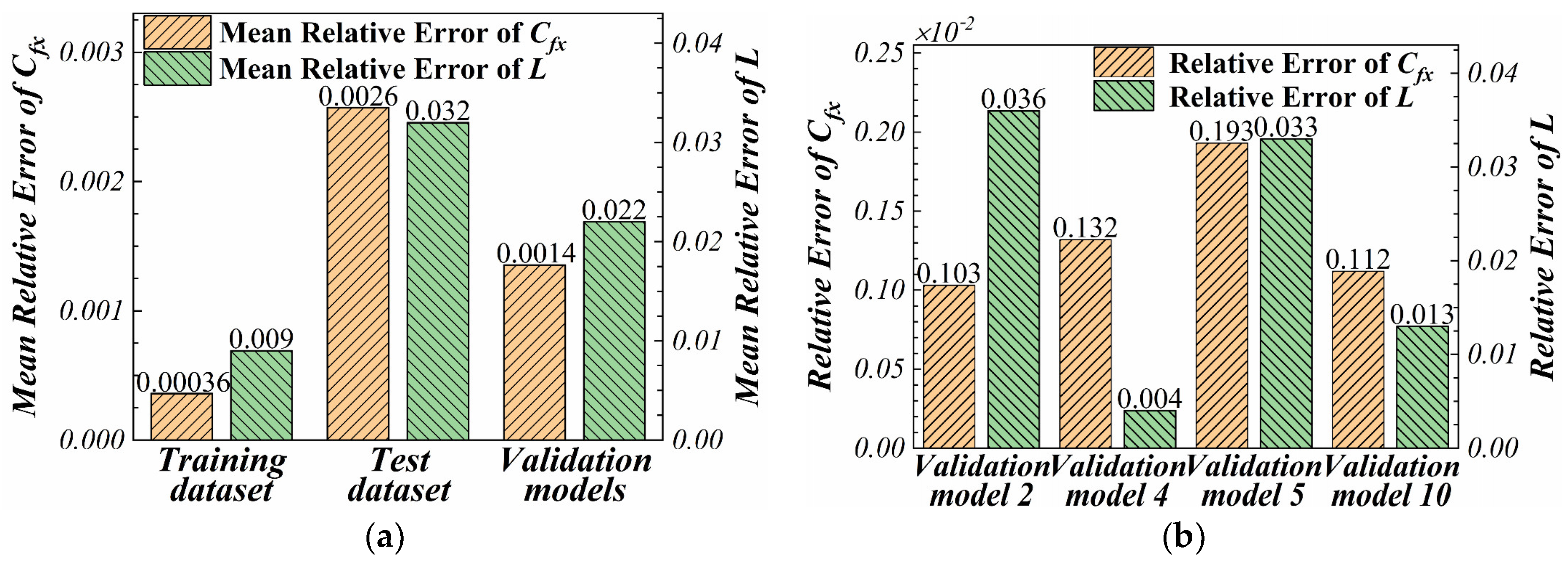
3.3. Mesh Validation
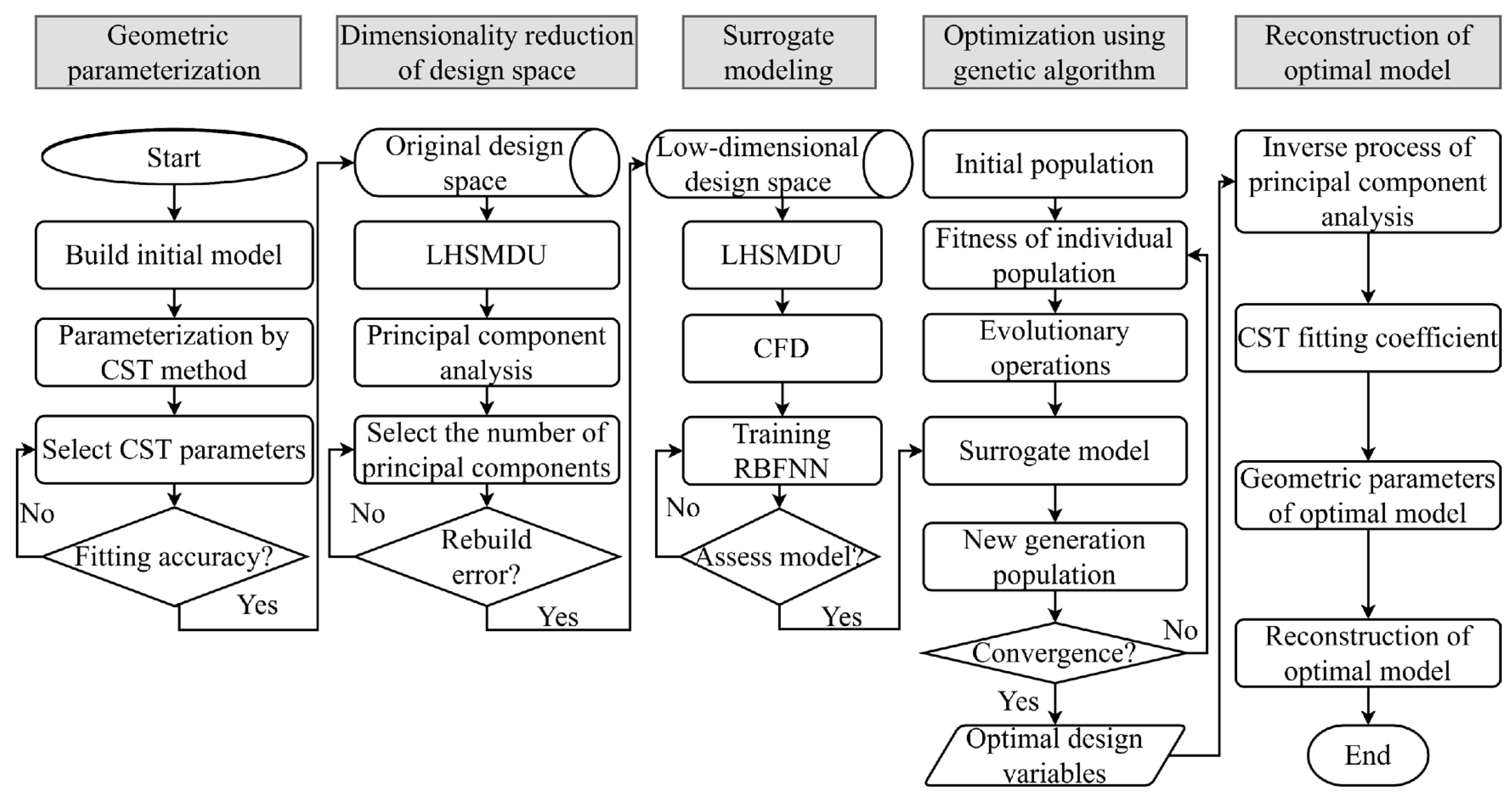
4. CST-PCA-RBFNN-Based Surrogate Model
4.1. CST Method for 3D Circular-to-Rectangular Transition Nozzle
4.2. Principal Component Analysis Method
5. Performance Analysis and Optimization of 3D Circular-to-Rectangular Transition Nozzle
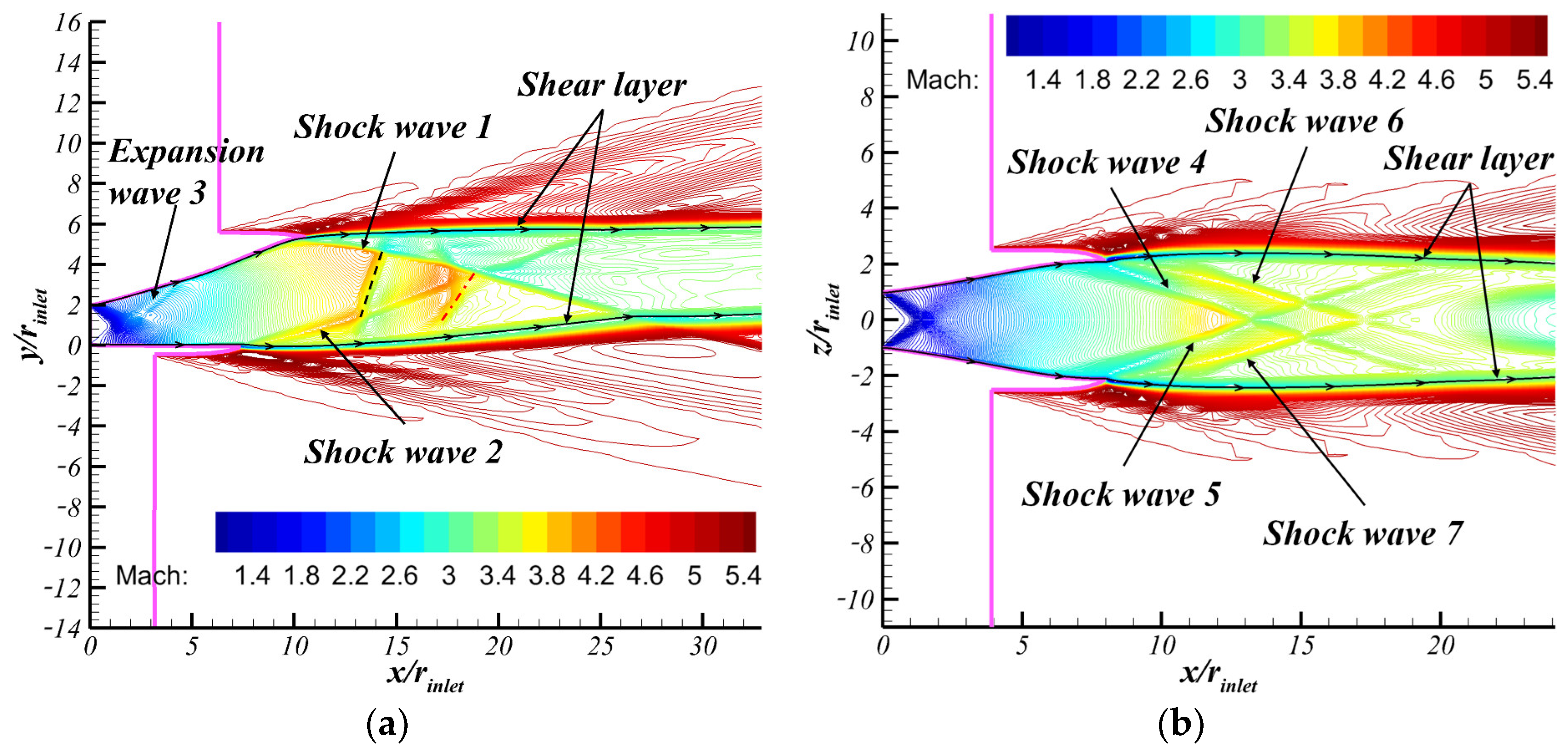
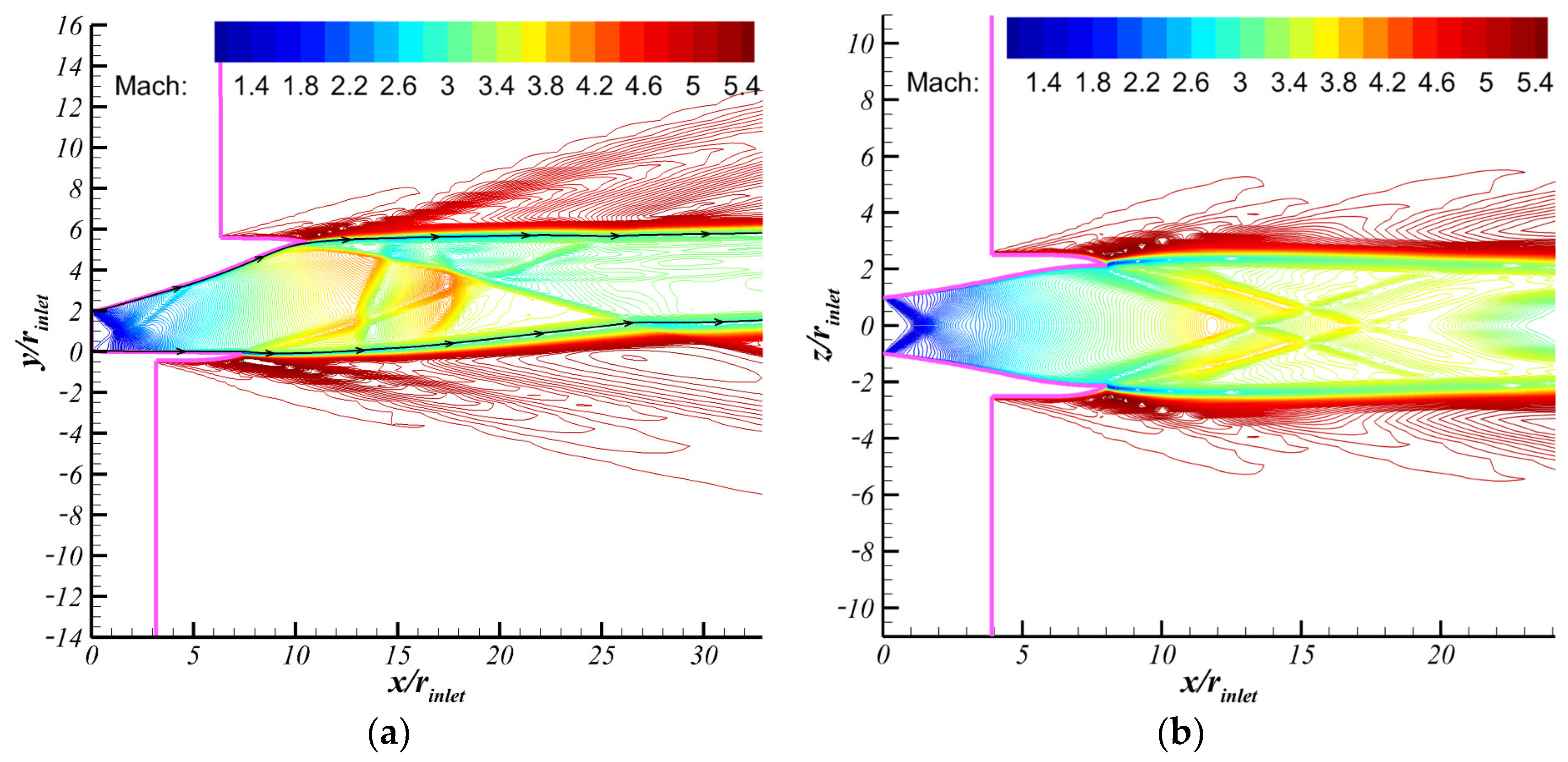
5.1. Flow Field Characteristics and Performance Analysis of Initial Model
5.2. Selection of Fitting Order of CST Method and Fitting Results
5.3. Optimal Design Based on Data Dimensionality Reduction
5.3.1. Optimization Task Description
5.3.2. Design Space Dimension Reduction
5.3.3. Optimization Based on the Surrogate Model
6. Conclusions
- (1)
- The validation of the CST-PCA-RBFNN-based surrogate model showed that it is feasible to parametrically represent the shape of a 3D circular-to-rectangular transition nozzle with circumferential control lines using the CST method with cylindrical coordinate form. The shape and aerodynamic performance of the approximate model can be comparable to the original model even if the fitting order of the CST method is low;
- (2)
- PCA is an effective and robust method for reducing data dimensions. The number of design variables was successfully reduced from 35 to 19 using PCA technique without affecting the prediction accuracy of RBFNN;
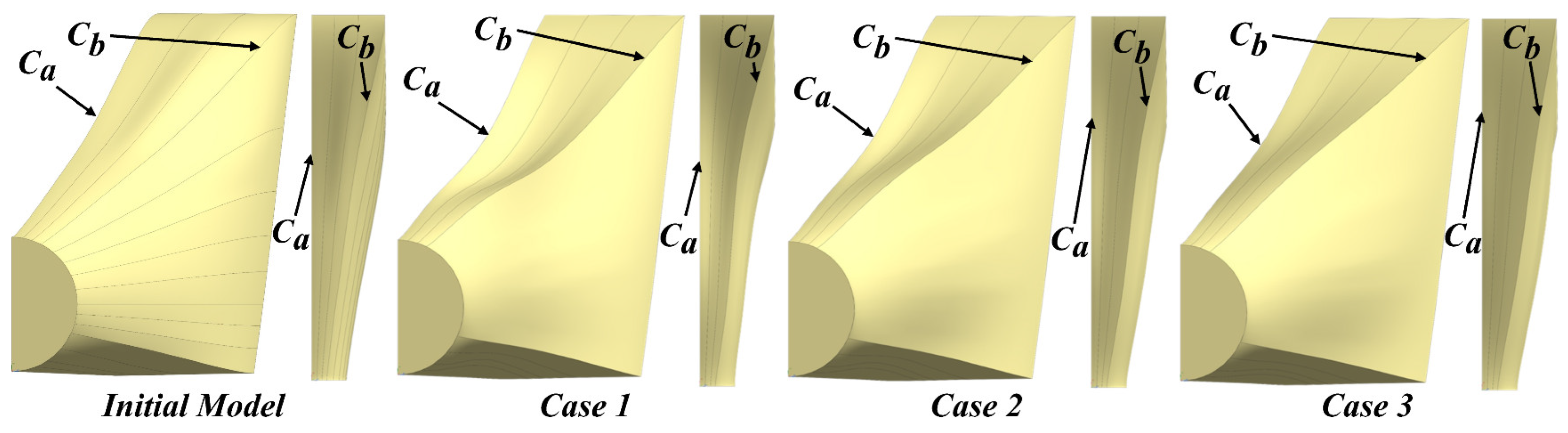
- (3)
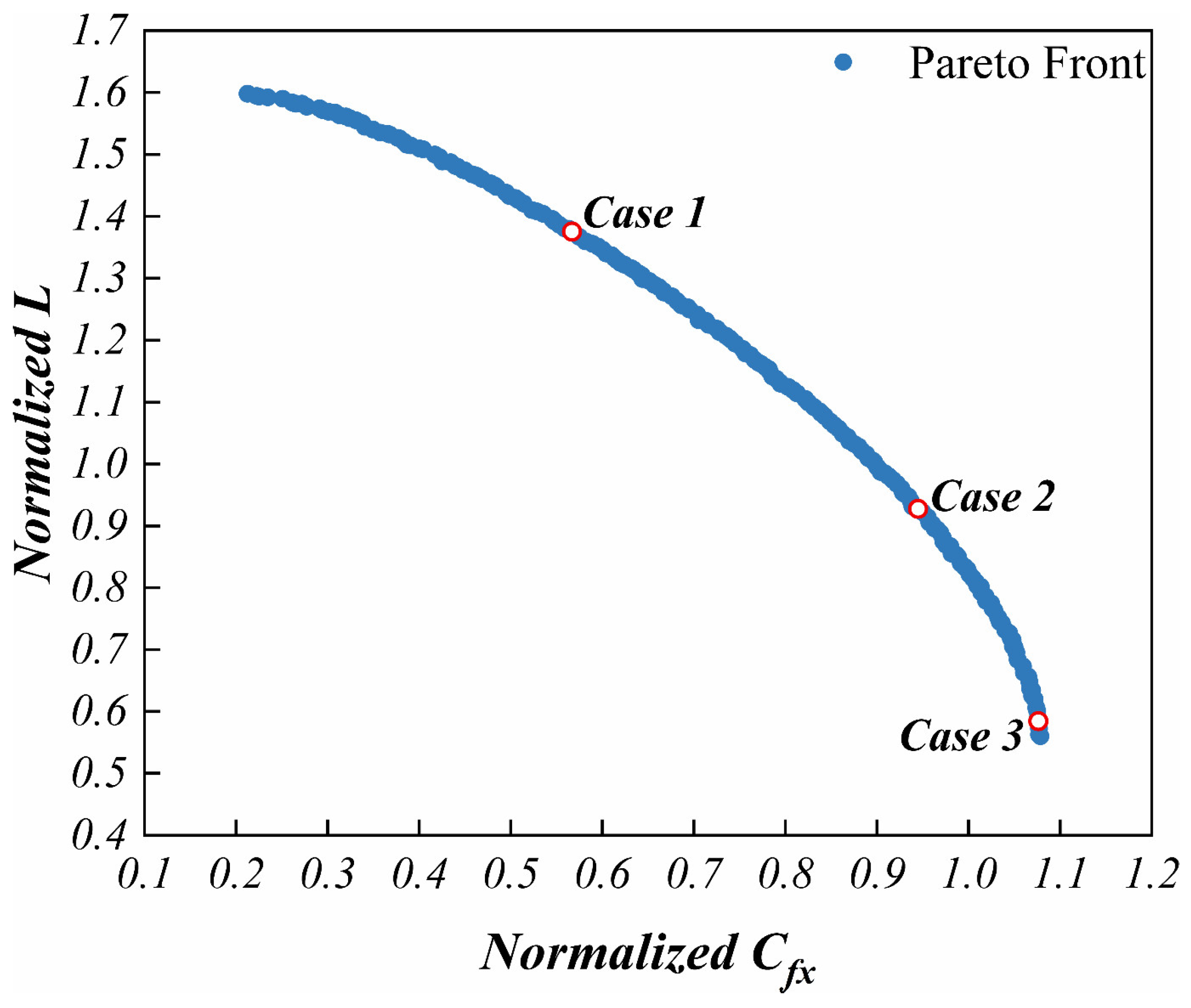
- Analysis of three cases on the Pareto front showed that the shape of the control line of the upper wall near the symmetry plane of the nozzle used in this study was crucial for the elimination of the reflected shock wave. The upper and side walls of the nozzle with fast expansion in the forepart and slow expansion in the afterpart can improve both Cfx and L;
- (4)
- Although the CST-PCA-RBFNN-based surrogate model proposed in this paper has limited control over the local surface deformation of the upper wall of the nozzle, it can significantly improve the Cfx and L of the nozzle, while satisfying the geometric constraints.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bulman, M.; Siebenhaar, A. The Rebirth of Round Hypersonic Propulsion. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006. [Google Scholar]
- Walker, S.; Rodgers, F.; Paull, A.; Van Wie, D. HyCAUSE Flight Test Program. In Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008. [Google Scholar]
- Bulman, M.; Siebenhaar, A. Combined Cycle Propulsion: Aerojet Innovations for Practical Hypersonic Vehicles. In Proceedings of the 17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, San Francisco, CA, USA, 11–14 April 2011. [Google Scholar]
- Ridgway, A.; Sam, A.A.; Pesyridis, A. Modelling a Hypersonic Single Expansion Ramp Nozzle of a Hypersonic Aircraft through Parametric Studies. Energies 2018, 11, 3449. [Google Scholar] [CrossRef] [Green Version]
- Shenkin, A.V.; Mazurov, A.P.; Bykov, A.P. Aerodynamic Design of Single-Expansion-Ramp Nozzle for Aircraft with Supersonic Cruise Speed of Flight. In Proceedings of the 29th Congress of the International Council for Aeronautical Science, St. Petersburg, Russia, 7–12 September 2014. [Google Scholar]
- Zhang, P.; Xu, J.; Quan, Z.; Mo, J. Effects of Nonuniform Mach-Number Entrance on Scramjet Nozzle Flowfield and Performance. Acta Astronaut. 2016, 129, 201–210. [Google Scholar] [CrossRef]
- Lv, Z.; Xu, J.; Mo, J. Design of a Three-Dimensional Scramjet Nozzle Considering Lateral Expansion and Geometric Constraints. Acta Astronaut. 2017, 141, 172–182. [Google Scholar] [CrossRef]
- You, Y.; Liang, D. Design Concept of Three-Dimensional Section Controllable Internal Waverider Hypersonic Inlet. Sci. China Ser. E-Technol. Sci. 2009, 52, 2017–2028. [Google Scholar] [CrossRef]
- Lu, X.; Yue, L.; Xiao, Y.; Zhang, X. Design of three-dimensional section controllable scramjet nozzle. In Proceedings of the 2nd National Hypersonic Science and Technology Academic Conference, Wuxi, Jiangsu, 26 October 2010. (In Chinese). [Google Scholar]
- Lv, Z.; Xu, J.; Mo, J. Design and Analysis on Three-Dimensional Scramjet Nozzles with Shape Transition. Aerosp. Sci. Technol. 2017, 71, 189–200. [Google Scholar] [CrossRef]
- Quan, Z.; Xu, J.; Mo, J. Design of nonlinearly compressed SERN profile. J. Propuls. Technol. 2012, 33, 951–955. (In Chinese) [Google Scholar]
- Hoffman, J.D. Design of Compressed Truncated Perfect Nozzles. J. Propuls. Power 1987, 3, 150–156. [Google Scholar] [CrossRef]
- Damira, S.; Marathe, A.; Sudhakar, K.; Issacs, A. Parametric Optimization of Single Expansion Ramp Nozzle (SERN). In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006. [Google Scholar]
- Gao, T.; Cui, K.; Wang, X.; Hu, S.; Yang, G.; Ren, L. Aerodynamic Optimization and Evaluation for the Three-Dimensional Afterbody/Nozzle Integrated Configuration of Hypersonic Vehicles. Chin. Sci. Bull. 2012, 57, 849–857. [Google Scholar] [CrossRef] [Green Version]
- Zhu, M.; Fu, L.; Zhang, S.; Zheng, Y. Design and Optimization of Three-Dimensional Supersonic Asymmetric Truncated Nozzle. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 2923–2935. [Google Scholar] [CrossRef]
- Kulfan, B.M. The “CST” Universal Parametric Geometry Representation Method, Recent Extensions and Applications. In Proceedings of the Royal Aeronautical Society Conference, Hamilton, London, UK, 23–24 October 2007. [Google Scholar]
- Akram, M.T.; Man-Hoe, K. CFD Analysis and Shape Optimization of Airfoils Using Class Shape Transformation and Genetic Algorithm—Part I. Appl. Sci. 2021, 11, 3791. [Google Scholar] [CrossRef]
- Su, H.; Gu, L.; Gong, C. Research on Geometry Modeling Method Based on Three-Dimensional CST Parameterization Technology. In Proceedings of the 16th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Wang, Q.; Zhao, Q.; Wu, Q. Aerodynamic Shape Optimization for Alleviating Dynamic Stall Characteristics of Helicopter Rotor Airfoil. Chin. J. Aeronaut. 2015, 28, 346–356. [Google Scholar] [CrossRef]
- Liu, C.; Duan, Y.; Cai, J.; Wang, J. Application of the 3D Multi-Block CST Method to Hypersonic Aircraft Optimization. Aerosp. Sci. Technol. 2016, 50, 295–303. [Google Scholar] [CrossRef]
- Christie, R.; Robinson, M.; Tejero, F.; MacManus, D.G. The Use of Hybrid Intuitive Class Shape Transformation Curves in Aerodynamic Design. Aerosp. Sci. Technol. 2019, 95, 105473. [Google Scholar] [CrossRef]
- Wang, J.; Cai, J.; Liu, C.; Duan, Y.; Yu, Y. Aerodynamic Configuration Integration Design of Hypersonic Cruise Aircraft with Inward-Turning Inlets. Chin. J. Aeronaut. 2017, 30, 1349–1362. [Google Scholar] [CrossRef]
- Berguin, S.H.; Mavris, D.N. Dimensionality Reduction in Aerodynamic Design Using Principal Component Analysis with Gradient Information. In Proceedings of the 10th AIAA Multidisciplinary Design Optimization Conference, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Berguin, S.H.; Mavris, D.N. Dimensionality Reduction Using Principal Component Analysis Applied to the Gradient. AIAA J. 2015, 53, 1078–1090. [Google Scholar] [CrossRef]
- Qiu, Y.; Bai, J.; Liu, N.; Wang, C. Global Aerodynamic Design Optimization Based on Data Dimensionality Reduction. Chin. J. Aeronaut. 2018, 31, 643–659. [Google Scholar] [CrossRef]
- Tao, J.; Sun, G.; Guo, L.; Wang, X. Application of a PCA-DBN-Based Surrogate Model to Robust Aerodynamic Design Optimization. Chin. J. Aeronaut. 2020, 33, 1573–1588. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Xu, J.; Wang, Y. Study of flow field characteristics of an over-under TBCC exhaust system during mode transition process. J. Exp. Fluid Mech. 2019, 33, 68–75. (In Chinese) [Google Scholar]
- Bare, E.A.; Capone, F.J. Static Internal Performance of Convergent Single-Expansion-Ramp Nozzles with Various Combinations of Internal Geometric Parameters; No. NAS 1.15:4112; NASA: Washington, DC, USA, 1989. [Google Scholar]
- Zhu, F.; Qin, N. Geometric Parameterisation and Aerodynamic Shape Optimisation. Ph.D. Thesis, University of Sheffield, Sheffield, South Yorkshire, UK, 2014. [Google Scholar]
- Ceze, M.; Hayashi, M.; Volpe, E. A Study of the CST Parameterization Characteristics. In Proceedings of the 27th AIAA Applied Aerodynamics Conference, San Antonio, TX, USA, 22–25 June 2009. [Google Scholar]
- Deutsch, J.L.; Deutsch, C.V. Latin Hypercube Sampling with Multidimensional Uniformity. J. Stat. Plan. Infer. 2012, 142, 763–772. [Google Scholar] [CrossRef]
- Sahilm89/Lhsmdu: Latin Hypercube Sampling with Multi-Dimensional Uniformity (LHSMDU): Speed Boost Minor Compatibility Fixes|Zenodo. Available online: https://zenodo.org/record/3929531#.YzvqlHZByUk (accessed on 4 October 2022).
- Cinquegrana, D.; Iuliano, E. Efficient Global Optimization of a Transonic Wing with Geometric Data Reduction. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
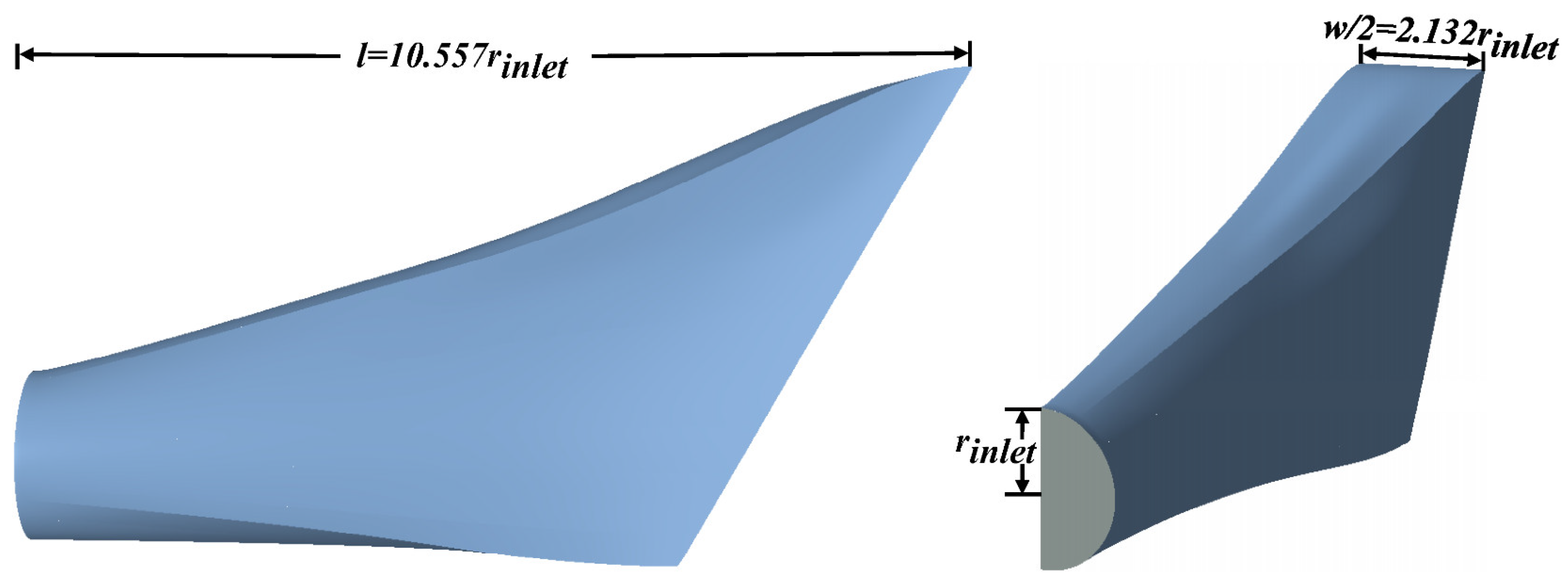





| Inlet Radius | Nozzle Length | Nozzle Width |
|---|---|---|
| = 100 mm | l ≤ 10.557 | w ≤ 4.597 |
| Ma∞ | NPR | Tt/K | |
|---|---|---|---|
| Initial Model | 5 | 77.995 | 2665 |
| Mesh | Number of Mesh Cells | Mesh Density Factor | Maximum Relative Error |
|---|---|---|---|
| Coarse | 888,571 | 0.502 | 2.698% |
| Medium | 1,770,061 | 1 | 0 |
| Fine | 3,563,615 | 2.013 | 0.375% |
| BX | 4 | 6 | 8 | |
|---|---|---|---|---|
| BR | ||||
| 4 | 33.3877 | 33.3858 | 33.3852 | |
| 6 | 26.2768 | 26.2773 | 26.2771 | |
| 8 | 20.8271 | 20.8242 | 20.8238 | |
| BX-BR | 4–4 | 4–6 | 4–8 | 6–4 | 8–4 | 8–8 |
|---|---|---|---|---|---|---|
| Cfx | 0.026% | 0.015% | 0.011% | 0.099% | 0.018% | 0.027% |
| L | 0.333% | 0.751% | 0.643% | 0.79% | 0.427% | 0.671% |
| Model | Performance Parameter | |||
|---|---|---|---|---|
| Cfx | L | |||
| Value | Improvement Rate (%) | Value/(N) | Improvement Rate (%) | |
| Initial model | 0.963997 | \ | −1204.228 | \ |
| Case 1 | 0.951866 | −1.258 | −301.502 | 74.963 |
| Case 2 | 0.966324 | 0.241 | −738.122 | 38.706 |
| Case 3 | 0.971154 | 0.742 | −1015.074 | 15.707 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Yang, Q.; Mu, Z.; Du, X.; Chen, L. Optimal Design of Three-Dimensional Circular-to-Rectangular Transition Nozzle Based on Data Dimensionality Reduction. Energies 2022, 15, 9316. https://doi.org/10.3390/en15249316
Yang H, Yang Q, Mu Z, Du X, Chen L. Optimal Design of Three-Dimensional Circular-to-Rectangular Transition Nozzle Based on Data Dimensionality Reduction. Energies. 2022; 15(24):9316. https://doi.org/10.3390/en15249316
Chicago/Turabian StyleYang, Haoqi, Qingzhen Yang, Zhongqiang Mu, Xubo Du, and Lingling Chen. 2022. "Optimal Design of Three-Dimensional Circular-to-Rectangular Transition Nozzle Based on Data Dimensionality Reduction" Energies 15, no. 24: 9316. https://doi.org/10.3390/en15249316
APA StyleYang, H., Yang, Q., Mu, Z., Du, X., & Chen, L. (2022). Optimal Design of Three-Dimensional Circular-to-Rectangular Transition Nozzle Based on Data Dimensionality Reduction. Energies, 15(24), 9316. https://doi.org/10.3390/en15249316






