A Comprehensive Review on Modular Multilevel Converters, Submodule Topologies, and Modulation Techniques
Abstract
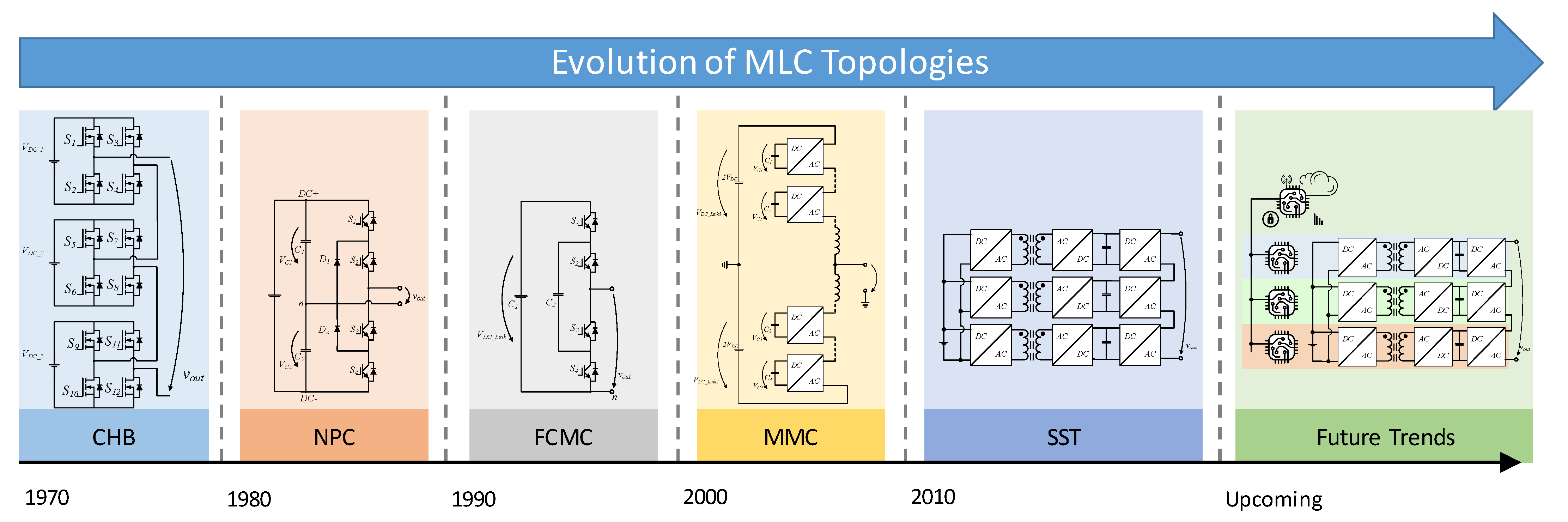
:1. Introduction
- Easily extendable due to modular converter substructures. Modularity and expandability allow the creation of redundant operating states, improving system response in case of failures (more fault tolerant);
- Lower harmonic content and more concentrated in the fundamental component and at high frequencies. As illustrated in Figure 1: (i) the greater the number of levels, the more closely the output waveform resembles a sinusoid; (ii) the higher-frequency harmonic content allows for easier filtering;
- Possibility of integrating less bulky passive filters, thus minimizing implementation costs and system losses, mainly copper and core losses in ferromagnetic elements;
- Possibility of reducing the voltage stress (dv/dt) of the power semiconductors. This feature enables the integration of more standard semiconductors with the higher commercially available stock and lower costs. Additionally, it allows for mitigating electromagnetic interference problems caused by high dv/dt values when switching semiconductors. Nevertheless, by reducing the dv/dt stress, it is also possible to reduce the galvanic isolation stress;
- Possibility of reducing switching frequencies, minimizing switching losses and semiconductor voltage stress;
- Simpler and faster maintenance service: just exchange the damaged submodule with a functional one;
- Enable the easy integration of renewable energy sources and energy storage systems.
2. Multilevel Converter
- The sizing of the inductive and capacitive elements: The inductor must be sized in order to decouple the DC component from the AC, as well as to minimize the short-circuiting of the DC bus;
- The pre-charging process of the capacitors: Whenever the MMC is initialized, the capacitors are discharged, requiring a pre-charging mechanism in order to minimize the inrush current;
- DC bus regulation: The DC bus must be constantly regulated to a reference voltage in order to allow the correct operation of the MMC, thus requiring several sensors and signal-conditioning circuits. The imbalance of DC bus voltages between the different submodules causes the emergence of circulating currents, requiring algorithms and mechanisms in order to mitigate this problem;
- The ripple in the DC bus: The harmonic spectrum of the DC bus voltage of each submodule will be concentrated in the fundamental frequency and in the second-order harmonic. Knowing that the voltage ripple is inversely proportional to the frequency of the fundamental component, this effect is more severe in variable speed applications, namely at start-up and at low motor rotating speeds. As such, capacitors with higher capacity are required, inflating implementation costs;
- Circulating currents: This effect does not affect the AC component of the output voltage and current. However, it increases the root mean square (RMS) and peak value of the arm current, consequently increasing the converter losses and the DC bus ripple;
- Fault-tolerance: The MMC is usually implemented with redundant submodules, ready to enter into operation in case of faults. One of the challenges is the decoupling of a damaged submodule and consequent coupling of an operational one, in a dynamic way, without the emergence of inrush currents. Another challenge is the development of protection mechanisms, namely circuit breakers, capable of shutting down the system in the event of a failure, which is especially important in HVDC applications.
2.1. Half-Bridge Submodule
2.2. Full-Bridge Submodule
2.3. Neutral Point Clamped Submodule
2.4. T-Type Neutral Point Clamping Submodule
2.5. Flying Capacitor Multilevel Converter Submodule
2.6. Submodule Topologies Comparison
3. Fault Tolerance Applied on MLC and Gate-Driver Circuits
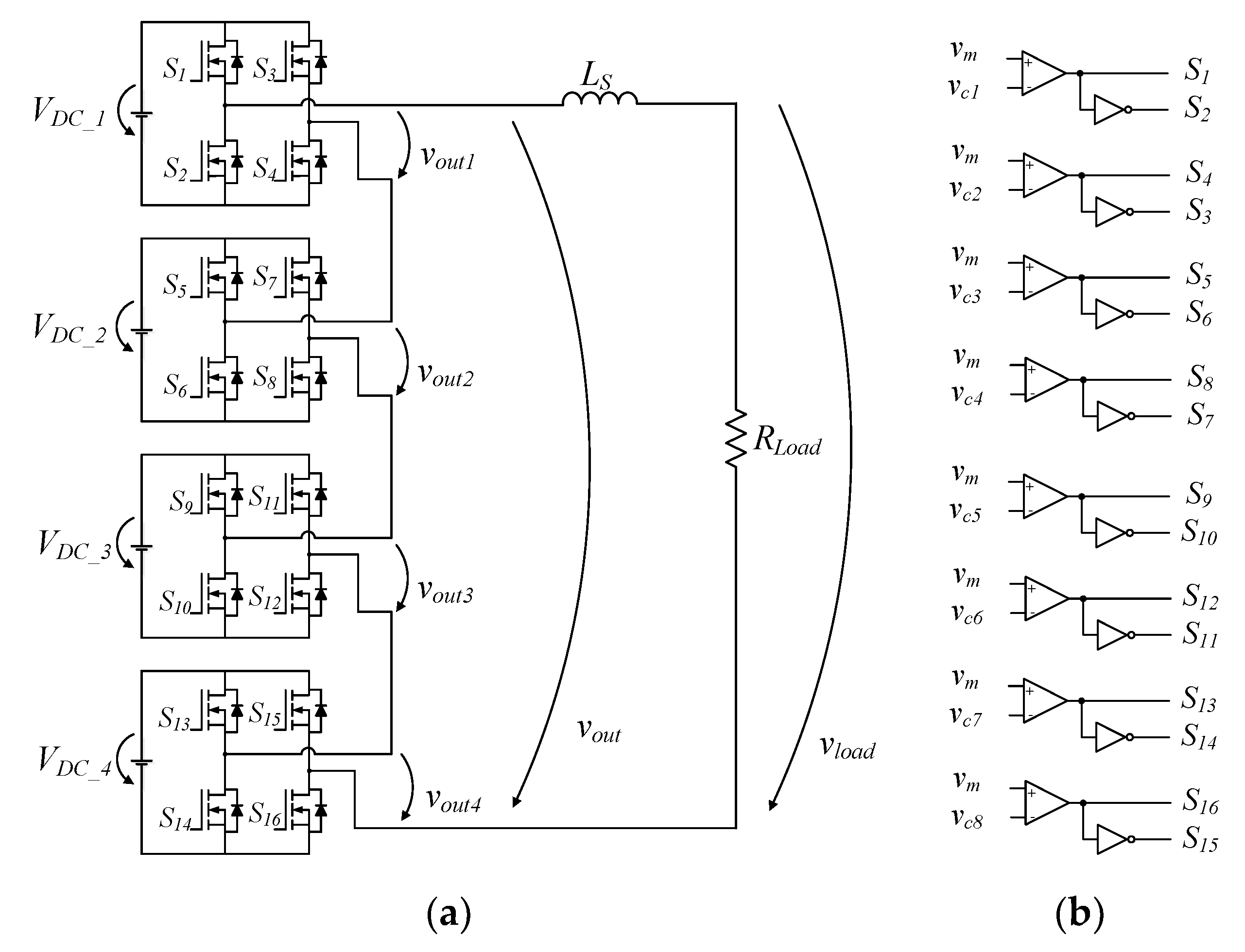
4. PWM Techniques Applied on MLC
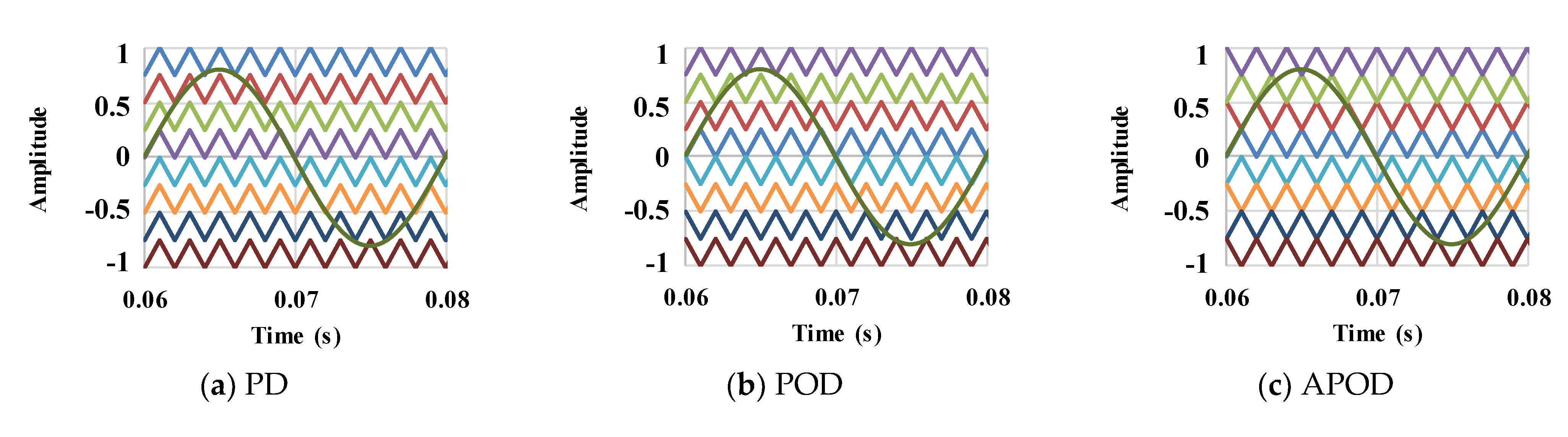
4.1. Level-Shift PWM Technique
4.2. Phase-Shift Carrier PWM Technique
4.3. Hybrid Carrier PWM Technique
4.4. Other Modulation Techniques
5. Simulation Results of PWM Techniques Applied on a Full-Bridge Cascade Converter
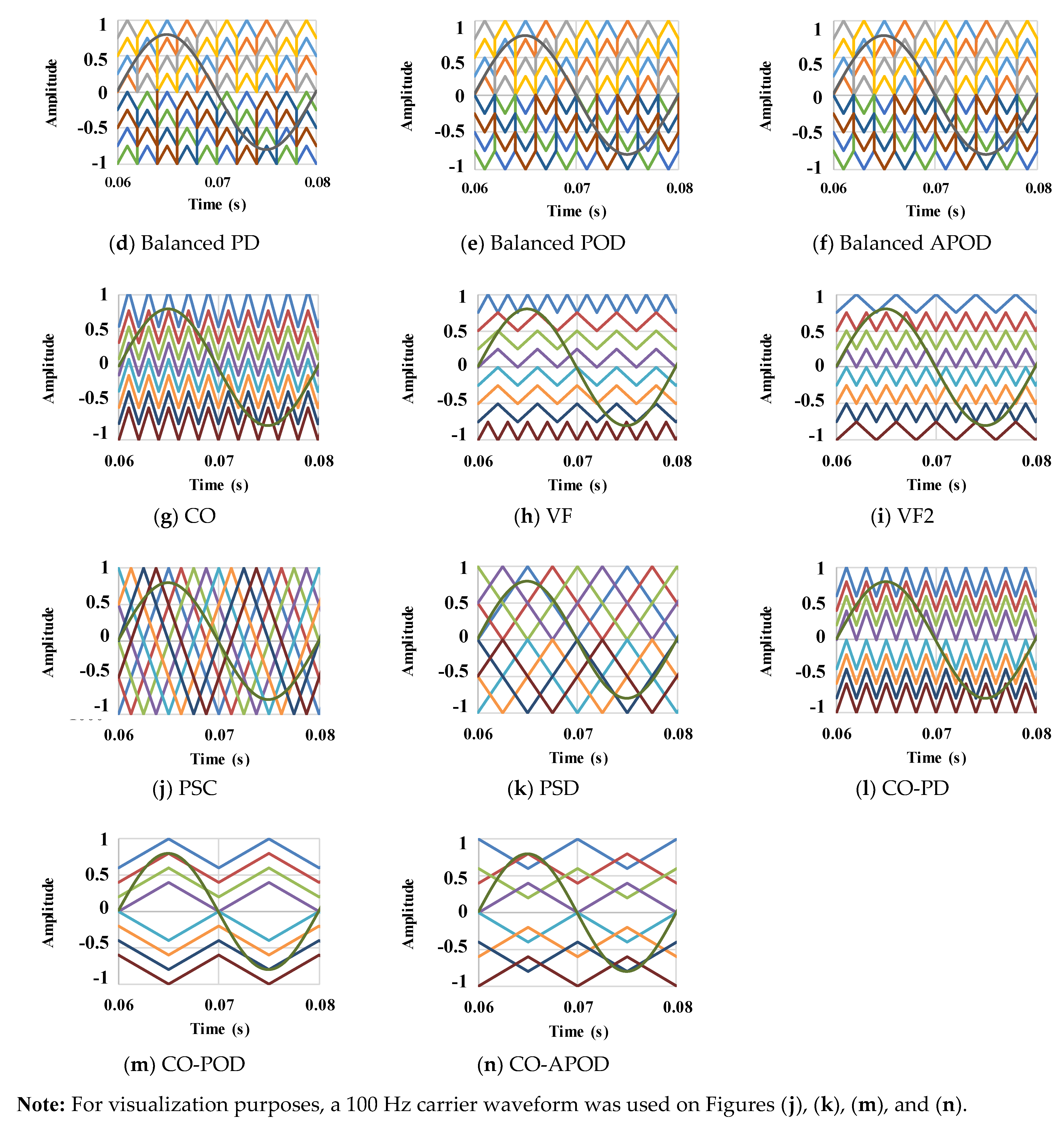
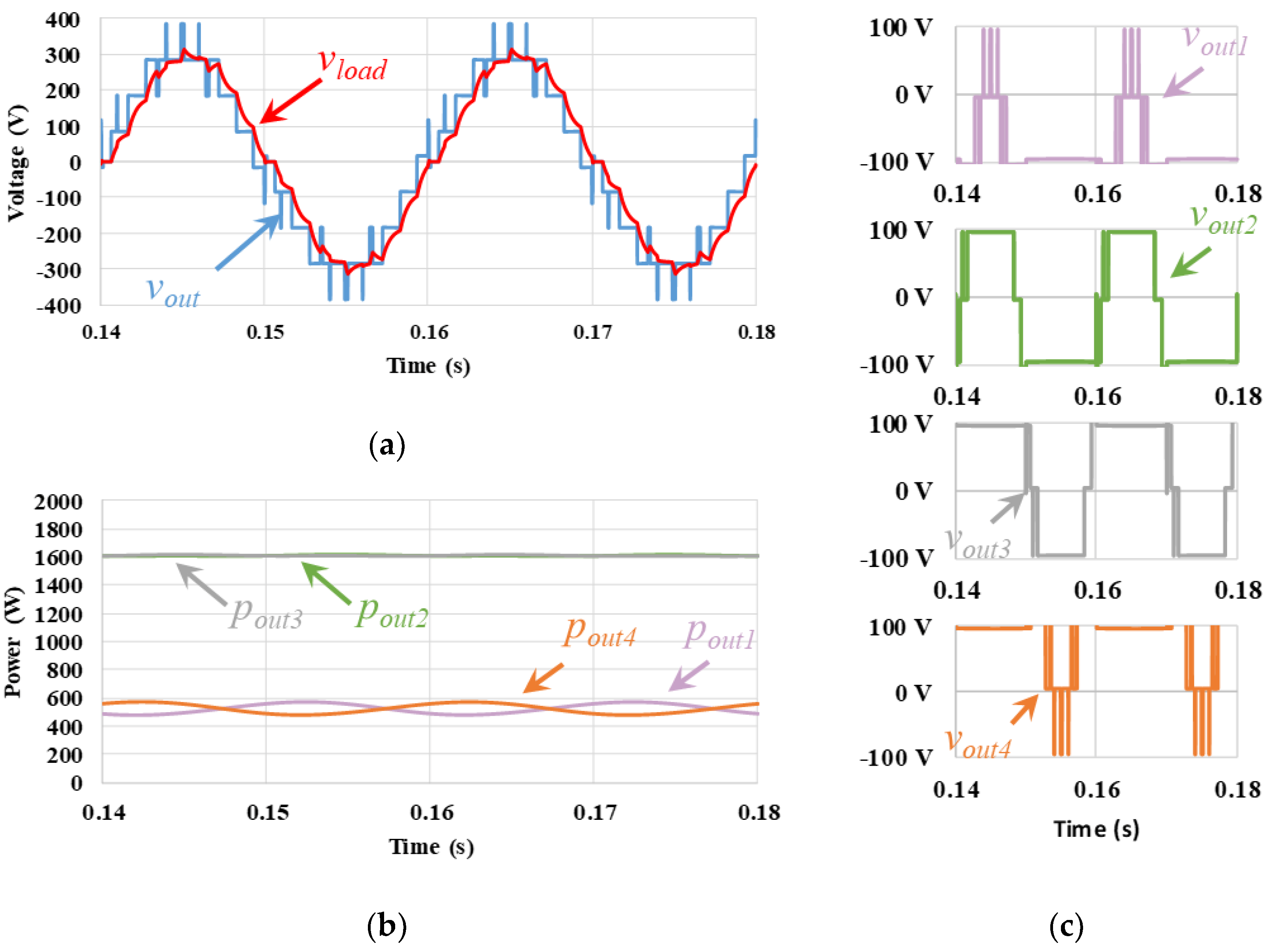
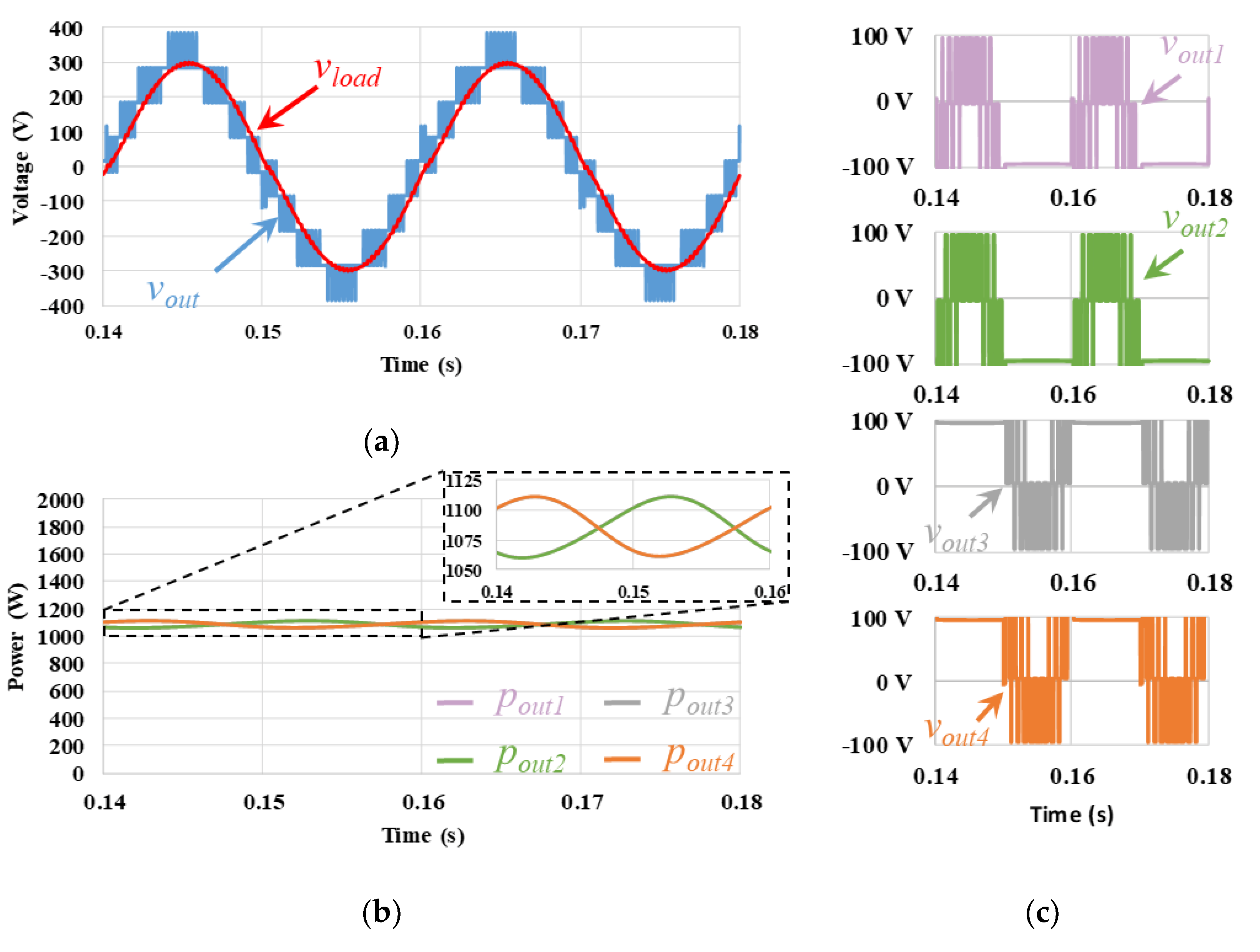
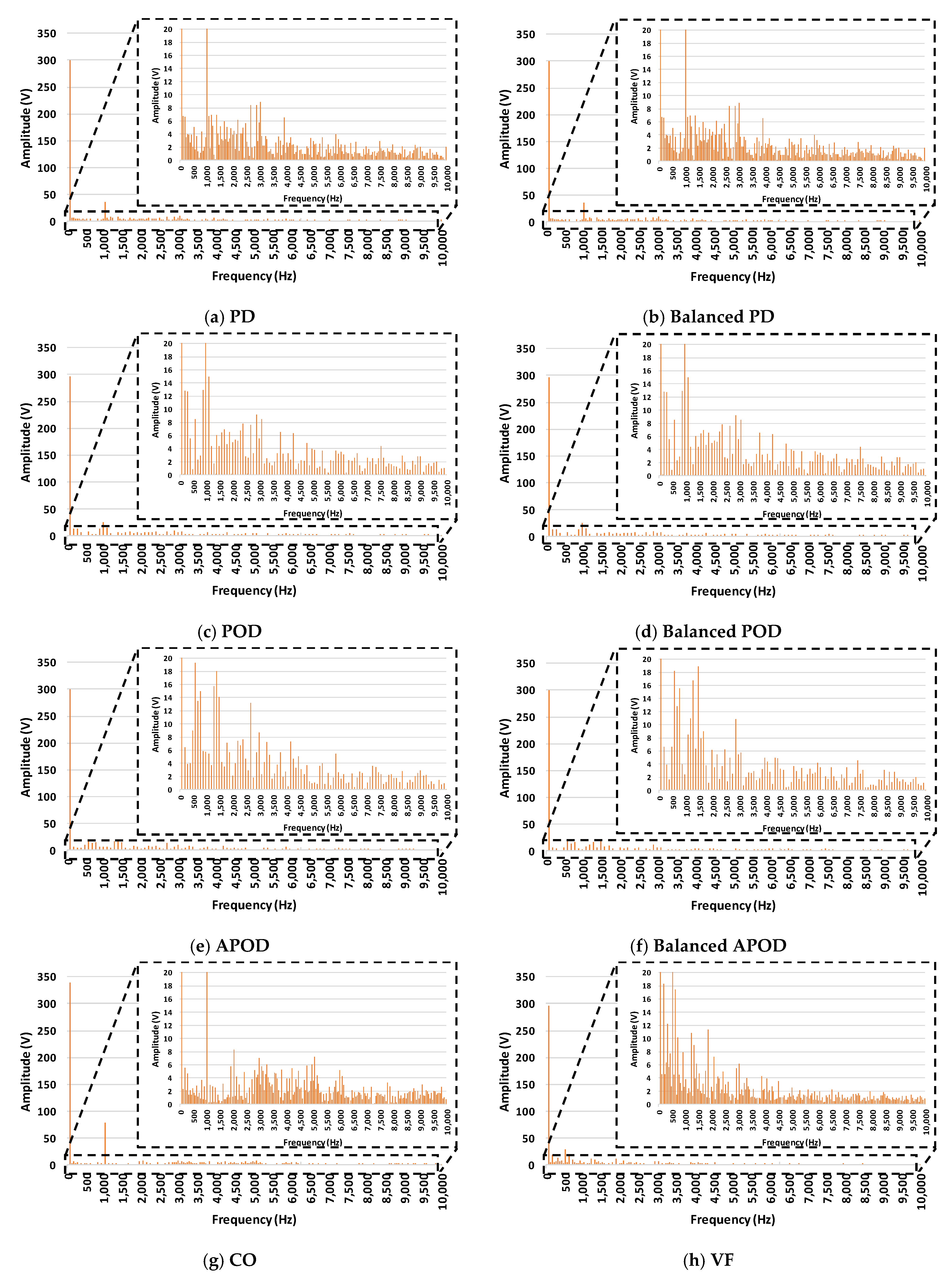
5.1. Basic Level-Shift PD, POD, and APOD PWM Techniques
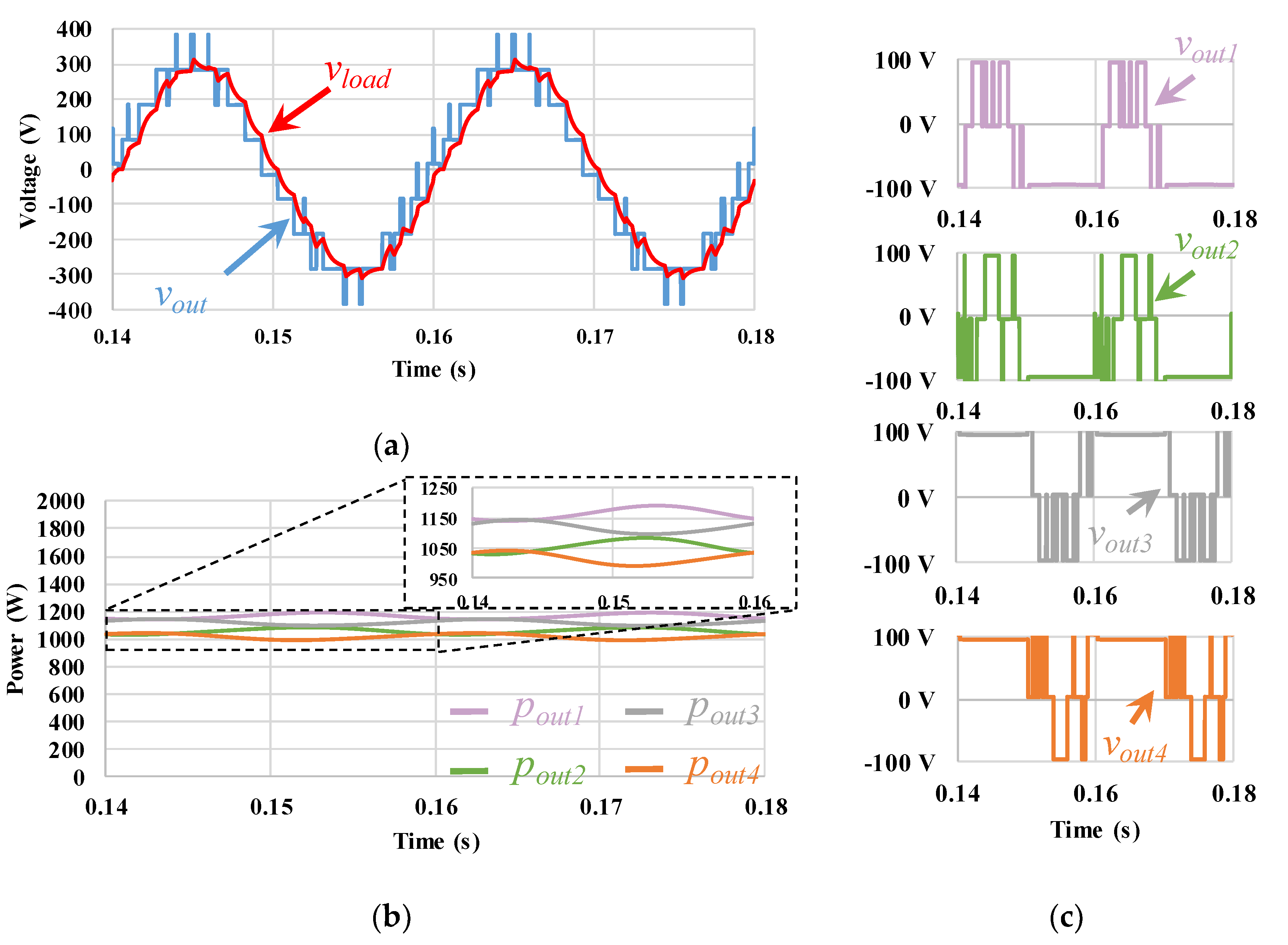
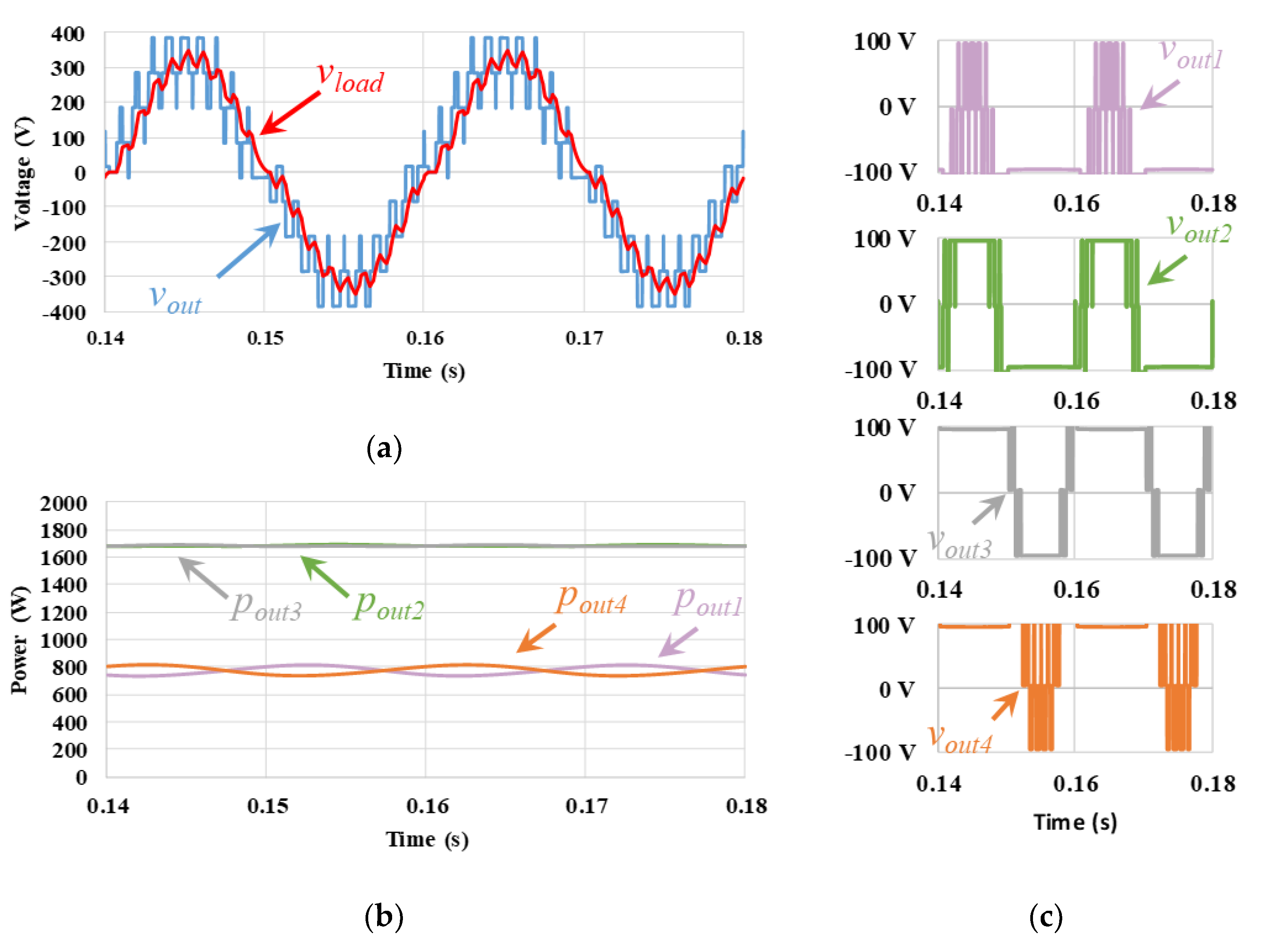
5.2. Power Balancing Level-Shift PD, POD, and APOD PWM Techniques
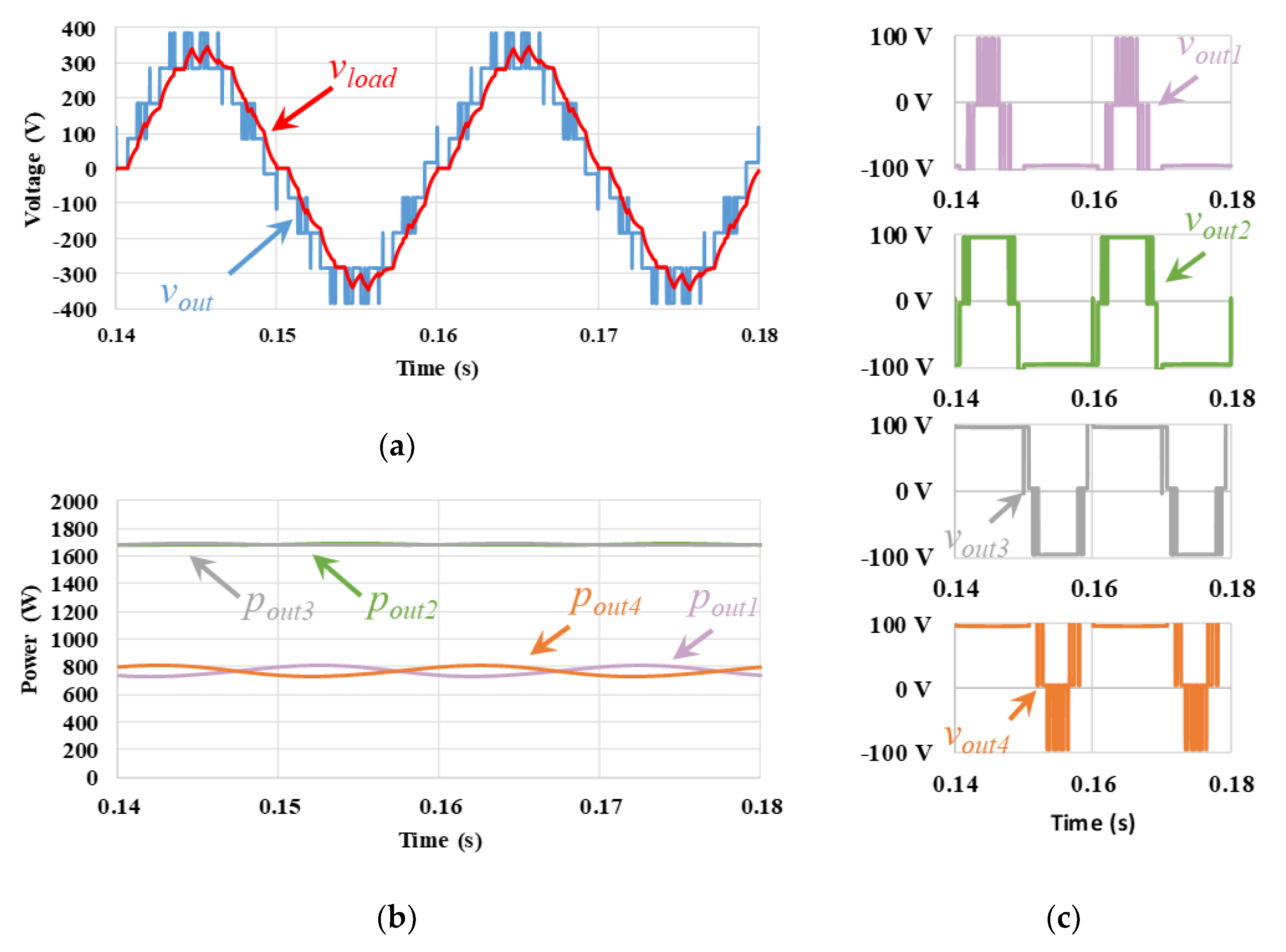
5.3. Level-Shift CO PWM Technique
5.4. Level-Shift VF and VF2 PWM Techniques
5.5. Phase-Shift Carrier PWM Technique
5.6. Hybrid Carrier PSD PWM Technique
5.7. Hybrid Carrier CO-PD, CO-POD, and CO-APOD PWM Techniques
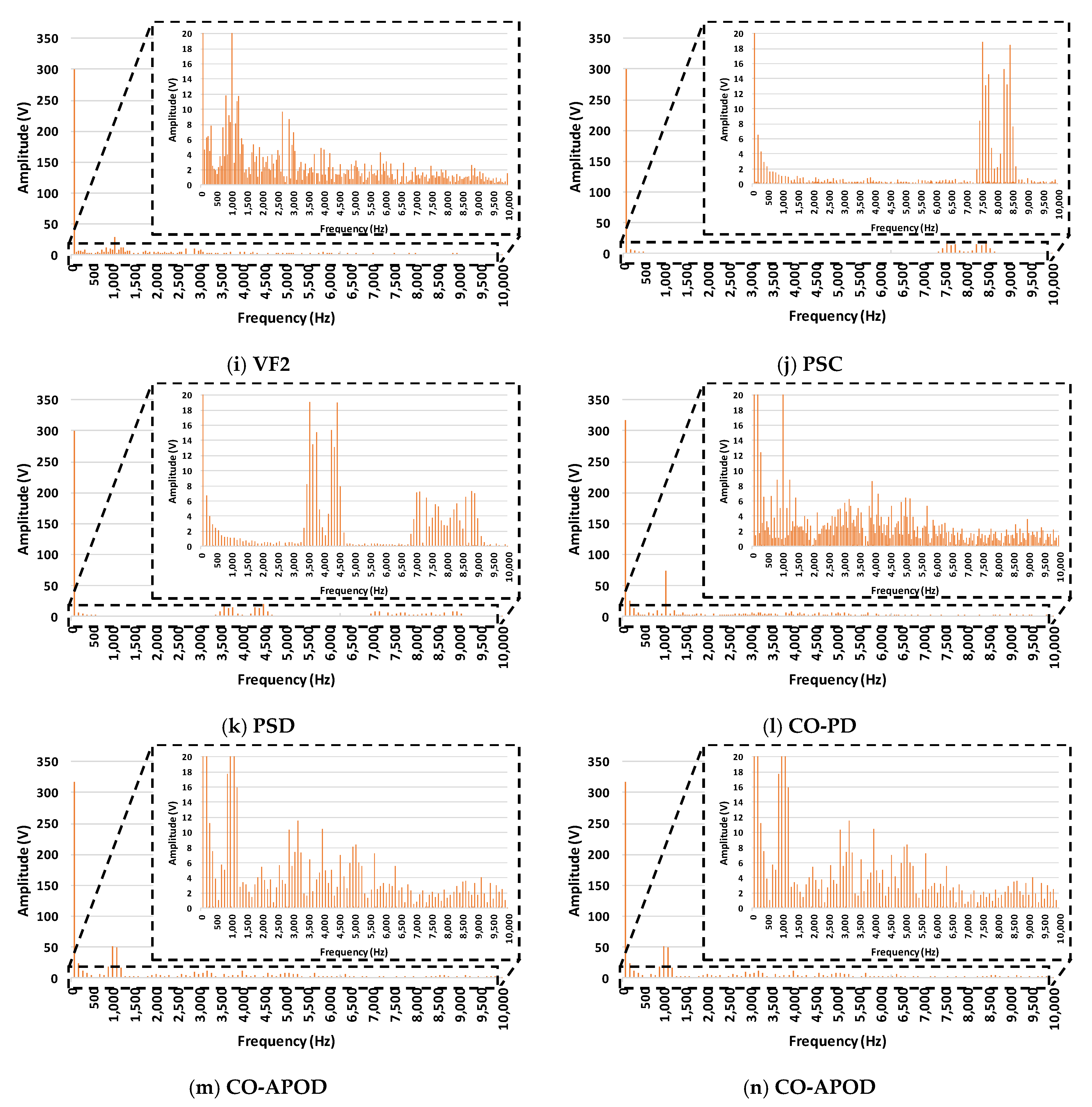
5.8. Comparative Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vijeh, M.; Rezanejad, M.; Samadaei, E.; Bertilsson, K. A general review of multilevel inverters based on main submodules: Structural point of view. IEEE Trans. Power Electron. 2019, 34, 9479–9502. [Google Scholar] [CrossRef]
- Barros, L.A.; Tanta, M.; Martins, A.P.; Afonso, J.L.; Pinto, J.G. Submodule Topologies and PWM Techniques Applied in Modular Multilevel Converters: Review and Analysis. In Proceedings of the International Conference on Sustainable Energy for Smart Cities, Viana do Castelo, Portugal, 3 December 2020; pp. 111–131. [Google Scholar]
- Gupta, K.K.; Bhatnagar, P. Multilevel Inverters: Conventional and Emerging Topologies and Their Control; Hayton, J., Ed.; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Rashid, M.H. Power Electronics Handbook, 4th ed.; Elsevier: Amsterdam, The Netherlands; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Sharifabadi, K.; Harnefors, L.; Nee, H.-P.; Norrga, S.; Teodorescu, R. Design, Control, and Application of Modular Multilevel Converters for HVDC Transmission Systems; IEEE Press: Piscataway, NJ, USA; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Feldman, R.; Tomasini, M.; Amankwah, E.; Clare, J.C.; Wheeler, P.W.; Trainer, D.R.; Whitehouse, R.S. A hybrid modular multilevel voltage source converter for HVDC power transmission. IEEE Trans. Ind. Appl. 2013, 49, 1577–1588. [Google Scholar] [CrossRef]
- Jung, J.-J.; Cui, S.; Lee, J.-H.; Sul, S.-K. A new topology of multilevel VSC converter for a hybrid HVDC transmission system. IEEE Trans. Power Electron. 2016, 32, 4199–4209. [Google Scholar] [CrossRef]
- Du, S.; Dekka, A.; Wu, B.; Zargari, N. Modular Multilevel Converters: Analysis, Control, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Engel, S.P.; Stieneker, M.; Soltau, N.; Rabiee, S.; Stagge, H.; De Doncker, R.W. Comparison of the modular multilevel DC converter and the dual-active bridge converter for power conversion in HVDC and MVDC grids. IEEE Trans Power Electron. 2014, 30, 124–137. [Google Scholar] [CrossRef]
- Huang, S. Distributed Modulation and Control of Modular Multilevel Converter for HVDC Application. Master’s Thesis, Aalborg University, Aalborg, Denmark, 2013. [Google Scholar]
- Song, G.; Wang, T.; Huang, X.; Zhang, C. An improved averaged value model of MMC-HVDC for power system faults simulation. Int. J. Electr. Power Energy Syst. 2019, 110, 223–231. [Google Scholar] [CrossRef]
- Li, X.; Song, Q.; Liu, W.; Rao, H.; Xu, S.; Li, L. Protection of nonpermanent faults on DC overhead lines in MMC-based HVDC systems. IEEE Trans. Power Deliv. 2012, 28, 483–490. [Google Scholar] [CrossRef]
- Son, G.T.; Lee, H.-J.; Nam, T.S.; Chung, Y.-H.; Lee, U.-H.; Baek, S.-T.; Hur, K.; Park, J.-W. Design and control of a modular multilevel HVDC converter with redundant power modules for noninterruptible energy transfer. IEEE Trans. Power Deliv. 2012, 27, 1611–1619. [Google Scholar]
- Ferreira, A.A. de A. Modular multilevel converters for power system applications. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2017. [Google Scholar]
- Zhou, L.; Fu, Q.; Li, X.; Liu, C. A novel photovoltaic grid-connected power conditioner employing hybrid multilevel inverter. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009; pp. 1–7. [Google Scholar]
- Latran, M.B.; Teke, A. Investigation of multilevel multifunctional grid connected inverter topologies and control strategies used in photovoltaic systems. Renew. Sustain. Energy Rev. 2015, 42, 361–376. [Google Scholar] [CrossRef]
- Lashab, A.; Sera, D.; Hahn, F.; Camurca, L.; Terriche, Y.; Liserre, M.; Guerrero, J.M. Cascaded multilevel PV inverter with improved harmonic performance during power imbalance between power cells. IEEE Trans. Ind. Appl. 2020, 56, 2788–2798. [Google Scholar] [CrossRef]
- Basu, T.S.; Maiti, S. A hybrid modular multilevel converter for solar power integration. IEEE Trans. Ind. Appl. 2019, 55, 5166–5177. [Google Scholar] [CrossRef]
- Acharya, A.B.; Ricco, M.; Sera, D.; Teoderscu, R.; Norum, L.E. Performance analysis of medium-voltage grid integration of PV plant using modular multilevel converter. IEEE Trans. Energy Convers. 2019, 34, 1731–1740. [Google Scholar] [CrossRef]
- Rojas, C.A.; Kouro, S.; Perez, M.A.; Echeverria, J. DC-DC MMC for HVdc grid interface of utility-scale photovoltaic conversion systems. IEEE Trans. Ind. Electron. 2017, 65, 352–362. [Google Scholar] [CrossRef]
- Nademi, H.; Das, A.; Burgos, R.; Norum, L.E. A new circuit performance of modular multilevel inverter suitable for photovoltaic conversion plants. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 4, 393–404. [Google Scholar] [CrossRef]
- Rong, F.; Gong, X.; Huang, S. A novel grid-connected PV system based on MMC to get the maximum power under partial shading conditions. IEEE Trans. Power Electron. 2016, 32, 4320–4333. [Google Scholar] [CrossRef]
- Debnath, S.; Saeedifard, M. A new hybrid modular multilevel converter for grid connection of large wind turbines. IEEE Trans. Sustain. Energy 2013, 4, 1051–1064. [Google Scholar] [CrossRef]
- Li, R.; Yu, L.; Xu, L.; Adam, G.P. Coordinated control of parallel DR-HVDC and MMC-HVDC systems for offshore wind energy transmission. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 2572–2582. [Google Scholar] [CrossRef]
- Karaagac, U.; Mahseredjian, J.; Cai, L.; Saad, H. Offshore wind farm modeling accuracy and efficiency in MMC-based multiterminal HVDC connection. IEEE Trans. Power Deliv. 2016, 32, 617–627. [Google Scholar] [CrossRef]
- Vidal-Albalate, R.; Beltran, H.; Rolán, A.; Belenguer, E.; Peña, R.; Blasco-Gimenez, R. Analysis of the performance of MMC under fault conditions in HVDC-based offshore wind farms. IEEE Trans. Power Deliv. 2015, 31, 839–847. [Google Scholar] [CrossRef] [Green Version]
- Islam, M.R.; Guo, Y.; Zhu, J. A high-frequency link multilevel cascaded medium-voltage converter for direct grid integration of renewable energy systems. IEEE Trans. Power Electron. 2013, 29, 4167–4182. [Google Scholar] [CrossRef]
- Kwon, K.; Choi, J. Single-Phase 13-Level Power Conditioning System for Peak Power Reduction of a High-Speed Railway Substation. Energies 2019, 12, 4405. [Google Scholar] [CrossRef] [Green Version]
- Bayat, H.; Yazdani, A. A hybrid MMC-based photovoltaic and battery energy storage system. IEEE Power Energy Technol. Syst. J. 2019, 6, 32–40. [Google Scholar] [CrossRef]
- Amin, M.; Rygg, A.; Molinas, M. Self-synchronization of wind farm in an MMC-based HVDC system: A stability investigation. IEEE Trans. Energy Convers. 2017, 32, 458–470. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, Y.; Yang, S.; Gao, F. Decoupled power control for a modular-multilevel-converter-based hybrid AC-DC grid integrated with hybrid energy storage. IEEE Trans. Ind. Electron. 2018, 66, 2926–2934. [Google Scholar] [CrossRef]
- Maharjan, L.; Yamagishi, T.; Akagi, H.; Asakura, J. Fault-tolerant operation of a battery-energy-storage system based on a multilevel cascade PWM converter with star configuration. IEEE Trans. Power Electron. 2010, 25, 2386–2396. [Google Scholar] [CrossRef]
- Maharjan, L.; Yamagishi, T.; Akagi, H. Active-power control of individual converter cells for a battery energy storage system based on a multilevel cascade PWM converter. IEEE Trans. Power Electron. 2010, 27, 1099–1107. [Google Scholar] [CrossRef]
- Zhou, Y.; Jiang, D.; Guo, J.; Hu, P.; Liang, Y. Analysis and control of modular multilevel converters under unbalanced conditions. IEEE Trans. Power Deliv. 2013, 28, 1986–1995. [Google Scholar] [CrossRef]
- Soong, T.; Lehn, P.W. Assessment of fault tolerance in modular multilevel converters with integrated energy storage. IEEE Trans. Power Electron. 2015, 31, 4085–4095. [Google Scholar] [CrossRef]
- Weiss, D.; Vasiladiotis, M.; Banceanu, C.; Drack, N.; Odegard, B.; Grondona, A. IGCT based modular multilevel converter for an AC-AC rail power supply. In Proceedings of the PCIM Europe 2017: International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 16–18 May 2017; pp. 1–8. [Google Scholar]
- ElGebaly, A.E.; Hassan, A.E.-W.; El-Nemr, M.K. Reactive Power Compensation by Multilevel Inverter STATCOM for Railways Power Grid. In Proceedings of the 2019 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Saint Petersburg, Moscow, 28–31 January 2019; pp. 2094–2099. [Google Scholar]
- Tanta, M.; Cunha, J.; Barros, L.A.; Monteiro, V.; Pinto, J.; Martins, A.P.; Afonso, J.L. Experimental Validation of a Reduced-Scale Rail Power Conditioner Based on Modular Multilevel Converter for AC Railway Power Grids. Energies 2021, 14, 484. [Google Scholar] [CrossRef]
- Dixon, J.; Pereda, J.; Castillo, C.; Bosch, S. Asymmetrical multilevel inverter for traction drives using only one DC supply. IEEE Trans. Veh. Technol. 2010, 59, 3736–3743. [Google Scholar] [CrossRef]
- Fazel, S.S.; Bernet, S.; Krug, D.; Jalili, K. Design and comparison of 4-kV neutral-point-clamped, flying-capacitor, and series-connected H-bridge multilevel converters. IEEE Trans. Ind. Appl. 2007, 43, 1032–1040. [Google Scholar] [CrossRef]
- Gan, C.; Sun, Q.; Wu, J.; Kong, W.; Shi, C.; Hu, Y. MMC-based SRM drives with decentralized battery energy storage system for hybrid electric vehicles. IEEE Trans. Power Electron. 2018, 34, 2608–2621. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, K.; Xu, L.; Li, Y. A hybrid cascaded multilevel converter for battery energy management applied in electric vehicles. IEEE Trans. Power Electron. 2013, 29, 3537–3546. [Google Scholar] [CrossRef]
- Ronanki, D.; Williamson, S.S. A simplified space vector pulse width modulation implementation in modular multilevel converters for electric ship propulsion systems. IEEE Trans. Transp. Electrif. 2018, 5, 335–342. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.; Zhao, S.; Wei, X.; Kang, Y. Design and implementation of a modular multilevel converter with hierarchical redundancy ability for electric ship MVDC system. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 5, 189–202. [Google Scholar] [CrossRef]
- Bina, M.T. A transformerless medium-voltage STATCOM topology based on extended modular multilevel converters. IEEE Trans. Power Electron. 2011, 26, 1534–1545. [Google Scholar]
- Cheng, Y.; Qian, C.; Crow, M.L.; Pekarek, S.; Atcitty, S. A comparison of diode-clamped and cascaded multilevel converters for a STATCOM with energy storage. IEEE Trans. Ind. Electron. 2006, 53, 1512–1521. [Google Scholar] [CrossRef]
- Merlin, M.M.; Green, T.C.; Mitcheson, P.D.; Trainer, D.R.; Critchley, R.; Crookes, W.; Hassan, F. The alternate arm converter: A new hybrid multilevel converter with dc-fault blocking capability. IEEE Trans. Power Deliv. 2013, 29, 310–317. [Google Scholar] [CrossRef] [Green Version]
- Song, W.; Huang, A.Q. Fault-tolerant design and control strategy for cascaded H-bridge multilevel converter-based STATCOM. IEEE Trans. Ind. Electron. 2009, 57, 2700–2708. [Google Scholar] [CrossRef]
- Akagi, H.; Inoue, S.; Yoshii, T. Control and performance of a transformerless cascade PWM STATCOM with star configuration. IEEE Trans. Ind. Appl. 2007, 43, 1041–1049. [Google Scholar] [CrossRef]
- Cupertino, A.F.; Farias, J.V.M.; Pereira, H.A.; Seleme, S.I.; Teodorescu, R. Comparison of DSCC and SDBC modular multilevel converters for STATCOM application during negative sequence compensation. IEEE Trans. Ind. Electron. 2018, 66, 2302–2312. [Google Scholar] [CrossRef]
- Gupta, R.; Ghosh, A.; Joshi, A. Control of cascaded transformer multilevel inverter based DSTATCOM. Electr. Power Syst. Res. 2007, 77, 989–999. [Google Scholar] [CrossRef]
- Liu, T.; Yang, X.; Chen, W.; Xuan, Y.; Li, Y.; Huang, L.; Hao, X. High-efficiency control strategy for 10-kV/1-MW solid-state transformer in PV application. IEEE Trans. Power Electron. 2020, 35, 11770–11782. [Google Scholar] [CrossRef]
- Liu, T.; Yang, X.; Chen, W.; Li, Y.; Xuan, Y.; Huang, L.; Hao, X. Design and implementation of high efficiency control scheme of dual active bridge based 10 kV/1 MW solid state transformer for PV application. IEEE Trans. Power Electron. 2018, 34, 4223–4238. [Google Scholar] [CrossRef]
- Parreiras, T.M.; Machado, A.P.; Amaral, F.V.; Lobato, G.C.; Brito, J.A.; Cardoso Filho, B. Forward dual-active-bridge solid-state transformer for a SiC-based cascaded multilevel converter cell in solar applications. IEEE Trans. Ind. Appl. 2018, 54, 6353–6363. [Google Scholar] [CrossRef]
- Liu, C.; Liu, C.; Cai, G.; Ying, H.; Zhang, Z.; Shan, R.; Pei, Z.; Song, X. An isolated modular multilevel converter (IM 2 C) topology based on high-frequency link (HFL) concept. IEEE Trans. Power Electron. 2019, 35, 1576–1588. [Google Scholar] [CrossRef]
- Madhusoodhanan, S.; Tripathi, A.; Patel, D.; Mainali, K.; Kadavelugu, A.; Hazra, S.; Bhattacharya, S.; Hatua, K. Solid-state transformer and MV grid tie applications enabled by 15 kV SiC IGBTs and 10 kV SiC MOSFETs based multilevel converters. IEEE Trans. Ind. Appl. 2015, 51, 3343–3360. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Pérez, M.A.; Leon, J.I. Recent advances and industrial applications of multilevel converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Akagi, H. Classification, terminology, and application of the modular multilevel cascade converter (MMCC). IEEE Trans. Power Electron. 2011, 26, 3119–3130. [Google Scholar] [CrossRef]
- Dekka, A.; Wu, B.; Fuentes, R.L.; Perez, M.; Zargari, N.R. Evolution of topologies, modeling, control schemes, and applications of modular multilevel converters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1631–1656. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, S.; Din, Z.; Hu, X. Hybrid multilevel converters: Topologies, evolutions and verifications. Energies 2019, 12, 615. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Chu, W.; Zhang, Z.; Zhu, Z. Power electronic transformer-based railway traction systems: Challenges and opportunities. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1237–1253. [Google Scholar] [CrossRef]
- Nami, A.; Liang, J.; Dijkhuizen, F.; Demetriades, G.D. Modular multilevel converters for HVDC applications: Review on converter cells and functionalities. IEEE Trans. Power Electron. 2015, 30, 18–36. [Google Scholar] [CrossRef]
- Perez, M.A.; Bernet, S.; Rodriguez, J.; Kouro, S.; Lizana, R. Circuit topologies, modeling, control schemes, and applications of modular multilevel converters. IEEE Trans. Power Electron. 2014, 30, 4–17. [Google Scholar] [CrossRef]
- Deng, F.; Lü, Y.; Liu, C.; Heng, Q.; Yu, Q.; Zhao, J. Overview on submodule topologies, modeling, modulation, control schemes, fault diagnosis, and tolerant control strategies of modular multilevel converters. Chin. J. Electr. Eng. 2020, 6, 1–21. [Google Scholar] [CrossRef]
- Antonio-Ferreira, A.; Collados-Rodriguez, C.; Gomis-Bellmunt, O. Modulation techniques applied to medium voltage modular multilevel converters for renewable energy integration: A review. Electr. Power Syst. Res. 2018, 155, 21–39. [Google Scholar] [CrossRef] [Green Version]
- Debnath, S.; Qin, J.; Bahrani, B.; Saeedifard, M.; Barbosa, P. Operation, control, and applications of the modular multilevel converter: A review. IEEE Trans. Power Electron. 2014, 30, 37–53. [Google Scholar] [CrossRef]
- Mcmurray, W. Fast Response Stepped-Wave Switching Power Converter Circuit. U.S. Patent 3581212, 25 May 1971. [Google Scholar]
- Huber, J.E.; Kolar, J.W. Solid-state transformers: On the origins and evolution of key concepts. IEEE Ind. Electron. Mag. 2016, 10, 19–28. [Google Scholar] [CrossRef]
- Rego, J.; Pereira, F.L.; Barros, L.A.M.; Martins, A.P.; Pinto, J.G. Development of a Modular Multilevel Cascade Converter based on Full-Bridge Submodules with a common DC-Bus. In Proceedings of the EAI SESC 2021—3rd EAI International Conference on Sustainable Energy for Smart Cities, Online Conference, 24–26 November 2021. [Google Scholar]
- Baker, R.H. Bridge Converter Circuit. U.S. Patent 4 270 163, 26 May 1991. [Google Scholar]
- Nabae, A.; Takahashi, I.; Akagi, H. A new neutral-point-clamped PWM inverter. IEEE Trans. Ind. Appl. 1981, 5, 518–523. [Google Scholar] [CrossRef]
- Meynard, T.; Foch, H. Multi-level conversion: High voltage choppers and voltage-source inverters. In Proceedings of the PESC’92 Record. 23rd Annual IEEE Power Electronics Specialists Conference, Toledo, Spain, 29 June–3 July 1992; pp. 397–403. [Google Scholar]
- Rashid, M.H. Power Electronics Handbook: Devices, Circuits, and Applications, 3rd ed.; Elsevier: Amsterdam, The Netherlands; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Maswood, A.I.; Tafti, H.D. Advanced Multilevel Converters and Applications in Grid Integration; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Brenna, M.; Foiadelli, F.; Zaninelli, D. Electrical Railway Transportation Systems; IEEE Press: Piscataway, NJ, USA; John Wiley & Sons: Hoboken, NJ, USA, 2018; Volume 67. [Google Scholar]
- Barros, L.A.M.; Tanta, M.; Martins, A.P.; Afonso, J.L.; Pinto, J.G. Opportunities and Challenges of Power Electronics Systems in Future Railway Electrification. In Proceedings of the IEEE CPE—POWERENG 2020: 14th International Conference on Compatibility, Power Electronics and Power Engineering, Setubal, Portugal, 8–10 July 2020. [Google Scholar]
- Kabalci, E. Multilevel Inverters: Control Methods and Advanced Power Electronic Applications; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Talon Louokdom, E.; Gavin, S.; Siemaszko, D.; Biya-Motto, F.; Essimbi Zobo, B.; Marchesoni, M.; Carpita, M. Small-Scale Modular Multilevel Converter for Multi-Terminal DC Networks Applications: System Control Validation. Energies 2018, 11, 1690. [Google Scholar] [CrossRef] [Green Version]
- Talon, E.; Gavin, S.; Siemaszko, D.; Biya-Motto, F.; Essimbi, B.; Carpita, M. Design and implementation of a multi-dsp based digital control system architecture for modular multilevel converters. In Proceedings of the 2016 IEEE International Power Electronics and Motion Control Conference (PEMC), Varna, Bulgaria, 25–28 September 2016; pp. 1182–1187. [Google Scholar]
- Toh, C.L.; Norum, L. A high speed control network synchronization jitter evaluation for embedded monitoring and control in modular multilevel converter. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar]
- Fey, J.-H.; Hinrichsen, F.; Carstens, G.; Mallwitz, R. Development of a modular multilevel converter demonstrator with EtherCAT communication. In Proceedings of the 2019 IEEE 13th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Sonderborg, Denmark, 23–25 April 2019; pp. 1–6. [Google Scholar]
- Rietmann, S.; Fuchs, S.; Hillers, A.; Biela, J. Field bus for data exchange and control of modular power electronic systems with high synchronisation accuracy. IEEJ J. Ind. Appl. 2019, 8, 295–305. [Google Scholar] [CrossRef] [Green Version]
- Ronanki, D.; Williamson, S.S. Modular multilevel converters for transportation electrification: Challenges and opportunities. IEEE Trans. Transp. Electrif. 2018, 4, 399–407. [Google Scholar] [CrossRef]
- Vahedi, H.; Al-Haddad, K.; Labbe, P.-A.; Rahmani, S. Cascaded multilevel inverter with multicarrier PWM technique and voltage balancing feature. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 2155–2160. [Google Scholar]
- Batschauer, A.L.; Mussa, S.A.; Heldwein, M.L. Three-phase hybrid multilevel inverter based on half-bridge modules. IEEE Trans. Ind. Electron. 2011, 59, 668–678. [Google Scholar] [CrossRef]
- Dujic, D.; Zhao, C.; Mester, A.; Steinke, J.K.; Weiss, M.; Lewdeni-Schmid, S.; Chaudhuri, T.; Stefanutti, P. Power electronic traction transformer-low voltage prototype. IEEE Trans. Power Electron. 2013, 28, 5522–5534. [Google Scholar] [CrossRef]
- Huang, A.Q. Medium-voltage solid-state transformer: Technology for a smarter and resilient grid. IEEE Ind. Electron. Mag. 2016, 10, 29–42. [Google Scholar] [CrossRef]
- Fan, H.; Li, H. High-frequency transformer isolated bidirectional DC-DC converter modules with high efficiency over wide load range for 20 kVA solid-state transformer. IEEE Trans. Power Electron. 2011, 26, 3599–3608. [Google Scholar] [CrossRef]
- Akagi, H. Multilevel converters: Fundamental circuits and systems. Proc. IEEE 2017, 105, 2048–2065. [Google Scholar] [CrossRef]
- Li, Z.; Wang, P.; Zhu, H.; Chu, Z.; Li, Y. An improved pulse width modulation method for chopper-cell-based modular multilevel converters. IEEE Trans. Power Electron. 2012, 27, 3472–3481. [Google Scholar] [CrossRef]
- Cottet, D.; van der Merwe, W.; Agostini, F.; Riedel, G.; Oikonomou, N.; Rüetschi, A.; Geyer, T.; Gradinger, T.; Velthuis, R.; Wunsch, B.; et al. Integration technologies for a fully modular and hot-swappable MV multi-level concept converter. In Proceedings of the PCIM Europe 2015; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Frankfurt am Main, Germany, 19–20 May 2015; pp. 1–8. [Google Scholar]
- Luo, F.L.; Ye, H. Advanced DC/AC Inverters: Applications in Renewable Energy; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Liao, J.; Corzine, K.; Ferdowsi, M. A new control method for single-DC-source cascaded H-bridge multilevel converters using phase-shift modulation. In Proceedings of the 2008 Twenty-Third Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 24–28 February 2008; pp. 886–890. [Google Scholar]
- Chattopadhyay, S.K.; Chakraborty, C. A new multilevel inverter topology with self-balancing level doubling network. IEEE Trans. Ind. Electron. 2013, 61, 4622–4631. [Google Scholar] [CrossRef]
- Farnesi, S.; Marchesoni, M.; Passalacqua, M.; Vaccaro, L. Solid-state transformers in locomotives fed through AC lines: A review and future developments. Energies 2019, 12, 4711. [Google Scholar] [CrossRef] [Green Version]
- Song, S.G.; Kang, F.S.; Park, S.-J. Cascaded multilevel inverter employing three-phase transformers and single DC input. IEEE Trans. Ind. Electron. 2009, 56, 2005–2014. [Google Scholar] [CrossRef]
- Flores, P.; Dixon, J.; Ortúzar, M.; Carmi, R.; Barriuso, P.; Morán, L. Static var compensator and active power filter with power injection capability, using 27-level inverters and photovoltaic cells. IEEE Trans. Ind. Electron. 2008, 56, 130–138. [Google Scholar] [CrossRef]
- Kang, F.-S.; Park, S.-J.; Lee, M.H.; Kim, C.-U. An efficient multilevel-synthesis approach and its application to a 27-level inverter. IEEE Trans. Ind. Electron. 2005, 52, 1600–1606. [Google Scholar] [CrossRef]
- Ortúzar, M.E.; Carmi, R.E.; Dixon, J.W.; Morán, L. Voltage-source active power filter based on multilevel converter and ultracapacitor DC link. IEEE Trans. Ind. Electron. 2006, 53, 477–485. [Google Scholar] [CrossRef]
- Gonzalez, S.A.; Verne, S.A.; Valla, M.I. Multilevel converters for industrial applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Tolbert, L.M.; Peng, F.Z.; Habetler, T.G. Multilevel PWM methods at low modulation indices. IEEE Trans. Power Electron. 2000, 15, 719–725. [Google Scholar] [CrossRef]
- Carpaneto, M.; Marchesoni, M.; Vaccaro, L. A new cascaded multilevel converter based on NPC cells. In Proceedings of the 2007 IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 1033–1038. [Google Scholar]
- Da Silva, G.P.; Trentini, F.; Odaguiri, V.T.; Bressan, M.V.; Heldwein, M.L.; Batschauer, A.L. Hybrid three-phase multilevel inverter based ON NPC cascaded to half-bridge cells. In Proceedings of the 2013 Brazilian Power Electronics Conference, Gramado, Brazil, 27–31 October 2013; pp. 72–78. [Google Scholar]
- Moonem, M.; Krishnaswami, H. Analysis and control of multi-level dual active bridge DC-DC converter. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 1556–1561. [Google Scholar]
- Yuan, Z.; Deshpande, A.; Narayanasamy, B.; Peng, H.; Emon, A.I.; Whitt, R.; Nafis, B.M.; Luo, F.; Huitink, D. Design and evaluation of a 150 kva sic mosfet based three level tnpc phase-leg pebb for aircraft motor driving application. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 6569–6574. [Google Scholar]
- Nami, A.; Adabi, J. A new T-type NPC-based submodule for modular multilevel cascaded converters. In Proceedings of the 5th Annual International Power Electronics, Drive Systems and Technologies Conference (PEDSTC 2014), Tehran, Iran, 5–6 February 2014; pp. 137–142. [Google Scholar]
- Hasan, N.S.; Rosmin, N.; Osman, D.A.A.; Musta’amal, A.H. Reviews on multilevel converter and modulation techniques. Renew. Sustain. Energy Rev. 2017, 80, 163–174. [Google Scholar] [CrossRef]
- Lei, Y.; Barth, C.; Qin, S.; Liu, W.-C.; Moon, I.; Stillwell, A.; Chou, D.; Foulkes, T.; Ye, Z.; Liao, Z.; et al. A 2-kW single-phase seven-level flying capacitor multilevel inverter with an active energy buffer. IEEE Trans. Power Electron. 2017, 32, 8570–8581. [Google Scholar] [CrossRef]
- Mortezaei, A.; Simões, M.G.; Busarello, T.D.C.; Marafão, F.P.; Al-Durra, A. Grid-connected symmetrical cascaded multilevel converter for power quality improvement. IEEE Trans. Ind. Appl. 2018, 54, 2792–2805. [Google Scholar] [CrossRef] [Green Version]
- Oliveira Pinto, J.G.; Macedo, R.; Monteiro, V.; Barros, L.; Sousa, T.; Afonso, J.L. Single-phase shunt active power filter based on a 5-level converter topology. Energies 2018, 11, 1019. [Google Scholar] [CrossRef] [Green Version]
- Acuna, P.; Morán, L.; Rivera, M.; Aguilera, R.; Burgos, R.; Agelidis, V.G. A single-objective predictive control method for a multivariable single-phase three-level NPC converter-based active power filter. IEEE Trans. Ind. Electron. 2015, 62, 4598–4607. [Google Scholar] [CrossRef]
- Adrikowski, T.; Bula, D.; Pasko, M. Three-phase active power filter with T-NPC type inverter. In Proceedings of the 2018 Progress in Applied Electrical Engineering (PAEE), Kościelisko, Poland, 18–22 June 2018; pp. 1–5. [Google Scholar]
- Antoniewicz, K.; Jasinski, M.; Kazmierkowski, M.P.; Malinowski, M. Model predictive control for three-level four-leg flying capacitor converter operating as shunt active power filter. IEEE Trans. Ind. Electron. 2016, 63, 5255–5262. [Google Scholar]
- Lin, B.-R.; Huang, C.-H. Implementation of a three-phase capacitor-clamped active power filter under unbalanced condition. IEEE Trans. Ind. Electron. 2006, 53, 1621–1630. [Google Scholar] [CrossRef]
- Manai, L.; Hakiri, D.; Besbes, M. Backstepping control of flying capacitor multilevel inverter-based active power filter. IET Power Electron. 2020, 13, 4610–4624. [Google Scholar] [CrossRef]
- Humayun, M.; Khan, M.M.; Hassan, M.U.; Zhang, W. Analysis of hybrid switches symmetric flying capacitor multilevel inverter based STATCOM. Int. J. Electr. Power Energy Syst. 2021, 131, 107054. [Google Scholar] [CrossRef]
- Liao, Z.; Pilawa-Podgurski, R.G.C.N. A High Power Density Multi-level Bipolar Active Single-phase Buffer with Full Capacitor Energy Utilization and Controlled Power Harmonics. IEEE Trans. Power Electron. 2021, 36, 13067–13079. [Google Scholar] [CrossRef]
- Abad, G.; Rodriguez, M.Á.; Poza, J. Three-level NPC converter-based predictive direct power control of the doubly fed induction machine at low constant switching frequency. IEEE Trans. Ind. Electron. 2008, 55, 4417–4429. [Google Scholar] [CrossRef]
- Akagi, H.; Isozaki, K. A hybrid active filter for a three-phase 12-pulse diode rectifier used as the front end of a medium-voltage motor drive. IEEE Trans. Power Electron. 2011, 27, 69–77. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Mascarella, D.; Joós, G.; Cyr, J.-M.; Xu, J. A dual three-level T-NPC inverter for high-power traction applications. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 668–678. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Cao, J.; Cheng, M.; Hu, Y. Direct torque control of T-NPC inverters-fed double-stator-winding PMSM drives with SVM. IEEE Trans. Power Electron. 2017, 33, 1541–1553. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Cheng, M.; Hu, Y. Remedial strategies of T-NPC three-level asymmetric six-phase PMSM drives based on SVM-DTC. IEEE Trans. Ind. Electron. 2017, 64, 6841–6853. [Google Scholar] [CrossRef] [Green Version]
- McGrath, B.P.; Holmes, D.G. Natural capacitor voltage balancing for a flying capacitor converter induction motor drive. IEEE Trans. Power Electron. 2009, 24, 1554–1561. [Google Scholar] [CrossRef]
- Krug, D.; Bernet, S.; Fazel, S.S.; Jalili, K.; Malinowski, M. Comparison of 2.3-kV medium-voltage multilevel converters for industrial medium-voltage drives. IEEE Trans. Ind. Electron. 2007, 54, 2979–2992. [Google Scholar] [CrossRef]
- Anderson, J.A.; Zulauf, G.; Papamanolis, P.; Hobi, S.; Miric, S.; Kolar, J.W. Three levels are not enough: Scaling laws for multilevel converters in AC/DC applications. IEEE Trans. Power Electron. 2020, 36, 3967–3986. [Google Scholar] [CrossRef]
- Teymour, H.R.; Sutanto, D.; Muttaqi, K.M.; Ciufo, P. Solar PV and battery storage integration using a new configuration of a three-level NPC inverter with advanced control strategy. IEEE Trans. Energy Convers. 2014, 29, 354–365. [Google Scholar]
- Tabart, Q.; Vechiu, I.; Etxeberria, A.; Bacha, S. Hybrid energy storage system microgrids integration for power quality improvement using four-leg three-level NPC inverter and second-order sliding mode control. IEEE Trans. Ind. Electron. 2017, 65, 424–435. [Google Scholar] [CrossRef]
- Jayan, V.; Ghias, A.M. A Weighting Factor Free Model Predictive Control for a Flying Capacitor Converter in a DC Microgrid. IEEE Trans. Energy Convers. 2021. [Google Scholar] [CrossRef]
- Zheng, L.; Kandula, R.P.; Divan, D. Current-Source Solid-State DC Transformer Integrating LVDC Microgrid, Energy Storage, and Renewable Energy Into MVDC Grid. IEEE Trans. Power Electron. 2021, 37, 1044–1058. [Google Scholar] [CrossRef]
- Ljøkelsøy, K.; Guidi, G. Development of a scale model of a Modular Multilevel Converters. Energy Procedia 2017, 137, 505–513. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Li, J.; Liu, W. A modular multilevel DC-link front-to-front DC solid-state transformer based on high-frequency dual active phase shift for HVDC grid integration. IEEE Trans. Ind. Electron. 2016, 64, 8919–8927. [Google Scholar] [CrossRef]
- Mueller, N.; Kouro, S.; Malinowski, M.; Rojas, C.A.; Jasinski, M.; Estay, G. Medium-voltage power converter interface for multigenerator marine energy conversion systems. IEEE Trans. Ind. Electron. 2016, 64, 1061–1070. [Google Scholar] [CrossRef]
- Modeer, T.; Pallo, N.; Foulkes, T.; Barth, C.B.; Pilawa-Podgurski, R.C.N. Design of a gan-based interleaved nine-level flying capacitor multilevel inverter for electric aircraft applications. IEEE Trans. Power Electron. 2020, 35, 12153–12165. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, Z.; Li, Y.; Peng, L. A modular DC solid state transformer for future onboard DC grid. In Proceedings of the 2016 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Toulouse, France, 2–4 November 2016; pp. 1–6. [Google Scholar]
- Zhou, L.; Fu, Q.; Li, X.; Liu, C. A novel multilevel power quality compensator for electrified railway. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 1141–1147. [Google Scholar]
- Youssef, M.Z.; Woronowicz, K.; Aditya, K.; Azeez, N.A.; Williamson, S.S. Design and development of an efficient multilevel DC/AC traction inverter for railway transportation electrification. IEEE Trans. Power Electron. 2016, 31, 3036–3042. [Google Scholar] [CrossRef]
- Ge, X.; Pu, J.; Gou, B.; Liu, Y.-C. An open-circuit fault diagnosis approach for single-phase three-level neutral-point-clamped converters. IEEE Trans. Power Electron. 2017, 33, 2559–2570. [Google Scholar] [CrossRef]
- Han, P.; He, X.; Ren, H.; Wang, Y.; Peng, X.; Shu, Z.; Gao, S.; Wang, Y.; Chen, Z. Fault diagnosis and system reconfiguration strategy of a single-phase three-level neutral-point-clamped cascaded inverter. IEEE Trans. Ind. Appl. 2019, 55, 3863–3876. [Google Scholar] [CrossRef]
- Zhao, C.; Dujic, D.; Mester, A.; Steinke, J.K.; Weiss, M.; Lewdeni-Schmid, S.; Chaudhuri, T.; Stefanutti, P. Power electronic traction transformer—Medium voltage prototype. IEEE Trans. Ind. Electron. 2013, 61, 3257–3268. [Google Scholar] [CrossRef]
- Kang, F.; Cho, S.E.; Park, S.-J.; Kim, C.-U.; Ise, T. A new control scheme of a cascaded transformer type multilevel PWM inverter for a residential photovoltaic power conditioning system. Sol. Energy 2005, 78, 727–738. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, T.; Mao, W.; Tan, D.; Chang, L. Multilevel inverters for grid-connected photovoltaic applications: Examining emerging trends. IEEE Power Electron. Mag. 2018, 5, 32–41. [Google Scholar] [CrossRef]
- Li, Y.; Yang, X.; Chen, W.; Liu, T.; Zhang, F. Neutral-point voltage analysis and suppression for NPC three-level photovoltaic converter in LVRT operation under imbalanced grid faults with selective hybrid SVPWM strategy. IEEE Trans. Power Electron. 2018, 34, 1334–1355. [Google Scholar] [CrossRef]
- Duman, T.; Marti, S.; Moonem, M.; Kader, A.; Rifath, A.A.; Krishnaswami, H. A modular multilevel converter with power mismatch control for grid-connected photovoltaic systems. Energies 2017, 10, 698. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Mu, X.; Li, Q.-K. Study of passivity-based decoupling control of T-NPC PV grid-connected inverter. IEEE Trans. Ind. Electron. 2017, 64, 7542–7551. [Google Scholar] [CrossRef]
- Wu, Y.; Zeng, G.; Liu, J.; Song, G.; Sun, J. Design and Implementation of a 125kW T-NPC PV Inverter. In Proceedings of the PCIM Asia 2015; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Shanghai, China, 24–26 June 2015; pp. 1–8. [Google Scholar]
- Alyami, S.; Sathik, M.J.; Almakhles, D.; Almutairi, A.; Obeidat, M. Seven Level T-Type Switched Capacitor Inverter Topology For PV Applications. IEEE Access 2021, 9, 85049–85059. [Google Scholar] [CrossRef]
- Fujii, K.; Noto, Y.; Okuma, Y. 1-MW solar power inverter with boost converter using all SiC power module. EPE J. 2016, 26, 165–173. [Google Scholar] [CrossRef]
- Madasamy, P.; Suresh Kumar, V.; Sanjeevikumar, P.; Holm-Nielsen, J.B.; Hosain, E.; Bharatiraja, C. A three-phase transformerless T-Type-NPC-MLI for grid connected PV systems with common-mode leakage current mitigation. Energies 2019, 12, 2434. [Google Scholar] [CrossRef] [Green Version]
- Anderson, J.A.; Hanak, E.J.; Schrittwieser, L.; Guacci, M.; Kolar, J.W.; Deboy, G. All-silicon 99.35% efficient three-phase seven-level hybrid neutral point clamped/flying capacitor inverter. CPSS Trans. Power Electron. Appl. 2019, 4, 50–61. [Google Scholar] [CrossRef]
- Park, S.-J.; Kang, F.-S.; Cho, S.E.; Moon, C.-J.; Nam, H.-K. A novel switching strategy for improving modularity and manufacturability of cascaded-transformer-based multilevel inverters. Electr. Power Syst. Res. 2005, 74, 409–416. [Google Scholar] [CrossRef]
- Tiwari, R.; Nilsen, R.; Nysveen, A. Active NPC Converter for Variable Speed Operation of Pumped Storage Hydropower Plant. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 19–21 October 2020; pp. 1211–1216. [Google Scholar]
- Desingu, K.; Selvaraj, R.; Chelliah, T.R.; Khare, D. Effective utilization of parallel-connected megawatt three-level back-to-back power converters in variable speed pumped storage units. IEEE Trans. Ind. Appl. 2019, 55, 6414–6426. [Google Scholar] [CrossRef]
- Bueno, E.J.; Cobreces, S.; RodrÍguez, F.J.; Hernandez, A.; Espinosa, F. Design of a back-to-back NPC converter interface for wind turbines with squirrel-cage induction generator. IEEE Trans. Energy Convers. 2008, 23, 932–945. [Google Scholar] [CrossRef]
- Senturk, O.S.; Helle, L.; Munk-Nielsen, S.; Rodriguez, P.; Teodorescu, R. Power capability investigation based on electrothermal models of press-pack IGBT three-level NPC and ANPC VSCs for multimegawatt wind turbines. IEEE Trans. Power Electron. 2012, 27, 3195–3206. [Google Scholar] [CrossRef]
- Eedara, A.K.; Koritala, C.S.; Rayapudi, S.R. Modified model predictive control of back-to-back T-type NPC converter interfacing wind turbine-driven PMSG and electric grid. Arab. J. Sci. Eng. 2019, 44, 7047–7065. [Google Scholar] [CrossRef]
- Lee, J.-S.; Lee, K.-B. Open-switch fault tolerance control for a three-level NPC/T-type rectifier in wind turbine systems. IEEE Trans. Ind. Electron. 2014, 62, 1012–1021. [Google Scholar] [CrossRef]
- Boumediene, B.; Smaili, A.; Allaoui, T.; Berkani, A.; Marignetti, F. Backstepping Control Strategy for Multi-source Energy System based Flying capacitor Inverter and PMSG. Przeglkad Elektrotechniczny 2021, 97, 21–29. [Google Scholar] [CrossRef]
- Gao, R.; Husain, I.; Wang, F.; Huang, A.Q. Solid-state transformer interfaced PMSG wind energy conversion system. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 1310–1317. [Google Scholar]
- She, X.; Huang, A.Q.; Wang, F.; Burgos, R. Wind energy system with integrated functions of active power transfer, reactive power compensation, and voltage conversion. IEEE Trans. Ind. Electron. 2012, 60, 4512–4524. [Google Scholar] [CrossRef]
- Gao, R.; She, X.; Husain, I.; Huang, A.Q. Solid-state-transformer-interfaced permanent magnet wind turbine distributed generation system with power management functions. IEEE Trans. Ind. Appl. 2017, 53, 3849–3861. [Google Scholar] [CrossRef]
- Ye, Y.; Zhang, G.; Huang, J.; Chen, S.; Wang, X. Comparative Analysis of Hybrid NPP and NPC Seven-Level Inverter with Switched-Capacitor. IEEE Access 2021, 9, 85852–85863. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, J.; Ma, G.; Sun, Z.; Liu, K.; Yao, C. Operation of a Seven-Level T-Type Active Neutral-Point-Clamped Converter with Modified Level-Shifted PWM. IEEE Trans. Ind. Electron. 2020, 68, 10970–10981. [Google Scholar] [CrossRef]
- McGrath, B.P.; Holmes, D.G. Analytical modelling of voltage balance dynamics for a flying capacitor multilevel converter. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 1810–1816. [Google Scholar]
- Feng, C.; Liang, J.; Agelidis, V.G. Modified phase-shifted PWM control for flying capacitor multilevel converters. IEEE Trans. Power Electron. 2007, 22, 178–185. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Corzine, K.A. Extended operation of flying capacitor multilevel inverters. IEEE Trans. Power Electron. 2006, 21, 140–147. [Google Scholar] [CrossRef]
- Obara, H.; Ohno, T.; Katayama, M.; Kawamura, A. Flying-Capacitor Linear Amplifier With Capacitor Voltage Balancing for High-Efficiency and Low Distortion. IEEE Trans. Ind. Appl. 2020, 57, 614–627. [Google Scholar] [CrossRef]
- Medium Voltage Wind Converters: ABB wind turbine converters PCS6000, full power converter, up to 12 MW. Manuf. ABB 2019.
- Multilevel Technology with ALSPA VDM; Alstom: Saint-Ouen, France, 2000.
- Wang, J.; Liang, J.; Gao, F.; Dong, X.; Wang, C.; Zhao, B. A closed-loop time-domain analysis method for modular multilevel converter. IEEE Trans. Power Electron. 2016, 32, 7494–7508. [Google Scholar] [CrossRef]
- Wang, D.; Tian, J.; Mao, C.; Lu, J.; Duan, Y.; Qiu, J.; Cai, H. A 10-kV/400-V 500-kVA electronic power transformer. IEEE Trans. Ind. Electron. 2016, 63, 6653–6663. [Google Scholar] [CrossRef]
- Du, S.; Wu, B.; Zargari, N.R.; Cheng, Z. A flying-capacitor modular multilevel converter for medium-voltage motor drive. IEEE Trans. Power Electron. 2016, 32, 2081–2089. [Google Scholar] [CrossRef]
- Delta MVD3000 Series: Medium Voltage Drive; Manufacturer: Delta Group: Tokyo, Japan, 2013.
- Engel, B.; Victor, M.; Bachmann, G.; Falk, A. 15 kV/16.7 Hz energy supply system with medium frequency transformer and 6.5 kV IGBTs in resonant operation. In Proceedings of the 10th European Conference on Power Electronics and Applications, EPE 2003, Toulouse, France, 2–4 September 2003; pp. 2–4. [Google Scholar]
- Steiner, M.; Reinold, H. Medium frequency topology in railway applications. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–10. [Google Scholar]
- Hugo, N.; Stefanutti, P.; Pellerin, M.; Akdag, A. Power electronics traction transformer. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–10. [Google Scholar]
- Dujic, D.; Mester, A.; Chaudhuri, T.; Coccia, A.; Canales, F.; Steinke, J.K. Laboratory scale prototype of a power electronic transformer for traction applications. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–10. [Google Scholar]
- Li, B.; Zhou, S.; Xu, D.; Finney, S.J.; Williams, B.W. A hybrid modular multilevel converter for medium-voltage variable-speed motor drives. IEEE Trans. Power Electron. 2016, 32, 4619–4630. [Google Scholar] [CrossRef] [Green Version]
- Delta MVD 1000 Series: Medium Voltage Drive; Manufacturer: Delta Group: Tokyo, Japan, 2014.
- Steurer, M.; Bogdan, F.; Bosworth, M.; Faruque, O.; Hauer, J.; Schoder, K.; Sloderbeck, M.; Soto, D.; Sun, K.; Winkelnkemper, M.; et al. Multifunctional megawatt scale medium voltage DC test bed based on modular multilevel converter (MMC) technology. In Proceedings of the 2015 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles (ESARS), Aachen, Germany, 3–5 March 2015; pp. 1–6. [Google Scholar]
- Christe, A.; Coulinge, E.; Dujic, D. Insulation coordination for a modular multilevel converter prototype. In Proceedings of the 2016 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016; pp. 1–9. [Google Scholar]
- Glinka, M. Prototype of multiphase modular-multilevel-converter with 2 MW power rating and 17-level-output-voltage. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No. 04CH37551), Aachen, Germany, 20–25 June 2004; Volume 4, pp. 2572–2576. [Google Scholar]
- Park, C.-H.; Negesse, B.B.; Kim, J.-M.; Kim, C.-K. Back-to-back 31 level modular multilevel converter with EtherCAT communication. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 1032–1039. [Google Scholar]
- Verdugo, C.; Kouro, S.; Rojas, C.A.; Perez, M.A.; Meynard, T.; Malinowski, M. Five-level T-type cascade converter for rooftop grid-connected photovoltaic systems. Energies 2019, 12, 1743. [Google Scholar] [CrossRef] [Green Version]
- Tu, P.; Yang, S.; Wang, P. Reliability-and cost-based redundancy design for modular multilevel converter. IEEE Trans. Ind. Electron. 2018, 66, 2333–2342. [Google Scholar] [CrossRef]
- He, J.; Chen, K.; Li, M.; Luo, Y.; Liang, C.; Xu, Y. Review of protection and fault handling for a flexible DC grid. Prot. Control Mod. Power Syst. 2020, 5, 1–15. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.; Yang, R.; Xu, R.; Xu, D.; Wang, W. Seamless transition control for modular multilevel converters when inserting a cold-reserve redundant submodule. IEEE Trans. Power Electron. 2015, 30, 4052–4057. [Google Scholar] [CrossRef]
- Li, J.; Yin, J. Fault-tolerant control strategies and capability without redundant sub-modules in modular multilevel converters. Energies 2019, 12, 1726. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Yuan, L.; Zhao, Z.; Lu, S.; Zhang, Y. Fault-tolerant control of MMC with hot reserved submodules based on carrier phase shift modulation. IEEE Trans. Power Electron. 2016, 32, 6778–6791. [Google Scholar] [CrossRef]
- Hu, P.; Jiang, D.; Zhou, Y.; Liang, Y.; Guo, J.; Lin, Z. Energy-balancing control strategy for modular multilevel converters under submodule fault conditions. IEEE Trans. Power Electron. 2013, 29, 5021–5030. [Google Scholar] [CrossRef]
- Aguayo-Alquicira, J.; Vásquez-Libreros, I.; Léon-Aldaco, D.; Estefany, S.; Ponce-Silva, M.; Lozoya-Ponce, R.E.; Flores-Rodr’\iguez, E.; Garc’\ia-Morales, J.; Reyes-Severiano, Y.; Carrillo-Santos, L.M.; et al. Reconfiguration Strategy for Fault Tolerance in a Cascaded Multilevel Inverter Using a Z-Source Converter. Electronics 2021, 10, 574. [Google Scholar] [CrossRef]
- Kang, J.; Kim, H.; Jung, H.-J.; Lee, D.-S.; Kim, C.-K.; Mantooth, H.A.; Hur, K. On exploiting active redundancy of a modular multilevel converter to balance reliability and operational flexibility. IEEE Trans. Power Electron. 2018, 34, 2234–2243. [Google Scholar] [CrossRef]
- Yang, Q.; Qin, J.; Saeedifard, M. Analysis, detection, and location of open-switch submodule failures in a modular multilevel converter. IEEE Trans. Power Deliv. 2015, 31, 155–164. [Google Scholar] [CrossRef]
- Campos-Delgado, D.U.; Espinoza-Trejo, D.R. An observer-based diagnosis scheme for single and simultaneous open-switch faults in induction motor drives. IEEE Trans. Ind. Electron. 2010, 58, 671–679. [Google Scholar] [CrossRef]
- Deng, F.; Chen, Z.; Khan, M.R.; Zhu, R. Fault detection and localization method for modular multilevel converters. IEEE Trans. Power Electron. 2014, 30, 2721–2732. [Google Scholar] [CrossRef]
- Li, B.; Shi, S.; Wang, B.; Wang, G.; Wang, W.; Xu, D. Fault diagnosis and tolerant control of single IGBT open-circuit failure in modular multilevel converters. IEEE Trans. Power Electron. 2015, 31, 3165–3176. [Google Scholar] [CrossRef]
- Shao, S.; Wheeler, P.W.; Clare, J.C.; Watson, A.J. Fault detection for modular multilevel converters based on sliding mode observer. IEEE Trans. Power Electron. 2013, 28, 4867–4872. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Zhang, Y.; Yang, R.; Wang, G.; Xu, D. An IGBT open-circuit fault detection method for modular multilevel converters. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Korea, 1–5 June 2015; pp. 1573–1578. [Google Scholar]
- Tang, S.; Wang, J.; Zheng, R.; Wang, D.; Zhang, C.; Yin, X.; Shuai, Z.; Shen, Z.J. Detection and Identification of Power Switch Failures Using Discrete Fourier Transform for DC-DC Flying Capacitor Buck Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 4062–4071. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, X.; Tolbert, L.M.; Wang, F.; Blalock, B.J. A di/dt feedback-based active gate driver for smart switching and fast overcurrent protection of IGBT modules. IEEE Trans. Power Electron. 2013, 29, 3720–3732. [Google Scholar] [CrossRef]
- Rodriguez-Blanco, M.A.; Claudio-Sanchez, A.; Theilliol, D.; Vela-Valdés, L.G.; Sibaja-Terán, P.; Hernández-González, L.; Aguayo-Alquicira, J. A failure-detection strategy for IGBT based on gate-voltage behavior applied to a motor drive system. IEEE Trans. Ind. Electron. 2010, 58, 1625–1633. [Google Scholar] [CrossRef]
- Abdelsalam, M.; Marei, M.I.; Tennakoon, S.B. An integrated control strategy with fault detection and tolerant control capability based on capacitor voltage estimation for modular multilevel converters. IEEE Trans. Ind. Appl. 2016, 53, 2840–2851. [Google Scholar] [CrossRef]
- Yaqobi, M.A.; Matayoshi, H.; Danish, M.S.S.; Lotfy, M.E.; Howlader, A.M.; Tomonobu, S. Low-voltage solid-state DC breaker for fault protection applications in isolated DC microgrid cluster. Appl. Sci. 2019, 9, 723. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Xu, J.; Lu, Y.; Zhao, C.; Zhang, J.; Jiang, C.; Qiu, S. An auxiliary DC circuit breaker utilizing an augmented MMC. IEEE Trans. Power Deliv. 2019, 34, 561–571. [Google Scholar] [CrossRef]
- Salimian, H.; Iman-Eini, H. Fault-tolerant operation of three-phase cascaded H-bridge converters using an auxiliary module. IEEE Trans. Ind. Electron. 2016, 64, 1018–1027. [Google Scholar] [CrossRef]
- Ahmed, N.; Ängquist, L.; Antonopoulos, A.; Harnefors, L.; Norrga, S.; Nee, H.-P. Performance of the modular multilevel converter with redundant submodules. In Proceedings of the IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 003922–003927. [Google Scholar]
- Lu, B.; Sharma, S.K. A literature review of IGBT fault diagnostic and protection methods for power inverters. IEEE Trans. Ind. Appl. 2009, 45, 1770–1777. [Google Scholar]
- Li, C.; Gole, A.M.; Zhao, C. A fast DC fault detection method using DC reactor voltages in HVdc grids. IEEE Trans. Power Deliv. 2018, 33, 2254–2264. [Google Scholar] [CrossRef]
- Jiang, W.; Zhu, C.; Xue, S.; Ren, K.; Yang, C. DC-Side-Fault-Tolerant Control of a Battery-Supercapacitor Hybrid Energy Storage System Based on Cascaded Multilevel Converter and Auxiliary Power Loop. IEEE Trans. Ind. Electron. 2019, 67, 7451–7460. [Google Scholar] [CrossRef]
- Anurag, A.; Acharya, S.; Prabowo, Y.; Gohil, G.; Bhattacharya, S. Design considerations and development of an innovative gate driver for medium-voltage power devices with high dv/dt. IEEE Trans. Power Electron. 2018, 34, 5256–5267. [Google Scholar] [CrossRef]
- Nguyen, V.-S.; Lefranc, P.; Crebier, J.-C. Gate driver supply architectures for common mode conducted EMI reduction in series connection of multiple power devices. IEEE Trans. Power Electron. 2018, 33, 10265–10276. [Google Scholar] [CrossRef]
- Ye, Z.; Lei, Y.; Liu, W.-C.; Shenoy, P.S.; Pilawa-Podgurski, R.C. Improved bootstrap methods for powering floating gate drivers of flying capacitor multilevel converters and hybrid switched-capacitor converters. IEEE Trans. Power Electron. 2019, 35, 5965–5977. [Google Scholar] [CrossRef]
- Darbas, C.; Olivier, J.-C.; Ginot, N.; Poitiers, F.; Batard, C. Cascaded Smart Gate Drivers for Modular Multilevel Converters Control: A Decentralized Voltage Balancing Algorithm. Energies 2021, 14, 3589. [Google Scholar] [CrossRef]
- Corentin, D.; Nicolas, G.; Jean-Christophe, O.; Frédèric, P. Modular Multilevel Converter with Distributed Galvanic Isolation: A Decentralized Voltage Balancing Algorithm with Smart Gate Drivers. In Proceedings of the 2020 22nd European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), Lyon, France, 7–11 September 2020; pp. 1–10. [Google Scholar]
- Busquets-Monge, S.; Rocabert, J.; Crebier, J.-C.; Peracaula, J. Diode-clamped multilevel converters with integrable gate-driver power-supply circuits. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar]
- Crébier, J.-C.; Rouger, N. Loss free gate driver unipolar power supply for high side power transistors. IEEE Trans. Power Electron. 2008, 23, 1565–1573. [Google Scholar] [CrossRef]
- Ghossein, L.; Morel, F.; Morel, H.; Dworakowski, P. State of the art of gate-drive power supplies for medium and high voltage applications. In Proceedings of the PCIM Europe 2016; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 10–12 May 2016; pp. 1–8. [Google Scholar]
- Zhang, X.; Li, H.; Brothers, J.A.; Wang, J.; Fu, L.; Perales, M.; Wu, J. A 15 kV SiC MOSFET gate drive with power over fiber based isolated power supply and comprehensive protection functions. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 1967–1973. [Google Scholar]
- Fujita, H. A resonant gate-drive circuit with optically isolated control signal and power supply for fast-switching and high-voltage power semiconductor devices. IEEE Trans. Power Electron. 2013, 28, 5423–5430. [Google Scholar] [CrossRef]
- Christe, A.; Polanco Lobos, I.A.; Petkovic, M.; Utvic, M.; Dujic, D. Auxiliary submodule power supply for a medium voltage modular multilevel converter. CPSS Trans. Power Electron. Appl. 2019, 4, 204–2018. [Google Scholar] [CrossRef]
- He, Q.; Zhu, Y.; Zhang, H.; Huang, A.; Cai, Q.-M.; Kim, H. A multilevel gate driver of SiC MOSFET s for mitigating coupling noise in bridge-leg converter. IEEE Trans. Electromagn. Compat. 2019, 61, 1988–1996. [Google Scholar] [CrossRef]
- Sochor, P.; Akagi, H. Theoretical and experimental comparison between phase-shifted PWM and level-shifted PWM in a modular multilevel SDBC inverter for utility-scale photovoltaic applications. IEEE Trans. Ind. Appl. 2017, 53, 4695–4707. [Google Scholar] [CrossRef]
- Tolbert, L.M.; Habetler, T.G. Novel multilevel inverter carrier-based PWM method. IEEE Trans. Ind. Appl. 1999, 35, 1098–1107. [Google Scholar] [CrossRef]
- Mo, R.; Li, H.; Shi, Y. A phase-shifted square wave modulation (PS-SWM) for modular multilevel converter (MMC) and DC transformer for medium voltage applications. IEEE Trans. Power Electron. 2018, 34, 6004–6008. [Google Scholar] [CrossRef]
- Xing, Z.; Ruan, X.; You, H.; Yang, X.; Yao, D.; Yuan, C. Soft-switching operation of isolated modular DC/DC converters for application in HVDC grids. IEEE Trans. Power Electron. 2015, 31, 2753–2766. [Google Scholar] [CrossRef]
- Agarwal, R.; Martin, S.; Li, H. Influence of Phase-Shifted Square Wave Modulation on Medium Frequency Transformer in a MMC Based SST. IEEE Access 2020, 8, 221093–221102. [Google Scholar] [CrossRef]
- Sha, G.; Duan, Q.; Sheng, W.; Ma, C.; Zhao, C.; Zhang, Y.; Tian, J. Research on Multi-Port DC-DC Converter Based on Modular Multilevel Converter and Cascaded H Bridges for MVDC Applications. IEEE Access 2021, 9, 95006–95022. [Google Scholar] [CrossRef]
- Ahmad, Y.; Pinto, S.F. Cascade multilevel STATCOM as a solution to improve the voltage profile of a power grid. In Proceedings of the 2018 International Young Engineers Forum (YEF-ECE), Costa da Caparica, Portugal, 4 May 2018; pp. 109–114. [Google Scholar]
- Zhao, F.; Xiao, G.; Liu, M.; Yang, D. A fast sorting strategy based on a two-way merge sort for balancing the capacitor voltages in modular multilevel converters. J. Power Electron. 2017, 17, 346–357. [Google Scholar] [CrossRef] [Green Version]
- Matar, M.; Paradis, D.; Iravani, R. FPGA-based implementation of modular multilevel converter model for real-time simulation of electromagnetic transients. In Proceedings of the International Conference on Power Systems Transients (IPST), Vancouver, BC, Canada, 18–20 July 2013. [Google Scholar]
- Bandaru, T.; Bhattacharya, T.; Chatterjee, D. Modified predictive sorting algorithm for full-bridge MMC in HVDC application. In Proceedings of the 2017 National Power Electronics Conference (NPEC), Pune, India, 18–20 December 2017; pp. 178–184. [Google Scholar]
- Qu, L.-P.; Lu, Z.; Liu, C.-J.; He, C.-L. A sort method of balancing capacitor voltage of mmc. In Proceedings of the 2019 18th International Symposium on Distributed Computing and Applications for Business Engineering and Science (DCABES), Wuhan, China, 8–10 November 2019; pp. 241–244. [Google Scholar]
- Joshi, S.D.; Ghat, M.B.; Shukla, A.; Chandorkar, M.C. Improved Balancing and Sensing of Submodule Capacitor Voltages in Modular Multilevel Converter. IEEE Trans. Ind. Appl. 2020, 57, 537–548. [Google Scholar] [CrossRef]
- Siemaszko, D. Fast sorting method for balancing capacitor voltages in modular multilevel converters. IEEE Trans. Power Electron. 2014, 30, 463–470. [Google Scholar] [CrossRef]
- Peng, H.; Xie, R.; Wang, K.; Deng, Y.; He, X.; Zhao, R. A capacitor voltage balancing method with fundamental sorting frequency for modular multilevel converters under staircase modulation. IEEE Trans. Power Electron. 2016, 31, 7809–7822. [Google Scholar] [CrossRef]
- Wang, K.; Deng, Y.; Peng, H.; Chen, G.; Li, G.; He, X. An improved CPS-PWM scheme-based voltage balancing strategy for MMC with fundamental frequency sorting algorithm. IEEE Trans. Ind. Electron. 2018, 66, 2387–2397. [Google Scholar] [CrossRef]
- Hu, P.; Teodorescu, R.; Wang, S.; Li, S.; Guerrero, J.M. A currentless sorting and selection-based capacitor-voltage-balancing method for modular multilevel converters. IEEE Trans. Power Electron. 2018, 34, 1022–1025. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Qin, J.; Zou, Y.; Duan, Q.; Sheng, W. Analysis of Capacitor Charging Characteristics and Low-Frequency Ripple Mitigation by Two New Voltage-Balancing Strategies for MMC-Based Solid-State Transformers. IEEE Trans. Power Electron. 2020, 36, 1004–1017. [Google Scholar] [CrossRef]
- Dekka, A.; Wu, B.; Zargari, N.R.; Fuentes, R.L. A space-vector PWM-based voltage-balancing approach with reduced current sensors for modular multilevel converter. IEEE Trans. Ind. Electron. 2016, 63, 2734–2745. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, Y.; Teo, K.H.; Harley, R.G. A simplified space vector modulation scheme for multilevel converters. IEEE Trans. Power Electron. 2015, 31, 1873–1886. [Google Scholar] [CrossRef]
- Babu, N.; Agarwal, P. Space vector modulation for three-level NPC inverter using two-level space vector diagram. In Proceedings of the 2016 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Trivandrum, India, 14–17 December 2016; pp. 1–6. [Google Scholar]
- Leon, J.I.; Vazquez, S.; Sanchez, J.A.; Portillo, R.; Franquelo, L.G.; Carrasco, J.M.; Dominguez, E. Conventional space-vector modulation techniques versus the single-phase modulator for multilevel converters. IEEE Trans. Ind. Electron. 2009, 57, 2473–2482. [Google Scholar] [CrossRef]
- Leon, J.I.; Portillo, R.; Vazquez, S.; Padilla, J.J.; Franquelo, L.G.; Carrasco, J.M. Simple unified approach to develop a time-domain modulation strategy for single-phase multilevel converters. IEEE Trans. Ind. Electron. 2008, 55, 3239–3248. [Google Scholar] [CrossRef]
- Tahir, S.; Wang, J.; Baloch, M.H.; Kaloi, G.S. Digital control techniques based on voltage source inverters in renewable energy applications: A review. Electronics 2018, 7, 18. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, D.; Costa, R.; Barros, L.A.M.; Pedrosa, D.; Pinto, J.G. A Comprehensive Comparison of Voltage and Current Control Techniques for Three-Phase VSI Converters. In Proceedings of the EAI SESC 2021—3rd EAI International Conference on Sustainable Energy for Smart Cities, Virtual Event, 24–26 November 2021. [Google Scholar]


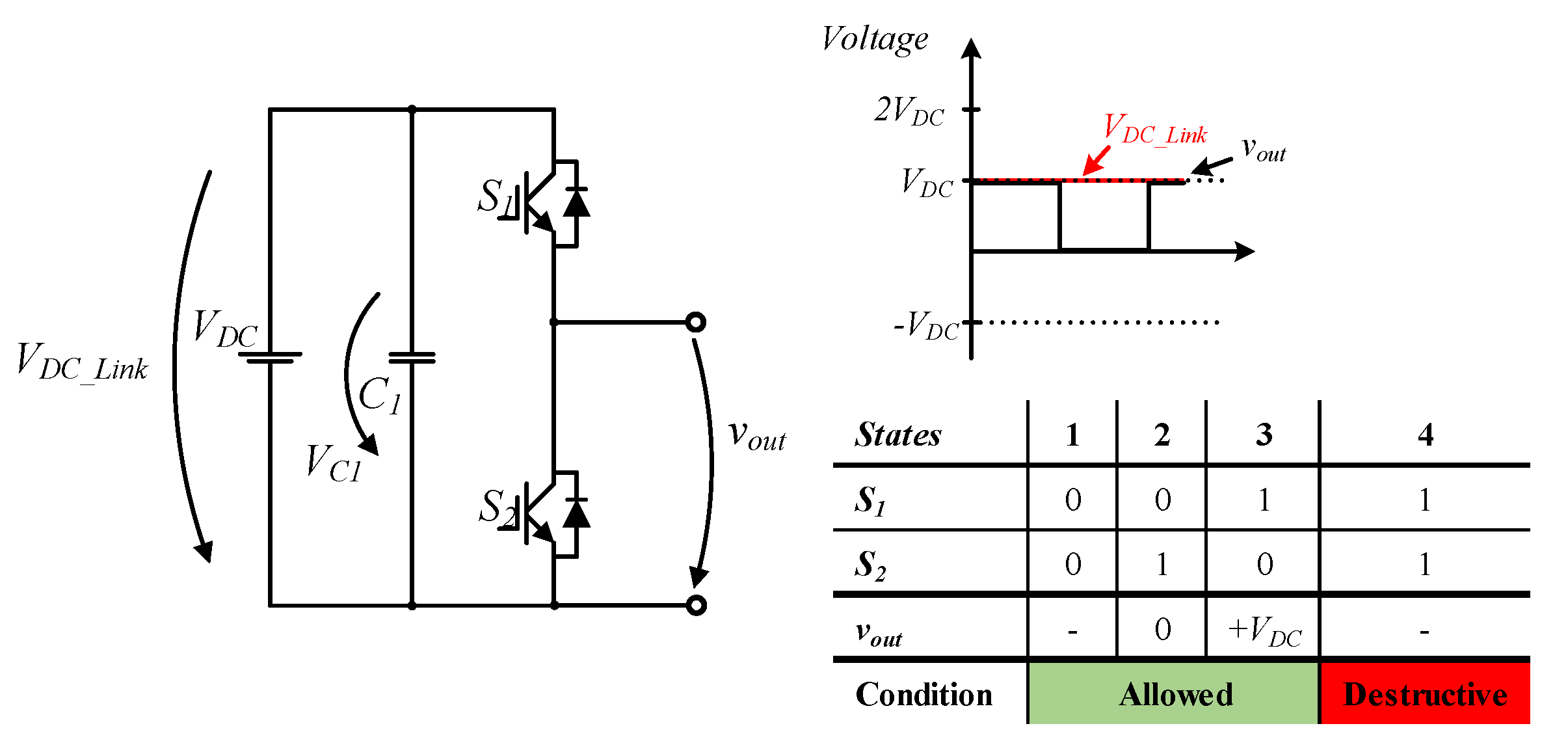
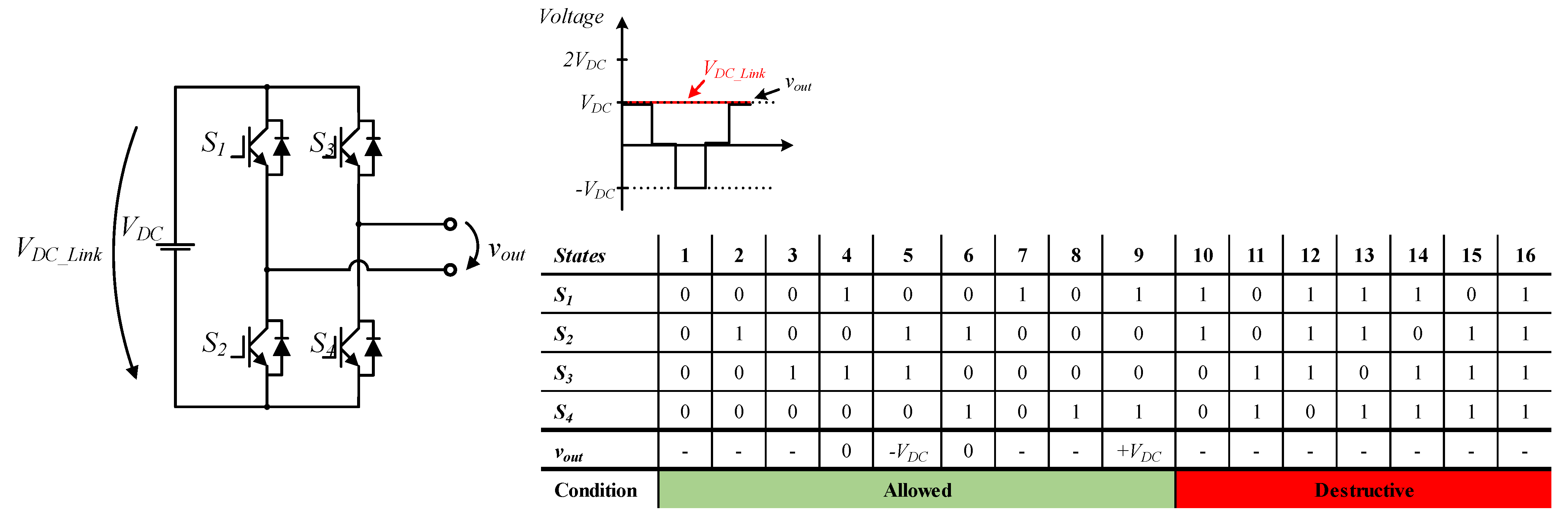
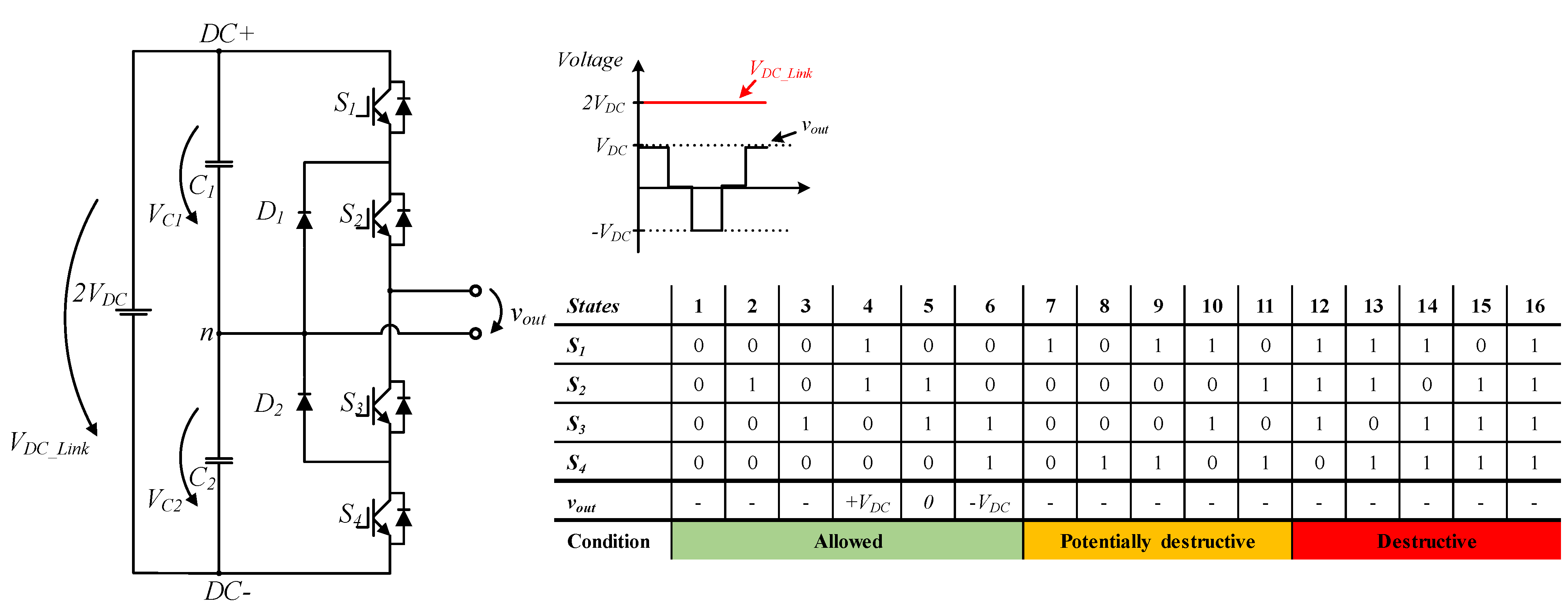
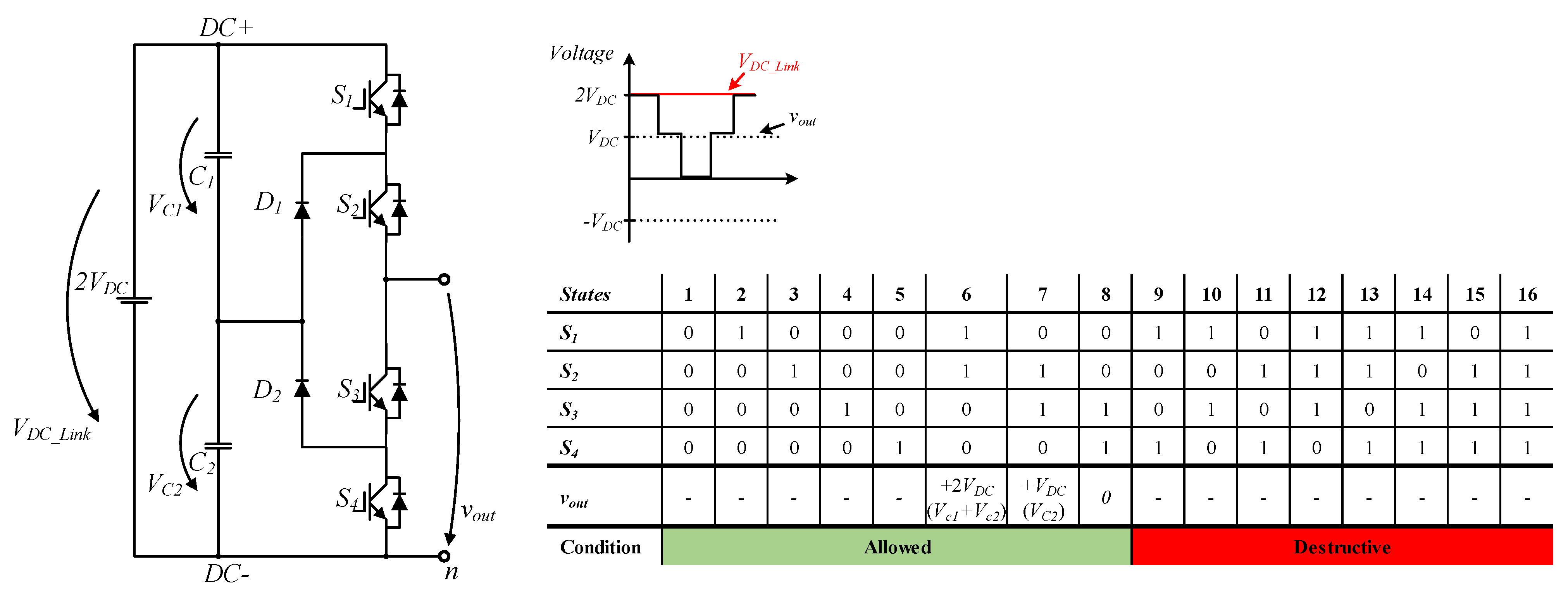

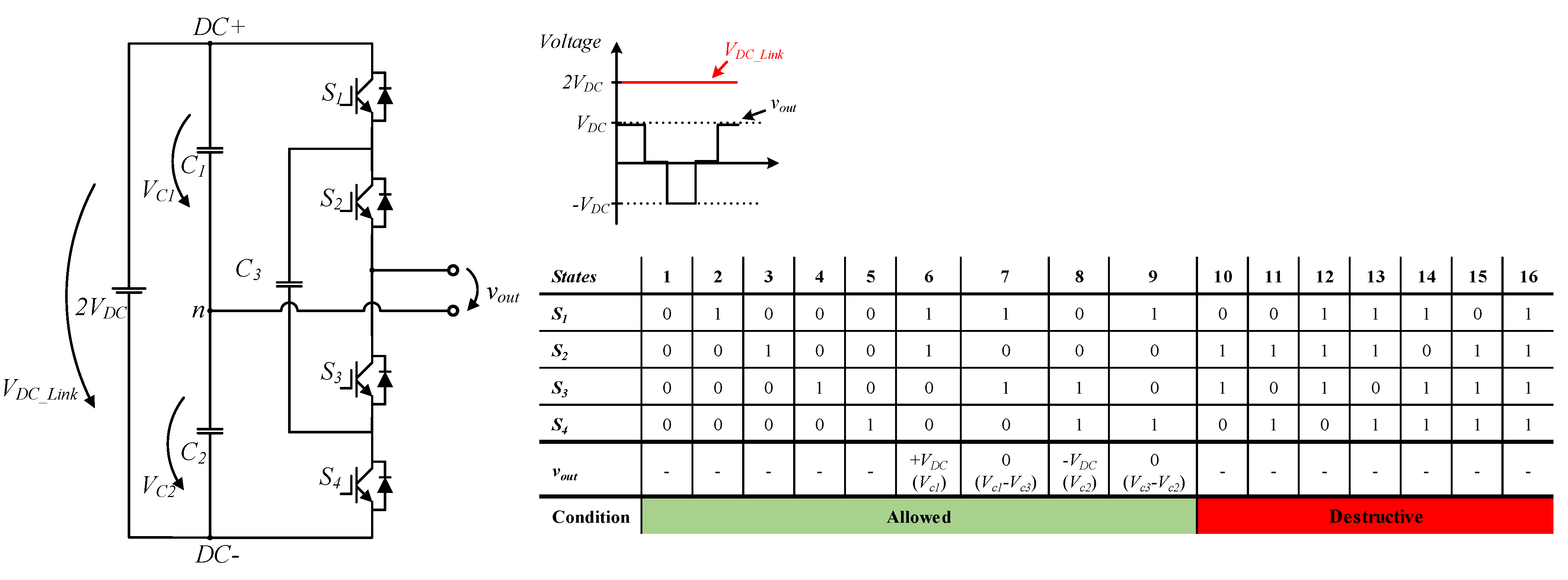
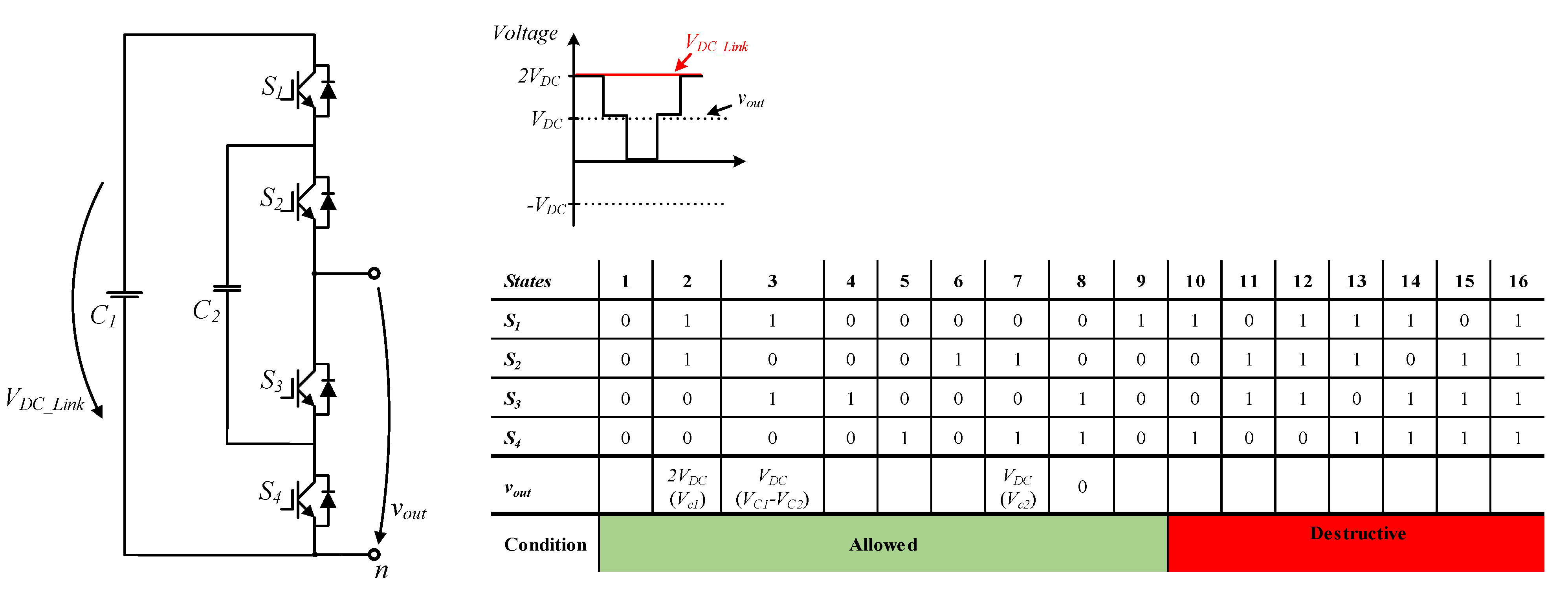



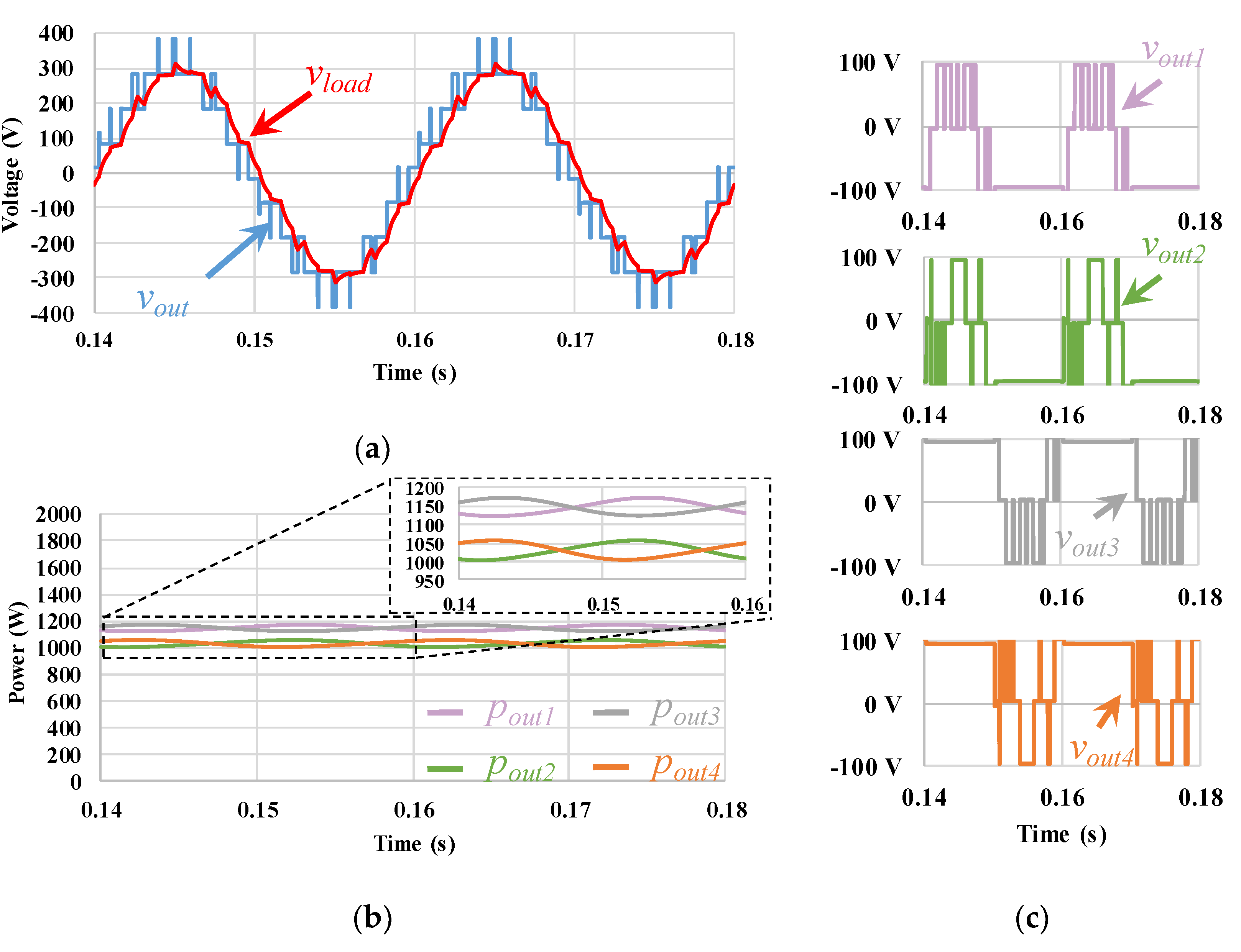

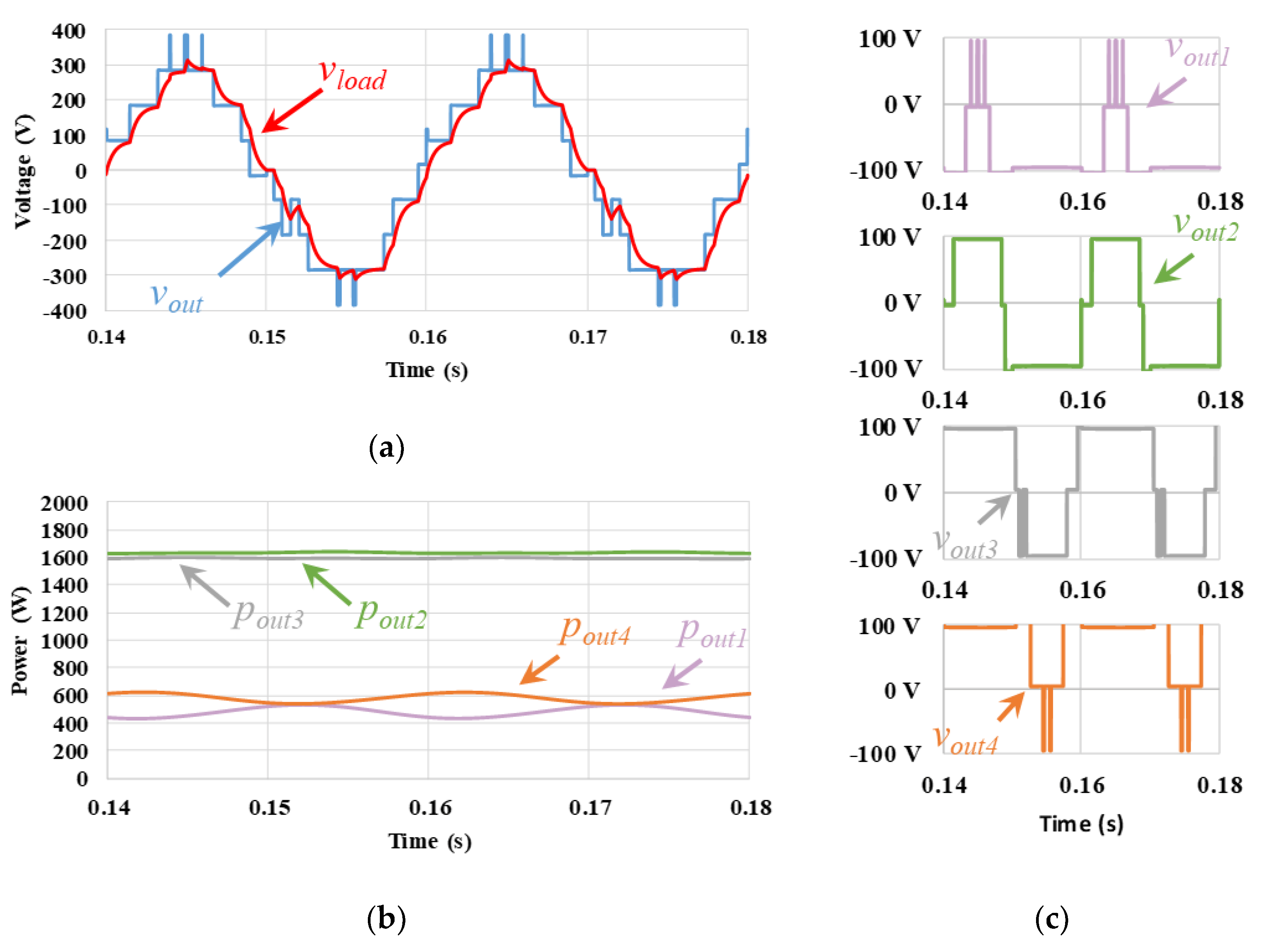
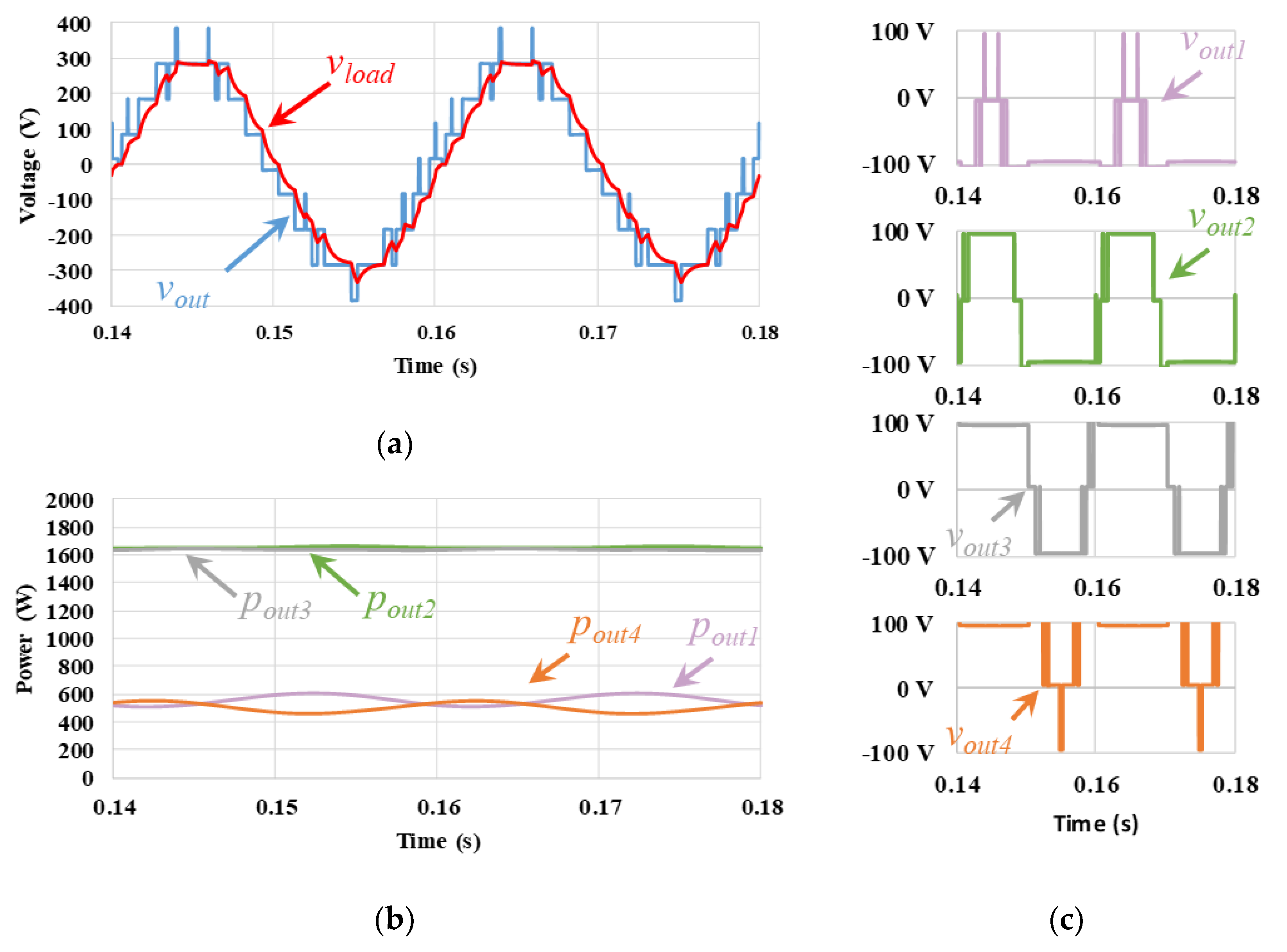
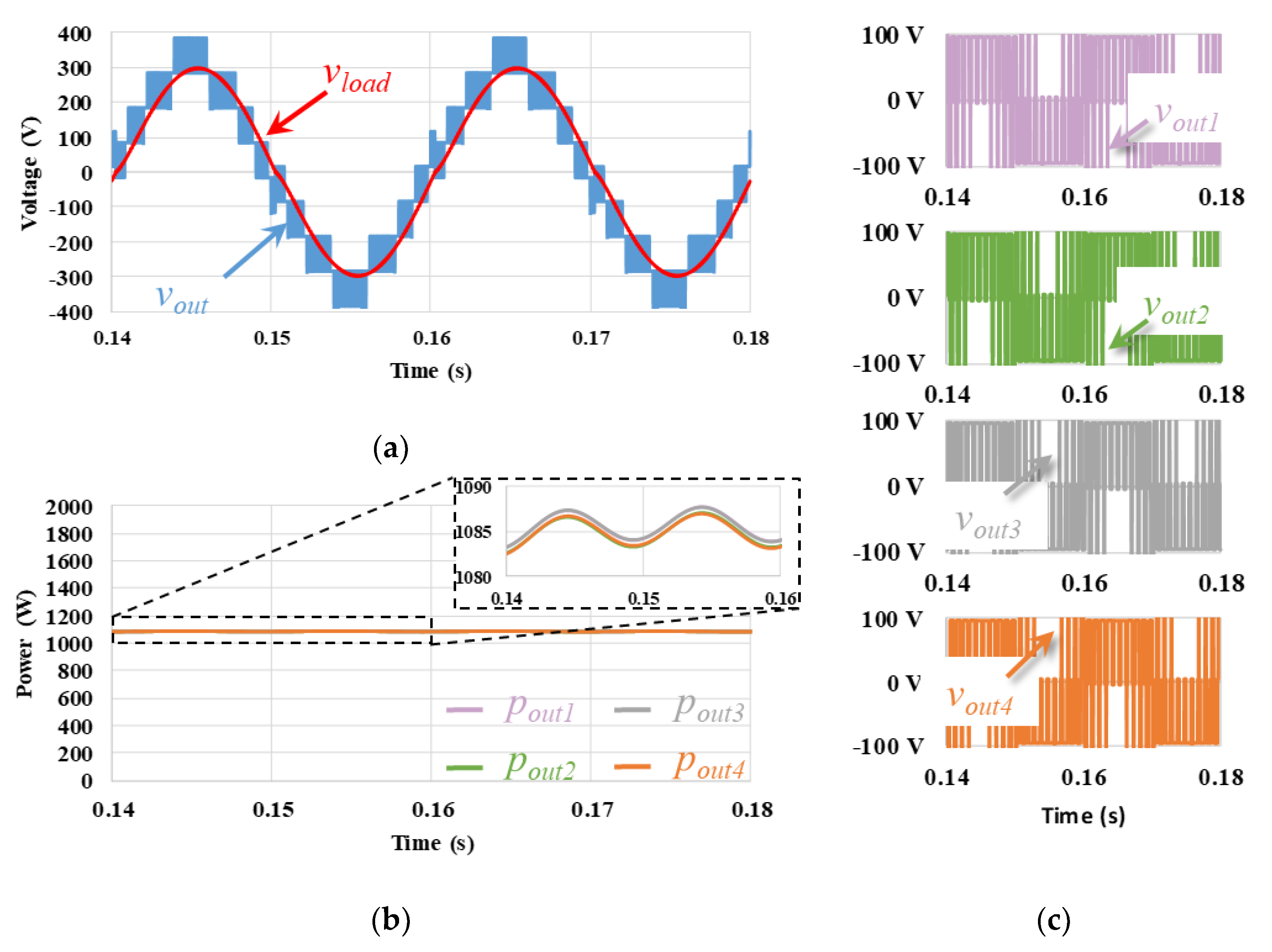

| Half-Bridge 1 | Half-Bridge 2 | Full-Bridge | NPC 1 | NPC 2 | T-NPC | FCMC 1 | FCMC 2 | |
|---|---|---|---|---|---|---|---|---|
| Number of output levels | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 |
| Number of DC bus capacitors | 2 | 1 | 1 | 2 | 2 | 2 | 2 | 2 |
| Number of IGBTs | 2 | 2 | 4 | 4 | 4 | 4 | 4 | 4 |
| Number of Diodes | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 2 |
| Max. Number of semiconductors in the conduction path | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 |
| Unipolar operation | no | no | yes | yes | no | yes | yes | no |
| Max voltage block | VDC | VDC | VDC | VDC | VDC | 2 VDC | VDC | VDC |
| DC bus voltage | 2 VDC | VDC | VDC | 2 VDC | 2 VDC | 2 VDC | 2 VDC | 2 VDC |
| Output frequency | fw | fw | 2 fw | fw | fw | fw | fw | fw |
| DC fault blocking | no | no | yes | no | no | no | no | no |
| Cell design complexity | * | * | * | ** | *** | ** | ** | *** |
| Cell control complexity | ** | ** | * | ** | *** | ** | *** | *** |
| Application | Half-Bridge | Full-Bridge | NPC | T-NPC | FCMC | SST |
|---|---|---|---|---|---|---|
| Active Filter | [45,51] | [48,49,50,109] | [46,110,111] | [112] | [113,114,115,116,117] | |
| Motor Drive | [42] | [42] | [118,119] | [120,121,122] | [123,124,125] | |
| Energy Storage | [31,35,41] | [32,33] | [46,126,127] | [128] | [129] | |
| HVDC | [7,11,12,13,24,25,30,130] | [6,7,130] | [6,131] | |||
| Marine | [43,44] | [132] | [133] | [134] | ||
| Railway | [38] | [135] | [136,137,138] | [86,139] | ||
| Photovoltaic | [18,21,22] | [17,18,140,141] | [142,143] | [144,145,146,147,148] | [149] | [52,53,54] |
| Pumping | [150] | [151,152] | ||||
| Wind | [23,24,25,26,30] | [27] | [153,154] | [155,156] | [157] | [158,159,160] |
| Others | [161,162] | [108,123,163,164,165,166] |
| Application | Half-bridge | Full-bridge | NPC | T-NPC | FCMC | SST |
|---|---|---|---|---|---|---|
| Max. Power | 1.5 kW 1, 10 kVA 4, 1.3 MW 12, 50 kW 17 | 5 MW 14, 500 kVA 15, 2 MW 16, 12.8 MW 13 | 12 MW-14.5 MVA 2 | 139 kVA 18 | 9.2 MVA 3, 5 kW 6 | 500 kVA 5, 1.5 MVA 8, 3 MVA 9, 1.2 MVA 10, 1.8 MVA 11 |
| Output Voltage | 230 V 1, 380 V 4, 4.16 kV 12 | 11 kV 7, 12 kV 14, 6.6 kV 15, 11 kV 13 | 3.4 kV 2 | 3.4 kV 2 | 6.6 kV 3 | 400 V 5, 15 kV 8, 9, 10, 11 |
| DC bus Voltage | 160 V 1, 400 V 4, 8 kV 12, 1.7 kV 17 | 24 kV 14, 10 kV 15 | 1.5 kV 5 | |||
| Switching Frequency | 40 kHz 1, 1 kHz 12 | 2 kHz 14, 2.5 kHz 16 | 8 kHz 18 | 350 V 6 | 400 Hz 10, 1 kHz 5, 5 kHz 8, 8 kHz 9 | |
| Power Semiconductor | IGBT 1, 4, 12 | IGBT 7, 13, 14, 15 | IGCT 2 | IGCT 18 | IGBT 3, | IGBT 5, 8, 9, 10, 11 |
| Number of Semiconductors | 16 1, 48 4, 60 12 | 300 7, 120 5, 13, 76 14, 128 16 | 48 2 | 48 18 | 36 3 | 216 5, 52 8, 96 9, 192 10, 72 11 |
| PWM Technique | PSC 1, 4, 12 | SVPWM 13 | PWM 2 | PWM 18 | PSC 5, | |
| Voltage levels | 5 1, 9 4, 31 17 | 19 13 | 3 2 | 3 18 | 7 3 | 13 5, 17 8, 9, 33 10, 19 11 |
| Variable | Value | |
|---|---|---|
| Fundamental Frequency | f | 50 Hz |
| Modulation Index | ma | 0.8 |
| Output Inductance | LS | 5 mH |
| Inductor Internal Resistance | RS | 100 mΩ |
| Load | RLoad | 10 Ω |
| DC bus Voltage | VDC | 100 V |
| Switching Frequency | fw | 1 kHz |
| Saturation Voltage 1 | VCE(sat) | 1.75 V |
| Transistor Resistance 1 | rCE | 8.1 mΩ |
| Diode Threshold Voltage 1 | VF | 2.2 V |
| Diode Resistance 1 | rF | 9 mΩ |
| Output Level | Number of Redundant States | Conditions |
|---|---|---|
| 4 VDC | 1 | +VDC + VDC + VDC + VDC |
| 3 VDC | 8 | + VDC + VDC + VDC + 0 |
| 2 VDC | 28 | +VDC + VDC + VDC − VDC + VDC + VDC +0 + 0 |
| VDC | 56 | +VDC + VDC − VDC + 0 + VDC + 0 + 0 + 0 |
| 0 | 70 | +VDC + VDC − VDC − VDC + VDC − VDC + 0 + 0 +0 + 0 + 0 + 0 |
| −VDC | 56 | −VDC − VDC + VDC + 0 − VDC + 0 + 0 + 0 |
| −2 VDC | 28 | −VDC − VDC − VDC + VDC −VDC − VDC + 0 + 0 |
| −3 VDC | 8 | −VDC − VDC − VDC + 0 |
| −4 VDC | 1 | −VDC − VDC − VDC − VDC |
| HB1 | HB2 | HB3 | HB4 | Total Power | Average Power | Imbalance | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pout1 | η%_1 | Pout2 | η%_2 | Pout3 | η%_3 | Pout4 | η%_4 | Pout | η%_avg | ||
| W | % | W | % | W | % | W | % | W | % | % | |
| PD | 569.3 | 88 | 1653.1 | 95.8 | 1638.9 | 95.8 | 496.4 | 86.5 | 4357.6 | 91.5 | 54.4 |
| POD | 523.7 | 87.4 | 1608.4 | 95.8 | 1608.4 | 95.8 | 523.8 | 87.4 | 4264.2 | 91.6 | 50.9 |
| APOD | 529.6 | 87.3 | 1649 | 95.8 | 1649 | 95.8 | 529.6 | 87.3 | 4357.2 | 91.6 | 51.4 |
| Balanced PD | 1164.9 | 94 | 1057.2 | 93.4 | 1119 | 93.7 | 1016.4 | 93.1 | 4357.5 | 93.5 | 6.70 |
| Balanced POD | 1119.4 | 93.9 | 1012.6 | 93.3 | 1119.4 | 93.9 | 1012.6 | 93.3 | 4264.0 | 93.6 | 5.01 |
| Balanced APOD | 1146.4 | 93.9 | 1030.4 | 93.2 | 1146.5 | 93.9 | 1030.4 | 93.2 | 4353.6 | 93.5 | 5.33 |
| CO | 908.8 | 91.2 | 1872.2 | 95.8 | 1868.8 | 95.7 | 928.3 | 91.4 | 5578 | 93.5 | 34.8 |
| VF | 481 | 86.3 | 1631.4 | 95.8 | 1591.9 | 95.7 | 579.7 | 88.4 | 4284 | 91.5 | 55.1 |
| VF2 | 557 | 87.8 | 1651.6 | 95.8 | 1637.4 | 95.8 | 504.3 | 86.7 | 4350.2 | 91.5 | 53.6 |
| PSC | 1085.5 | 93.6 | 1084.8 | 93.5 | 1085.5 | 93.6 | 1084.8 | 93.5 | 4340.4 | 93.5 | 0.0320 |
| PSD | 1085.1 | 93.5 | 1084.9 | 93.5 | 1084.9 | 93.5 | 1085.2 | 93.5 | 4340.1 | 93.5 | 0.0117 |
| CO-PD | 772.6 | 90.7 | 1681.9 | 95.7 | 1680.4 | 95.7 | 774.1 | 90.7 | 4909 | 93.5 | 37.1 |
| CO-POD | 775.4 | 90.7 | 1684.9 | 95.7 | 1684.9 | 95.7 | 775.4 | 90.7 | 4920.7 | 93.2 | 37.0 |
| CO-APOD | 767.1 | 90.6 | 1681.7 | 95.7 | 1681.7 | 95.7 | 767.1 | 90.6 | 4897.7 | 93.2 | 37.4 |
| vout | vload | |
|---|---|---|
| PD | 18.2% | 6.03% |
| POD | 17.9% | 6.82% |
| APOD | 18.7% | 5.96% |
| Balanced PD | 17.9% | 6.81% |
| Balanced POD | 17.9% | 6.81% |
| Balanced APOD | 17.9% | 5.68% |
| CO | 26.0% | 7.61% |
| VF | 18.9% | 9.99% |
| VF2 | 18.1% | 6.45% |
| PSC | 18.8% | 2.56% |
| PSD | 18.9% | 2.77% |
| CO-PD | 28.6% | 11.1% |
| CO-POD | 28.6% | 10.7% |
| CO-APOD | 19.6% | 8.87% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barros, L.A.M.; Martins, A.P.; Pinto, J.G. A Comprehensive Review on Modular Multilevel Converters, Submodule Topologies, and Modulation Techniques. Energies 2022, 15, 1078. https://doi.org/10.3390/en15031078
Barros LAM, Martins AP, Pinto JG. A Comprehensive Review on Modular Multilevel Converters, Submodule Topologies, and Modulation Techniques. Energies. 2022; 15(3):1078. https://doi.org/10.3390/en15031078
Chicago/Turabian StyleBarros, Luis A. M., António P. Martins, and José Gabriel Pinto. 2022. "A Comprehensive Review on Modular Multilevel Converters, Submodule Topologies, and Modulation Techniques" Energies 15, no. 3: 1078. https://doi.org/10.3390/en15031078
APA StyleBarros, L. A. M., Martins, A. P., & Pinto, J. G. (2022). A Comprehensive Review on Modular Multilevel Converters, Submodule Topologies, and Modulation Techniques. Energies, 15(3), 1078. https://doi.org/10.3390/en15031078







