A Parameter Estimation Method for a Photovoltaic Power Generation System Based on a Two-Diode Model
Abstract
:1. Introduction
- A PV power generation system based on a two-diode model is established in the MATLAB/SIMULINK environment, which can be used for parameter estimation of PV power plants of different types and scales.
- Converting the seven parameters of the two-diode model into 17 parameters according to different environmental conditions provides more precise parameter estimates for the PV model.
- A parameter elimination technique that combines parameter sensitivity analysis and the overall effect method is used to remove the parameters that have little effect on the output.
- To enhance the global search ability of GWO, a dynamic crowding distance (DCD) algorithm is used to eliminate the agents with higher density region in the optimization process.
2. The PV Power Generation Models
2.1. Single-Diode Model
2.2. Two-Diode Model
3. The Proposed Method
3.1. Establishment of PV Power Generation Model
3.2. Parameter Selection
3.3. Enhanced Gray Wolf Optimizer (EGWO)
3.3.1. Surrounding Prey
3.3.2. Attacking Prey
3.3.3. Search for Other Prey
3.3.4. Dynamic Crowding Distance (DCD)
4. Numerical Results
4.1. Establishment of PV Power Generation Model
4.2. Parameter Selection for Optimization
4.3. Parameter Optimization
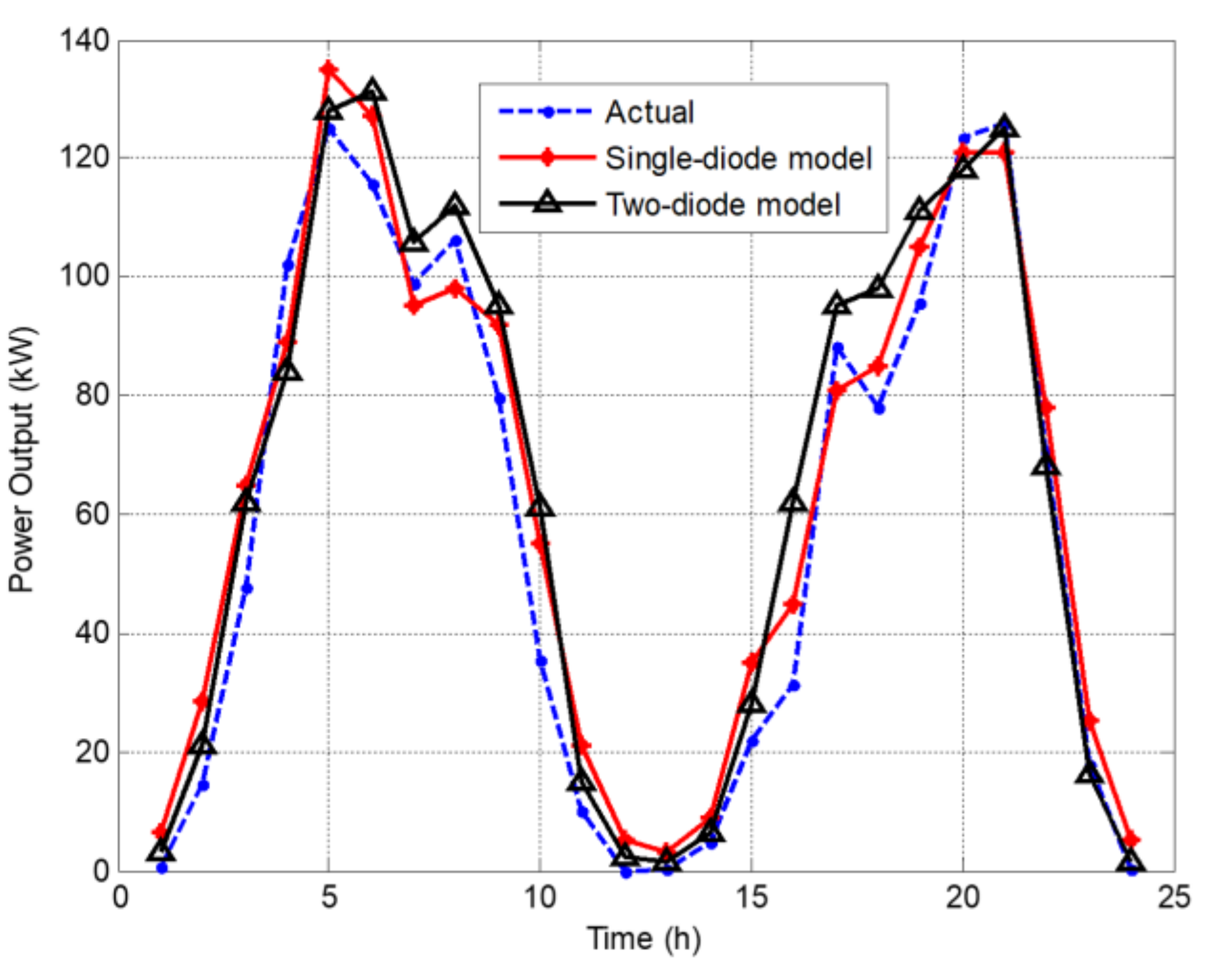
4.4. Discussion
- A photovoltaic power generation system based on a two-diode model is established in the MATLAB/SIMULINK environment, which can be applied to PV power plants of different types and scales only by changing the number of modules in series and parallel.
- As shown in Table 6, whether a single-diode model or a two-diode model is used, it is more accurate to convert the original model to a more refined model with more parameters according to different environmental conditions.
- Although the proposed EGWO takes approximately 9 min to complete the parameter optimization, it only needs to be executed offline, and usually needs to be performed once a month or when a new PV array is installed.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Temperature coefficient at the maximum power point | |
| Temperature coefficient for the short-circuit current | |
| Temperature coefficient for the open-circuit voltage | |
| Eigenvalue of the ith output | |
| The jth parameter | |
| Coefficient vector | |
| C | Number of feasible agents |
| Coefficient vector | |
| Diversity of the ith agent | |
| Dynamic crowding distance | |
| Differential evolution | |
| Enhanced gray wolf optimizer | |
| The effect of the jth parameter with respect to the overall variables | |
| Gap energy | |
| Gap energy under STC | |
| Fitness value of the ith feasible agent | |
| Fitness value of the jth feasible agent | |
| Maximum fitness value | |
| Minimum fitness value | |
| G | Solar irradiance |
| Solar irradiance under STC | |
| Gray wolf optimizer | |
| I | Output current |
| Photo current | |
| Photo current under STC | |
| Maximum output current | |
| Maximum output current under STC | |
| Saturation current | |
| Saturation current under STC | |
| Short-circuit current | |
| Short-circuit current under STC | |
| k | Boltzmann constant ( |
| Ideal factor | |
| Ideal factor under STC | |
| no | Number of outputs |
| N | Number of data points |
| Estimated value of the jth agent | |
| Measured value of the jth agent | |
| Capacity of the PV power generation | |
| Estimated value | |
| Actual value | |
| Particle swarm optimization | |
| Photovoltaic | |
| Location of the gray wolf | |
| 𝑃𝑖𝑗 | Principal component element for the jth parameter of the ith output |
| Positions of wolf | |
| Positions of wolf | |
| Positions of wolf | |
| Number of the parameter | |
| q | Electron charge |
| Series resistance | |
| Series resistance under STC | |
| Parallel resistance | |
| Parallel resistance under STC | |
| Sensitivity coefficient in the steady state | |
| Standard test condition | |
| t | Current iteration |
| Surface temperature | |
| Surface temperature under STC | |
| Output voltage | |
| Maximum output voltage | |
| Maximum output voltage under STC | |
| Open-circuit voltage | |
| Open-circuit voltage under STC | |
| Thermal voltage | |
| Whale optimizer | |
| Location vector of agent | |
| Location vector of the prey | |
| The ith output |
References
- Liu, J.; Fang, W.; Zhang, X.; Yang, C. An Improved Photovoltaic Power Forecasting Model with the Assistance of Aerosol Index Data. IEEE Trans. Sustain. Energy 2015, 6, 434–442. [Google Scholar] [CrossRef]
- Wang, F.; Yu, Y.; Zhang, Z.; Li, J.; Zhen, Z.; Li, K. Wavelet Decomposition and Convolutional LSTM Networks Based Improved Deep Learning Model for Solar Irradiance Forecasting. Appl. Sci. 2018, 8, 1286. [Google Scholar] [CrossRef] [Green Version]
- Ramli, A.M.; Makbui, B.; Houssem, R.E.H. Estimation of Solar Radiation on PV Panel Surface with Optimum Tilt Angle Using Vortex Search Algorithm. IET Renew. Power Gener. 2018, 12, 1138–1145. [Google Scholar] [CrossRef]
- Sun, Y.; Szucs, G.; Brandt, A.R. Solar PV Output Prediction from Video Streams Using Convolutional Neural Networks. Energy Environ. Sci. 2018, 11, 1811–1818. [Google Scholar] [CrossRef]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Liang, Z.; Wei, Z.; Sun, G. Hybrid Method for Short-Term Photovoltaic Power Forecasting Based on Deep Convolutional Neural Network. IET Gener. Transm. Distrib. 2018, 12, 4557–4567. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Lu, S.; Hamann, H.F.; Hodge, B.M.; Lehman, B. A Solar Time Based Analog Ensemble Method for Regional Solar Power Forecasting. IEEE Trans. Sustain. Energy 2019, 10, 268–279. [Google Scholar] [CrossRef]
- Lee, W.; Kim, K.; Park, J.; Kim, J.; Kim, Y. Forecasting Solar Power Using Long-Short Term Memory and Convolutional Neural Networks. IEEE Access 2018, 6, 73068–73080. [Google Scholar] [CrossRef]
- Agoua, X.G.; Girard, R.; Kariniotakis, G. Probabilistic Models for Spatio-Temporal Photovoltaic Power Forecasting. IEEE Trans. Sustain. Energy 2019, 10, 780–789. [Google Scholar] [CrossRef] [Green Version]
- Aprillia, H.; Yang, H.T.; Huang, C.M. Short-Term PV Power Forecasting Using a Convolutional Neural Network-Salp Swarm Algorithm. Energies 2020, 13, 1879. [Google Scholar] [CrossRef]
- Lateko, H.; Yang, H.T.; Huang, C.M.; Aprillia, H.; Hsu, C.Y.; Zhong, J.L.; Phuong, N.H. Stacking Ensemble Method with the RNN Meta-Learner for Short-Term PV Power Forecasting. Energies 2021, 14, 4733. [Google Scholar] [CrossRef]
- Pavan, A.M.; Mellit, A.; Lughi, V. Explicit Empirical Model for General Photovoltaic Devices: Experimental Validation at Maximum Power Point. Sol. Energy 2014, 101, 105–116. [Google Scholar] [CrossRef]
- Mattei, M.; Notton, G.; Cristofari, C.; Muselli, M.; Poggi, P. Calculation of the Polycrystalline PV Module Temperature Using a Simple Method of Energy Balance. Renew. Energy 2006, 31, 553–567. [Google Scholar] [CrossRef]
- Jadli, U.; Thakur, P.; Shukla, R.D. A New Parameter Estimation Method of Solar Photovoltaic. IEEE J. Photovolt. 2018, 8, 239–247. [Google Scholar] [CrossRef]
- Sabudin, S.N.M.; Jamil, N.M. Parameter Estimation in Mathematical Modeling for Photovoltaic Panel. Mater. Sci. Eng. 2019, 536, 1–11. [Google Scholar]
- Huang, Y.C.; Huang, C.M.; Chen, S.J.; Yang, S.P. Optimization of Module Parameters for PV Power Estimation Using a Hybrid Algorithm. IEEE Trans. Sustain. Energy 2020, 11, 2210–2219. [Google Scholar] [CrossRef]
- Hou, J.; Xu, P. The Matlab/Simulink Simulation Model of the PV Array Based on the Four-Parameter Model. Renew. Energy Resour. 2013, 31, 10–19. [Google Scholar]
- Chouder, A.; Silvestre, S.; Sadaoui, N.; Rahmani, L. Modeling and Simulation of a Grid Connected PV System Based on the Evaluation of Main PV Module Parameters. Simul. Model. Pract. Theory 2012, 20, 46–58. [Google Scholar] [CrossRef]
- Ye, M.; Wang, X.; Xu, Y. Parameter extraction of solar cells using particle swarm optimization. J. Appl. Phys. 2009, 105, 094502. [Google Scholar] [CrossRef]
- Cárdenas-Bravo, C.; Barraza, R.; Sánchez-Squella, A.; Valdivia-Lefort, P.; Castillo-Burns, F. Estimation of Single-Diode Photovoltaic Model Using the Differential Evolution Algorithm with Adaptive Boundaries. Energies 2021, 14, 3925. [Google Scholar] [CrossRef]
- Stornelli, V.; Muttillo, M.; de Rubeis, T.; Nardi, I. A New Simplified Five-Parameter Estimation Method for Single-Diode Model of Photovoltaic Panels. Energies 2019, 12, 4271. [Google Scholar] [CrossRef] [Green Version]
- Valdivia-González, A.; Zaldívar, D.; Cuevas, E.; Pérez-Cisneros, M.; Fausto, F.; González, A. A Chaos-Embedded Gravitational Search Algorithm for the Identification of Electrical Parameters of Photovoltaic Cells. Energies 2017, 10, 1052. [Google Scholar] [CrossRef] [Green Version]
- Al-Shamma’a, A.A.; Omotoso, H.O.; Alturki, F.A.; Farh, H.M.H.; Alkuhayli, A.; Alsharabi, K.; Noman, A.M. Parameter Estimation of Photovoltaic Cell Modules Using Bonobo Optimizer. Energies 2022, 15, 140. [Google Scholar] [CrossRef]
- Kang, T.; Yao, J.; Jin, M.; Yang, S.; Duong, T. A Novel Improved Cuckoo Search Algorithm for Parameter Estimation of Photovoltaic (PV) Models. Energies 2018, 11, 1060. [Google Scholar] [CrossRef] [Green Version]
- Oliva, D.; Ewees, A.A.; Aziz, M.A.E.; Hassanien, A.E.; Cisneros, M.P. A Chaotic Improved Artificial Bee Colony for Parameter Estimation of Photovoltaic Cells. Energies 2017, 10, 865. [Google Scholar] [CrossRef] [Green Version]
- Kurobe, K.I.; Matsunami, H. New Two-Diode Model for Detailed Analysis of Multicrystalline Silicon Solar Cell. Jpn. J. Appl. Phys. 2005, 44, 8314–8322. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. An Accurate and Fast Computational Algorithm for the Two-Diode Model of PV Module Based on Hybrid Method. IEEE Trans. Ind. Electron. 2017, 64, 6212–6222. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Taheri, H. Accurate MATLAB Simulink PV System Simulator Based on a Two-Diode Model. J. Electron. 2011, 11, 179–187. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, A.B.; Reda, M.; Attia, E.F.; Sameh, S.A.; Mohamed, A. Efficient Ranking-Based Whale Optimizer for Parameter Extraction of Three-Diode Photovoltaic Model: Analysis and Validations. Energies 2021, 14, 3729. [Google Scholar]
- Elazab, O.S.; Hasanien, H.M.; Alsaidan, I.; Abdelaziz, A.Y.; Muyeen, S.M. Parameter Estimation of Three Diode Photovoltaic Model Using Grasshopper Optimization Algorithm. Energies 2020, 13, 497. [Google Scholar] [CrossRef] [Green Version]
- Dunteman, G.H. Principal Components Analysis; Sage: Newbury Park, CA, USA, 1989. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Luo, B.; Zheng, J.; Wu, X.J. Dynamic crowding distance: A new diversity maintenance strategy for MOEAs. In Proceedings of the 2008 Fourth International Conference on Natural Computation, Jinan, China, 18–20 October 2008; pp. 580–585. [Google Scholar]
- Mirjalili, S. Grey Wolf Optimizer (GWO), Version 1.6, 2018. Available online: https://www.mathworks.com/matlabcentral/fileexchange/44974-grey-wolf-optimizer-gwo (accessed on 25 September 2021).
- Biswas, P. Particle Swarm Optimization (PSO), Version 1.5.0.2. Available online: https://www.mathworks.com/matlabcentral/leexchange/43541-particle-swarm-optimization-pso (accessed on 8 February 2022).
- Mirjalili, S. The Whale Optimization Algorithm, Version 1.0.0.0. Available online: https://www.mathworks.com/matlabcentral/_leexchange/55667-the-whale-optimization-algorithm (accessed on 8 February 2022).










| No | Parameter | Reference Value | No | Parameter | Reference Value |
|---|---|---|---|---|---|
| 1 | IL,ref (A) | 3.45 | 10 | Io1,ref (A) | 1.16 × 10−15 |
| 2 | Voc,ref (V) | 66.4 | 11 | Io2,ref (A) | 1.07 × 10−15 |
| 3 | Isc,ref (A) | 3.66 | 12 | nI1,ref | 1.8609 |
| 4 | Vmp,ref (V) | 52.0 | 13 | nI2,ref | 1.8609 |
| 5 | Imp,ref (A) | 3.51 | 14 | αIsc (A/K) | 6.81 × 10−4 |
| 6 | Gref (W/m2) | 1000 | 15 | αImp (A/K) | 6.50 × 10−4 |
| 7 | Tref (K) | 298 | 16 | (V/K) | −0.166 |
| 8 | Rs,ref (Ω) | 2.4089 | 17 | Eg,ref (eV) | 1.121 |
| 9 | Rsh,ref (Ω) | 150 |
| No. | Parameter | Power | Current | Voltage | |
|---|---|---|---|---|---|
| 1 | IL,ref (A) | 0.6210 | 0.0312 | 4.2 × 10−6 | 0.9532 |
| 2 | Voc,ref (V) | 0.001 | 0.002 | 0.0098 | 0.3440 |
| 3 | Isc,ref (A) | −0.120 | −0.0025 | −0.0001 | 0.8031 |
| 4 | Vmp,ref (V) | 0.004 | 0.00075 | 5.1 × 10−5 | 0.4680 |
| 5 | Imp,ref (A) | 0.052 | 0.001 | 3.2 × 10−5 | 0.7865 |
| 6 | Gref (W/m2) | −0.194 | −0.0038 | −0.0025 | 0.9425 |
| 7 | Tref (°K) | 0.490 | 0.0125 | 0.14525 | 0.8821 |
| 8 | Rs,ref (Ω) | −0.1155 | −0.02201 | −0.0000 | 0.7971 |
| 9 | Rsh,ref (Ω) | 0.0015 | 1.3 × 10−5 | 0.0011 | 0.3635 |
| 10 | Io1,ref (A) | 3.5 × 10−6 | 1.2 × 10−6 | 4.8 × 10−5 | 0.0806 |
| 11 | Io2,ref (A) | 2.9 × 10−6 | 0.6 × 10−6 | 1.6 × 10−5 | 0.0912 |
| 12 | nI1,ref | 0.0410 | 0.0023 | 8.5 × 10−5 | 0.3131 |
| 13 | nI2,ref | 0.0410 | 0.0023 | 8.5 × 10−5 | 0.3131 |
| 14 | (A/K) | 5.1 × 10−6 | 1.8 × 10−6 | 1.2 × 10−7 | 0.0112 |
| 15 | (A/K) | 0.00067 | 0.00032 | 2.9 × 10−7 | 0.2302 |
| 16 | (V/K) | 0.00024 | 0.00011 | −9.3 × 10−7 | 0.2031 |
| 17 | Eg,ref (eV) | 5.1 × 10−6 | 1.8 × 10−6 | 0.8 × 10−5 | 0.0633 |
| No. | Parameter | Reference | Range | Optimization |
|---|---|---|---|---|
| 1 | IL,ref (A) | 3.45 | 3.4~3.5 | 3.42 |
| 2 | Voc,ref (V) | 66.4 | 63~69 | 66.35 |
| 3 | Isc,ref (A) | 3.66 | 3.5~5.4 | 3.71 |
| 4 | Vmp,ref (V) | 52.0 | 41~55 | 51.62 |
| 5 | Imp,ref (A) | 3.51 | 3.43~3.65 | 3.508 |
| 6 | Gref (W/m2) | 1000 | 950~1050 | 1015.3 |
| 7 | Tref (K) | 298 | 282~310 | 295.6 |
| 8 | Rs,ref (Ω) | 2.4089 | 2.3~2.5 | 2.424 |
| 9 | Rsh,ref (Ω) | 150 | 130~170 | 148 |
| 10 | nI1,ref | 1.8609 | 1.75~1.95 | 1.86 |
| 11 | (A/K) | 6.50 × 10−4 | 4.50 × 10−4~8.50 × 10−4 | 4.93 × 10−4 |
| 12 | (V/K) | −0.166 | −0.145~−0.185 | −0.171 |
| Weather Types | Optimization | MRE (%) |
|---|---|---|
| Sunny day | Before optimization | 3.7532 |
| After optimization | 1.2542 | |
| Rainy day | Before optimization | 1.1991 |
| After optimization | 0.6931 | |
| Cloudy day | Before optimization | 1.7640 |
| After optimization | 0.9277 | |
| Slightly cloudy day | Before optimization | 1.9742 |
| After optimization | 1.7337 |
| Weather Type | Method | MRE (%) |
|---|---|---|
| Sunny day | Before optimization | 3.7532 |
| PSO [18,34] WO [28,35] EGWO [31,33] | 1.8321 1.6235 1.2542 | |
| Rainy day | Before optimization | 1.1991 |
| PSO [18,34] WO [28,35] EGWO [31,33] | 0.9125 0.9012 0.6931 | |
| Cloudy day | Before optimization | 1.7640 |
| PSO [18,34] WO [28,35] EGWO [31,33] | 0.9936 0.9312 0.9277 | |
| Slightly cloudy day | Before optimization | 1.9742 |
| PSO [18,34] WO [28,35] EGWO [31,33] | 1.7452 1.7545 1.7337 |
| Weather Type | Single-Diode Model 1 | Two-Diode Model 2 | Single-Diode Model 3 | Two-Diode Model 4 |
|---|---|---|---|---|
| Sunny day (25–26 July) | 2.8521 | 2.8011 | 2.2951 | 1.7487 |
| Rainy day (8–9 December) | 1.8922 | 1.8910 | 1.7973 | 1.7869 |
| Cloudy day (1–2 November) | 2.2324 | 2.2025 | 2.0390 | 1.7340 |
| Slightly cloudy day (21–22 June) | 2.8865 | 2.6698 | 2.6538 | 2.0996 |
| Weather Type | Time Period | Single-Diode Model MRE (%) | Two-Diode Model MRE (%) |
|---|---|---|---|
| Sunny day (25–26 July) | Morning 1 | 2.1855 | 1.3590 |
| Noon 2 | 3.2484 | 2.4492 | |
| Afternoon 3 | 1.4296 | 1.3600 | |
| Average error | 2.2951 | 1.7487 | |
| Rainy day (8–9 December) | Morning 1 | 2.0953 | 2.0278 |
| Noon 2 | 1.4920 | 1.9675 | |
| Afternoon 3 | 1.8045 | 1.3655 | |
| Average error | 1.7973 | 1.7869 | |
| Cloudy day (1–2 November) | Morning 1 | 2.4880 | 1.0525 |
| Noon 2 | 2.5213 | 2.1633 | |
| Afternoon 3 | 1.8313 | 1.8188 | |
| Average error | 2.0390 | 1.7340 | |
| Slightly cloudy day (21–22 June) | Morning 1 | 2.3463 | 2.0363 |
| Noon 2 | 2.6648 | 2.9756 | |
| Afternoon 3 | 2.8888 | 1.2744 | |
| Average error | 2.6538 | 2.0996 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.-M.; Chen, S.-J.; Yang, S.-P. A Parameter Estimation Method for a Photovoltaic Power Generation System Based on a Two-Diode Model. Energies 2022, 15, 1460. https://doi.org/10.3390/en15041460
Huang C-M, Chen S-J, Yang S-P. A Parameter Estimation Method for a Photovoltaic Power Generation System Based on a Two-Diode Model. Energies. 2022; 15(4):1460. https://doi.org/10.3390/en15041460
Chicago/Turabian StyleHuang, Chao-Ming, Shin-Ju Chen, and Sung-Pei Yang. 2022. "A Parameter Estimation Method for a Photovoltaic Power Generation System Based on a Two-Diode Model" Energies 15, no. 4: 1460. https://doi.org/10.3390/en15041460
APA StyleHuang, C.-M., Chen, S.-J., & Yang, S.-P. (2022). A Parameter Estimation Method for a Photovoltaic Power Generation System Based on a Two-Diode Model. Energies, 15(4), 1460. https://doi.org/10.3390/en15041460






