Transmission System Electromechanical Stability Analysis with High Penetration of Renewable Generation and Battery Energy Storage System Application
Abstract
:1. Introduction
1.1. Energy Storage Systems in the Expansion of Renewable Sources
1.2. Transient and Electromechanical Stability
1.3. Grid Codes
1.4. Work Objectives and Contributions
- Evolution of studies related to the joint and simultaneous operation of renewable sources, storage systems, and electrical systems. Three-phase modeling of the transmission system, allowing more excellent coverage in the analysis of electromechanical stability.
- Modeling, simulations, and analyses carried out considering the current Brazilian grid codes with the possibility of replication in other countries.
- Design, control, and coupling of BESS to the solar plant, contributing to smoothing the power delivered to the grid and minimizing the operational uncertainties.
2. Proposed Modeling for Transient Analysis
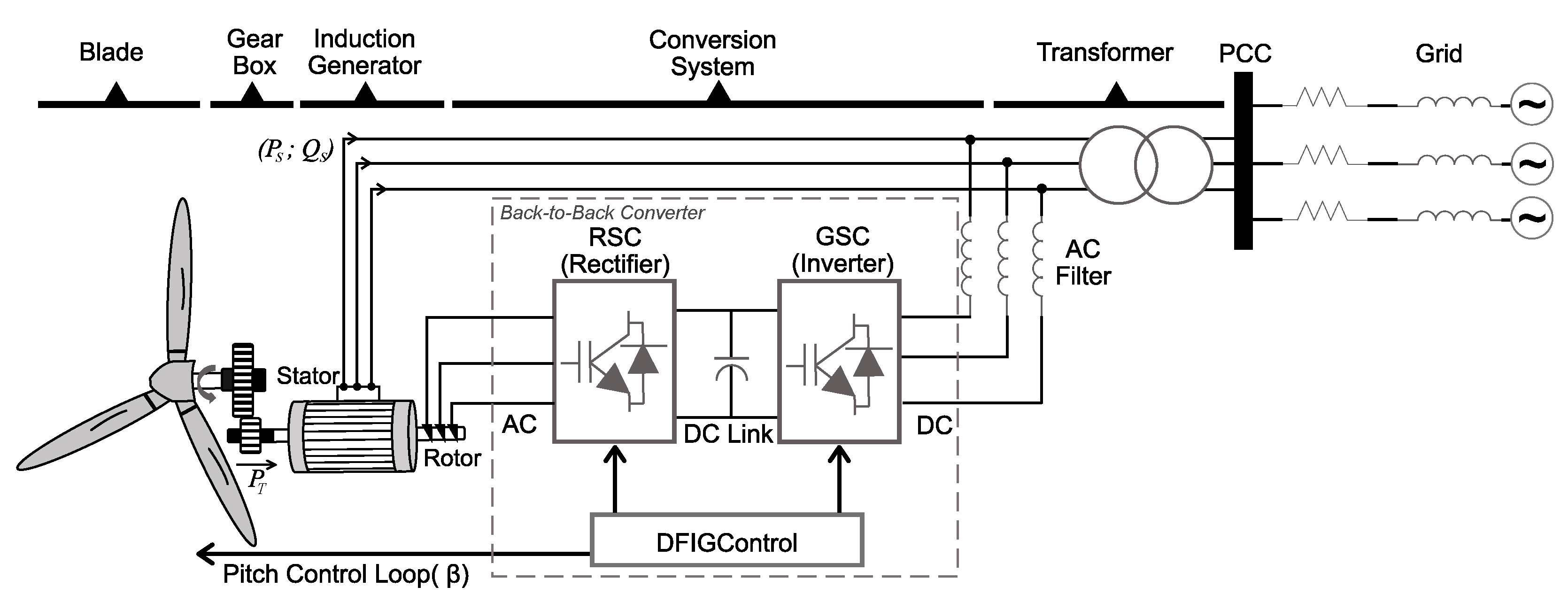
2.1. Wind Power Plant
2.2. Solar Power Plant
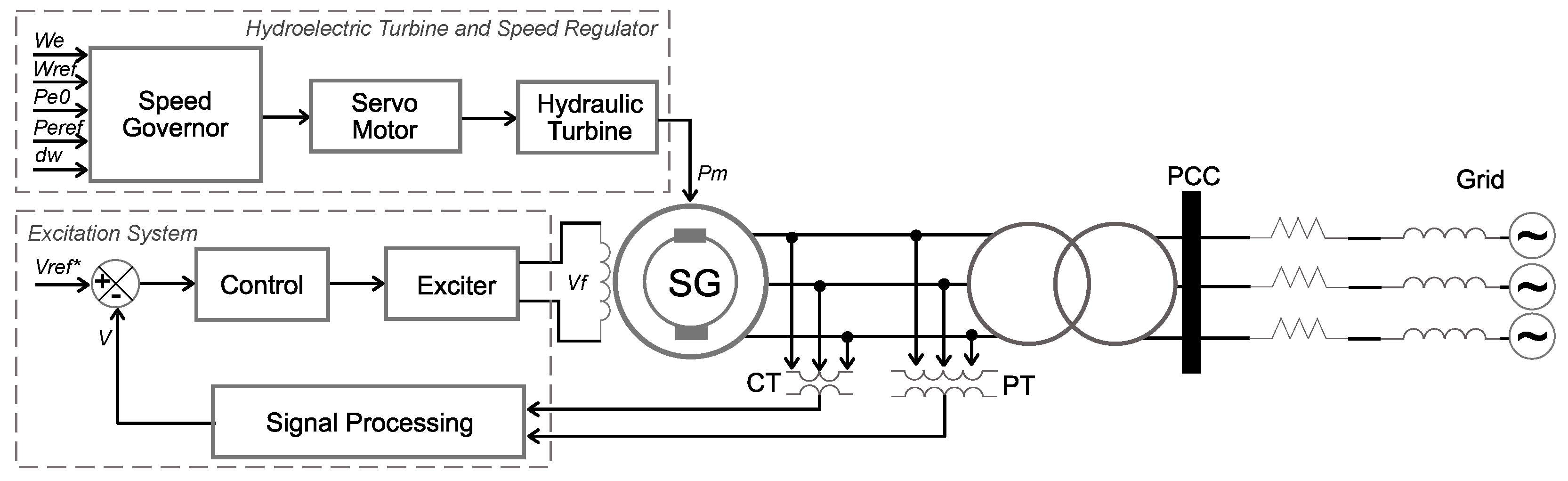
2.3. Hydroelectric Power Plant
2.4. Transmission Grid
2.4.1. Lines, Transformers, and Loads
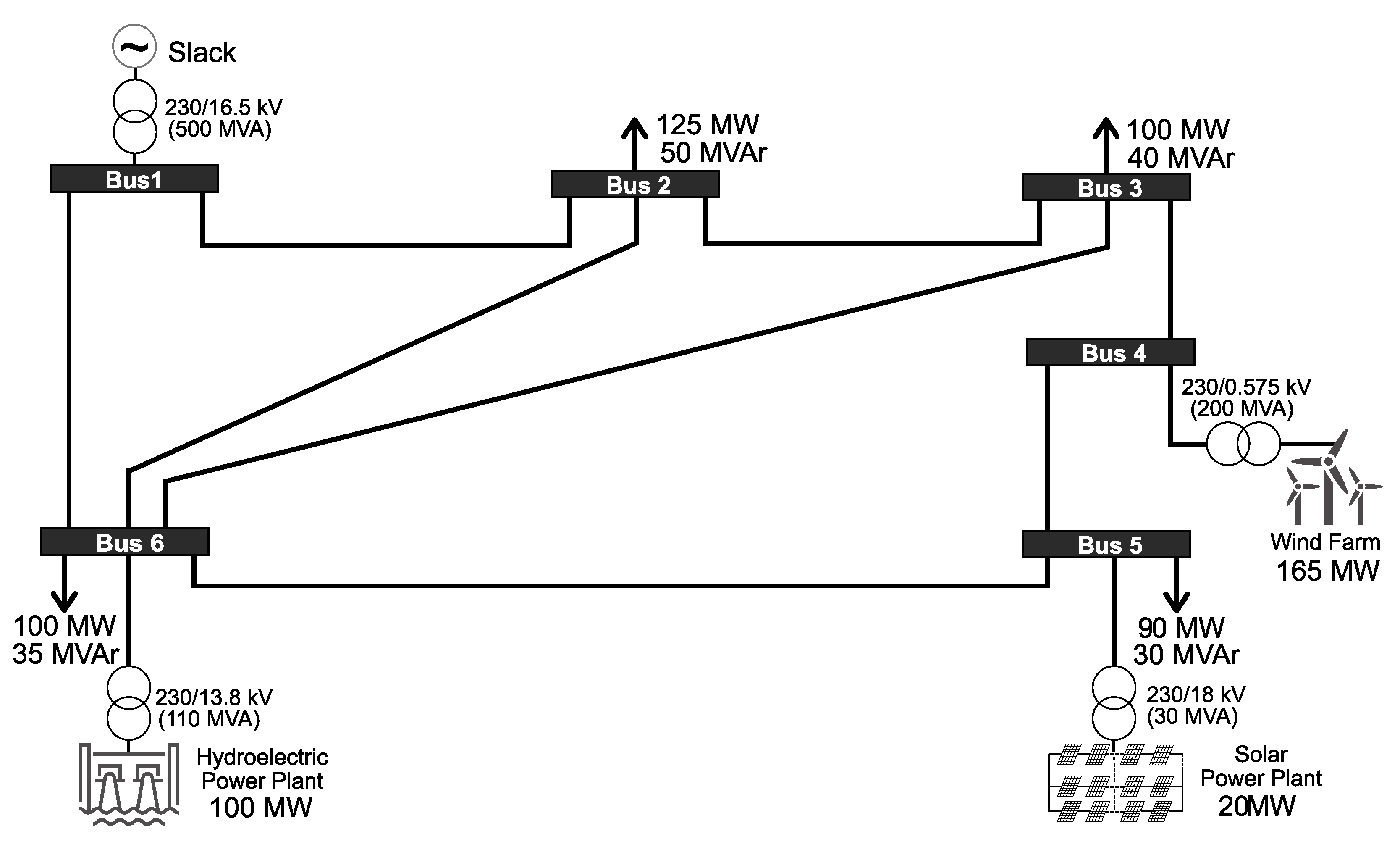
2.4.2. Test Transmission Grid
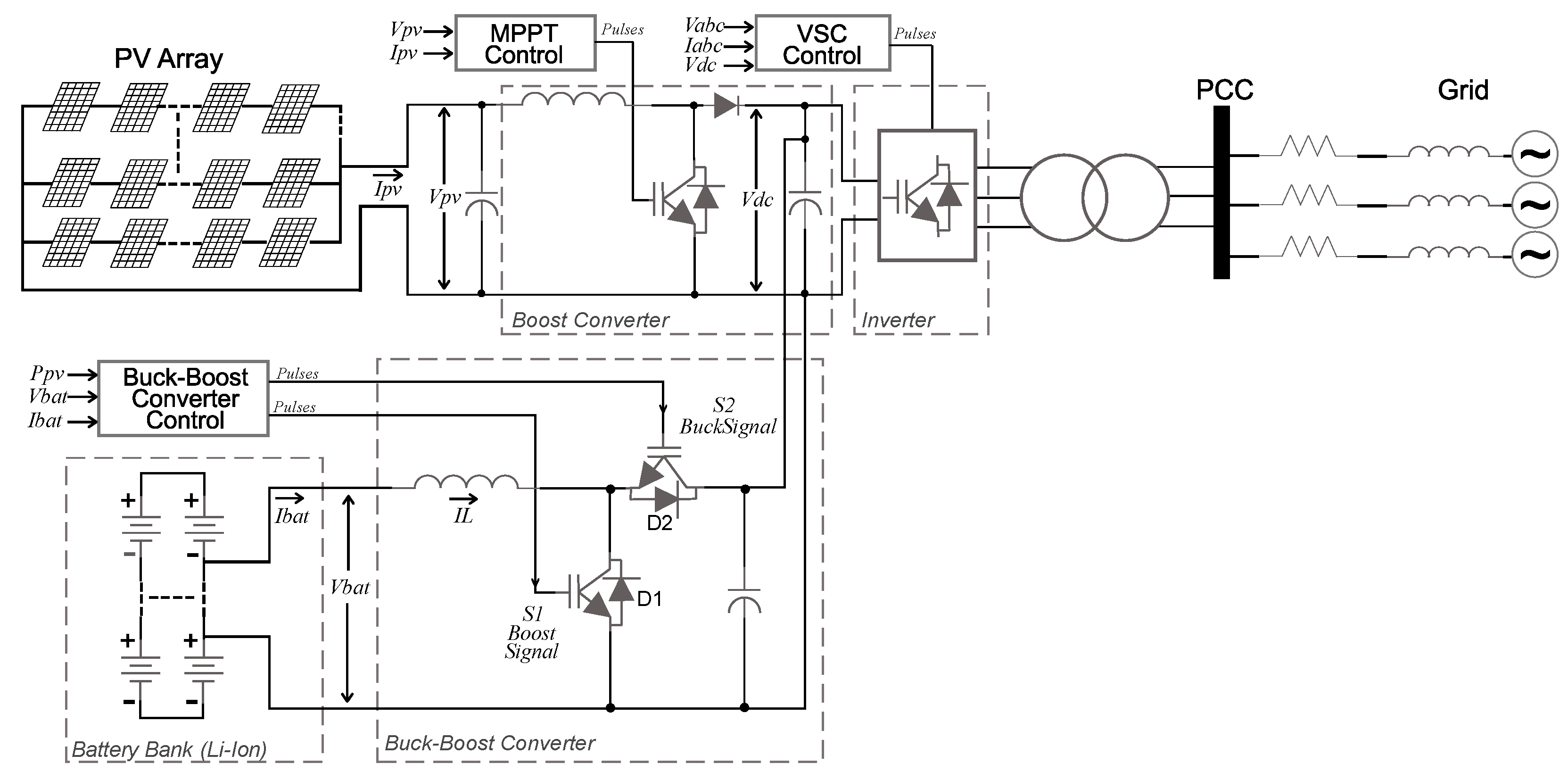
3. Proposal for Coupling BESS to the Solar PV Plant
3.1. Modeling the Lithium-Ion Battery Bank
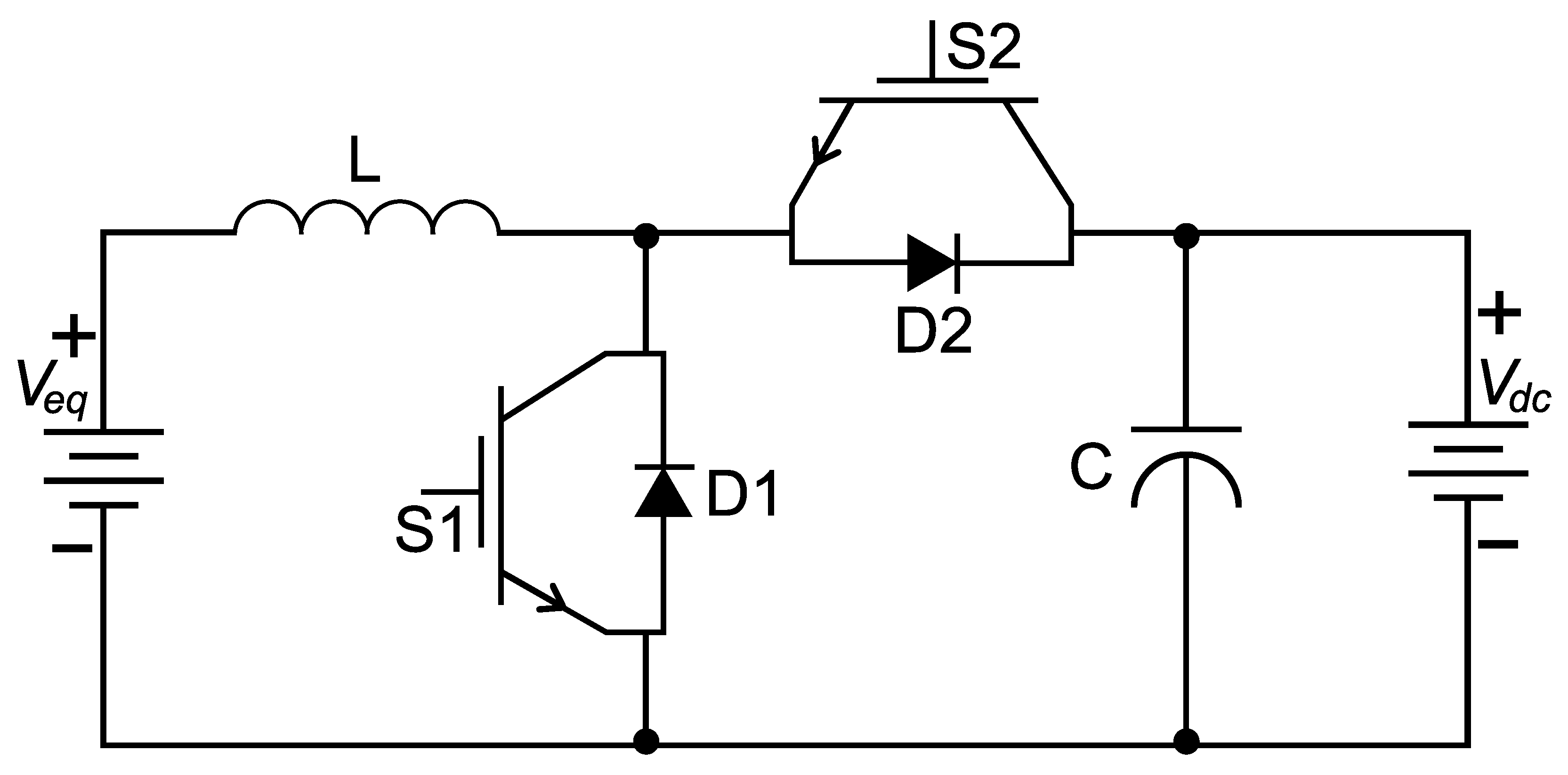
3.2. Bidirectional Buck–Boost Converter
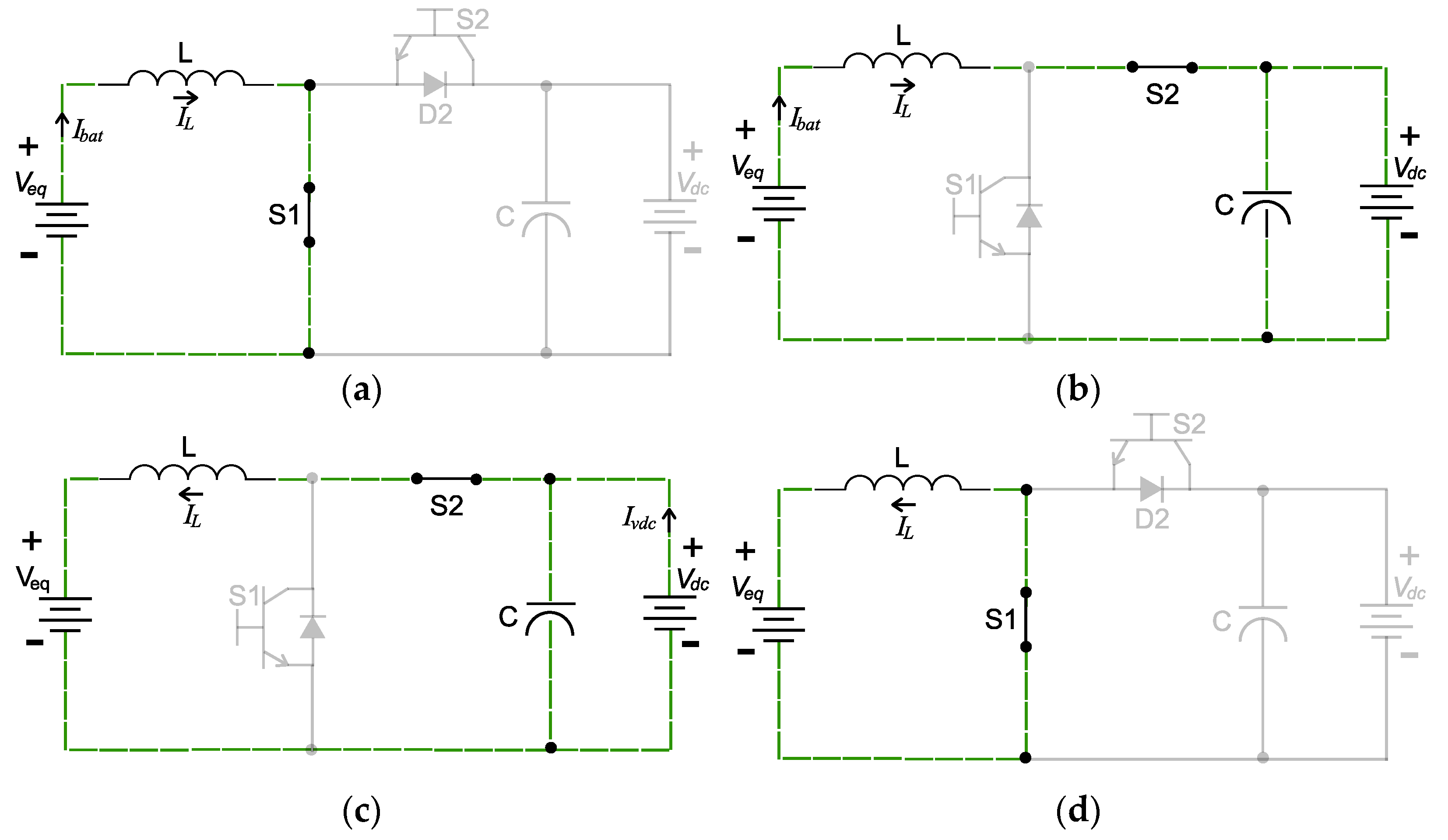
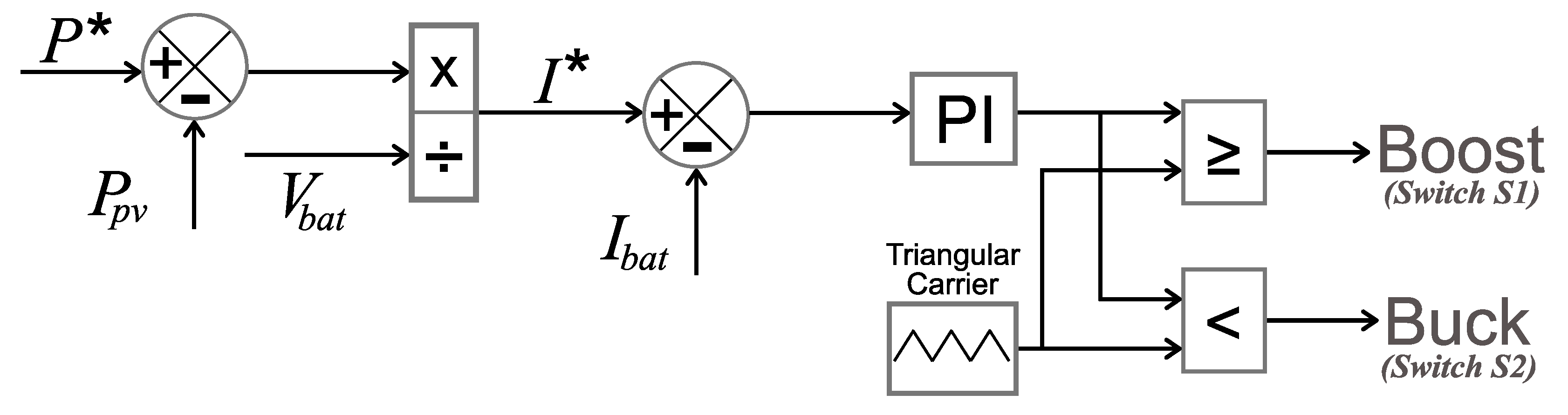
3.2.1. Converter Switching and Control Strategy
- Stage 1 (discharge, boost), power flow from the battery bank () to the DC link (): When switch is on, the diode is reverse-polarized, and then the batteries deliver current to inductor (Figure 7a). When switch is on, the diode is reverse-polarized, and inductor S1 supplies power to the DC link (Figure 7b).
4. Tests and Results
4.1. Electromechanical Stability Analysis: Initial Guidelines and Assumptions
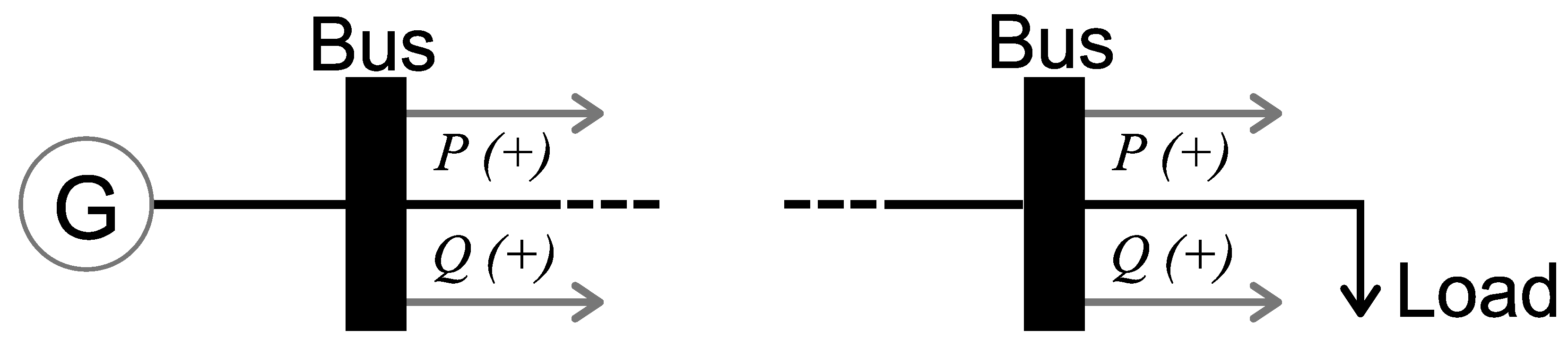
- The analyses were conducted on the basis of the current Brazilian grid code, Grid Proceedings [38]. The main tables and figures used for the analysis are in Appendix B, and the sign convention is illustrated in Figure 9;
- According to guidelines for electrical studies obtained, all simulations were performed under a time horizon of 15 s (using an initial state vector to start the system in the steady state) [38];
- In the variables calculated and presented in pu (values per unit), the base power was 100 MW, and the base voltage was equal to the rated voltage of the bus itself;
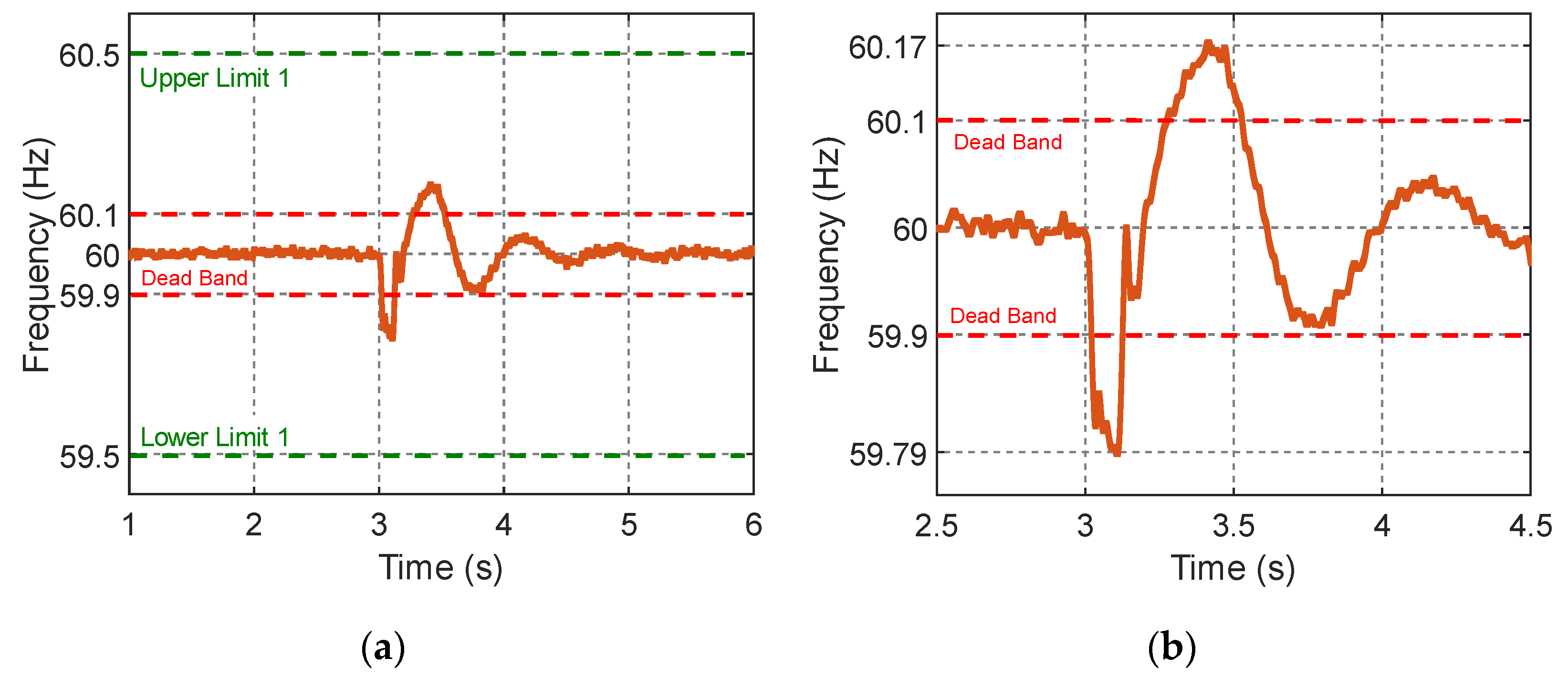
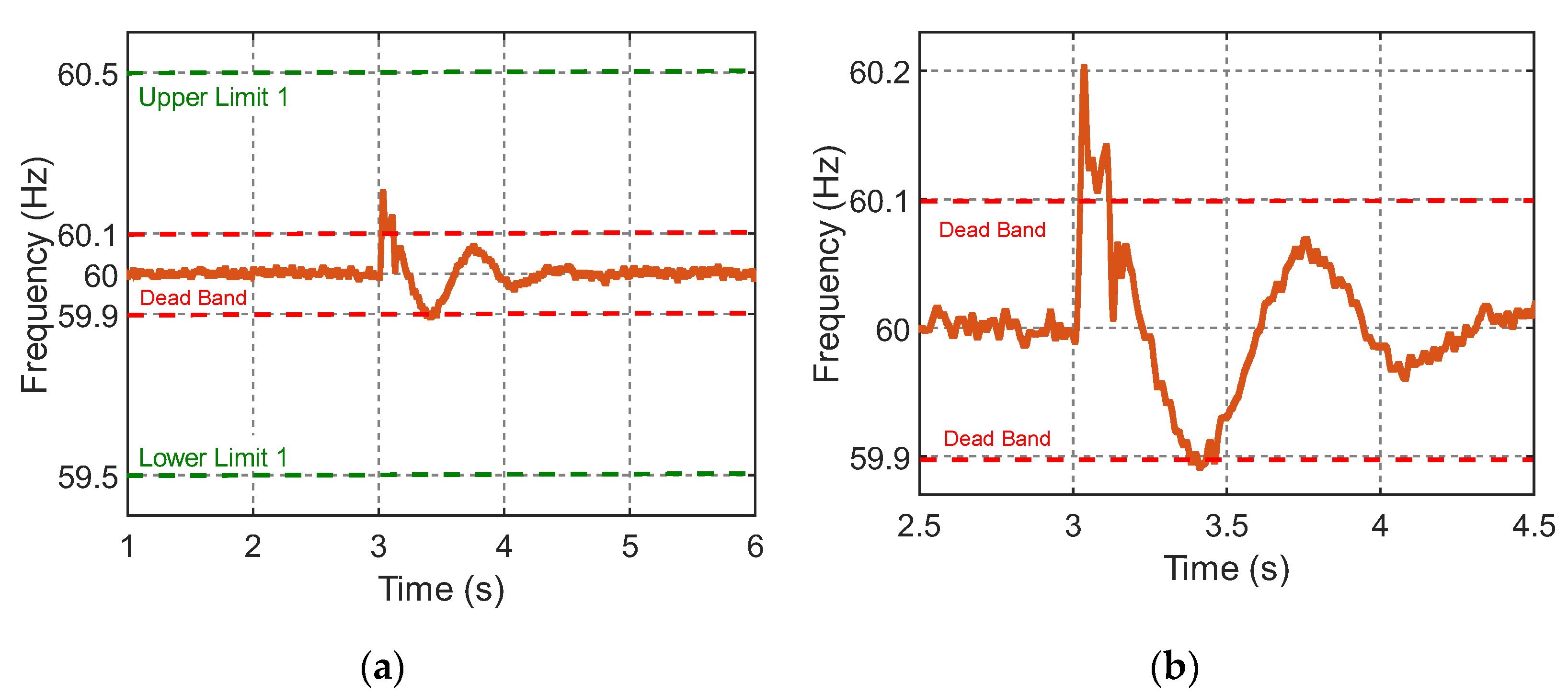
- The Brazilian standard frequency is 60 Hz where, as established in [38], under normal conditions (permanent regime, without the occurrence of disturbances), it should not exceed ±0.1 Hz. Its means that deviations from the nominal regime frequency must be within the limits of 59.9 Hz to 60.1 Hz. The literature defines as steady-state oscillation dead zone or dead band [4];
- Regarding voltage, the operating limit in the steady state is understood by the ratio 0.95 < V < 1.05, and the generators need to operate in this range without being turned off [38]. To this end, the graphs contain a red dotted line showing the upper (1.05) and lower (0.95) limits;
- The scenarios were designed to cover different operating conditions of the EPS, following the preoperational studies required by the ONS to request access to the grid commissioning, among others [38].
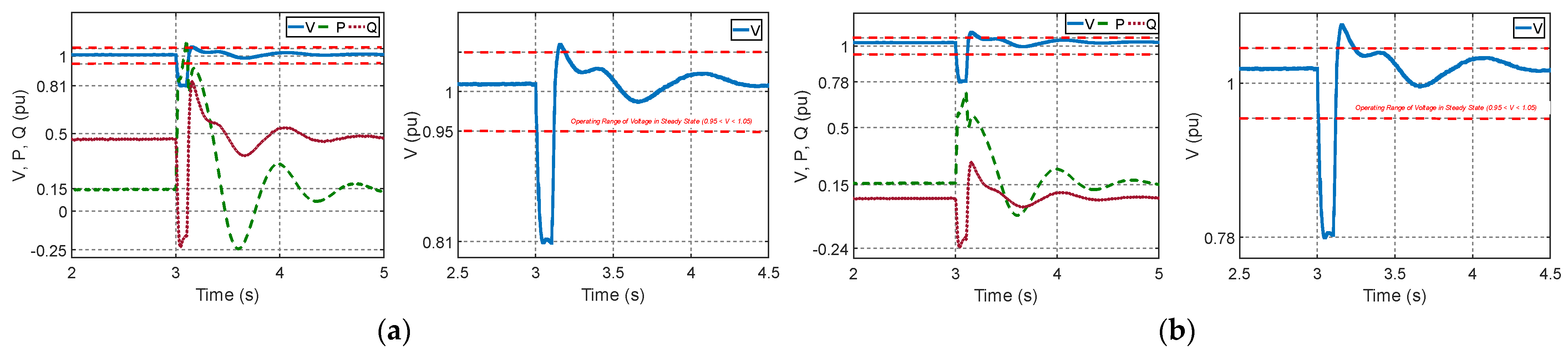
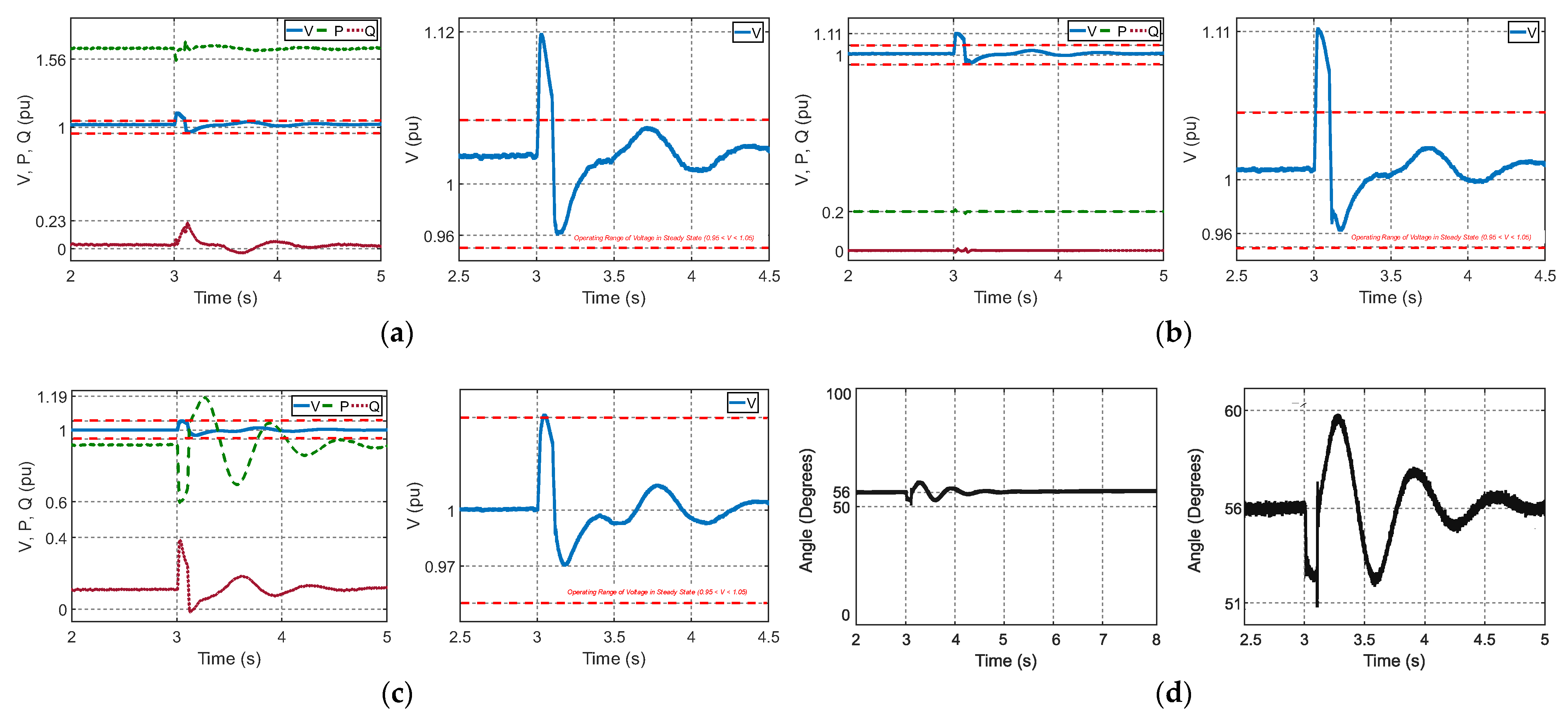
4.2. Scenario 1: Three-Phase Fault at Wind Power Plant Terminals
4.2.1. Generators Analysis
4.2.2. Bus and System Frequency Analysis
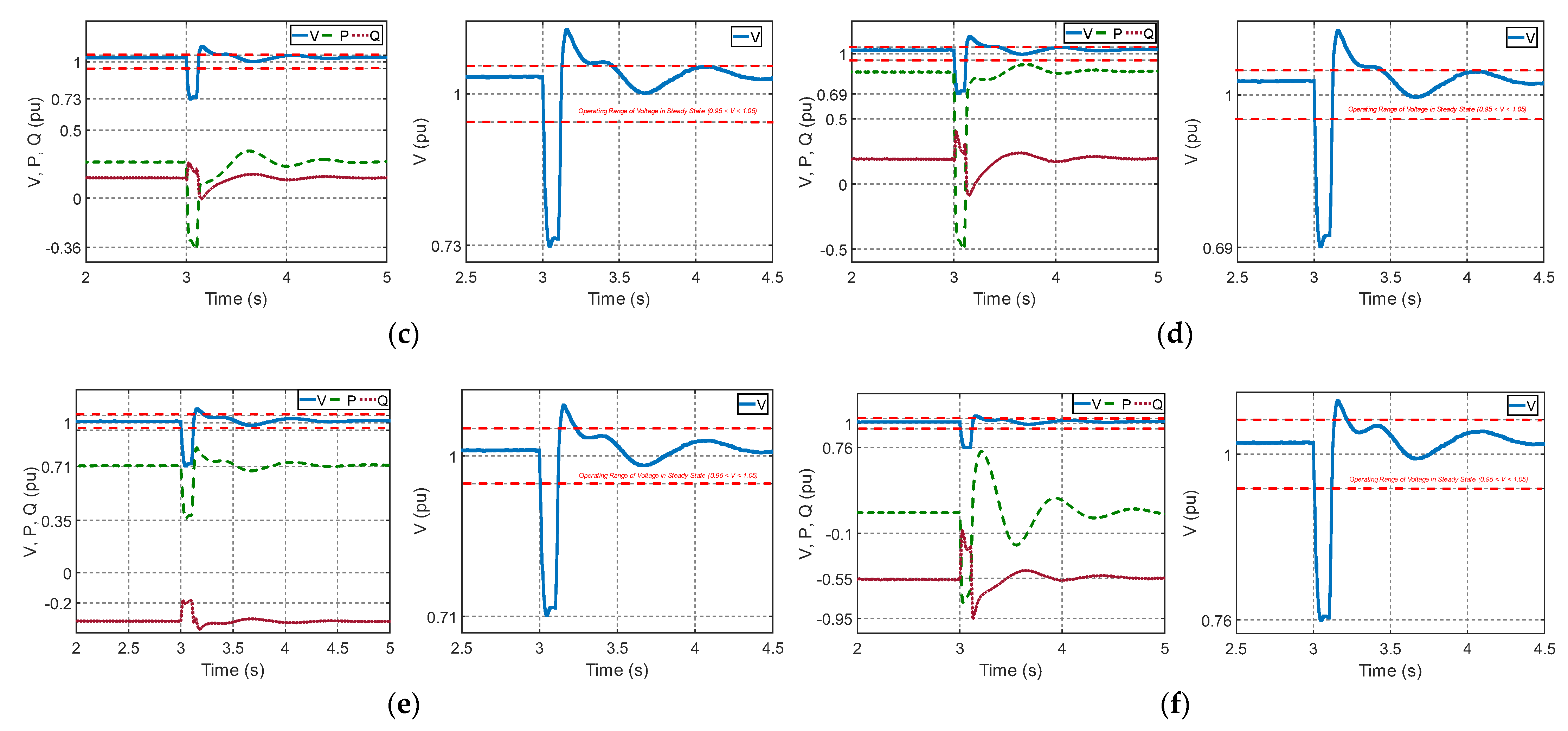
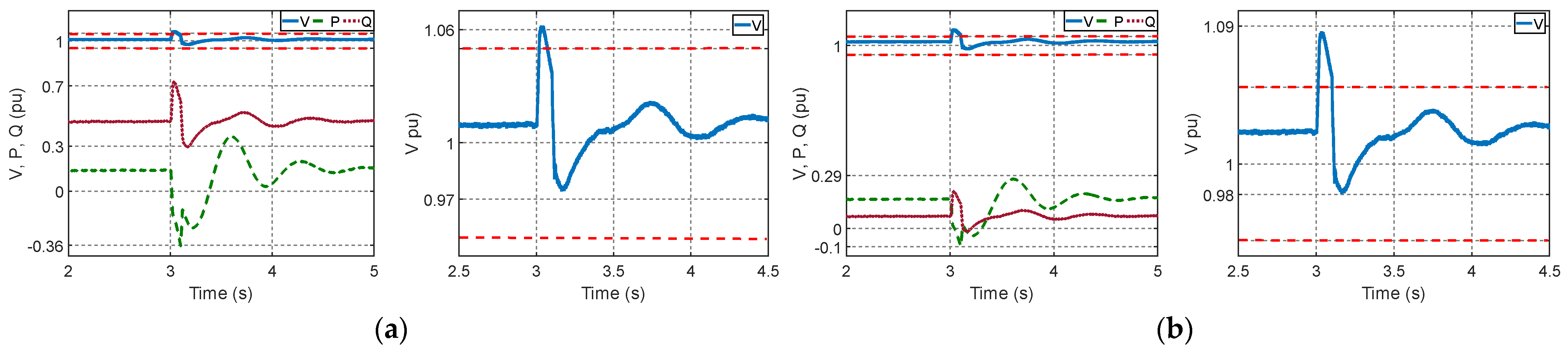
4.3. Scenario 2: Load Rejection at Bus 5
4.3.1. Generators Analysis
4.3.2. Bus and System Frequency Analysis
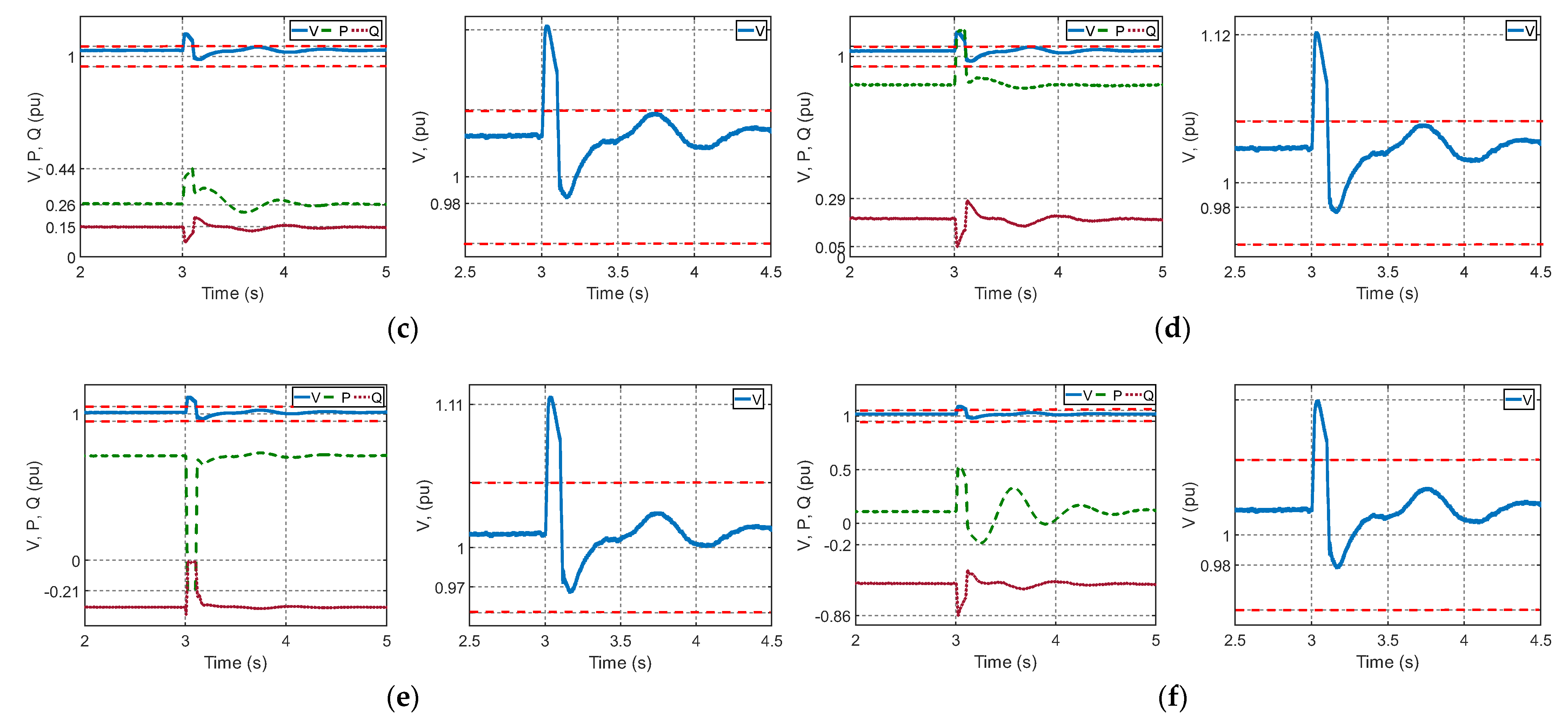
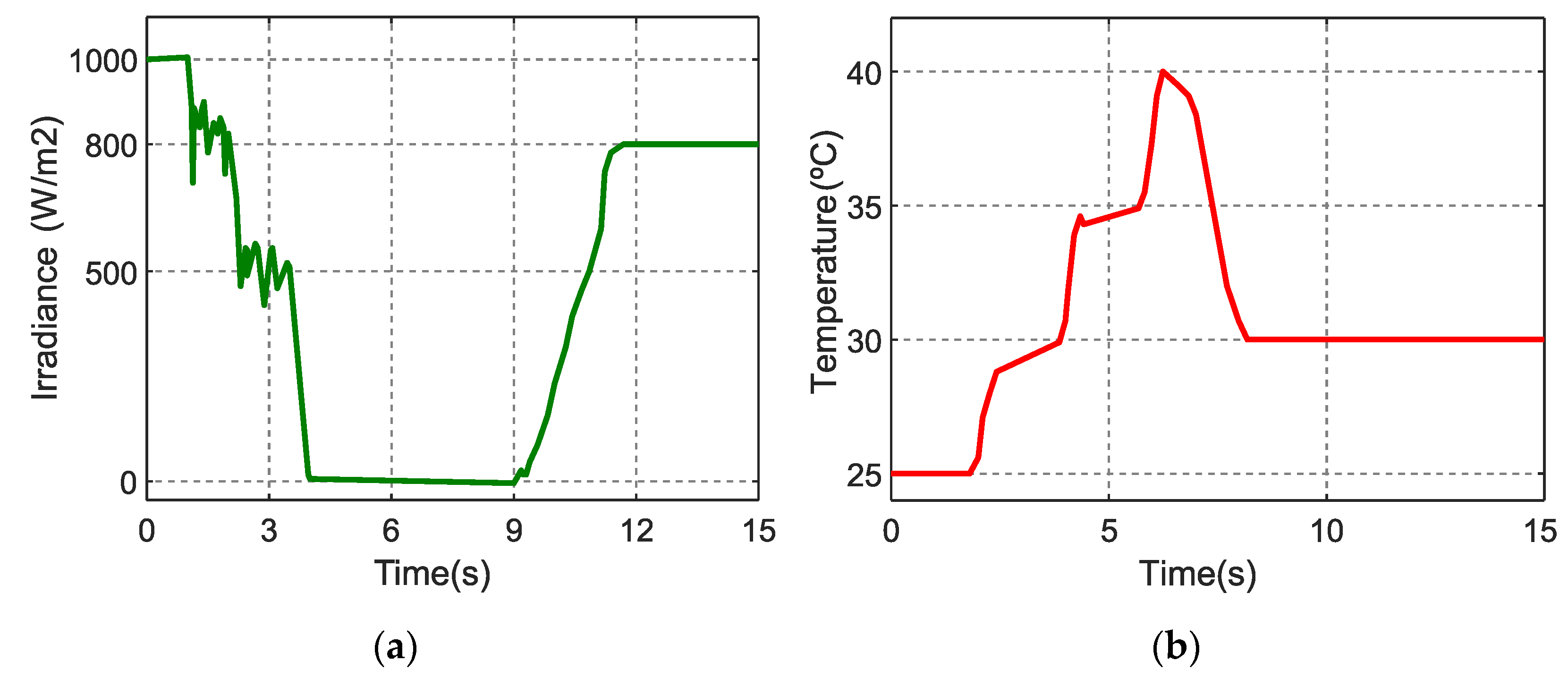
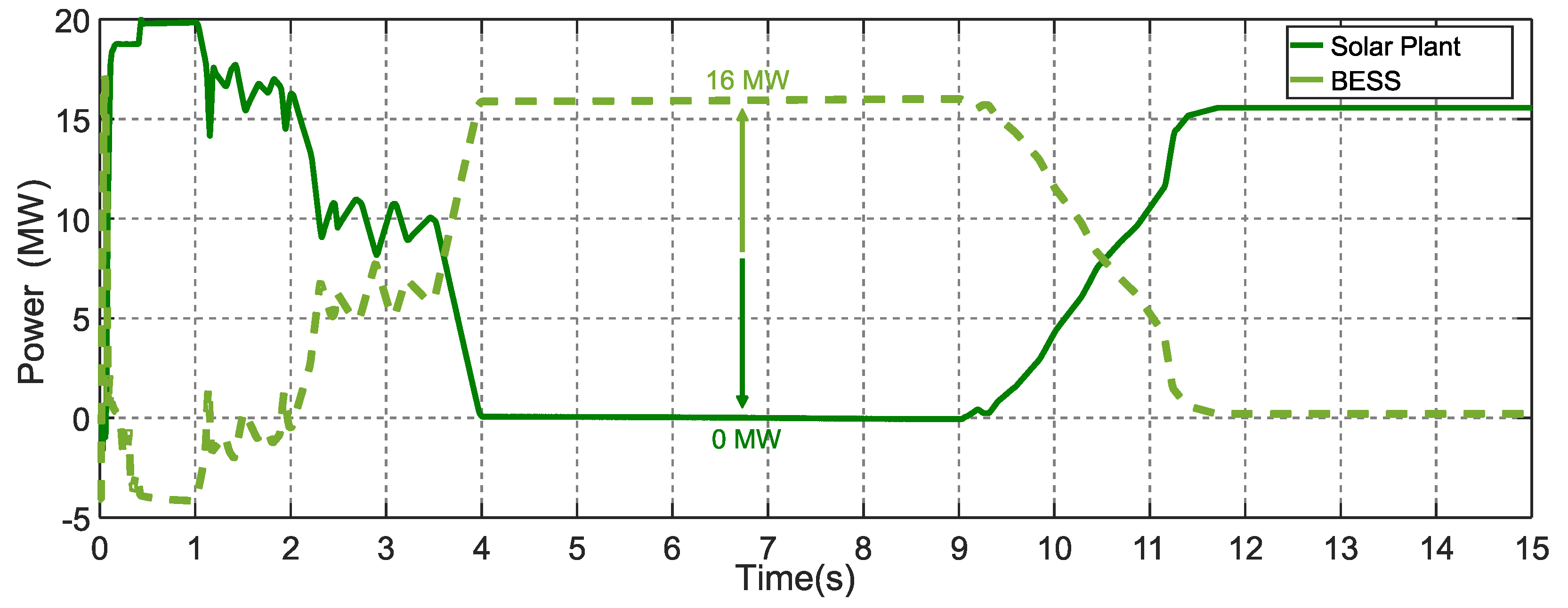
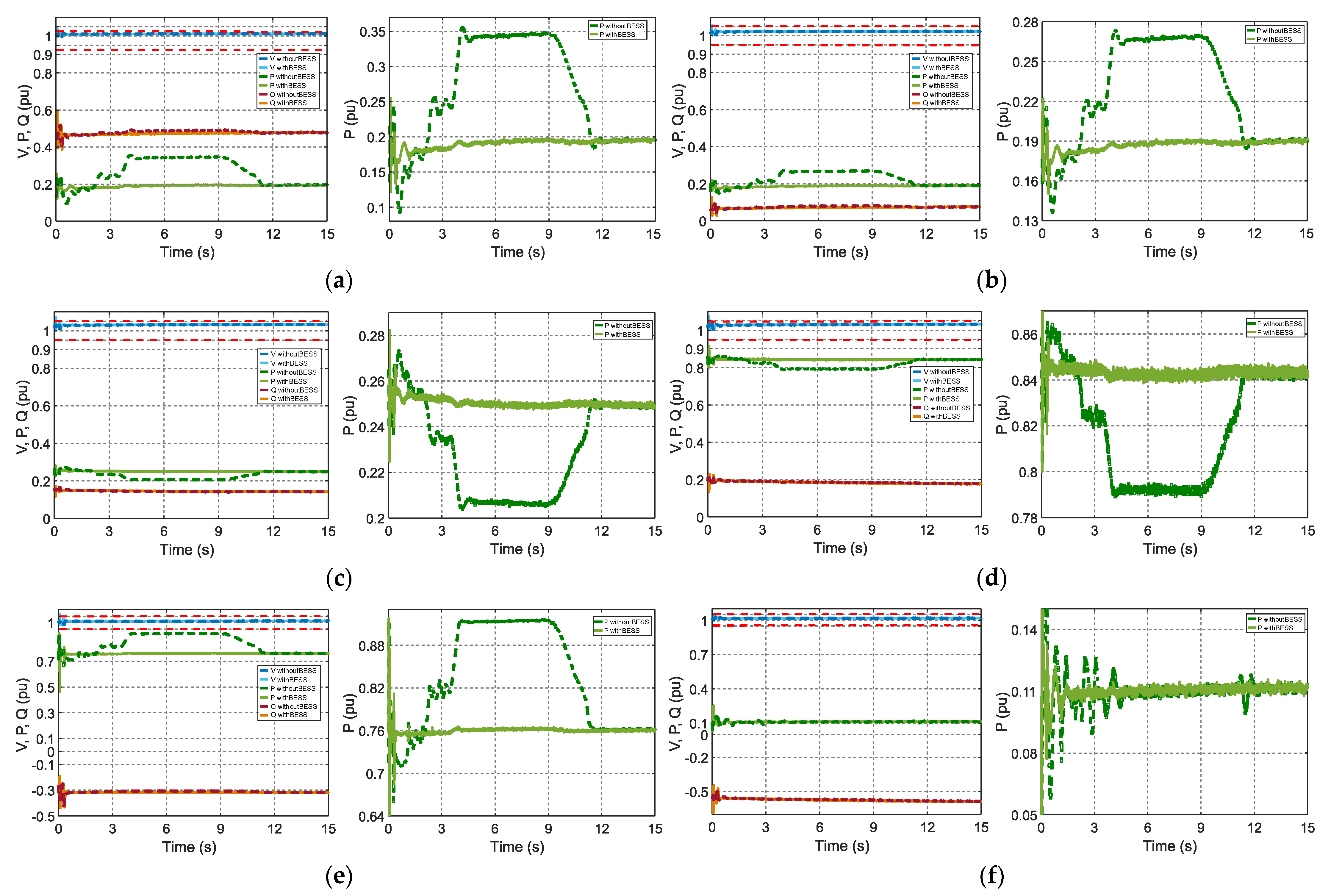
4.4. Scenario 3: Power Variation at the Solar Power Plant and BESS Performance
4.4.1. Solar Plant in Conjunction with BESS Analysis
4.4.2. Bus and System Frequency Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Description | Value | Unit |
|---|---|---|
| Rated power of a DFIG turbine | 1.5 | MW |
| Number of turbines | 110 | unit |
| Full power | 165 | MW |
| Rated voltage rms (L–L) | 575 | V |
| Number of poles | 3 | unit |
| Stator resistance | 0.023 | Ω |
| Rotor resistance | 0.019 | Ω |
| Stator inductance | 0.18 | H |
| Rotor inductance | 0.16 | H |
| DC link voltage | 1150 | V |
| DC link capacitor | 10 | µF |
| Wind speed to rated power | 15 | m/s |
| Wind turbine inertia constant | 4.32 | s |
| Maximum pitch angle | 27 | ° |
| Description | Value | Unit |
|---|---|---|
| Interconnected power plants in the PCC | 2 | unit |
| Rated power (per plant) | 10 | MW |
| Rated power (total) | 20 | MW |
| PV module model | SPR-305-WHT-D | - |
| Number of modules in series (per plant) | 50 | unit |
| Number of modules in parallel (per plant) | 660 | unit |
| Maximum rated power of the module | 30,523 | W |
| Number of cells per module | 96 | unit |
| Voltage at the maximum power point | 54.7 | V |
| Current at the maximum power point | 5.58 | A |
| Open-circuit voltage | 64.2 | V |
| Short-circuit current | 5.96 | A |
| Description | Value | Unit |
|---|---|---|
| Rated energy | 48 | MWh |
| Nominal capacity | 40,000 | Ah |
| Rated voltage | 1200 | V |
| Voltage at full load | 1413.559 | V |
| Rated discharge current | 8698.652 | A |
| Initial state of charge | 50 | % |
| Capacity at rated voltage | 19,230.77 | Ah |
| Voltage constant | 1301.5896 | V |
| Internal resistance | 0.0006 | Ω |
| Polarization resistance | 0.00074744 | Ω |
| Exponential zone | 1301; 4000 | V; Ah |
| Description | Value | Unit |
|---|---|---|
| Inductor | 5 | mH |
| Output capacitor | 8 | µF |
| IGBT resistance | 0.001 | Ω |
| Switching frequency | 12 | kHz |
| Input voltage | 1200 | V |
| Output voltage | 5000 | V |
| Sn (MVA) | Pm (pu) | H (s) | Rs (pu) | XI (pu) | Xd (pu) | X’d (pu) |
|---|---|---|---|---|---|---|
| 100 | 0.85 | 3.01 | 0.0031 | 0.005 | 1.3125 | 0.1813 |
| X″d (pu) | Xq (pu) | X″q (pu) | T′do (pu) | T″do (pu) | T′qo (pu) | ρ |
| 0.13 | 1.2578 | 0.1 | 5.89 | 0.04 | 0.099 | 20 |
| Tr (s) | Ka | Ta (s) | Ke | Te (s) | Tb (s) | Tc (s) | Kf | Tf (s) | Efmax (pu) | Kp |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.005 | 250 | 0.1 | 1 | 0.65 | 0 | 0 | 0.048 | 0.95 | 7 | 0 |
| Ta (s) | Ka | Rp | Kp | Ki | Kd | Td (s) | β | Tw (s) |
|---|---|---|---|---|---|---|---|---|
| 0.07 | 3.33 | 0.05 | 1.163 | 0.105 | 0 | 0.01 | 0 | 2.67 |
| Branch | R (pu) | X (pu) | Bsh (pu) |
|---|---|---|---|
| 1–2 | 0.01 | 0.085 | 0.088 |
| 1–6 | 0.039 | 0.17 | 0.179 |
| 2–3 | 0.032 | 0.161 | 0.153 |
| 2–6 | 0.032 | 0.161 | 0.153 |
| 3–4 | 0.0085 | 0.072 | 0.0745 |
| 3–6 | 0.032 | 0.161 | 0.153 |
| 4–5 | 0.0119 | 0.1008 | 0.1045 |
| 5–6 | 0.017 | 0.092 | 0.079 |
| Sn (MVA) | V1 (kV) | R1 (pu) | L1 (pu) | V2 (kV) | R2 (pu) | L2 (pu) | Rm (pu) | Lm (pu) | Tap | |
|---|---|---|---|---|---|---|---|---|---|---|
| Slack | 500 | 16.5 | 0 | 0.0576 | 230 | 0 | 0.0576 | 500 | 500 | 1 |
| Hydro | 110 | 13.8 | 0 | 0.0576 | 230 | 0 | 0.0576 | 500 | 500 | 1 |
| Wind | 200 | 0.575 | 0 | 0.0576 | 230 | 0 | 0.0576 | 500 | 500 | 1 |
| Solar | 30 | 18 | 0 | 0.0576 | 230 | 0 | 0.0576 | 500 | 500 | 1 |
Appendix B


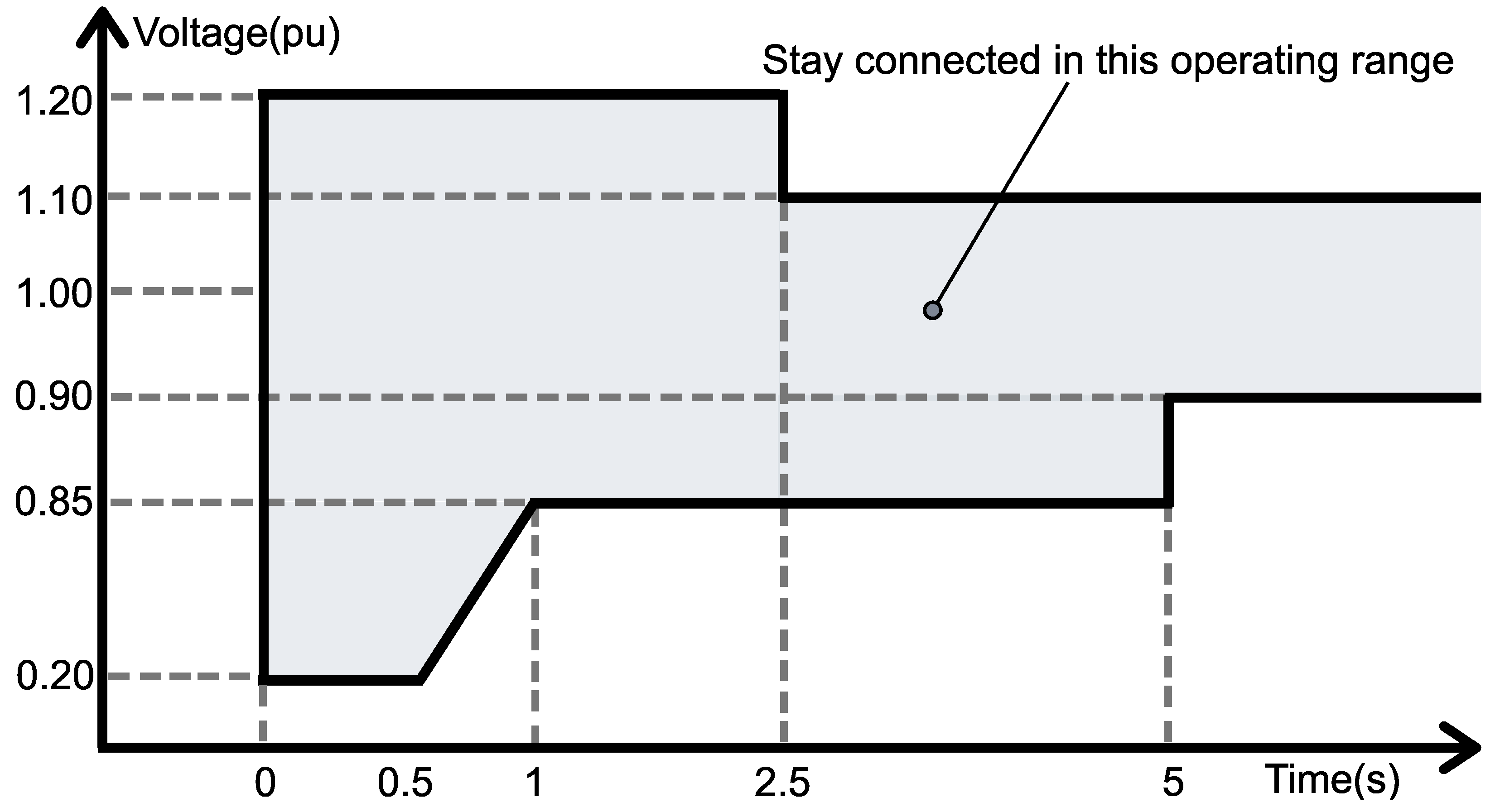
| Frequency Range (Hz) | Maximum Exposure Time (s) |
|---|---|
| f > 66.0 Hz | 0 |
| 63.5 Hz < f ≤ 66.0 Hz | 30 |
| 62.0 Hz < f ≤ 63.5 Hz | 150 |
| 60.5 Hz < f ≤ 62.0 Hz | 270 |
| 58.5 Hz ≤ f < 59.5 Hz | 390 |
| 57.5 Hz ≤ f < 58.5 Hz | 45 |
| 56.5 Hz ≤ f < 57.5 Hz | 15 |
| f < 56.5 Hz | 0 |
| Type of STVV | Duration of STVV | Amplitude of STVV Concerning the Rated Voltage (ARV) |
|---|---|---|
| Momentary voltage interruption (MVI) | ≤3 s | ARV < 0.1 pu |
| Momentary voltage sag (MVS) | ≥1 cycle and ≤3 s | 0.1 ≤ ARV < 0.9 pu |
| Momentary voltage rise (MVR) | ≥1 cycle and ≤3 s | ARV > 1.1 pu |
| Temporary voltage interruption (TVI) | >3 s and ≤1 min | ARV < 0.1 pu |
| Temporary voltage sag (TVS) | >3 s and ≤1 min | 0.1 ≤ ARV < 0.9 pu |
| Temporary voltage rise (TVR) | >3 s and ≤1 min | ARV > 1.1 pu |
References
- Sauer, P.W.; Pai, M.A.; Chow, J.H. Power System Dynamics and Stability: With Synchrophasor Measurement and Power System Toolbox, 2nd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2017; ISBN 9781119355755. [Google Scholar]
- Venkataraman, S.; Ziesler, C.; Johnson, P.; Van Kempen, S. Integrated Wind, Solar, and Energy Storage: Designing Plants with a Better Generation Profile and Lower Overall Cost. IEEE Power Energy Mag. 2018, 16, 74–83. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control, 1st ed.; McGraw-Hill Inc.: New York, NY, USA, 1994; ISBN 007035958. [Google Scholar]
- Attya, A.B.; Dominguez-Garcia, J.L.; Anaya-Lara, O. A review on frequency support provision by wind power plants: Current and future challenges. Renew. Sustain. Energy Rev. 2018, 81, 2071–2087. [Google Scholar] [CrossRef] [Green Version]
- Ullah, K.; Basit, A.; Ullah, Z.; Aslam, S.; Herodotou, H. Automatic Generation Control Strategies in Conventional and Modern Power Systems: A Comprehensive Overview. Energies 2021, 14, 2376. [Google Scholar] [CrossRef]
- Rahman, M.J.; Tafticht, T.; Doumbia, M.L.; Mutombo, N.M.-A. Dynamic Stability of Wind Power Flow and Network Frequency for a High Penetration Wind-Based Energy Storage System Using Fuzzy Logic Controller. Energies 2021, 14, 4111. [Google Scholar] [CrossRef]
- Asiaban, S.; Kayedpour, N.; Samani, A.E.; Bozalakov, D.; De Kooning, J.D.M.; Crevecoeur, G.; Vandevelde, L. Wind and Solar Intermittency and the Associated Integration Challenges: A Comprehensive Review including the Status in the Belgian Power System. Energies 2021, 14, 2630. [Google Scholar] [CrossRef]
- Dreidy, M.; Mokhlis, H.; Mekhilef, S. Inertia response and frequency control techniques for renewable energy sources: A review. Renew. Sustain. Energy Rev. 2017, 69, 144–155. [Google Scholar] [CrossRef]
- Robyns, B.; François, B.; Delille, G.; Saudemont, C. Energy Storage in Electric Power Grids; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; ISBN 9781119058724. [Google Scholar]
- Tielens, P.; Van Hertem, D. The relevance of inertia in power systems. Renew. Sustain. Energy Rev. 2016, 55, 999–1009. [Google Scholar] [CrossRef]
- Nadeem, F.; Hussain, S.M.S.; Tiwari, P.K.; Goswami, A.K.; Ustun, T.S. Comparative review of energy storage systems, their roles, and impacts on future power systems. IEEE Access 2019, 7, 4555–4585. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Energy Storage Data. Available online: https://www.iea.org/fuels-and-technologies/energy-storage (accessed on 5 February 2022).
- Dehghani-Sanij, A.R.; Tharumalingam, E.; Dusseault, M.B.; Fraser, R. Study of energy storage systems and environmental challenges of batteries. Renew. Sustain. Energy Rev. 2019, 104, 192–208. [Google Scholar] [CrossRef]
- Wan, C.; Qian, W.; Zhao, C.; Song, Y.; Yang, G. Probabilistic Forecasting Based Sizing and Control of Hybrid Energy Storage for Wind Power Smoothing. IEEE Trans. Sustain. Energy 2021, 12, 1841–1852. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Ciupageanu, D.A.; Micangeli, A.; Ottaviano, P.A.; Pelosi, D. Real time power management strategy for hybrid energy storage systems coupled with variable energy sources in power smoothing applications. Energy Rep. 2021, 7, 2872–2882. [Google Scholar] [CrossRef]
- Rallabandi, V.; Akeyo, O.M.; Jewell, N.; Ionel, D.M. Incorporating battery energy storage systems into multi-MW grid connected PV systems. IEEE Trans. Ind. Appl. 2019, 55, 638–647. [Google Scholar] [CrossRef]
- Huang, J.; Jiang, Z.; Negnevitsky, M. Ancillary Service by Tiered Energy Storage Systems. J. Energy Eng. 2022, 148, 04021059. [Google Scholar] [CrossRef]
- Gomez, L.A.G.; Grilo, A.P.; Salles, M.B.C.; Filho, A.J.S. Combined Control of DFIG-Based Wind Turbine and Battery Energy Storage System for Frequency Response in Microgrids. Energies 2020, 13, 894. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Z.; Zecchino, A.; Cherkaoui, R.; Paolone, M. Real-Time Control of Battery Energy Storage Systems to Provide Ancillary Services Considering Voltage-Dependent Capability of DC-AC Converters. IEEE Trans. Smart Grid 2021, 12, 4164–4175. [Google Scholar] [CrossRef]
- Mustafa, M.B.; Keatley, P.; Huang, Y.; Agbonaye, O.; Ademulegun, O.O.; Hewitt, N. Evaluation of a battery energy storage system in hospitals for arbitrage and ancillary services. J. Energy Storage 2021, 43, 103183. [Google Scholar] [CrossRef]
- Ghiasi, M. Detailed study, multi-objective optimization, and design of an AC-DC smart microgrid with hybrid renewable energy resources. Energy 2019, 169, 496–507. [Google Scholar] [CrossRef]
- Murty, V.V.; Kumar, A. Optimal Energy Management and Techno-economic Analysis in Microgrid with Hybrid Renewable Energy Sources. J. Mod. Power Syst. Clean Energy 2020, 8, 929–940. [Google Scholar] [CrossRef]
- Ghiasi, M.; Esmaeilnamazi, S.; Ghiasi, R.; Fathi, M. Role of Renewable Energy Sources in Evaluating Technical and Economic Efficiency of Power Quality. Technol. Econ. Smart Grids Sustain. Energy 2020, 5, 1. [Google Scholar] [CrossRef] [Green Version]
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; et al. Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar] [CrossRef]
- Sauer, P.W.M.P. Power System Dynamics and Stability, 1st ed.; Prentice Hall: Urbana, IL, USA, 1997; ISBN 9781588746733. [Google Scholar]
- Eremia, M.; Shahidehpour, M. Handbook of Electrical Power System Dynamics: Modeling, Stability, and Control, 1st ed.; Eremia, M., Shahidehpour, M., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; ISBN 9781118497173. [Google Scholar]
- Alzahrani, S.; Shah, R.; Mithulananthan, N. Examination of Effective VAr with Respect to Dynamic Voltage Stability in Renewable Rich Power Grids. IEEE Access 2021, 9, 75494–75508. [Google Scholar] [CrossRef]
- Niu, S.; Zhang, Z.; Ke, X.; Zhang, G.; Huo, C.; Qin, B. Impact of renewable energy penetration rate on power system transient voltage stability. Energy Rep. 2022, 8, 487–492. [Google Scholar] [CrossRef]
- Collados-Rodriguez, C.; Cheah-Mane, M.; Prieto-Araujo, E.; Gomis-Bellmunt, O. Stability and operation limits of power systems with high penetration of power electronics. Int. J. Electr. Power Energy Syst. 2022, 138, 107728. [Google Scholar] [CrossRef]
- Eftekharnejad, S.; Vittal, V.; Heydt, G.T.; Keel, B.; Loehr, J. Impact of increased penetration of photovoltaic generation on power systems. IEEE Trans. Power Syst. 2013, 28, 893–901. [Google Scholar] [CrossRef]
- Xiong, L.; Li, P.; Wu, F.W.; Wang, J. Stability Enhancement of Power Systems with High DFIG-Wind Turbine Penetration via Virtual Inertia Planning. IEEE Trans. Power Syst. 2019, 34, 1352–1361. [Google Scholar] [CrossRef]
- Hansen, A.D.; Das, K.; Sørensen, P.; Singh, P.; Gavrilovic, A. European and Indian Grid Codes for Utility Scale Hybrid Power Plants. Energies 2021, 14, 4335. [Google Scholar] [CrossRef]
- Roberts, C. Review of International Grid Codes; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2018.
- International Renewable Energy Agency (IRENA). Scaling up Variable Renewable Power: The Role of Grid Codes; International Renewable Energy Agency (IRENA): Abu Dhabi, United Arab Emirates, 2016. [Google Scholar]
- Rodrigues, E.M.G.; Osório, G.J.; Godina, R.; Bizuayehu, A.W.; Lujano-Rojas, J.M.; Catalão, J.P.S. Grid code reinforcements for deeper renewable generation in insular energy systems. Renew. Sustain. Energy Rev. 2016, 53, 163–177. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q.; Hannan, M.A.; Jern, K.P.; Mansur, M.; Mahlia, T.M.I. Grid-connected renewable energy sources: Review of the recent integration requirements and control methods. J. Clean. Prod. 2020, 253, 119831. [Google Scholar] [CrossRef]
- Vrana, T.K.; Attya, A.; Trilla, L. Future-oriented generic grid code regarding wind power plants in Europe. Int. J. Electr. Power Energy Syst. 2021, 125, 106490. [Google Scholar] [CrossRef]
- Operador Nacional do Sistema Elétrico (ONS). Procedimentos de Rede. Available online: http://www.ons.org.br/paginas/sobre-o-ons/procedimentos-de-rede/vigentes (accessed on 22 February 2022).
- Abad, G.; López, J.; Rodríguez, M.A.; Marroyo, L.; Iwanski, G. Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation, 1st ed.; IEEE Press, Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; ISBN 9781118104965. [Google Scholar]
- Wu, B.; Lang, Y.; Zargari, N.; Kouro, S. Power Conversion and Control of Wind Energy Systems, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; ISBN 9780470593653. [Google Scholar]
- Edgar, N.; Sanchez, R.R.-C. Doubly Fed Induction Generators Control for Wind Energy, 1st ed.; CRC Press: Boca Raton, FL, USA, 2016; ISBN 978-1-4987-4584-0. [Google Scholar]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; ISBN 9780470551578. [Google Scholar]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook, 2nd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2011; ISBN 9781119992714. [Google Scholar]
- Ackermann, T. Wind Power in Power Systems, 2nd ed.; Ackermann, T., Ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2012; ISBN 9781119941842. [Google Scholar]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 2nd ed.; Kluwer Academic Publishers: Norwell, MA, USA, 2000; ISBN 0471017507. [Google Scholar]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics Converters: Applications, and Design, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003; ISBN 9780511544828. [Google Scholar]
- Masters, G.M. Renewable and Efficient Electric Power Systems, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; ISBN 9780471668824. [Google Scholar]
- Esram, T.; Chapman, P.L. Comparison of photovoltaic array maximum power point tracking techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef] [Green Version]
- Glover, J.D.; Sarma, M.S.; Overbye, T.J. Power System Analysis and Design; Cengage Learning: Stamford, CT, USA, 2011; ISBN 978-1-111-42577. [Google Scholar]
- Anderson, P.M.; Fouad, A.A. Power System Control and Stability, 2nd ed.; IEEE Press: Hoboken, NJ, USA, 2003; ISBN 9780471238621. [Google Scholar]
- Mathworks Simscape Electrical Reference (Specialized Power Systems) Version 7.1; Mathworks: Natick, MA, USA, 2019.
- De Mello, F.P.; Koessler, R.J.; Aaee, J.; Anderson, P.M.; Doudna, J.H.; Fish, J.H.; Hamm, P.A.L.; Kundur, P.; Lee, D.C.; Rogers, G.J.; et al. Hydraulic turbine and turbine control models for system dynamic studies. IEEE Trans. Power Syst. 1992, 7, 167–179. [Google Scholar] [CrossRef]
- IEEE. 421.5-1992 IEEE Recommended Practice for Excitation System Models for Power System Stability Studies; IEEE: Piscataway, NJ, USA, 1992. [Google Scholar]
- Arrillaga, J.; Watson, N.R. Computer Modelling of Electrical Power Systems, 2nd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2013; ISBN 9781118878286. [Google Scholar]
- Fitzgerald, A.E.; Kingsley, C.; Umans, S.D. Electric Machinery, 6th ed.; Mc Graw Hill: New York, NY, USA, 2003; ISBN 0073660094. [Google Scholar]
- IEEE Task Force. Load representation for dynamic performance analysis (of power systems). IEEE Trans. Power Syst. 1993, 8, 472–482. [Google Scholar] [CrossRef]
- Stagg, G.W.; El-Abiad, A.H. Computer Methods in Power System Analysis; McGraw-Hill Inc.: New York, NY, USA, 1968; ISBN 67-12963. [Google Scholar]
- Luque, A.; Hegedus, S. Handbook of Photovoltaic Science and Engineering, 1st ed.; Luque, A., Hegedus, S., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2003; ISBN 9780470014004. [Google Scholar]
- Tremblay, O.; Dessaint, L.-A. Experimental Validation of a Battery Dynamic Model for EV Applications. World Electr. Veh. J. 2009, 3, 289–298. [Google Scholar] [CrossRef] [Green Version]
- Sarrias, R.; Fernández, L.M.; García, C.A.; Jurado, F. Coordinate operation of power sources in a doubly-fed induction generator wind turbine/battery hybrid power system. J. Power Sources 2012, 205, 354–366. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.-A.; Dekkiche, A.-I. A Generic Battery Model for the Dynamic Simulation of Hybrid Electric Vehicles. In Proceedings of the 2007 IEEE Vehicle Power and Propulsion Conference, Arlington, TX, USA, 9–12 September 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 284–289. [Google Scholar]
- Saw, L.H.; Somasundaram, K.; Ye, Y.; Tay, A.A.O. Electro-thermal analysis of Lithium Iron Phosphate battery for electric vehicles. J. Power Sources 2014, 249, 231–238. [Google Scholar] [CrossRef]
- Caricchi, F.; Crescimbini, F.; Capponi, F.G.; Solero, L. Study of bi-directional buck-boost converter topologies for application in electrical vehicle motor drives. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition-APEC, Anaheim, CA, USA, 15–19 February 1998; IEEE: Piscataway, NJ, USA, 1998; Volume 1, pp. 287–293. [Google Scholar]
- Perez, F.; Custodio, J.F.; De Souza, V.G.; Filho, H.K.R.; Motoki, E.M.; Ribeiro, P.F. Application of energy storage elements on a PV system in the smart grid context. In Proceedings of the 2015 IEEE PES Innovative Smart Grid Technologies Latin America, ISGT LATAM 2015, Montevideo, Uruguay, 5–7 October 2015; IEEE: Piscataway, NJ, USA, 2016; pp. 751–756. [Google Scholar]
- Lopes, J.C.; Sousa, T.; da Silva Benedito, R.; Trigoso, F.B.M.; Garzon Medina, D.O. Application of Battery Energy Storage System in Photovoltaic Power Plants Connected to the Distribution Grid. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Conference-Latin America (ISGT Latin America), Gramado City, Brazil, 15–18 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Perelmuter, V. Renewable Energy Systems: Simulation with Simulink® and SimPowerSystems™, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781498765985. [Google Scholar]
- Slootweg, J.G.; Polinder, H.; Kling, W.L. Representing Wind Turbine Electrical Generating Systems in Fundamental Frequency Simulations. IEEE Trans. Energy Convers. 2003, 18, 516–524. [Google Scholar] [CrossRef] [Green Version]
- Agência Nacional de Energia Elétrica (ANEEL). Resolução Normativa Aneel No 903, de 8 de Dezembro de. 2020. Available online: https://www.in.gov.br/en/web/dou/-/resolucao-normativa-aneel-n-903-de-8-de-dezembro-de-2020-294345560 (accessed on 4 February 2022).



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopes, J.C.; Sousa, T. Transmission System Electromechanical Stability Analysis with High Penetration of Renewable Generation and Battery Energy Storage System Application. Energies 2022, 15, 2060. https://doi.org/10.3390/en15062060
Lopes JC, Sousa T. Transmission System Electromechanical Stability Analysis with High Penetration of Renewable Generation and Battery Energy Storage System Application. Energies. 2022; 15(6):2060. https://doi.org/10.3390/en15062060
Chicago/Turabian StyleLopes, José Calixto, and Thales Sousa. 2022. "Transmission System Electromechanical Stability Analysis with High Penetration of Renewable Generation and Battery Energy Storage System Application" Energies 15, no. 6: 2060. https://doi.org/10.3390/en15062060
APA StyleLopes, J. C., & Sousa, T. (2022). Transmission System Electromechanical Stability Analysis with High Penetration of Renewable Generation and Battery Energy Storage System Application. Energies, 15(6), 2060. https://doi.org/10.3390/en15062060







