Flux-Weakening Drive for IPMSM Based on Model Predictive Control
Abstract
:1. Introduction
2. IPMSM Model
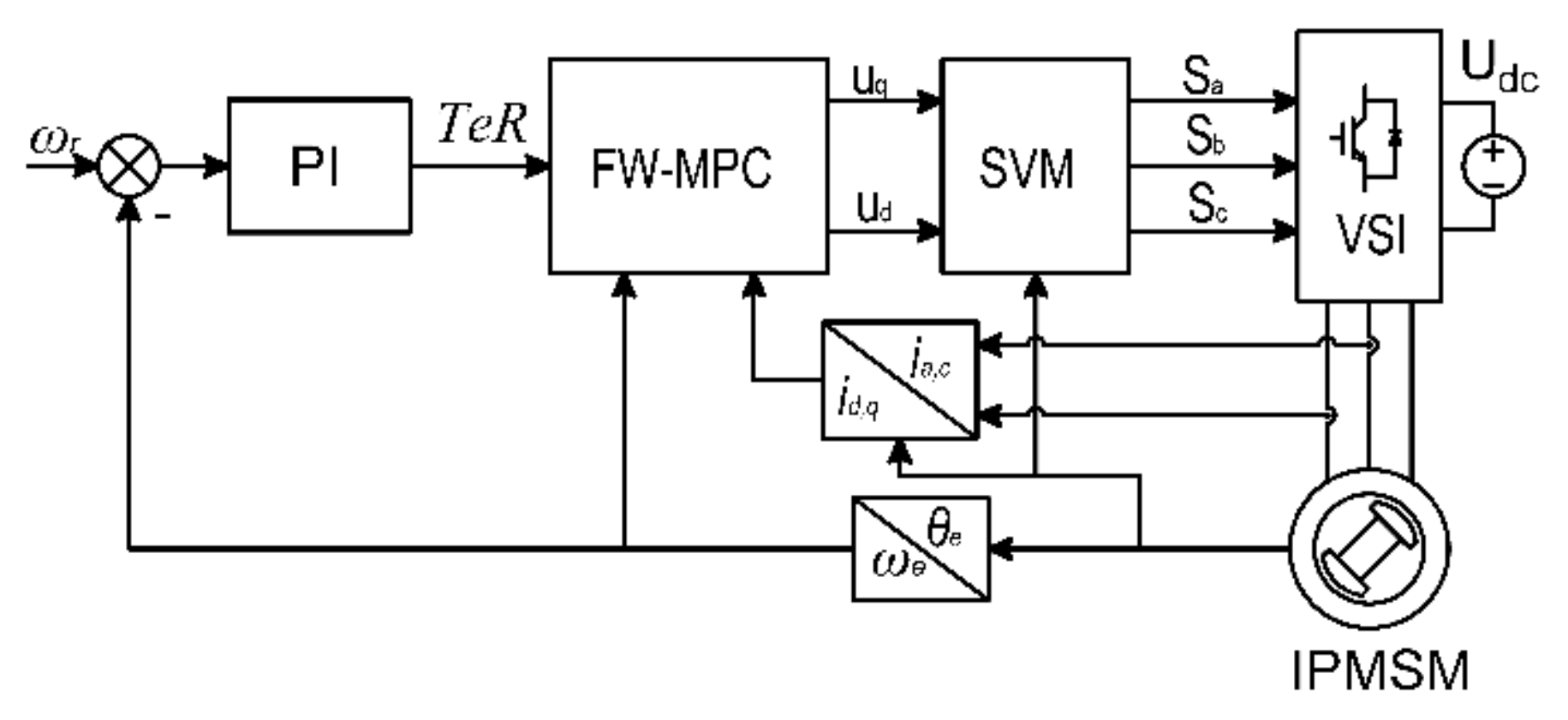
3. Control System
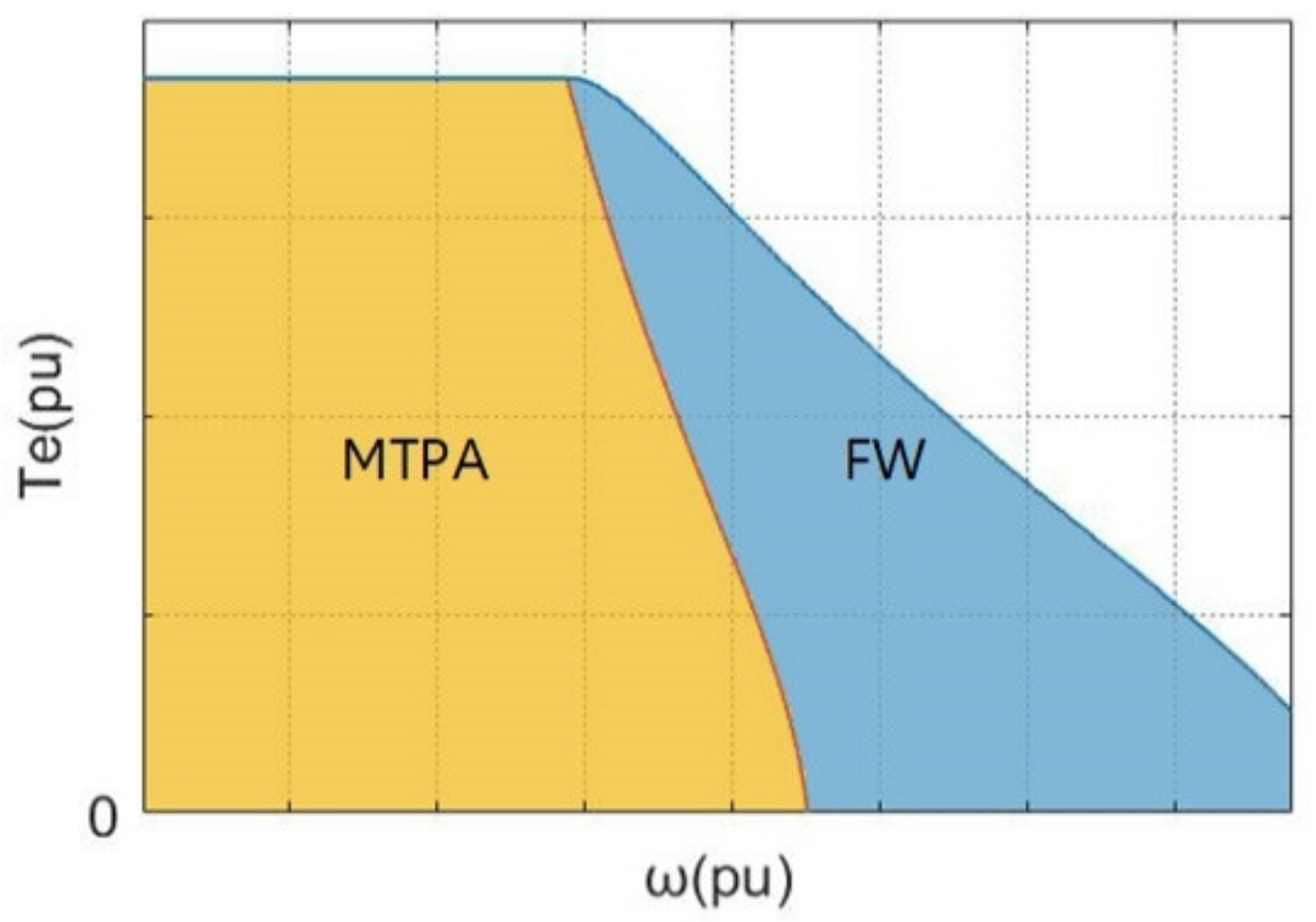
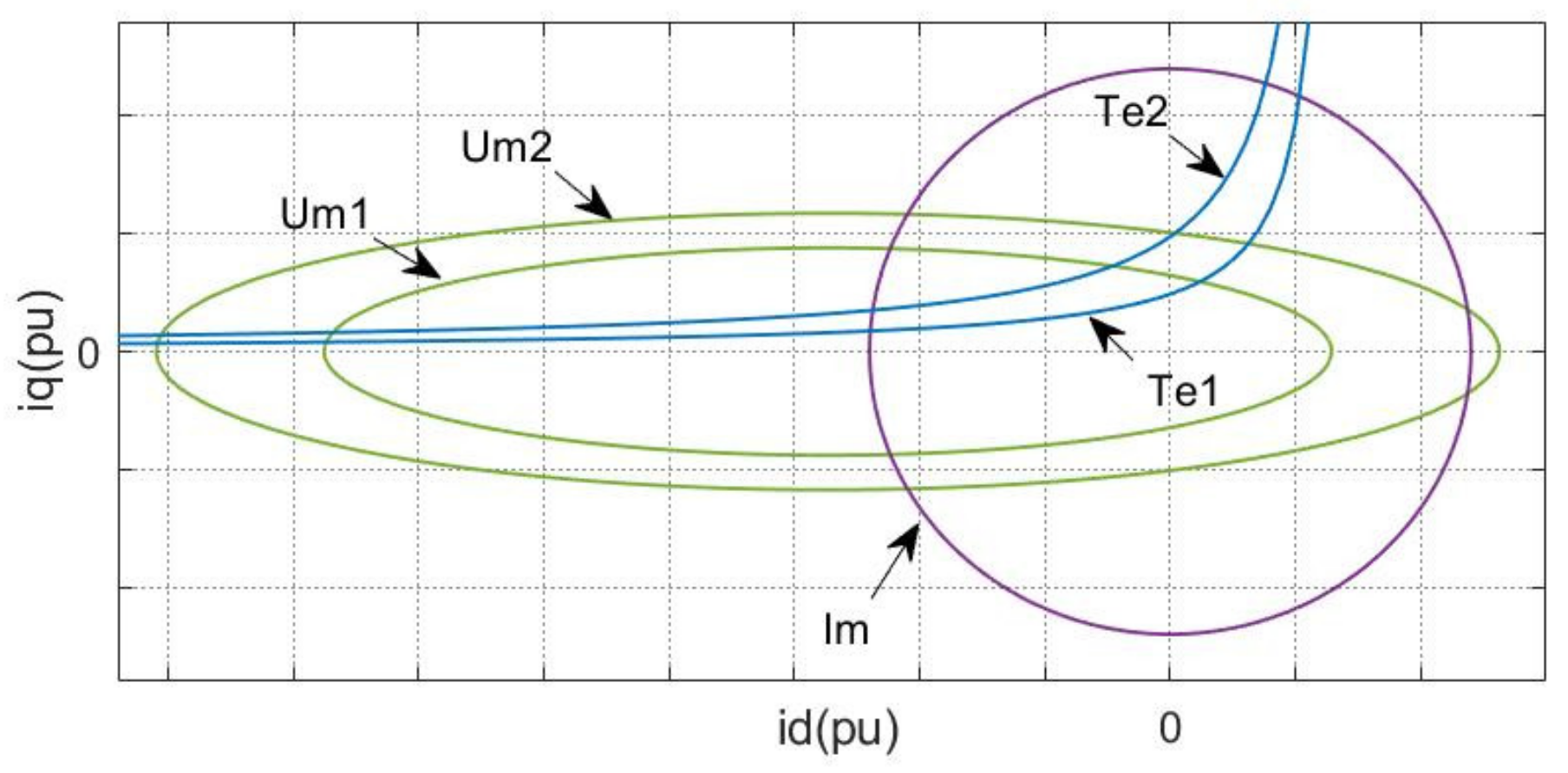
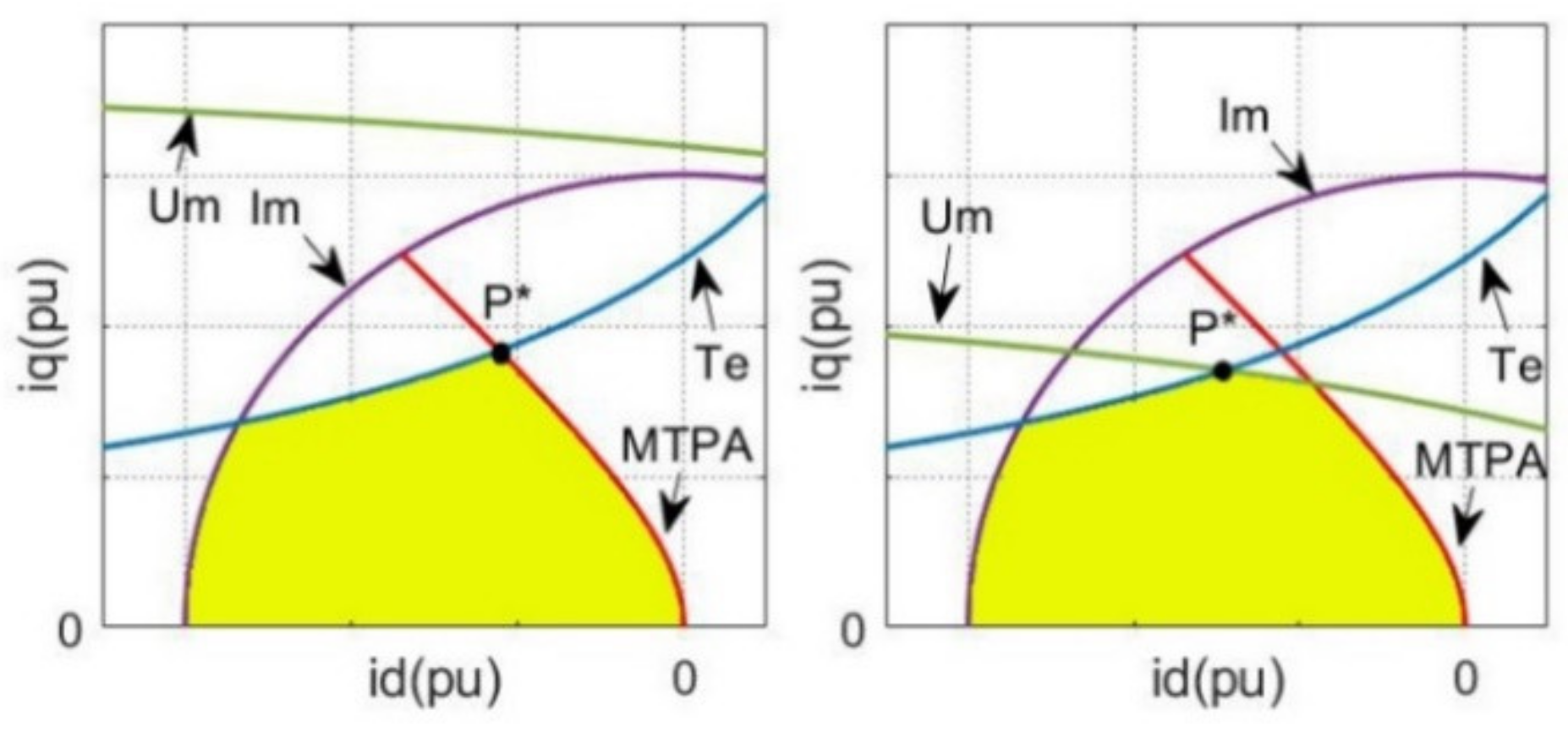
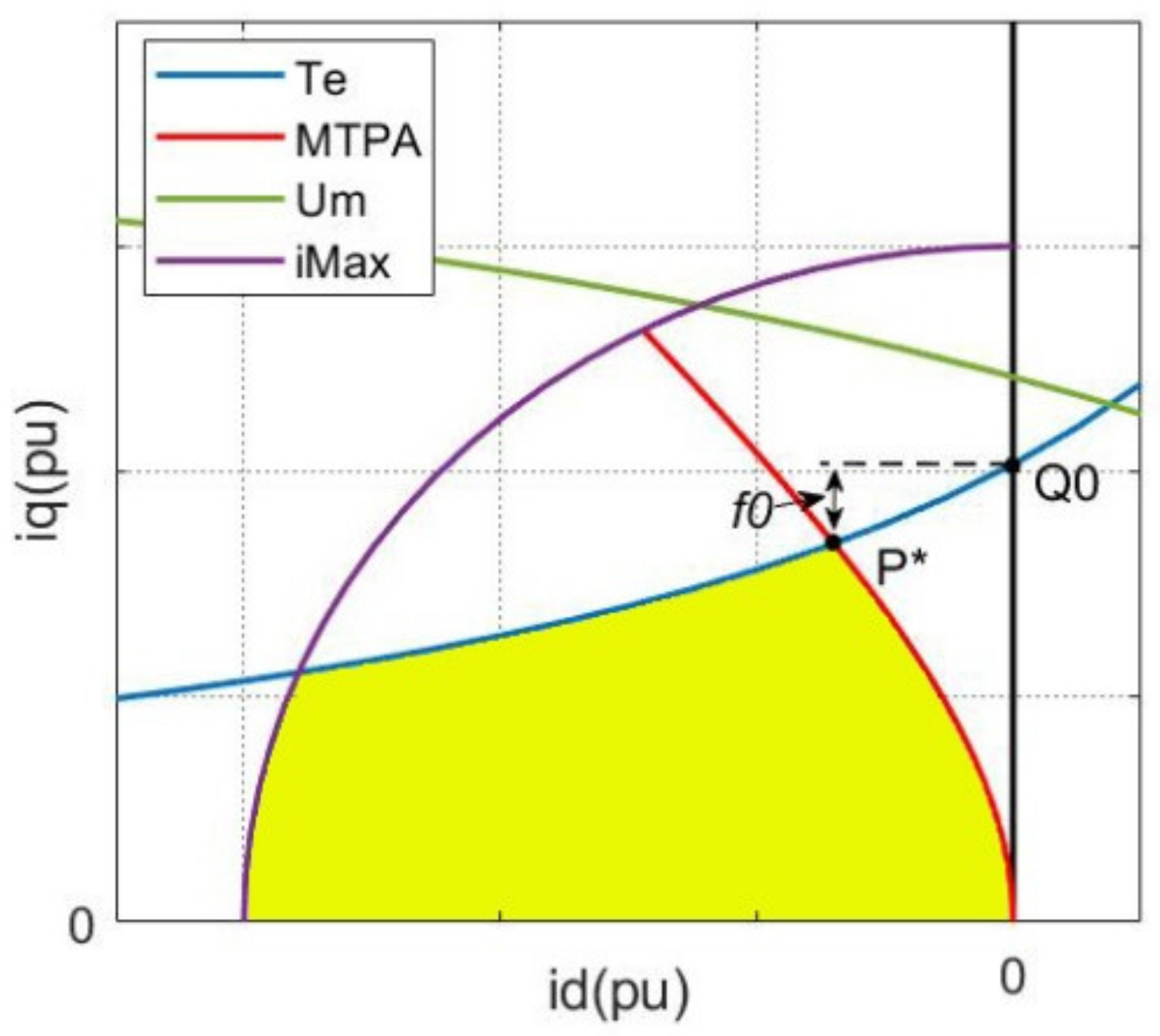
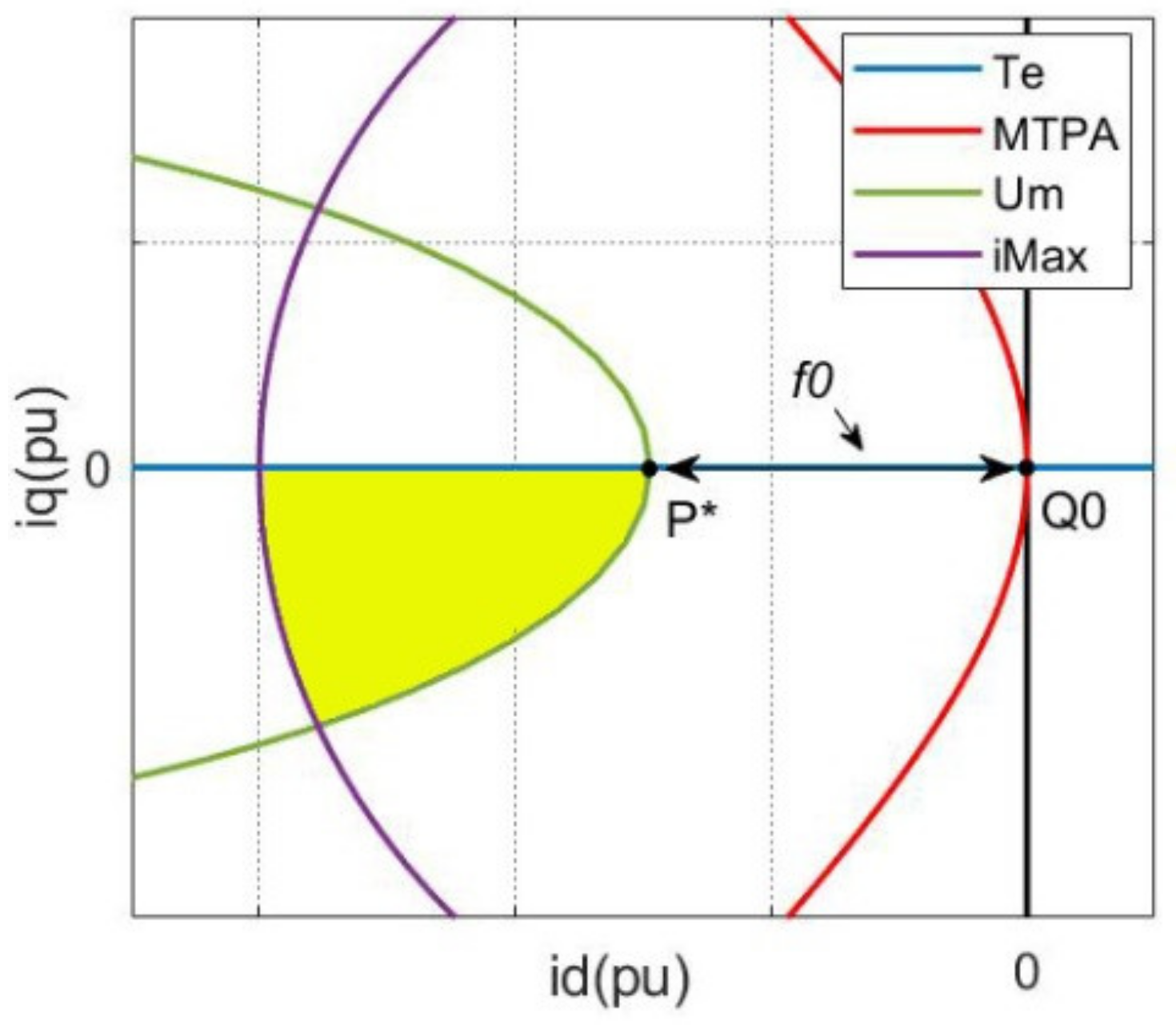
3.1. Equivalent Optimization Problem
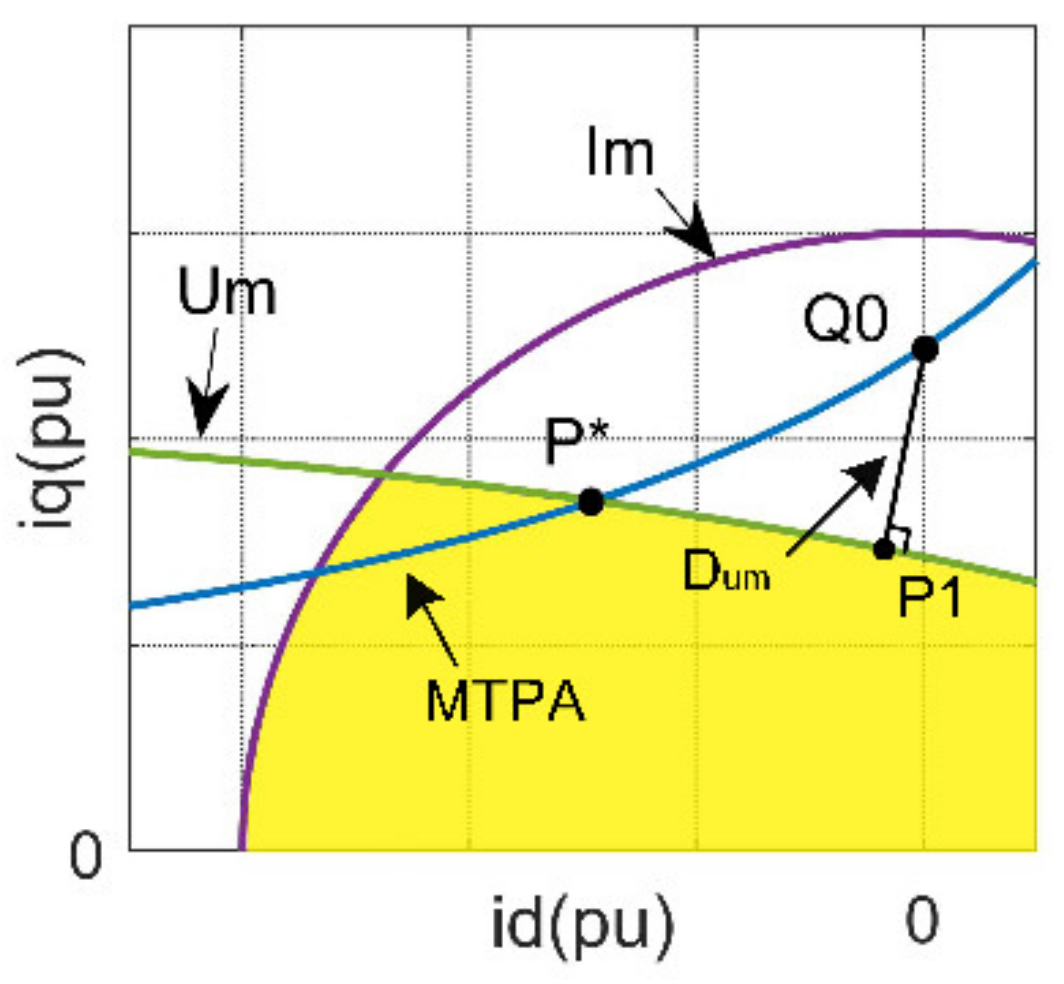
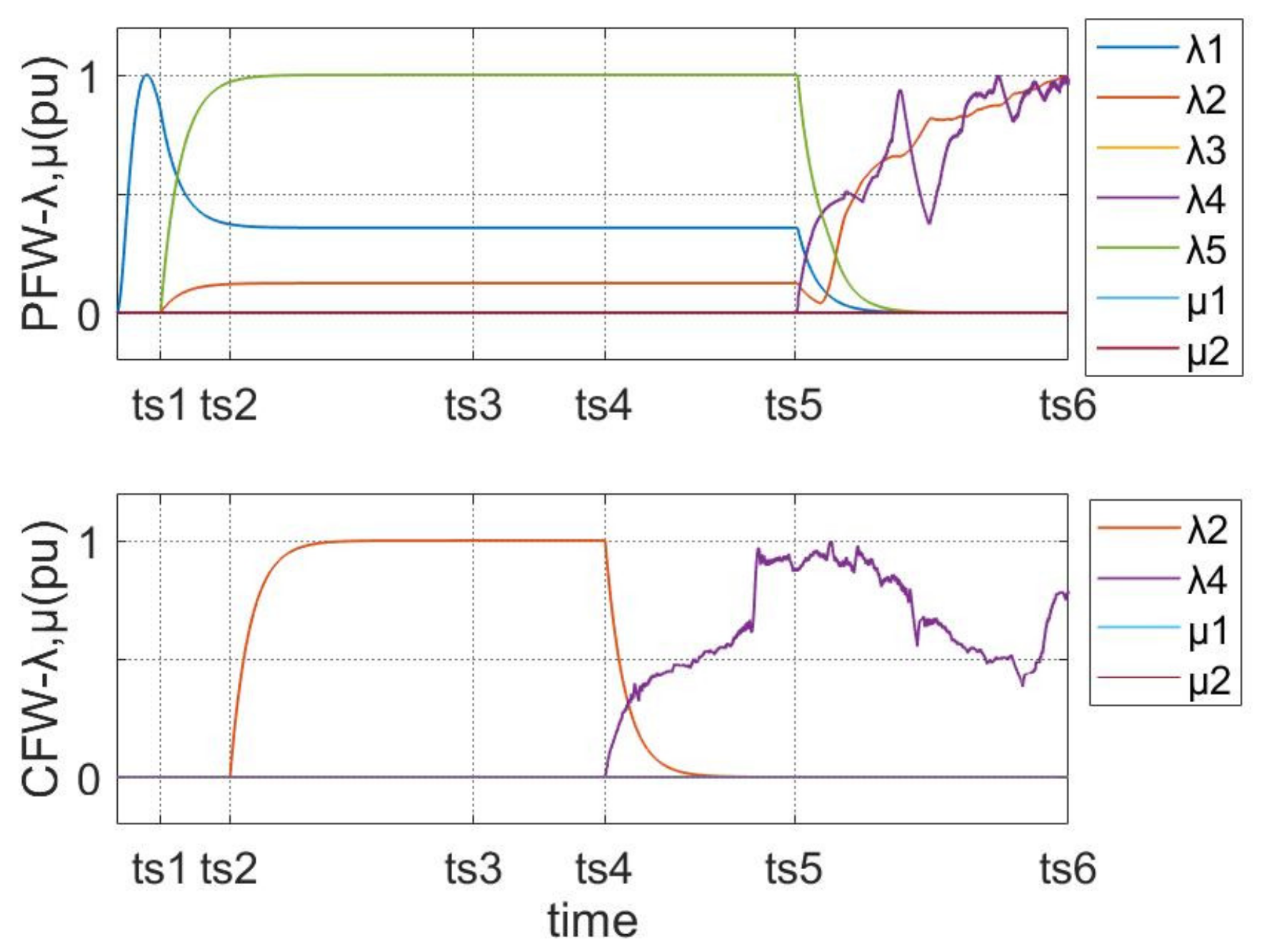
3.2. Proposed FW-MPC Strategy
3.3. Classical FW-MPC
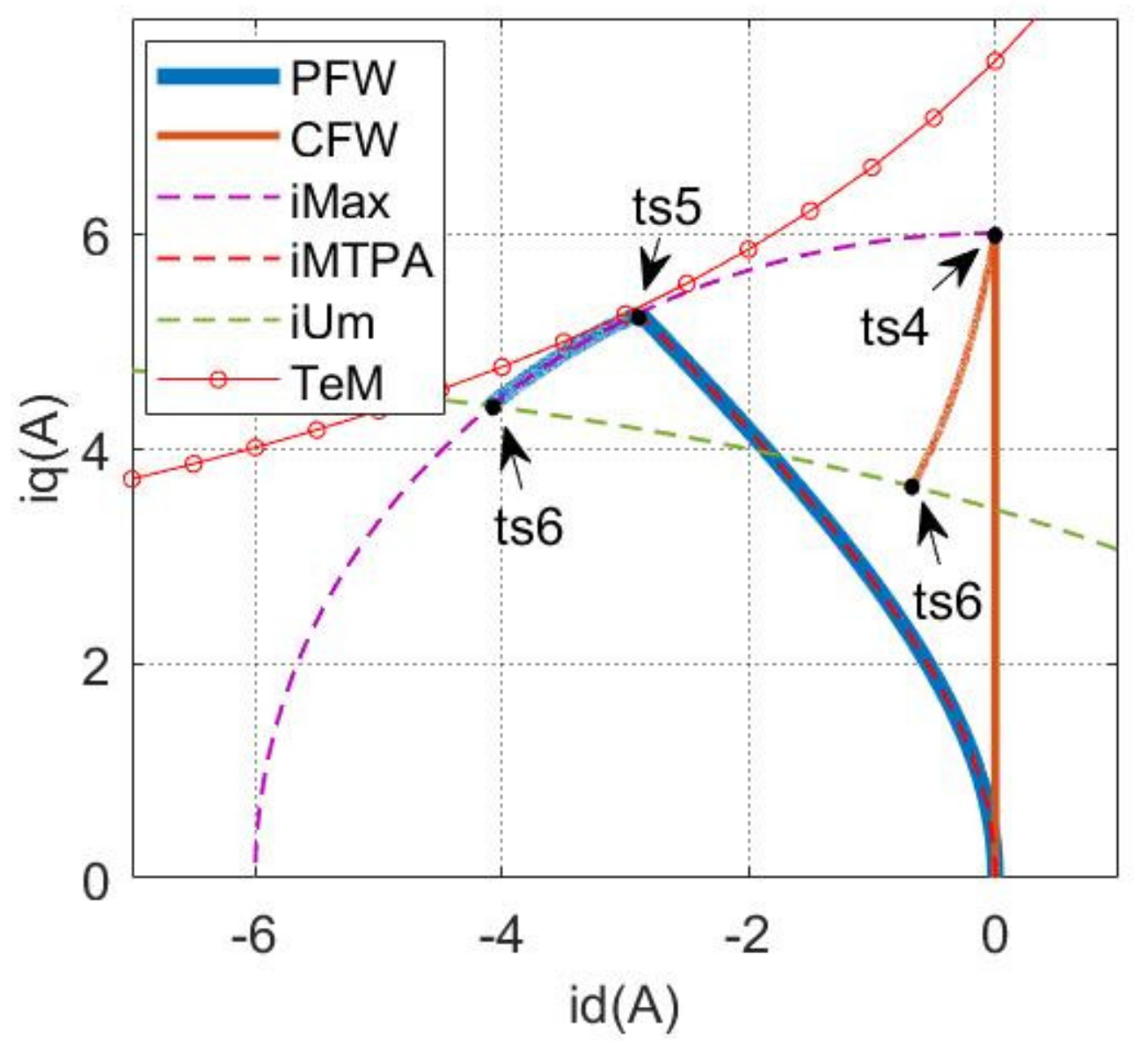
4. Simulation Results
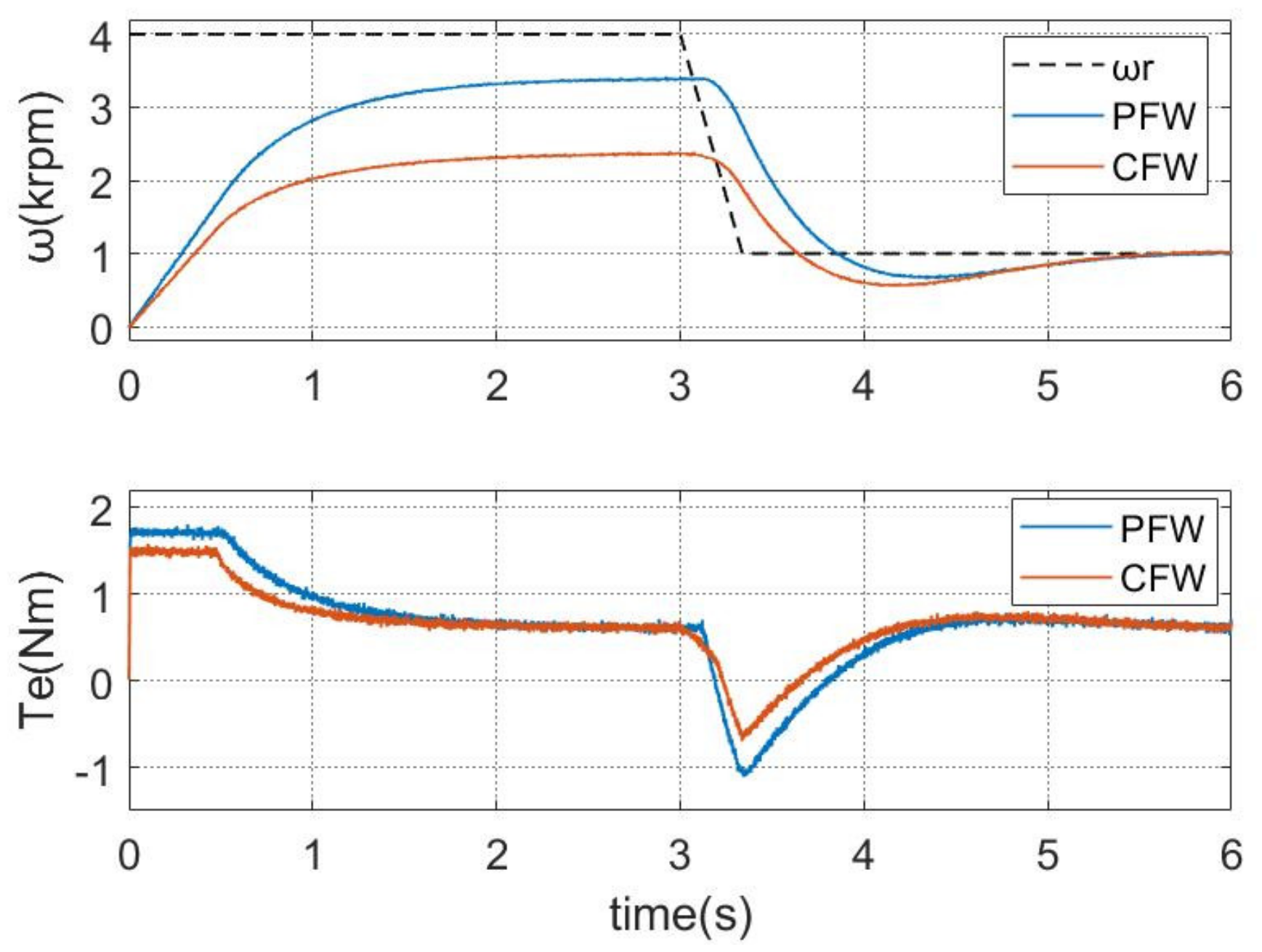
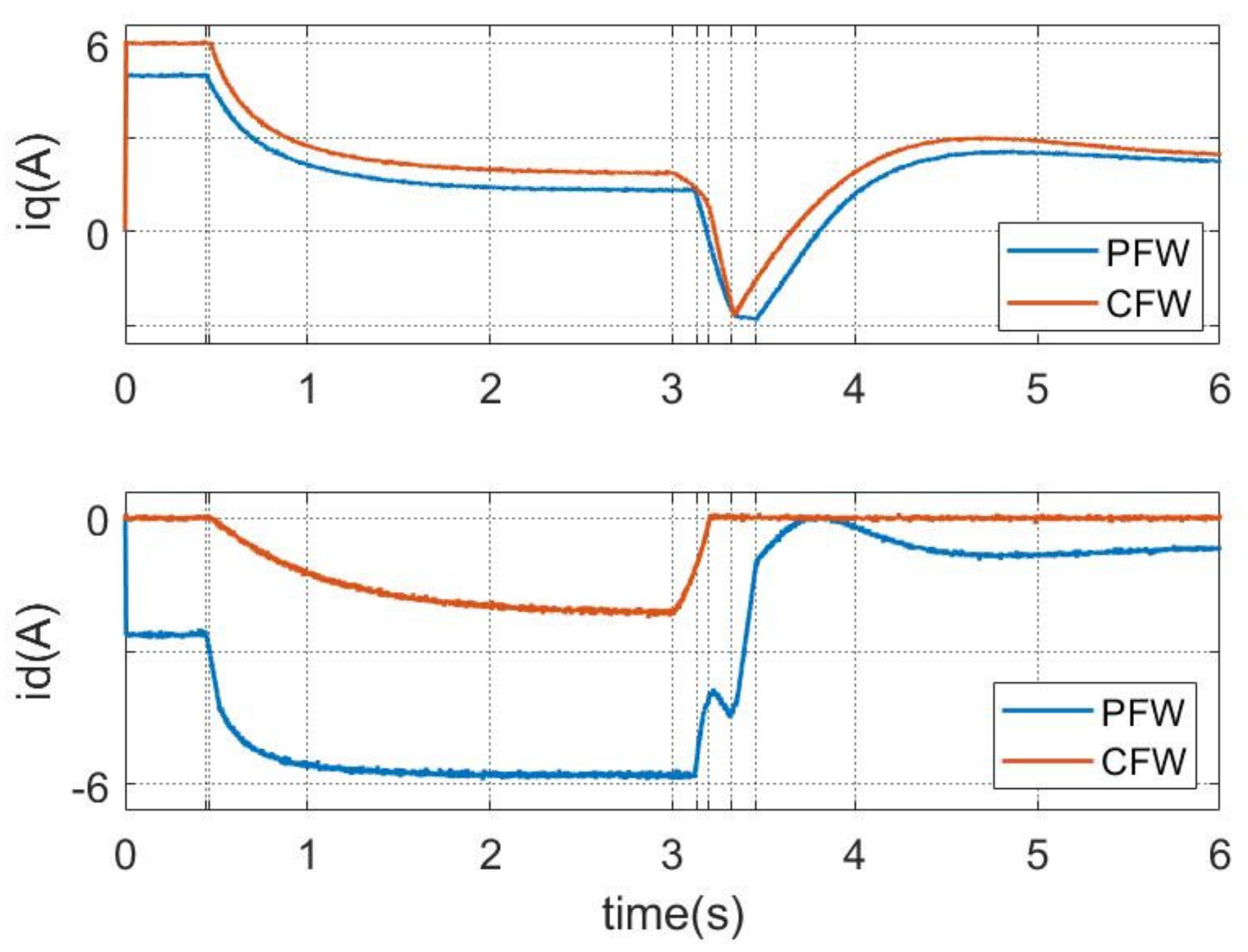
5. Experimental Results
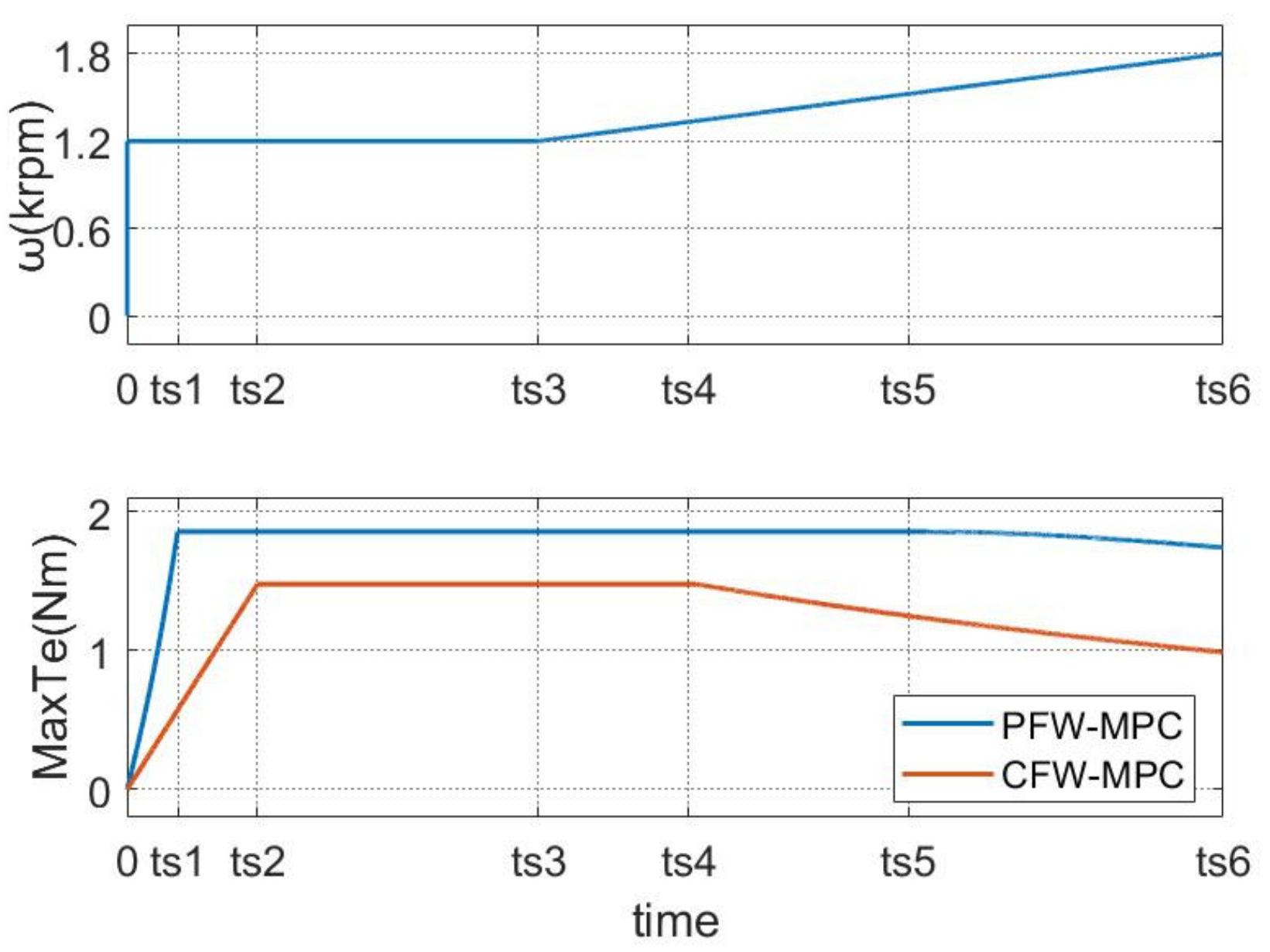
5.1. Speed and Torque
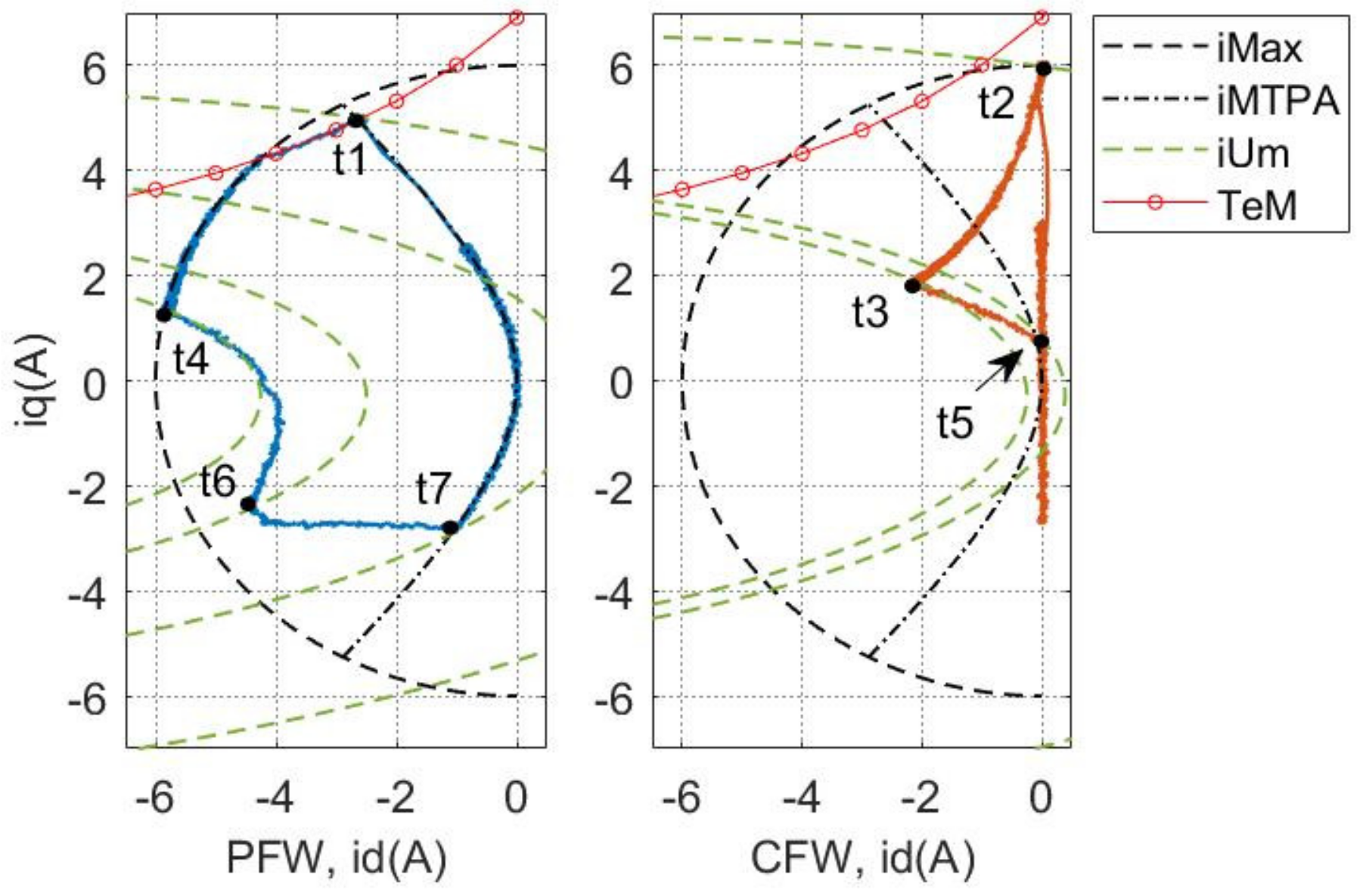
5.2. Current Trajectory
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| id, iq | Stator dq-axis currents. |
| ud, uq | dq-axis stator voltages. |
| Ld, Lq | dq-axis inductances. |
| Rs | Stator winding resistance. |
| Ts | Sampling period. |
| ωe | Rotor electrical angular speed. |
| Te | Electrical torque. |
| φf | Flux linkage. |
| θe | Rotation angle. |
| p | Pole pairs. |
| A, B, C | State parameter matrix |
| W | Disturbance parameter matrix |
References
- Gu, A.; Guo, Y.; Dong, J.; Ruan, B.; Lian, Y.; Zhang, S.; Song, X. Modeling and Analysis of the Flux-Weakening Range of Interior Permanent Magnet Synchronous Machines with Segmented Permanent Magnets. In Proceedings of the 2020 8th International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, Asia, 7–10 December 2020; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2021. [Google Scholar]
- Yamazaki, K.; Kumagai, M.; Ikemi, T.; Ohki, S. A Novel Rotor Design of Interior Permanent-Magnet Synchronous Motors to Cope with Both Maximum Torque and Iron-Loss Reduction. IEEE Trans. Ind. Appl. 2013, 49, 2478–2486. [Google Scholar] [CrossRef]
- Dutta, R.; Rahman, M. A Comparative Analysis of Two Test Methods of Measuring d- and q-Axes Inductances of Interior Permanent-Magnet Machine. IEEE Trans. Magn. 2006, 42, 3712–3718. [Google Scholar] [CrossRef]
- Inoue, T.; Inoue, Y.; Morimoto, S.; Sanada, M. Maximum Torque Per Ampere Control of a Direct Torque-Controlled PMSM in a Stator Flux Linkage Synchronous Frame. IEEE Trans. Ind. Appl. 2016, 52, 2360–2367. [Google Scholar] [CrossRef]
- Preindl, M.; Bolognani, S. Model Predictive Direct Torque Control with Finite Control Set for PMSM Drive Systems, Part 1: Maximum Torque Per Ampere Operation. IEEE Trans. Ind. Inform. 2013, 9, 1912–1921. [Google Scholar] [CrossRef]
- Sun, T.; Wang, J.; Chen, X. Maximum Torque Per Ampere (MTPA) Control for Interior Permanent Magnet Synchronous Machine Drives Based on Virtual Signal Injection. IEEE Trans. Power Electron. 2014, 30, 5036–5045. [Google Scholar] [CrossRef]
- Ekanayake, S.; Dutta, R.; Rahman, M.F.; Xiao, D. Direct torque and flux control of interior permanent magnet synchronous machine in deep flux-weakening region. IET Electr. Power Appl. 2017, 12, 98–105. [Google Scholar] [CrossRef] [Green Version]
- Cheng, B.; Tesch, T.R. Torque Feedforward Control Technique for Permanent-Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2010, 57, 969–974. [Google Scholar] [CrossRef]
- Ge, H.; Miao, Y.; Bilgin, B.; Nahid-Mobarakeh, B.; Emadi, A. Speed Range Extended Maximum Torque Per Ampere Control for PM Drives Considering Inverter and Motor Nonlinearities. IEEE Trans. Power Electron. 2016, 32, 7151–7159. [Google Scholar] [CrossRef]
- Ding, D.; Wang, G.; Zhao, N.; Zhang, G.; Xu, D. Enhanced Flux-Weakening Control Method for Reduced DC-Link Capacitance IPMSM Drives. IEEE Trans. Power Electron. 2018, 34, 7788–7799. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, M.; Wang, C.; You, X. A Single Current Regulator Flux-Weakening Control for PMSM under Square-Wave Mode with Wider Operation Range. IEEE Trans. Transp. Electrif. 2021, 8, 1063–1071. [Google Scholar] [CrossRef]
- Pellegrino, G.; Armando, E.G.; Guglielmi, P. Direct-Flux Vector Control of IPM Motor Drives in the Maximum Torque Per Voltage Speed Range. IEEE Trans. Ind. Electron. 2011, 59, 3780–3788. [Google Scholar] [CrossRef]
- Jang-Mok, K.; Seung-Ki, S. Speed control of interior permanent magnet synchronous motor drive for the flux weakening operation. IEEE Trans. Ind. Appl. 1997, 33, 43–48. [Google Scholar] [CrossRef]
- Bedetti, N.; Calligaro, S.; Petrella, R. Analytical Design and Autotuning of Adaptive Flux-Weakening Voltage Regulation Loop in IPMSM Drives with Accurate Torque Regulation. IEEE Trans. Ind. Appl. 2020, 56, 301–313. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, X.; Wang, J.; Niu, F.; Zhang, J.; Fang, Y.; Wu, L. Improved Flux-Weakening Control of IPMSMs Based on Torque Feedforward Technique. IEEE Trans. Power Electron. 2018, 33, 10970–10978. [Google Scholar] [CrossRef]
- Bolognani, S.; Calligaro, S.; Petrella, R. Adaptive Flux-Weakening Controller for Interior Permanent Magnet Synchronous Motor Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 236–248. [Google Scholar] [CrossRef]
- Hoang, K.D.; Aorith, H.K.A. Online Control of IPMSM Drives for Traction Applications Considering Machine Parameter and Inverter Nonlinearities. IEEE Trans. Transp. Electrif. 2015, 1, 312–325. [Google Scholar] [CrossRef] [Green Version]
- Jung, S.-Y.; Hong, J.; Nam, K. Current Minimizing Torque Control of the IPMSM Using Ferrari’s Method. IEEE Trans. Power Electron. 2013, 28, 5603–5617. [Google Scholar] [CrossRef]
- Kwon, T.; Choi, G.; Kwak, M.; Sul, S. Novel Flux-Weakening Control of an IPMSM for Quasi-Six-Step Operation. IEEE Trans. Ind. Appl. 2008, 44, 1722–1731. [Google Scholar] [CrossRef]
- Mynar, Z.; Vesely, L.; Vaclavek, P. PMSM Model Predictive Control With Field-Weakening Implementation. IEEE Trans. Ind. Electron. 2016, 63, 5156–5166. [Google Scholar] [CrossRef]
- Xie, W.; Wang, X.; Wang, F.; Xu, W.; Kennel, R.; Gerling, D. Dynamic Loss Minimization of Finite Control Set-Model Predictive Torque Control for Electric Drive System. IEEE Trans. Power Electron. 2015, 31, 849–860. [Google Scholar] [CrossRef]
- Zhang, G.; Furusho, J. Speed control of two-inertia system by PI/PID control. IEEE Trans. Ind. Electron. 1999, 47, 603–609. [Google Scholar] [CrossRef]
- Consoli, A.; Scelba, G.; Scarcella, G.; Cacciato, M. An Effective Energy-Saving Scalar Control for Industrial IPMSM Drives. IEEE Trans. Ind. Electron. 2012, 60, 3658–3669. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Mayne, D.Q.; Diehl, M. Model Predictive Control: Theory, Computation, and Design; Nob Hill Publishing: Madison, WI, USA, 2017. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Raković, S.V. Model predictive control: Classical, robust, and stochastic. IEEE Control. Syst. Mag. 2016, 36, 102–105. [Google Scholar]



| Strategy Type | Feedback FW | Look-Up Tables | FW-MPC |
|---|---|---|---|
| Advantages | Simple | Algorithm Simple | Optimal FW |
| Disadvantages | Time Delay | Current Ripple; Need Lots of Data | Complex |
| Udc | 70 V |
| Im | 6 A |
| Ld | 9 mH |
| Lq | 27.4 mH |
| Rs | 0.83 Ω |
| φf | 122 mWb |
| p | 2 |
| Ts | 100 µs |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Qi, R. Flux-Weakening Drive for IPMSM Based on Model Predictive Control. Energies 2022, 15, 2543. https://doi.org/10.3390/en15072543
Zhang Y, Qi R. Flux-Weakening Drive for IPMSM Based on Model Predictive Control. Energies. 2022; 15(7):2543. https://doi.org/10.3390/en15072543
Chicago/Turabian StyleZhang, Yunfei, and Rong Qi. 2022. "Flux-Weakening Drive for IPMSM Based on Model Predictive Control" Energies 15, no. 7: 2543. https://doi.org/10.3390/en15072543
APA StyleZhang, Y., & Qi, R. (2022). Flux-Weakening Drive for IPMSM Based on Model Predictive Control. Energies, 15(7), 2543. https://doi.org/10.3390/en15072543






