Performance Evaluation of Centrifugal Refrigeration Compressor Using R1234yf and R1234ze(E) as Drop-In Replacements for R134a Refrigerant
Abstract
:1. Introduction
2. Comparative Analysis of Refrigerant Physical Properties
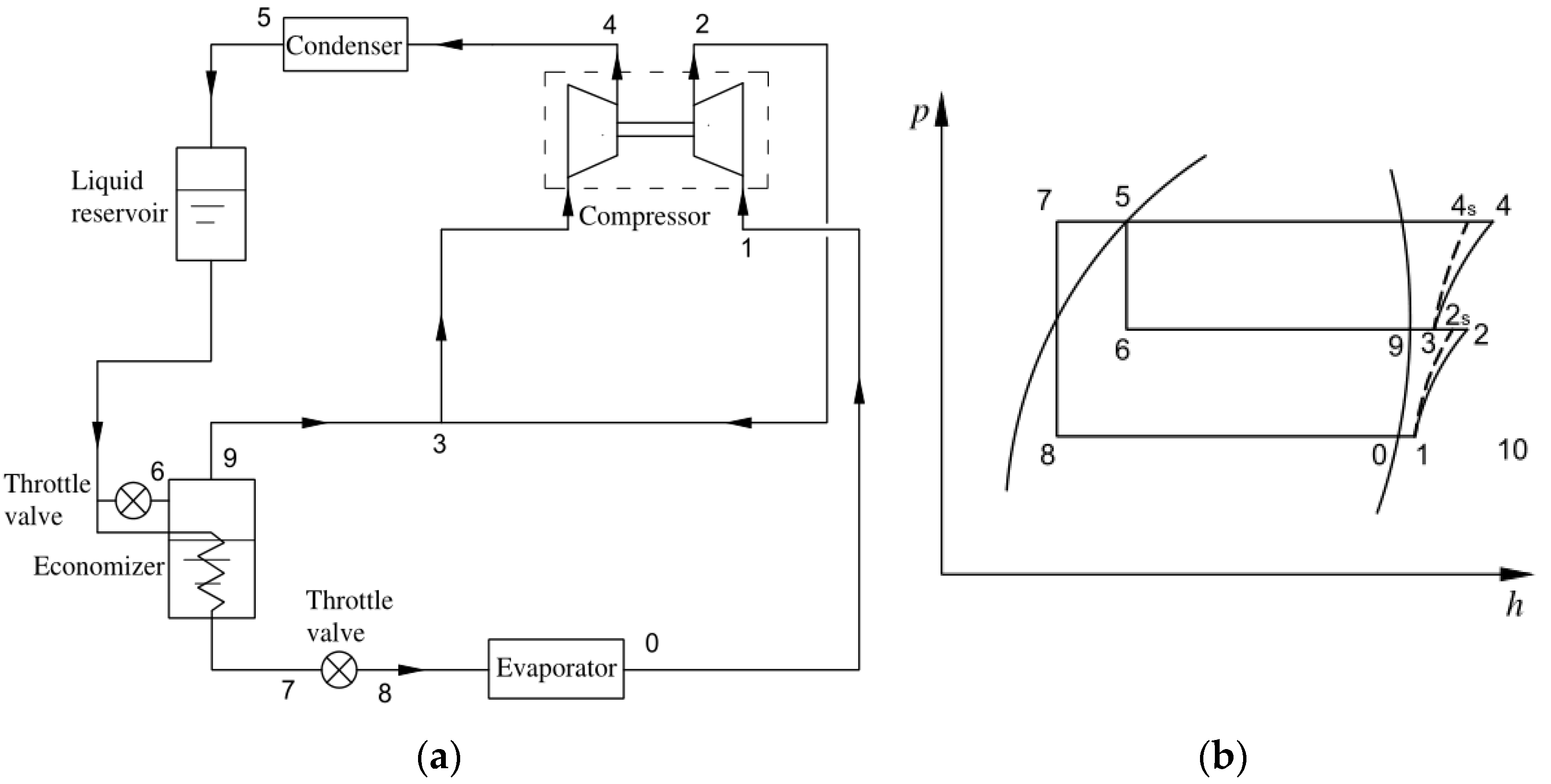
3. Refrigeration Cycle System
4. Numerical Calculation Methods
4.1. Basic Governing Equations
- (1)
- Mass conservation equation
- (2)
- Momentum conservation equation
- (3)
- Energy conservation equation
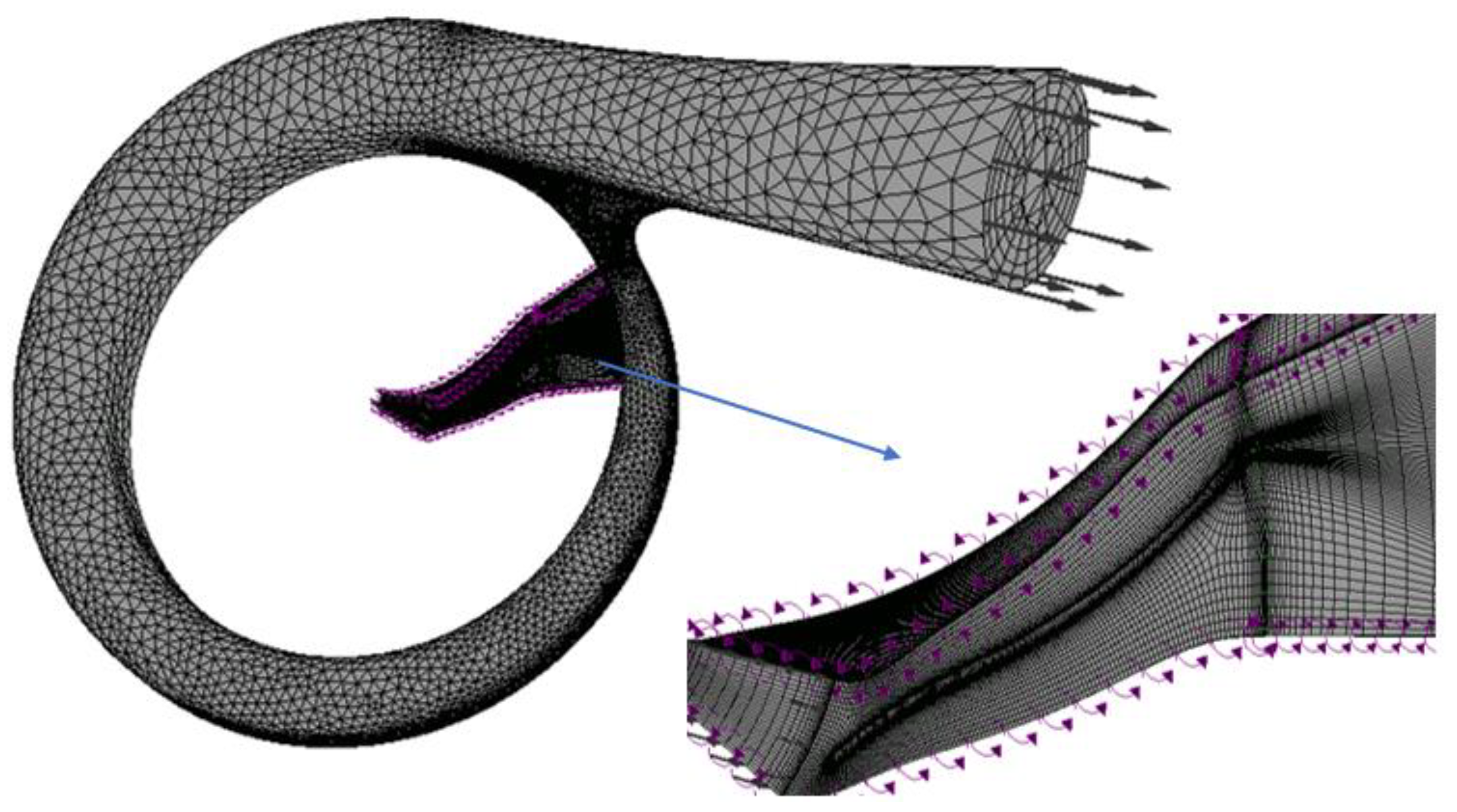
4.2. Geometrical Model
4.3. Meshing
4.4. Calculation Parameters and Boundary Conditions
4.5. Performance Parameters
5. Results and Discussions
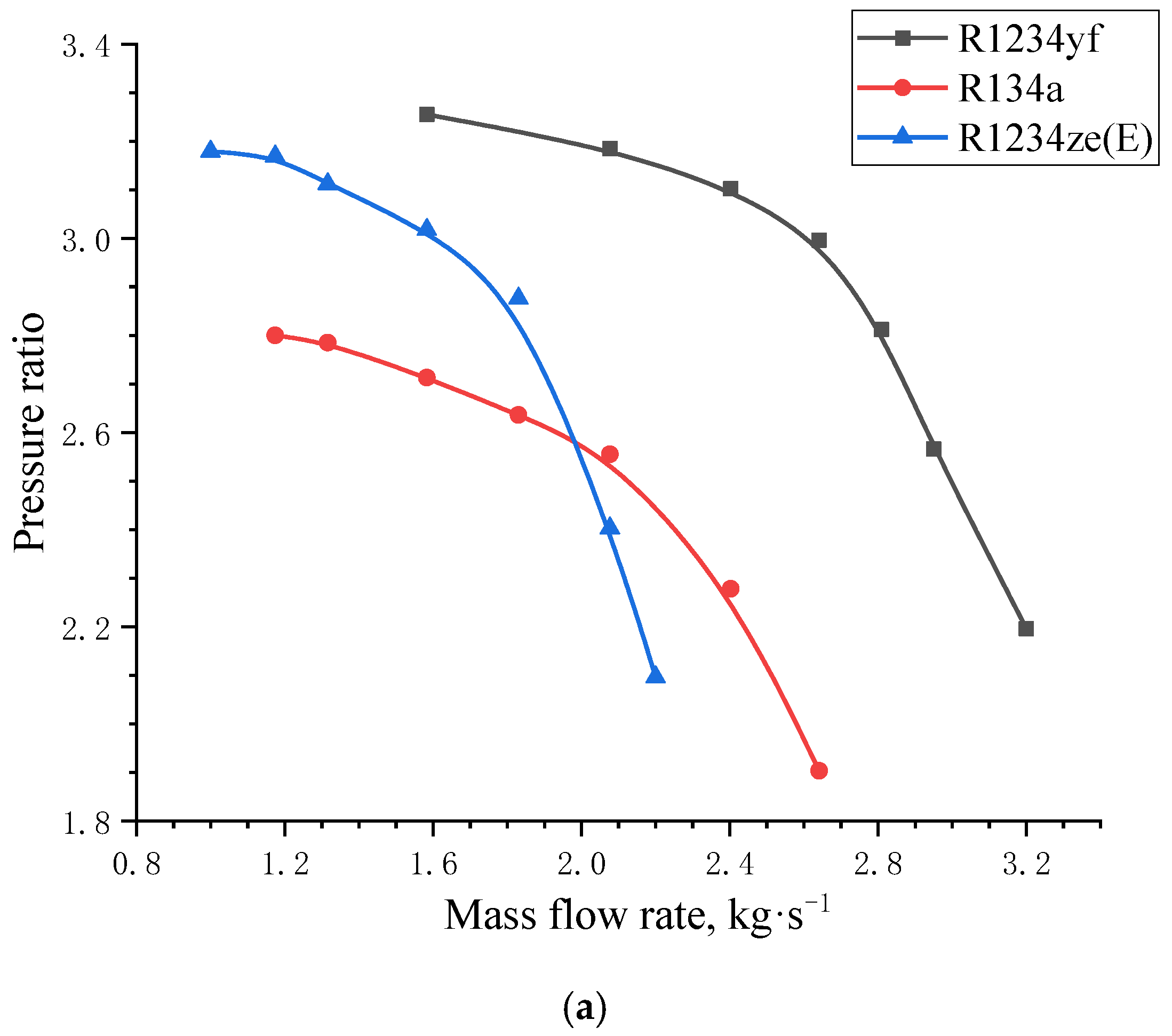
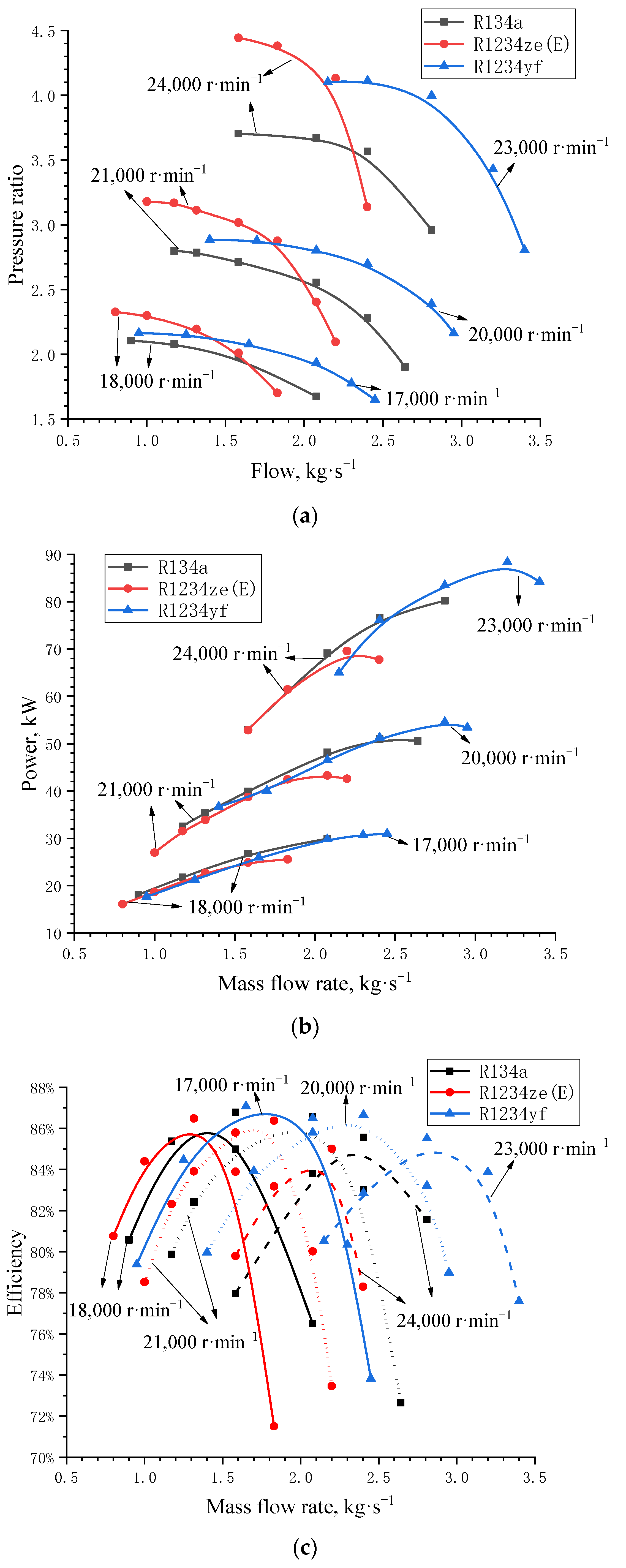
5.1. Centrifugal Compressor Performance
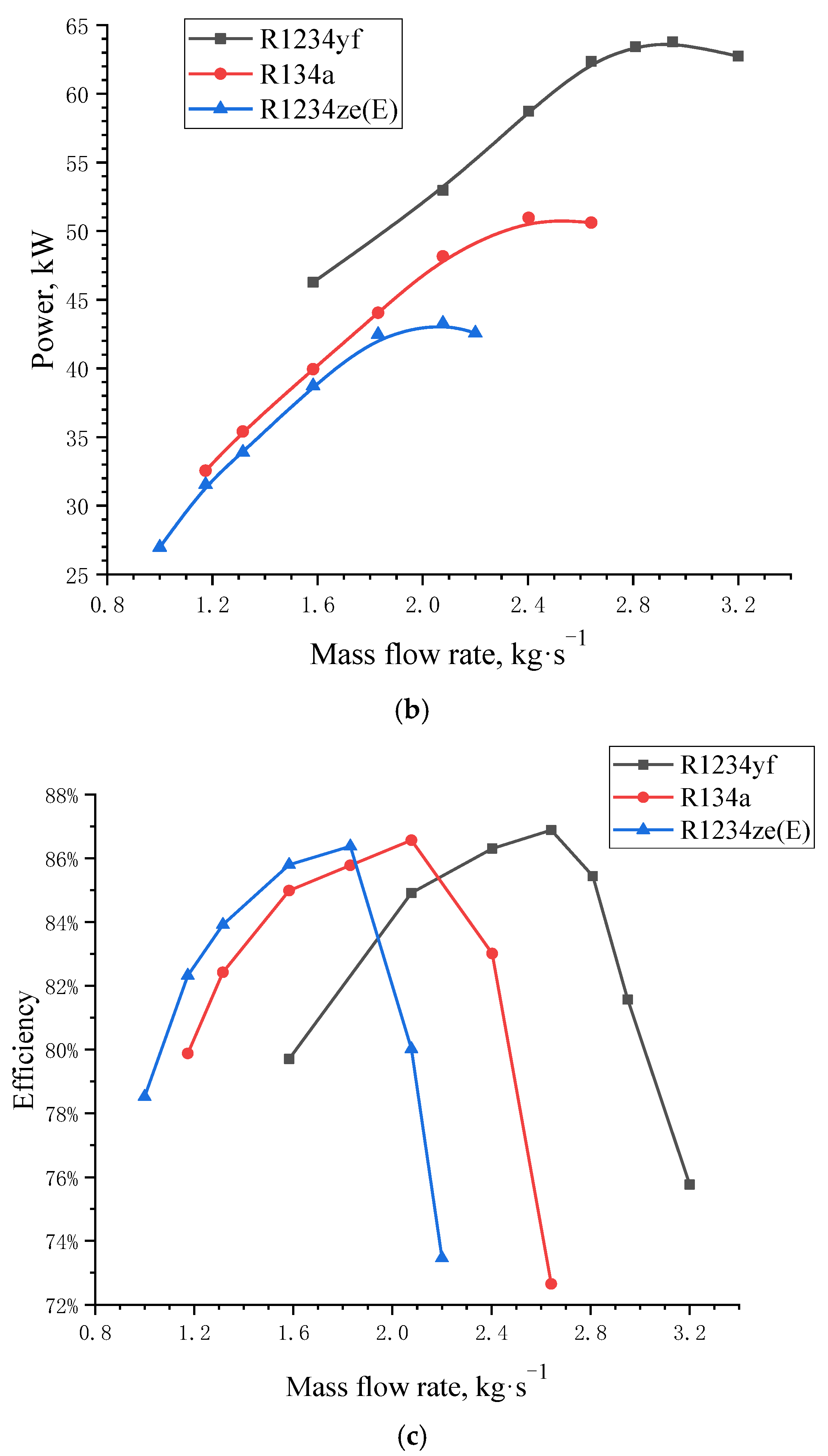
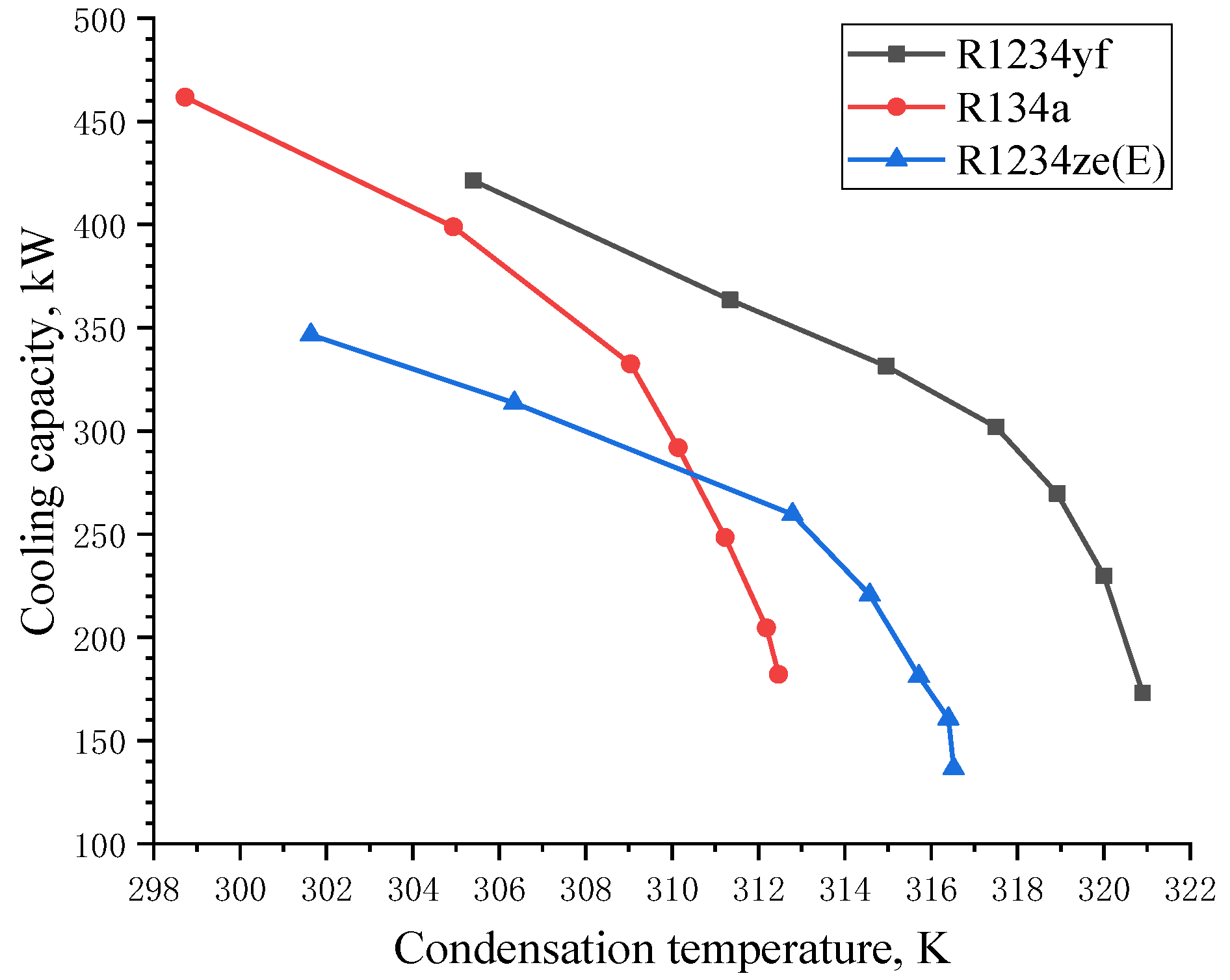
5.2. Cooling Capacity
5.3. Coefficient of Performance (COP)
5.4. COP Comparison under Same Conditions
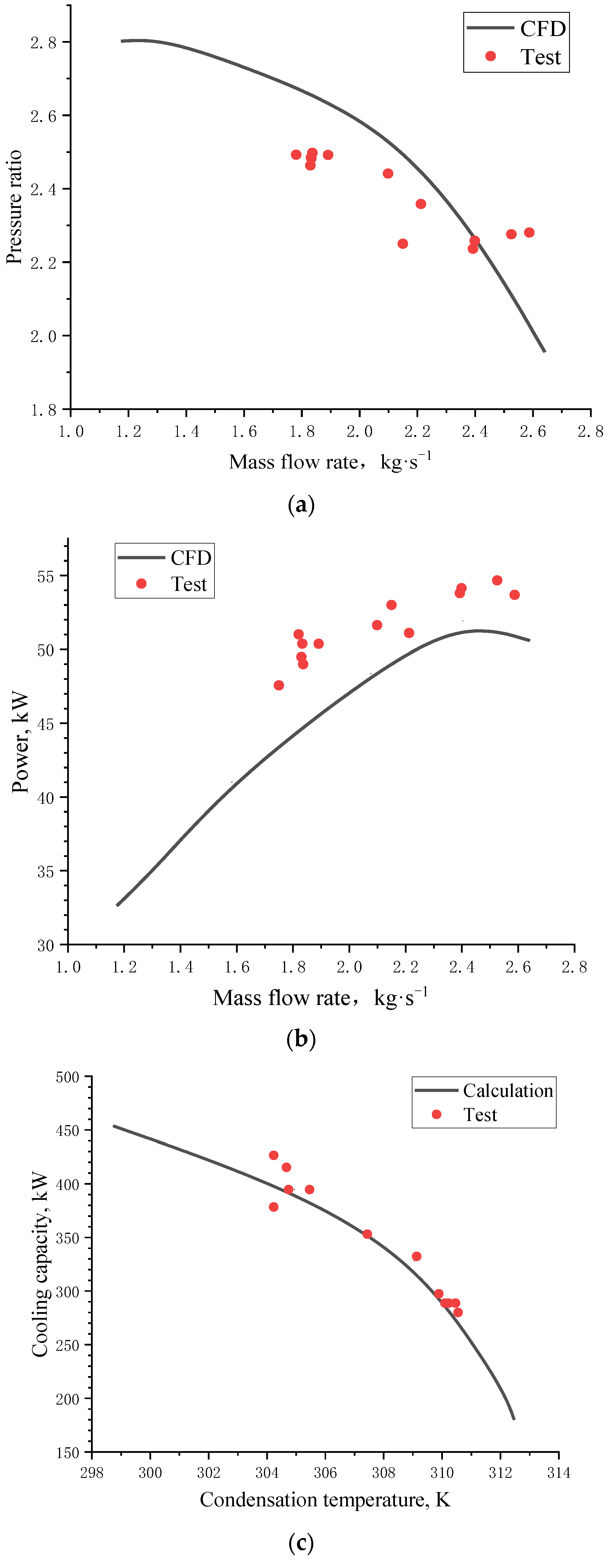
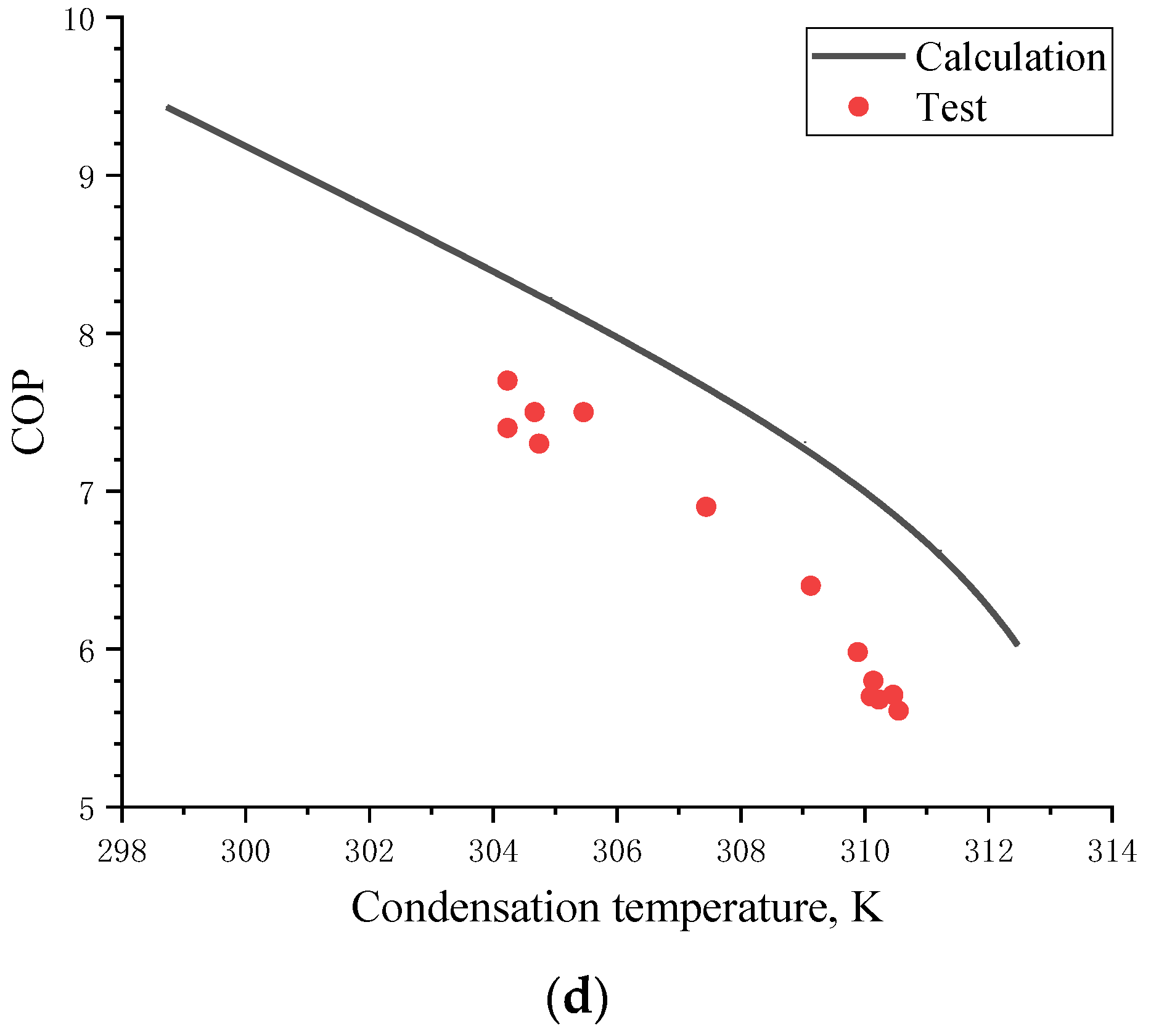
5.5. Results Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meng, Z.; Zhang, H.; Qiu, J.; Lei, M. Theoretical analysis of R1234ze(E), R152a, and R1234ze(E)/R152a mixtures as replacements of R134a in vapor compression system. Adv. Mech. Eng. 2016, 8, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Shin, Y.; Chung, J. Performance Prediction of Centrifugal Compressor for Drop-In Testing Using Low Global Warming Potential Alternative Refrigerants and Performance Test Codes. Energies 2017, 10, 2043. [Google Scholar] [CrossRef] [Green Version]
- Atmaca, A.U.; Erek, A.; Ekren, O. Investigation of new generation refrigerants under two different ejector mixing theories. Energy Procedia 2017, 136, 394–401. [Google Scholar] [CrossRef]
- Jribi, S.; Saha, B.B.; Koyama, S.; Chakraborty, A.; Ng, K.C. Study on activated carbon/HFO-1234ze(E) based adsorption cooling cycle. Appl. Therm. Eng. 2013, 50, 1570–1575. [Google Scholar] [CrossRef]
- Janković, Z.; Sieres Atienza, J.; Martínez Suárez, J.A. Thermodynamic and heat transfer analyses for R1234yf and R1234ze(E) as drop-in replacements for R134a in a small power refrigerating system. Appl. Therm. Eng. 2015, 80, 42–54. [Google Scholar] [CrossRef]
- Sieres, J.; Santos, J.M. Experimental analysis of R1234yf as a drop-in replacement for R134a in a small power refrigerating system. Int. J. Refrig. 2018, 91, 230–238. [Google Scholar] [CrossRef]
- Lee, Y.; Jung, D. A brief performance comparison of R1234yf and R134a in a bench tester for automobile applications. Appl. Therm. Eng. 2012, 35, 240–242. [Google Scholar] [CrossRef]
- Pabon, J.J.G.; Khosravi, A.; Belman-Flores, J.M.; Machado, L.; Revellin, R. Applications of refrigerant R1234yf in heating, air conditioning and refrigeration systems: A decade of researches. Int. J. Refrig. 2020, 118, 104–113. [Google Scholar] [CrossRef]
- Niu, Y.; Liu, J.; Zhou, Y.; Lin, E. General introduction of R1234yf and R1234ze(E). Refrig. Air Cond. 2015, 15, 82–91. [Google Scholar]
- Zhang, X.; Liu, X.; Li, J.; Wu, J.; Wang, R. Status and development trend of products and technologies for industrial and commercial refrigerant compressor. Refrig. Air Cond. 2017, 17, 49–57. [Google Scholar]
- Aral, M.C.; Suhermanto, M.; Hosoz, M. Performance evaluation of an automotive air conditioning and heat pump system using R1234yf and R134a. Sci. Technol. Built Environ. 2020, 27, 44–60. [Google Scholar] [CrossRef]
- Qi, Z. Performance improvement potentials of R1234yf mobile air conditioning system. Int. J. Refrig. 2015, 58, 35–40. [Google Scholar] [CrossRef]
- Mota-Babiloni, A.; Navarro-Esbrí, J.; Barragán, Á.; Molés, F.; Peris, B. Drop-in energy performance evaluation of R1234yf and R1234ze(E) in a vapor compression system as R134a replacements. Appl. Therm. Eng. 2014, 71, 259–265. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Liang, K.; Li, Z.; Zhao, Y.; Xu, J.; Jiang, H. Experimental assessment of alternative low global warming potential refrigerants for automotive air conditioners application. Case Stud. Therm. Eng. 2020, 22, 100800. [Google Scholar] [CrossRef]
- Yang, C.; Nalbandian, H.; Lin, F. Flow Boiling Heat Transfer and Pressure Drop of Refrigerants HFO-1234yf and HFO-134a in Small Circular Tube. Int. J. Heat Mass Transf. 2018, 121, 726–735. [Google Scholar] [CrossRef]
- Yang, C.; Nalbandian, H. Condensation Heat Transfer and Pressure Drop of Refrigerants HFO-1234yf and HFO-134a in Small Circular Tube. Int. J. Heat Mass Transf. 2018, 127, 218–227. [Google Scholar] [CrossRef]
- Nagata, R.; Kondou, C.; Koyama, S. Comparative Assessment of Condensation and Pool Boiling Heat Transfer on Horizontal Plain Single Tubes for R1234ze(e), R1234ze(z), and R1233zd(e). Int. J. Refrig. 2016, 63, 157–170. [Google Scholar] [CrossRef] [Green Version]
- Ubara, T.; Asano, H.; Sugimoto, K. Falling film evaporation and pool boiling heat transfer of R1233zd(E) on thermal spray coated tube. Appl. Therm. Eng. 2021, 196, 117329. [Google Scholar] [CrossRef]
- Elbarghthi, A.F.A.; Mohamed, S.; Nguyen, V.V.; Dvorak, V. CFD Based Design for Ejector Cooling System Using HFOS (1234ze(E) and 1234yf). Energies 2020, 13, 1408. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, V.V.; Varga, S.; Dvorak, V. HFO1234ze(e) As an Alternative Refrigerant for Ejector Cooling Technology. Energies 2019, 12, 4045. [Google Scholar] [CrossRef] [Green Version]
- Bansal, P.; Shen, B. Analysis of environmentally friendly refrigerant options for window air conditioners. Sci. Technol. Built Environ. 2015, 21, 483–490. [Google Scholar] [CrossRef]
- Uusitalo, A.; Turunen-Saaresti, T.; Honkatukia, J.; Tiainen, J.; Jaatinen-Värri, A. Numerical analysis of working fluids for large scale centrifugal compressor driven cascade heat pumps upgrading waste heat. Appl. Energy 2020, 269, 115056. [Google Scholar] [CrossRef]
- Wu, D.; Hu, B.; Wang, R.Z. Vapor compression heat pumps with pure Low-GWP refrigerants. Renew. Sustain. Energy Rev. 2021, 138, 110571. [Google Scholar] [CrossRef]
- Xue, F.; Su, X.; Wang, Z. Application study of R1233zd(E) into centrifugal chiller. Refrig. Air Cond. 2019, 19, 24–29. [Google Scholar]
- JB/T 12843-2016; Centrifugal Refrigerant Compressors. Ministry of Industry and Information Technology of the People’s Republic China: Beijing, China, 2016. (In Chinese)
- Pakle, S.; Jiang, K. Design of a transonic centrifugal compressor for High-speed turbomachinery. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 235, 2112–2125. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties—REFPROP. 9.0; NIST NSRDS: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Salhi, K.; Mohamed Ramadan, K.; Hadjiat, M.M.; Hamidat, A. Energetic and Exergetic Performance of Solar-Assisted Direct Expansion Air-Conditioning System with Low-GWP Refrigerants in Different Climate Locations. Arab. J. Sci. Eng. 2020, 45, 5385–5398. [Google Scholar] [CrossRef]
- De Paula, C.H.; Duarte, W.M.; Rocha, T.T.M.; de Oliveira, R.N.; Mendes, R.d.P.; Maia, A.A.T. Thermo-economic and environmental analysis of a small capacity vapor compression refrigeration system using R290, R1234yf, and R600a. Int. J. Refrig. 2020, 118, 250–260. [Google Scholar] [CrossRef]
- Xue, X.; Wang, T. Stall recognition for centrifugal compressors during speed transients. Appl. Therm. Eng. 2019, 153, 104–112. [Google Scholar] [CrossRef]
- Ma, X. Research on Performance Optimization and State Evaluation Methods of Centrifugal Compressors; Southwest Petroleum University: Chengdu, China, 2013. [Google Scholar]





| R134a | R1234yf | R1234ze(E) | R1233zd(E) | |
|---|---|---|---|---|
| Molecular formula | CH2FCF3 | C3H2F4 | C3H2F4 | C3H2ClF3 |
| Molecular weight | 102.0 | 114.04 | 114.04 | 130.5 |
| Critical pressure (MPa) | 4.059 | 3.382 | 3.636 | 3.624 |
| Critical temperature (°C) | 101.6 | 94.7 | 109.4 | 166.5 |
| Normal boiling point (°C) | −26.07 | −29.45 | −18.97 | 18.3 |
| GWP | 1430 | 4 | 6 | 1 |
| ODP | 0 | 0 | 0 | 0 |
| Security level | A1 | A2L | A1 | A1 |
| R134a | R1234yf | R1234ze(E) | R1233zd(E) | |
|---|---|---|---|---|
| Evaporation temperature (°C) | 5.5 | 5.5 | 5.5 | 5.5 |
| Condensation temperature (°C) | 37 | 37 | 37 | 37 |
| Superheating temperature (°C) | 3 | 3 | 3 | 3 |
| Subcooling temperature (°C) | 4 | 4 | 4 | 4 |
| Cooling capacity (kJ·m−3) | 2717.4 | 2590.8 | 2033.0 | 593.1 |
| R134a | R1234yf | R1234ze(E) | R1233zd(E) | |
|---|---|---|---|---|
| Evaporation temperature (°C) | 5.5 | |||
| Evaporation pressure (kPa) | 355.78 | 379.04 | 263.96 | 60.707 |
| Condensation pressure (kPa) | Set according to different working conditions | |||
| Superheating temperature (°C) | 3 | |||
| Subcooling temperature (°C) | 4 | |||
| Design Parameters | First Stage Impeller | Second Stage Impeller |
|---|---|---|
| Impeller hub diameter (mm) | 25.0 | 37.0 |
| Impeller inlet diameter (mm) | 66.7 | 64.5 |
| Impeller outlet diameter (mm) | 127.2 | 114.3 |
| Impeller outlet width (mm) | 5.7 | 4.9 |
| Number of blades | 16 | 16 |
| Diffuser inlet radius (mm) | 66.0 | 59.5 |
| Diffuser outlet radius (mm) | 94.0 | 85.4 |
| Diffuser width (mm) | 6.7 | 5.8 |
| Radius at 0° of volute profile (mm) | 94.0 | 85.4 |
| Radius at 360° of volute profile (mm) | 138.7 | 131.4 |
| Condensation Temperature (K) | COP of R134a | COP of R1234ze(E) | Percentage of Reduction |
|---|---|---|---|
| 300.8 | 10.360 | 9.822 | 5.19% |
| 310.5 | 6.852 | 6.477 | 5.47% |
| 322.8 | 4.435 | 4.224 | 4.76% |
| Condensation Temperature (K) | COP of R134a | COP of R1234ze(E) | Percentage of Reduction |
|---|---|---|---|
| 296.0 | 12.318 | 11.462 | 6.95% |
| 305.2 | 8.163 | 7.416 | 9.15% |
| 319.4 | 4.990 | 4.457 | 10.7% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, K.; Zhao, Y.; Liu, G.; Yang, Q.; Yu, G.; Li, L. Performance Evaluation of Centrifugal Refrigeration Compressor Using R1234yf and R1234ze(E) as Drop-In Replacements for R134a Refrigerant. Energies 2022, 15, 2552. https://doi.org/10.3390/en15072552
Yi K, Zhao Y, Liu G, Yang Q, Yu G, Li L. Performance Evaluation of Centrifugal Refrigeration Compressor Using R1234yf and R1234ze(E) as Drop-In Replacements for R134a Refrigerant. Energies. 2022; 15(7):2552. https://doi.org/10.3390/en15072552
Chicago/Turabian StyleYi, Kexin, Yuanyang Zhao, Guangbin Liu, Qichao Yang, Guoxin Yu, and Liansheng Li. 2022. "Performance Evaluation of Centrifugal Refrigeration Compressor Using R1234yf and R1234ze(E) as Drop-In Replacements for R134a Refrigerant" Energies 15, no. 7: 2552. https://doi.org/10.3390/en15072552
APA StyleYi, K., Zhao, Y., Liu, G., Yang, Q., Yu, G., & Li, L. (2022). Performance Evaluation of Centrifugal Refrigeration Compressor Using R1234yf and R1234ze(E) as Drop-In Replacements for R134a Refrigerant. Energies, 15(7), 2552. https://doi.org/10.3390/en15072552






