Piezoelectric Energy Harvesting from Roadways under Open-Traffic Conditions: Analysis and Optimization with Scaling Law Method

Abstract

Piezoelectric energy harvesting from roadways, which converts ambient vibration energy of roads into electric energy, has a wide range of potential applications in intelligent transportation systems. On-site open-traffic tests revealed that energy harvested by piezoelectric energy harvester (PEH) units embedded in roadways is far less than the value in laboratories, which may be because the parameters of traffic flow load (frequency, distribution, wave shape, etc.) and the road structure are significantly different from the pre-established conditions in laboratories or even on-site tests with only one vehicle passing. To address this issue, an analytical model for piezoelectric energy harvesting from roadways under open-traffic conditions was proposed to examine the mechanical response of the road structure and the electrical performance of the stack PEH units embedded in the road. The influence of all parameters in the energy-harvesting system was then obtained with the scaling law method, revealing that the energy harvested by PEH units is determined by the energy coefficient, the system’s intrinsic parameter, normalized parameters of roadways, and the normalized embedded position of PEH units. It is found that that the energy-harvesting system’s intrinsic parameter should be approximately 0.8 to ensure maximum energy-harvesting efficiency. Meanwhile, the pavement with lower bending stiffness and higher linear density while the foundation with small stiffness and smaller damping coefficient would be more suitable for energy harvesting. Furthermore, the lateral embedded position of PEH units should be carefully chosen, since the units embedded in an optimal position can harvest three times more than that embedded in other positions. The concise criteria presented in this study will be used as a reference not only for material selection, dimension optimization, and embedded positions determination of PEH units but also for choosing of the optimal roadways to achieve maximum piezoelectric energy harvesting efficiency under open-traffic conditions.

1. Introduction

With the increase in global highway mileage and car ownership, considerable vibration energy is accumulated in the roadways and then dissipated in vain. Harvesting the ubiquitous vibration energy from roads would be potential to provide electricity for sensors embedded in infrastructures and for traffic auxiliary facilities such as street lights and signage. This would be of special importance when grid power supply and battery replacement are inconvenient [1,2,3,4].

Piezoelectric energy harvesters (PEHs) have attracted extensive attention both from the industry and research community in the recent yeas, because they are easily fabricated, deployable for all kinds of roads, and independent from weather conditions [5]. In 2008, Innowattech, an Israeli company, fabricated a road-capable PEH and then carried out on-site tests [6,7]. It claimed that for a single lane, 1 km-long PEH, as high as 200 kWh electricity can be harvested in one hour. Nevertheless, neither detailed information regarding structural design nor experimental raw data can be found about the PEH. Afterward, PEHs with different piezoelectric materials [8,9,10], structural design strategies [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26], package methods [27,28], series-parallel connections [29,30], energy-harvesting circuits [31,32], etc. are extensively investigated with enormous carefully designed laboratory tests, theoretical analyses [33,34,35,36], and finite element simulations [37,38]. These research studies have greatly promoted the development of PEHs in laboratory experiments and thus lay a solid foundation for future field studies.

Several research groups have conducted field tests in recent years. Wang et al. carried out a series of on-site experiments since 2016 to investigate the electrical performance of PEH units under vehicles with different axle loads and driving speeds, and four LED Chinese characters were lit up successfully with the harvested energy [39,40,41]. Hwang et al. fabricated a kind of road-capable PEHs, which provided sufficient electric energy for a temperature sensor to measure data 14 times in 16 s and then transmitted the data wirelessly [42]. Song et al. installed a PEH in a speed bump, and a 10,000 $\mathsf{\mu }\mathrm{F}$ capacitor was charged up to 6 V when a vehicle passed the PEH nine times at 30 km/h [43]. Chen et al. demonstrated an innovative roadway PEH by incorporating a compression-to-compression force amplification mechanism to achieve a high energy density [44]. Recently, Hong et al. developed a uniform stress distribution road piezoelectric generator, which can provide sufficient energy to charge a mobile phone battery for 53 s when a compact vehicle compressed 25 units at a speed of 100 km/h [45]. These on-site experiments studied the scenario that only one vehicle passes this PEH.

Nevertheless, under real traffic conditions, the vehicles’ types, axle loads, traffic speeds, and following distances would change with certain randomness (Figure 1). To evaluate the performance of PEHs under open-traffic conditions, Wang et al. installed a piezoelectric micro-energy collection-storage system in roadways, and the harvested electric energy was used to charge a capacitor. The results showed that only 76 mJ electrical energy was stored in the capacitor after 1200 random automobiles passed this PEH in 3 h [46].

These on-site experiments fully validated the feasibility of harvesting vibration energy of the pavement structure with PEHs to power low-energy electronics. Nevertheless, when comparing the energy gathered in on-site tests with that in laboratory experiments, it would be found that the energy-harvesting efficiency drops dramatically in on-site tests, especially under open-traffic conditions. This would be because the parameters of traffic load (frequency, load distribution, waveform, etc.) and the roadways (material, structure, etc.) would be significantly different from the simulation conditions in laboratories, and the influence of these huge differences have yet not been clarified in the research to date.

To fill this research gap, a theoretical model is proposed to examine the electric performance of PEH units under open-traffic conditions. The structure of the roadway is simplified as a composite beam resting on the Kelvin–Voigt foundation, and the distribution of the traffic flow load along the transverse direction is simplified as a pair of parabolas, whereas the traffic load along the longitudinal direction is equalized as a series of half-cycle sinusoidal pulses, as shown in detail in Section 2. Then, the scaling law method is applied to analyze this system (Section 3), and the effects of four combined normalized parameters that can fully determine the amount of energy harvested by PEH units under traffic load are examined systematically (Section 4). The objective of this present study is to identify criteria to guide the design and arrangement of PEH units as well as the selection of proper roadways for achieving maximum energy-harvesting efficiency under open-traffic conditions.

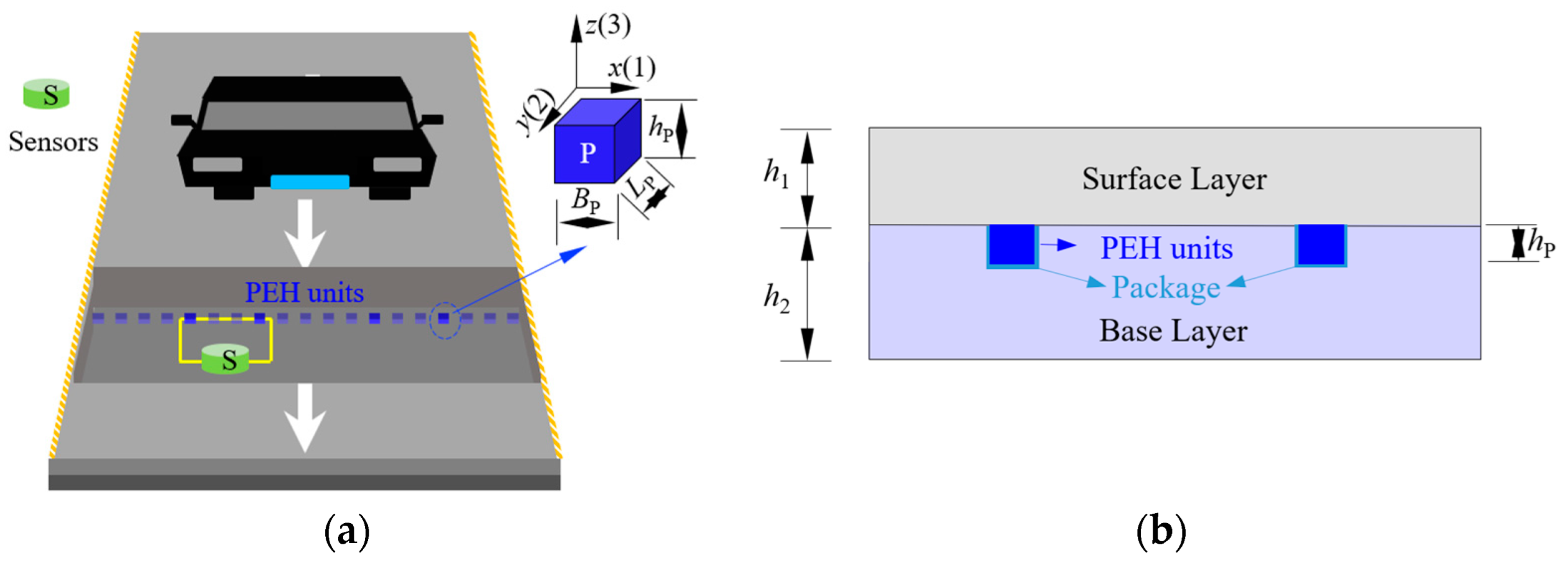
2. Electromechanical Modeling

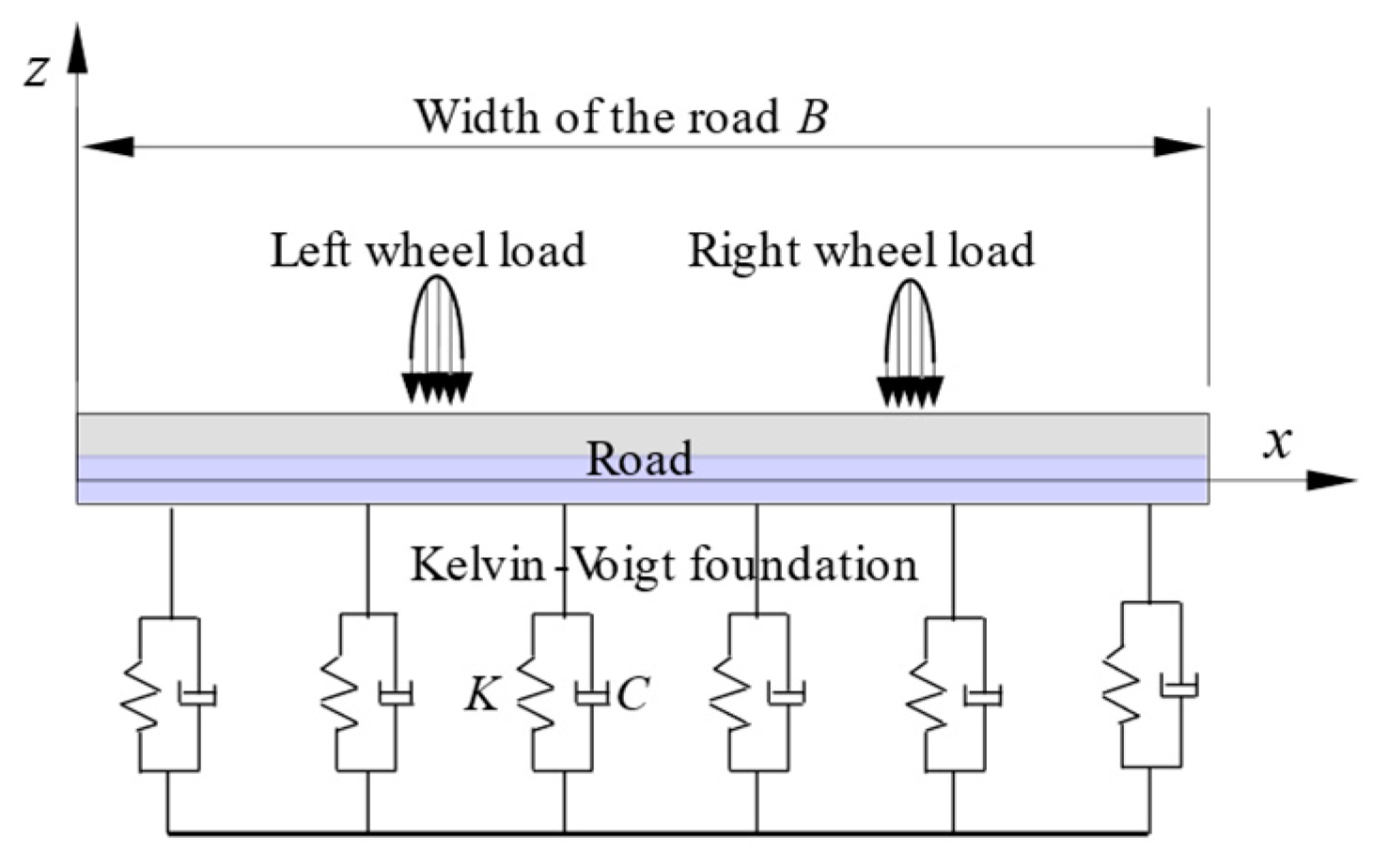
2.1. Mechanical Response of Roadways under Traffic Flow Load

The road structure under traffic load can be modeled as a composite beam resting on the Kelvin–Voigt foundation (Figure 2), and the corresponding governing equation can be expressed as [33,34,35,36]

$$D\frac{{\partial }^{4}w\left(x,t\right)}{\partial x^4}+\rho \frac{{\partial }^{2}w\left(x,t\right)}{\partial t^2}+C\frac{\partial w\left(x,t\right)}{\partial t}+Kw\left(x,t\right)=q\left(x,t\right),$$

(1)

where $w\left(x,t\right)$ is the deflection of the composite beam, $D$ and $\rho$ are the bending stiffness and linear density of the composite beam, $C$ and $K$ are the damping coefficient and stiffness of the foundation, and $q\left(x,t\right)$ stands for the distribution of traffic load.

The traffic load $q\left(x,t\right)$ can be described as follows:

$$q\left(x,t\right)=q_0{f}_{\mathrm{B}}\left(x\right)f_{\mathrm{L}}\left(t\right),$$

(2)

where $q_0$ is the amplitude of traffic load, which is directly depending on the axle loads of the vehicle; $f_{\mathrm{B}}\left(x\right)$ stands for the distribution of traffic load along the width direction of the road; and $f_{\mathrm{L}}\left(t\right)$ stands for the time-history of traffic load along the driving direction (Figure 2).

The shape of the load distribution of a single tire applied on the pavements can be simplified as a parabola line [8]. Then, the distribution of traffic load along the width direction can be described as follows:

$$f_{\mathrm{B}}\left(x\right)=\{\begin{array}{ll}-4{\left(x-x_{\mathrm{C}}-B_{\mathrm{V}}/2\right)}^2/B_{\mathrm{C}}^2+1\hfill & x\in \left[x_{\mathrm{C}}+\frac{B_{\mathrm{V}}-B_{\mathrm{C}}}{2},x_{\mathrm{C}}+\frac{B_{\mathrm{V}}+B_{\mathrm{C}}}{2}\right]\hfill \\ -4{\left(x-x_{\mathrm{C}}+B_{\mathrm{V}}/2\right)}^2/B_{\mathrm{C}}^2+1\hfill & x\in \left[x_{\mathrm{C}}-\frac{B_{\mathrm{V}}+B_{\mathrm{C}}}{2},x_{\mathrm{C}}-\frac{B_{\mathrm{V}}-B_{\mathrm{C}}}{2}\right]\hfill \\ 0\hfill & \mathrm{other}\hfill \end{array},$$

(3)

in which $x_{\mathrm{C}}$ stands for the wheel path position, i.e., the distance from the center of the vehicle to the roadside; $B_{\mathrm{V}}$ stands for the track width, i.e., the lateral distance between the centerlines of the two tires; and $B_{\mathrm{C}}$ stands for the width of the contact area between tires and roads (Figure 3a).

The time-history waveform of the traffic load applied by a single tire on a PEH can be simplified as a half-cycle sinusoidal pulse $f\left(t\right)=\sin \left(\omega t\right)$, in which $t\in \left[0,\pi /\omega \right]$. Thus, for a vehicle with speed $v$ and wheelbase $L_{\mathrm{W}}$ (the distance between the front and rear axles) that passes the PEH, the time-history of traffic load along the driving direction can be obtained as

$$f_{\mathrm{L}}\left(t\right)=\{\begin{array}{ll}\sin \left(\mathsf{\pi }t/t_1\right)\hfill & t\in \left[0,t_1\right]\hfill \\ \sin \left[\mathsf{\pi }\left(t-t_1-t_2\right)/t_1\right]\hfill & t\in \left[t_1+t_2,2t_1+t_2\right]\hfill \\ 0\hfill & \mathrm{other}\hfill \end{array},$$

(4)

in which $t_1=\left(L_{\mathrm{C}}+L_{\mathrm{P}}\right)/v$, and $t_2=L_{\mathrm{W}}/v$. Here, $L_{\mathrm{C}}$ stands for the length of the contact area between tires and roads, and $L_{\mathrm{P}}$ stands for the length of a PEH unit. The following distance, that is, the distance between two consecutive vehicles traveling along the same direction, is denoted as $L_{\mathrm{S}}$, and then, the period $T$ of the traffic load can be expressed as $T=\left(L_{\mathrm{W}}+L_{\mathrm{S}}\right)/v$; thus, $f_{\mathrm{L}}\left(t\right)=f_{\mathrm{L}}\left(t+T\right)$ (Figure 3b).

Substituting Equations (2)–(4) into Equation (1), the deflection of the composite beam $w\left(x,t\right)$ can be obtained readily.

2.2. Electromechanical Modeling of PEHs

Previous research studies suggest that multilayer stack structural PEHs are of good durability under traffic load and also convenient for on-site installation [47,48,49]. Here, this type of PEHs is used as a typical example in the forthcoming analysis. The PEHs embedded in the pavement would endure stress and strain when traffic flow load is applied on the road. Then, according to the constitutive relationship of piezoelectric material, the accumulated charge of the ith PEH (dimension: $L_{\mathrm{P}}\times B_{\mathrm{P}}\times h_{\mathrm{P}}$) can be obtained as

$$Q_i\left(t\right)=C_{\mathrm{P}}{V}_i-\alpha \frac{\partial w^2\left(x,t\right)}{\partial x^2}|{}_{x=x_i}$$

(5)

where $V_i$ is the voltage drop across the PEH, $C_{\mathrm{P}}=\frac{L_{\mathrm{P}}{B}_{\mathrm{P}}}{h_{\mathrm{P}}}\left({\epsilon }_{33}-\frac{2d_{31}^2}{s_{11}+s_{12}}\right)$ is the equivalent capacitance of the PEH unit, and $\alpha =\frac{L_{\mathrm{P}}{B}_{\mathrm{P}}{d}_{31}{h}_c{Y}_2}{\left(s_{11}+s_{12}\right)Y_{\mathrm{P}}}$ is the equivalent force factor. Here, $d_{31}$, ${\epsilon }_{33}$, $s_{11}$, and $s_{12}$ are the piezoelectric constant, dielectric constant, and elastic constants of the piezoelectric material, respectively; $x_i$ is the embedded position of the ith PHE unit; $Y_2$ and $Y_{\mathrm{P}}$ are the Young’s modulus of the base layer of road and piezoelectric material; and $h_c$ is the distance from the center of piezoelectric layer to the neutral axis of the whole composite cross-section.

When the PEH unit is connected to a resistor with resistance R, the current in this circuit would be $I_i=-\mathrm{d}{Q}_i\left(t\right)/\mathrm{d}t=V_i/R$, and then, the governing equation for this circuit can be written as follows:

$$\frac{\mathrm{d}{V}_i\left(t\right)}{\mathrm{d}t}+\frac{V_i\left(t\right)}{R{C}_{\mathrm{P}}}=\frac{\alpha }{C_{\mathrm{P}}}\frac{\partial w^3\left(x,t\right)}{\partial x^2\partial t}|{}_{x=x_i}$$

(6)

With the initial condition $V_i\left(0\right)=0$, the voltage across the ith PEH unit can be derived as

$$V_i\left(t\right)=\frac{\alpha }{C_{\mathrm{P}}}\exp \left(-\frac{t}{R{C}_{\mathrm{P}}}\right){\displaystyle {\mathsf{\int }}_0^t\exp \left(\frac{t^{\prime }}{R{C}_{\mathrm{P}}}\right)\left[\frac{\partial w^3\left(x,t\right)}{\partial x^2\partial t}|{}_{x=x_i}\right]\mathrm{d}{t}^{\prime }}$$

(7)

So, when the wheel path position of a vehicle is $x_{\mathrm{C}}$, the energy harvested by the ith PEH in a period T as the vehicle passes can be obtained as

$${\stackrel{⌢}{E}}_i\left(x_{\mathrm{C}}\right)=\left[{\displaystyle {\mathsf{\int }}_0^T{V}_i^2\left(t\right)\mathrm{d}t}\right]/R$$

(8)

According to the standard <BS 5400, Steel, Concrete and Composite Bridges-Part 10: Code of Practice for Fatigue>, which is published by the British Standards Institution in 1980, the distribution of the wheel path position $x_{\mathrm{C}}$ follows a Gaussian distribution, i.e., $p\left(x_{\mathrm{C}}\right)~\mathrm{N}\left(\mu ,{\sigma }^2\right)$. Thus, considering the lateral wheel path distribution, the energy harvested by the ith PEH in a period T can be obtained as

$$E_i={\displaystyle {\mathsf{\int }}_{\min \left(x_{\mathrm{C}}\right)}^{\max \left(x_{\mathrm{C}}\right)}{\stackrel{⌢}{E}}_i\left(x_{\mathrm{C}}\right)p\left(x_{\mathrm{C}}\right)\mathrm{d}{x}_{\mathrm{C}}}$$

(9)

3. Scaling Law Analysis

From the above-mentioned theoretical model, it can be seen that as many as 24 parameters are contained in the piezoelectric energy-harvesting system under traffic flow load. There are eight traffic flow load parameters, i.e., the amplitude of traffic load $q_0$, wheel path position $x_{\mathrm{C}}$, track width $B_{\mathrm{V}}$, wheelbase $L_{\mathrm{W}}$, following distance $L_{\mathrm{S}}$, traffic speed $v$, the length $L_{\mathrm{C}}$ and width $B_{\mathrm{C}}$ of the contact area between tires and roads. There are also eight road material and structure parameters, i.e., thickness, density and modulus of the surface layer and base layer of the road, the stiffness $K$, and damping coefficient $C$ of foundation. The total number of the parameters of PEH units is also 8, and these parameters are the size ($L_{\mathrm{P}}$, $B_{\mathrm{P}}$, and $h_{\mathrm{P}}$), piezoelectric constant $d_{31}$, dielectric constant ${\epsilon }_{33}$, elastic constants ($s_{11}$ and $s_{12}$), and the embedded position $x_i$. All these parameters would influence the energy-harvesting efficiency of the piezoelectric energy harvesting system. The traditional approach to examine the influence of these parameters on the energy-harvesting efficiency is based on single parameter analysis, which requires other parameters to be fixed when examining the influence of a concerned parameter. This approach is effective for a simple system but would be insufficient for a complex system, since it is unable to provide a comprehensive understanding of the interaction between these parameters in the system. By contrast, based on the deep understanding about the whole system, the scaling law analysis can provide a comprehensive understanding of the relation between these parameters. Through in-depth analysis of each equation in the piezoelectric energy-harvesting system, the following dimensionless parameters are selected for the scaling law analysis.

The normalized lateral embedded position of a PEH unit $\overline{x}$ is defined as $\overline{x}=x/B$, in which B is the width of the road; then, the lateral distribution of traffic load along the width of road can be normalized as

$${\overline{f}}_{\mathrm{B}}\left(\overline{x}\right)=\{\begin{array}{ll}-{\left(\overline{x}-\frac{x_{\mathrm{C}}}{B}-\frac{B_{\mathrm{V}}}{2B}\right)}^2{\left(\frac{2B}{B_C}\right)}^2+1\hfill & \overline{x}\in \left[\frac{x_{\mathrm{C}}}{B}+\frac{B_{\mathrm{V}}}{2B}-\frac{B_{\mathrm{C}}}{2B},\frac{x_{\mathrm{C}}}{B}+\frac{B_{\mathrm{V}}}{2B}+\frac{B_{\mathrm{C}}}{2B}\right]\hfill \\ -{\left(\overline{x}-\frac{x_{\mathrm{C}}}{B}+\frac{B_{\mathrm{V}}}{2B}\right)}^2{\left(\frac{2B}{B_C}\right)}^2+1\hfill & \overline{x}\in \left[\frac{x_{\mathrm{C}}}{B}-\frac{B_{\mathrm{V}}}{2B}-\frac{B_{\mathrm{C}}}{2B},\frac{x_{\mathrm{C}}}{B}-\frac{B_{\mathrm{V}}}{2B}+\frac{B_{\mathrm{C}}}{2B}\right]\hfill \\ 0\hfill & \mathrm{other}\hfill \end{array}$$

(10)

Normalized time $\overline{t}$ is defined as $\overline{t}=t/t_1$, in which $t_1=\left(L_{\mathrm{C}}+L_{\mathrm{P}}\right)/v$ is the time needed for a single tire to pass a PEH unit, as aforementioned. Then, the time-history of traffic load along the driving direction can be normalized as

$${\overline{f}}_{\mathrm{L}}\left(\overline{t}\right)=\{\begin{array}{ll}\sin \left(\mathsf{\pi }\overline{t}\right)\hfill & t\in \left[0,1\right]\hfill \\ \sin \left[\mathsf{\pi }\left(\overline{t}-1-t_2/t_1\right)\right]\hfill & t\in \left[1+t_2/t_1,2+t_2/t_1\right]\hfill \\ 0\hfill & \mathrm{other}\hfill \end{array}$$

(11)

Normalized parameters $\overline{w}=\frac{wD}{q_0{B}^4}$, $\overline{\rho }=\frac{\rho B^4}{D{t}_1^2}$, $\overline{C}=\frac{C{B}^4}{D{t}_1}$, and $\overline{K}=\frac{K{B}^4}{D}$ are defined and then substituted into Equation (1), and the governing equation for the vibration of the roadway under traffic flow load can be rewritten as

$$\frac{{\partial }^4\overline{w}\left(\overline{x},\overline{t}\right)}{\partial {\overline{x}}^4}+\overline{\rho }\frac{{\partial }^2\overline{w}\left(\overline{x},\overline{t}\right)}{\partial {\overline{t}}^2}+\overline{C}\frac{\partial \overline{w}\left(\overline{x},\overline{t}\right)}{\partial \overline{t}}+\overline{K}\overline{w}\left(\overline{x},\overline{t}\right)={\overline{f}}_{\mathrm{B}}\left(\overline{x}\right){\overline{f}}_{\mathrm{L}}\left(\overline{t}\right)$$

(12)

The normalized output voltage of the ith PEH unit ${\overline{V}}_i$ can be defined as ${\overline{V}}_i=V_i/V_0$, in which $V_0=\frac{\alpha }{C_{\mathrm{P}}}\frac{q_0{B}^2}{D}$; then, ${\overline{V}}_i$ can be derived as

$${\overline{V}}_i\left(\overline{t}\right)=\pi \exp \left(-\frac{\pi \overline{t}}{R\omega C_{\mathrm{P}}}\right){\displaystyle {\mathsf{\int }}_0^{\overline{t}}\exp \left(\frac{\pi \overline{t\prime }}{R\omega C_{\mathrm{P}}}\right)\left[\frac{\partial {\overline{w}}^3\left(\overline{x},\overline{t}\right)}{\partial {\overline{x}}^2\partial \overline{t}}|{}_{\overline{x}={\overline{x}}_i}\right]\mathrm{d}\overline{t\prime }}$$

(13)

in which $\omega =\pi /t_1$.

The normalized energy harvested by the ith PEH unit ${\overline{E}}_i$ can be defined as ${\overline{E}}_i=E_i/E_{{}_{\mathrm{eff}0}}$. Here, $E_{{}_{\mathrm{eff}0}}={\alpha }^2{\left(q_0{B}^2/D\right)}^2/C_{\mathrm{P}}$ is the energy coefficient. Then, ${\overline{E}}_i$ can be obtained as

$${\overline{E}}_{\mathrm{i}}={\overline{E}}_{\mathrm{i}}\left(R\omega C_{\mathrm{P}},\overline{K},\overline{C},\overline{\rho },{\overline{x}}_i\right)$$

(14)

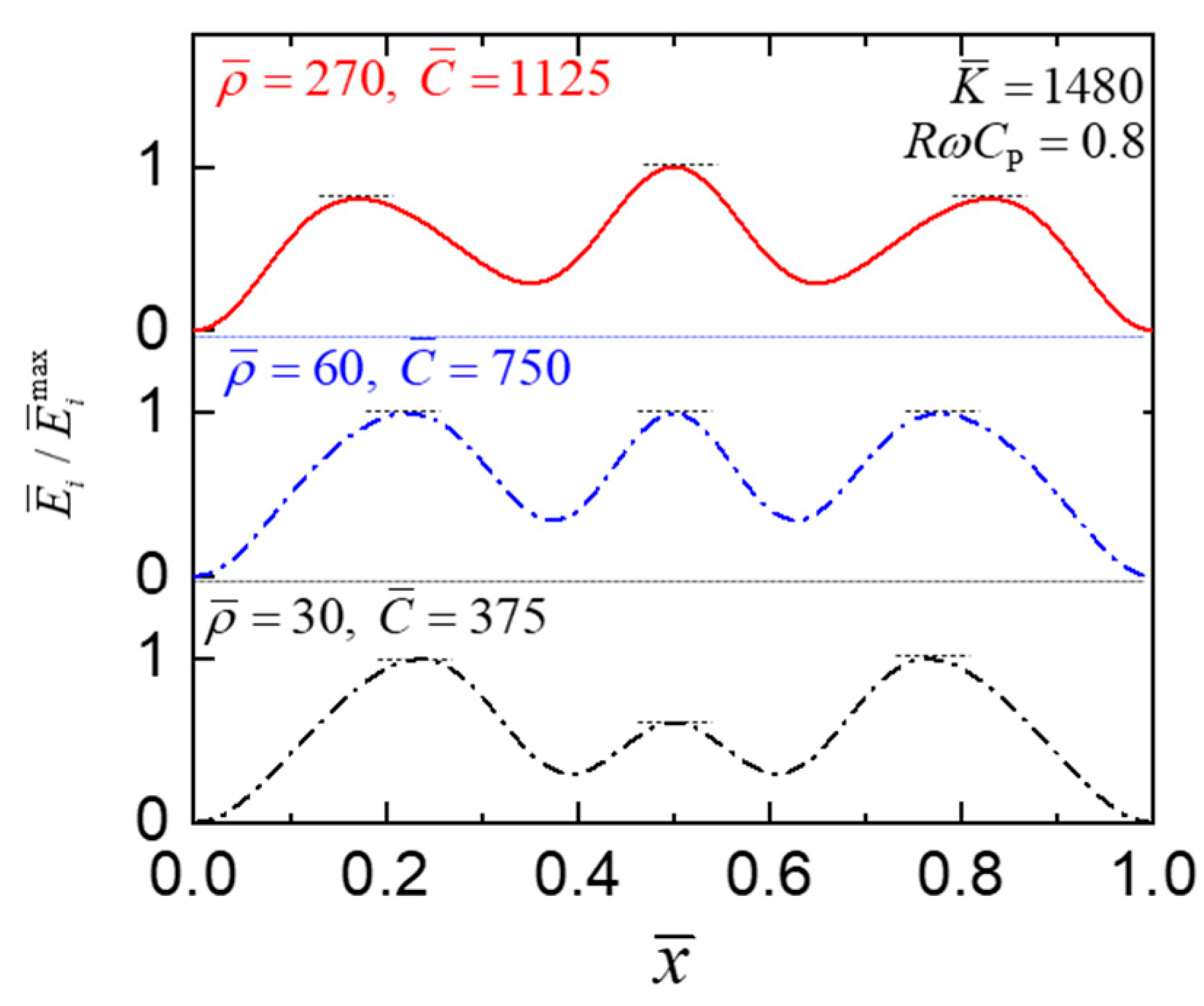
4. Results and Optimization Criteria

From Equation (14), it can be seen that the energy $E_i$ harvested by a PEH unit in a period T is linear with the energy coefficient $E_{{}_{\mathrm{eff}0}}$, and it is also influenced by the system’s intrinsic parameter $R\omega C_{\mathrm{P}}$, the normalized stiffness $\overline{K}$ and the normalized damping coefficient $\overline{C}$ of the foundation, the normalized linear density $\overline{\rho }$ of the pavement, and also the unit’s lateral embedded position ${\overline{x}}_i=x_i/B$.

4.1. Influence of Energy Coefficient $E_{{}_{\mathrm{eff}0}}$

Substitute the expressions of $\alpha$ and $C_{\mathrm{P}}$ into $E_{{}_{\mathrm{eff}0}}={\alpha }^2{\left(q_0{B}^2/D\right)}^2/C_{\mathrm{P}}$, the energy coefficient $E_{{}_{\mathrm{eff}0}}$ can be rewritten as

$$E_{{}_{\mathrm{eff}0}}=\left(L_{\mathrm{P}}{B}_{\mathrm{P}}{h}_{\mathrm{P}}\right)q_0^2\frac{B^4}{D^2}\frac{Y_2^2}{Y_{\mathrm{P}}^2}{h}_{\mathrm{c}}^2\frac{d_{31}^2}{\left[{\epsilon }_{33}-2d_{31}^2/\left(s_{11}+s_{12}\right)\right]{\left(s_{11}+s_{12}\right)}^2},$$

(15)

Equation (15) shows that when normalized energy ${\overline{E}}_{\mathrm{i}}$ is fixed, the energy harvested by PEH units would be linear to the energy coefficient $E_{{}_{\mathrm{eff}0}}$. This would arrive at the following conclusions. ① Energy harvested by the PEH units is linear to the total volume of piezoelectric material ($V_{\mathrm{P}}=L_{\mathrm{P}}{B}_{\mathrm{P}}{h}_{\mathrm{P}}$). Therefore, when evaluating the energy efficiency of different PEHs, the energy harvested per unit volume piezoelectric material should be applied to compare. ② Energy harvested by PEH units is directly proportional to the square of the amplitude of traffic load, i.e., $E_{\mathrm{i}}\propto q_0^2$. ③ Energy harvested by PEH units is linear to the combination coefficient $\frac{B^4}{D^2}\frac{Y_2^2}{Y_{\mathrm{P}}^2}$ of the pavement structure. This means the larger the ratio of the fourth power of the road’s width to the square of the road’s bending stiffness ($D^2$), the larger the ratio of the road’s base layer’s Young’s modulus $Y_2$ to the piezoelectric material’s Young’s modulus $Y_{\mathrm{P}}$; then, the PEH units embedded in the road can harvest energy more efficiently. This relationship can guide the choice of suitable roadways for embedding PEH units. ④ Energy harvested by PEH units is directly proportional to the square of the distance from the center of the piezoelectric layer to the neutral axis of the whole composite cross-section, i.e., $E_{\mathrm{i}}\propto h_{\mathrm{c}}^2$. This relationship can be used to determine the embedded depth of PEH units. ⑤ The larger the combination coefficient $d_{31}^2/\left[{\epsilon }_{33}-2d_{31}^2/\left(s_{11}+s_{12}\right)\right]/{\left(s_{11}+s_{12}\right)}^2$ of the piezoelectric material, the higher the energy-harvesting efficiency. This relationship could be used as a guideline for choosing proper piezoelectric material.

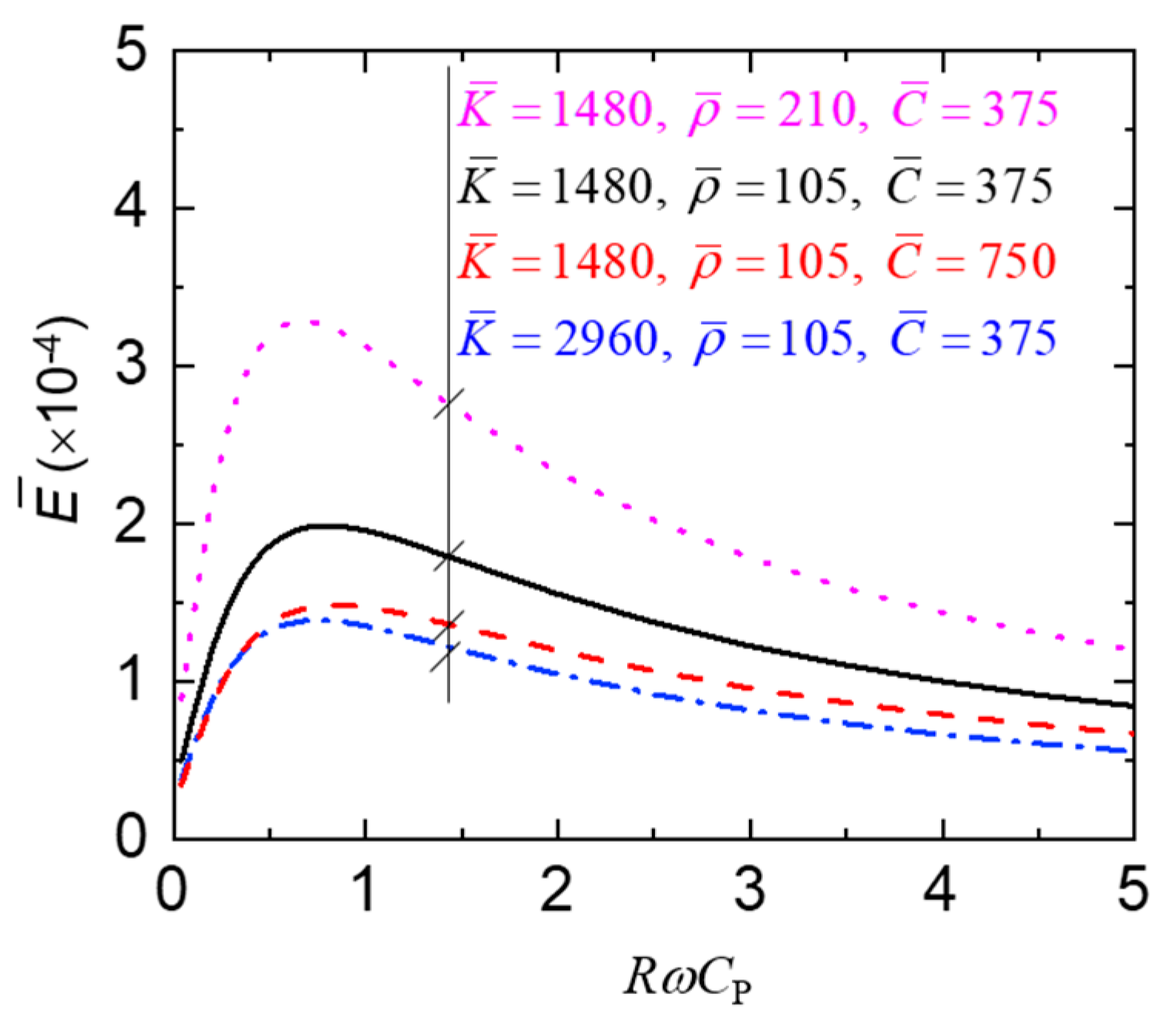
4.2. Influence of System’s Intrinsic Parameter $R\omega C_{\mathrm{P}}$

In the piezoelectric energy-harvesting systems, $R\omega C_{\mathrm{P}}$ is an intrinsic normalized parameter that denotes the effect of matching between the external resistance $R$, the equivalent capacitance of the PHE and the frequency of the excitation $\omega$. In practical applications, the external resistance $R$ of the electronics embedded in the pavement, the excitation frequency $\omega$ of the traffic load, and the equivalent capacitance of the PHE $C_{\mathrm{P}}$ codetermine the value of $R\omega C_{\mathrm{P}}$. For a typical road [50] with common traffic speed $v=20\mathrm{m}/\mathrm{s}$, the normalized parameters can be calculated as $\overline{\rho }=\frac{\rho B^4}{D{t}_1^2}=105$, $\overline{C}=\frac{C{B}^4}{D{t}_1}=375$, $\overline{K}=\frac{K{B}^4}{D}=1480$. Then, when the parameters of roads and traffic speed are changed, the $\overline{\rho }$, $\overline{C}$, $\overline{K}$ would be changed accordingly. Therefore, the variance of the values of $\overline{\rho }$, $\overline{C}$, and $\overline{K}$ can cover different kinds of roads under various traffic speeds. The influence of the system’s intrinsic parameter $R\omega C_{\mathrm{P}}$ on the energy-harvesting efficiency is investigated under four typical types of roads (Figure 4). Here, the vertical coordinate $\overline{E}={\displaystyle \sum _{i=1}^N{\overline{E}}_i}$ denotes the energy harvested by all of the PEH units embedded in the pavement. In other words, the total length of these units equals the overall width of the pavement. For all these four distinct kinds of roads, the optimal $R\omega C_{\mathrm{P}}$, which is corresponding to the maximum harvested energy, is 0.75, 0.80, 0.85, 0.75, respectively (as shown by the four lines from up to down in Figure 4). Thus, in practical application, it is acceptable to make $R\omega C_{\mathrm{P}}=0.8$, since this can guarantee 95% of the highest energy harvesting efficiency for the four different road conditions (Figure 4). Generally, there are two ways to satisfy this criterion. ① Adjust the external impedance $R$. Once the PEH unit is designed, the equivalent capacitance $C_{\mathrm{P}}$ of the device is determined. Then, the external impedance $R$ should be adjusted according to the traffic speeds (such as expressway with high traffic speed, urban roads with low traffic speed) to ensure $R\omega C_{\mathrm{P}}=0.8$, since $\omega =\pi v/\left(L_{\mathrm{C}}+L_{\mathrm{P}}\right)$. ② Adjust the design of PEH units. Under certain circumstances, the external impedance $R$ of the electronics may be unchangeable. So, the equivalent capacitance $C_{\mathrm{P}}$ of the PEH units should be adjusted to make $R\omega C_{\mathrm{P}}=0.8$. Since $C_{\mathrm{P}}=\frac{L_{\mathrm{P}}{B}_{\mathrm{P}}}{h_{\mathrm{P}}}\left({\epsilon }_{33}-\frac{2d_{31}^2}{s_{11}+s_{12}}\right)$, the dimension of PHE ($L_{\mathrm{P}}$, $B_{\mathrm{P}}$, $h_{\mathrm{P}}$) can be tuned to make $C_{\mathrm{P}}$ satisfy this criterion.

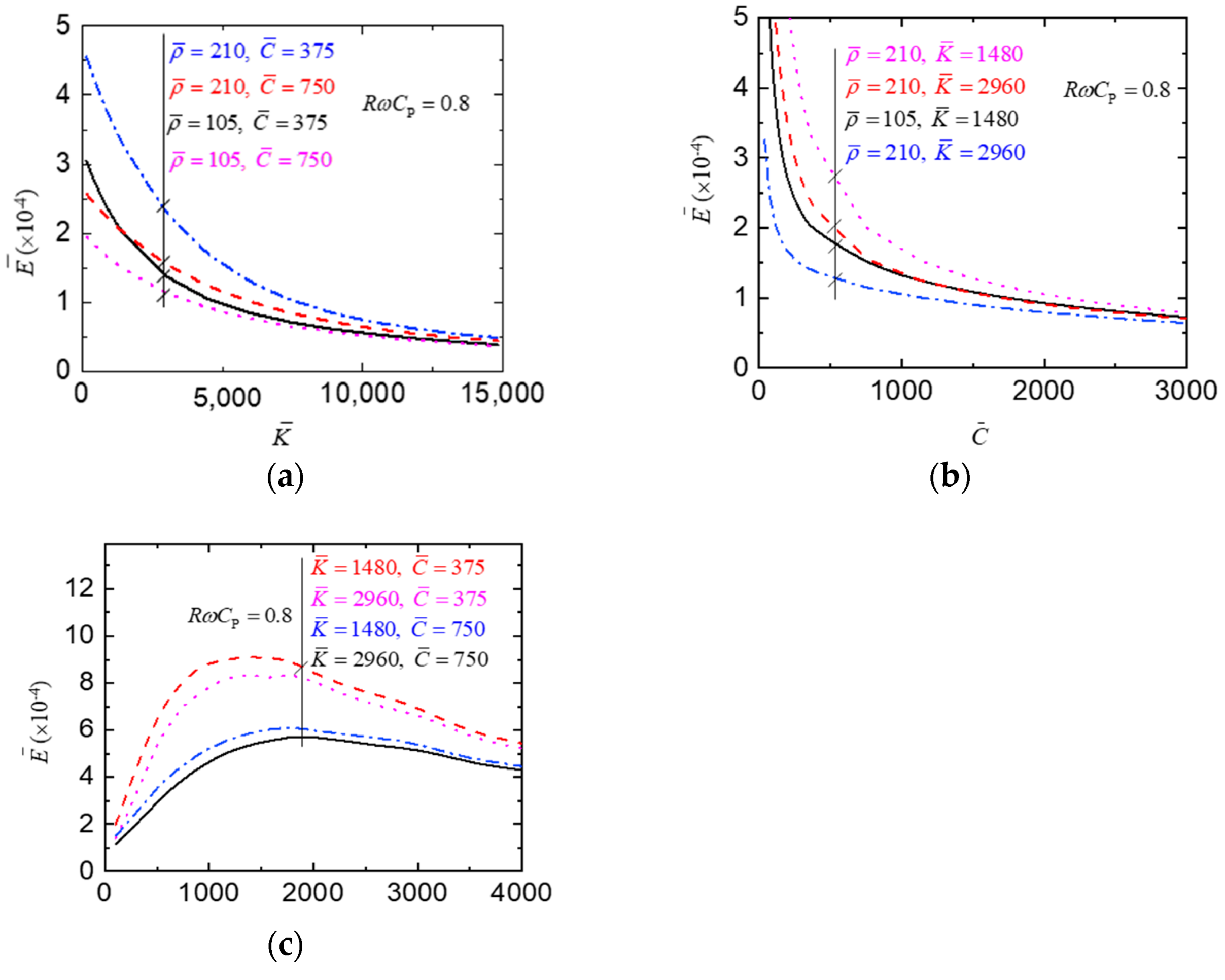
4.3. Influence of Normalized Parameters ($\overline{K}$, $\overline{C}$, and $\overline{\rho }$) of Roads

The influence of normalized foundation stiffness $\overline{K}$ of the foundation is evaluated for four typical roads with varied normalized linear density $\overline{\rho }$ and damping coefficient $\overline{C}$ (Figure 5a). The results show that the normalized harvested $\overline{E}$ would decrease with the increase in the normalized foundation stiffness $\overline{K}$ for all these four different roads. This is because the strain of piezoelectric material would be reduced with the increasing of the normalized foundation stiffness $\overline{K}$, whereas the traffic load and other parameters of the road are unchanged. Thus, the roadways with lower foundation stiffness are preferred to achieve higher energy harvesting efficiency.

The influence of the normalized damping coefficient $\overline{C}$ of the foundation is also investigated under four typical roads (Figure 5b). The results show that the normalized harvested $\overline{E}$ would decrease with the increase in the normalized foundation damping coefficient $\overline{C}$ for all these four different roads. This is because the vibration of PEH units would decay more quickly if the damping coefficient of the foundation is larger; consequently, the electric output power of PEH units would also decrease more quickly, resulting in the decease of the energy harvested by PEH units. Thus, the roads with lower foundation damping coefficients are preferred to maximize higher energy harvesting efficiency.

The influence of the pavement’s normalized linear density $\overline{\rho }$ is investigated under four typical roads similarly (Figure 5c). The results reveal that the harvested energy of PEH units would increase first and then decrease with the increasing normalized linear density $\overline{\rho }$. This is because the fundamental natural frequency (${\omega }_{\mathrm{n}}=\sqrt{\left(1+\overline{K}\right)/\overline{\rho }}$) would decrease and normalized excitation frequency $s=\omega /{\omega }_{\mathrm{n}}$ would increase with the increasing of normalized linear density $\overline{\rho }$. From the frequency response function $H\left(s\right)$ in basic vibration theories, it can be seen that the response of the system would increase first and then decrease with the normalized excitation frequency s, which would cause the energy gathered by PEH units to change in the same way.

In practical conditions, the traffic condition with smaller $\overline{K}$, smaller $\overline{C}$ and moderate $\overline{\rho }$ (approximate 1000) would guarantee the highest energy-harvesting efficiency.

4.4. Influence of Normalized Lateral Embedded Position ${\overline{x}}_i$ of PEH Units

The influence of the normalized lateral embedded position ${\overline{x}}_i$ of PEH units is investigated under three distinct types of roads, i.e., type 1 with $\overline{\rho }=270,\overline{C}=1125,\overline{K}=1480$, type 2 with $\overline{\rho }=60,\overline{C}=750,\overline{K}=1480$, and type 3 with $\overline{\rho }=30,\overline{C}=375,\overline{K}=1480$, as shown in Figure 6. It can be seen that the PEH units embedded at the middle of the pavement (${\overline{x}}_i=0.5$) could harvest more energy than the units embedded near the wheels (${\overline{x}}_i=0.25$, 0.75) when $\overline{\rho }=270$, $\overline{C}=1125$, and $\overline{K}=1480$. According to the definition of these normalized parameters, it can be known that this would be corresponding to the condition that the velocity of vehicles is relatively high. By contrast, when $\overline{\rho }=30$, $\overline{C}=375$, and $\overline{K}=1480$, which means that the speed of vehicles is relatively low, PEH units embedded near the wheels (${\overline{x}}_i=0.25$, 0.75) would harvest more energy than those embedded at the middle of the pavement (${\overline{x}}_i=0.5$). When $\overline{\rho }=60$, $\overline{C}=750$, and $\overline{K}=1480$, the energy harvested by PEH units embedded at the middle of the pavement would be similar to that embedded near the wheels. In short, the lateral embedded positions of PEH units should be carefully chosen, since the unit embedded at optimal positions would harvest as much as four times that patched at bed locations (Figure 6), and the optimal lateral embedded positions should be adjusted according to the normalized road parameters ($\overline{K}$, $\overline{C}$, and $\overline{\rho }$), which are dependent both on the parameters of roads and the speed of vehicles.

4.5. Energy Harvested by PEH Units: A Numerical Example

Based on the above calculations, for a typical road ($\overline{\rho }=105$, $\overline{C}=375$, and $\overline{K}=1480$) [50], as a vehicle ($q_0=0.7\mathrm{MPa}$) passes with common traffic speed $v=20\mathrm{m}/\mathrm{s}$, the PEH unit (parameters are listed in

Table 1. Parameters of the PEH units.

Geometry and Material Parameters	Value
Length of a PEH unit, LP (m)	0.05
Width of a PEH unit, BP (m)	0.05
Thickness of a PEH unit, hP (m)	0.02
Piezoelectric constant, d31 (C/N)	−2.74 × 10−10
Dielectric constants, ε33 (F/m)	3.98 × 10−8
Elastic compliances, s11 (Pa−1)	16.5 × 10−12
Elastic compliances, s12 (Pa−1)	−4.78 × 10−12

) that are embedded in the optimal lateral positions of the pavement can harvest 0.68 mJ. If 1000 such vehicles pass this unit in one hour, then it can be estimated that the energy harvested by the piezoelectric material can achieve as 13,600 J/m³.

5. Conclusions

An integrated electromechanical model incorporating a composite beam resting on the Kelvin–Voigt foundation is proposed to investigate the piezoelectric energy harvesting of pavements under open-traffic conditions, and the electric performance of PEH units embedded in the pavement is theoretically calculated with this model. A concise scaling law is established to reveal the intrinsic relationship between the energy-harvesting efficiency of PEH units and four combined parameters in the system, i.e., the energy coefficient, the energy harvesting system’s intrinsic parameter, normalized parameters of roadways, and normalized lateral embedded position of PEH units. The results reveal that the energy-harvesting system’s intrinsic parameter should be approximately 0.8 to ensure maximum energy harvesting efficiency. Meanwhile, when the pavement has lower bending stiffness and higher linear density and the foundation has small stiffness and smaller damping coefficient, the roadway would be more suitable for energy harvesting. Furthermore, the optimal lateral embedded position of PEH units should be adjusted with the parameters of roads and traffic speeds. This theoretical model can be used as a reference for material selection, structural optimization, and lateral embedded position determination of PEH units, as well as the selection of the roadway to achieve optimal efficiency for PEHs embedded in pavement under on-site open-traffic conditions.