Reliability Assessment of SiC-Based Depot Charging Infrastructure with Smart and Bidirectional (V2X) Charging Strategies for Electric Buses
Abstract
:1. Introduction
2. Methodology
2.1. System and Control Architecture
2.2. Smart Charging Scheduling Algorithm
2.3. Low-Level Controller
2.4. Electro-Thermal Modelling
2.5. Lifetime Estimation Framework
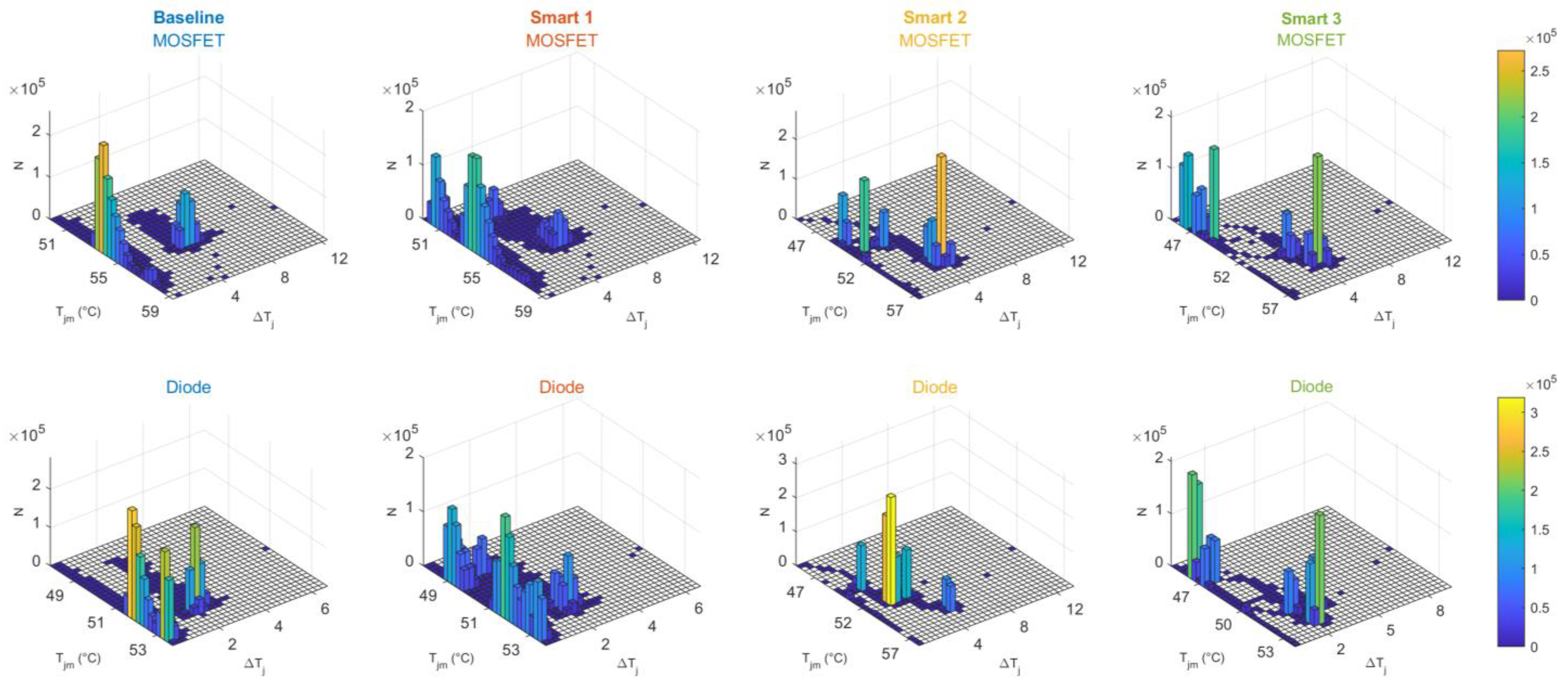
3. Results & Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Transport and Environment (T&E). Addressing the Heavy-Duty Climate Problem. Brussels, Belgium, September 2022. Available online: https://www.transportenvironment.org/discover/addressing-the-heavy-duty-climate-problem/ (accessed on 23 November 2022).
- Gandoman, F.H.; Ahmadi, A.; Bossche, P.V.D.; Van Mierlo, J.; Omar, N.; Nezhad, A.E.; Mavalizadeh, H.; Mayet, C. Status and future perspectives of reliability assessment for electric vehicles. Reliab. Eng. Syst. Saf. 2018, 183, 1–16. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Wang, H.; Vernica, I.; Liu, B.; Davari, P. Reliability of Power Electronic Systems for EV/HEV Applications. Proc. IEEE 2020, 109, 1060–1076. [Google Scholar] [CrossRef]
- Hanif, A.; Yu, Y.; DeVoto, D.; Khan, F.H. A Comprehensive Review Toward the State-of-the-Art in Failure and Lifetime Predictions of Power Electronic Devices. IEEE Trans. Power Electron. 2018, 34, 4729–4746. [Google Scholar] [CrossRef]
- Li, S.; Lu, S.; Mi, C.C. Revolution of Electric Vehicle Charging Technologies Accelerated by Wide Bandgap Devices. Proc. IEEE 2021, 109, 985–1003. [Google Scholar] [CrossRef]
- Ding, X.; Du, M.; Zhou, T.; Guo, H.; Zhang, C. Comprehensive comparison between silicon carbide MOSFETs and silicon IGBTs based traction systems for electric vehicles. Appl. Energy 2017, 194, 626–634. [Google Scholar] [CrossRef]
- Yu, S.; Wang, J.; Zhang, X.; Liu, Y.; Jiang, N.; Wang, W. The Potential Impact of Using Traction Inverters with SiC MOSFETs for Electric Buses. IEEE Access 2021, 9, 51561–51572. [Google Scholar] [CrossRef]
- Chakraborty, S.; Hasan, M.M.; Paul, M.; Tran, D.-D.; Geury, T.; Davari, P.; Blaabjerg, F.; El Baghdadi, M.; Hegazy, O. Real-Life Mission Profile-Oriented Lifetime Estimation of a SiC Interleaved Bidirectional HV DC/DC Converter for Electric Vehicle Drivetrains. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 5142–5167. [Google Scholar] [CrossRef]
- Barbagallo, C.; Rizzo, S.A.; Scelba, G.; Scarcella, G.; Cacciato, M. On the Lifetime Estimation of SiC Power MOSFETs for Motor Drive Applications. Electronics 2021, 10, 324. [Google Scholar] [CrossRef]
- Karunarathna, J.; Madawala, U.; Baguley, C.; Blaabjerg, F.; Sandelic, M. Reliability Analysis of Fast Electric Vehicle Charging Systems. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 1607–1612. [Google Scholar] [CrossRef]
- Manzolli, J.A.; Trovão, J.P.; Antunes, C.H. A review of electric bus vehicles research topics—Methods and trends. Renew. Sustain. Energy Rev. 2022, 159, 112211. [Google Scholar] [CrossRef]
- Pearre, N.S.; Ribberink, H. Review of research on V2X technologies, strategies, and operations. Renew. Sustain. Energy Rev. 2019, 105, 61–70. [Google Scholar] [CrossRef]
- Jahic, A.; Eskander, M.; Schulz, D. Charging Schedule for Load Peak Minimization on Large-Scale Electric Bus Depots. Appl. Sci. 2019, 9, 1748. [Google Scholar] [CrossRef] [Green Version]
- Elliott, M.; Kittner, N. Operational grid and environmental impacts for a V2G-enabled electric school bus fleet using DC fast chargers. Sustain. Prod. Consum. 2022, 30, 316–330. [Google Scholar] [CrossRef]
- Fan, H.; Wang, D.; Yu, Z.; Du, L. Bi-Level Optimal Scheduling of Electric Bus Fleets in Regional Integrated Electricity-Gas-Heat Energy Systems. IEEE Trans. Transp. Electrif. 2022. [Google Scholar] [CrossRef]
- Verbrugge, B.; Rauf, A.M.; Rasool, H.; Abdel-Monem, M.; Geury, T.; El Baghdadi, M.; Hegazy, O. Real-Time Charging Scheduling and Optimization of Electric Buses in a Depot. Energies 2022, 15, 5023. [Google Scholar] [CrossRef]
- Rafique, S.; Nizami, M.; Irshad, U.; Hossain, M.; Mukhopadhyay, S. A two-stage multi-objective stochastic optimization strategy to minimize cost for electric bus depot operators. J. Clean. Prod. 2021, 332, 129856. [Google Scholar] [CrossRef]
- Manzolli, J.A.; Trovão, J.P.F.; Antunes, C.H. Electric bus coordinated charging strategy considering V2G and battery degradation. Energy 2022, 254, 124252. [Google Scholar] [CrossRef]
- Houbbadi, A.; Trigui, R.; Pelissier, S.; Redondo-Iglesias, E.; Bouton, T. Optimal Scheduling to Manage an Electric Bus Fleet Overnight Charging. Energies 2019, 12, 2727. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Bryant, A.; Mawby, P.; Xiang, D.; Ran, L.; Tavner, P. An Industry-Based Survey of Reliability in Power Electronic Converters. IEEE Trans. Ind. Appl. 2011, 47, 1441–1451. [Google Scholar] [CrossRef]
- Verbrugge, B.; Hasan, M.M.; Rasool, H.; Geury, T.; El Baghdadi, M.; Hegazy, O. Smart Integration of Electric Buses in Cities: A Technological Review. Sustainability 2021, 13, 12189. [Google Scholar] [CrossRef]
- Rasool, H.; Verbrugge, B.; Zhaksylyk, A.; Tran, T.M.; El Baghdadi, M.; Geury, T.; Hegazy, O. Design Optimization and Electro-Thermal Modeling of an Off-Board Charging System for Electric Bus Applications. IEEE Access 2021, 9, 84501–84519. [Google Scholar] [CrossRef]
- Chakraborty, S.; Mazuela, M.; Tran, D.-D.; Corea-Araujo, J.A.; Lan, Y.; Loiti, A.A.; Garmier, P.; Aizpuru, I.; Hegazy, O. Scalable Modeling Approach and Robust Hardware-in-the-Loop Testing of an Optimized Interleaved Bidirectional HV DC/DC Converter for Electric Vehicle Drivetrains. IEEE Access 2020, 8, 115515–115536. [Google Scholar] [CrossRef]
- Rasool, H.; Verbrugge, B.; Jaman, S.; Abramushkina, E.; Geury, T.; El Baghdadi, M.; Hegazy, O. Design and Real-Time Implementation of a Control System for SiC Off-Board Chargers of Battery Electric Buses. Energies 2022, 15, 1434. [Google Scholar] [CrossRef]
- Samavatian, V.; Iman-Eini, H.; Avenas, Y. An efficient online time-temperature-dependent creep-fatigue rainflow counting algorithm. Int. J. Fatigue 2018, 116, 284–292. [Google Scholar] [CrossRef]
- Wintrich, A.; Nicolai, U.; Tursky, W.; Reimann, T. Application Manual Power Semiconductors; SEMIKRON International GmbH: Nuremberg, Germany, 2011. [Google Scholar]
- Karimi, S.; Zadeh, M.; Suul, J.A. A Multilayer Framework for Reliability Assessment of Shore-to-Ship Fast Charging System Design. IEEE Trans. Transp. Electrif. 2021, 8, 3028–3040. [Google Scholar] [CrossRef]
- Baba, S.; Gieraltowski, A.; Jasinski, M.T.; Blaabjerg, F.; Bahman, A.S.; Zelechowski, M. Active Power Cycling Test Bench for SiC Power MOSFETs—Principles, Design, and Implementation. IEEE Trans. Power Electron. 2020, 36, 2661–2675. [Google Scholar] [CrossRef]
- Pu, S.; Yang, F.; Vankayalapati, B.T.; Akin, B. Aging Mechanisms and Accelerated Lifetime Tests for SiC MOSFETs: An Overview. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 1232–1254. [Google Scholar] [CrossRef]

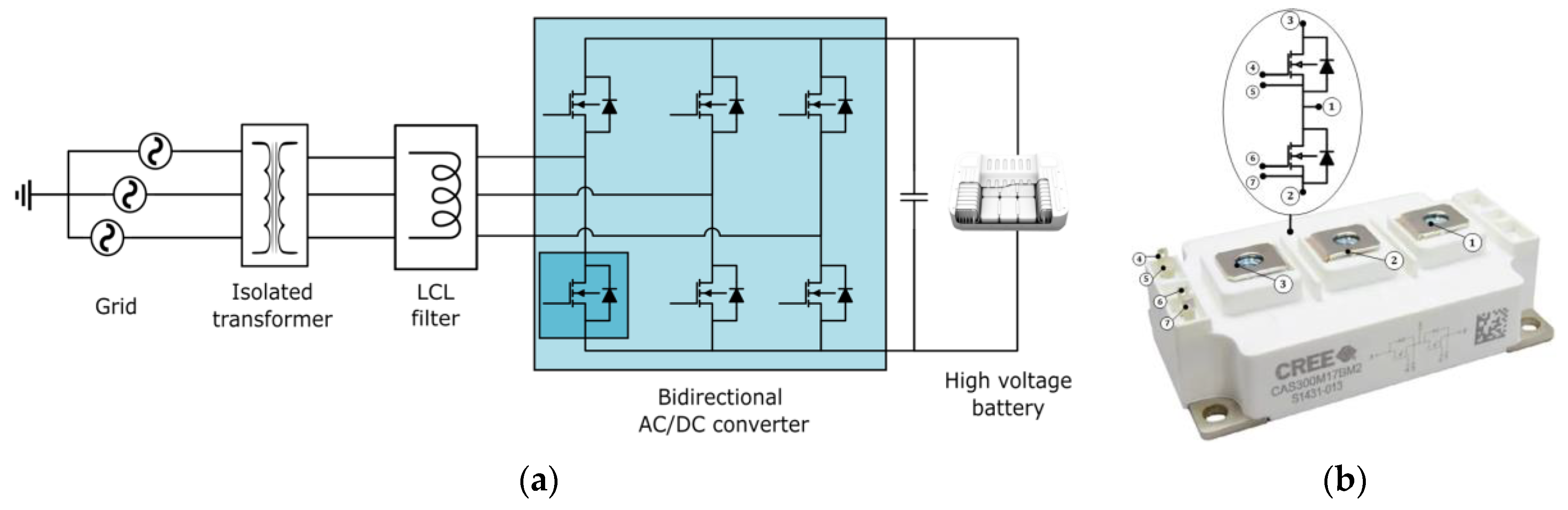
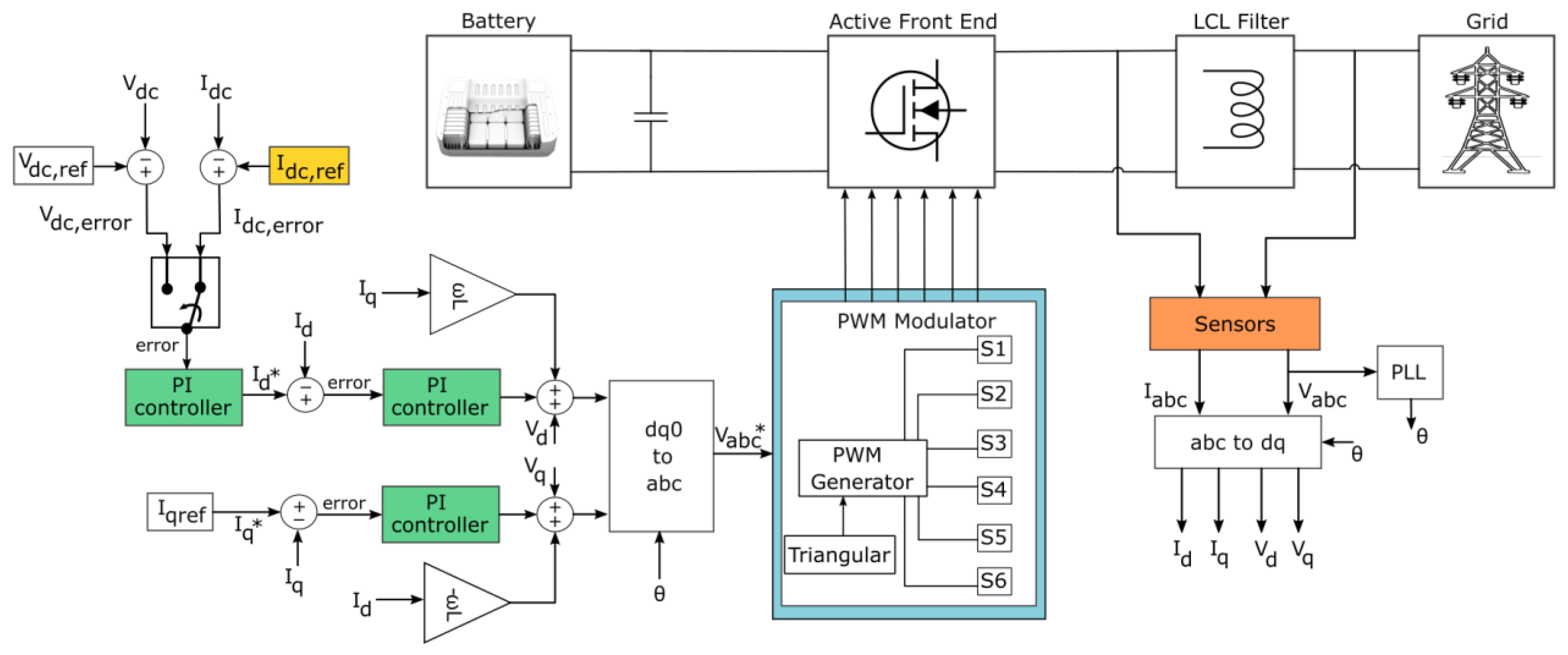

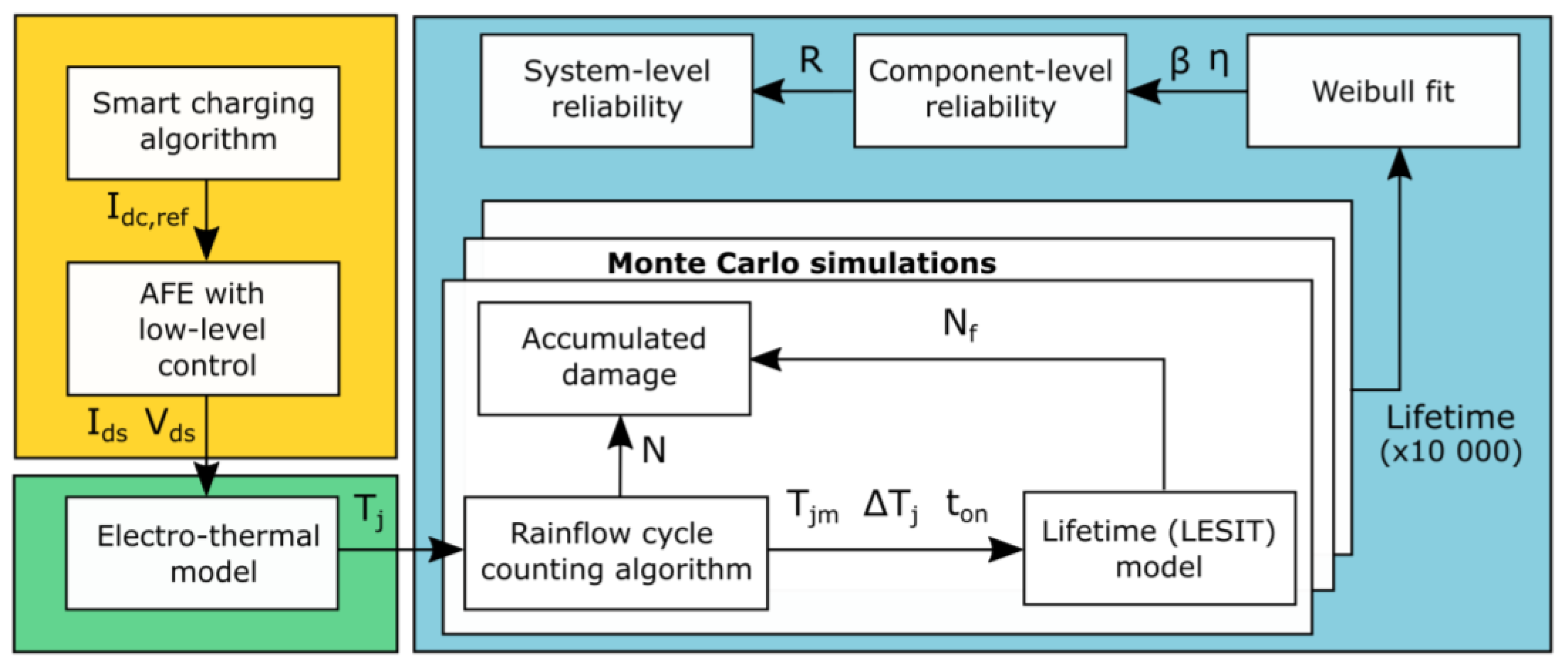

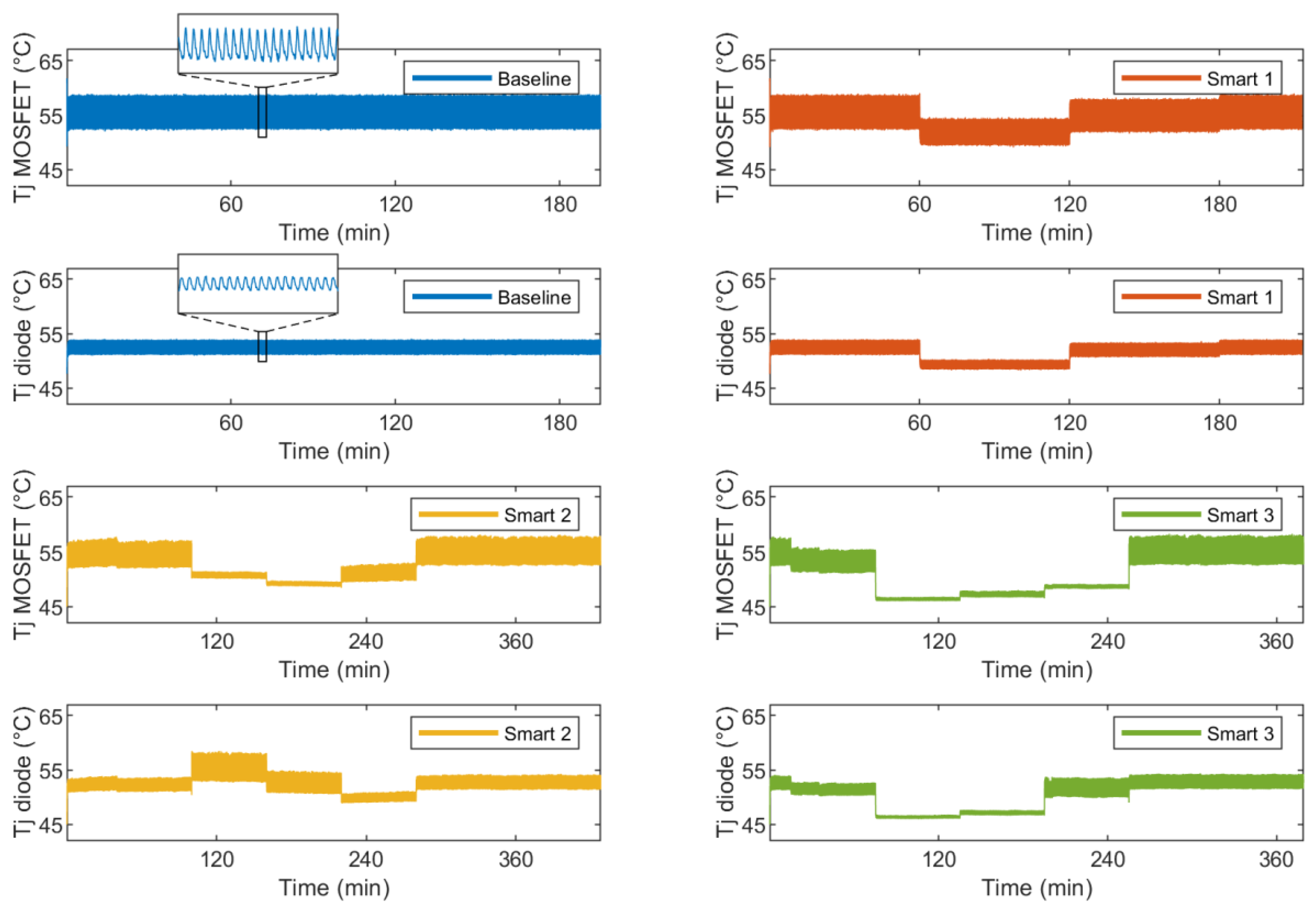

| Parameter | Value |
|---|---|
| Maximum power (kW) | 100 |
| Power factor | 0.99 |
| Switching frequency (kHz) | 40 |
| AC voltage (V) | 400 |
| DC voltage range (V) | 600–800 |
| Power electronic module | SiC half bridge module (CAS300M17BM2) |
| Controller | Control Parameters | gM (dB) | PM (deg) | ωcp (rad/s) | ωcg (rad/s) |
|---|---|---|---|---|---|
| Id/Iq Current Control | Kp = 1.8, Ki = 18,411 | 43.9 | 65.1 | 1.51 × 104 | 7.86 × 105 |
| Vdc/Idc Voltage/Current control | Kp = 0.25, Ki = 18 | 43.9 | 86.2 | 281 | 2.45 × 104 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verbrugge, B.; Rasool, H.; Hasan, M.M.; Chakraborty, S.; Geury, T.; El Baghdadi, M.; Hegazy, O. Reliability Assessment of SiC-Based Depot Charging Infrastructure with Smart and Bidirectional (V2X) Charging Strategies for Electric Buses. Energies 2023, 16, 153. https://doi.org/10.3390/en16010153
Verbrugge B, Rasool H, Hasan MM, Chakraborty S, Geury T, El Baghdadi M, Hegazy O. Reliability Assessment of SiC-Based Depot Charging Infrastructure with Smart and Bidirectional (V2X) Charging Strategies for Electric Buses. Energies. 2023; 16(1):153. https://doi.org/10.3390/en16010153
Chicago/Turabian StyleVerbrugge, Boud, Haaris Rasool, Mohammed Mahedi Hasan, Sajib Chakraborty, Thomas Geury, Mohamed El Baghdadi, and Omar Hegazy. 2023. "Reliability Assessment of SiC-Based Depot Charging Infrastructure with Smart and Bidirectional (V2X) Charging Strategies for Electric Buses" Energies 16, no. 1: 153. https://doi.org/10.3390/en16010153
APA StyleVerbrugge, B., Rasool, H., Hasan, M. M., Chakraborty, S., Geury, T., El Baghdadi, M., & Hegazy, O. (2023). Reliability Assessment of SiC-Based Depot Charging Infrastructure with Smart and Bidirectional (V2X) Charging Strategies for Electric Buses. Energies, 16(1), 153. https://doi.org/10.3390/en16010153








