Declining Discount Rates for Energy Policy Investments in CEE EU Member Countries
Abstract
1. Introduction
2. Dilemmas in Evaluating Energy-Related Investments
2.1. Energy Policy Investment Requirements in CEE EU Member Countries in the Light of European Union Strategic Goals
2.2. Social Discount Rate in Energy Investments Evaluation
3. Materials and Methods
3.1. Constant SDR: Ramsey Equation and Gollier’s Precautionary Term
3.2. Time-Declining SDR Based on Expected Net Present Value
3.3. Data Sources
4. Results
4.1. Estimation of the Constant SDR
4.2. Estimation of Declining SDR
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Steffen, B.; Patt, A. A Historical Turning Point? Early Evidence on How the Russia-Ukraine War Changes Public Support for Clean Energy Policies. Energy Res. Soc. Sci. 2022, 91, 102758. [Google Scholar] [CrossRef]
- Żuk, P.; Żuk, P. National Energy Security or Acceleration of Transition? Energy Policy after the War in Ukraine. Joule 2022, 6, 709–712. [Google Scholar] [CrossRef]
- Zakeri, B.; Paulavets, K.; Barreto-Gomez, L.; Echeverri, L.G.; Pachauri, S.; Boza-Kiss, B.; Zimm, C.; Rogelj, J.; Creutzig, F.; Ürge-Vorsatz, D. Pandemic, War, and Global Energy Transitions. Energies 2022, 15, 6114. [Google Scholar] [CrossRef]
- Kong, D.; Yang, X.; Xu, J. Energy Price and Cost Induced Innovation: Evidence from China. Energy 2020, 192, 116586. [Google Scholar] [CrossRef]
- Peña-Ramos, J.A.; del Pino-García, M.; Sánchez-Bayón, A. The Spanish Energy Transition into the EU Green Deal: Alignments and Paradoxes. Energies 2021, 14, 2535. [Google Scholar] [CrossRef]
- Ostrowski, W. The Twenty Years’ Crisis of European Energy Security: Central and Eastern Europe and the US. Geopolitics 2022, 27, 875–897. [Google Scholar] [CrossRef]
- Ciołek, M.; Emerling, I.; Olejko, K.; Sadowska, B.; Wójcik-Jurkiewicz, M. Assumptions of the Energy Policy of the Country versus Investment Outlays Related to the Purchase of Alternative Fuels: Poland as a Case Study. Energies 2022, 15, 1945. [Google Scholar] [CrossRef]
- Delivering the European Green Deal. Available online: https://ec.europa.eu/info/strategy/priorities-2019-2024/european-green-deal/delivering-european-green-deal_en (accessed on 15 November 2022).
- Economic Appraisal Vademecum 2021–2027—General Principles and Sector Applications; European Commission: Brussels, Belgium, 2021.
- Gardiner, S.M. A Perfect Moral Storm: Climate Change, Intergenerational Ethics and the Problem of Moral Corruption. Environ. Values 2006, 15, 397–413. [Google Scholar] [CrossRef]
- Taebi, B. Intergenerational Risks of Nuclear Energy. In Handbook of Risk Theory Epistemology, Decision Theory, Ethics, and Social Implications of Risk; Roeser, S., Hillerbrand, R., Sandin, P., Peterson, M., Eds.; Springer: Dordrecht, The Netherlands; Heidelberg, Germany; London, UK; New York, NY, USA, 2012; pp. 295–318. [Google Scholar]
- van den Bergh, J.C.J.M.; Botzen, W.J.W. Monetary Valuation of the Social Cost of CO2 Emissions: A Critical Survey. Ecol. Econ. 2015, 114, 33–46. [Google Scholar] [CrossRef]
- Florio, M.; Sirtori, E. The Social Cost of Capital: Recent Estimates for the EU Countries; CSIL Centre for Industrial Studies: Milano, Italy, 2013. [Google Scholar]
- Florio, M. Applied Welfare Economics: Cost-Benefit Analysis of Projects and Policies; Routledge: New York, NY, USA, 2014; ISBN 1-317-81425-8. [Google Scholar]
- Catalano, J.; Pancotti, C. Estimation of SDR in Selected Countries; Working Papers; CSIL Centre for Industrial Studies: Milano, Italy, 2022. [Google Scholar]
- Guide to Cost-Benefit Analysis of Investment Projects. Economic Appraisal Tool for Cohesion Policy 2014–2020; European Commission: Brussels, Belgium, 2015.
- The Green Book Central Government Guidance on Appraisal and Evaluation 2020; HM Treasury: London, UK, 2020.
- Arrow, K.; Cropper, M.; Gollier, C.; Groom, B.; Heal, G.; Newell, R.; Nordhaus, W.; Pindyck, R.; Pizer, W.; Portney, P.; et al. Determining Benefits and Costs for Future Generations. Science 2013, 341, 349–350. [Google Scholar] [CrossRef]
- Freeman, M.C.; Groom, B. Positively Gamma Discounting: Combining the Opinions of Experts on the Social Discount Rate. Econ. J. 2015, 125, 1015–1024. [Google Scholar] [CrossRef]
- Gollier, C.; Hammitt, J.K. The Long-Run Discount Rate Controversy. Annu. Rev. Resour. Econ. 2014, 6, 273–295. [Google Scholar] [CrossRef]
- Circular A-4. Available online: https://obamawhitehouse.archives.gov/node/15644 (accessed on 26 October 2022).
- Seçilmiş, E.; Akbulut, H. Social Discount Rates for Six Transition Countries. Ekon. Cas. 2019, 67, 629–646. [Google Scholar]
- Foltyn-Zarychta, M.; Buła, R.; Pera, K. Discounting for Energy Transition Policies—Estimation of the Social Discount Rate for Poland. Energies 2021, 14, 741. [Google Scholar] [CrossRef]
- Maselli, G.; Nesticò, A. The Role of Discounting in Energy Policy Investments. Energies 2021, 14, 6055. [Google Scholar] [CrossRef]
- Moser, C.; Stauffacher, M.; Smieszek, T.; Seidl, R.; Krütli, P.; Scholz, R.W. Psychological Factors in Discounting Negative Impacts of Nuclear Waste. J. Environ. Psychol. 2013, 35, 121–131. [Google Scholar] [CrossRef]
- Foltyn-Zarychta, M. Future-Generation Perception: Equal or Not Equal? Long-Term Individual Discount Rates for Poland. Energies 2021, 14, 8218. [Google Scholar] [CrossRef]
- Foltyn-Zarychta, M. Ocena Inwestycji Międzypokoleniowych-Kryteria Etyczne w Ekonomicznej Ocenie Efektywności Projektów Inwestycyjnych; C.H. Beck: Warszawa, Poland, 2018. [Google Scholar]
- Ramsey, F.P. A Mathematical Theory of Saving. Econ. J. 1928, 38, 543–559. [Google Scholar] [CrossRef]
- Gollier, C. Pricing the Planet’s Future: The Economics of Discounting in an Uncertain World; Princeton University Press: Princeton, NJ, USA, 2012; ISBN 978-1-4008-4540-8. [Google Scholar]
- Weitzman, M.L. Why the Far-Distant Future Should Be Discounted at Its Lowest Possible Rate. J. Environ. Econ. Manag. 1998, 36, 201–208. [Google Scholar] [CrossRef]
- Primary Energy Consumption by Source. Available online: https://ourworldindata.org/grapher/primary-energy-source-bar (accessed on 1 November 2022).
- Statistical Review of World Energy|Energy Economics|Home. Available online: https://www.bp.com/en/global/corporate/energy-economics/statistical-review-of-world-energy.html (accessed on 1 November 2022).
- Andrew, R.; Peters, G. The Global Carbon Project’s Fossil CO2 Emissions Dataset; CICERO Center for International Climate Research: Oslo, Norway, 2021. [Google Scholar] [CrossRef]
- Friedlingstein, P.; Jones, M.W.; O’Sullivan, M.; Andrew, R.M.; Bakker, D.C.E.; Hauck, J.; Le Quéré, C.; Peters, G.P.; Peters, W.; Pongratz, J.; et al. Global Carbon Budget 2021. Earth Syst. Sci. Data 2021, 14, 1917–2005. [Google Scholar] [CrossRef]
- Available online: https://www.iea.org/data-and-statistics/data-product/co2-emissions-from-fuel-combustion-highlights (accessed on 1 November 2022).
- Energy Policy: General Principles|Fact Sheets on the European Union|European Parliament. Available online: https://www.europarl.europa.eu/factsheets/en/sheet/68/energy-policy-general-principles (accessed on 1 November 2022).
- Energy and the Green Deal. Available online: https://ec.europa.eu/info/strategy/priorities-2019-2024/european-green-deal/energy-and-green-deal_en (accessed on 1 November 2022).
- European Commision 2050 Long-Term Strategy. Available online: https://climate.ec.europa.eu/eu-action/climate-strategies-targets/2050-long-term-strategy_en (accessed on 1 November 2022).
- Espinosa, V.I.; Peña-Ramos, J.A.; Recuero-López, F. The Political Economy of Rent-Seeking: Evidence from Spain’s Support Policies for Renewable Energy. Energies 2021, 14, 4197. [Google Scholar] [CrossRef]
- The European Green Deal. Available online: https://ec.europa.eu/commission/presscorner/detail/en/ip_19_6691 (accessed on 1 November 2022).
- Proposal for a Regulation of the European Parliament and of the Council Establishing the Just Transition Fund; EU: Brussels, Belgium, 2020.
- National Long-Term Strategies. Available online: https://ec.europa.eu/info/energy-climate-change-environment/implementation-eu-countries/energy-and-climate-governance-and-reporting/national-long-term-strategies_en (accessed on 1 November 2022).
- Atlason, R.S.; Unnthorsson, R. Energy Return on Investment of Hydroelectric Power Generation Calculated Using a Standardised Methodology. Renew. Energy 2014, 66, 364–370. [Google Scholar] [CrossRef]
- Jansen, J.; Bakker, S. Social Cost-Benefit Analysis of Climate Change Mitigation Options in a European Context; Energy Research Centre of The Netherlands: The Hague, The Netherlands, 2006. [Google Scholar]
- IPCC. Climate Change 2014: Mitigation of Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; ISBN 978-1-107-05821-7. [Google Scholar]
- Ürge-Vorsatz, D.; Tirado Herrero, S. Building Synergies between Climate Change Mitigation and Energy Poverty Alleviation. Energy Policy 2012, 49, 83–90. [Google Scholar] [CrossRef]
- Feng, T.; Du, H.; Coffman, D.; Qu, A.; Dong, Z. Clean Heating and Heating Poverty: A Perspective Based on Cost-Benefit Analysis. Energy Policy 2021, 152, 112205. [Google Scholar] [CrossRef]
- Mishan, E.J. Cost-Benefit Analysis: An Informal Introduction; Praeger Publishers: New York, NY, USA, 1976; ISBN 978-0-275-85690-8. [Google Scholar]
- Stern, N. The Economics of Climate Change: The Stern Review; Cambridge University Press: Cambridge, UK, 2007; ISBN 978-0-521-70080-1. [Google Scholar]
- Ilg, P.; Gabbert, S.; Weikard, H. Nuclear Waste Management under Approaching Disaster: A Comparison of Decommissioning Strategies for the German Repository Asse II. Risk Anal. 2017, 37, 1213–1232. [Google Scholar] [CrossRef]
- Arrow, K.J.; Cropper, M.L.; Gollier, C.; Groom, B.; Heal, G.M.; Newell, R.G.; Nordhaus, W.D.; Pindyck, R.S.; Pizer, W.A.; Portney, P.R.; et al. Should Governments Use a Declining Discount Rate in Project Analysis? Rev. Environ. Econ. Policy 2014, 8, 145–163. [Google Scholar] [CrossRef]
- Dasgupta, P. Discounting Climate Change. J. Risk Uncertain. 2008, 37, 141–169. [Google Scholar] [CrossRef]
- Lind, R.C.; Arrow, K.J.; Corey, G.R.; Dasgupta, P.; Sen, A.K.; Stauffer, T.; Stiglitz, J.E.; Stockfisch, J.A. Discounting for Time and Risk in Energy Policy; Routledge: New York, NY, USA, 2013; ISBN 1-135-98518-9. [Google Scholar]
- Azar, C.; Sterner, T. Discounting and Distributional Considerations in the Context of Global Warming. Ecol. Econ. 1996, 19, 169–184. [Google Scholar] [CrossRef]
- Spackman, M. Social Discounting and the Cost of Public Funds: A Practitioner’s Perspective. J. Benefit-Cost Anal. 2020, 11, 244–271. [Google Scholar] [CrossRef]
- Poterba, J. The Rate of Return to Corporate Capital and Factor Shares: New Estimates Using Revised National Income Accounts and Capital Stock Data; National Bureau of Economic Research, Inc.: Cambridge, MA, USA, 1999. [Google Scholar]
- Kuo, C.-Y.; Jenkins, G.P.; Mphahlele, M.B. The Economic Opportunity Cost of Capital in South Africa. S. Afr. J. Econ. 2003, 71, 523–543. [Google Scholar] [CrossRef]
- Burgess, D.F.; Zerbe, R.O. Appropriate Discounting for Benefit-Cost Analysis. J. Benefit-Cost Anal. 2011, 2, 1–20. [Google Scholar] [CrossRef]
- Evans, D.J. The Elasticity of Marginal Utility of Consumption: Estimates for 20 OECD Countries. Fisc. Stud. 2005, 26, 197–224. [Google Scholar] [CrossRef]
- Nesticò, A.; Maselli, G. A Protocol for the Estimate of the Social Rate of Time Preference: The Case Studies of Italy and the USA. J. Econ. Stud. 2020, 47, 527–545. [Google Scholar] [CrossRef]
- Jouini, E.; Marin, J.-M.; Napp, C. Discounting and Divergence of Opinion. J. Econ. Theory 2010, 145, 830–859. [Google Scholar] [CrossRef]
- Gollier, C. Time Horizon and the Discount Rate. J. Econ. Theory 2002, 107, 463–473. [Google Scholar] [CrossRef]
- Cropper, M.L.; Freeman, M.C.; Groom, B.; Pizer, W.A. Declining Discount Rates. Am. Econ. Rev. 2014, 104, 538–543. [Google Scholar] [CrossRef]
- Costanza, R.; Kubiszewski, I.; Stoeckl, N.; Kompas, T. Pluralistic Discounting Recognizing Different Capital Contributions: An Example Estimating the Net Present Value of Global Ecosystem Services. Ecol. Econ. 2021, 183, 106961. [Google Scholar] [CrossRef]
- Page, E.A. Climate Change, Justice and Future Generations; Edward Elgar Publishing: Cheltenham, UK, 2006; ISBN 978-1-84542-471-8. [Google Scholar]
- Roser, D.; Seidel, C. Climate Justice: An Introduction; Routledge: London, UK, 2016; ISBN 978-1-315-61796-1. [Google Scholar]
- Sumaila, U.R.; Walters, C. Intergenerational Discounting: A New Intuitive Approach. Ecol. Econ. 2005, 52, 135–142. [Google Scholar] [CrossRef]
- Cropper, M.L.; Aydede, S.K.; Portney, P.R. Preferences for Life Saving Programs: How the Public Discounts Time and Age. J. Risk Uncertain. 1994, 8, 243–265. [Google Scholar] [CrossRef]
- Weitzman, M.L. Gamma Discounting. Am. Econ. Rev. 2001, 91, 260–271. [Google Scholar] [CrossRef]
- Almansa, C.; Martínez-Paz, J.M. What Weight Should Be Assigned to Future Environmental Impacts? A Probabilistic Cost Benefit Analysis Using Recent Advances on Discounting. Sci. Total Environ. 2011, 409, 1305–1314. [Google Scholar] [CrossRef] [PubMed]
- Drupp, M.A.; Freeman, M.C.; Groom, B.; Nesje, F. Discounting Disentangled. Am. Econ. J. Econ. Policy 2018, 10, 109–134. [Google Scholar] [CrossRef]
- Rendall, M. Discounting, Climate Change, and the Ecological Fallacy. Ethics 2019, 129, 441–463. [Google Scholar] [CrossRef]
- Gollier, C. Discounting an Uncertain Future. J. Public Econ. 2002, 85, 149–166. [Google Scholar] [CrossRef]
- Gollier, C. Maximizing the Expected Net Future Value as an Alternative Strategy to Gamma Discounting. Financ. Res. Lett. 2004, 1, 85–89. [Google Scholar] [CrossRef]
- Gollier, C.; Weitzman, M.L. How Should the Distant Future Be Discounted When Discount Rates Are Uncertain? Econ. Lett. 2010, 107, 350–353. [Google Scholar] [CrossRef]
- Newell, R.G.; Pizer, W.A. Discounting the Distant Future: How Much Do Uncertain Rates Increase Valuations? J. Environ. Econ. Manag. 2003, 46, 52–71. [Google Scholar] [CrossRef]
- Gollier, C.; Koundouri, P.; Pantelidis, T. Declining Discount Rates: Economic Justifications and Implications for Long-Run Policy. Econ. Policy 2008, 23, 758–795. [Google Scholar] [CrossRef]
- Feldstein, M.S. The Derivation of Social Time Preference Rates. Kyklos 1965, 18, 277–287. [Google Scholar] [CrossRef]
- Moore, M.A.; Vining, A.R. The Social Rate of Time Preference and the Social Discount Rate; Mercatus Center at George Mason University: Arlington, TX, USA, 2018. [Google Scholar]
- Groom, B.; Maddison, D. New Estimates of the Elasticity of Marginal Utility for the UK. Environ. Resour. Econ. 2019, 72, 1155–1182. [Google Scholar] [CrossRef]
- Akbulut, H.; Seçilmiş, E. Estimation of a Social Discount Rate for Turkey. Socio-Econ. Plan. Sci. 2019, 67, 78–85. [Google Scholar] [CrossRef]
- Spackman, M. Discount Rates and Rates of Return in the Public Sector: Economic Issues; Government Economic Service Working Paper; HM Treasury: London, UK, 1991; Volume 113.
- Eckstein, O. Investment Criteria for Economic Development and the Theory of Intertemporal Welfare Economics. Q. J. Econ. 1957, 71, 56. [Google Scholar] [CrossRef]
- Feldstein, M.S. The Social Time Preference Discount Rate in Cost Benefit Analysis. Econ. J. 1964, 74, 360–379. [Google Scholar] [CrossRef]
- World Population Prospects-Population Division-United Nations. Available online: https://population.un.org/wpp/Download/Standard/Population/ (accessed on 6 November 2022).
- Stern, N. Welfare Weights and the Elasticity of the Marginal Valuation of Income. In Studies in Modern Economic Analysis: The Proceedings of the Association of University Teachers of Economics, Edinburgh, 1976; Basil Blackwell: Oxford, UK, 1977. [Google Scholar]
- OECD Tax Statistics. Available online: https://www.oecd-ilibrary.org/taxation/data/oecd-tax-statistics_tax-data-en (accessed on 6 November 2022).
- The OECD Tax-Benefit Web Calculator. Available online: https://www.oecd.org/els/soc/tax-benefit-web-calculator/ (accessed on 27 October 2022).
- Freeman, M.; Groom, B.; Spackman, M. Social Discount Rates for Cost-Benefit Analysis: A Report for HM Treasury; HM Treasury: London, UK, 2018.
- Kula, E. Estimation of a Social Rate of Interest for India. J. Agric. Econ. 2004, 55, 91–99. [Google Scholar] [CrossRef]
- Kula, E. Derivation of Social Time Preference Rates for the United States and Canada. Q. J. Econ. 1984, 99, 873–882. [Google Scholar] [CrossRef]
- Kula, E. Social Interest Rate for Public Sector Appraisal in the United Kingdom, the United States and Canada. Null 1987, 2, 169–174. [Google Scholar] [CrossRef][Green Version]
- The World Bank. World Development Indicators. Available online: https://databank.worldbank.org/source/world-development-indicators (accessed on 6 November 2022).
- The Green Book. 2022. Available online: https://www.gov.uk/government/publications/the-green-book-appraisal-and-evaluation-in-central-governent/the-green-book-2020 (accessed on 8 November 2022).
- Evans, D.J.; Sezer, H. Social Discount Rates for Member Countries of the European Union. J. Econ. Stud. 2005, 32, 47–59. [Google Scholar] [CrossRef]
- Kazlauskienė, V.; Stundžienė, A. Estimation of Social Discount Rate for Lithuania. Trendy Ekon. Manag. 2016, 10, 39–47. [Google Scholar] [CrossRef][Green Version]
- Guide to Cost-Benefit Analysis of Investment Projects; European Commission: Brussels, Belgium, 2008.
- Addicott, E.T.; Fenichel, E.P.; Kotchen, M.J. Even the Representative Agent Must Die: Using Demographics to Inform Long-Term Social Discount Rates. J. Assoc. Environ. Resour. Econ. 2019, 7, 379–415. [Google Scholar] [CrossRef]
- Hansson, S.O. Philosophical Problems in Cost–Benefit Analysis. Econ. Philos. 2007, 23, 163–183. [Google Scholar] [CrossRef]





| Country/Entity | tCO₂ per Person | Country | kgCO₂ per GDP $ |
|---|---|---|---|
| Czech Republic | 8.58 | Poland | 0.28 |
| Poland | 8.02 | Bulgaria | 0.28 |
| Estonia | 7.04 | Czech Republic | 0.27 |
| Slovenia | 6.19 | Estonia | 0.24 |
| Slovakia | 5.70 | Slovenia | 0.20 |
| Bulgaria | 5.32 | Slovakia | 0.19 |
| Lithuania | 5.02 | Hungary | 0.18 |
| Hungary | 4.89 | Lithuania | 0.16 |
| Romania | 3.85 | Romania | 0.16 |
| Latvia | 3.71 | Latvia | 0.15 |
| EU27 | 5.89 | EU27 | 0.17 |
| Period | PV[1, E(R)] | E[PV(1, R)] | Certainty Equivalent R | E[PV(1, R)]: PV[1, E(R)] |
|---|---|---|---|---|
| 1 | 0.9512294 | 0.9514197 | 4.8580% | 1.00 |
| 10 | 0.6065307 | 0.6187018 | 4.5192% | 1.02 |
| 30 | 0.2231302 | 0.2645130 | 3.8636% | 1.19 |
| 50 | 0.0820850 | 0.1266638 | 3.4253% | 1.54 |
| 100 | 0.0067379 | 0.0253495 | 3.0266% | 3.76 |
| 150 | 0.0005531 | 0.0055683 | 2.9652% | 10.07 |
| 200 | 0.0000454 | 0.0012398 | 2.9568% | 27.31 |
| 250 | 0.0000037 | 0.0002766 | 2.9556% | 74.21 |
| 300 | 0.0000003 | 0.0000617 | 2.9555% | 201.72 |
| Average Death Rate | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Period | Bulgaria | Czechia | Estonia | Hungary | Latvia | Lithuania | Poland | Romania | Slovakia | Slovenia | CEE EU Members |
| 1960–1970 | 0.85% | 1.09% | 1.06% | 1.05% | 1.04% | 0.82% | 0.77% | 0.89% | 0.82% | 0.98% | 1.18% |
| 1971–1980 | 1.02% | 1.25% | 1.16% | 1.24% | 1.21% | 0.95% | 0.88% | 0.96% | 0.96% | 0.99% | 1.11% |
| 1981–1990 | 1.17% | 1.26% | 1.21% | 1.37% | 1.26% | 1.05% | 0.99% | 1.06% | 1.01% | 1.00% | 1.13% |
| 1991–2000 | 1.36% | 1.12% | 1.37% | 1.40% | 1.44% | 1.17% | 1.00% | 1.18% | 0.98% | 0.96% | 1.09% |
| 2001–2010 | 1.46% | 1.04% | 1.28% | 1.31% | 1.44% | 1.29% | 0.97% | 1.23% | 0.98% | 0.93% | 0.99% |
| 2011–2020 | 1.54% | 1.05% | 1.17% | 1.33% | 1.45% | 1.41% | 1.06% | 1.33% | 0.98% | 0.97% | 0.87% |
| 1960–2020 | 1.23% | 1.14% | 1.21% | 1.28% | 1.30% | 1.11% | 0.94% | 1.10% | 0.95% | 0.97% | 1.06% |
| Bulgaria | Czechia | Estonia | Hungary | Latvia | Lithuania | Poland | Romania | Slovakia | Slovenia | CEE EU Members | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| l | 1.23% | 1.14% | 1.21% | 1.29% | 1.31% | 1.12% | 0.95% | 1.11% | 0.96% | 0.98% | 1.06% |
| η | 1.0001 | 1.3478 | 1.2553 | 1.3346 | 1.1349 | 1.2429 | 1.1136 | 1.0511 | 1.3318 | 1.3770 | 1.0638 |
| g | 2.65% | 1.34% | 3.61% | 1.93% | 4.06% | 4.55% | 3.15% | 4.54% | 2.49% | 1.44% | 3.21% |
| σ2 | 0.0087 | 0.0008 | 0.0025 | 0.0008 | 0.0034 | 0.0030 | 0.0005 | 0.0036 | 0.0008 | 0.0013 | 0.0004 |
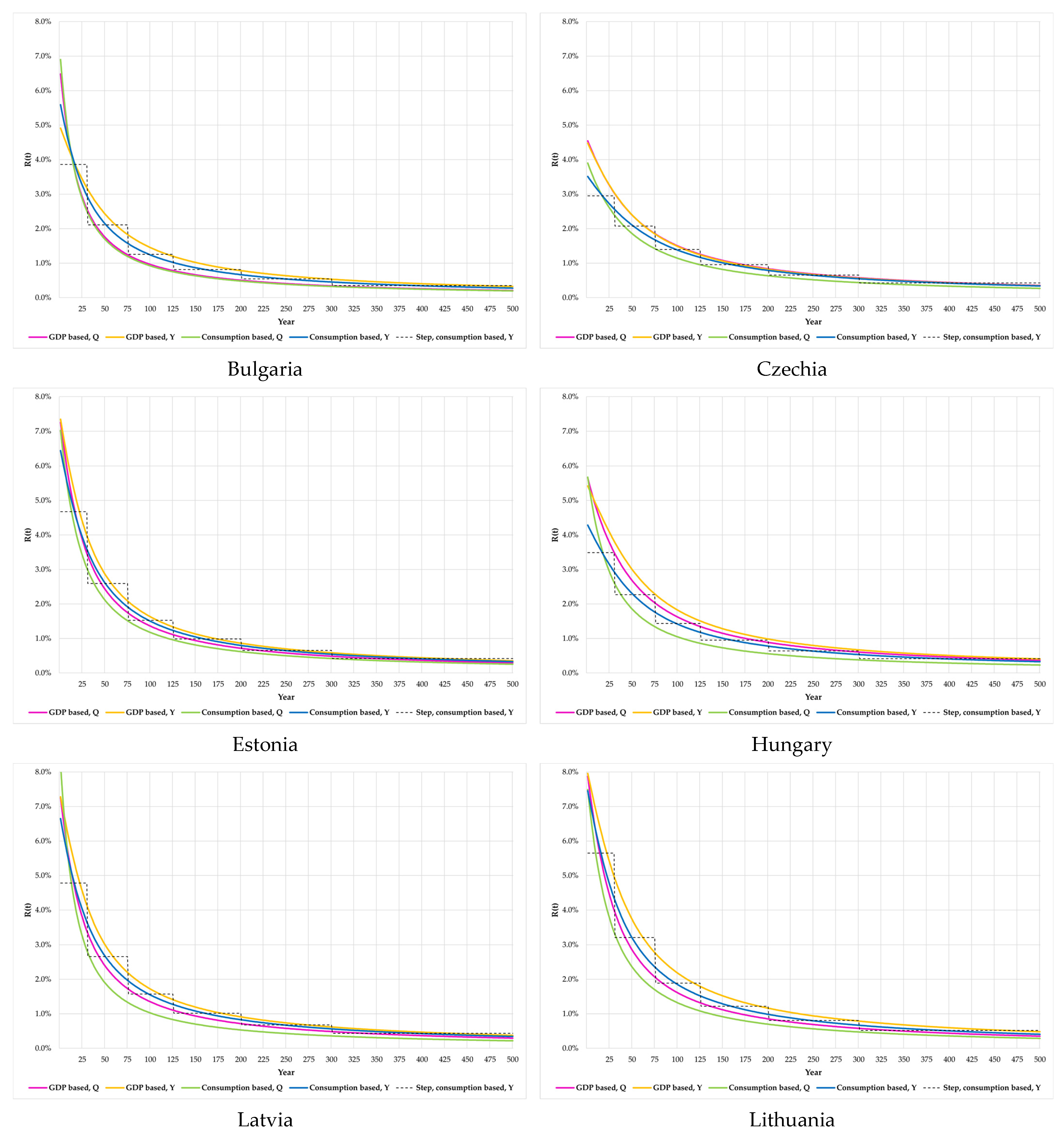
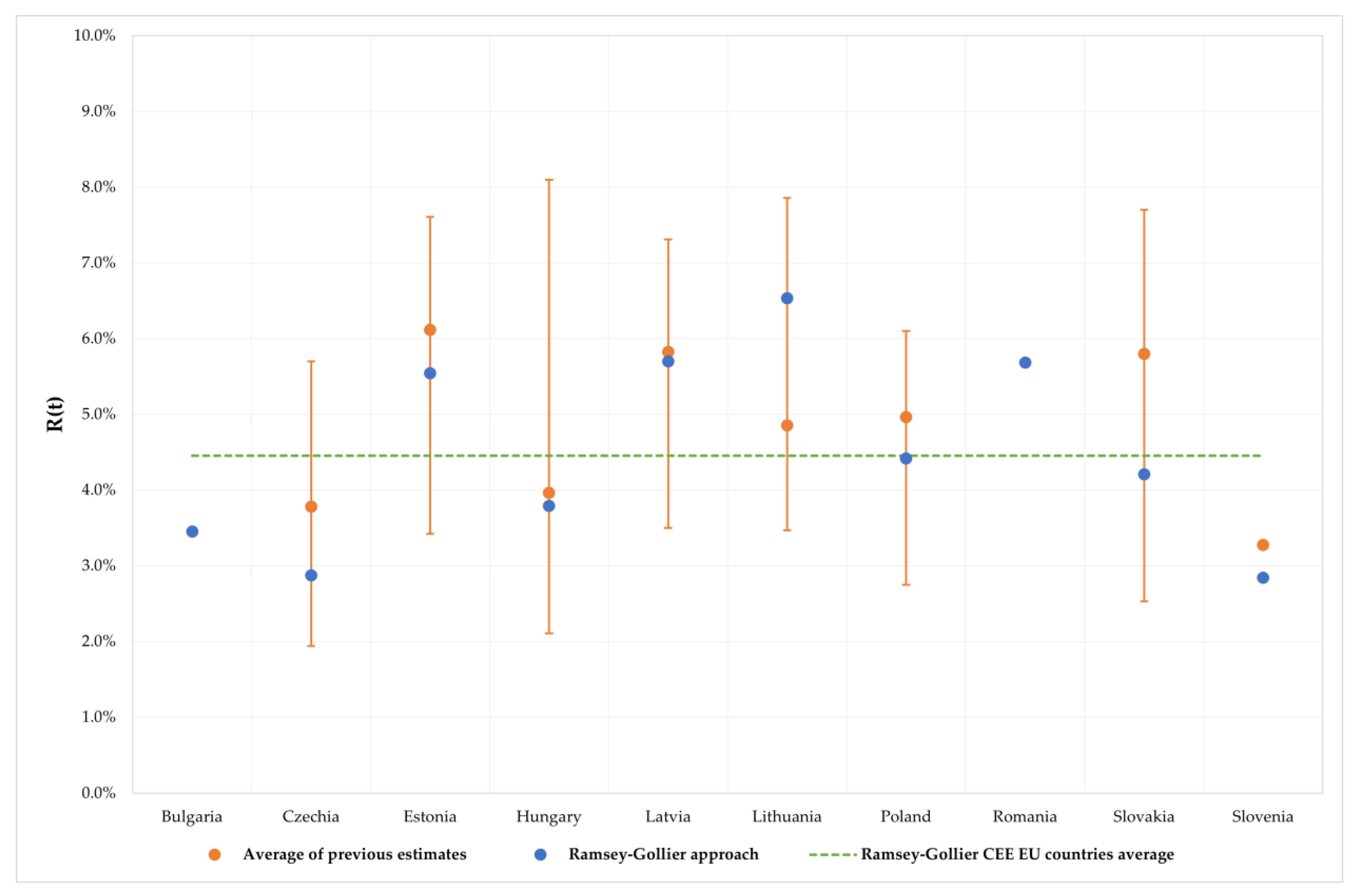
| SDR (Ramsey) | 3.89% | 2.95% | 5.74% | 3.86% | 5.92% | 6.77% | 4.45% | 5.88% | 4.28% | 2.96% | 4.48% |
| SDR (Ramsey-Gollier) | 3.45% | 2.87% | 5.54% | 3.79% | 5.70% | 6.54% | 4.42% | 5.68% | 4.21% | 2.84% | 4.45% |
| Bulgaria | Czechia | Estonia | Hungary | Latvia | Lithuania | Poland | Romania | Slovakia | Slovenia | CEE EU Members | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Trials | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 |
| Base case | 3.45% | 2.87% | 5.54% | 3.79% | 5.70% | 6.54% | 4.42% | 5.68% | 4.21% | 2.84% | 4.45% |
| Mean | 3.47% | 2.82% | 5.54% | 3.80% | 5.77% | 6.56% | 4.40% | 5.61% | 4.23% | 2.90% | 4.46% |
| Median | 4.89% | 3.44% | 6.20% | 4.44% | 6.26% | 7.37% | 4.67% | 6.27% | 4.58% | 3.51% | 4.88% |
| Standard deviation | 10.51% | 4.40% | 7.09% | 4.19% | 7.42% | 7.74% | 2.83% | 7.13% | 4.15% | 5.53% | 2.50% |
| Skewness | 2.25 | 1.72 | 0.68 | 0.57 | 0.58 | 1.43 | 0.62 | 0.15 | 0.18 | 1.39 | 0.56 |
| Excess kurtosis | 7.30 | 4.60 | 0.83 | −0.00 | 1.08 | 3.64 | 0.80 | −0.42 | −0.66 | 3.69 | −0.11 |
| Coefficient of variation | 3.03 | 1.56 | 1.28 | 1.10 | 1.29 | 1.18 | 0.64 | 1.27 | 0.98 | 1.90 | 0.56 |
| Min | −55.09% | −18.44% | −24.88% | −11.83% | −23.08% | −32.56% | −7.29% | −17.74% | −9.10% | −22.88% | −4.43% |
| Max | 28.91% | 13.94% | 26.71% | 15.79% | 28.56% | 27.33% | 12.24% | 32.33% | 16.25% | 21.95% | 11.58% |
| Mean stand. error | 0.11% | 0.04% | 0.07% | 0.04% | 0.07% | 0.08% | 0.03% | 0.07% | 0.04% | 0.06% | 0.02% |
| Nonnegative trials | 7594 | 8302 | 8160 | 8164 | 8271 | 8741 | 9344 | 7660 | 8174 | 7945 | 9396 |
| SDR | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Period | Bulgaria | Czechia | Estonia | Hungary | Latvia | Lithuania | Poland | Romania | Slovakia | Slovenia | CEE EU Members |
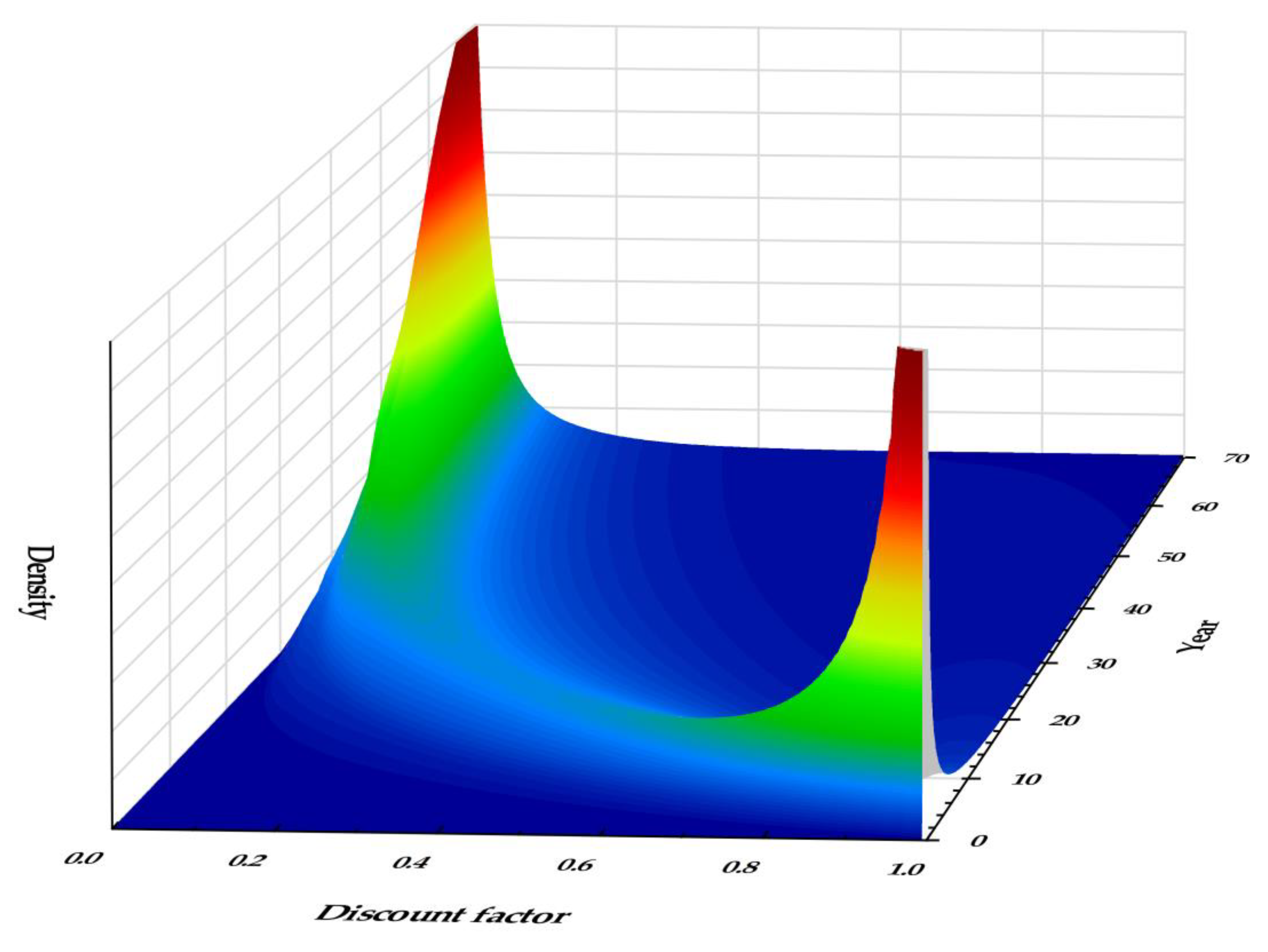
| 1–30 | 3.86% | 2.95% | 4.67% | 3.49% | 4.78% | 5.65% | 4.06% | 4.43% | 3.58% | 3.06% | 4.09% |
| 31–75 | 2.11% | 2.07% | 2.59% | 2.27% | 2.66% | 3.21% | 3.09% | 2.31% | 2.25% | 2.00% | 3.13% |
| 76–125 | 1.26% | 1.40% | 1.53% | 1.44% | 1.57% | 1.89% | 2.15% | 1.33% | 1.41% | 1.29% | 2.17% |
| 126–200 | 0.82% | 0.96% | 0.98% | 0.95% | 1.02% | 1.22% | 1.49% | 0.85% | 0.94% | 0.87% | 1.49% |
| 201–300 | 0.55% | 0.66% | 0.65% | 0.64% | 0.68% | 0.81% | 1.02% | 0.57% | 0.63% | 0.59% | 1.03% |
| 301–500 | 0.35% | 0.43% | 0.42% | 0.41% | 0.43% | 0.52% | 0.67% | 0.36% | 0.41% | 0.38% | 0.68% |
| SDR | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Period | Bulgaria | Czechia | Estonia | Hungary | Latvia | Lithuania | Poland | Romania | Slovakia | Slovenia | CEE EU Members |
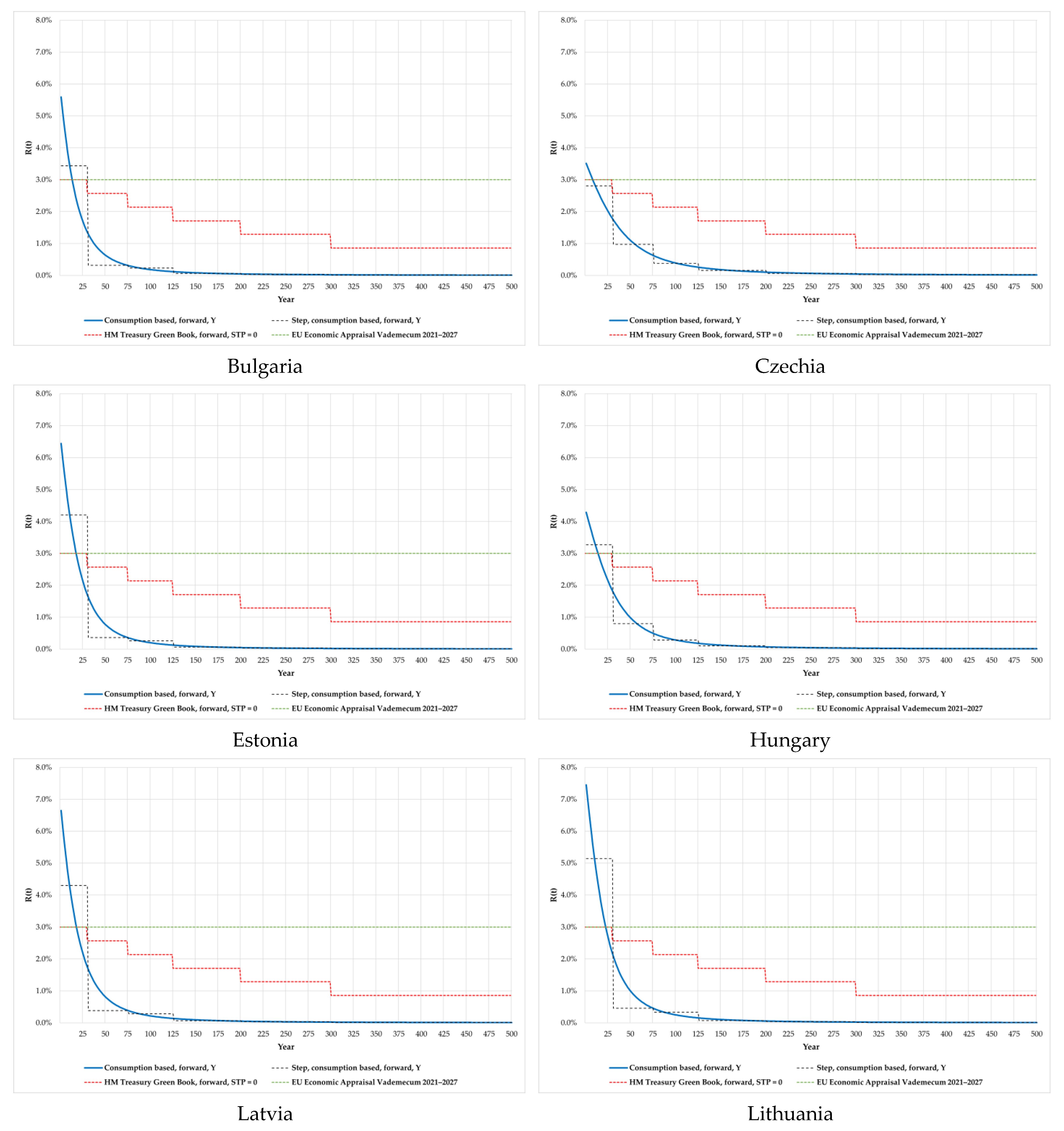
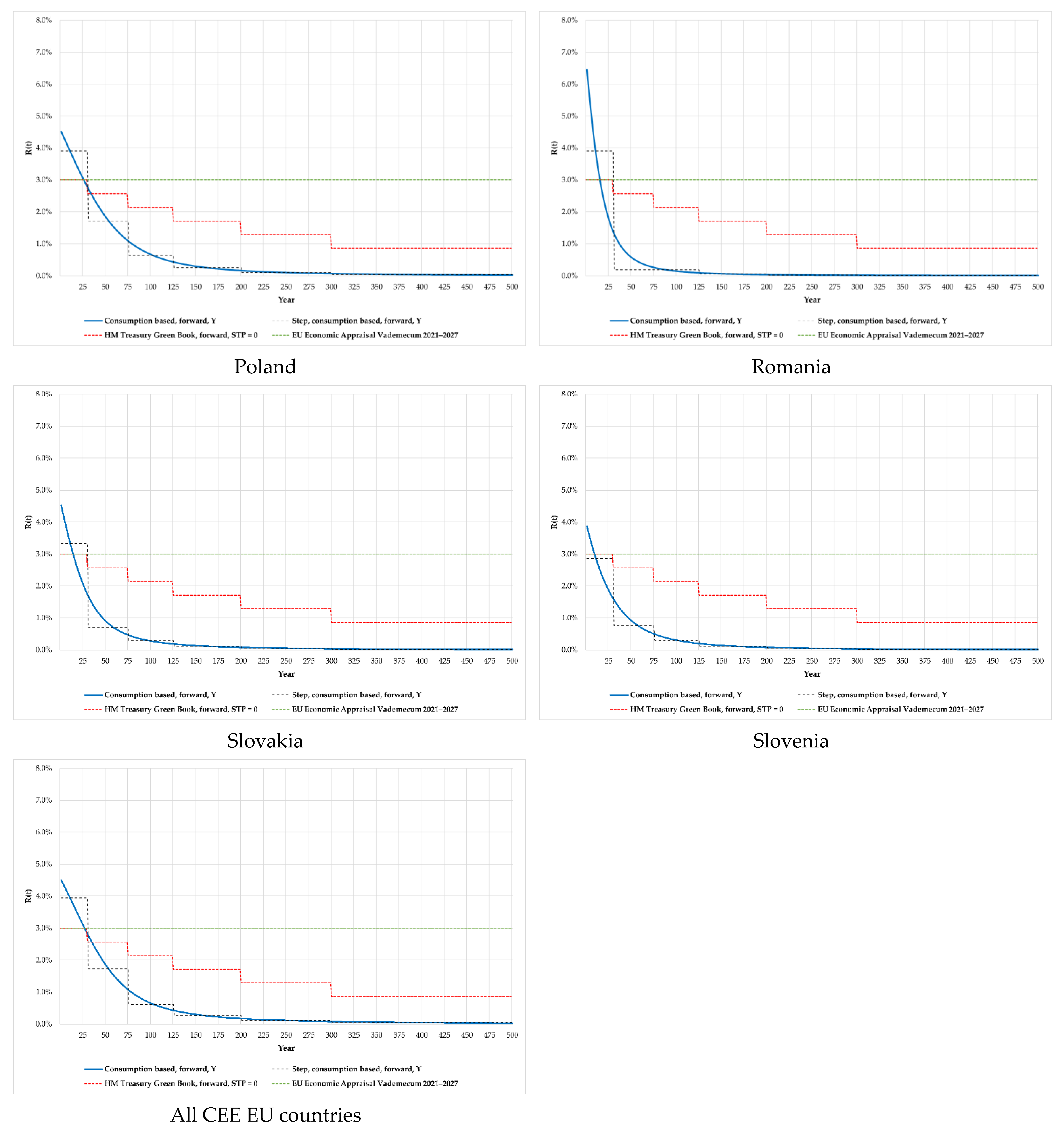
| 1–30 | 3.43% | 2.81% | 4.20% | 3.27% | 4.30% | 5.14% | 3.90% | 3.90% | 3.33% | 2.86% | 3.94% |
| 31–75 | 0.32% | 0.97% | 0.36% | 0.80% | 0.38% | 0.46% | 1.71% | 0.19% | 0.69% | 0.76% | 1.73% |
| 76–125 | 0.23% | 0.38% | 0.26% | 0.29% | 0.28% | 0.34% | 0.64% | 0.19% | 0.29% | 0.31% | 0.61% |
| 126–200 | 0.06% | 0.16% | 0.06% | 0.11% | 0.07% | 0.07% | 0.25% | 0.05% | 0.11% | 0.12% | 0.26% |
| 201–300 | 0.03% | 0.06% | 0.03% | 0.05% | 0.04% | 0.04% | 0.10% | 0.02% | 0.05% | 0.05% | 0.11% |
| 301–500 | 0.01% | 0.03% | 0.01% | 0.02% | 0.01% | 0.01% | 0.04% | 0.01% | 0.02% | 0.02% | 0.05% |
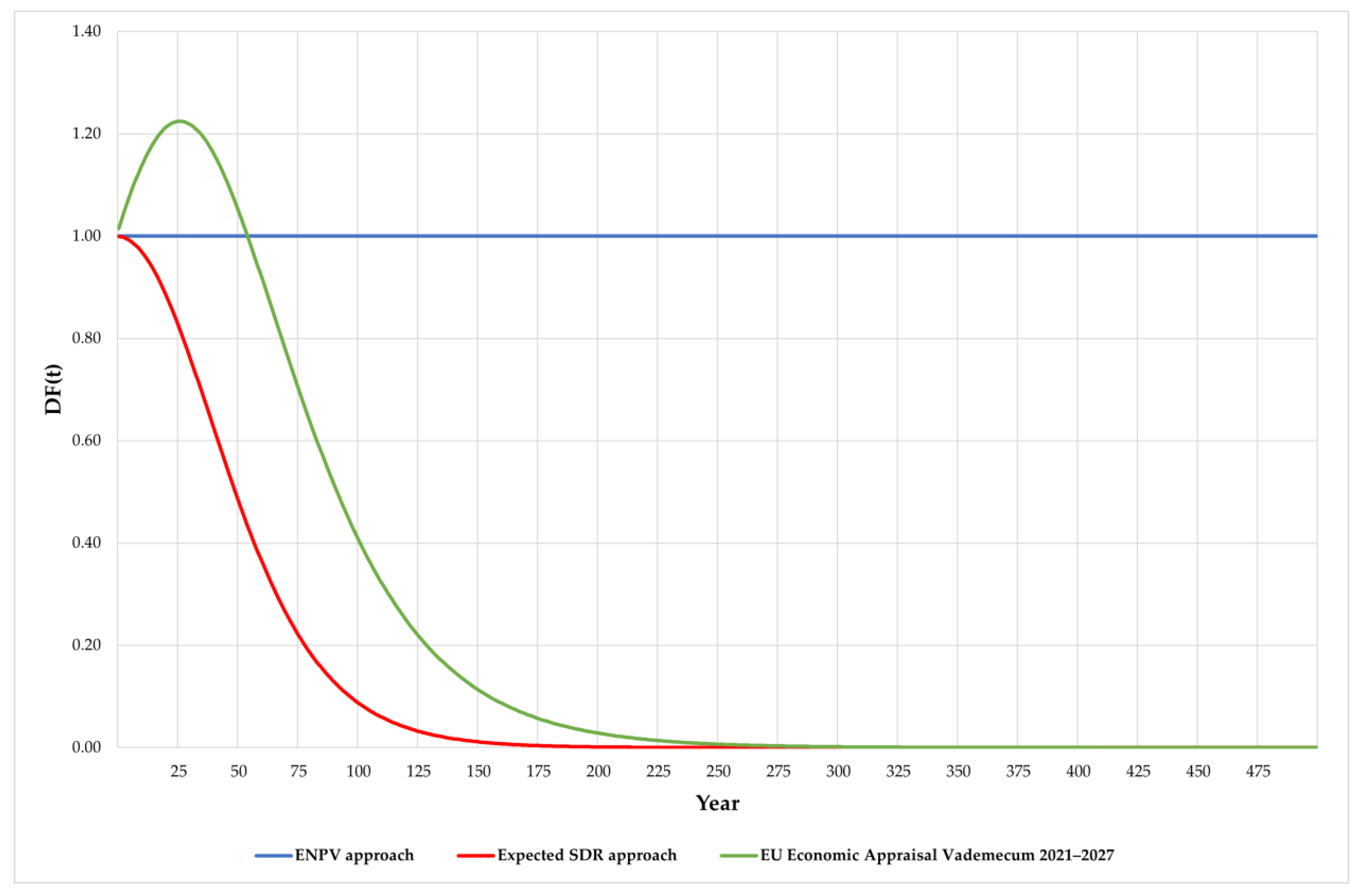
| Period | PV[1, 3%] | PV[1, E(R)] | E[PV(1, R)] | Certainty Equivalent R | E[PV(1, R)]: PV[1, 3%] | E[PV(1, R)]: PV[1, E(R)] |
|---|---|---|---|---|---|---|
| 1 | 0.970446 | 0.955719 | 0.955985 | 4.5013% | 0.99 | 1.00 |
| 10 | 0.740818 | 0.635776 | 0.654067 | 4.2455% | 0.88 | 1.03 |
| 30 | 0.406570 | 0.256988 | 0.333167 | 3.6637% | 0.82 | 1.30 |
| 50 | 0.223130 | 0.103877 | 0.210442 | 3.1171% | 0.94 | 2.03 |
| 100 | 0.049787 | 0.010790 | 0.119964 | 2.1206% | 2.41 | 11.12 |
| 150 | 0.011109 | 0.001121 | 0.096249 | 1.5605% | 8.66 | 85.87 |
| 200 | 0.002479 | 0.000116 | 0.085982 | 1.2268% | 34.69 | 738.46 |
| 250 | 0.000553 | 0.000012 | 0.080290 | 1.0088% | 145.17 | 6638.40 |
| 300 | 0.000123 | 0.000001 | 0.076687 | 0.8560% | 621.40 | 61,038.40 |
| Social Cost of Carbon | Nuclear Decommissioning | Nuclear Decommissioning (Delayed, 50 Years) | |
|---|---|---|---|
| $/tC | bn £ | bn £ | |
| Ramsey-Gollier SDR | 4.48 | 36.46 | 3.93 |
| Declining SDR | 27.93 | 43.07 | 15.18 |
| SDR = 3% | 10.45 | 46.65 | 10.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buła, R.; Foltyn-Zarychta, M. Declining Discount Rates for Energy Policy Investments in CEE EU Member Countries. Energies 2023, 16, 321. https://doi.org/10.3390/en16010321
Buła R, Foltyn-Zarychta M. Declining Discount Rates for Energy Policy Investments in CEE EU Member Countries. Energies. 2023; 16(1):321. https://doi.org/10.3390/en16010321
Chicago/Turabian StyleBuła, Rafał, and Monika Foltyn-Zarychta. 2023. "Declining Discount Rates for Energy Policy Investments in CEE EU Member Countries" Energies 16, no. 1: 321. https://doi.org/10.3390/en16010321
APA StyleBuła, R., & Foltyn-Zarychta, M. (2023). Declining Discount Rates for Energy Policy Investments in CEE EU Member Countries. Energies, 16(1), 321. https://doi.org/10.3390/en16010321







