Pre-Sizing Approach of a Fuel Cell-Battery Hybrid Power System with Interleaved Converters
Abstract
:1. Introduction
2. State-of-the-Art
2.1. Architecture/Components
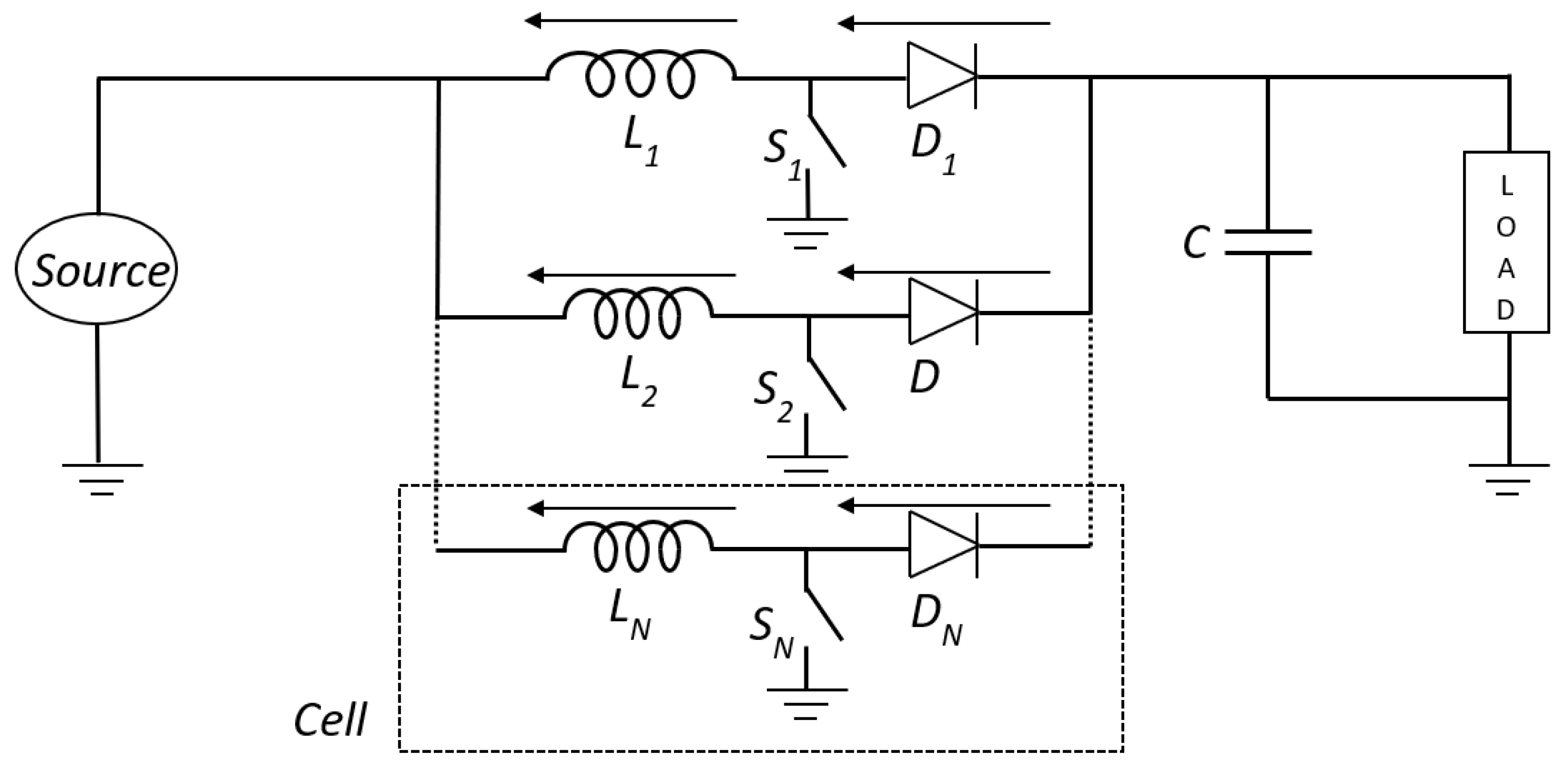
- The two-converter structure, consisting of the association of a converter for each source. Although it is the arrangement with the largest number of degrees of freedom, it remains a complex system in terms of control design.
- The direct parallel structure, which directly connects the sources to the load. This disposition, however, requires an over-sized FC to provide the demanded power to the load.
- The one-converter structure, which only places one converter at one source (usually the FC) to downsize the associated source. It presents some constraints related to the management of the battery state of charge.
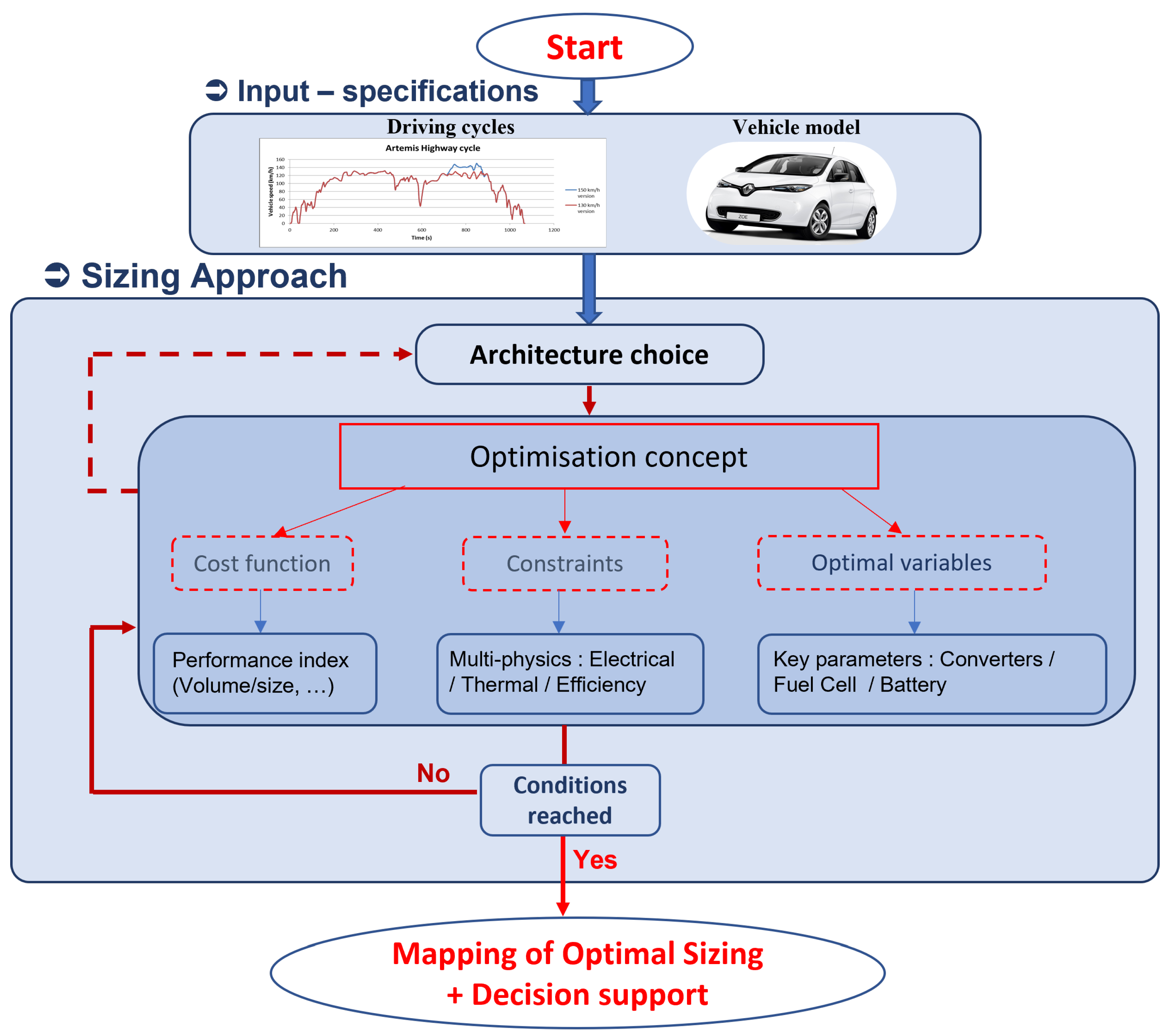
2.2. Design Approach
3. Implementation and Modelling
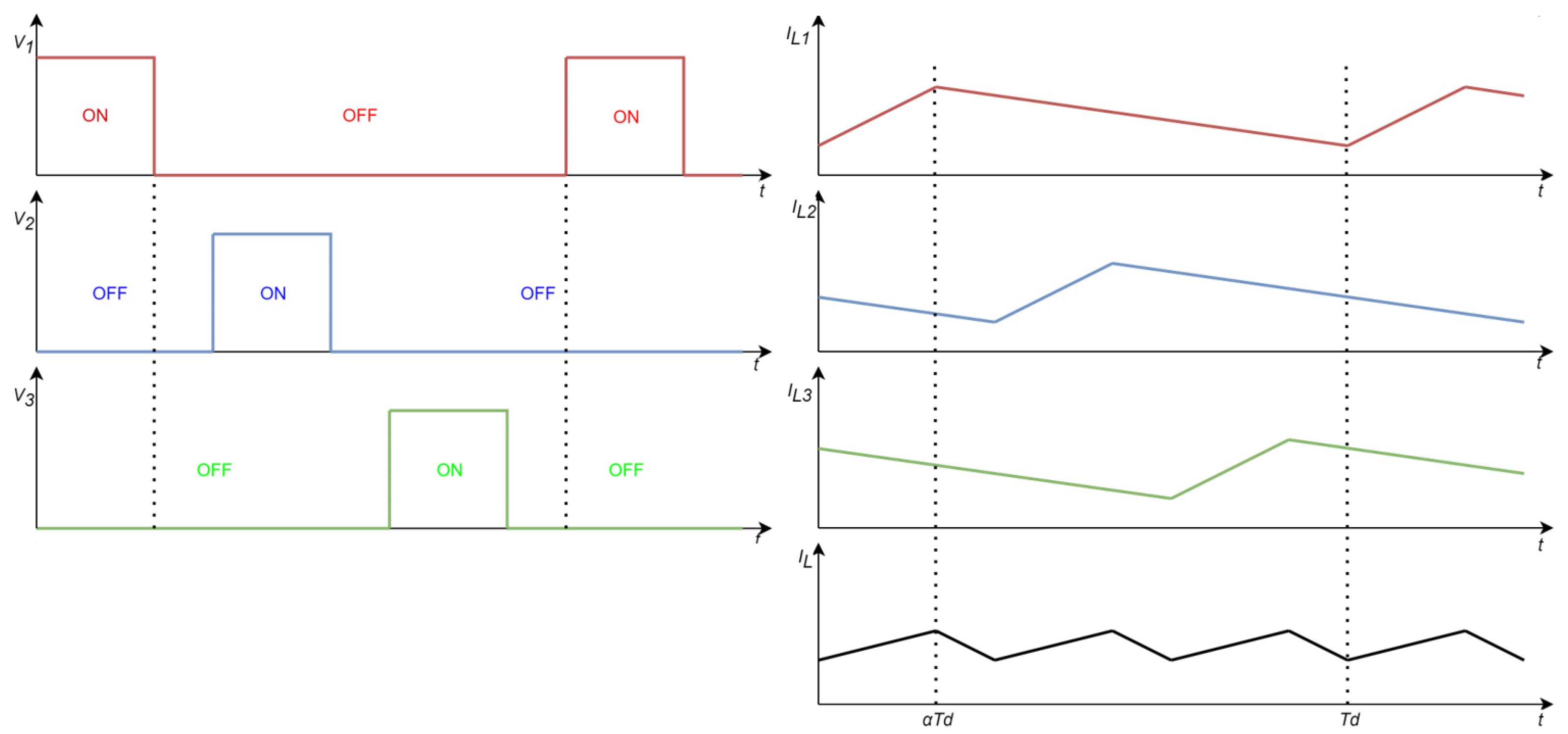
3.1. Approach Description
3.2. Volume Cost Function
3.2.1. Fuel Cell Volume
3.2.2. Battery Volume
3.2.3. Converter Volume
- Inductance volume:
- Capacitor volume:
- CActive component volume:
3.3. Constraints
3.3.1. Fuel Cell System
- Behaviour:
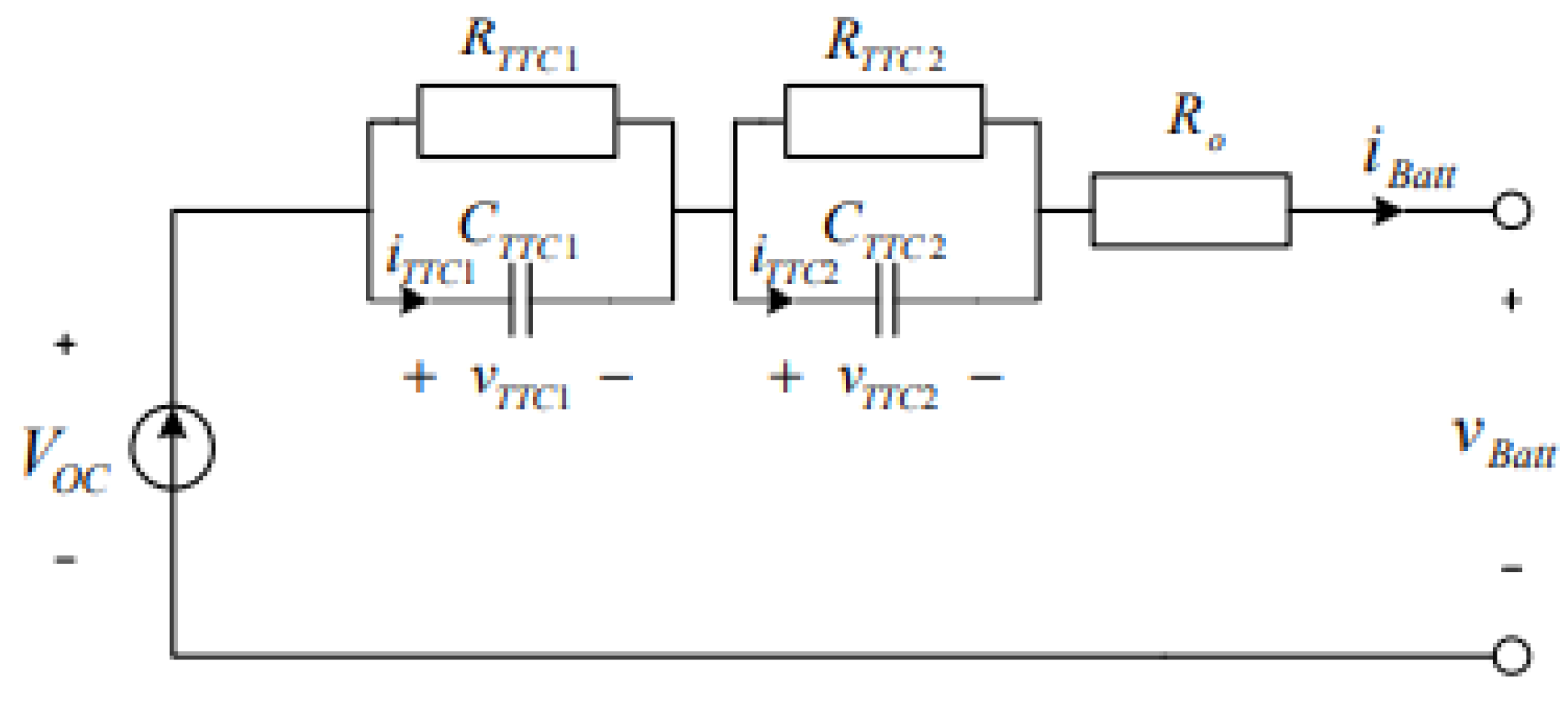
3.3.2. Battery Pack
- Behaviour:
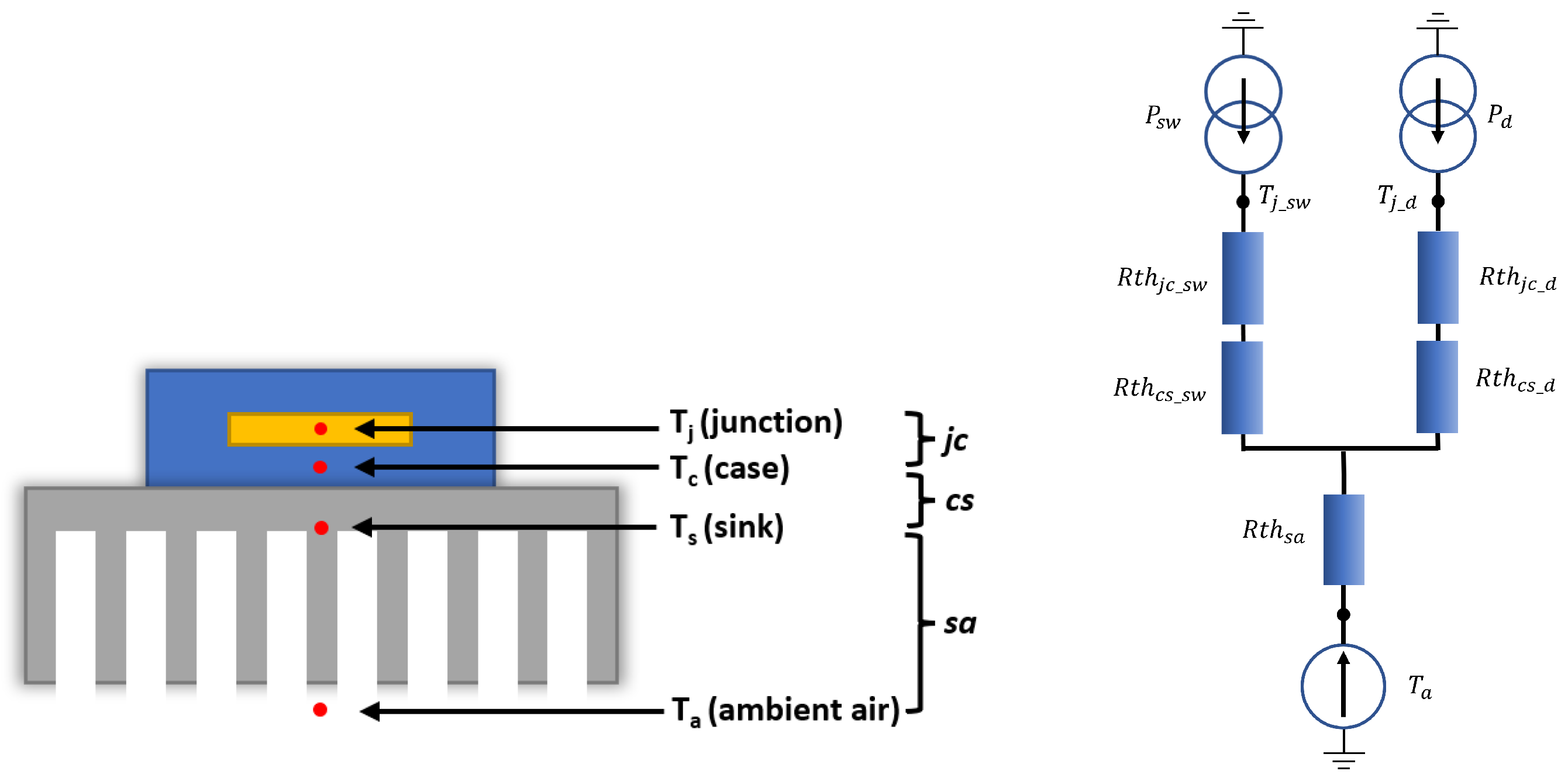
3.3.3. Converter
- Behaviour:
- Electrical constraints:
- Efficiency:
- Switching losses when opening the semi-conductor ;
- Conduction losses ;
- Switching losses when closing ;
- Thermal:
4. Results and Analysis
4.1. Use Case
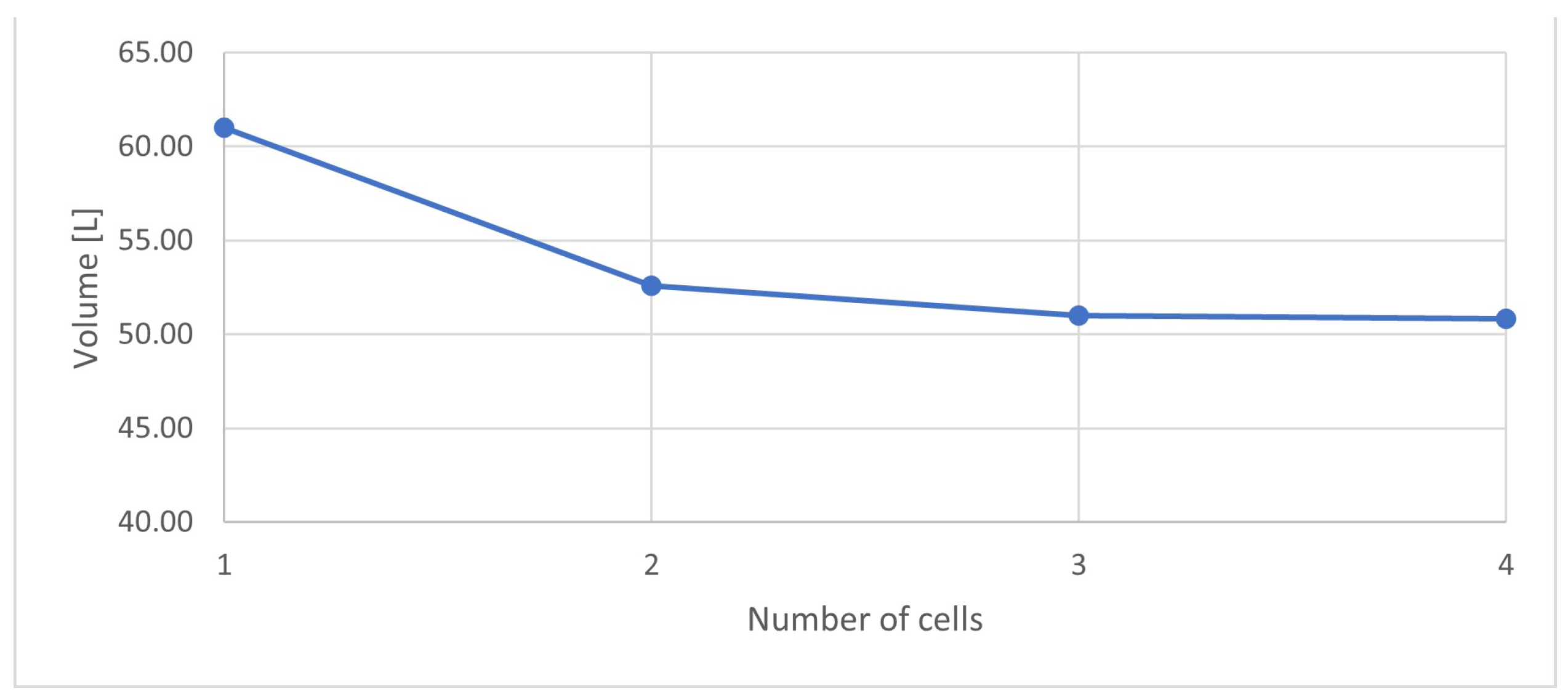
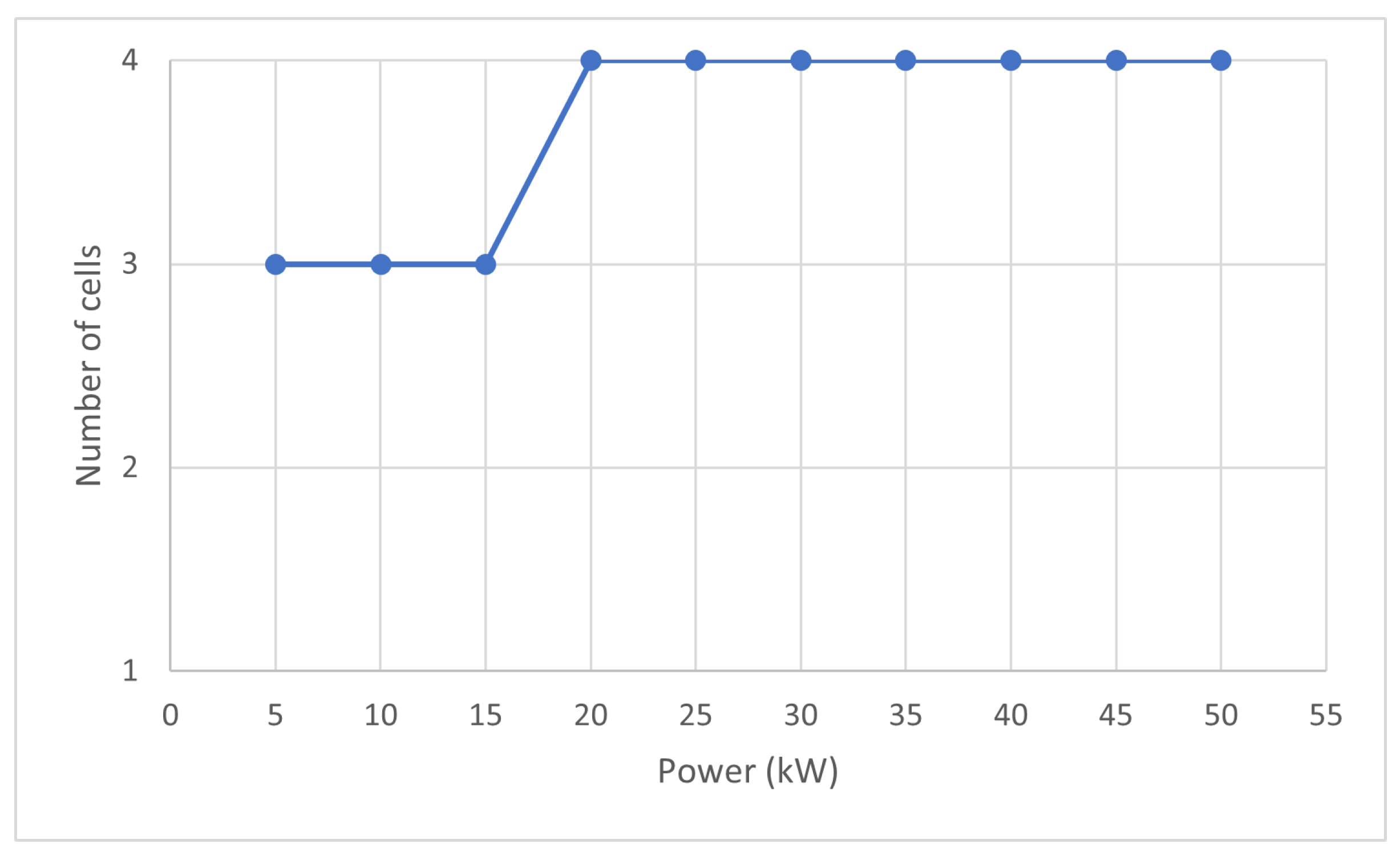
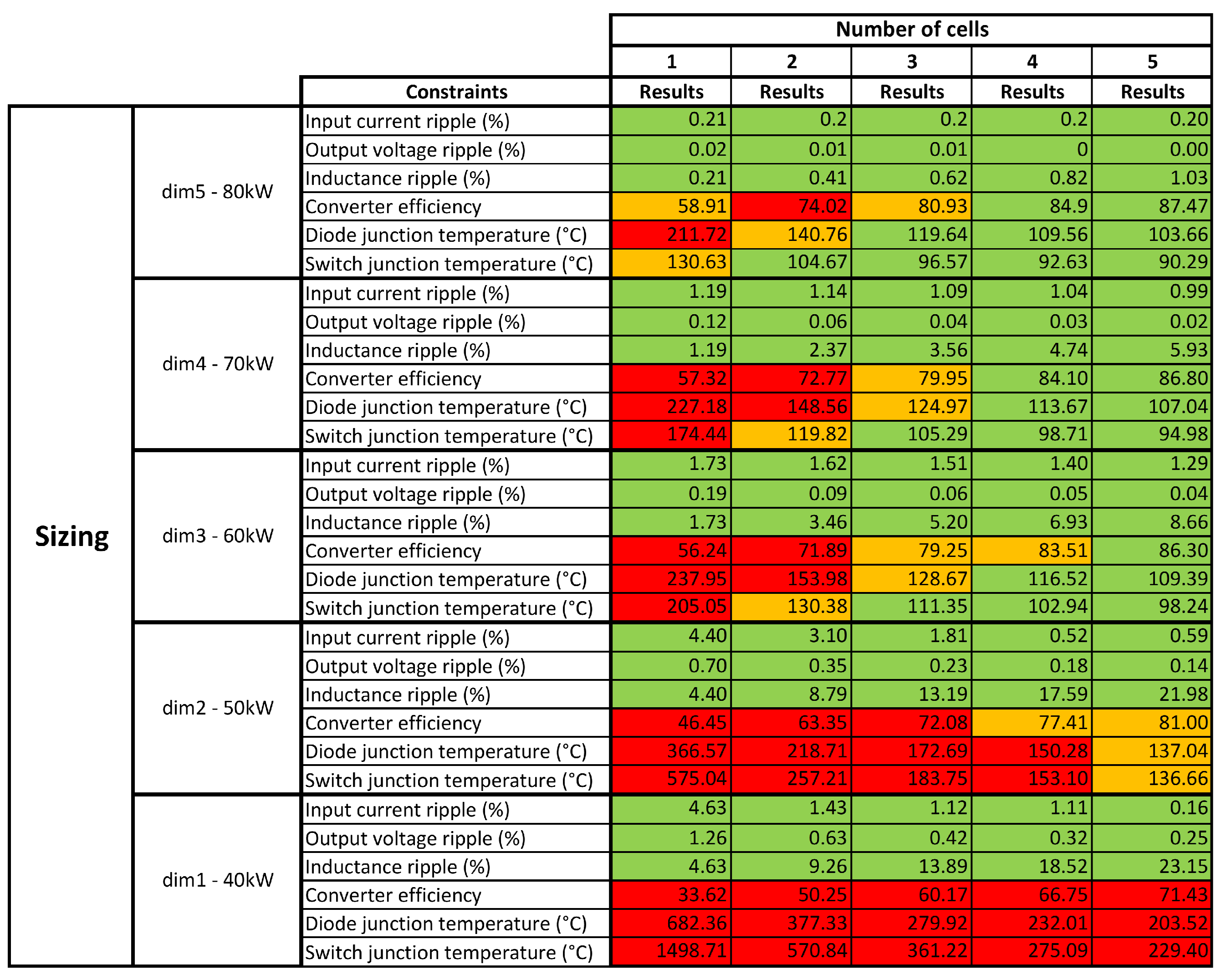
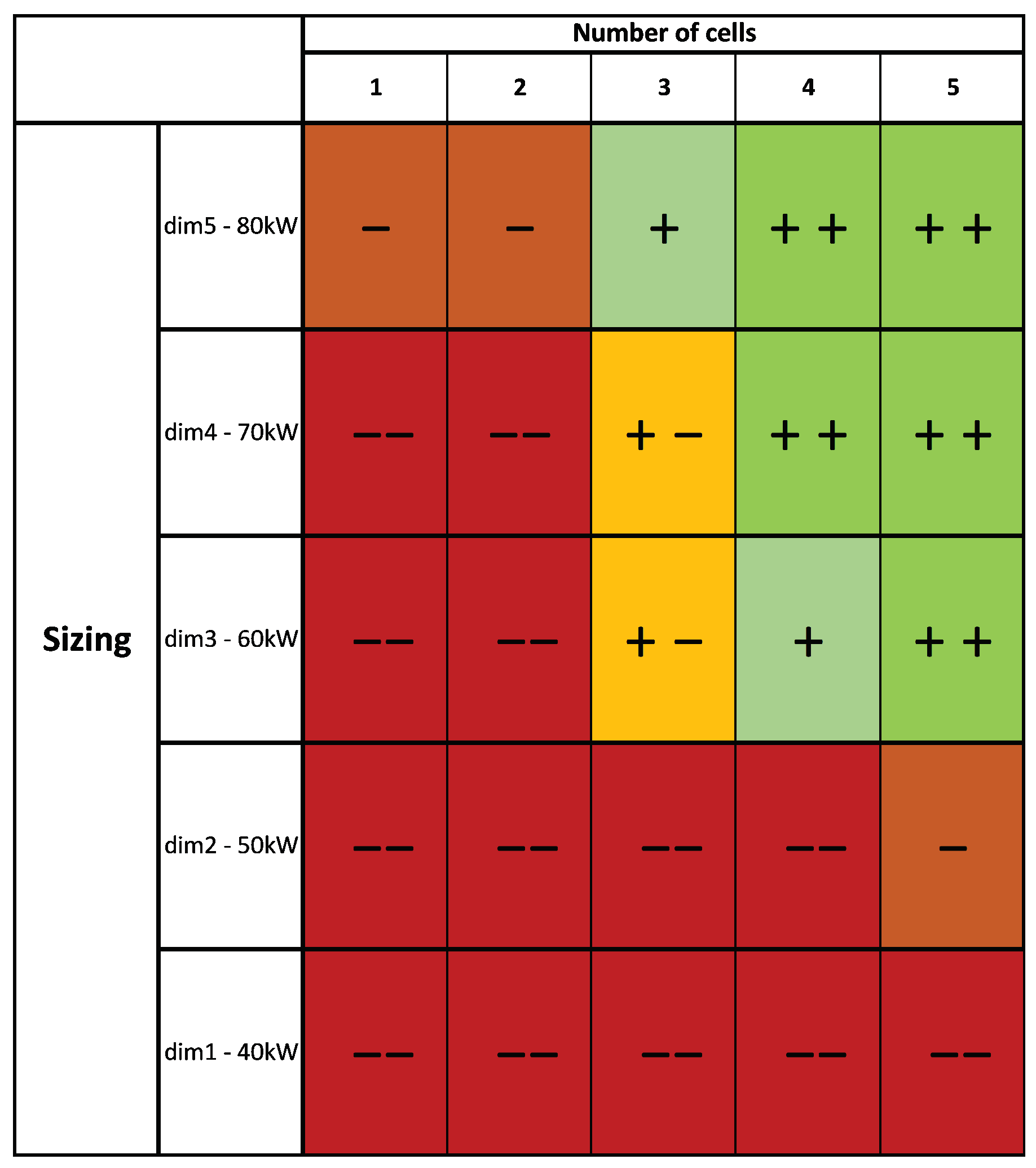
4.2. Optimisation Results
- Output network voltage: 360 V
- Output power: 20 kW
- Number of cells:
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EV | Electric vehicle |
| HEV | Hybrid electric vehicle |
| FCEV | Fuel cell electric vehicle |
| PEMFC | Proton exchange membrane fuel cell |
| FC | Fuel cell |
| ESS | Energy storage system |
| SoC | State of charge |
| SoH | State of health |
| DC | Direct current |
| PSO | Particle swarm optimisation |
| GA | Genetic algorithm |
| RMS | Root mean square |
| CCM | Continuous conduction mode |
| DCM | Discontinuous conduction mode |
References
- Ogunbode, C.A.; Doran, R.; Böhm, G. Exposure to the IPCC special report on 1.5 °C global warming is linked to perceived threat and increased concern about climate change. Clim. Chang. 2020, 158, 361–375. [Google Scholar] [CrossRef]
- Chakraborty, S.; Kumar, N.M.; Jayakumar, A.; Dash, S.K.; Elangovan, D. Selected Aspects of Sustainable Mobility Reveals Implementable Approaches and Conceivable Actions. Sustainability 2021, 13, 12918. [Google Scholar] [CrossRef]
- Muneer, T.; Kolhe, M.; Doyle, A. Electric Vehicles: Prospects and Challenges; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Zhang, F.; Hu, X.; Langari, R.; Cao, D. Energy management strategies of connected HEVs and PHEVs: Recent progress and outlook. Prog. Energy Combust. Sci. 2019, 73, 235–256. [Google Scholar] [CrossRef]
- Jayakumar, A.; Chalmers, A.; Lie, T.T. Review of prospects for adoption of fuel cell electric vehicles in New Zealand. IET Electr. Syst. Transp. 2017, 7, 259–266. [Google Scholar] [CrossRef]
- Ceschia, A.; Azib, T.; Bethoux, O.; Alves, F. Optimal design methodology for sizing a fuel cell/battery hybrid power source. Proc. Inst. Mech. Eng. Part A: J. Power Energy 2021, 235, 3–16. [Google Scholar] [CrossRef]
- Zivanov, M.; Sasic, B.; Lazic, M. Desing of Multiphase Boost Converter for Hybrid Fuel Cell/Battery Power Sources. In Paths to Sustainable Energy; Nathwani, J., Ng, A., Eds.; IntechOpen: Rijeka, Croatia, 2010; Chapter 19. [Google Scholar] [CrossRef]
- Saadi, R.; Hammoudi, M.; Kraa, O.; Ayad, M.; Bahri, M. A robust control of a 4-leg floating interleaved boost converter for fuel cell electric vehicle application. Math. Comput. Simul. 2020, 167, 32–47. [Google Scholar] [CrossRef]
- Sorlei, I.S.; Bizon, N.; Thounthong, P.; Varlam, M.; Carcadea, E.; Culcer, M.; Iliescu, M.; Raceanu, M. Fuel cell electric vehicles—A brief review of current topologies and energy management strategies. Energies 2021, 14, 252. [Google Scholar] [CrossRef]
- Samosir, A.S.; Mohd Yatim, A.H. Simulation and implementation of interleaved boost DC-DC converter for fuel cell application. Int. J. Power Electron. Drive Syst. 2011, 1, 168–174. [Google Scholar] [CrossRef]
- Faraj, K.S.; Hussein, J. Analysis and comparison of DC-DC boost converter and interleaved DC-DC boost converter. Eng. Technol. J. 2020, 38, 622–635. [Google Scholar] [CrossRef]
- Kascak, S.; Prazenica, M.; Jarabicova, M.; Paskala, M. Interleaved DC/DC boost converter with coupled inductors. Adv. Electr. Electron. Eng. 2018, 16, 147–154. [Google Scholar] [CrossRef]
- Guilbert, D.; Gaillard, A.; N’Diaye, A.; Djerdir, A. Energy efficiency and fault tolerance comparison of DC/DC converters topologies for fuel cell electric vehicles. In Proceedings of the 2013 IEEE Transportation Electrification Conference and Expo (ITEC), Metro Detroit, MI, USA, 16–19 June 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Farhani, S.; N’Diaye, A.; Djerdir, A.; Bacha, F. Design and practical study of three phase interleaved boost converter for fuel cell electric vehicle. J. Power Sources 2020, 479, 228815. [Google Scholar] [CrossRef]
- Younsi, M.O.; Bendali, M.; Azib, T.; Larouci, C.; Marchand, C.; Coquery, G. Current-sharing control technique of interleaved buck converter for automotive application. In Proceedings of the 7th IET International Conference on Power Electronics, Machines and Drives (PEMD 2014), Manchester, UK, 8–10 April 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Bendali, M.; Larouci, C.; Azib, T.; Marchand, C.; Coquery, G. Design methodology with optimization of an interleaved buck converter for automotive application. In Proceedings of the Eurocon 2013, Zagreb, Croatia, 1–4 July 2013; pp. 1066–1072. [Google Scholar] [CrossRef]
- Pniak, L.; Revol, B.; Quéval, L.; Magambo, J.S.N.T.; Béthoux, O. Pre-sizing of a modular high power density DC/DC converter with GaN components. Math. Comput. Simul. 2023. [CrossRef]
- Delhommais, M.; Delaforge, T.; Schanen, J.L.; Wurtz, F.; Rigaud, C. A Predesign Methodology for Power Electronics Based on Optimization and Continuous Models: Application to an Interleaved Buck Converter. Designs 2022, 6, 68. [Google Scholar] [CrossRef]
- Xun, Q.; Liu, Y.; Holmberg, E. A comparative study of fuel cell electric vehicles hybridization with battery or supercapacitor. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 389–394. [Google Scholar] [CrossRef]
- Pan, G.; Bai, Y.; Song, H.; Qu, Y.; Wang, Y.; Wang, X. Hydrogen Fuel Cell Power System—Development Perspectives for Hybrid Topologies. Energies 2023, 16, 2680. [Google Scholar] [CrossRef]
- Azib, T.; Bethoux, O.; Remy, G.; Marchand, C.; Berthelot, É. An innovative control strategy of a single converter for hybrid fuel cell/supercapacitor power source. IEEE Trans. Ind. Electron. 2010, 57, 4024–4031. [Google Scholar] [CrossRef]
- Thounthong, P.; Davat, B.; Rael, S.; Sethakul, P. Fuel cell high-power applications. IEEE Ind. Electron. Mag. 2009, 3, 32–46. [Google Scholar] [CrossRef]
- Dicks, A.; Rand, D.A.J. Fuel Cell Systems Explained, 3rd ed.; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Mebarki, N.; Rekioua, T.; Mokrani, Z.; Rekioua, D.; Bacha, S. PEM fuel cell/battery storage system supplying electric vehicle. Int. J. Hydrog. Energy 2016, 41, 20993–21005. [Google Scholar] [CrossRef]
- Ajayan, S.; Selvakumar, A.I. Modeling and simulation of PEM fuel cell electric vehicle with multiple power sources. Int. J. Recent Technol. Eng. 2020, 8, 2967–2975. [Google Scholar] [CrossRef]
- Visvanathan, V.K.; Palaniswamy, K.; Ponnaiyan, D.; Chandran, M.; Kumaresan, T.; Ramasamy, J.; Sundaram, S. Fuel Cell Products for Sustainable Transportation and Stationary Power Generation: Review on Market Perspective. Energies 2023, 16, 2748. [Google Scholar] [CrossRef]
- Saadi, A.; Becherif, M.; Aboubou, A.; Ayad, M. Comparison of proton exchange membrane fuel cell static models. Renew. Energ. 2013, 56, 64–71. [Google Scholar] [CrossRef]
- Saldaña, G.; San Martín, J.I.; Zamora, I.; Asensio, F.J.; Oñederra, O. Analysis of the current electric battery models for electric vehicle simulation. Energies 2019, 12, 2750. [Google Scholar] [CrossRef]
- Kabalo, M.; Blunier, B.; Bouquain, D.; Miraoui, A. State-of-the-art of DC-DC converters for fuel cell vehicles. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- İnci, M.; Büyük, M.; Demir, M.H.; İlbey, G. A review and research on fuel cell electric vehicles: Topologies, power electronic converters, energy management methods, technical challenges, marketing and future aspects. Renew. Sust. Energ. Rev. 2021, 137, 110648. [Google Scholar] [CrossRef]
- Ceschia, A.; Azib, T.; Bethoux, O.; Alves, F. Multi-Criteria Optimal Design for FUEL Cell Hybrid Power Sources. Energies 2022, 15, 3364. [Google Scholar] [CrossRef]
- Niu, M.; Wan, C.; Xu, Z. A review on applications of heuristic optimization algorithms for optimal power flow in modern power systems. J. Mod. Power Syst. Clean Energy 2014, 2, 289–297. [Google Scholar] [CrossRef]
- Rahmat-Samii, Y. Genetic algorithm (GA) and particle swarm optimization (PSO) in engineering electromagnetics. In Proceedings of the 17th International Conference on Applied Electromagnetics and Communications, Dubrovnik, Croatia, 1–3 October 2003; pp. 1–5. [Google Scholar] [CrossRef]
- Ceschia, A.; Azib, T.; Bethoux, O.; Alves, F. Reliability Impact in Optimal Sizing of Fuel Cell/Battery Hybrid Power Sources. Energies 2020, 13, 3510. [Google Scholar] [CrossRef]
- Martin, E.; Papageorgopoulos, D. DOE Hydrogen and Fuel Cells Program Record; Technical Report; US Departament of Energy: Washington, DC, USA, 2015. [Google Scholar]
- Raggl, K.; Nussbaumer, T.; Kolar, J.W. Model based optimization of EMC input filters. In Proceedings of the 2008 11th Workshop on Control and Modeling for Power Electronics, Zurich, Switzerland, 17–20 August 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Ejjabraoui, K.; Larouci, C.; Lefranc, P.; Marchand, C. A pre-sizing approach of DC-DC converters, application to design a Buck converter for the automotive domain. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 517–523. [Google Scholar] [CrossRef]
- Lin, X.; Perez, H.E.; Mohan, S.; Siegel, J.B.; Stefanopoulou, A.G.; Ding, Y.; Castanier, M.P. A lumped-parameter electro-thermal model for cylindrical batteries. J. Power Sources 2014, 257, 1–11. [Google Scholar] [CrossRef]
- Tran, M.K.; DaCosta, A.; Mevawalla, A.; Panchal, S.; Fowler, M. Comparative study of equivalent circuit models performance in four common lithium-ion batteries: LFP, NMC, LMO, NCA. Batteries 2021, 7, 51. [Google Scholar] [CrossRef]
- Aitakkache, M.; Enrici, P.; Matt, D.; Boubaker, N.; Piscini, L. Concept, Feasibility of Cylindrical Bar Winding for Low Voltage Permanent Magnet Synchronous Motor. Energies 2022, 15, 1507. [Google Scholar] [CrossRef]
- Liu, J.; Wilson, T.; Wong, R.; Wunderlich, R.; Lee, F. A method for inductor core loss estimation in power factor correction applications. In Proceedings of the APEC. Seventeenth Annual IEEE Applied Power Electronics Conference and Exposition (Cat. No.02CH37335), Dallas, TX, USA, 10–14 March 2002; pp. 439–445. [Google Scholar] [CrossRef]
- Azib, T.; Larouci, C.; Chaibet, A.; Boukhnifer, M. Online energy management strategy of a hybrid fuel cell/battery/ultracapacitor vehicular power system. IEEJ Trans. Electr. Electron. Eng. 2014, 9, 548–554. [Google Scholar] [CrossRef]





| Formalism | Mathematical Definition |
|---|---|
| Cost function | |
| Optimisation parameters | Converter parameters, FC parameters, and BAT parameters |
| Constraints | |
| Parameter | Values |
|---|---|
| M | 1425 (kg) |
| L | 4.804 (m) |
| l | 1.730 (m) |
| H | 1.568 (m) |
| S | l × H (m2) |
| Cx | 0.29 |
| Cr | 0.012 |
| α | 0 |
| g | 9.81 (m·s−2) |
| ρ | 1.184 (kg·m−3) |
| Formalism | Mathematical Definition |
|---|---|
| Cost function | |
| Optimisation parameters | Inductance, capacitance, frequency, magnetic density, wire diameter, winding number, heat sink thermal resistance, active surface area, number of FC cells |
| Constraints | Input current ripple |
| Inductance current ripple | |
| Output voltage ripple | |
| Junction temperature MOSFET °C | |
| Junction temperature diode °C | |
| Efficiency | |
| Output voltage | |
| Input converter current < limited FC current | |
| Parameter | Values |
|---|---|
| L | 0.001 (H) |
| C | 0.001 (F) |
| freq | 10,000 (Hz) |
| B | 1.2 (T) |
| Diameter | 1 · 10−4 (m) |
| Winding number | 300 |
| Heat sink thermal resistance | 0.5 °(C/W) |
| Number of FC cells | 240 |
| Active surface area | 140 (m2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mercier, V.; Ceschia, A.; Azib, T.; Larouci, C. Pre-Sizing Approach of a Fuel Cell-Battery Hybrid Power System with Interleaved Converters. Energies 2023, 16, 4068. https://doi.org/10.3390/en16104068
Mercier V, Ceschia A, Azib T, Larouci C. Pre-Sizing Approach of a Fuel Cell-Battery Hybrid Power System with Interleaved Converters. Energies. 2023; 16(10):4068. https://doi.org/10.3390/en16104068
Chicago/Turabian StyleMercier, Victor, Adriano Ceschia, Toufik Azib, and Cherif Larouci. 2023. "Pre-Sizing Approach of a Fuel Cell-Battery Hybrid Power System with Interleaved Converters" Energies 16, no. 10: 4068. https://doi.org/10.3390/en16104068
APA StyleMercier, V., Ceschia, A., Azib, T., & Larouci, C. (2023). Pre-Sizing Approach of a Fuel Cell-Battery Hybrid Power System with Interleaved Converters. Energies, 16(10), 4068. https://doi.org/10.3390/en16104068







