Influence of Stator Core Seams on No-Load Performance of Module-Combined Stator Permanent Magnet Motor and Its Weakening Method

Abstract

In this paper, a module-combined stator is proposed, which is used for large and ultra-low-speed permanent magnet synchronous motors, and the influence of stator core seams on the no-load performance is studied. A method is proposed to weaken the negative influence of stator iron core seams on the no-load performance of permanent magnet synchronous motors. Firstly, the magnetic circuit model of the motor considering the stator iron core seams was deduced theoretically, and the selection principle of stator core seam number was given a description. The influence of different seam parameters on the no-load performance and the influence of different pole-slot fits and the number of parallel branches on the no-load performance are analyzed. The proposed structure of the stator iron core, which can weaken the influence of stator iron core seams on the no-load performance of the motor, is proposed. Using analysis and simulation experiments, the effectiveness of the proposed stator iron core structures in weakening the negative influence of the stator iron core seams on the no-load performance was verified.

1. Introduction

For large and ultra-low-speed motors, module-combined stator permanent magnet motors are used to reduce the assembly difficulty and improve the fault tolerance [1,2,3]. The stator module combination structure of permanent magnet motors has three main schemes:

Scheme 1: A single set of stator teeth and a stator yoke are superposed to form a tooth–yoke sub-module, and the coil is wound on the tooth–yoke sub-module [4,5];

Scheme 2: A stator sector piece with a single set of stator teeth is separately superposed onto a sub-module stator, and the wound coil is directly wound onto the stator tooth module. This stator tooth module and the stator yoke are fixed via a separate connecting piece or a pigeon tail slot on the stator sheet [6,7];

Scheme 3: A stator sector piece that can wind one group of three-phase windings is separately superposed into a sub-module stator. The windings are wound on a single tooth when the seams of the stator core module are in the yoke and the pitch y = 1, while the seams of the stator core module are in the tooth or pitch Y > 1. The windings are divided into two different span specifications: large and small-span windings [8,9,10,11,12].

A novel cogging torque mitigation method for modular permanent magnet (PM) machines with flux gaps in alternate stator teeth has been proposed [13,14]. The influence of these flux gaps on the electromagnetic performance of modular PM machines, such as on the winding factor, open-circuit air-gap flux densities, back electromotive force, cogging torque, on-load torque, inductance, magnetic saturation and copper losses, were comprehensively investigated and general rules have been established [15].

In this paper, a module-combined stator is proposed for large and ultra-low-speed permanent magnet synchronous motors, and the influence of the stator core seams was studied. For large and ultra-low-speed motors (<60 rpm), copper loss (>80% total loss) is mainly dependent on the no-load back electromotive force and the same coil parameters and cogging torque can significantly influence the motor parameter measurement accuracy of the converter; therefore, this paper mainly studied the performance of the no-load back electromotive force and cogging torque. Firstly, a magnetic circuit model considering the stator core seams was established. The effect of the dimension parameters of the seams on the no-load performance of the motor was studied using different pole slot fits and number of parallel branches. Based on the comparison of the effects of different parts of the stator core seams, two kinds of stator sheet structures are proposed to weaken the adverse effects of the stator core seams.

2. Magnetic Circuit Model with Consideration of Stator Core Seams

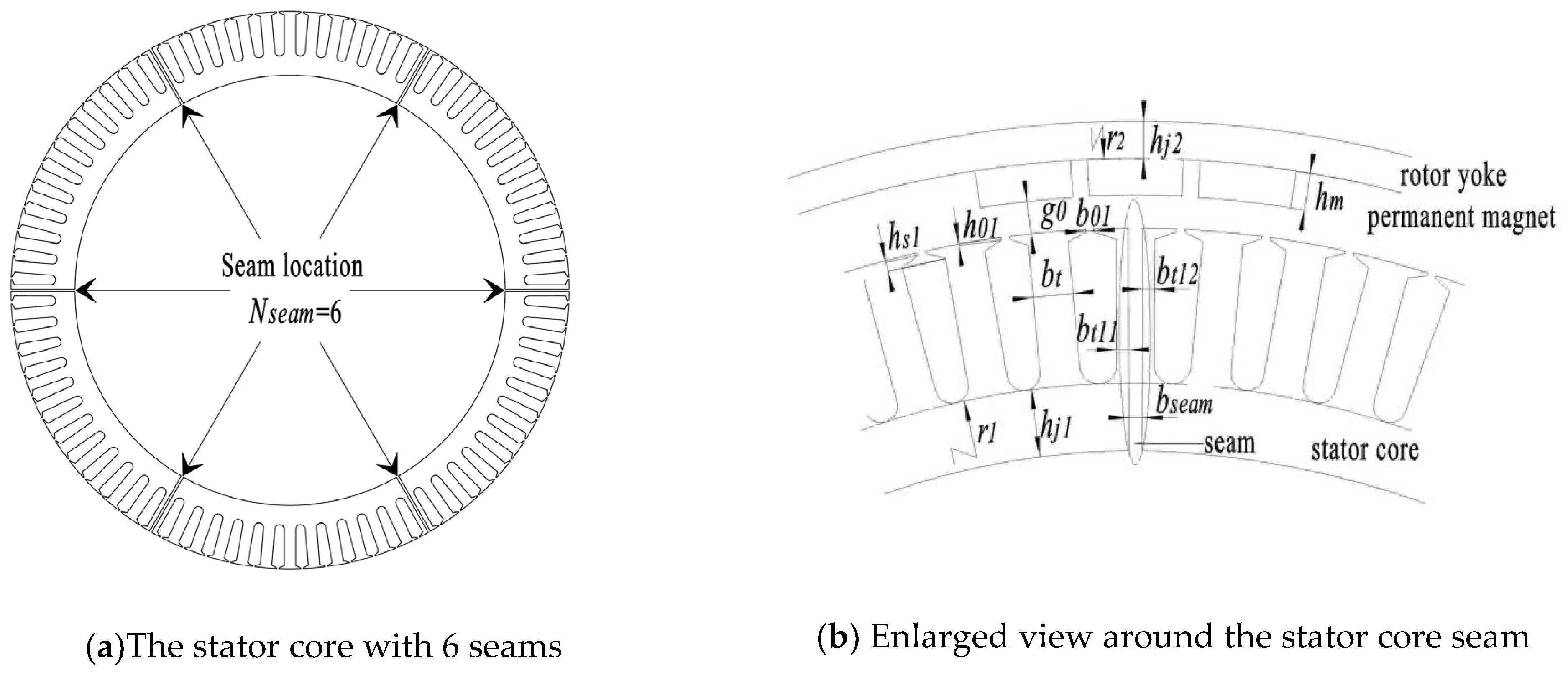
A schematic of stator core seams with an outer rotor permanent magnet surface mounting motor is given in Figure 1. In the enlarged view around the stator core seams in Figure 1b, N_seam is the seam number; h_j2 is the height of the rotor yoke; h_m and r₂ are the inner diameter and thickness of the permanent magnet, respectively; g₀ is the air gap between the stator and rotor; h₀₁ and b₀₁ are the height and width of the stator notch, respectively; b_t is the regular tooth width; b_t11 and b_t12 are the left tooth width and the right tooth width, respectively, with the seam on the tooth; b_seam is the seam width; r₁ is the radius of the slot bottom; h_j1 is the height of the stator yoke; and h_s1 is the radial projection height from the slot shoulder bottom to the slot notch.

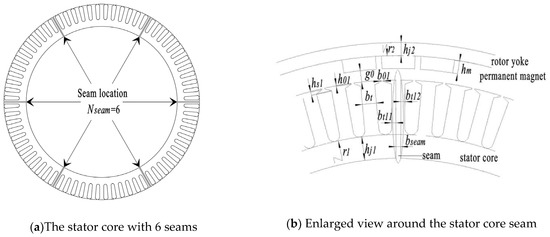
Figure 1. The schematic drawing of stator with seams (N_seam = 6).

2.1. The Selection Principle of Seam Number

The number of slots per pole per phase in a multi-pole, ultra-low-speed permanent magnet synchronous motor with fewer slots is shown in Expression (1).

$$q=\frac{Q_s}{2pm}=b+\frac{c}{d}$$

(1)

where q is the number of slots per pole per phase, Q_S is the number of stator slots, p is the number of motor pole pairs, m is motor phase, and c and d are the minimum forms of the numerator or denominator.

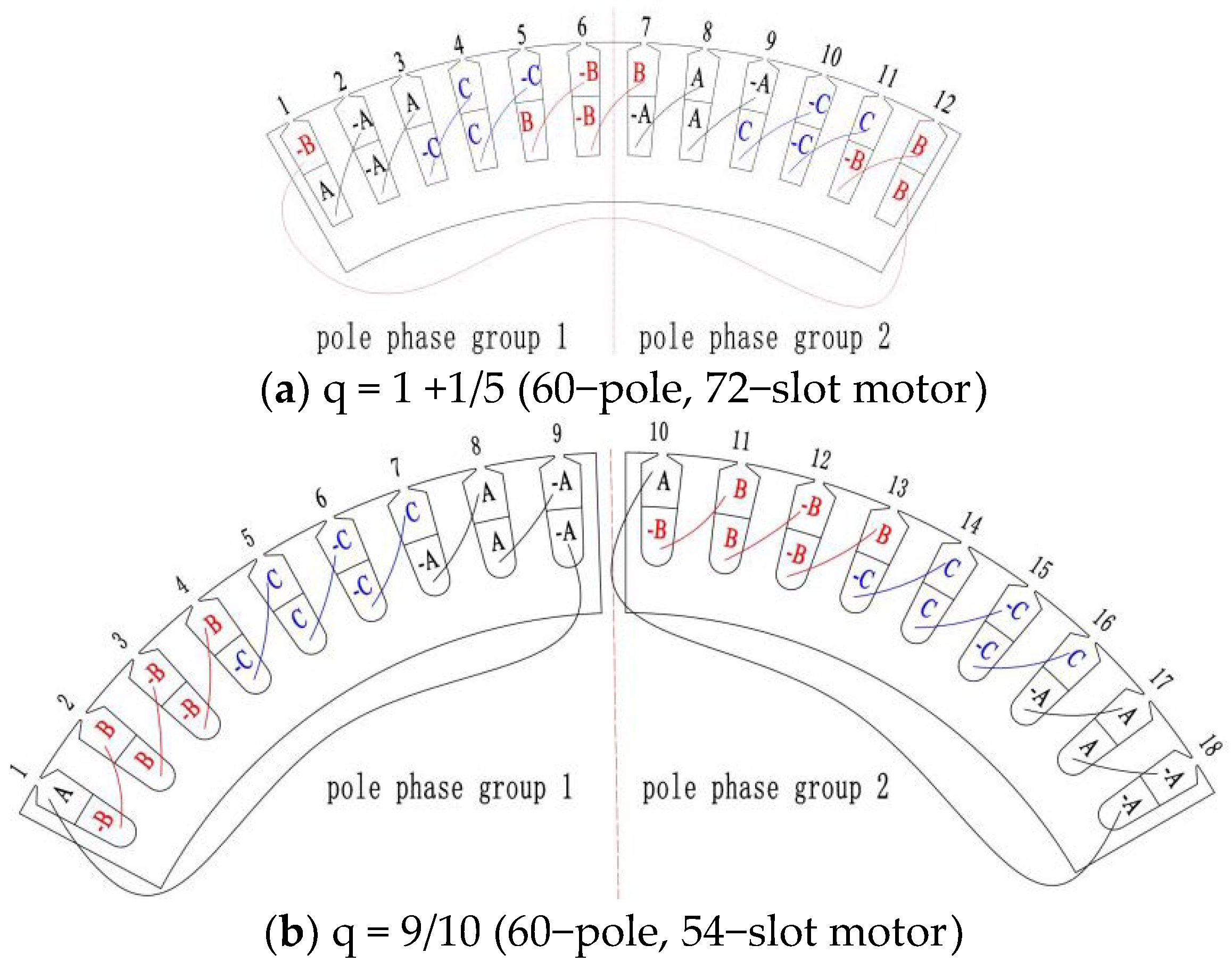
The maximum number of pole phase groups is 2p/d. When d is even, the value of seam number N_seam should be the divisor of 2p/d because the large span coil must connect at least one pole phase group as shown in Figure 2a. When d is odd, the value of seam number N_seam should be the divisor of p/d because the large span coil must connect at least two pole phase groups as shown in Figure 2b.

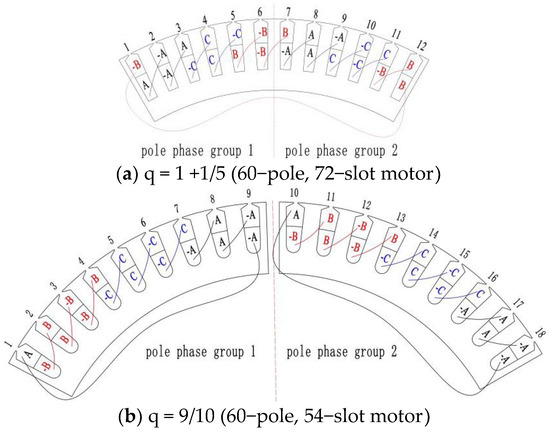
Figure 2. Pole phase groups with two different pole slot combinations.

2.2. The Magnetic Circuit

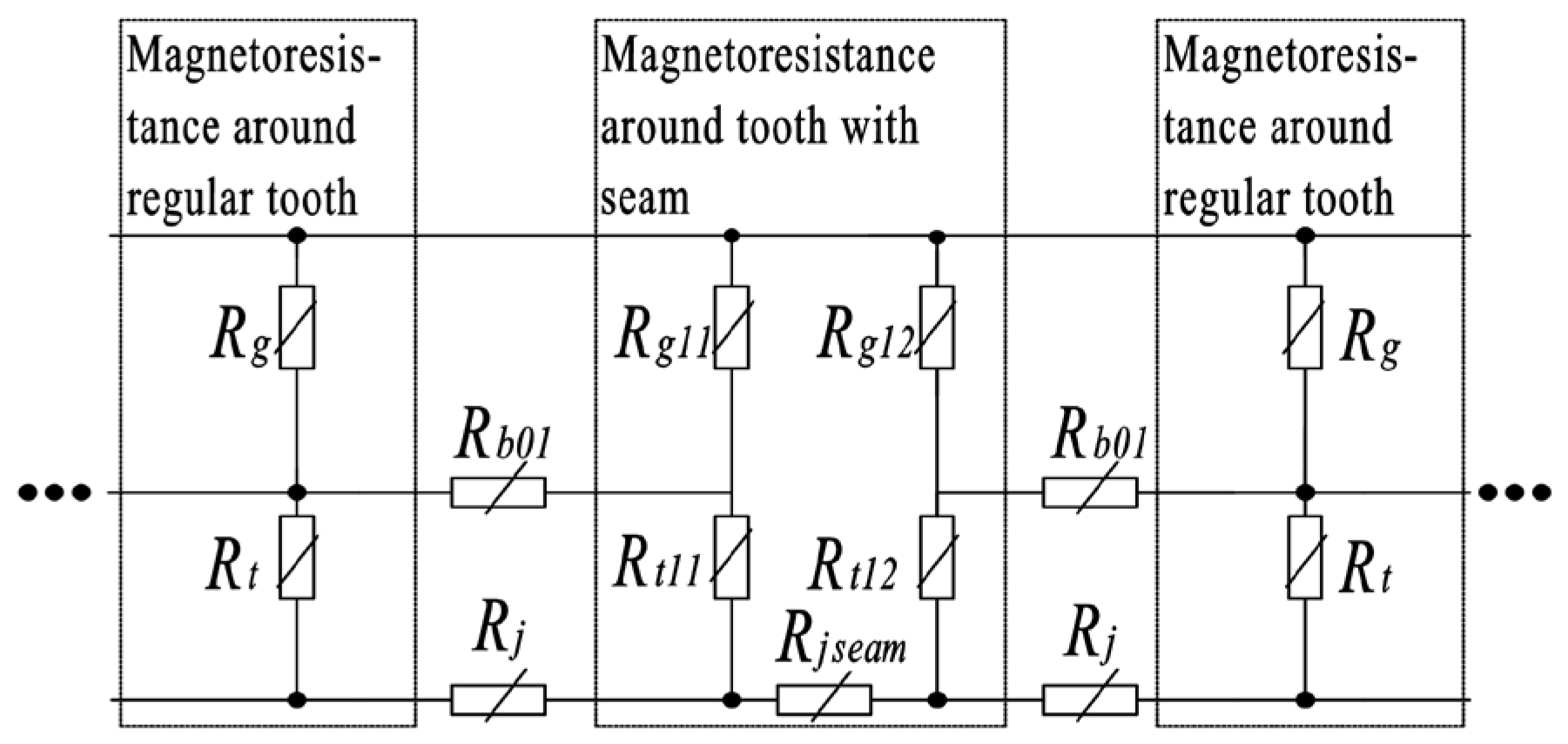
The magnetic circuit model considering the stator core seams is given in Figure 3. In order to facilitate the modeling, the following assumptions were made:

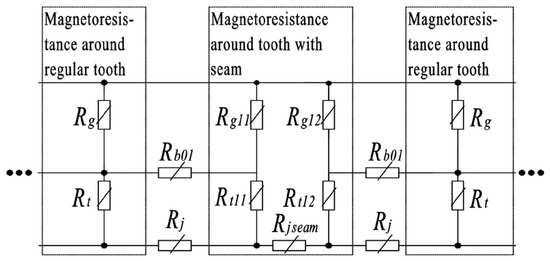
Figure 3. Distribution of air gaps and stator magnetoresistance around the stator core seam.

• The flux in the left tooth and right tooth with the seam on the tooth are linearly proportional to the tooth width;
• The magnetic resistance of each segment was simplified to a rectangle in the calculation of the magnetic resistance;
• The magnetic permeability of the ferromagnetic material was set to be invariable, and the corresponding magnetic resistance was assumed to be invariable.

In Figure 3, R_g is the equivalent air gap magnetoresistance corresponding to the regular tooth; R_g11 and R_g12 are the equivalent air gap magnetoresistances corresponding to the left and right tooth with the seam, respectively; R_b01 is the stator slot leakage magnetoresistance; R_t is the regular tooth magnetoresistance; R_b01 is the stator slot leakage magnetoresistance; R_t11 and R_t12 are the left and right tooth magnetoresistances with the seam, respectively; R_j is the regular stator yoke magnetoresistance; and R_jseam is the stator yoke magnetoresistance with the seam.

The expression of magnetoresistance R is shown in (2), where l is the length of the magnetic path, μ is the magnetoconductivity of the medium, and S is the sectional area of the medium.

$$R=\frac{l}{\mu S}$$

(2)

Based on the expression (2), R_g, R_g11, and R_g12 can be expressed as:

$$\left\{\begin{array}{l}{R}_g=\frac{Q_s{k}_{\delta }{g}_0}{2\pi {\mu }_0(r_2 - h_m - 0.5g_0)L_{Fe}}\\ R_{g11}=\frac{Q_s{k}_{\delta 1}\frac{b_{t11} + b_{t12}}{b_{t11}}{g}_0}{2\pi {\mu }_0(r_2 - h_m - 0.5g_0)L_{Fe}}\\ R_{g12}=\frac{Q_s{k}_{\delta 1}\frac{b_{t11} + b_{t12}}{b_{t12}}{g}_0}{2\pi {\mu }_0(r_2 - h_m - 0.5g_0)L_{Fe}}\end{array}\right.$$

(3)

where k_δ and k_δ1 are the air gap coefficients corresponding to the regular stator tooth and stator tooth with the seam, respectively; g₀ is the air gap between stator and rotor, μ₀ is the vacuum magnetic permeability, r₂ is the inner diameter of rotor yoke, h_m is the magnetization direction length of permanent magnets, L_Fe is the iron core length of the stator and rotor, b_t11 is the tooth width on the left of the seam, and b_t12 is the tooth width on the right of the seam. Referring to reference [16,17,18], k_δ and k_δ1 can be expressed as:

$$\left\{\begin{array}{l}{k}_{\delta }=\frac{1}{1 - \frac{Q_s{b}_{01}}{2\pi \left(r_2 - h_m - g_0\right)}\sigma }\\ \sigma =\frac{2}{\pi }\left\{{\tan }^{-1}\frac{0.5b_{01}}{h_m + g_0} - \frac{h_m + g_0}{b_0{}_1}\ln \left(1 + {\left(\frac{0.5b_{01}}{h_m + g_0}\right)}^2\right)\right\}\\ k_{\delta 1}=\frac{1}{1 - \frac{Q_s\left(b_{01} + b_{seam}\right)}{4\pi \left(r_2 - h_m - g_0\right)}{\sigma }_1}\\ {\sigma }_1=\frac{2}{\pi }\ln \left\{\begin{array}{l}{\tan }^{-1}\frac{b_{01} + b_{seam}}{4\left(h_m + g_0\right)} - \\ \frac{2\left(h_m + g_0\right)}{b_{01} + b_{seam}}\left(1 + {\left(\frac{b_{01} + b_{seam}}{4\left(h_m + g_0\right)}\right)}^2\right)\end{array}\right\}\end{array}\right.$$

(4)

where b₀₁ is the width of the top stator slot, and b_seam is the width of the stator core seam. The stator tooth magnetoresistance and yoke magnetoresistance can be expressed as follows, where μ_Fe is the relative magnetic permeability of the stator:

$$\left\{\begin{array}{l}{R}_t=\frac{r_2 - h_m - g_0 - r_1}{{\mu }_{Fe}{\mu }_0{b}_t{L}_{Fe}}\\ R_{t11}=\frac{r_2 - h_m - g_0 - r_1}{{\mu }_{Fe}{\mu }_0{b}_{t11}{L}_{Fe}}\\ R_{t12}=\frac{r_2 - h_m - g_0 - r_1}{{\mu }_{Fe}{\mu }_0{b}_{t12}{L}_{Fe}}\\ R_{jseam}=\frac{b_{seam}}{{\mu }_0{h}_{j1}{L}_{Fe}}\end{array}\right.$$

(5)

where r₁ is the outer diameter of the stator yoke, μ_fe is the magnetic permeability of the stator core, b_t is the width of the stator tooth without seam, and h_j1 is the radial height of the stator yoke.

3. Influence of Seams on No-Load Performance

3.1. Influence of Different Seam Numbers and Seam Widths on No-Load Performance

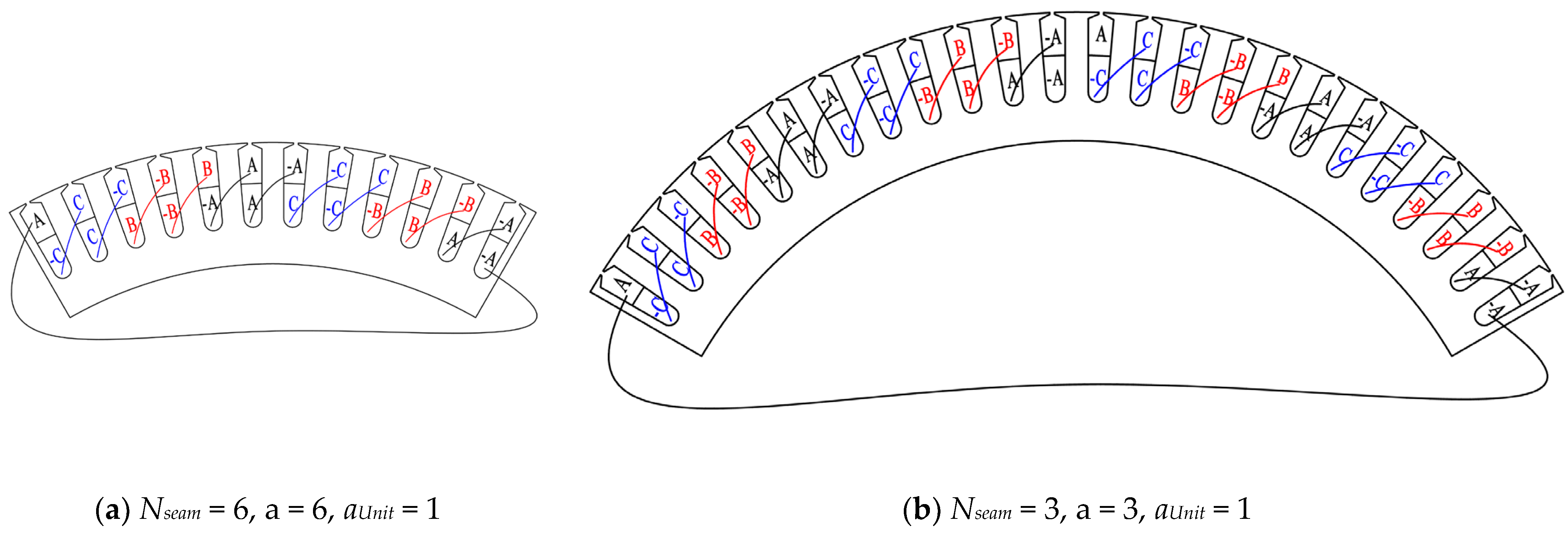
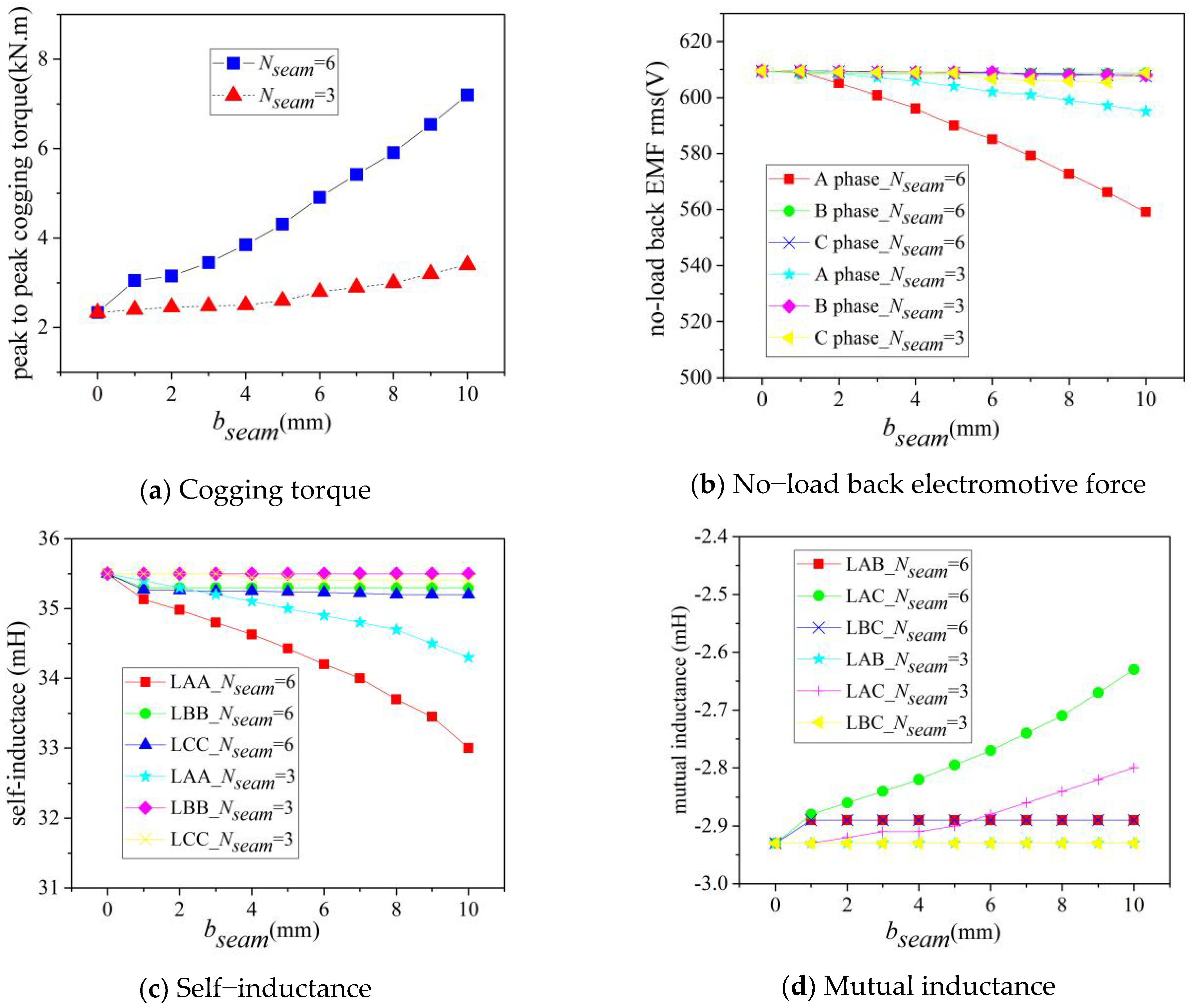
The motor parameters are given in Table 1. The winding end connection diagram is shown in Figure 4 in the case of N_seam = 3, a = 3, a_Unit = 1 and N_seam = 6, a = 6, a_Unit = 1, where a is the number of parallel branches of the whole stator and a_Unit is the number of parallel branches of one stator sub-module. The influence of the seam number N_seam and the seam width b_seam on the no-load motor performance is shown in Figure 5. It can be seen from Figure 5 that:

Table 1. Parameters of the 60-pole 72-slot motor.

Parameter	Values and Unit
Rated power of motor	220 kW
Rated voltage	660 V
Rated speed	30 r/min
Rated frequency	15 Hz
Number of rotor poles	60
Number of stator slots	72
Number of groups per pole per phase	12
Rotor structure	Out rotor with permanent magnet surface mounting
Outside diameter of rotor	1270 mm
Thickness of rotor yoke	50 mm
Core length	1000 mm
Thickness of PM	8 mm
Pole arc coefficient of PM	0.83
PM material	N42UH
Br at 20 °C	1.3T
Hc at 20 °C	971 kA/m
Relative magnet permeability	1.06
Air gap	2.3 mm
Outside diameter of stator	1149.4 mm
Slot height	80 mm
Stator yoke height	50 mm
Pitch	1
No-load back electromotive force	609.5 V

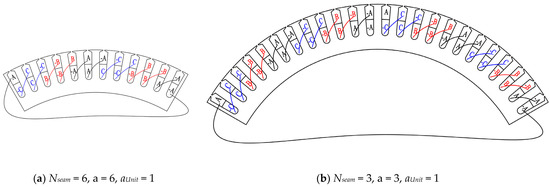
Figure 4. Single-stator unit winding end connection diagram with different N_seam values.

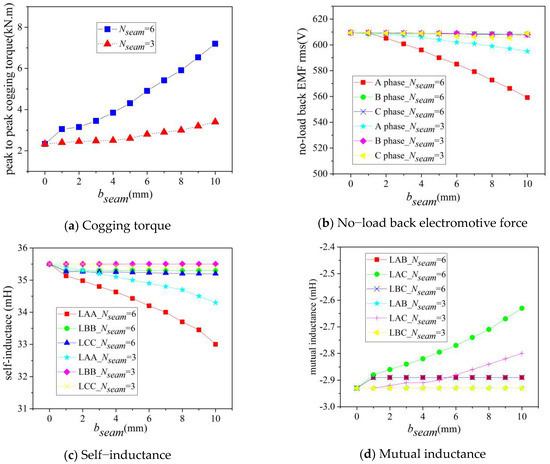
Figure 5. The relationships of no-load performance using different seam numbers and seam widths.

(1)

The cogging torque amplitude was directly proportional to the seam number N_seam and the seam width b_seam;

(2)

The effective value of no-load phase back electromotive force, the amplitude of the self-inductance, and mutual inductance were inversely proportional to the seam number N_seam and the seam width b_seam;

(3)

The self-inductance L_AA and mutual inductance L_AC of A phase, which were closest to the seam, were the most affected by the seam number N_seam and the seam width b_seam because the maximum mutual inductance variation extent (0.35 mH), which is influenced by the seam number N_seam and the seam width b_seam, has little influence on motor performance; the mutual inductances that are influenced by the seam number N_seam and the seam width b_seam are ignored in the following chapters.

3.2. The Relationship between Motor No-Load Performance and the Number of Parallel Branches in One Unit with Same Seam

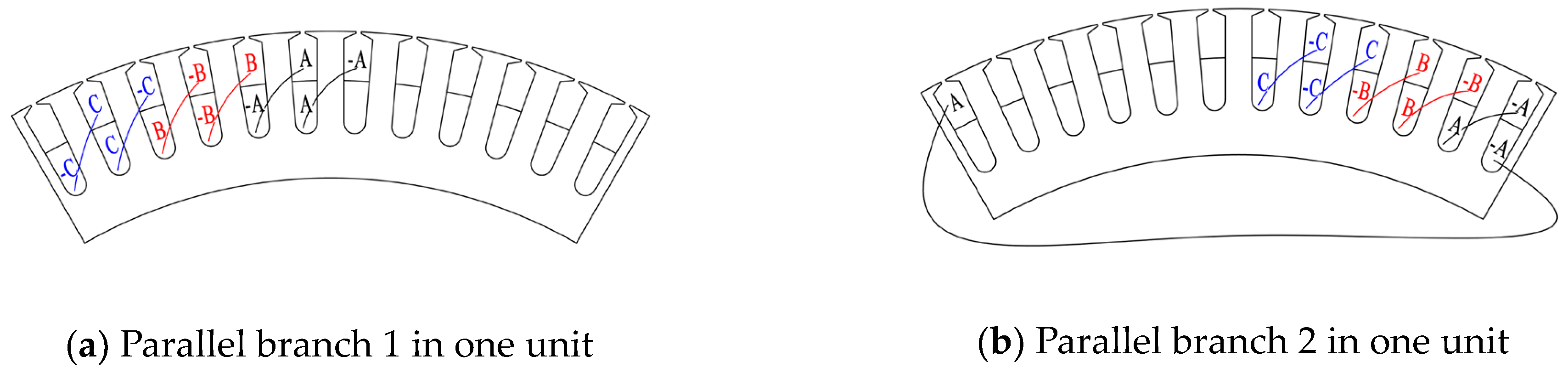
Winding end connection diagram with two parallel branches in one stator unit are shown in Figure 6, Where N_seam = 6, a = 12, a_Unit = 2. The no-load performance with a different number of parallel branches in one stator unit a_Unit is shown in Figure 7; the no-load cogging torque is not shown because the stator winding connection style had no influence on it. The winding end connection diagrams with a_Unit = 1 and a_Unit = 2 are shown in Figure 4a and Figure 6, respectively.

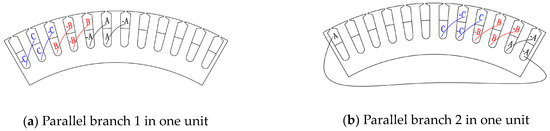
Figure 6. Winding end connection diagram with two parallel branches in one stator unit (N_seam = 6, a = 12, a_Unit = 2).

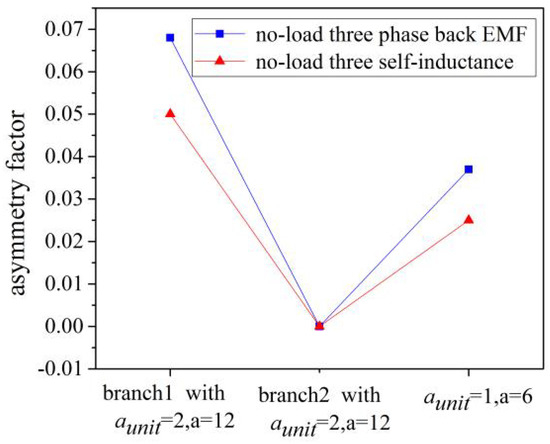
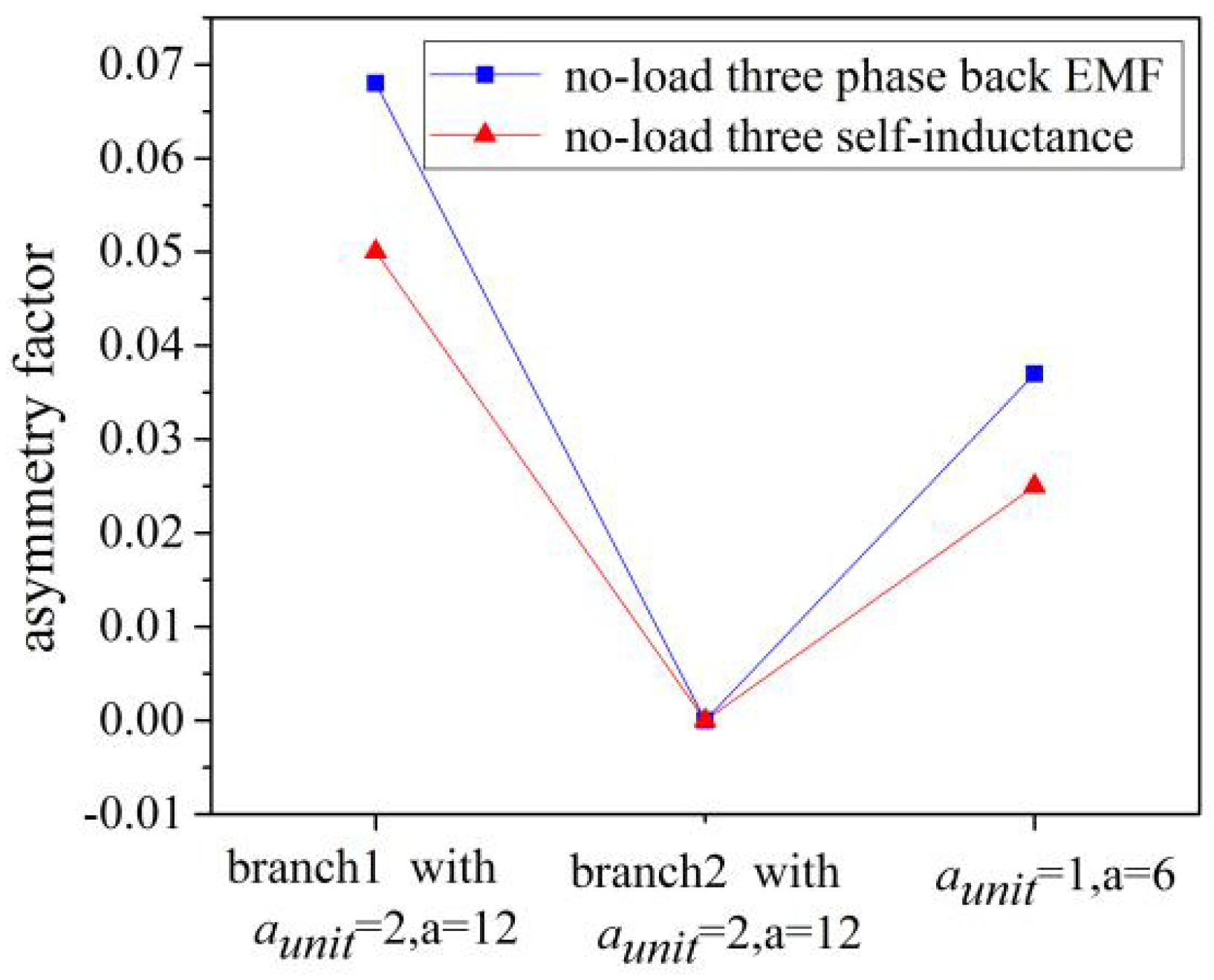
Figure 7. Asymmetry factor of no-load three-phase back electromotive force and self-induction using different motor parallel branches (b_seam = 5 mm).

Additionally, the asymmetry factor for the back electromotive force in this paper is max{|E_A − E_av|;|E_B − E_av|;|E_C − E_av|} and the asymmetry factor for self-inductance is max{|L_AA − L_av|;|L_BB − L_av|;|L_CC − L_av|}, where E_A is the effective values of A phase winding no-load back electromotive force, E_B is the effective values of B phase winding no-load back electromotive force, E_C is the effective values of C phase winding no-load back electromotive force, E_av = (E_A + E_B + E_C)/3; L_AA, L_BB, L_CC are the average no-load self-inductance value of A phase winding, B phase winding, and C phase winding, respectively, and L_av = (L_AA + L_BB + L_CC)/3.

It can be seen from Figure 7 that the asymmetry factor of the no-load three-phase back electromotive force’s effective values and the inductance were inversely proportional to the number of parallel branches in one stator unit a_Unit.

3.3. The Relationship between Motor No-Load Performance and Slot–Pole Combination with Same Seam Parameters

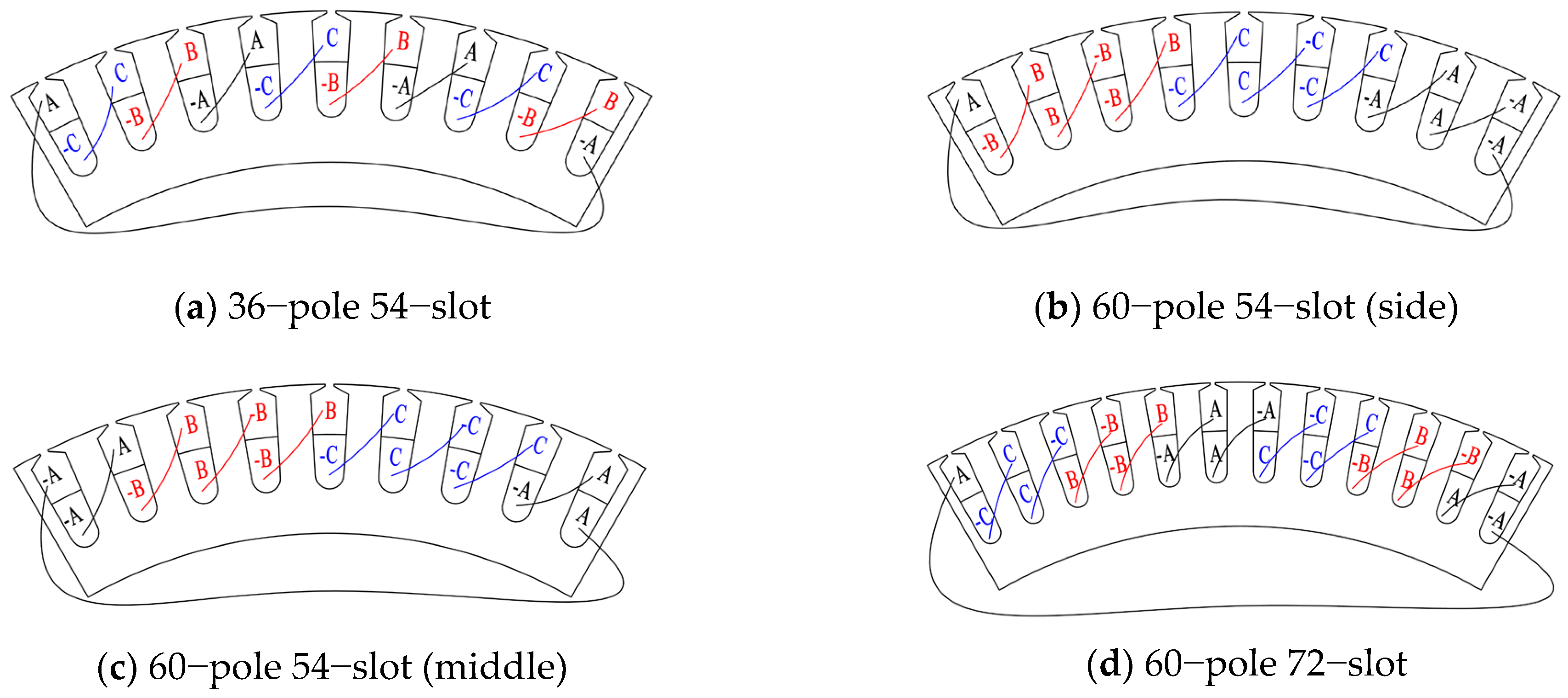
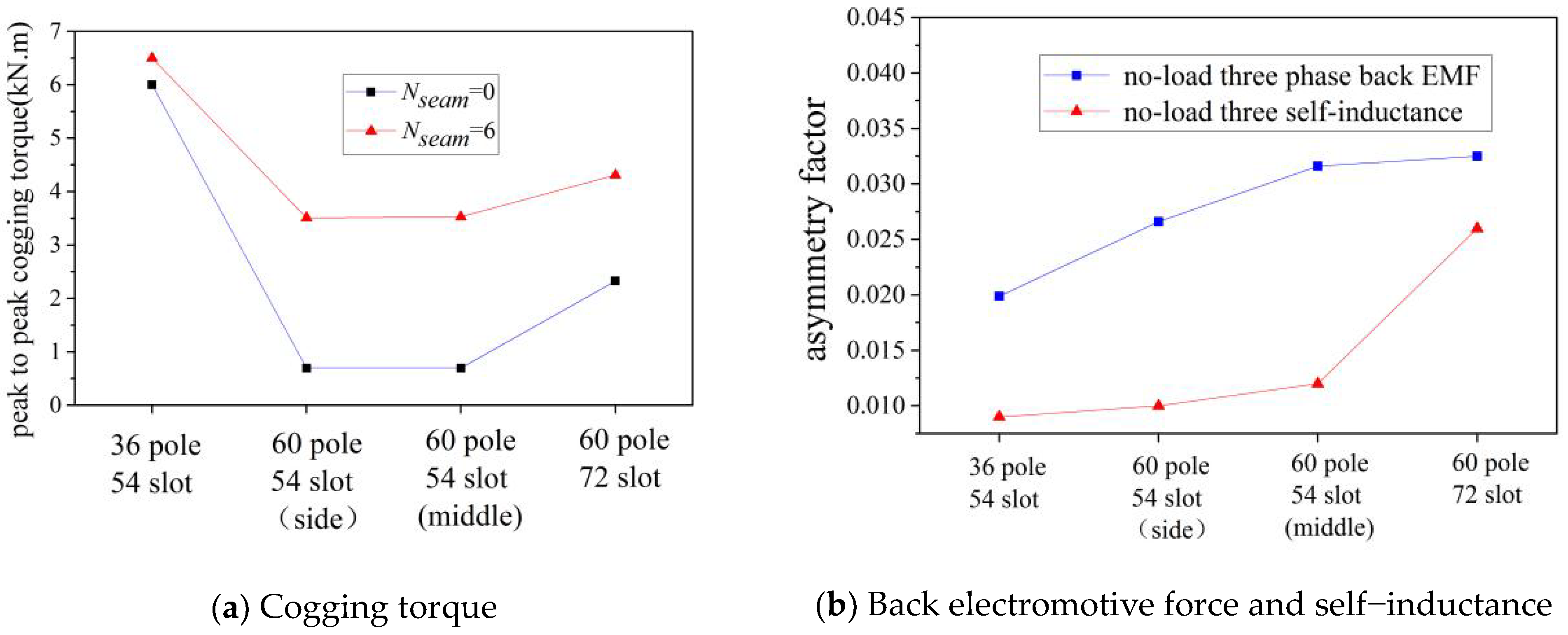
The stator winding wiring diagrams with different pole slots are shown in Figure 8, where the winding wiring diagram of a 60-pole, 54-slot stator is divided into two kinds according to the position of the seam on the A phase winding. The no-load performance, which is shown in Figure 9, showed that:

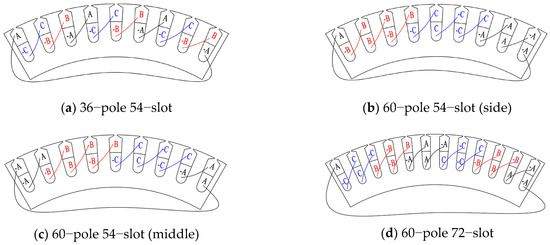
Figure 8. Stator winding wiring diagram with different pole slots (N_seam = 6, a = 6, a_Unit = 1).

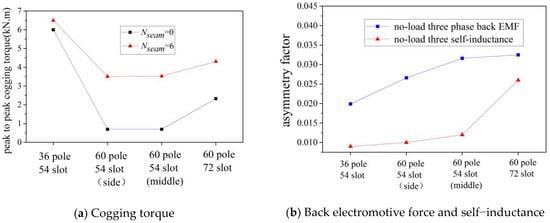
Figure 9. The relationship between no-load motor performance and slot–pole combination (b_seam = 5 mm).

(1)

More stator slots with the same rotor poles can weaken the no-load motor performance impact of seams: with the same 54-slot stator sheet parameter, the no-load motor performance impact of a seam with the 36-pole scheme was less than the 60-pole scheme; with the same 60-pole rotor parameter, the no-load motor performance impact of a seam with a 72-slot scheme was less than that of a 54-slot scheme;

(2)

When the number of stator teeth that continuously wind the same phase coil in one polar phase group was more than three, the seam on the side of the same phase coil tooth weakened the no-load motor performance impact of the seam. The no-load motor performance impact of the seam in Figure 8b was less than that in Figure 8c, where the seam is in the middle of the same phase coil tooth.

In conclusion, the following electromagnetic parameters can weaken the no-load motor performance impact of seams:

(1)

Reduce the number of the stator core seams and width of the stator core seams;

(2)

Reduce the number of parallel branches in one stator sub-module;

(3)

Adopt fewer poles and more slots;

(4)

When the number of stator teeth that continuously wind the same phase coil in one polar phase group is more than three, place the seam on the same side as the phase coil tooth.

4. Stator Sheet Structures That Can Weaken the Impact of Seams

4.1. No-Load Motor Performance Impact of Seams on Different Parts of Tooth

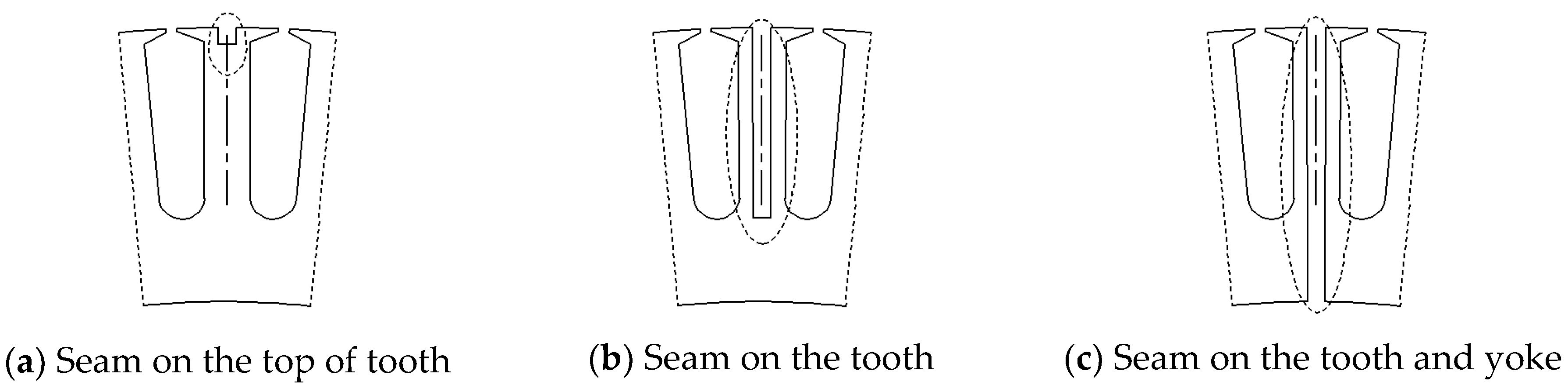
Figure 10 shows a schematic drawing of a seam on different parts of tooth. The corresponding results, which are shown in Figure 11, showed that:

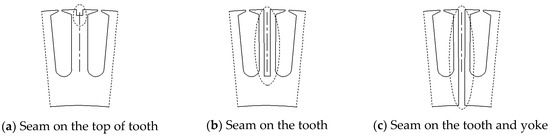
Figure 10. Schematic drawing of a seam on a stator core.

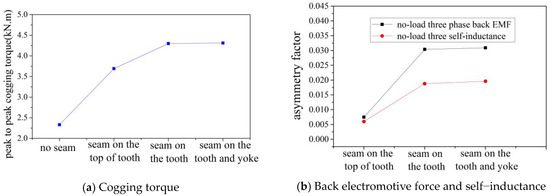
Figure 11. The corresponding no-load performance of seam location on stator core (N_seam = 6, b_seam = 5 mm, a = 6).

(1)

The no-load cogging torque was chiefly affected by a seam on the top of the tooth (compare Figure 10a,c);

(2)

The no-load back electromotive force and self-inductance were mainly affected by a seam on the top of the tooth (compare Figure 10a–c);

(3)

The no-load motor performance impact of a seam on the yoke was negligible (compare Figure 10b,c).

4.2. Proposed New Stator Sheet Structures

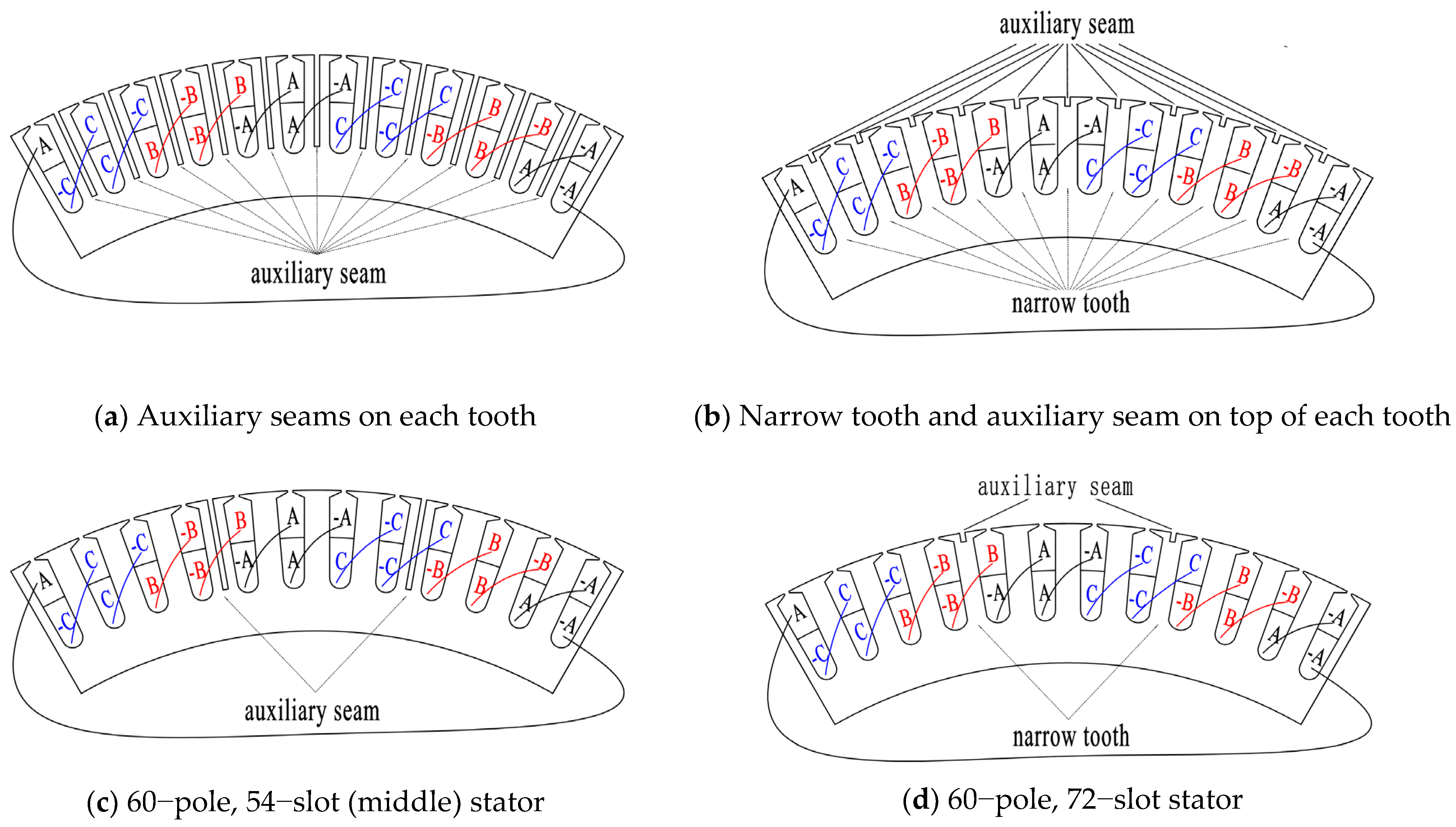
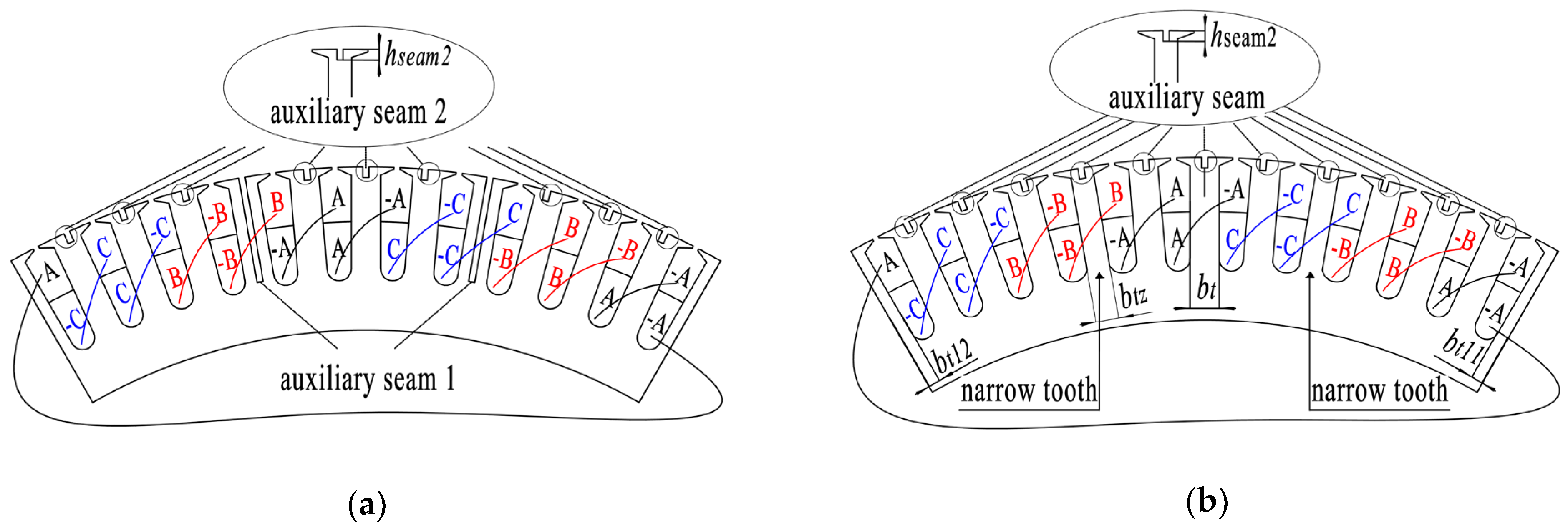
According to the conclusions from Section 3.1, the new stator sheet structures, which are shown in Figure 12, adopt the method of an opening auxiliary seam on the top of the tooth to balance the no-load cogging torque impact of a seam, and narrow the tooth or auxiliary seam on the whole tooth to balance the no-load back electromotive force and self-inductance. In Figure 12, the width of narrow tooth b_tz = b_t11 + b_t12 = b_t − b_seam.

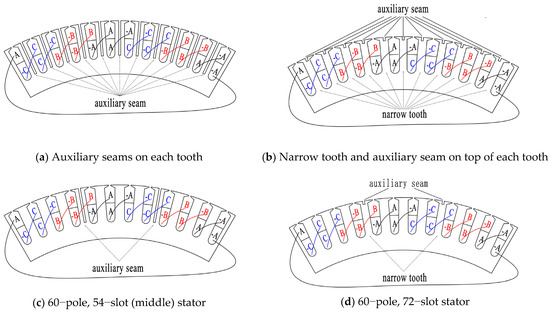
Figure 12. Stator winding wiring diagrams with different pole slots (N_seam = 6, a = 6, a_Unit = 1).

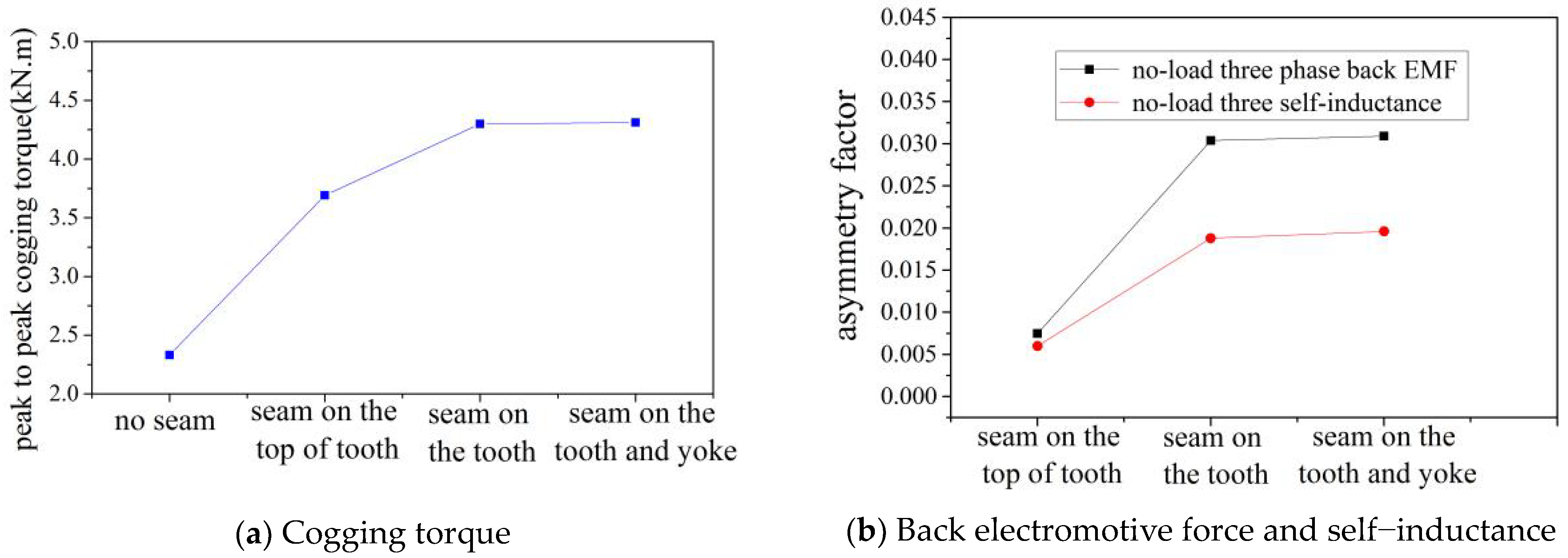
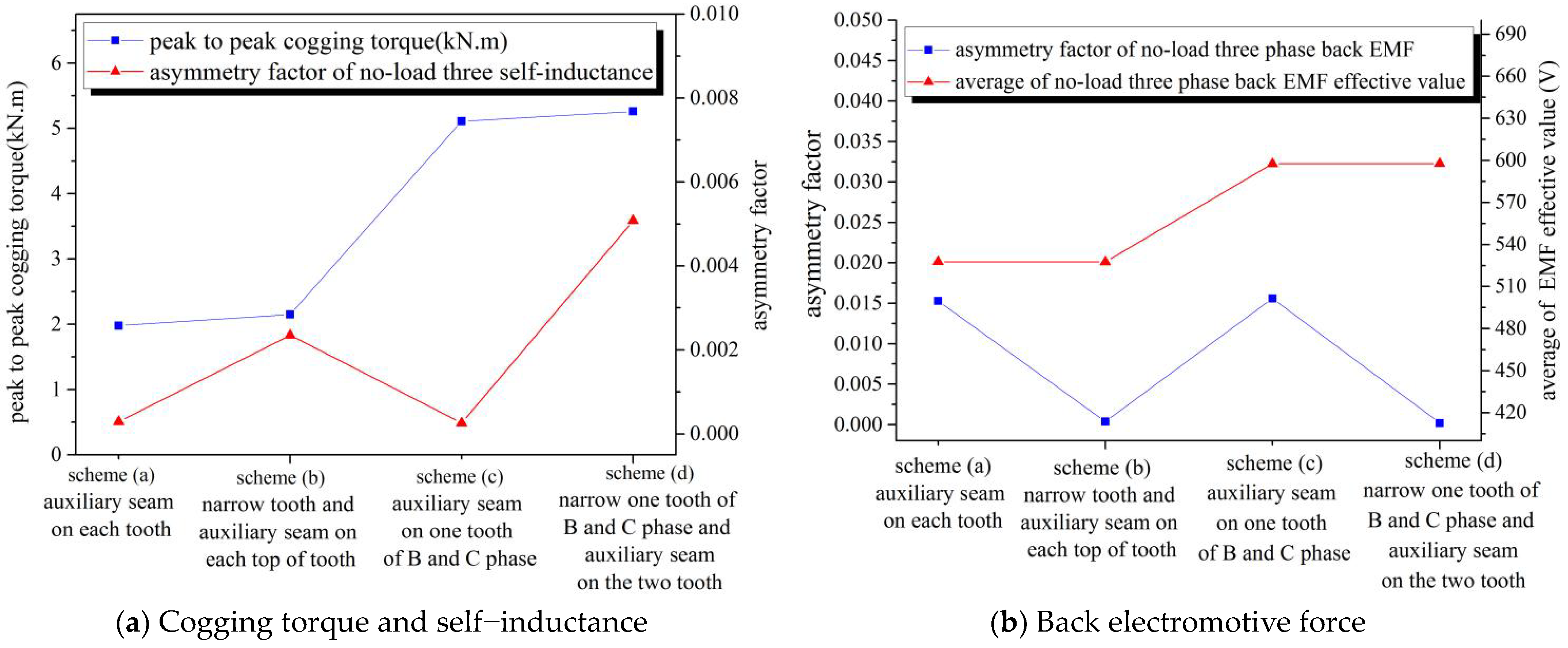
Figure 13 shows that:

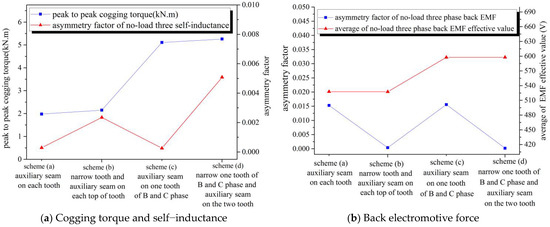
Figure 13. Comparison of no-load performance with auxiliary seam and narrow tooth (b_seam = 5 mm).

(1)

Compared with the narrow tooth and auxiliary seam on the top of the tooth scheme (Figure 12b,d), an auxiliary seam (Figure 12a,c) was better at weakening the no-load cogging torque and self-inductance impact of the seam but worse at weakening the no-load asymmetry factor of the back electromotive force impact of the seam;

(2)

Compared with one tooth of B and C phase with an auxiliary seam or narrow tooth (Figure 12c,d), each whole tooth with an auxiliary seam or narrow tooth (Figure 12a,b) weakened the no-load cogging torque and self-inductance impact of the seam better, but reduced the back electromotive force value more.

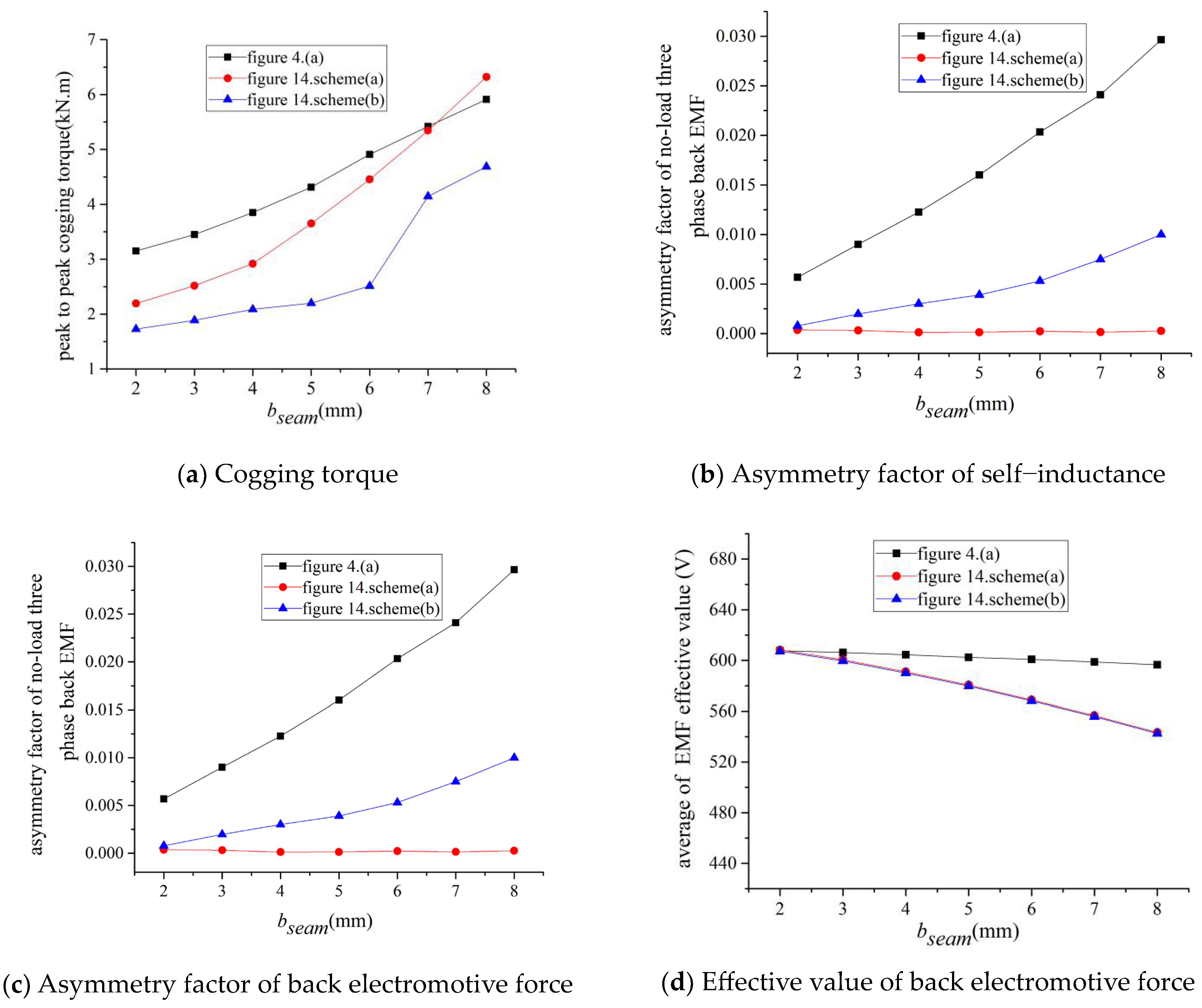
Learning from the strengths and weaknesses shown in Figure 12, Figure 14 was proposed on the basis of Figure 12b,d. An auxiliary seam 2 was added to balance the air-gap magnetic field to reduce the negative impact of the seam on the cogging torque, where the width of auxiliary seam 2 is equal to the width of auxiliary seam 1.

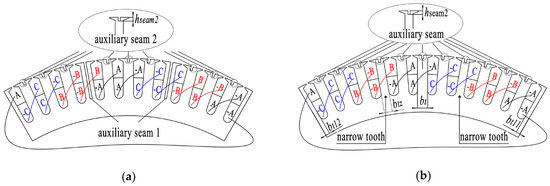
Figure 14. Winding end connection diagram with double auxiliary seams scheme (N_seam = 6, a_Unit = 1). (a) Auxiliary seam 1 on one tooth of B and C phase and auxiliary seam 2 on other tooth, (b) Narrow tooth of B and C phase + auxiliary seam 1 on the narrow tooth + auxiliary seam 2 on the other tooth.

The results in Figure 15 and Figure 16 show that:

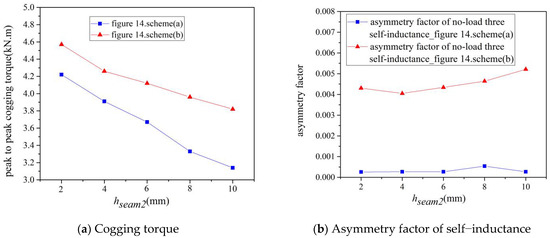
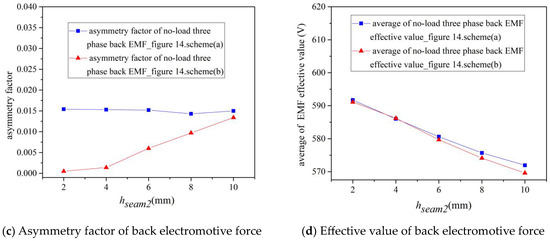
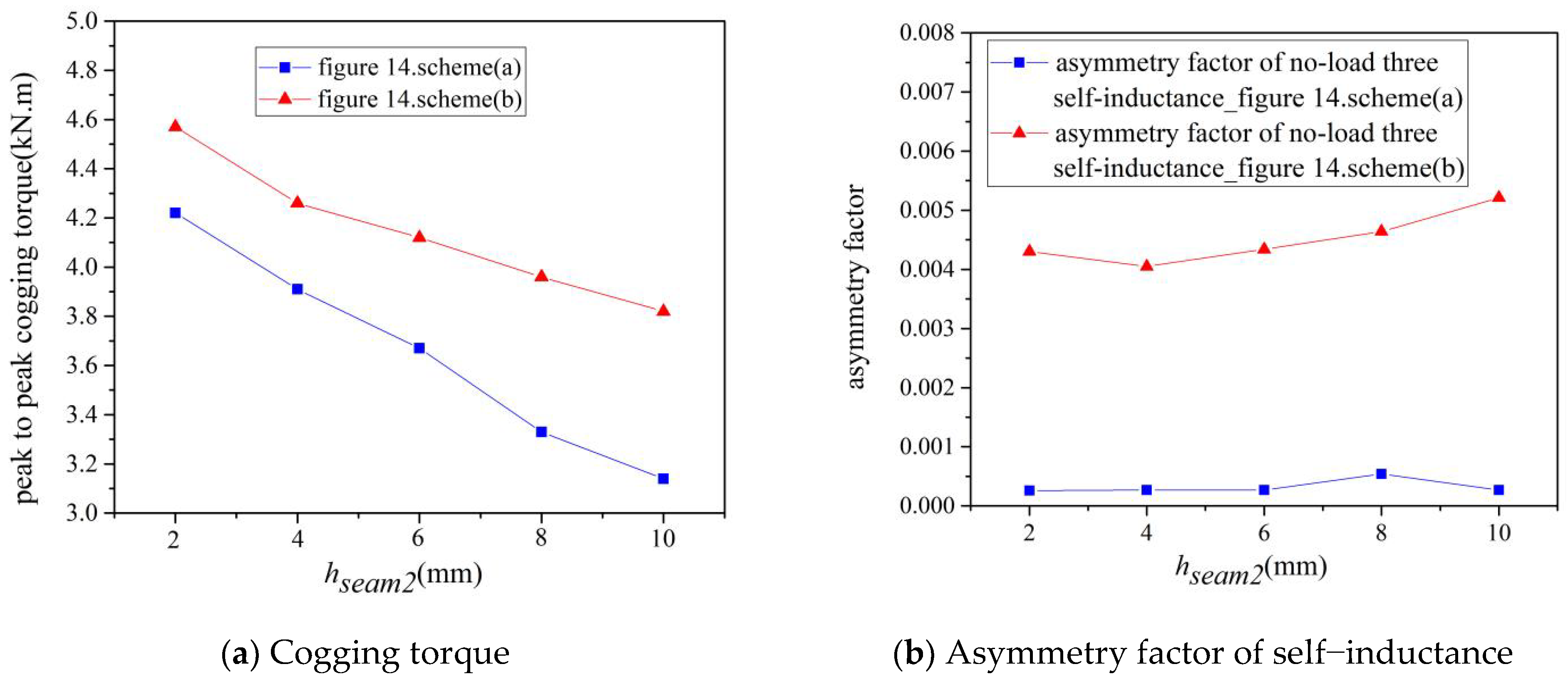
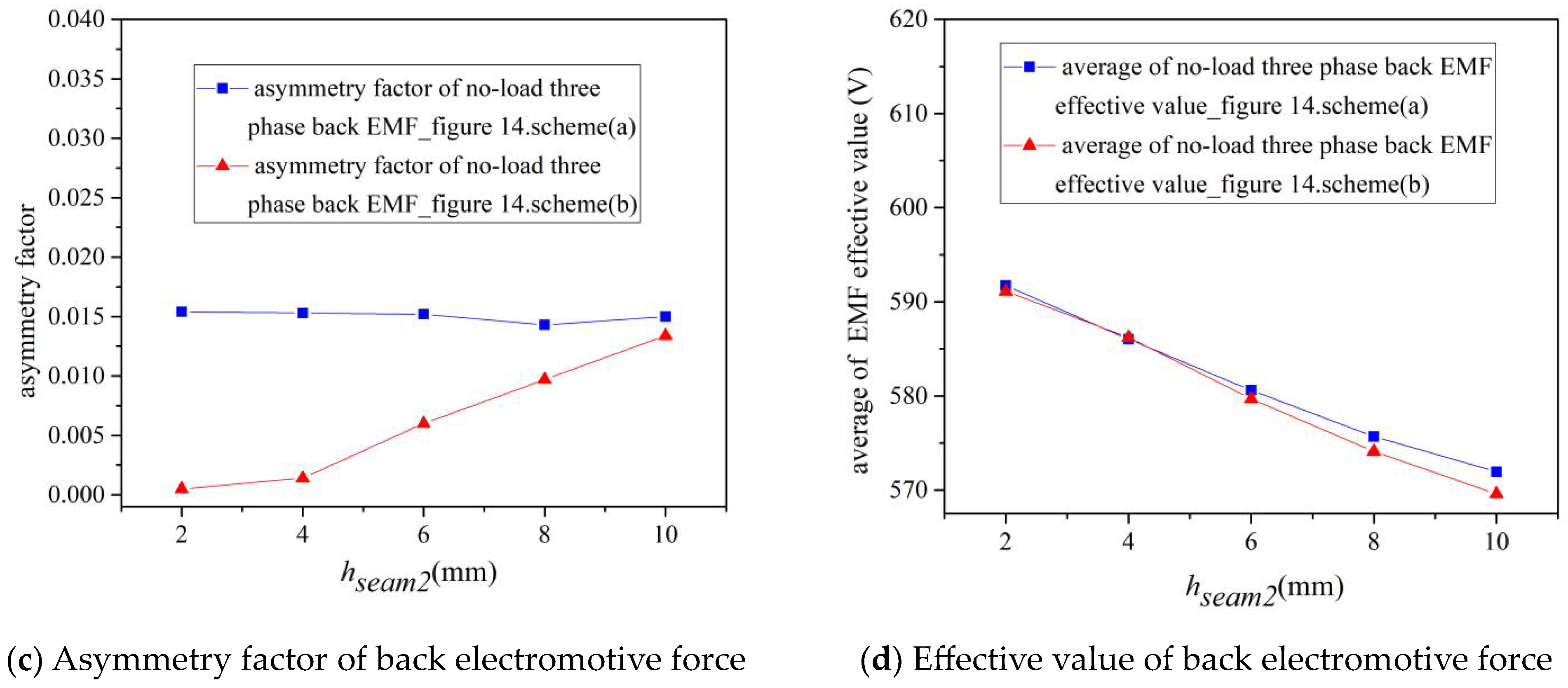
Figure 15. The corresponding no-load performance with double auxiliary seam scheme and different h_seam2 (b_seam = 5 mm).

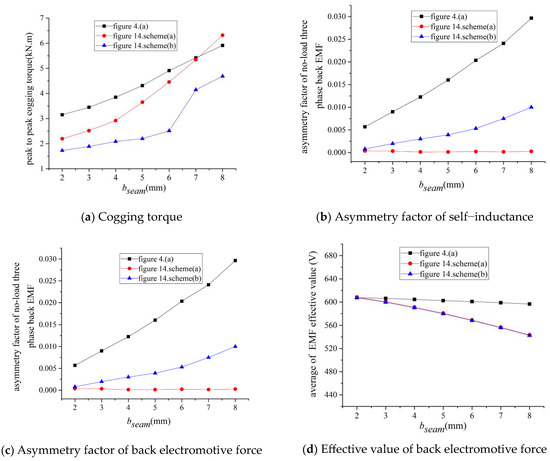
Figure 16. The corresponding no-load performance using double auxiliary seam scheme and different b_seam (h_seam2 = 6 mm).

(1)

Auxiliary seam 2 can effectively weaken no-load cogging torque (compare with Figure 12b,d); meanwhile, auxiliary seam 2 weakened the no-load back electromotive force value less when compared with the results in Figure 12a,c;

(2)

Increasing the height of auxiliary seam h_seam2 can weaken the no-load cogging torque, but increase the asymmetry factor of no-load back electromotive force and decrease the value of no-load back electromotive force;

(3)

When the seam width b_seam is increased (Figure 16), the cogging torque decreased to a smaller degree, and the asymmetry factor decreased, while no-load self-inductance and phase electromotive force remained nearly constant. Both schemes decreased the effective value of the back electromotive force to a greater degree, especially the Figure 14b scheme.

The disadvantage of the Figure 14a scheme is that auxiliary seam 1 produces difficulties on the core, especially if the seam width b_seam is too small. The disadvantage of the Figure 14b scheme is the effects on the asymmetry factor of no-load back electromotive force, especially if the seam width b_seam is too large. Therefore, when the seam width b_seam is larger, Figure 14a is the better scheme; when the seam width b_seam is smaller, Figure 14b is the better scheme.

5. Discussion

To model the impact of stator core seams on stator module-combined permanent magnet synchronous motors, a magnetic circuit model considering the stator core seam was deduced theoretically. The selection of electromagnetic parameters to weaken the impact of seams on the no-load performance is summarized as follows: (A) reduce the number and width of the seams; (B) reduce the number of parallel branches under the one stator sub-module; (C) adopt a scheme with fewer poles and more slots; and (D) when the number of stator teeth that continuously wind the same phase coil in one polar phase group is more than 3, place the seam on the same side as the phase coil tooth. The new stator core structures, which are shown in Figure 14, can significantly weaken the impact of seams on the no-load performance, while reducing the decreasing value of the no-load back electromotive force.

This study mainly focused on the seam on the stator core tooth; however, the influence of seams on the stator core yoke was not studied in this paper. The maximum modular number, arrangement of coils in the groove, and winding end wiring modes with different modular seam locations will be investigated in future studies.