Forecasting the Return of Carbon Price in the Chinese Market Based on an Improved Stacking Ensemble Algorithm

Abstract

Recently, carbon price forecasting has become critical for financial markets and environmental protection. Due to their dynamic, nonlinear, and high noise characteristics, predicting carbon prices is difficult. Machine learning forecasting often uses stacked ensemble algorithms. As a result, common stacking has many limitations when applied to time series data, as its cross-validation process disrupts the temporal sequentiality of the data. Using a double sliding window scheme, we proposed an improved stacking ensemble algorithm that avoided overfitting risks and maintained temporal sequentiality. We replaced cross-validation with walk-forward validation. Our empirical experiment involved the design of two dynamic forecasting frameworks utilizing the improved algorithm. This incorporated forecasting models from different domains as base learners. We used three popular machine learning models as the meta-model to integrate the predictions of each base learner, further narrowing the gap between the final predictions and the observations. The empirical part of this study used the return of carbon prices from the Shenzhen carbon market in China as the prediction target. This verified the enhanced accuracy of the modified stacking algorithm through the use of five statistical metrics and the model confidence set (MCS). Furthermore, we constructed a portfolio to examine the practical usefulness of the improved stacking algorithm. Empirical results showed that the improved stacking algorithm could significantly and robustly improve model prediction accuracy. Support vector machines (SVR) aggregated results better than the other two meta-models (Random forest and XGBoost) in the aggregation step. In different volatility states, the modified stacking algorithm performed differently. We also found that aggressive investment strategies can help investors achieve higher investment returns with carbon option assets.

1. Introduction

In recent years, with the aggravation of global warming, the topic of carbon dioxide emissions has attracted widespread attention. Governments worldwide have implemented numerous mitigation tools to address this challenge [1]. China, the second largest economy globally, produces the greatest carbon emissions, which means that it is of great significance to accurately predict the trend of its carbon return and grasp the fluctuation characteristics of its carbon markets [2]. More specifically, accurate expected carbon return provides a scientific basis for investors and regulators in the carbon market, reduces market risks, and effectively promotes the healthy development of the carbon financial market [3]. Therefore, accurate prediction of carbon returns takes priority in academic research and practical applications, from the perspectives of both guiding investment and environmental protection.

Multi-model integration is a technical approach to improve model performance by integrating the results of multiple models. With the great popularity of machine learning in the forecasting field, ensemble learning, as the most frequently used multi-model integration technique in machine learning applications, has attracted more and more attention. Bagging, boosting, and stacking are three classic ensemble learning algorithms, which are the foundation for a series of ensemble algorithms. The core idea of bagging and boosting is to change the way training data are fed to the model to construct a better model, while stacking uses cross-validation to collect and integrate the results of different models, which focuses more on using the diversity of different models in capturing sample information. However, the common stacking algorithm uses cross-validation, aiming to avoid overfitting, but, at the same time, this process also disrupts the temporal sequentiality of the samples. Therefore, some necessary improvements are required to adopt the stacking algorithm for time series prediction.

1.1. Literature Review

In order to clearly show the progress of the relevant work, the literature review is partitioned into some sub-sections. The first sub-section provides a detailed overview of the current work on carbon market prediction and its limitations. The second sub-section introduces the development of ensemble learning, especially the stacking algorithms. Finally, we summarize the feasibility of combining carbon price prediction with the stacking algorithm based on the literature review.

1.1.1. Progress in Carbon Market Prediction

The prediction of carbon return (in this study, carbon return refers to the log return of carbon prices, and the calculation follows Equation (29)) is complex and challenging work. Fan et al. [4] enumerated the chaotic characteristics of the carbon market and summarized that the carbon price is dynamically nonlinear, non-stationary, and abundantly noisy. Many scholars have made attempts in different ways to obtain more accurate predictions. The first is to elaborate the predicting model frameworks to boost the predicting performance based on historical data, which is regarded as the modeling paradigm in carbon market prediction studies. They must focus on fitting the dynamic characteristics of the carbon price, by itself, more accurately. According to our survey, the predictive models for carbon market prediction can be divided into three types of methods, which are traditional statistical or econometric methods, single-model machine learning methods, and hybrid models based on decomposition and integration.

Traditional statistical and econometric methods, such as ARIMA [5], GARCH-type models [6,7], and HAR-RV [8], are simple, effective, and lightweight, but can only reflect linear changes and have high requirements for data distribution. With the increasing popularity of artificial intelligence technology in recent years, many scholars have tried to apply machine learning models to estimate the variability of the carbon market. There is increasing evidence to show that machine learning methods outperform other models for nonlinear time series prediction [9]. Compared with the traditional model, the machine learning-based predictive models, such as Support Vector Machine (SVM) [10], Artificial Neural Network (ANN) [11], Convolutional Neural Network (CNN), and Long Short-Term Memory network (LSTM) [12], have greater forecasting accuracy when applied to carbon market prediction. The shortcomings of these models are embodied in the results being highly dependent on parameter tuning, which can be blamed for overfitting the nonlinearity of data. These shortcomings were recognized as inherent and difficult to overcome until the work of Ji et al. [12], which combined the machine learning method and traditional econometric method into the same forecasting framework to promote strengths and palliate weaknesses.

As for the hybrid model, most of them follow three steps, which are time series decomposition, separate forecast, and result aggregation. In different cases, the choice of method for the three steps varies, but they all aim to bring a competitive accuracy to carbon market prediction. Some advanced signal decomposition methods, such as EMD [13], VMD [14], and CEEMDAN [3], have been introduced to decompose the original time series into several independent series of simple patterns, and then different prediction methods are used to predict the decomposed sequences separately. Some researchers have contributed to finding a more suitable prediction model for the second step; for example, Qin et al. [15] innovatively adopted Local Polynomial Prediction (LPP) and Sun and Duan [16] used the improved Extreme Learning Machine (ELM). Thirdly, the final result is obtained by integrating the predicted results through different strategies [17,18]. According to current studies, the hybrid model produces the most stable and accurate predictions. However, using such a hybrid model has the potential risk of losing essential information or introducing overwhelming noise during the process of decomposition. As of yet, a perfect solution to solving the overfitting problem has not been proposed.

Additionally, Fan et al. [4] have pointed out that the carbon market is affected by the market mechanism, climate agreements, climate change, economic situation, and other factors, showing a trend of instability and fluctuation. Despite this, in most of the current carbon prediction literature, multi-variable prediction has received little attention, and the potential predictive power of related variables is ignored [19]. The introduction of multi-variable techniques into carbon return prediction has great potential and needs to be explored. Current multivariate prediction of the carbon market is mostly related to energy commodities [20,21]. A notable exception is Tan et al. [19], who comprehensively assessed the predictive power of 53 commodity and financial predictors related to European carbon futures return. These works consider carbon-related variables, but the prediction model they chose still has room for improvement.

According to previous studies [22,23], the relationship between the return and the volatility is close. At present, there is a considerable amount of literature focusing on the volatility of the carbon market. Benz and Trück [24] constructed a stochastic model using Markov switching and AR-GARCH models, as well as in-sample and out-of-sample predictive analysis. Their model captures features such as skewness and excessive kurtosis in carbon price volatility and, in particular, distinguishes different stages of volatility in returns. Byun and Cho [7] explored the ability of the GARCH-type model, implied volatility, and K-nearest neighbour method to predict carbon price volatility and proved that the GARCH-type model has the best effect, based on empirical results. Segnon et al. [6] reviewed the price volatility models, ranging from simple GARCH-type models to recently popular volatility models with long-term dependence and state transitions. For investors in the market, carbon returns can better reflect the profits generated by carbon assets. Thus, how to use volatility information to ferret out the potential carbon return is an unstudied but attractive direction.

1.1.2. Development of Ensemble Learning

The core idea of ensemble learning is to aggregate multiple base learners into a strong learner with superior generalization performance by combining strategies. Dasarathy and Sheela [25] proposed a composite classifier system consisting of two or more component classifiers of different types, which is widely recognized as the origin of ensemble learning. Schapire [26] proposed the boosting algorithm, which converts a weak learner into a strong learner. The stacking algorithm was proposed by Wolpert [27], in which the core idea is to aggregate the results of multiple base models through a complex level-2 model. Breiman [28] proposed the bagging algorithm, which aggregates the results of various models trained by subsamples. These three classic ensemble algorithms laid a solid foundation for the development of ensemble learning in the future.

In general, there are three main differences between ensemble algorithms: the process to feed training data, the ways to generate individual learners, and the combination strategies. These three aspects also represent the directions in which ensemble learning researchers can innovate and improve the algorithm. For the stacking algorithm, the main innovations of the previous studies concentrated on the selection and generation of base learners, the optimization of combination strategies, and the extension of applications.

Impressive work on base learners for stacking ensemble algorithms includes the following: Ding and Wu [29] used an artificial bee colony algorithm to construct the base learners, and their improved stacking ensemble algorithm performs well on multiple datasets, which proves the successful introduction of the bee colony algorithm. Bakurov et al. [30] chose four predictive models of different types as primary models to maintain the diversity in order to improve the generalization performance. Agarwal and Chowdary [31] proposed an improved stacking algorithm called A-stacking. They clustered the training set and then selected the results of the best base learner in each cluster as the input to the level-2 meta-learner.

Many researchers have introduced different combination strategies to optimize the common stacking algorithm. Varshini et al. [32] used generalized linear models, decision trees, Support Vector Machines, and Random Forests as meta-learners for the combination step. Lacy et al. [33] compared the differences between using linear and nonlinear models as the meta-learner. Menahem et al. [34] proposed an improved stacking model called “Troika”, and their main work was to add a third layer to further aggregate the results of the meta-learner. Pari et al. [35] added a middle layer to combine the results of base learners, and then used the combined results as input for the meta-learner.

Due to its excellent performance, stacking has been applied in various fields, including computer science [36], medicine [37], engineering [38], and finance [39]. However, the application of the stacking algorithm for predicting carbon market changes has not attracted much attention, even though it has a wide field of application with good prospects.

1.1.3. Literature Review Summary

Firstly, current research on carbon market forecasting is aimed at finding the best model to measure and predict the dynamic changes in the carbon market. However, as mentioned above, it is difficult to break through the inherent limitations of a specific forecast model, whether for machine learning models or statistical models. The hybrid model can, to some extent, take advantage of multiple models, but its potential risks mentioned above cannot be ignored. Stacking is a popular ensemble algorithm in machine learning, which mitigates overfitting while integrating multiple models. Compared to the hybrid model, the stacking algorithm has no decomposition step in the integration process, so there is no risk of information leakage or noise introduction. The idea of introducing stacking is a good attempt to overcome the drawbacks of hybrid models, but considering the problem of cross-validation failure on time series data prediction, some improvements are necessary.

Secondly, the current innovative work on the common stacking algorithm focuses on the generation of base learners and the improvement of combination strategies, but there are few improvements for cross-validation, which is necessary for applying stacking to time series data prediction and is of great significance for extending its application area.

Finally, the multiple variables related to carbon prices and hidden information in carbon price volatility have not received much attention in carbon market forecasting, which would help a lot in building more reliable and systematic forecasts.

1.2. Objectives and Contributions

In this paper, we focus on several core issues, which are reflected in the following three questions:

• How to modify the common stacking algorithm to maintain the sequentiality of the time series training data and at the same time improve the predictive power?;
• How to apply the improved stacking ensemble algorithm to carbon return prediction?;
• How to evaluate the improved algorithm’s practical power and provide investment guidance based on the results?

For the first question, we elaborately designed a double sliding window scheme to replace the cross-validation scheme of the common stacking algorithm. The improved stacking ensemble algorithm uses a sliding window scheme in both the base learner training phase and the meta-learner aggregation phase. This improvement ensures that the time series sample are sequential in order and, similar to cross-validation, the dataset is divided and fed to the base learner, thus effectively avoiding overfitting.

For the second question, we designed two forecasting frameworks based on the improved stacking algorithm for the empirical experiment. One is a homogeneous ensemble framework that combines model selection methods based on factor-augmented regression with Random Forest (RF), Support Vector Regression (SVR), and eXtreme gradient boosting (XGBoost) in machine learning. The other is a heterogeneous ensemble framework, which incorporates seven forecasting models as base learners: MMA (Mallows Model Average), LASSO regression, Ridge regression, E-net regression, Random Forest, Support Vector Regression, and XGBoost. The three popular aggregation models of machine learning are used as the meta-learners of the framework. With 34 carbon price-related variables as features and the return of carbon price as the target variable, we constructed six ensemble models based on the improved stacking algorithm.

For the final question, we introduced a new perspective to examine the performance of the improved algorithm by dividing the carbon return series into turmoil and tranquil states, which made the evaluation more practically valid. To implement this purpose, we adopted the SWARCH (Markov-switching GARCH) model to divide the carbon market into “high” and “low” volatility states, and the subsequent assessments were distinguished into two parts. Five statistical accuracy metrics and the model confidence set (MCS) were used to evaluate the performance of the improved algorithm in improving accuracy. In addition, we constructed a systematic portfolio experiment to verify the economic impact of the improved stacking algorithm on different volatility states. As far as we know, this study is the first work to apply the carbon return prediction model for practical usage and examine it under different volatile levels.

The main contributions of this paper can be briefly summarized as follows:

• This study innovatively improves the common stacking algorithm for better application to time series forecasting, and the results show that the modified algorithm can significantly improve the accuracy and increase the economic gain;
• The two ensemble forecasting frameworks we constructed are robust and accurate for predicting carbon price return;
• We novelly explored the predictability of carbon option returns using the stacking ensemble algorithm from a statistical and economic perspective, and the characteristics of carbon assets we obtained are very enlightening to relevant practitioners and academics;
• We linked the carbon return forecast with the volatility of the carbon market, opening up a new perspective to capture the variations of predictability of returns under different market conditions.

The rest of the paper is organized as follows. Section 2 includes the innovative work of this study and introduces the algorithm, the forecasting models involved, and the evaluation criteria. Section 3 provides a brief introduction and exploratory analysis of the data. Section 4 presents the empirical results, including accuracy metrics results, MCS analysis, and portfolio results. The research conclusions and future work are discussed in Section 5.

2. Methodology and Models

2.1. Improvement on the Stacking Ensemble Algorithm

2.1.1. The Common Stacking Algorithm

The core idea of the stacking ensemble algorithm is to divide the training process into two layers (two levels). First, multiple individual learners (called base learners) are trained in the first layer (level-1) using the original dataset. Next, the output of the base learners is used as input features for the learners in the second layer (level-2). The learner called meta-learner in the second layer is used for aggregation. The stacking algorithm uses a complex model to aggregate results instead of the simple strategy of averaging or voting used in most ensemble learning algorithms, thus further reducing the bias and variance and improving the generalizability. Figure 1 shows the workflow of the common stacking ensemble algorithm.

However, there is a high risk of overfitting if all the original datasets are directly used to train the base learner to generate the input for the meta-learner. Therefore, the common stacking algorithm includes a step of k-fold cross-validation.

The stacking algorithm with cross-validation first divides the original data into a training set D and a test set $D_{test}$, then generates the training set of the meta-learner on the training set D by k-fold ways, and, finally, evaluates the performance of the ensemble model on the test set $D_{test}$. Figure 2 shows the topological structure of the stacking algorithm with cross-validation.

To better understand the stacking algorithm with k-fold cross-validation, the process of the algorithm is next described in two specific steps. (The pseudocode of the algorithm is given in Algorithm 1). According to Algorithm 1, it is assumed that the base learners consist of N different models (${\eta }_1,{\eta }_2,\dots ,{\eta }_N$) and the meta-learner is $\eta$.

Training with k-fold cross-validation: Divide the original training set $D=\{(x_1,y_1),$ $(x_2,y_2),\dots ,(x_m,y_m)\}$ into k similarly sized and disjointed sets $D_1,D_2,\dots ,D_k$, and for any $u\ne v,D_u\cap D_v=Ø$. Let $D_j$ and ${\overline{D}}_j=D\setminus D_j$ denote the test set and training set of the j-th fold, respectively. Next, train the base learners ${\eta }_1,{\eta }_2,\dots ,{\eta }_N$ on ${\overline{D}}_j$ and use the trained base learners to make predictions on $D_j$. Assuming that a certain sample of the test set $D_j$ is $x_i$, a set of N predictions for $x_i$ is generated, denoted as $x_i^{\prime }=({\eta }_1^{\left(j\right)}\left(x_i\right),{\eta }_2^{\left(j\right)}\left(x_i\right),\dots ,{\eta }_N^{\left(j\right)}\left(x_i\right))$. When j gradually increases from 1 to k, (i.e., after k iterations) the predictions corresponding to all samples on the training set D are obtained, and—taking $x_i^{\prime }$ as the features’ input to the meta-learner and $y_i$ as the target variable—the new training set $D^{\prime }={\left\{(x_i^{\prime },y_i)\right\}}_{i=1}^m$ of the meta-learner is generated.

Prediction on test set: During training, as j increases from 1 to k, each base learner ${\eta }_t$ is trained k times using different ${\overline{D}}_j$, while each trained base learner makes predictions on $D_j$ and, at the same time, makes out-of-sample predictions for x on $D_{test}$, generating k predictions $({\eta }_n^{\left(1\right)}\left(x\right),{\eta }_n^{\left(2\right)}\left(x\right),\dots ,{\eta }_n^{\left(k\right)}\left(x\right))$. Then, take the average of these k results as the final prediction of the base learner ${\eta }_n$ for the sample x on the test set $D_{test}$:

$$\begin{array}{c}\hfill {\overline{\eta }}_n\left(\mathit{x}\right)=\frac{1}{k}\sum _{j=1}^k{\eta }_n^{\left(j\right)}\left(\mathit{x}\right)\end{array}$$

(1)

Therefore, for N base learners, N predictions are generated for sample x on $D_{test}$, and $\left({\overline{\eta }}_1\left(\mathit{x}\right),{\overline{\eta }}_2\left(\mathit{x}\right),\dots ,{\overline{\eta }}_N\left(\mathit{x}\right)\right)$ are used as N feature inputs to the trained meta-learner; thus, the final predictions of the algorithm for samples on $D_{test}$ are obtained.    

Algorithm 1: Common stacking algorithm with k-fold cross-validation

Input: Training set: $D=(x_1,y_1)(x_2,y_2),\dots ,(x_m,y_m)$, Test set $D_{test}=(x,y)$             Base learners: ${\eta }_1,{\eta }_2,\dots ,{\eta }_N$             Meta-learner: $\eta$ Output:$H\left(x\right)={\eta }^{{}^{\prime }}\left({\overline{\eta }}_1\left(\mathit{x}\right),{\overline{\eta }}_2\left(\mathit{x}\right),\dots ,{\overline{\eta }}_N\left(\mathit{x}\right)\right)$ 1: level-1: Train the base learners with k-fold cross-validation 2: for $j=1,\dots ,k$ do 3:      Divide D into $D_j$ and ${\overline{D}}_j=D\setminus D_j$ 4:      for $n=1,\dots ,N$ do 5:         Train base learner ${\eta }_n$ on ${\overline{D}}_j$$\Rightarrow {\eta }_n^{\left(j\right)}(D\setminus D_j)$ 6:      end for 7: end for 8: for $x_i\in D_j$ do 9:      Use the trained base learner to make prediction for $x_i$$\Rightarrow {\eta }_n^{\left(j\right)}\left(x_i\right)$ 10: end for 11: for $x\in D_{test}$ do 12:      Use the trained base learner to make prediction for x$\Rightarrow {\eta }_n^{\left(j\right)}\left(x\right)$ 13: end for 14: level-2: Train the meta-learner 15: for $i=1,2,\dots ,m$ do 16:      Generate $D^{\prime }={\left\{(x_i^{\prime },y_i)\right\}}_{i=1}^m$ with $x_i^{\prime }=({\eta }_1^{\left(j\right)}\left(x_i\right),{\eta }_2^{\left(j\right)}\left(x_i\right),\dots ,{\eta }_N^{\left(j\right)}\left(x_i\right))$ to train meta-learner η$\Rightarrow {\eta }^{\prime }=\eta \left(D^{\prime }\right)$ 17: end for 18: Make prediction on test set $D_{test}$ 19: for $x\in D_{test}$ do 20:      (1) Generate new features for x with ${\overline{\eta }}_t\left(\mathit{x}\right)=\frac{1}{k}{\sum }_{j=1}^k{\eta }_n^{\left(j\right)}\left(\mathit{x}\right)$ 21:      (2) Input $\left({\overline{\eta }}_1\left(\mathit{x}\right),{\overline{\eta }}_2\left(\mathit{x}\right),\dots ,{\overline{\eta }}_N\left(\mathit{x}\right)\right)$ into trained meta-model ${\eta }^{\prime }$ to obtain the             final prediction $\Rightarrow {\eta }^{\prime }\left({\overline{\eta }}_1\left(\mathit{x}\right),{\overline{\eta }}_2\left(\mathit{x}\right),\dots ,{\overline{\eta }}_N\left(\mathit{x}\right)\right)$ 22: end for

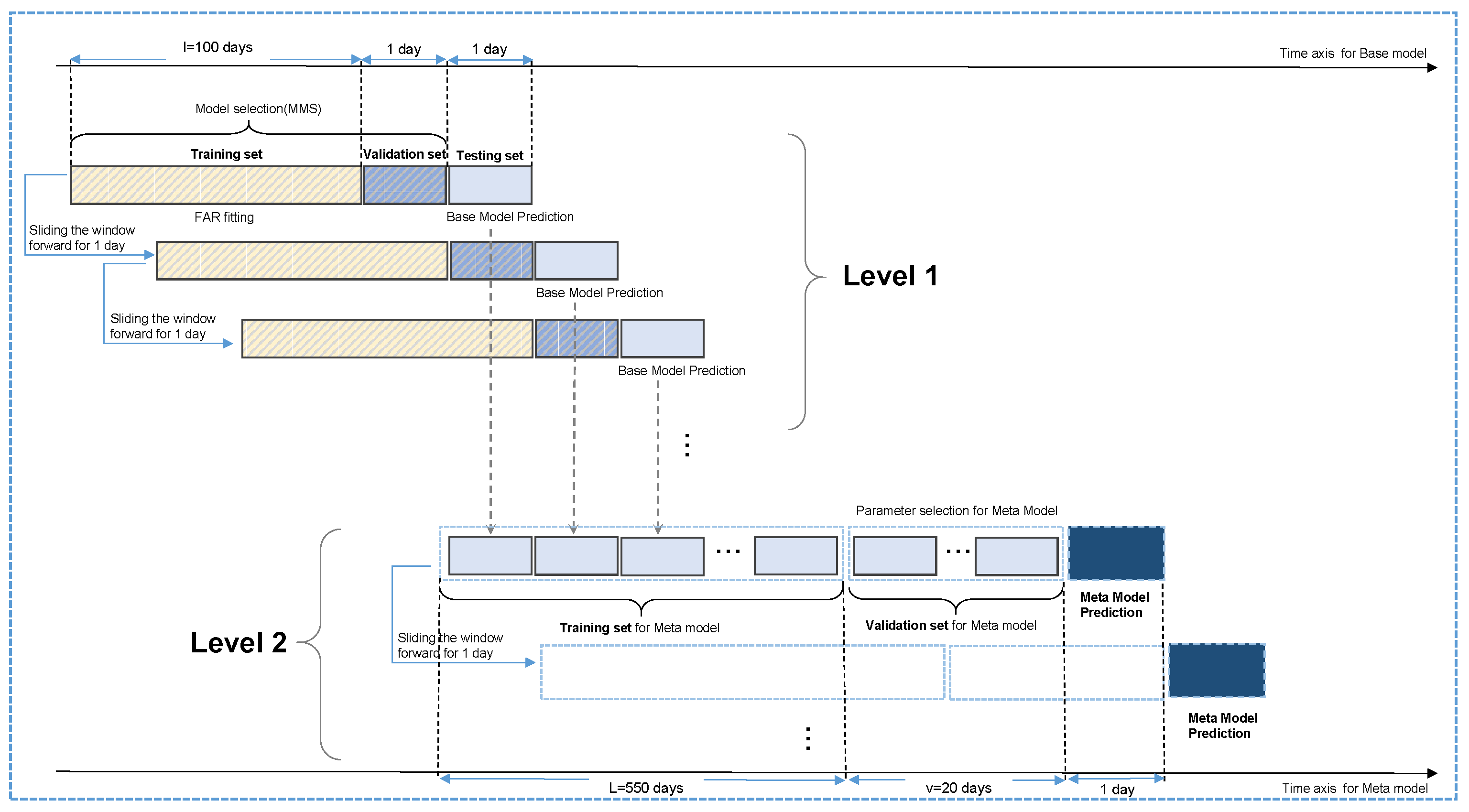
2.1.2. Our Improved Stacking Algorithm

Since the cross-validation process uses a k-fold scheme, the common stacking ensemble algorithm disrupts the temporal sequentiality of the time series data, which leads to information loss and the failure of many time series-related prediction models. To solve this problem, this study proposes a double sliding window scheme that maintains the advantages of the common stacking algorithm against overfitting while ensuring input is in chronological order.

We call the improved stacking algorithm the “stacking ensemble algorithm with walk-forward validation”. The improved algorithm still has two layers which are similar to the common algorithm, namely, the base learner training layer (level-1) and the meta-learner aggregation layer (level-2). Figure 3 shows the workflow of the improved stacking ensemble algorithm.

Training base learner with walk-forward validation: Assume that the whole original time series dataset is $D=\{(x_1,y_1),\dots ,(x_t,y_t),\dots ,(x_n,y_n)\}$, the base learner is composed of M different models (${\eta }_1,\dots ,{\eta }_m,\dots ,{\eta }_M$), and the meta-learner is $\eta$. First, determine the size of the sliding window in the first layer as l, and use the first training set $D_1=\{(x_1,y_1),\dots ,(x_l,y_l)\}\subset D$ to train M different base learners at the same time and obtain the next period prediction (${\widehat{y}}_{l+1}^{\left(m\right)}={\eta }_m\left(x_{l+1}\right)$) to form the prediction set $({\widehat{y}}_{l+1}^{\left(1\right)},{\widehat{y}}_{l+1}^{\left(2\right)},\dots ,{\widehat{y}}_{l+1}^{\left(M\right)})$. Next, slide the training set window forward one period in chronological order to obtain the second training set $D_2=\{(x_2,y_2),\dots ,(x_{l+1},y_{l+1})\}\subset D$, and then use the training set $D_2$ to train T base learners and obtain a set of $l+2$ period predictions ${\widehat{y}}_{l+2}$,..., carrying on until the entire dataset D is traversed. In this way, a set of predictions ${\{{\widehat{y}}_t=({\widehat{y}}_t^{\left(1\right)},{\widehat{y}}_t^{\left(2\right)},\dots ,{\widehat{y}}_t^{\left(M\right)})\}}_{t=l+1}^n$ of the base learner for $y_t$ are obtained, and the vector ${\widehat{y}}_t$ corresponds to the observation $y_t$ to form a new dataset, denoted as $Y=\{(y_t^{\prime },y_t):t=l+1,\dots ,n\}$, which is the input to the meta-learner in the next layer.

Training meta-model and making final prediction: Connect the new datasets Y collected in the first layer in chronological order so that the predictions of M base learners correspond to the M input features of the meta-learner. Next, determine the size of the training set window (L) and the size of the validation set window (v) in the second layer. Then, train the meta-learner on the first training set $Y_1=\{(y_{l+1}^{\prime },y_{l+1}),\dots ,(y_{l+L}^{\prime },y_{l+L})\}\subset Y$. After the training is complete, evaluate the accuracy of the meta-learner on the interval of length v (i.e., $t=l+L+1,\dots ,l+L+v$), and adjust the hyperparameters of the meta-learner according to the model accuracy for the validation set. Once the optimal parameters are obtained, the data from the validation set are then incorporated into the training set to retrain the meta-learner. At this time, with the optimal parameters, the meta-learner is retrained using $Y_1^{\prime }=\{(y_{l+1}^{\prime },y_{l+1}),\dots ,(y_{l+L+v}^{\prime },y_{l+L+v})\}$ (the retrained meta-model is denoted as ${\eta }^{\prime }$) and is used to make the prediction at the next period $t=l+L+v+1$ (${\widehat{y}}_{l+L+v+1}={\eta }^{\prime }\left(y_{l+L+v+1}^{\prime }\right)$), which is the final prediction of the algorithm. Next, slide the training set window forward one period in chronological order in the second layer and repeat the above "training-validation-retraining-prediction" process to obtain the final predictions at the next period. After the new dataset Y is traversed, all the final predictions of the algorithm are collected. Algorithm 2 shows the pseudo-code of the improved stacking ensemble algorithm.   

Algorithm 2: Improved stacking algorithm with walk-forward validation

Input: Dataset: $D=\{(x_1,y_1),\dots ,(x_t,y_t),\dots ,(x_n,y_n)\}$             Base learners: ${\eta }_1,\dots ,{\eta }_m,\dots ,{\eta }_M$             Meta-learner: $\eta$ Output: $H\left(x_t\right)={\eta }^{\prime }\left(y_t^{\prime }\right),t=l+L+v+1,\dots ,n$ 1: level-1: Training base learners with walk-forward validation 2: for $t=l+1,\dots ,n$ do 3:      for $i=1,\dots ,m,\dots ,M$ do 4:         ${\widehat{y}}_t^{\left(i\right)}={\eta }_i\left(x_t\right)$ 5:      end for 6: end for 7: level-2: Training meta-learner and make the final prediction 8: for $t=l+L+1,\dots ,n$ do 9:      Connect ${\widehat{y}}_t^{\left(i\right)}$ to obtain $y_t^{{}^{\prime }}=({\widehat{y}}_t^{\left(1\right)},{\widehat{y}}_t^{\left(2\right)},\dots ,{\widehat{y}}_t^{\left(M\right)})$ 10:      Train η using $Y_t^1=\{(y_{t-L}^{{}^{\prime }},y_{t-L}),\dots ,(y_{t-1}^{{}^{\prime }},y_{t-1})\}$ to obtain trained meta-learner            $\Rightarrow {\eta }^{{}^{\prime }}=\eta \left(Y_t^1\right)$ 11:      while $t\le \delta \le t+v-1$ do 12:         $H\left(x_{\delta }\right)={\eta }^{\prime }\left(y_{\delta }^{\prime }\right)$ 13:      end while 14:      Adjust the hyperparameters of ${\eta }^{\prime }$ according to $H\left(x_{\delta }\right)$ 15:      if Find the best hyperparameter of ${\eta }^{\prime }$ then 16:         Retrain ${\eta }^{\prime }$ using $Y_t^2=\{(y_{t-L}^{\prime },y_{t-L}),\dots ,(y_{t+v-1}^{\prime },y_{t+v-1})\}$ on $(t-L,t+v-1)$               to obtain retrained meta-learner $\Rightarrow {\eta }^{\prime }=\eta \left(Y_t^2\right)$ 17:      end if 18:      Predict $y_{t+v}$ using the retrained meta-learner ${\eta }^{\prime }$$\Rightarrow H\left(x_{t+v}\right)={\eta }^{\prime }\left(y_{t+v}^{\prime }\right)$ 19: end for 20: Isolating the test set on the timeline $D_{test}$ 21: $D_{test}=D\setminus D_{l+L+v}$

2.1.3. Forecasting Framework for Empirical Experiments

Ensemble learning is classified into homogeneous ensemble and heterogeneous ensemble according to the different settings of learners. If the base learners are all composed of the same type of models, then it is called a homogeneous ensemble, and if the base learners are composed of different types of models, then it is called a heterogeneous ensemble [40]. Stacking algorithms can be homogeneous or heterogeneous [41]. Therefore, we innovatively designed two ensemble frameworks called homogeneous ensemble framework and heterogeneous ensemble framework for predicting the return of carbon price based on the improved stacking ensemble algorithm, and the empirical experiment design in this study follows the setup of the ensemble framework.

The details of the homogeneous ensemble framework are discussed below: First, we chose factor-augmented regression as the level-1 base learner (called base model) (the type of all base models is factor-augmented regression, but their input independent variables are different (recall Section 2.2)) in the homogeneous ensemble framework, because it has been proven to have good performance in predicting carbon returns in the study of Tan et al. [19]. Moreover, we further expanded their work by elaborately adding Mallows model selection in the forecasting framework. The training and prediction of the base models were performed under a sliding window scheme. The window size was $l+1$, which means that the prediction on data t was obtained by training the model on data from time $t-l$ to $t-1$. After collecting the predictions of all the base models (a set of candidate models, recall Section 2.2), instead of directly using all of them as input to the meta-model, we added a model selection step to filter out the underperforming base models through the Mallows model selection criteria, and only the best one remained. Since the model selection criteria are based on the prediction at time $t=l+1$ and all fitted values of the previous period l, we used the prediction of the remaining best base model at time $l+2$ as the input to the meta-model to isolate the training set and the testing set, while the data at time t was regarded as the validation set. After the above steps are completed, the size-fixed window slides forward for one day in the time axis and repeats the same "train-predict" process to obtain the prediction at time $l+3$ …Finally, when the sliding window slides to the end of the original dataset, a set of predictions are collected from the best base model. However, there were still errors between these predictions and the observations.

The next part of the ensemble framework was to use machine learning models as the level-2 aggregation meta-learner (also called meta-model) to bridge the gap between the predictions of base models and the observations. The predictions collected from the level-1 layer were concatenated in chronological order and combined with real observations to form data to train the meta-model. In the level-2 layer, the size of the fixed window was set to $L+v$, where $L=550$ days was the sample size of the training set and v = 20 days was the sample size of the validation set. After training the meta-model on the training set, predicting the carbon return on the validation set and calculating the out-of-sample R-squared ($\mathbb{A}$ represented the validation set period, and $\overline{y}$ was the prediction of the historical average model (HA). The historical average model is widely used as the benchmark model—calculated by ${\overline{y}}_{t|t-1}=\frac{1}{t-1}{\displaystyle \sum _{T=1}^{t-1}}{y}_T$), as proposed by Campbell and Thompson [42]—to search for the best hyperparameter. The out-of-sample R-squared is of the following form:

$$\begin{array}{c}\hfill R_{os}^2=1-\frac{{\sum }_{t\in \mathbb{A}}{\left(y_t-{\widehat{y}}_{t\mid t-1}\right)}^2}{{\sum }_{t\in \mathbb{A}}{\left(y_t-{\overline{y}}_{t\mid t-1}\right)}^2}\end{array}$$

(2)

The best hyperparameter settings are those that enable the meta-model to obtain the highest $R_{os}^2$ on the validation set. Once the parameters of the meta-model were fixed, we re-trained the meta-model on the new dataset formed by the previous training set and validation set. The final prediction at time $t=l+L+v+1$ comes from the re-trained meta-model, and then the size-fixed window slides forward for one day in the time axis and the above process is repeated until all remaining final predictions are collected. The topological structure diagram of the homogeneous ensemble framework is visualized in Figure 4.

The benefit of homogeneity is to reduce the risk of additional noise from different models, but it neglects that different models have their own advantages in capturing information in different dimensions. As such, we fine-tuned the details of the homogeneous ensemble framework to construct the heterogeneous ensemble framework, to incorporate diverse models so as to break through the accuracy limits of a single model.

The core idea of the heterogeneous ensemble framework is still the improved stacking algorithm: First, we chose seven different prevailing predictive models (i.e., LASSO, Ridge regression, E-net, MMA, SVM, RF, and XGBoost (See Section 2.2 and the Appendix A for a description of these models)) of penalty regression, model average, and machine learning as level-1 base learners. These models were used to train all base learners at window size l = 100 days, and the predicted carbon return at time $t=l+1$ was obtained from the trained base models. To achieve a balance of prediction accuracy among all base models, no validation process was included to calibrate the base models specifically. This highlights the final difference between the base model and the ensemble model in accuracy caused by the improved stacking algorithm. Next in the process, the size-fixed window slides forward for one day in the time axis and the “train-predict” process is repeated, and predictions of the base models at time $t=l+2$ are obtained, and so on… Finally, when the sliding window slides to the end of the original dataset, seven sets of predictions are collected, each from a different base model, which serve as feature inputs for the meta-learner. In the level-2 layer of the heterogeneous ensemble framework, the partition of datasets, the determination of hyperparameters, the designed size of the window, and the sliding scheme are basically the same as those in the homogeneous ensemble framework. The specific details can be found in the heterogeneous ensemble framework in Figure 5.

The purpose of stacking is to improve the final prediction accuracy, not to find the optimal or best base model. We included a variety of different models so that the base predictions were versatile. It is possible that there is a better list of base models and meta-models, but this is not the core issue of this paper. Our choices for meta-model included SVM, RF, and XGBoost, which are popular machine learning models for performing integration tasks in industry and academic circles. As mentioned above, the core issue of this study is the benefits brought by the improved stacking algorithm, and we acknowledge that more refined tuning of parameters and model selection may lead to better final results.

2.2. Forecasting Models

Considering the large number of models involved in the ensemble algorithm, we mainly introduced factor-augmented regression combined with Mallows model selection theory (FAR+MMS) and Mallows model average (MMA) in this subsection. As for the rest of the prediction models (LASSO, Ridge regression, E-net, Support Vector Regression(SVR), Random Forest(RF), and eXtreme gradient boosting(XGBoost)), since they are widely used, brief introduction to each of them is provided in Appendix A. According to the experimental design in Section 2.1.3, we summarize the use of models as follows: for the homogeneous ensemble framework, FAR was chosen as the base model and filtered by MMS (FAR+MMS); for the heterogeneous ensemble framework, MMA, LASSO, Ridge regression, E-net, SVR, RF, and XGBoost were chosen as the base model. The selection of these base models was based on relevant research on carbon market prediction for better comparison (FAR [19], SVR [43,44], RF [45,46], XGBoost [47,48]). Meanwhile, SVR, RF, and XGBoost are also used as the meta-model for two ensemble frameworks to form six ensemble models (homo_svr,homo_rf,homo_xgb;hete_svr,hete_rf,hete_xgb). The hyperparameters of each model are listed in

Table A3. List of hyperparameters.

Model Name	Explanations	Hyperparameters
$\mathit{Base\; Model}$
FAR	Factor-augmented regression	$p_{max}=q_{max}=4,r=7$
FAR+MMS	Mallows Model Selection	-
MMA	Mallows Model Averaging	-
E-net	Elastic-net	$\alpha =0.168,l_{1}ratio=0.1$
lasso	Lasso regression	-
ridge	Ridge regression	-
svr	Support Vector Regression	kernel:rbf, gamma:auto, C:[0.5,1]
XGBoost	eXtreme Gradient Boosting	max_depth:3, learning_rate:0.04, subsample:0.3, colsample_bytree:0.8, reg_alpha:0.05, reg_lambda:0.05, n_estimators:50
rf	Random Forest	n_estimators:50, max_features:sqrt, max_depth:4, min_samples_split:2, min_samples_leaf:4
$\mathit{Ensemble\; Model}$
homo_rf	RF as meta-model for homogeneous ensemble	n_estimators:180, max_features:sqrt, max_depth:2, min_samples_split:2, min_samples_leaf:4
homo_svr	SVR as meta-model for homogeneous ensemble	c = 0.5
homo_xgb	XGBoost as meta-model for homogeneous ensemble	max_depth:2, learning_rate:0.1, subsample:0.95, colsample_bytree:0.7, reg_alpha:0.2, reg_lambda:0.05, n_estimators:50
hete_rf	RF as meta-model for heterogeneous ensemble	n_estimators:70, max_features:sqrt, max_depth:3, min_samples_split:2, min_samples_leaf:2
hete_svr	SVR as meta-model for heterogeneous ensemble	c = 8
hete_xgb	XGBoost as meta-model heterogeneous ensemble	max_depth:2, learning_rate:0.06, subsample:0.6, colsample_bytree:0.6, reg_alpha:0.2, reg_lambda:0.06, n_estimators:80

of Appendix B.

Factor-augmented regression (FAR): In the following discussion of factor-augmented regression, we follow the study of Kim and Swanson [49] and Cheng and Hansen [50]. Factor-augmented regression extracts the common factors through the dimension reduction techniques of ‘factor decomposition’ and builds a concise and effective model with rich information.

Let $X_{it}$ be the observation for $t=1,\dots ,T$ and $i=1,\dots ,N$, and $y_{t+h}$ be the predicted target variables. We begin with the following factor model:

$$\begin{array}{c}\hfill X_{it}={\lambda }_i^{\prime }{F}_t+e_{it},\end{array}$$

(3)

where $F_t$ is a $1\times r$ vector of common factors, ${\lambda }_i$ is a $1\times r$ vector called the factor loading, and $e_{it}$ is the idiosyncratic component of $X_{it}$. Let X be a $T\times N$ dimensional matrix of observations and $F=(F_1,\dots ,F_T)$ be a $T\times r$ dimensional matrix of common factors; then, Equation (3) can be converted to matrix notation:

$$\begin{array}{c}\hfill X=F{\mathsf{\Lambda }}^{\prime }+e,\end{array}$$

(4)

where $\mathsf{\Lambda }=({\lambda }_1,\dots ,{\lambda }_N)$ is $N\times r$, and e is a $T\times N$ error matrix. Once F is extracted, we construct the following factor-augmented regression model:

$$\begin{array}{c}\hfill y_{t+h}={\alpha }_0+\alpha \left(L\right)y_t+\beta {\left(L\right)}^{\prime }{F}_t+{ϵ}_{t+h},\end{array}$$

(5)

where $h\ge 1$ is the forecast horizon, $\alpha \left(L\right)$ and $\beta \left(L\right)$ are lag polynomials of order p and q, respectively, for some $0\le p\le p_{max}$ and $0\le q\le q_{max}$. $p_{max}$ and $q_{max}$ are, respectively, the maximum lag of $y_t$ and $F_t$.

For the empirical experiment, this paper adopts the approximate model structure proposed by Cheng and Hansen [50], which can be written as follows:

$$\begin{array}{c}\hfill y_{t+h}=z_t^{\prime }b+{ϵ}_{t+h},\end{array}$$

(6)

where $z_t=(1,y_t,\dots ,y_{t-p_{max}},F_t^{\prime },\dots ,F_{t-q_{max}}^{\prime })$, and b includes all coefficients from Equation (5).

Sequentially nested subsets of $z_t$ are taken in order from smallest to largest in size to construct M candidate models. M approximating models are considered, indexed by $m=1,\dots ,M$, where each approximating model m specifies a subset $z_t\left(m\right)$ of the regressors $z_t$. Thus, the first model sets $z_t\left(1\right)=1$, the second model sets $z_t\left(2\right)=(1,y_t)$, etc., expanding to a total of $M=(1+p_{max})(1+\tilde{r})$ sequentially nested models, where $\tilde{r}$ is the number of common factors retained. The approximate form of the mth candidate model is thus written as follows:

$$\begin{array}{c}\hfill y_{t+h}=z_t\left(m\right)b\left(m\right)+{ϵ}_{t+h}.\end{array}$$

(7)

Let ${\tilde{z}}_t\left(m\right)$ denote $z_t\left(m\right)$, the factors $F_t$ of which are replaced by their estimates ${\tilde{F}}_t$, leading to $\tilde{Z}\left(m\right)={({\tilde{z}}_1\left(m\right),\dots {\tilde{z}}_{T-h}\left(m\right))}^{\prime }$. Consequently, the least squares estimate of $b\left(m\right)$ is $\widehat{b}\left(m\right)={\left(\tilde{Z}{\left(m\right)}^{\prime }\tilde{Z}\left(m\right)\right)}^{-1}\tilde{Z}{\left(m\right)}^{\prime }y$ with residual ${\widehat{ϵ}}_{t+h}\left(m\right)=y_{t+h}-{\tilde{z}}_t{\left(m\right)}^{\prime }\widehat{b}\left(m\right)$. The prediction of the mth candidate model at time T is expressed as follows:

$$\begin{array}{c}\hfill {\widehat{y}}_{T+h|T}\left(m\right)={\tilde{z}}_T{\left(m\right)}^{\prime }\widehat{b}\left(m\right).\end{array}$$

(8)

Mallows Model Selection (MMS): When factor-augmented regression is used as the base model of the homogeneous ensemble algorithm, we need to select the best model from M candidate models. We refer to the model selection criteria of factor-augmented regression derived by Cheng and Hansen [50] under the Mallows [51] criterion.

The Mallows criterion is an unbiased estimate of the expected squared fit under the assumption of independent observations and homoskedastic regression. We directly present the criteria for model selection below:

$$\begin{array}{c}\hfill S_T\left(m\right)=\frac{1}{T}\sum _{t=1}^T{\widehat{ϵ}}_t{\left(m\right)}^2+\frac{2{\widehat{\sigma }}_T^2}{T}k\left(m\right),\end{array}$$

(9)

where $k\left(m\right)=dim\left(z_t\left(m\right)\right)$ denotes the number of regressors in the mth model, and ${\widehat{\sigma }}_T^2=(T-K{\left(M\right)}^{-1}{\sum }_{t=1}^T){\widehat{ϵ}}_t{\left(M\right)}^2$ denotes the preliminary estimate of ${\sigma }^2$.

The best model selected under the Mallows criterion is the model $\widehat{m}$ that satisfies equation $\widehat{m}=argmi{n}_{1\le m\le M}{S}_T\left(m\right)$. To sum up, there are three steps: estimating the parameters of each model m, calculating the $S_T\left(m\right)$ for each model, and selecting the prediction of the model with the minimum $S_T\left(m\right)$.

Mallows Model Averaging (MMA): Cheng and Hansen [50] obtain edthe model average form suitable for factor-augmented regression by minimizing the Mallows criteria [51], which was further work after the MMA (Mallows Model Averaging) proposed by Hansen [52]. In this paper, we follow Cheng and Hansen [50] to use factor-augmented regressions with nested subsets of regressors as candidate models, and the final forecast combinations of candidate models are as follows:

$$\begin{array}{c}\hfill {\widehat{y}}_{T+h\mid T}\left(w\right)=\sum _{m=1}^{M}w\left(m\right){\widehat{y}}_{T+h\mid T}\left(m\right)\end{array}$$

(10)

where ${\widehat{y}}_{T+h\mid T}\left(m\right)$ is the prediction of the mth candidate model, and $w\left(m\right)$ represents its weight, which minimizes the following objective function:

$$\begin{array}{c}\hfill \underset{w}{\min }\frac{1}{T}\sum _{t=1}^T{\left(\sum _{m=1}^{M}w\left(m\right){\widehat{\epsilon }}_t\left(m\right)\right)}^2+\frac{2{\widehat{\sigma }}_T^2}{T}\sum _{m=1}^{M}w\left(m\right)k\left(m\right),\end{array}$$

(11)

where $k\left(m\right)=dim\left(z_t\left(m\right)\right)$ denotes the number of regressors in the mth model, and ${\widehat{\sigma }}_T^2=(T-K{\left(M\right)}^{-1}{\sum }_{t=1}^T){\widehat{ϵ}}_t{\left(M\right)}^2$ denotes the preliminary estimate of ${\sigma }^2$.

2.3. Statistical and Economic Evaluation

2.3.1. Judgment on Different Volatile Intervals

Hamilton and Susmel [53] incorporated Markov switching (MS) and ARCH models to construct a new model named SWARCH (switching ARCH), which aimed to distinguish the volatility state between the tranquil and turmoil periods. The SWARCH model has been proven to be robust in differentiating the volatility states of the time series dynamics in subsequent empirical studies. Liu and Lee [54] adopted the SWARCH model to reveal the pattern of regime-switching in the INE crude oil futures market and explore how external shock turns the crude oil futures market from stable to volatile. Wang et al. [55] classified stock market crises based on SWARCH filtering probabilities of the high volatility regime. Shi et al. [56] used the SWARCH model to measure the significance of firm-specific news sentiment in quantifying intraday volatility persistence in the calm (low-volatility) state and the turbulent (high-volatility) state. We needed to figure out whether the proposed ensemble algorithm could effectively work in different volatility state episodes, and the typical AR(p)–SWARCH(K,q) model was the optimal choice to divide the carbon return series into different volatility states:

$$\begin{array}{cc}\hfill y_t& =u+{\theta }_1{y}_{t-1}+{\theta }_2{y}_{t-2}+\dots +{\theta }_p{y}_{t-p}+{ϵ}_t,{ϵ}_t|{\mathcal{I}}_{t-1}\sim N(0,h_t);\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \frac{h_t^2}{{\gamma }_{s_t}}& ={\alpha }_0+{\alpha }_1\frac{{ϵ}_{t-1}^2}{{\gamma }_{s_{t-1}}}+\dots +{\alpha }_q\frac{{ϵ}_{t-q}^2}{{\gamma }_{s_{t-q}}},s_t\in \{1,\dots ,K\},\hfill \end{array}$$

(13)

where u is a constant; ${ϵ}_t$ is the residual of a normal distribution with zero mean and variance of $h_t$; ${\theta }_1,{\theta }_2,\dots ,{\theta }_p$ and ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_q$ are parameters to be estimated; and $\gamma$ denotes a set of scaling parameters related to the latent state variable $s_t$, which is a Markov chain with K regimes. In our study, we uniformly set the lag p and q to be 1, and the input of the SWARCH model was the actual observations of carbon return.

In this study, R package MSGARCH [57] is applied to calculate the filtering probability according to the following formulation:

$$\begin{array}{c}\hfill P(s_t=j|Y_t;{\mathit{\theta }}_t),j=1,\dots ,K\end{array}$$

(14)

where $Y_t$ are historic observations of price log return at time t, and ${\mathit{\theta }}_t$ denotes the parameter vector. In the experiment, we set K to 3 to increase the differentiation between high and low volatility states; thus, $s_t=3$ means that the carbon market is in a state of high volatility, and the rest of $s_t$ represents a low volatility state. The criteria are written as follows:

$$\begin{array}{c}\hfill C_t=\left\{\begin{array}{cc}1,\hfill & P(s_t=3|Y_t;{\mathit{\theta }}_t)\ge 0.5,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(15)

2.3.2. Prediction Accuracy Metrics

In order to evaluate the performance of the ensemble algorithm in prediction accuracy, we explored five statistical metrics from different perspectives: root mean square error (RMSE), symmetric mean absolute percentage error (SMAPE), mean absolute error (MAE), Theil U statistic 1 (U1), and out-of-sample $R^2$ ($R_{os}^2$) [42]. RMSE reflects the deviation between the prediction and the true value. SMAPE measures the relative error in the sense of ratio. MAE intuitively represents the absolute value of error. U1 considers both the prediction and the observation as the measurement basis, and it evaluates the prediction power of the model. Lastly, $R_{os}^2$ evaluates the superiority of the model by comparing it with the historical average benchmark model (HA).

Table 1. Statistical evaluation indexes.

Evaluation Index	Definition	Equation
RMSE	Root mean square error	$\sqrt{\frac{1}{n}{\sum }_{t=1}^n{\left({\widehat{y}}_t-y_t\right)}^2}$
SMAPE	Symmetric mean absolute percentage error	$\frac{1}{n}{\sum }_{t=1}^n\frac{|{\widehat{y}}_t-y_t|}{\left(\right|{\widehat{y}}_t+y_t\left|\right)/2}$
MAE	Mean absolute error	$\frac{1}{n}{\sum }_{t=1}^n\left|{\widehat{y}}_t-y_t\right|$
U1	Theil U statistic 1	$\sqrt{\frac{1}{n}{\sum }_{t=1}^n{\left({\widehat{y}}_t-y_t\right)}^2}/\left(\sqrt{\frac{1}{n}{\sum }_{t=1}^n{y}_t^2}+\sqrt{\frac{1}{n}{\sum }_{t=1}^n{\widehat{y}}_t^2}\right)$
${\mathrm{R}}_{\mathrm{os}}^2$	Out-of-sample ${\mathrm{R}}^2$ statistic	$1-\frac{{\sum }_{t=1}^n{\left(y_t-{\widehat{y}}_{t|t-1}\right)}^2}{{\sum }_{t=1}^n{\left(y_t-{\overline{y}}_{t|t-1}\right)}^2}$

lists the details of the above evaluation metrics. For the four measures RMSE, SMAPE, MAE, and U1, the smaller the value, the higher the prediction accuracy of the model. $R_{os}^2$ represents the proportion of improvement in forecasting accuracy of the measured model compared to the historical average benchmark model. Campbell and Thompson [42] indicated that even very small positive $R_{os}^2$ can signal superior predictive accuracy relative to the benchmark.

2.3.3. Model Confidence Set

Using only the statistical metrics in Table 1 as the criteria for evaluating the model accuracy, the results are easily influenced by the sample, and such an evaluation is not robust. A small number of singularities can significantly affect the computation of the model loss function, leading to an abnormal increase in the loss value and, ultimately, invalidating the evaluation of the model accuracy. The model confidence set (MCS) proposed by Hansen et al. [58] is designed to overcome the above problem, so this paper uses the MCS to verify the usefulness of the improved stacking algorithm in improving the accuracy of the model from the perspective of hypothesis testing.

The process of the MCS is as follows: Firstly, suppose there are $m_0$ prediction models, denoted as ${\mathcal{M}}_0=\{1,2,3,\dots ,m_0\}$, and there are M real observations $y_t$ on the test set. Then, each prediction model in ${\mathcal{M}}_0$ generates M corresponding predictions ${\widehat{y}}_t(t=1,2,\dots ,M)$. For each ${\widehat{y}}_t$, the corresponding predicted loss value $L_{t,j}$, $j=1,2,\dots ,m_0$ is calculated according to the chosen loss function. Next, the difference between the loss values of the two prediction models $u,v(u,v\in {\mathcal{M}}_0)$ in ${\mathcal{M}}_0$ is calculated, which is denoted as $d_{t,uv}$ and is computed as follows:

$$\begin{array}{c}\hfill d_{t,uv}=L_{t,u}-L_{t,v}.\end{array}$$

(16)

Secondly, define the set of best models ${\mathcal{M}}^{*}$:

$$\begin{array}{c}\hfill {\mathcal{M}}^{*}\equiv \{u\in {\mathcal{M}}_0:E\left(d_{t,uv}\right)\le 0,\mathrm{for}\mathrm{all}v\in {\mathcal{M}}_0\}.\end{array}$$

(17)

The models with poor accuracy in the model set ${\mathcal{M}}_0$ are filtered out by continuous significance tests, and the model with the best prediction accuracy is left at the end. In each significance test, the null hypothesis states that the two models have the same prediction accuracy, expressed as follows:

$$\begin{array}{c}\hfill H_{0,\mathcal{M}}:E\left(d_{t,uv}\right)=0,\mathrm{for}\mathrm{all}u,v\in \mathcal{M}\subset {\mathcal{M}}_0.\end{array}$$

(18)

The equivalence test is used to test the null hypothesis, and the elimination rule is used to filter out the models that reject the null hypothesis. The specific process is divided into the following three steps: (1) Let $\mathcal{M}={\mathcal{M}}_0$; (2) Test the null hypothesis at the significance level $\alpha$ using the equivalence test; (3) If the null hypothesis is not rejected, consider ${\mathcal{M}}_{1-\alpha }^{*}=\mathcal{M}$; otherwise, the model for which the null hypothesis is rejected is filtered out from $\mathcal{M}$. The testing and filtering continue until the null hypothesis is no longer rejected, and the final retained models in ${\mathcal{M}}_{1-\alpha }^{*}$ are the models with the best accuracy at the confidence level of $1-\alpha$. If the p value of the prediction model is greater than the given significance level $\alpha$, it belongs to the highest accuracy model set, and a larger p value represents higher prediction accuracy.

In this study, we chose three loss functions for the MCS: Mean Squared Error (MSE), Mean Absolute Error (MAE), and Huber loss (In this study, we set $\delta =1$), which are calculated as follows:

$$\begin{array}{ll}\hfill & \mathrm{MSE}:\frac{1}{n}\sum _{t=1}^n{\left(y_t-{\widehat{y}}_t\right)}^2,\hfill \end{array}$$

(19)

$$\begin{array}{ll}\hfill & \mathrm{MAE}:\frac{1}{n}\sum _{t=1}^n\left|y_t-{\widehat{y}}_t\right|,\hfill \end{array}$$

(20)

$$\begin{array}{ll}\hfill & \mathrm{Huber}\mathrm{Loss}:\left\{\begin{array}{c}\frac{1}{2}{(y_t-{\widehat{y}}_t)}^2,|y_t-{\widehat{y}}_t|\le \delta \hfill \\ \delta |y_t-{\widehat{y}}_t|-\frac{1}{2}{\delta }^2,|y_t-{\widehat{y}}_t|>\delta \hfill \end{array}\right.\hfill \end{array}$$

(21)

The test statistic is as follows:

$$\begin{array}{cc}\hfill & T_R=\underset{u,v\in \mathcal{M}}{max}\frac{\left|{\overline{d}}_{uv}\right|}{\sqrt{\widehat{var}\left({\overline{d}}_{uv}\right)}},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & T_{MAX}=\underset{u\in \mathcal{M}}{max}\frac{{\overline{d}}_{u.}}{\sqrt{\widehat{var}\left({\overline{d}}_u\right)}}.\hfill \end{array}$$

(23)

where ${\overline{d}}_{uv}=\frac{1}{M}{\displaystyle \sum _{t=1}^M}{d}_{t,uv}$, and ${\overline{d}}_{u.}=\frac{1}{m_0}{\displaystyle \sum _{u\in \mathcal{M}}}{\overline{d}}_{uv}$ The null hypothesis is rejected when the statistic is greater than the critical value. Since the distributions of $T_R$ and $T_{MAX}$ are very complex, this study uses block bootstrap to obtain the p-value of the test (we set the ’block size’ parameter of bootstrap to 2 and the number of simulations to 10,000, referring to the study of Hansen et al. [58] for the specific procedure).

2.3.4. Investment Portfolio

Additionally, we measured the gains generated by the developed ensemble framework using portfolio strategy from the perspective of economic value. More specifically, following Campbell and Thompson [42], Rapach et al. [59] and Zhao and Cheng [60], we calculated realized utility gains for a mean-variance investor who allocates his portfolio daily between carbon emission option and risk-free bills with weights ${\omega }_t$ and $1-{\omega }_t$, based on the prediction of carbon return. At time t, the investor determines the amount of funds allocated to two assets in the next period ($t+1$) according to $\omega$. The weight ${\omega }_t$ is determined by the following formula:

$$\begin{array}{c}\hfill {\omega }_t=\frac{1}{\gamma }·\frac{{\widehat{y}}_{t+1}}{{\widehat{\sigma }}_{t+1}^2}\end{array}$$

(24)

where ${\widehat{\sigma }}_{t+1}^2$ is the sample variance of carbon return with a rolling window of 50 days (Zhao and Cheng [60] used monthly data in their empirical experiment and estimated ${\widehat{\sigma }}_{t+1}^2$ as the sample variance of quarterly returns within a fixed ten-year rolling-window; referring to this, we decided to set the window size to 50 for the daily data used in the portfolio), ${\widehat{y}}_{t+1}$ is the prediction of carbon return at time $t+1$, and $\gamma$ is a relative risk aversion parameter which describes the trading style of the investor, to some extent—the lower the value of $\gamma$, the more aggressive the investors. ${\omega }_t$ is constrained between $-1.5$ and $1.5$ (if ${\omega }_t\le -1.5$, ${\omega }_t$ is set to $-1.5$, and if ${\omega }_t\ge 1.5$, then ${\omega }_t$ is set to $1.5$) (According to Campbell and Thompson [42] and Rapach et al. [59], ${\omega }_t$ is set between 0 and 1.5 to preclude short sales and prevent more than 50% leverage. There are also some studies that add the option of short selling [61]. Considering the actual trading situation of carbon options, we chose the latter range of ${\omega }_t$). We explored the average utility level of the ensemble models under fixed threshold bounds of ${\omega }_t$ with different $\gamma$. The realized return is calculated as shown:

$$\begin{array}{c}\hfill R_{t+1}={\omega }_t{y}_{t+1}+(1-{\omega }_t)r_{t+1},\end{array}$$

(25)

in which $y_{t+1}$ is the observation of carbon return, and $r_{t+1}$ is a risk-free rate. (We chose 1-year China government bond yield as the risk-free rate.) Then, we calculated the universally acknowledged certainty equivalent return (CER):

$$\begin{array}{c}\hfill CER={\widehat{\mu }}_R-\frac{1}{2}\gamma {\widehat{\sigma }}_R^2\end{array}$$

(26)

where ${\widehat{\mu }}_R$ and ${\widehat{\sigma }}_R^2$ are the sample mean and variance of series $R_t$. The difference between $CER$ calculated by the forecast model and the historical average model (HA) is called utility gain, which is multiplied by 400 as an annualized percentage return. As such, the following metrics are obtained:

$$\begin{array}{c}\hfill U{G}^{model}=400(CE{R}^{model}-CE{R}^{HA}).\end{array}$$

(27)

Utility gain ($U{G}^{model}$) can be interpreted as the portfolio management fees that investors are willing to pay to obtain the additional information provided by the forecasting ‘$model$’ compared to using only a historical average model (HA).

We employed another popular criterion, called Sharpe ratio (SR), to evaluate the performance of the portfolio above. It is constructed based on the portfolio excess returns:

$$\begin{array}{c}\hfill SR=\frac{{\mu }_p}{{\sigma }_p}\end{array}$$

(28)

where ${\mu }_p$ and ${\sigma }_p$ are, respectively, the means and standard deviations of portfolio excess returns. The Sharpe ratio is the economic indicator that evaluates the portfolio returns against its corresponding volatile risks.

3. Data Description

In this section, we provide an introduction to our data, including composition and source of variables, partition time node of dataset, and data cleaning approach. We collected 895 daily settlement prices of carbon emission options in the carbon emission trading markets of Shenzhen, China, from 27 March 2018 to 6 July 2022. The last 224 samples of the dataset from 10 May 2021 to 6 July 2022 were used as test sets. The main reason for choosing Shenzhen’s carbon market is that it is the first carbon market in China, with a large scale, more complete data, and a strong influence on carbon prices in other markets. We employed the log return (computed as Equation (29)) of the carbon price (SZA) as the target for prediction, which is widely used as the continuously compounded return of carbon.

In terms of the predictors, we followed Tan et al. [19] to consider three categories of variables:

• Commodity variables, including energy and non-energy commodity futures, based on settlement prices and a price index from the Chinese market. For energy commodities, the selections were as follows: (1) China Liquefied Natural Gas Price Index (LNG); (2) thermal coal (SPcoa); (3) INE crude oil (SPcru). For non-energy commodities, the variables were subdivided into non-ferrous metals and agricultural products. Non-ferrous metals were (1) aluminum (SPalu); (2) zinc (SPzin); (3) lead (SPlea); (4) nickel (SPnic); (5) tin (SPtin); (6) silver (SPsil); (7) gold (SPgol); and (8) cathode copper (SPcop). Agricultural products were (1) yellow corn (SPcor); (2) egg (SPegg); (3) cotton (SPcot); and (4) high-quality strong gluten wheat (SPwhe) (except for LNG, other variables were option settlement price (active contract));
• Stock and bond market variables, including some composite indexes and rate variables. For the stock market, the predictors were (1) SSE: Average P/E ratio (SSEPE); (2) SSE Composite Index (SSECI); (3) CSI 300 Index (CSI300); (4) SSE 180 Index (SSE180); (5) SZSE Composite Index (SZSECI); (6) CSI 100 Index (CSI100); and (7) CSI 500 Index (CSI500). For the bond market, the predictors were (1) SSE Government Bond (SSEGBI); (2) SSE Corporate Bond Index (SSECBI); (3) SSE Enterprise Bond Index (SSEEBI); (4) CCDC government bond yield: 3-months (Gb3M); (5) CCDC government bond yield: 10-years (Gb10Y); (6) CCDC corporate bond yield (AAA): 3-months (Cb3M); (7) CCDC corporate bond yield (AAA): 10-years (Cb10M); (8) CCDC coal industry bond yield (AAA): 3-months (coalb3M); and (9) CCDC coal industry bond yield (AAA): 5-years (coalb5Y);
• Economic and industry composite variables, including (1) Financial Conditions Index (FCI); (2) China Securities Industry Index: energy (CSIIene); and (3) Wind Industry Index: energy (Windene). These three indexes were used to depict the financial sector and the energy sector as a whole, sectors which are closely related to the carbon option return.

We transformed the original data into two forms as follows: (i) Logarithmic difference method (LD) (according to Equation (29)); (ii) First-order difference method (FD) (according to Equation (30)). The transformation alleviates the heteroscedasticity of time series data and makes the data stable.

$$\begin{array}{c}\hfill y_t=ln{P}_t-ln{P}_{t-1}\end{array}$$

(29)

$$\begin{array}{c}\hfill y_t=P_t-P_{t-1}\end{array}$$

(30)

Table A1. Descriptive statistics.

Variables	Mean	Std. Dev.	Skew.	Kurt.	ADF Test	Jarque–Bera
SZA	0.00034	0.18722	0.28	11.27	−18.85 ***	4857.24 ***
LNG	0.00068	0.00047	0.34	33.09	−9.76 ***	41764.82 ***
SPcoa	0.00042	0.00050	−2.14	24.06	−8.86 ***	22770.72 ***
SPcru	0.00044	0.00052	−0.33	10.50	−25.58 ***	4217.38 ***
SPcor	0.00046	0.00005	0.68	4.42	−26.42 ***	815.51 ***
SPegg	0.00020	0.00045	4.68	63.46	−8.15 ***	156892.57 ***
SPcot	−0.00013	0.00018	0.06	8.94	−25.61 ***	3045.48 ***
SPwhe	0.00031	0.00015	3.16	43.93	−8.06 ***	75088.17 ***
SPalu	0.00032	0.00013	−0.58	17.67	−7.01 ***	11956.52 ***
SPzin	−0.00001	0.00017	0.60	9.79	−26.96 ***	3712.28 ***
SPlea	−0.00021	0.00010	−0.31	4.56	−16.78 ***	806.90 ***
SPnic	0.00063	0.00028	0.14	5.36	−12.91 ***	1096.74 ***
SPtin	0.00035	0.00020	0.16	12.29	−6.73 ***	5760.94 ***
SPsil	0.00020	0.00023	−0.98	11.20	−15.31 ***	4924.58 ***
SPgol	0.00038	0.00006	−0.82	10.13	−9.97 ***	4013.54 ***
SPcop	0.00020	0.00013	2.12	49.51	−27.06 ***	94123.69 ***
SSEPE	−0.00032	0.00024	−4.40	49.17	−9.80 ***	95125.33 ***
SSECI	0.00003	0.00015	−0.39	3.76	−30.72 ***	563.26 ***
CSI300	0.00008	0.00018	−0.41	3.33	−11.46 ***	448.50 ***
SSE180	0.00005	0.00017	−0.25	3.18	−11.65 ***	394.53 ***
SZSECI	0.00021	0.00023	−0.62	3.52	−10.88 ***	532.07 ***
CSI100	0.00003	0.00018	−0.35	2.87	−10.28 ***	331.63 ***
CSI500	0.00007	0.00022	−0.59	3.79	−29.92 ***	599.16 ***
SSEGBI	0.00021	0.00000	4.96	57.39	−5.88 ***	129320.39 ***
SSECBI	0.00023	0.00000	3.96	27.77	−5.29 ***	31781.76 ***
SSEEBI	0.00021	0.00000	2.68	20.55	−5.10 ***	17187.30 ***
Gb3M	−0.00081	0.00075	−1.71	17.74	−10.91 ***	12447.21 ***
Gb10Y	−0.00034	0.00008	−1.76	18.40	−7.98 ***	13377.39 ***
Cb3M	−0.00108	0.00031	−1.36	16.33	−15.98 ***	10454.93 ***
Cb10M	−0.00044	0.00002	−2.11	27.65	−6.90 ***	29825.27 ***
coalb3M	−0.00108	0.00033	−1.17	15.50	−16.51 ***	9368.78 ***
coalb5Y	−0.00060	0.00006	−0.81	10.93	−8.55 ***	4653.14 ***
FCI	−0.00450	0.01904	−0.81	17.78	−8.76 ***	12151.94 ***
CSIIene	0.00018	0.00034	0.20	5.04	−31.51 ***	974.00 ***
Windene	0.00025	0.00032	0.05	4.83	−31.17 ***	888.71 ***

Note: ADF test tests the null hypothesis that the series has the unit root, which means that the series is nonstationary. Jarque-Bera test tests the null hypothesis that the series follows a normal distribution. ^*** indicates that the null hypothesis is rejected at the statistical significance of 1%.

summarizes the statistical descriptions of all variables. From the results of the ADF test (Augmented Dickey–Fuller test) and Jarque–Bera test, the transformed data are stationary and show the characteristics of non-normal distribution.

Table A2. Explanation of variables.

Label	Variable	Transform.
SZA	Option Settlement Price: Carbon Emission Right (Shenzhen)	LD
Panel A: Energy and non-energy commodities
LNG	China Liquified Natural Gas Price Index	LD
SPcoa	Futures settlement price (active contract): Coal	LD
SPcru	Futures settlement price (active contract): Crude oil	LD
SPcor	Futures settlement price (active contract): Corn	LD
SPegg	Futures settlement price (active contract): Egg	LD
SPcot	Futures settlement price (active contract): Cotton	LD
SPwhe	Futures settlement price (active contract): Wheat	LD
SPalu	Futures settlement price (active contract): Aluminium	LD
SPzin	Futures settlement price (active contract): Zinc	LD
SPlea	Futures settlement price (active contract): Lead	LD
SPnic	Futures settlement price (active contract): Nickel	LD
SPtin	Futures settlement price (active contract): Tin	LD
SPsil	Futures settlement price (active contract): Silver	LD
SPgol	Futures settlement price (active contract): Gold	LD
SPcop	Futures settlement price (active contract): Copper	LD
SZA	Option Settlement Price: Carbon Emission Right (Shenzhen)	LD
Panel B: Financial variables
SSEPE	SSE Average P/E ratio	LD
SSECI	SSE Composite Index	LD
CSI300	CSI 300 Index	LD
SSE180	SSE 180 Index	LD
SZSECI	SZSE Composite Index	LD
CSI100	CSI 100 Index	LD
CSI500	CSI 500 Index	LD
SSEGBI	SSE Government Bond Index	LD
SSECBI	SSE Corporate Bond Index	LD
SSEEBI	SSE Enterprise Bond Index	LD
Gb3M	CCDC government bond yield: 3-months	LD
Gb10Y	CCDC government bond yield: 10-years	LD
Cb3M	CCDC corporate bond yield (AAA): 3-months	LD
Cb10M	CCDC corporate bond yield (AAA): 10-years	LD
coalb3M	CCDC coal industry bond yield (AAA): 3-months	LD
coalb5Y	CCDC coal industry bond yield (AAA): 5-years	LD
Panel C: Economic and industry index
FCI	Financial Conditions Index	FD
CSIIene	China Securities Industry Index: Energy	LD
Windene	WIND Industry Index: Energy	LD

Note: 1. Shanghai Stock Exchange; 2. China Securities Index; 3. Shenzhen Stock Exchange; 4. China Central Depository & Clearing Co., Ltd., Beijing, China.

(see Appendix B) provides an explanation of all variables involved. All variables are available from the WIND (WIND is a popular financial database in mainland China, which contains both micro- and macro-economic variable data for researchers and practitioners) database. Since there are some missing data in the original samples at different time points, we adopted an approach to fill in the missing data with the mean value of the previous and the next points to deal with this problem. In addition, we calculated the correlation of each variable and drew a heat map (shown in Figure A2 in Appendix B).

4. Empirical Results

In this section, we compare the performance difference of the forecasting model before and after using the improved stacking algorithm from the perspective of accuracy through statistical metrics and model confidence set, and evaluate the increase in economic gains brought by the improved algorithms through a portfolio. Also, we systematically explore the performance of the ensemble algorithm in high and low volatility states so that potential investors can make more rational use of the improved stacking ensemble algorithm to invest in carbon assets profitably.

4.1. Out-of-Sample Accuracy Performance

As mentioned in the data description section, the test data to compare model performance covered 224 samples from 10 May 2021 to 6 July 2022. The accuracy of the forecasting model was measured by five statistical metrics, and the models included base models before the ensemble process and six ensemble models using different frameworks. More specifically, we explored in detail the positive effect of our improved stacking algorithm on carbon return prediction from two dimensions: the whole mixing interval and the intervals with high or low volatility. In addition, to further analyze the robustness of the ensemble algorithm, we compare the performance of different ensemble models at different sliding window sizes in the third part of this section.

4.1.1. Accuracy for the Whole Test Set

The accuracy performance of the ensemble models on the whole test set covering 224 samples is presented in

Table 2. Comparison of model accuracy for the whole test data.

	RMSE	SMAPE	MAE	U1	${\mathbf{R}}_{\mathbf{os}}^2$
Homogeneous ensemble
Base Model
FAR	0.4701	0.2774	0.2959	0.1738	0.1828
FAR+MMS	0.4513	0.2706	0.2872	0.1671	0.2469
Ensemble Model
homo_rf	0.4317	0.2544	0.2698	0.1530	0.3107
homo_svr	0.4229	0.2458	0.2605	0.1475	0.3386
homo_xgb	0.4270	0.2510	0.2660	0.1512	0.3257
Heterogeneous ensemble
Base Model
MMA	0.4616	0.2733	0.2910	0.1712	0.2120
E-net	0.4832	0.2616	0.2827	0.1679	0.1364
lasso	0.4868	0.2683	0.2895	0.1662	0.1238
ridge	0.4825	0.2647	0.2855	0.1677	0.1390
SVR	0.4668	0.2542	0.2734	0.1602	0.1943
XGBoost	0.5022	0.2863	0.3087	0.1713	0.0671
RF	0.4992	0.2708	0.2936	0.1629	0.0783
Ensemble Model
hete_rf	0.4387	0.2541	0.2702	0.1544	0.2884
hete_svr	0.4340	0.2445	0.2602	0.1535	0.3034
hete_xgb	0.4393	0.2446	0.2611	0.1536	0.2862

Note: Explanation of ensemble model name abbreviations: ‘homo’ stands for homogeneous and the suffix connecting ‘homo’ represents the name of the meta-model used in the stacking algorithm. For example, ‘homo_rf’ denotes the ensemble model using homogeneous ensemble framework and random forest as the meta-model. ‘hete’ stands for heterogeneous, and its rules for abbreviation are similar to ‘homo’.FAR+MMS denotes the best factor-augmented regression selected by Mallows model selection criteria.

, according to the different ensemble frameworks applied. For homogeneous ensemble, it can be clearly seen from the table that, after adding the model selection process, compared with only using factor-augmented regression, the model achieved better performance in the five accuracy evaluation metrics.

We introduced an index PI to quantitatively measure the percentage of improvement in the evaluation index. For homogeneous ensemble, ‘base_model’ indicates FAR, while it indicates ‘base model with the best performance’ for the heterogeneous ensemble; ‘index’ represents one of the five precision evaluation indexes.

$$\begin{array}{c}\hfill {\mathbf{PI}}_{Index}^{ensemble\_model}=\left|\frac{{\mathbf{Index}}_{base\_model}-{\mathbf{Index}}_{ensemble\_model}}{{\mathbf{Index}}_{base\_model}}\right|\times 100\%,\end{array}$$

(31)

where ‘$P{I}_{Index}^{ensemble\_model}$’ is interpreted as the rate of improvement generated by the ’ensemble model’ in terms of ‘index’.

Among the three ensemble models under the homogeneous ensemble framework, $homo\_svr$ achieved the best performance in five statistical error indicators, with $P{I}_{RMSE}^{homo\_svr}$ = 10.04%, $P{I}_{SMAPE}^{homo\_svr}=11.41\%$, $P{I}_{MAE}^{homo\_svr}=11.95\%$, $P{I}_{U1}^{homo\_svr}=15.13\%$, and $P{I}_{R_{os}^2}^{homo\_svr}=84.52\%$. For heterogeneous ensemble, more forecasting models joined the comparison; however, even the best performers of the base models could not beat the ensemble model in the accuracy metrics. The best $PI$ was still obtained by ‘$hete\_svr$’, with values of $P{I}_{RMSE}^{hete\_svr}=5.98\%$, $P{I}_{SMAPE}^{hete\_svr}=3.85\%$, $P{I}_{MAE}^{hete\_svr}=4.85\%$, $P{I}_{U1}^{hete\_svr}=4.19\%$, and $P{I}_{R_{os}^2}^{hete\_svr}=42.80\%$.

In addition, the positive $PI$ indicates that, compared with the base model, the accuracy of each of the three ensemble models was improved after the integration process. Considering the results of homogeneous ensemble and heterogeneous ensemble, as a level-2 model for performing aggregation tasks, the advantage of SVR in improving accuracy is outstanding, and all the ensemble models play a positive role in improving prediction accuracy. Figure 6 provides more intuitive support for this view. The accuracy error in the ensemble models shrinks to the minimum range compared to the base model. (In order to unify the measurement criteria and more intuitively represent the comparison of the accuracy of the integrated model, $R_{os}^2$ was converted to $1-R_{os}^2$, which means that the smaller the $1-R_{os}^2$ shown in Figure 6, the higher the accuracy).

4.1.2. Accuracy for the Different Volatility Intervals

In order to validate the effectiveness of the improved stacking algorithm in improving the prediction accuracy in more detail, we used the MSGARCH model to divide the timeline of the entire dataset into ‘high volatility state’ and ‘low volatility state’, which, respectively, represent whether the current state is high volatility or low volatility. The volatility state of the whole time series is shown in Figure 7. According to the division results, the first 112 samples of the test set, from 10 May 2021 to 22 November 2021, were in a high volatility state, and the remaining half were in a low volatility state. The carbon return curves predicted by the six ensemble models are shown in Figure 8. Visually, from Figure 8, these ensemble models achieved good results in predicting the trend of carbon return, but the precision differences between the models under different volatility states, as well as before and after the ensemble process, need to be verified by quantitative calculation.

Table 3. Comparison of model accuracy for the period with different volatility using homogeneous ensemble.

	RMSE			SMAPE			MAE			U1			${\mathbf{R}}_{\mathbf{os}}^2$
	High	Low		High	Low		High	Low		High	Low		High	Low
Base Model
FAR	0.6041	0.2775		0.3691	0.1858		0.4020	0.1897		0.2757	0.0945		0.2330	−0.1846
FAR+MMS	0.5864	0.2518		0.3657	0.1755		0.3960	0.1784		0.2732	0.0862		0.2773	0.0251
Ensemble Model
homo_rf	0.5617	0.2392		0.3408	0.1680		0.3692	0.1704		0.2451	0.0797		0.3368	0.1199
homo_svr	0.5482	0.2390		0.3285	0.1630		0.3554	0.1656		0.2311	0.0790		0.3683	0.1213
homo_xgb	0.5542	0.2399		0.3373	0.1648		0.3646	0.1673		0.2416	0.0799		0.3545	0.1148
Percentage of improvement(%)
	8.1735	13.7447		9.0900	11.0440		9.6952	11.5317		13.2126	15.8577		-	-

and

Table 4. Comparison of model accuracy for the period with different volatility using heterogeneous ensemble.

	RMSE			SMAPE			MAE			U1			${\mathbf{R}}_{\mathbf{os}}^2$
	High	Low		High	Low		High	Low		High	Low		High	Low
Base Model
MMA	0.6056	0.2437		0.3753	0.1713		0.4081	0.1740		0.2815	0.0855		0.2292	0.0863
E-net	0.6376	0.2460		0.3654	0.1579		0.4045	0.1609		0.2750	0.0807		0.1456	0.0688
lasso	0.6384	0.2575		0.3683	0.1683		0.4075	0.1715		0.2685	0.0857		0.1434	−0.0197
ridge	0.6345	0.2511		0.3642	0.1652		0.4026	0.1683		0.2737	0.0845		0.1539	0.0298
SVR	0.6154	0.2388		0.3530	0.1555		0.3887	0.1581		0.2592	0.0758		0.2040	0.1231
XGBoost	0.6573	0.2692		0.3900	0.1827		0.4313	0.1860		0.2724	0.0910		0.0919	−0.1143
RF	0.6643	0.2390		0.3775	0.1642		0.4207	0.1666		0.2605	0.0800		0.0724	0.1214
Ensemble Model
hete_rf	0.5769	0.2283		0.3458	0.1625		0.3759	0.1646		0.2470	0.0772		0.3006	0.1986
hete_svr	0.5686	0.2311		0.3362	0.1527		0.3652	0.1551		0.2418	0.0776		0.3205	0.1784
hete_xgb	0.5765	0.2318		0.3323	0.1569		0.3628	0.1593		0.2430	0.0786		0.3016	0.1734
Percentage of improvement(%)
	9.7761	7.5941		8.7461	5.4426		10.0423	5.7167		9.7016	6.6027		-	-

show the calculation results of five statistical accuracy metrics of models when adopting two different ensemble frameworks under high and low volatility states. Compared to the results for the whole test data, a similar conclusion can be drawn, that the stacking algorithm always improves the precision of the model, whether in the high or low volatility state. However, with different ensemble frameworks and different level-2 meta-models, the ensemble models show some specific patterns in periods with different volatility.

As shown in Table 3, $homo\_svr$ is still the most competitive model in both high and low volatility states compared to the other two. However, based on the results in Table 4, $hete\_rf$ achieves the best performance for three indicators (RMSE, U1, ${\mathrm{R}}_{\mathrm{os}}^2$) in low volatility state, while in high volatility state, $hete\_svr$ is superior in these three indicators while $hete\_xgb$ is optimal in the other two (SMAPE, MAE). These results illustrate that ‘$RF$’ and ‘$XGBoost$’ can also be taken into consideration to be the level-2 model, depending on the ensemble mode and the volatility state. Moreover, we calculated the percentage of precision improvement on average for RMSE, SMAPE, MAE, and U1, (For homogeneous ensemble [shown in Table 3], the result was based on the mean of the three ensemble models over the value of ‘FAR’; for heterogeneous ensemble [shown in Table 4], the result was based on the mean of the three ensemble models over the mean of all base models; we did not calculate the percentage increase in ${\mathrm{R}}_{\mathrm{os}}^2$, because ${\mathrm{R}}_{\mathrm{os}}^2$ can be negative), which are listed at the bottom of Table 3 and Table 4. An interesting generalization is observed that, for the homogeneous ensemble, the ensemble process can improve the precision more significantly in the period with low volatility than that in the period with high volatility, while it is the opposite for the heterogeneous ensemble. The above results indicate that, in order to improve the accuracy of the forecasting model, it is more advantageous to choose the homogeneous ensemble framework when the carbon return is in the low volatility period, while the heterogeneous ensemble framework is a better choice when the carbon price is in the high volatility period.

In addition, to verify the effectiveness and advancement of the ensemble models, other popular methods related to carbon market prediction, especially deep learning models (LSTM [62], GRU [63], EMD+LSTM [48]), were considered.

Table 5. Comparison of accuracy between integrated models and deep learning models.

	RMSE				SMAPE				MAE				U1				${\mathbf{R}}_{\mathbf{os}}^2$
	Whole	High	Low		Whole	High	Low		Whole	High	Low		Whole	High	Low		Whole	High	Low
Ensemble Model
homo_rf	0.4317	0.5617	0.2392		0.2544	0.3408	0.1680		0.2698	0.3692	0.1704		0.1530	0.2451	0.0797		0.3107	0.3368	0.1199
homo_svr	0.4229	0.5482	0.2390		0.2458	0.3285	0.1630		0.2605	0.3554	0.1656		0.1475	0.2311	0.0790		0.3386	0.3683	0.1213
homo_xgb	0.4270	0.5542	0.2399		0.2510	0.3373	0.1648		0.2660	0.3646	0.1673		0.1512	0.2416	0.0799		0.3257	0.3545	0.1148
hete_rf	0.4387	0.5769	0.2283		0.2541	0.3458	0.1625		0.2702	0.3759	0.1646		0.1544	0.2470	0.0772		0.2884	0.3006	0.1986
hete_svr	0.4340	0.5686	0.2311		0.2445	0.3362	0.1527		0.2602	0.3652	0.1551		0.1535	0.2418	0.0776		0.3034	0.3205	0.1784
hete_xgb	0.4393	0.5765	0.2318		0.2446	0.3323	0.1569		0.2611	0.3628	0.1593		0.1536	0.2430	0.0786		0.2862	0.3016	0.1734
Deep Learning Model
LSTM	0.4415	0.5280	0.3334		0.2943	0.3373	0.2513		0.3086	0.3607	0.2566		0.1972	0.2155	0.1861		0.2790	0.4141	−0.7100
GRU	0.4696	0.5471	0.3763		0.3401	0.3765	0.3038		0.3552	0.4000	0.3104		0.2059	0.2218	0.1964		0.1846	0.3709	−1.1785
EMD+LSTM	0.4560	0.5358	0.3588		0.3123	0.3436	0.2809		0.3270	0.3672	0.2868		0.1631	0.1879	0.1467		0.2311	0.3966	−0.9798

shows the accuracy comparison between the ensemble models and other prediction models. It can be seen from the results that our proposed ensemble models outperform the other models.

4.1.3. Robustness Analysis for Different Rolling Window Sizes

Arbitrary choices of window sizes have consequences on how the sample is split into in-sample and out-of-sample portions, which may lead to different empirical results in practice [64]. The results of the above two sections were obtained under the condition that the window size was 100; we also expanded the window size to 200 and 300 to check the robustness of the experimental results.

Table A4. Comparison of model accuracy at different window sizes.

w = 200
	RMSE				SMAPE				MAE				U1				${\mathrm{R}}_{\mathrm{os}}^{\mathbf{2}}$
	Whole	High	Low		Whole	High	Low		Whole	High	Low		Whole	High	Low		Whole	High	Low
Base Model
FAR	0.4369	0.5620	0.2568		0.2595	0.3481	0.1708		0.2749	0.3758	0.1740		0.1630	0.2569	0.0935		0.2942	0.3363	−0.0142
FAR+MMS	0.4362	0.5604	0.2578		0.2704	0.3601	0.1807		0.2851	0.3866	0.1836		0.1632	0.2595	0.0942		0.2965	0.3400	−0.0222
MMA	0.4378	0.5641	0.2549		0.2713	0.3634	0.1792		0.2862	0.3903	0.1821		0.1631	0.2601	0.0926		0.2913	0.3311	0.0003
E-net	0.4658	0.6127	0.2419		0.2552	0.3551	0.1553		0.2742	0.3903	0.1582		0.1641	0.2681	0.0793		0.1977	0.2111	0.0996
lasso	0.4756	0.6280	0.2410		0.2573	0.3578	0.1569		0.2776	0.3956	0.1596		0.1690	0.2767	0.0784		0.1634	0.1711	0.1067
ridge	0.4692	0.6157	0.2473		0.2598	0.3571	0.1626		0.2791	0.3926	0.1656		0.1662	0.2704	0.0843		0.1859	0.2032	0.0590
SVR	0.4507	0.5916	0.2372		0.2477	0.3430	0.1524		0.2652	0.3754	0.1551		0.1564	0.2523	0.0771		0.2488	0.2643	0.1346
XGBoost	0.4759	0.6242	0.2518		0.2763	0.3786	0.1740		0.2955	0.4144	0.1767		0.1647	0.2611	0.0916		0.1623	0.1811	0.0248
RF	0.4884	0.6469	0.2420		0.2645	0.3670	0.1621		0.2861	0.4075	0.1647		0.1620	0.2615	0.0795		0.1180	0.1206	0.0990
Ensemble Model
homo_rf	0.4268	0.5528	0.2426		0.2608	0.3509	0.1707		0.2751	0.3770	0.1732		0.1530	0.2433	0.0841		0.3262	0.3578	0.0950
homo_svr	0.4059	0.5231	0.2365		0.2402	0.3188	0.1616		0.2533	0.3426	0.1640		0.1372	0.2109	0.0802		0.3906	0.4250	0.1394
homo_xgb	0.4210	0.5472	0.2347		0.2508	0.3395	0.1622		0.2650	0.3654	0.1646		0.1456	0.2316	0.0788		0.3445	0.3707	0.1529
hete_rf	0.4311	0.5668	0.2248		0.2540	0.3468	0.1613		0.2693	0.3752	0.1633		0.1536	0.2449	0.0778		0.3126	0.3249	0.2227
hete_svr	0.4169	0.5422	0.2317		0.2413	0.3260	0.1565		0.2555	0.3520	0.1590		0.1442	0.2267	0.0788		0.3572	0.3821	0.1744
hete_xgb	0.4196	0.5500	0.2226		0.2511	0.3446	0.1576		0.2653	0.3708	0.1597		0.1477	0.2333	0.0788		0.3489	0.3641	0.2375
Percentage of improvement(%)
homogeneous	4.3389	3.7271	7.3429		3.4248	3.3781	3.5201		3.7968	3.7642	3.8672		10.8676	11.0036	13.2982		-	-	-
heterogeneous	9.3613	9.6233	7.6670		4.9431	5.8698	2.8976		6.1368	7.3688	3.2041		9.2448	11.1046	5.7464		-	-	-
w = 300
	RMSE				SMAPE				MAE				U1				${\mathrm{R}}_{\mathrm{os}}^{\mathbf{2}}$
	Whole	High	Low		Whole	High	Low		Whole	High	Low		Whole	High	Low		Whole	High	Low
Base Model
FAR	0.4432	0.5723	0.2555		0.2631	0.3554	0.1708		0.2792	0.3844	0.1740		0.1614	0.2574	0.0900		0.2737	0.3117	−0.0043
FAR+MMS	0.4363	0.5592	0.2609		0.2723	0.3573	0.1872		0.2870	0.3837	0.1902		0.1636	0.2572	0.0964		0.2959	0.3428	−0.0473
MMA	0.4378	0.5609	0.2620		0.2721	0.3557	0.1884		0.2869	0.3825	0.1914		0.1637	0.2568	0.0958		0.2912	0.3387	−0.0561
E-net	0.4657	0.6120	0.2431		0.2549	0.3537	0.1561		0.2740	0.3889	0.1591		0.1645	0.2671	0.0804		0.1981	0.2127	0.0907
lasso	0.4681	0.6163	0.2415		0.2544	0.3531	0.1557		0.2737	0.3890	0.1585		0.1654	0.2695	0.0792		0.1898	0.2016	0.1031
ridge	0.4685	0.6158	0.2447		0.2573	0.3553	0.1592		0.2766	0.3909	0.1622		0.1661	0.2696	0.0825		0.1881	0.2031	0.0788
SVR	0.4473	0.5868	0.2363		0.2471	0.3420	0.1523		0.2643	0.3737	0.1549		0.1559	0.2514	0.0774		0.2601	0.2764	0.1410
XGBoost	0.4838	0.6417	0.2376		0.2681	0.3808	0.1554		0.2886	0.4193	0.1580		0.1715	0.2752	0.0837		0.1343	0.1346	0.1316
RF	0.4916	0.6485	0.2504		0.2742	0.3710	0.1775		0.2960	0.4119	0.1802		0.1791	0.2781	0.0967		0.1064	0.1161	0.0355
Ensemble Model
homo_rf	0.4299	0.5564	0.2450		0.2588	0.3432	0.1744		0.2736	0.3702	0.1769		0.1527	0.2381	0.0867		0.3166	0.3494	0.0766
homo_svr	0.4234	0.5492	0.2387		0.2464	0.3278	0.1651		0.2612	0.3547	0.1676		0.1445	0.2230	0.0813		0.3369	0.3660	0.1235
homo_xgb	0.4255	0.5496	0.2448		0.2543	0.3393	0.1694		0.2688	0.3656	0.1721		0.1477	0.2316	0.0831		0.3305	0.3650	0.0780
hete_rf	0.4343	0.5667	0.2367		0.2569	0.3381	0.1757		0.2725	0.3670	0.1779		0.1546	0.2377	0.0860		0.3026	0.3250	0.1384
hete_svr	0.4169	0.5417	0.2328		0.2408	0.3262	0.1553		0.2549	0.3521	0.1578		0.1440	0.2221	0.0786		0.3572	0.3833	0.1664
hete_xgb	0.4276	0.5586	0.2319		0.2526	0.3439	0.1614		0.2675	0.3713	0.1637		0.1494	0.2334	0.0813		0.3237	0.3443	0.1731
Percentage of improvement(%)
homogeneous	3.8109	3.5846	4.9584		3.7821	5.2603	0.7060		4.0542	5.4235	1.0293		8.1069	10.2943	6.9572		-	-	-
heterogeneous	8.5464	9.1647	4.6173		4.2287	6.3325	−0.3874		5.3811	7.6877	−0.0795		10.3723	13.3881	3.6899		-	-	-

(see Appendix B) lists the accuracy performance of models using two different ensemble frameworks at different window sizes. As seen in Table A4, the forecasting accuracy of the ensemble models is still better than that of the base models after the expansion of window size, which further confirms the most important conclusion, that the ensemble algorithm we developed can improve the predictive power of forecasting models to an impressive extent with regard to robustness. We also notice that, with the expansion of window size, the forecasting accuracy of the ensemble models decreases and the range of improvement in precision brought by the ensemble algorithm also decreases. Thus, setting the window size to 100 is a good choice to let the ensemble algorithm unleash its full power. Of course, the selection of window size is not the focus of this paper; accordingly, the following portfolio research was also carried out on the results with a window size of 100.

4.2. Analysis of MCS

The p-values of the ensemble model constructed by the improved stacking algorithm with regard to the MCS are shown in

Table 6. The p-value of MCS.

	MSE			MAE			Huber Loss
	${\mathit{T}}_{\mathit{R}}$	${\mathit{T}}_{\mathit{MAX}}$		${\mathit{T}}_{\mathit{R}}$	${\mathit{T}}_{\mathit{MAX}}$		${\mathit{T}}_{\mathit{R}}$	${\mathit{T}}_{\mathit{MAX}}$
Homogeneous ensemble
FAR	0.1075	0.0969		0.0416	0.0801		0.0862	0.0541
FAR+MMS	0.2132	0.2082		0.0752	0.0801		0.2302	0.1569
homo_rf	0.6814	0.6707		0.2739	0.163		0.8326	0.8531
homo_xgb	0.6814	0.6707		0.3961	0.3961		0.8326	0.8531
homo_svr	1.0000	1.0000		1.0000	1.0000		1.0000	1.0000
Heterogeneous ensemble
MMA	0.3683	0.3922		0.0876	0.3015		0.2629	0.3739
E-net	0.3683	0.3922		0.2946	0.3015		0.2629	0.3739
lasso	0.3683	0.3776		0.1881	0.3015		0.2509	0.2619
ridge	0.3683	0.3776		0.2921	0.3015		0.2629	0.3158
SVR	0.3244	0.3922		0.3658	0.3676		0.2509	0.3739
XGBoost	0.0778	0.0536		0.0104	0.0184		0.0443	0.0316
RF	0.3683	0.3550		0.0926	0.3015		0.1578	0.2619
hete_rf	0.8630	0.7634		0.2921	0.3676		0.8959	0.7860
hete_xgb	0.8630	0.6902		0.8846	0.8846		0.8959	0.7514
hete_svr	1.0000	1.0000		1.0000	1.0000		1.0000	1.0000

Note: The value in bold indicates that the corresponding model has the best prediction accuracy.

. The significance level $\alpha$ was set to 0.05. According to the results in Table 6, there was a significant boost in the accuracy of the model after using the improved stacking algorithm (seen in the larger p-values), which means that the improved stacking ensemble algorithm passes the hypothesis test for improving the accuracy; the improvement is proven to be robust. Moreover, $hom{o}_{svr}$ and $het{e}_{svr}$, respectively, achieved the highest p-values in homogeneous ensemble and heterogeneous ensemble, which indicates the significant advantage of support vector regression (SVR) as an aggregation meta-model for the ensemble algorithm.

4.3. Investment Gains from a Portfolio Perspective

Thus far, the advantages of the improved stacking ensemble algorithms in improving the accuracy of prediction have been comprehensively proven. However, translating such advantages into investment gains in practical business scenarios is a direction of more concern for market participants. We calculated the annualized utility gain (recall Equation (27)) generated by the mean-variance investor who constructs a portfolio strategy between carbon option and risk-free asset based on the predictions of the ensemble models. Inspired by Tan et al. [19] and Zhao and Cheng [60], we chose the 1-year China government bond as the alternative allocation asset, meaning that the 1-year China government bond yield was substituted into Equation (25) to represent the risk-free rate.

4.3.1. Influence of Risk Preference on Portfolio Construction

As mentioned in the section about economic evaluation (see Section 4.2), the risk aversion parameter $\gamma$ measures the extent of the investor’s aversion to risky assets and aggressive investment. The lower the value of $\gamma$, the greater the tolerance of investors to risk. It can be inferred from the calculation formula of weight $\omega$ (recall Equation (24)) that a lower $\gamma$ value leads to a higher weight assigned to the carbon option in the portfolio. As such, we conducted the robustness test on the annualized utility gain generated by investors with different risk preferences. The results were calculated by the predictions over three periods: the whole test set interval, high volatility interval, and low-volatility interval, which are shown in Figure 9 and Figure 10.

Figure 9 reveals a phenomenon that, when $\gamma$ is extremely small, $hete\_rf$ is the model to obtain the maximum utility gain, but when $\gamma$ increases to more than 0.5, $homo\_svr$ begins to take the lead, and when it exceeds 0.9, the annualized utility gain (UG) of all ensemble models gradually turns negative. Moreover, it is obvious that the annualized utility gain in all ensemble models over the whole prediction interval with mixed volatility state decreases with the increase in investor risk aversion parameter $\gamma$.

Figure 10a depicts how the various ensemble models perform in terms of utility gain in the high volatility interval. Under this condition, the dominance of the ensemble models based on the homogeneous ensemble framework is very clear. In the high volatility interval, with extremely small $\gamma$ (e.g., $\gamma =0.1$), $homo\_xgb$ produces the largest annualized utility gain. Then, when $\gamma =0.2\sim 0.4$, $homo\_rf$ slightly leads the others. Finally, when $\gamma$ exceeds 0.4, $homo\_svr$ always performs the best.

As for Figure 10b, the excellence of $hete\_rf$ in the low volatility interval is outstanding, which can be demonstrated from two aspects. Firstly, within the range of $\gamma$ plotted in (b), the annualized utility gain obtained by $hete\_rf$ is much higher than that obtained by other ensemble models. Secondly, with the increase in $\gamma$, the annualized utility gain of other ensemble models rapidly drops below 0, while that of $hete\_rf$ stays positive until $\gamma$ is greater than 1.9 (specific values can be found in

Table A5. The annualized utility gain in the high volatility state with different $\gamma$ values.

$\mathit{\gamma }$	homo_rf	homo_svr	homo_xgb	hete_rf	hete_svr	hete_xgb
0.1	127.7197	123.8112	130.1952	124.2137	125.9954	123.8034
0.2	106.8630	101.8535	105.7327	103.7007	105.0748	105.3883
0.3	88.2185	85.6709	87.1185	83.8264	86.4316	85.9962
0.4	70.2675	68.8990	70.2145	65.6354	68.6525	67.9815
0.5	52.7011	59.8317	54.7938	47.4687	49.0159	50.8217
0.6	38.3261	49.1146	45.4186	33.7303	30.2269	37.5260
0.7	29.1157	37.5849	34.7880	23.8302	20.6855	28.0542
0.8	19.5876	26.3511	24.5970	14.0808	11.0149	18.0043
0.9	10.2042	15.6767	14.6974	3.9732	1.5389	7.7412
1.0	0.8623	5.4678	4.9580	−6.3192	−7.4124	−1.6894
1.1	−8.2981	−4.2715	−4.6567	−15.5063	−16.6081	−10.8347
1.2	−17.4042	−13.3336	−14.0189	−24.3991	−25.6488	−19.2512
1.3	−26.3873	−22.1643	−23.2896	−33.1668	−34.0418	−27.5019
1.4	−35.2305	−30.8520	−32.3527	−41.2748	−42.2087	−35.9446
1.5	−43.9335	−39.4210	−41.2813	−48.5382	−49.5585	−44.2988
1.6	−52.3764	−47.8206	−49.8819	−55.5433	−56.5896	−52.5452
1.7	−59.5221	−56.0732	−57.9944	−62.5579	−63.4440	−60.4958
1.8	−66.6184	−63.7761	−65.4391	−62.2680	−67.9305	−68.0212
1.9	−67.0725	−71.0538	−70.1967	−61.9225	−72.4949	−71.0244
2.0	−66.7368	−78.2603	−74.9988	−61.8104	−77.0745	−67.9159

and

Table A6. The annualized utility gain in the low volatility state with different $\gamma$ values.

$\mathit{\gamma }$	homo_rf	homo_svr	homo_xgb	hete_rf	hete_svr	hete_xgb
0.1	10.5833	11.0648	9.6583	21.7402	14.0093	6.2470
0.2	9.2922	8.0546	9.5888	19.7474	9.3324	6.7526
0.3	7.1480	5.2682	8.1578	16.5444	5.6646	6.6055
0.4	4.1519	3.3513	5.8763	12.7961	2.8451	5.2168
0.5	1.6063	2.2058	3.1016	9.3113	1.1212	3.6444
0.6	−0.2334	1.1163	0.3678	7.7594	−0.2119	2.3696
0.7	−0.2521	−0.1230	−1.8165	7.5543	−1.7435	1.4899
0.8	−0.2480	−1.4857	−2.2543	7.3756	−3.3473	0.5143
0.9	−0.2202	−2.8608	−2.3471	6.8545	−3.4884	−0.1160
1.0	−0.4539	−4.2558	−2.5065	6.2759	−3.6066	−0.6956
1.1	−0.8144	−5.6323	−2.5351	5.6874	−3.4685	−0.8434
1.2	−1.2150	−6.6567	−2.6040	5.0897	−3.4482	−0.9459
1.3	−1.6539	−6.5332	−2.9180	4.4465	−3.5440	−1.1259
1.4	−2.1931	−6.5012	−3.3178	3.7551	−3.7335	−1.3668
1.5	−2.6683	−6.5235	−3.7421	3.0814	−3.9281	−1.6564
1.6	−3.1688	−6.6074	−4.2389	2.4251	−4.1701	−1.9855
1.7	−3.7310	−6.7433	−4.7852	1.7832	−4.4465	−2.3472
1.8	−4.2997	−6.9287	−5.3504	1.1336	−4.7509	−2.7454
1.9	−4.8519	−7.1635	−5.8327	0.4947	−5.0776	−3.1775
2.0	−5.3919	−7.4461	−6.3234	−0.0607	−5.3202	−3.6242

of Appendix B). $homo\_rf$ has significantly better performance and better robustness in terms of economic returns in the low volatility interval of the test set.

To summarize, for the carbon option, investors with risk-preferred attitudes are more likely to obtain high economic gains, and under the portfolio strategy in this paper, using the homogeneous ensemble is more conducive to achieving high economic returns when the market is in a high volatility state. Also, ‘$hete\_rf$’ compared to the other ensemble models has significant advantages in the portfolio during the low volatility period. Considering the difference in magnitude of the annualized utility gain between high and low volatility states, we find that the improved stacking algorithm exerts significantly greater advantage in the high volatility state.

4.3.2. Functionality of Ensemble Strategy in Improving Economic Gains

In the previous subsection, the performance of the ensemble models is shown through portfolios constructed by investors with different risk appetites. In this section, we further explore the function of the stacking algorithms we proposed in improving the economic gains of the model quantitatively. We report the comparison of annualized utility gain and Sharpe ratio with $\gamma =0.3$ between the base models and the ensemble models, in

Table 7. Annualized utility gains and Sharpe ratio at $\gamma =0.3$.

	UG				SR
	Whole	High	Low		Whole	High	Low
Base Model
FAR	40.0720	77.1260	5.1235		0.2445	0.3445	0.0876
FAR+MMS	45.7422	88.4737	5.6559		0.2650	0.3759	0.0899
MMA	42.4660	79.2613	7.9127		0.2526	0.3485	0.1066
E-net	42.3854	80.5625	6.3027		0.2551	0.3581	0.0947
lasso	41.8589	80.7737	4.9107		0.2572	0.3668	0.0837
ridge	40.2578	81.0734	1.8021		0.2466	0.3582	0.0615
svr	41.7817	71.9543	13.1367		0.2549	0.3344	0.1537
XGBoost	9.6912	19.3971	0.3235		0.1320	0.1810	0.0520
rf	27.1812	41.1122	13.6153		0.2007	0.2448	0.1538
Ensemble Model
homo_rf	46.4293	88.2185	7.1480		0.2689	0.3774	0.1010
homo_svr	44.2339	85.6709	5.2682		0.2608	0.3702	0.0867
homo_xgb	46.4102	87.1185	8.1578		0.2681	0.3730	0.1086
hete_rf	49.2886	83.8264	16.5444		0.2810	0.3678	0.1690
hete_svr	44.8457	86.4316	5.6646		0.2638	0.3742	0.0899
hete_xgb	45.1008	85.9962	6.6055		0.2649	0.3725	0.0968
buy&hold	-	-	-		0.0119	0.0050	0.0187

Note: The values in bold represent the best model for the corresponding metric.

, to show the impact of ‘ensemble’.

As detailed in Table 7, $hete\_rf$ achieves the best results for annualized utility gain and Sharpe ratio over both the whole test set and low volatility interval. In the high volatility interval, $homo\_rf$ is the best ensemble model, with $UG=88.2185$ and Sharpe ratio = 0.3774. Moreover, whether the stacking ensemble algorithm is homogeneous or heterogeneous, the ensemble process can always improve the portfolio return, based on the comparison of the performance of ensemble models with that of base models. In other words, ensemble strategy plays a positive role in improving the economic gains of prediction.

We use PI (Equation (31)) to show the extent of improvement brought by ensemble strategy on the two indicators, the best of which are $P{I}_{UG}^{hete\_rf}=16\%$ and $P{I}_{SR}^{homo\_rf}=9.96\%$ for the whole test set, $P{I}_{UG}^{homo\_rf}=14.33\%$ and $P{I}_{SR}^{homo\_rf}=9.55\%$ for the high volatility interval, and $P{I}_{UG}^{homo\_xgb}=58.70\%$ and $P{I}_{SR}^{homo\_xgb}=23.99\%$ for the low volatility interval. In terms of the absolute value of annualized utility gain and Sharpe ratio (SR), the heterogeneous ensemble framework performs better, and the homogeneous ensemble framework is superior for the improvement degree compared to the base model. An extra finding is that, compared to FAR, FAR+MMS in the homogeneous ensemble makes a significant improvement in obtaining economic gains, which means that our innovation in adding model selection to the homogeneous ensemble is successful. As well, to confirm the usefulness of the modified stacking algorithms, it is also necessary to show the performance of the $buy\&hold$ strategy (buy on the first day and sell on the last) in the comparison in terms of Sharpe ratio. Table 7 lists the obtained Sharpe ratio using the $buy\&hold$ strategy at the bottom. The Sharpe ratio of using the $buy\&hold$ strategy to invest in carbon option assets is much lower than that of using other prediction models in the table, which means that the additional information provided by the model is very valuable.

A counter-intuitive phenomenon occurs, in that $homo\_svr$ and $hete\_svr$ outperform other ensemble models in accuracy but $homo\_rf$ and $hete\_rf$ make more economic gains in the portfolio. Considering the portfolio strategy we have adopted, this problem is not difficult to explain. First, the premise of our portfolio is that the investors are mean-variance types, and from the whole calculation process of certainty equivalent return (CER), we can infer that a more fluctuant prediction of carbon return will result in a realized return with higher volatility, which means that CER will be penalized more by variance in Equation (26). We list the sample variance of the real carbon return and predictions made by each ensemble model in

Table 8. Variance in real observation and predicted value by ensemble models.

	homo_rf	homo_svr	homo_xgb	hete_rf	hete_svr	hete_xgb	Observation
Whole	0.0715	0.0656	0.0775	0.0547	0.0884	0.0624	0.2715
High	0.1166	0.1041	0.1264	0.0970	0.1508	0.1048	0.4800
Low	0.0258	0.0256	0.0278	0.0108	0.0246	0.0171	0.0655

. As can be seen from Table 8, real carbon return has a relatively greater variance, which makes the prediction of $hete\_svr$ tend to have high fluctuation since $hete\_svr$ has higher accuracy. (In fact, according to the values, the prediction of $hete\_svr$ does have a relatively larger variance compared to other integrated models.) The variance in the prediction made by $hete\_rf$ is the smallest in all intervals, which is beneficial to achieve a more robust certainty equivalent return (CER) in the portfolio. This reasonable inference of the result indicates that, for investors of mean-variance type, the forecast model with stable prediction is more conducive to obtaining high returns when investing in carbon assets.

Since the historical average (HA) model reflects historical information from the average, we added another baseline for comparison from recent information. We took the carbon return at day t as the prediction of the next day (day $t+1$), and calculated the annualized utility gains based on this strategy (i.e., calculate the CER based on this strategy, and replace $CE{R}^{HA}$ in Equation (27) with it to obtain the corresponding annualized utility gains), as shown in

Table 9. Annualized utility gains using another baseline.

	UG
	Whole	High	Low
Base Model
FAR	144.9971	263.4732	25.9002
FAR+MMS	150.6673	268.8209	26.4326
MMA	147.3911	265.6085	28.6894
E-net	147.3105	266.9096	27.0794
lasso	146.7839	267.1209	25.6873
ridge	145.1829	267.4206	22.5788
svr	146.7068	258.3015	33.9134
XGBoost	114.6163	205.7443	21.1002
rf	132.1063	227.4593	34.3919
Ensemble Model
homo_rf	151.3544	274.5656	27.9247
homo_svr	149.1590	272.0181	26.0448
homo_xgb	151.3353	273.4657	28.9345
hete_rf	154.2137	270.1735	37.3211
hete_svr	149.7708	272.7787	26.4413
hete_xgb	150.0259	272.3434	27.3822

. The results show that, even if this strategy is used as a benchmark, the improvement brought by the modified stacking algorithm is still significant, and for assets with sharp price fluctuations such as carbon options, using only the information from the previous day is risky (it can be seen that the $UG$ in Table 9 is much greater than that in Table 7).

5. Conclusions and Future Works

Through implementing comprehensive empirical experiments, we proved that the improved stacking ensemble algorithm can effectively improve the accuracy of models in predicting carbon returns. Support vector regression has advantages in improving prediction accuracy as meta-models for the improved stacking ensemble algorithm. When the carbon market is in a low volatility state, the improvement in homogeneous ensemble is greater, while in a high volatility state, heterogeneous integration is a better choice. Based on the results of detailed portfolio experiments, we find interesting generalizations about forecasts using stacking algorithms and characteristics of carbon assets. Not only did we provide supportive evidence for the existing research on carbon return prediction, but they we also explored supplementary research discussing the predictive model’s practical significance in investment. Firstly, the improved stacking ensemble algorithm significantly improves the economic benefits of carbon asset in portfolios. Secondly, if investing in carbon assets, a risk-prone investor is more likely to receive higher returns. Meanwhile, the empirical results demonstrate that different stacking ensemble frameworks perform diversely during turmoil and tranquil periods. We recommend the ensemble technique in practice since it brings stable forecasting performance and attractive investing gains, even when the volatility situation varies from low to high. Last but not least, the details of our innovation on stacking algorithm provide a valuable reference for researchers who study time series prediction.

However, there are still some limitations requiring further discussion in future work. We do not attempt to construct the optimal portfolio strategy in this study since the main focus, as mentioned, is the economic impact of ensemble strategy on the forecasting model and the optimal ensemble models in different market situations. In future works, we plan to test whether the improved stacking algorithm can continue to play a constructive role as investment portfolios vary across multiple financial assets. Additionally, we intend to set our sights on the broader carbon market to test the robustness of this ensemble algorithm.