Optimum Scenarios of EV Charging Infrastructure: A Case Study for the Saudi Arabia Market
Abstract
1. Introduction
1.1. Top Barriers to EV Adoption
1.2. KSA Market Status
2. Literature Review
3. Main Objective of the Study
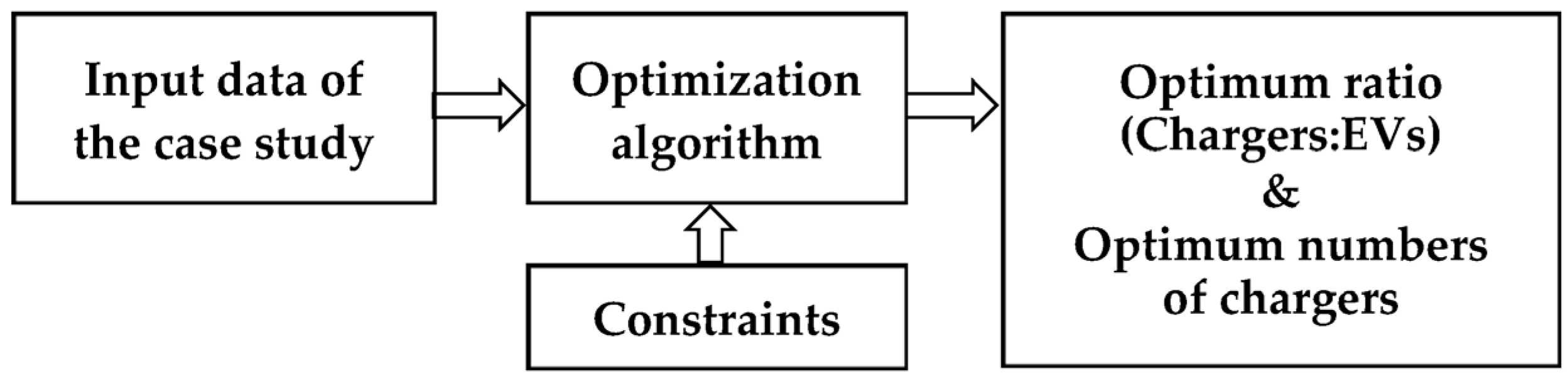
4. Methods
4.1. Charging Mix Scheme
4.2. Trade-Off between Cost and Quality of Service
4.3. Problem Formulation
- J is the customized objective function to be minimized.
- L1, L2, L3, L4 are the number of chargers whose power ratings are 5 kW, 25 kW, 50 kW and 120 kW, respectively.
- is the total cost function (see Appendix A).
- is the total charging time function (see Appendix A).
- is the objective function term concerning the total cost.
- is the objective function term concerning the total charging time.
- is the weight factor of the total cost term.
- is the weight factor of the total charging time term.
- is the objective function term concerning the total cost.
- is the weight factor of the cost term of chargers of type i
- is the total cost of all chargers of type i:
- is the objective function term concerning the total charging time.
- is the weight factor of the charging time term of chargers of type i
- is the total charging time of all chargers of type i.
- The applied (considered) constraints are:
- Number of home chargers of 5 kW: ;
- Number of residential chargers of 25 kW: ;
- Number of public chargers of 50 kW: ;
- Number of public chargers of 120 kW: ;
- Charging power: .
4.4. Variables and Parameters Affecting the Study
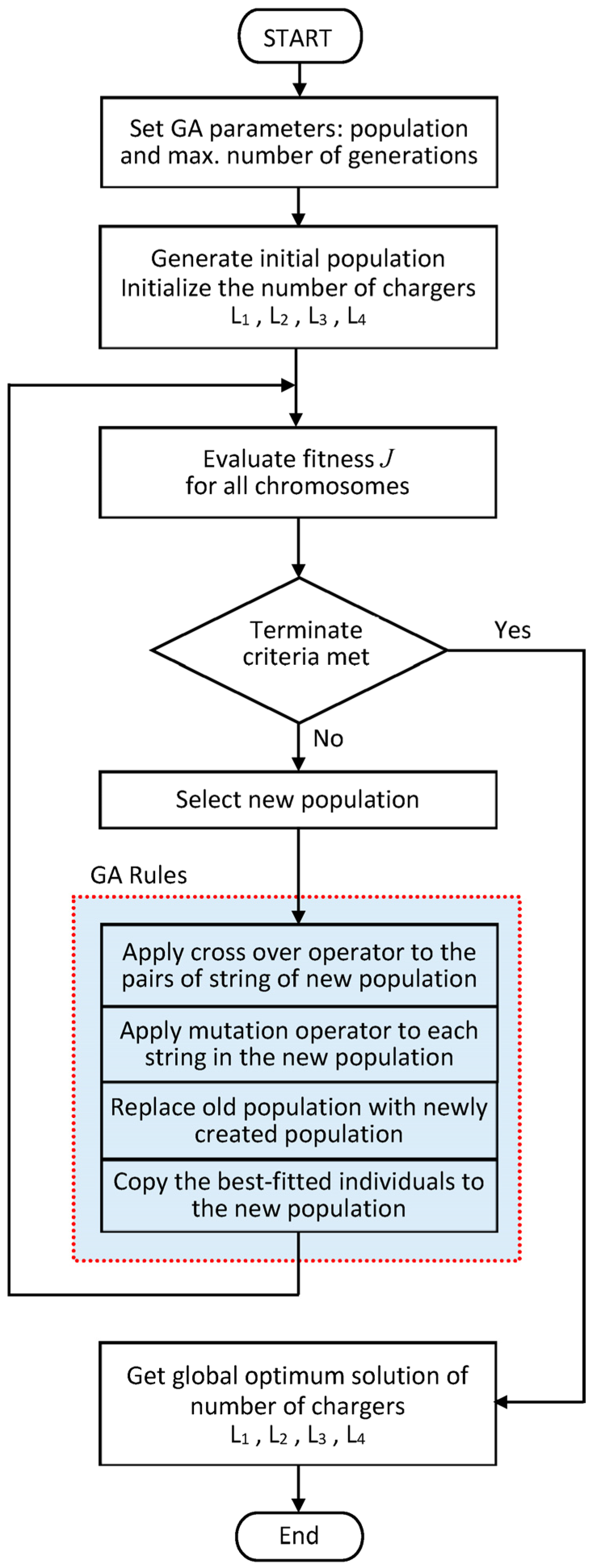
4.5. Evolutionary Search Algorithms
- Particle Swarm Optimization
- b.
- Genetic Algorithm
5. Assumptions and Inputs of the Study
6. Results
6.1. Extreme Optimization Results
6.2. Optimization Results for Minimum Costs and Charging Time Simultaneously
6.3. Comparison with the Typical Ratios of Many Countries
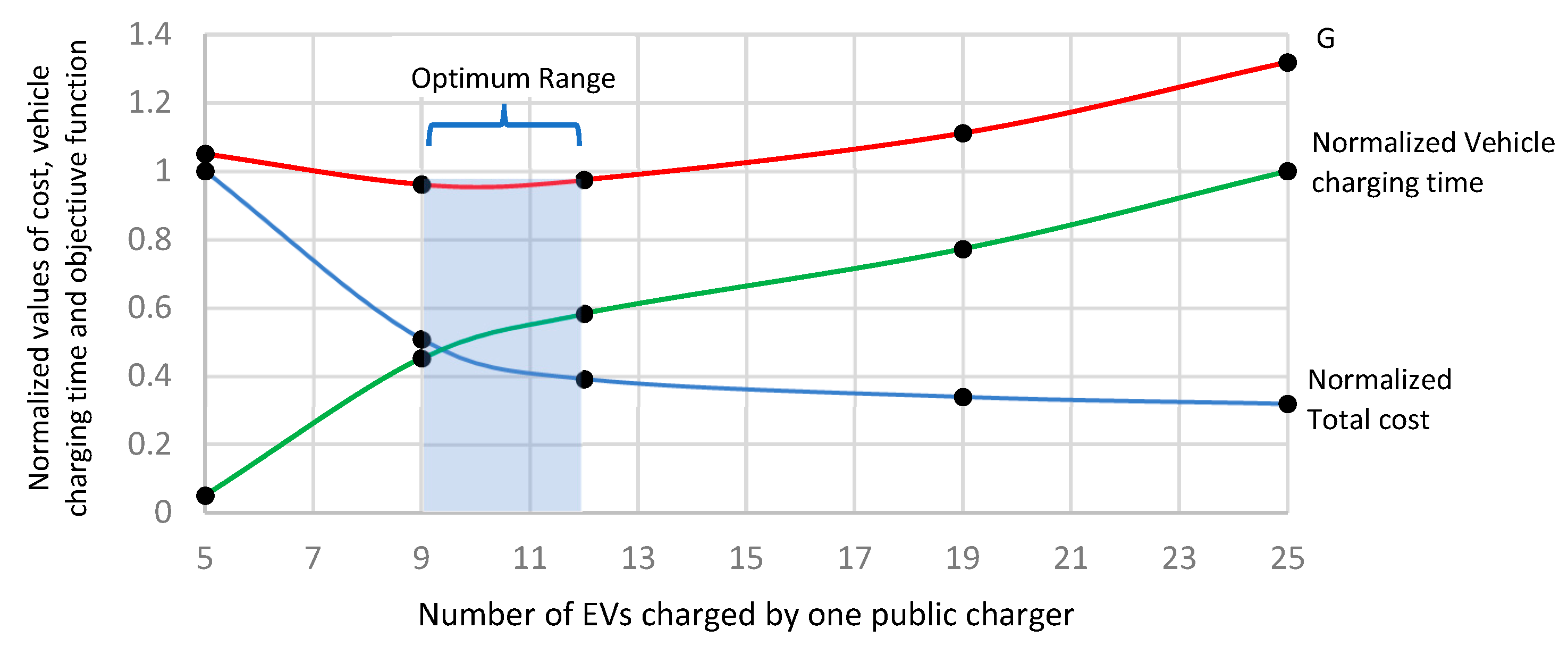
6.4. Optimum Range of the Ratio (Chargers:EVs)
6.5. Additional Cost (Power Generation Cost)
6.6. Recommendations for Highways
7. Discussion
8. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CEER | Trademark of the EV vehicles to be fabricated in the KSA |
| DWC | Dynamic wireless charger |
| EMS | Energy management system |
| EV | Electric vehicle |
| GA | Genetic algorithms |
| ICE | Internal combustion engine |
| IOV | Internet of vehicles |
| IPT | Inductive power transfer |
| PSO | Particle swarm optimization |
| PCP | Public charging points |
| PV | Photovoltaic |
| SASO | Saudi standards organization |
| SOC | State of charge of EV battery |
| TTC | Technology Transfer Centers |
| VDSC | Vehicle directed smart charging |
| Symbols | |
| Bcap | Battery capacity (kWh) |
| Ci | Total cost of chargers of type i |
| CCi | Capital cost of an individual charger of type i: |
| Total cost of all chargers; | |
| D1 | Daily covered distance during working days (km) |
| D2 | Daily covered distance during weekends (km) |
| Davg | Average daily covered distance (km) |
| d | Distances: 10 km; 20 km;……250 (km) |
| Ti | Total charging time with chargers of type i |
| Total charging time with all chargers; | |
| MCi | Running (maintenance) cost of an individual charger of type i |
| NEVd1 | Number of EVs that have covered a distance d (km) during a working day |
| NEVd2 | Number of EVs that have covered a distance d (km) during a weekend day |
| SOCf | Final state of charge of EV battery |
| SOCi | Initial state of charge of EV battery |
| Li | Number of the charger of type i |
| M | Iteration number in the PSO algorithm |
| k | Particle (bird) number in the PSO algorithm |
| i | Type number of chargers, it takes numerical values from 1 to 4 |
| J | Objective function |
| w | Inertia factor in the PSO algorithm |
| wc | Cost-term weight factor |
| wci | Cost-term weight factor of charger i |
| wt | Charging-term weight factor |
| wti | Charging-term weight factor of charger I |
| EV efficiency (kW/km) | |
| Charging power of individual charger of type i | |
| Total possible charging power of all chargers of type i | |
| Total possible charging power of all chargers | |
| Minimum required power to charge all vehicles; | |
| Position of the particle number m at the iteration number k | |
| Velocity of the particle number m at the iteration number k |
Appendix A
- (a)
- Computation of total cost of the different types of chargers:
- is the total cost of all chargers of type i;
- is the number of chargers of type i obtained from the optimization algorithm;
- is the capital cost of an individual charger of type i;
- is the total cost of all chargers;
- is the running (maintenance) cost of an individual charger of type i;
- i takes values from 1 to 4.
- (b)
- Computation of charging time with the different types of chargers:
- is the total charging time of all chargers of type i;
- is the total charging time with all chargers.
- (c)
- Computation of average daily covered distance and needed charging power:
- is the total required charging power for all vehicles;
- (d)
- Computation of resultant (actual) charging power with different types of chargers:
- is the total charging power of all chargers of type i;
- is the charging power of individual charger of type i.
Appendix B
- Optimization Software
| Item | Parameter |
|---|---|
| Software package | Matlab R2016 64 Bit, Mathworks, Inc. |
| Machine | Intel core i7, Ram 16 GB |
| (Simulation platform) | PSO: Matlab m.file |
| GA: Optimization toolbox 7.5, Mathworks, Inc. |
References
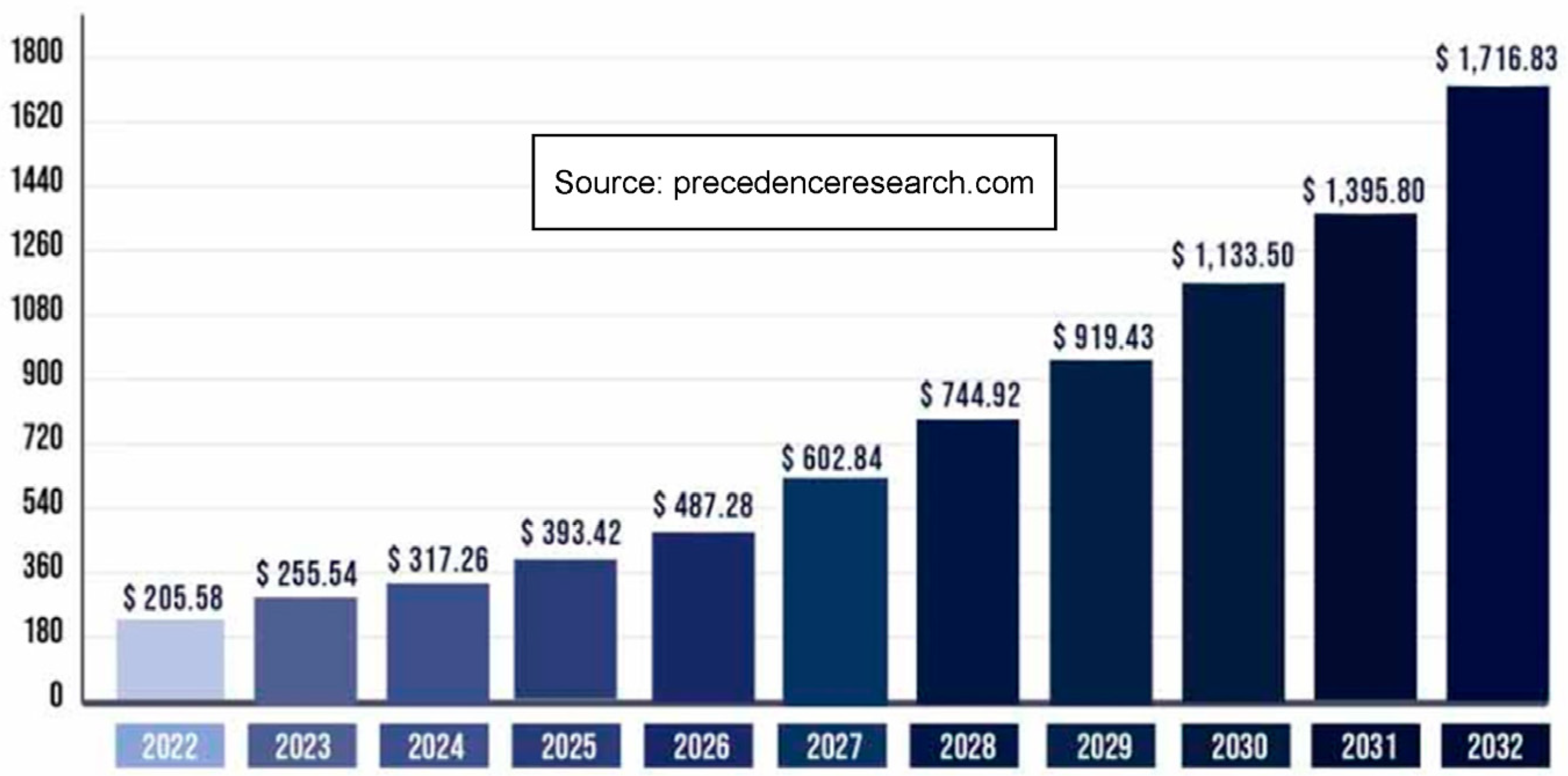
- Available online: https://www.precedenceresearch.com/electric-vehicle-market (accessed on 30 June 2023).
- IEA Technology Report. Available online: https://www.iea.org/reports/global-ev-outlook-2021 (accessed on 1 March 2023).
- Alotaibi, S.; Omer, S.; Su, Y. Identification of Potential Barriers to Electric Vehicle Adoption in Oil-Producing Nations—The Case of Saudi Arabia. Electricity 2022, 3, 365–395. [Google Scholar] [CrossRef]
- Available online: https://www.exro.com/industry-insights/barriers-to-electric-vehicle-adoption-in-2022#:~:text=Charging%20infrastructure%2C%20electric%20vehicle%20performance,barriers%20to%20electric%20vehicle%20adoption (accessed on 10 January 2023).
- Available online: https://www.exro.com/industry-insights/barriers-to-ev-adoption-part-2 (accessed on 10 January 2023).
- National Industrial Development Center NIDC. Available online: https://www.ic.gov.sa/en/ (accessed on 10 January 2023).
- Available online: https://english.alarabiya.net/business/technology/2022/11/17/Saudi-Arabia-s-electric-vehicle-maker-Ceer-appoints-CEO (accessed on 20 December 2022).
- Available online: https://www.saudiembassy.net/news/hrh-crown-prince-launches-ceer-first-saudi-electric-vehicle-brand (accessed on 20 December 2022).
- Available online: https://english.aawsat.com/home/article/3967641/crown-prince-launches-ceer-1st-saudi-electric-vehicle-brand (accessed on 23 December 2022).
- Available online: https://www.zeaara.com/blog/riyadhcarstats.html (accessed on 5 January 2023).
- Available online: https://www.arabnews.com/node/2034146/business-economy (accessed on 9 January 2023).
- Nezamuddin, O.N.; Nicholas, C.L.; Santos, E.C. The Problem of Electric Vehicle Charging: State-of-the-Art and an Innovative Solution. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4663–4673. [Google Scholar] [CrossRef]
- Ucer, E.; Koyuncu, I.; Kisacikoglu, M.C.; Yavuz, M.; Meintz, A.; Rames, C. Modeling and Analysis of a Fast Charging Station and Evaluation of Service Quality for Electric Vehicles. IEEE Trans. Transp. Electrif. 2019, 5, 215–225. [Google Scholar] [CrossRef]
- Tu, H.; Feng, H.; Srdic, S.; Lukic, S. Extreme Fast Charging of Electric Vehicles: A Technology Overview. IEEE Trans. Transp. Electrif. 2019, 5, 861–878. [Google Scholar] [CrossRef]
- Kabir, M.E.; Assi, C.; Alameddine, H.; Antoun, J.; Yan, J. Demand-Aware Provisioning of Electric Vehicles Fast Charging Infrastructure. IEEE Trans. Veh. Technol. 2020, 69, 6952–6963. [Google Scholar] [CrossRef]
- Shao, C.; Qian, T.; Wang, Y.; Wang, X. Coordinated Planning of Extreme Fast Charging Stations and Power Distribution Networks Considering On-Site Storage. IEEE Trans. Intell. Transp. Syst. 2021, 22, 493–504. [Google Scholar] [CrossRef]
- Abdullah, H.M.; Gastli, A.; Ben-Brahim, L.; Mohammed, S.O. Planning and Optimizing Electric-Vehicle Charging Infrastructure through System Dynamics. IEEE Access 2022, 10, 17495–17514. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, X.-P.; Wang, J.; Li, J.; Wu, C.; Hu, M.; Bian, H. A Review on Electric Vehicle Charging Infrastructure Development in the UK. J. Mod. Power Syst. Clean Energy 2020, 8, 193–205. [Google Scholar] [CrossRef]
- Ding, Z.; Teng, F.; Sarikprueck, P.; Hu, Z. Technical Review on Advanced Approaches for Electric Vehicle Charging Demand Management, Part II: Applications in Transportation System Coordination and Infrastructure Planning. IEEE Trans. Ind. Appl. 2020, 56, 5695–5703. [Google Scholar] [CrossRef]
- Marquez-Fernandez, F.J.; Bischoff, J.; Domingues-Olavarria, G.; Alakula, M. Assessment of Future EV Charging Infrastructure Scenarios for Long-Distance Transport in Sweden. IEEE Trans. Transp. Electrif. 2022, 8, 615–626. [Google Scholar] [CrossRef]
- Mirheli, A.; Hajibabai, L. Hierarchical Optimization of Charging Infrastructure Design and Facility Utilization. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15574–15587. [Google Scholar] [CrossRef]
- Nicolaides, D.; Cebon, D.; Miles, J. An Urban Charging Infrastructure for Electric Road Freight Operations: A Case Study for Cambridge UK. IEEE Syst. J. 2019, 13, 2057–2068. [Google Scholar] [CrossRef]
- Li, C.; Dong, Z.; Chen, G.; Zhou, B.; Zhang, J.; Yu, X. Data-Driven Planning of Electric Vehicle Charging Infrastructure: A Case Study of Sydney, Australia. IEEE Trans. Smart Grid 2021, 12, 3289–3304. [Google Scholar] [CrossRef]
- Brenna, M.; Lazaroiu, G.C.; Roscia, M.; Saadatmandi, S. Dynamic Model for the EV’s Charging Infrastructure Planning through Finite Element Method. IEEE Access 2020, 8, 102399–102408. [Google Scholar] [CrossRef]
- Abdullah, H.M.; Gastli, A.; Ben-Brahim, L.; Mohammed, S.O. Integrated Multi-Criteria Model for Long-Term Placement of Electric Vehicle Chargers. IEEE Access 2022, 10, 123452–123473. [Google Scholar] [CrossRef]
- Fathollahi, A.; Derakhshandeh, S.Y.; Ghiasian, A.; Masoum, M.A. Optimal Siting and Sizing of Wireless EV Charging Infrastructures Considering Traffic Network and Power Distribution System. IEEE Access 2022, 10, 117105–117117. [Google Scholar] [CrossRef]
- Sadhukhan, A.; Ahmad, M.S.; Sivasubramani, S. Optimal Allocation of EV Charging Stations in a Radial Distribution Network Using Probabilistic Load Modeling. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11376–11385. [Google Scholar] [CrossRef]
- Zeb, M.Z.; Imran, K.; Khattak, A.; Janjua, A.K.; Pal, A.; Nadeem, M.; Zhang, J.; Khan, S. Optimal Placement of Electric Vehicle Charging Stations in the Active Distribution Network. IEEE Access 2020, 8, 68124–68134. [Google Scholar] [CrossRef]
- Deb, S.; Tammi, K.; Gao, X.-Z.; Kalita, K.; Mahanta, P.; Cross, S. A Robust Two-Stage Planning Model for the Charging Station Placement Problem Considering Road Traffic Uncertainty. IEEE Trans. Intell. Transp. Syst. 2022, 23, 6571–6585. [Google Scholar] [CrossRef]
- Frendo, O.; Gaertner, N.; Stuckenschmidt, H. Open Source Algorithm for Smart Charging of Electric Vehicle Fleets. IEEE Trans. Ind. Inform. 2021, 17, 6014–6022. [Google Scholar] [CrossRef]
- Hussain, S.; Ahmed, M.A.; Kim, Y.-C. Efficient Power Management Algorithm Based on Fuzzy Logic Inference for Electric Vehicles Parking Lot. IEEE Access 2019, 7, 65467–65485. [Google Scholar] [CrossRef]
- ElGhanam, E.; Sharf, H.; Odeh, Y.; Hassan, M.S.; Osman, A.H. On the Coordination of Charging Demand of Electric Vehicles in a Network of Dynamic Wireless Charging Systems. IEEE Access 2022, 10, 62879–62892. [Google Scholar] [CrossRef]
- Jeong, S.; Jang, Y.J.; Kum, D.; Lee, M.S. Charging Automation for Electric Vehicles: Is a Smaller Battery Good for the Wireless Charging Electric Vehicles? IEEE Trans. Autom. Sci. Eng. 2019, 16, 486–497. [Google Scholar] [CrossRef]
- Ejaz, W.; Naeem, M.; Sharma, S.K.; Khattak, A.M.; Ramzan, M.R.; Ali, A.; Anpalagan, A. Iov-Based Deployment and Scheduling of Charging Infrastructure in Intelligent Transportation Systems. IEEE Sens. J. 2021, 21, 15504–15514. [Google Scholar] [CrossRef]
- Mokgonyana, L.; Smith, K.; Galloway, S. Reconfigurable Low Voltage Direct Current Charging Networks for Plug-in Electric Vehicles. IEEE Trans. Smart Grid 2019, 10, 5458–5467. [Google Scholar] [CrossRef]
- Mobarak, M.H.; Bauman, J. Vehicle-Directed Smart Charging Strategies to Mitigate the Effect of Long-Range EV Charging on Distribution Transformer Aging. IEEE Trans. Transp. Electrif. 2019, 5, 1097–1111. [Google Scholar] [CrossRef]
- Danish, S.M.; Zhang, K.; Jacobsen, H.-A.; Ashraf, N.; Qureshi, H.K. Blockev: Efficient and Secure Charging Station Selection for Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 4194–4211. [Google Scholar] [CrossRef]
- Frendo, O.; Gaertner, N.; Stuckenschmidt, H. Improving Smart Charging Prioritization by Predicting Electric Vehicle Departure Time. IEEE Trans. Intell. Transp. Syst. 2021, 22, 6646–6653. [Google Scholar] [CrossRef]
- Kabir, M.E.; Sorkhoh, I.; Moussa, B.; Assi, C. Joint Routing and Scheduling of Mobile Charging Infrastructure for V2V Energy Transfer. IEEE Trans. Intell. Veh. 2021, 6, 736–746. [Google Scholar] [CrossRef]
- Lasla, N.; Al-Ammari, M.; Abdallah, M.; Younis, M. Blockchain Based Trading Platform for Electric Vehicle Charging in Smart Cities. IEEE Open J. Intell. Transp. Syst. 2020, 1, 80–92. [Google Scholar] [CrossRef]
- Khalid, M.R.; Khan, I.A.; Hameed, S.; Asghar, M.S.; Ro, J.-S. A Comprehensive Review on Structural Topologies, Power Levels, Energy Storage Systems, and Standards for Electric Vehicle Charging Stations and Their Impacts on Grid. IEEE Access 2021, 9, 128069–128094. [Google Scholar] [CrossRef]
- Shahriar, S.; Al-Ali, A.R.; Osman, A.H.; Dhou, S.; Nijim, M. Machine Learning Approaches for EV Charging Behavior: A Review. IEEE Access 2020, 8, 168980–168993. [Google Scholar] [CrossRef]
- Shahriar, S.; Al-Ali, A.R.; Osman, A.H.; Dhou, S.; Nijim, M. Prediction of EV Charging Behavior Using Machine Learning. IEEE Access 2021, 9, 111576–111586. [Google Scholar] [CrossRef]
- Lee, Z.J.; Sharma, S.; Johansson, D.; Low, S.H. ACN-SIM: An Open-Source Simulator for Data-Driven Electric Vehicle Charging Research. IEEE Trans. Smart Grid 2021, 12, 5113–5123. [Google Scholar] [CrossRef]
- Chaudhari, K.; Kandasamy, N.K.; Krishnan, A.; Ukil, A.; Gooi, H.B. Agent-Based Aggregated Behavior Modeling for Electric Vehicle Charging Load. IEEE Trans. Ind. Inform. 2019, 15, 856–868. [Google Scholar] [CrossRef]
- Chavhan, S.; Dubey, N.; Lal, A.; Khetan, D.; Gupta, D.; Khanna, A.; Rodrigues, J.J.; Pinheiro, P.R. Next-Generation Smart Electric Vehicles Cyber Physical System for Charging Slots Booking in Charging Stations. IEEE Access 2020, 8, 160145–160157. [Google Scholar] [CrossRef]
- Ahmed, M.A.; El-Sharkawy, M.R.; Kim, Y.-C. Remote Monitoring of Electric Vehicle Charging stations in Smart Campus Parking Lot. J. Mod. Power Syst. Clean Energy 2020, 8, 124–132. [Google Scholar] [CrossRef]
- Lee, Z.J.; Lee, G.; Lee, T.; Jin, C.; Lee, R.; Low, Z.; Chang, D.; Ortega, C.; Low, S.H. Adaptive Charging Networks: A Framework for Smart Electric Vehicle Charging. IEEE Trans. Smart Grid 2021, 12, 4339–4350. [Google Scholar] [CrossRef]
- Cao, Y.; Kaiwartya, O.; Zhuang, Y.; Ahmad, N.; Sun, Y.; Lloret, J. A Decentralized Deadline-Driven Electric Vehicle Charging Recommendation. IEEE Syst. J. 2019, 13, 3410–3421. [Google Scholar] [CrossRef]
- Tucker, N.; Alizadeh, M. An Online Admission Control Mechanism for Electric Vehicles at Public Parking Infrastructures. IEEE Trans. Smart Grid 2020, 11, 161–170. [Google Scholar] [CrossRef]
- Kong, P.-Y. Autonomous Robot-like Mobile Chargers for Electric Vehicles at Public Parking Facilities. IEEE Trans. Smart Grid 2019, 10, 5952–5963. [Google Scholar] [CrossRef]
- Ahmad, M.S.; Sivasubramani, S. Optimal Number of Electric Vehicles for Existing Networks Considering Economic and Emission Dispatch. IEEE Trans. Ind. Inform. 2019, 15, 1926–1935. [Google Scholar] [CrossRef]
- Badia, B.; Berry, R.A.; Wei, E. Investment in EV Charging Spots for Parking. IEEE Trans. Netw. Sci. Eng. 2020, 7, 650–661. [Google Scholar] [CrossRef]
- Azab, M. Multi-Objective Design Approach of Passive Filters for Single-Phase Distributed Energy Grid Integration Systems Using Particle Swarm Optimization. Energy Rep. 2020, 6, 157–172. [Google Scholar] [CrossRef]
- Azab, M.; Serrano-Fontova, A. Optimal Tuning of Fractional Order Controllers for Dual Active Bridge-Based DC Microgrid Including Voltage Stability Assessment. Electronics 2021, 10, 1109. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Bell, D. A Novel Particle Swarm Optimization Approach for Patient Clustering from Emergency Departments. IEEE Trans. Evol. Comput. 2019, 23, 632–644. [Google Scholar] [CrossRef]
- Azab, M. Design Approach and Performance Analysis of Trap Filter for Three-Phase PV Grid Integration Systems Using Evolutionary Search Algorithms. J. King Saud Univ. Eng. Sci. 2021, 33, 491–506. [Google Scholar] [CrossRef]
- Corus, D.; Oliveto, P.S. Standard Steady State Genetic Algorithms Can Hillclimb Faster than Mutation-Only Evolutionary Algorithms. IEEE Trans. Evol. Comput. 2018, 22, 720–732. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Fan, K.; Ma, W.; Lei, H. Prediction Method for Low Speed Characteristics of Compressor Based on Modified Similarity Theory with Genetic Algorithm. IEEE Access 2018, 6, 36834–36839. [Google Scholar] [CrossRef]
- Mohammadi, A.; Asadi, H.; Mohamed, S.; Nelson, K.; Nahavandi, S. Multiobjective and Interactive Genetic Algorithms for Weight Tuning of a Model Predictive Control-Based Motion Cueing Algorithm. IEEE Trans. Cybern. 2019, 49, 3471–3481. [Google Scholar] [CrossRef]
- Dalla Chiara, B.; Deflorio, F.; Pellicelli, M.; Castello, L.; Eid, M. Perspectives on Electrification for the Automotive Sector: A Critical Review of Average Daily Distances by Light-Duty Vehicles, Required Range, and Economic Outcomes. Sustainability 2019, 11, 5784. [Google Scholar] [CrossRef]
- Smart, J.; Powell, W.; Schey, S. Extended Range Electric Vehicle Driving and Charging Behavior Observed Early in the EV Project. SAE Tech. Pap. Ser. 2013, 1–9. [Google Scholar] [CrossRef]
- He, J.; Yamamoto, T. Characterization of Daily Travel Distance of a University Car Fleet for the Purpose of Replacing Conventional Vehicles with Electric Vehicles. Sustainability 2020, 12, 690. [Google Scholar] [CrossRef]
- Plötz, P.; Jakobsson, N.; Sprei, F. On the Distribution of Individual Daily Driving Distances. Transp. Res. Part B Methodol. 2017, 101, 213–227. [Google Scholar] [CrossRef]
- Available online: https://www.statista.com/chart/26325/ratio-electric-vehicles-to-public-charging-points/ (accessed on 20 June 2023).
- Available online: https://www.statista.com/statistics/975223/saudi-arabia-electricity-generation-capacity/#:~:text=As%20of%202021%2C%20the%20electricity,capacity%20of%20around%2053.6%20gigawatts (accessed on 20 June 2023).
- Available online: https://datasource.kapsarc.org/explore/dataset/electric-power-generation-capacity-and-number-of-subscribers/table/?disjunctive.indicators&refine.indicators=%2APower%2BGeneration%2BCapacity%2B%28MW%29 (accessed on 13 October 2022).
- Available online: https://www.kapsarc.org/wp-content/uploads/2020/12/KS-2020-DP25-Saudi-Arabia-Energy-Report.pdf (accessed on 8 February 2023).



| Item | Estimated Quantity |
|---|---|
| Estimated fabricated EVs (by 2025/2026) | 150,000 |
| Approved importers by SASO* (until 2022) | 16 |
| Estimated conventional cars in Riyadh | 4,800,000 |
| Estimated market share of EVs and HEV | 3% |
| Estimated imported EV and HEV (by 2025) | 50,000–60,000 |
| Rating of Charger [kW] | Charging Time [Hour] |
|---|---|
| 5 | 15 |
| 10 | 7.5 |
| 25 | 3 |
| 50 | 1.5 |
| 120 | 0.62 |
| 150 | 0.50 |
| Case | Action | ||
|---|---|---|---|
| Crowded cities | Assign higher priority to the charging time term | 0.1–0.3 | 0.9–0.7 |
| Limited funds | Assign higher priority to the cost term | 0.9–0.7 | 0.1–0.3 |
| Equal importance | Same priority | 1 | 1 |
| Ignored Constraint | Algorithm Action | Consequence |
|---|---|---|
| Minimum value of the total generated charging power | Few numbers of chargers | Insufficient charging power |
| Maximum value of home chargers | Large numbers of home chargers | Unrealistic results |
| Variable & Parameters Affecting the Case Study |
|---|
| Number of running EVs in that province |
| Types of EV chargers and their power rating |
| Initial (capital) costs of EV chargers |
| Running (maintenance) costs of EV chargers |
| Estimated daily travelled distances during working days |
| Estimated travelled distances during weekends |
| Battery capacity of EVs |
| EV efficiency (required power/km) or distance travelled with 1 kW |
| Initial and desired State of Charge (SOC) of EV battery |
| Upgrade costs of existing gasoline stations to host EV chargers |
| EVs density on specific roads |
| Highway lengths and distances between cities |
| Particles (Birds) | Max. Iterations | Inertia w | α | β |
|---|---|---|---|---|
| 500 | 300 | 2 | 0.5 | 0.5 |
| PS 1 | Creation Function | Fitness Scaling | Selection | Reproduction | Mutation | Crossover Function | |
|---|---|---|---|---|---|---|---|
| Elite Count | Crossover Fraction | ||||||
| 100 | Uniform | Rank | Stochastic | 0.05 PS | 0.8 | Constrain | Scattered |
| Item | Estimated Quantity | |
|---|---|---|
| Number of EVs | 150,000 | |
| Residential chargers: charger_1; charger_2 | Power ratings | 5 kW, 25 kW (AC Type) |
| Prices (initial cost) | 400 USD, 1600 USD | |
| Maintenance cost/year | 27 USD, 53 USD | |
| Public chargers: charger_3; charger_4 | Power ratings | 50 kW, 120 kW (DC, DC Fast) |
| Prices (initial cost) | 10,667 USD, 40,000 USD | |
| Maintenance cost/year | 533 USD, 1067 USD | |
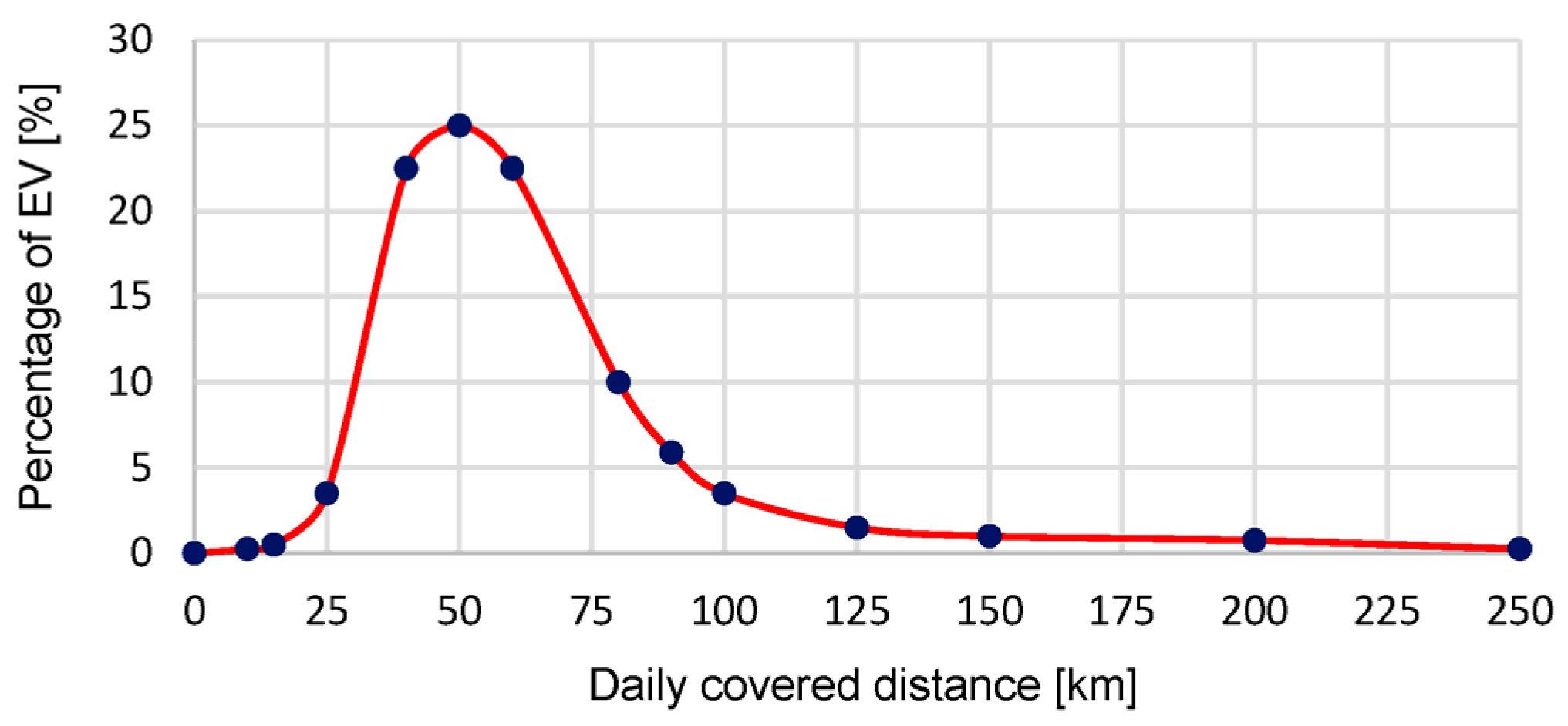
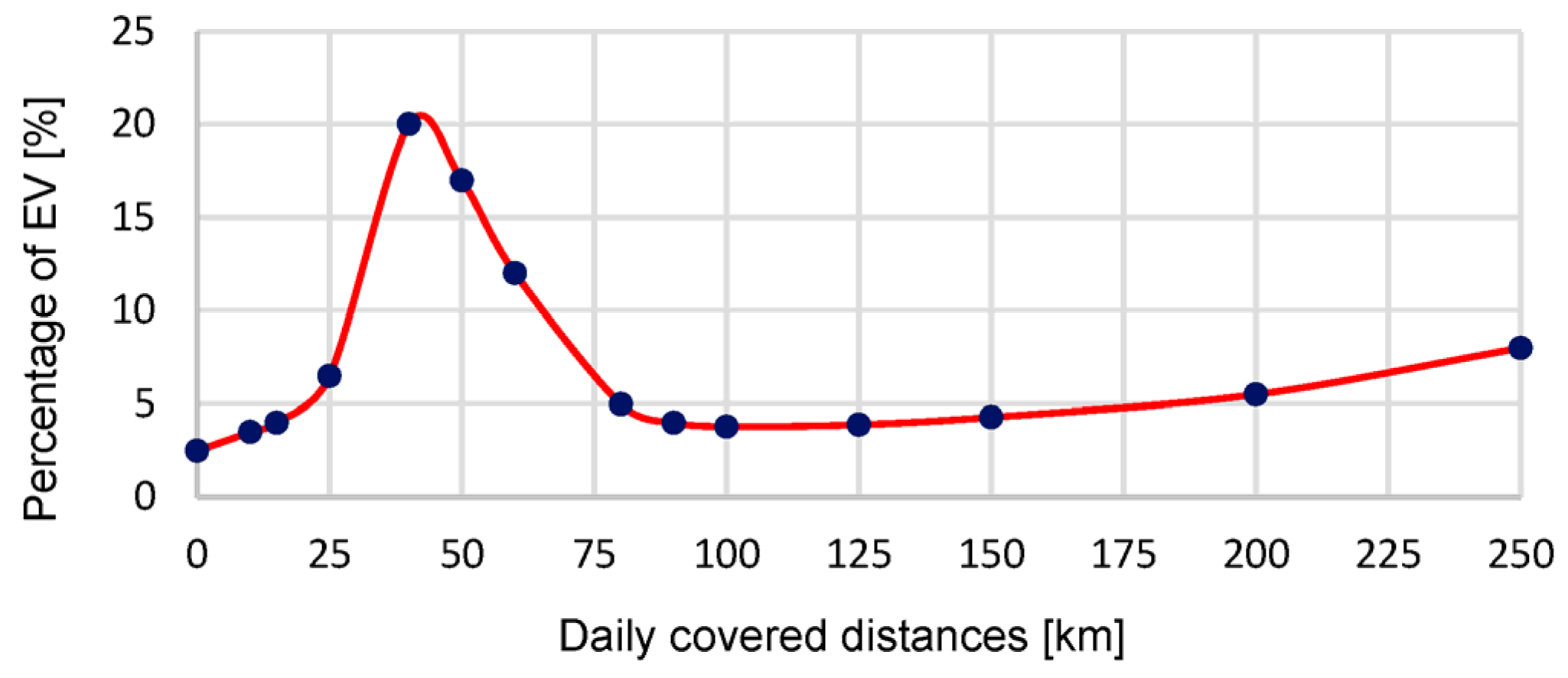
| Estimated daily travelled distances during working days | Profile shown in Figure 6 | |
| Estimated travelled distances during weekends | Profile shown in Figure 7 | |
| Battery capacity of EVs | 75 kWh | |
| EV efficiency: (travelled distance with 1 kW) | 4 km | |
| Initial and desired SOC of EV battery | Worst case: 0% to 100% | |
| Worst case initial and final SOC of EV battery | 0% → 100% | |
| Minimum required charging power (GW) | 2.432 GW | |
| Optimization Goal | Total Cost Optimized Only | Charging Time Optimized Only | |
|---|---|---|---|
| Optimization Results | |||
| Overall cost (million USD) | 186.67 | 720.01 | |
| Overall charging time (Mh) | 1.325 | 0.04202 | |
| # of charger_1 of 5 kW: L1 | 72,331 | 185 | |
| # of charger_2 of 25 kW: L2 | 79,741 | 2754 | |
| # of charger_3 of 50 kW: L3 | 411 | 15,792 | |
| # of charger_4 of 120 kW: L4 | 476 | 13,113 | |
| Ratio (Chargers: EVs) | 0.006 | 0.1927 | |
| # of EVs served by one public charging point (PCP) | 167 | 5 | |
| Optimization Goal | Total Cost Optimized Only | Optimized Cost and Charging Time Simultaneously | Charging Time Optimized Only | ||||
|---|---|---|---|---|---|---|---|
| Obtained Results | |||||||
| Total cost (million USD) | 186.67 | 229.63 | 244.1 | 282.05 | 366.13 | 720.01 | |
| Total charging time (Mh) | 1.325 | 0.830 | 0.641 | 0.484 | 0.376 | 0.04202 | |
| Charging power (GW) | 2.432 | 2.432 | 2.432 | 2.432 | 2.432 | 2.432 | |
| # of charger_1 of 5 kW: L1 | 72,331 | 39,683 | 27,213 | 17,820 | 12,887 | 185 | |
| # of charger_2 of 25 kW: L2 | 79,741 | 75,352 | 73,849 | 66,574 | 53,472 | 2754 | |
| # of charger_3 of 50 kW: L3 | 411 | 5393 | 7411 | 11,524 | 13,654 | 15,792 | |
| # of charger_4 of 120 kW: L4 | 476 | 675 | 667 | 860 | 2908 | 13,113 | |
| Ratio (Chargers:EVs) | 0.006 | 0.04 | 0.053 | 0.082 | 0.1104 | 0.1927 | |
| # of EVs served by one PCP | 167 | 25 | 19 | 12 | 9 | 5 | |
| Country | EU Recommend | Korea | Chile | NL | China | Italy | Japan | UK | US | India | NZ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | 1:10 | 1:2 | 1:3 | 1:5 | 1:6 | 1:8 | 1:10 | 1:13 | 1:18 | 1:22 | 1:52 |
| Ratio (Chargers:EVs) | Cost (Million USD) |
|---|---|
| 1:5 | 720 |
| 1:9 | 366 |
| 1:11 | 290 |
| 1:12 | 282 |
| 1:19 | 244 |
| 1:22 | 236 |
| 1:25 | 229 |
| Ratio (Chargers:EVs) | Cost (Million USD) | Vehicle Charging Time (Hour) |
|---|---|---|
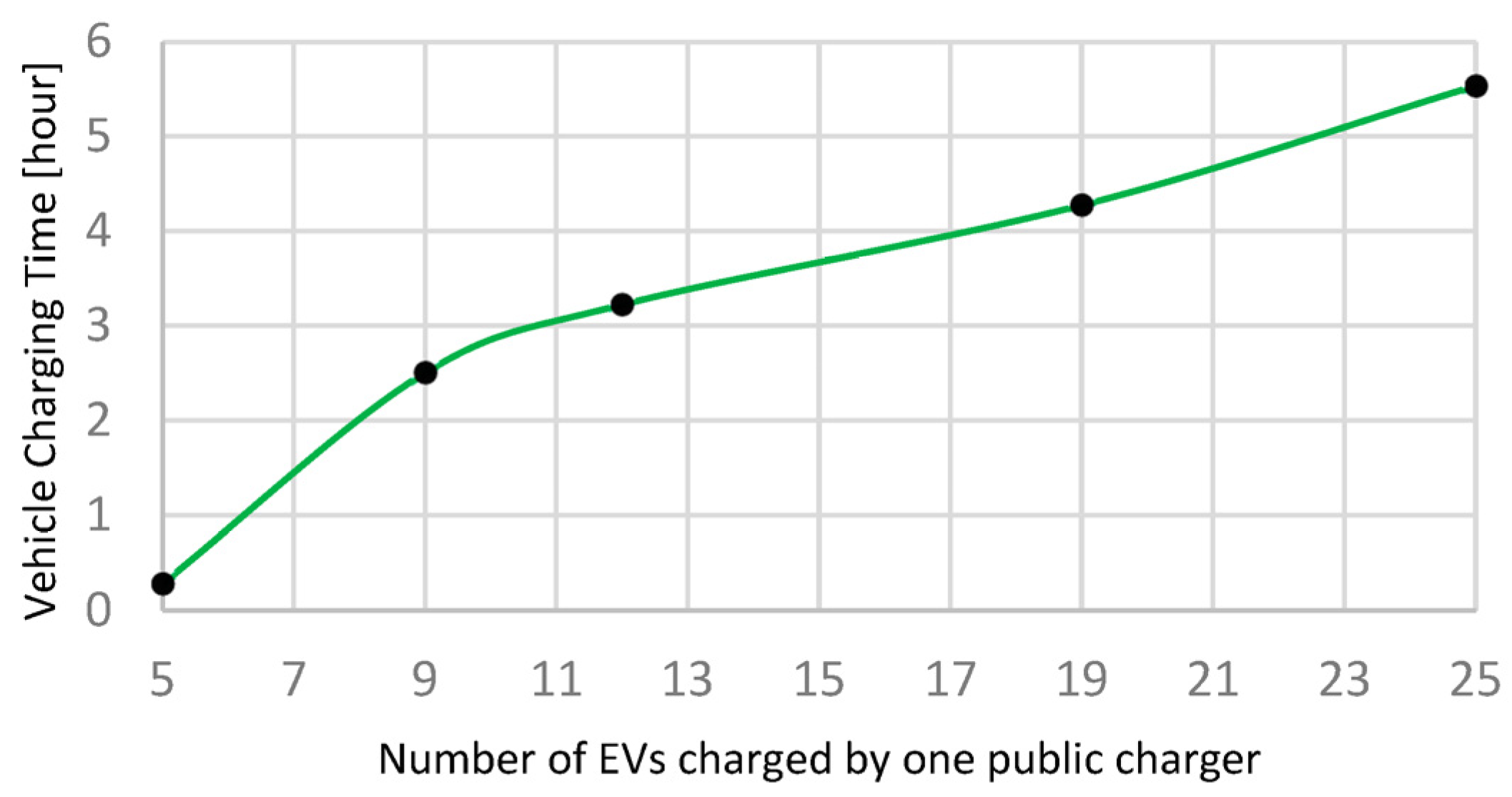
| 1:9 | 366 | 2.5 |
| 1:11 | 290 | 3:05 |
| 1:12 | 282 | 3.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azab, M. Optimum Scenarios of EV Charging Infrastructure: A Case Study for the Saudi Arabia Market. Energies 2023, 16, 5186. https://doi.org/10.3390/en16135186
Azab M. Optimum Scenarios of EV Charging Infrastructure: A Case Study for the Saudi Arabia Market. Energies. 2023; 16(13):5186. https://doi.org/10.3390/en16135186
Chicago/Turabian StyleAzab, Mohamed. 2023. "Optimum Scenarios of EV Charging Infrastructure: A Case Study for the Saudi Arabia Market" Energies 16, no. 13: 5186. https://doi.org/10.3390/en16135186
APA StyleAzab, M. (2023). Optimum Scenarios of EV Charging Infrastructure: A Case Study for the Saudi Arabia Market. Energies, 16(13), 5186. https://doi.org/10.3390/en16135186







