Modern Optimization Algorithm for Improved Performance of Maximum Power Point Tracker of Partially Shaded PV Systems
Abstract
:1. Introduction
1.1. Motivation
1.2. Innovation and Contribution
- Evaluation of the application of the DOA in a photovoltaic MPPT as a function of conversion time and failure rate.
- Calculate the best swarm size to achieve the shortest time of convergence while maintaining a zero failure rate.
- Evaluating the performance of the MPPT with different initialization strategies.
- Using a novel strategy for avoiding the stagnation of search agents in LPs.
1.3. Paper Outlines
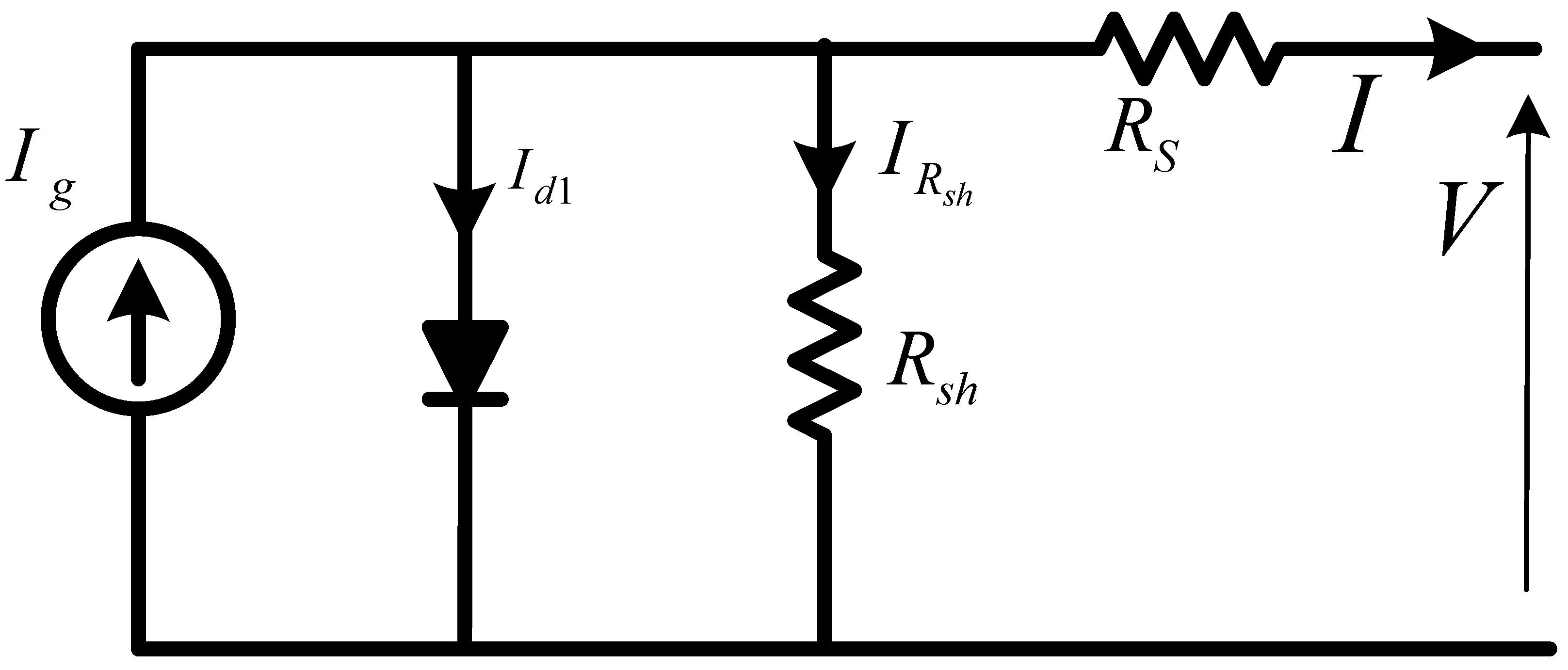
2. PV Array Modelling
3. Dandelion Optimization Algorithm
3.1. Rising Stage
3.2. Mutation Sowing
3.3. Selection Stage
3.4. Improved DOA for MPPT of PV Systems
4. Simulation Work
4.1. Optimal Design of the Boost Converter
4.2. The Best Initialization
4.3. Optimal Swarm Size
4.4. Real-Time Simulation Results
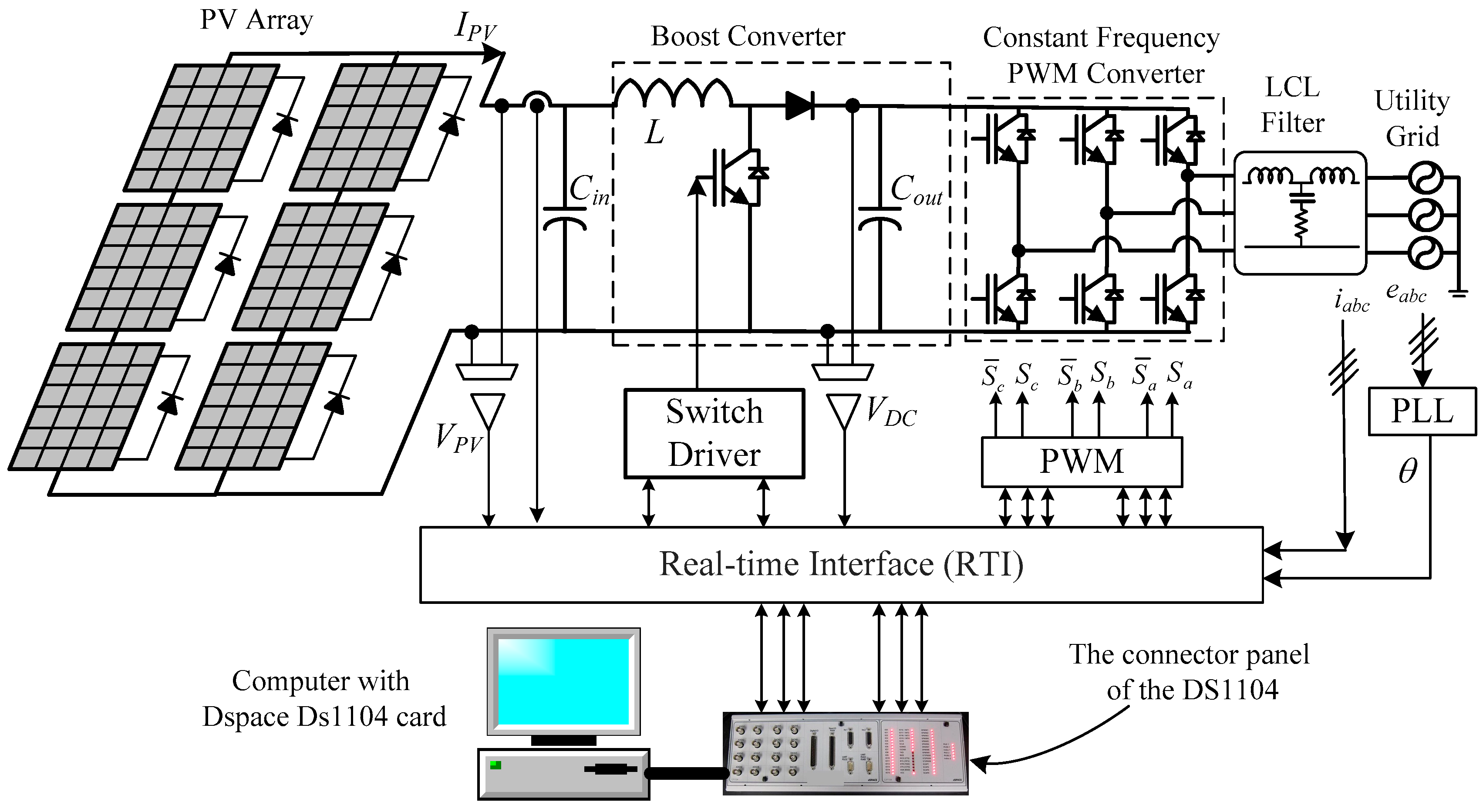
5. Experimental Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hansen, K.; Breyer, C.; Lund, H. Status and perspectives on 100% renewable energy systems. Energy 2019, 175, 471–480. [Google Scholar] [CrossRef]
- PowerWeb, a Forecast International Inc. Renewable Energy. Available online: http://www.fi-powerweb.com/Renewable-Energy.html (accessed on 10 January 2023).
- Lavrik, A.; Zhukovskiy, Y.; Tcvetkov, P. Optimizing the size of autonomous hybrid microgrids with regard to load shifting. Energies 2021, 14, 5059. [Google Scholar] [CrossRef]
- Muna, Y.B.; Kuo, C.C. Feasibility and techno-economic analysis of electric vehicle charging of PV/Wind/Diesel/Battery hybrid energy system with different battery technology. Energies 2022, 15, 4364. [Google Scholar] [CrossRef]
- Eltamaly, A. Performance of MPPT techniques of photovoltaic systems under normal and partial shading conditions. In Advances in Renewable Energies and Power Technologies; Elsevier: Amsterdam, The Netherlands, 2018; pp. 115–161. [Google Scholar]
- Premkumar, M.; Subramaniam, U.; Babu, T.S.; Elavarasan, R.M.; Mihet-Popa, L. Evaluation of mathematical model to characterize the performance of conventional and hybrid PV array topologies under static and dynamic shading patterns. Energies 2020, 13, 3216. [Google Scholar] [CrossRef]
- Eltamaly, A. Modeling of fuzzy logic controller for photovoltaic maximum power point tracker. In Solar Future 2010 Conference; Yeditepe University: Istanbul, Turkey, 2010. [Google Scholar]
- Solis-Cisneros, H.; Sevilla-Camacho, P.; Robles-Ocampo, J.; Zuñiga-Reyes, M.; Rodríguez-Resendíz, J.; Muñiz-Soria, J.; Hernández-Gutiérrez, C. A dynamic reconfiguration method based on neuro-fuzzy control algorithm for partially shaded PV arrays. Sustain. Energy Technol. Assess. 2022, 52, 102147. [Google Scholar] [CrossRef]
- Eltamaly, S. A novel particle swarm optimization optimal control parameter determination strategy for maximum power point trackers of partially shaded photovoltaic systems. Eng. Optim. 2022, 54, 634–650. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Al-Saud, M.S.; Abokhalil, A.G. A Novel Bat Algorithm Strategy for Maximum Power Point Tracker of Photovoltaic Energy Systems Under Dynamic Partial Shading. IEEE Access 2020, 8, 10048–10060. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A New MPPT Design Using Grey Wolf Optimization Technique for Photovoltaic System Under Partial Shading Conditions. IEEE Trans. Sustain. Energy 2015, 7, 181–188. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A novel musical chairs algorithm applied for MPPT of PV systems. Renew. Sustain. Energy Rev. 2021, 146, 111135. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z. A Deterministic Particle Swarm Optimization Maximum Power Point Tracker for Photovoltaic System under Partial Shading Condition. IEEE Trans. Ind. Electron. 2012, 60, 3195–3206. [Google Scholar] [CrossRef]
- Imtiaz, T.; Khan, B.H.; Khanam, N. Fast and improved PSO (FIPSO)-based deterministic and adaptive MPPT technique under partial shading conditions. IET Renew. Power Gener. 2020, 14, 3164–3171. [Google Scholar] [CrossRef]
- Merchaoui, M.; Sakly, A.; Mimouni, M. Improved fast particle swarm optimization based PV MPPT. In Proceedings of the 2018 9th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 20–22 March 2018; pp. 1–7. [Google Scholar]
- Jordehi, A.R. Time varying acceleration coefficients particle swarm optimisation (TVACPSO): A new optimisation algorithm for estimating parameters of PV cells and modules. Energy Convers. Manag. 2016, 129, 262–274. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence (Cat. No. 98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Jiao, B.; Lian, Z.; Gu, X. A dynamic inertia weight particle swarm optimization algorithm. Chaos Solitons Fractals 2008, 37, 698–705. [Google Scholar] [CrossRef]
- Koh, J.S.; Tan, R.H.; Lim, W.H.; Tan, N.M. A Modified Particle Swarm Optimization for Efficient Maximum Power Point Tracking under Partial Shading Condition. IEEE Trans. Sustain. Energy 2023, 14, 1822–1834. [Google Scholar] [CrossRef]
- Amoh Mensah, A.; Wei, X.; Otuo-Acheampong, D.; Mbuzi, T. Maximum power point tracking techniques using improved incremental conductance and particle swarm optimizer for solar power generation systems. Energy Harvest. Syst. 2023. [Google Scholar] [CrossRef]
- Chatterjee, A.; Siarry, P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization. Comput. Oper. Res. 2006, 33, 859–871. [Google Scholar] [CrossRef]
- Abdulkadir, M.; Yatim, A.H.M.; Yusuf, S.T. An Improved PSO-Based MPPT Control Strategy for Photovoltaic Systems. Int. J. Photoenergy 2014, 2014, 818232. [Google Scholar] [CrossRef] [Green Version]
- Sundareswaran, K.; Peddapati, S.; Palani, S. MPPT of PV Systems Under Partial Shaded Conditions Through a Colony of Flashing Fireflies. IEEE Trans. Energy Convers. 2014, 29, 463–472. [Google Scholar]
- Eltamaly, A.M. Optimal control parameters for bat algorithm in maximum power point tracker of photovoltaic energy systems. Int. Trans. Electr. Energy Syst. 2021, 31, e12839. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Huang, S.-C.; Huang, J.-W.; Liang, W.-C. A Particle Swarm Optimization-Based Maximum Power Point Tracking Algorithm for PV Systems Operating Under Partially Shaded Conditions. IEEE Trans. Energy Convers. 2012, 27, 1027–1035. [Google Scholar] [CrossRef]
- Chaieb, H.; Sakly, A. Comparison between P&O and PSO methods based MPPT algorithm for photovoltaic systems. In Proceedings of the 2015 16th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Monastir, Tunisia, 21–23 December 2015; pp. 694–696. [Google Scholar]
- Sundareswaran, K.; Kumar, V.V.; Palani, S. Application of a combined particle swarm optimization and perturb and observe method for MPPT in PV systems under partial shading conditions. Renew. Energy 2015, 75, 308–317. [Google Scholar] [CrossRef]
- Eltamaly, A.M. An Improved Cuckoo Search Algorithm for Maximum Power Point Tracking of Photovoltaic Systems under Partial Shading Conditions. Energies 2021, 14, 953. [Google Scholar] [CrossRef]
- da Rocha, M.; Sampaio, L.; da Silva, S. Comparative analysis of MPPT algorithms based on Bat algorithm for PV systems under partial shading condition. Sustain. Energy Technol. Assess. 2020, 40, 100761. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A Grey Wolf-Assisted Perturb & Observe MPPT Algorithm for a PV System. IEEE Trans. Energy Convers. 2017, 32, 340–347. [Google Scholar]
- Ahmed, C.; Mohammed V University in Rabat; Cherkaoui, M.; Mokhlis, M. PSO-SMC Controller Based GMPPT Technique for Photovoltaic Panel Under Partial Shading Effect. Int. J. Intell. Eng. Syst. 2020, 13, 307–316. [Google Scholar] [CrossRef]
- Kamal, N.A.; Azar, A.T.; Elbasuony, G.S.; Almustafa, K.M.; Almakhles, D. PSO-based adaptive perturb and observe MPPT technique for photovoltaic systems. In International Conference on Advanced Intelligent Systems and Informatics; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Chtita, S.; Motahhir, S.; El Hammoumi, A.; Chouder, A.; Benyoucef, A.S.; El Ghzizal, A.; Derouich, A.; Abouhawwash, M.; Askar, S.S. A novel hybrid GWO–PSO-based maximum power point tracking for photovoltaic systems operating under partial shading conditions. Sci. Rep. 2022, 12, 10637. [Google Scholar] [CrossRef]
- Davoodkhani, F.; Nowdeh, S.A.; Abdelaziz, A.Y.; Mansoori, S.; Nasri, S.; Alijani, M. A new hybrid method based on gray wolf optimizer-crow search algorithm for maximum power point tracking of photovoltaic energy system. In Modern Maximum Power Point Tracking Techniques for Photovoltaic Energy Systems; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Seyedmahmoudian, M.; Rahmani, R.; Mekhilef, S.; Oo, A.M.T.; Stojcevski, A.; Soon, T.K.; Ghandhari, A.S. Simulation and Hardware Implementation of New Maximum Power Point Tracking Technique for Partially Shaded PV System Using Hybrid DEPSO Method. IEEE Trans. Sustain. Energy 2015, 6, 850–862. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Photovoltaic Maximum Power Point Trackers: An Overview. In Advanced Technologies for Solar Photovoltaics Energy Systems. Green Energy and Technology; Motahhir, S., Eltamaly, A.M., Eds.; Springer: Cham, Switzerland, 2021; pp. 117–200. [Google Scholar] [CrossRef]
- Furtado, A.M.S.; Bradaschia, F.; Cavalcanti, M.C.; Limongi, L.R. A Reduced Voltage Range Global Maximum Power Point Tracking Algorithm for Photovoltaic Systems Under Partial Shading Conditions. IEEE Trans. Ind. Electron. 2018, 65, 3252–3262. [Google Scholar] [CrossRef]
- Xu, S.; Gao, Y.; Zhou, G.; Mao, G. A Global Maximum Power Point Tracking Algorithm for Photovoltaic Systems Under Partially Shaded Conditions Using Modified Maximum Power Trapezium Method. IEEE Trans. Ind. Electron. 2020, 68, 370–380. [Google Scholar] [CrossRef]
- Kermadi, M.; Salam, Z.; Ahmed, J.; Berkouk, E.M. A High-Performance Global Maximum Power Point Tracker of PV System for Rapidly Changing Partial Shading Conditions. IEEE Trans. Ind. Electron. 2020, 68, 2236–2245. [Google Scholar] [CrossRef]
- Boztepe, M.; Guinjoan, F.; Velasco-Quesada, G.; Silvestre, S.; Chouder, A.; Karatepe, E. Global MPPT Scheme for Photovoltaic String Inverters Based on Restricted Voltage Window Search Algorithm. IEEE Trans. Ind. Electron. 2013, 61, 3302–3312. [Google Scholar] [CrossRef]
- Kermadi, M.; Salam, Z.; Ahmed, J.; Berkouk, E.M. An Effective Hybrid Maximum Power Point Tracker of Photovoltaic Arrays for Complex Partial Shading Conditions. IEEE Trans. Ind. Electron. 2019, 66, 6990–7000. [Google Scholar] [CrossRef]
- Kermadi, M.; Salam, Z.; Eltamaly, A.M.; Ahmed, J.; Mekhilef, S.; Larbes, C.; Berkouk, E.M. Recent developments of MPPT techniques for PV systems under partial shading conditions: A critical review and performance evaluation. IET Renew. Power Gener. 2020, 14, 3401–3417. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Al-Saud, M.; Abokhalil, A.G. A novel scanning bat algorithm strategy for maximum power point tracker of partially shaded photovoltaic energy systems. Ain Shams Eng. J. 2020, 11, 1093–1103. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability. Appl. Energy 2014, 119, 118–130. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Farh, H.M.H.; Al Saud, M.S. Impact of PSO Reinitialization on the Accuracy of Dynamic Global Maximum Power Detection of Variant Partially Shaded PV Systems. Sustainability 2019, 11, 2091. [Google Scholar] [CrossRef] [Green Version]
- Cortés, B.; Tapia, R.; Flores, J.J. System-Independent Irradiance Sensorless ANN-Based MPPT for Photovoltaic Systems in Electric Vehicles. Energies 2021, 14, 4820. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Al-Saud, M.S.; Abo-Khalil, A.G. Performance Improvement of PV Systems’ Maximum Power Point Tracker Based on a Scanning PSO Particle Strategy. Sustainability 2020, 12, 1185. [Google Scholar] [CrossRef] [Green Version]
- Sevilla-Camacho, P.-Y.; Zuniga-Reyes, M.-A.; Robles-Ocampo, J.-B.; Castillo-Palomera, R.; Muniz, J.; Rodriguez-Resendiz, J. A Novel Fault Detection and Location Method for PV Arrays Based on Frequency Analysis. IEEE Access 2019, 7, 72050–72061. [Google Scholar] [CrossRef]
- Li, X.-G.; Han, S.-F.; Zhao, L.; Gong, C.-Q.; Liu, X.-J. New Dandelion Algorithm Optimizes Extreme Learning Machine for Biomedical Classification Problems. Comput. Intell. Neurosci. 2017, 2017, 4523754. [Google Scholar] [CrossRef] [Green Version]
- Eltamaly, A.M. Performance of smart maximum power point tracker under partial shading conditions of photovoltaic systems. J. Renew. Sustain. Energy 2015, 7, 043141. [Google Scholar] [CrossRef]
- Cotfas, D.; Cotfas, P.; Kaplanis, S. Methods to determine the dc parameters of solar cells: A critical review. Renew. Sustain. Energy Rev. 2013, 28, 588–596. [Google Scholar] [CrossRef]
- Khanna, V.; Das, B.; Bisht, D.; Vandana; Singh, P. A three diode model for industrial solar cells and estimation of solar cell parameters using PSO algorithm. Renew. Energy 2015, 78, 105–113. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Musical chairs algorithm for parameters estimation of PV cells. Sol. Energy 2022, 241, 601–620. [Google Scholar] [CrossRef]
- Gong, C.; Han, S.; Li, X.; Zhao, L.; Liu, X. A new dandelion algorithm and optimization for extreme learning machine. J. Exp. Theor. Artif. Intell. 2018, 30, 39–52. [Google Scholar] [CrossRef]
- Liu, X.; Qin, X. A probability-based core dandelion guided dandelion algorithm and application to traffic flow prediction. Eng. Appl. Artif. Intell. 2020, 96, 103922. [Google Scholar] [CrossRef]
- Abbassi, R.; Saidi, S.; Abbassi, A.; Jerbi, H.; Kchaou, M.; Alhasnawi, B.N. Accurate Key Parameters Estimation of PEMFCs’ Models Based on Dandelion Optimization Algorithm. Mathematics 2023, 11, 1298. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Ma, S.; Chen, M. Dandelion Optimizer: A nature-inspired metaheuristic algorithm for engineering applications. Eng. Appl. Artif. Intell. 2022, 114, 105075. [Google Scholar] [CrossRef]
- Alharbi, M.; Ragab, M.; AboRas, K.M.; Kotb, H.; Dashtdar, M.; Shouran, M.; Elgamli, E. Innovative AVR-LFC Design for a Multi-Area Power System Using Hybrid Fractional-Order PI and PIDD2 Controllers Based on Dandelion Optimizer. Mathematics 2023, 11, 1387. [Google Scholar] [CrossRef]
- Ali, M.H.; Soliman, A.M.A.; Ahmed, M.F.; Adel, A.H. Optimization of Reactive Power Dispatch Considering DG Units Uncertainty By Dandelion Optimizer Algorithm. Int. J. Renew. Energy Res. IJRER 2022, 12, 1805–1818. [Google Scholar]
- Zhu, H.; Liu, G.; Zhou, M.; Xie, Y.; Abusorrah, A.; Kang, Q. Optimizing Weighted Extreme Learning Machines for imbalanced classification and application to credit card fraud detection. Neurocomputing 2020, 407, 50–62. [Google Scholar] [CrossRef]
- Zamuda, A.; Brest, J.; Mezura-Montes, E. Structured Population Size Reduction Differential Evolution with Multiple Mutation Strategies on CEC 2013 Real Parameter Optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 1925–1931. [Google Scholar]
- Eltamaly, A.M.; Rabie, A.H. A Novel Musical Chairs Optimization Algorithm. Arab. J. Sci. Eng. 2023. [Google Scholar] [CrossRef]
- Brest, J.; Maučec, M.S. Population size reduction for the differential evolution algorithm. Appl. Intell. 2008, 29, 228–247. [Google Scholar] [CrossRef]
- Noman, N.; Iba, H. Accelerating Differential Evolution Using an Adaptive Local Search. IEEE Trans. Evol. Comput. 2008, 12, 107–125. [Google Scholar] [CrossRef]
- Neri, F.; Tirronen, V. Scale factor local search in differential evolution. Memetic Comput. 2009, 1, 153–171. [Google Scholar] [CrossRef]
- Neri, F.; Iacca, G.; Mininno, E. Disturbed Exploitation compact Differential Evolution for limited memory optimization problems. Inf. Sci. 2011, 181, 2469–2487. [Google Scholar] [CrossRef]
- Caraffini, F.; Iacca, G.; Neri, F.; Picinali, L.; Mininno, E. A CMA-ES super-fit scheme for the re-sampled inheritance search. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 1123–1130. [Google Scholar]
- Das, S.K.; Verma, D.; Nema, S.; Nema, R.K. Shading mitigation techniques: State-of-the-art in photovoltaic applications. Renew. Sustain. Energy Rev. 2017, 78, 369–390. [Google Scholar] [CrossRef]
- Amara, K.; Bakir, T.; Malek, A.; Hocine, D.; Bourennane, E.B.; Fekik, A.; Zaouia, M. An optimized steepest gradient based maximum power point tracking for PV control systems. Int. J. Electr. Eng. Inform. 2019, 11, 662–683. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A novel strategy for optimal PSO control parameters determination for PV energy systems. Sustainability 2021, 13, 1008. [Google Scholar] [CrossRef]
- Estévez-Bén, A.A.; Alvarez-Diazcomas, A.; Rodriguez-Resendiz, J. Transformerless Multilevel Voltage-Source Inverter Topology Comparative Study for PV Systems. Energies 2020, 13, 3261. [Google Scholar] [CrossRef]
- Lopez, H.; Resendiz, J.R.; Guo, X.; Vazquez, N.; Carrillo-Serrano, R.V. Transformerless Common-Mode Current-Source Inverter Grid-Connected for PV Applications. IEEE Access 2018, 6, 62944–62953. [Google Scholar] [CrossRef]


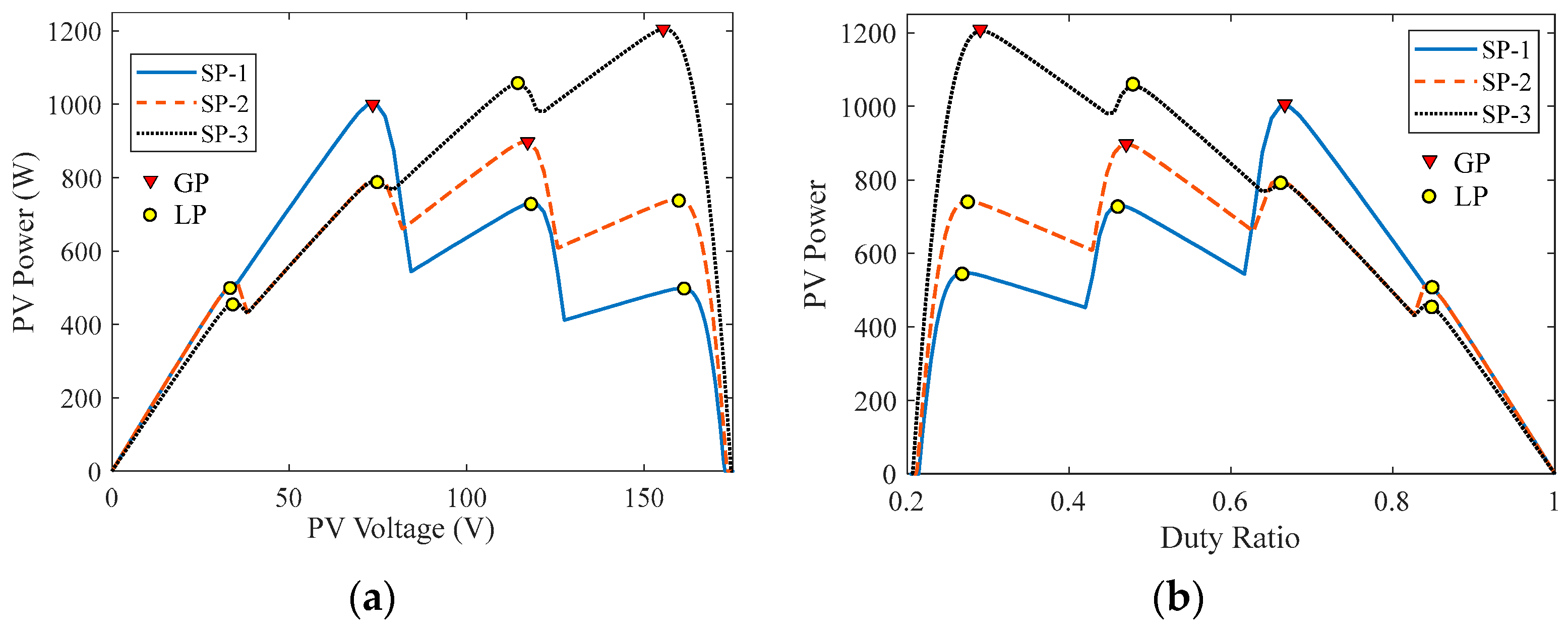
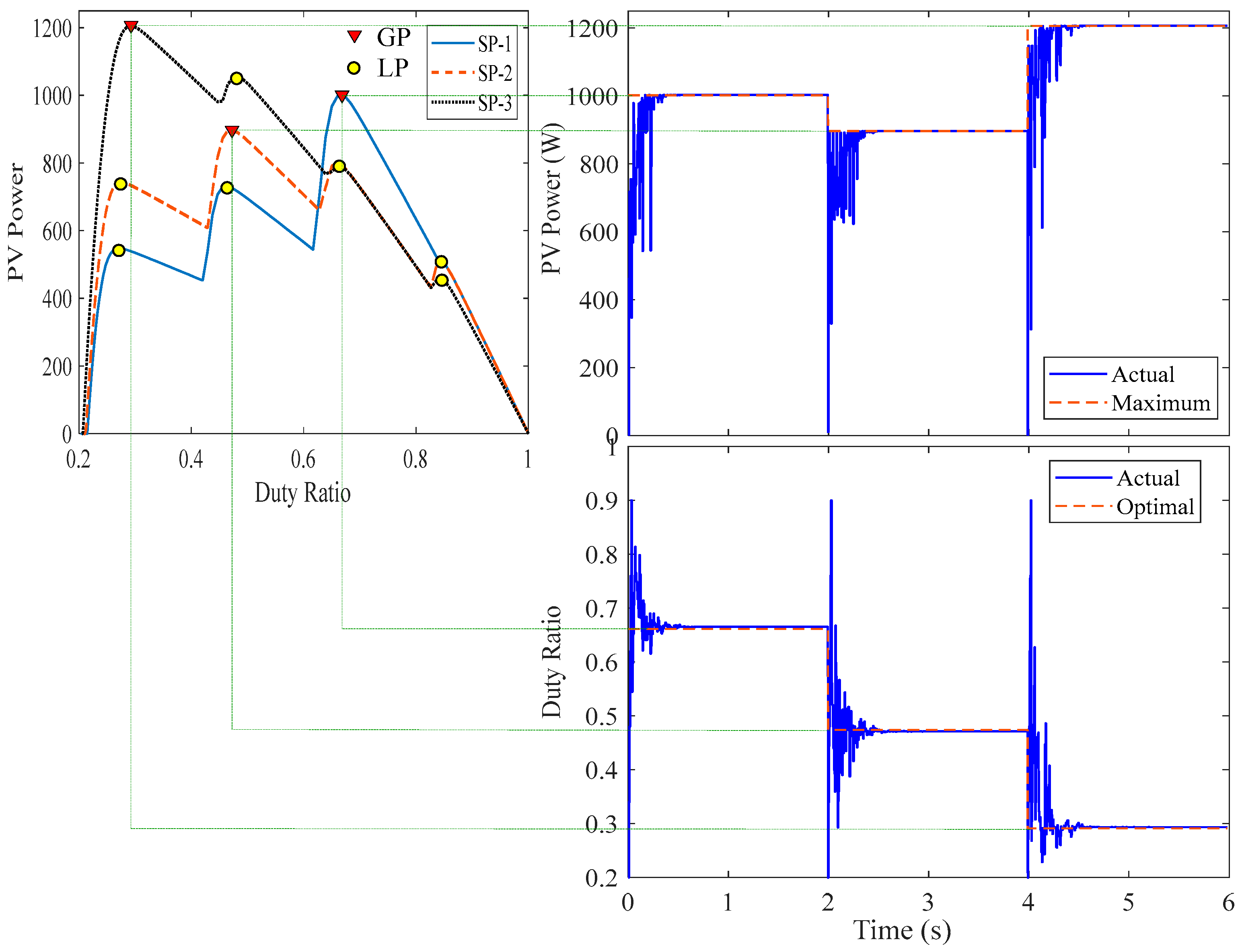
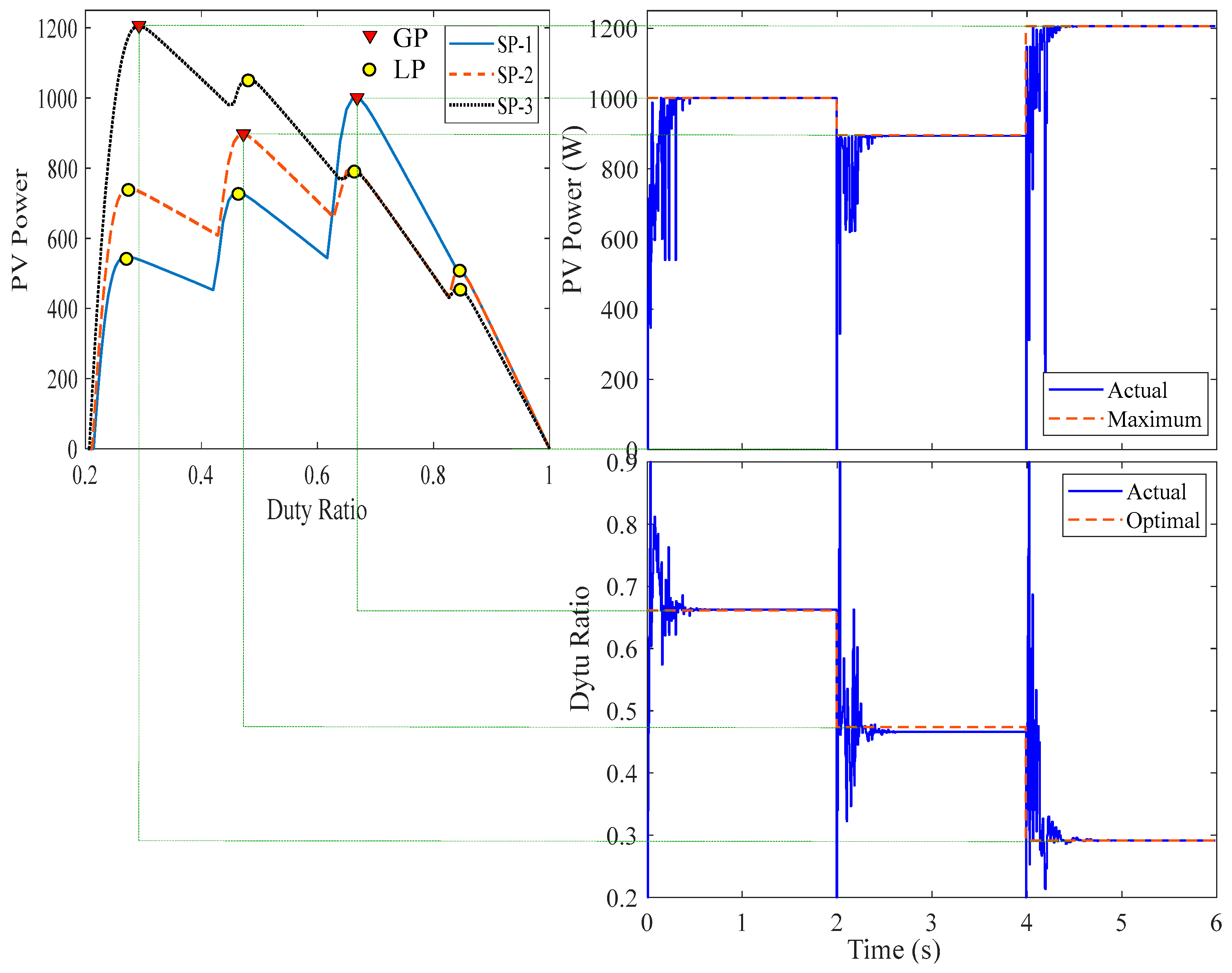




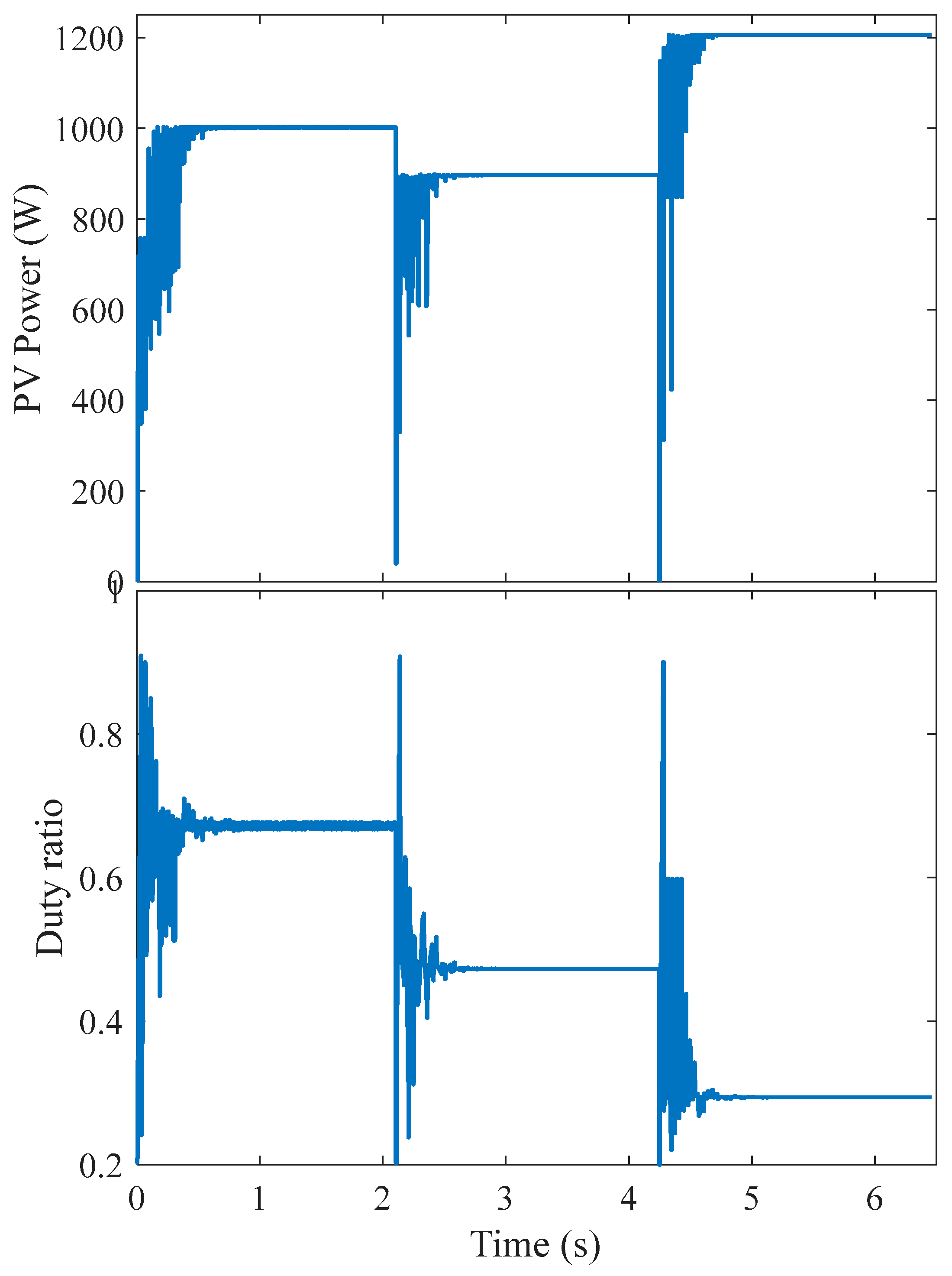

| Name | Solar Irradiances (W/m2) | GP Parameters | |||||
|---|---|---|---|---|---|---|---|
| G1 | G2 | G3 | G4 | d | V (V) | P (W) | |
| SP-1 | 1000 | 900 | 400 | 200 | 0.6613 | 74.51140 | 1001.4 |
| SP-2 | 1000 | 700 | 500 | 300 | 0.4740 | 115.7296 | 897.32 |
| SP-3 | 900 | 700 | 600 | 500 | 0.2912 | 155.9261 | 1205.8 |
| MPPT | Control Paramters |
|---|---|
| MCA [12] | Pa = 0.25, β = 1.5, α = 0.8 |
| PSO [9] | ω = 0.7298, cl = 1.4962, cg = 1.49618 |
| GWO [11] | A = 2→0, r1 = r2 = random [0, 1] |
| DOA [60] | β = 1.5, ω = 1.0 |
| Initialization Strategy | Convergence Time (s) | Failure Rate (%) |
|---|---|---|
| Random Duty Ratio | 0.49 | 2 |
| Equal Distance | 0.41 | 0 |
| Anticipated Position of the Peaks | 0.40 | 0 |
| Swarm Size | Convergence Time (s) | Failure Rate (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| DOA | MCA | PSO | GWO | DOA | MCA | PSO | GWO | |
| 3 | 0.35 | 0.38 | 0.68 | 0.49 | 6.5 | 8.1 | 11.7 | 8.8 |
| 4 | 0.39 | 0.40 | 0.82 | 0.61 | 3.3 | 4.5 | 5.8 | 4.5 |
| 5 | 0.40 | 0.41 | 1.07 | 0.78 | 1.1 | 2.1 | 3.5 | 2.2 |
| 6 | 0.41 | 0.43 | 1.25 | 0.92 | 0 | 0 | 0 | 0 |
| 7 | 0.48 | 0.51 | 1.36 | 1.06 | 0 | 0 | 0 | 0 |
| 8 | 0.57 | 0.57 | 1.44 | 1.15 | 0 | 0 | 0 | 0 |
| 9 | 0.62 | 0.61 | 1.52 | 1.21 | 0 | 0 | 0 | 0 |
| 10 | 0.65 | 0.62 | 1.58 | 1.29 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eltamaly, A.M.; Almutairi, Z.A.; Abdelhamid, M.A. Modern Optimization Algorithm for Improved Performance of Maximum Power Point Tracker of Partially Shaded PV Systems. Energies 2023, 16, 5228. https://doi.org/10.3390/en16135228
Eltamaly AM, Almutairi ZA, Abdelhamid MA. Modern Optimization Algorithm for Improved Performance of Maximum Power Point Tracker of Partially Shaded PV Systems. Energies. 2023; 16(13):5228. https://doi.org/10.3390/en16135228
Chicago/Turabian StyleEltamaly, Ali M., Zeyad A. Almutairi, and Mohamed A. Abdelhamid. 2023. "Modern Optimization Algorithm for Improved Performance of Maximum Power Point Tracker of Partially Shaded PV Systems" Energies 16, no. 13: 5228. https://doi.org/10.3390/en16135228
APA StyleEltamaly, A. M., Almutairi, Z. A., & Abdelhamid, M. A. (2023). Modern Optimization Algorithm for Improved Performance of Maximum Power Point Tracker of Partially Shaded PV Systems. Energies, 16(13), 5228. https://doi.org/10.3390/en16135228









