Inrush Current Reduction Strategy for a Three-Phase Dy Transformer Based on Pre-Magnetization of the Columns and Controlled Switching
Abstract
:1. Introduction
State of the Art
- Starting/switching phase angle of voltage;
- Residual flux in core;
- Magnitude of voltage;
- Saturation flux;
- Core material;
- Supply/source impedance;
- Load and size of transformer.
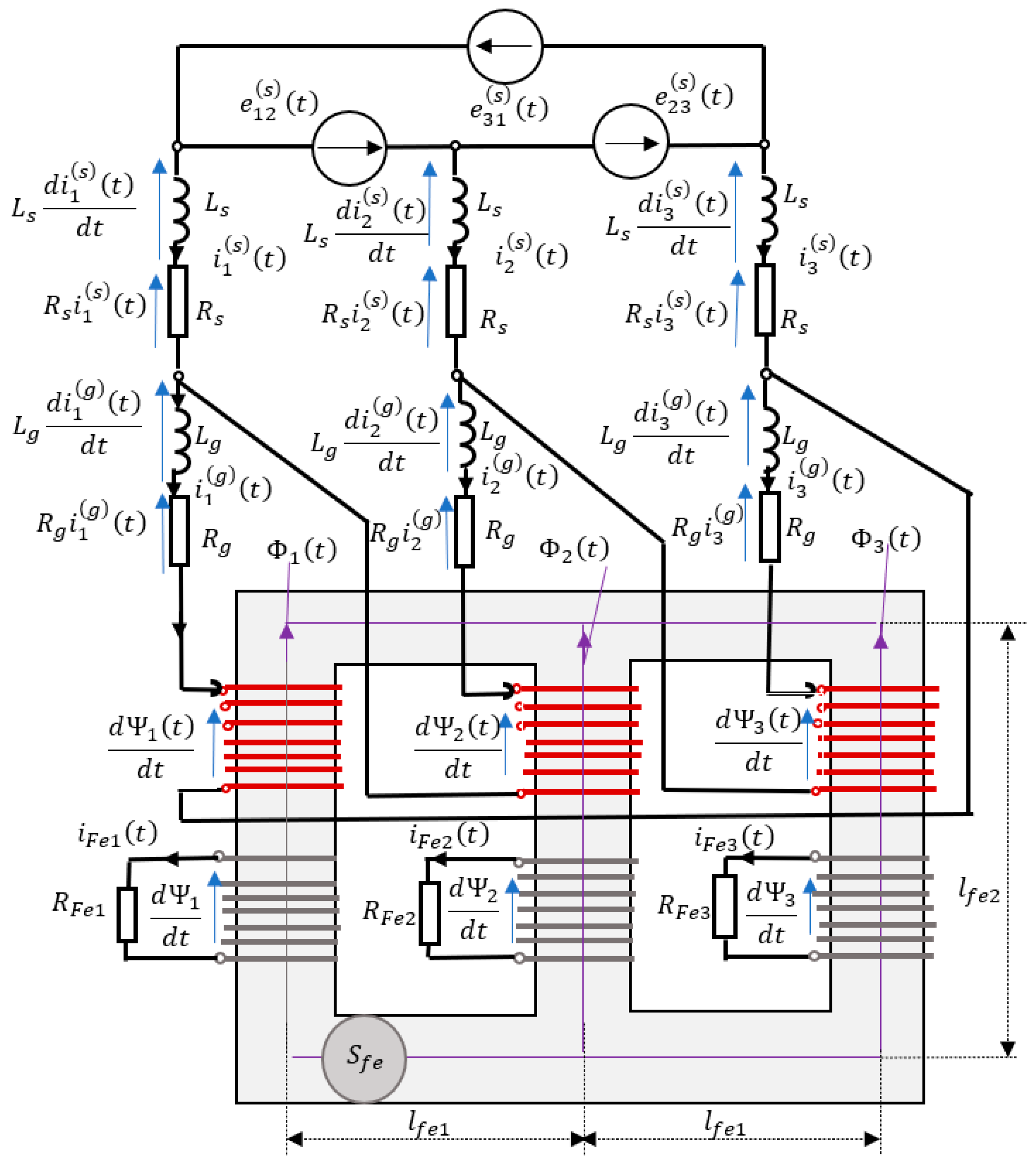
2. Model of a Three-Phase Transformer with Connection Group Dy with a Non-Linear Magnetization Curve in the No-Load State
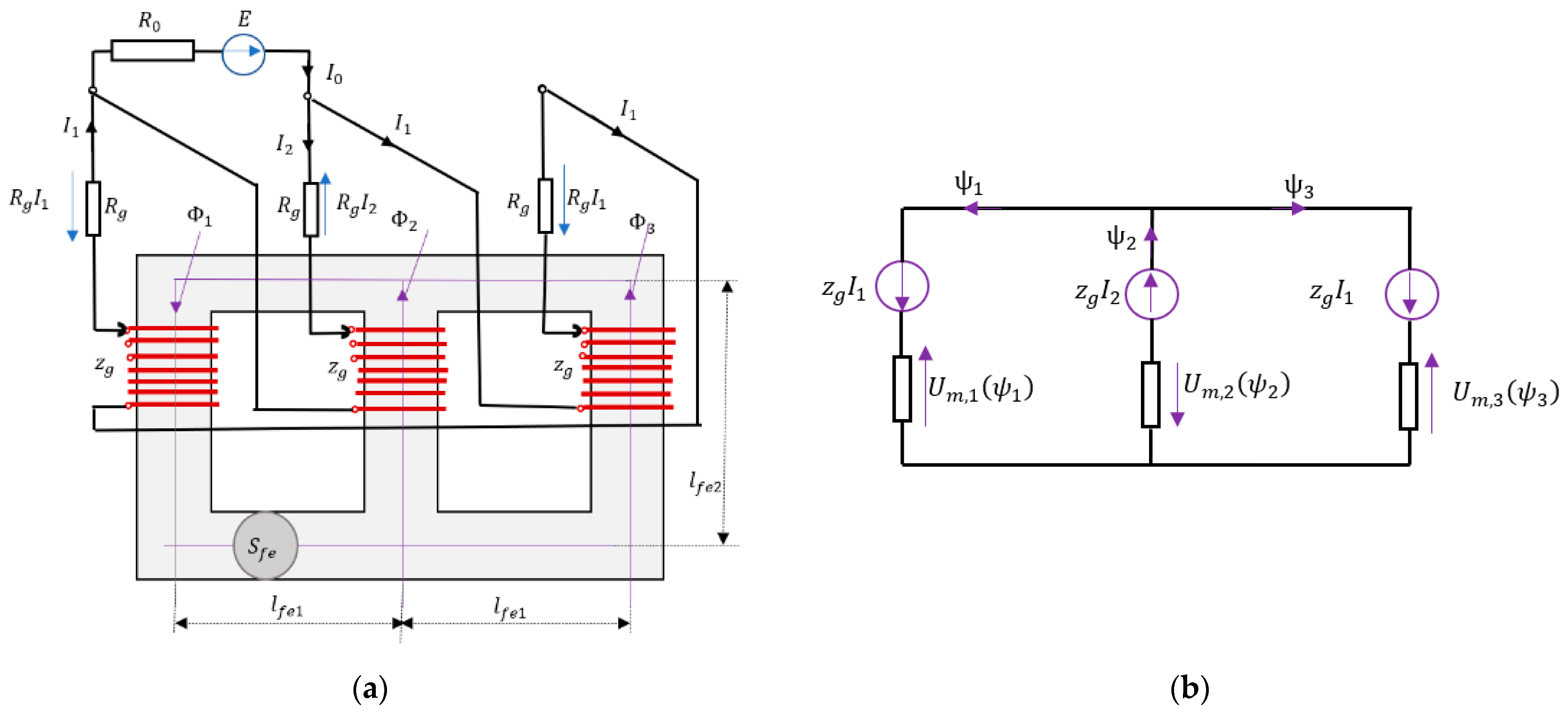
2.1. Model Concept
2.2. Residual Magnetism
2.3. Dynamic Equations of the Unloaded Transformer Dy
3. Investigation
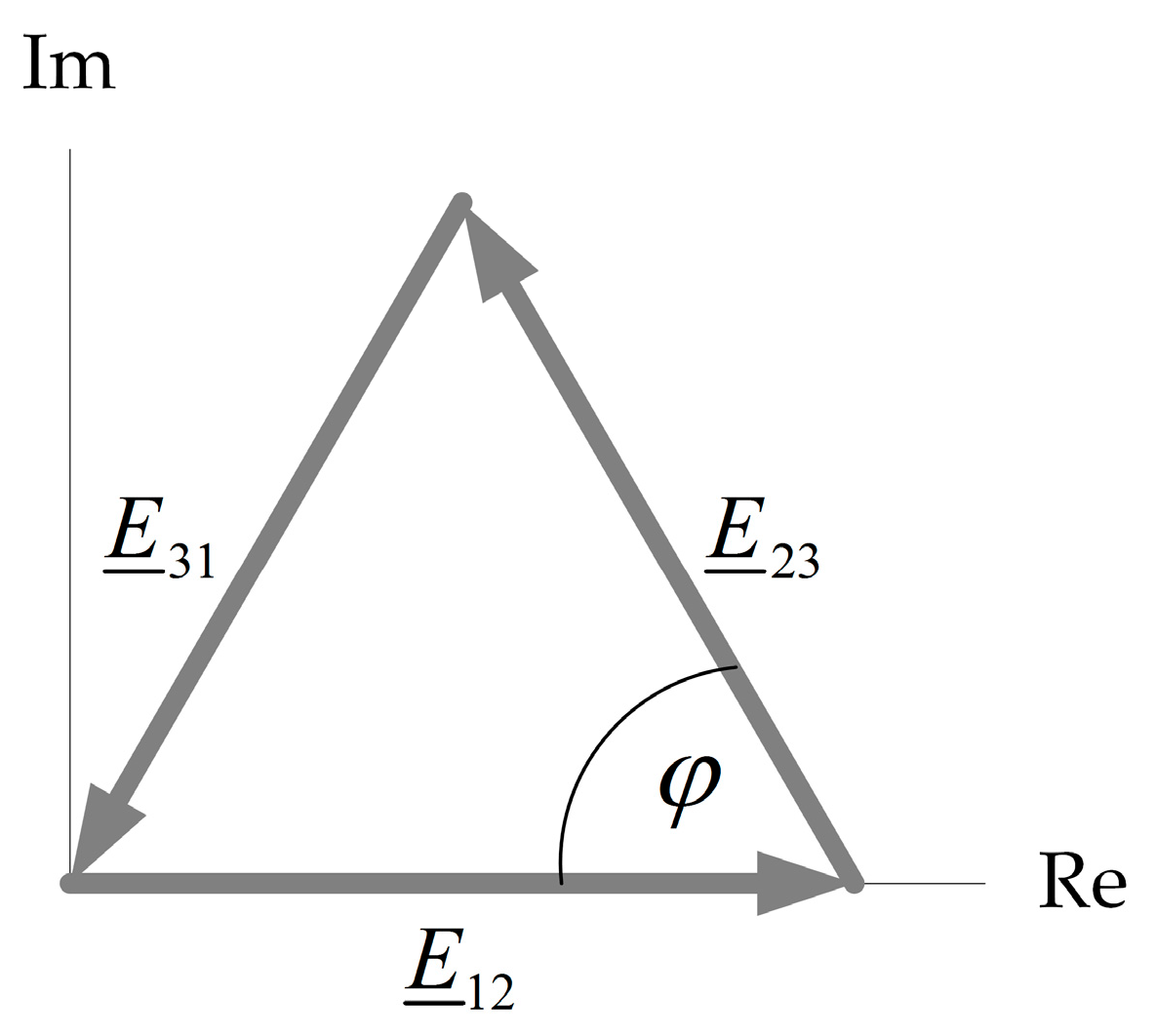
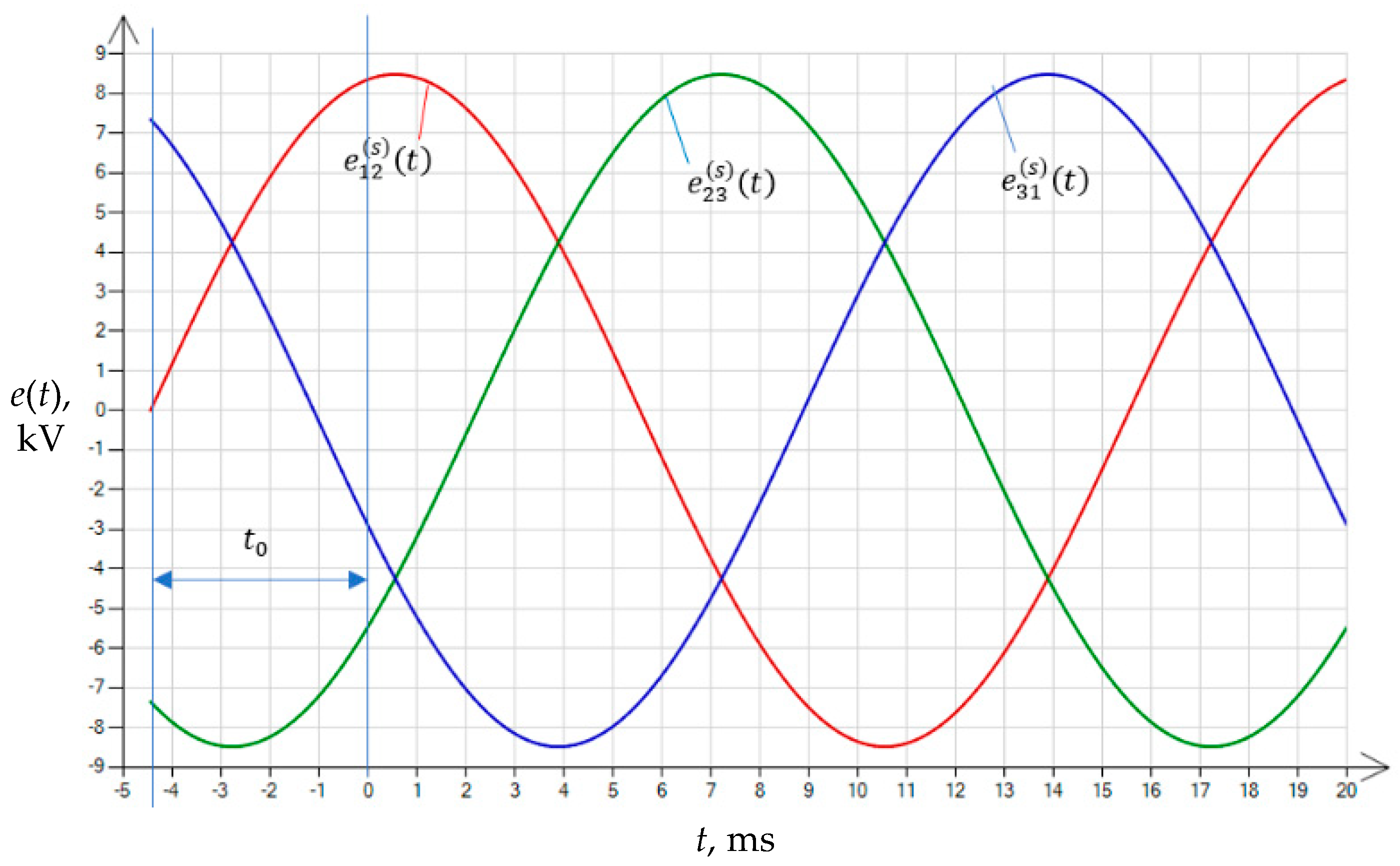
3.1. Definition of Supply Voltages Together with the Method That Takes into Account the Time Instant Determined (Set) in the Supply Voltage Waveform
3.2. Study of the Influence of Residual Magnetism on the Maximum Values of Inrush Currents of an Unloaded Transformer
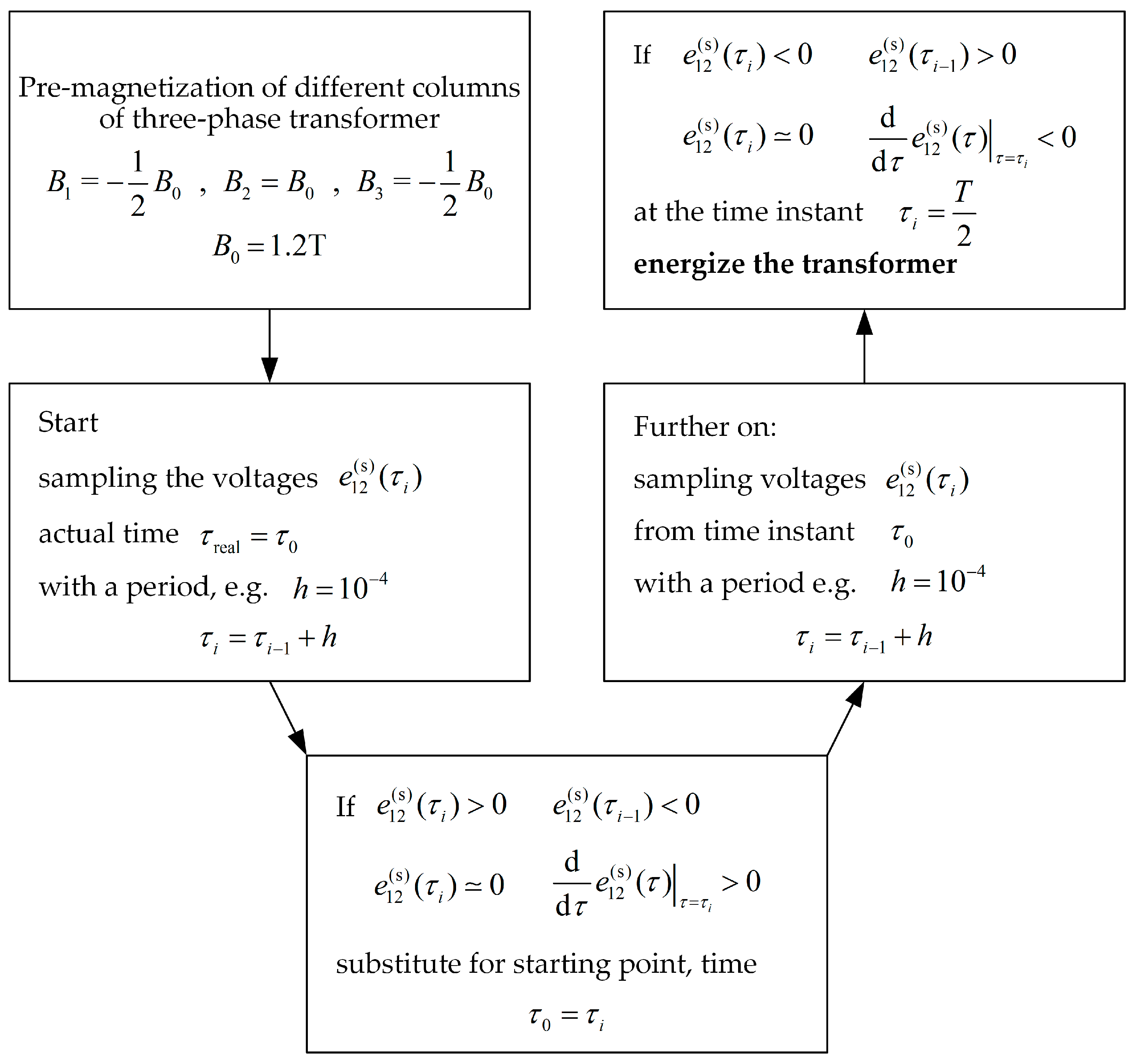
3.3. Implementation of Calculations—Calculation Algorithm
4. Simulation Results
5. Algorithm for Selecting the Time Instant Specified in the Waveform of the Switched Supply Voltage
5.1. Method of Implementation of Pre-Magnetization of the Core Columns of the Tested Transformer
5.2. Selection of the Currents Required for Core Pre-Magnetization
5.3. The Strategy of Energizing a Three-Phase, Three-Column Transformer Where Primary Winding Is Delta-Connected and Where the Columns Are Pre-Magnetized According to (20) at Specific Time Instants in the Supply Voltage Waveforms
6. The Simplifications Implied by Using the Model Formulated in this Paper
- The initial magnetization state of the transformer core can be taken into account as residual magnetism in the form of (assignable) initial conditions for the state variables , which are essentially flux linkages and , where is the residual flux density in the different columns of the transformer core.
- The integration of the equations with the initial conditions formulated in this way leads in the first instance to a solution () located deep in the saturation region of the ferromagnetic core curve; the maximum inrush currents of the unloaded transformer determined from this solution are calculated accurately.
- Taking any initial conditions (e.g., zero) for the systems of Equations (5) and (8) as the starting point leads to a steady-state solution, which is the limit cycle of the transient state solution; the trajectories of the transition to this limit cycle have no physical interpretation in this case, since the assumed mathematical model does not take into account magnetic hysteresis (it does not track the history of core magnetization).
- The model is suitable for the study of steady-state conditions of the transformer when the resistances are determined based on the idling losses, in which eddy currents and magnetic hysteresis are taken into account.
- The completed tests have shown that there is no significant influence* of the parameter of the model on the maximum values of the inrush currents of the unloaded transformer in the first period of the transient state caused by energizing the transformer (*—lossiness values provided by the manufacturer of the transformer plates vary within wide limits).
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| e | sinusoidal supply voltage |
| Ψk | flux linkage associated with the transformer’s primary coil, computed as Ψk(t) = zgΦk(t), in the column of the transformer |
| ik(g) | transformer primary current |
| RFe,k | equivalent resistance representing the iron core losses |
| iFe,k | active component of the transformer’s idle current |
| Rs | equivalent resistance of the power grid (power source) |
| Ls | equivalent inductance (reactance) of the power grid (power source) |
| Rg | primary winding resistance |
| Lg | leakage inductance of the primary winding |
| H | magnetic field strength |
| Φ | main flux leakage (effective value of the flux) |
| Bk | flux density |
| sFe | cross-sectional area of the core of the transformer |
| zg | number of turns in the primary windings |
| φ0 | phase of the initial supplied voltage |
| ω | pulse |
Appendix A
| Quantity, Unit | Value |
|---|---|
| Primary voltage PRI/phase to phase, V | 6000 |
| Secondary voltage SEC/phase to phase, V | 230 |
| Frequency | 50 |
| Rated primary current, A | 800 |
| Number of primary winding turns, N | 160 |
| Iron power loss (for 1.7 T), W/kg | 1.05 |
| Copper power loss, kW | 50 |
| Short-circuit voltage, % | 5 |
| Core cross-sections, m2 | 0.110565 |
| Column length, m | 2 |
| Length of the yoke, m | 0.76 |
| Equivalent resistance of the network, Ω | 0.1 |
| Equivalent reactance of the network, Ω | 0.2 |
| 1 | 29.9624271037522 |
| 2 | −76.4912078883278 |
| 3 | 420.867774746849 |
| 4 | −1274.37623231261 |
| 5 | 2196.27285444425 |
| 6 | −2301.93260519503 |
| 7 | 1516.77585894405 |
| 8 | −630.577358829122 |
| 9 | 160.397849549712 |
| 10 | −22.7840824031901 |
| 11 | 1.38472183966324 |
References
- CIGRÉ Working Group. C4.307. Transformer Energization in Power Systems: A Study Guide, 568th ed.; CIGRÉ Publication: Paris, France, 2014; pp. 8–73. [Google Scholar]
- Kulkarn, S.V.; Khaparde, S.A. Transformer Engineering: Design, Technology, and Diagnostics, 2nd ed.; Taylor & Francis Inc.: Boca Raton, FL, USA, 2012; pp. 1–750. [Google Scholar]
- Majka, Ł.; Baron, B.; Zydroń, P. Measurement-based stiff equation methodology for single phase transformer inrush current computations. Energies 2022, 15, 7651. [Google Scholar] [CrossRef]
- Barros, R.M.R.; da Costa, E.G.; Araujo, J.F.; de Andrade, F.L.M.; Ferreira, T.V. Contribution of inrush current to mechanical failure of power transformers windings. High Volt. 2019, 4, 300–307. [Google Scholar] [CrossRef]
- Steurer, M.; Frohlich, K. The impact of inrush currents on the mechanical stress of high voltage power transformer coils. IEEE Trans. Power Deliv. 2002, 17, 155–160. [Google Scholar] [CrossRef]
- Pandey, S.B.; Lin, C. Estimation for a life model of transformer insulation under combined electrical and thermal stress. IEEE Trans. Reliab. 1992, 41, 466–468. [Google Scholar] [CrossRef]
- Alassi, A.; Ahmed, K.H.; Egea-Alvarez, A.; Foote, C. Transformer Inrush Current Mitigation Techniques for Grid-Forming Inverters Dominated Grids. IEEE Trans. Power Deliv. 2023, 38, 1610–1620. [Google Scholar] [CrossRef]
- Hamilton, R. Analysis of transformer inrush current and comparison of harmonic restraint methods in transformer protection. IEEE Trans. Ind. Appl. 2013, 49, 1890–1899. [Google Scholar] [CrossRef]
- Ni, R.; Wang, P.; Moxley, R.; Flemming, S.; Schneider, S. False Trips on Transformer Inrush-Avoiding the Unavoidable. In Proceedings of the 68th Annual Conference for Protective Relay Engineers, College Station, TX, USA, 30 March–2 April 2015. [Google Scholar]
- Nagpal, M.; Martinich, T.G.; Moshref, A.; Morison, K.; Kundur, P.P. Assessing and limiting impact of transformer inrush current on power quality. IEEE Trans. Power Deliv. 2006, 21, 890–896. [Google Scholar] [CrossRef]
- Blume, L.F.; Camilli, G.; Farnham, S.B.; Peterson, H.A. Transformer magnetizing inrush currents and influence on system operation. Trans. Am. Inst. Electr. Eng. 1944, 63, 366–375. [Google Scholar] [CrossRef]
- Horiszny, J. Analysis and Reduction of Transformer Inrush Current; Gdansk University of Technology: Gdańsk, Poland, 2016; p. monograph 159. (In Polish) [Google Scholar]
- Chiesa, N.; Mork, B.A.; Høidalen, H.K. Transformer model for inrush current calculations: Simulations, measurements and sensitivity analysis. IEEE Trans. Power Deliv. 2010, 25, 2599–2608. [Google Scholar] [CrossRef]
- Brunke, J.H.; Frohlich, K.J. Elimination of transformer inrush currents by controlled switching. Part I. Theoretical considerations. IEEE Trans. Power Deliv. 2001, 16, 276–280. [Google Scholar] [CrossRef]
- Leite, J.V.; Benabou, A.; Sadowski, N. Transformer Inrush Currents Taking into Account Vector Hysteresis. IEEE Trans. Magn. 2010, 46, 3237–3240. [Google Scholar] [CrossRef]
- Cui, Y.; Abdulsalam, S.G.; Chen, S.; Xu, W. A sequential phase energization technique for transformer inrush current reduction. Part I: Simulation and experimental results. IEEE Trans. Power Del. 2005, 20, 943–949. [Google Scholar] [CrossRef]
- Chraygane, M.; El Ghazal, N.; Fadel, M.; Bahani, B.; Belhaiba, A.; Ferfra, M.; Bassoui, M. Improved modeling of new three-phase high voltage transformer with magnetic shunts. Arch. Electr. Eng. 2015, 64, 157–172. [Google Scholar] [CrossRef]
- Horiszny, J. Research of leakage magnetic field in deenergized transformer. Compel-Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 1657–1667. [Google Scholar] [CrossRef]
- Mitra, J.; Xu, X.; Benidris, M. Reduction of three-phase transformer inrush currents using controlled switching. IEEE Trans. Ind. Appl. 2020, 56, 890–897. [Google Scholar] [CrossRef]
- Ni, H.; Fang, S.; Lin, H. A simplified phase-controlled switching strategy for inrush current reduction. IEEE Trans. Power Del. 2021, 36, 215–222. [Google Scholar] [CrossRef]
- Cano-González, R.; Bachiller-Soler, A.; Rosendo-Macías, J.A.; Álvarez-Cordero, G. Inrush current mitigation in three-phase transformers with isolated neutral. Electr. Power Syst. Res. 2015, 121, 14–19. [Google Scholar] [CrossRef]
- Nicolet, A.; Delince, F. Implicit Runge–Kutta methods for transient magnetic field computation. IEEE Trans. Magn. 1996, 32, 1405–1408. [Google Scholar] [CrossRef]
- Noda, T.; Takenaka, K.; Inoue, T. Numerical integration by the 2-stage diagonally implicit Runge–Kutta method for electromagnetic transient simulations. IEEE Trans. Power Del. 2009, 24, 390–399. [Google Scholar] [CrossRef]
- Pries, J.; Hoffmann, H. State Algorithms for Nonlinear Time-Periodic Magnetic Diffusion Problems Using Diagonally Implicit Runge–Kutta Methods. Magn. IEEE Trans. 2015, 51, 7208612. [Google Scholar] [CrossRef]
- Sowa, M. Ferromagnetic coil frequency response and dynamics modeling with fractional elements. Electr. Eng. 2021, 103, 1737–1752. [Google Scholar] [CrossRef]
- Sowa, M.; Majka, Ł.; Wajda, K. Excitation system voltage regulator modeling with the use of fractional calculus. AEU-Int. J. Electron. Commun. 2023, 159, 154471. [Google Scholar] [CrossRef]
- Baron, B.; Kolańska-Płuska, J.; Lukaniszyn, M.; Spałek, D.; Kraszewski, T. Solution of nonlinear stiff differential equations for a three-phase no-load transformer using a Runge-Kutta implicit method. Arch. Electr. Eng. 2022, 71, 1081–1106. [Google Scholar]
- Baron, B.; Kolańska-Płuska, J.; Waindok, A.; Kraszewski, T.; Kawala-Sterniuk, A. Application of Runge–Kutta implicit methods for solving stiff non-linear differential equations of a single-phase transformer model in the no-load state. Innovation Management and information Technology impact on Global Economy in the Era of Pandemic. In Proceedings of the 37th International Business Information Management Association Conference (IBIMA), Cordoba, Spain, 1–2 April 2021; pp. 8071–8087. [Google Scholar]
- Baron, B.; Kolańska-Płuska, J.; Kraszewski, T. Application of Runge–Kutta implicit methods to solve the rigid differential equations of a single-phase idle transformer model. Pozn. Univ. Technol. Acad. J. Electr. Eng. 2019, 100, 75–86. (In Polish) [Google Scholar]
- Baron, B.; Kolańska-Płuska, J. Numerical Methods of Solving Ordinary Differential Equations in C#; Politechnika Opolska Publisher: Opole, Poland, 2015. (In Polish) [Google Scholar]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Dekker, K.; Verwer, J.G. Stability of Runge–Kutta Methods for Stiff Nonlinear Differential Equations; North-Holland: Amsterdam, The Netherlands; New York, NY, USA; Oxford, UK, 1984. [Google Scholar]
- Dos Passos, W. Numerical Methods Algorithms and Tools in C#; CRC Press, Taylor & Francis Group LLC: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2010; ebook-PDF; Available online: https://vdocuments.mx/numerical-methods-algorithms-and-tools-in-c-586e04e116cbc.html?page=1 (accessed on 11 April 2023).
- Majka, Ł.; Szuster, D. Application of the stationary DC decay test to industrial turbogenerator model parameter estimation. Przegląd Elektrotechniczny 2014, 90, 242–245. [Google Scholar]
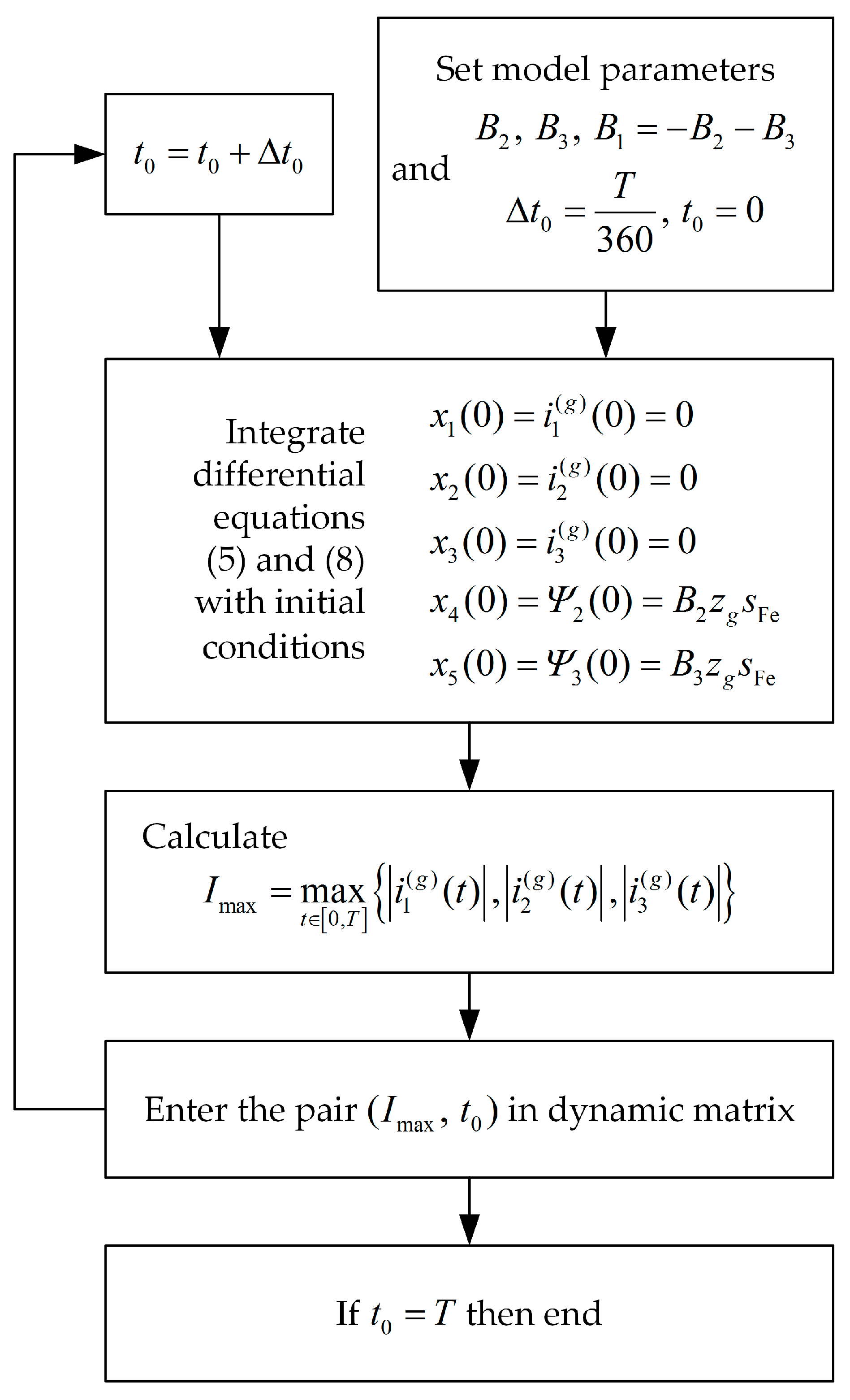
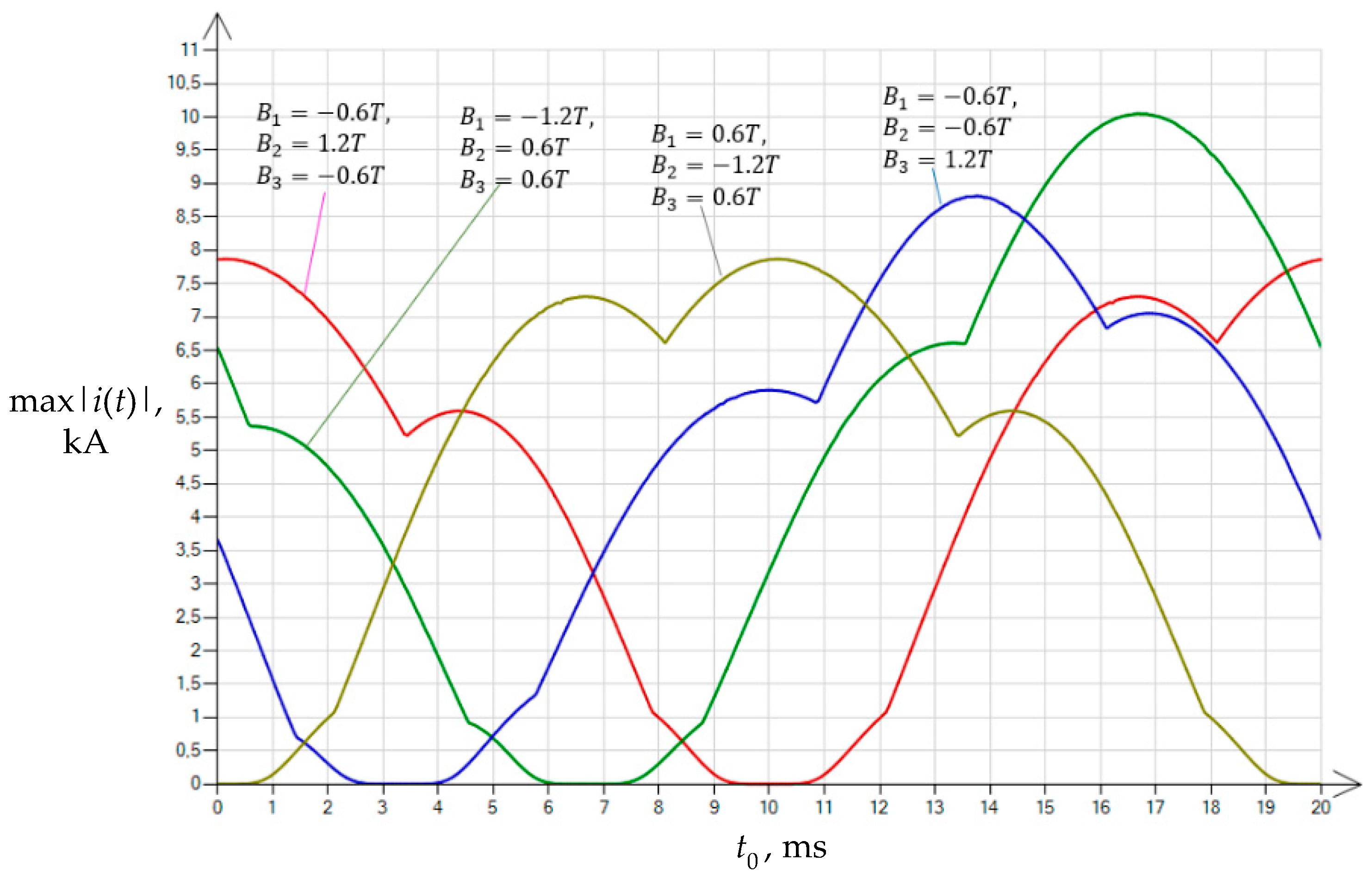

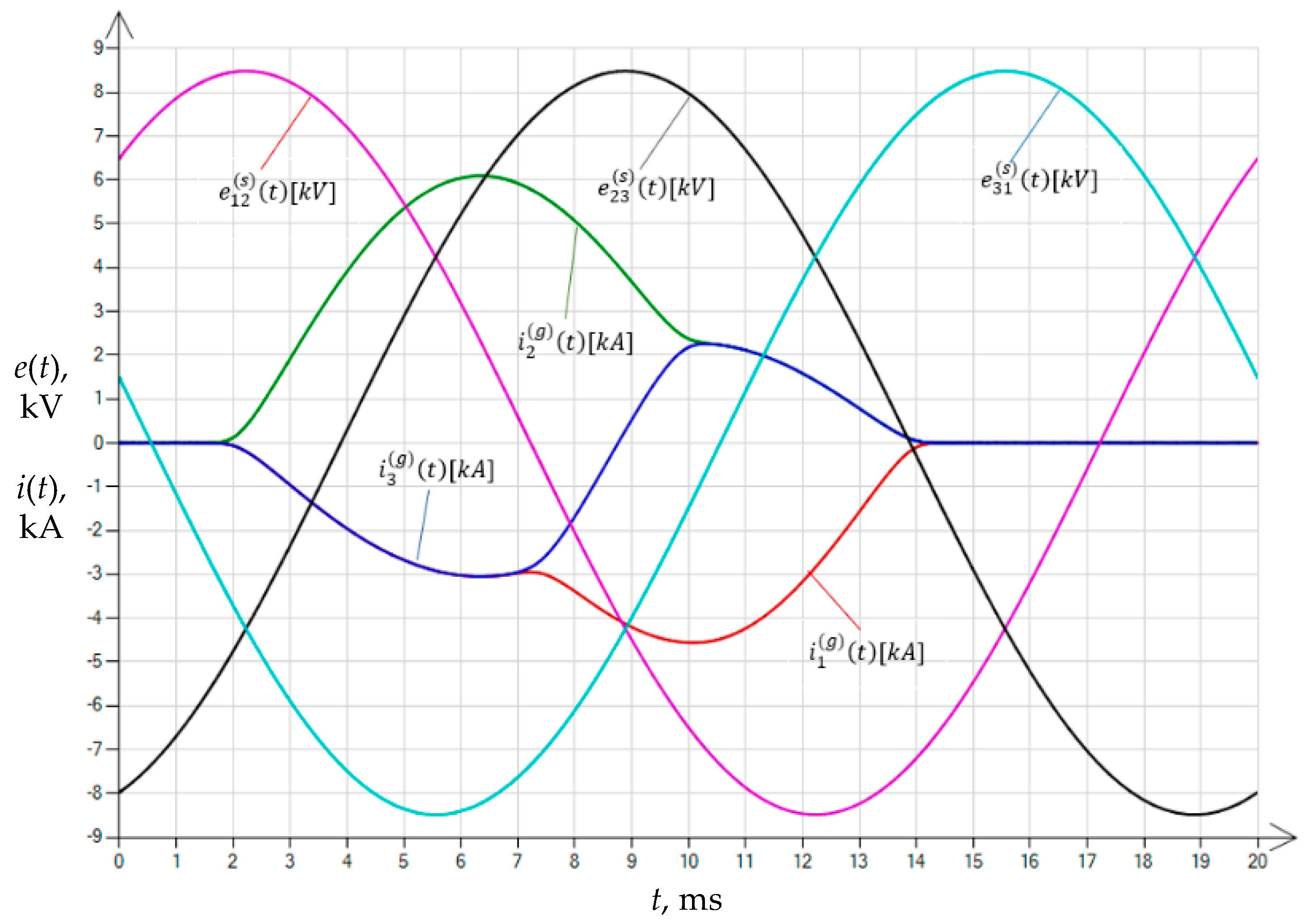
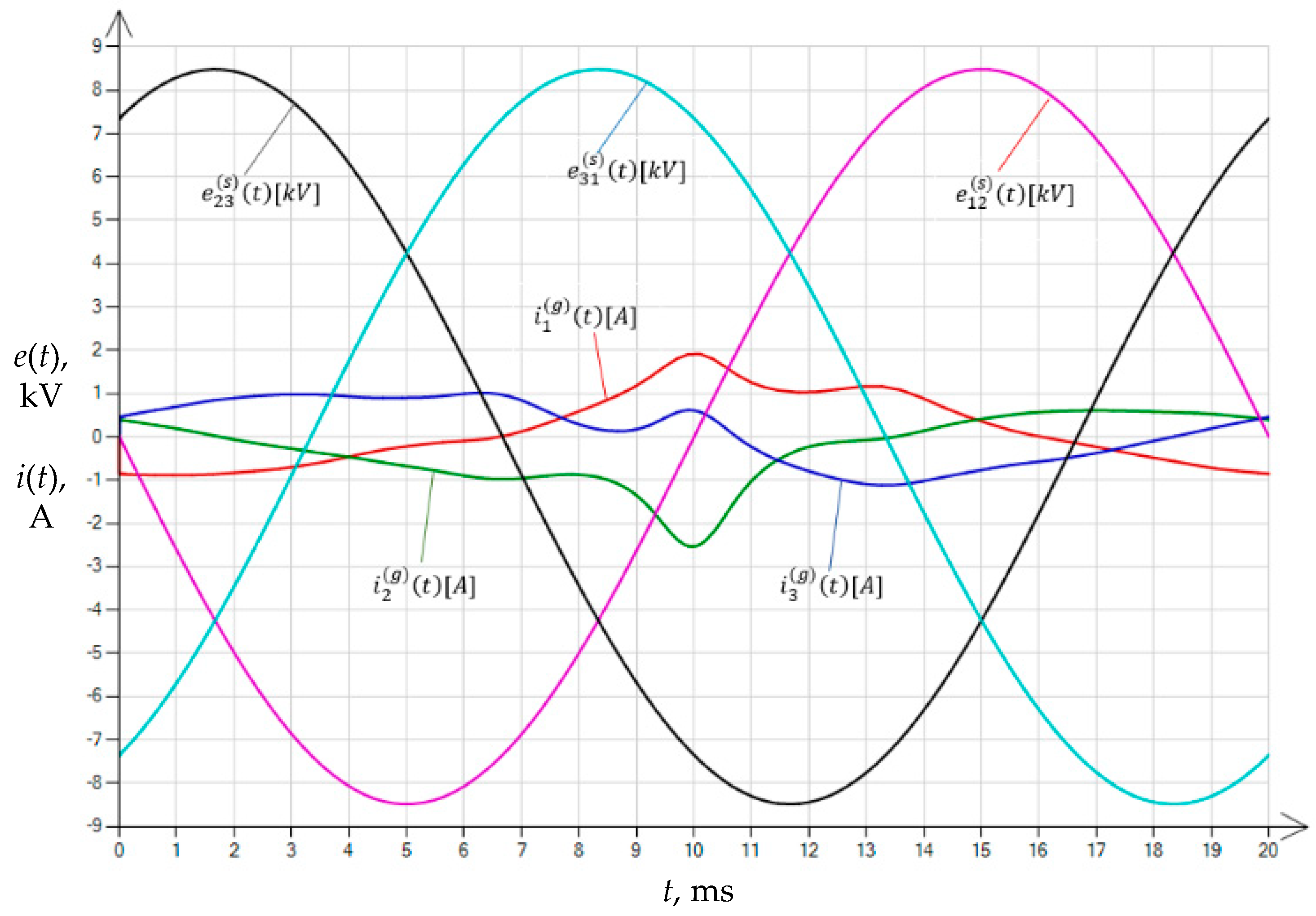

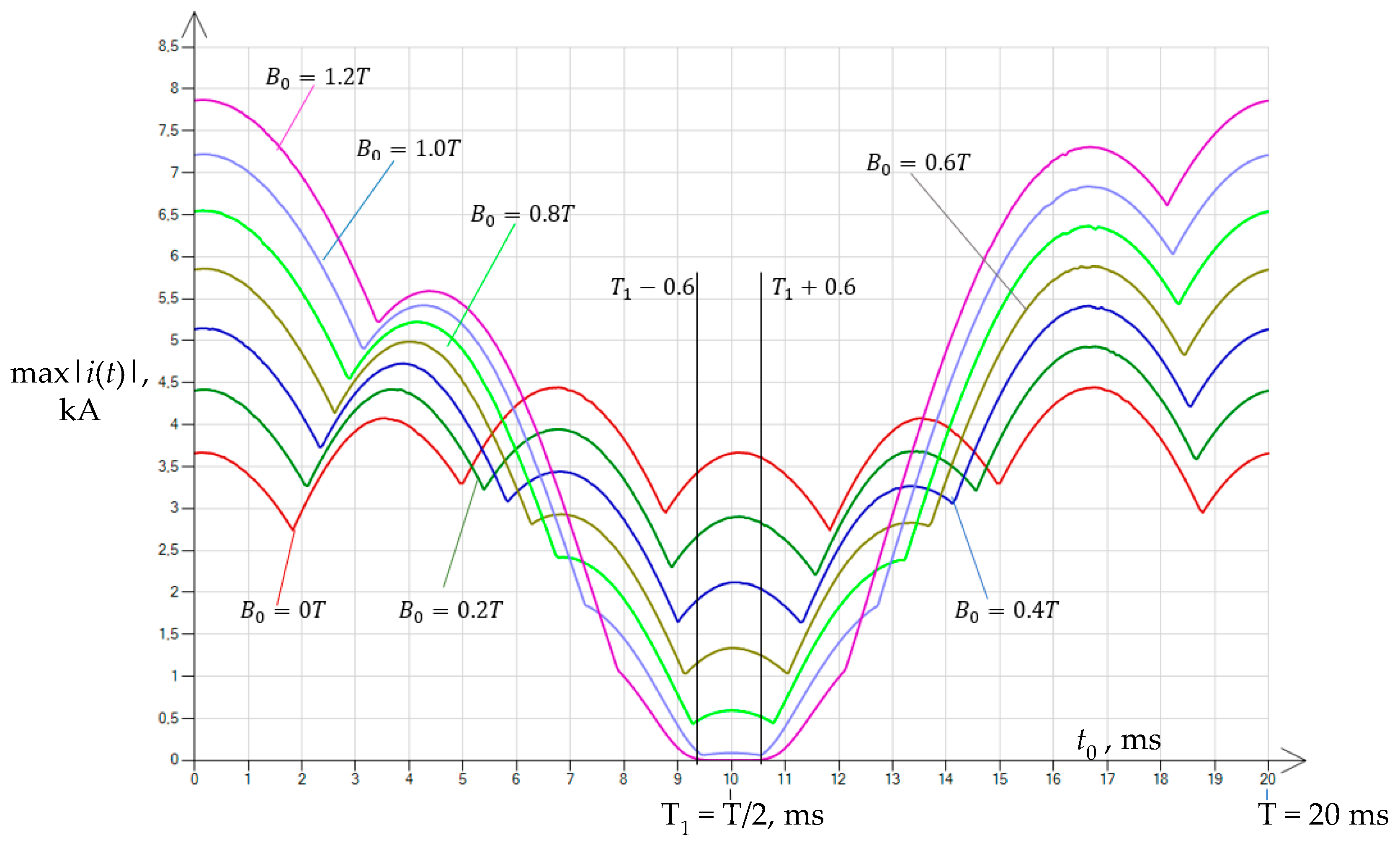

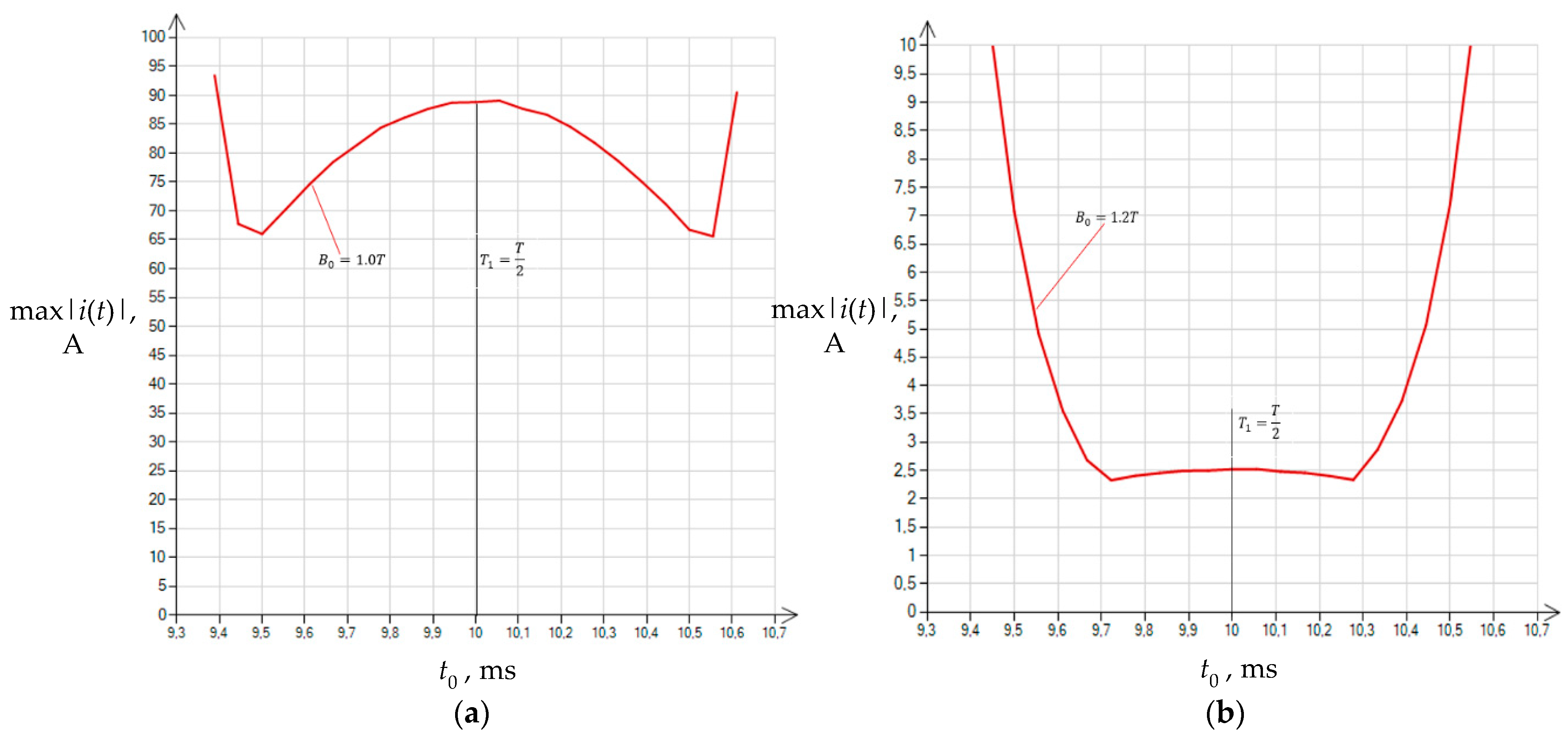
| Variant | |||
|---|---|---|---|
| 1 | −0.6 | 1.2 | −0.6 |
| 2 | −1.2 | 0.6 | 0.6 |
| 3 | −0.6 | −0.6 | 1.2 |
| 4 | 0.6 | −1.2 | 0.6 |
| Type | ||||||
|---|---|---|---|---|---|---|
| 1 | −1 | 0 | 0 | |||
| 2 | 1 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łukaniszyn, M.; Baron, B.; Kolańska-Płuska, J.; Majka, Ł. Inrush Current Reduction Strategy for a Three-Phase Dy Transformer Based on Pre-Magnetization of the Columns and Controlled Switching. Energies 2023, 16, 5238. https://doi.org/10.3390/en16135238
Łukaniszyn M, Baron B, Kolańska-Płuska J, Majka Ł. Inrush Current Reduction Strategy for a Three-Phase Dy Transformer Based on Pre-Magnetization of the Columns and Controlled Switching. Energies. 2023; 16(13):5238. https://doi.org/10.3390/en16135238
Chicago/Turabian StyleŁukaniszyn, Marian, Bernard Baron, Joanna Kolańska-Płuska, and Łukasz Majka. 2023. "Inrush Current Reduction Strategy for a Three-Phase Dy Transformer Based on Pre-Magnetization of the Columns and Controlled Switching" Energies 16, no. 13: 5238. https://doi.org/10.3390/en16135238






