Optimal Parameter Identification of a PEM Fuel Cell Using Recent Optimization Algorithms
Abstract
:1. Introduction
2. Electrochemical Reaction Inside a PEMFC
Fuel Cell Modeling Mathematically
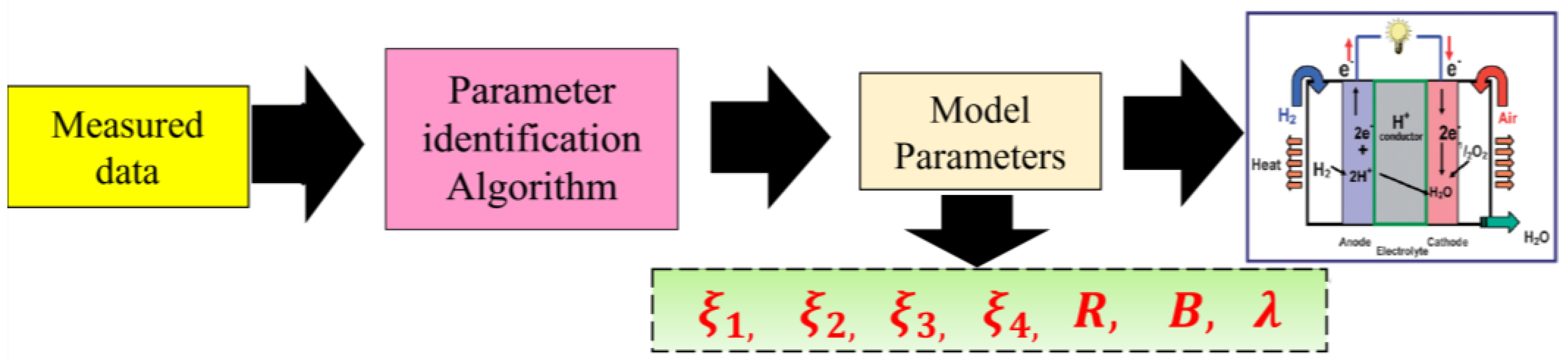
3. PEMFC-Parameter-Estimation Approach
4. Bald Eagle Search Algorithm
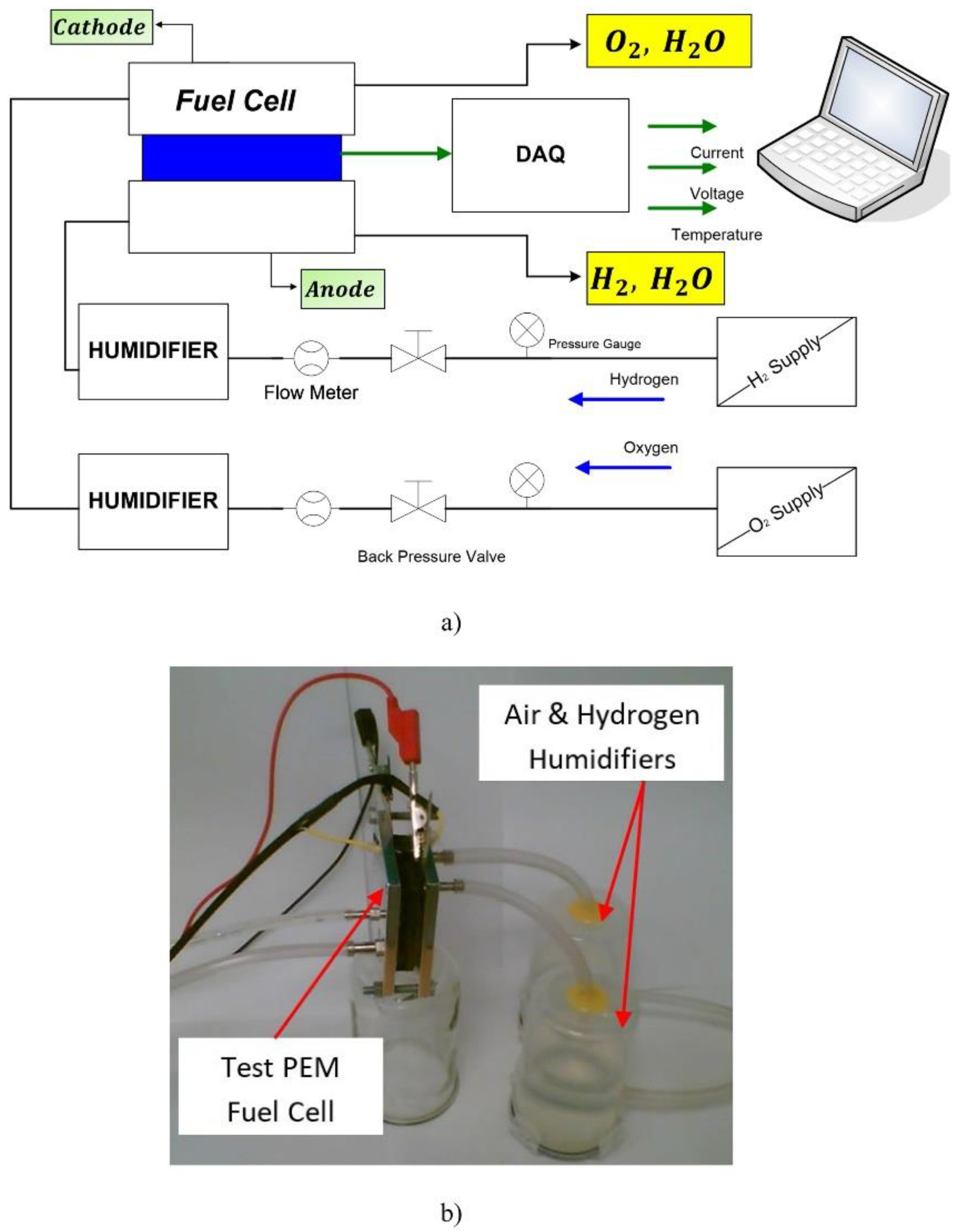
5. Experimental Procedure
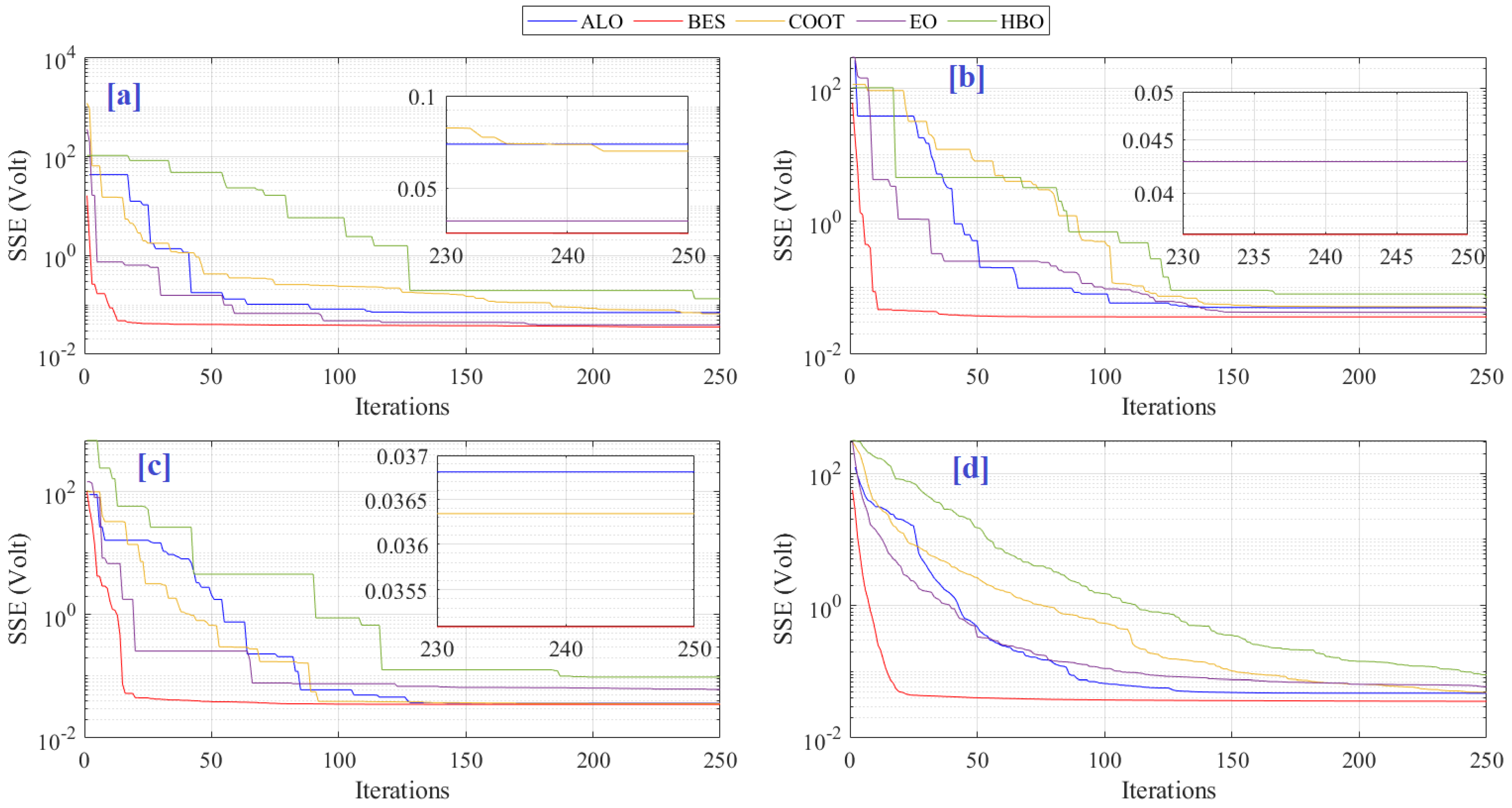
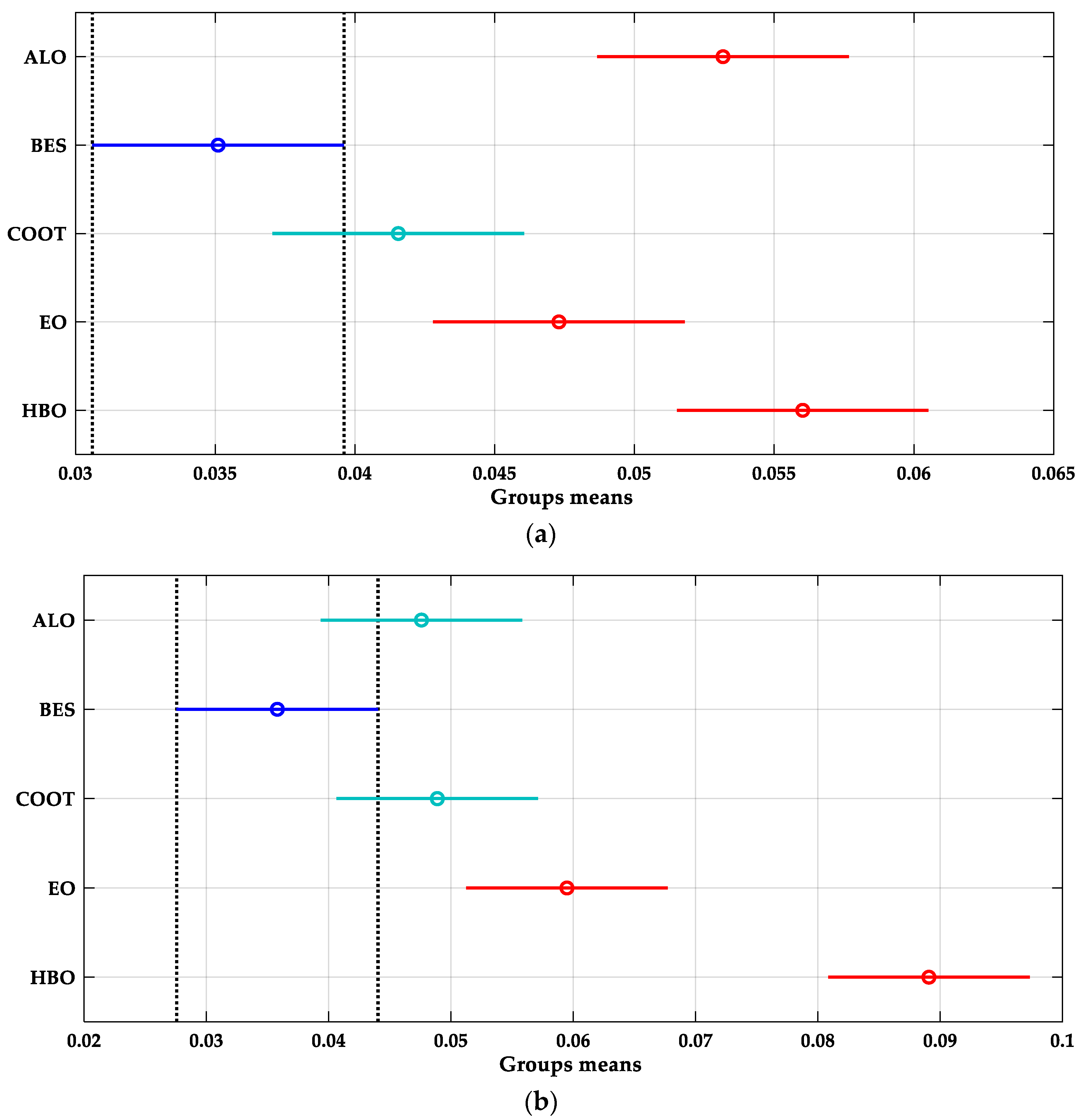
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Variable | ALO | BES | COOT | EO | HBO |
|---|---|---|---|---|---|
| nmax 500 | |||||
| 0.11768 | 0 | 0.0287 | 0.03125 | 0.31464 | |
| 0.000544 | 0 | 0.000444 | 0.000316 | 0.001607 | |
| 0.0000117 | 0 | 0.0000345 | 0.0000142 | 0.000041 | |
| 0 | 0 | 0 | 0 | 1 × 10−6 | |
| 0 | 0 | 1.01675 | 0.0006 | 0.00813 | |
| 0 | 0 | 2.4 × 10−5 | 1.6 × 10−5 | 0.000571 | |
| 0 | 0 | 1.2 × 10−5 | 1 × 10−6 | 0.000049 | |
| nmax 250 | |||||
| 0.17366 | 0 | 0.12019 | 0.07958 | 0.04924 | |
| 0.0002 | 0 | 0.00019 | 0.00016 | 0.00024 | |
| 2.23 × 10−5 | 0 | 3.67 × 10−5 | 5.7 × 10−6 | 5.2 × 10−6 | |
| 0 | 0 | 0 | 0 | 0 | |
| 2 × 10−5 | 0 | 5.23322 | 2.23775 | 6.8724 | |
| 0.00011 | 0 | 0.000128 | 9.2 × 10−5 | 0.001531 | |
| 0.00001 | 0 | 0.000105 | 3.9 × 10−5 | 0.00027 | |
References
- Ali, M.N.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Promising MPPT methods combining metaheuristic, fuzzy-logic and ANN techniques for grid-connected photovoltaic. Sensors 2021, 21, 1244. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X.; Liu, Y.; Bucknall, R. A novel design of a solid oxide fuel cell-based combined cooling, heat and power residential system in the U. K. IEEE Trans. Ind. Appl. 2021, 57, 805–813. [Google Scholar] [CrossRef]
- Ihonen, J.; Koski, P.; Pulkkinen, V.; Keränen, T.; Karimäki, H.; Auvinen, S.; Nikiforow, K.; Kotisaari, M.; Tuiskula, H.; Viitakangas, J. Operational experiences of PEMFC pilot plant using low grade hydrogen from sodium chlorate production process. Int. J. Hydrogen Energy 2017, 42, 27269–27283. [Google Scholar] [CrossRef]
- Qiu, Y.; Wu, P.; Miao, T.; Liang, J.; Jiao, K.; Li, T.; Lin, J.; Zhang, J. An intelligent approach for contact pressure optimization of PEM fuel cell gas diffusion layers. Appl. Sci. 2020, 10, 4194. [Google Scholar] [CrossRef]
- Ahmed, K.; Farrok, O.; Rahman, M.M.; Ali, M.S.; Haque, M.M.; Azad, A.K. Proton exchange membrane hydrogen fuel cell as the grid connected power generator. Energies 2020, 13, 6679. [Google Scholar] [CrossRef]
- Nikiforow, K.; Pennanen, J.; Ihonen, J.; Uski, S.; Koski, P. Power ramp rate capabilities of a 5 kW proton exchange membrane fuel cell system with discrete ejector control. J. Power Sources 2018, 381, 30–37. [Google Scholar] [CrossRef]
- Menesy, A.S.; Sultan, H.M.; Korashy, A.; Banakhr, F.A.; Ashmawy, M.G.; Kamel, S. Effective parameter extraction of different polymer electrolyte membrane fuel cell stack models using a modified artificial ecosystem optimization algorithm. IEEE Access 2020, 8, 31892–31909. [Google Scholar] [CrossRef]
- Tanveer, W.H.; Rezk, H.; Nassef, A.; Abdelkareem, M.A.; Kolosz, B.; Karuppasamy, K.; Aslam, J.; Gilani, S.O. Improving fuel cell performance via optimal parameters identification through fuzzy logic based-modeling and optimization. Energy 2020, 204, 117976. [Google Scholar] [CrossRef]
- Sundén, B. Fuel cell types—Overview. In Hydrogen, Batteries and Fuel Cells; Sundén, B., Ed.; Academic Press: Cambridge, MA, USA, 2019; pp. 123–144. [Google Scholar] [CrossRef]
- Fathy, A.; Rezk, H. Multi-verse optimizer for identifying the optimal parameters of PEMFC model. Energy 2018, 143, 634–644. [Google Scholar] [CrossRef]
- Ashraf, H.; Abdellatif, S.O.; Elkholy, M.M.; El-Fergany, A.A. Computational techniques based on artificial intelligence for extracting optimal parameters of PEMFCs: Survey and insights. Arch. Comput. Methods Eng. 2022, 29, 3943–3972. [Google Scholar] [CrossRef]
- Rezk, H.; Olabi, A.G.; Sayed, E.; Wilberforce, T. Role of Metaheuristics in Optimizing Microgrids Operating and Management Issues: A Comprehensive Review. Sustainability 2023, 15, 4982. [Google Scholar] [CrossRef]
- Zhu, Y.; Yousefi, N. Optimal parameter identification of PEMFC stacks using adaptive sparrow search algorithm. Int. J. Hydrogen Energy 2021, 46, 9541–9552. [Google Scholar] [CrossRef]
- Yousri, D.; Mirjalili, S.; Machado, J.T.; Thanikanti, S.B.; Fathy, A.; Elbaksawi, O. Efficient fractional-order modified Harris Hawks optimizer for proton exchange membrane fuel cell modeling. Eng. Appl. Artif. Intell. 2021, 100, 104193. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, W.; Wang, H.; Yildizbasi, A. Developed coyote optimization algorithm and its application to optimal parameters estimation of PEMFC model. Energy Rep. 2020, 6, 1106–1117. [Google Scholar] [CrossRef]
- Bao, S.; Ebadi, A.; Toughani, M.; Dalle, J.; Maseleno, A.; Baharuddin; Yıldızbası, A. A new method for optimal parameters identification of a PEMFC using an improved version of monarch butterfly optimization algorithm. Int. J. Hydrogen Energy 2020, 45, 17882–17892. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; El-Fergany, A.; Chakrabortty, R.K.; Ryan, M.J. Adaptive and efficient optimization model for optimal parameters of proton exchange membrane fuel cells: A comprehensive analysis. Energy 2021, 233, 121096. [Google Scholar] [CrossRef]
- Wilberforce, T.; Rezk, H.; Olabi, A.G.; Epelle, E.I.; Abdelkareem, M.A. Comparative analysis on parametric estimation of a PEM fuel cell using metaheuristics algorithms. Energy 2023, 262 Pt B, 125530. [Google Scholar] [CrossRef]
- Fathy, A.; Elaziz, M.A.; Alharbi, A.G. A novel approach based on hybrid vortex search algorithm and differential evolution for identifying the optimal parameters of PEM fuel cell. Renew. Energy 2020, 146, 1833–1845. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, W.; Wang, H. Optimal parameter estimation for PEMFC using modified monarch butterfly optimization. Int. J. Energy Res. 2020, 44, 8427–8441. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Ali, H.; Abdul-Ghaffar, H.; Abdelsalam, H.A.; Abd El Sattar, M. Accurate parameters extraction of PEMFC model based on metaheuristics algorithms. Energy Rep. 2021, 7, 6854–6867. [Google Scholar] [CrossRef]
- Gupta, J.; Nijhawan, P.; Ganguli, S. Optimal parameter estimation of PEM fuel cell using slime mould algorithm. Int. J. Energy Res. 2021, 45, 14732–14744. [Google Scholar] [CrossRef]
- Qin, F.; Liu, P.; Niu, H.; Song, H.; Yousefi, N. Parameter estimation of PEMFC based on improved fluid search optimization algorithm. Energy Rep. 2020, 6, 1224–1232. [Google Scholar] [CrossRef]
- Yang, B.; Li, D.; Zeng, C.; Chen, Y.; Guo, Z.; Wang, J.; Shu, H.; Yu, T.; Zhu, J. Parameter extraction of PEMFC via Bayesian regularization neural network based meta-heuristic algorithms. Energy 2021, 228, 120592. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, W.; Wang, H.; Razmjooy, N. A new technique for optimal estimation of the circuit-based PEMFCs using developed Sunflower Optimization Algorithm. Energy Rep. 2020, 6, 662–671. [Google Scholar] [CrossRef]
- Sun, S.; Su, Y.; Yin, C.; Jermsittiparsert, K. Optimal parameters estimation of PEMFCs model using converged moth search algorithm. Energy Rep. 2020, 6, 1501–1509. [Google Scholar] [CrossRef]
- Chen, Y.; Pi, D.; Wang, B.; Chen, J.; Xu, Y. Bi-subgroup optimization algorithm for parameter estimation of a PEMFC model. Expert Syst. Appl. 2022, 196, 116646. [Google Scholar] [CrossRef]
- Syah, R.; Isola, L.A.; Guerrero, J.W.G.; Suksatan, W.; Sunarsi, D.; Elveny, M.; Alkaim, A.F.; Thangavelu, L.; Aravindhan, S. Optimal parameters estimation of the PEMFC using a balanced version of Water Strider Algorithm. Energy Rep. 2021, 7, 6876–6886. [Google Scholar] [CrossRef]
- Guo, H.; Tao, H.; Salih, S.Q.; Yaseen, Z.M. Optimized parameter estimation of a PEMFC model based on improved grass fibrous root optimization algorithm. Energy Rep. 2020, 6, 1510–1519. [Google Scholar] [CrossRef]
- Özdemir, M.T. Optimal parameter estimation of polymer electrolyte membrane fuel cells model with chaos embedded particle swarm optimization. Int. J. Hydrogen Energy 2021, 46, 16465–16480. [Google Scholar] [CrossRef]
- Mossa, M.A.; Kamel, O.M.; Sultan, H.M.; Diab, A.A.Z. Parameter estimation of PEMFC model based on Harris Hawks’ optimization and atom search optimization algorithms. Neural Comput. Appl. 2021, 33, 5555–5570. [Google Scholar] [CrossRef]
- Rezk, H.; Ferahtia, S.; Djeroui, A.; Chouder, A.; Houari, A.; Machmoum, M.; Abdelkareem, M.A. Optimal parameter estimation strategy of PEM fuel cell using gradient-based optimizer. Energy 2022, 239, 122096. [Google Scholar] [CrossRef]
- Zhang, G.; Xiao, C.; Razmjooy, N. Optimal parameter extraction of PEM fuel cells by meta-heuristics. Int. J. Ambient Energy 2020, 43, 2510–2519. [Google Scholar] [CrossRef]
- Han, W.; Li, D.; Yu, D.; Ebrahimian, H. Optimal parameters of PEM fuel cells using chaotic binary shark smell optimizer. Energy Sources A Recov. Util. Environ. Eff. 2019, 1–15. [Google Scholar] [CrossRef]
- Fathy, A.; Babu, T.S.; Abdelkareem, M.A.; Rezk, H.; Yousri, D. Recent approach based heterogeneous comprehensive learning archimedes optimization algorithm for identifying the optimal parameters of different fuel cells. Energy 2022, 248, 123587. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, W.; Wang, H.; Ashourian, M. Parameter identification of PEMFC based on convolutional neural network optimized by balanced deer hunting optimization algorithm. Energy Rep. 2020, 6, 1572–1580. [Google Scholar] [CrossRef]
- Sultan, H.M.; Menesy, A.S.; Kamel, S.; Hasanien, H.M.; Al-Durra, A. Identifying optimal parameters of proton exchange membrane fuel cell using water cycle algorithm. In Proceedings of the 2020 2nd International Conference on Smart Power & Internet Energy Systems, Bangkok, Thailand, 15–18 September 2020; pp. 176–181. [Google Scholar]
- Alsaidan, I.; Shaheen, M.A.; Hasanien, H.M.; Alaraj, M.; Alnafisah, A.S. A PEMFC model optimization using the enhanced bald eagle algorithm. Ain Shams Eng. J. 2022, 13, 101749. [Google Scholar] [CrossRef]
- Abaza, A.; El-Sehiemy, R.A.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M. Optimal estimation of proton exchange membrane fuel cells parameter based on coyote optimization algorithm. Appl. Sci. 2021, 11, 2052. [Google Scholar] [CrossRef]
- Blanco-Cocom, L.; Botello-Rionda, S.; Ordoñez, L.; Valdez, S.I. Robust parameter estimation of a PEMFC via optimization based on probabilistic model building. Math. Comput. Simul. 2021, 185, 218–237. [Google Scholar] [CrossRef]
- Lu, X.; Kanghong, D.; Guo, L.; Wang, P.; Yildizbasi, A. Optimal estimation of the proton exchange membrane fuel cell model parameters based on extended version of crow search algorithm. J. Clean. Prod. 2020, 272, 122640. [Google Scholar] [CrossRef]
- Menesy, A.S.; Sultan, H.M.; Kamel, S. Extracting model parameters of proton exchange membrane fuel cell using equilibrium optimizer algorithm. In Proceedings of the 2020 International Youth Conference on Radio Electronics, Electrical and Power Engineering, Moscow, Russia, 12–14 March 2020; pp. 1–7. [Google Scholar]
- Duan, B.; Cao, Q.; Afshar, N. Optimal parameter identification for the proton exchange membrane fuel cell using satin bowerbird optimizer. Int. J. Energy Res. 2019, 43, 8623–8632. [Google Scholar] [CrossRef]
- Fathy, A.; Aleem, S.A.; Rezk, H. A novel approach for PEM fuel cell parameter estimation using LSHADE-EpSin optimization algorithm. Int. J. Energy Res. 2021, 45, 6922–6942. [Google Scholar] [CrossRef]
- Isa, Z.M.; Nayan, N.M.; Arshad, M.H.; Kajaan, N.A.M. Optimizing PEMFC model parameters using ant lion optimizer and dragonfly algorithm: A comparative study. Int. J. Electr. Comput. Eng. 2019, 9, 5295. [Google Scholar] [CrossRef]
- Song, Y.; Tan, X.; Mizzi, S. Optimal parameter extraction of the proton exchange membrane fuel cells based on a new Harris Hawks optimization algorithm. Energy Sources A Recov. Util. Environ. Eff. 2020, 1–18. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, Q.; Zhang, L.; Dai, J.; Razmjooy, N. Model parameter estimation of the PEMFCs using improved barnacles mating optimization algorithm. Energy 2020, 212, 118738. [Google Scholar] [CrossRef]
- Sun, X.; Wang, G.; Xu, L.; Yuan, H.; Yousefi, N. Optimal estimation of the PEM fuel cells applying deep belief network optimized by improved archimedes optimization algorithm. Energy 2021, 237, 121532. [Google Scholar] [CrossRef]
- Hasanien, H.M.; Shaheen, M.A.; Turky, R.A.; Qais, M.H.; Alghuwainem, S.; Kamel, S.; Tostado-Véliz, M.; Jurado, F. Precise modeling of PEM fuel cell using a novel enhanced transient search optimization algorithm. Energy 2022, 247, 123530. [Google Scholar] [CrossRef]
- Ćalasan, M.; Aleem, S.H.A.; Hasanien, H.M.; Alaas, Z.M.; Ali, Z.M. An innovative approach for mathematical modeling and parameter estimation of PEM fuel cells based on iterative Lambert W function. Energy 2022, 264, 126165. [Google Scholar] [CrossRef]
- Wilberforce, T.; Olabi, A.G.; Rezk, H.; Abdelaziz, A.Y.; Abdelkareem, M.A.; Sayed, E.T. Boosting the output power of PEM fuel cells by identifying best-operating conditions. Energy Convers. Manag. 2022, 270, 116205. [Google Scholar] [CrossRef]
- Rezk, H.; Wilberforce, T.; Sayed, E.T.; Alahmadi, A.N.M.; Olabi, A.G. Finding best operational conditions of PEM fuel cell using adaptive neuro-fuzzy inference system and metaheuristics. Energy Rep. 2022, 8, 6181–6190. [Google Scholar] [CrossRef]
- Wilberforce, T.; Olabi, A.G.; Monopoli, D.; Dassisti, M.; Sayed, E.T.; Abdelkareem, M.A. Design optimization of proton exchange membrane fuel cell bipolar plate. Energy Convers. Manag. 2023, 277, 116586. [Google Scholar] [CrossRef]
- Ashraf, H.; Abdellatif, S.O.; Elkholy, M.M.; Attia, A. El-Fergany. Honey badger optimizer for extracting the ungiven parameters of PEMFC model: Steady-state assessment. Energy Convers. Manag. 2022, 258, 115521. [Google Scholar] [CrossRef]
- Eelsayed, S.K.; Ahmed, A.; Ehab Ehab Elsayed Elattar, Attia El-Fergany. Steady-state modelling of pem fuel cells using gradient-based optimizer. Dyna 2021, 96, 520–527. [Google Scholar] [CrossRef] [PubMed]








| Data | |
|---|---|
| No. of cells | 48 |
| Area | 62.5 cm2 |
| 178 | |
| 1 bar | |
| 1 bar | |
| Temperature | 323 K |
| RHa (%) | 100 |
| RHa (%) | 100 |
| Parameter | |||||||
|---|---|---|---|---|---|---|---|
| Max. | −1.19969 | 0.001 | 3.6 × 10−5 | −2.6 × 10−4 | 10 | 0.0136 | 1 × 10-4 |
| Min. | 0.8532 | 0.005 | 9.8 × 10−5 | −9.54 × 10−5 | 24 | 0.5 | 8 × 10-4 |
| Variable | ALO | BES | COOT | EO | HBO |
|---|---|---|---|---|---|
| nmax 500 | |||||
| −1.00213 | −0.88445 | −0.85575 | −0.8532 | −1.19909 | |
| 0.003131 | 0.002587 | 0.003031 | 0.002271 | 0.004194 | |
| 6.35 × 10−5 | 5.18 × 10−5 | 8.63 × 10−5 | 3.76 × 10−5 | 9.28 × 10−5 | |
| −1.02 × 10−5 | −1.02 × 10−4 | −1.02 × 10−4 | −1.02 × 10−4 | −1.03 × 10−4 | |
| 24 | 24 | 22.98325 | 23.9994 | 23.99187 | |
| 0.147078 | 0.147078 | 0.147054 | 0.147062 | 0.147649 | |
| 5.82 × 10−4 | 5.82 × 10−4 | 5.70 × 10−4 | 5.83 × 10−4 | 5.33 × 10−4 | |
| t (s) | 2.217 | 1.101 | 1.359 | 1.503 | 1.896 |
| nmax 250 | |||||
| −0.90198 | −1.07564 | −0.95545 | −1.15522 | −1.0264 | |
| 2.81 × 10−3 | 3.01 × 10−3 | 3.20 × 10−3 | 3.17 × 10−3 | 2.77 × 10−3 | |
| 6.31 × 10−5 | 4.08 × 10−5 | 7.75 × 10−5 | 3.51 × 10−5 | 3.56 × 10−5 | |
| −0.0001 | −0.0001 | −0.0001 | −0.0001 | −0.0001 | |
| 23.99998 | 24 | 18.76678 | 21.76225 | 17.1276 | |
| 0.147188 | 0.147078 | 0.147206 | 0.14717 | 0.148609 | |
| 5.72 × 10−4 | 5.82 × 10−4 | 4.77 × 10−4 | 5.43 × 10−4 | 3.12 × 10−4 | |
| Metric | ALO | BES | COOT | EO | HBO |
|---|---|---|---|---|---|
| nmax 500 | |||||
| Best | 0.03551 | 0.035099 | 0.035203 | 0.035099 | 0.035512 |
| Worst | 0.088554 | 0.03516 | 0.057578 | 0.080252 | 0.140873 |
| Mean | 0.053168 | 0.035102 | 0.04155 | 0.047299 | 0.056021 |
| StD | 0.015021 | 1.15 × 10−8 | 0.006312 | 0.012671 | 0.019082 |
| Median | 0.047477 | 0.035099 | 0.039141 | 0.042721 | 0.053123 |
| Variance | 0.000226 | 1.33 × 10−10 | 0.00004 | 0.000161 | 0.000364 |
| nmax 250 | |||||
| Best | 0.035665 | 0.035099 | 0.035972 | 0.035377 | 0.041025 |
| Worst | 0.084315 | 0.041652 | 0.089465 | 0.09115 | 0.277627 |
| Mean | 0.04758 | 0.035794 | 0.048877 | 0.059477 | 0.089071 |
| StD | 0.010739 | 0.001557 | 0.013843 | 0.016703 | 0.045321 |
| Median | 0.043887 | 0.035107 | 0.043326 | 0.060752 | 0.083815 |
| Variance | 0.000115 | 2.42487 × 10−6 | 0.000192 | 0.000279 | 0.002054 |
| Run | ALO | BES | COOT | EO | HBO | ALO | BES | COOT | EO | HBO |
|---|---|---|---|---|---|---|---|---|---|---|
| nmax 500 | nmax 250 | |||||||||
| 1 | 0.061045 | 0.035099 | 0.041897 | 0.043371 | 0.061045 | 0.069544 | 0.03559 | 0.066005 | 0.039074 | 0.069544 |
| 2 | 0.03551 | 0.035099 | 0.057578 | 0.035206 | 0.03551 | 0.042054 | 0.035159 | 0.089465 | 0.08997 | 0.042054 |
| 3 | 0.044722 | 0.0351 | 0.037212 | 0.054035 | 0.044722 | 0.038159 | 0.035099 | 0.037021 | 0.060585 | 0.038159 |
| 4 | 0.045554 | 0.035099 | 0.036802 | 0.03593 | 0.045554 | 0.049855 | 0.035102 | 0.041889 | 0.06092 | 0.049855 |
| 5 | 0.058755 | 0.03516 | 0.04322 | 0.043943 | 0.058755 | 0.042842 | 0.035105 | 0.052037 | 0.080191 | 0.042842 |
| 6 | 0.036432 | 0.035099 | 0.043051 | 0.037184 | 0.036432 | 0.042523 | 0.041652 | 0.050637 | 0.043589 | 0.042523 |
| 7 | 0.04339 | 0.035099 | 0.042054 | 0.03805 | 0.04339 | 0.063406 | 0.035103 | 0.053675 | 0.035407 | 0.063406 |
| 8 | 0.083922 | 0.035099 | 0.041 | 0.036183 | 0.083922 | 0.04853 | 0.035099 | 0.036328 | 0.047768 | 0.04853 |
| 9 | 0.087286 | 0.035121 | 0.054107 | 0.041179 | 0.087286 | 0.038219 | 0.035338 | 0.081844 | 0.078667 | 0.038219 |
| 10 | 0.069625 | 0.035099 | 0.03661 | 0.048265 | 0.069625 | 0.043728 | 0.035105 | 0.079143 | 0.063174 | 0.043728 |
| 11 | 0.059361 | 0.035099 | 0.049718 | 0.065185 | 0.059361 | 0.041954 | 0.035981 | 0.051543 | 0.043901 | 0.041954 |
| 12 | 0.049401 | 0.035099 | 0.037363 | 0.035099 | 0.049401 | 0.054698 | 0.035099 | 0.041514 | 0.035377 | 0.054698 |
| 13 | 0.088554 | 0.035099 | 0.035631 | 0.039107 | 0.088554 | 0.041833 | 0.040977 | 0.039554 | 0.080345 | 0.041833 |
| 14 | 0.06482 | 0.035099 | 0.049396 | 0.044619 | 0.06482 | 0.050085 | 0.036513 | 0.051696 | 0.042868 | 0.050085 |
| 15 | 0.037251 | 0.035099 | 0.038151 | 0.035113 | 0.037251 | 0.04126 | 0.03664 | 0.051652 | 0.080236 | 0.04126 |
| 16 | 0.040361 | 0.035099 | 0.03612 | 0.049796 | 0.040361 | 0.035745 | 0.035557 | 0.036767 | 0.046892 | 0.035745 |
| 17 | 0.039375 | 0.035099 | 0.046439 | 0.051557 | 0.039375 | 0.036448 | 0.035099 | 0.043006 | 0.078408 | 0.036448 |
| 18 | 0.039232 | 0.035099 | 0.049288 | 0.080252 | 0.039232 | 0.044045 | 0.035099 | 0.055907 | 0.057489 | 0.044045 |
| 19 | 0.051856 | 0.035099 | 0.036807 | 0.071827 | 0.051856 | 0.058844 | 0.035192 | 0.057119 | 0.09115 | 0.058844 |
| 20 | 0.057312 | 0.035099 | 0.054051 | 0.04207 | 0.057312 | 0.084315 | 0.035099 | 0.041082 | 0.037868 | 0.084315 |
| 21 | 0.068326 | 0.035099 | 0.036793 | 0.039929 | 0.068326 | 0.048396 | 0.035099 | 0.044696 | 0.043607 | 0.048396 |
| 22 | 0.042721 | 0.035099 | 0.036611 | 0.039384 | 0.042721 | 0.045652 | 0.036608 | 0.03902 | 0.060021 | 0.045652 |
| 23 | 0.045484 | 0.035099 | 0.040131 | 0.036169 | 0.045484 | 0.035665 | 0.036399 | 0.038404 | 0.072356 | 0.035665 |
| 24 | 0.040642 | 0.035099 | 0.040156 | 0.047737 | 0.040642 | 0.050396 | 0.035099 | 0.043646 | 0.066669 | 0.050396 |
| 25 | 0.05499 | 0.035099 | 0.03577 | 0.039146 | 0.05499 | 0.055817 | 0.035426 | 0.038915 | 0.066761 | 0.055817 |
| 26 | 0.04306 | 0.035101 | 0.045983 | 0.077701 | 0.04306 | 0.048563 | 0.035109 | 0.040728 | 0.047401 | 0.048563 |
| 27 | 0.068888 | 0.035099 | 0.035447 | 0.059882 | 0.068888 | 0.042822 | 0.035099 | 0.037187 | 0.037412 | 0.042822 |
| 28 | 0.044559 | 0.035099 | 0.035203 | 0.039904 | 0.044559 | 0.056942 | 0.035186 | 0.05352 | 0.067886 | 0.056942 |
| 29 | 0.054714 | 0.035099 | 0.036305 | 0.062891 | 0.054714 | 0.038241 | 0.035099 | 0.035972 | 0.066791 | 0.038241 |
| 30 | 0.0379 | 0.035099 | 0.037609 | 0.048247 | 0.0379 | 0.036811 | 0.035099 | 0.036341 | 0.06152 | 0.036811 |
| Run | Current Density | ALO | BES | COOT | EO | HBO | ALO | BES | COOT | EO | HBO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| nmax 500 | nmax 250 | ||||||||||
| 1 | 0.00615 | 0.01268 | 0.04476 | 0.07324 | 0.00669 | 0.12212 | 0.03292 | 0.04531 | 0.16414 | 0.07084 | 0.24777 |
| 2 | 0.02665 | 0.00782 | 0.00088 | 0.00502 | 0.00114 | 0.00392 | 0.00956 | 0.00077 | 0.00548 | 0.00112 | 0.05217 |
| 3 | 0.041 | 0.0338 | 0.05721 | 0.06767 | 0.0459 | 0.06785 | 0.02748 | 0.05718 | 0.07668 | 0.06293 | 0.04065 |
| 4 | 0.05371 | 0.0633 | 0.09384 | 0.10689 | 0.07679 | 0.11161 | 0.05492 | 0.09383 | 0.12629 | 0.10205 | 0.09686 |
| 5 | 0.10086 | 0.07999 | 0.04275 | 0.02929 | 0.06626 | 0.01962 | 0.08972 | 0.04277 | 0.00546 | 0.03275 | 0.00866 |
| 6 | 0.11398 | 0.05669 | 0.02037 | 0.00796 | 0.04362 | 0.00139 | 0.06595 | 0.02041 | 0.02775 | 0.01083 | 0.01661 |
| 7 | 0.16031 | 0.02646 | 0.0019 | 0.00935 | 0.01714 | 0.01462 | 0.03298 | 0.00186 | 0.04268 | 0.0086 | 0.04014 |
| 8 | 0.20787 | 0.01186 | 0.00405 | 0.00594 | 0.00783 | 0.00423 | 0.01483 | 0.00406 | 0.03121 | 0.00713 | 0.03589 |
| 9 | 0.23411 | 0.04643 | 0.03831 | 0.03923 | 0.04569 | 0.04545 | 0.04741 | 0.03825 | 0.01984 | 0.03717 | 0.01142 |
| 10 | 0.2829 | 0.01971 | 0.02662 | 0.03181 | 0.02539 | 0.04699 | 0.01732 | 0.02642 | 0.02491 | 0.02864 | 0.00943 |
| 11 | 0.30873 | 0.00237 | 0.01707 | 0.02387 | 0.01145 | 0.04384 | 0.00154 | 0.01678 | 0.02401 | 0.0204 | 0.00452 |
| 12 | 0.32922 | 0.02677 | 0.04735 | 0.05507 | 0.03845 | 0.07873 | 0.02184 | 0.04699 | 0.06083 | 0.05152 | 0.03793 |
| 13 | 0.36243 | 0.03256 | 0.00342 | 0.00506 | 0.01703 | 0.03428 | 0.03875 | 0.00388 | 0.01968 | 0.00165 | 0.00934 |
| 14 | 0.40344 | 0.0167 | 0.02034 | 0.02843 | 0.00245 | 0.06324 | 0.02363 | 0.01981 | 0.05289 | 0.02569 | 0.01487 |
| 15 | 0.43623 | 0.04365 | 0.00362 | 0.00309 | 0.02313 | 0.04067 | 0.0504 | 0.00412 | 0.03369 | 0.00123 | 0.01316 |
| 16 | 0.47108 | 0.08116 | 0.04297 | 0.03871 | 0.06164 | 0.00087 | 0.08681 | 0.04327 | 0.00448 | 0.0394 | 0.06301 |
| 17 | 0.50511 | 0.10926 | 0.08048 | 0.07946 | 0.0946 | 0.04551 | 0.11271 | 0.08031 | 0.04633 | 0.07889 | 0.11956 |
| 18 | 0.53832 | 0.0314 | 0.02332 | 0.02593 | 0.02755 | 0.00217 | 0.03138 | 0.02224 | 0.00115 | 0.02432 | 0.0935 |
| 19 | 0.56498 | 0.00843 | 0.01338 | 0.01879 | 0.00357 | 0.01068 | 0.01251 | 0.011 | 0.00932 | 0.01684 | 0.12236 |
| 20 | 0.59122 | 0.13831 | 0.06751 | 0.0602 | 0.0999 | 0.04179 | 0.14793 | 0.072 | 0.04172 | 0.06146 | 0.09935 |
| SSE | 0.06104 | 0.0351 | 0.0419 | 0.04337 | 0.05577 | 0.06954 | 0.03559 | 0.066 | 0.03907 | 0.06954 | |
| RMSE | 0.05525 | 0.04189 | 0.04577 | 0.04657 | 0.05281 | 0.05897 | 0.04218 | 0.05745 | 0.0442 | 0.05897 | |
| MAE | 0.04247 | 0.03251 | 0.03575 | 0.03581 | 0.03998 | 0.04603 | 0.03256 | 0.04093 | 0.03417 | 0.04603 | |
| Source | df | SS | MS | F | Prob | |
|---|---|---|---|---|---|---|
| Columns | 500-25 | 4 | 0.0087 | 0.00218 | 13.31 | 2.919 × 10−9 |
| 250-25 | 0.0491 | 0.01227 | 22.44 | 1.942 × 10−14 | ||
| Error | 500-25 | 145 | 0.0237 | 0.00016 | ||
| 250-25 | 0.0793 | 0.00055 | ||||
| Total | 500-25 | 149 | 0.0324 | |||
| 250-25 | 0.1283 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezk, H.; Wilberforce, T.; Olabi, A.G.; Ghoniem, R.M.; Sayed, E.T.; Ali Abdelkareem, M. Optimal Parameter Identification of a PEM Fuel Cell Using Recent Optimization Algorithms. Energies 2023, 16, 5246. https://doi.org/10.3390/en16145246
Rezk H, Wilberforce T, Olabi AG, Ghoniem RM, Sayed ET, Ali Abdelkareem M. Optimal Parameter Identification of a PEM Fuel Cell Using Recent Optimization Algorithms. Energies. 2023; 16(14):5246. https://doi.org/10.3390/en16145246
Chicago/Turabian StyleRezk, Hegazy, Tabbi Wilberforce, A. G. Olabi, Rania M. Ghoniem, Enas Taha Sayed, and Mohammad Ali Abdelkareem. 2023. "Optimal Parameter Identification of a PEM Fuel Cell Using Recent Optimization Algorithms" Energies 16, no. 14: 5246. https://doi.org/10.3390/en16145246
APA StyleRezk, H., Wilberforce, T., Olabi, A. G., Ghoniem, R. M., Sayed, E. T., & Ali Abdelkareem, M. (2023). Optimal Parameter Identification of a PEM Fuel Cell Using Recent Optimization Algorithms. Energies, 16(14), 5246. https://doi.org/10.3390/en16145246












