Operation Optimization of Wind/Battery Storage/Alkaline Electrolyzer System Considering Dynamic Hydrogen Production Efficiency

Abstract

Hydrogen energy is regarded as a key path to combat climate change and promote sustainable economic and social development. The fluctuation of renewable energy leads to frequent start/stop cycles in hydrogen electrolysis equipment. However, electrochemical energy storage, with its fast response characteristics, helps regulate the power of hydrogen electrolysis, enabling smooth operation. In this study, a multi-objective constrained operation optimization model for a wind/battery storage/alkaline electrolyzer system is constructed. Both profit maximization and power abandonment rate minimization are considered. In addition, some constraints, such as minimum start/stop times, upper and lower power limits, and input fluctuation limits, are also taken into account. Then, the non-dominated sorting genetic algorithm II (NSGA-II) algorithm and the entropy method are used to optimize the operation strategy of the hybrid energy system by considering dynamic hydrogen production efficiency, and through optimization to obtain the best hydrogen production power of the system under the two objectives. The change in dynamic hydrogen production efficiency is mainly related to the change in electrolyzer power, and the system can be better adjusted according to the actual supply of renewable energy to avoid the waste of renewable energy. Our results show that the distribution of Pareto solutions is uniform, which indicates the suitability of the NSGA-II algorithm. In addition, the optimal solution indicates that the battery storage and alkaline electrolyzer can complement each other in operation and achieve the absorption of wind power. The dynamic hydrogen production efficiency can make the electrolyzer operate more efficiently, which paves the way for system optimization. A sensitivity analysis reveals that the profit is sensitive to the price of hydrogen energy.

1. Introduction

China is characterized by being “rich in coal and short of oil and gas”, which has led to a high dependence on crude oil and natural gas resources. However, with increasing fossil fuel consumption and environmental pollution, the development of clean and efficient new energy sources has become an inevitable trend. In the context of energy transition and the goal of carbon peak and carbon neutrality, China has launched a comprehensive initiative to deeply transform its energy supply structure, aiming for a clean, low-carbon, and safe direction in terms of consumption and demand. China has begun to focus on constructing a new zero-carbon energy system based on renewable energy. Among these initiatives, the hydrogen economy represents an important means of realizing a low-carbon, green energy supply. It is also seen as a key pathway to combat climate change and promote sustainable economic and social development [1]. The hydrogen economy is a proposed system where hydrogen is produced and used extensively as the primary energy carrier. The successful development of the hydrogen economy means innumerable advantages for the environment, energy security, the economy, and final users [2]. However, like other energy production methods, hydrogen comes with challenges, including high costs and safety concerns across its entire value chain [3]. Hydrogen energy has garnered significant attention due to its potential to promote energy transformation, drive deep decarbonization, and ensure energy security. In recent years, there have been progressive research and a practical application of the hydrogen economy on the international stage, accompanied by increased government investments in hydrogen energy technology. This has resulted in the rapid growth of the hydrogen energy industry. As a clean and zero-carbon energy source for the future, hydrogen energy presents unprecedented development opportunities and has sparked a global energy revolution. Currently, as depicted in Figure 1, major economies worldwide have put forth strategies, planning policies, and major projects to foster the development of hydrogen energy [4]. China possesses numerous inherent advantages for the development of hydrogen energy, including abundant renewable energy resources, diverse application scenarios, and well-established infrastructure. These factors provide a robust foundation for the long-term growth of the hydrogen energy industry [5].

As a widely utilized secondary energy source, hydrogen can serve as an alternative energy solution across various production and consumption sectors, including heavy industry, transportation, construction, and the electric power industry [6]. For example, the synergies of green hydrogen can contribute to the clean and sustainable development of offshore and coastal industries, offering opportunities for the diffusion of clean energy [7]. In recent years, power systems globally have encountered mounting challenges due to the risks associated with integrating new energy sources into the grid. This situation presents new prospects for hydrogen energy to propel the advancement of power systems. One notable application scenario for hydrogen energy is its utilization in consuming renewable energy that cannot be connected to the grid.

Solar, wind, and other renewable energy sources are characterized by intermittency and significant fluctuations in power output. The issues related to excess solar and wind power curtailment have become increasingly evident with the growing penetration of photovoltaic and wind power systems. To ensure the secure and stable operation of the power grid, it is necessary to maintain a certain level of power generation to meet electricity demand. This requires either storing surplus power in backup systems or finding alternative methods to achieve a balance between supply and demand. While traditional battery storage is effective for short-term power supply and demand management, it is not suitable for large-scale and long-term energy storage due to inherent challenges, such as battery self-discharge [8]. Hydrogen energy possesses various advantages, such as a high energy density and the ease of storage and transportation. Hydrogen energy storage, characterized by its high energy storage density, provides a unique solution for converting surplus electricity into hydrogen production and storage. The stored hydrogen can then be efficiently utilized to generate electricity when needed, ensuring a real-time balance between electricity supply and demand while promoting the utilization of renewable energy sources [9]. The integration of photovoltaics (PVs), energy storage, and electrolysis in a PV–storage–electrolysis hydrogen system is an effective approach for harnessing renewable energy. To enhance the utilization of photovoltaic energy, enable the grid integration of PV power generation as per dispatch requirements, and produce electrolysis hydrogen during low-demand periods, optimizing the operation of the PV–storage–electrolysis hydrogen system is crucial. This optimization problem directly influences the system’s overall economic viability and the power abandonment rate [10].

To alleviate the pressure caused by the global energy crisis, especially in the power sector, various renewable energy generation technologies have been developed and applied, with wind and photovoltaic power generation accounting for the largest share [11]. However, the uncertainty and variability of these renewable energy generation sources have put forward important requirements for the operational flexibility of power systems, which also poses new challenges for the efficient energy utilization of energy systems. Many research scholars have carried out many inspiring works on how to utilize the role of the energy system for energy saving and emission reduction, rational allocation of multiple energy sources, and analysis of the interdependence between different energy systems [12].

The process of constructing an optimization model for renewable energy system operation focuses on factors such as the state of the load and the influence of prices. In the literature, a novel fuel cell/battery hybrid power system with simple, low-cost, and highly stable load-sharing characteristics was proposed [13]. This hybrid system aims to shift the power sharing dominance from the battery to the fuel cell, reducing the duration of battery-dominated operation. It not only significantly improves the fuel cell efficiency under partial load conditions but also enhances the effectiveness of battery recharging, especially during periods of less frequent demand, resulting in overall improved efficiency. Abdelkafi et al. [14] studied the design of a comprehensive power supervisory approach to manage the power flow between energy and storage elements. The objective was to develop an energy management algorithm capable of handling wind speed fluctuations, load power variations, and the slow dynamics of the hydrogen system. The control strategy needed to respond quickly, enabling optimized energy management of all hybrid unit elements and ensuring a high-quality, three-phase load energy supply at all times. Carapellucci et al. [15] developed a computer code to evaluate the energy and economic performance of power generation islands that utilize renewable energy sources with hydrogen storage systems. This code is based on a database containing information about renewable energy sources, technologies, and electrical and hydrogen loads, as well as energy and economic models of the system components. The system optimization aims to minimize the cost per unit of electricity by adjusting the margin factor of system components and the limit state-of-charge value of the battery bank. Avril et al. [16] presented a multi-objective design of a weakly connected system that aims to minimize the total level cost and grid connection while satisfying consumer satisfaction constraints. They proposed using a multi-objective code based on particle swarm optimization to determine the optimal combination of different energy devices. Yang Q et al. [17] proposed an improved evolutionary algorithm to solve the capacity optimization problem of hybrid PV/wind systems. Their objective function considers both investment and operation costs while ensuring the basic requirements of a stand-alone power system. Cai et al. [18] established an improved frequency response model based on the classical system frequency response model. They considered factors such as the rotating standby capacity, static load model, and turbine speed regulation system. Additionally, they introduced a low-frequency load shedding module and proposed an optimization method for low-frequency load shedding based on the improved frequency response model and comprehensive node index. Li et al. [19] established the operation mechanism and mathematical model of an integrated energy system. They then proposed a low-carbon eco-economic dispatch model aimed at minimizing the economic cost and optimizing the operation of the integrated energy system, taking into account the increased penetration of wind power. In a study by Deng et al. [20], a mathematical model of a power plant system integrating a tower CSP-S-CO₂ Brayton cycle was developed to minimize the levelized cost of electricity (LCOE) of the plant, and the parameters of the integrated system were optimized using the joint cubic equation method. A sensitivity analysis of the key parameters of the cycle was also performed. Comodi et al. [21] proposed an innovative energy community optimization design model aimed at reducing its carbon footprint. The community is modeled as a spatially staggered network of energy centers, each with its own electricity, heating, and cooling needs. This model aims to define the optimal combination of energy systems, thermal and electrical energy storage, and energy network infrastructure needed to meet the energy needs of users in the region.

In summary, numerous studies have proposed various methods to optimize renewable energy systems. These methods include utilizing fuel cell/battery hybrid power systems, employing overall power supervision methods, utilizing computer codes, and implementing multi-objective design approaches. The objectives of these methods encompass cost reduction, enhanced efficiency, and meeting consumer demands. Various types of renewable energy systems are mentioned, such as photovoltaic/wind hybrid systems, integrated energy systems, and power plants integrating a CSP-S-CO₂ Brayton cycle. Additionally, several research methods are utilized in constructing optimization models for renewable energy systems. These methods primarily involve multi-objective optimization utilizing genetic algorithms, modeling research based on energy hubs, linear thermal–electric joint scheduling methods that consider the thermal storage characteristics of regional heating networks, energy-aware optimization strategies, and other approaches. The ultimate aim of these methods is to enhance the operational efficiency and benefits of renewable energy systems. They demonstrate high feasibility and practicality.

Zhang et al. [22] conducted a study on the development of an efficient solar energy system that integrates power generation and hydrogen production. The system comprises a tower-type solar power generation and thermal energy storage system, a proton exchange membrane electrolytic water system, and a reheated steam Rankine cycle with a heat-return heater. It also includes an organic Rankine cycle waste heat recovery sub-system with a heat-return heater, allowing for energy ladder utilization. In a separate study, Seyed et al. [23] explored the utilization of thermoelectric generators as an alternative to organic Rankine cycle condensers. They employed a genetic-algorithm-based multi-objective optimization approach to evaluate and compare the performance of systems with and without thermoelectric generator configurations. Their goal was to determine the optimal operating conditions of the system. The results indicated that integrating thermoelectric generators can enhance output power and fuel efficiency while reducing the overall production cost. An analysis of the main output equipment’s efficiency under static conditions and the characteristic relationship between the efficiency and power of each piece of energy conversion equipment was conducted to develop a more precise dispatch strategy [24]. Researchers proposed a linear combined heat and power scheduling method that considers the heat storage characteristics of district heating networks [25]. This method coordinates the short-time optimal operation of the power district thermal system and improves the scheduling flexibility of the power system to adapt to the random access of large-scale wind power. Li et al. [26] studied an efficiency model for the operation of various types of equipment that was developed based on a modeling study of energy hubs and the conversion relationship between energy sources. Zhou et al. [27] proposed the optimal energy management principles for independent photovoltaic hydrogen production systems. This approach assigns higher priority to the energy flow route with higher transmission efficiency in any possible operational situation. Based on this optimal energy management strategy, researchers developed a direct system sizing approach to pre-size the system components, including PV panels, electrolyzers, hydrogen storage tanks, fuel cells, and batteries, while considering the mismatch between intermittent solar radiation and time-varying load demand. The proposed system sizing method provides a fast and simple way to evaluate the economic feasibility of PV hydrogen production systems in terms of hardware cost. Conficoni et al. [28] studied an energy-aware optimization strategy that was proposed to utilize a heterogeneous cooling system in a holistic manner with the aim of minimizing the overall cooling system power consumption while satisfying the system thermal constraints. This strategy achieves the minimization of system energy use power consumption by downscaling the complex constraints. Ferrario et al. [29] evaluated four storage configurations based on different energy management strategies and analyzed system performance parameters. In order to address the suboptimal and optimal regions separately, multidimensional sensitivity analysis and PSO parallel approach are used to optimize the energy storage size. Lingkang et al. [30] considered the seasonal energy storage behavior of an energy storage system, such as energy power coupling, self-discharge loss, and minimum charging state. Scholars have proposed a new approach to perform the optimal sizing of AC-linked solar PV/proton exchange membrane systems. The innovation lies in the proposal of the solar-plant-to-electrolyzer-capacity ratio (AC/AC ratio) as the optimization variable [31]. Others have conducted techno-economic analyses based on a dataset of electricity generation from an actual wind farm, with a large number of system configurations and different component sizes and layouts to assess their performance. A sensitivity analysis of different components and tariff strategies was performed to evaluate the effectiveness of different storage technologies and to help understand how to facilitate the penetration of green hydrogen in heavy industry. However, an optimization study of the system power allocation was not performed [32].

Currently, there is no operational optimization of renewable energy hydrogen production systems that considers dynamic efficiency. Dynamic hydrogen production efficiency, which varies with electrolyzer power, is important, as it determines the accuracy of hydrogen production measurements. Therefore, we develop an operational optimization method for a renewable-energy-based hydrogen production system that takes into account dynamic efficiency. The purpose is to optimize the operating power of each component in the wind/battery storage/alkaline electrolyzer system, resulting in a minimized power abandonment rate and a maximized profit. Therefore, we need to research and develop an operational optimization method for renewable-energy-based hydrogen production systems that take into account dynamic efficiency. The variation in dynamic hydrogen production efficiency is mainly associated with changes in electrolyzer power, which is crucial, as it determines the accuracy of hydrogen production measurements.

2. System Introduction

2.1. System Structure

The system integrates various elements, including renewable energy generation, power storage, hydrogen production, and hydrogen transportation (Figure 2). The electricity generated by a wind turbine can be directly supplied to the power grid or stored in batteries for future use, optimized by the control system. Another portion of the electricity is utilized in an electrolyzer device, which separates water (H₂O) into hydrogen gas (H₂) and oxygen gas (O₂). The generated hydrogen gas is then compressed and stored in hydrogen tanks for further transportation and utilization. In this process, the electrolyzer, compressor, and hydrogen tanks are essential components for hydrogen production through water electrolysis. Hydrogen gas can be transported to various demand points and enter the hydrogen market through various methods, such as liquid transportation, gas transportation, or pipeline transportation. Liquid transportation is suitable for long-distance transport, while gas and pipeline transportation are commonly used for short-distance distribution. The term “Electricity Flow” refers to the movement of electricity from the wind turbine through the control system to the power grid, batteries, and electrolyzer. “H₂ Flow” represents the process of hydrogen gas being produced by the electrolyzer, compressed, stored, and ultimately transported to the hydrogen market.

2.2. Wind Power Sub-System

The wind power sub-system converts wind power to electricity. The real-time power output is dependent on the wind speed at the height of the hub. It could be calculated as follows:

$$P_{WT}(t)=\left\{\begin{array}{l}0,v(t)<v_{in}orv(t)>v_{out}\\ P_r\cdot \frac{v(t)-v_{in}}{v_r-v_{in}},v_{in}\le v(t)\le v_r\\ P_r,v_r\le v(t)\le v_{out}\end{array}\right.$$

(1)

where $P_r$ is the rated power output of the wind turbine; $v\left(t\right)$ is the real-time wind speed at time t; and $v_{in}$, $v_r$, and $v_{out}$ represent the cut-in, rated, and cut-out wind speed, respectively.

Furthermore, considering the relationship between the wind speed and the height of the wind measurement, the real-time speed should be calculated and discounted by the wind tower as follows:

$$v(t)=v_{ref}(t)\cdot (\frac{H_{WT}}{H_{ref}}{)}^{\gamma }$$

(2)

where $v_{ref}(t)$ is the wind speed at the coherent wind measurement tower, $H_{WT}$ and $H_{ref}$ are the heights of the wind turbines and the tower, and $\gamma$ is the friction coefficient. Detailed values of the relevant parameters applied in WT are illustrated in

Table 1. Technical parameters of wind turbines.

Parameters	Values
Rated capacity	10 kW
Height of the turbine hub	20 m
Cut-in speed	3 m/s
Rated speed	11 m/s
Cut-out speed	25 m/s
Friction coefficient	1/7

.

2.3. Battery Storage Sub-System

The battery storage sub-system has two states: charging and discharging. When the entire system requires additional power supply, the battery storage sub-system discharges, and the power can be depicted as follows:

$$P_{BS}\left(t\right)=P_{demand}\left(t\right)/{\eta }_{dis}$$

(3)

When the entire system has a power surplus, the battery storage sub-system charges, and the power can be depicted as follows:

$$P_{BS}\left(t\right)=P_{surplus}\left(t\right)/{\eta }_{ch}$$

(4)

where ${\eta }_{dis}$ and ${\eta }_{ch}$ represent the discharge and charging efficiencies, respectively.

The charging and discharging state constraints are as follows:

$$x^{ch}+x^{dis}\le 1$$

(5)

where $x^{ch}$ is the charging state of the battery storage system; $x^{dis}$ is the charging state of the battery storage system. Both are Boolean variables that restrict the battery storage from discharging, charging, or neither discharging nor charging at the same time.

2.4. Alkaline Electrolyzer Sub-System

The alkaline electrolyzer sub-system could utilize surplus electricity to electrolyze water into hydrogen and oxygen, or surplus hydrogen to produce electricity. Let $P_g\left(t\right)$ be the sum of the power output of WT units at time t, and let $P_L\left(t\right)$ be the sum of the power load at time t; the residual hydrogen volume of the hydrogen tanks at time t could be determined as the following two formulas:

$$SO{C}_{HT}(t)=SO{C}_{HT}(t-1)+{\eta }_{EL}[P_g(t)-\frac{P_L(t)}{{\eta }_{inv}}]\cdot \rho$$

(6)

where ${\eta }_{EL}$ represents the conversion efficiencies of the electrolyzer (65% in this study), $\rho$ is the volume of hydrogen that can be produced per kWh of electricity, $\eta$ is the amount of electricity generated per m³ of hydrogen, and $SO{C}_{HT}\left(t\right)$ is the remaining capacity of the hydrogen storage tank.

3. Operation Optimization Model

3.1. Objectives

It is recommended to choose the wind power curve, which can better reflect the volatility and instability of renewable energy, and the granularity is one minute. The maximum consumption of new energy is expressed by the power abandonment rate, with a lower power abandonment rate indicating a greater consumption of new energy. The objective is to maximize profit and minimize the power abandonment rate and establish an optimization model for the operation of a wind energy/storage/alkaline electrolysis cell system. Specifically,

$$f{\left(x\right)}_1=f_1-f_2+f_3+f_4+f_5$$

(7)

$${f\left(x\right)}_2=\frac{\left(p_{re}-p_{el}-p_{ba}\right)}{p_{re}}$$

(8)

the objective function $f{\left(x\right)}_1$ represents the profit, where $f_1$ is the revenue of hydrogen production, including hydrogen production and hydrogen price; $f_2$ is the operating cost of the electrolyzer; $f_3$ is the battery storage operating cost; $f_4$ is the cost of purchased electricity, that is, the additional product of the electricity obtained from the grid and the electricity price; and $f_5$ is the cost brought by the water consumption of hydrogen production. The objective function $f{\left(x\right)}_2$ represents the power abandonment rate, where $p_{re}$ is the renewable energy power, $p_{el}$ is the electrolysis power, and $p_{ba}$ is the battery storage power.

3.2. Constraints

The optimization model for the wind energy/storage/alkaline electrolysis cell system includes various constraints related to renewable energy, hydrogen energy storage, and battery storage. The renewable energy constraints encompass power offset and capacity limitations. The hydrogen energy storage constraints involve the minimum start/stop times, upper and lower power limits, and input fluctuation limits. The battery storage constraints encompass state-of-charge (SOC) limits and charge–discharge conservation.

3.2.1. Renewable Energy Constraints

1. The power offset constraint is

$$p_{\mathit{grid}}\left(t\right)-p_{\mathit{ret}}\left(t\right)\le {\gamma }_{\mathit{max}}{C}_v$$

(9)

where $p_{\mathit{grid}}\left(t\right)$ is the grid-connected power of the power station at time t; $p_{\mathit{ret}}\left(t\right)$ is the planned output at time t, which is obtained via a scenario analysis; and ${\gamma }_{\mathit{max}}$ is the maximum offset rate specified. $C_v$ is the installed capacity of renewable energy. According to the “Technical Regulations for Grid-Connected Photovoltaic Power Plants of State Grid Corporation of China”, the grid-connected power of the wind energy storage system should align with the dispatch curve, allowing for a certain power deviation within a specified ratio.

2. The renewable energy capacity constraint is

$$0\le P_{grid}\left(t\right)\le C_v$$

(10)

3.2.2. Hydrogen Energy Storage Constraint

1. The power offset constraint is

$$\left\{\begin{array}{c}{\displaystyle \sum _{i=0}^{T_{on}-1}}{u}_{t+i}\ge T_{on}\left(u_t-u_{t-1}\right)\\ {\displaystyle \sum _{i=0}^{T_{off}-1}}(1-u_{t+i})\ge T_{off}(u_{t-1}-u_t)\end{array}\right.$$

(11)

where $T_{on}$ and $T_{off}$ are the minimum start-up and shutdown times of the electrolysis cell, and $u_t$ represents the start/stop status of the electrolysis cell at time t, where 1 represents the start and 0 represents the stop.

2. The upper and lower limit constraints of the electrolysis cell power is

$$P_{el-min}\le P_{el}\le P_{el-max}$$

(12)

where $P_{el-min}$ and $P_{el-max}$ represent the lower and upper limits of the electrolysis cell power, respectively.

3. The fluctuation input limit constraint is

$$P_{el}\ge 20\%P_{el-rated}$$

(13)

Fluctuating inputs can significantly impact the service life of hydrogen production equipment. Therefore, when the fluctuating inputs exceed the tolerance range of the electrolysis cell, the input power needs to be stabilized within the allowable range through electrochemical coordination. $P_{el-rated}$ is the rated power. When the input power is less than $P_{el-rated}$ due to fluctuations, some sub-electrolysis cells will be in intermittent operation, causing the operating temperature of the electrolysis cell to be lower than the rated state, and its efficiency will be lower. At the same time, there will be a risk of hydrogen–oxygen crossover causing an explosion.

$$P_{el}\le P_{el-rated}$$

(14)

The electrolysis cell is designed with a specific rated power. If the overload power exceeds the rated power for an extended period, it will cause irreversible damage to the electrolysis cell’s service life. Therefore, it is crucial to avoid long-term overload conditions.

3.2.3. Battery Storage Constraints

1. The energy storage SOC constraint is given by

$${SOC}_{min}\le SOC\left(i\right)\le {SOC}_{max}$$

(15)

2. The charge and discharge conservation constraint is given by

$$E_{q{d}_{E}SS}=E_{e{l}_{E}ss}$$

(16)

Within a time unit cycle, the electricity obtained from the consumption of discarded electricity in the battery storage should align with the total electricity delivered to the hydrogen energy storage system. Here, $E_{qd\_ESS}$ represents the electricity obtained through the consumption of discarded electricity, and $E_{el\_Ess}$ represents the electricity delivered to hydrogen energy storage.

3.2.4. Parameter Settings

The intermittent fluctuations of renewable energy sources, such as wind and solar power, can result in significant power variations in hydrogen production facilities, affecting the operational lifespan of electrolytic hydrogen production systems. To address this issue, the proposed approach utilizes battery storage as an auxiliary regulation device, leveraging its fast and precise adjustment capabilities. This approach involves a power allocation method for the coupled system of renewable energy sources, hydrogen production, and battery storage. This study focuses on a wind power plant in the Shanghai region of China and optimizes the operation of the wind power/energy storage/alkaline electrolyzer system. This optimization determines the optimal charging and discharging power for energy storage, as well as the optimal power for hydrogen production based on relevant basic parameters. Currently, the statistical calculation of hydrogen production utilizes a fitting approach to derive the hydrogen production rate curve. The confidence interval of the linear model coefficients is set at 95%, as shown in Figure 3. The fitting curve equation is $\mathrm{y}=-0.003158x^3+0.02249{\mathrm{x}}^2+16.75\mathrm{x}-44.67$. The fitted dynamic efficiency range is 35.46% to 54.39%.

Since the method proposed in this study was specifically designed for wind turbine systems, a real-value representation was used for all objective functions. The crossover and mutation operators were implemented using simulated binary crossover and mutation. The specific parameters of the algorithm and constraint bars were set as shown in

Table 2. Model parameter setting table.

Parameters	Values
Population size	200
Maximum number of generations	20
Latitude	2000
Crossover probability	0.9
Crossover operator	20
Mutation operator	20
Hydrogen price	60 CNY/kg
Operating cost of electrolyzer	0.001 CNY/kg
Operating cost of battery storage	0.007 CNY/kg
Rated power of electrolyzer	40 WM
Battery rated power	40 WM
Battery rated capacity	40 WMh
Minimum boot time	10 min
Minimum downtime	5 min
Battery initial soc	12 MW

.

3.3. Solution Method

3.3.1. NSGA-II

During the analysis and research of multi-objective optimization problems, it was often observed that improving one objective may compromise the performance of another objective. This conflict arises due to the inherent nature of conflicting objectives. However, in multi-objective optimization problems, it is possible to assign weights to each objective function to obtain the optimal solutions for each objective to the best extent possible. Therefore, in this model, the non-dominated sorting genetic algorithm II (NSGA-II) is employed to solve the model and obtain the solutions on the Pareto front. The entropy weight method is then utilized to identify compromise solutions (Figure 4).

3.3.2. Entropy Weight Method

The entropy weight method is an objective multicriteria decision-making method. It is based on the concept of information entropy and calculates and compares the information entropy among decision variables to determine the weights of each variable in the decision-making process. The entropy weight method does not rely on subjective evaluations or personal preferences. Instead, it relies on mathematical models and data analyses to determine decision weights. Therefore, it is considered an objective decision-making method. The specific calculation steps are as follows:

• For standardized processing, in order to solve the problem of the homogeneity of different index values, we can use the following formula to standardize each index:

$$z_{ij}=\frac{x_{ij}}{\sqrt{{\sum }_{i=1}^n{x}_{ij}^2}}$$

(17)

2.

The proportion of the sample under the indicator can be calculated as follows:

$$p_{ij}=\frac{z_{ij}}{{\sum }_{i=1}^n{z}_{ij}}$$

(18)

3.

For the index, its information entropy calculation formula is as follows:

$$e_j=-\frac{1}{\ln \left(n\right)}\sum _{i=1}^n{p}_{ij}\ln \left(p_{ij}\right),j =\left\{1,2,3\dots ,\left.m\right\}\right.$$

(19)

4.

The information utility value, defined as $d_j$, can be calculated as follows:

$$d_j=1-e_j$$

(20)

5.

The entropy weight of each indicator can be obtained by normalizing the information utility value:

$$w_j=\frac{d_j}{{\sum }_{i=1}^m{d}_j},j=\left\{1,2,3\dots ,\left.m\right\}\right.$$

(21)

6.

After the entropy weight of each indicator is calculated, the comprehensive score of each sample can be obtained for ranking.

$$s_j=\sum _{j=1}^m{w}_j{p}_{ij},i=\left\{1,\dots ,\left.n\right\}\right.$$

(22)

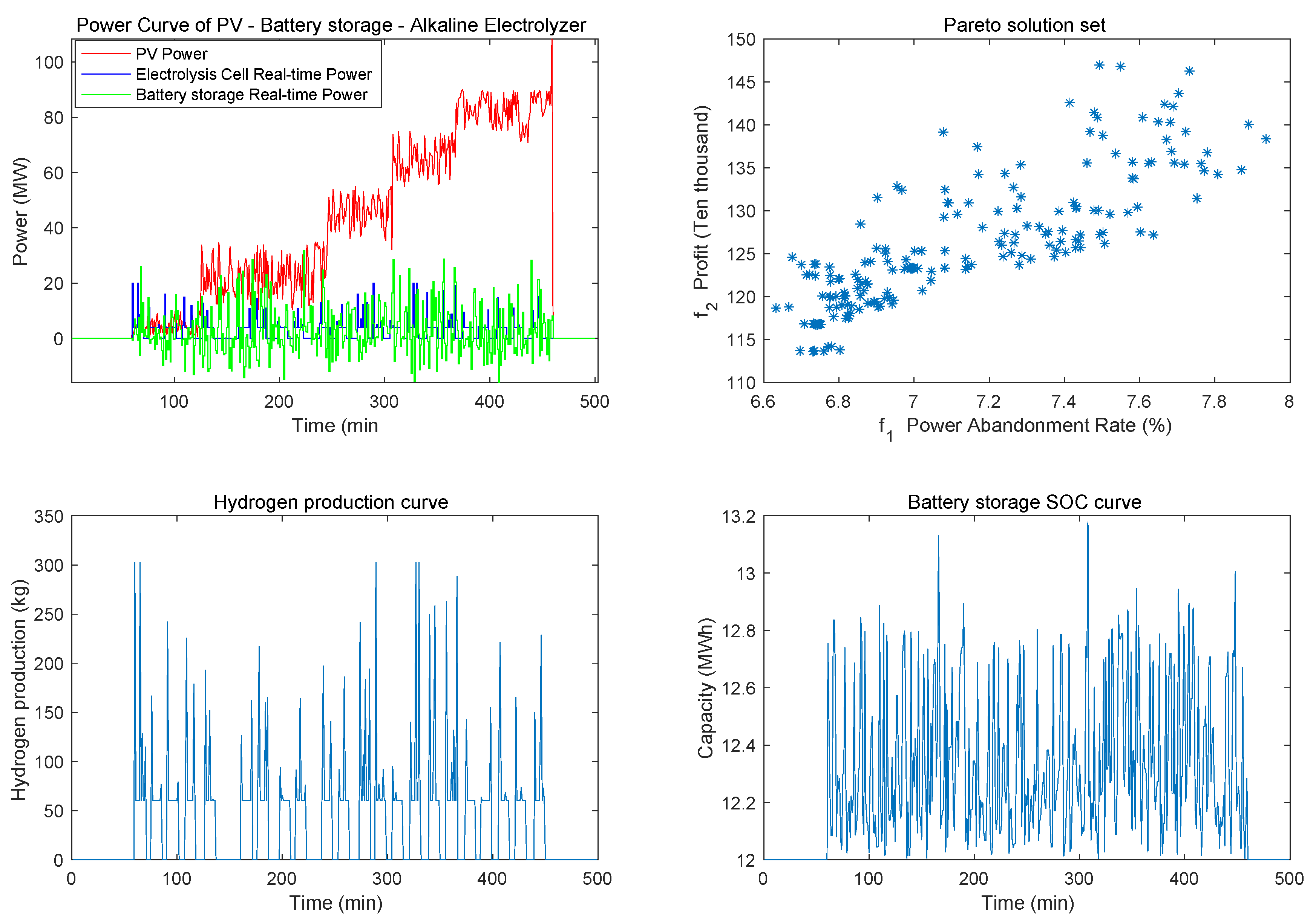
4. Results and Discussion

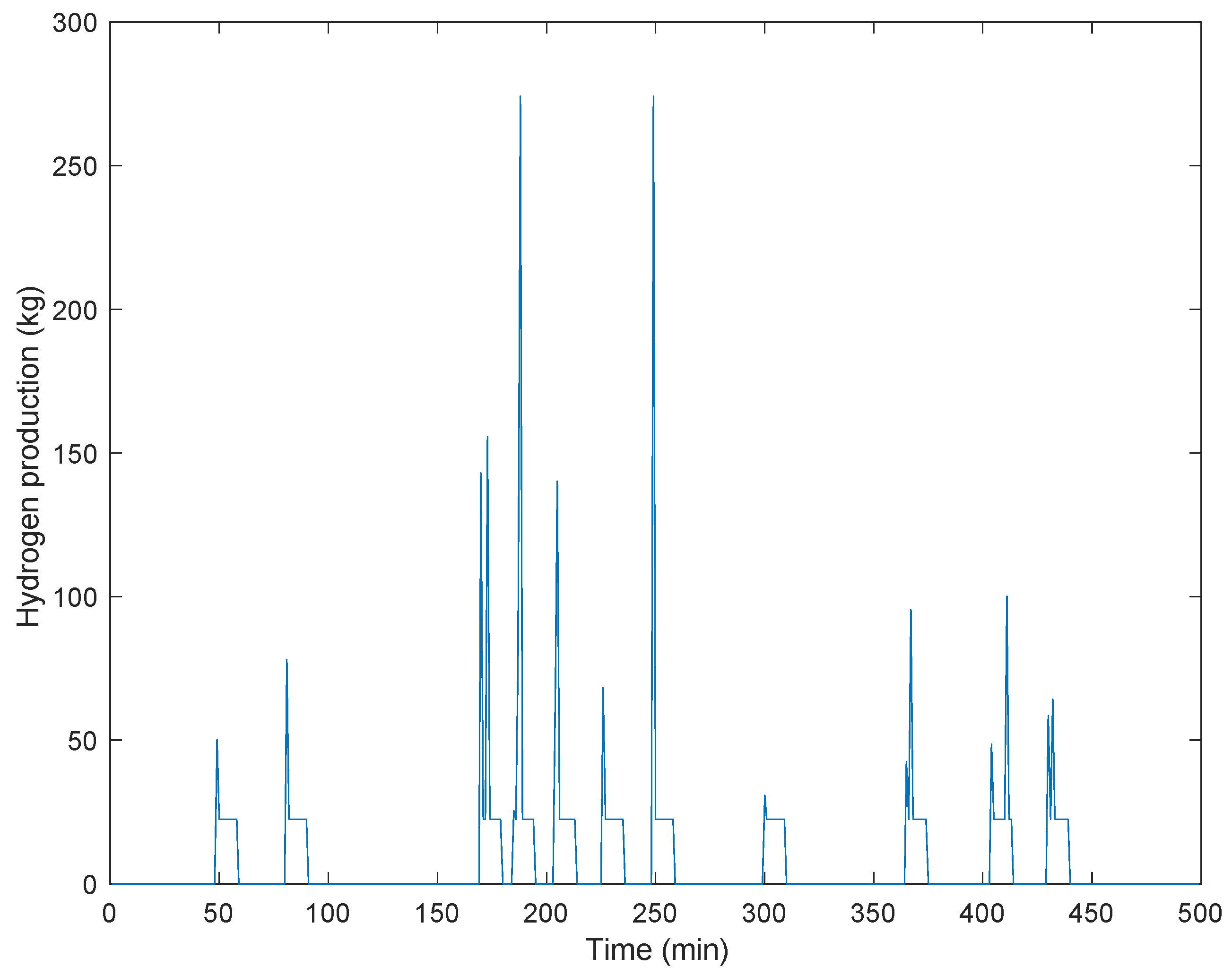
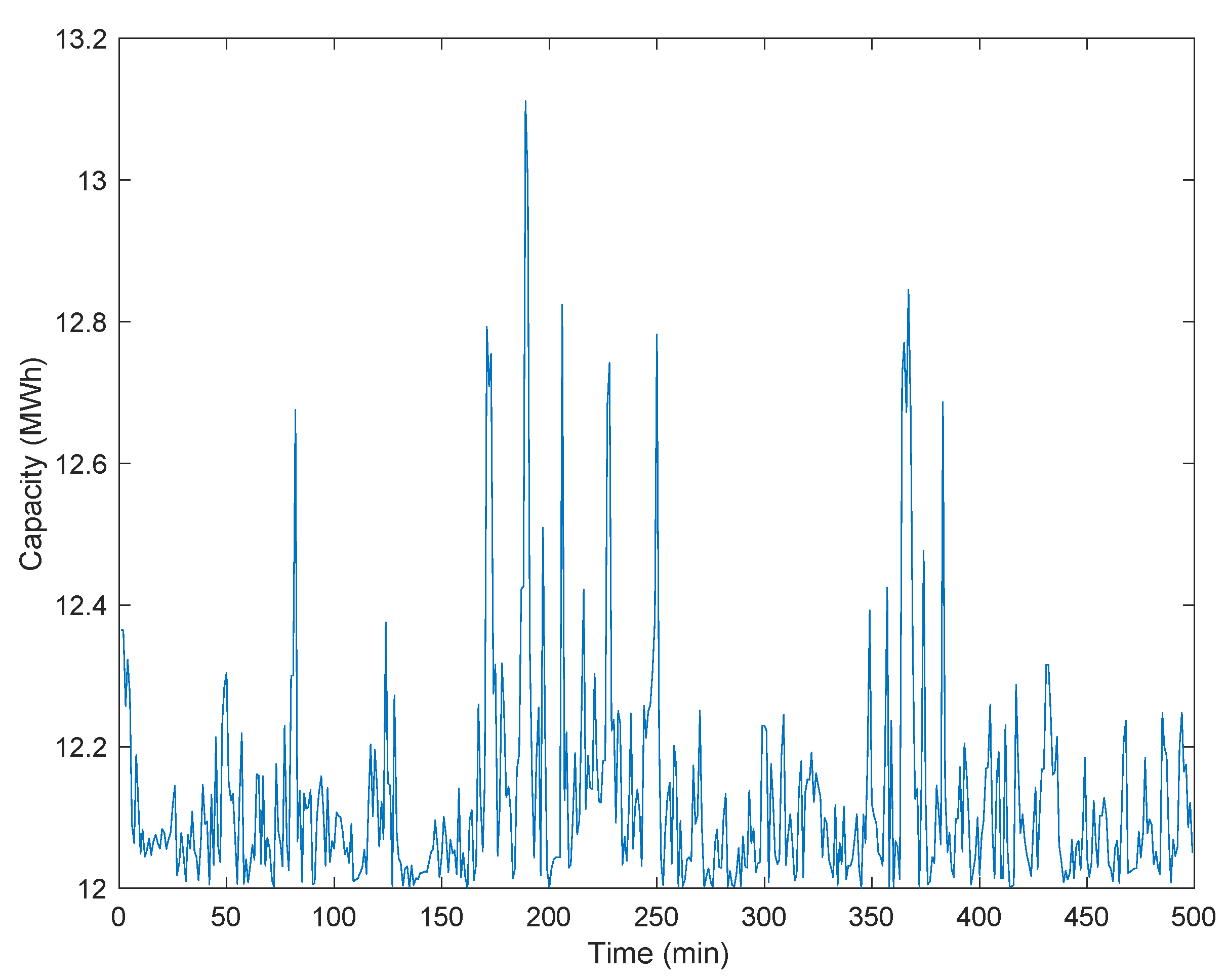
4.1. Results

The programming was conducted in the MATLAB R2022a environment, and the computation process took 15 min. The resulting Pareto front solution set is depicted in Figure 5. The figure illustrates that the power abandonment rate varies between 2.6% and 4.0%, while the profit ranges from CNY 3 million to 4.4 million. The figure demonstrates a more uniform distribution of Pareto solutions, indicating the effectiveness of the solution algorithm. By analyzing the relationship among these solutions, the weights for the two objectives (the power abandonment rate and profit) were determined as follows: $\mathrm{w}1$ = 0.797 and $\mathrm{w}2$ = 0.203. By plugging the known conditions into the model and solving it, a compromise solution was found, representing the optimal hydrogen production rate within 500 min, as illustrated in Figure 6. At the optimal hydrogen production rate, the hydrogen production remains stable for a certain period and then gradually declines. This occurs because the electrolyzer operates at its optimal current density and voltage, achieving the most efficient state for the hydrogen production reaction. Over time, as the concentration of hydrogen increases and the reactant levels decrease within the electrolyzer, the hydrogen production rate begins to decrease. The peak point represents the highest efficiency of hydrogen production within the electrolyzer at the optimal hydrogen production rate. The rate at which hydrogen production declines depends on the reactant consumption rate and the design parameters of the electrolyzer. Understanding the hydrogen production curve at the optimal hydrogen production rate can assist managers in optimizing electrolyzer operations, leading to improved hydrogen production and energy efficiency.

Additionally, it is important to control the range of the battery state of charge (SOC) to avoid exceeding the limits of the SOC curve in order to protect the safety and stability of the battery. The SOC curve for battery storage is shown in Figure 7.

The optimal power curves for the charging and discharging battery storage and hydrogen production in the electrolyzer provide decision-makers with a clear understanding of the power range and fluctuations in wind power generation, battery storage, and alkaline electrolyzer systems. By compensating for deficiencies in wind power generation and utilizing excess wind power, the battery storage and the electrolyzer can collaborate to optimize system performance, subject to certain constraints. The figure illustrates that, when there are significant fluctuations in wind power or when it is insufficient to initiate the electrolyzer, the battery discharges to produce hydrogen for the electrolyzer. This process aptly compensates for the fluctuation and instability of wind power. This information holds great value for decision-makers in effectively managing the power range and fluctuations within the wind power/battery storage/alkaline electrolyzer system (Figure 8).

4.2. Discussion

Through the process of modeling and identifying a solution, a comprehensive comparison of different future scenarios of hydrogen prices was conducted, taking into account the power abandonment rate. The figure presented showcases the variations in the power abandonment rate and profit in relation to the fluctuation of hydrogen prices. The horizontal axis ranges from 20 to 100 CNY/kg with a 5 CNY/kg interval, representing the price of hydrogen. The left vertical axis illustrates the power abandonment rate (%), while the right vertical axis represents profit (ten thousand).

The wind/battery storage/alkaline electrolyzer system is a complex system involving the comprehensive optimization of multiple variables and objectives. Through the entropy weight method, the importance of different objectives can be given according to the weight to achieve multi-objective optimization. During optimization, the system tries to find a balanced strategy with the goal of minimizing curtailment and maximizing profit. It can be seen that the higher the hydrogen price, the higher the profit, and the change in the power abandonment rate may be due to the greater volatility of wind power resources. Even if the hydrogen price rises, the system may still not be able to eliminate all power curtailment. In the case of large fluctuations in wind power resources, there may still be some periods or situations where electrolyzers and batteries cannot fully absorb all wind power, thus increasing the power abandonment rate to a certain extent (Figure 9). In summary, this figure shows the impact of hydrogen prices on the power abandonment rate and profit, that is, the impact of hydrogen prices on power supply and economic benefits. Specifically, a moderate increase in the price of hydrogen can help reduce the power abandonment rate and increase profits, but the effect may reverse when the price is too high. From this observation, it is evident that the hydrogen price plays a crucial role in the renewable energy consumption of the wind power/hydrogen/battery storage coupled system, considering the objective of maximizing profits. Maximizing the consumption of renewable energy while significantly reducing costs can bring about favorable economic benefits and is suitable for the development of future low-carbon clean power systems.

Compared with Figure 9, under the given electrolyzer efficiency, when the static efficiency of the electrolyzer is 60%, the hydrogen production may be higher than the dynamic efficiency, and it can be clearly seen that the number of operations of the electrolyzer with a constant efficiency is reduced, illustrating that it is not adjusted according to the actual supply of renewable energy, which may lead to the waste of energy or an inability to fully utilize renewable energy. In addition, hydrogen production at a constant efficiency does not consider the optimal efficiency of the electrolyzer under different loads, and it cannot maximize efficiency (Figure 10).

We randomly selected 500 min of photovoltaic power generation data from a day, with these data representing the actual power generation power of the photovoltaic system in different time periods. These data may be affected by the weather, the solar radiation intensity, and other environmental factors. Using the same wind power installed capacity and constraint configuration, through this optimization model, the following results were obtained: the electrolyzer utilized the power of photovoltaic power generation and battery to the maximum extent to achieve efficient hydrogen production (Figure 11).

Considering that the entropy weight method may ignore the consistency of the decision matrix and overemphasize the diversity between the standards, we used the CRITIC method to determine the weight of the two objectives, which is a weight based on the calculation methods of the AHP and the entropy weight method, because it can take into account the consistency of the judgment matrix and the degree of contradiction between each standard, so the accuracy of determining the weight of each standard is relatively higher. This method first calculates the consistency index of each standard, and then it determines the weight of each target according to the relative size of these consistency indexes. At this time, we obtained the weight of curtailment rate as 0.52147 and the weight of the profit as 0.47853. This shows that, in the optimization of the wind/battery storage/alkaline electrolyzer system, the importance of reducing the curtailment rate is slightly higher than that of increasing profits (Figure 12).

In conclusion, the power optimization solution obtained through the analysis of the wind power/battery storage/alkaline electrolyzer system takes into account both the hydrogen production cost and the requirement of maximizing the consumption of renewable energy generation. This approach ensures a more even distribution of resources and enhances the efficiency of the power system to a certain extent.

5. Conclusions

Hydrogen technology has the potential to play a significant role in microgrids and standalone applications, but it also faces certain limitations and challenges. Ensuring a consistent and reliable supply of renewable energy for hydrogen production can be a challenge, particularly in remote or off-grid areas. In the case of large fluctuations in renewable energy and batteries that cannot meet constraints such as charging and discharging, disconnecting from the grid may cause the frequent start and stop of the electrolyzer, shorten the life of the electrolyzer, and increase operating costs. Owing to the great advantages and potential of hydrogen energy, its development and utilization have become increasingly popular. Nevertheless, there is less research on the optimal operation of wind/battery storage/alkaline electrolyzers. Therefore, this study established a multi-energy operation optimization model by considering the dynamic efficiency of hydrogen production. In terms of hydrogen production, a wind/battery storage/alkaline electrolyzer system considering dynamic hydrogen production efficiency can effectively meet the challenges brought about by the fluctuation of renewable energy. Battery storage can store surplus renewable energy and release it when needed to balance the difference between energy supply and demand. And the optimization algorithm can be used to find the relatively optimal power allocation strategy to ensure the minimum power abandonment rate and maximize profit. The main conclusions are as follows:

(1)

The hydrogen production efficiency of the alkaline electrolyzer has a non-linear relationship with its input power. Compared with constant efficiency, dynamic hydrogen production can be combined with post-optimization to make more effective use of renewable energy. The trend of hydrogen production efficiency is to increase first and then decrease. Therefore, it is significant to consider the dynamic efficiency of hydrogen production.

(2)

The distribution of Pareto solutions was uniform, which indicates the suitability of the NSGA-II algorithm. The weights of the power abandonment rate (objective 1) and profit (objective 2) were 0.421 and 0.579, respectively.

(3)

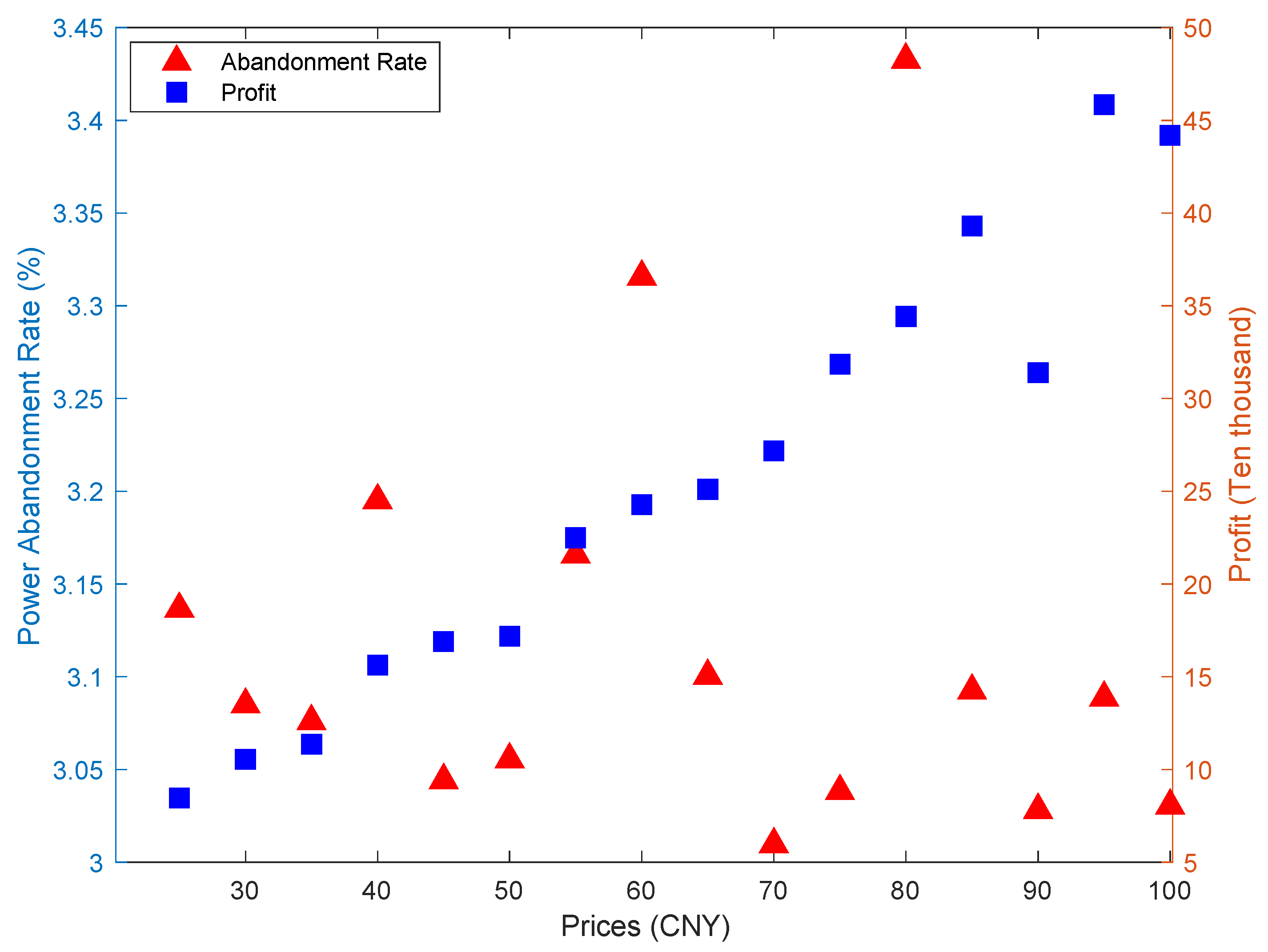
Profits are sensitive to hydrogen prices. As the hydrogen price rises, the profit gradually increases, and the power abandonment rate changes accordingly. This may be due to the large fluctuation of wind power resources. Even if the hydrogen price rises, the system may still not be able to eliminate all power curtailment. The system will find a balanced strategy. Therefore, policymakers should pay close attention to hydrogen prices.

In a future study, a hybrid electrolysis system including alkaline electrolyzers and proton exchange membrane electrolyzers will be considered. Research and analyses of various optimization algorithms, such as the grasshopper optimization algorithm [33], improving the strength Pareto evolutionary algorithm (SPEA2) [34], the multi-objective heat transfer search algorithm for truss optimization (MOHTS) [35], the multi-objective passing vehicle search algorithm for structure optimization (MOPVS) [36], a novel physics-based multi-object thermal exchange optimization algorithm to design truss structures (MOETO) [37], a decomposition-based multi-objective heat transfer search algorithm for structure optimization (MOHTS/D) [38], NSGA-II, and a multi-target solving device analysis, will be carried out, as well as the study and application of hydrogen dynamics.