High Static Gain DC–DC Double Boost Quadratic Converter
Abstract
:1. Introduction
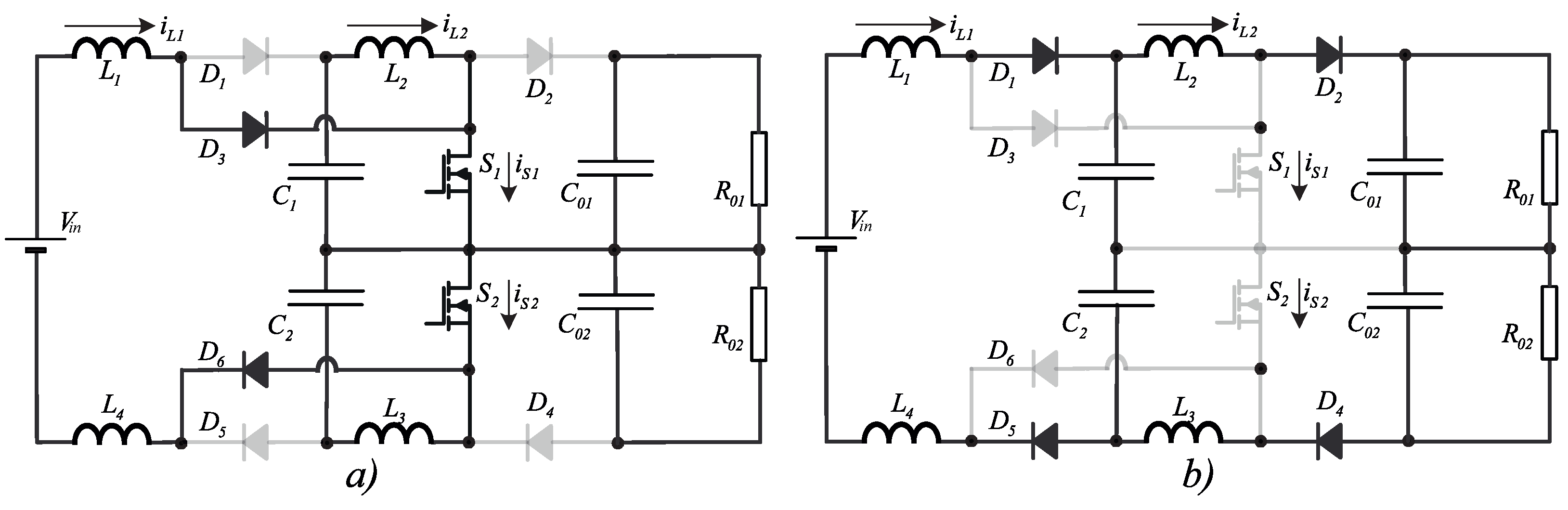
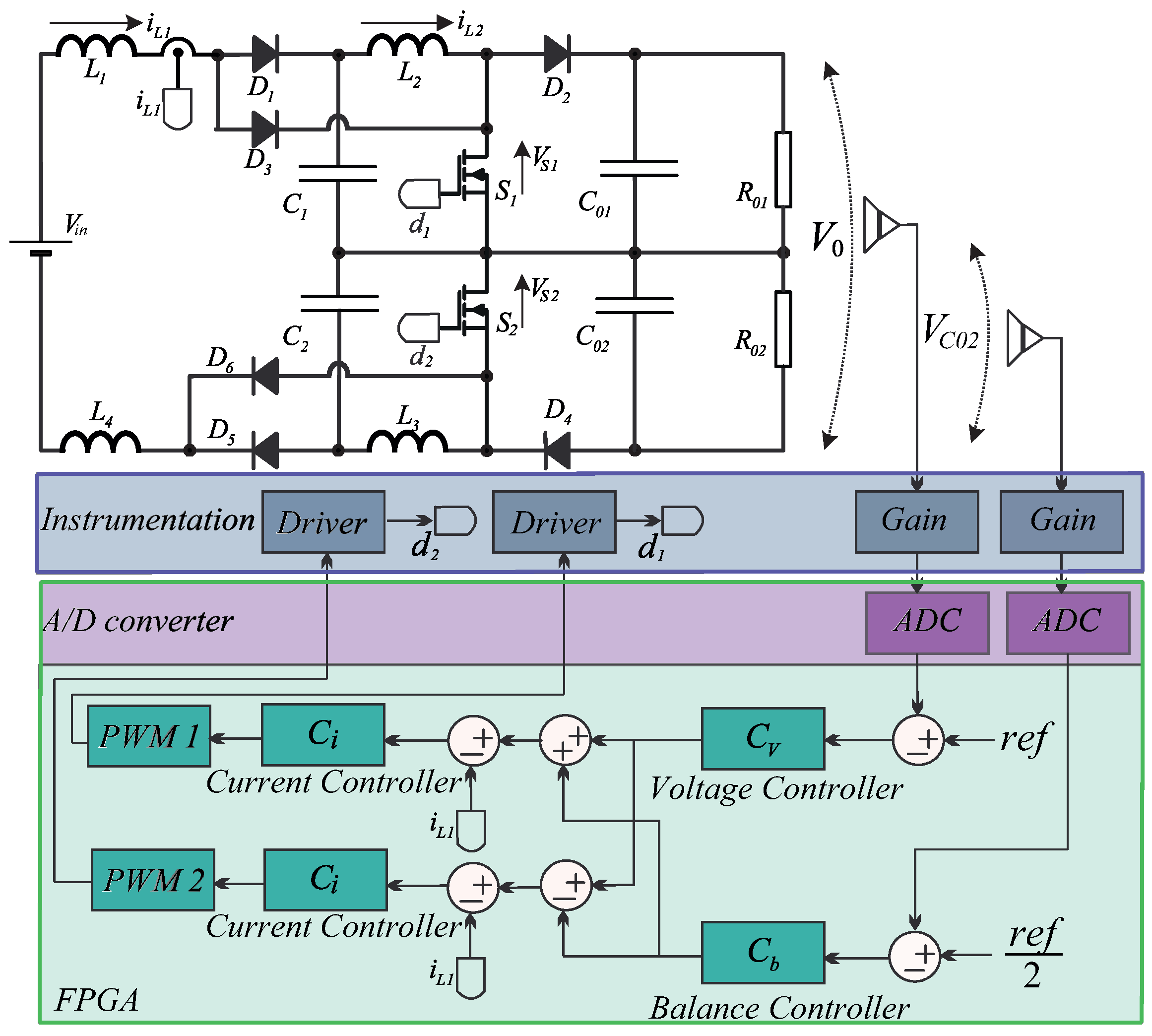
2. Converter Topology
2.1. Operation in Continuous Conduction Mode (CCM)
2.1.1. First Stage: (, )
2.1.2. Second Stage: (, )
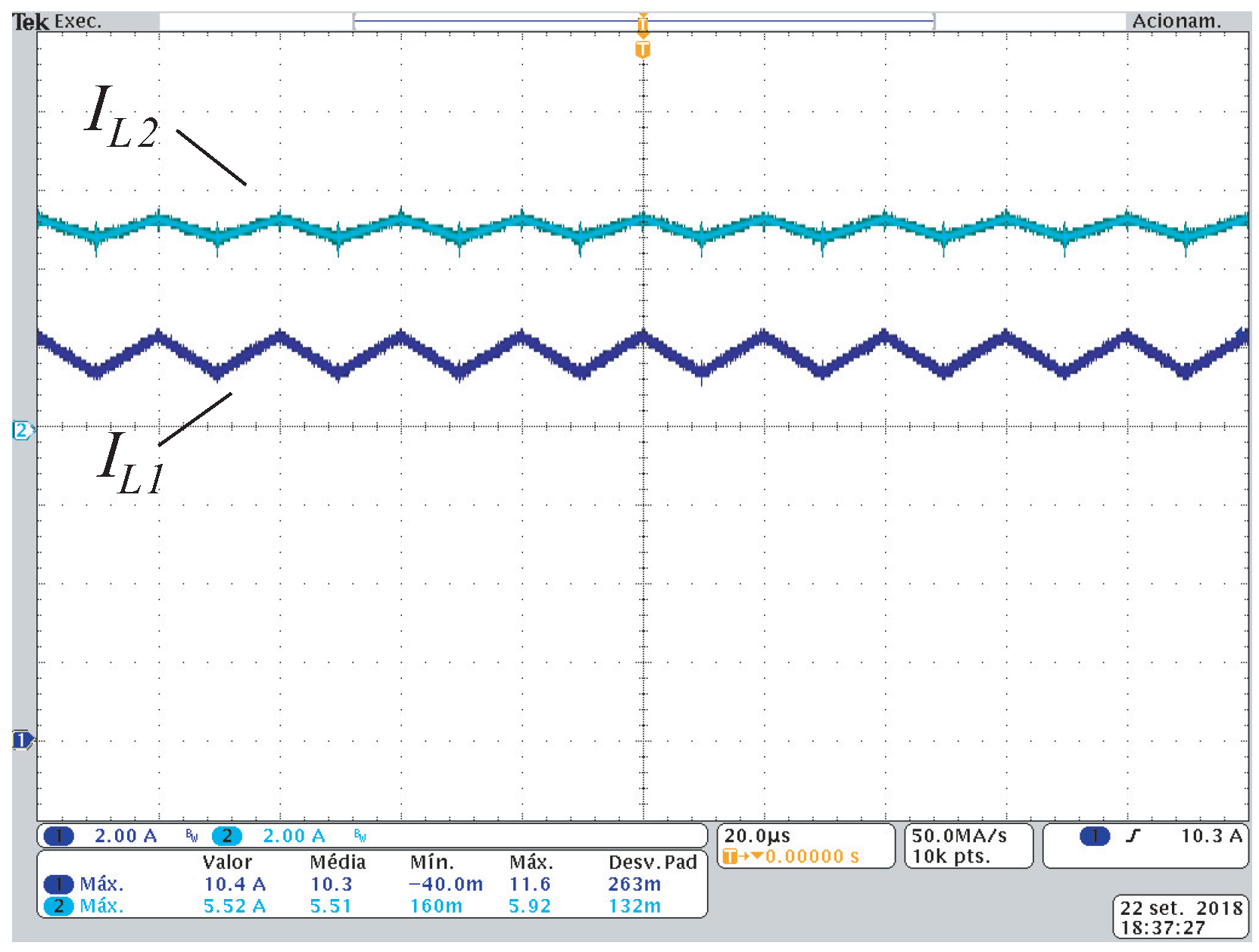
2.1.3. Current Ripple in Inductors and
2.1.4. Converter Component Design
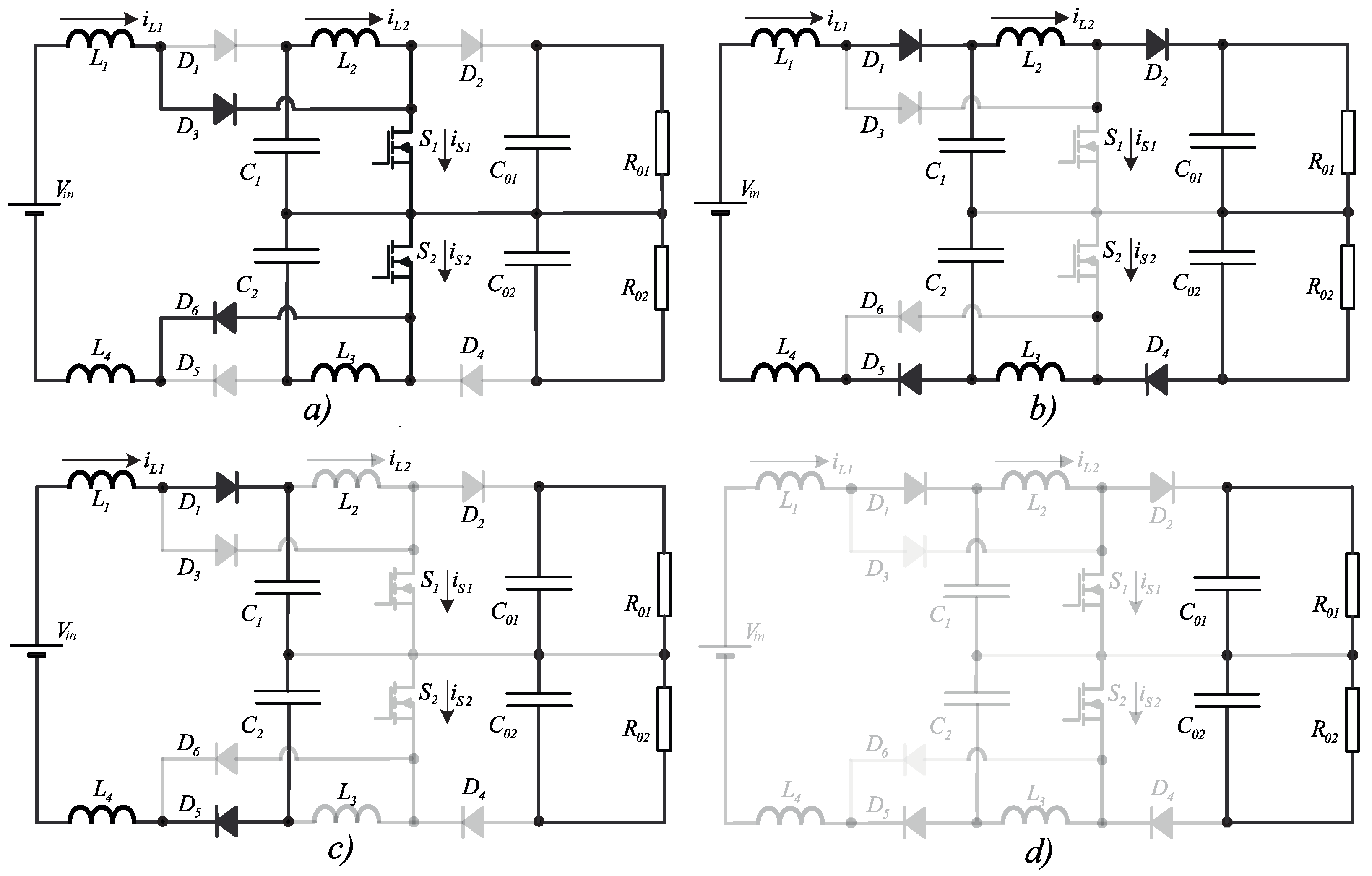
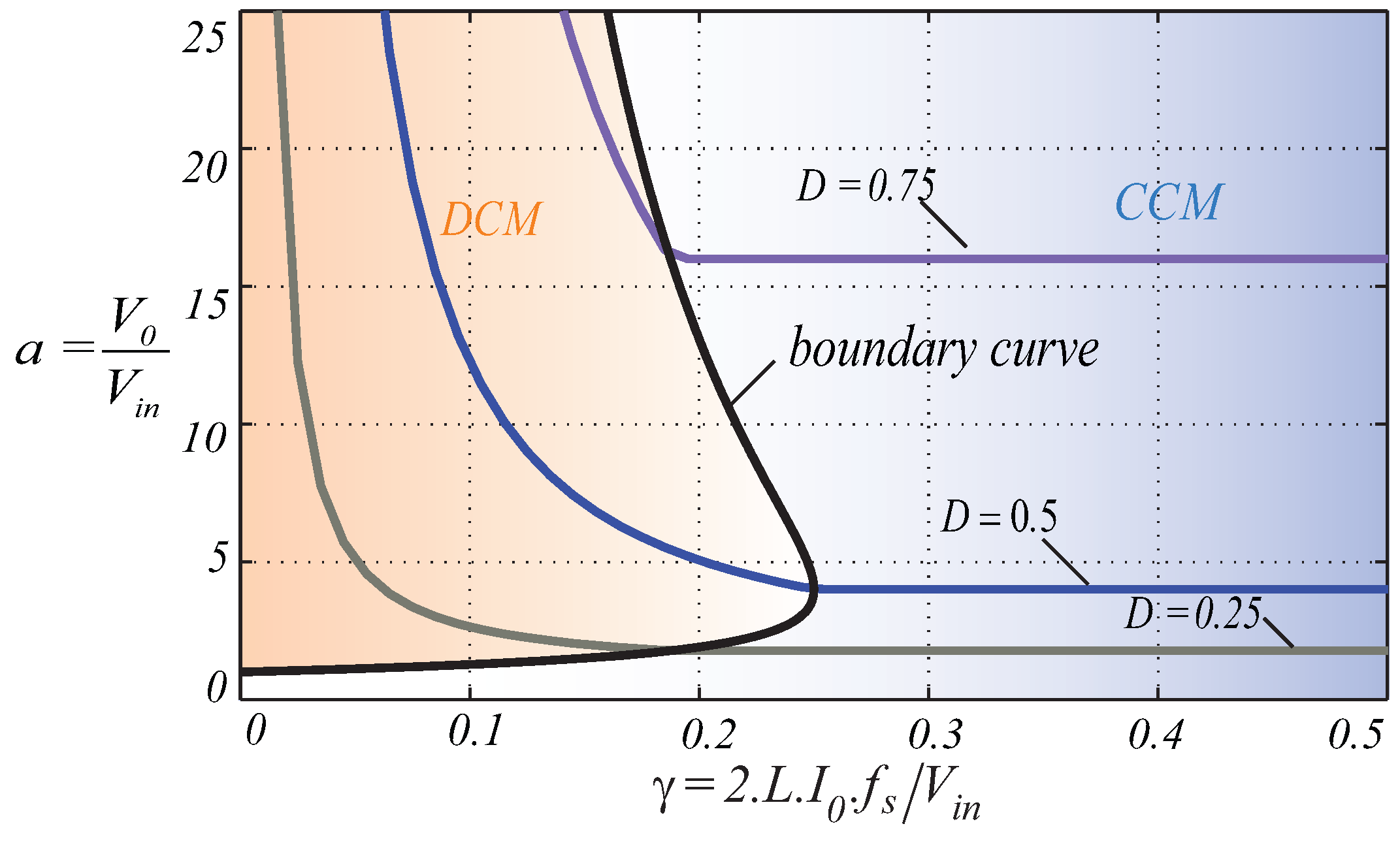
2.2. Operation in Critical Conduction Mode
2.3. Operation in Discontinuous Conduction Mode
2.3.1. Third Stage: (, )
2.3.2. Fourth Stage: (, )
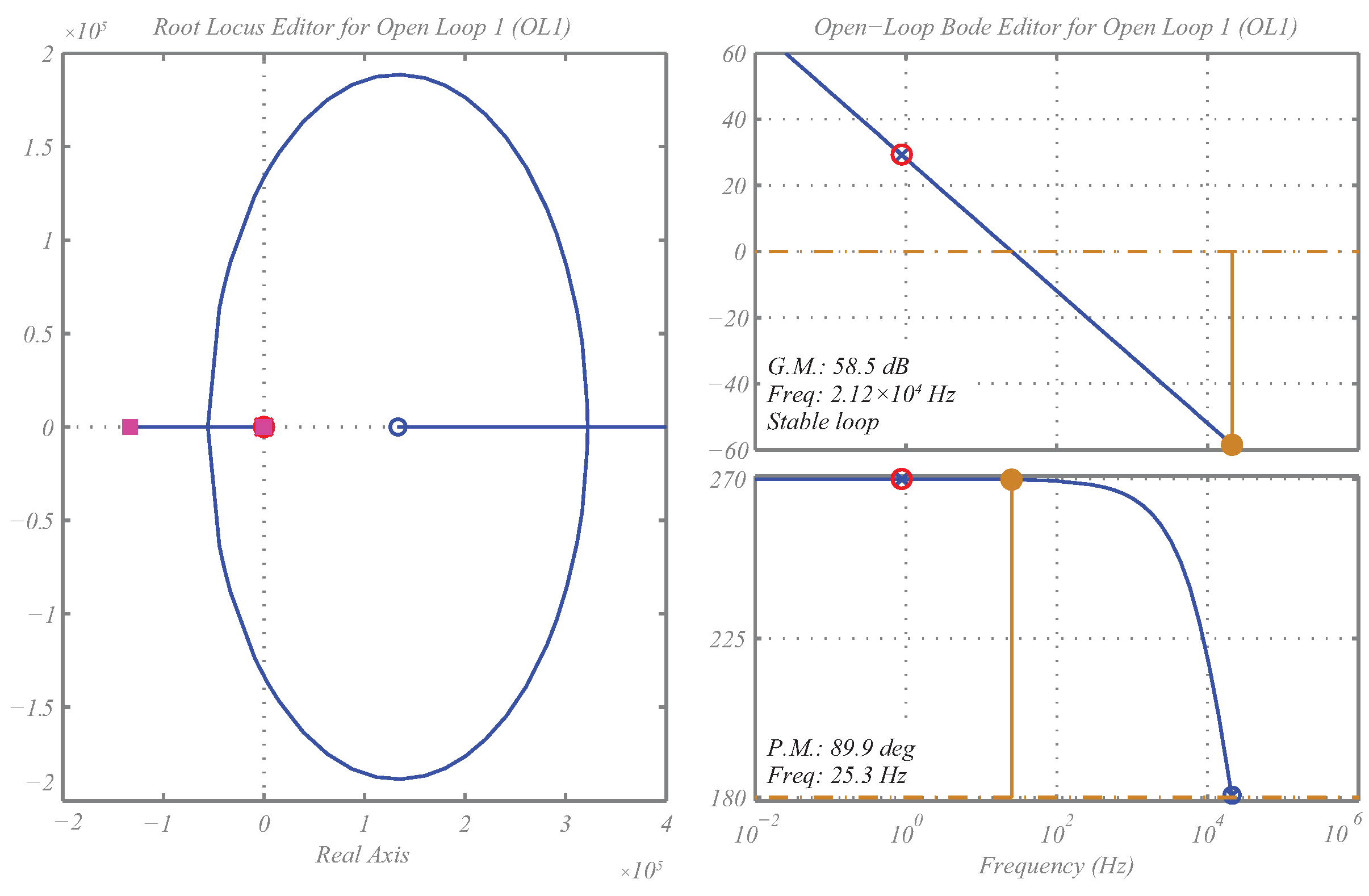
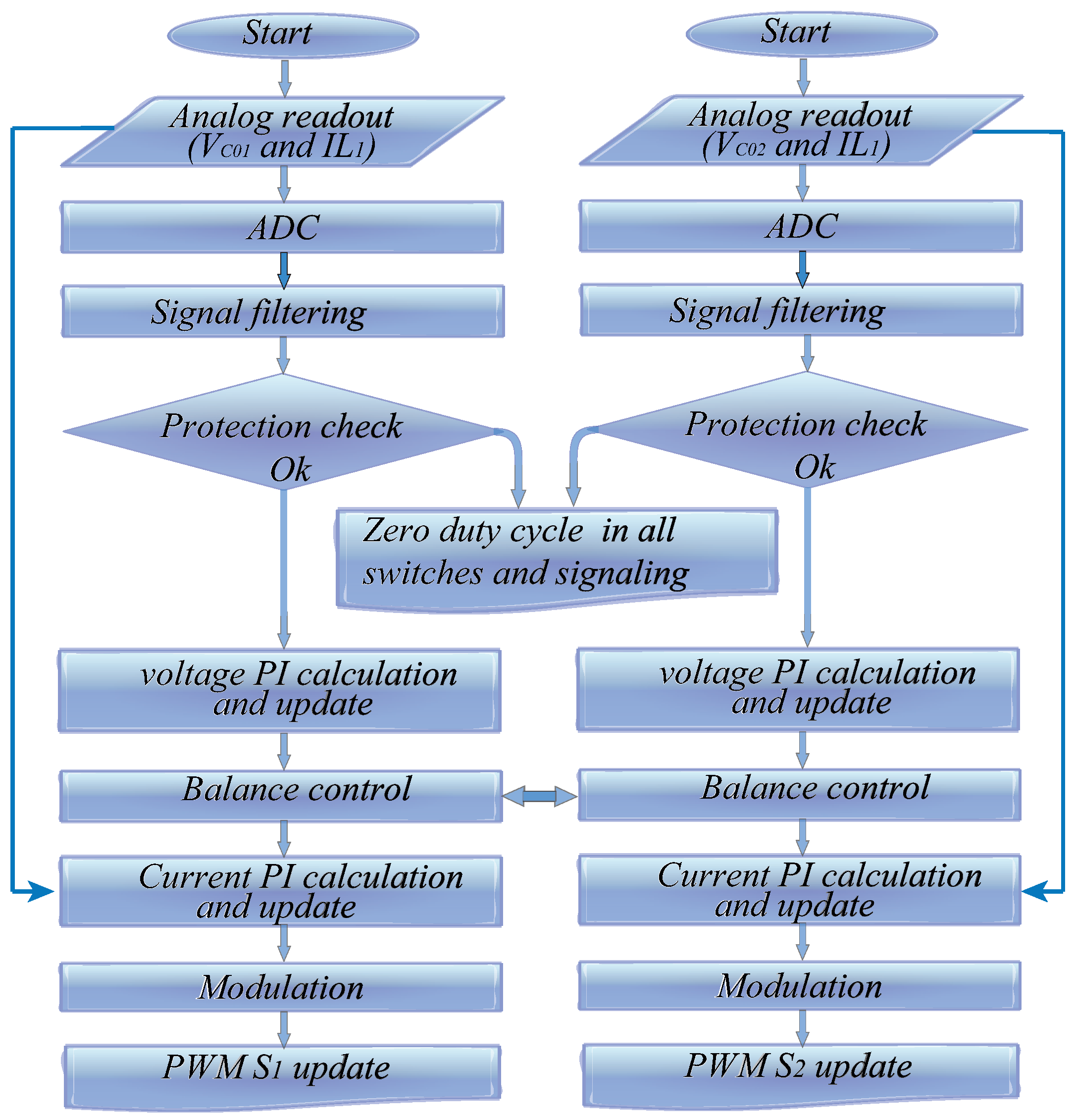
3. Dynamic Modeling and Converter Control
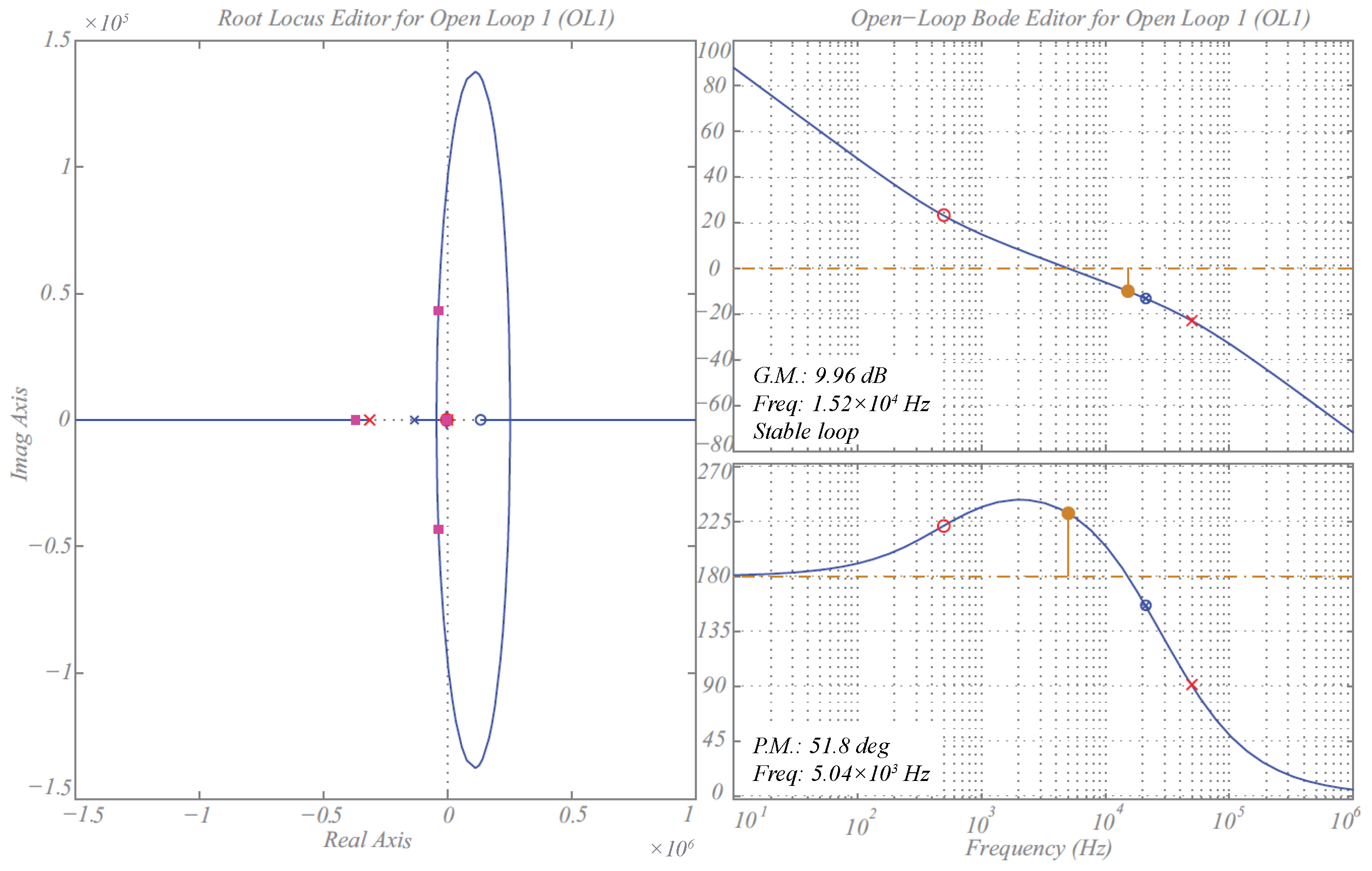

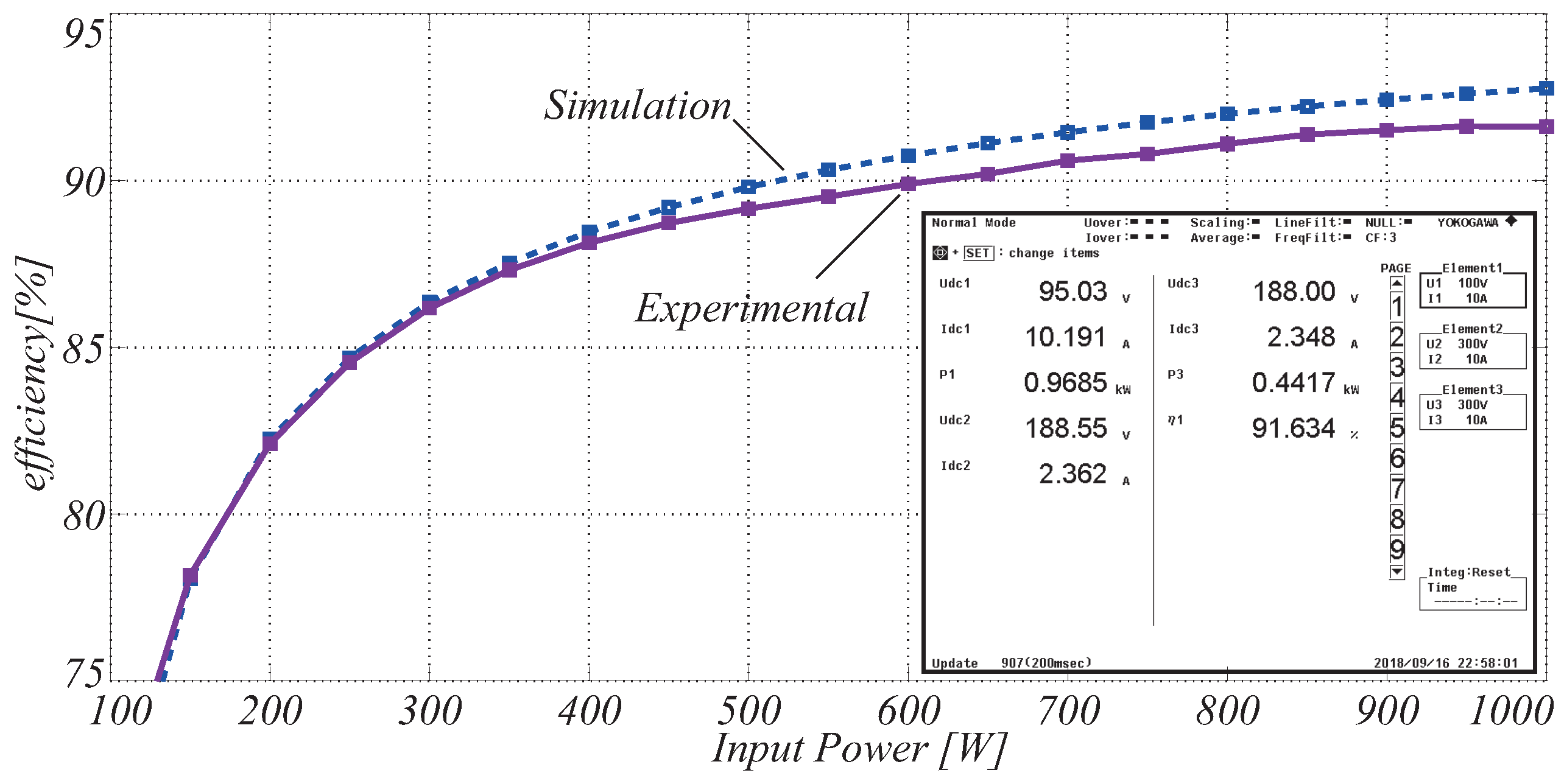
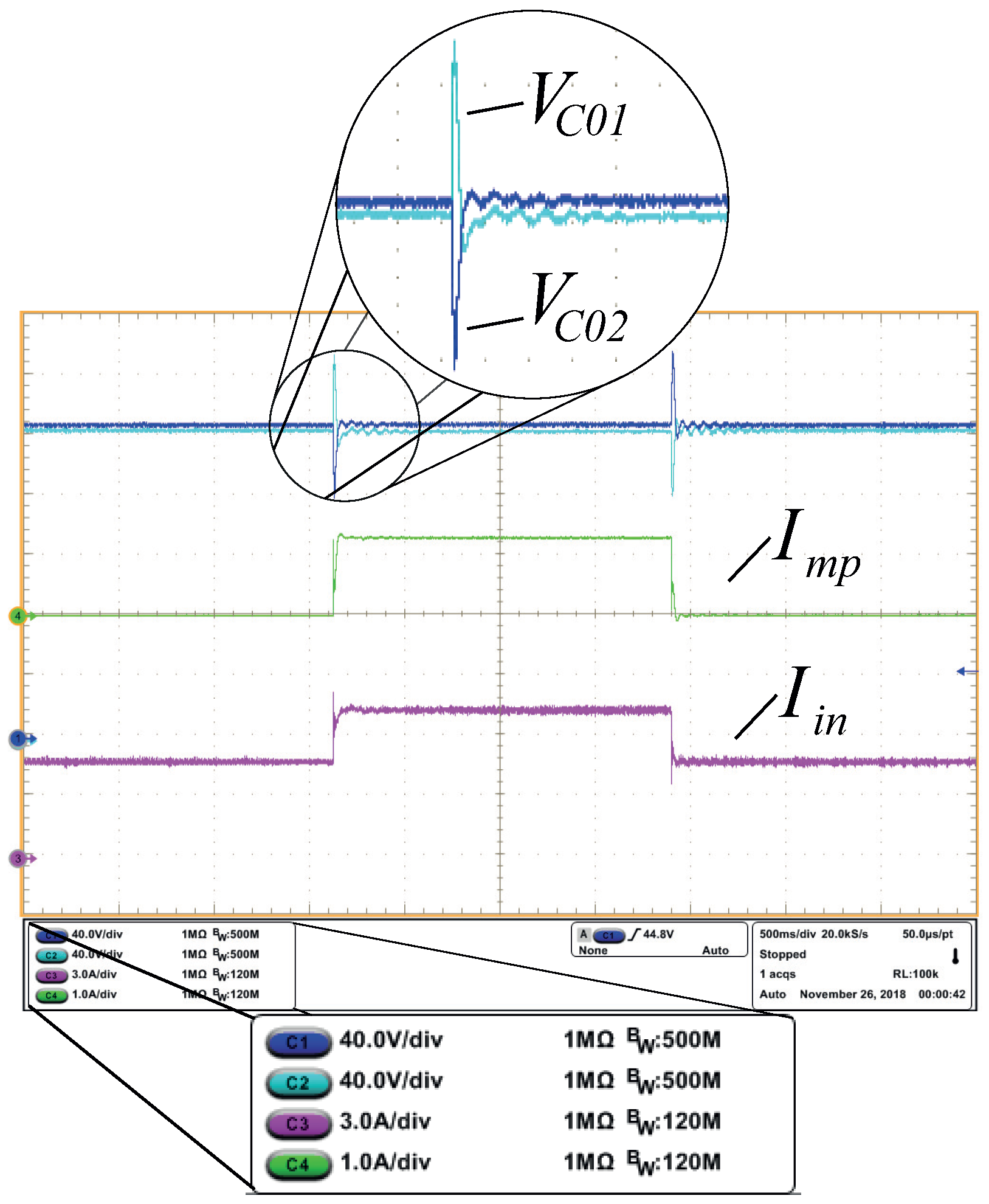
4. Experimental Results
4.1. Converter Operating Open Loop
4.2. Converter Operating in Closed Loop
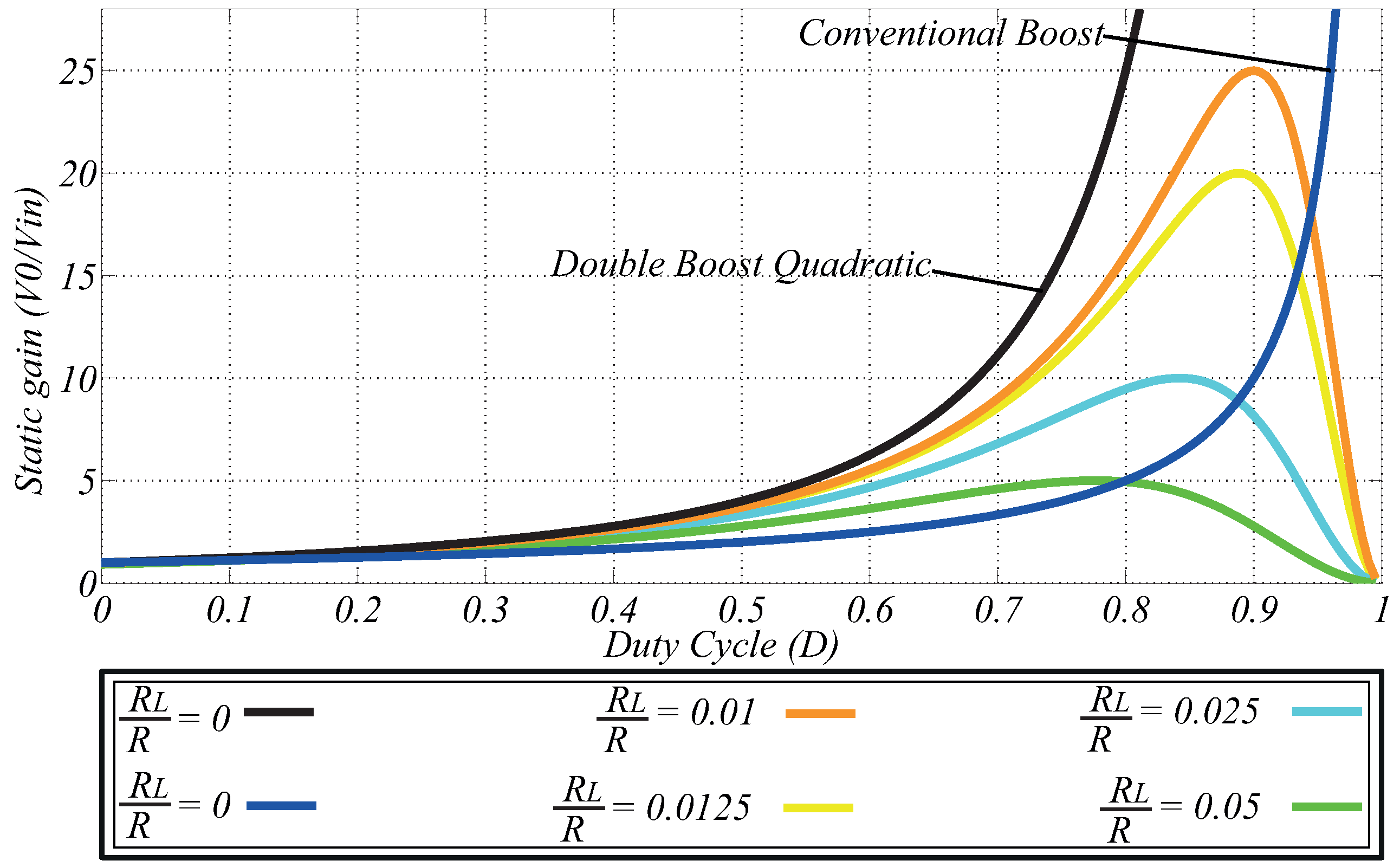
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Danielis, R.; Scorrano, M.; Massi Pavan, A.; Blasuttigh, N. Simulating the Diffusion of Residential Rooftop Photovoltaic, Battery Storage Systems and Electric Cars in Italy. An Exploratory Study Combining a Discrete Choice and Agent-Based Modelling Approach. Enegies 2023, 16, 557. [Google Scholar] [CrossRef]
- Sumathy, P.; Navamani, J.D.; Lavanya, A.; Sathik, J.; Zahira, R.; Essa, F.A. PV Powered High Voltage Pulse Converter with Switching Cells for Food Processing Application. Energies 2023, 16, 1010. [Google Scholar] [CrossRef]
- Karbowniczak, A.; Latała, H.; Ne˛cka, K.; Kurpaska, S.; Książek, L. Modelling of Energy Storage System from Photoelectric Conversion in a Phase Change Battery. Energies 2022, 15, 1132. [Google Scholar] [CrossRef]
- Kishore, P.M.; Bhimasingu, R. Dual-input and triple-output boost hybrid converter suitable for grid-connected renewable energy sources. IET Power Electron. 2020, 13, 808–820. [Google Scholar] [CrossRef]
- Khodair, D.; Motahhir, S.; Mostafa, H.H.; Shaker, A.; Munim, H.A.E.; Abouelatta, M.; Saeed, A. Modeling and Simulation of Modified MPPT Techniques under Varying Operating Climatic Conditions. Energies 2023, 16, 549. [Google Scholar] [CrossRef]
- Pellitteri, F.; Di Dio, V.; Puccio, C.; Miceli, R. A Model of DC-DC Converter with Switched-Capacitor Structure for Electric Vehicle Applications. Energies 2022, 15, 1224. [Google Scholar] [CrossRef]
- Yalla, N.; Agarwal, P.; Venkata, J.S.P.A.; Bussa, V.K. Reduced switching state multilevel improved power factor converter for level-3 electric vehicle applications. IET Power Electron. 2020, 13, 693–702. [Google Scholar] [CrossRef]
- Russo, A.; Cavallo, A. Stability and Control for Buck–Boost Converter for Aeronautic Power Management. Energies 2023, 16, 988. [Google Scholar] [CrossRef]
- Li, H.; Gu, Y.; Zhang, X.; Liu, Z.; Zhang, L.; Zeng, Y. A Fault-Tolerant Strategy for Three-Level Flying-Capacitor DC/DC Converter in Spacecraft Power System. Energies 2023, 16, 556. [Google Scholar] [CrossRef]
- Zhou, G.; Tian, Q.; Leng, M.; Fan, X.; Bi, Q. Energy management and control strategy for DC microgrid based on DMPPT technique. IET Power Electron. 2020, 13, 658–668. [Google Scholar] [CrossRef]
- Kumar, R.; Wu, C.-C.; Liu, C.-Y.; Hsiao, Y.-L.; Chieng, W.-H.; Chang, E.-Y. Discontinuous Current Mode Modeling and Zero Current Switching of Flyback Converter. Energies 2021, 14, 5996. [Google Scholar] [CrossRef]
- Farakhor, A.; Abapour, M.; Sabahi, M. Study on the derivation of the continuous input current high-voltage gain DC/DC converters. IET Power Electron. 2018, 11, 1–9. [Google Scholar] [CrossRef]
- Sedaghati, F.; Pourfajar, S. Analysis and implementation of a boost DC-DC converter with high voltage gain and continuous input current. IET Power Electron. 2020, 13, 798–807. [Google Scholar] [CrossRef]
- Samuel, V.J.; Keerthi, G.; Mahalingam, P. Coupled inductor-based DC-DC converter with high voltage conversion ratio and smooth input current. IET Power Electron. 2020, 13, 733–743. [Google Scholar] [CrossRef]
- Middlebrook, R.D. Transformerless DC-to-DC converters with large conversion ratios. IET Power Electron. 1988, 3, 484–488. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.; Sun, Y. Overview of Dual-Active-Bridge Isolated Bidirectional DC-DC Converter for High-Frequency-Link Power-Conversion System. IET Power Electron. 2014, 29, 4091–4106. [Google Scholar] [CrossRef]
- Jeferson, F. Conversor CC-CC Híbrido Isolado Para Utilização em Sistemas MVDC. Ph.D. Thesis, Universidade Federal de Santa Catarina, Florianópolis, Brazil, 2020. [Google Scholar]
- Jéssika Melo de, A. Conversores CC-CC Não-Isolados Elevadores Baseados na Conexão Diferencial de Conversores Com Tensão de Saída de Mesma Polaridade. Ph.D. Thesis, Universidade Federal de Santa Catarina, Florianópolis, Brazil, 2022. [Google Scholar]
- Jamshidpour, E.; Poure, P.; Saadate, S. Unified Switch Fault Detection for Cascaded Non-Isolated DC-DC Converters. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Forouzesh, M.; Siwakoti, Y.P.; Gorji, S.A.; Blaabjerg, F.; Lehman, B. Step-Up DC-DC Converters: A Comprehensive Review of Voltage-Boosting Techniques, Topologies, and Applications. IET Power Electron. 2017, 32, 9143–9178. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, L.; Sumner, M.; Wang, P. Single-Switch, Wide Voltage-Gain Range, Boost DC-DC Converter for Fuel Cell Vehicles. IEEE Trans. Veh. Technol. 2018, 67, 134–145. [Google Scholar] [CrossRef]
- Julio Cesar, D. Família de Retificadores Boost Unidirecionais Híbridos Monofásicos Com Célula de Capacitor Chaveado. Ph.D. Thesis, Universidade Federal de Santa Catarina, Florianópolis, Brazil, 2017. [Google Scholar]
- Axelrod, B.; Berkovich, Y.; Ioinovici, A. Switched-Capacitor/Switched-Inductor Structures for Getting Transformerless Hybrid DC-DC PWM Converters. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 687–696. [Google Scholar] [CrossRef]
- Fardahar, S.M.; Sabahi, M. New Expandable Switched-Capacitor/Switched-Inductor High-Voltage Conversion Ratio Bidirectional DC-DC Converter. IEEE Trans. Power Electron. 2020, 35, 2480–2487. [Google Scholar] [CrossRef]
- Liu, H.; Li, F. A Novel High Step-up Converter with a Quasi-active Switched-Inductor Structure for Renewable Energy Systems. IEEE Trans. Power Electron. 2016, 31, 5030–5039. [Google Scholar] [CrossRef]
- Samiullah, M.; Iqbal, A.; Ashraf, I.; Maroti, P.K. Voltage Lift Switched Inductor Double Leg Converter with Extended Duty Ratio for DC Microgrid Application. IEEE Access 2021, 9, 85310–85325. [Google Scholar] [CrossRef]
- Lenon, S. Metodologia Para Concepção de Conversores CC-CC de Alto Ganho Baseados em Topologias Básicas Com Indutor Acoplado e Células Multiplicadoras de Tensão. Ph.D. Thesis, Universidade Federal de Santa Catarina, Florianópolis, Brazil, 2020. [Google Scholar]
- Wu, T.-F.; Yu, T.-H. Unified approach to developing single-stage power converters. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 211–223. [Google Scholar] [CrossRef]
- de Azevedo Ayres, W.; Bridi, É.; Sartori, H.C.; Pinheiro, J.R. Conversor de Alto Ganho de Tensão Dual Boost Quadrático; SEPOC: Santa Maria, Brasil, 2018. [Google Scholar]
- Marcos Antônio, S. Metodologia Aplicada à Derivação e Modelagem de Conversores CC-CC Diferenciais de Alto Ganho. Ph.D. Thesis, Universidade Federal de Santa Catarina, Florianópolis, Brazil, 2020. [Google Scholar]
- Matsuo, H.; Harada, K. The Cascade Connection of Switching Regulators. IEEE Trans. Ind. Appl. 1976, IA-12, 192–198. [Google Scholar] [CrossRef]
- Maksimovic, D.; Cuk, S. General properties and synthesis of PWM DC-to-DC converters. In Proceedings of the 20th Annual IEEE Power Electronics Specialists Conference, PESC’89 Record, Milwaukee, WI, USA, 26–29 June 1989; Volume 2, pp. 515–525. [Google Scholar]
- Maksimovic, D.; Cuk, S. Switching converters with wide DC conversion range. IEEE Trans. Power Electron. 1991, 6, 151–157. [Google Scholar] [CrossRef]
- Barreto, L.H.S.C.; Coelho, E.A.A.; Farias, V.J.; de Freitas, L.C.; Vieira, J.B., Jr. An optimal lossless commutation quadratic PWM Boost converter. In Proceedings of the Seventeenth Annual IEEE Applied Power Electronics Conference and Exposition, APEC, Dallas, TX, USA, 10–14 March 2002; Volume 2, pp. 624–629. [Google Scholar]
- Novaes, Y.R.; Barbi, I.; Rufer, A. A New Three-Level Quadratic (T-LQ) DC/DC Converter Suitable for Fuel Cell Applications. IEEJ Trans. Ind. Appl. 2008, 124, 459–467. [Google Scholar] [CrossRef]
- Cordeiro, A.; Pires, V.F.; Foito, D.; Pires, A.J.; Martins, J.F. Three-level quadratic boost DC-DC converter associated to a SRM drive for water pumping photovoltaic powered systems. Sol. Energy 2020, 209, 42–56. [Google Scholar] [CrossRef]
- de Sá, F.L.; Ruiz-Caballero, D.; Mussa, S.A. A new DC-DC double Boost Quadratic converter. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar] [CrossRef]
- Erickson, R.W. Fundamentals of Power electronics. In Lectures on Power Electronics, 1st ed.; Chapman & Hall: New York, NY, USA, 1997. [Google Scholar]
- Silva, G.V.; Coelho, R.F.; Lazzarin, T.B. Modeling the Switched Capacitor Cell Boost Converter Using a Reduced Order Equivalent Converter. IEEE Trans. Power Electron. 2017, 22, 288–297. [Google Scholar]
- Sun, J.; Bass, R.M. Modeling and practical design issues for average current control. In Proceedings of the Fourteenth Annual Applied Power Electronics Conference and Exposition, APEC ’99, Dallas, TX, USA, 14–18 March 1999; Volume 2, pp. 980–986. [Google Scholar]
- Guepfrih, M.F.; Waltrich, G.; Lazzarin, T.B. Quadratic-boost-double-flyback converter. IET Power Electron. 2019, 12, 1–12. [Google Scholar] [CrossRef]
- Silva Junior, E.T. Boost Converter Analysis and Design of the Compensators. Master’s Dissertation, University Federal of Santa Catarina UFSC, INEP, Florianópolis, Brazil, 1994. [Google Scholar]
- Ogata, K. Modern Control Engineering, 5th ed.; Prentice & Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Brockveld, S.L.; Waltrich, G. Boost-flyback converter with interleaved input current and output voltage series connection. IET Power Electron. 2018, 11, 1–9. [Google Scholar] [CrossRef]
- Martins, A.S.; Kassick, E.V.; Barbi, I. Control strategy for the double-boost converter in continuous conduction mode applied to power factor correction. In Proceedings of the 27th Annual IEEE Power Electronics Specialists Conference, PESC’96 Record, Baveno, Italy, 23–27 June 1996; Volume 2, pp. 1066–1072. [Google Scholar]
- Padilha, F.J.C.; Bellar, M.D. Modeling and control of the half bridge voltage doubler boost converter. In Proceedings of the 2003 IEEE International Symposium on Industrial Electronics. ISIE’03, Rio de Janeiro, Brazil, 9–11 June 2003; Volume 2, pp. 741–745. [Google Scholar]
- Zhou, J.; Cheng, S.; Hu, Z.; Liu, J. Balancing control of neutral-point voltage for three-level T-type inverter based on hybrid variable virtual space vector. IET Power Electron. 2020, 13, 744–750. [Google Scholar] [CrossRef]
- BeMicro Max10, FPGA Evaluation Kit; Altera: San Jose, CA, USA; Analog Devices: Wilmington, MA, USA, 2014.
- Lahari, M.V.P.; Vedula, S.V.; Rao, V.U. Real time models for FPGA based control of power electronic converters: A graphical programming approach. In Proceedings of the IEEE IAS Joint Industrial and Commercial Power Systems/ Petroleum and Chemical Industry Conference (ICPSPCIC), Hyderabad, India, 19–21 November 2015; pp. 60–65. [Google Scholar]
- Fiori, M.; Barbosa, L.R. Three-Level Boost Quadratic G Converter. IEEE Trans. Power Electron. 2017, 22, 131–138. [Google Scholar]






| Component | Calculation to Obtain Parameters |
|---|---|
| Inductor | |
| Inductor | |
| Intermediate Capacitor | |
| Output Capacitor | |
| Load Resistance R |
| Component | Description | Equating Efforts |
|---|---|---|
| Switch | Average Current | |
| RMS current | ||
| Maximum Current | ||
| Maximum voltage | ||
| Diode | Average Current | |
| RMS current | ||
| Maximum Current | ||
| Maximum voltage | ||
| Diode | Average Current | |
| RMS current | ||
| Maximum Current | ||
| Maximum voltage | ||
| Diode | Average Current | |
| RMS current | ||
| Maximum Current | ||
| Maximum voltage | ||
| Inductor | Average Current | |
| RMS current | ||
| Maximum Current | ||
| Maximum voltage | ||
| Inductor | Average Current | |
| RMS current | ||
| Maximum Current | ||
| Maximum voltage | ||
| Capacitor | Average Current | |
| RMS current | ||
| Capacitor | Average Current | |
| RMS current |
| Description | Parameters |
|---|---|
| Output Voltage | V |
| Input Voltage | V |
| Intermediate Capacitor | F |
| Output Capacitor | F |
| Load Resistance | ohms |
| Switching Frequency | kHz |
| Duty Cycle | |
| Input Inductance | mH |
| Intermediate Inductance | mH |
| Switch Models (MOSFET)— | |
| Diodes Models (Ultrafast)— |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Sá, F.L.; Ruiz-Caballero, D.; Dal’Agnol, C.; da Silva, W.R.; Mussa, S.A. High Static Gain DC–DC Double Boost Quadratic Converter. Energies 2023, 16, 6362. https://doi.org/10.3390/en16176362
de Sá FL, Ruiz-Caballero D, Dal’Agnol C, da Silva WR, Mussa SA. High Static Gain DC–DC Double Boost Quadratic Converter. Energies. 2023; 16(17):6362. https://doi.org/10.3390/en16176362
Chicago/Turabian Stylede Sá, Franciéli Lima, Domingo Ruiz-Caballero, Cleiton Dal’Agnol, William Rafhael da Silva, and Samir Ahmad Mussa. 2023. "High Static Gain DC–DC Double Boost Quadratic Converter" Energies 16, no. 17: 6362. https://doi.org/10.3390/en16176362
APA Stylede Sá, F. L., Ruiz-Caballero, D., Dal’Agnol, C., da Silva, W. R., & Mussa, S. A. (2023). High Static Gain DC–DC Double Boost Quadratic Converter. Energies, 16(17), 6362. https://doi.org/10.3390/en16176362






