Multi-Angle Reliability Evaluation of Grid-Connected Wind Farms with Energy Storage Based on Latin Hypercube Important Sampling
Abstract
:1. Introduction
- (1)
- To solve the issues of poor convergence and low accuracy of grid reliability evaluation of wind farms and energy storage, this paper proposes a power system reliability evaluation method based on LHIS. First, the sample space probability distribution of the sample object is optimized, and the optimized probability distribution is stratified sampled. Then, the correlation of the sampling matrix is reduced.
- (2)
- To solve the problem of the lack of risk analysis and the severity of the consequences in the case, this paper evaluates the power grid from two perspectives: the operational risk and the contribution to system reliability. Three operation scenarios are set for connecting wind farms with energy storage systems at different nodes, connecting wind farms of different capacities with energy storage systems, and connecting wind farms with different energy storage capacities. It has been verified that the method can evaluate the reliability of the grid more comprehensively and accurately.
2. Wind Farm Output Model
3. Reliability Evaluation for Power Systems with Wind Farms and Energy Storage Systems Based on the Latin Hypercube Importance Sampling Method
3.1. Charge and Discharge Model of Energy Storage System
3.2. Latin Hypercube Important Sampling (LHIS)
3.2.1. Sampling Principle
- (1)
- Optimize the spatial probability distribution of the sampling objects based on the IS method. Then, make the mathematical expectation of the original sample of the sampling object unchanged and replace the original sample space probability distribution with the new probability distribution . If the new variance is 0, then the is the optimal probability distribution at this time. The method is as follows [22]:
- (2)
- Sample the optimized probability distribution based on the LHS method. Stratify the input random variables and select the random sampling points in each hypercube as the sampling points, according to the importance shown in the original probability density function, usually the boundary of the hypercube closest to the expected value. The calculation formula of is as follows (assuming that the sampling number, , is even) [11]:
- (3)
- Reduce the correlation of the sampling matrix based on the Cholesky decomposition method. If K components are sampled, and the sampling times of each component is N, then all of the sampled values will form an initial sampling matrix, , of order . The accuracy of the evaluation results is greatly affected by the correlation of the sampled values in the sampling matrix, therefore, the correlation between the lines of the sampling matrix should be reduced.
3.2.2. Sampling the Power Systems with Wind Farms and Storage Systems
3.3. Evaluation Indicators
3.3.1. Comprehensive Risk Indicator ()
3.3.2. Wind Storage Generation Interrupted Energy Benefit (WSGIEB)
3.4. Evaluation Process
- (1)
- Input the original data, calculation accuracy, and evaluation time of the power system. Sample the power system based on the LHIS method and obtain the initial sampling matrix .
- (2)
- Select the states of the system components in time sequence and calculate the output of wind farms () and the output of conventional power plants ().
- (3)
- Judge the energy storage systems’ operation state and determine the charging power () or discharging power () of the energy storage systems according to the output conditions of the wind farms and the conventional power plants. Calculate the total output of the conventional power plants, wind farms, and energy storage systems.
- (4)
- Calculate the probability power flow of the system, the load cutting, the line power exceeding the limit, the node voltage exceeding the limit, and the power shortage. Calculate the evaluation indicator and judge whether the calculation results converge [32]. If the results do not converge, increase the time by one and return to Step 3.
- (5)
- If the results converge, end the cycle and output evaluation indicators.
4. Simulation Analysis
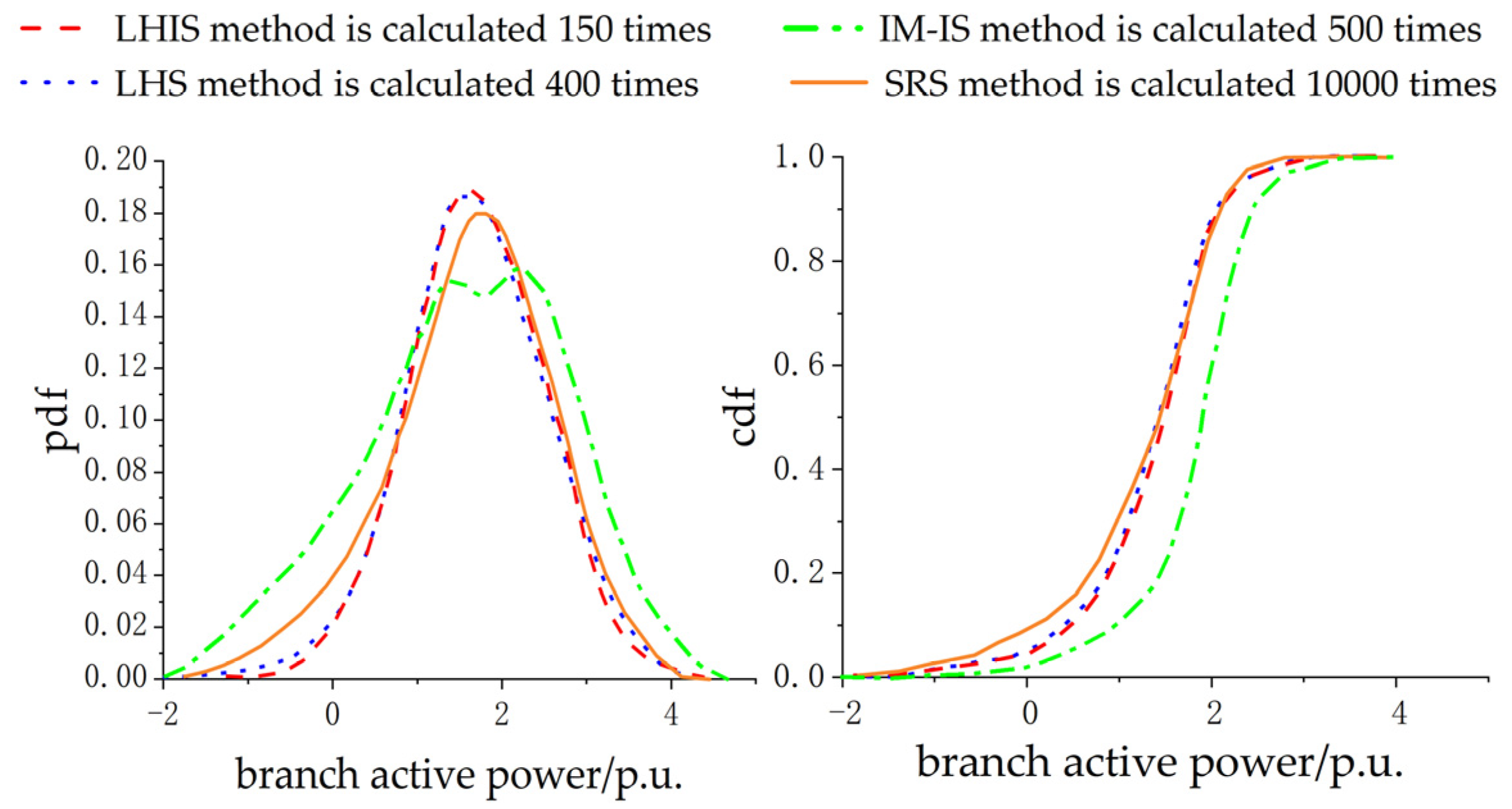
4.1. Verification of Evaluation Methods
4.2. Connecting Wind Farms with Energy Storage Systems at Different Nodes
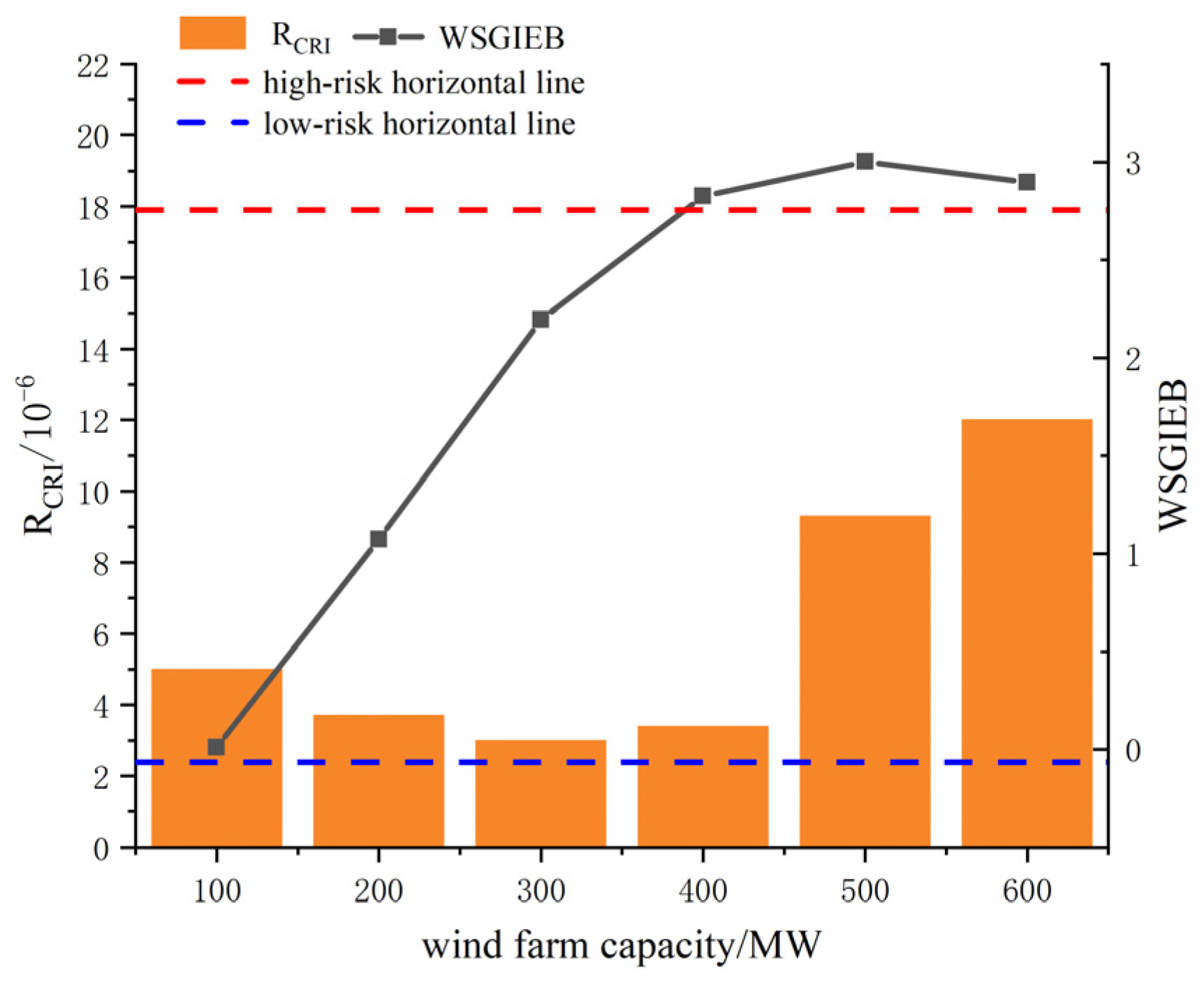
4.3. Connecting Wind Farms of Different Capacities with Energy Storage Systems
4.4. Connecting Wind Farms with Different Energy Storage Capacities
5. Conclusions
- (1)
- Through comparative experiments with the LHIS method, the LHS method, and the IM-IS method, it can be concluded that the calculation efficiency of the LHIS method is 40% higher than that of the LHS method and 47% higher than that of the IM-IS method. The calculation accuracy of the LHIS method is 20% higher than that of the LHS method and 33% higher than that of the IM-IS method.
- (2)
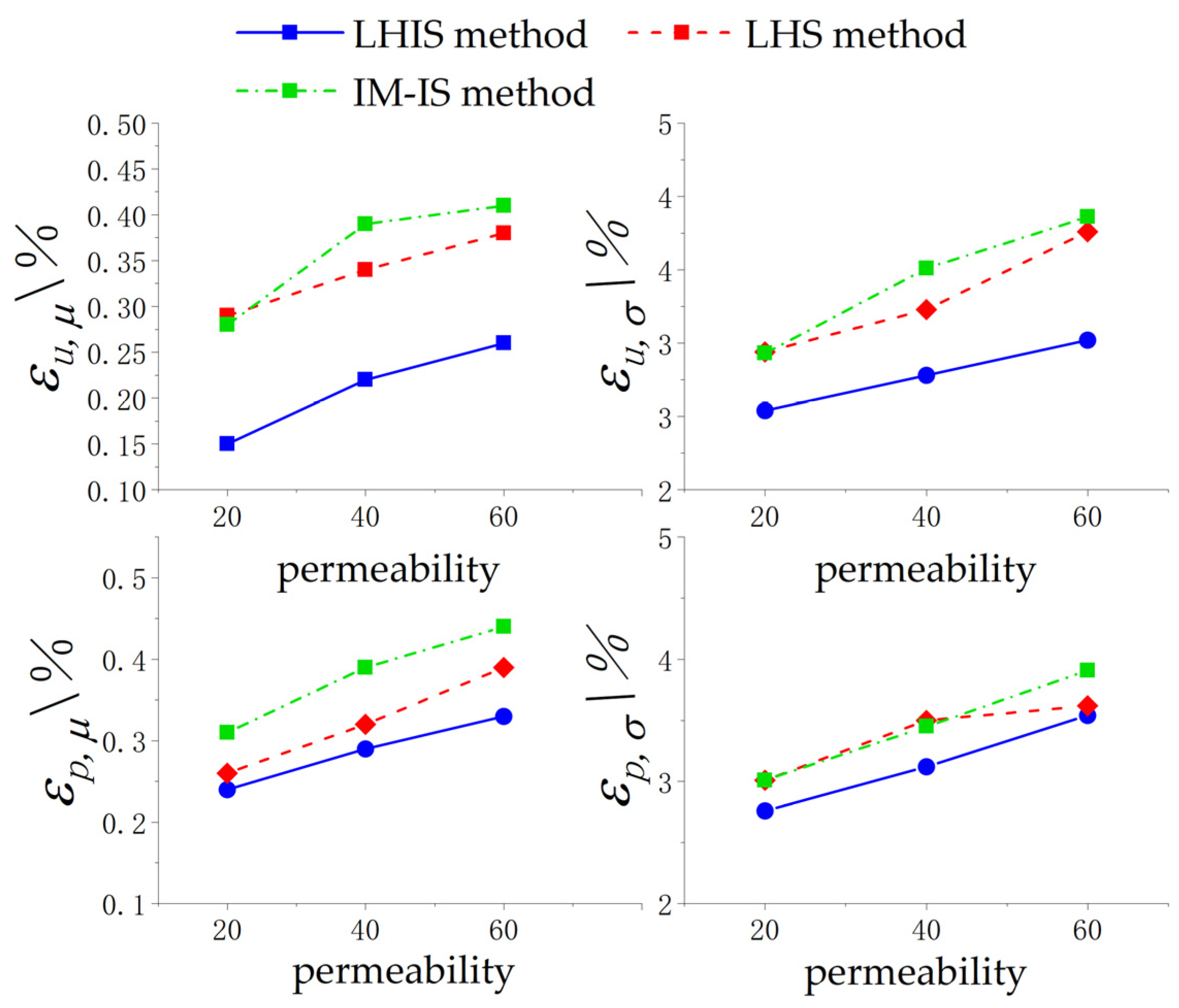
- The LHIS method is universal to the reliability analysis of power systems under different permeability conditions. When the permeability reaches 60%, the relative error of expectation does not exceed 0.3%, and the relative error of standard deviation does not exceed 3%. Simultaneously, the calculation time does not exceed 6 s. The LHIS method ensures the high precision of the results and a fast calculation time under high permeability conditions.
- (3)
- This paper proposed a comprehensive risk indicator to evaluate the operational risk and the wind storage generation interrupted energy benefit (WSGIEB) to evaluate the contribution of the reliability, which solved the problem of a lack of risk analysis of operation state in traditional power system reliability evaluation. Combined with the operation risk division table, the operation of the power system in this state can be more intuitively obtained.
- (4)
- By analyzing different wind farms with different energy storage system connection strategies, it can be confirmed that the LHIS method can accurately evaluate the reliability of power systems and provide useful references for power system design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, X.M.; Cheng, S.J.; Wen, J.Y. Analysis on the application prospect of energy storage technology in solving large-scale wind power grid connection problems. Power Syst. Autom. 2013, 37, 14–18. [Google Scholar] [CrossRef]
- Ni, W.; Lv, L.; Xiang, Y.; Liu, J.Y.; Huang, Y.; Wang, P.F. Reliability assessment of integrated energy systems based on Markov Process Monte Carlo method. Power Grid Technol. 2020, 44, 150–158. [Google Scholar] [CrossRef]
- Gong, L.X.; Liu, T.Q.; He, C.; Nan, L.; Su, X.N.; Hu, X.T. Considering comprehensive gas-electric combined system reliability assessment of demand response. Electr. Power Autom. Equip. 2021, 9, 39–47. [Google Scholar] [CrossRef]
- Li, Y. Reliability Assessment of Power System with Large-Scale Renewable Energy. Master’s Thesis, Ningxia University, Yinchuan, China, 2020. [Google Scholar]
- Zhao, Y.; Wang, J.; Geng, L.; Wang, Y.P.; Shuang, Y.J. Extended cross entropy method for non sequential Monte Carlo simulation of power grid reliability. Chin. J. Electr. Eng. 2017, 37, 1963–1974. [Google Scholar] [CrossRef]
- Jirutitijaroen, P.; Singh, C. Comparison of Simulation Methods for Power System Reliability Indexes and Their Distributions. IEEE Trans. Power Syst. 2008, 23, 486–493. [Google Scholar] [CrossRef]
- Huang, Y.S.; Chen, S.H.; Chen, Z.; Hu, W.; Huang, Q. Improved probabilistic load flow method based on D-vine Copulas and Latin hypercube sampling in distribution network with multiple wind generators. IET Gener. Transm. Distrib. 2020, 14, 893–899. [Google Scholar] [CrossRef]
- Tómasson, E.; Söder, L. Generation adequacy analysis of multi-area power systems with a high share of wind power. IEEE Trans. Power Syst. 2018, 33, 3854–3862. [Google Scholar] [CrossRef]
- Tómasson, E.; Söder, L. Improve important sampling for reliability evaluation of composite power systems. IEEE Trans. Power Syst. 2017, 32, 2426–2434. [Google Scholar] [CrossRef]
- Cai, J.L.; Xu, Q.S.; Cao, M.J.; Yang, B. A novel importance sampling method of power system reliability assessment considering multi-state units and correlation between wind speed and load. Int. J. Electr. Power Energy Syst. 2019, 109, 217–226. [Google Scholar] [CrossRef]
- Zhang, W.F.; Che, Y.B.; Liu, Y.S. Improved Latin Hypercube Sampling Method for Reliability Evaluation of Power Systems. Autom. Electr. Power Syst. 2015, 39, 52–57. [Google Scholar] [CrossRef]
- Oh, U.; Lee, Y.; Choi, J.; Karki, R. Reliability evaluation of power system considering wind generator-s coordinated with multi-energy storage systems. IET Gener. Transm. Distrib. 2020, 14, 786–796. [Google Scholar] [CrossRef]
- Yuan, M.F.; Zhao, F.Z.; Wang, S.T. Reliability assessment of wind power storage power generation system based on Monte Carlo simulation. Electr. Appl. Energy Effic. Manag. Technol. 2020, 590, 28–34. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, W.X.; Zhang, J.H.; Yu, Y.; Yu, J.X.; Liu, D.X. Risk assessment of power generation system with battery storage wind farm. J. Sol. Energy 2014, 35, 207–213. [Google Scholar] [CrossRef]
- Yang, X.Y.; Yang, Y.W.; Liu, Y.Q.; Deng, Z.Q. A reliability assessment approach for electric power systems considering wind power uncertainty. IEEE Access 2020, 8, 12467–12478. [Google Scholar] [CrossRef]
- Song, T.H.; Li, K.J.; Han, X.Q.; Chen, W.H.; Jia, Y.B.; Wen, F.S. Cooperative operation strategy of energy storage system in multiple application scenarios. Power Syst. Autom. 2021, 45, 43–51. [Google Scholar] [CrossRef]
- Parvini, Z.; Abbaspour, A.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M. Operational reliability studies of power systems in the presence of energy storage systems. IEEE Trans. Power Syst. 2018, 33, 3691–3700. [Google Scholar] [CrossRef]
- Ponkumar, G.; Jayaprakash, S.; Kanagarathinam, K. Advanced Machine Learning Techniques for Accurate Very-Short-Term Wind Power Forecasting in Wind Energy Systems Using Historical Data Analysis. Energies 2023, 16, 5459. [Google Scholar] [CrossRef]
- Pan, C.Q.; Wang, C.; Zhao, Z.Y.; Wang, J.; Bie, Z. A copula function based Monte Carlo simulation method of multivariate wind speed and PV power spatio-temporal series. Energy Procedia 2019, 15, 213–218. [Google Scholar] [CrossRef]
- Huang, D.; Yang, X.; Gao, L.; Zang, C.; Chen, H.Y. Multi-objective cooperative game interval economic scheduling considering wind power and energy storage connected to power grid. Control Theory Appl. 2021, 38, 1061–1070. [Google Scholar] [CrossRef]
- Shezan, S.A.; Kamwa, I.; Ishraque, M.F.; Muyeen, S.M.; Hasan, K.N.; Saidur, R.; Rizvi, S.M.; Shafiullah, M.; Al-Sulaiman, F.A. Evaluation of Different Optimization Techniques and Control Strategies of Hybrid Microgrid. Energies 2023, 16, 1792. [Google Scholar] [CrossRef]
- Cai, J.L.; Hao, L.L.; Zhang, K.Q. Non-parametric importance stratified sampling method for Reliability evaluation of power systems with renewable energy. Autom. Electr. Power Syst. 2012, 46, 104–115. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.; Ren, H.; Cheng, X.Y.; Xie, K.G. Optimal f-divergence importance sampling method for reliability evaluation of large power grids. J. Electr. Eng. China 2022, 42, 5067–5079. [Google Scholar] [CrossRef]
- Li, H.; Hu, X.D.; Xuan, W.B. Important sampling effect increment method for reliability evaluation of power systems. J. Power Syst. Autom. 2020, 32, 117–124. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, S.; Wang, B.Q.; Zhang, J.H.; Zhao, T.Y. Probabilistic reliability assessment of power systems with wind power based on Latin Hypercube sampling. Trans. China Electrotech. Soc. 2016, 31, 193–206. [Google Scholar] [CrossRef]
- Osama, A.A.; Chung, C.Y. A hybrid framework for short-term risk assessment of wind-integrated composite power systems. IEEE Trans. Power Syst. 2019, 34, 2334–2344. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Wu, L.; Lu, P.; Zhang, S.H. Transmission line overload risk assessment for power systems with wind and load-power generation correlation. IEEE Trans. Smart Grid 2015, 6, 1233–1242. [Google Scholar] [CrossRef]
- Ma, Y.F.; Yang, X.K.; Wang, Z.J.; Dong, L.; Zhao, S.Q.; Cai, Y.Q. Operation risk assessment of large-scale wind power grid connected power system based on value-at-risk. Power Grid Technol. 2021, 45, 849–855. [Google Scholar] [CrossRef]
- Ma, Y.F.; Luo, Z.R.; Zhao, S.Q.; Wang, Z.J.; Xie, J.R.; Zeng, S.M. Risk assessment of wind power system based on improved Monte Carlo mixed sampling. Power Syst. Prot. Control 2022, 50, 75–83. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Li, Y.T.; He, L.Z.; Yao, F. Application of monte carlo method in static safety risk assessment of power system. Electr. Meas. Instrum. 2015, 52, 106–111. [Google Scholar] [CrossRef]
- Shang, H.Y.; Liu, T.Q.; Bu, T.; He, C.; Yin, Y.; Ding, L.J. Risk assessment of high proportion new energy grid connected systems based on the ALARP criterion. Power Autom. Equip. 2021, 41, 196–203. [Google Scholar] [CrossRef]
- Gao, F.Y.; Yuan, C.; Li, Z.J.; Qi, X.D.; Zhuang, S.X. Probabilistic power flow calculation based on approximate Bayesian calculation combined with Markov chain Monte Carlo. J. Sol. Energy 2021, 42, 265–272. [Google Scholar] [CrossRef]





| Year | Forced Outage Rate | MTTR | Year | Forced Outage Rate | MTTR |
|---|---|---|---|---|---|
| 2021 | 0.085 | 3.14 | 2013 | 0.169 | 3.54 |
| 2020 | 0.233 | 2.75 | 2012 | 0.214 | 1.59 |
| 2019 | 0.200 | 2.37 | 2011 | 0.209 | 2.51 |
| 2018 | 0.251 | 2.64 | 2010 | 0.173 | 1.86 |
| 2017 | 0.253 | 3.00 | 2009 | 0.194 | 1.78 |
| 2016 | 0.231 | 2.09 | 2008 | 0.212 | 2.01 |
| 2015 | 0.282 | 6.87 | 2007 | 0.100 | 0.78 |
| 2014 | 0.224 | 4.42 | -- |
| Risk Grade | Value-at-Risk |
|---|---|
| High risk | Over 1.79 × 10−5 |
| Medium risk | 2.39 × 10−6~1.79 × 10−5 |
| Low risk | Less than 2.39 × 10−6 |
| LHIS (s) | LHS (s) | IM-IS (s) | |
|---|---|---|---|
| (0.2%) | 5.002 | 9.241 | 9.545 |
| (0.2%) | 5.091 | 9.327 | 10.001 |
| (3%) | 6.147 | 10.202 | 11.563 |
| (3%) | 6.463 | 10.731 | 11.799 |
| LHIS | LHS | IM-IS | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 20% | 40% | 60% | 20% | 40% | 60% | 20% | 40% | 60% | |
| (%) | 0.15 | 0.22 | 0.26 | 0.29 | 0.34 | 0.38 | 0.28 | 0.39 | 0.41 |
| (%) | 2.54 | 2.78 | 2.89 | 2.94 | 3.23 | 3.76 | 2.93 | 3.51 | 3.86 |
| (%) | 0.24 | 0.29 | 0.30 | 0.26 | 0.32 | 0.39 | 0.31 | 0.39 | 0.44 |
| (%) | 2.76 | 2.85 | 2.98 | 3.01 | 3.45 | 3.62 | 3.31 | 3.50 | 4.05 |
| Permeability | LHIS (s) | LHS (s) | IM-IS (s) |
|---|---|---|---|
| 20% | 5.216 | 9.321 | 11.624 |
| 40% | 5.425 | 10.012 | 12.043 |
| 60% | 5.514 | 10.424 | 12.398 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Zhang, Y.; Wang, Y.; Liang, K.; Zhao, H.; Yang, A. Multi-Angle Reliability Evaluation of Grid-Connected Wind Farms with Energy Storage Based on Latin Hypercube Important Sampling. Energies 2023, 16, 6427. https://doi.org/10.3390/en16186427
Yang W, Zhang Y, Wang Y, Liang K, Zhao H, Yang A. Multi-Angle Reliability Evaluation of Grid-Connected Wind Farms with Energy Storage Based on Latin Hypercube Important Sampling. Energies. 2023; 16(18):6427. https://doi.org/10.3390/en16186427
Chicago/Turabian StyleYang, Weixin, Yangfan Zhang, Yu Wang, Kai Liang, Hongshan Zhao, and Ao Yang. 2023. "Multi-Angle Reliability Evaluation of Grid-Connected Wind Farms with Energy Storage Based on Latin Hypercube Important Sampling" Energies 16, no. 18: 6427. https://doi.org/10.3390/en16186427
APA StyleYang, W., Zhang, Y., Wang, Y., Liang, K., Zhao, H., & Yang, A. (2023). Multi-Angle Reliability Evaluation of Grid-Connected Wind Farms with Energy Storage Based on Latin Hypercube Important Sampling. Energies, 16(18), 6427. https://doi.org/10.3390/en16186427





