Current Pulse-Based Measurement Technique for Zinc–Air Battery Parameters
Abstract
:1. Introduction
2. Zinc–Air Battery Model
2.1. Electrochemical Model
2.1.1. Electrode Reaction and Theoretical Electric Potential
2.1.2. Zinc–Air Battery Polarization
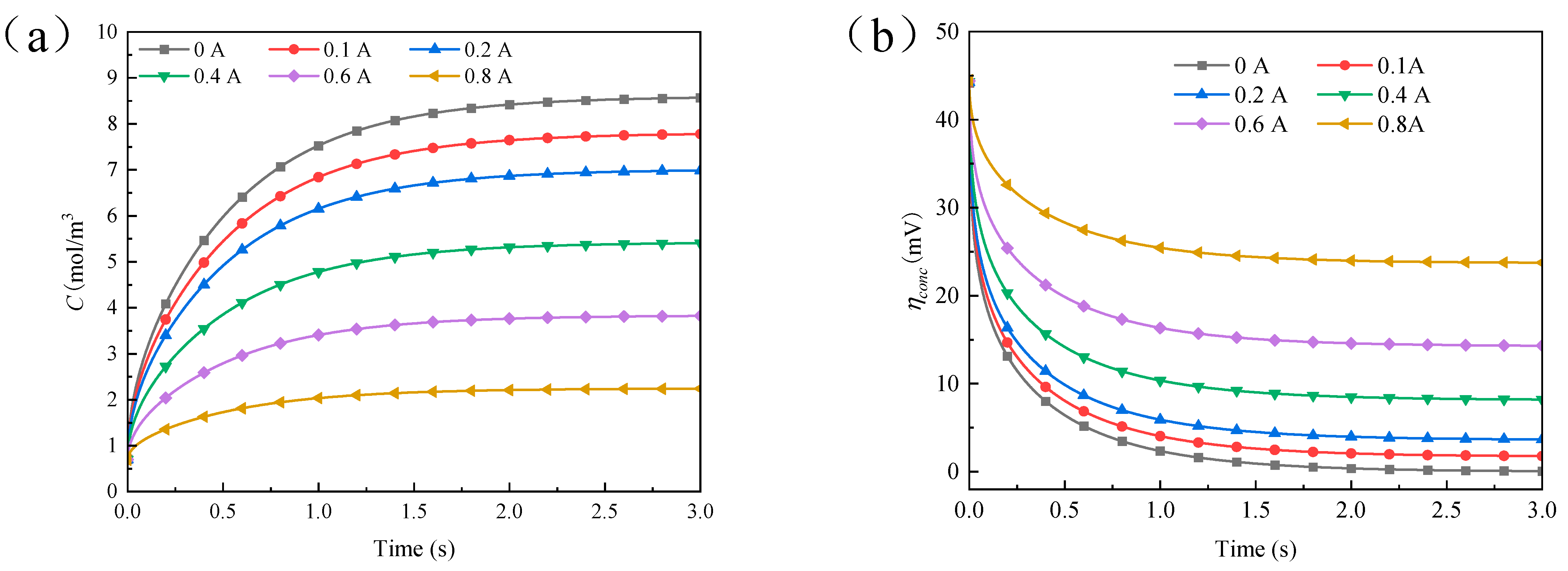
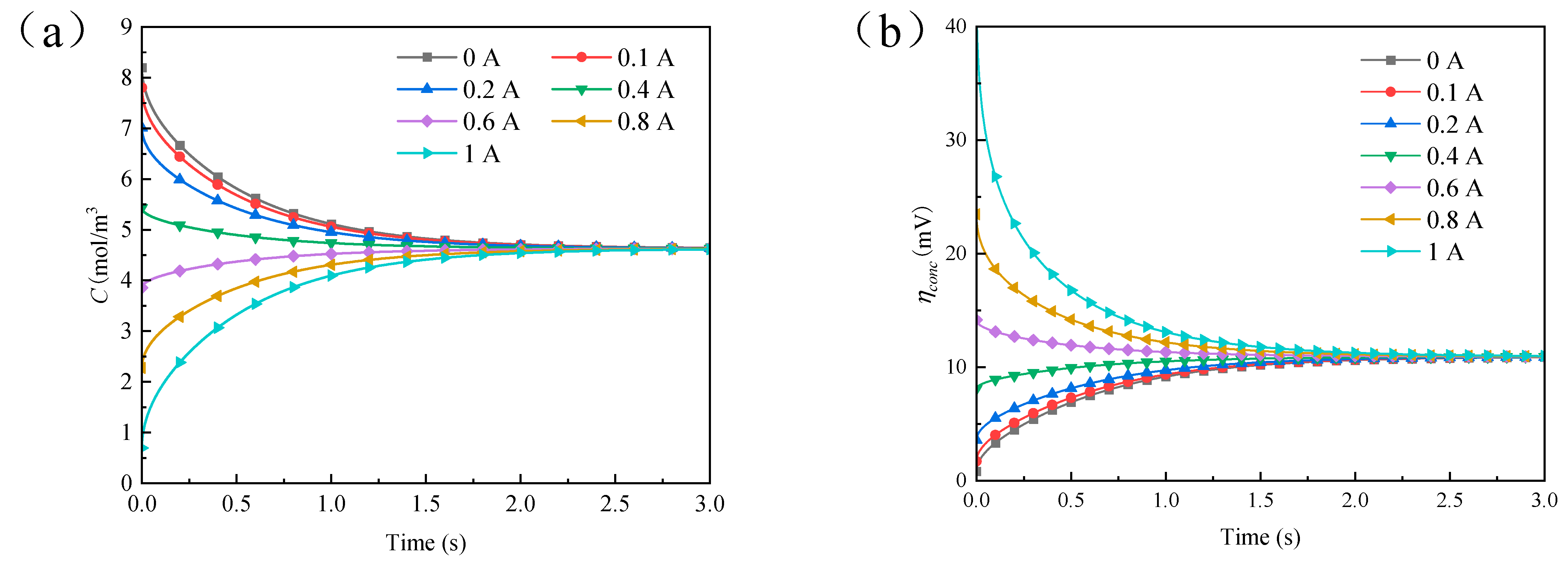
- Concentration polarization (ηconc): Polarization caused by a decrease in the concentration of reactants on the electrode surface has a response time of seconds due to the fact that the rate of reactant transport in a chemical reaction is less than the rate of reactant consumption. In zinc–air batteries, this can be calculated using the following equation:
- 2.
- Electrochemical polarization (ηact): Polarization stems from the discrepancy between the electrochemical reaction rate of the cathodic and anodic active materials and the rate of electron mobility. This phenomenon manifests with a response time measured within the microsecond scale;
- 3.
- Ohmic polarization (ηohmic): Polarization due to the electrolyte, electrode material, diaphragm resistance, and contact resistance existing between the various constituent parts occurs instantaneously.
2.1.3. Output Voltage
2.2. Equivalent Circuit Model
2.3. Gas Diffusion Model
3. Experimental Section
3.1. Experimental Setup
3.2. Experimental Operation
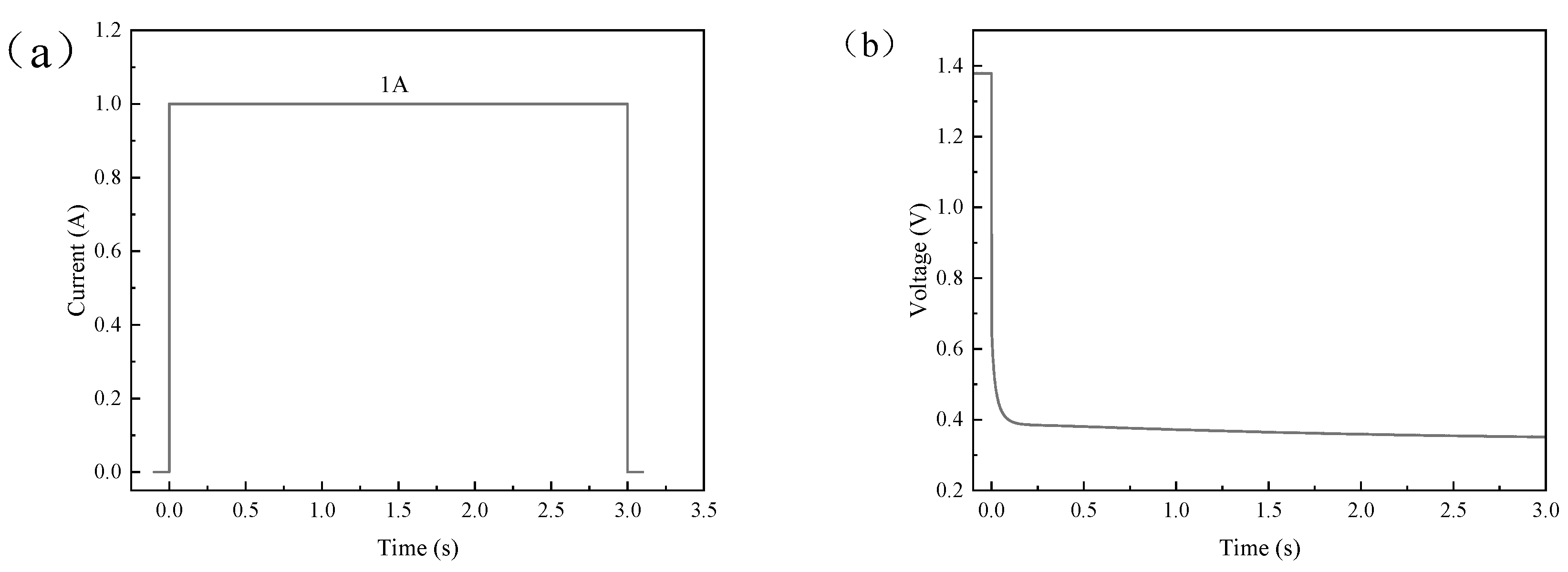
3.2.1. Single Current Pulse
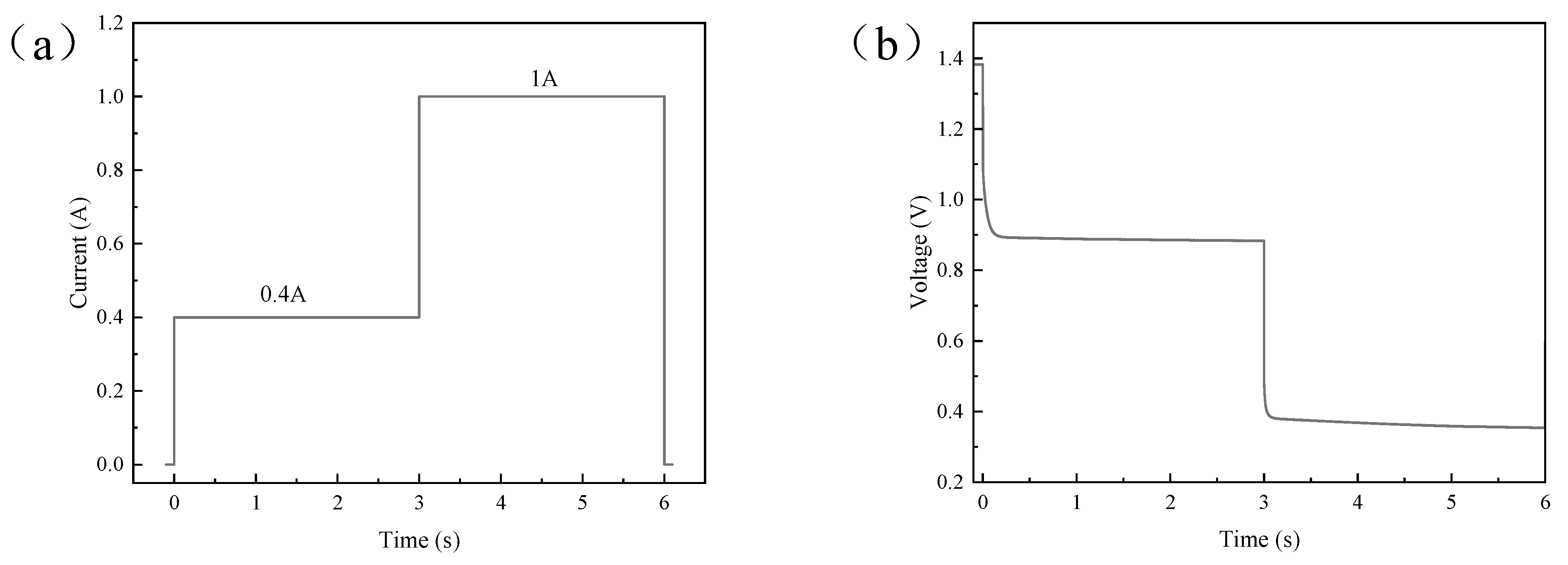
3.2.2. Step Current Pulses
4. Results and Discussion
4.1. Calculation of Zinc–Air Battery Parameters
4.1.1. Calculation of Circuit Parameters
4.1.2. Calculation of Effective Diffusion Coefficient
4.2. Results and Discussion of Single Current Pulse Experiment
4.3. Results and Discussion of Step Current Pulse Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Olabi, A.G.; Onumaegbu, C.; Wilberforce, T.; Ramadan, M.; Abdelkareem, M.A.; Al Alami, A.H. Critical review of energy storage systems. Energy 2021, 214, 118987. [Google Scholar] [CrossRef]
- Deng, W.; Xu, Y.; Zhang, X.; Li, C.; Liu, Y.; Xiang, K.; Chen, H. (NH4)2Co2V10O28·16H2O/(NH4)2V10O25·8H2O heterostructure as cathode for high-performance aqueous Zn-ion batteries. J. Alloys Compd. 2022, 903, 163824. [Google Scholar] [CrossRef]
- Deng, W.; Li, Y.; Xu, D.; Zhou, W.; Xiang, K.; Chen, H. Three-dimensional hierarchically porous nitrogen-doped carbon from water hyacinth as selenium host for high-performance lithium–selenium batteries. Rare Met. 2022, 41, 3432–3445. [Google Scholar] [CrossRef]
- Li, D.; Guo, H.; Jiang, S.; Zeng, G.; Zhou, W.; Li, Z. Microstructures and electrochemical performances of TiO2-coated Mg–Zr co-doped NCM as a cathode material for lithium-ion batteries with high power and long circular life. New J. Chem. 2021, 45, 19446–19455. [Google Scholar] [CrossRef]
- Su, D.; Xiao, Y.; Liu, Y.; Xu, S.; Fang, S.; Cao, S.; Wang, X. Surface-confined polymerization to construct binary Fe3N/Co–N–C encapsulated MXene composites for high-performance zinc-air battery. Carbon 2023, 201, 269–277. [Google Scholar] [CrossRef]
- Wen, X.; Luo, J.; Xiang, K.; Zhou, W.; Zhang, C.; Chen, H. High-performance monoclinic WO3 nanospheres with the novel NH4+ diffusion behaviors for aqueous ammonium-ion batteries. Chem. Eng. J. 2023, 458, 141381. [Google Scholar] [CrossRef]
- Zeng, X.; Li, M.; Abd El-Hady, D.; Alshitari, W.; Al-Bogami, A.S.; Lu, J.; Amine, K. Commercialization of Lithium Battery Technologies for Electric Vehicles. Adv. Energy Mater. 2019, 9, 1900161. [Google Scholar] [CrossRef]
- Chavan, S.; Venkateswarlu, B.; Prabakaran, R.; Salman, M.; Joo, S.W.; Choi, G.S.; Kim, S.C. Thermal runaway and mitigation strategies for electric vehicle lithium-ion batteries using battery cooling approach: A review of the current status and challenges. J. Energy Storage 2023, 72, 108569. [Google Scholar] [CrossRef]
- Han, S.; Zhenghao, M.; Meilin, L.; Xiaohui, Y.; Xiaoxue, W. Global supply sustainability assessment of critical metals for clean energy technology. Resour. Policy 2023, 85, 103994. [Google Scholar] [CrossRef]
- Zhou, W.; Zeng, G.; Jin, H.; Jiang, S.; Huang, M.; Zhang, C.; Chen, H. Bio-Template Synthesis of V2O3@ Carbonized Dictyophora Composites for Advanced Aqueous Zinc-Ion Batteries. Molecules 2023, 28, 2147. [Google Scholar] [CrossRef]
- Wang, H.; Xu, L.; Deng, D.; Liu, X.; Li, H.; Su, D. Regulated electronic structure and improved electrocatalytic performances of S-doped FeWO4 for rechargeable zinc-air batteries. J. Energy Chem. 2023, 76, 359–367. [Google Scholar] [CrossRef]
- Xu, M.; Dou, H.; Zhang, Z.; Zheng, Y.; Ren, B.; Ma, Q.; Wen, G.; Luo, D.; Yu, A.; Zhang, L. Hierarchically Nanostructured Solid-State Electrolyte for Flexible Rechargeable Zinc–Air Batteries. Angew. Chem. Int. Ed. 2022, 134, e202117703. [Google Scholar] [CrossRef]
- Jiao, M.; Zhang, Q.; Ye, C.; Liu, Z.; Zhong, X.; Wang, J.; Li, C.; Dai, L.; Zhou, G.; Cheng, H. Recycling spent LiNi1−x−yMnxCoyO2 cathodes to bifunctional NiMnCo catalysts for zinc-air batteries. Proc. Natl. Acad. Sci. USA 2022, 119, e2092765177. [Google Scholar] [CrossRef]
- He, Y.; Shang, W.; Ni, M.; Huang, Y.; Zhao, H.; Tan, P. In-situ observation of the gas evolution process on the air electrode of Zn-air batteries during charging. Chem. Eng. J. 2022, 427, 130862. [Google Scholar] [CrossRef]
- Pei, Z.; Ding, L.; Wang, C.; Meng, Q.; Chen, Y. Make It Stereoscopic: Interfacial Design for Full-Temperature Adaptive Flexible Zinc-Air Batteries. Energy Environ. Sci. 2021, 14, 4926–4935. [Google Scholar] [CrossRef]
- Cuadras, A.; Miró, P.; Ovejas, V.J.; Estrany, F. Entropy generation model to estimate battery ageing. J. Energy Storage 2020, 32, 101740. [Google Scholar] [CrossRef]
- Wang, H.; Sayed, S.Y.; Luber, E.J.; Olsen, B.C.; Shirurkar, S.M.; Venkatakrishnan, S.; Tefashe, U.M.; Farquhar, A.K.; Smotkin, E.S.; McCreery, R.L. Redox flow batteries: How to determine electrochemical kinetic parameters. ACS Nano 2020, 14, 2575–2584. [Google Scholar] [CrossRef]
- Shang, Y.; Lu, G.; Kang, Y.; Zhou, Z.; Duan, B.; Zhang, C. A multi-fault diagnosis method based on modified Sample Entropy for lithium-ion battery strings. J. Power Source 2020, 446, 227275. [Google Scholar] [CrossRef]
- Arregi, O.; Agirrezabala, E.; Iraola, U.; Milo, A.; Yeregui, J.; Nogueras, U.; Sánchez, R.; Gil, I. A New Equivalent Circuit Model Parametrization Methodology Based on Current Pulse Tests for Different Battery Technologies. Energies 2021, 14, 7255. [Google Scholar] [CrossRef]
- Wang, K.; Yu, J. Lifetime simulation of rechargeable zinc-air battery based on electrode aging. J. Energy Storage 2020, 28, 101191. [Google Scholar] [CrossRef]
- Schmitt, T.; Arlt, T.; Manke, I.; Latz, A.; Horstmann, B. Zinc electrode shape-change in secondary air batteries: A 2D modeling approach. J. Power Source 2019, 432, 119–132. [Google Scholar] [CrossRef]
- He, Y.; Cui, Y.; Shang, W.; Zhao, Z.; Tan, P. Insight into the bubble-induced overpotential towards high-rate charging of Zn-air batteries. Chem. Eng. J. 2022, 448, 137782. [Google Scholar] [CrossRef]
- Tran, M.; DaCosta, A.; Mevawalla, A.; Panchal, S.; Fowler, M. Comparative study of equivalent circuit models performance in four common lithium-ion batteries: LFP, NMC, LMO, NCA. Batteries 2021, 7, 51. [Google Scholar] [CrossRef]
- Xiong, B.; Yang, Y.; Tang, J.; Li, Y.; Wei, Z.; Su, Y.; Zhang, Q. An enhanced equivalent circuit model of vanadium redox flow battery energy storage systems considering thermal effects. IEEE Access 2019, 7, 162297–162308. [Google Scholar] [CrossRef]
- Petrone, G.; Zamboni, W.; Spagnuolo, G. An interval arithmetic-based method for parametric identification of a fuel cell equivalent circuit model. Appl. Energ. 2019, 242, 1226–1236. [Google Scholar] [CrossRef]
- Lao-Atiman, W.; Olaru, S.; Diop, S.; Skogestad, S.; Arpornwichanop, A.; Cheacharoen, R.; Kheawhom, S. Linear parameter-varying model for a refuellable zinc–air battery. R. Soc. Open Sci. 2020, 7, 201107. [Google Scholar] [CrossRef]
- Ji, Y.; Qiu, S.; Li, G. Simulation of second-order RC equivalent circuit model of lithium battery based on variable resistance and capacitance. J. Cent. South Univ. 2020, 27, 2606–2613. [Google Scholar] [CrossRef]
- Leong, K.W.; Wang, Y.; Ni, M.; Pan, W.; Luo, S.; Leung, D.Y.C. Rechargeable Zn-air batteries: Recent trends and future perspectives. Renew. Sustain. Energy Rev. 2022, 154, 111771. [Google Scholar] [CrossRef]
- O’Hayre, R.; Cha, S.; Colella, W.; Prinz, F.B. Fuel Cell Fundamentals, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 203–237. [Google Scholar]
- Dongfang, C.; Pucheng, P.; Xin, S.; Peng, R. Electrochemical impedance equivalent circuit model for zinc-air fuel cells. J. Tsinghua Univ. Sci. Technol. 2020, 60, 139–146. [Google Scholar]






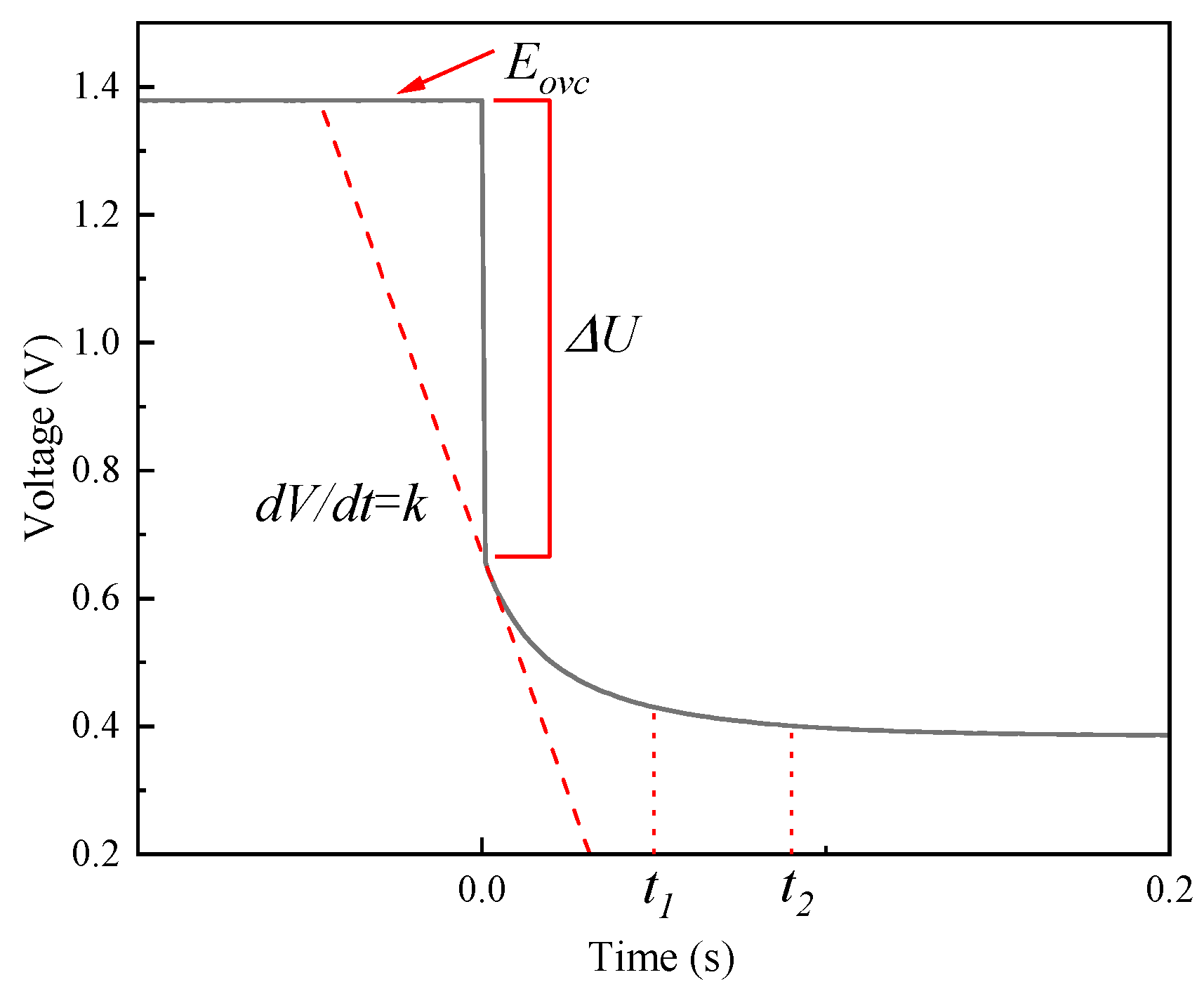
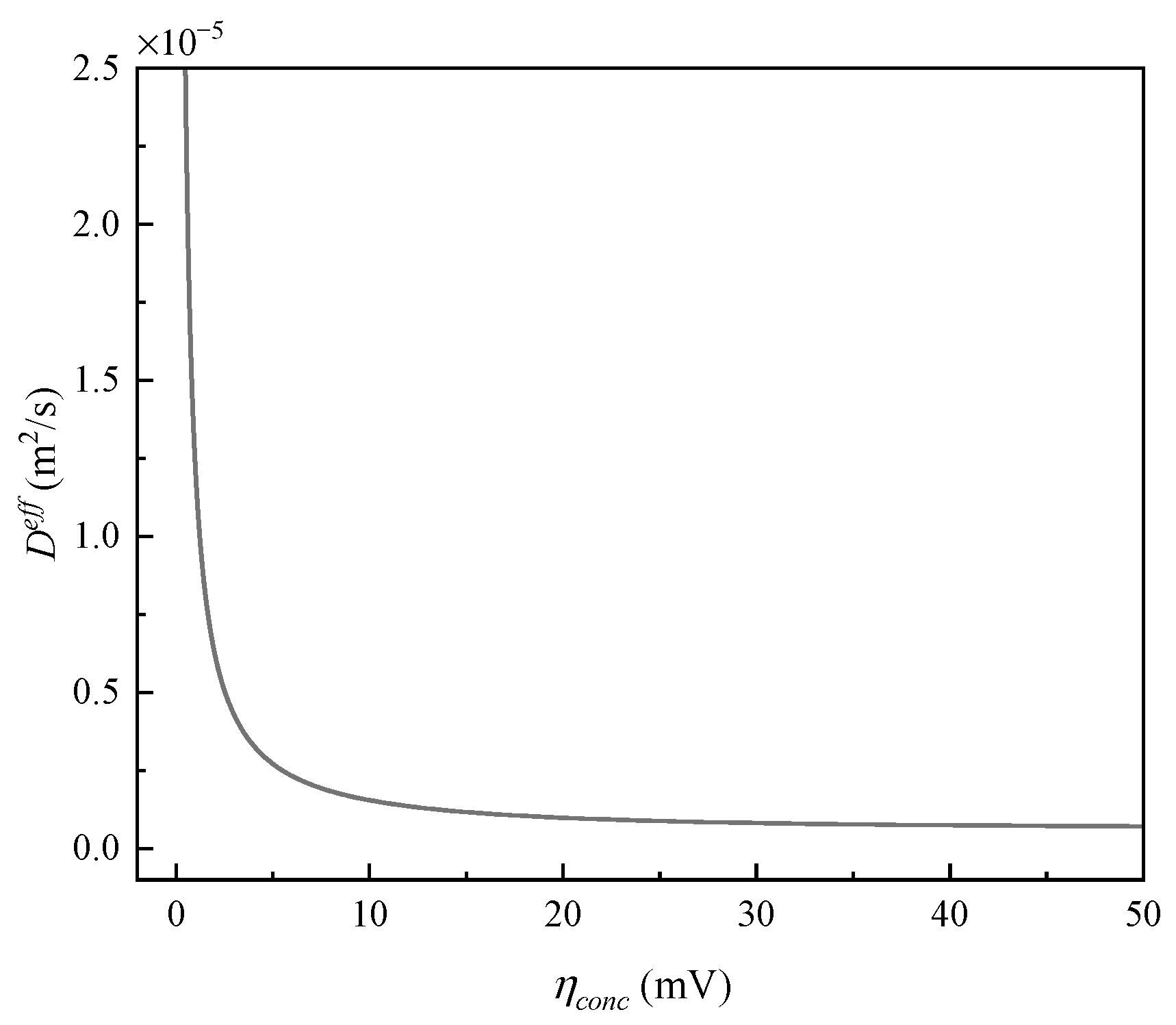
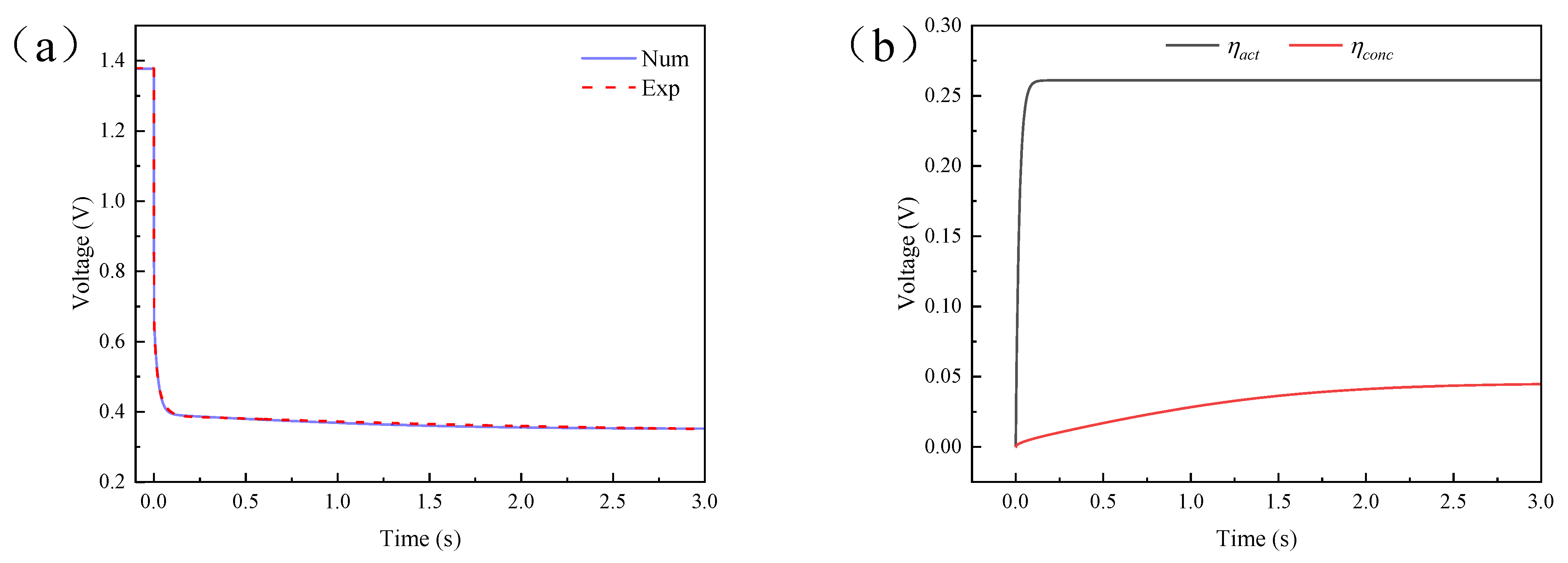
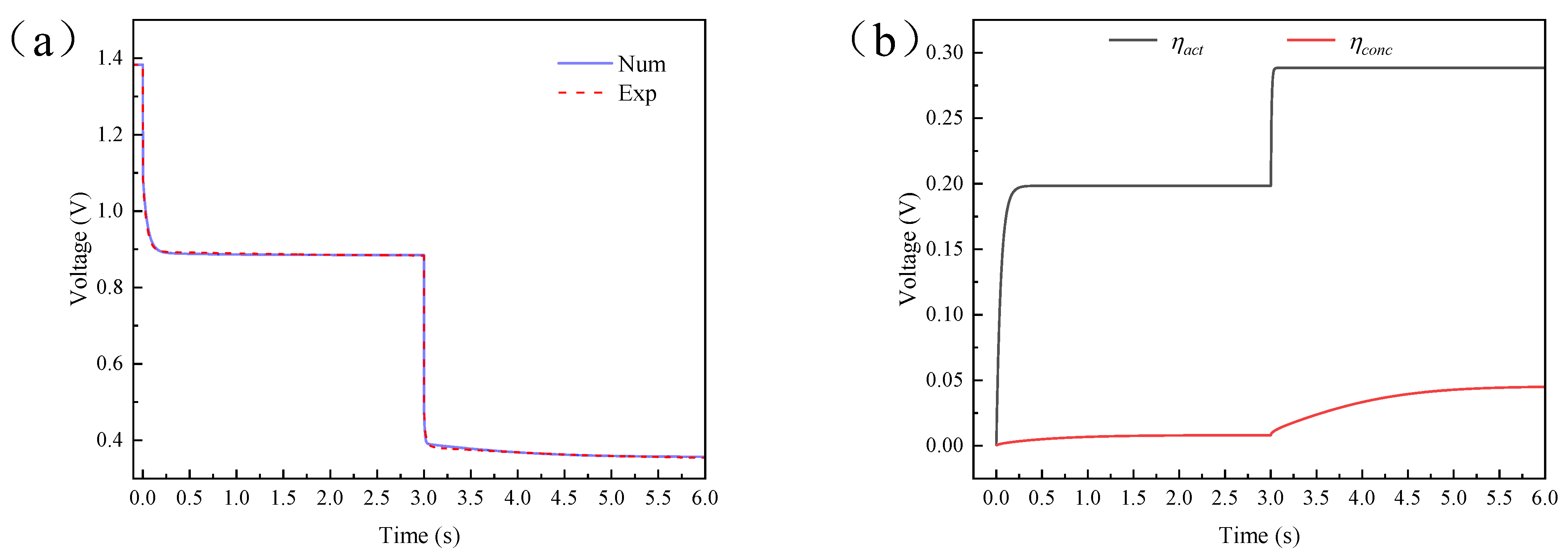
| Parameter | Value | Unit |
|---|---|---|
| 7.25 × 10−7 | m/s2 | |
| R | 8.3145 | J/(mol·K) |
| T | 298.15 | K |
| F | 96,485 | C/mol |
| C* | 8.6 | mol/m3 |
| α | 0.5 | - |
| As | 4.5 × 10−4 | m2 |
| l | 0.001 | m |
| EOCV | RL | Rt | Cd | C1 | C2 | |
|---|---|---|---|---|---|---|
| 1.378 V | 0.721 Ω | 0.261 Ω | 0.079 F | 8.6 mol/m3 | 8.6 mol/m3 | 7.25 × 10−7 m/s2 |
| EOCV | RL | Rt | Cd | C1 | C2 | |
|---|---|---|---|---|---|---|
| 1.383 V | 0.729 Ω | 0.496 Ω | 0.10 F | 8.6 mol/m3 | 8.6 mol/m3 | 7.25 × 10−7 m/s2 |
| 0.883 V | 0.653 Ω | 0.155 Ω | 0.057 F | 8.6 mol/m3 | 5.43 mol/m3 | 7.25 × 10−7 m/s2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, L.; Xu, X. Current Pulse-Based Measurement Technique for Zinc–Air Battery Parameters. Energies 2023, 16, 6448. https://doi.org/10.3390/en16186448
Hu L, Xu X. Current Pulse-Based Measurement Technique for Zinc–Air Battery Parameters. Energies. 2023; 16(18):6448. https://doi.org/10.3390/en16186448
Chicago/Turabian StyleHu, Lin, and Xianzhi Xu. 2023. "Current Pulse-Based Measurement Technique for Zinc–Air Battery Parameters" Energies 16, no. 18: 6448. https://doi.org/10.3390/en16186448
APA StyleHu, L., & Xu, X. (2023). Current Pulse-Based Measurement Technique for Zinc–Air Battery Parameters. Energies, 16(18), 6448. https://doi.org/10.3390/en16186448





