Nonlinear Predictive Control of Interior Permanent Magnet Synchronous Machine with Extra Current Constraint
Abstract
:1. Introduction
2. Linear Constraint of the Armature Current
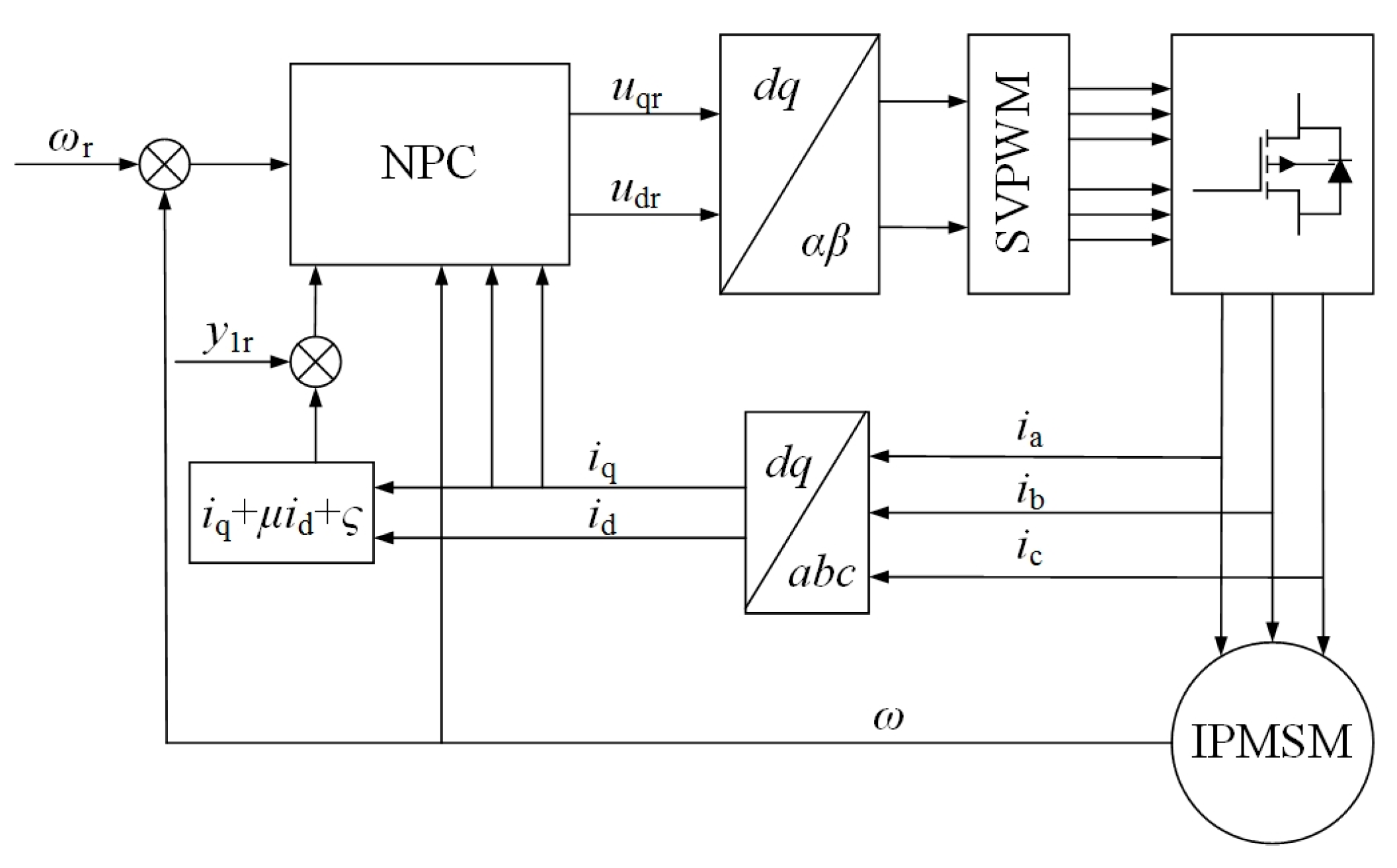
3. Proposed Controller for the IPMSM
3.1. Design of the Controller
3.2. Constraints of the Controller
3.3. Stability Analysis
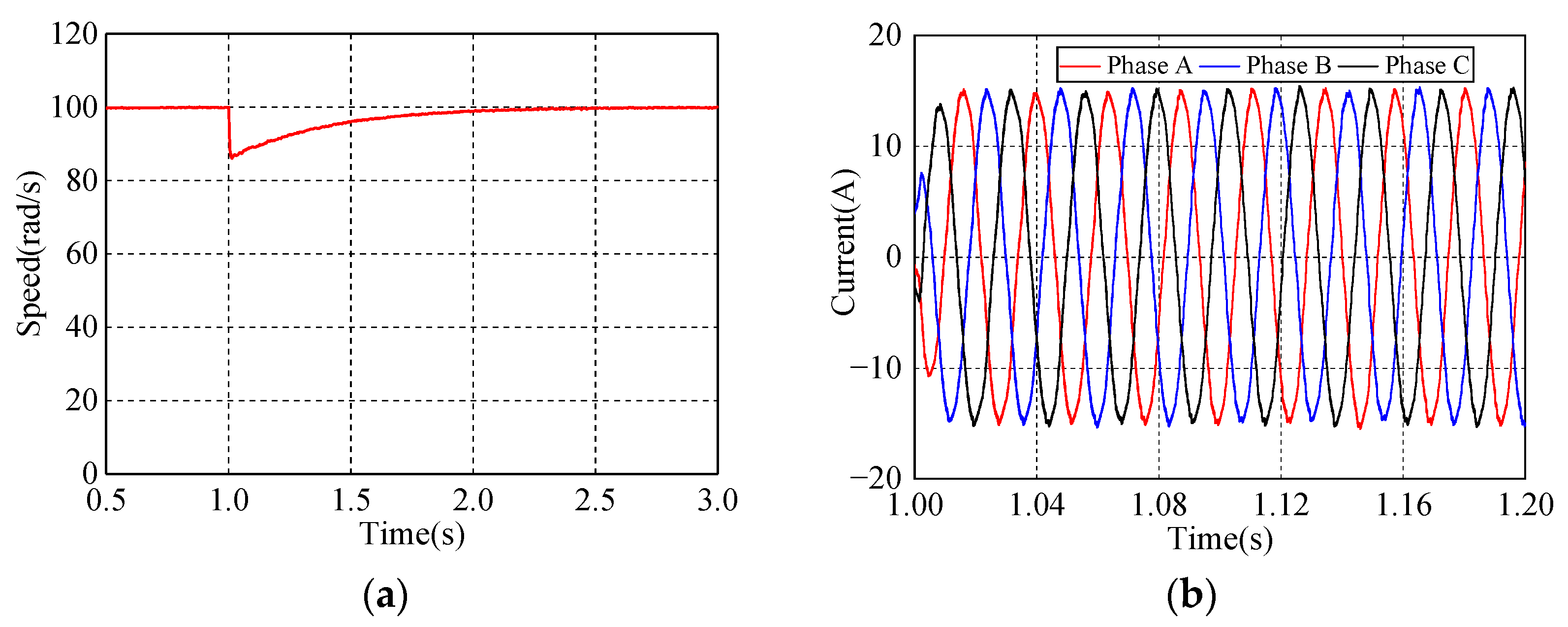
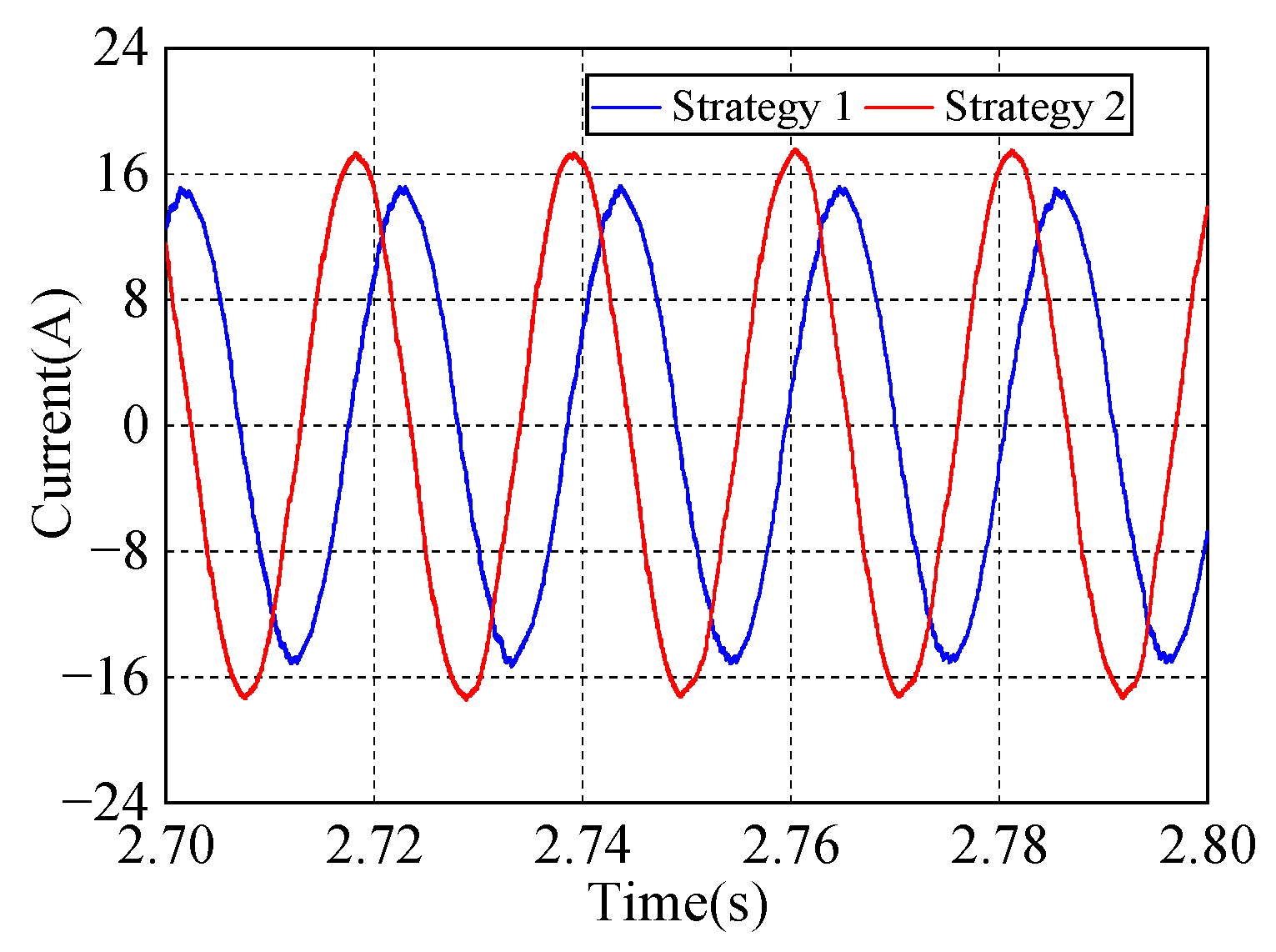
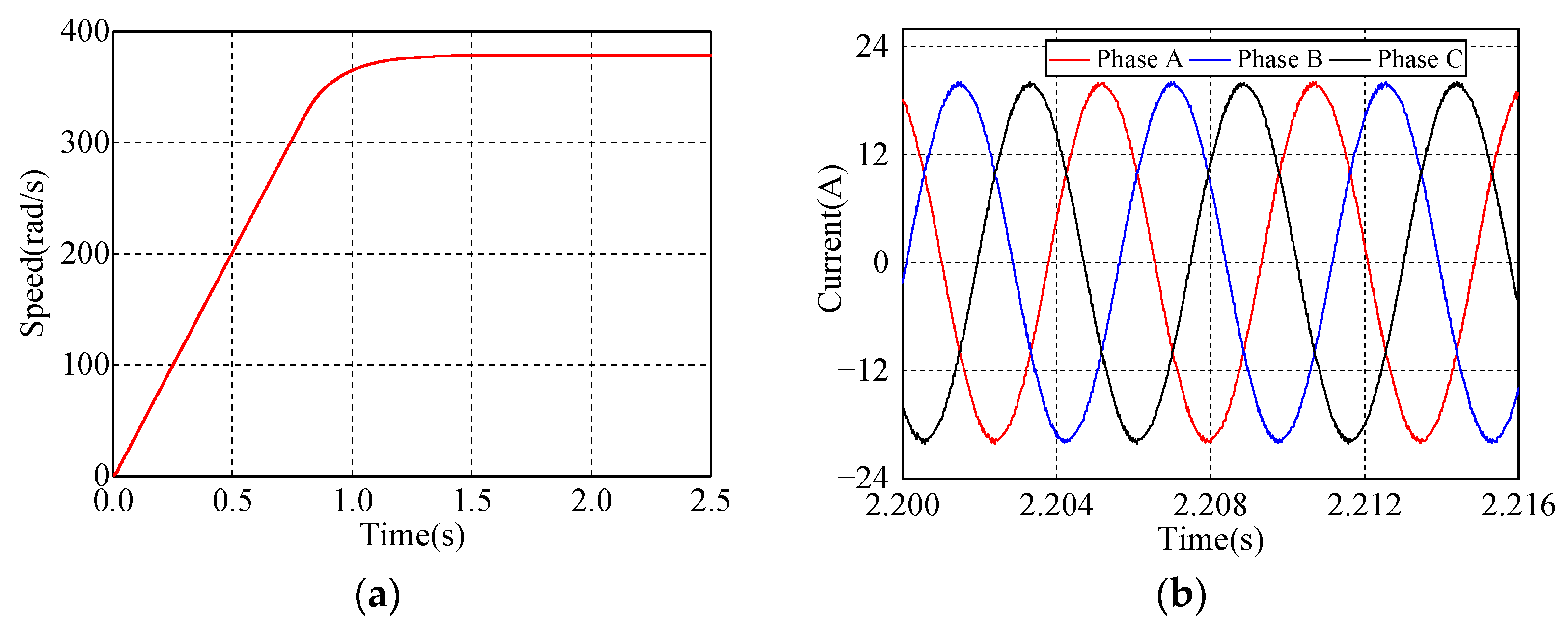
4. Simulation Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, L.; Yin, H.; Wang, D.; Fang, Y. A nonlinear subdomain and magnetic circuit hybrid model for open−circuit field prediction in surface−mounted PM machines. IEEE Trans. Energy Convers. 2019, 34, 1485–1495. [Google Scholar] [CrossRef]
- Hajdinjak, M.; Miljavec, D. Analytical calculation of the magnetic field distribution in slotless brushless machines with U−shaped interior permanent magnets. IEEE Trans. Ind. Electron. 2020, 67, 6721–6731. [Google Scholar] [CrossRef]
- Peng, B.; Wang, X.; Zhao, W.; Ren, J. Study on shaft voltage in fractional slot permanent magnet machine with different pole and slot number combinations. IEEE Trans. Magn. 2019, 55, 8102305. [Google Scholar] [CrossRef]
- Riaz, S.; Lin, H.; Anwar, M.B.; Ali, H. Design of PD−type second−order ILC law for PMSM servo position control. J. Phys. Conf. Ser. 2020, 1707, 012002. [Google Scholar] [CrossRef]
- Liu, G.; Chen, B.; Wang, K.; Song, X. Selective current harmonic suppression for high−speed PMSM based on high−precision harmonic detection method. IEEE Trans. Ind. Informat. 2019, 15, 3457–3468. [Google Scholar] [CrossRef]
- Junejo, A.K.; Xu, W.; Mu, C.; Ismail, M.M.; Liu, Y. Adaptive speed control of PMSM drive system based a new sliding−mode reaching law. IEEE Trans. Power Electron. 2020, 35, 12110–12121. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, L.; Ji, W. Improved non−singular fast terminal sliding mode control with disturbance observer for PMSM drives. IEEE Trans. Transp. Electrif. 2021, 7, 2753–2762. [Google Scholar] [CrossRef]
- Nawaz, M.K.; Dou, M.; Riaz, S.; Sardar, M.U. Current control of permanent magnet synchronous motors using improved model predictive control. Math. Probl. Eng. 2022, 2022, 1736931. [Google Scholar]
- Chen, W.-H.; Ballance, D.J.; Gawthrop, P.J. Optimal control of nonlinear systems: A predictive control approach. Automatica 2003, 39, 633–641. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Junejo, A.K.; Tang, Y.; Shahab, M.; Habib, H.U.R.; Liu, Y.; Huang, S. Composite speed control of PMSM drive system based on finite time sliding mode observer. IEEE Access 2021, 9, 151803–151813. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, W.; Mu, C.; Liu, Y. Improved deadbeat predictive current control combined sliding mode strategy for PMSM drive system. IEEE Trans. Veh. Technol. 2018, 67, 251–263. [Google Scholar] [CrossRef]
- Liu, X.; Yu, H.; Yu, J.; Zhao, L. Combined speed and current terminal sliding mode control with nonlinear disturbance observer for PMSM drive. IEEE Access 2018, 6, 29594–29601. [Google Scholar] [CrossRef]
- Bolognani, S.; Peretti, L.; Zigliotto, M. Design and implementation of model predictive control for electrical motor drives. IEEE Trans. Ind. Electron. 2009, 56, 1925–1936. [Google Scholar] [CrossRef]
- Sun, C.; Sun, D.; Chen, W.; Nian, H. Improved model predictive control with new cost function for hybrid-inverter open-winding PMSM system based on energy storage model. IEEE Trans. Power Electron. 2021, 36, 10705–10715. [Google Scholar] [CrossRef]
- Xue, C.; Zhou, D.; Li, Y. Finite-control-set model predictive control for three-level NPC inverter-fed PMSM Drives with LC filter. IEEE Trans. Ind. Electron. 2021, 68, 11980–11991. [Google Scholar] [CrossRef]
- Abu−Ali, M.; Berkel, F.; Manderla, M.; Reimann, S.; Kennel, R.; Abdelrahem, M. Deep learning-based long-horizon MPC: Robust, high performing, and computationally efficient control for PMSM drives. IEEE Trans. Power Electron. 2022, 37, 12486–12501. [Google Scholar]
- Wang, L.; Chai, S.; Rogers, E.; Freeman, C.T. Multivariable repetitive -predictive controllers using frequency decomposition. IEEE Trans. Control Syst. Technol. 2012, 20, 1597–1604. [Google Scholar] [CrossRef] [Green Version]
- Preindl, M.; Schaltz, E.; Thogersen, P. Switching frequency reduction using model predictive direct current control for high power voltage source inverters. IEEE Trans. Ind. Electron. 2011, 58, 2826–2835. [Google Scholar] [CrossRef]
- Zheng, C.; Yang, J.; Gong, Z.; Xiao, Z.; Dong, X. Cascade-free modulated predictive direct speed control of PMSM drives. Energies 2022, 15, 7200. [Google Scholar] [CrossRef]
- Akpunar, A.; Iplikci, S. Runge-Kutta model predictive speed control for permanent magnet synchronous motors. Energies 2020, 13, 1216. [Google Scholar] [CrossRef] [Green Version]
- Shao, M.; Deng, Y.; Li, H.; Liu, J.; Fei, Q. Sliding mode observer-based parameter identification and disturbance compensation for optimizing the mode predictive control of PMSM. Energies 2019, 12, 1857. [Google Scholar] [CrossRef] [Green Version]
- Tang, M.; Zhuang, S. On speed control of a permanent magnet synchronous motor with current predictive compensation. Energies 2019, 12, 65. [Google Scholar] [CrossRef]
- Yang, J.; Zheng, W.X.; Li, S.; Wu, B.; Cheng, M. Design of a prediction-accuracy-enhanced continuous-time MPC for disturbed systems via a disturbance observer. IEEE Trans. Ind. Electron. 2015, 62, 5807–5815. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, B.; Mei, Y. Deadbeat predictive current control of permanent-magnet synchronous motors with stator current and disturbance observer. IEEE Trans. Power Electron. 2017, 32, 3818–3834. [Google Scholar] [CrossRef]
- Hedjar, R.; Toumi, R.; Boucher, P.; Dumur, D. Finite horizon nonlinear predictive control by the Taylor approximation: Application to robot tracking trajectory. Int. J. Appl. Math. Comput. Sci. 2005, 15, 527–540. [Google Scholar]
- Errouissi, R.; Ouhrouche, M.; Chen, W.-H.; Trzynadlowski, A.M. Robust nonlinear predictive controller for permanent-magnet synchronous motors with an optimized cost function. IEEE Trans. Ind. Electron. 2012, 59, 2849–2858. [Google Scholar] [CrossRef]
- Tao, G. A simple alternative to the Barbalat lemma. IEEE Trans. Autom. Contr. 1997, 42, 698. [Google Scholar] [CrossRef]









| Parameters | Values |
|---|---|
| Rated power | 11 kW |
| d-axis inductances | 18.88 mH |
| q-axis inductances | 30.56 mH |
| Phase resistance | 0.32 Ω |
| PM flux | 0.317 Wb |
| Winding turns per slot | 18 |
| Number of pole pairs | 3 |
| Number of slots | 36 |
| Parallel branches per phase | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, M.; Cai, H.; Zhao, W.; Ren, J. Nonlinear Predictive Control of Interior Permanent Magnet Synchronous Machine with Extra Current Constraint. Energies 2023, 16, 716. https://doi.org/10.3390/en16020716
Tian M, Cai H, Zhao W, Ren J. Nonlinear Predictive Control of Interior Permanent Magnet Synchronous Machine with Extra Current Constraint. Energies. 2023; 16(2):716. https://doi.org/10.3390/en16020716
Chicago/Turabian StyleTian, Mengmeng, Hailiang Cai, Wenliang Zhao, and Jie Ren. 2023. "Nonlinear Predictive Control of Interior Permanent Magnet Synchronous Machine with Extra Current Constraint" Energies 16, no. 2: 716. https://doi.org/10.3390/en16020716
APA StyleTian, M., Cai, H., Zhao, W., & Ren, J. (2023). Nonlinear Predictive Control of Interior Permanent Magnet Synchronous Machine with Extra Current Constraint. Energies, 16(2), 716. https://doi.org/10.3390/en16020716







