Optimal Design of Corona Ring for 132 kV Insulator at High Voltage Transmission Lines Based on Optimisation Techniques
Abstract
:1. Introduction
2. Proposed Methodology
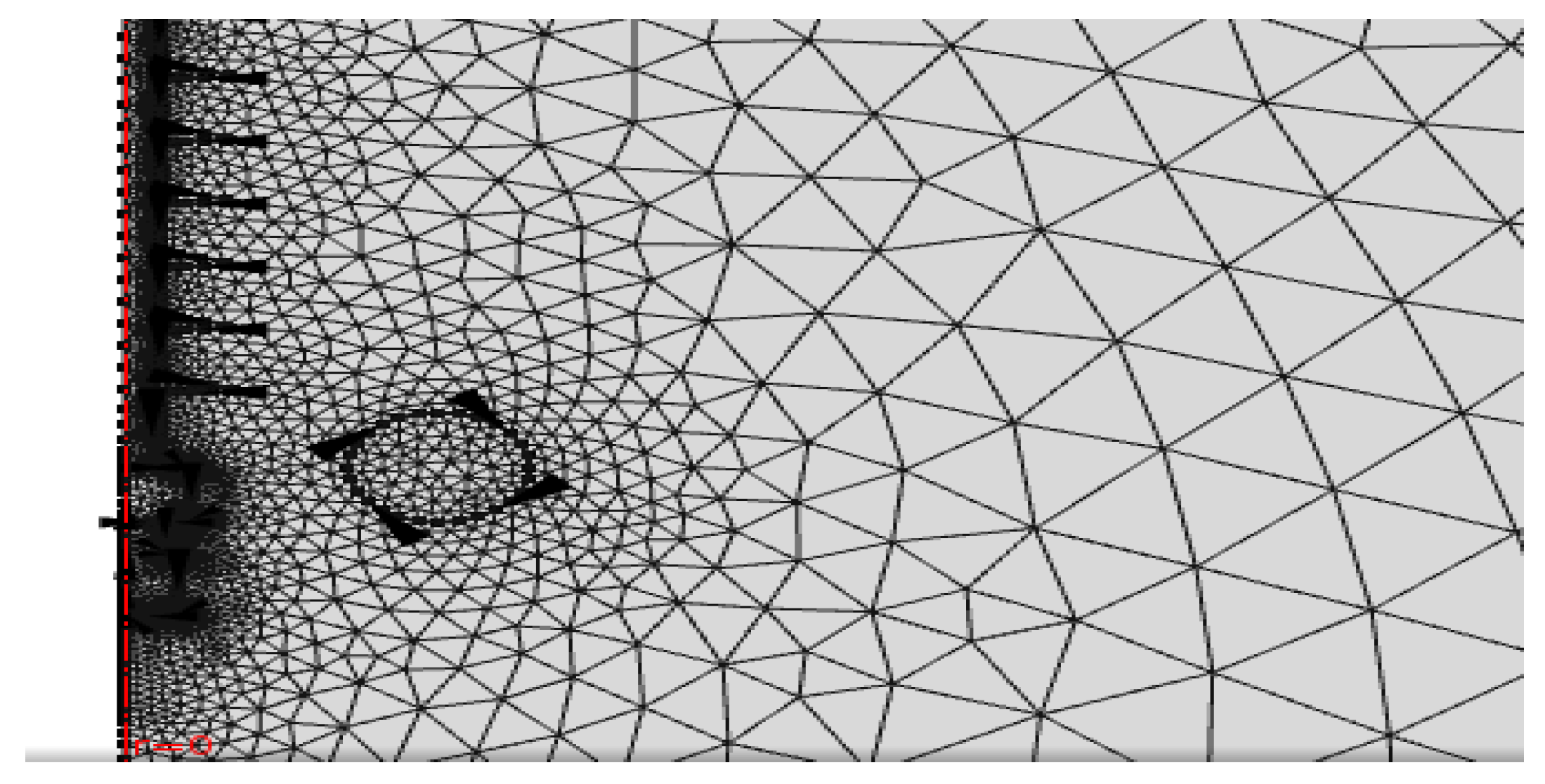
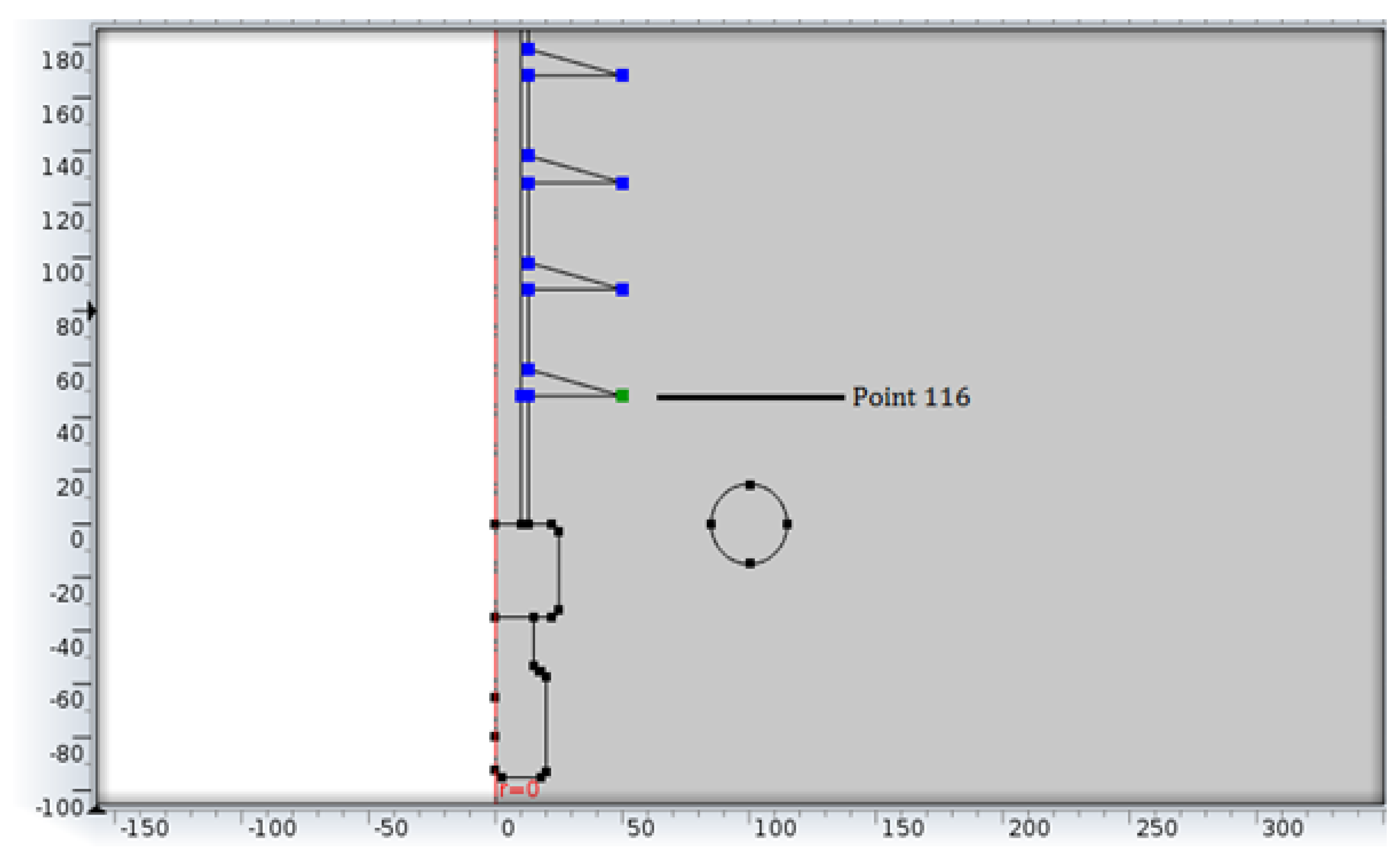
2.1. Model of 132 kV Non-Ceramic Insulator Model and Corona Ring
2.2. Objective Function for the Optimisation
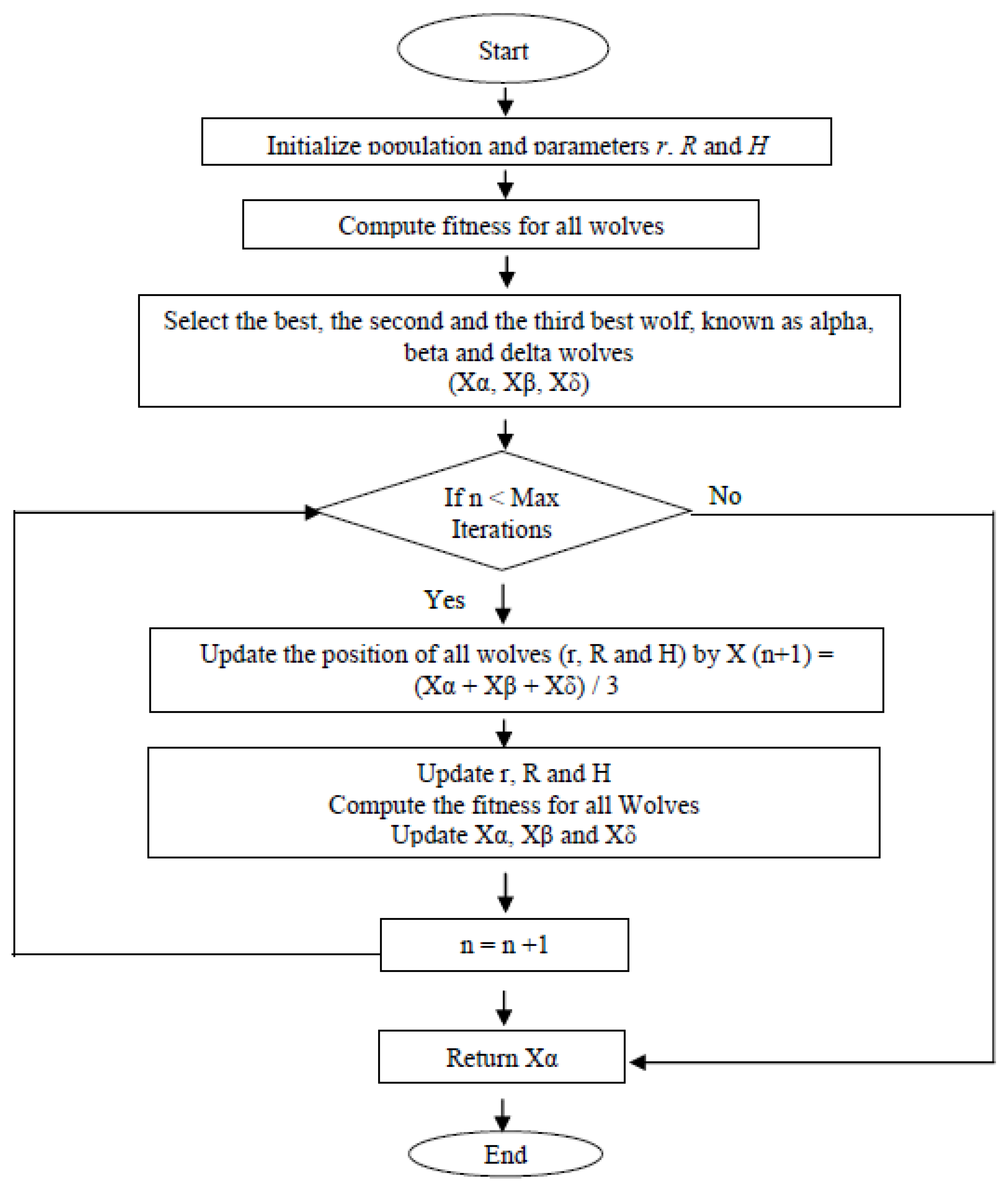
2.3. Grey Wolf Optimisation (GWO)
2.4. Imperialist Competitive Algorithm (ICA)
3. Results and Discussion
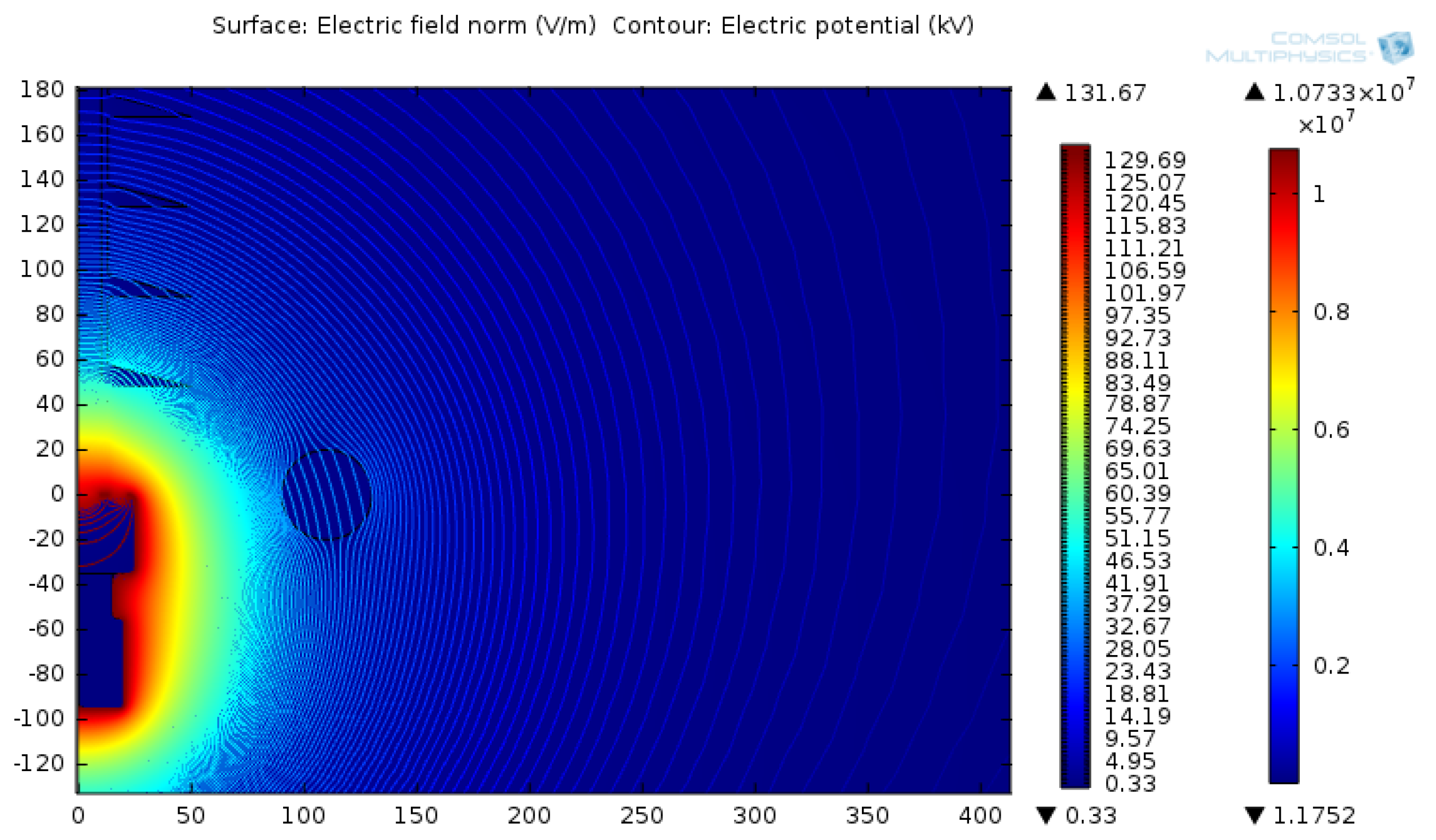
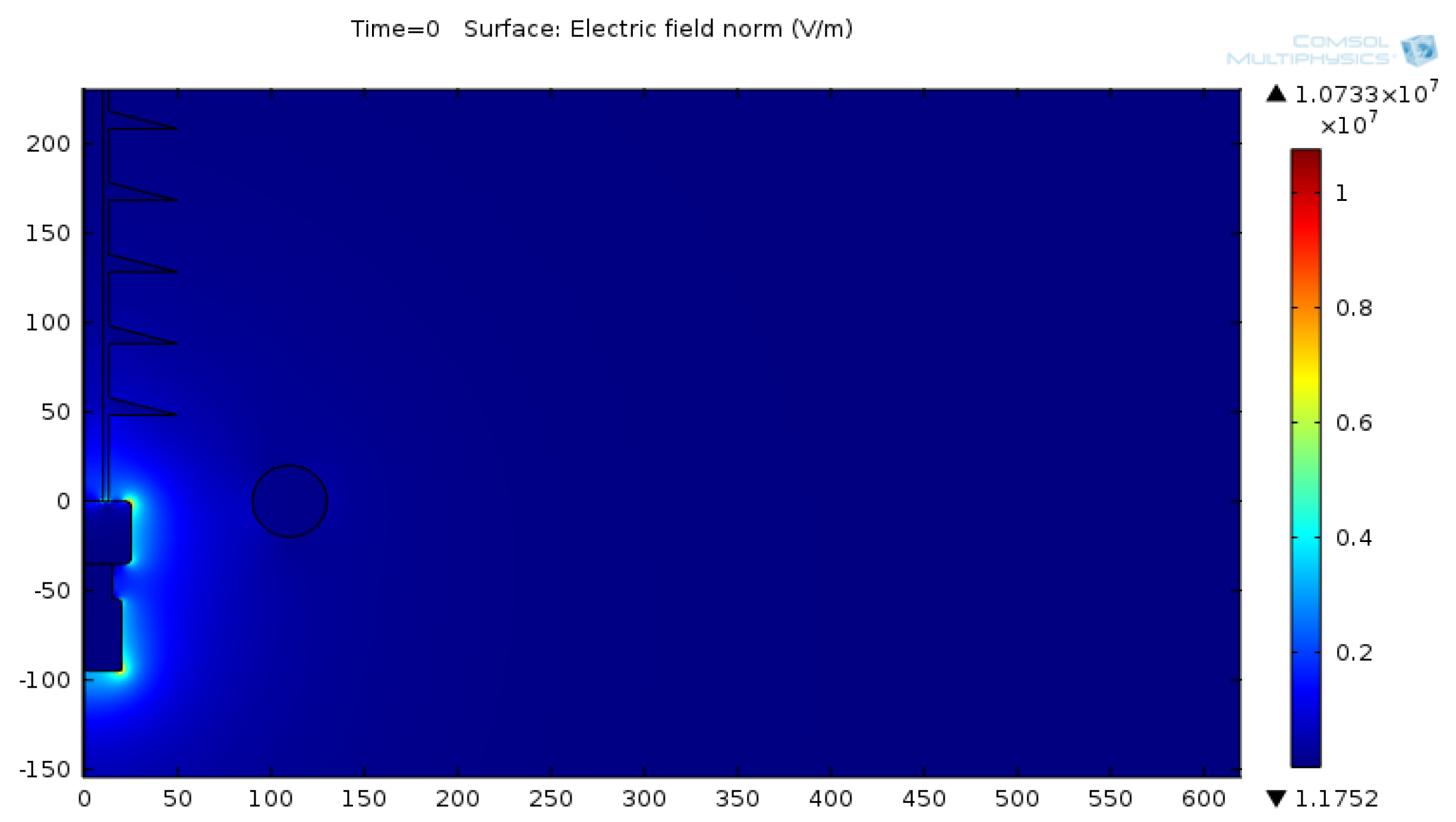
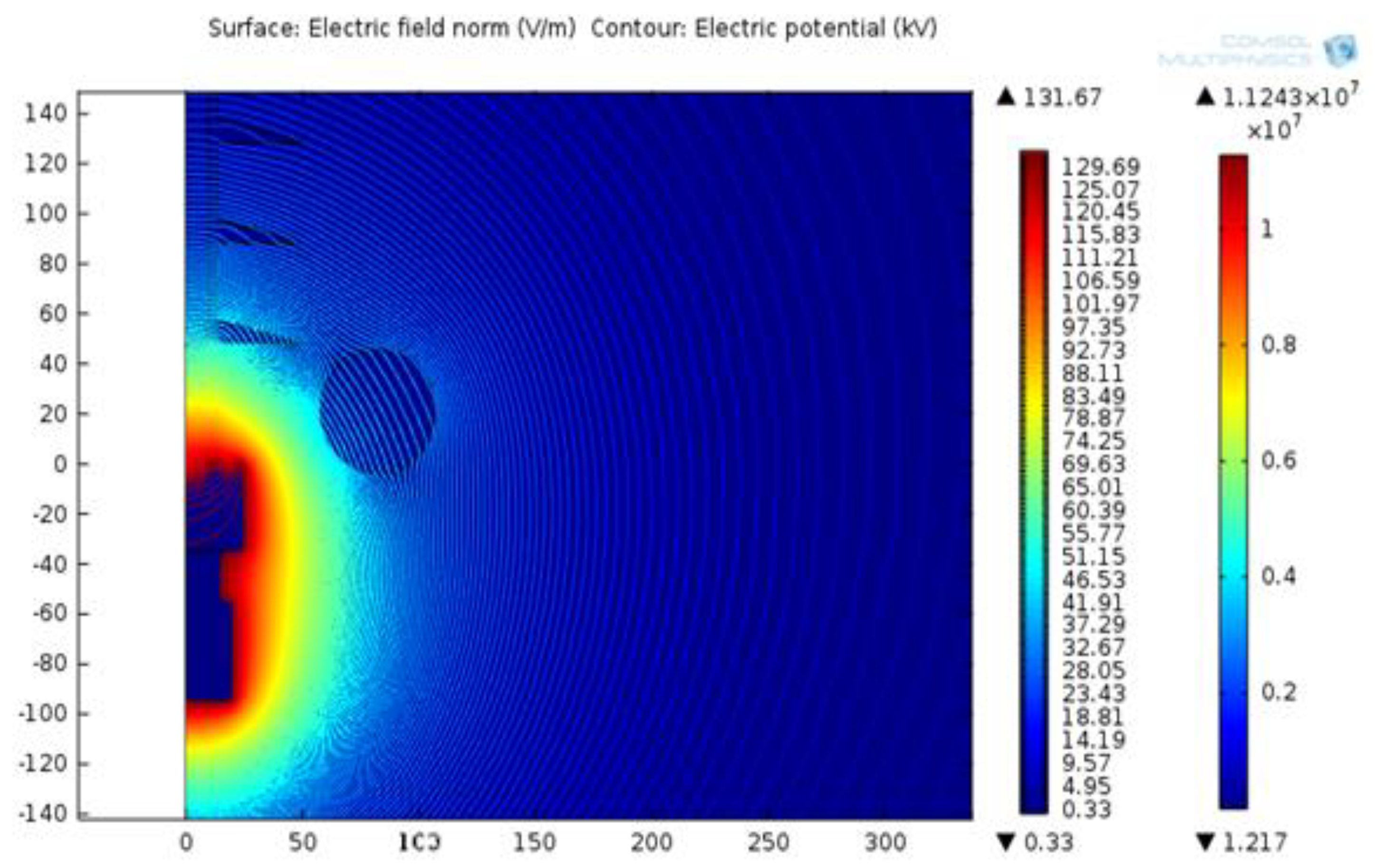
3.1. Distributions of Electric Field and Electric Potential on 132 kV Insulator String
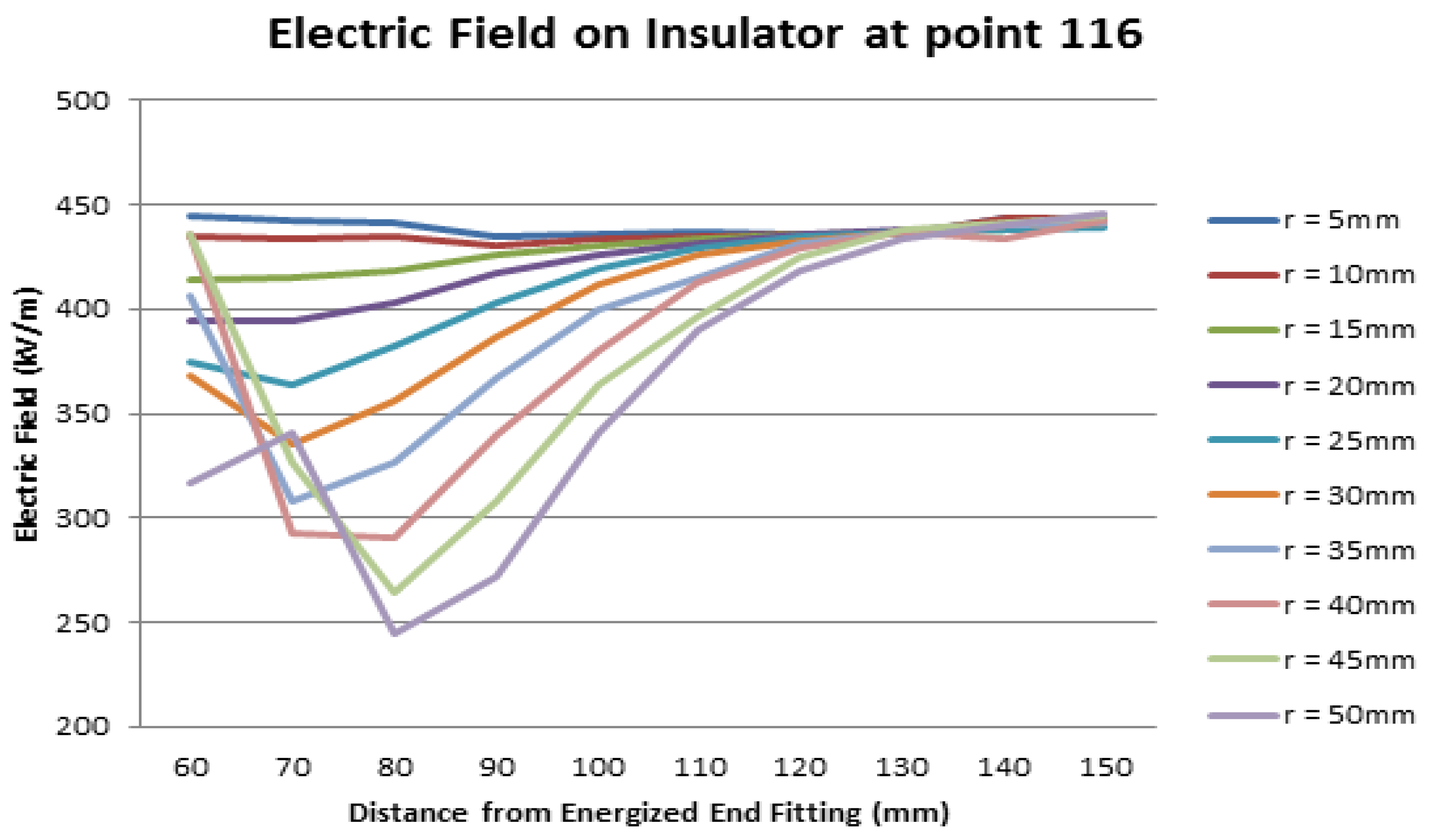
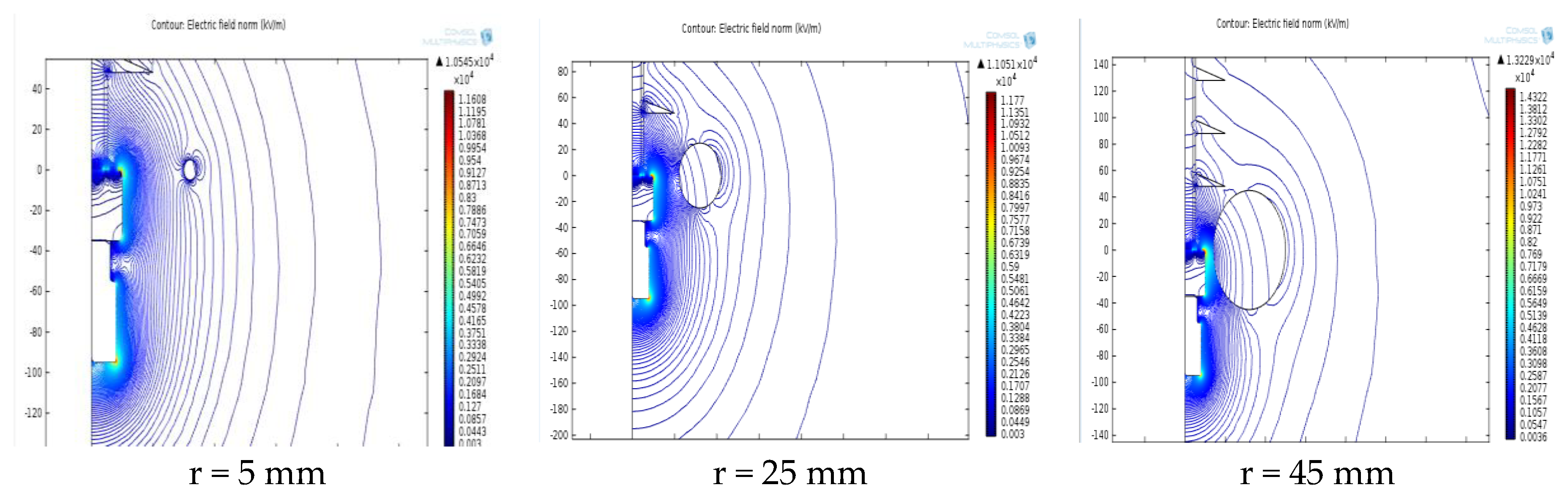
3.2. Simulation Results Using Various Parameter Values of Corona Ring in 132 kV Insulator String
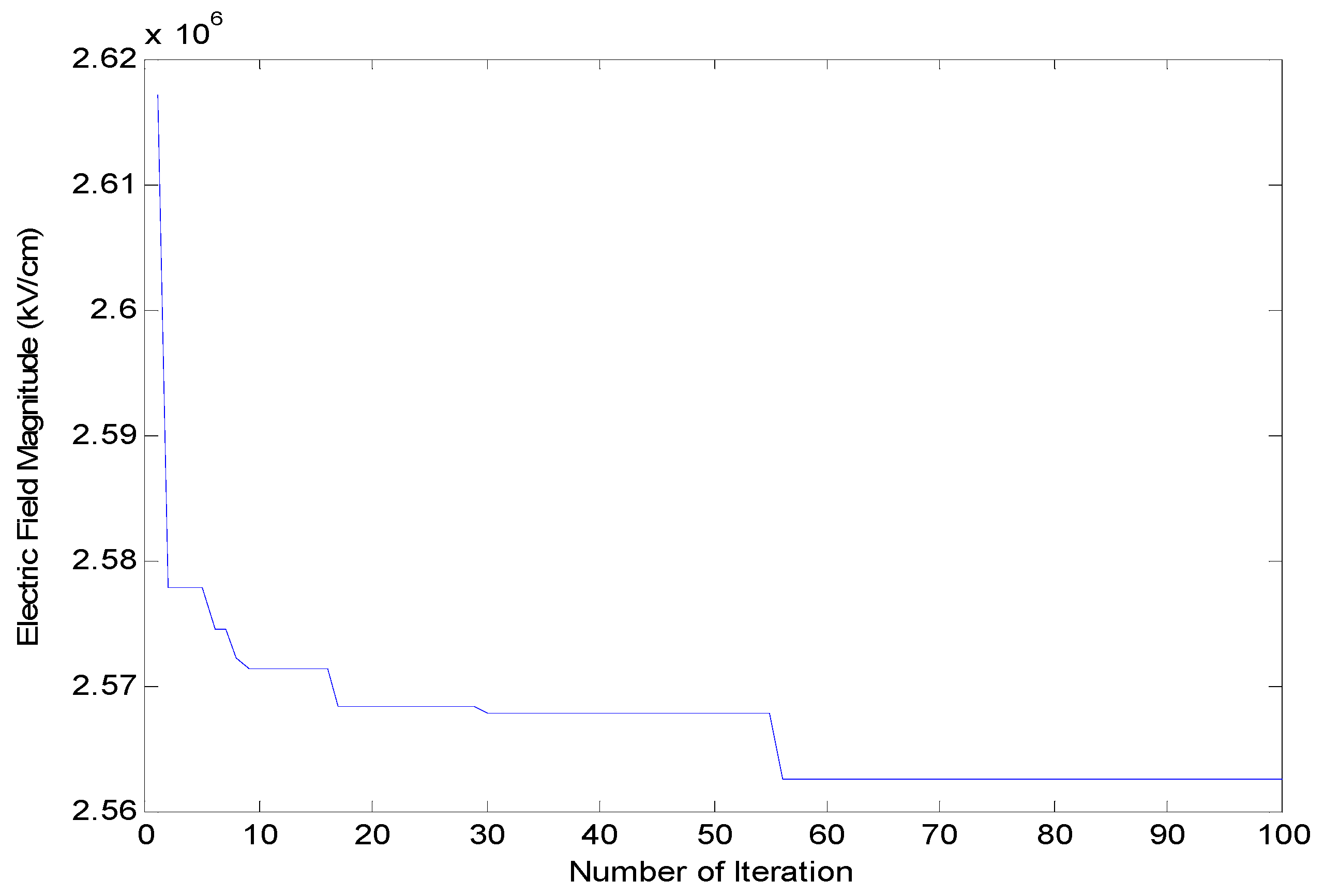
3.3. Optimisation Results Using ICA and GWO for 132 kV Insulator String
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Murawwi, E.A.; El-Hag, A. Corona ring design for a 400 kV non-ceramic insulator. In Proceedings of the 2nd International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, United Arab Emirates, 15–17 November 2011; pp. 1–4. [Google Scholar]
- Barros, R.M.R.; Costa, E.G.D.; Ferreira, T.V.; Araujo, J.F.; Andrade, F.L.M. A new approach for optimal design of corona ring. In Proceedings of the IEEE International Power Modulator and High Voltage Conference (IPMHVC), San Francisco, CA, USA, 6–9 July 2016; pp. 684–687. [Google Scholar]
- Arumugam, S.; Haba, Y.; Koerner, G.; Uhrlandt, D.; Paschen, M. Understanding partial discharges in low-power relay and silicone cable modified to suit high-voltage requirement of deep sea electrical system. Int. Trans. Electr. Energy Syst. 2018, 28, e2542. [Google Scholar] [CrossRef]
- Riba, J.R.; Capelli, F. Analysis of Capacitance to Ground Formulas for Different High-Voltage Electrodes. Energies 2018, 11, 1090. [Google Scholar] [CrossRef] [Green Version]
- Hu, H.; Zhang, X.; Liu, Y.; Guo, L. Optimization of the Electric Field Distribution at the End of the Stator in a Large Generator. Energies 2018, 11, 2510. [Google Scholar] [CrossRef] [Green Version]
- Mohammad, S.; Hoseini, H.F.; Mahdi, M.A.; Tavakoli, M. Electric Field Distributions around Silicon Rubber Insulators in Polluted and Cleaned Area. Int. J. Sci. Eng. Investig. 2013, 2, 137–140. [Google Scholar]
- Zhang, D.; Liu, J.; Fengbo, T.; Huang, X.; Yang, C.; Zhang, Z. Research on the Non-Contact Pollution Monitoring Method of Composite Insulator Based on Space Electric Field. Energies 2021, 14, 2116. [Google Scholar] [CrossRef]
- Phillips, A.J.; Kuffel, J.; Baker, A.; Burnham, J.; Carreira, A.; Cherney, E.; Chisholm, W.; Farzaneh, M.; Gemignani, R.; Gillespie, A.; et al. Electric Fields on AC Composite Transmission Line Insulators. IEEE Trans. Power Deliv. 2008, 23, 823–830. [Google Scholar] [CrossRef]
- Yang, W.; Zhu, T.; Tian, Y.; Zhu, S.; Yang, X. Computation and Analysis of Electric Field Distribution Under Lightning Impulse Voltage for 1000-kV Gas-Insulated-Switchgear Spacer. J. Electr. Eng. Technol. 2020, 15, 1745–1758. [Google Scholar] [CrossRef]
- Niedospial, E. Design and application of corona and grading rings for composite insulators. In Proceedings of the PES T&D, Orlando, FL, USA, 7–10 May 2012; pp. 1–3. [Google Scholar]
- Terrab, H.; Kara, A. Parameters design optimization of 230 kV corona ring based on electric field analysis and response surface methodology. Electr. Power Syst. Res. 2017, 163, 782–788. [Google Scholar] [CrossRef]
- Can, Y.; Aydogan, O.; Suat, I. Electric field distributions around composite insulators under AC and impulse voltages. In Proceedings of the Modern Electric Power Systems, Wroclaw, Poland, 20–22 September 2010; pp. 1–6. [Google Scholar]
- Sima, W.; Wu, K.; Yang, Q.; Sun, C. Corona Ring Design of ±800kV DC Composite Insulator Based on Computer Analysis. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena, Denver, CO, USA, 15–18 October 2006; pp. 457–460. [Google Scholar]
- Lalitha, M.; Kumar, K.V.; Samala, V. Design and simulation of voltage and electric field distribution on disc insulators using finite element method in Opera software. In Proceedings of the International Conference on Smart Electric Grid (ISEG), Guntur, India, 19–20 September 2014; pp. 1–6. [Google Scholar]
- Rout, U.K.; Sahu, R.K.; Panda, S. Gravitational Search Algorithm based Automatic Generation Control for interconnected power system. In Proceedings of the International Conference on Circuits, Power and Computing Technologies (ICCPCT), Nagercoil, India, 20–21 March 2013; pp. 558–563. [Google Scholar]
- Gierczak, M.; Markowski, P.M.; Dziedzic, A. The Modeling of Magnetic Fields in Electromagnetic Microgenerators Using the Finite Element Method. Energies 2022, 15, 1014. [Google Scholar] [CrossRef]
- Stefanini, D.; Seifert, J.M.; Clemens, M.; Weida, D. Three dimensional FEM electrical field calculations for EHV composite insulator strings. In Proceedings of the IEEE International Power Modulator and High Voltage Conference, Atlanta, GA, USA, 23–27 May 2010. [Google Scholar]
- Bakar, A.; Abidin, A.; Illias, H.; Mokhlis, H.; Abd Halim, S.; Hassan, N.; Tan, C.K. Determination of the striking distance of a lightning rod using finite element analysis. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 4083–4097. [Google Scholar] [CrossRef]
- Marghny, M.; Zanaty, E.A.; Dukhan, W.H.; Reyad, O. A hybrid multi-objective optimization algorithm for software requirement problem. Alex. Eng. J. 2022, 61, 6991–7005. [Google Scholar] [CrossRef]
- Yan, C.; Chen, J.; Ma, Y. Grey Wolf Optimization Algorithm with Improved Convergence Factor and Position Update Strategy. In Proceedings of the 11th International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 24–25 August 2019; pp. 41–44. [Google Scholar]
- Sabo, A.; Abdul, W.N.I.; Othman, M.L.; Mohd, J.M.Z.A.; Beiranvand, H. Optimal design of power system stabilizer for multimachine power system using farmland fertility algorithm. Int. Trans. Electr. Energy Syst. 2020, 30, e12657. [Google Scholar] [CrossRef]
- Ibrahim, K.S.M.H.; Huang, Y.F.; Ahmed, A.N.; Koo, C.H.; El-Shafie, A. A review of the hybrid artificial intelligence and optimization modelling of hydrological streamflow forecasting. Alex. Eng. J. 2022, 61, 279–303. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Djerioui, A.; Houari, A.; Machmoum, M.; Ghanes, M. Grey Wolf Optimizer-Based Predictive Torque Control for Electric Buses Applications. Energies 2020, 13, 5013. [Google Scholar] [CrossRef]
- Yu, H.; Yu, Y.; Liu, Y.; Wang, Y.; Gao, S. Chaotic grey wolf optimization. In Proceedings of the International Conference on Progress in Informatics and Computing, Shanghai, China, 23–25 December 2016; pp. 103–113. [Google Scholar]
- Du, M.; Zhao, Y.; Liu, C.; Zhu, Z. Lifecycle cost forecast of 110 kV power transformers based on support vector regression and gray wolf optimization. Alex. Eng. J. 2021, 60, 5393–5399. [Google Scholar] [CrossRef]
- Han, Y.; Tong, X. Multi-Step Short-Term Wind Power Prediction Based on Three-level Decomposition and Improved Grey Wolf Optimization. IEEE Access 2020, 8, 67124–67136. [Google Scholar] [CrossRef]
- Ansari, M.M.; Guo, C.; Shaikh, M.S.; Chopra, N.; Haq, I.; Shen, L. Planning for Distribution System with Grey Wolf Optimization Method. J. Electr. Eng. Technol. 2020, 15, 1485–1499. [Google Scholar] [CrossRef]
- Naserbegi, A.; Aghaie, M.; Zolfaghari, A. Implementation of Grey Wolf Optimization (GWO) algorithm to multi-objective loading pattern optimization of a PWR reactor. Ann. Nucl. Energy 2020, 148, 107703. [Google Scholar] [CrossRef]
- Eid, A. Allocation of distributed generations in radial distribution systems using adaptive PSO and modified GSA multi-objective optimizations. Alex. Eng. J. 2020, 59, 4771–4786. [Google Scholar] [CrossRef]
- Bashiri, M.; Bagheri, M. Using Imperialist competitive algorithm optimization in multi-response nonlinear programming. Int. J. Ind. Eng. Prod. Res. 2012, 24, 229–235. [Google Scholar]






| Typical System Voltage | No. of Sheds | Length (mm) | Cantilever Strength (kN) | Creepage Distance (mm) |
|---|---|---|---|---|
| 132 kV | 40 | 1650 | 6.8 | 3914 |
| Materials | Relative Permittivity, εr | Electrical Conductivity, σ (S/m) | Density, ρ (kg/m3) | Heat Capacity at a Constant Pressure, Cp (J/kgK) | Thermal Conductivity, k (W/mK) |
|---|---|---|---|---|---|
| Aluminium | 1 | 3.774 × 107 | 2700 | 900 | 160 |
| Silicone rubber | 4.2 | 1 × 10−14 | 2203 | 1925 | 1.38 |
| Fiberglass | 4.2 | 1 × 10−14 | 80 | 390 | 0.47 |
| Iron | 1 | 1.12 × 107 | 7870 | 440 | 76.2 |
| Air | 1 | 0 | 1 | 450 | 0.024 |
| Boundary | Boundary Setting |
|---|---|
| Terminal | Applied voltage 132 kV |
| Air | Electric insulation |
| Ground | 0 V |
| All interior boundary | Continuity |
| Ring Diameter, R (mm) | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Points (116) Electric field (kV/cm) | 4.314 | 4.325 | 4.333 | 4.338 | 4.348 | 4.354 | 4.356 | 4.356 | 4.355 | 4.359 | r = 5 mm |
| 4.299 | 4.219 | 4.265 | 4.303 | 4.331 | 4.346 | 4.355 | 4.356 | 4.356 | 4.362 | r = 10 mm | |
| 13.967 | 4.086 | 4.162 | 4.252 | 4.289 | 4.327 | 4.344 | 4.363 | 4.364 | 4.365 | r = 15 mm | |
| 17.757 | 11.700 | 4.010 | 4.161 | 4.248 | 4.313 | 4.341 | 4.361 | 4.366 | 4.373 | r = 20 mm | |
| 24.604 | 14.296 | 3.827 | 4.021 | 4.156 | 4.283 | 4.331 | 4.354 | 4.378 | 4.379 | r = 25 mm | |
| 37.636 | 18.451 | 11.923 | 3.866 | 4.077 | 4.231 | 4.319 | 4.361 | 4.387 | 4.393 | r = 30 mm | |
| 67.285 | 25.481 | 14.739 | 3.658 | 3.968 | 4.125 | 4.305 | 4.359 | 4.387 | 4.405 | r = 35 mm | |
| N/A | 39.141 | 18.650 | 12.110 | 3.802 | 4.104 | 4.277 | 4.346 | 4.399 | 4.409 | r = 40 mm | |
| N/A | 70.143 | 25.970 | 14.866 | 3.619 | 3.954 | 4.208 | 4.324 | 4.392 | 4.431 | r = 45 mm | |
| N/A | N/A | 41.386 | 18.944 | 12.132 | 3.808 | 4.099 | 4.260 | 4.356 | 4.399 | r = 50 mm |
| Cases | Parameters: Description |
|---|---|
| Case 1 | Diameter of ring tube, r |
| Case 2 | Diameter of ring tube, r |
| Ring diameter, R | |
| Case 3 | Diameter of ring tube, r |
| Vertical position of the ring along the insulator, H | |
| Ring diameter, R |
| Parameters | Lower Limit | Upper Limit |
|---|---|---|
| Ring diameter | Rmin = 60 mm | Rmax = 150 mm |
| Diameter of ring tube | rmin = 5 mm | rmax = 50 mm |
| Vertical position of the ring along the insulator | Hmin = 0 mm | Hmax = 100 mm |
| Case | Optimised Parameters | Parameter Measurements (mm) | Electric Fields at Point 116 (kV/cm) | Without Optimisations | ||
|---|---|---|---|---|---|---|
| ICA | GWO | ICA | GWO | |||
| Case 1 | r | 24.114 | 24.1 | 3.871 | 3.859 | 3.827 |
| Case 2 | r | 23.999 | 24.22 | 3.92 | 3.899 | 3.827 |
| R | 82.145 | 81.37 | ||||
| Case 3 | r | 25.112 | 24.9 | 3.777 | 3.724 | 3.827 |
| R | 83.147 | 82.18 | ||||
| H | 21.718 | 20.98 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aramugam, K.; Illias, H.A.; Ching, Y.C.; Ali, M.S.; Makmud, M.Z.H. Optimal Design of Corona Ring for 132 kV Insulator at High Voltage Transmission Lines Based on Optimisation Techniques. Energies 2023, 16, 778. https://doi.org/10.3390/en16020778
Aramugam K, Illias HA, Ching YC, Ali MS, Makmud MZH. Optimal Design of Corona Ring for 132 kV Insulator at High Voltage Transmission Lines Based on Optimisation Techniques. Energies. 2023; 16(2):778. https://doi.org/10.3390/en16020778
Chicago/Turabian StyleAramugam, Kalaiselvi, Hazlee Azil Illias, Yern Chee Ching, Mohd Syukri Ali, and Mohamad Zul Hilmey Makmud. 2023. "Optimal Design of Corona Ring for 132 kV Insulator at High Voltage Transmission Lines Based on Optimisation Techniques" Energies 16, no. 2: 778. https://doi.org/10.3390/en16020778
APA StyleAramugam, K., Illias, H. A., Ching, Y. C., Ali, M. S., & Makmud, M. Z. H. (2023). Optimal Design of Corona Ring for 132 kV Insulator at High Voltage Transmission Lines Based on Optimisation Techniques. Energies, 16(2), 778. https://doi.org/10.3390/en16020778









