Techno-Economic Strategy for the Load Dispatch and Power Flow in Power Grids Using Peafowl Optimization Algorithm

Abstract

The purpose of this paper is to address an urgent operational issue referring to optimal power flow (OPF), which is associated with a number of technical and financial aspects relating to issues of environmental concern. In the last few decades, OPF has become one of the most significant issues in nonlinear optimization research. OPF generally improves the performance of electric power distribution, transmission, and production within the constraints of the control system. It is the purpose of an OPF to determine the most optimal way to run a power system. For the power system, OPFs can be created with a variety of financial and technical objectives. Based on these findings, this paper proposes the peafowl optimization algorithm (POA). A powerful meta-heuristic optimization algorithm inspired by collective foraging activities among peafowl swarms. By balancing local exploitation with worldwide exploration, the OPF is able to strike a balance between exploration and exploitation. In order to solve optimization problems involving OPF, using the standard IEEE 14-bus and 57-bus electrical network, a POA has been employed to find the optimal values of the control variables. Further, there are five study cases, namely, reducing fuel costs, real energy losses, voltage skew, fuel cost as well as reducing energy loss and voltage skew, and reducing fuel costs as well as reducing energy loss and voltage deviation, as well as reducing emissions costs. The use of these cases facilitates a fair and comprehensive evaluation of the superiority and effectiveness of POA in comparison with the coot optimization algorithm (COOT), golden jackal optimization algorithm (GJO), heap-based optimizer (HPO), leader slime mold algorithm (LSMA), reptile search algorithm (RSA), sand cat optimization algorithm (SCSO), and the skills optimization algorithm (SOA). Based on simulations, POA has been demonstrated to outperform its rivals, including COOT, GJO, HPO, LSMA, RSA, SCSO, and SOA. In addition, the results indicate that POA is capable of identifying the most appropriate worldwide solutions. It is also successfully investigating preferred search locations, ensuring a fast convergence speed and enhancing the search engine’s capabilities.

1. Introduction

Electricity consumption is increasing immensely, making it increasingly relevant to conduct scientific research in the area of electrical power systems for operation and planning. The complexity and nonlinear nature of electrical power grids require efficient operation within their operating limits [1]. The optimal power flow (OPF) framework is one of the main strategies that might help attain this objective. In order to operate an electric power network, OPF technologies are essential. Power grid management settings are adjusted optimally using optimization techniques while dealing with a variety of restrictions. By focusing on both single and multiple objective frameworks, this article aims at resolving the OPF issue [2,3]. As a result, different power grid requirements will be met from a technical, as well as a financial, perspective. As well as for planning future growth, the OPF findings are necessary for the efficient operation, planning, and management of the current electrical grid. For a particular electrical network, the OPF solution should govern the variables that control or make decisions in a practical area that optimizes predefined objective functions. Often, fuel cost minimization is incorporated as a primary objective function (OF) when formulating the OPF problem, along with other objectives, such as voltage profile enhancement (VPE), real power loss minimization (RPLM), and emissions cost minimization (ECM), based on adapting control variables under both operational and tangible constraints. Conventional optimization methods (COTs) were used in the early decades to solve OPF problems, including linear programming, non-linear programming, mixed integer programming, and interior point methods. Many COTs are used by industry despite their exceptional convergence characteristics. Unlike hill-climbing algorithms, most traditional algorithms are deterministic and cannot locate the most efficient solution on the planet or manage binary or integer variables well. Additionally, COTs cannot address the OPF issue since traditional optimization techniques (apart from linear programming and convex optimization) require starting points. Despite their shortcomings, metaheuristic optimization algorithms are a promising solution for various applications due to their ability to exploit the rapid growth of computational intelligence over the years [4,5,6]. There has been significant progress in solving OPF using multiple metaheuristic optimization techniques over the last ten years, including hybrid approaches, swarm approaches, artificial neural networks with fuzzy logic, and bio-inspired approaches. A summary of the previous approaches to solving this problem can be found in Table 1. These methodologies may be classified according to the single or multiple aims, contributions, and key conclusions of each application.

Table 1. Applied techniques for the optimal power flow (OPF) issue.

Year	Title	Contribution	Ref
2015	Scheduling OPF from distributed photovoltaic systems, wind turbines, and diesel generators using batteries	A model has been developed in order to reduce the operation costs of the hybrid system. In addition, it has been evaluated the most suitable power flow considering the intermittent solar and wind resources, the condition of the batteries, and the varying load demand. This is when a particular scenario regarding the cost of wind generation is considered.	[7]
2015	An algorithm for wind-integrated multi-objective dynamic economic dispatch that utilizes a hybrid flower pollination algorithm (FBA) with time-varying fuzzy selection mechanisms.	To solve the economic dispatch issue, the author used a hybrid FBA.	[8]
2016	OPF-based Jaya algorithm (JA)	To address various issues related to OPF, the JA has been applied to the newly designed IEEE 30-bus and IEEE 118-bus. In this work, three main aim functions are considered for the OPF solution: reduction of real power losses, enhancement of voltage stability, and minimization of generation costs. The impact of distributed generation (DG) is also incorporated into the OPF issue through a modified formulation.	[9]
2017	OPF incorporated the stochastic wind and solar power	The OPF problem was successfully handled in a small system using only the IEEE 30-bus thanks to a history-based adaptation approach of differential evolution algorithms.	[10]
2017	OPF-based modified particle swarm (MPSO) for hybridization of the distributed renewable generation	A MPSO optimizer has been developed to determine the appropriate hourly load flow in the 30-bus IEEE system. A few buses have been equipped with solar panels and wind turbines to see how they perform as DG.	[11]
2017	Solving OPF problems using biogeography-based optimizer (BBO) and grey wolf optimizer (GWO)	Various OPF approaches have been developed to address its multi-constrained problems in the power system, including BBO and GWO. The suggested methods have been evaluated in conjunction with the IEEE 30-bus test system in a variety of situations, as well as the 9-bus test system.	[12]
2018	Crow search algorithm (CSA) for single-objective OPF in power systems	The best power solution for electric power systems is found using the CSA. Different restricted objective functions, total fuel expenditure, active power loss, and pollutant emissions are advised to be considered. Systems based on IEEE 118-bus and IEEE 30-bus are utilized to test the proposed method.	[13]
2018	A stud krill herd (SKH) algorithm-based OPF solution network	A SKH technique is illustrated in relation to the OPF issues of the IEEE 14-bus, IEEE 30-bus, and IEEE 57-bus systems. A variety of objective functions were evaluated, including the effect of valve point loading, active power loss, L-index, and emissions.	[14]
2019	A modified Jaya algorithm (MJAYA) for OPF that incorporates renewable energy sources (RES) as part of cost, emissions, power loss, and voltage profile considerations	An MJAYA optimizer uses four alternative objective measures: cost minimization, emissions minimization, transmission power loss minimization, and voltage profile improvement. RES and OPF can be addressed using these methods. The proposed optimizer was applied to two different test systems, IEEE 30-bus and IEEE 118-bus.	[15]
2020	Using a heuristic algorithm, a stochastic RES is incorporated into the OPF scheme	Using the GWO method, the OPF issue was solved by incorporating intermittent solar and wind power generation.	[16]
2020	For the purposes of addressing OPF issues, the krill herd algorithm (KHA) is taken into account in accordance with FACTS devices and stochastic wind power generation	A KHA was used in conjunction with FACTS devices in order to handle the OPF issue in cases of overestimation and underestimation of wind production costs.	[17]
2020	The modified artificial bee colonies optimizer (MABCO) with different objective functions of OPF constraints	MABCO has been assigned the responsibility for handling the OPF issue. Through the application of the proposed algorithm to the IEEE 30-bus system, it has been demonstrated to minimize four distinct objective functions: fuel costs for thermal units, active power losses in transmission lines, emissions produced by fossil-fueled thermal units, and deviations at load buses.	[18]
2021	Using a multi-operator differential evolution algorithm (MODEA), the OPF considers intermittent solar and wind generation	The OPF issue was solved using MODEA approach by incorporating sporadic solar and wind power generation in one scenario. This was done in order to correct the overestimation and underestimation of wind energy costs.	[19]
2021	Using the barnacles mating optimizer (BMO) to resolve the issue of OPF with stochastic wind-solar-small hydropower	The BMO addressed the OPF issue by combining FACTS devices and stochastic wind power generation into one scenario.	[20]
2021	An approach to robust optimization using Rao algorithms (RA) for OPF problems	There are three common IEEE systems (30-bus, 57-bus, and 118-bus) in which RAs are used to address OPF issues by taking into account technical and financial goals.	[21]
2021	Using artificial ecosystem optimization (AEO) to find the most suitable solution for OPF concerns	The OPF issue may be resolved through the use of AEO. A five-goal function evaluation of the proposed technique is carried out on IEEE 30-bus systems and includes fuel cost, pollution, power loss, voltage deviations, and L-index.	[22]
2021	The application of a multi-objective backtracking search algorithm (MOBSA) to multi-objective OPF	A MOBSA optimizer is used to formulate and solve the OPF issue in electrical power systems. A number of objective functions are considered, including voltage variation, power losses, and fuel costs. An optimal compromise between all the Pareto optimum options is determined by applying a fuzzy membership strategy to the BSA approach. To analyze, validate, and test the MOBSA approach’s capability for bi- and tri-objectives, it has been applied in different IEEE networks.	[23]
2021	OPF based on firefly algorithm (FA) for minimizing power loss	The FA has been used to solve the OPF issue. The FA was proposed to optimize the control variables in order to reduce the actual power loss experienced by the transmission system. On the IEEE 14-bus and 30-bus systems, the proposed algorithm was then assessed using the MATLAB program.	[24]
2021	Using a multi-objective PSO (MOPSO) to solve the OPF problem in power systems	In a power system with conflicting objectives, it is suggested that a MOPSO approach be used to address the limited OPF problem. In addition, the operator will be provided with the most appropriate optimum solution from the ideal Pareto set based on fuzzy set theory. To confirm the applicability and effectiveness of the recommended strategy, the IEEE 30-bus standard system was used.	[25]
2021	OPF solution-based jellyfish search optimization (JFO) considering uncertainty of RES	The JFO has been used to establish optimum solutions for the redesigned IEEE 30-bus test system.	[26]
2022	The Archimedes optimization algorithm (AOA) is used for OPF problems	The AOA has been presented as a revolutionary metaheuristic approach for the minimization of various objective functions when using RES to solve OPF optimization problems.	[27]
2022	The enhanced slime mold algorithm (ESMA) for the solution of OPF problems	An ESMA based on neighborhood dimension learning (NDL) was used to address the OPF problem. In order to demonstrate the validity of the method, 23 benchmark functions have been demonstrated, along with comparisons to the original SMA and three more contemporary optimization techniques. A modified power flow model has been developed that incorporates both conventional and renewable energy sources, which are represented, respectively, by thermal power generators (TPGs) and wind and solar photovoltaic generators.	[28]
2022	The modified whale optimization algorithm (MWOA) for solving problems of the OPF	MWOA has been designed to address both single-objective and multi-objective OPF issues. IEEE 30-bus was used to evaluate the suggested approach.	[29]
2022	A multi-objective OPF that considers stochastic wind and solar energy	In order to solve the most efficient power flow with stochastic wind and solar energy, a multi-objective evolutionary approach based on non-dominated sorting with constraint management methodology is proposed. Based on a modified IEEE 30-bus and IEEE 57-bus systems, the proposed technique was tested for its effectiveness in solving big dimensional problems.	[30]

There is no optimization procedure that can achieve the global optimum for every optimization problem. Research is being conducted on contemporary metaheuristic algorithms with the objective of addressing the multi-objective and single-objective aspects of the OPF issue as a non-linear, difficult engineering problem. A variety of engineering applications have benefited from the use of these algorithms because of their simple structure, decreased operator requirements, speedy convergence properties, and enhanced balancing capabilities. POA is a promising tool for solving nonlinear, restricted optimization problems since it is widely used and has a great deal of significance.

Therefore, the following accomplishments of this research might be summed up:

• An innovative approach is presented to solve the OPF issue in power systems. This method guarantees quick convergence and increased search efficiency.
• Describing the five objective functions used in the OPF issue formulation, a number of validations of the suggested approaches have been conducted for both single-objective and multi-objective OPF optimizations. Using pricing and weighting factors, the proposed methods for addressing optimization issues are applied to account for the multi-objective functions (fuel cost, power losses, voltage variation, and emissions).
• A challenging test suite for metaheuristic literary works is evaluated using IEEE 14-bus and IEEE 57-bus testing systems. In statistical evaluations, a boxplot is produced that is highly accurate in reducing the OF with the lowest values, demonstrating the robustness of the proposed POA algorithm.

Following is the breakdown of this essay: Section 2 introduces the OPF’s mathematical formulation model. Section 3 covers the simulation findings and includes the demonstration. This section compares and analyzes the selected metaheuristic algorithms. The study and analysis are summarized and drawn in Section 4.

2. Mathematical Formulation for OPF

OPF often seeks to reduce certain goal functions. An objective function is given by F, and equality and inequality constraints are given by g and h in the network of a power system. The OPF is estimated as follows:

$$min F\left(x, u\right)$$

(1)

Conditional on:

$$g_j\left(x,u\right)=0; j=1,2,\dots ,m$$

$$h_j\left(x,u\right)\le 0; j=1,2,\dots ,p$$

From Equation (1), x represents the dependent variables, and u represents the control variables. Both $g_j$ and $h_j$ imply a need for equality and inequality. A limitation on equality is indicated by the variable m, whereas an inequality is indicated by the variable p.

The variables ($x$) can be expressed by (2):

$$x=\left[P_{G1},V_{L1}\dots V_{L,NPQ},Q_{G,1}\dots Q_{G,NG},S_{TL,1}\dots S_{TL,NTL}\right]$$

(2)

Here, by (2), a slack bus’s power is indicated by $P_{G1}$, a load bus’s voltage is indicated by $V_L$, a generator’s reactive output power is indicated by $Q_G$, and a transmission line’s apparent power flow is indicated by $S_{TL}$. A load bus is identified by NPQ, a generation bus by NG, and a transmission line by NTL.

The controlled variables (u) can be formulated by (3):

$$u=\left[P_{G,2}\dots P_{G,NG},V_{G,1}\dots V_{G,NG},Q_{C,1}\dots Q_{C,NC},T_1\dots T_{NT}\right]$$

(3)

As shown in the equation, $P_G$ represents the generator’s actual output power, $V_G$ represents the generator’s bus voltage, $Q_C$ represents the injected shunt compensator’s reactive power, T represents the transformer’s tap setting, NC represents the shunt reactive compensation unit number, and NT represents the transformer number.

2.1. Objective Functions of OPF

The last instance addressed the multi-objective OPF, while the prior three cases dealt with addressing single-objective OPF.

2.1.1. Fuel Costs Minimization

In order to reduce total fuel costs, this objective function is the OPF issue’s main goal. It may be shown as a quadratic polynomial function for every generator using the examples below:

$$F_1={\displaystyle \sum }_{i=1}^{NG}{F}_i\left(P_{Gi}\right)={\displaystyle \sum }_{i=1}^{NPV}\left(a_i+b_i{P}_{Gi}+c_i{P^2}_{Gi}\right)\frac{\$}{h}$$

(4)

Based on Equation (4), $F_i$ indicates the fuel cost at the ith generator. In addition, the $a_i$, $b_i$, and $c_i$ are the cost coefficients.

2.1.2. Generation Emissions Minimization

Pollution may be decreased by limiting the gas thermal power plants release. Here is how the emission gases’ objective function works:

$$F_2={\displaystyle \sum }_{i=1}^{NG}\left({\gamma }_i{P^2}_{Gi}+{\beta }_i{P}_{Gi}+{\alpha }_i+{\mathsf{\zeta }}_{i}exp({\lambda }_i{P}_{Gi}\right)$$

(5)

From Equation (5) at ith generators, the emission coefficients are ${\gamma }_i$, ${\beta }_i$, ${\alpha }_i$, ${\mathsf{\zeta }}_i$, and ${\lambda }_i$.

2.1.3. Active Power Losses Minimization

Minimizing actual power loss is the desired objective function, and it may be demonstrated as follows:

$$F_3={\displaystyle \sum }_{i=1}^{NTL}{G}_{ij}\left({V^2}_i+{V^2}_j-2V_i{V}_j\cos {\delta }_{ij}\right)$$

(6)

where $G_{ij}$ the transmission conductance, $NTL$ is the transmission lines number, and ${\delta }_{ij}$ is the voltages phase difference.

2.1.4. Voltage Deviation Minimization

This objective function, which may be stated as follows, seeks to minimize the variations in the voltage on the load buses from a specified value:

$$F_4=VD={\displaystyle \sum }_{i=1}^{NPQ}\left|V_i-1\right|$$

(7)

2.1.5. Multi-Objective Functions

Multi-objective problems are defined as problems in which several independent objective functions are optimized simultaneously by the following Equation (8):

$$Min F\left(x,u\right)=\left[F_1\left(x,u\right),F_2\left(x,u\right),\dots ,F_i\left(x,u\right)\right]$$

(8)

From Equation (8), i is the number of objectives.

Multi-objective functions can be solved using the Pareto approach or weight factors as follows:

$$Min F_5={\displaystyle \sum }_{i=1}^4{w}_i F_i\left(x,u\right)$$

$$F\left(x,u\right)=w_1{F}_1+w_2{F}_2+w_3{F}_3+w_4{F}_4$$

(9)

$$F\left(x,u\right)=w_1{\displaystyle \sum }_{i=1}^{NG}\left(a_i+b_i{P}_{Gi}+c_i{P^2}_{Gi}\right)+w_2{\displaystyle \sum }_{i=1}^{NG}\left({\gamma }_i{P^2}_{Gi}+{\beta }_i{P}_{Gi}+{\alpha }_i+{\mathsf{\zeta }}_i \exp ({\lambda }_i{P}_{Gi}\right)$$

$$+w_3{\displaystyle \sum }_{i=1}^{NTL}{G}_{ij}\left({V^2}_i+{V^2}_j-2V_i{V}_j\cos {\delta }_{ij}\right)+w_4{\displaystyle \sum }_{i=1}^{NPQ}\left|V_i-1\right|$$

(10)

In order to determine the weighting factors $w_1$, $w_2$, $w_3$ and $w_4$, each goal’s relative importance can be considered. The weighting factors can be considered based on the following formula:

$${\displaystyle \sum }_{i=1}^n{w}_i=1$$

(11)

2.2. System Constraints

In the system, there are already a number of restrictions that fall under the following categories:

2.2.1. The Equality Constraints

The equality constraints can be estimated by the following equations:

$$P_{Gi}-P_{Di}=\left|V_i\right|{\displaystyle \sum }_{j=1}^{NB}\left|V_j\right|\left(G_{ij}\cos {\delta }_{ij}+B_{ij}sin{\delta }_{ij}\right)$$

(12)

$$Q_{Gi}-Q_{Di}=\left|V_i\right|{\displaystyle \sum }_{j=1}^{NB}\left|V_j\right|\left(G_{ij}\cos {\delta }_{ij}+B_{ij}sin{\delta }_{ij}\right)$$

(13)

There are two types of demand for a load on a bus, active and reactive. They are represented by $P_{Di}$ and $Q_{Di}$, respectively. Conductance and susceptibility are represented by $G_{ij}$ and $B_{ij}$, respectively, surrounded by nodes i and j.

2.2.2. Inequality Constraints

The operation limits for a power system are determined by its equipment, the transmission load, and the voltage of the load buses. It is possible to categorize inequality constraints as follows:

(a) 

Generators’ active output power

$${P_{Gi}}^{min}\le P_{Gi}\le {P_{Gi}}^{max} i=1,2,\dots ,NG$$

(14)

(b) 

Bus voltages at generators

$${V_{Gi}}^{min}\le V_{Gi}\le {V_{Gi}}^{max} i=1,2,\dots ,NG$$

(15)

(c) 

Generators’ reactive output power

$${Q_{Gi}}^{min}\le Q_{Gi}\le {Q_{Gi}}^{max} i=1,2,\dots ,NG$$

(16)

(d) 

Setting the transformer’s tap

$${T_i}^{min}\le T_i\le {T_i}^{max} i=1,2,\dots ,NT$$

(17)

(e) 

Shunt VAR compensator

$${Q_{Ci}}^{min}\le Q_{Ci}\le {Q_{Ci}}^{max} i=1,2,\dots ,NC$$

(18)

(f) 

A transmission line’s apparent power flow

$$S_{Li}\le {S_{Li}}^{min} i=1,2,\dots ,NTL$$

(19)

(g) 

Voltage boundaries on the load bus

$${V_{Li}}^{min}\le V_{Li}\le {V_{Li}}^{max} i=1,2,\dots ,NPQ$$

(20)

A quadratic penalty formulation of the objective function can be used to easily incorporate the dependent control variables into an optimization solution as follows:

$$F_g\left(x,u\right)=F_i\left(x,u\right)+K_G{\left(\Delta P_{G1}\right)}^2+K_Q{\displaystyle \sum }_{i=1}^{NPV}{\left(\Delta Q_{Gi}\right)}^2+K_V{\displaystyle \sum }_{i=1}^{NPQ}{\left(\Delta V_{Li}\right)}^2+K_S{\displaystyle \sum }_{i=1}^{NTL}{\left(\Delta S_{Li}\right)}^2$$

(21)

where $K_G$, $K_Q$, $K_V$, and $K_S$ are penalty factors with large positive values, and also $\Delta P_{G1}$, $\Delta Q_{Gi}$, $\Delta V_{Li}$, and $\Delta S_{Li}$ are penalty conditions that can be stated as follows:

$$\Delta P_{G1}=\left\{\begin{array}{c}\left(P_{G1}-{P_{G1}}^{max}\right) P_{G1}>{P_{G1}}^{max}\\ \left(P_{G1}-{P_{G1}}^{min}\right) P_{G1}<{P_{G1}}^{min}\\ 0 {P_{G1}}^{min}<P_{G1}<{P_{G1}}^{max}\end{array}\right.$$

(22)

$$\Delta Q_{Gi}=\left\{\begin{array}{c}\left(Q_{Gi}-{Q_{Gi}}^{max}\right) Q_{Gi}>{Q_{Gi}}^{max}\\ \left(Q_{Gi}-{Q_{Gi}}^{min}\right) Q_{Gi}<{Q_{Gi}}^{min}\\ 0 {Q_{Gi}}^{min}<Q_{Gi}<{Q_{Gi}}^{max}\end{array}\right.$$

(23)

$$\Delta V_{Li}=\left\{\begin{array}{c}\left(V_{Li}-{V_{Li}}^{max}\right) V_{Li}>{V_{Li}}^{max}\\ \left(V_{Li}-{V_{Li}}^{min}\right) V_{Li}<{V_{Li}}^{min}\\ 0 {V_{Li}}^{min}<V_{Li}<{V_{Li}}^{max}\end{array}\right.$$

(24)

$$\Delta S_{Li}=\left\{\begin{array}{c} \left(S_{Li}-{S_{Li}}^{max}\right) S_{Li}>{S_{Li}}^{max}\\ \left(S_{Li}-{S_{Li}}^{min}\right) S_{Li}<{S_{Li}}^{min}\\ 0 {S_{Li}}^{min}<S_{Li}<{S_{Li}}^{max}{S_{Li}}^{max}\end{array} \right.$$

(25)

2.3. Peafowl Optimization Algorithm (POA)

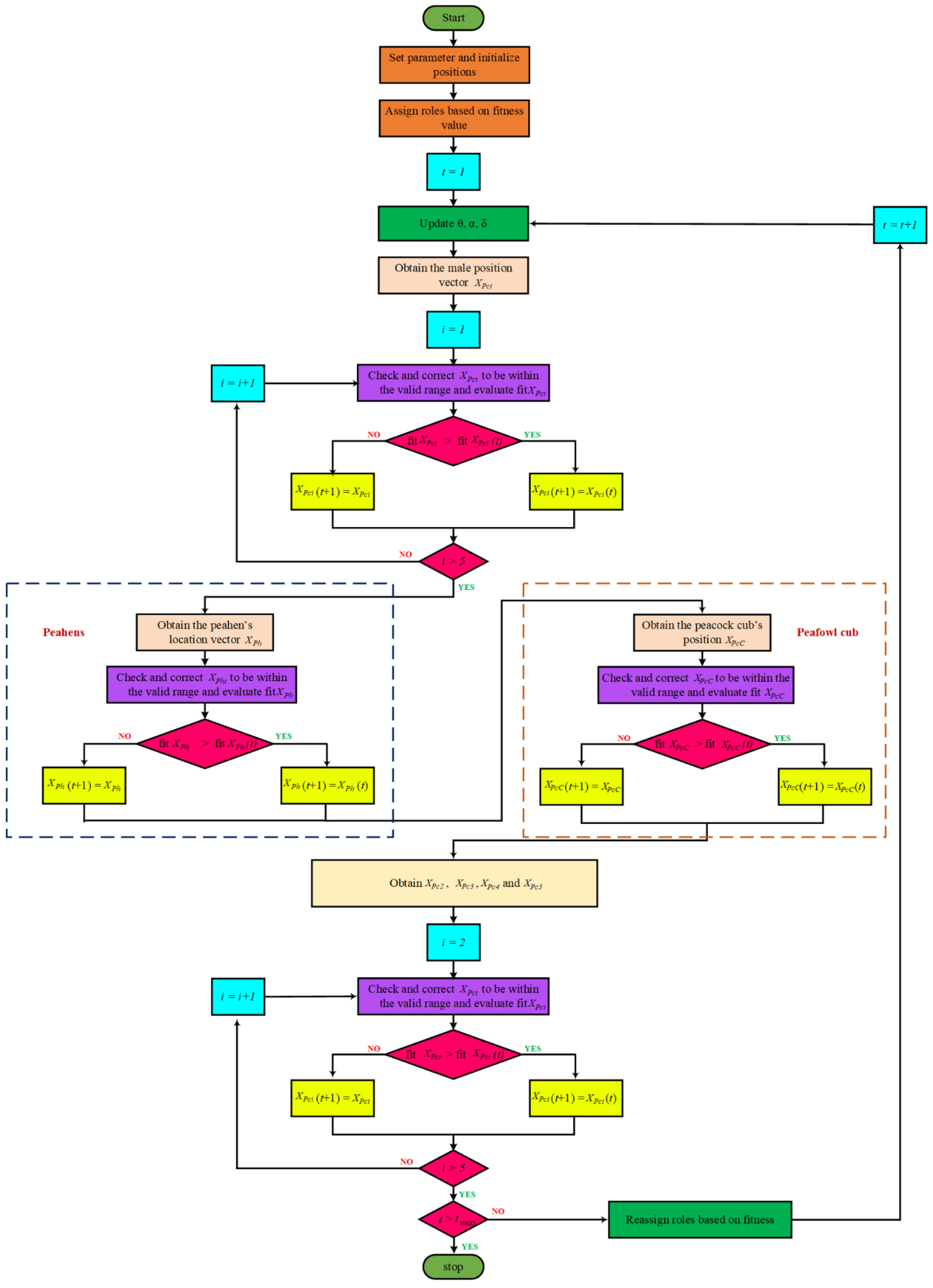
The main inspiration for this algorithm is from the observation of the living habits and behaviors of green peafowls in Yunnan Province in China. Male peafowls are referred to as peacocks, and female peafowls as peahens. Peafowl activities primarily fall into four categories: breeding behavior, food-seeking activity, social behavior, and spatial behavior [31]. The top five solutions to real-world optimization problems are referred to as adult peacocks. The individual roles of these artificial peafowl swarms may vary over time. Therefore, it is necessary to redistribute them based on fitness values after every iteration in order to maintain POA enforcement. Peacocks will rotate around food sources once they have discovered them in order to exhibit and brag to attract peahens’ attention and boost the likelihood of mating. As a result, peahens are likely to use a variety of seeking and approaching strategies throughout the entire search process in order to dynamically control their behavior throughout. In Figure 1, which illustrates the whole execution flowchart of the POA-based OPF, the maximum iteration number is denoted by the symbol $t_{max}$.

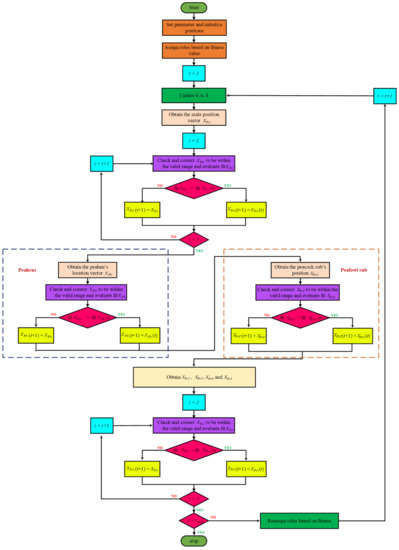
Figure 1. Flowchart of POA for the OPF problem.

For the POA technique, the control variables of the OPF problem are coded as the positions of the peacocks based on the fitness function (objective function) represented by Equations (4)–(8).

However, the advantages of the POA technique can be deduced as follows:

• During the entire search process, both peahens and peafowl cubs use adaptive seeking and approaching mechanisms. As a result, they are able to dynamically alter their behavior at various stages, thereby maintaining a healthy balance between local exploitation and global exploration. By combining global and local search operators, POA achieves a balance between the two, and prevents local optimum formation.
• In order to find the most effective solutions for today, the five peacocks will rotate and dance as they search throughout the area for solutions. In addition to spinning in situ, the peacock also circles its food source. This is a very unique rotating dance mechanism of the peacock that involves two distinct modes of rotation. There is significance in the fact that a strategy was used to force the present optimal solution to perform a neighboring search, which has never been attempted before. As a result, local optimum situations can be identified.
• As a general rule, POA is designed to explore the optimal search areas and to return the most relevant answers overall.
• The POA outperforms in terms of estimation accuracy, convergence speed, and stability.

3. Simulation Results

A test of the effectiveness of the recommended techniques for single OPF issues has been conducted using the IEEE 14-bus network and the IEEE 57-bus network. The number of populations, the number of iterations, and the number of runs is 50, 200, and 20, respectively. This work is carried out using the MATLAB R2022a programming language and a computer with an Intel^® CoreTM i7-8550U processor and 16 GB of RAM. Five case studies are presented in the following sections:

–

Minimization of fuel operation costs.

–

Reducing transmission power losses to a minimum.

–

Minimization of voltage deviation.

–

Minimization of fuel operational costs, transmission power losses, and voltage level deviations.

–

Minimization of the emission index, fuel operational costs, voltage deviations, and transmission power losses.

3.1. Standard IEEE-14 Bus Test System

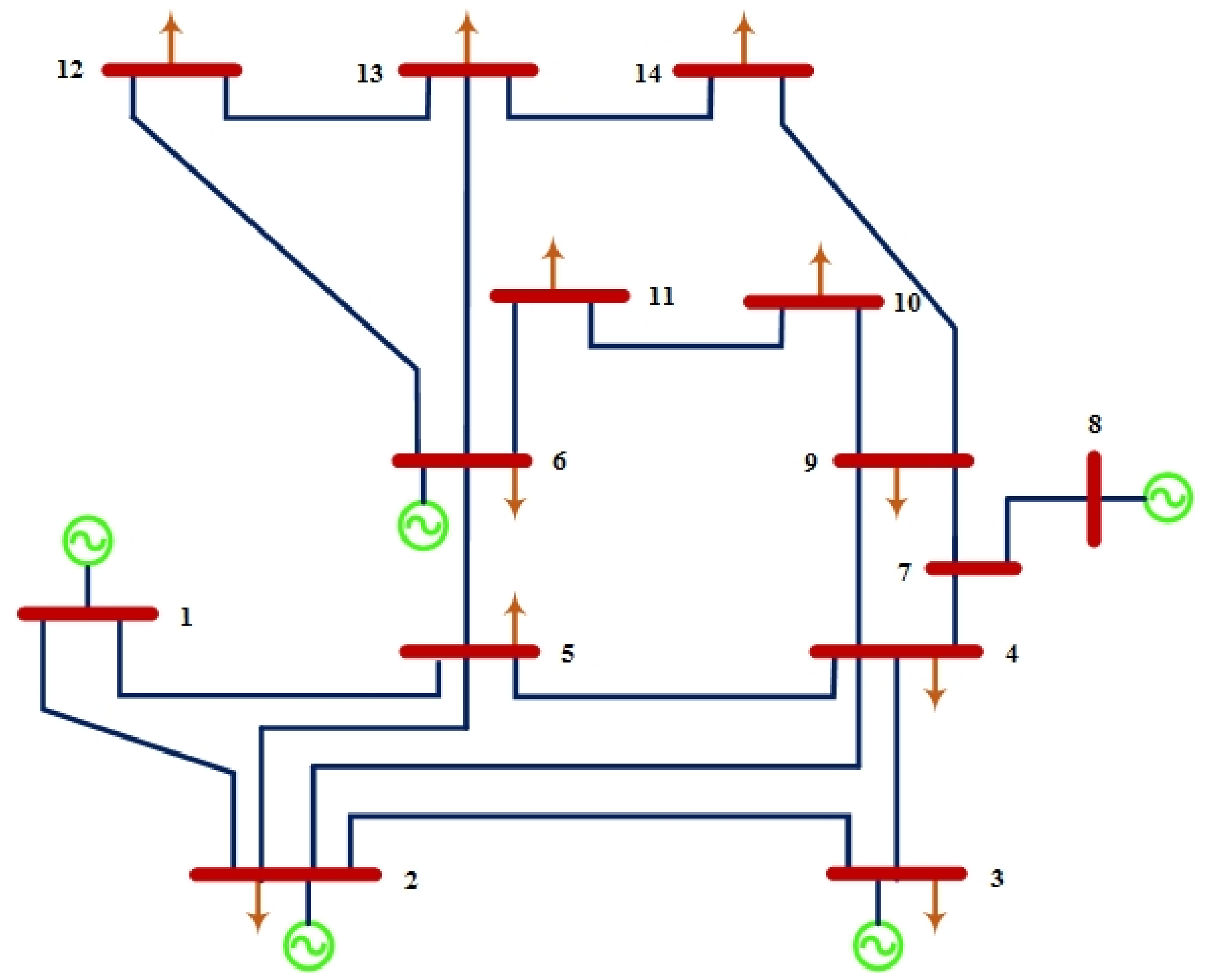
A single-line schematic is shown in Figure 2 based on the IEEE 14-bus standard system [1]. An IEEE type-1 exciter is included in three of its five synchronous machines, which are synchronous compensators used solely for reactive power support. There are eleven loads in the system, totaling 259 MW and 81.3 MVAR.

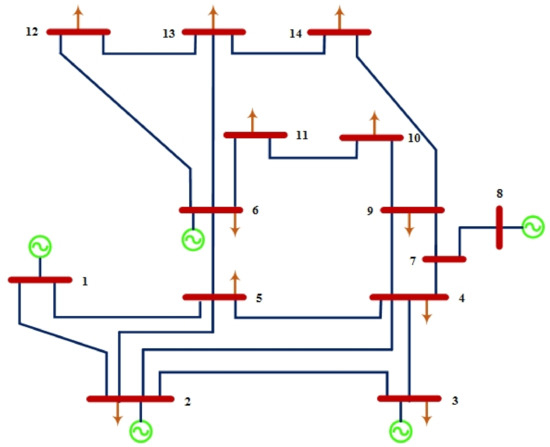
Figure 2. Standard IEEE 14-bus.

• Case 1: Fuel Cost Minimization

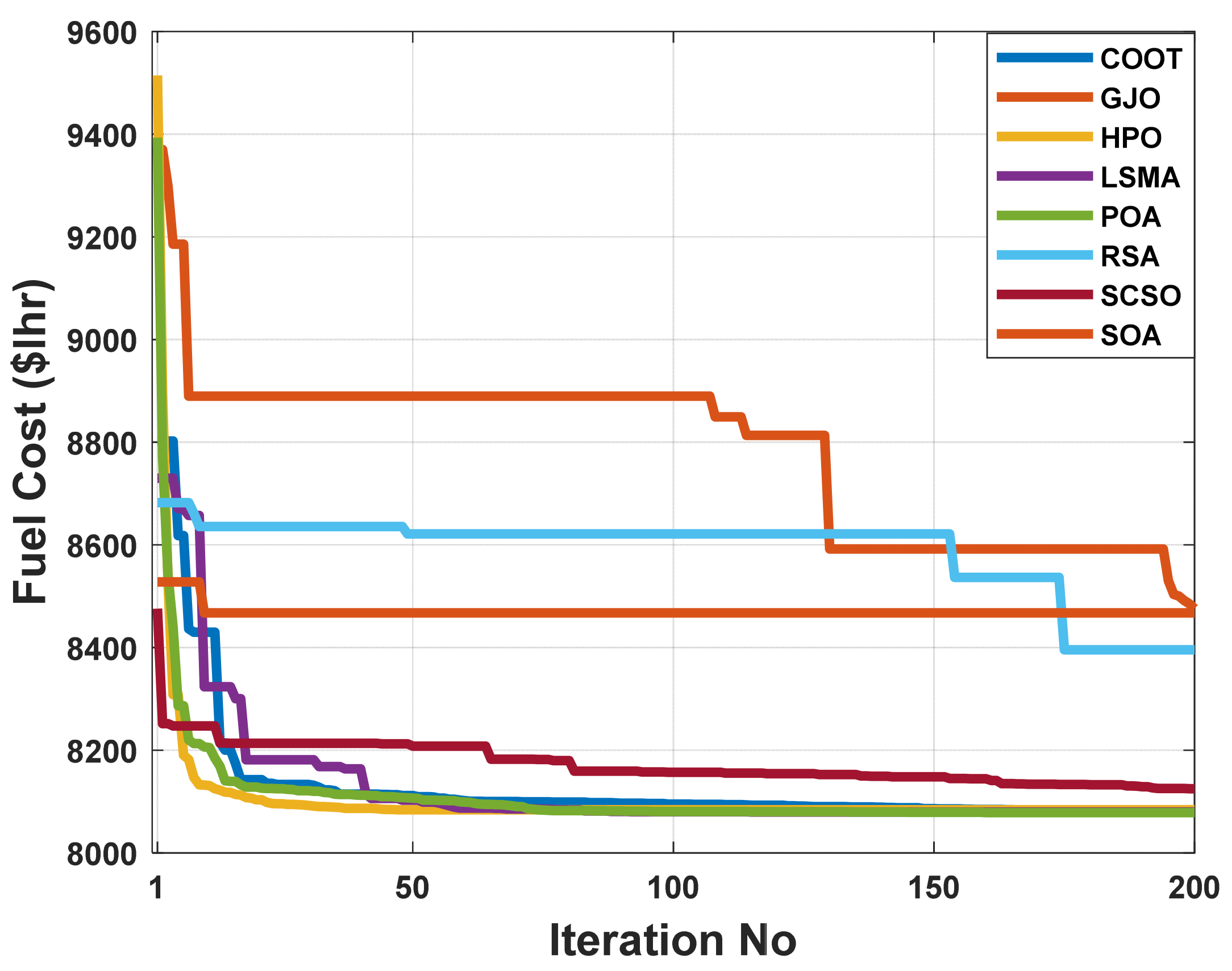
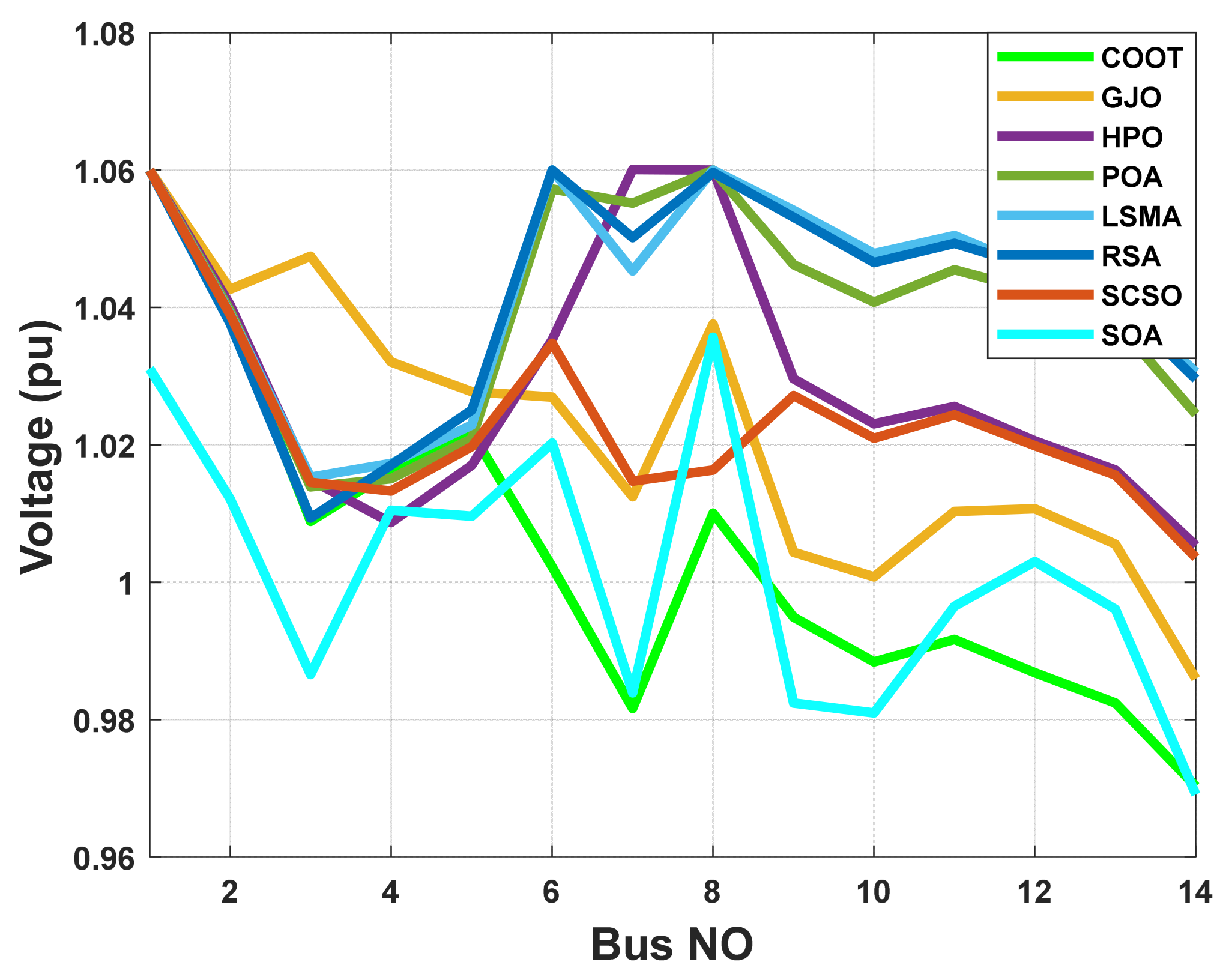
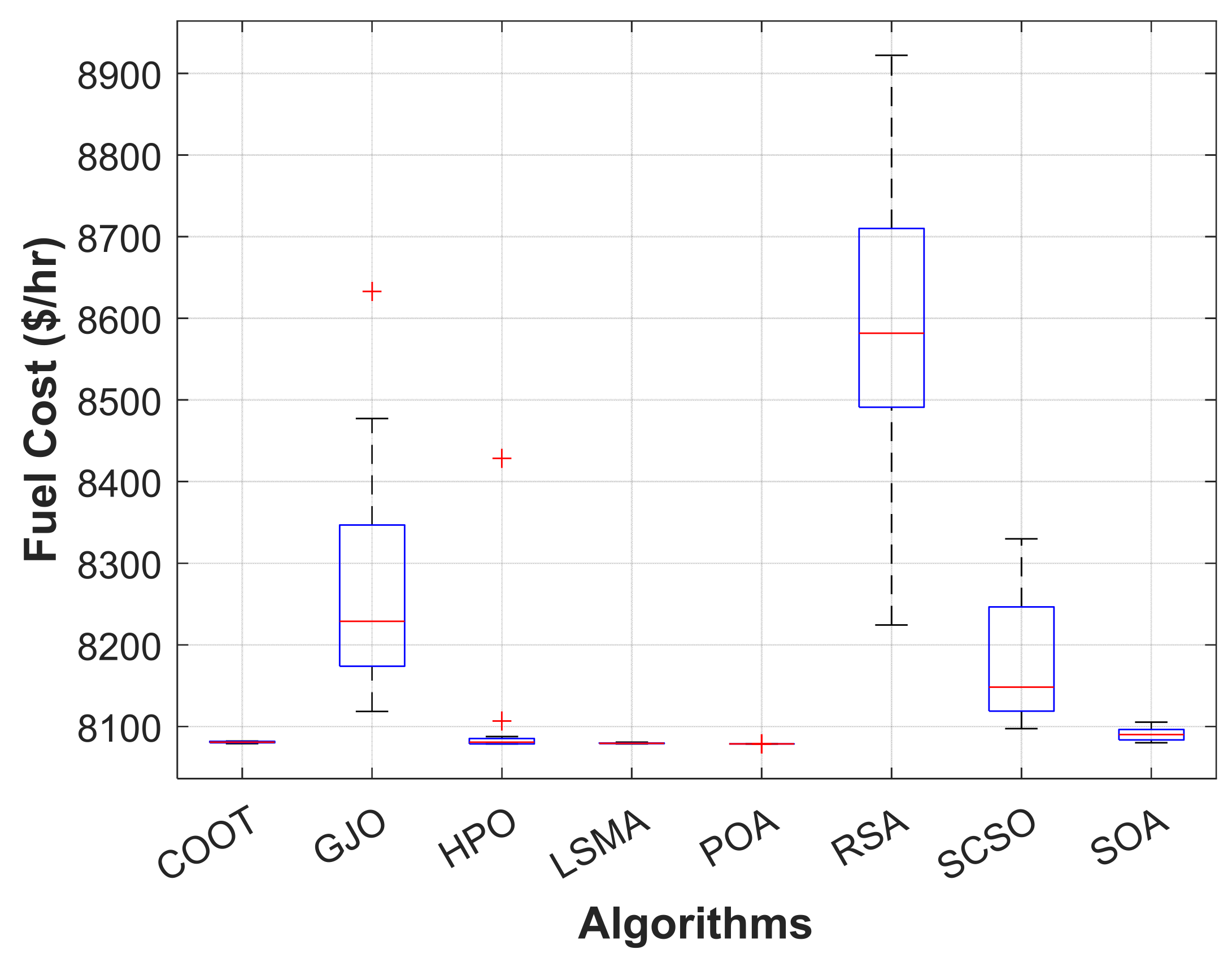
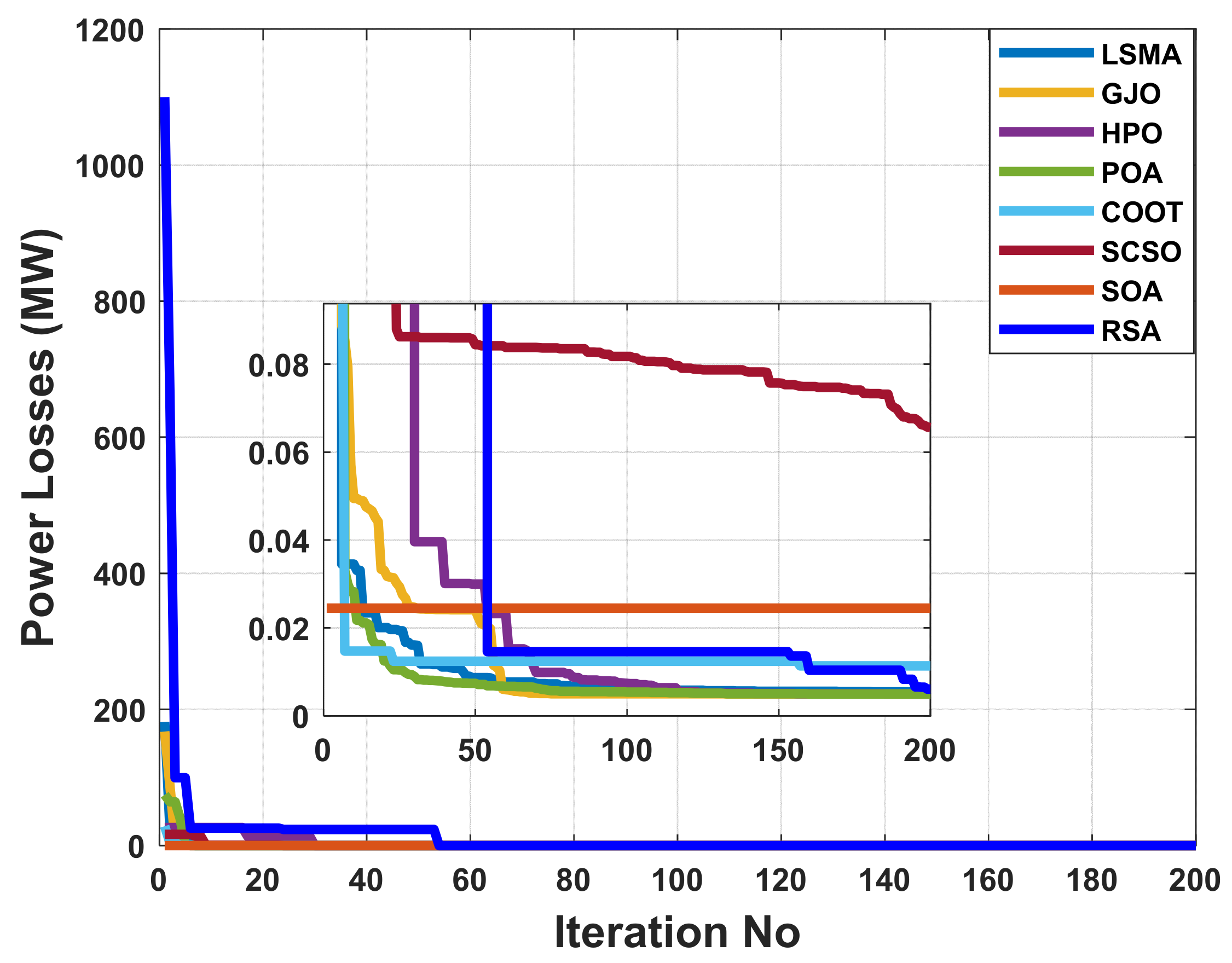
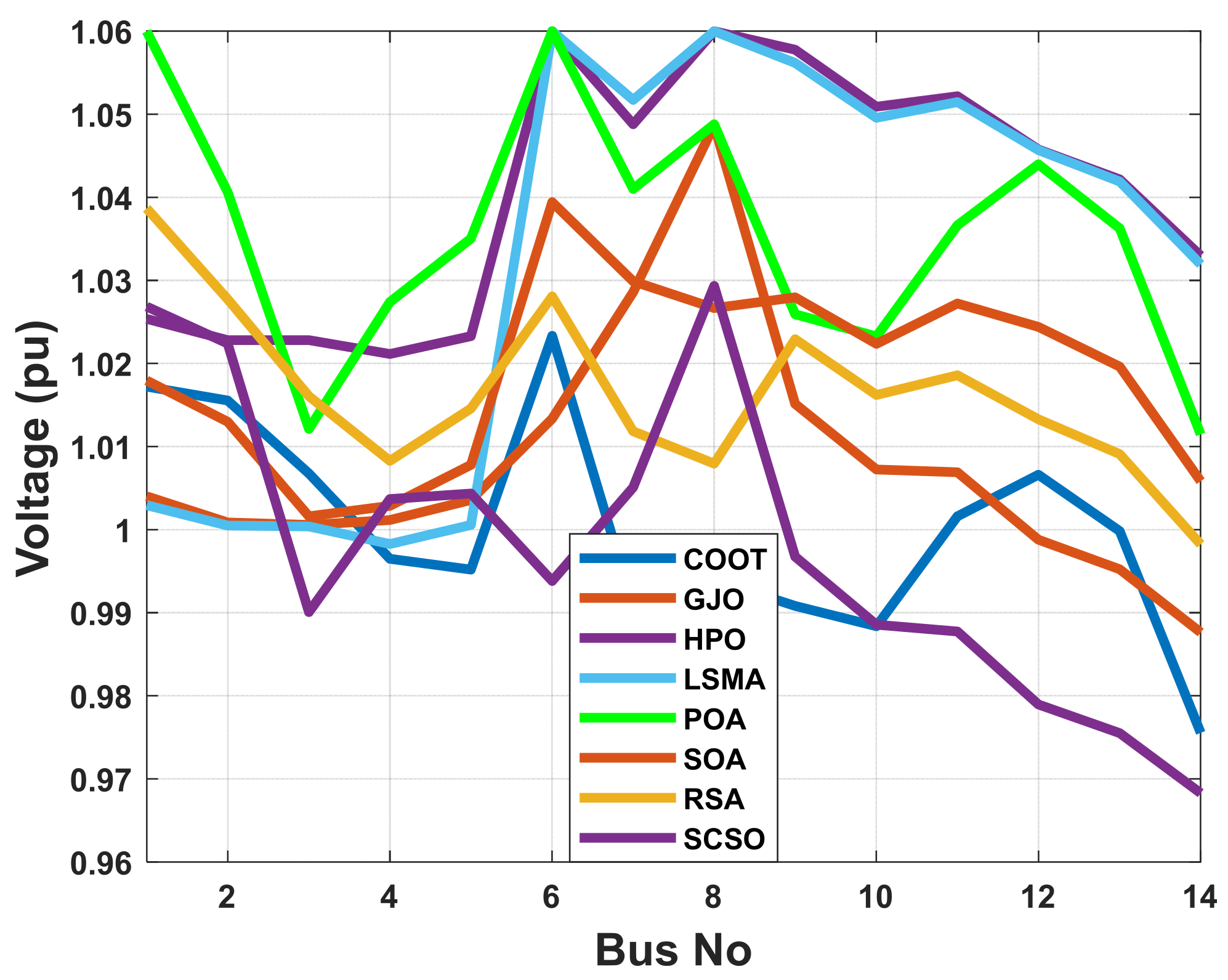
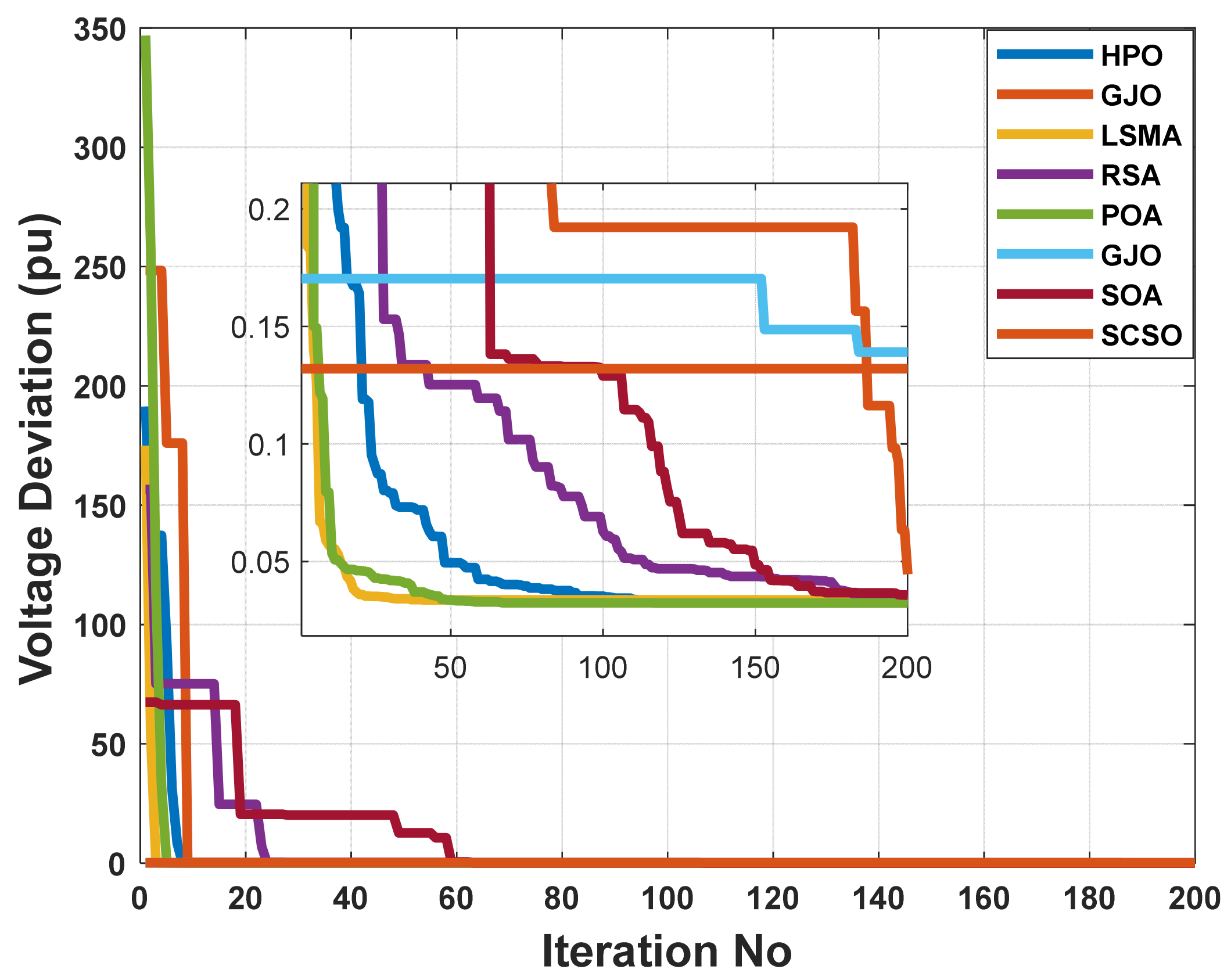
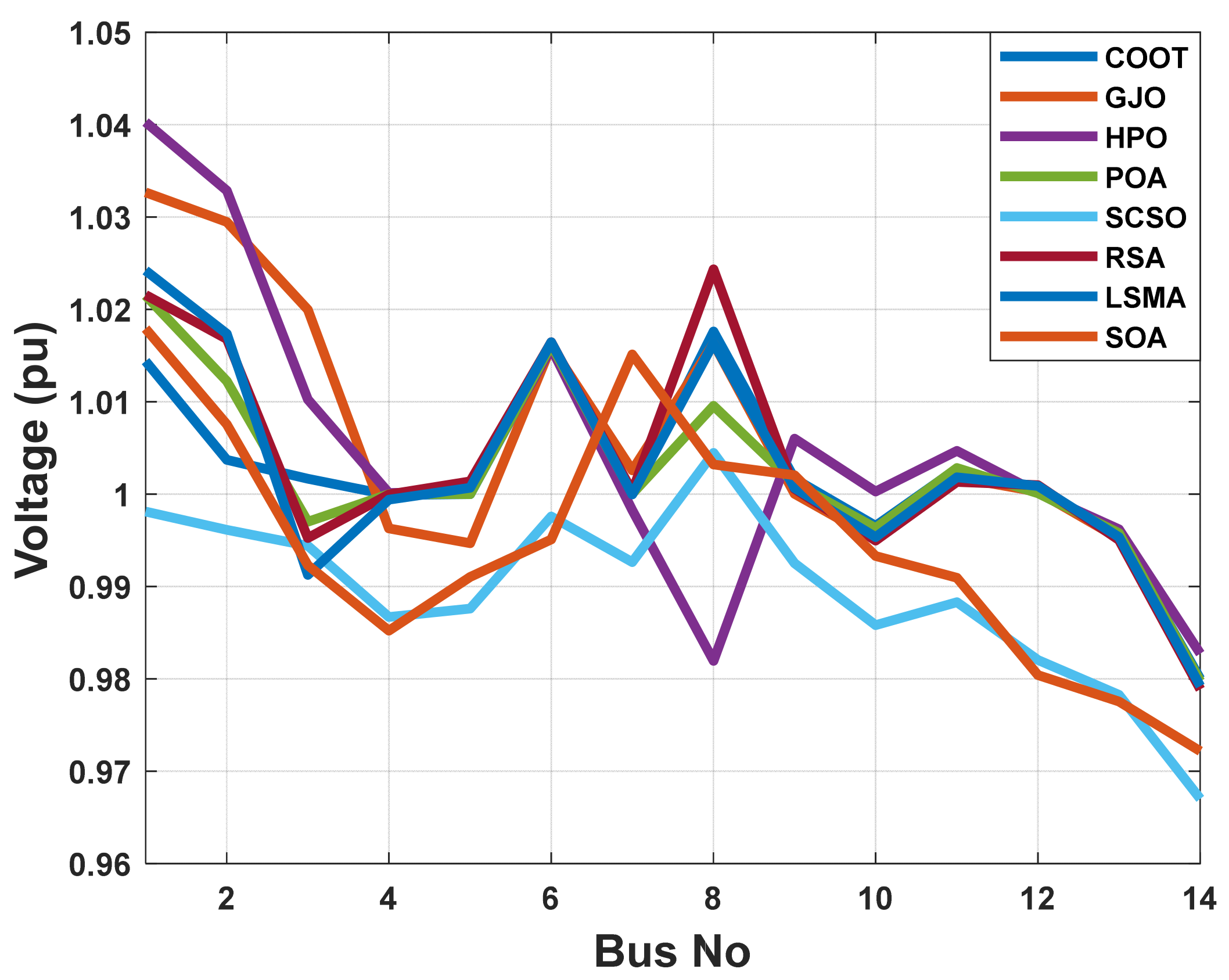
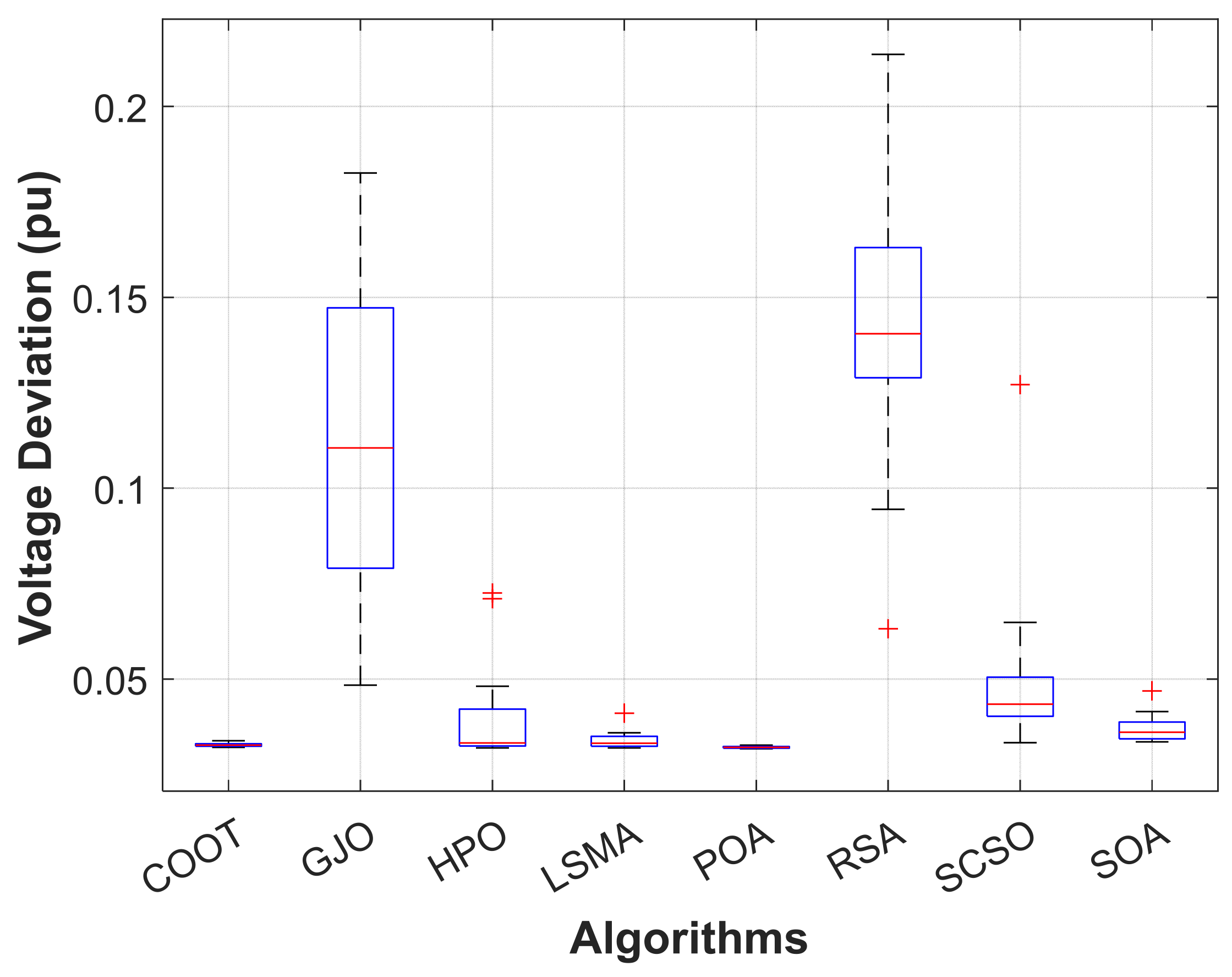
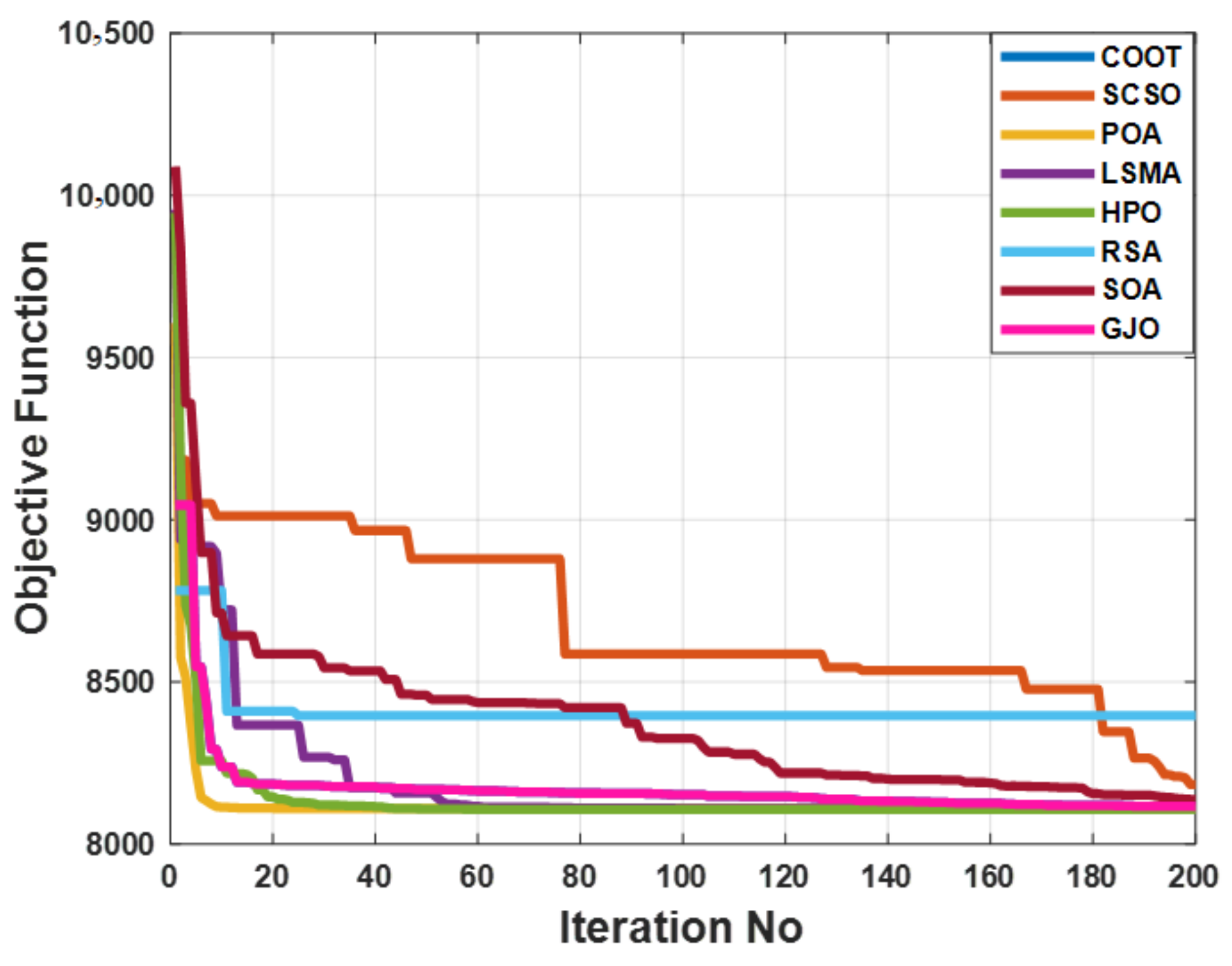
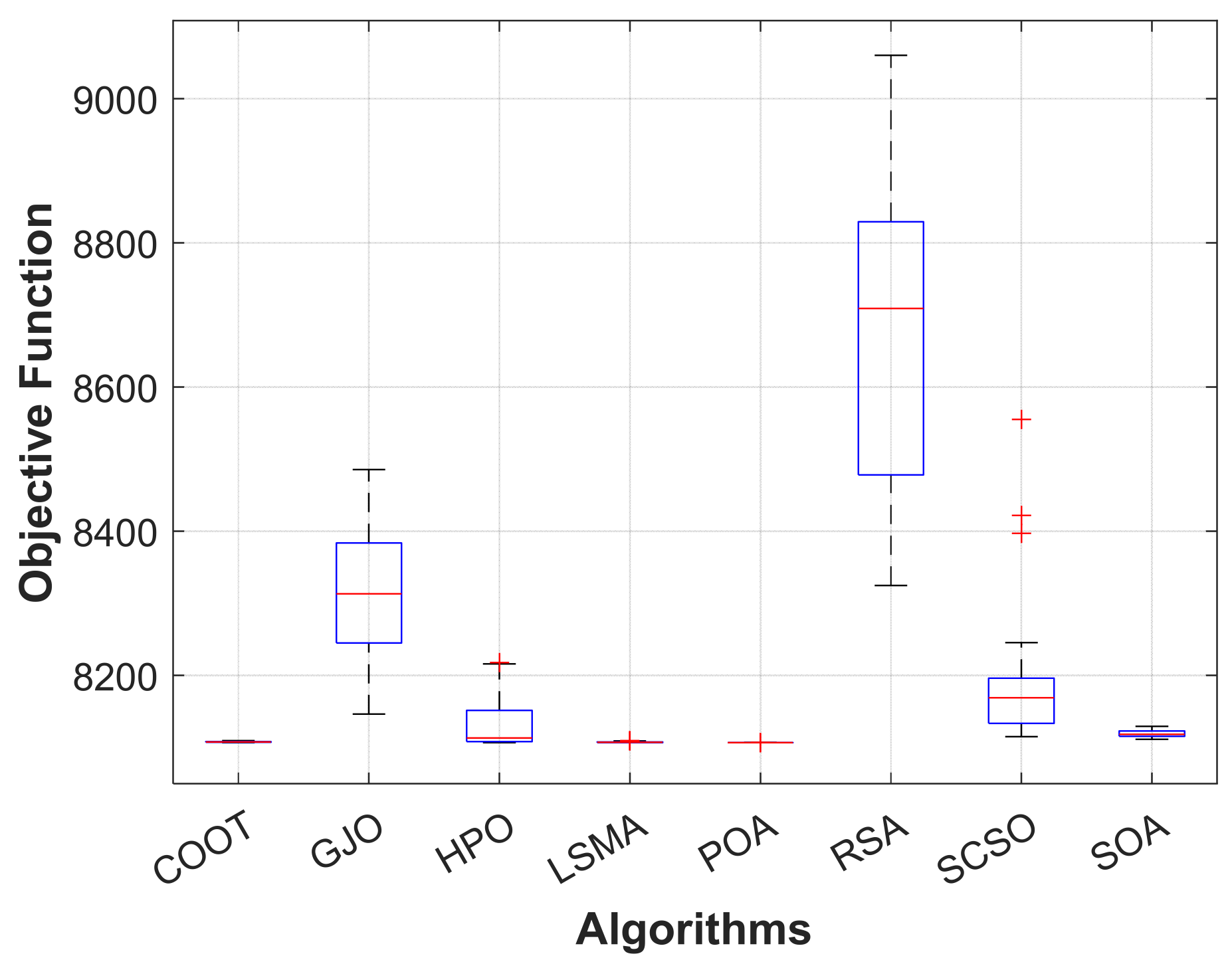
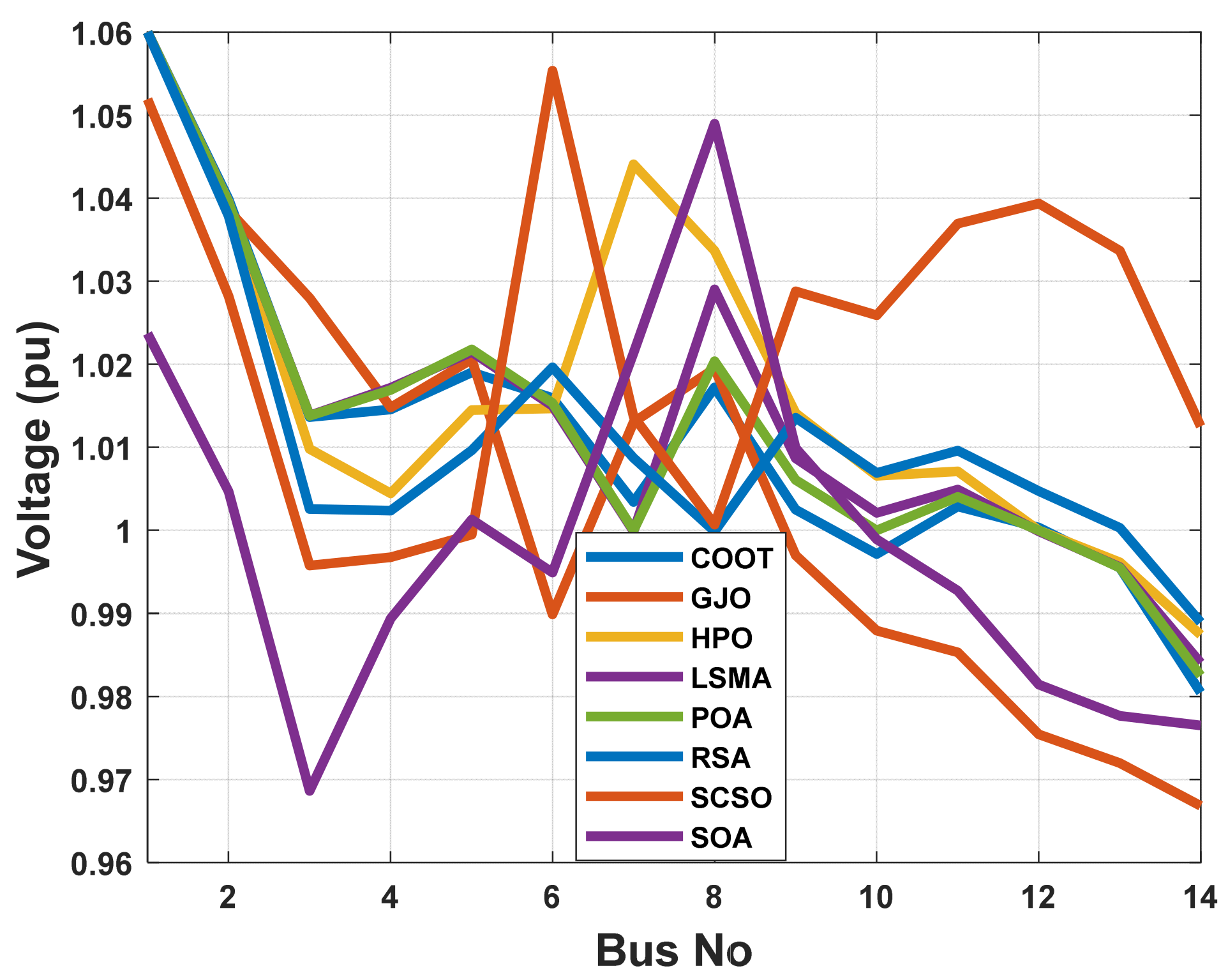
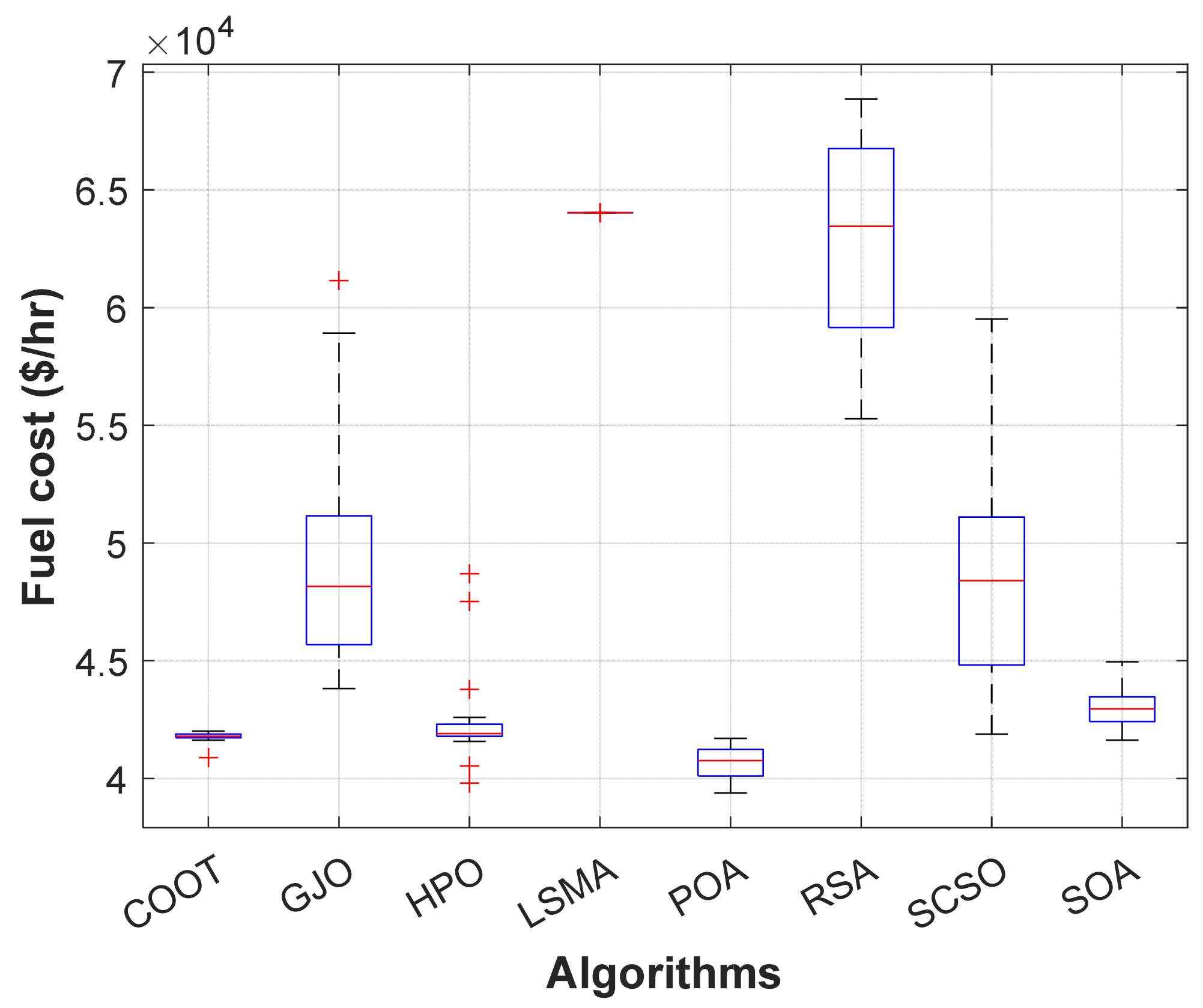
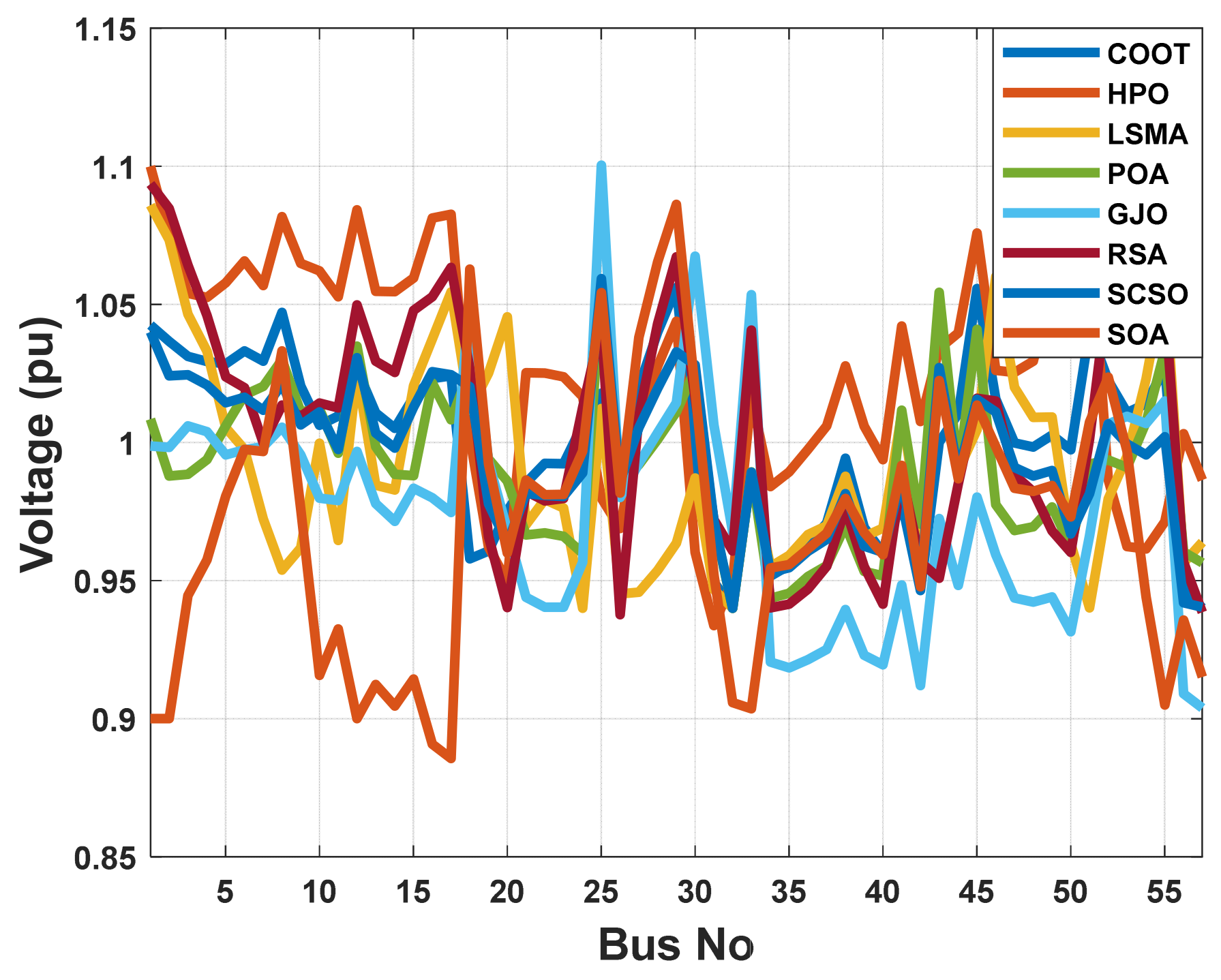
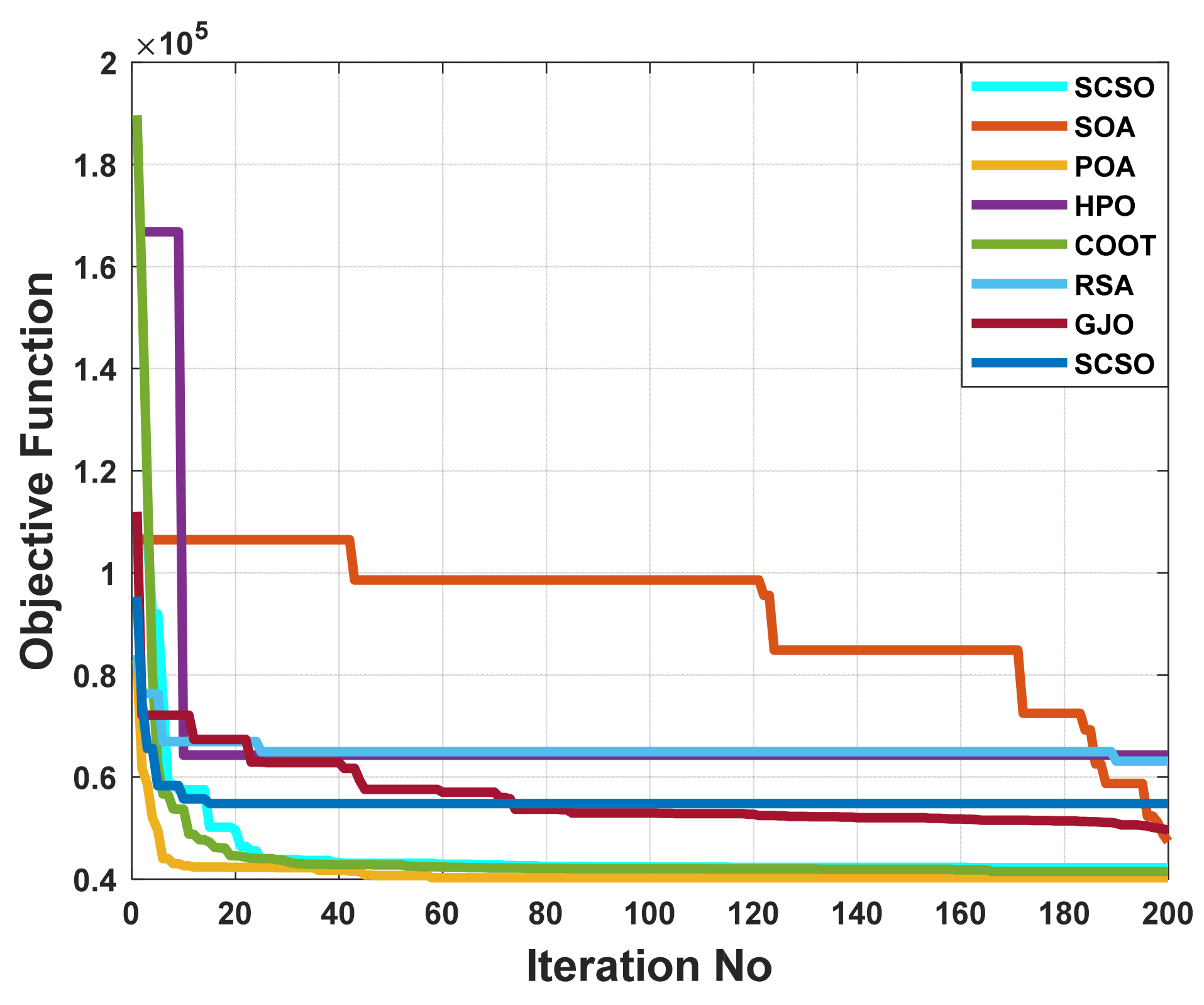
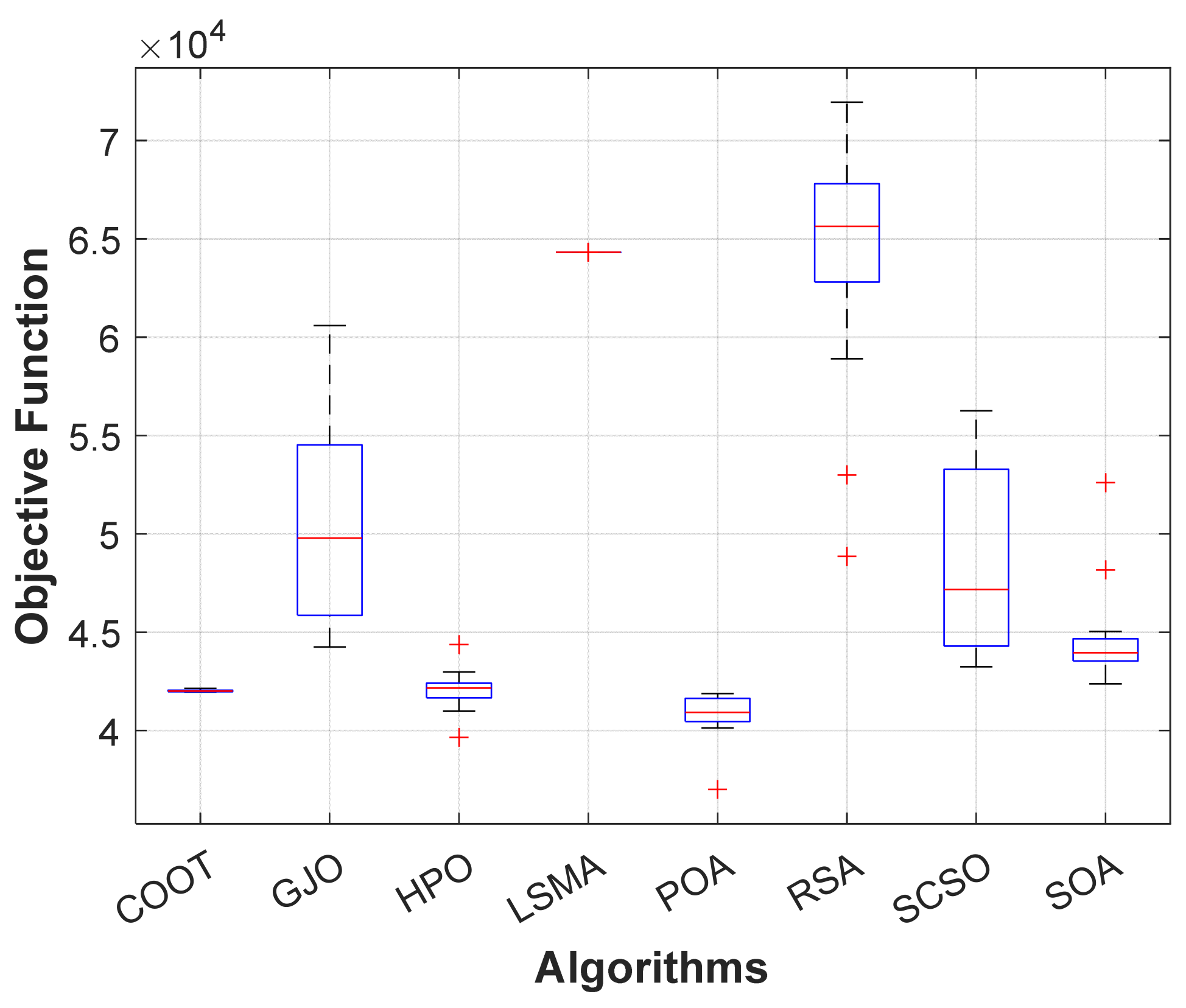
When using the POA algorithm, fuel cost reduction is regarded as the target function. Figure 3 depicts the convergence graph of fuel cost reduction using the POA algorithm. The approach needs 70 iterations to get the optimal solution, demonstrating the remarkable convergence rate of the POA algorithm. Table 2 lists the optimal cost-minimization values and the appropriate changes to the design variables. When the POA algorithm is used, the findings show a considerable reduction in fuel costs to 8078.658 USD/h. Additionally, for this scenario, the average computing time for a single loop is 0.067 s. These outcomes demonstrate how the POA algorithm performs well in terms of solution optimality and quick convergence. To further verify the effectiveness of the POA method, the fuel cost determined using different alternative heuristic optimization techniques is compared with it. Table 2 shows how superior the POA algorithm is to earlier methods. Particularly, the majority of acquired solutions using heuristic optimization algorithms are feasible, primarily due to voltage magnitude accepted at all system load buses, as shown in Figure 4. Comparing the proposed POA’s boxplots to those of other methods, it can be noted that they are extremely tight for reducing fuel costs, with the lowest values as indicated in Figure 5.

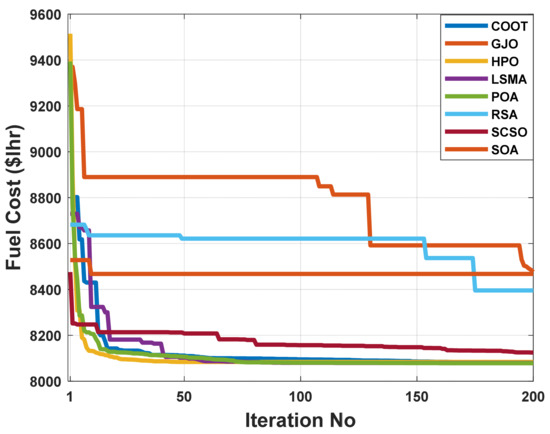
Figure 3. The convergence characteristics of POA and other compared algorithms for case 1 in a standard IEEE 14-bus test system.

Table 2. Optimal control variables for IEEE 14-bus test system for minimizing fuel cost.

Items	COOT	GJO	HPO	LSMA	POA	RSA	SCSO	SOA
${\mathit{P}}_{\mathit{G}\mathbf{1}}$(MW)	194.2744	129.678	196.5432	194.734	194.429	128.388	193.96	194.92
${\mathit{P}}_{\mathit{G}\mathbf{2}}$(MW)	36.93928	15.96422	37.12171	36.74314	36.7	38.36	32.55	34.19
${\mathit{P}}_{\mathit{G}\mathbf{3}}$(MW)	28.84738	80.16223	34.55253	27.80827	28.9	43.78	3.764	21.99
${\mathit{P}}_{\mathit{G}\mathbf{6}}$(MW)	0.043025	2.255178	0.244163	0.037901	1.23 × 10−06	51.83	31.49	2.682
${\mathit{P}}_{\mathit{G}\mathbf{8}}$(MW)	8.193937	35.06381	4.71 × 10−22	8.957517	8.09	2.441	7.236	14.53
${\mathit{V}}_{\mathbf{1}}$(pu)	1.06	1.06	1.06	1.06	1.06	1.030	1.06	1.06
${\mathit{V}}_{\mathbf{2}}$(pu)	1.039008	1.042636	1.040393	1.039566	1.03	1.007	1.037	1.03
${\mathit{V}}_{\mathbf{3}}$(pu)	1.008855	1.047458	1.014896	1.013919	1.01	0.995	1.009	1.01
${\mathit{V}}_{\mathbf{6}}$(pu)	1.002211	1.02698	1.035305	1.057227	1.05	0.983	1.06	1.03
${\mathit{V}}_{\mathbf{8}}$(pu)	1.010036	1.037573	1.06	1.059998	1.06	0.997	1.059	1.01
${\mathit{T}}_{\mathbf{8}}$(4–7)	1.09827	1.030069	0.9	0.949798	1.00	1.0481	0.983101	1.02
${\mathit{T}}_{\mathbf{9}}$(4–9)	0.918073	1.065814	1.1	0.990355	0.9	0.9944	0.907155	0.90
${\mathit{T}}_{\mathbf{10}}$(5–6)	1.025153	0.952079	0.990377	0.968266	0.97	1.0134	0.974561	0.98
${\mathit{Q}}_{\mathbf{14}}$(MVAR)	1.644 × 10−15	9.176 × 10−15	2.338 × 10−15	9.562 × 10−15	4.10 × 10−15	2.220 × 10−14	4.862 × 10−15	2.35 × 10−15
Fuel Cost (USD/h)	8081.805	8476.019	8083.802	8079.477	8078.658	8380.422	8124.842	8085.33
Power Losses (MW)	9.298071	4.123752	9.461673	9.281052	9.223268	5.803744	10.0213	9.33603
Voltage Deviation (pu)	0.141726	0.118	0.206451	0.328433	0.35572	0.277329	0.357644	0.15944
Time (s)	11.65	11.099	11.635	11.7	13.52	10.06	10.99	19

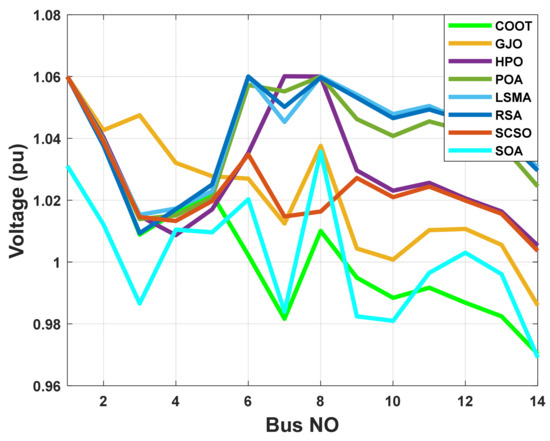
Figure 4. The voltage profile of the POA and other compared algorithms for case 1 in a standard IEEE 14-bus test system.

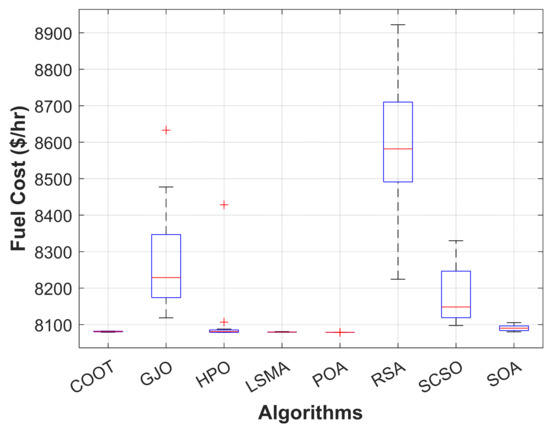
Figure 5. Boxplot of POA and other compared algorithms for case 1 in a standard IEEE 14-bus test system.

• Case 2: Power Losses Minimization

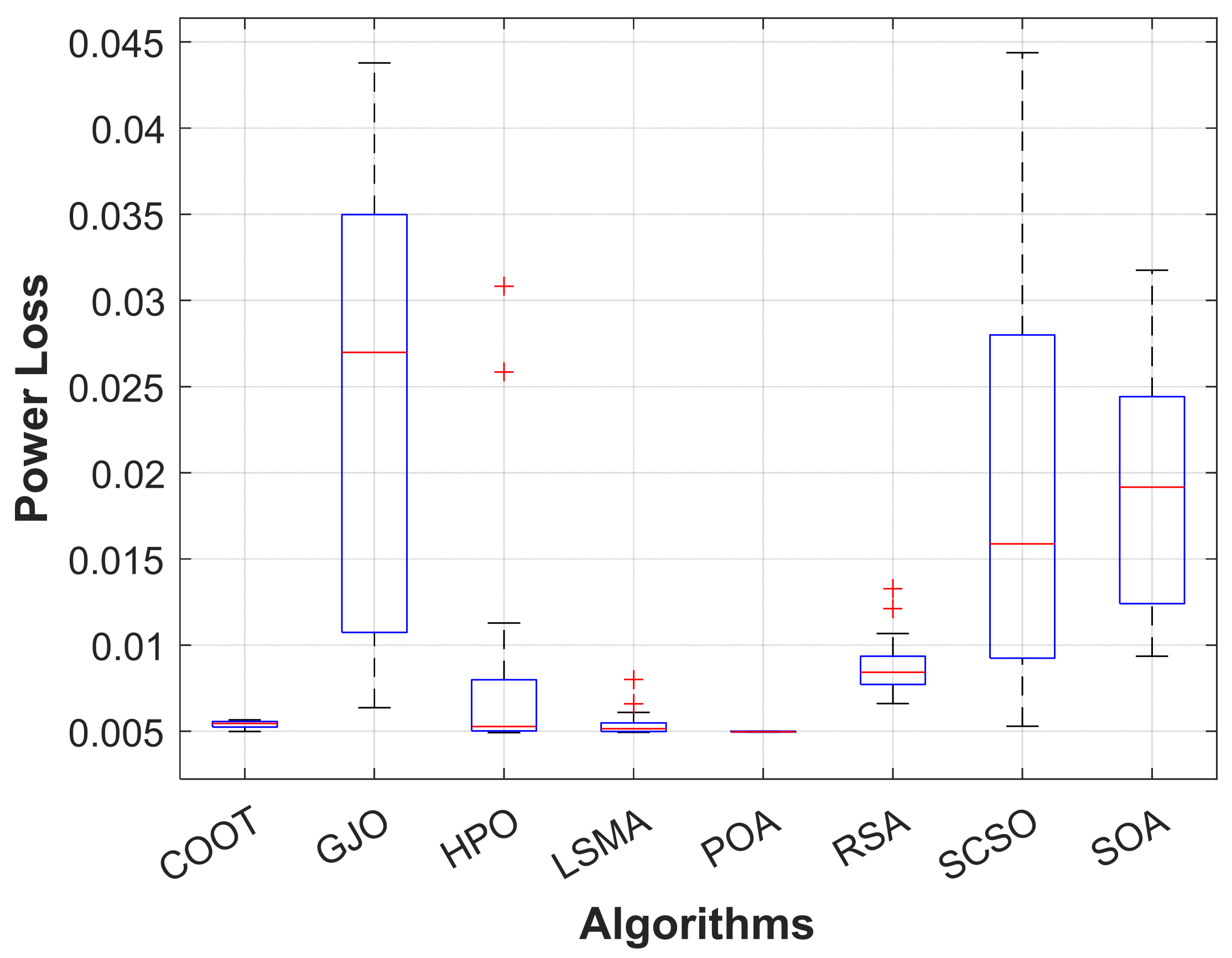
Real power loss was the desired outcome here. The POA algorithm was utilized to arrive at the most efficient solution, the results of which are given in Table 3. The POA algorithm is extremely useful for establishing the precise settings of the control variable, which diminishes system losses. As a result, when the POA algorithm is used, real power losses are reduced to 0.498 MW. In Figure 6, real power losses utilizing the POA method are steeply convergent while taking other comparative techniques into account. Within 50 iterations, the algorithm reaches the optimum solution, demonstrating how rapidly it converges. The evaluated real power loss is compared to that found before using published population-based optimization techniques in order to assess the performance of the approach. Table 3 demonstrates how the POA algorithm outperforms these prior methods. As shown in Figure 7, heuristic optimization algorithms produce feasible results. The reason for this is the magnitude of voltage accepted on all system load buses. Figure 8 shows a boxplot of results for each approach with further analysis to support the performance of the suggested technique.

Table 3. Optimal control variables for the IEEE-14 bus test system for minimizing real power loss.

Items	COOT	GJO	HPO	LSMA	POA	RSA	SCSO	SOA
${\mathit{P}}_{\mathit{G}\mathbf{1}}$(MW)	1.028704	7.30612	0.006377	1.08788	0.209838	5.644483	149.1941	24.4800
${\mathit{P}}_{\mathit{G}\mathbf{2}}$(MW)	21.53073	0	18.91011	24.51901	21.70094	49.14867	2.239793	72.77672
${\mathit{P}}_{\mathit{G}\mathbf{3}}$(MW)	94.78993	97.16583	94.3017	94.85178	94.53314	82.37025	25.19207	57.78994
${\mathit{P}}_{\mathit{G}\mathbf{6}}$(MW)	45.78516	59.43502	46.27993	44.64214	46.79586	63.20229	77.6015	43.74909
${\mathit{P}}_{\mathit{G}\mathbf{8}}$(MW)	96.40808	95.69824	100	94.39515	96.2584	59.77316	11.33366	61.70674
${\mathit{V}}_{\mathbf{1}}$(pu)	1.004006	1.057386	1.025368	1.05901	1.002925	0.995467	1.06	1.017939
${\mathit{V}}_{\mathbf{2}}$(pu)	1.000842	1.053487	1.022796	1.056491	1.000486	0.988651	1.040647	1.012964
${\mathit{V}}_{\mathbf{3}}$(pu)	1.000543	1.06	1.022816	1.056017	1.000374	0.999657	1.012128	1.001584
${\mathit{V}}_{\mathbf{6}}$(pu)	1.013361	1.056341	1.06	1.059655	1.06	0.979288	1.06	1.039418
${\mathit{V}}_{\mathbf{8}}$(pu)	1.04868	1.037111	1.06	1.059991	1.06	0.978301	1.048782	1.026664
${\mathit{T}}_{\mathbf{8}}$(4–7)	0.951231	1.053539	0.980815	1.027193	0.946883	0.988243	0.968271	0.958376
${\mathit{T}}_{\mathbf{9}}$(4–9)	1.002595	0.9	0.9	0.911704	0.900002	0.999006	1.033692	0.952294
${\mathit{T}}_{\mathbf{10}}$(5–6)	1.001186	0.979693	0.968031	0.995208	0.946987	0.995788	0.975498	0.977932
${\mathit{Q}}_{\mathbf{14}}$(MVAR)	1.39 × 10−14	1.92 × 10−14	1.767 × 10−15	2.447 × 10−15	7.37 × 10−20	2.22 × 10−14	1.53 × 10−14	1.12 × 10−14
Fuel Cost (USD/h)	10250.21	10461.7	10301.34	10217.05	10263.37	10058.48	8620.656	9915.479
Power Losses (MW)	0.542603	0.605205	0.498118	0.495957	0.49818	1.138851	6.561136	1.502544
Voltage Deviation (pu)	0.080938	0.358553	0.37494	0.439738	0.330684	0.302505	0.280935	0.167852
Time (s)	9.89	11.2237	12.35	10.78	12.7	10.59	11.994	22.42

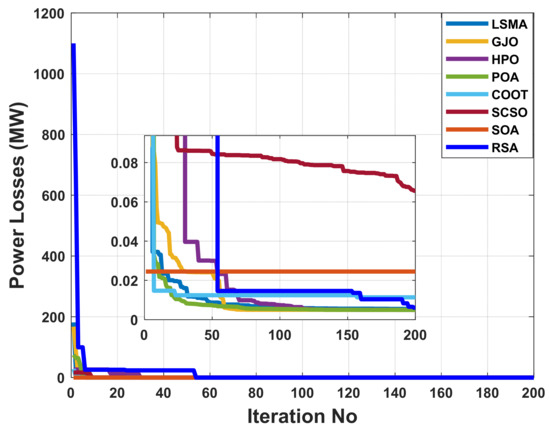
Figure 6. The convergence characteristics of POA and other compared algorithms for case 2 in a standard IEEE 14-bus test system.

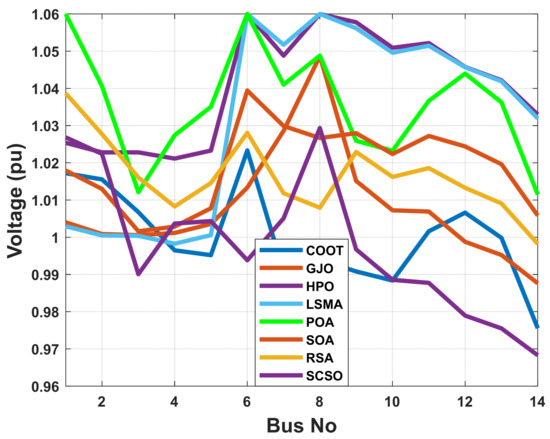
Figure 7. The voltage profile of the POA and other compared algorithms for case 2 in a standard IEEE 14-bus test system.

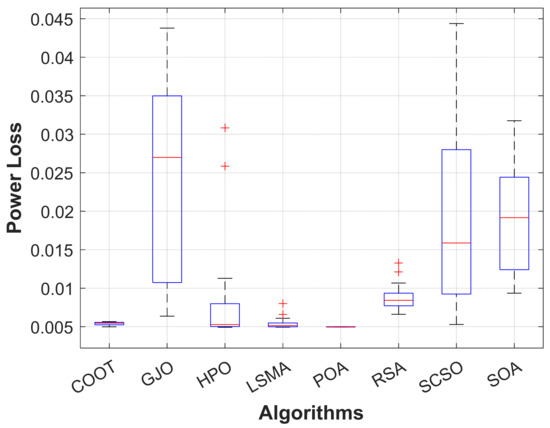
Figure 8. Boxplot of POA and other compared algorithms for case 2 in a standard IEEE 14-bus test system.

• Case 3: Voltage Deviation Minimization

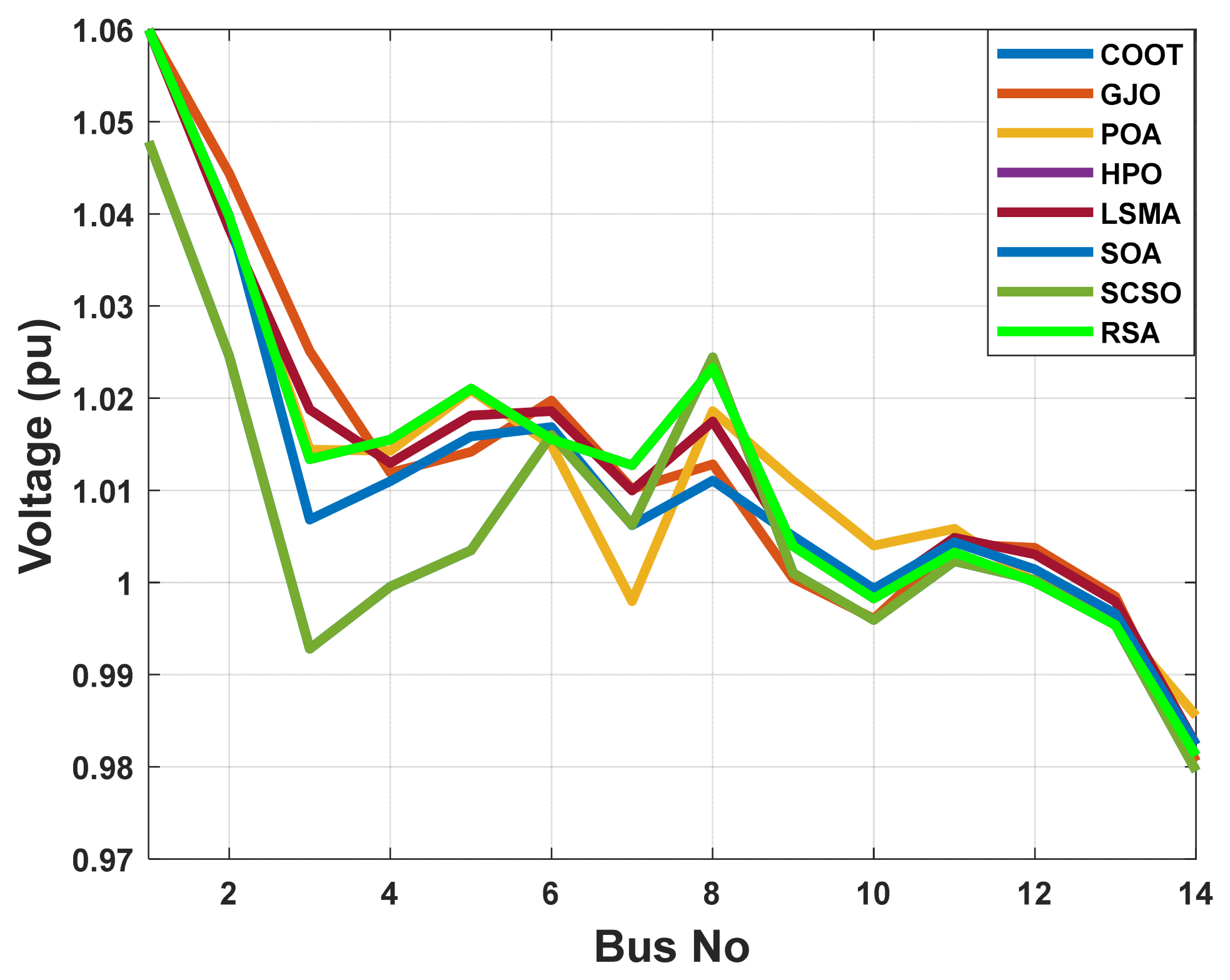
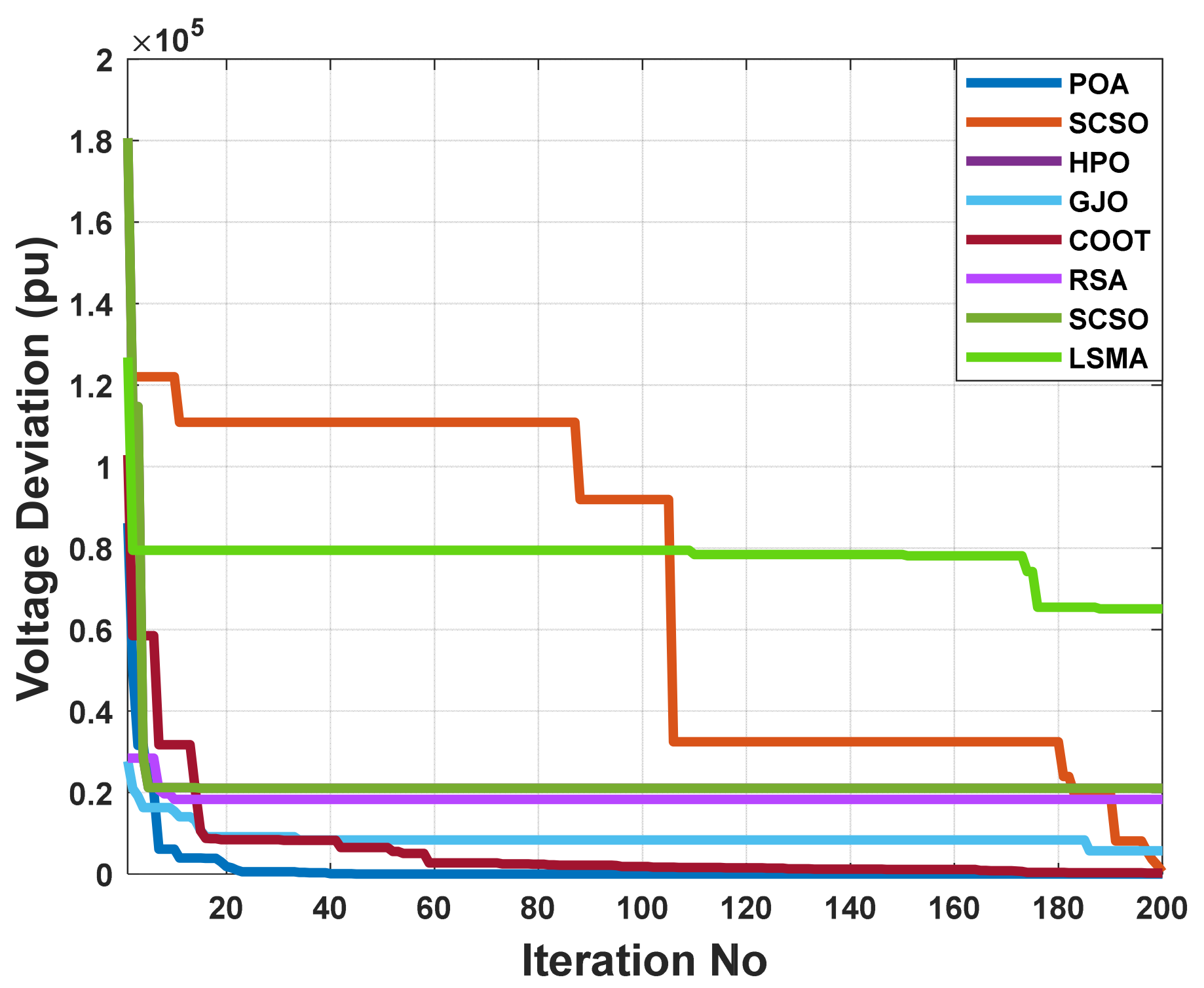
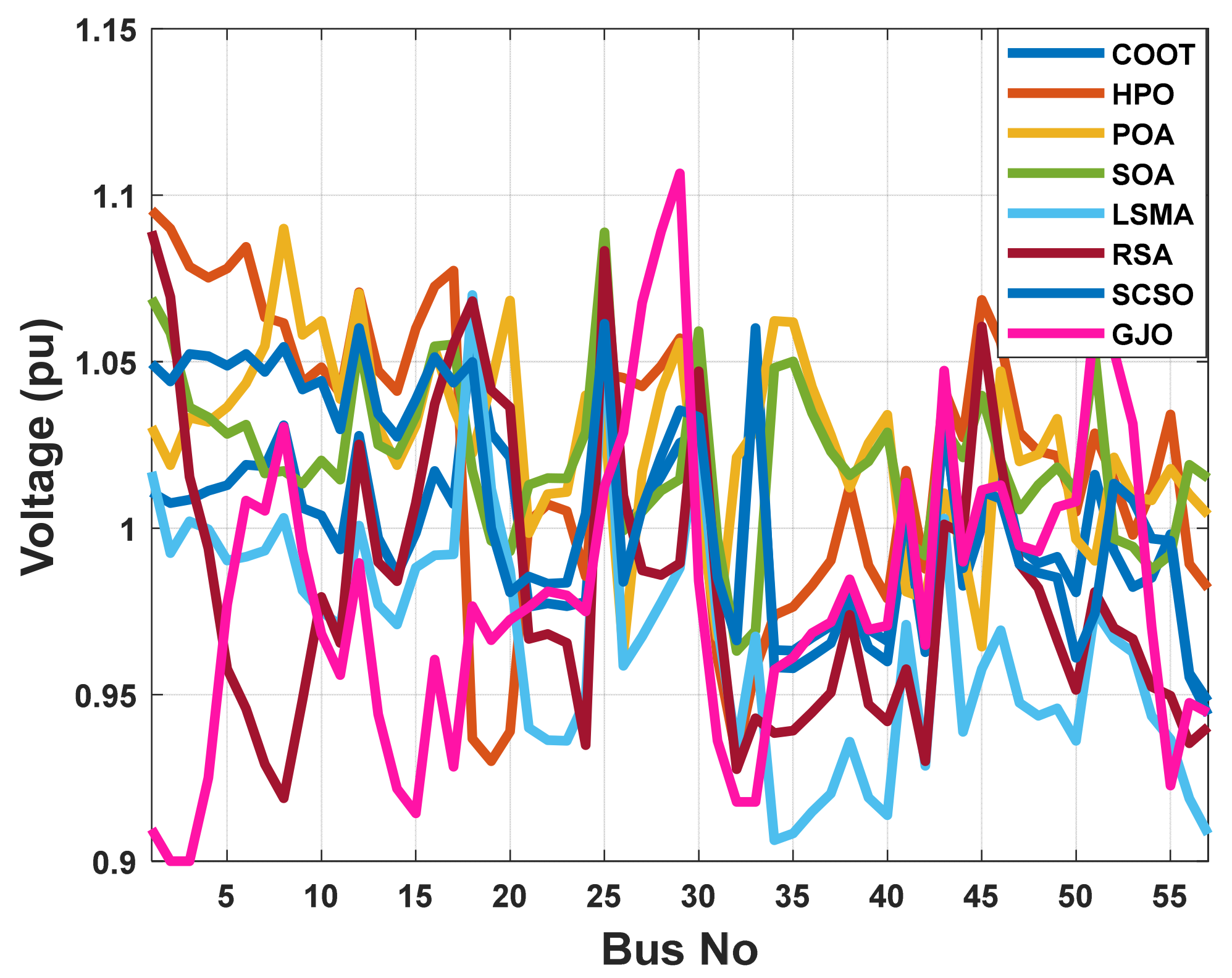
The aim function to be improved using the POA algorithm in this part is decreasing voltage deviation. In Table 4, it is shown that the voltage deviation index is brought down to 0.032 pu by employing the POA algorithm. The POA method significantly outperforms other population-based optimization strategies in Table 4 and Figure 9 when comparing solutions obtained using these methods. Figure 10 illustrates the voltage profiles of all buses using different proposed methods. Figure 11 displays the boxplots for minimizing the voltage deviation with the lowest values by the proposed POA algorithm.

Table 4. Optimal control variables for the IEEE 14-bus test system for minimizing voltage deviation.

Items	COOT	GJO	HPO	LSMA	POA	RSA	SCSO	SOA
${\mathit{P}}_{\mathit{G}\mathbf{1}}$(MW)	56.73424	38.2107	36.84806	78.24469	66.54202	2.165307	15.34358	40.87647
${\mathit{P}}_{\mathit{G}\mathbf{2}}$(MW)	86.90402	140	140	24.61071	40.97941	72.4793	137.0081	105.3721
${\mathit{P}}_{\mathit{G}\mathbf{3}}$(MW)	23.47437	85.04849	34.64746	77.72378	31.34806	100	21.9077	15.24737
${\mathit{P}}_{\mathit{G}\mathbf{6}}$(MW)	24.24789	0.155591	37.42394	8.8394	22.88459	15.44516	58.94462	51.81955
${\mathit{P}}_{\mathit{G}\mathbf{8}}$(MW)	71.11909	0	14.65117	71.89589	99.94992	70.09576	29.79057	49.48359
${\mathit{V}}_{\mathbf{1}}$(pu)	1.014407	1.032659	1.014542	1.040268	1.021496	0.998107	1.021559	1.0242
${\mathit{V}}_{\mathbf{2}}$(pu)	1.003701	1.029464	1.006344	1.032852	1.012234	0.996127	1.016798	1.017348
${\mathit{V}}_{\mathbf{3}}$(pu)	1.001659	1.019954	1.007583	1.010254	0.99702	0.9944	0.995242	0.991246
${\mathit{V}}_{\mathbf{6}}$(pu)	1.01599	1.016016	1.016608	1.015819	1.01616	0.997579	1.016431	1.016443
${\mathit{V}}_{\mathbf{8}}$(pu)	1.017618	1.016309	1.038365	0.981946	1.009543	1.004469	1.02433	1.016361
${\mathit{T}}_{\mathbf{8}}$(4–7)	1.011072	1.002471	1.047192	0.983767	0.987685	0.994753	1.02698	1.013982
${\mathit{T}}_{\mathbf{9}}$(4–9)	0.969511	0.978497	0.948759	0.941214	0.982657	0.96332	0.941012	0.950879
${\mathit{T}}_{\mathbf{10}}$(5–6)	0.973489	0.926223	0.971961	0.921935	0.950704	0.985221	0.950169	0.944359
${\mathit{Q}}_{\mathbf{14}}$(MVAR)	1.122 × 10−15	1.342 × 10−16	1.452 × 10−14	9.856 × 10−15	2.43 × 10−18	2.22 × 10−14	1.78 × 10−15	1.27 × 10−14
Fuel Cost (USD/h)	9714.967	12007.54	11992.44	8923.21	9043.051	10379.56	12224.1	10488.37
Power Losses (MW)	3.479607	4.414777	4.570637	2.314479	2.70401	1.185523	3.994572	3.799099
Voltage Deviation (pu)	0.032572	0.044547	0.033617	0.034367	0.032281	0.13911	0.03566	0.034761
Time (s)	11.17	10.74	11.69	11.06	12.67	10.32	11.67	19.127

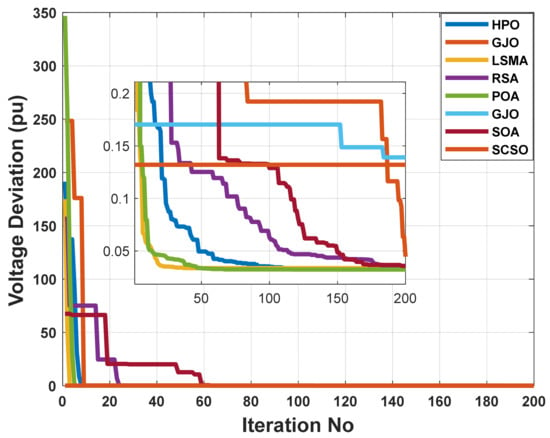
Figure 9. The convergence characteristics of POA and other compared algorithms for case 3 in a standard IEEE 14-bus test system.

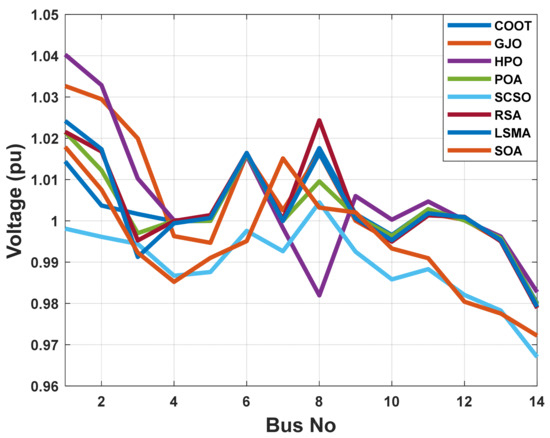
Figure 10. The voltage profile of the POA and other compared algorithms for case 3 in a standard IEEE 14-bus test system.

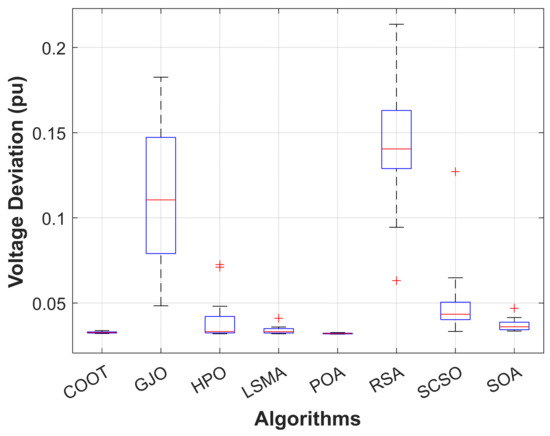
Figure 11. Boxplot of POA and other compared algorithms for case 3 in a standard IEEE 14-bus test system.

• Case 4: Multi-Objective Function without Emissions Minimization

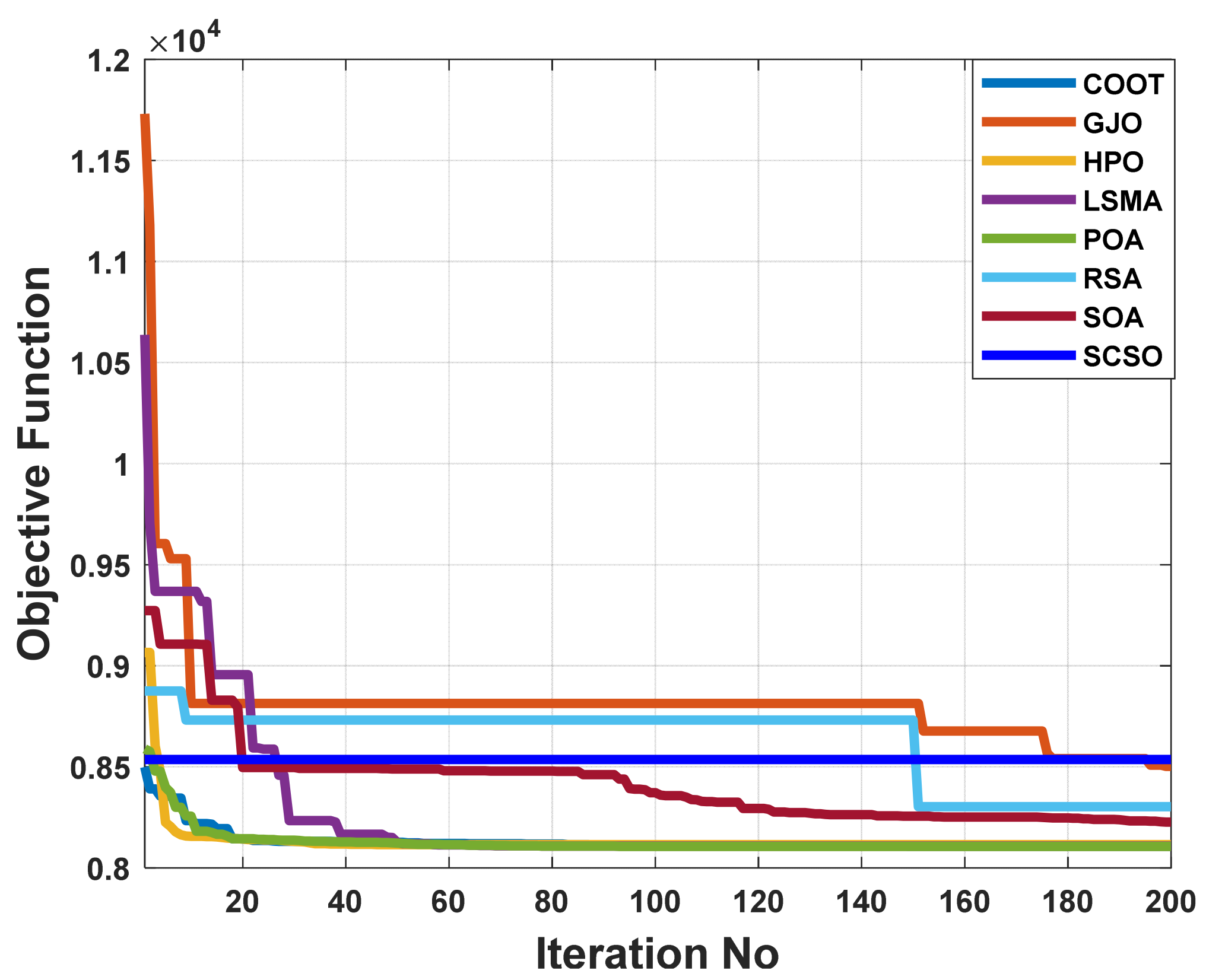
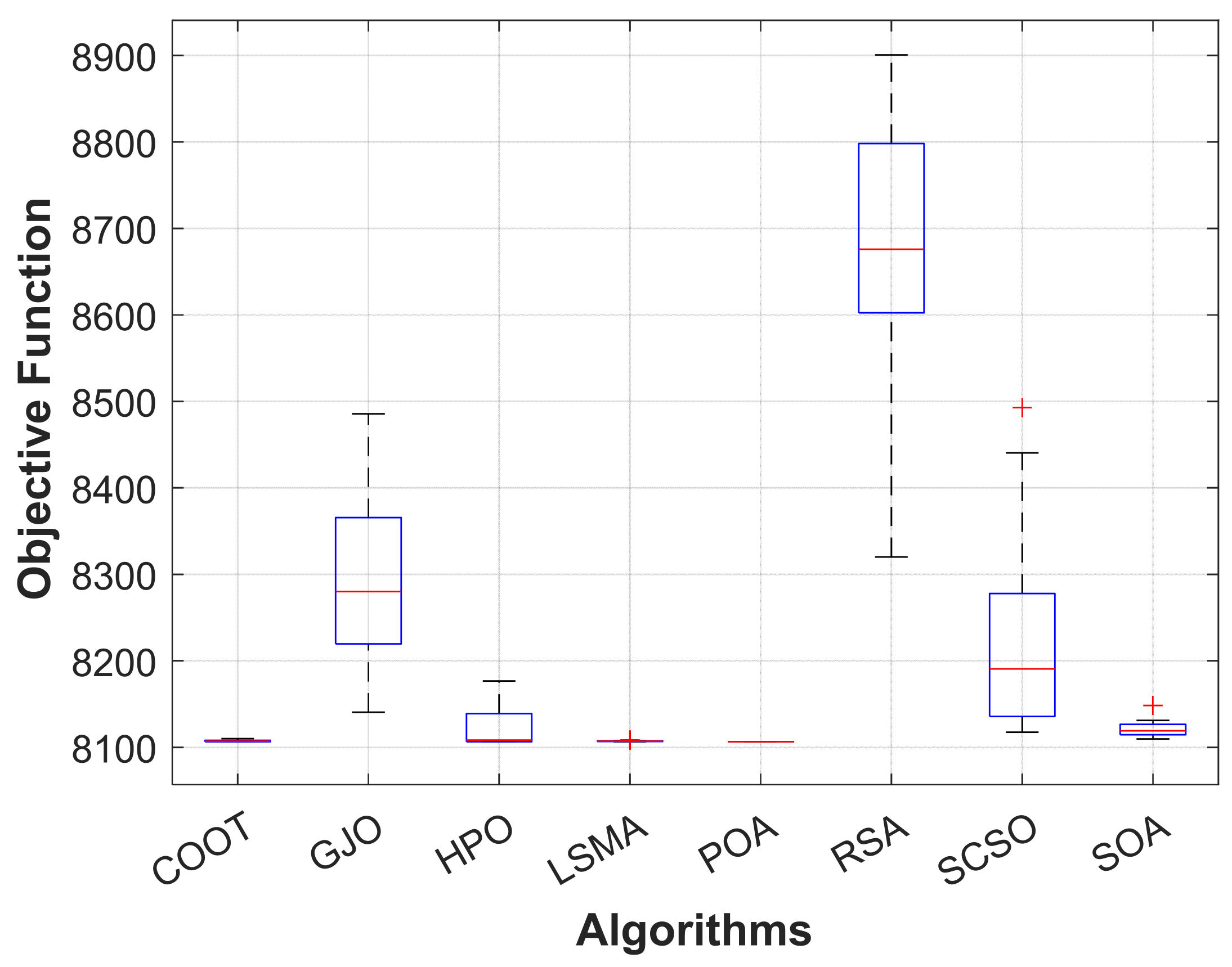
For maximizing the advantages of the suggested test system, a weighted multi-objective function is provided here that incorporates reduction of fuel operational cost, transmission power loss, and voltage-level deviation. Table 5 illustrates how the multi-objective OPF issue was addressed using the POA and taking other comparative algorithms in the IEEE 14-bus system into account. These results indicate that POA is more efficient than other comparable algorithms for solving the multi-objective OF problem. It has been shown that the total cost function 8106.371 USD/h is superior to all other algorithms, which achieved 8115.557 USD/h, 8183.349 USD/h, 8109.171 USD/h, 8107.896 USD/h, 8394.928 USD/h, 8136.388 USD/h, and 8120.729 USD/h, respectively, by COOT, GJO, HPO, LSMA, RSA, SCSO, and SOA. Figure 12 illustrates that, for all comparison methods, the voltage profiles of all buses are within the predetermined limits, as in prior examples. In addition, Figure 13 demonstrates that despite being compared to other algorithms, the POA still exhibits rapid and smooth convergence properties. When compared to previous approaches, it can be shown that the boxplots of the proposed POA are extremely tight for reducing the OF with the lowest values, as illustrated in Figure 14.

Table 5. Optimal control variables for the IEEE 14-bus test system for minimizing multi-objective function without emissions.

Items	COOT	GJO	HPO	LSMA	POA	RSA	SCSO	SOA
${\mathit{P}}_{\mathit{G}\mathbf{1}}$(MW)	192.0215	162.9969	195.4545	193.0184	193.2524	141.194	177.598	191.5900
${\mathit{P}}_{\mathit{G}\mathbf{2}}$(MW)	36.78655	36.59235	37.05394	36.62079	36.64604	48.6672	32.6814	37.37917
${\mathit{P}}_{\mathit{G}\mathbf{3}}$(MW)	27.86653	64.57128	35.81917	29.60956	30.11561	16.17147	47.99072	13.14186
${\mathit{P}}_{\mathit{G}\mathbf{6}}$(MW)	0.132856	0.244825	0	0.000432	0	24.22994	8.506282	9.812656
${\mathit{P}}_{\mathit{G}\mathbf{8}}$(MW)	11.55978	1.464105	0	8.907496	8.150998	35.56969	0	16.5847
${\mathit{V}}_{\mathbf{1}}$(pu)	1.047839	1.06	1.06	1.06	1.06	1.01601	1.06	1.06
${\mathit{V}}_{\mathbf{2}}$(pu)	1.024612	1.044424	1.039532	1.039728	1.039569	1.001019	1.038401	1.039804
${\mathit{V}}_{\mathbf{3}}$(pu)	0.992798	1.025107	1.014412	1.013371	1.013683	0.982475	1.018758	1.006805
${\mathit{V}}_{\mathbf{6}}$(pu)	1.016025	1.019745	1.014881	1.01553	1.015322	0.985291	1.018599	1.016864
${\mathit{V}}_{\mathbf{8}}$(pu)	1.024438	1.012836	1.01861	1.023279	1.01441	0.982821	1.017488	1.011079
${\mathit{T}}_{\mathbf{8}}$(4–7)	1.00257	0.984234	1.066152	0.996172	1.043162	0.960429	0.998169	1.006025
${\mathit{T}}_{\mathbf{9}}$(4–9)	0.996333	1.036421	0.9	1.022018	0.945132	0.998466	1.000417	0.975196
${\mathit{T}}_{\mathbf{10}}$(5–6)	0.972437	0.956601	1.015417	1.007059	1.010104	1.033504	0.988647	0.976105
${\mathit{Q}}_{\mathbf{14}}$(MVAR)	1.250 × 10−14	1.170 × 10−14	0	2.17 × 10−14	2.216 × 10−14	2.220 × 10−14	1.641 × 10−17	6.906 × 10−15
Objective Functions	8115.557	8183.349	8109.171	8107.896	8106.371	8394.928	8136.388	8120.729
Fuel Cost (USD/h)	8092.53	8162.663	8082.842	8081.42	8081.095	8307.168	8113.44	8095.161
Power Losses (MW)	9.367238	6.869502	9.327685	9.156709	9.165079	6.832808	7.776665	9.508475
Voltage Deviation (pu)	0.042924	0.069475	0.076715	0.0816	0.06944	0.21886	0.073951	0.065511
Time (s)	9.84	13.68	11.46	11.11	12.5	10.4	11.26	18.58

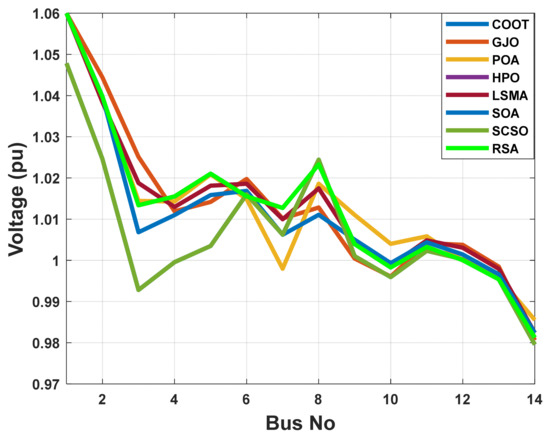
Figure 12. The voltage profile of the POA and other compared algorithms for case 4 in a standard IEEE 14-bus test system.

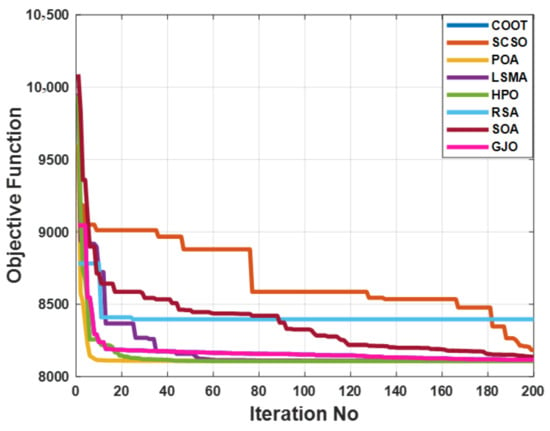
Figure 13. The convergence characteristics of POA and other compared algorithms for case 4 in a standard IEEE 14-bus test system.

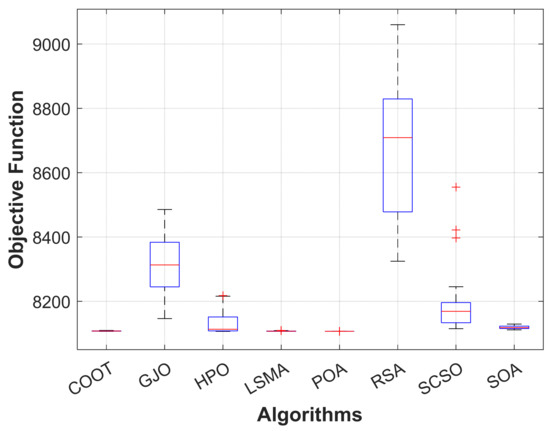
Figure 14. Boxplot of POA and other compared algorithms for case 4 in a standard IEEE 14-bus test system.

• Case 5: Multi-Objective Function with Emissions Minimization

Table 6 displays the most effective outcomes of using the POA algorithm to solve a multi-objective OPF problem while taking emissions for the IEEE 14-bus testing system into account. The POA outperforms other comparable algorithms, as indicated in this table. Additionally, the POA provides 8106.437 USD/h compared to 8107.453 USD/h, 8502.7213 USD/h, 8114.69152 USD/h, 8107.0404 USD/h, 8303.238 USD/h, 8225.998 USD/h, and 8126.254 USD/h by the COOT, GJO, HPO, LSMA, RSA, SCSO, and SOA, respectively. Figure 15 shows the voltage profile for each bus, and it can be seen that all values are within the set ranges. Additionally, Figure 16 displays the convergence characteristics for this example acquired by POA and other algorithms. As can be seen, POA surpasses all other algorithms due to its rapid speed convergence. As illustrated in Figure 17, the boxplots of the proposed POA are extremely narrow as compared to previous strategies for reducing the OF with the lowest values.

Table 6. Optimal control variables for the IEEE 14-bus test system for minimizing multi-objective function with emissions.

Items	COOT	GJO	HPO	LSMA	POA	RSA	SCSO	SOA
${\mathit{P}}_{\mathit{G}\mathbf{1}}$(MW)	193.5845	180.49407	193.33818	193.59468	193.2785	145.7119	170.8183	189.4911
${\mathit{P}}_{\mathit{G}\mathbf{2}}$(MW)	36.72527	0	36.64361	36.4865	36.64462	37.25915	18.91234	31.0333
${\mathit{P}}_{\mathit{G}\mathbf{3}}$(MW)	31.24205	69.69709	30.29847	32.23486	30.11637	60.74761	46.6554	26.13053
${\mathit{P}}_{\mathit{G}\mathbf{6}}$(MW)	0.001082	5.720682	0	2.51 × 10−9	0	16.45116	6.012253	9.001716
${\mathit{P}}_{\mathit{G}\mathbf{8}}$(MW)	6.656068	9.862208	7.997534	5.848945	8.125942	5.174346	23.28307	12.27411
${\mathit{V}}_{\mathbf{1}}$(pu)	1.059998	1.06	1.06	1.06	1.06	1.016093	1.06	1.06
${\mathit{V}}_{\mathbf{2}}$(pu)	1.039893	1.038542	1.039565	1.039456	1.039491	0.991845	1.040546	1.037875
${\mathit{V}}_{\mathbf{3}}$(pu)	1.013661	1.028002	1.009789	1.013851	1.013812	0.991781	1.020862	1.002555
${\mathit{V}}_{\mathbf{6}}$(pu)	1.015953	0.989869	1.014682	1.014984	1.015319	0.986511	1.014955	1.019656
${\mathit{V}}_{\mathbf{8}}$(pu)	1.01721	1.019496	1.033687	1.029013	1.020388	1.001773	1.009211	0.999885
${\mathit{T}}_{\mathbf{8}}$(4–7)	1.02359	0.977262	0.9	1.069538	1.051967	1.066974	1.017782	0.990329
${\mathit{T}}_{\mathbf{9}}$(4–9)	0.984422	1.027489	1.099999	0.927031	0.945896	0.987889	0.961107	0.924403
${\mathit{T}}_{\mathbf{10}}$(5–6)	0.993893	1.025831	1.010783	1.002535	1.006555	0.9909	0.979511	0.969252
${\mathit{Q}}_{\mathbf{14}}$(MVAR)	2.021 × 10−14	1.5587 × 10−16	1.55978 × 10−14	7.3102 × 10−16	0	2.220 × 10−14	5.927 × 10−15	2.028 × 10−15
Objective Functions	8107.453	8502.7213	8114.69152	8107.0404	8106.437	8303.238	8225.998	8126.254
Fuel Cost (USD/h)	8082.077	8472.77	8085.404	8081.216	8081.022	8254.88	8205.161	8101.703
Power Losses (MW)	9.209041	6.774051	9.277797	9.164991	9.165493	6.344187	6.681433	8.930808
Voltage Deviation (pu)	0.069581	0.164027	0.107256	0.074943	0.070824	0.300865	0.074756	0.066895
Time (s)	11.758	12.14	11.29	11.64	12.82	10.32	11.78	20.21

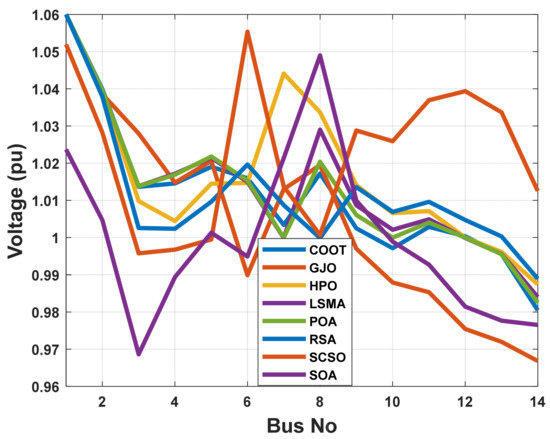
Figure 15. The voltage profile of the POA and other compared algorithms for case 5 in a standard IEEE 14-bus test system.

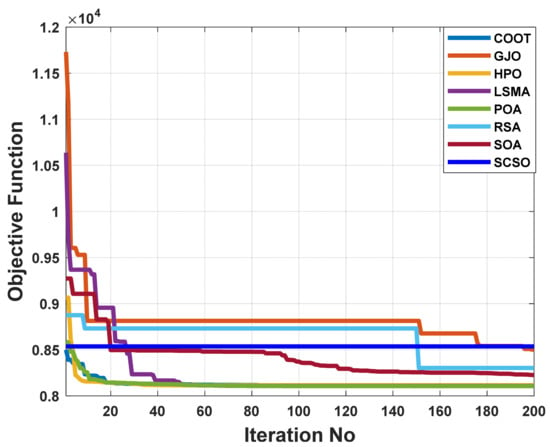
Figure 16. The convergence characteristics of POA and other compared algorithms for case 5 in a standard IEEE 14-bus test system.

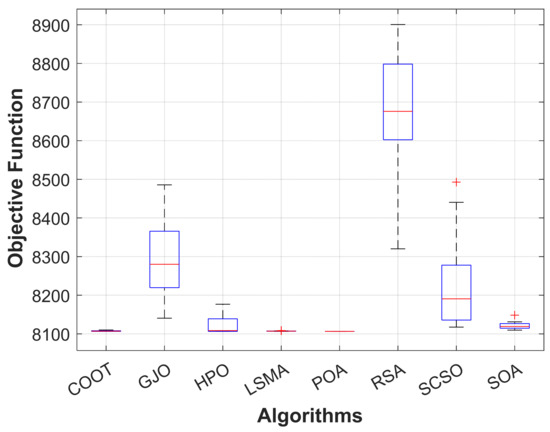
Figure 17. Boxplot of POA and other compared algorithms for case 5 in a standard IEEE 14-bus test system.

3.2. Standard IEEE 57-Bus Test System

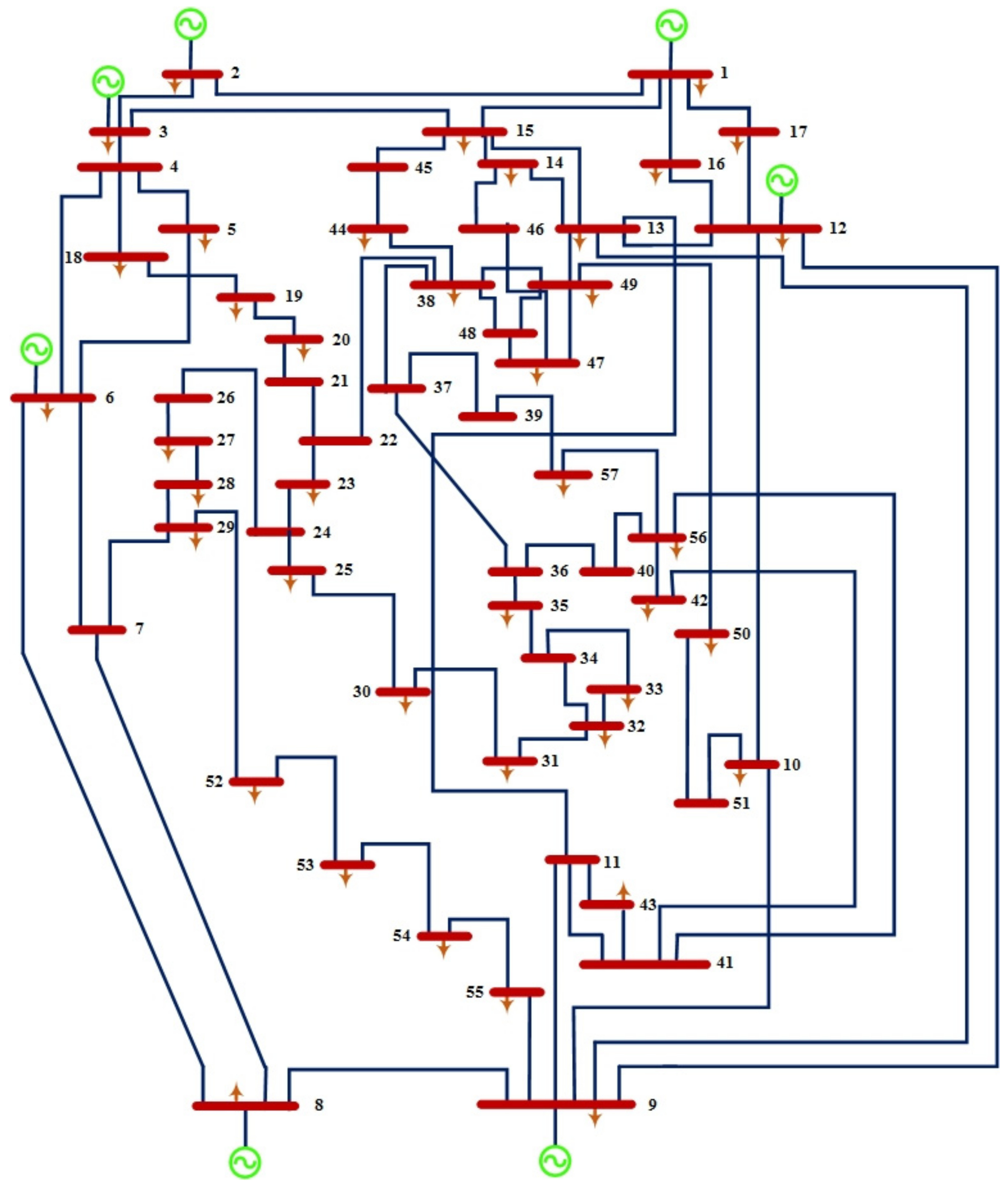
To assess the scalability of the suggested methods, a large-scale IEEE 57-bus test system is taken into consideration. Approximately 1975.9 megawatts are the total capacity of this system as illustrated in Figure 18. This system is made up of seven generators located at buses 1, 2, 3, 6, 8, 9, and 12, and 80 transmission lines.

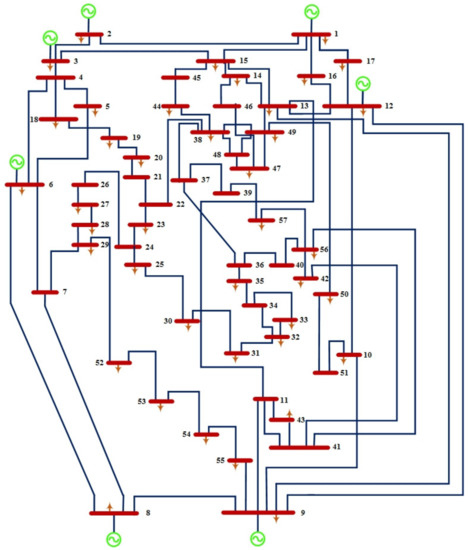
Figure 18. Standard IEEE 57 bus.

• Case 1: Fuel Cost Minimization

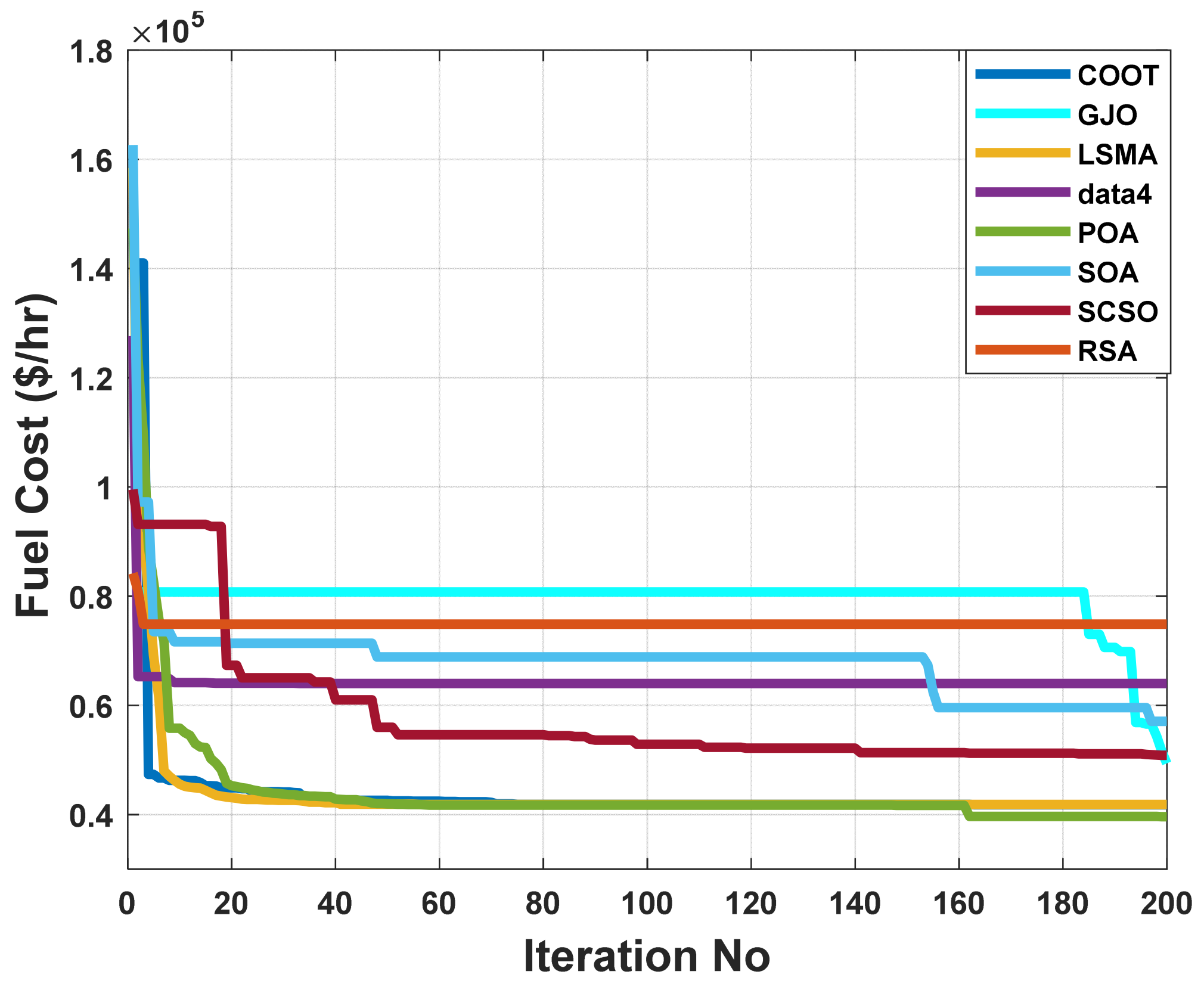
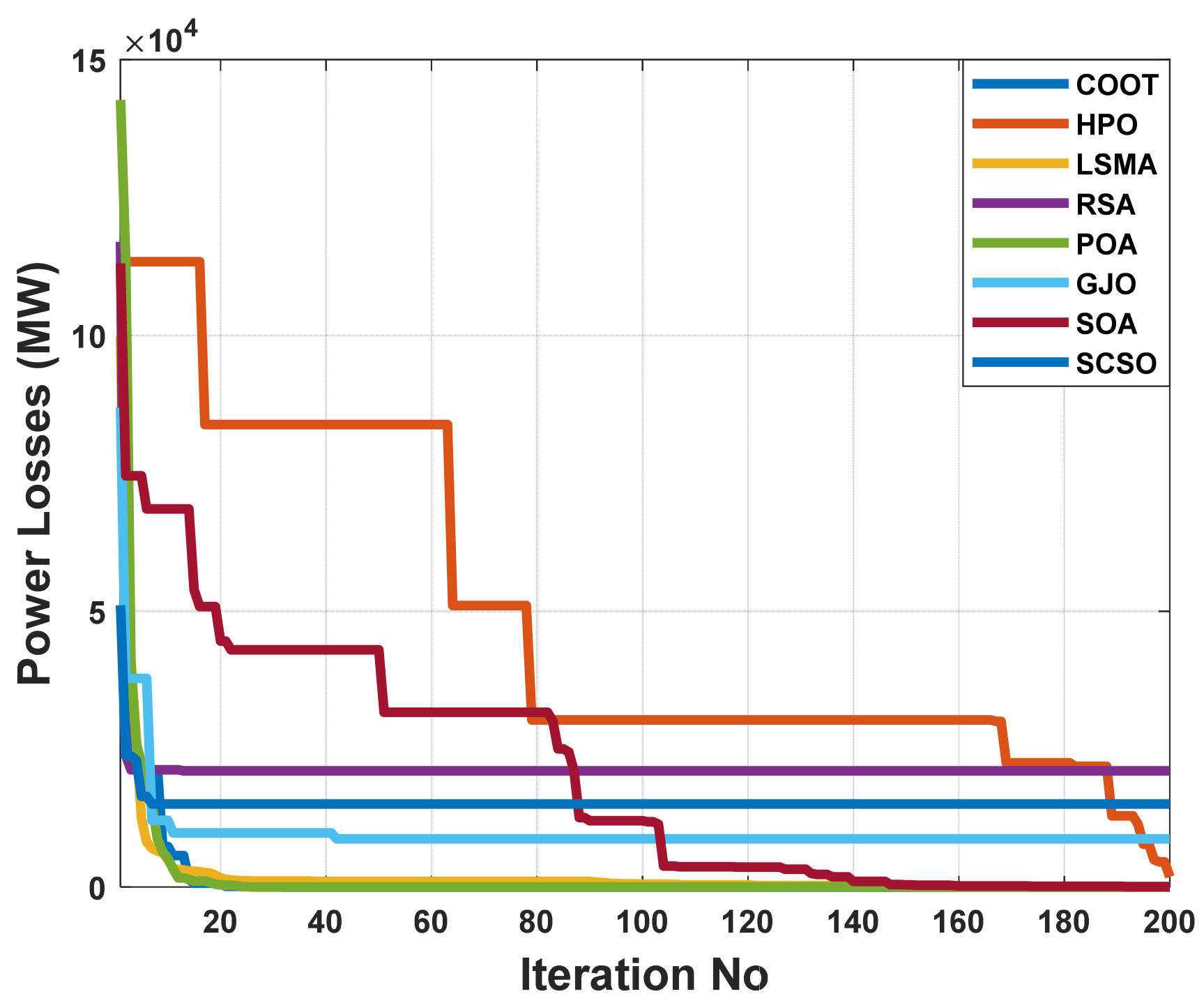
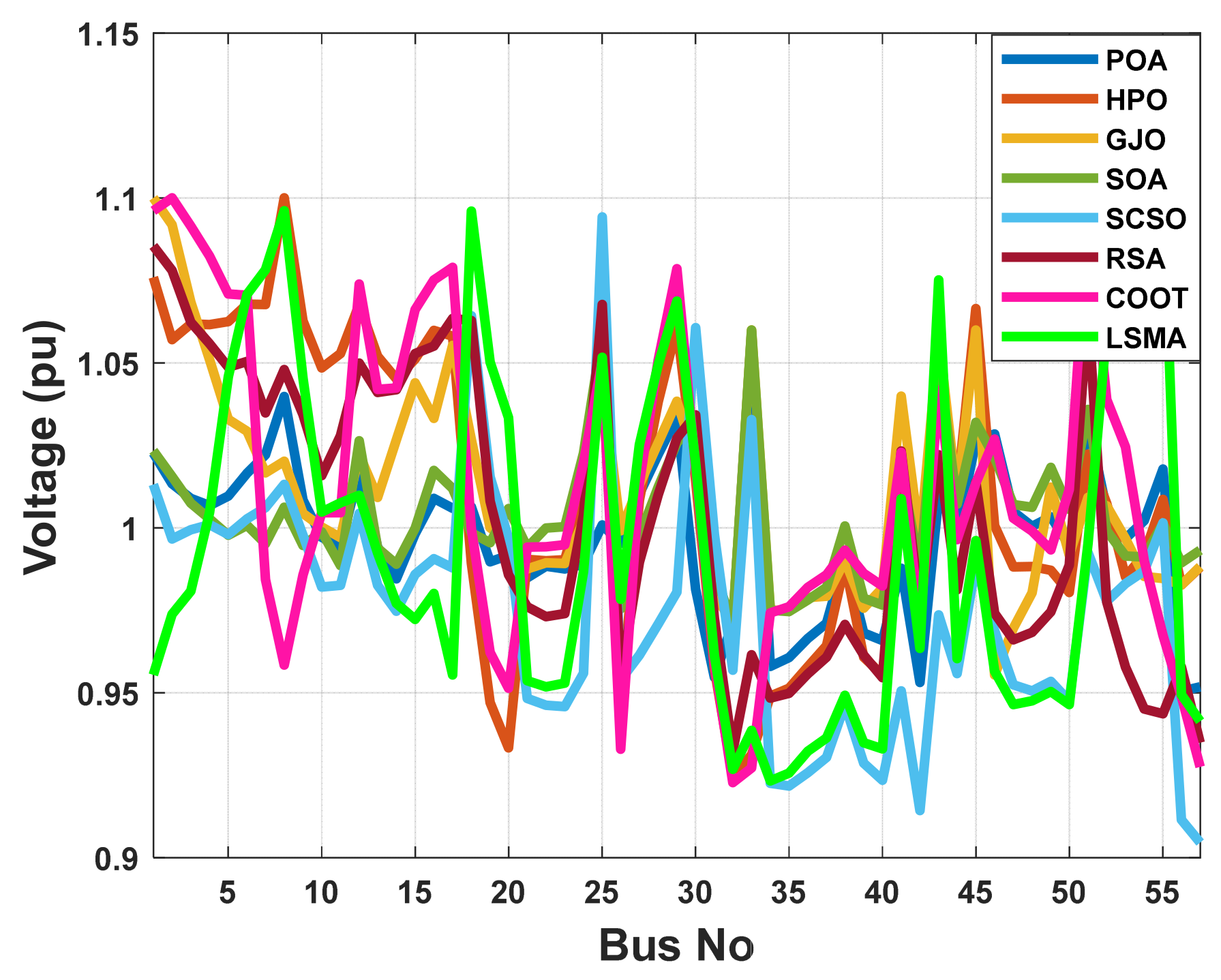
When using the POA algorithm, fuel cost reduction is a target function. Figure 19 depicts the convergence graph of fuel cost reduction using the POA algorithm. The approach needs 40 iterations to get the optimal solution, demonstrating the remarkable convergence rate of the POA algorithm. Table 7 lists the optimal cost-minimization values and the appropriate changes to the design variables. Using the POA algorithm, the findings show a significant reduction in fuel costs to 40687.44 dollars/h. Additionally, for this scenario, the average computing time for a single loop is 2.3 s. These results demonstrate how the POA algorithm performs well in terms of solution optimality and quick convergence. To further verify the effectiveness of the POA method, the fuel cost determined by different alternative heuristic optimization techniques is compared with it. Table 7 shows how superior the POA algorithm is to earlier methods. The majority of solutions found using heuristic optimization techniques are impractical, mainly due to voltage magnitude infringements at one or more system load buses, as shown in Figure 20. Figure 21 displays the boxplots for minimizing the fuel cost with the lowest values by the proposed POA algorithm.

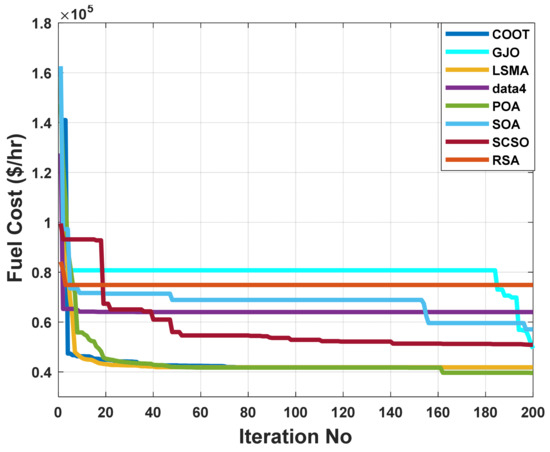
Figure 19. The convergence characteristics of POA and other compared algorithms for case 1 in a standard IEEE 57-bus test system.

Table 7. Optimal control variables for IEEE 57-bus test system for minimizing fuel cost.

Items	COOT	GJO	HPO	LSMA	POA	RSA	SCSO	SOA
${\mathit{P}}_{\mathit{G}\mathbf{1}}$(MW)	197.7838	371.690	142.5807	167.437	120.455	425.759	454.697	233.953
${\mathit{P}}_{\mathit{G}\mathbf{2}}$(MW)	31.24513	100	100	78.61242	57.30494	96.56606	6.909926	75.69572
${\mathit{P}}_{\mathit{G}\mathbf{3}}$(MW)	56.93642	112.6899	51.99754	110.0574	48.50211	99.89622	43.97356	103.7388
${\mathit{P}}_{\mathit{G}\mathbf{6}}$(MW)	59.77353	28.81841	100	78.61242	81.38164	99.82272	48.52389	67.52995
${\mathit{P}}_{\mathit{G}\mathbf{8}}$(MW)	504.3633	252.0763	476.7618	432.3683	461.5699	327.1145	372.6451	420.6549
${\mathit{P}}_{\mathit{G}\mathbf{9}}$(MW)	66.66147	21.2803	82.70673	78.61242	99.47932	100	35.79731	59.3668
${\mathit{P}}_{\mathit{G}\mathbf{12}}$(MW)	350.2702	391.6082	325.7042	322.3109	372.0019	137.6043	319.1894	307.3434
${\mathit{V}}_{\mathbf{1}}$(pu)	1.048887	1.047444	1.069788	1.057225	0.984398	1.004495	0.979297	1.04642
${\mathit{V}}_{\mathbf{2}}$(pu)	1.024585	1.039486	1.060676	1.057225	0.981031	1.001261	0.965505	1.045545
${\mathit{V}}_{\mathbf{3}}$(pu)	1.019626	1.050245	1.04188	1.057225	0.979223	0.999685	0.983364	1.048618
${\mathit{V}}_{\mathbf{6}}$(pu)	1.028053	1.045172	1.01975	1.057225	1.000974	0.998841	1.046333	1.056115
${\mathit{V}}_{\mathbf{8}}$(pu)	1.029975	1.076081	1.030599	1.057225	1.027746	1.018083	1.09642	1.048946
${\mathit{V}}_{\mathbf{9}}$(pu)	1.012998	1.047681	1.02844	1.057225	0.997744	0.996577	1.026543	1.026946
${\mathit{V}}_{\mathbf{12}}$(pu)	1.035543	1.061038	1.071861	1.057225	1.000793	0.998037	1.00491	1.040067
${\mathit{T}}_{\mathbf{19}}$(4–18)	1.058144	0.947804	0.949381	1.057225	0.996549	1.005289	0.936907	1.041311
${\mathit{T}}_{\mathbf{20}}$(4–18)	0.970199	1.013505	1.028492	1.057225	1.000884	1.000067	0.911137	1.000879
${\mathit{T}}_{\mathbf{31}}$(21–20)	1.040849	1.066533	0.977381	1.057225	1.03221	1.007842	0.967188	1.047449
${\mathit{T}}_{\mathbf{35}}$(24–25)	0.970862	1.06634	0.9	1.057225	0.96404	0.999705	1.052234	0.991579
${\mathit{T}}_{\mathbf{36}}$(24–25)	0.977253	1.088629	0.909488	1.057225	0.955274	1.0002	1.037244	1.046058
${\mathit{T}}_{\mathbf{37}}$(24–26)	0.990529	0.953116	1.081878	1.057225	1.023043	0.996146	1.070401	1.027622
${\mathit{T}}_{\mathbf{41}}$(7–29)	0.947611	1.096667	0.912128	1.057225	0.974603	1.001424	1.078433	1.041304
${\mathit{T}}_{\mathbf{46}}$(34–32)	1.001128	1.034269	1.013036	1.057225	0.993301	1.028964	1.000778	1.031106
${\mathit{T}}_{\mathbf{54}}$(11–41)	0.947226	0.915234	1.1	1.057225	0.929266	0.993404	1.08784	0.980267
${\mathit{T}}_{\mathbf{58}}$(15–45)	0.976558	0.956786	1.1	1.057225	0.943817	0.998996	0.973629	1.010064
${\mathit{T}}_{\mathbf{59}}$(14–46)	0.964372	0.976524	0.956153	1.057225	0.971547	0.999587	1.077907	1.012034
${\mathit{T}}_{\mathbf{65}}$(10–51)	1.063189	1.049839	1.096226	1.057225	0.991905	0.997932	0.913759	1.030253
${\mathit{T}}_{\mathbf{66}}$(13–49)	0.941266	0.965933	0.980817	1.057225	0.966859	0.9957	0.919586	1.015465
${\mathit{T}}_{\mathbf{71}}$(11–43)	1.008708	0.996256	0.941791	1.057225	0.922381	0.992983	0.910013	0.990072
${\mathit{T}}_{\mathbf{73}}$(40–56)	1.021312	1.0381	0.900003	1.057225	1.023472	0.986722	1.048906	0.969576
${\mathit{T}}_{\mathbf{76}}$(39–57)	0.956721	1.061383	1.052962	1.057225	0.984479	0.997449	0.924498	1.019591
${\mathit{T}}_{\mathbf{80}}$(9–55)	1.033859	1.021458	1.1	1.057225	1.015375	1.021489	1.005122	1.043914
${\mathit{Q}}_{\mathbf{18}}$(MVAR)	18.36787	3.828557	0	23.58372	14.00844	30	8.58643	20.09548
${\mathit{Q}}_{\mathbf{25}}$(MVAR)	10.63048	20.57741	9.836345	23.58372	12.66613	30	21.6348	24.9082
${\mathit{Q}}_{\mathbf{53}}$(MVAR)	14.86012	7.538395	8.378733	23.58372	19.40512	30	13.24130	22.9107
Fuel Cost (USD/h)	42040.09	48929.76	42243.82	42970.85	40687.44	51502.33	50391.52	43471.69
Power Losses (MW)	19.95473	29.79418	45.48402	17.21084	23.40391	59.49587	55.70792	35.89089
Voltage Deviation (pu)	0.895417	1.485768	1.502203	2.546091	1.01512	1.969187	1.800056	1.487702
Time (s)	388.2	521.06	477.71	51.31	469.76	375.34	657.12	881.29

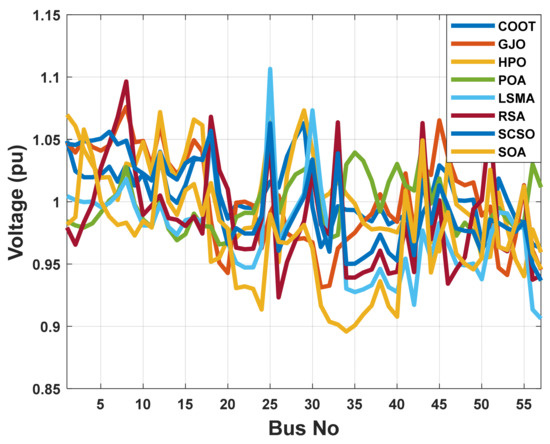
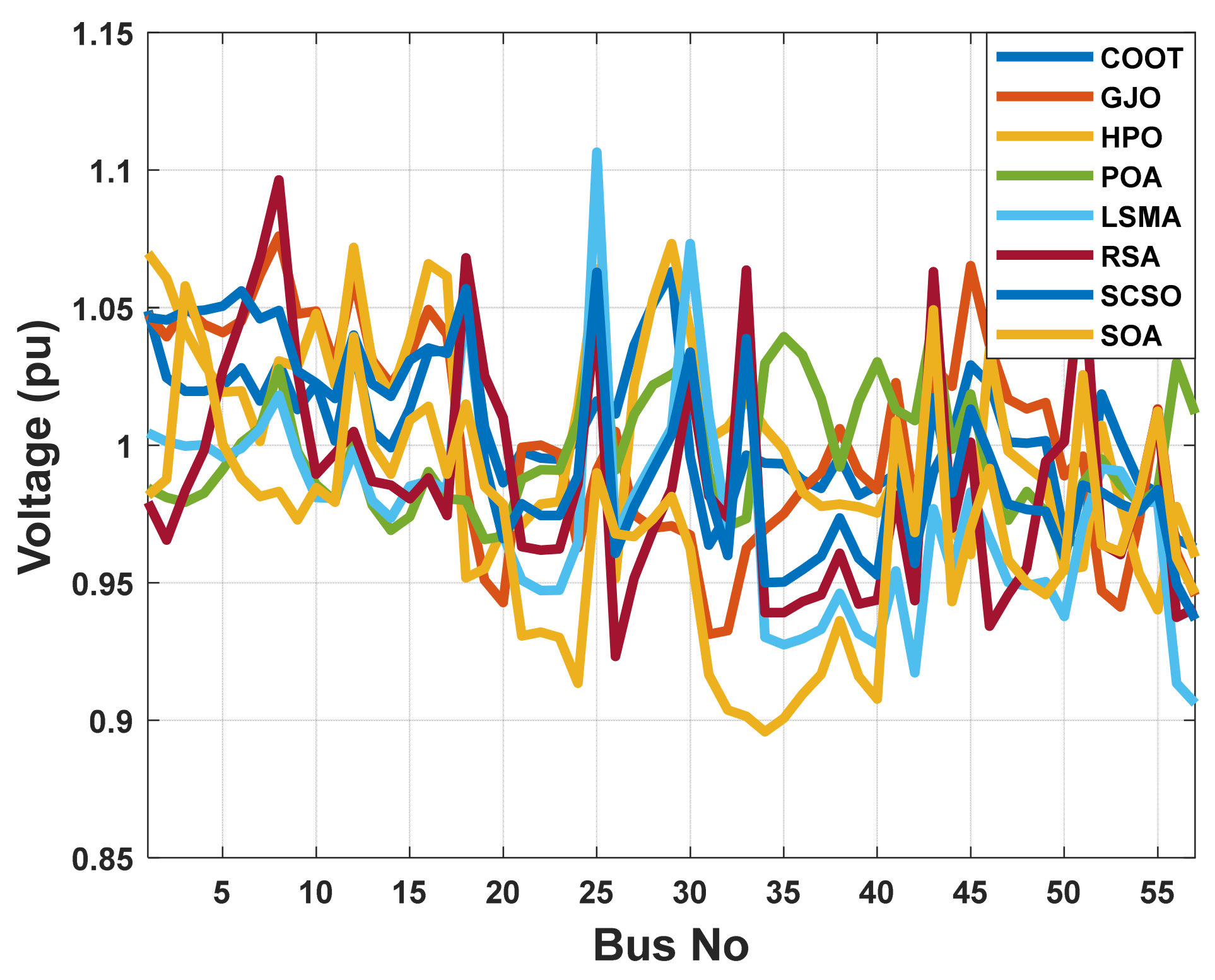
Figure 20. The voltage profile of the POA and other compared algorithms for case 1 in a standard IEEE 57-bus test system.

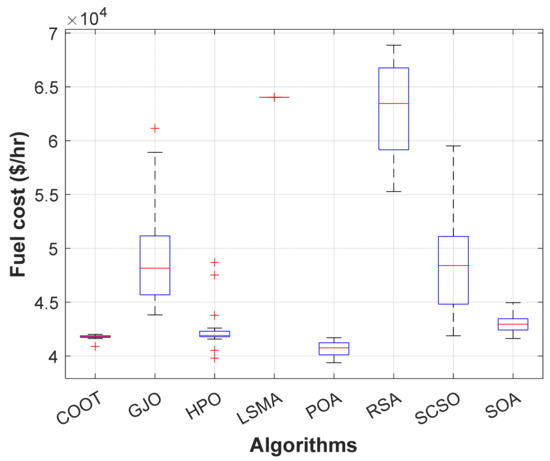
Figure 21. Boxplot of POA and other compared algorithms for case 1 in a standard IEEE 57-bus test system.

• Case 2: Power Losses Minimization

Real power loss was the desired outcome here. Table 8 shows the results of the POA algorithm used to determine the most appropriate solution. In order to minimize system losses, the POA algorithm is extremely useful for setting the precise parameters of the control variable. Therefore, when the POA algorithm is applied, real power losses are drastically reduced to 17.34087 MW. According to Figure 22, real power losses utilizing the POA method are steeply convergent. Within 20 iterations, the algorithm fully converges to the optimum solution, showing the rapid convergence of the POA algorithm. The evaluated real power loss is compared to that found before using published population-based optimization techniques in order to assess the performance of the approach. Table 8 shows how the POA algorithm outperforms these prior methods. Figure 23 illustrates how most of the solutions found using heuristic optimization techniques are impractical. This is mostly due to voltage magnitude infringements at one or more of the system load buses.

Table 8. Optimal control variables for the IEEE-57 bus test system for minimizing real power loss.

Items	COOT	GJO	HPO	LSMA	POA	RSA	SCSO	SOA
${\mathit{P}}_{\mathit{G}\mathbf{1}}$(MW)	367.3958	502.8752	26.61482	245.443	188.6494	577.923	527.628	305.193
${\mathit{P}}_{\mathit{G}\mathbf{2}}$(MW)	45.55037	43.33367	62.04805	100	77.10654	98.63242	73.88113	63.83717
${\mathit{P}}_{\mathit{G}\mathbf{3}}$(MW)	101.9771	6.952017	139.6707	99.40716	107.9492	96.88607	138.0824	96.19934
${\mathit{P}}_{\mathit{G}\mathbf{6}}$(MW)	55.38195	34.46028	0.009616	90.80443	77.10654	91.1916	70.47633	66.0404
${\mathit{P}}_{\mathit{G}\mathbf{8}}$(MW)	359.7809	199.4968	550	271.8845	424.086	192.3662	15.37014	417.5567
${\mathit{P}}_{\mathit{G}\mathbf{9}}$(MW)	43.08224	95.36671	100	51.24983	77.10654	98.62073	81.71518	68.3154
${\mathit{P}}_{\mathit{G}\mathbf{12}}$(MW)	298.9079	396.3917	404.7581	409.7099	316.1368	147.2975	390.0653	255.7295
${\mathit{V}}_{\mathbf{1}}$(pu)	1.042538	1.1	1.085981	1.00969	1.054213	0.998668	1.093626	1.040023
${\mathit{V}}_{\mathbf{2}}$(pu)	1.036595	1.07494	1.073359	1.008916	1.054213	0.998175	1.084741	1.024141
${\mathit{V}}_{\mathbf{3}}$(pu)	1.031164	1.053998	1.046523	1.011108	1.054213	1.005981	1.064192	1.024557
${\mathit{V}}_{\mathbf{6}}$(pu)	1.033186	1.065752	0.997431	1.032578	1.054213	0.997352	1.019788	1.016406
${\mathit{V}}_{\mathbf{8}}$(pu)	1.04704	1.081742	0.95378	1.059654	1.054213	1.005464	1.013539	1.021042
${\mathit{V}}_{\mathbf{9}}$(pu)	1.020408	1.064906	0.961834	1.024166	1.054213	0.995451	1.009436	1.006408
${\mathit{V}}_{\mathbf{12}}$(pu)	1.026629	1.084197	1.025306	1.028605	1.054213	0.996747	1.049852	1.030716
${\mathit{T}}_{\mathbf{19}}$(4–18)	1.042645	0.917592	1.1	0.954046	1.054213	0.994249	1.097842	0.996223
${\mathit{T}}_{\mathbf{20}}$(4–18)	1.060135	0.9989	1.095099	1.04727	1.054213	1.00528	0.989782	1.016827
${\mathit{T}}_{\mathbf{31}}$(21–20)	0.984235	1.1	0.900853	1.003333	1.054213	0.998001	1.080062	1.032004
${\mathit{T}}_{\mathbf{35}}$(24–25)	1.04114	1.043938	0.990581	1.02104	1.054213	0.990241	0.959514	0.988035
${\mathit{T}}_{\mathbf{36}}$(24–25)	1.002672	0.936991	0.9	0.952104	1.054213	0.99943	0.927372	1.009631
${\mathit{T}}_{\mathbf{37}}$(24–26)	1.024837	1.055624	0.989079	1.002447	1.054213	0.97587	1.094129	1.001701
${\mathit{T}}_{\mathbf{41}}$(7–29)	0.965366	0.991475	1.022613	1.023964	1.054213	0.98583	0.922529	0.977251
${\mathit{T}}_{\mathbf{46}}$(34–32)	1.020165	1.023924	1.015032	1.042105	1.054213	1.018907	1.009522	1.047081
${\mathit{T}}_{\mathbf{54}}$(11–41)	1.016565	0.934885	0.9	0.97541	1.054213	0.998228	0.90391	1.00784
${\mathit{T}}_{\mathbf{58}}$(15–45)	0.94758	0.975701	1.015761	0.92678	1.054213	1.000497	1.027763	0.993082
${\mathit{T}}_{\mathbf{59}}$(14–46)	0.982257	1.035633	0.900006	0.9728	1.054213	1.006188	0.993364	0.975842
${\mathit{T}}_{\mathbf{65}}$(10–51)	0.95562	0.9733	1.072133	1.063133	1.054213	1.001608	1.00022	1.025286
${\mathit{T}}_{\mathbf{66}}$(13–49)	0.98052	0.926186	0.900336	0.90975	1.054213	0.999628	1.073005	0.966189
${\mathit{T}}_{\mathbf{71}}$(11–43)	0.999161	1.019114	0.937224	0.985258	1.054213	0.99522	1.078198	0.955134
${\mathit{T}}_{\mathbf{73}}$(40–56)	0.961773	0.933596	1.088143	1.048763	1.054213	0.993784	0.900907	1.028046
${\mathit{T}}_{\mathbf{76}}$(39–57)	1.002686	1.045105	0.9	0.947493	1.054213	0.983648	1.056531	0.965162
${\mathit{T}}_{\mathbf{80}}$(9–55)	0.990639	1.095884	0.9	1.01055	1.054213	0.982561	0.966574	1.004182
${\mathit{Q}}_{\mathbf{18}}$(MVAR)	7.330008	3.517719	25.20328	13.7767	23.13196	30	10.48645	19.13057
${\mathit{Q}}_{\mathbf{25}}$(MVAR)	13.9093	1.614847	9.225315	16.9723	23.13196	30	9.489179	22.32273
${\mathit{Q}}_{\mathbf{53}}$(MVAR)	12.49768	2.55233	29.984736	11.14232	23.13196	30	29.89042	20.20811
Fuel Cost (USD/h)	47221.91	54746.02	45980.64	44621.4	43062.37	61885.15	61914.4	45076
Power Losses (MW)	27.86184	40.78486	38.91329	17.688	17.34087	74.24726	65.2568	28.78647
Voltage Deviation (pu)	1.232325	1.776749	1.494146	1.082698	2.530102	2.088162	1.767814	1.140811

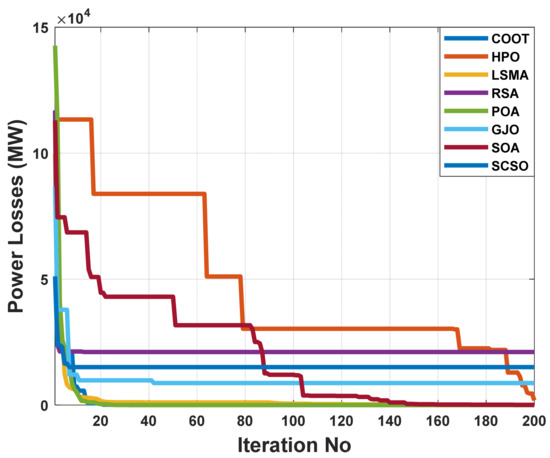
Figure 22. The convergence characteristics of POA and other compared algorithms for case 2 in a standard IEEE 57-bus test system.

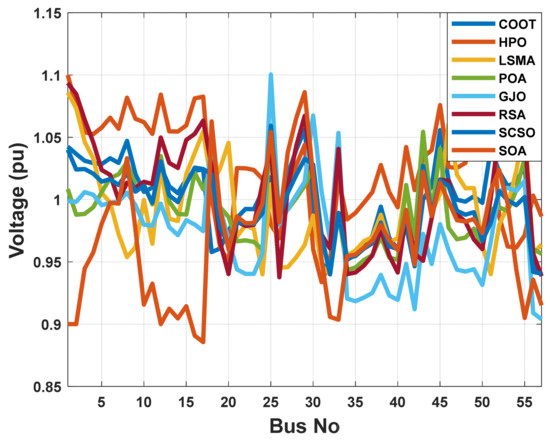
Figure 23. The voltage profile of the POA and other compared algorithms for case 2 in a standard IEEE 57-bus test system.

• Case 3: Voltage Deviation Minimization

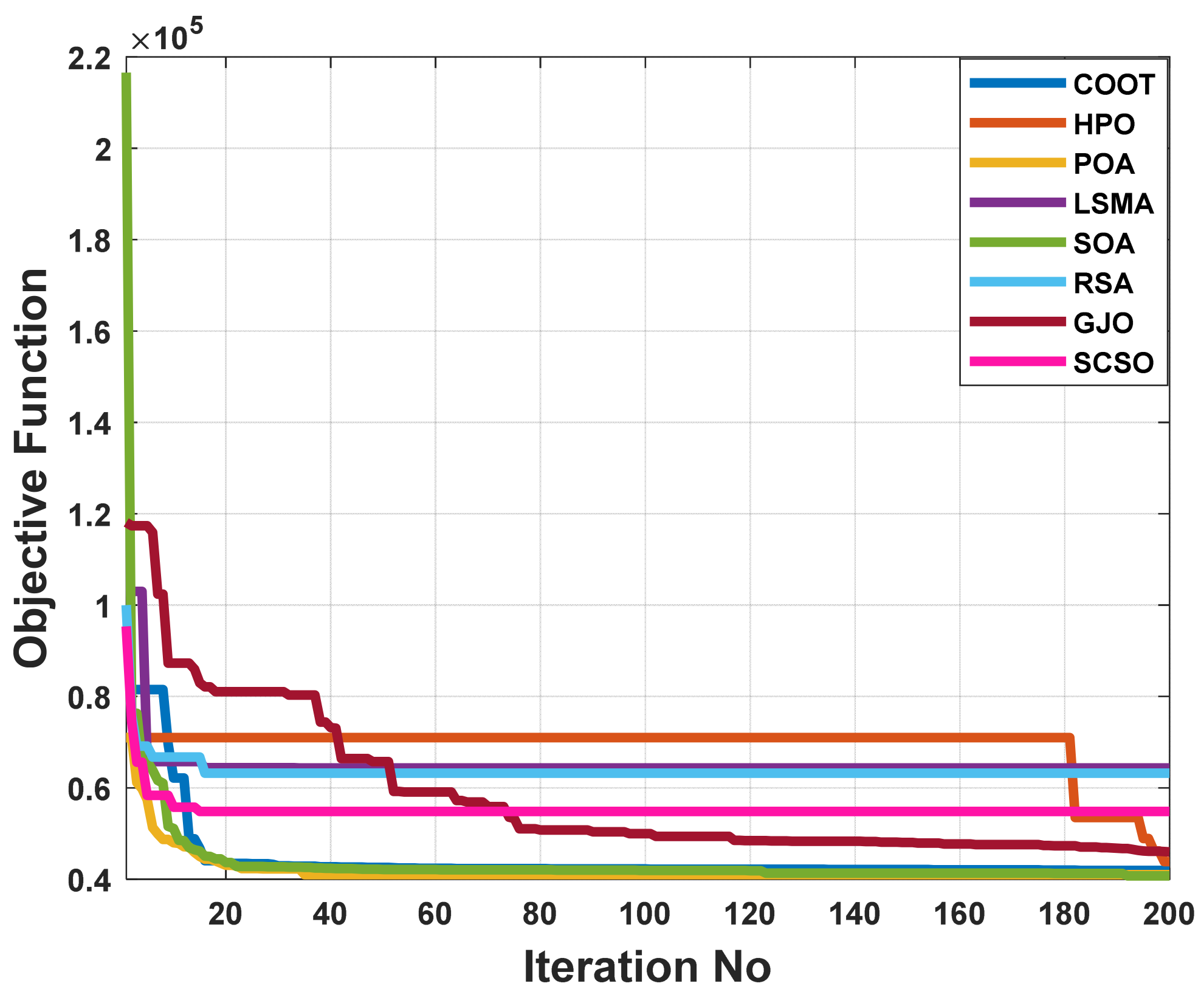
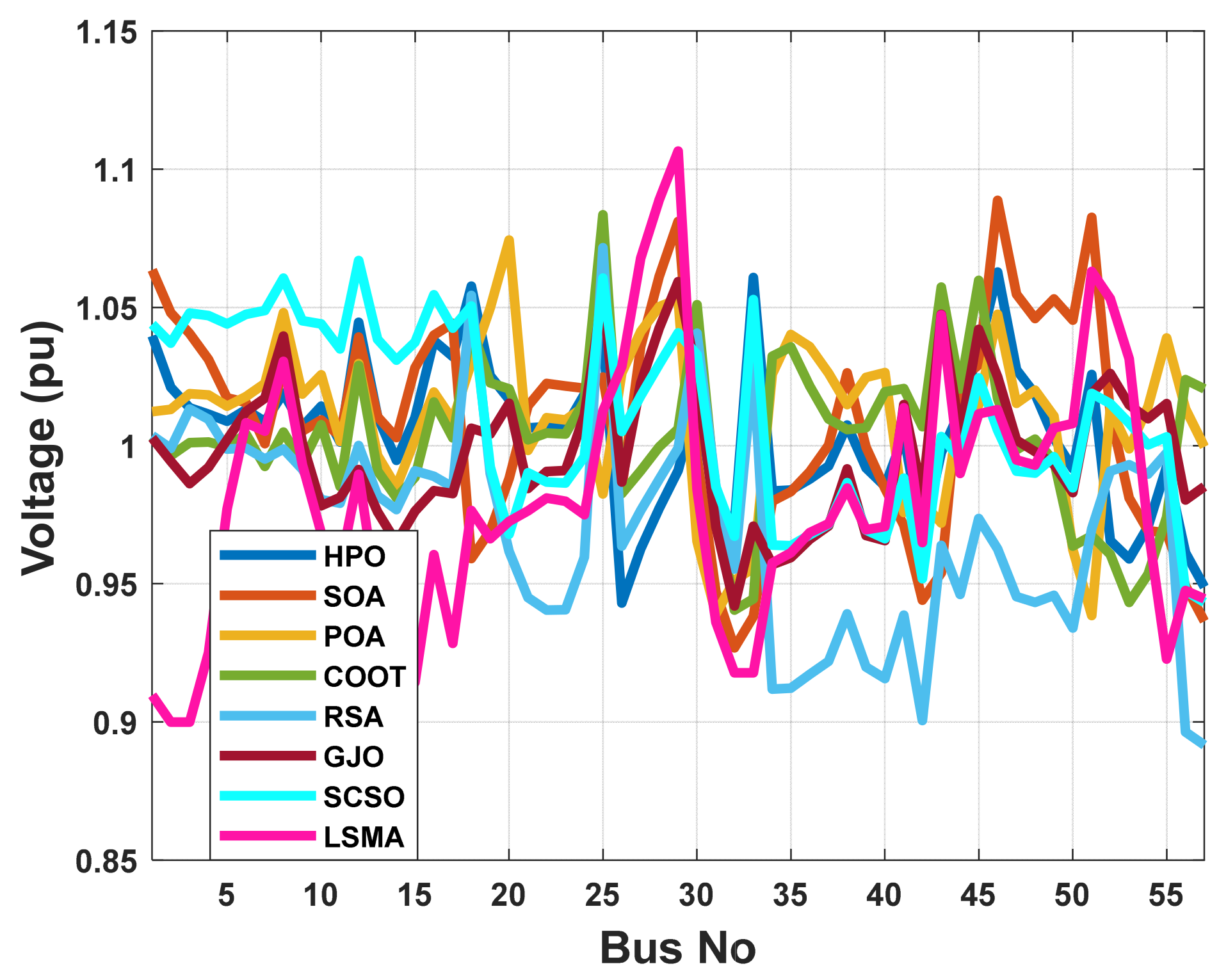
The aim function to be improved using the POA algorithm in this part is decreasing voltage deviation. The voltage profile performance can be illustrated by Figure 24. Figure 25 illustrates the pattern of decreasing system voltage divergence. Table 9 indicates that the voltage deviation index is brought down to 0.755485 pu by using the POA algorithm. The POA method significantly outperforms other population-based optimization strategies in Table 9, which compares solutions obtained using these methods.

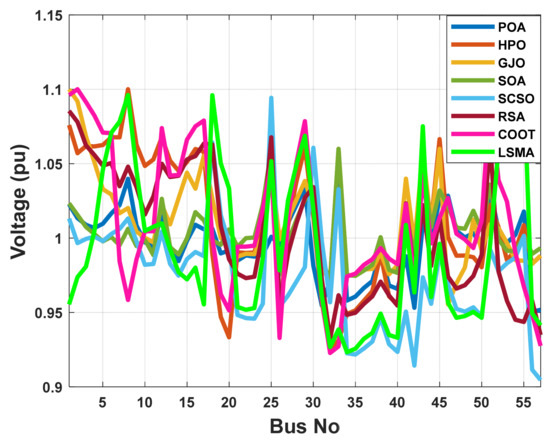
Figure 24. The voltage profile of the POA and other compared algorithms for case 3 in a standard IEEE 57-bus test system.

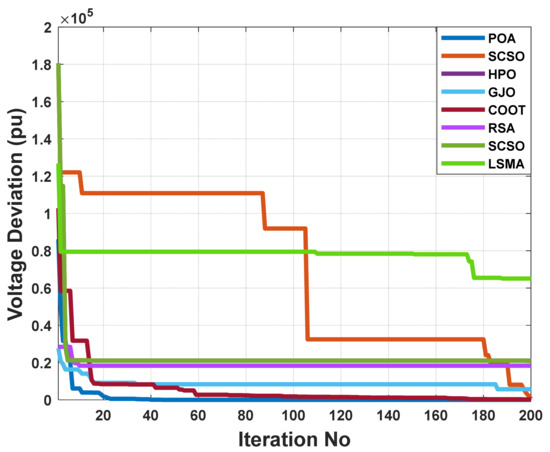
Figure 25. The convergence characteristics of POA and other compared algorithms for case 3 in a standard IEEE-57 bus test system.

Table 9. Optimal control variables for the IEEE-57 bus test system for minimizing voltage deviation.

Items	COOT	GJO	HPO	LSMA	POA	RSA	SCSO	SOA
${\mathit{P}}_{\mathit{G}\mathbf{1}}$(MW)	421.1214	525.4485	358.60363	188.3940	320.4316	573.5604	594.3406	311.848
${\mathit{P}}_{\mathit{G}\mathbf{2}}$(MW)	72.25687	12.98853	90.75598	77.12462	86.46992	99.98832	0	74.3561
${\mathit{P}}_{\mathit{G}\mathbf{3}}$(MW)	88.35667	12.13086	140	107.9745	82.74629	109.6236	28.6272	89.80432
${\mathit{P}}_{\mathit{G}\mathbf{6}}$(MW)	28.03546	62.41389	59.692	77.12462	25.79468	99.99411	74.46495	76.8283
${\mathit{P}}_{\mathit{G}\mathbf{8}}$(MW)	352.0251	490.2188	550	424.1854	406.7538	127.9425	331.5351	365.9131
${\mathit{P}}_{\mathit{G}\mathbf{9}}$(MW)	61.77203	12.80034	99.98592	77.12462	71.12463	100	9.145451	59.96798
${\mathit{P}}_{\mathit{G}\mathbf{12}}$(MW)	254.0532	170.3655	0.007318	316.2109	279.1839	192.2922	254.1349	291.7019
${\mathit{V}}_{\mathbf{1}}$(pu)	1.022639	1.075929	1.1	1.054249	1.023386	1.013123	0.955836	1.06744
${\mathit{V}}_{\mathbf{2}}$(pu)	1.013317	1.057024	1.091839	1.054249	1.015561	0.99666	0.920465	1.05153
${\mathit{V}}_{\mathbf{3}}$(pu)	1.008901	1.061775	1.068392	1.054249	1.007436	0.999425	0.939305	1.032994
${\mathit{V}}_{\mathbf{6}}$(pu)	1.016556	1.067814	1.029314	1.054249	1.00075	1.00272	0.9	1.017289
${\mathit{V}}_{\mathbf{8}}$(pu)	1.039839	1.1	1.020164	1.054249	1.006194	1.013188	0.97823	1.0183
${\mathit{V}}_{\mathbf{9}}$(pu)	1.008448	1.062705	1.00434	1.054249	0.994658	0.997722	0.953705	1.002052
${\mathit{V}}_{\mathbf{12}}$(pu)	1.017573	1.067726	1.022264	1.054249	1.026377	1.0044	0.963754	1.022894
${\mathit{T}}_{\mathbf{19}}$(4–18)	1.040873	1.037222	1.1	1.054249	1.056896	1.001071	0.9820	1.006171
${\mathit{T}}_{\mathbf{20}}$(4–18)	0.963618	1.074576	0.973951	1.054249	0.990877	0.994484	0.9000	1.014352
${\mathit{T}}_{\mathbf{31}}$(21–20)	0.983409	1.078305	0.98273	1.054249	0.968187	0.964269	0.9000	1.002956
${\mathit{T}}_{\mathbf{35}}$(24–25)	1.041545	1.087195	1.1	1.054249	0.954261	0.98741	0.9000	0.996873
${\mathit{T}}_{\mathbf{36}}$(24–25)	1.023486	0.925179	1.1	1.054249	1.1	1.00195	0.9713	1.005973
${\mathit{T}}_{\mathbf{37}}$(24–26)	0.993722	1.073618	0.998933	1.054249	1.048433	1.002152	0.9000	0.988807
${\mathit{T}}_{\mathbf{41}}$(7–29)	0.983896	0.987871	0.979029	1.054249	0.96581	1.028714	0.9263	0.979444
${\mathit{T}}_{\mathbf{46}}$(34–32)	0.992286	1.050329	1.035477	1.054249	1.048452	1.027416	0.9000	1.051059
${\mathit{T}}_{\mathbf{54}}$(11–41)	0.976077	1.049094	0.9	1.054249	0.987147	0.99798	0.9907	0.987646
${\mathit{T}}_{\mathbf{58}}$(15–45)	0.969508	0.963389	0.965711	1.054249	0.966374	0.993585	1.0186	0.985214
${\mathit{T}}_{\mathbf{59}}$(14–46)	0.943704	1.03972	1.099498	1.054249	0.96269	0.999218	0.9000	0.947937
${\mathit{T}}_{\mathbf{65}}$(10–51)	0.955431	1.013208	0.984817	1.054249	0.956463	0.975024	0.9000	0.978016
${\mathit{T}}_{\mathbf{66}}$(13–49)	0.956819	1.049629	0.905424	1.054249	0.92454	1.0013	0.9000	0.972732
${\mathit{T}}_{\mathbf{71}}$(11–43)	0.974798	1.022256	0.934631	1.054249	0.927742	0.998117	0.9064	0.988604
${\mathit{T}}_{\mathbf{73}}$(40–56)	1.026217	0.939216	1.1	1.054249	0.971578	0.9868	0.9519	1.017982
${\mathit{T}}_{\mathbf{76}}$(39–57)	0.951803	0.9	0.9	1.054249	0.914743	0.999575	0.9720	0.970088
${\mathit{T}}_{\mathbf{80}}$(9–55)	0.987809	1.046058	1.020461	1.054249	0.992554	0.996514	0.9000	0.982761
${\mathit{Q}}_{\mathbf{18}}$(MVAR)	3.15308	15.8537	1.82 × 10−7	23.13738	7.5638	30	7.73267	19.0887
${\mathit{Q}}_{\mathbf{25}}$(MVAR)	13.1228	11.17404	24.2134	23.13738	25.109	30	11.2909	20.5717
${\mathit{Q}}_{\mathbf{53}}$(MVAR)	14.8217	0.578587	20.6549	23.13738	18.3045	30	0	15.2484
Fuel Cost (USD/h)	49437.71	55266.44	52806.22	43060.77	45118.17	62449.96	59709	45062.7
Power Losses (MW)	50.50726	35.68396	72.51459	17.33857	45.76651	69.3365	94.990	28.76144
Voltage Deviation (pu)	0.900456	1.681832	1.101717	2.53029	0.755485	1.965747	2.42513	0.961458

• Case 4: Multi-Objective Function without Emissions Minimization

For maximizing the benefits of the suggested test system, a weighted multi-objective function is provided here. This function combines reductions in fuel operational costs, transmission power losses, and voltage-level deviations. As shown in Table 10, the multi-objective OPF issue has been addressed utilizing the POA and other comparative algorithms within the IEEE 57-bus system. It is evident from these results that POA is more efficient than other comparable algorithms when it comes to solving multi-objective OF problems. There is a superior total cost function of 41,764.3 USD/h compared to all other algorithms, which achieve 41,976.43 USD/h, 43,824.11 USD/h, 42,223.671 USD/h, 64,314.49 USD/h, 63,232.87 USD/h, 45,964.76 USD/h, and 42,897.4 USD/h, respectively, by using COOT, GJO, HPO, LSMA, RSA, SCSO, and SOA. A comparison of the POA with other algorithms demonstrates that the POA exhibits rapid and smooth convergence properties despite being compared with other algorithms as shown in Figure 26. Moreover, Figure 27 illustrates that the voltage profiles of all buses fall within the predetermined limits for POA for all comparison methods.

Table 10. Optimal control variables for the IEEE 57-bus test system for minimizing multi-objective function without emissions.

Items	COOT	GJO	HPO	LSMA	POA	RSA	SCSO	SOA
${\mathit{P}}_{\mathit{G}\mathbf{1}}$(MW)	143.623	157.8655	136.1501	164.7678	121.0508	516.7867	300.4537	163.6008
${\mathit{P}}_{\mathit{G}\mathbf{2}}$(MW)	95.50346	96.66898	92.77499	78.80253	99.49578	58.61703	99.20256	77.66144
${\mathit{P}}_{\mathit{G}\mathbf{3}}$(MW)	51.6136	34.16096	52.82851	110.3235	45.9514	93.78267	15.56203	102.953
${\mathit{P}}_{\mathit{G}\mathbf{6}}$(MW)	45.9964	81.04082	17.42949	78.80253	42.58585	98.92257	27.96472	82.65552
${\mathit{P}}_{\mathit{G}\mathbf{8}}$(MW)	493.3967	546.2633	522.5906	433.4139	507.3556	249.1353	425.4817	438.6529
${\mathit{P}}_{\mathit{G}\mathbf{9}}$(MW)	77.41605	43.24442	53.8094	78.80253	56.28702	91.10879	15.57721	76.99095
${\mathit{P}}_{\mathit{G}\mathbf{12}}$(MW)	360.5917	314.5936	390.0989	323.0904	369.7469	181.8416	394.9684	324.7219
${\mathit{V}}_{\mathbf{1}}$(pu)	1.010821	1.095558	1.030438	1.057605	1.069032	1.016942	1.089165	1.049457
${\mathit{V}}_{\mathbf{2}}$(pu)	1.00752	1.089988	1.01893	1.057605	1.058611	0.992543	1.069507	1.044066
${\mathit{V}}_{\mathbf{3}}$(pu)	1.008595	1.078525	1.033196	1.057605	1.036323	1.002037	1.015472	1.052305
${\mathit{V}}_{\mathbf{6}}$(pu)	1.019076	1.084493	1.043557	1.057605	1.031085	0.991385	0.945824	1.05237
${\mathit{V}}_{\mathbf{8}}$(pu)	1.03088	1.061628	1.089941	1.057605	1.017217	1.003066	0.918915	1.054463
${\mathit{V}}_{\mathbf{9}}$(pu)	1.006087	1.043752	1.058084	1.057605	1.013366	0.981323	0.94846	1.041638
${\mathit{V}}_{\mathbf{12}}$(pu)	1.027734	1.070866	1.070544	1.057605	1.056079	1.000824	1.025206	1.060138
${\mathit{T}}_{\mathbf{19}}$(4–18)	1.026778	0.902624	1.066358	1.057605	0.9	0.99679	0.98803	1.042515
${\mathit{T}}_{\mathbf{20}}$(4–18)	0.988586	1.1	0.972051	1.057605	1.035692	0.982485	0.952147	1.033824
${\mathit{T}}_{\mathbf{31}}$(21–20)	0.961711	1.049479	0.900006	1.057605	1.037126	0.973817	0.935748	1.026349
${\mathit{T}}_{\mathbf{35}}$(24–25)	0.988476	0.969389	1.000309	1.057605	0.900434	0.990506	0.9	1.01238
${\mathit{T}}_{\mathbf{36}}$(24–25)	1.030513	0.999585	1.087473	1.057605	0.970427	1.044842	0.96527	1.071951
${\mathit{T}}_{\mathbf{37}}$(24–26)	0.973038	0.937815	1.099902	1.057605	1.035169	0.987916	0.919489	1.019389
${\mathit{T}}_{\mathbf{41}}$(7–29)	0.991395	1.003775	0.98553	1.057605	1.001553	1.005509	0.946868	1.010111
${\mathit{T}}_{\mathbf{46}}$(34–32)	1.024185	1.06815	0.993316	1.057605	1.04226	1.008054	1.062274	1.039037
${\mathit{T}}_{\mathbf{54}}$(11–41)	0.986205	1.030859	1.071105	1.057605	1.027471	0.965091	1.062132	0.984209
${\mathit{T}}_{\mathbf{58}}$(15–45)	0.997118	0.975627	1.1	1.057605	0.984413	1.037131	0.923144	1.024104
${\mathit{T}}_{\mathbf{59}}$(14–46)	0.950359	0.968253	0.953752	1.057605	0.993008	0.989257	0.944164	1.006946
${\mathit{T}}_{\mathbf{65}}$(10–51)	0.97996	1.013855	1.075006	1.057605	0.959907	0.987179	0.990935	1.067964
${\mathit{T}}_{\mathbf{66}}$(13–49)	0.97179	0.991058	0.9	1.057605	0.958867	0.99701	1.026386	1.008685
${\mathit{T}}_{\mathbf{71}}$(11–43)	0.944231	0.987932	1.014904	1.057605	0.970531	0.954439	0.947065	0.985541
${\mathit{T}}_{\mathbf{73}}$(40–56)	0.979475	0.919486	0.935276	1.057605	0.96477	0.987912	0.961167	0.999985
${\mathit{T}}_{\mathbf{76}}$(39–57)	0.98793	0.980401	0.980505	1.057605	0.944449	0.998591	0.925594	1.012483
${\mathit{T}}_{\mathbf{80}}$(9–55)	1.005002	1.000079	1.038643	1.057605	1.02328	1.055628	1.00378	1.04901
${\mathit{Q}}_{\mathbf{18}}$(MVAR)	23.0086	2.6995373	0.104336	23.64076	19.70416	30	19.75618	24.3374
${\mathit{Q}}_{\mathbf{25}}$(MVAR)	22.5812	19.99087	15.12682	23.64076	16.51699	30	28.1742	24.9488
${\mathit{Q}}_{\mathbf{53}}$(MVAR)	13.9403	3.345749	14.42611	23.64076	26.39929	30	28.9131	25.81277
Objective Functions	41976.43	43824.11	42223.671	64314.49	41764.3	63232.87	45964.76	42897.4
Fuel Cost (USD/h)	41783.88	42122.54	41825.63	42965.23	40760.63	56355.88	44666.85	42682.41
Power Losses (MW)	41.4021	24.90775	57.85032	17.20324	26.13897	42.46369	29.02817	38.0977
Voltage Deviation (pu)	1.095638	1.774337	1.431168	2.548151	1.161998	2.246715	1.914592	1.368907

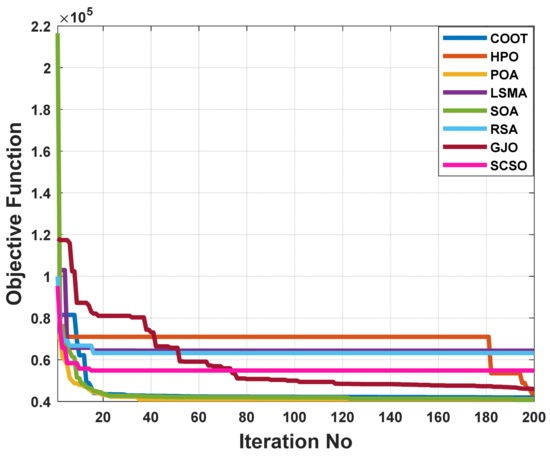
Figure 26. The convergence characteristics of POA and other compared algorithms for case 4 in a standard IEEE 57- bus test system.

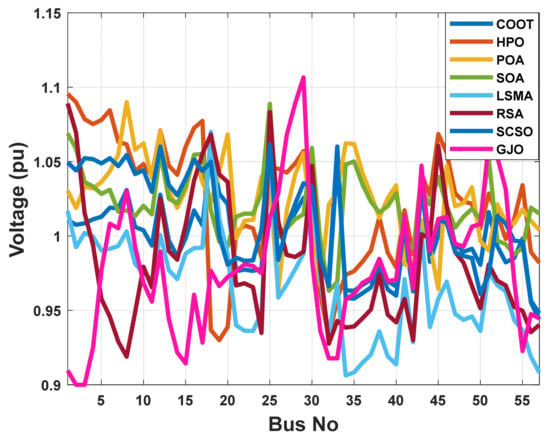
Figure 27. The voltage profile of the POA and other compared algorithms for case 4 in a standard IEEE 57-bus test system.

• Case 5: Multi-Objective Function with Emissions Minimization

Table 11 displays the most effective outcomes of using the POA algorithm to solve a multi-objective OPF problem while taking emissions for the IEEE 57-bus testing system into account. The POA outperforms other comparable algorithms, as seen in this table. POA is also providing 41,380.89 USD/h against 42,310.05 USD/h, 47,363.09 USD/h, 64,312.7 USD/h, 42,337.87 USD/h, 63,175.39 USD/h, 49,580.09 USD/h, and 43,524.05 USD/h by COOT, GJO, HPO, LSMA, RSA, SCSO, and SOA, respectively. Figure 28 shows the voltage profile for each bus. Additionally, Figure 29 displays the convergence characteristics for this example acquired by POA and other algorithms. As can be seen, POA surpasses all other algorithms due to its rapid speed convergence. As shown in Figure 30, each approach is represented as a boxplot with further analysis supporting its performance.

Table 11. Optimal control variables for the IEEE 57-bus test system for minimizing multi-objective function with emissions.

Items	COOT	GJO	HPO	LSMA	POA	RSA	SCSO	SOA
${\mathit{P}}_{\mathit{G}\mathbf{1}}$(MW)	157.0896	322.5358	168.3039	153.4498	105.9981	445.3433	419.376	216.2357
${\mathit{P}}_{\mathit{G}\mathbf{2}}$(MW)	47.48924	23.25643	78.55071	99.9776	79.16808	100	47.45904	59.13851
${\mathit{P}}_{\mathit{G}\mathbf{3}}$(MW)	73.52258	57.1142	109.971	42.50658	47.43168	102.246	56.53641	107.2786
${\mathit{P}}_{\mathit{G}\mathbf{6}}$(MW)	71.36369	55.55387	78.55071	71.92552	10.38385	98.78829	76.79583	68.17841
${\mathit{P}}_{\mathit{G}\mathbf{8}}$(MW)	481.9199	408.7232	432.0289	447.7161	550	205.9314	433.7121	391.9606
${\mathit{P}}_{\mathit{G}\mathbf{9}}$(MW)	40.78315	23.4726	78.55071	76.92445	80.99457	99.97366	78.52864	80.36427
${\mathit{P}}_{\mathit{G}\mathbf{12}}$(MW)	395.5245	379.6115	322.0579	370.6479	369.5153	233.0069	169.9581	342.4249
${\mathit{V}}_{\mathbf{1}}$(pu)	1.039707	1.063608	1.057101	1.003219	1.012285	1.003658	1.00281	1.043929
${\mathit{V}}_{\mathbf{2}}$(pu)	1.021049	1.048051	1.057101	0.996317	1.013079	0.998963	0.99439	1.037034
${\mathit{V}}_{\mathbf{3}}$(pu)	1.013695	1.040502	1.057101	1.001063	1.018794	1.013156	0.98623	1.047918
${\mathit{V}}_{\mathbf{6}}$(pu)	1.012959	1.015672	1.057101	1.004153	1.017731	0.999136	1.012292	1.047485
${\mathit{V}}_{\mathbf{8}}$(pu)	1.019015	1.029036	1.057101	1.00482	1.048083	0.998688	1.039675	1.06055
${\mathit{V}}_{\mathbf{9}}$(pu)	1.006806	1.005213	1.057101	0.993639	1.018648	0.991483	1.001037	1.045169
${\mathit{V}}_{\mathbf{12}}$(pu)	1.044617	1.039267	1.057101	1.028938	1.02962	0.99997	0.991365	1.066996
${\mathit{T}}_{\mathbf{19}}$(4–18)	0.982872	0.999949	1.057101	0.91143	1.063171	1.00971	1.008624	1.01952
${\mathit{T}}_{\mathbf{20}}$(4–18)	0.967336	1.073089	1.057101	0.992341	1.026559	1.004591	0.991413	1.021341
${\mathit{T}}_{\mathbf{31}}$(21–20)	0.996597	0.998337	1.057101	0.987006	0.9	1.013441	0.946955	1.054483
${\mathit{T}}_{\mathbf{35}}$(24–25)	1.061537	1.066385	1.057101	1.029215	0.931084	0.996408	0.953579	1.00248
${\mathit{T}}_{\mathbf{36}}$(24–25)	1.070802	0.9	1.057101	1.033502	0.994979	1.054513	1.012286	1.042586
${\mathit{T}}_{\mathbf{37}}$(24–26)	1.078596	1.041821	1.057101	1.037292	0.986429	0.995274	1.025393	0.988943
${\mathit{T}}_{\mathbf{41}}$(7–29)	1.015138	0.906204	1.057101	0.977811	0.96218	0.997808	0.953248	1.006311
${\mathit{T}}_{\mathbf{46}}$(34–32)	1.043536	1.06632	1.057101	1.051063	0.957042	1.001245	1.039402	1.03881
${\mathit{T}}_{\mathbf{54}}$(11–41)	0.922432	0.96831	1.057101	0.955169	0.96859	1.00914	0.969531	1.0052
${\mathit{T}}_{\mathbf{58}}$(15–45)	0.973685	1.008302	1.057101	0.913597	0.986897	1.016269	0.92691	1.005755
${\mathit{T}}_{\mathbf{59}}$(14–46)	0.912198	0.9	1.057101	0.95304	0.915573	1.006454	0.927957	1.018402
${\mathit{T}}_{\mathbf{65}}$(10–51)	0.980815	0.924335	1.057101	1.040334	1.1	0.999182	0.949914	1.015991
${\mathit{T}}_{\mathbf{66}}$(13–49)	1.012088	0.916659	1.057101	0.952983	0.906462	1.002239	0.964772	1.004249
${\mathit{T}}_{\mathbf{71}}$(11–43)	1.003818	1.056396	1.057101	0.917139	1.029909	1.00369	0.924282	1.023534
${\mathit{T}}_{\mathbf{73}}$(40–56)	0.980575	0.926906	1.057101	1.026154	0.9	1.007135	0.99156	1.004644
${\mathit{T}}_{\mathbf{76}}$(39–57)	1.03927	1.072478	1.057101	0.907699	1.025613	0.988551	0.907312	0.982117
${\mathit{T}}_{\mathbf{80}}$(9–55)	1.007899	1.037999	1.057101	1.013152	0.973004	0.996485	0.985401	1.044155
${\mathit{Q}}_{\mathbf{18}}$(MVAR)	17.30864	9.431689	23.5652	22.4933	19.41307	30	11.55227	23.69138
${\mathit{Q}}_{\mathbf{25}}$(MVAR)	20.1859	4.378543	23.56521	21.80043	7.7245948	30	19.81482	23.25284
${\mathit{Q}}_{\mathbf{53}}$(MVAR)	14.56342	0	23.56521	5.31018	4.9146352	30	16.33104	22.1113
Objective Functions	42310.05	47363.09	64312.7	42337.87	41380.89	63175.39	49580.09	43524.05
Fuel Cost (USD/h)	42110	44739.72	42972.97	41614.88	40971	52672.29	49401.58	43312.4
Power Losses (MW)	41.29439	19.79479	17.21373	29.29512	28.98564	50.29164	33.81916	36.88689
Voltage Deviation (pu)	1.090954	1.611049	2.545424	1.108771	1.265823	2.102887	1.108747	1.343105
Time (s)	460.23	574.68	444.36	57.43	416.94	415.28	589.99	855.862

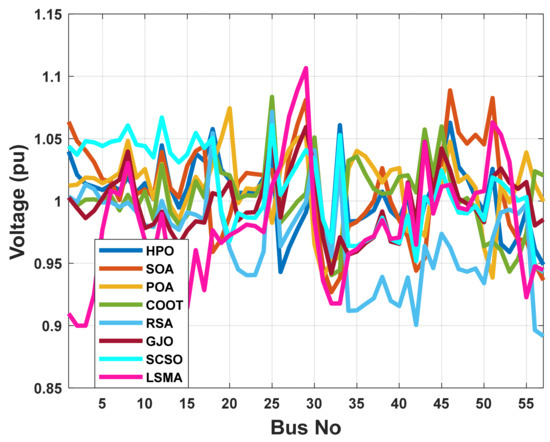
Figure 28. The voltage profile of the POA and other compared algorithms for case 5 in a standard IEEE 57-bus test system.

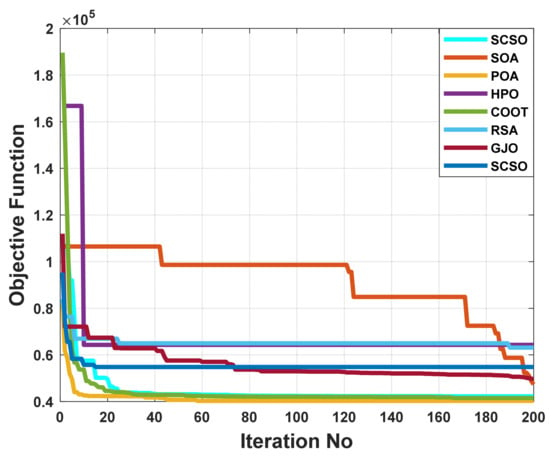
Figure 29. The convergence characteristics of POA and other compared algorithms for case 5 in a standard IEEE 57-bus test system.

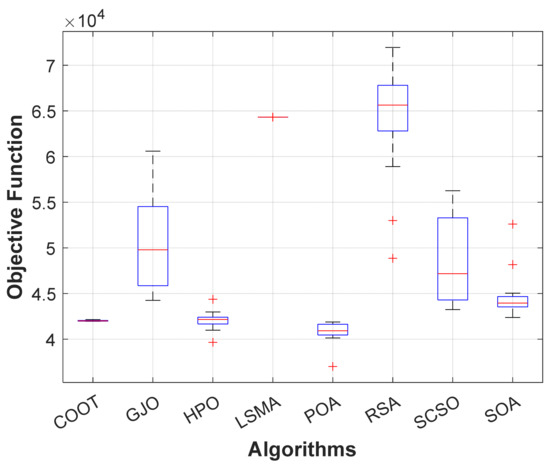
Figure 30. Boxplot of POA and other compared algorithms for case 5 in a standard IEEE 57-bus test system.

4. Conclusions

In order to address the OPF issue, this study proposes a novel optimization method inspired by peafowl (Pavo muticus/cristatus) called POA. Peafowl swarms demonstrate distinct courting, food-seeking, and chasing behaviors. The following is a summary of the major innovations made in this paper and its results: (a) POA combines global and local exploitation and exploratory searching operators to achieve a reasonable trade-off between the two, and to prevent local optimum formation. There are many examples of peacocks performing rotation dancing operations, peahens and peafowl cubs using adaptive search behavior at various stages of their search, and interactions among peacock species. (b) Instead of remaining motionless, the five peacocks that represent the most effective solutions for today will rotate and dance as they search for solutions throughout the area. Peacocks have a unique rotating dance mechanism that includes two distinct modes of rotation: spinning in-situ and circling the food source. It is significant to note that a strategy is used that forces the present optimal solution to perform a neighboring search which has never been done before. In this way, local optimum situations may be broken out. (c) Both peahens and peafowl cubs employ adaptive seeking and approaching mechanisms during the entire search process in order to dynamically alter their behavior at various stages, thus ensuring a healthy balance between local exploitation and global exploration. (d) A number of analyses were conducted in order to demonstrate the effectiveness and reliability of the proposed POA. According to the simulation results, POA typically explores the optimal searching regions and provides the most appropriate overall answers. (e) POA is used in the estimation of control variables in practical engineering applications to verify its performance in real-world scenarios. Actual case studies have shown that POA outperforms other algorithms in terms of estimation accuracy, convergence speed, and stability.

This study was worthwhile, but there are some critical issues that need to be addressed in the next study. Firstly, it would be possible to address the limitations and restrictions of the proposed technique by reducing the complexity of parameter tweaking. Secondly, in this paper, multi-objective optimization problems are simplified by converting them to a single item before carrying out the actual optimization operation by constructing a weighted sum of all the objectives. The major advantage of the weighted sum method is its ability to identify a single unique solution for actual implementation. In the future, the authors will use the well-known ε-constraint method to generate multiple Pareto optimal solutions. With regard to future extensions of this work, the authors will add some indices such as VSI, and use the Pareto state for the proposed multi-objective function optimization problem. According to the previous discussion that illustrated the developed POA’s superiority, it can open a wide range of future works. In the future, it should be possible to address the limitations and restrictions of the proposed technique. The complexity of parameter tweaking might be further reduced, and the implementation of online estimation may be more challenging. The study of the OPF problem while considering degradation processes is an insightful and fruitful study area that will prove crucial for engineering applications, such as state-of-health monitoring and performance prediction. It can also be extended to real-world applications such as energy management and load management, conventional and smart grid applications, industry and engineering applications, and smart home applications.