A Study of Passenger Car Cabin Pre-Ventilation under the Sun
Abstract
:1. Introduction
2. Methodology
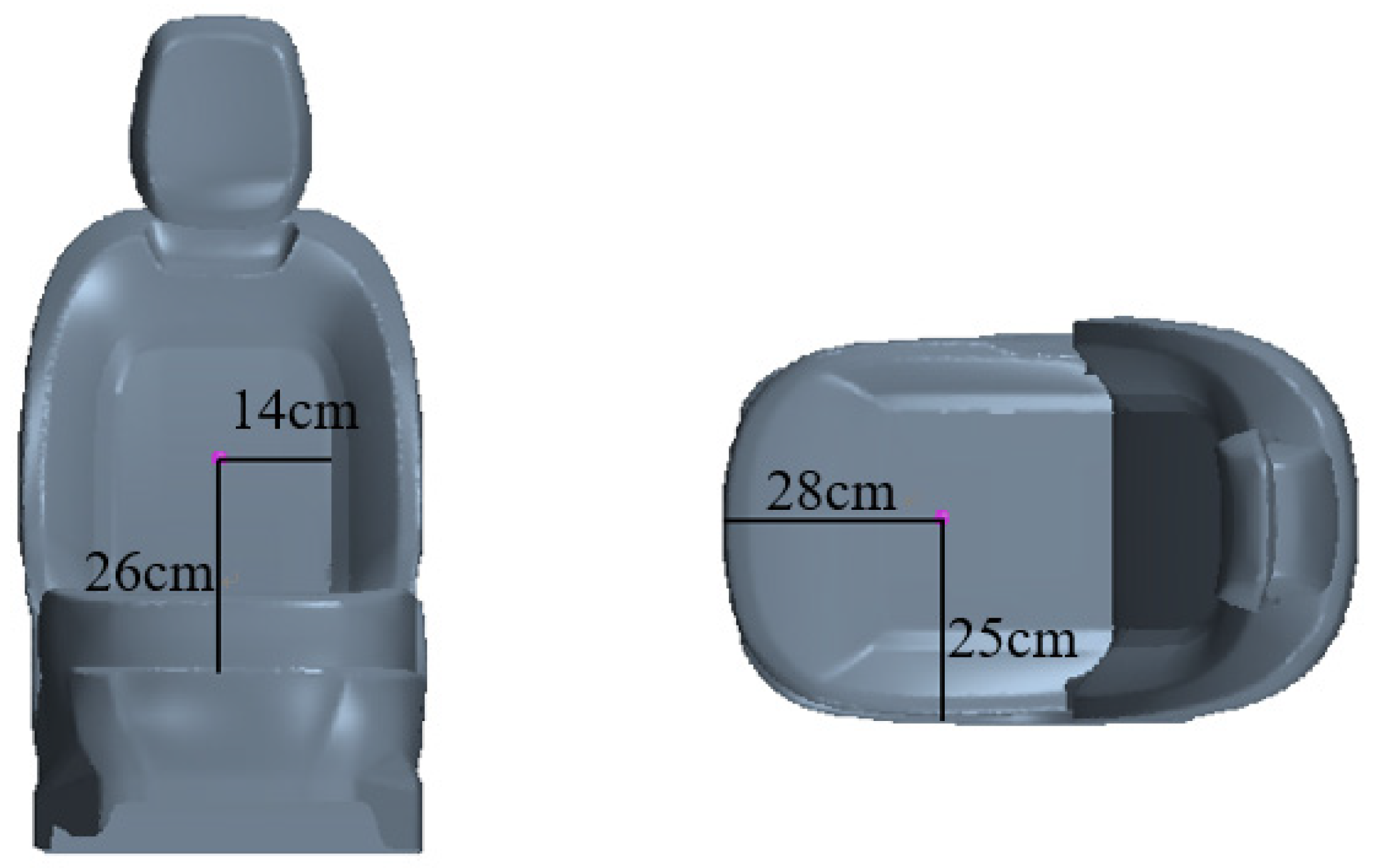
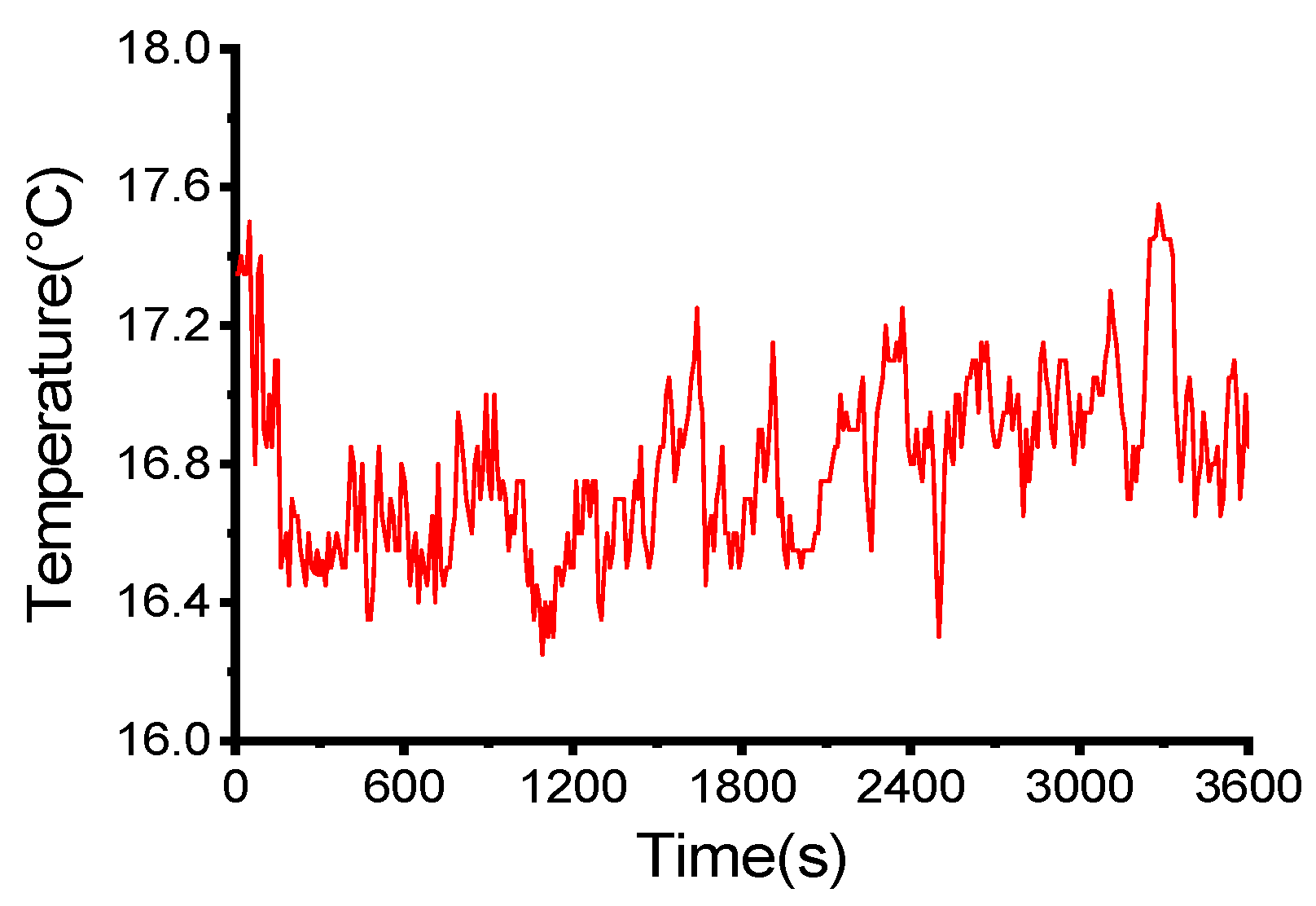
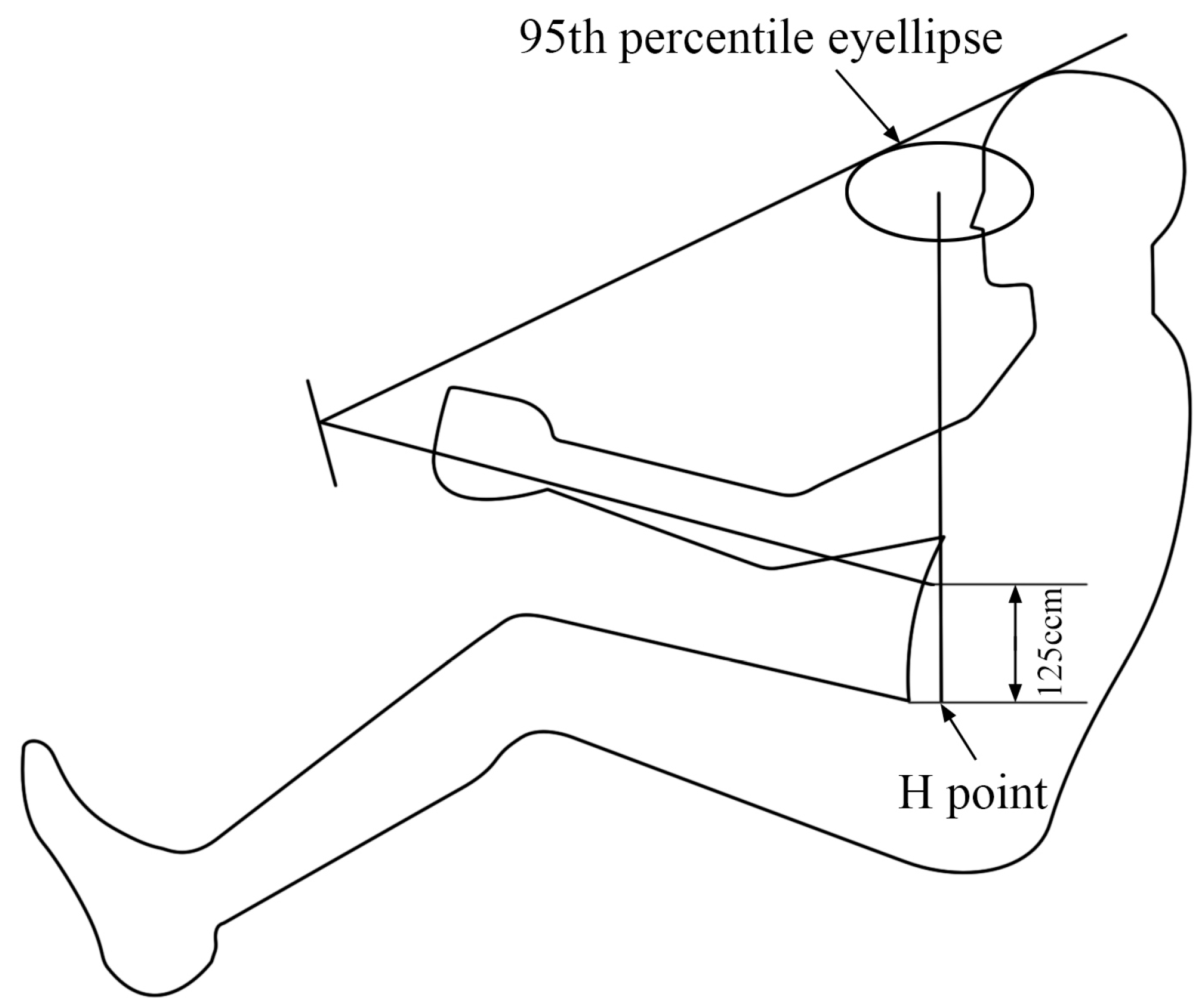
2.1. Occupant Cabin Temperature Rise Test Experiment Methods
2.2. Analysis of Temperature Rise Process of Occupant Cabin
2.3. Simulation of the Temperature Rise of the Vehicle Cabin
2.3.1. The Setting of the Temperature Rise Model of the Occupant Cabin
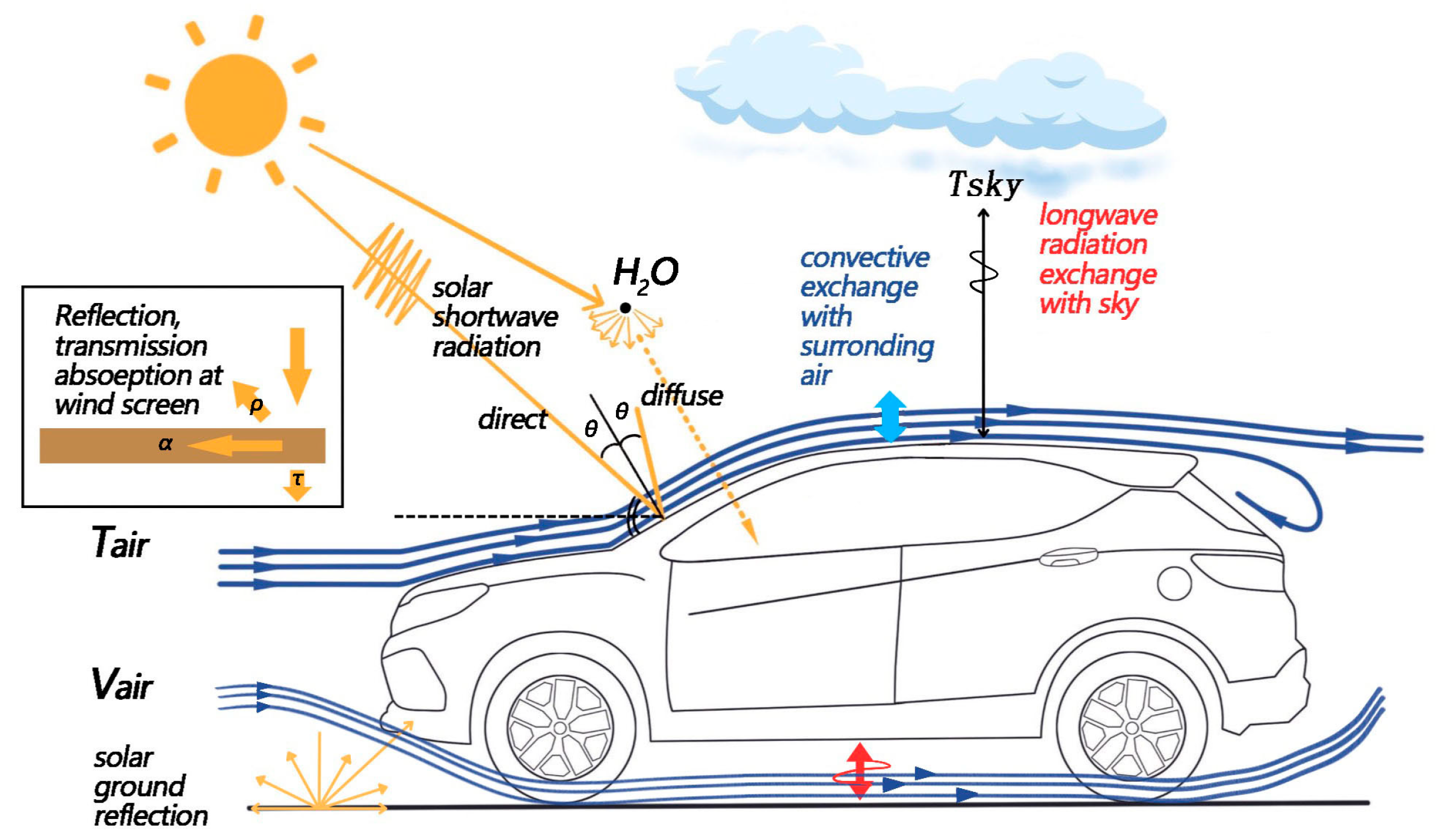
2.3.2. Establishment of Radiation Model
2.3.3. Simulation of Outdoor Parking Temperature Rise in Autumn
3. Simulation of the Temperature Distribution of the Occupant Cabin
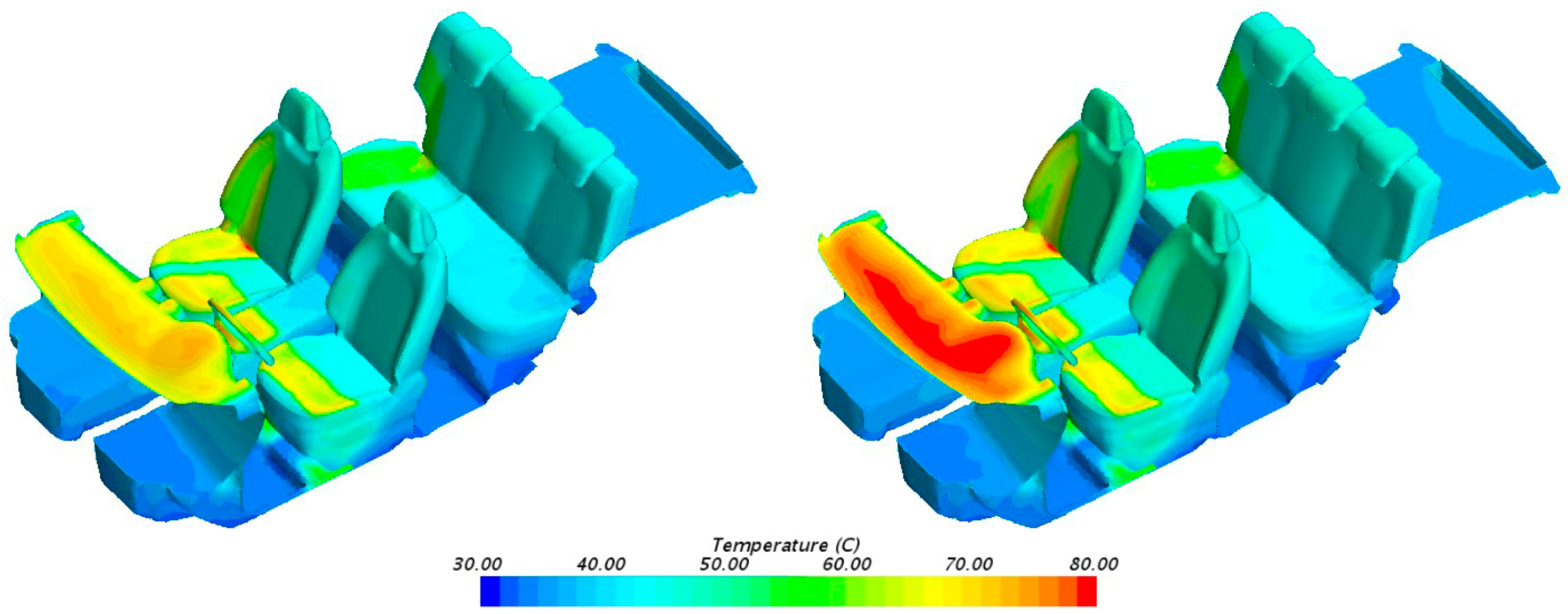
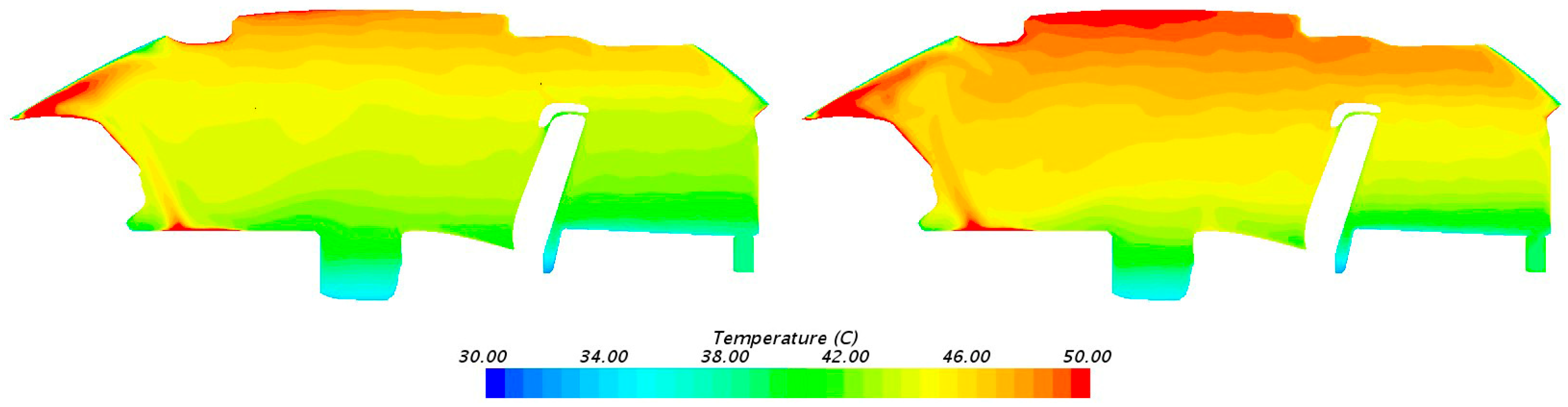
3.1. Analysis of the Influence of the Greenhouse Effect on the Temperature of the Occupant Cabin
3.2. Simulation of the Greenhouse Effect in the Occupant Cabin
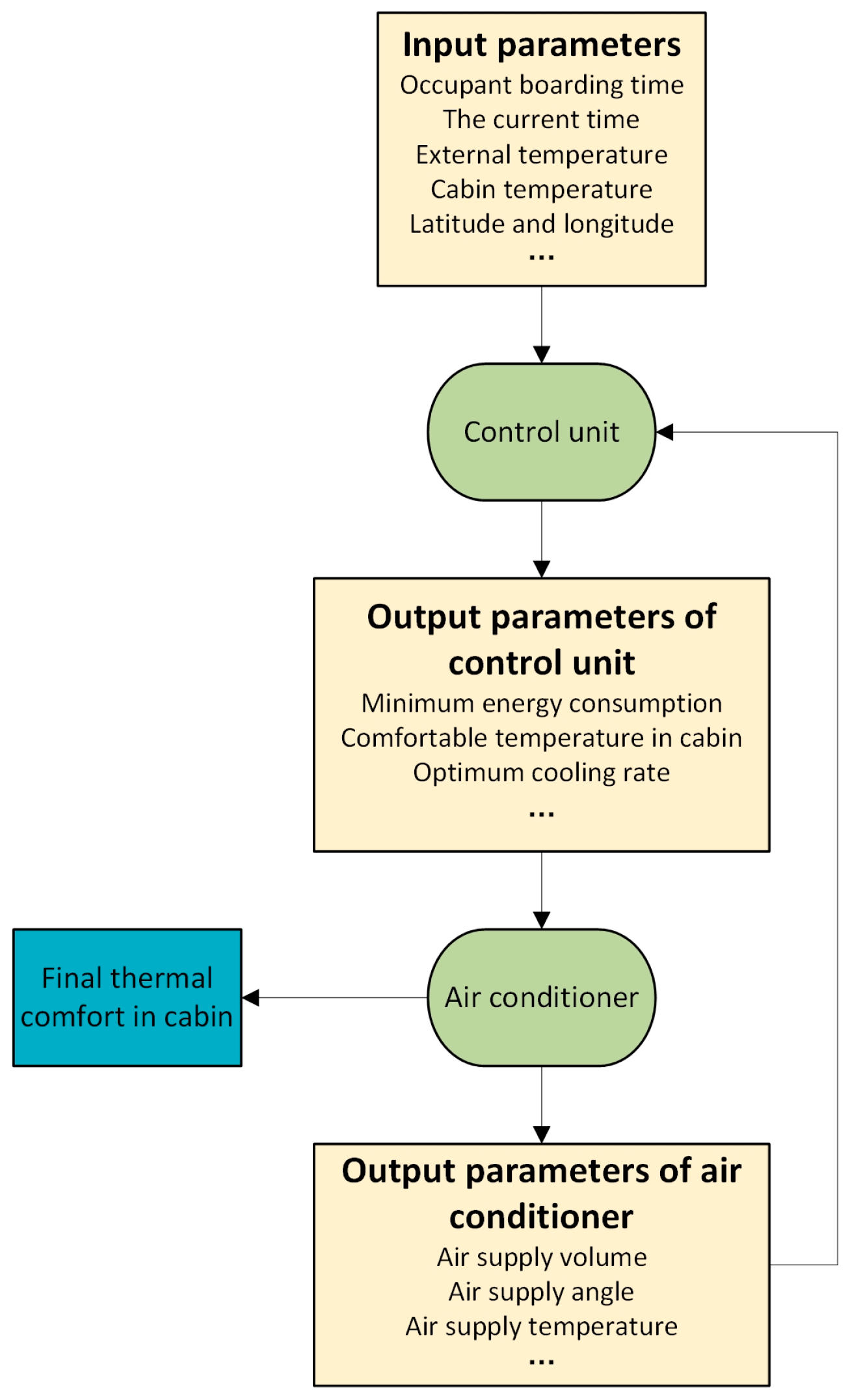
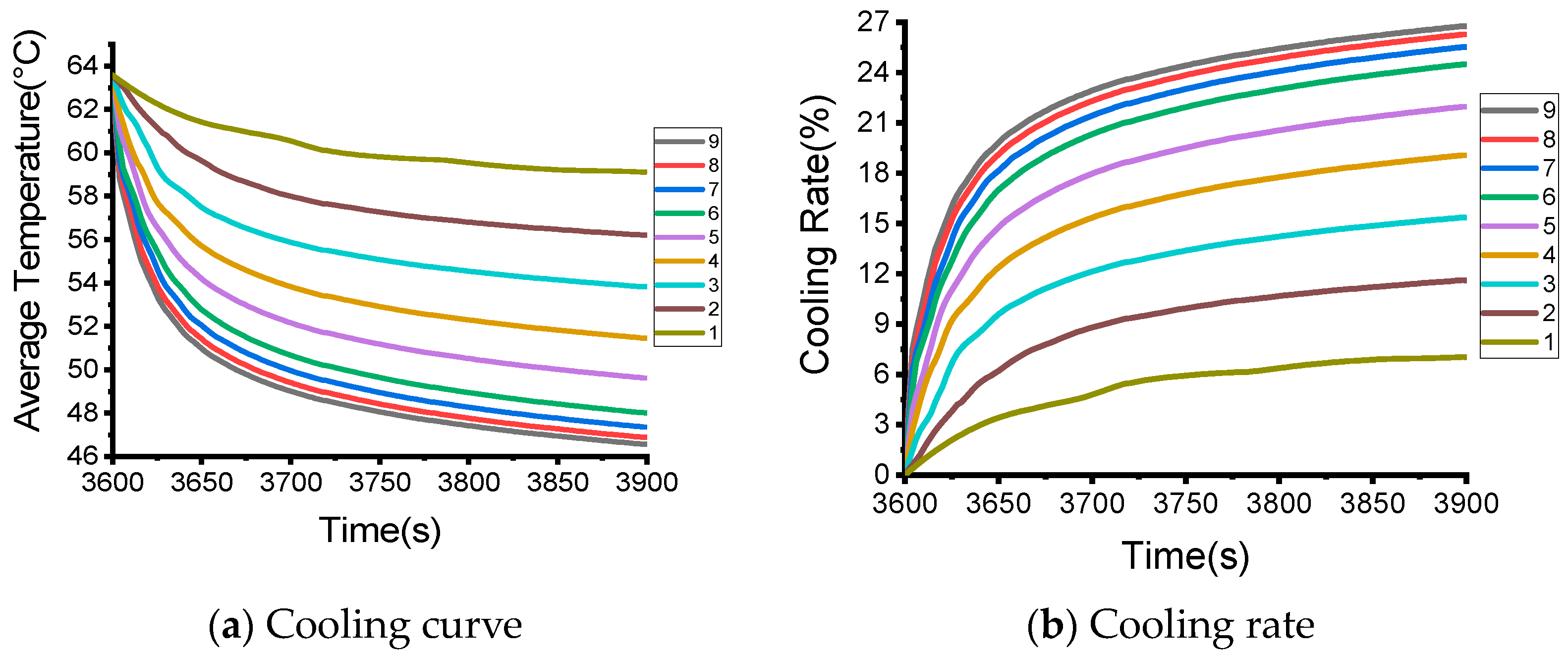
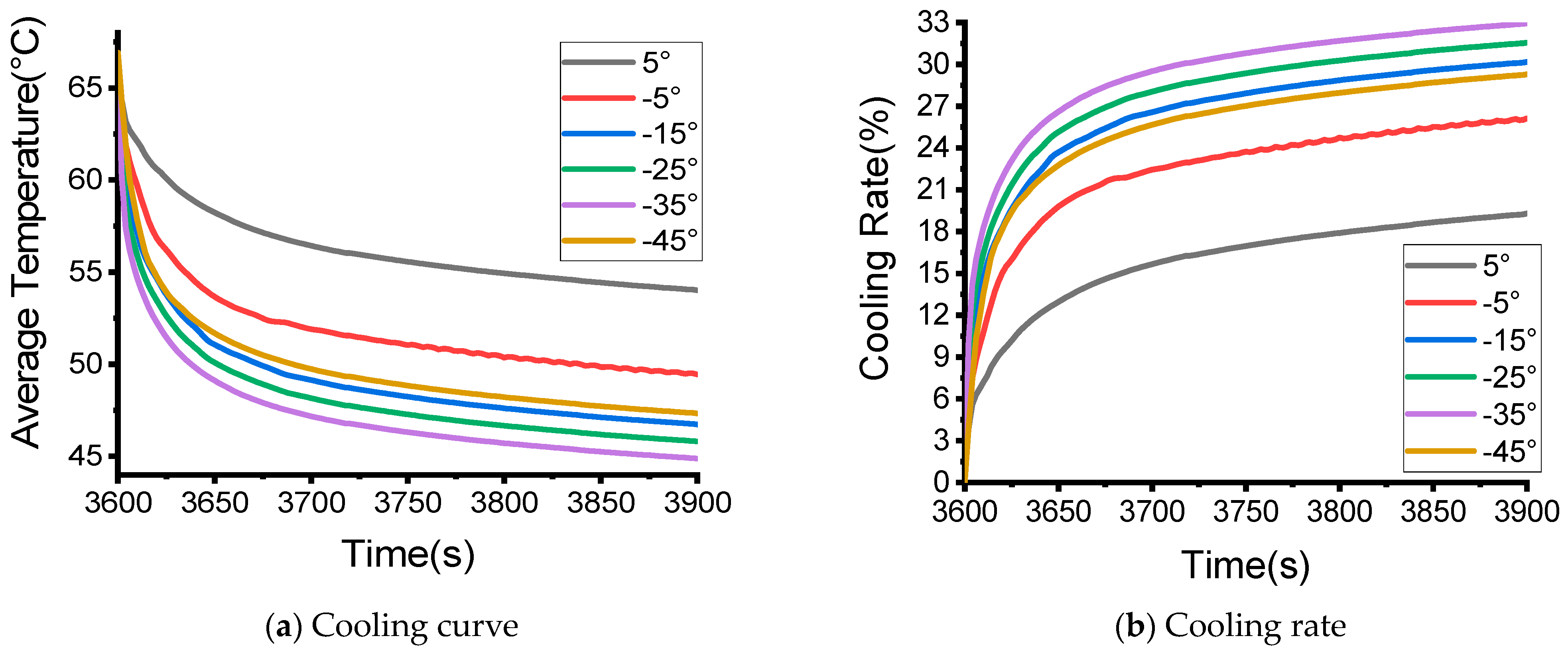
4. Characteristics of Pre-Cooling Ventilation in Occupant Cabin
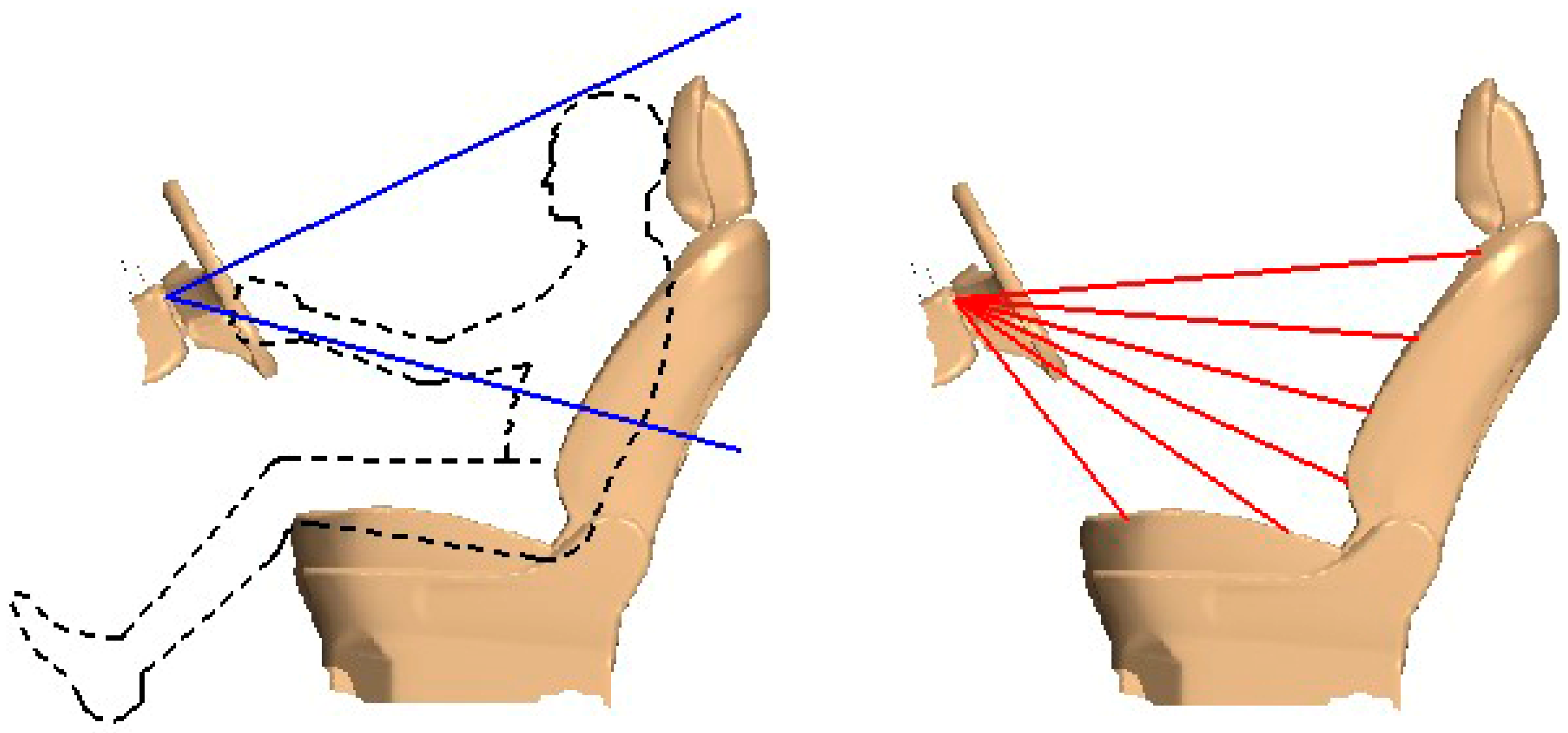
4.1. Working Condition Setting
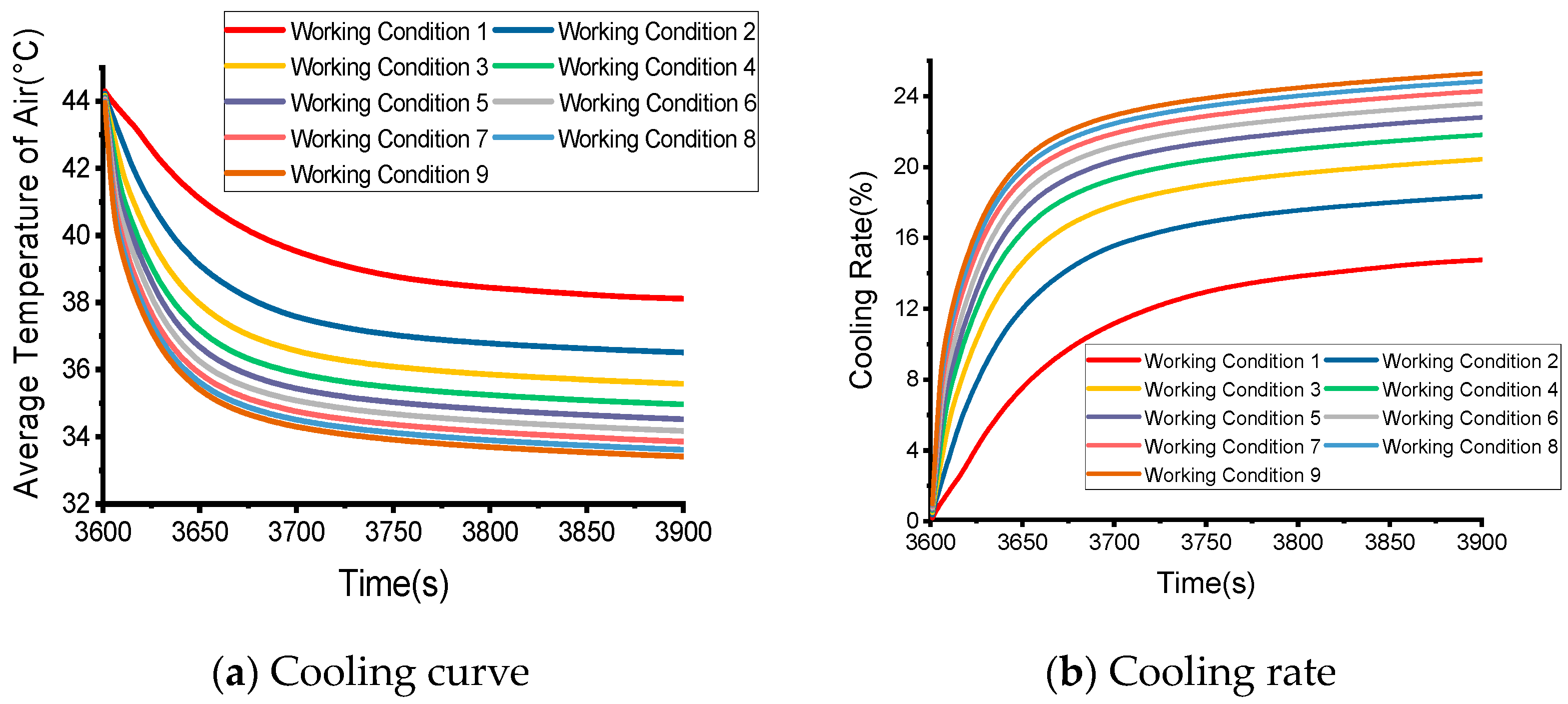
4.2. Simulation Analysis of the Average Air Temperature in the Occupant Cabin
4.3. Simulation Analysis of the Average Temperature of the Seat
5. Conclusions
- (a)
- There are large differences in the surface convective heat transfer coefficients of different parts of the vehicle body, and there are large errors in their solution using empirical formulas. The solution accuracy can be improved by establishing a virtual wind tunnel and using the CAS model outside the vehicle body.
- (b)
- At the same solar radiation intensity, compared to gray body heat radiation, a multi-band heat radiation model that takes into account the greenhouse effect shows an increase in the overall temperature of the passenger cabin. For areas close to the front windshield, such as front seats and dashboards, etc., the impact of the greenhouse effect is more significant.
- (c)
- In the process of ventilation and cooling, the cooling effect of the air in the passenger cabin is mainly determined by the air supply volume, and the air supply angle has a limited impact on the cooling effect. For the driver’s seat, adjusting the air supply volume and air supply angle has a great impact on the cooling effect. The larger the total air supply, the better the cooling effect. However, as the air supply increases, the effect of increasing the cooling rate gradually weakens. Adjusting the air supply angle of the air outlet can change the flow field distribution near the seat surface, and the average cooling rate can be improved by adjusting the air supply angle reasonably, which can reduce energy consumption.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Al-Kayiem, H.H.; Sidik, M.F.B.M.; Munusammy, Y.R. Study on the Thermal Accumulation and Distribution Inside a Parked Car Cabin. Am. J. Appl. Sci. 2010, 7, 784–789. [Google Scholar] [CrossRef]
- Wyon, D.P.; Wyon, I.; Norin, F.J.E. Effects of moderate heat stress on driver vigilance in a moving vehicle. Ergonomics 1996, 39, 61–75. [Google Scholar] [CrossRef] [PubMed]
- Lenzuni, P.; Capone, P.; Freda, D.; Del Gaudio, M. Is driving in a hot vehicle safe? Int. J. Hyperth. 2014, 30, 250–257. [Google Scholar] [CrossRef] [PubMed]
- Grundstein, A.; Dowd, J.; Meentemeyer, V. Quantifying the Heat-Related Hazard for Children in Motor Vehicles. Bull. Am. Meteorol. Soc. 2010, 91, 1183–1191. [Google Scholar] [CrossRef]
- Li, L. Simulation and Experimental of Vehicle Cabin and Components Thermal Load under Natural Exposure. Master’s Thesis, South China University of Technology, Guangzhou, China, 2015. [Google Scholar]
- Hu, C. A Study of the Characteristics of Sunning and Ventilation Cooling in Parked Vehicle. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2016. [Google Scholar]
- Ravindra, K.; Agarwal, N.; Mor, S. Assessment of thermal comfort parameters in various car models and mitigation strategies for extreme heat-health risks in the tropical climate. J. Environ. Manag. 2020, 267, 110655. [Google Scholar] [CrossRef] [PubMed]
- Mezrhab, A.; Bouzidi, M. Computation of thermal comfort inside a passenger car cabin. Appl. Therm. Eng. 2006, 26, 1697–1704. [Google Scholar] [CrossRef]
- Lahimer, A.A.; Alghoul, M.A.; Sopian, K. Potential of Solar Reflective Cover on Regulating the Car Cabin Conditions and Fuel Consumption. Appl. Therm. Eng. 2018, 143, 59–71. [Google Scholar] [CrossRef]
- Dadour, I.R.; Almanjahie, I.; Fowkes, N.D.; Keady, G.; Vijayan, K. Temperature variations in a parked vehicle. Forensic Sci. Int. 2011, 207, 205–211. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Lai, D.; Chen, Q. Experimental investigation of thermal comfort in a passenger car under driving conditions. Build. Environ. 2018, 149, 109–119. [Google Scholar] [CrossRef]
- Chen, S.; Du, B.; Li, Q.; Xue, D. The influence of different orientations and ventilation cases on temperature distribution of the car cabin in the hot soak. Case Stud. Therm. Eng. 2022, 39, 102401. [Google Scholar] [CrossRef]
- Marshall, G.J.; Mahony, C.P.; Rhodes, M.J.; Daniewicz, S.R.; Tsolas, N.; Thompson, S.M. Thermal Management of Vehicle Cabins, External Surfaces, and Onboard Electronics: An Overview. Engineering 2019, 5, 954–969. [Google Scholar] [CrossRef]
- Tan, L.; Yuan, Y. Computational fluid dynamics simulation and performance optimization of an electrical vehicle Air conditioning system. Alex. Eng. J. 2022, 61, 315–328. [Google Scholar] [CrossRef]
- Hariharan, C.; Sanjana, S.; Saravanan, S.; Sundar, S.S.; Prakash, A.S.; Raj, A.A. CFD studies for energy conservation in the HVAC system of a hatchback model passenger car. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 45, 4724–4741. [Google Scholar]
- Lu, K.; Gu, Z.; Jia, X.; Yin, Y. Analysis and Improvement of the Effects of Air-conditioning System on the Thermal Comfort of Passenger Cabin in a Heavy Truck. Automot. Eng. 2011, 33, 162–166. [Google Scholar]
- Gu, Z.; Shen, H.; Yang, Z.; Yin, Y. Improvement of vehicle air-conditioning duct and analysis of its impact on occupant thermal comfort. J. Chongqing Univ. 2013, 36, 91–96. [Google Scholar]
- Wang, J.; Xue, C.; Hu, X.; Cao, J.; Yue, L.; Shi, R. Simulation of airflow in passenger cabin based on air-conditioning supply parameters. J. Jilin Univ. (Eng. Technol. Ed.) 2017, 47, 50–57. [Google Scholar]
- Khatoon, S.; Kim, M.-H. Thermal Comfort in the Passenger Compartment Using a 3-D Numerical Analysis and Comparison with Fanger’s Comfort Models. Energies 2020, 13, 690. [Google Scholar] [CrossRef]
- Tobias, D.; Pascal, L.; Andre, V.; Daniel, S.; Mikhail, K.; Johannes, B. Vertical ventilation concepts for future passenger cars. Build. Environ. 2018, 129, 142–153. [Google Scholar]
- Lyu, H.; Chen, B.; Gao, T.; Li, Y.; Shi, J.; Chen, J. Analysis on Thermal Comfort in Car Passenger Cabin Based on Flow Field and Temperature Field. Automot. Eng. 2020, 42, 234–239. [Google Scholar]
- Sen, S.; Selokar, M. Numerical Simulation and Validation of Cabin Aiming and Cool-Down of a Passenger Car. Sae Int. J. Passeng. Cars-Mech. Syst. 2016, 9, 52–61. [Google Scholar] [CrossRef]
- Tang, J.; Gu, Z.; Mo, Z.; Wen, Q.; Zhang, S. Optimization of vehicle air-conditioning grilles and the improvement of passenger thermal comfort. J. Hefei Univ. Technol. (Nat. Sci.) 2016, 39, 309–313, 394. [Google Scholar]
- Singh, O.P.; Raut, R.; Biswas, M.; Singh, R. Effect of Dynamic Vents on the Thermal Comfort of a Passenger Car. Stroj. Vestn.-J. Mech. Eng. 2015, 61, 561–570. [Google Scholar] [CrossRef]
- Zhao, J. Design and Implementation of Communication Module for Car Air-Conditioning Remote Control System Based on FPGA. Master’s Thesis, Jilin University, Changchun, China, 2012. [Google Scholar]
- Guo, P.; Hu, X.; Gao, H.; Wang, M.; Sang, T.; Wang, J.; Cao, J. Influence of Parked Car Ventilation Parameters on Driver Cabin Cooling after Hot Soak. J. South China Univ. Technol. (Nat. Sci. Ed.) 2020, 48, 76–83. [Google Scholar]
- Chen, Z.; Qian, J.; Ye, Y. Predicting Theory of Effective Thermal Conductivity of Complex Material. J. Univ. Sci. Technol. China 1992, 22, 416–424. [Google Scholar]
- Zhen, J.; Guo, Q.; Zhou, J. Simulation of Heat Transfer in Multi-Layered Medium. Appl. Phys. 2019, 9, 7–12. [Google Scholar] [CrossRef]
- Li, G.; Ma, H. Numerical Simulations for the Laminar Natural Convection of High Rayleigh Numbers in an Enclosure. J. Huazhong Univ. Sci. Technol. 2004, 3, 14–17. [Google Scholar]
- Tao, W. Thermal, 5th ed.; Higher Education Press: Beijing, China, 2019; pp. 154–196. [Google Scholar]
- Standard Tables for Reference Solar Spectral Irradiance: Direct Normal and Hemispherical on 37° Tilted Surface. Available online: https://www.astm.org/standards/g173 (accessed on 5 May 2023).
- Shi, J.; Qi, W.; Xu, Q.; Zhou, S.; Wang, G. Etiological Analysis of Subambient Temperature Burn in 351 Cases of Hefei Area. Chin. J. Reparative Reconstr. Surg. 2010, 24, 665–667. [Google Scholar]
- Danca, P.; Vartires, A.; Dogeanu, A. An Overview of Current Methods for Thermal Comfort Assessment in Vehicle Cabin. Energy Procedia 2016, 85, 162–169. [Google Scholar] [CrossRef]





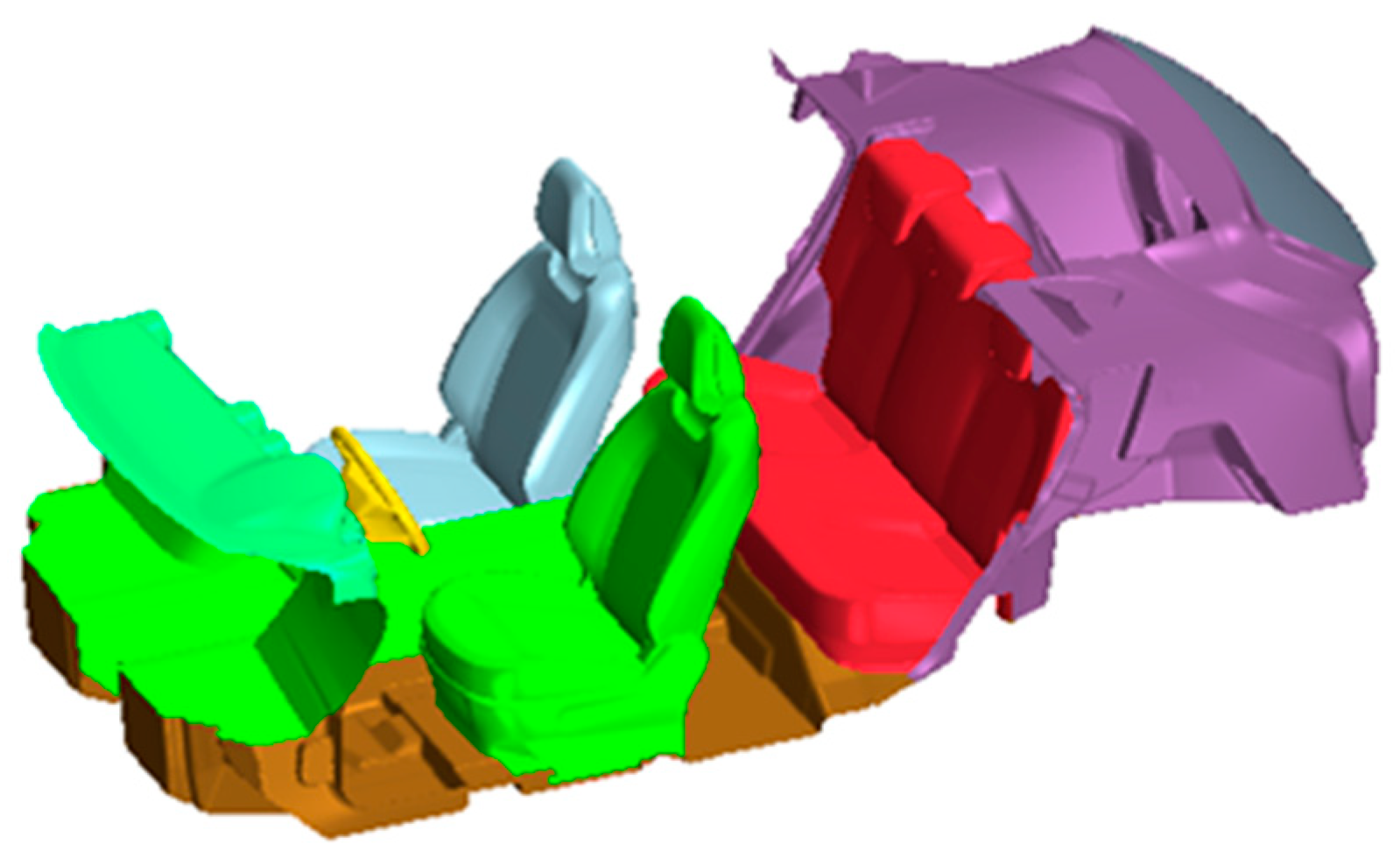
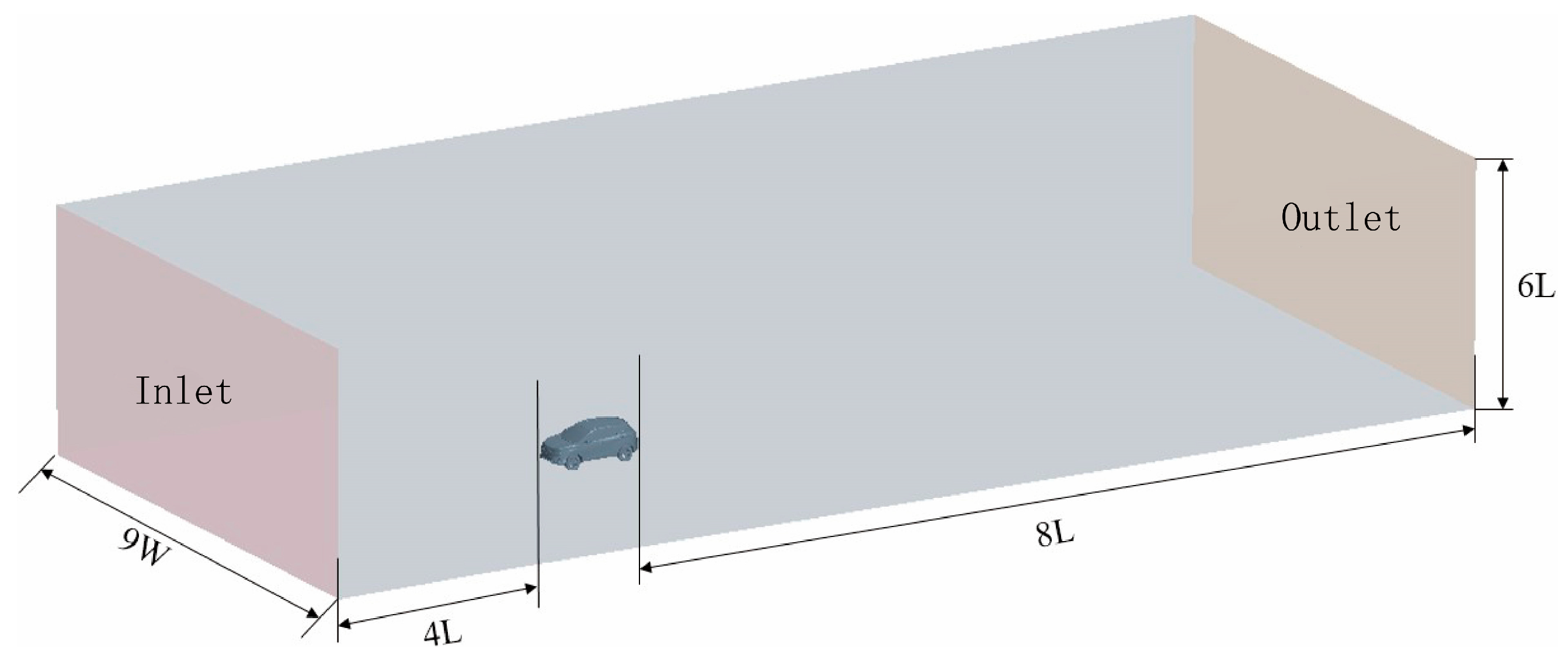
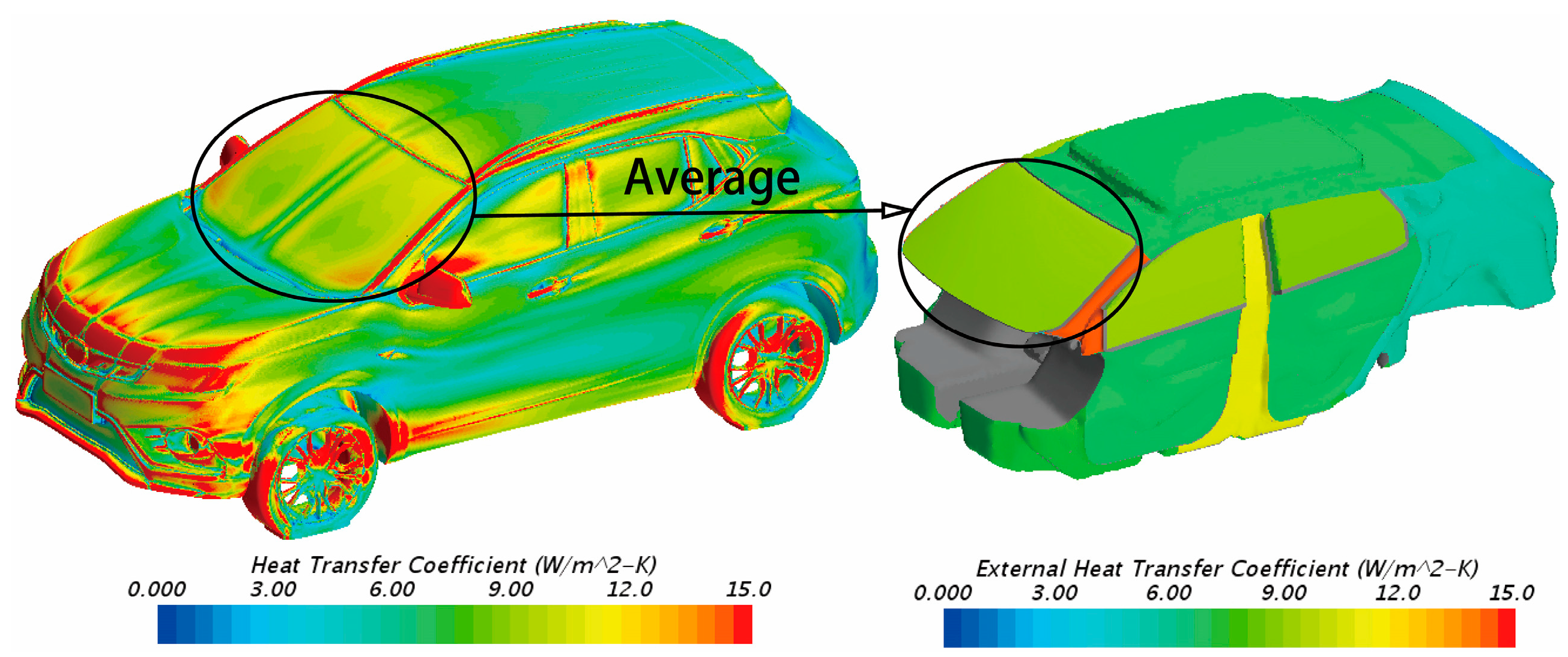
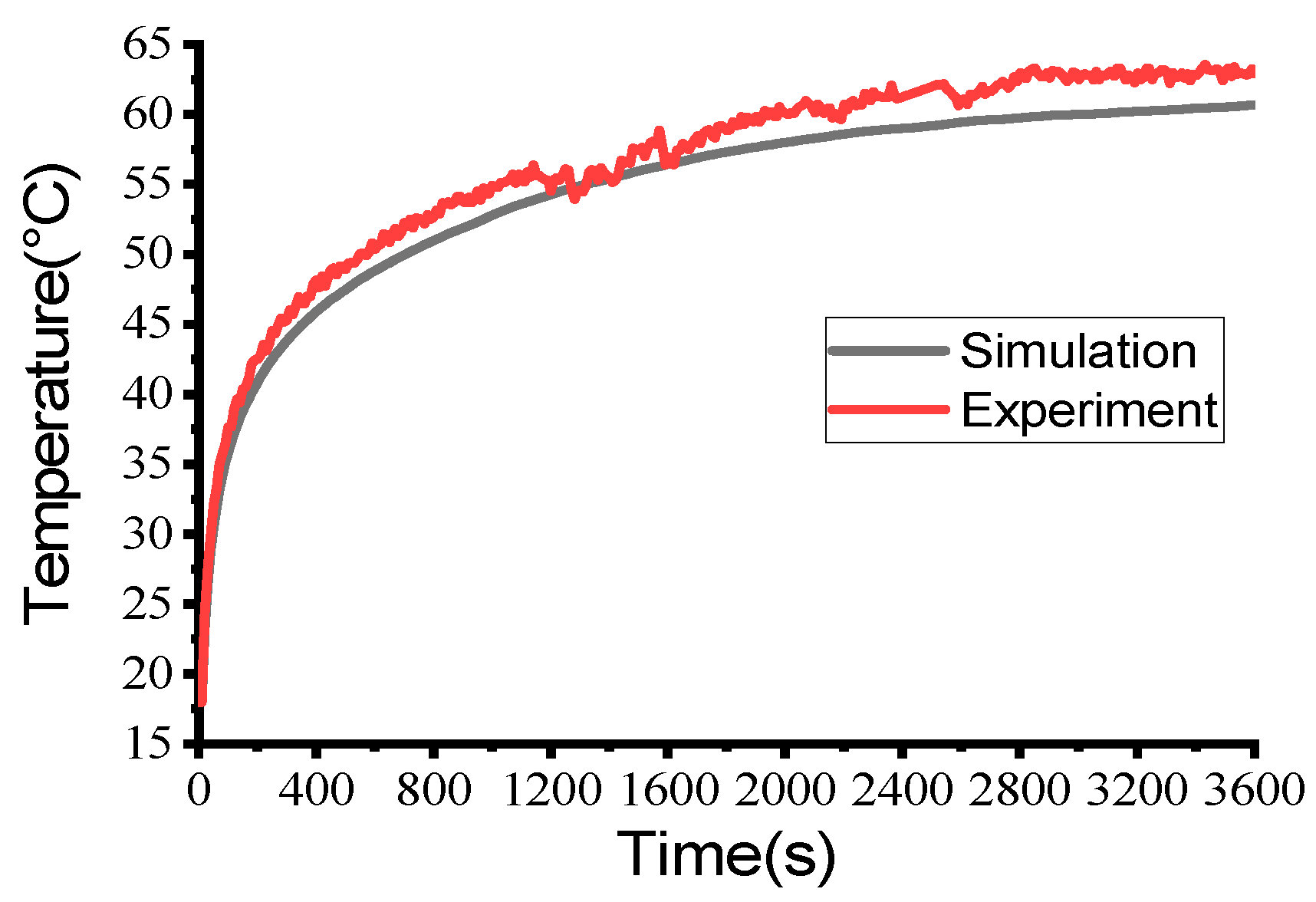

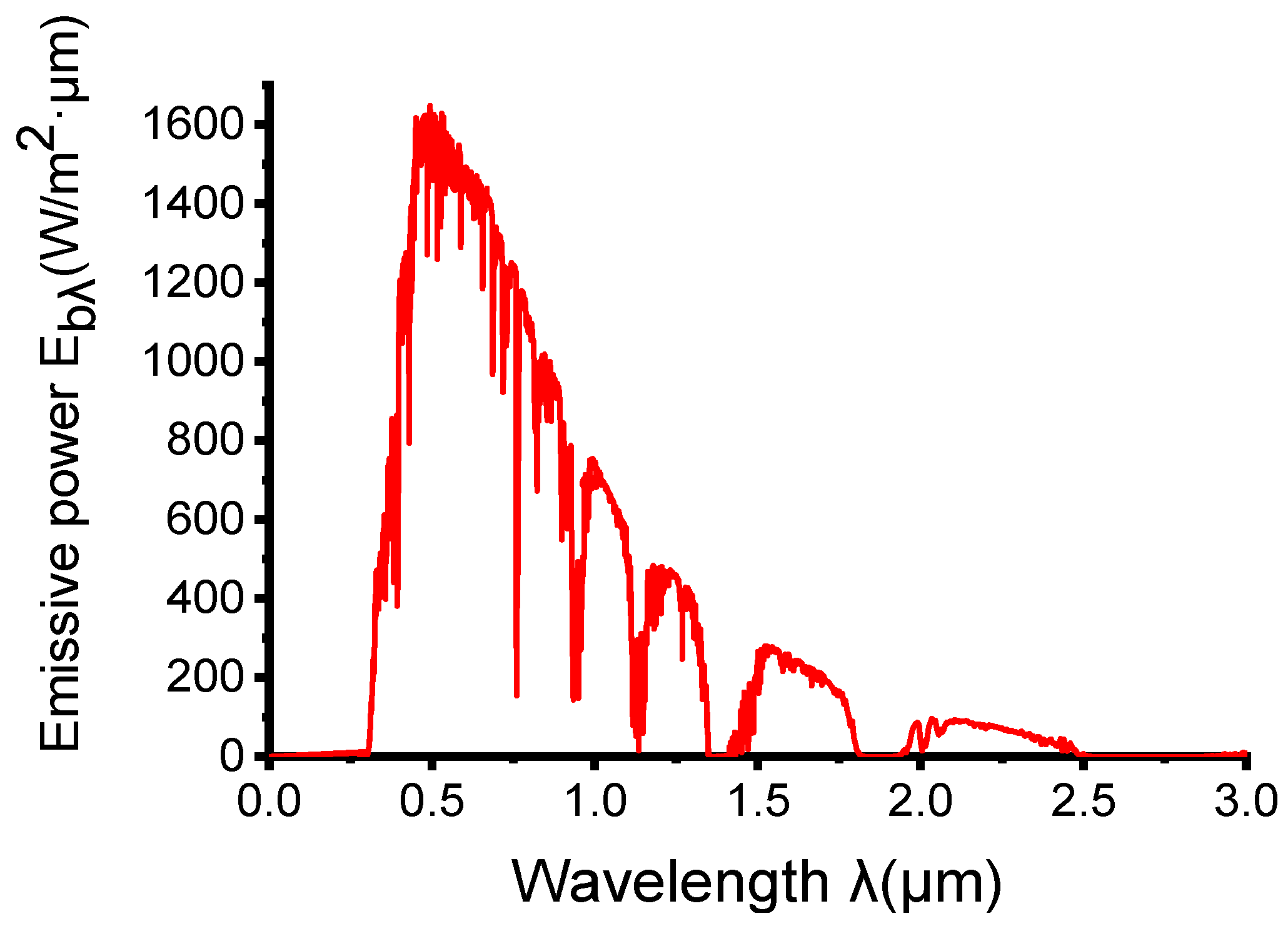
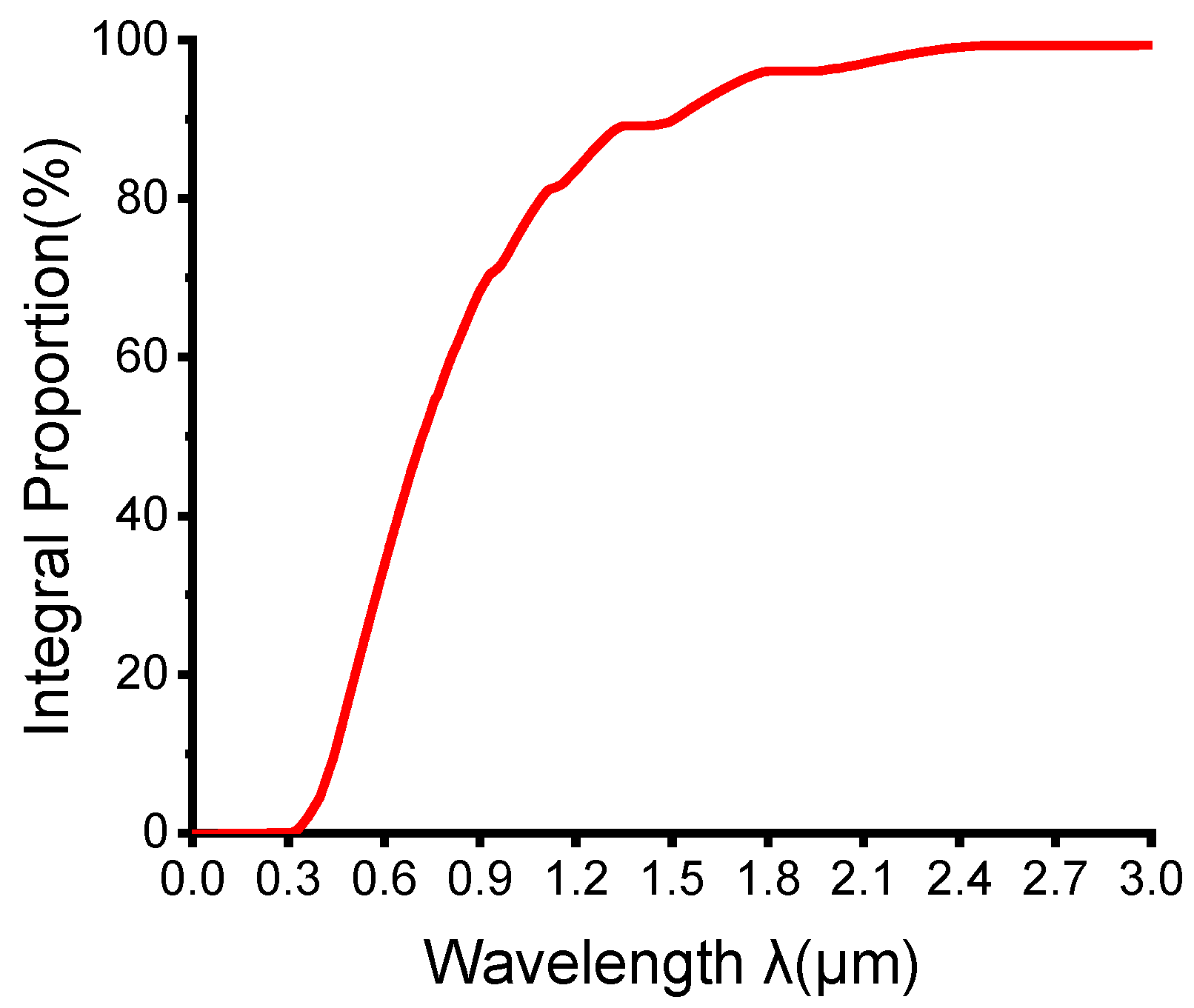
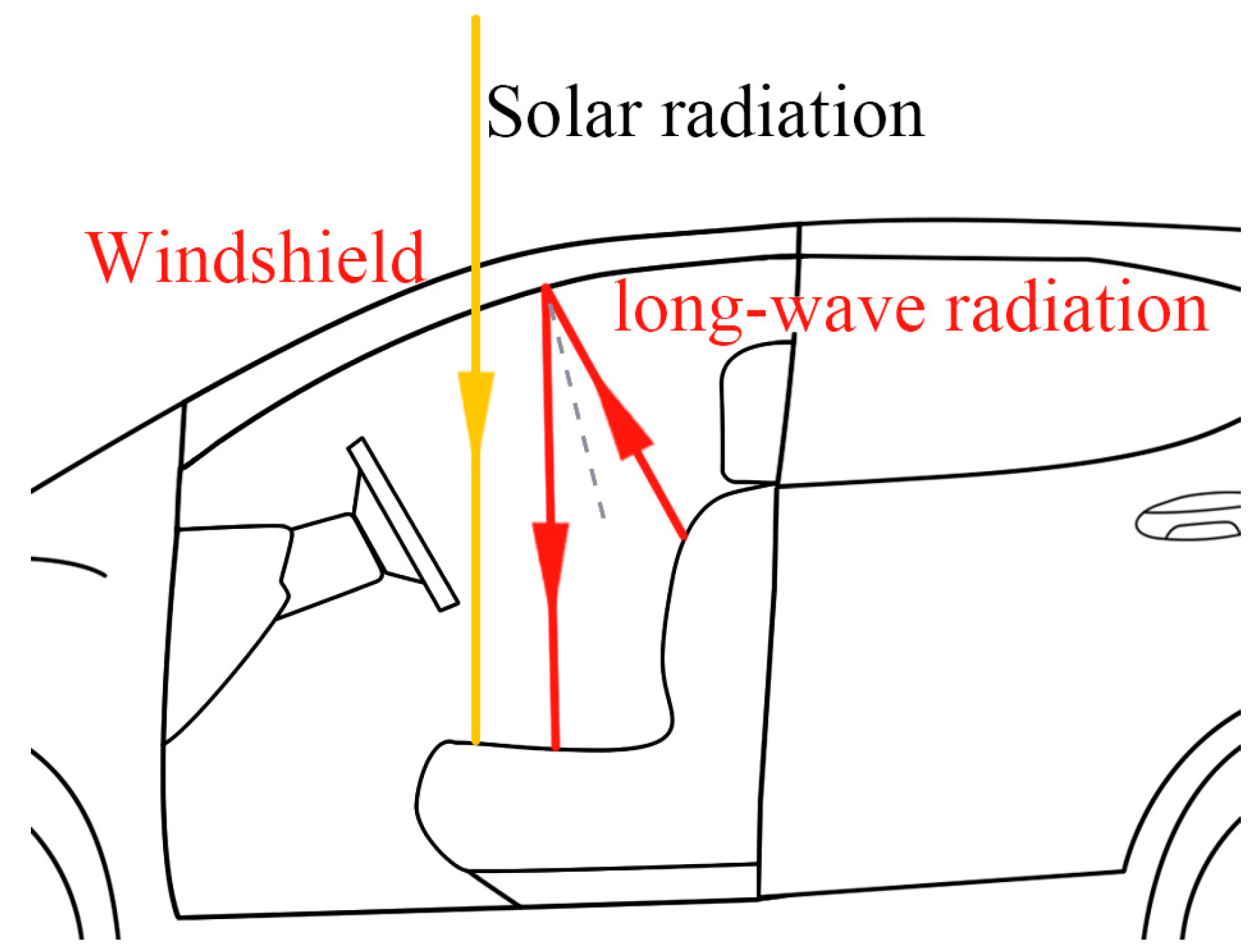
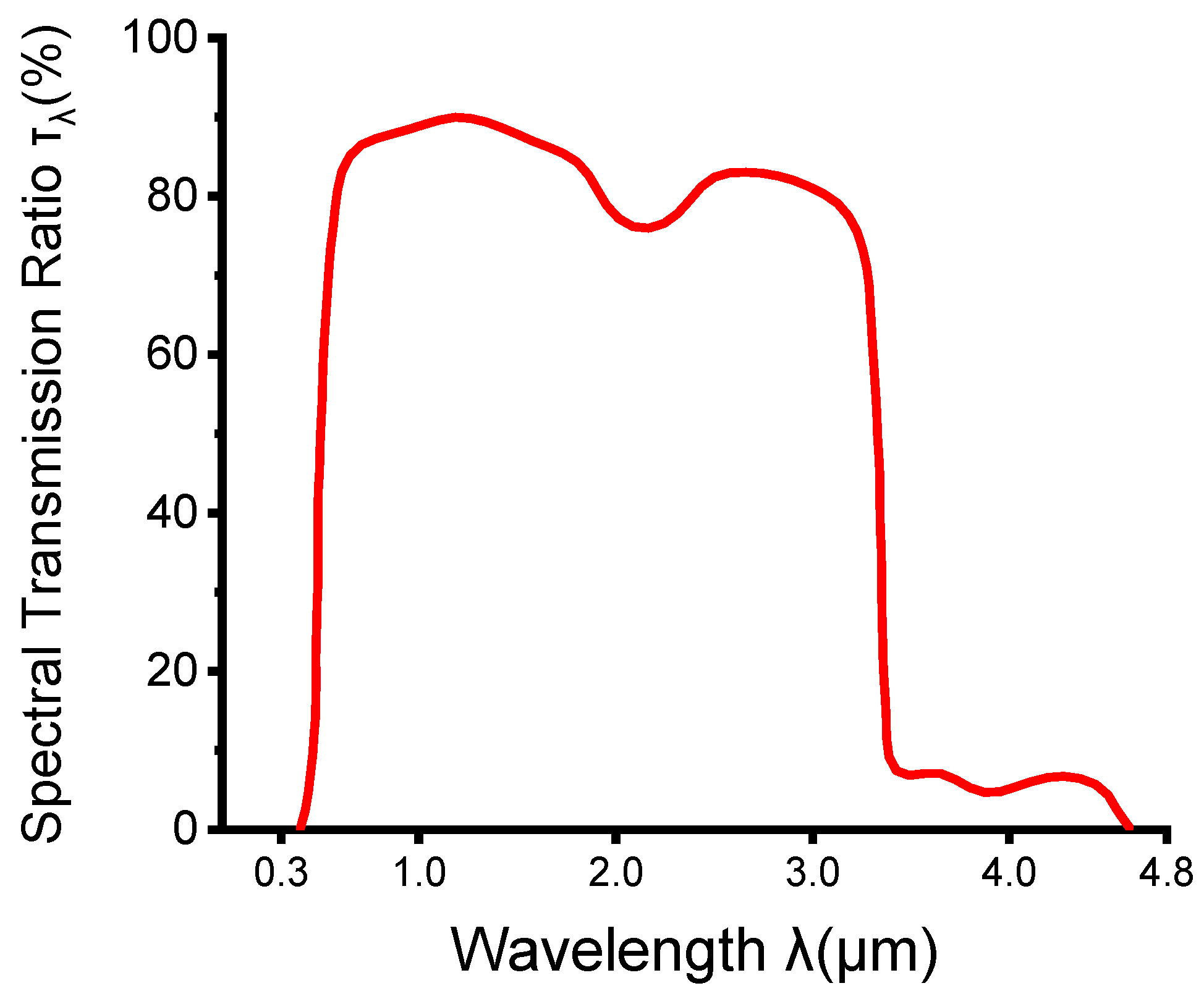






| Region | Multi-Section Radiation Conditions | |
|---|---|---|
| 0–3 μm | 3–400 μm | |
| Front windshield | 0.7 | 0.1 |
| Side window 1 | 0.7 | 0.1 |
| Side window 2 | 0.4 | 0.1 |
| Rear windshield | 0.4 | 0.1 |
| Occupant Cabin Parts | Absorption Rate α | Reflectivity ρ |
|---|---|---|
| Seats | 0.6 | 0.4 |
| Dashboard | 0.9 | 0.1 |
| Steering wheel | 0.85 | 0.15 |
| Doors | 0.6 | 0.4 |
| Roof | 0.6 | 0.4 |
| Floor | 0.5 | 0.5 |
| A pillar | 0.6 | 0.4 |
| B pillar | 0.6 | 0.4 |
| Temperature/°C | Density/kg·m−3 | Thermal Conductivity × 102/W·(m·K)−1 | Dynamic Viscosity × 106/kg·(m·s)−1 | Specific Heat Capacity/kJ·(kg·K)−1 |
|---|---|---|---|---|
| 30 | 1.165 | 2.67 | 18.6 | 1.005 |
| 40 | 1.128 | 2.76 | 19.1 | 1.005 |
| 50 | 1.093 | 2.83 | 19.6 | 1.005 |
| 60 | 1.060 | 2.90 | 20.1 | 1.005 |
| 70 | 1.029 | 2.96 | 20.6 | 1.009 |
| 80 | 1.000 | 3.05 | 21.1 | 1.009 |
| 90 | 0.972 | 3.13 | 21.5 | 1.009 |
| Region | Working Condition 1 | Base Working Condition | |
|---|---|---|---|
| / | 0–3 μm | 3–400 μm | |
| Front windshield | 0.7 | 0.7 | 0.1 |
| Side window 1 | 0.7 | 0.7 | 0.1 |
| Side window 2 | 0.4 | 0.4 | 0.1 |
| Rear windshield | 0.4 | 0.4 | 0.1 |
| Working Condition | Total Air Supply/m3·h−1 | Air Supply of Each Air Outlet/m3·h−1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 100 | 25 |
| 2 | 200 | 50 |
| 3 | 300 | 75 |
| 4 | 400 | 100 |
| 5 | 500 | 125 |
| 6 | 600 | 150 |
| 7 | 700 | 175 |
| 8 | 800 | 200 |
| 9 | 900 | 225 |
| Working Condition | Longitudinal Air Supply Angle (Deg.) |
|---|---|
| 1 | 25 |
| 2 | 15 |
| 3 | 5 |
| 4 | −5 |
| 5 | −15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, Z.; Liu, S.; Wang, G.; Chang, H. A Study of Passenger Car Cabin Pre-Ventilation under the Sun. Energies 2023, 16, 7154. https://doi.org/10.3390/en16207154
Zhang Y, Li Z, Liu S, Wang G, Chang H. A Study of Passenger Car Cabin Pre-Ventilation under the Sun. Energies. 2023; 16(20):7154. https://doi.org/10.3390/en16207154
Chicago/Turabian StyleZhang, Yingchao, Ziqiao Li, Shengda Liu, Guohua Wang, and He Chang. 2023. "A Study of Passenger Car Cabin Pre-Ventilation under the Sun" Energies 16, no. 20: 7154. https://doi.org/10.3390/en16207154
APA StyleZhang, Y., Li, Z., Liu, S., Wang, G., & Chang, H. (2023). A Study of Passenger Car Cabin Pre-Ventilation under the Sun. Energies, 16(20), 7154. https://doi.org/10.3390/en16207154







