Using the Exact Equivalent π-Circuit Model for Representing Three-Phase Transmission Lines Directly in the Time Domain
Abstract
:1. Introduction
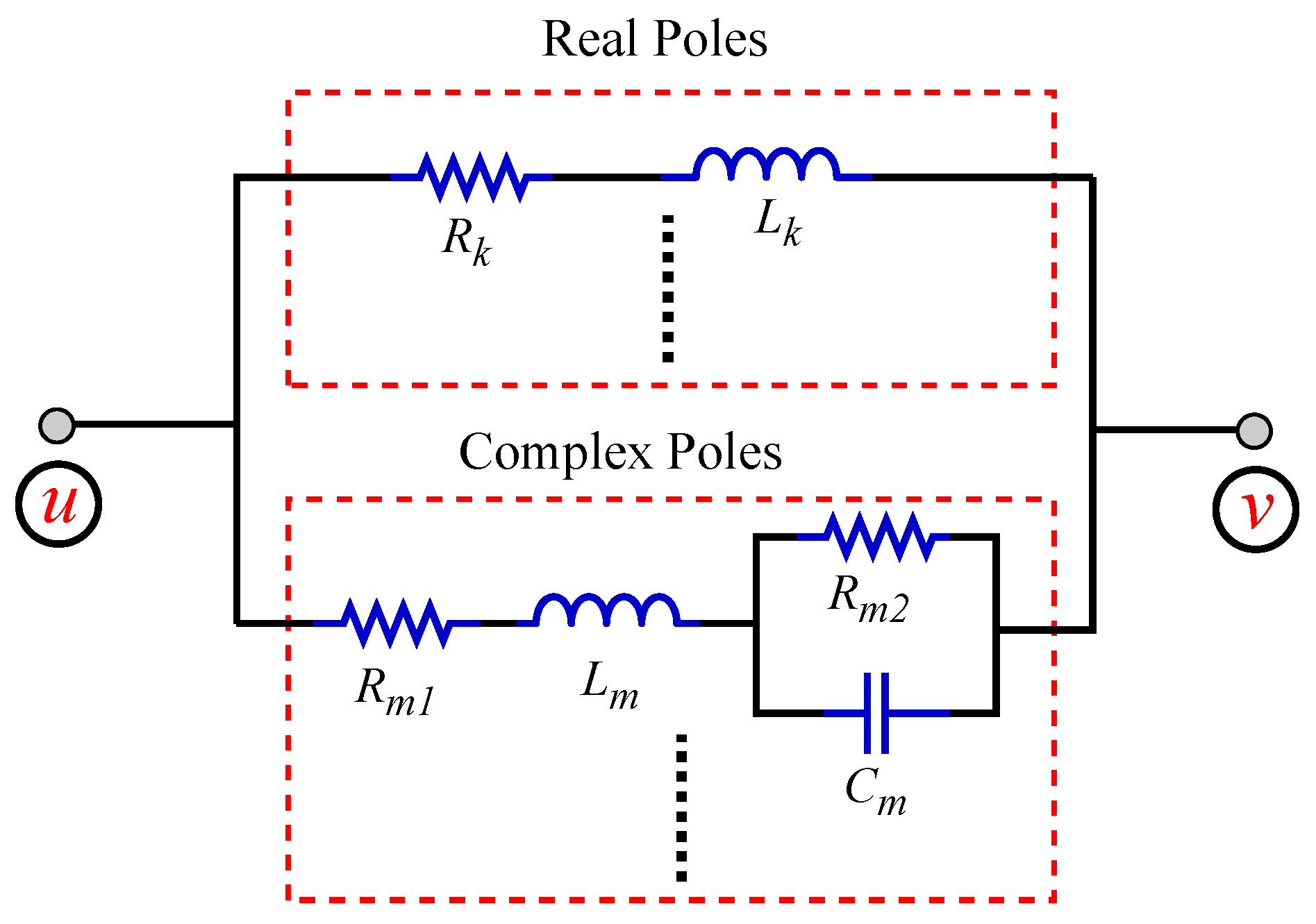
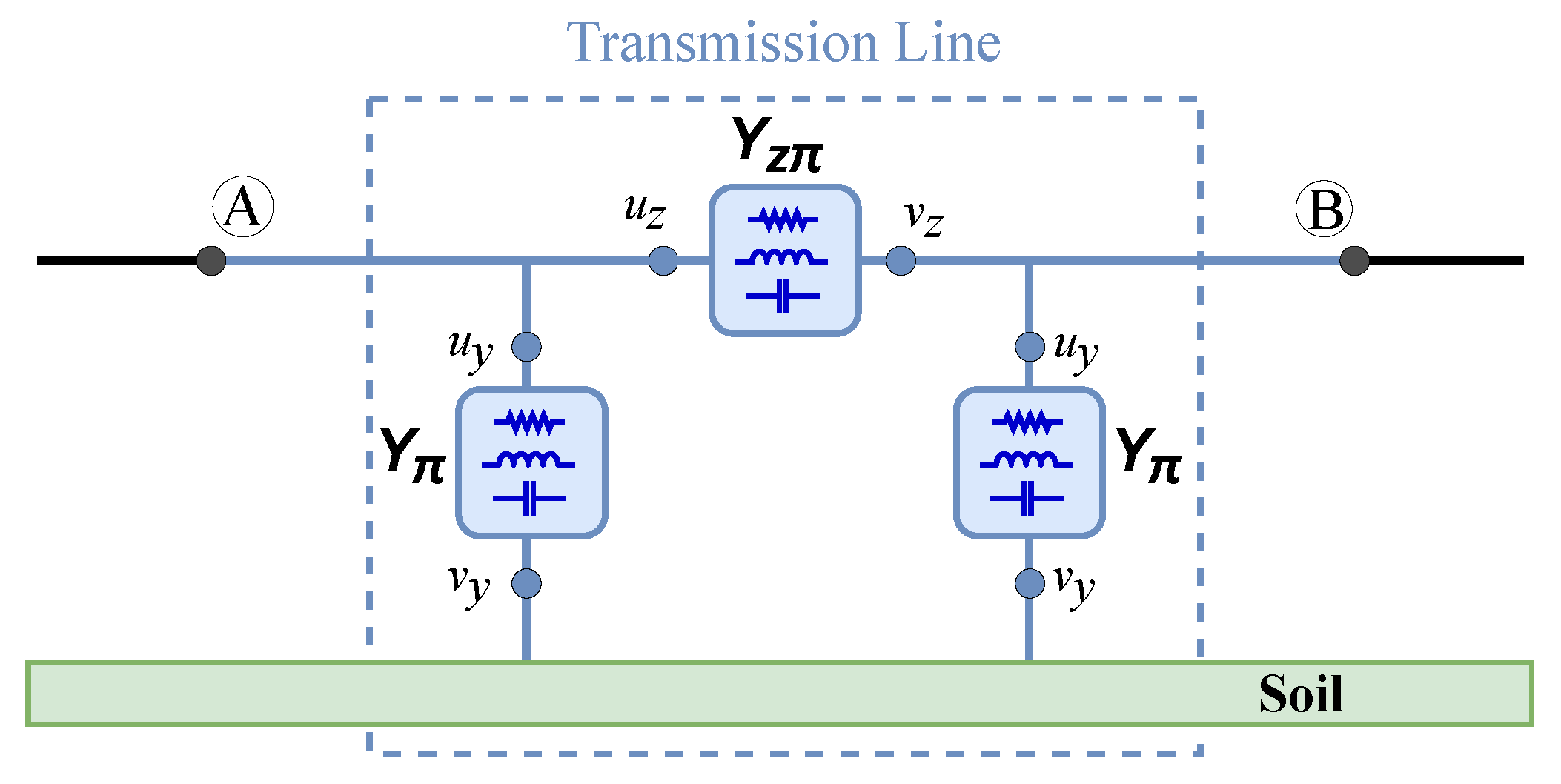
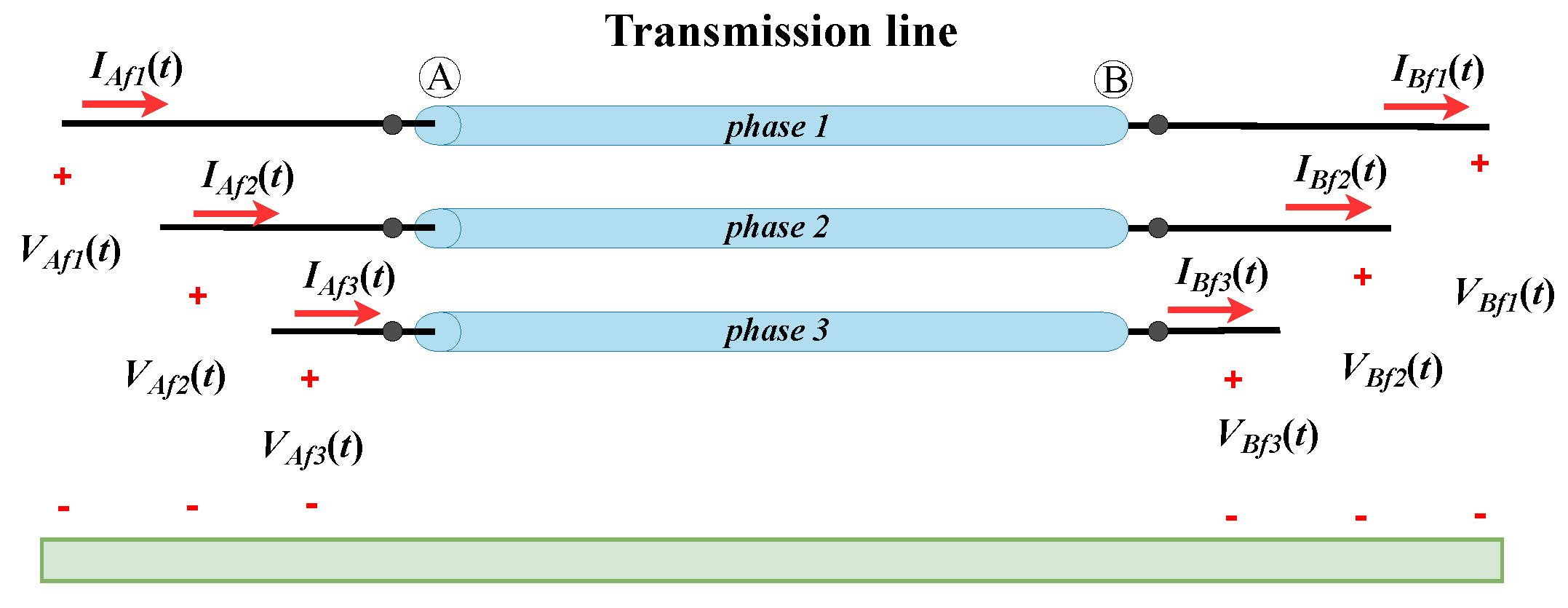
2. Exact Equivalent π-Circuit of a TL Formed by Circuit Elements

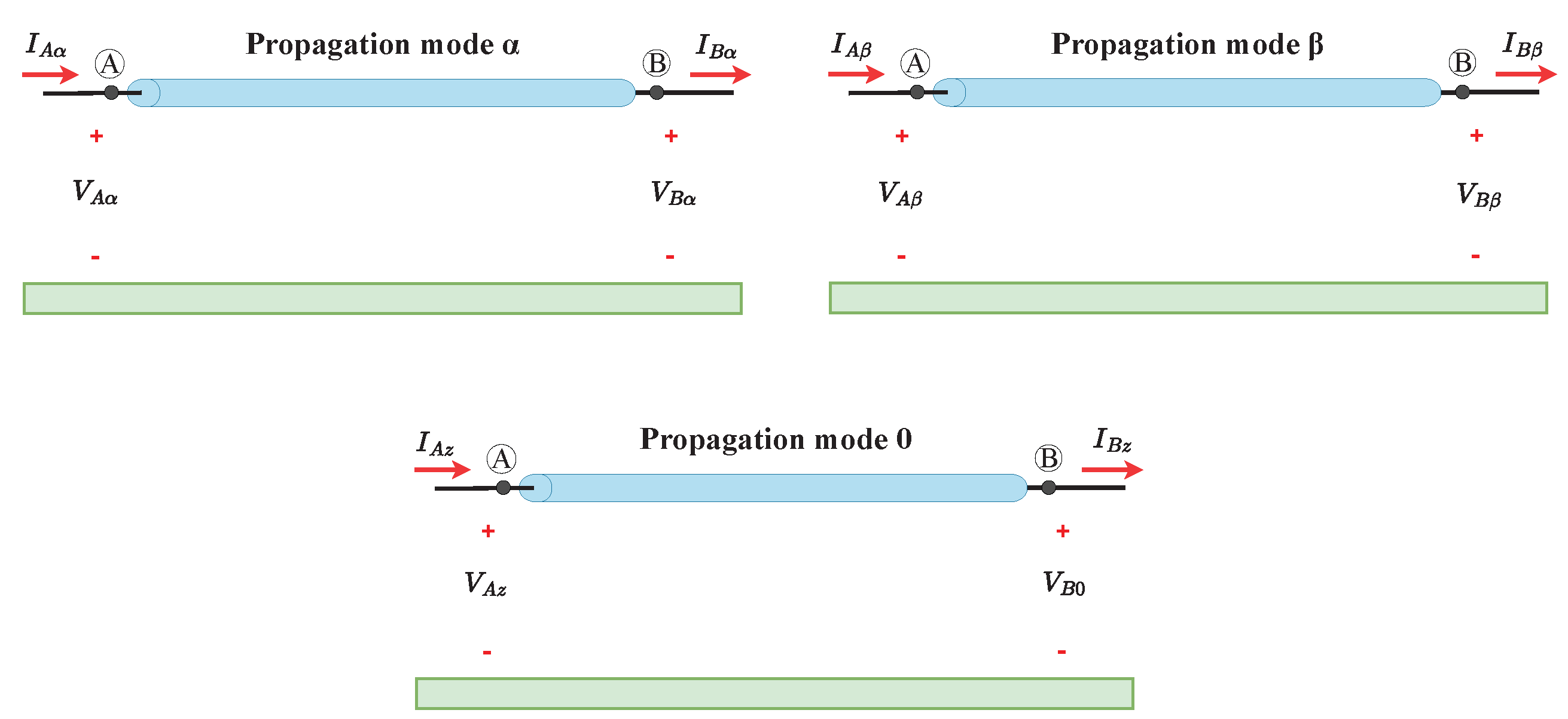
3. Representation of a Perfectly Transposed TL in the Mode Domain
4. Representation of Propagation Modes Using the Exact Equivalent π Circuit

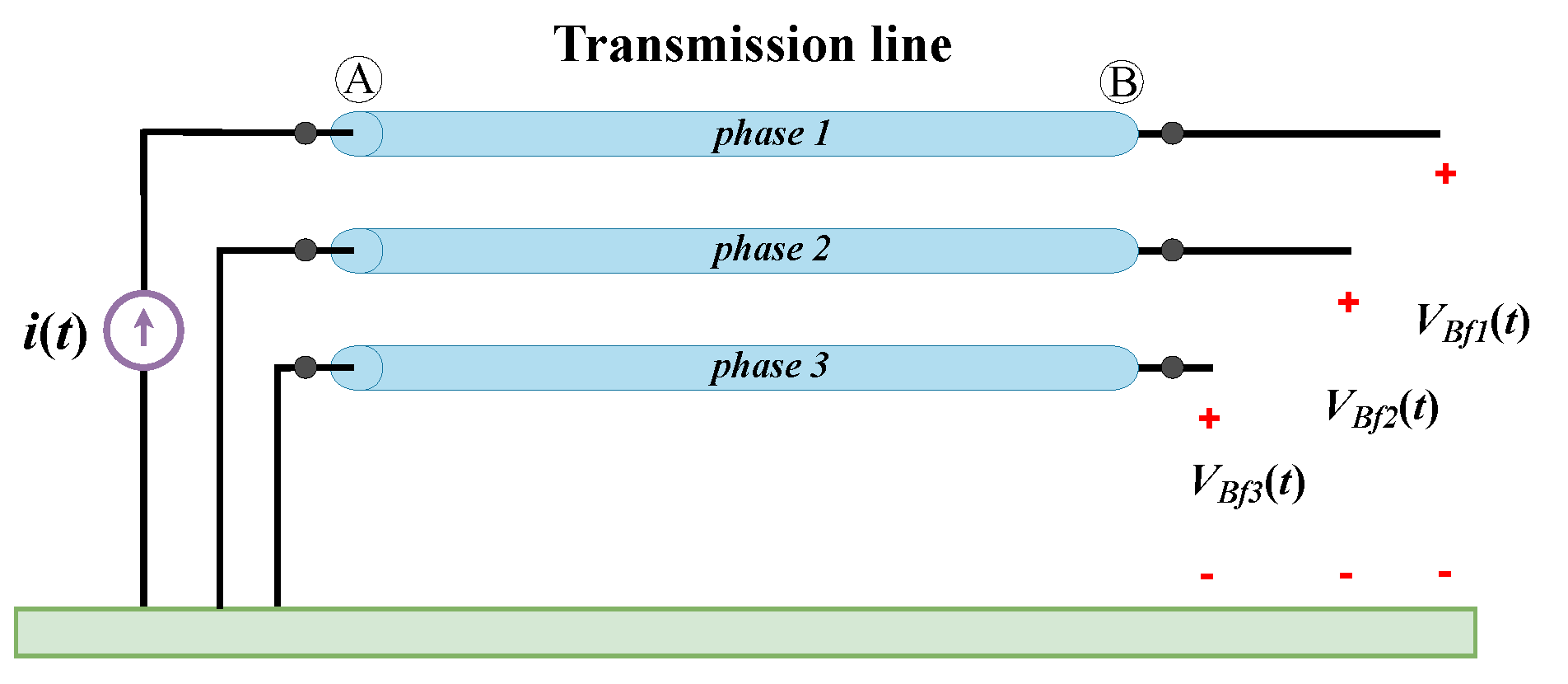
5. Methodology for the Implementation of a Proposed Model in ATP Software

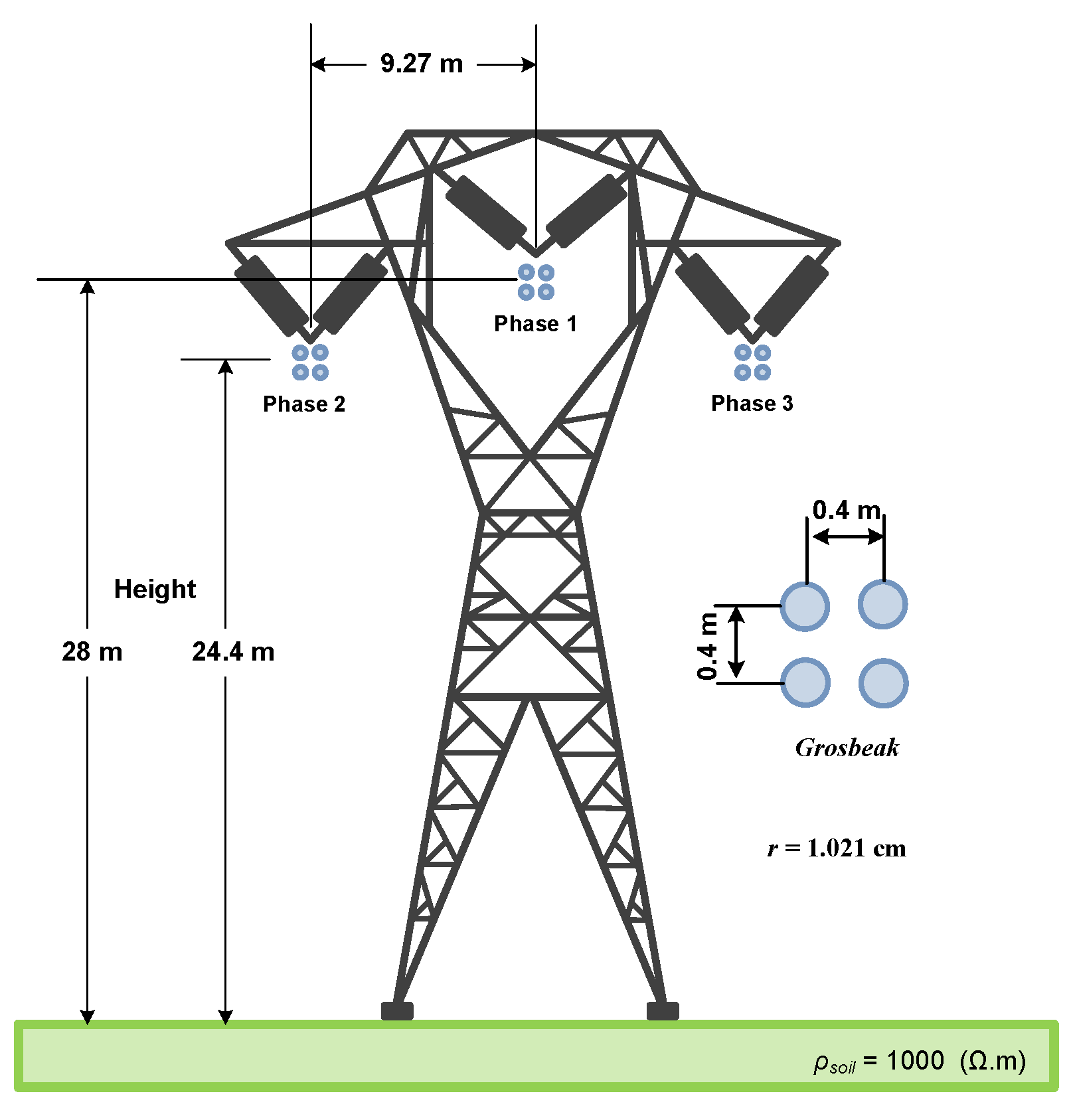
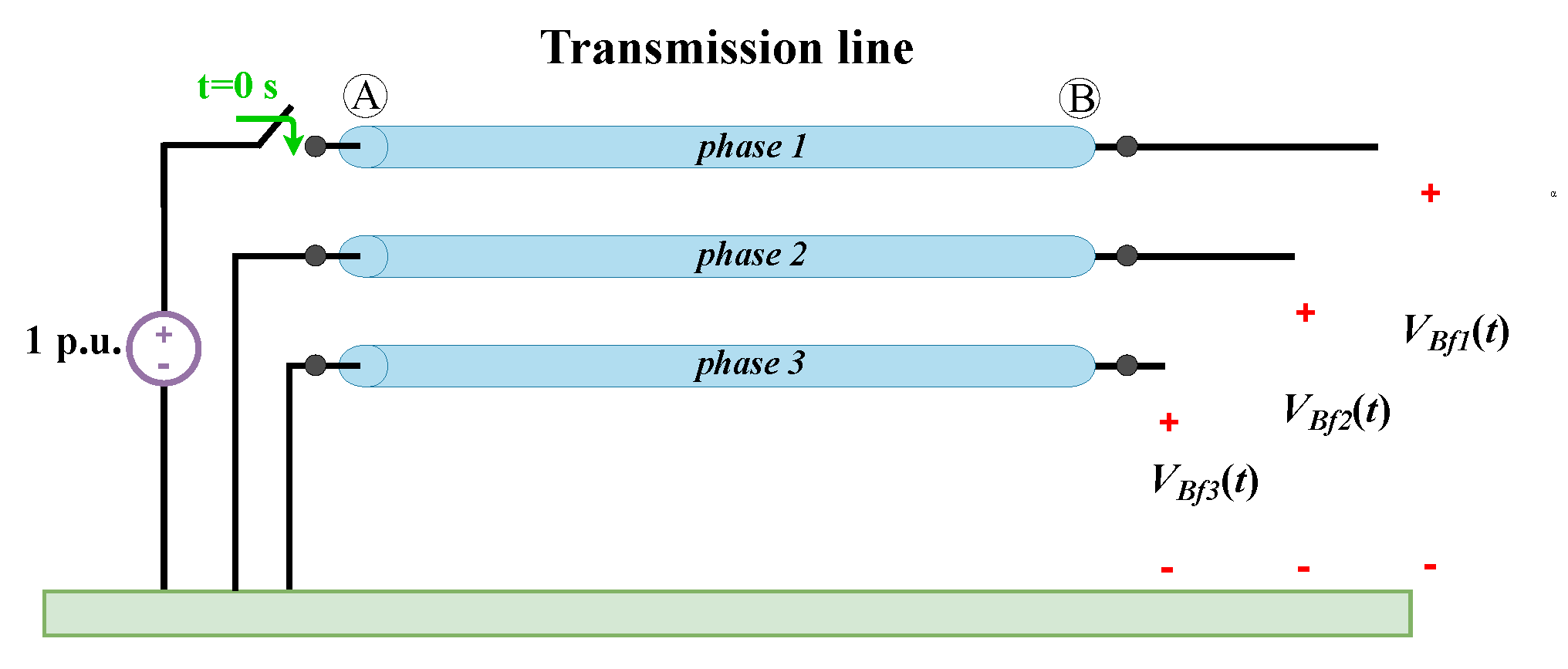
6. Results and Discussion
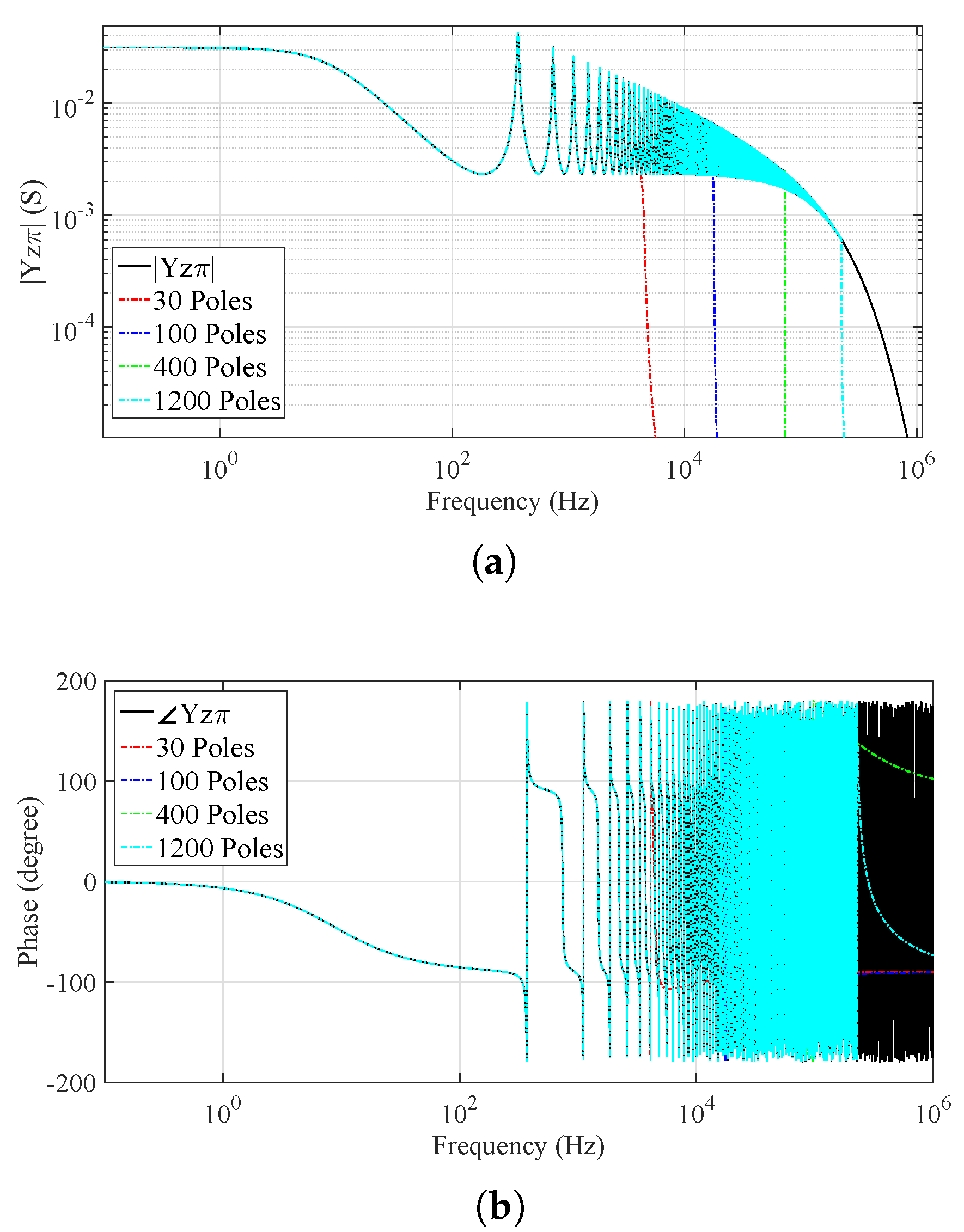
6.1. Rational Approximation of the Admittance Curves of and in the Propagation Modes
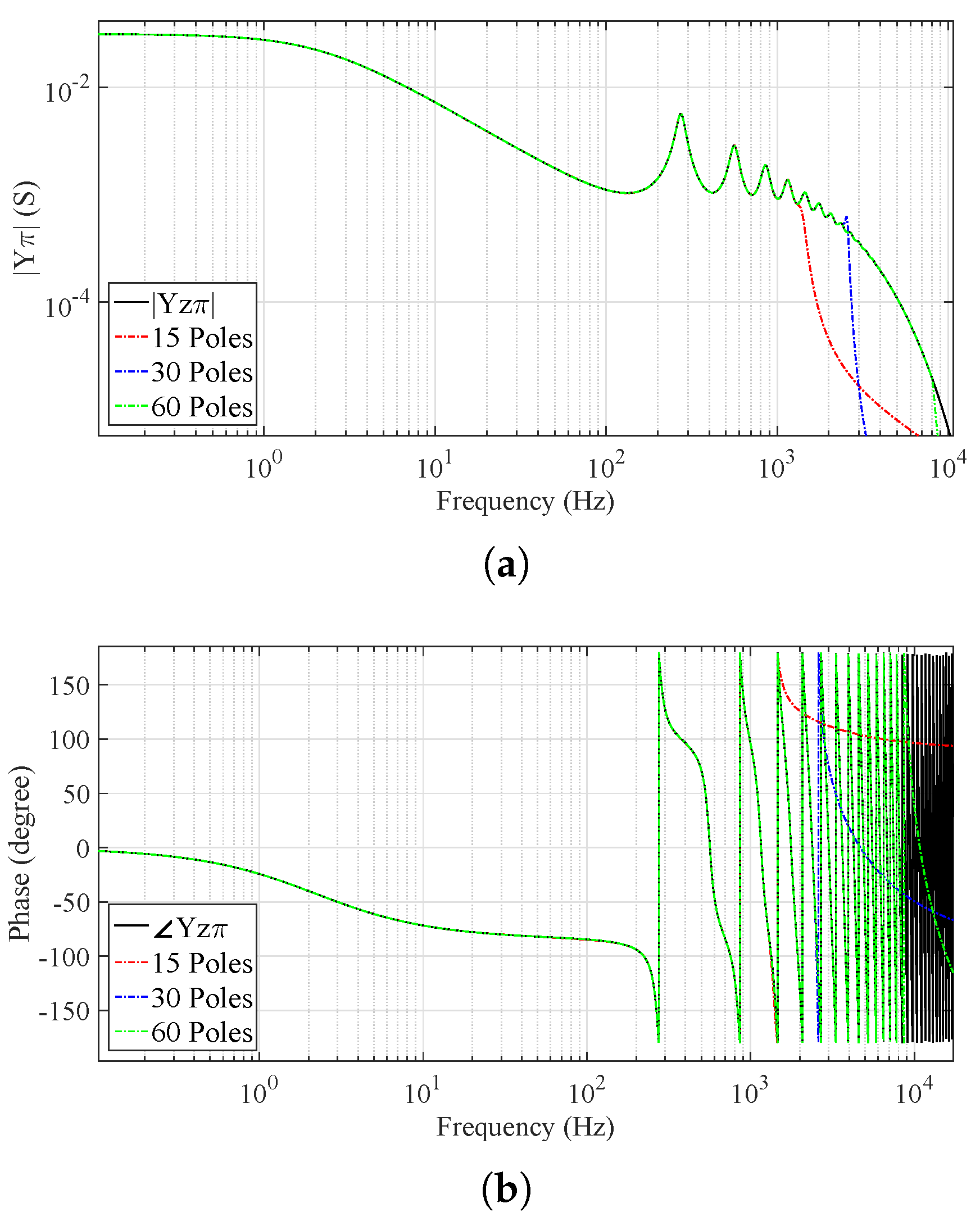

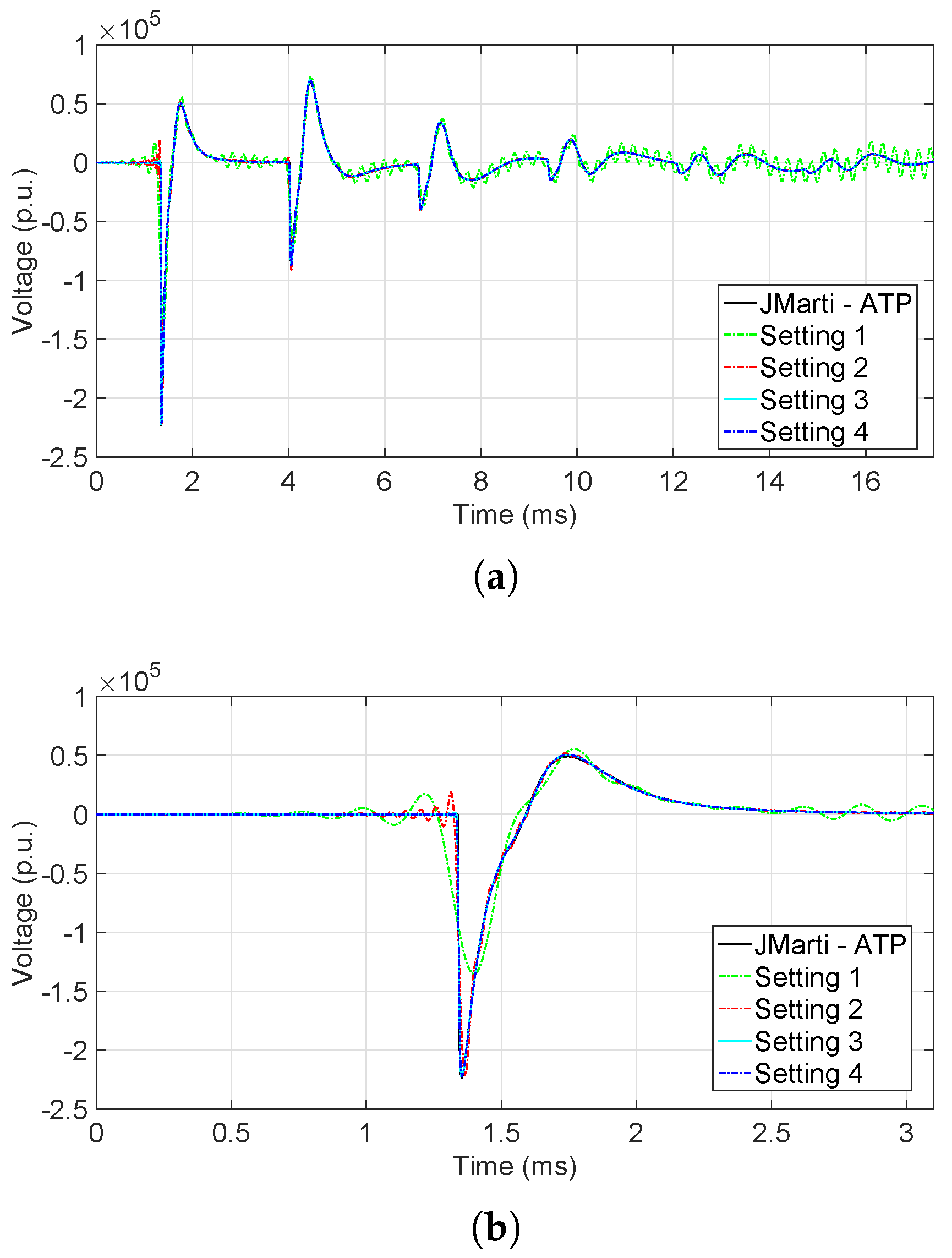
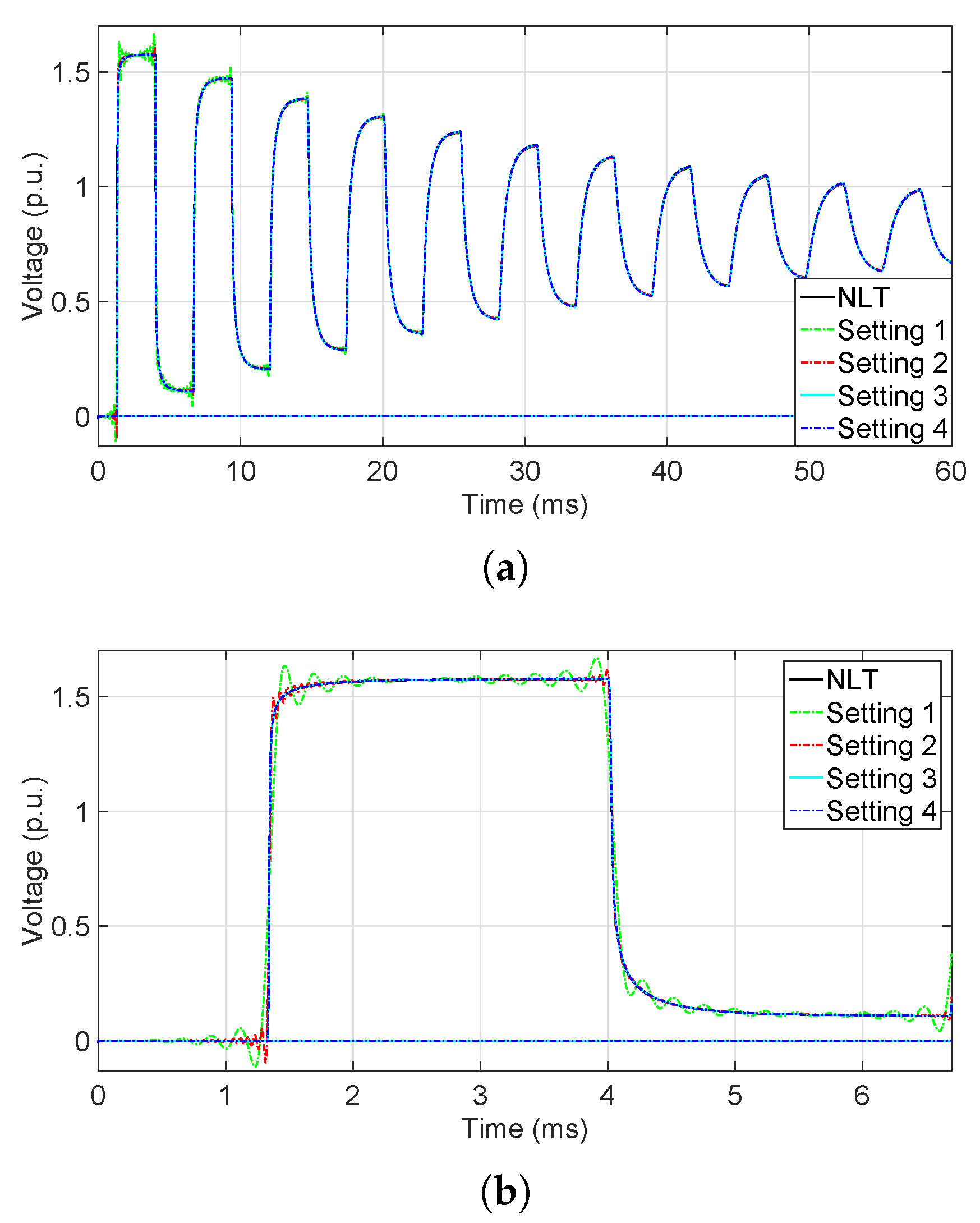
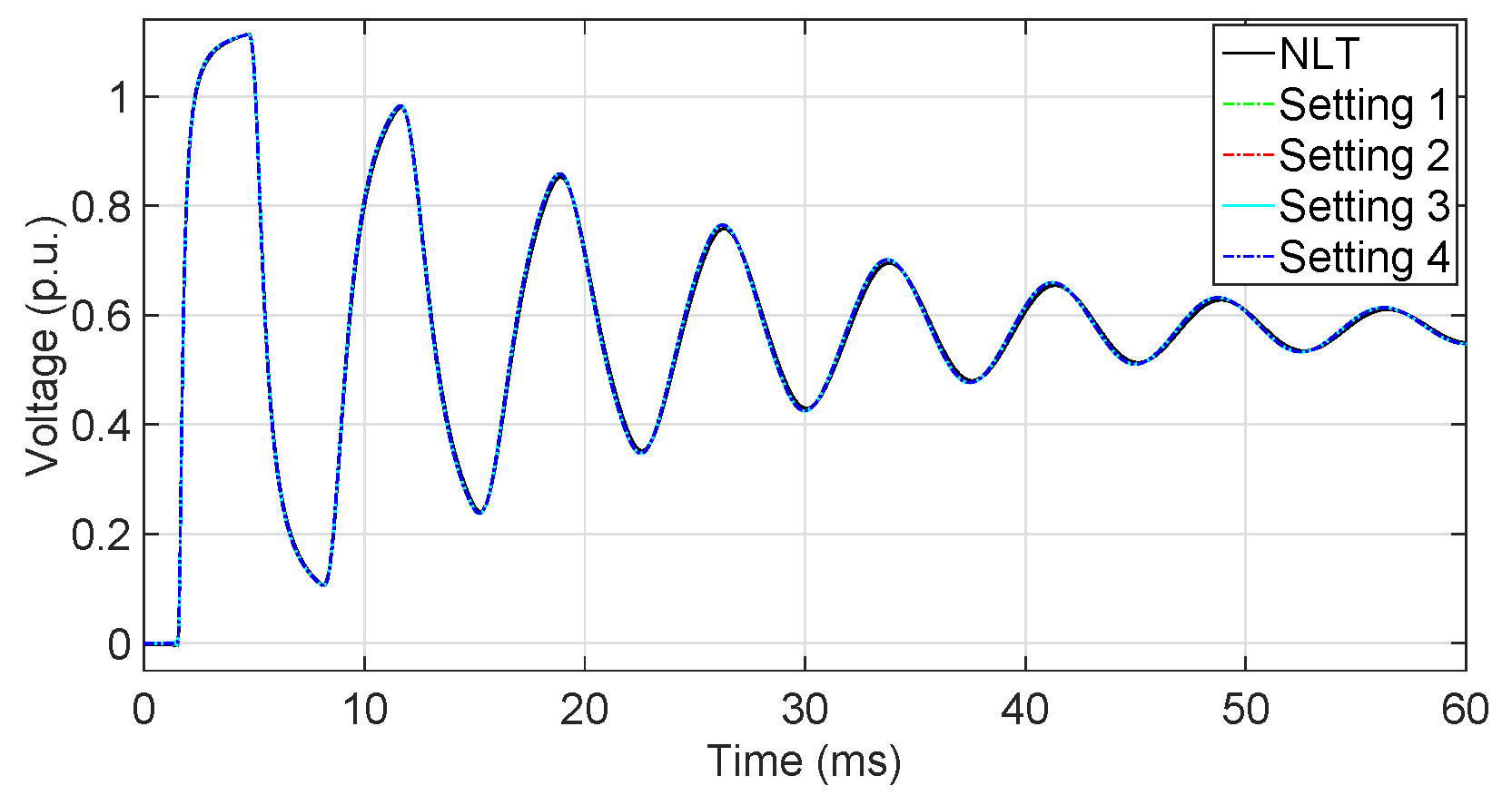
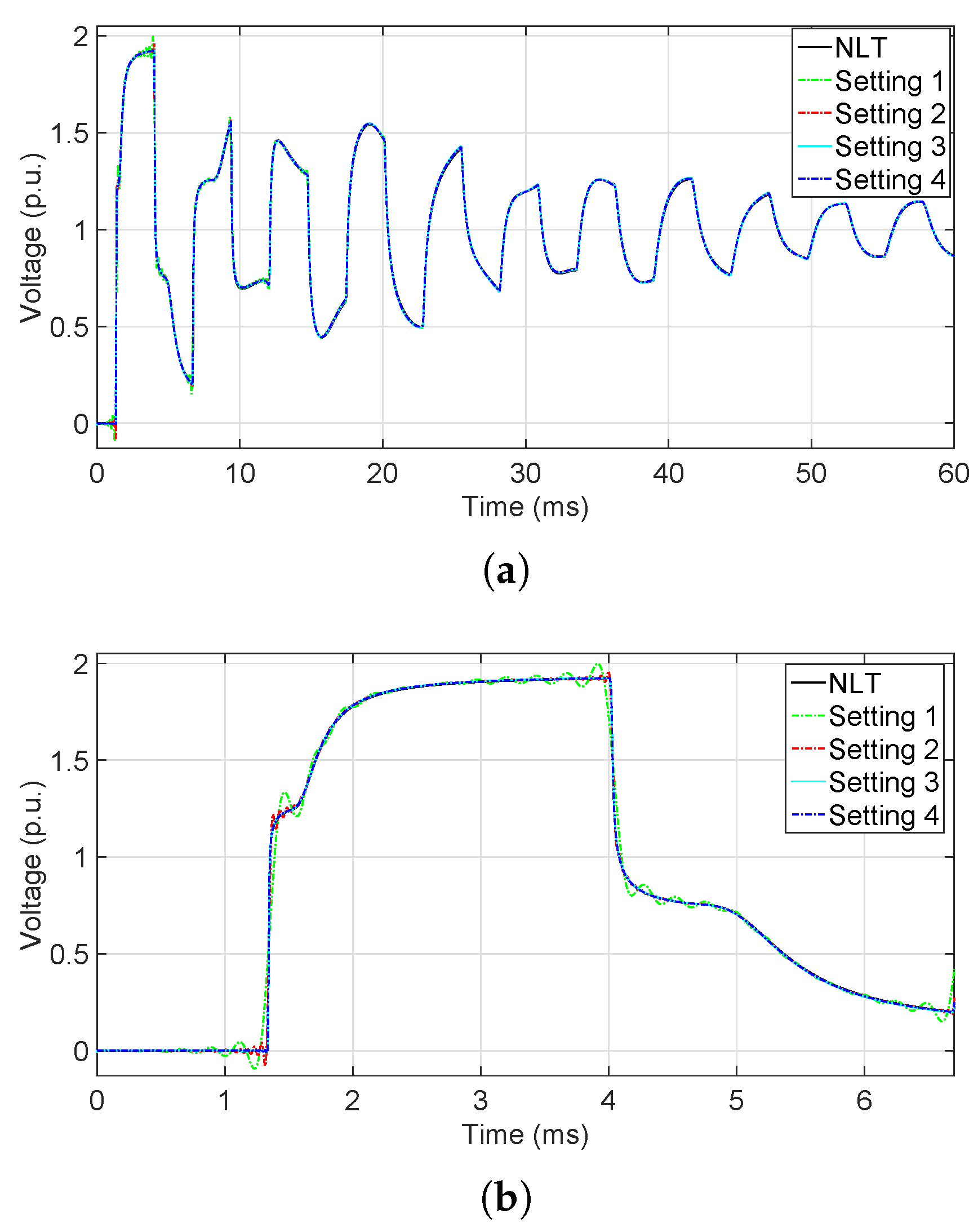
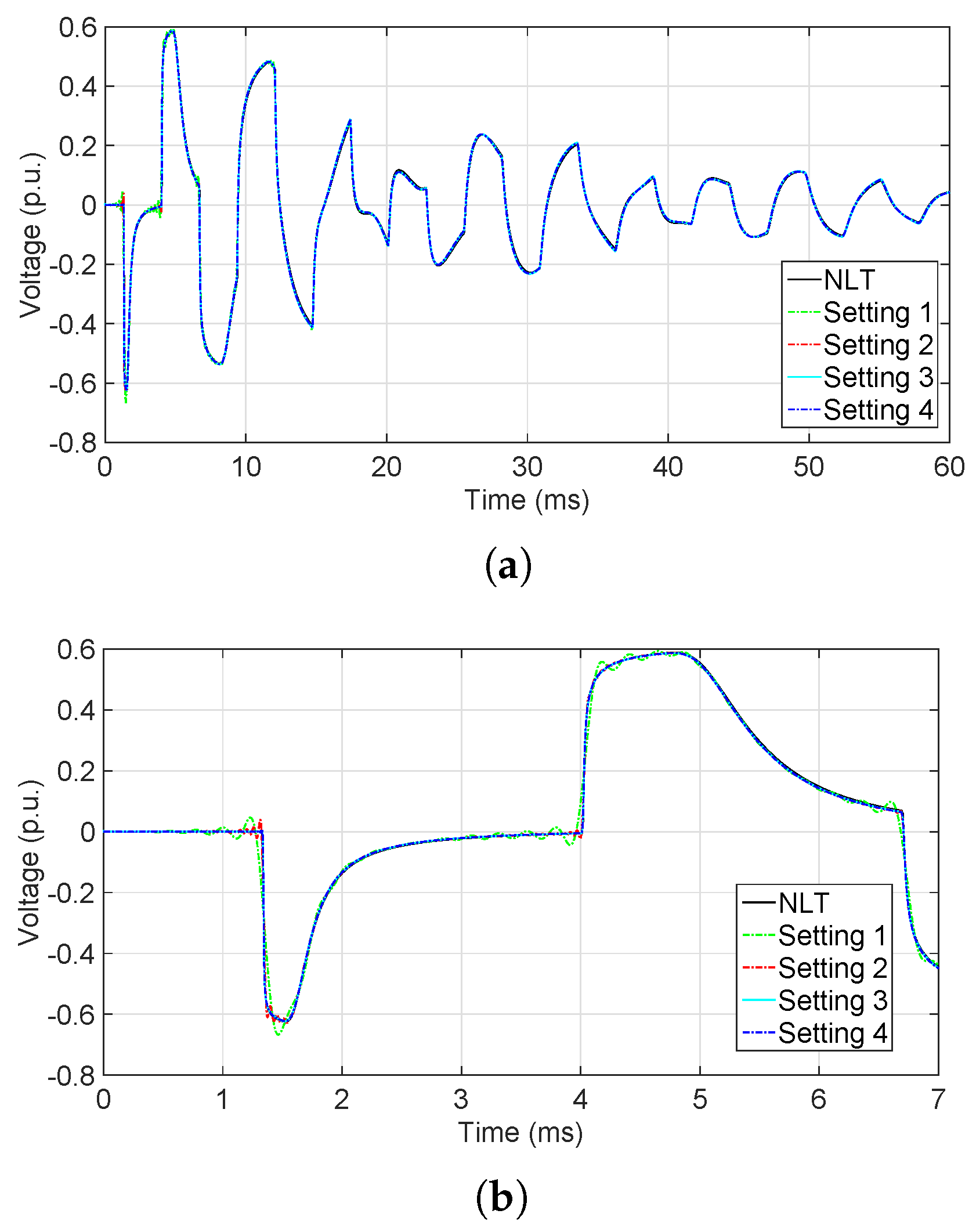
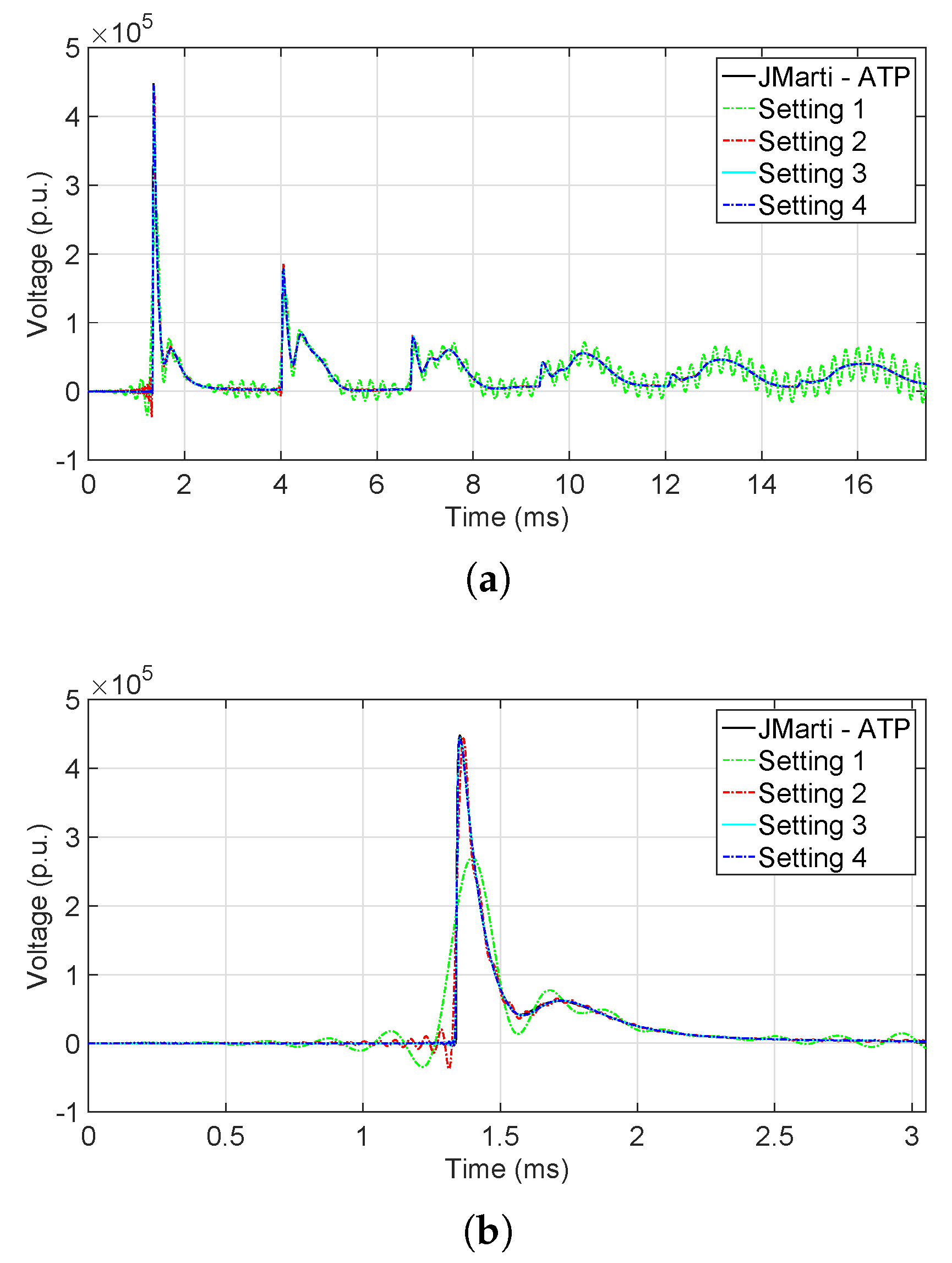
6.2. Time-Domain Analysis
6.2.1. Low-Frequency Analysis
6.2.2. High-Frequency Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MTL | Multiconductor transmission line |
| TL | Transmission line |
| NR | Newton–Raphson |
| EMTP | Electromagnetic Transients Program |
| ATP | Alternative Transient Program |
| ULM | Universal line model |
| PSCAD | Power systems computer-aided design |
| EMTP-RV | Electromagnetic Transients Program—Restructured Version |
| VF | Vector fitting |
| pul | Per unit length |
References
- Morched, A.; Gustavsen, B.; Tartibi, M. A universal model for accurate calculation of electromagnetic transients on overhead lines and underground cables. IEEE Trans. Power Deliv. 1999, 14, 1032–1038. [Google Scholar] [CrossRef]
- Vega, M.G.; Naredo, J.; Ramos-Leaños, O. Minimum Delay Systems for the Modeling of Transmission Lines at EMT Power System Studies. Signal 2017, 10, 11. [Google Scholar]
- Kocar, I.; Mahseredjian, J. New procedure for computation of time delays in propagation function fitting for transient modeling of cables. IEEE Trans. Power Deliv. 2015, 31, 613–621. [Google Scholar] [CrossRef]
- Torrez Caballero, P.; Marques Costa, E.C.; Kurokawa, S. Modal decoupling of overhead transmission lines using real and constant matrices: Influence of the line length. Int. J. Electr. Power Energy Syst. 2017, 92, 202–211. [Google Scholar] [CrossRef]
- Colqui, J.S.L.; Eraso, L.C.T.; Caballero, P.T.; Pissolato Filho, J.; Kurokawa, S. Implementation of Modal Domain Transmission Line Models in the ATP Software. IEEE Access 2022, 10, 15924–15934. [Google Scholar] [CrossRef]
- Wedepohl, L.; Nguyen, H.; Irwin, G. Frequency-dependent transformation matrices for untransposed transmission lines using Newton-Raphson method. IEEE Trans. Power Syst. 1996, 11, 1538–1546. [Google Scholar] [CrossRef]
- Nguyen, T.; Chan, H. Evaluation of modal transformation matrices for overhead transmission lines and underground cables by optimization method. IEEE Trans. Power Deliv. 2002, 17, 200–209. [Google Scholar] [CrossRef]
- Chrysochos, A.I.; Papadopoulos, T.A.; Papagiannis, G.K. Robust Calculation of Frequency-Dependent Transmission-Line Transformation Matrices Using the Levenberg–Marquardt Method. IEEE Trans. Power Deliv. 2014, 29, 1621–1629. [Google Scholar] [CrossRef]
- Uribe, F.A.; Naredo, J.L.; Moreno, P.; Guardado, L. Electromagnetic transients in underground transmission systems through the numerical Laplace transform. Int. J. Electr. Power Energy Syst. 2002, 24, 215–221. [Google Scholar] [CrossRef]
- Moreno, P.; Ramirez, A. Implementation of the Numerical Laplace Transform: A Review Task Force on Frequency Domain Methods for EMT Studies. IEEE Trans. Power Deliv. 2008, 23, 2599–2609. [Google Scholar] [CrossRef]
- Alameri, H.A.; Gomez, P. Laplace Domain Modeling of Power Components for Transient Converter-Grid Interaction Studies. In Proceedings of the 2021 North American Power Symposium (NAPS), College Station, TX, USA, 14–16 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Camara, F.; Lima, A.C.; Correia de Barros, M.T.; da Silva, F.F.; Bak, C.L. Admittance-based modelling of cables and overhead lines by idempotent decomposition. Electr. Power Syst. Res. 2023, 224, 109596. [Google Scholar] [CrossRef]
- Mikulović, J.Č.; Šekara, T.B. The numerical method of inverse Laplace transform for calculation of overvoltages in power transformers and test results. Serbian J. Electr. Eng. 2014, 11, 243–256. [Google Scholar] [CrossRef]
- Mamiş, M. Computation of electromagnetic transients on transmission lines with nonlinear components. IEE Proc.-Gener. Transm. Distrib. 2003, 150, 200–204. [Google Scholar] [CrossRef]
- Marti, L. Simulation of transients in underground cables with frequency-dependent modal transformation matrices. IEEE Trans. Power Deliv. 1988, 3, 1099–1110. [Google Scholar] [CrossRef]
- De Conti, A.; Emídio, M.P.S. Extension of a modal-domain transmission line model to include frequency-dependent ground parameters. Electr. Power Syst. Res. 2016, 138, 120–130. [Google Scholar] [CrossRef]
- Challa, K.K.; Gurrala, G. Development of an Experimental Scaled-Down Frequency Dependent Transmission Line Model. IEEE Access 2021, 9, 64639–64652. [Google Scholar] [CrossRef]
- Macias, J.R.; Exposito, A.G.; Soler, A.B. A comparison of techniques for state-space transient analysis of transmission lines. IEEE Trans. Power Deliv. 2005, 20, 894–903. [Google Scholar] [CrossRef]
- Kurokawa, S.; Yamanaka, F.N.; Prado, A.J.; Pissolato, J. Inclusion of the frequency effect in the lumped parameters transmission line model: State space formulation. Electr. Power Syst. Res. 2009, 79, 1155–1163. [Google Scholar] [CrossRef]
- Araujo, A.; Silva, R.; Kurokawa, S. Comparing lumped and distributed parameters models in transmission lines during transient conditions. In Proceedings of the 2014 IEEE Pes T&d Conference and Exposition, Chicago, IL, USA, 14–17 April 2014; pp. 1–5. [Google Scholar]
- Ametani, A. Electromagnetic transients program: History and future. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 1150–1158. [Google Scholar] [CrossRef]
- Martí, J.R. Accurate Modeling of Frequency-Dependent Transmission Lines in Electromagnetic Transient Simulations. IEEE Power Eng. Rev. 1982, PER-2, 29–30. [Google Scholar] [CrossRef]
- Caballero, P.T.; Costa, E.C.M.; Kurokawa, S. Frequency-dependent line model in the time domain for simulation of fast and impulsive transients. Int. J. Electr. Power Energy Syst. 2016, 80, 179–189. [Google Scholar] [CrossRef]
- Bode, H.W. Network Analysis and Feedback Amplifier Design; D.V. Nostrand: New York, NY, USA, 1945. [Google Scholar]
- Bañuelos-Cabral, E.; Gutiérrez-Robles, J.; García-Sánchez, J.; Sotelo-Castañón, J.; Galván-Sánchez, V. Accuracy enhancement of the JMarti model by using real poles through vector fitting. Electr. Eng. 2019, 101, 635–646. [Google Scholar] [CrossRef]
- Colqui, J.S.L.; Araújo, A.R.J.D.; Pascoalato, T.F.G.; Kurokawa, S.; Filho, J.P. Transient Analysis on Multiphase Transmission Line Above Lossy Ground Combining Vector Fitting Technique in ATP Tool. IEEE Access 2022, 10, 86204–86214. [Google Scholar] [CrossRef]
- De Lauretis, M.; Ekman, J.; Antonini, G.; Romano, D. Enhanced delay-rational Green’s method for cable time domain analysis. In Proceedings of the 2015 International Conference on Electromagnetics in Advanced Applications (ICEAA), Turin, Italy, 7–11 September 2015; pp. 1228–1231. [Google Scholar] [CrossRef]
- Gustavsen, B. Optimal time delay extraction for transmission line modeling. IEEE Trans. Power Deliv. 2016, 32, 45–54. [Google Scholar] [CrossRef]
- Balestero, P.J.R.; Colqui, J.S.L.; Kurokawa, S. Using the Exact Equivalent π-Circuit of Transmission Lines for Electromagnetic Transient Simulations in the Time Domain. IEEE Access 2022, 10, 90847–90856. [Google Scholar] [CrossRef]
- Singh, A.; Marti, J.R.; Srivastava, K.D. Algorithms for fast simulation of transformer windings for diagnostic testing of power transformers. IEEE Trans. Power Deliv. 2010, 25, 1564–1572. [Google Scholar] [CrossRef]
- Dommel, H.W. EMTP Theory Book; Microtran Power System Analysis Corporation: Vancouver, BC, Canada, 1996. [Google Scholar]
- Portela, C.; Tavares, M. Modeling, simulation and optimization of transmission lines. Applicability and limitations of some used procedures. In Proceedings of the 2002 Transmission and Distribution Latin America Conference, Sao Paulo, Brazil, 18–22 March 2002. [Google Scholar]
- Glover, J.D.; Sarma, M.S.; Overbye, T. Power System Analysis & Design, SI Version; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Paul, C.R. Decoupling the multiconductor transmission line equations. IEEE Trans. Microw. Theory Tech. 1996, 44, 1429–1440. [Google Scholar] [CrossRef]
- Marti, J.; Marti, L.; Dommel, H. Transmission line models for steady-state and transients analysis. In Proceedings of the Joint International Power Conference Athens Power Tech, Athens, Greece, 5–8 September 1993; Volume 2, pp. 744–750. [Google Scholar]
- Gustavsen, B.; Semlyen, A. Rational approximation of frequency domain responses by vector fitting. IEEE Trans. Power Deliv. 1999, 14, 1052–1059. [Google Scholar] [CrossRef]
- Deschrijver, D.; Mrozowski, M.; Dhaene, T.; De Zutter, D. Macromodeling of multiport systems using a fast implementation of the vector fitting method. IEEE Microw. Wirel. Compon. Lett. 2008, 18, 383–385. [Google Scholar] [CrossRef]
- Gustavsen, B. Improving the pole relocating properties of vector fitting. IEEE Trans. Power Deliv. 2006, 21, 1587–1592. [Google Scholar] [CrossRef]
- Gustavsen, B.; Semlyen, A. Enforcing passivity for admittance matrices approximated by rational functions. IEEE Trans. Power Syst. 2001, 16, 97–104. [Google Scholar] [CrossRef]
- Gustavsen, B. Computer code for rational approximation of frequency dependent admittance matrices. IEEE Trans. Power Deliv. 2002, 17, 1093–1098. [Google Scholar] [CrossRef]
- Antonini, G. SPICE equivalent circuits of frequency-domain responses. IEEE Trans. Electromagn. Compat. 2003, 45, 502–512. [Google Scholar] [CrossRef]
- Budner, A. Introduction of Frequency-Dependent Line Parameters into an Electromagnetic. IEEE Trans. Power Appar. Syst. 1970, PAS-89, 88–97. [Google Scholar] [CrossRef]
- Portela, C.; Tavares, M. Six-phase transmission line-propagation characteristics and new three-phase representation. IEEE Trans. Power Deliv. 1993, 8, 1470–1483. [Google Scholar] [CrossRef]
- Clarke, E. Circuit Analysis of A–C Power Systems: Graph. Darst; Wiley: Hoboken, NJ, USA, 1950. [Google Scholar]
- Sajid Leon Colqui, J.; Carlos Timaná, L.; Kurokawa, S.; Ricardo Justo De Araújo, A.; Pissolato Filho, J. Lightning Current on the Frequency-Dependent Lumped Parameter Model Representing Short Transmission Lines. In Proceedings of the 2021 35th International Conference on Lightning Protection (ICLP) and XVI International Symposium on Lightning Protection (SIPDA), Colombo, Sri Lanka, 20–26 September 2021; Volume 1, pp. 1–8. [Google Scholar] [CrossRef]
- Jia, W.; Xiaoqing, Z. Double-exponential expression of lightning current waveforms. In Proceedings of the 2006 4th Asia-Pacific Conference on Environmental Electromagnetics, Dalian, China, 1–4 August 2006; pp. 320–323. [Google Scholar]

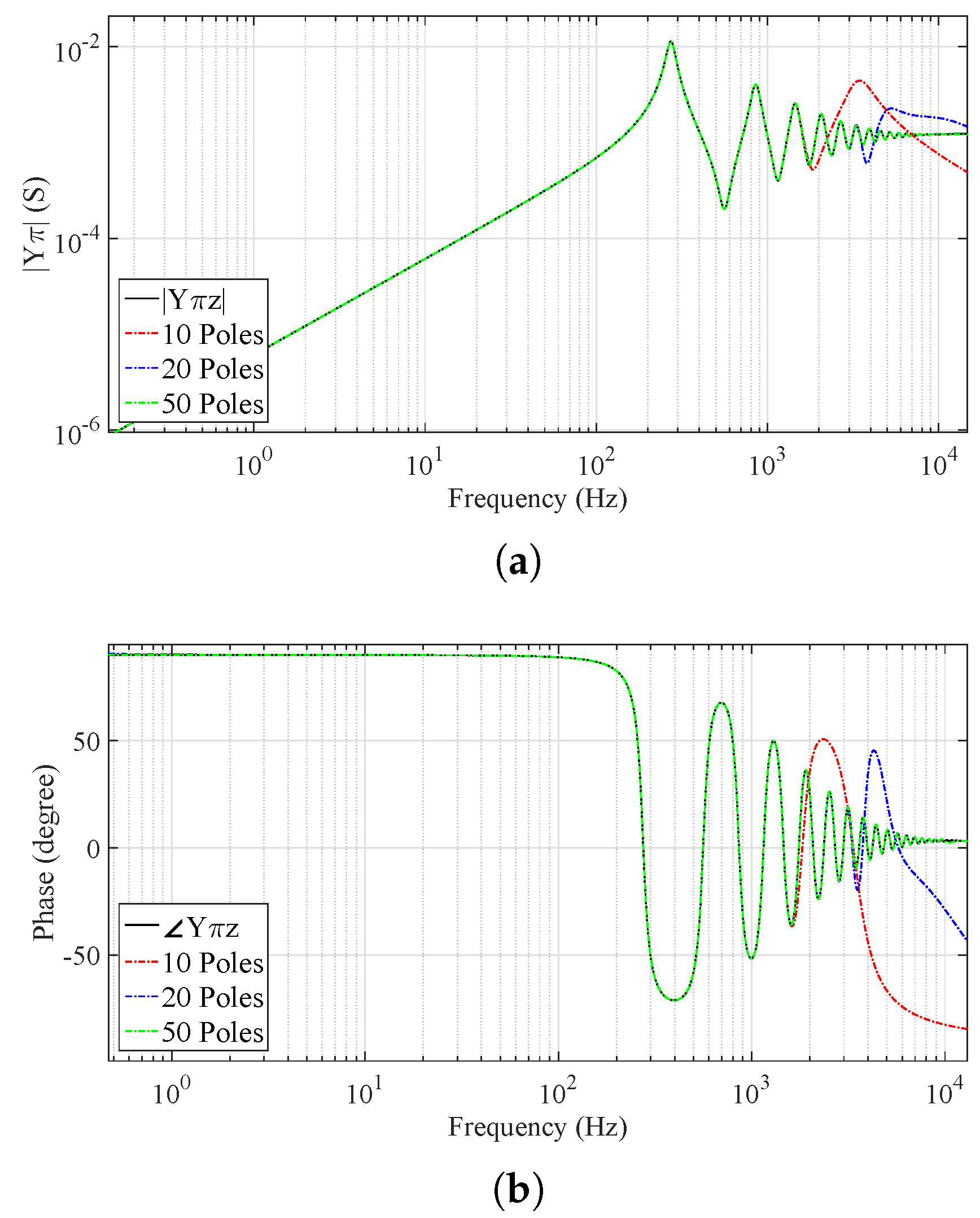
| Poles | ||||
|---|---|---|---|---|
| Modes and | Mode 0 | |||
| Settings | ||||
| 1 | 30 | 20 | 60 | 50 |
| 2 | 100 | 80 | 60 | 50 |
| 3 | 400 | 260 | 60 | 50 |
| 4 | 1200 | 570 | 60 | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robles Balestero, J.P.; Leon Colqui, J.S.; Kurokawa, S. Using the Exact Equivalent π-Circuit Model for Representing Three-Phase Transmission Lines Directly in the Time Domain. Energies 2023, 16, 7192. https://doi.org/10.3390/en16207192
Robles Balestero JP, Leon Colqui JS, Kurokawa S. Using the Exact Equivalent π-Circuit Model for Representing Three-Phase Transmission Lines Directly in the Time Domain. Energies. 2023; 16(20):7192. https://doi.org/10.3390/en16207192
Chicago/Turabian StyleRobles Balestero, Juan Paulo, Jaimis Sajid Leon Colqui, and Sérgio Kurokawa. 2023. "Using the Exact Equivalent π-Circuit Model for Representing Three-Phase Transmission Lines Directly in the Time Domain" Energies 16, no. 20: 7192. https://doi.org/10.3390/en16207192
APA StyleRobles Balestero, J. P., Leon Colqui, J. S., & Kurokawa, S. (2023). Using the Exact Equivalent π-Circuit Model for Representing Three-Phase Transmission Lines Directly in the Time Domain. Energies, 16(20), 7192. https://doi.org/10.3390/en16207192








