Analysis and Design of Resonant DC/AC Converters with Energy Dosing for Induction Heating
Abstract
:1. Introduction
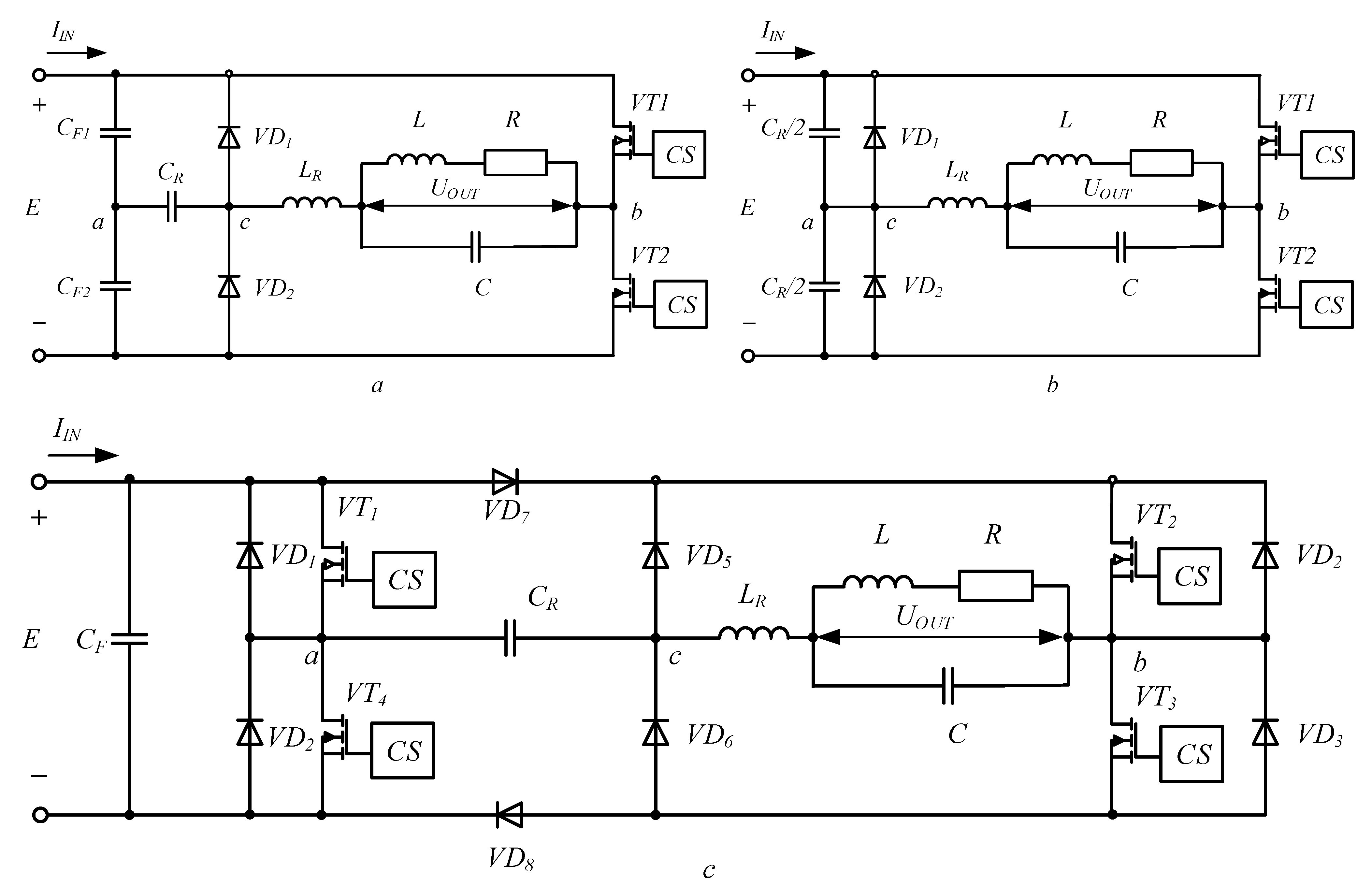
2. Basic Relations in the Analysis of Resonant DC/AC Converters with Energy Dosing
- (1)
- It is possible for the parallel load circuit to work on resonance, inductive or capacitive tuning (represented by the first harmonic as R, R-L, R-C) and together with the resonant elements of the circuit form an equivalent oscillating circuit with a frequency of angular natural oscillations ω0 (ω0 = 2.π.f0, f0—resonant frequency) greater than, less than or equal to the angular control frequency ω (ω = 2.π.f, f—working frequency);
- (2)
- The energy and power consumed by the power source and transmitted to the load by means of capacitors CR/2 are constant and independent of the load parameters;
- (3)
- The voltage uCR on the resonant capacitors is constant in the interval, and due to the operation of the limiting diodes, it is fixed at the level E/2 for the half-bridge scheme and E for the full-bridge scheme;
- (4)
- The voltage on the load uT in all appropriate/energy modes is sinusoidal;
- (5)
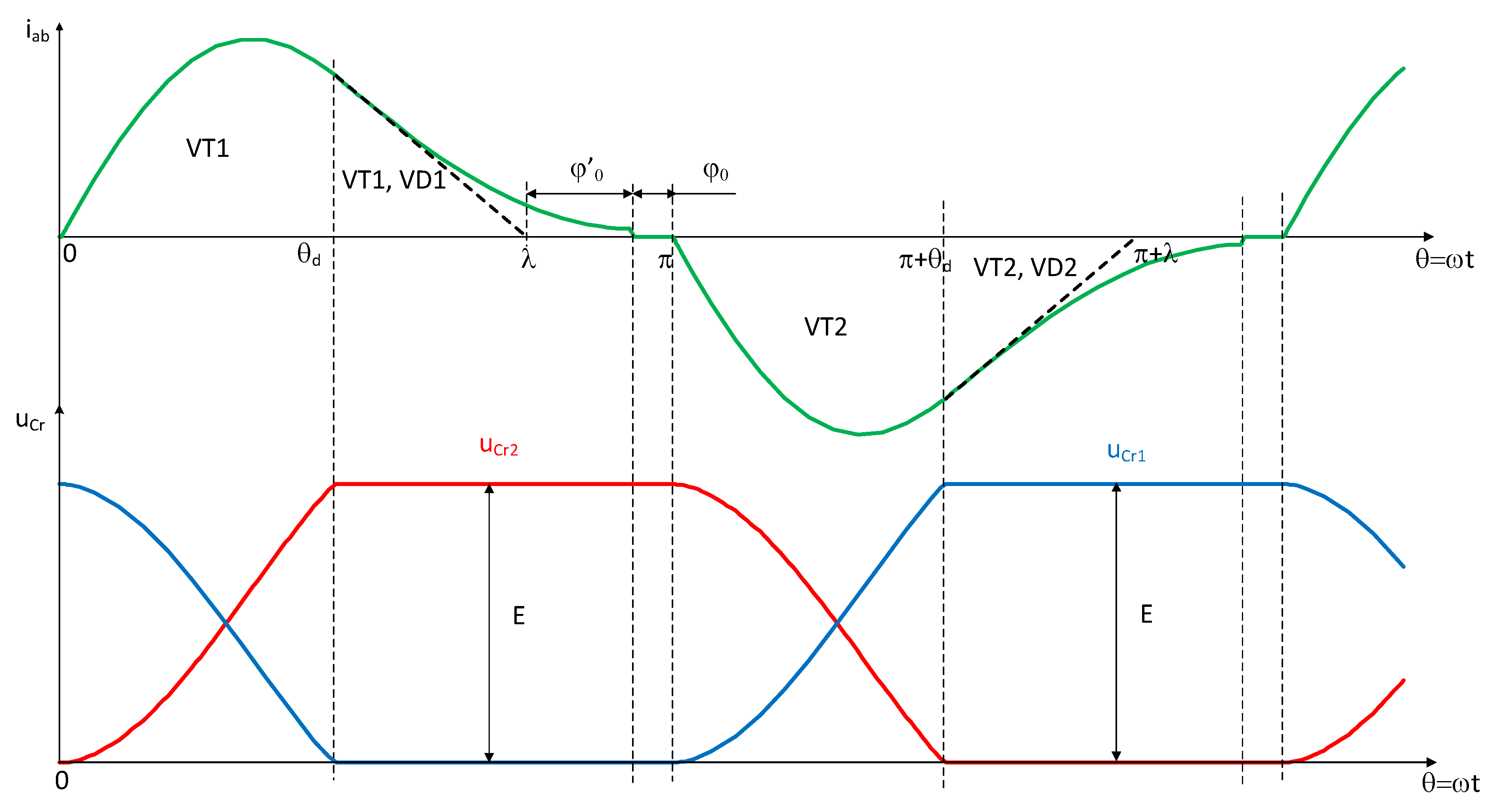
- The shape of the current pulse through the resonant inductance differs from the sinusoidal one, with the maximum shifted to the left of its middle. As a result, its first harmonic is also shifted to the left relative to the beginning of the half-period by an angle φ1. This circumstance should be taken into account in the analysis and design of the circuit, and the alternating voltages can be replaced by equivalent sinusoids, but in no case should this be done for the alternating current (due to its nonsinusoidal shape).
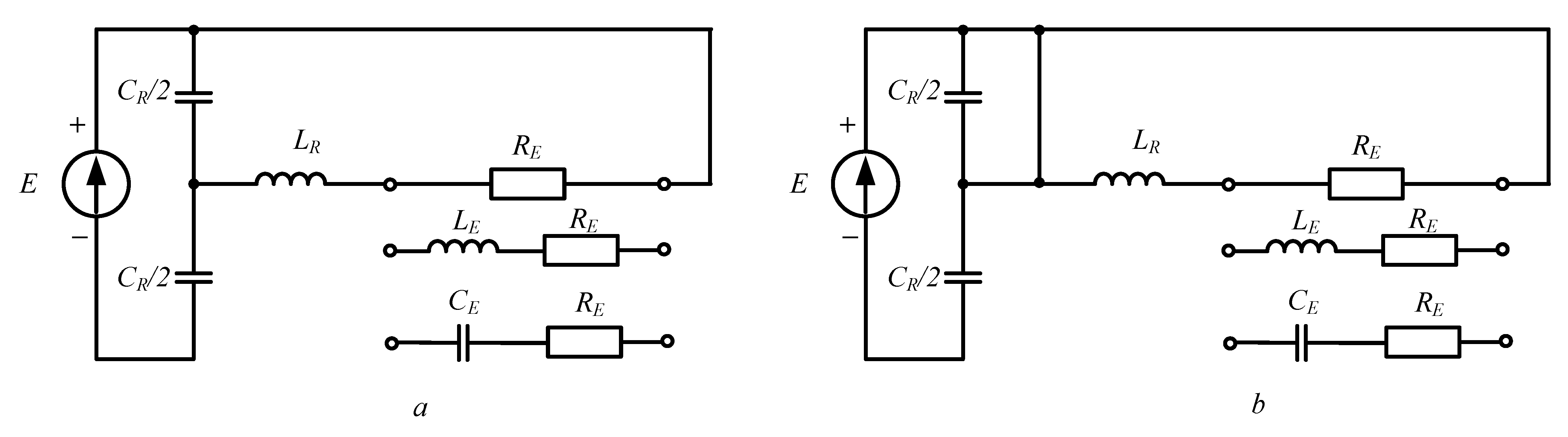
- δ—angle between the first harmonic of the generated voltage and the first harmonic of the current in the AC circuit. It is more convenient here to work with the tangent of this angle—, where CE and RE are the equivalent capacity and active resistance of the parallel load circuit, which are brought into the series resonance circuit of DC/AC converter;
- Q—quality factor of a series resonant circuit
- ξ0, ξ—disturbances, respectively, of the parallel load circuit and of the series resonant circuitwhere ω0p is the angular resonant frequency of the parallel load circuit, ω0 is the angular resonant frequency of the series AC circuit and ω is the angular control frequency;
- cosφT—load power factor L-R
2.1. Features and Modes of Operation of the Inverter in the Interval of Energy Consumption from the Power Source
2.2. Features and Modes of Operation of the Inverter in the Interval of the Short Circuit of the AC Circuit
2.3. Determination of the Main Electrical and Phase Quantities in RI with ED
3. Methodology for Engineering Design of RI with ED
- (1)
- The engineering design of the RI power circuit and the load is a joint process in which the RI design plays a dominant role. The determination of the voltage uCR, which is also the load voltage, is a key point in determining its equivalent active resistance R and inductance L;
- (2)
- It is necessary that the phase difference between the current and the voltage of the load parallel resonant circuit is equal to the pause between the control pulses of the transistors and is maintained in this state by the control system in the process of operation. In such an operating mode, the transistors work with soft commutations—they turn on at zero current and zero voltage. To satisfy the specified condition, the frequency of natural oscillations of the equivalent circuit of the AC circuit of the RI must be greater than the control frequency, i.e., ω0/ω > 1. The research carried out in [31,32] showed that at values of the pause between the control pulses, most often φ0 = 0.1π, ω0p/ω = 1.2–1.4 can be assumed;
- (3)
- The energy and power consumed by the power source and transferred to the load through the capacitor CR are unchanged;
- (4)
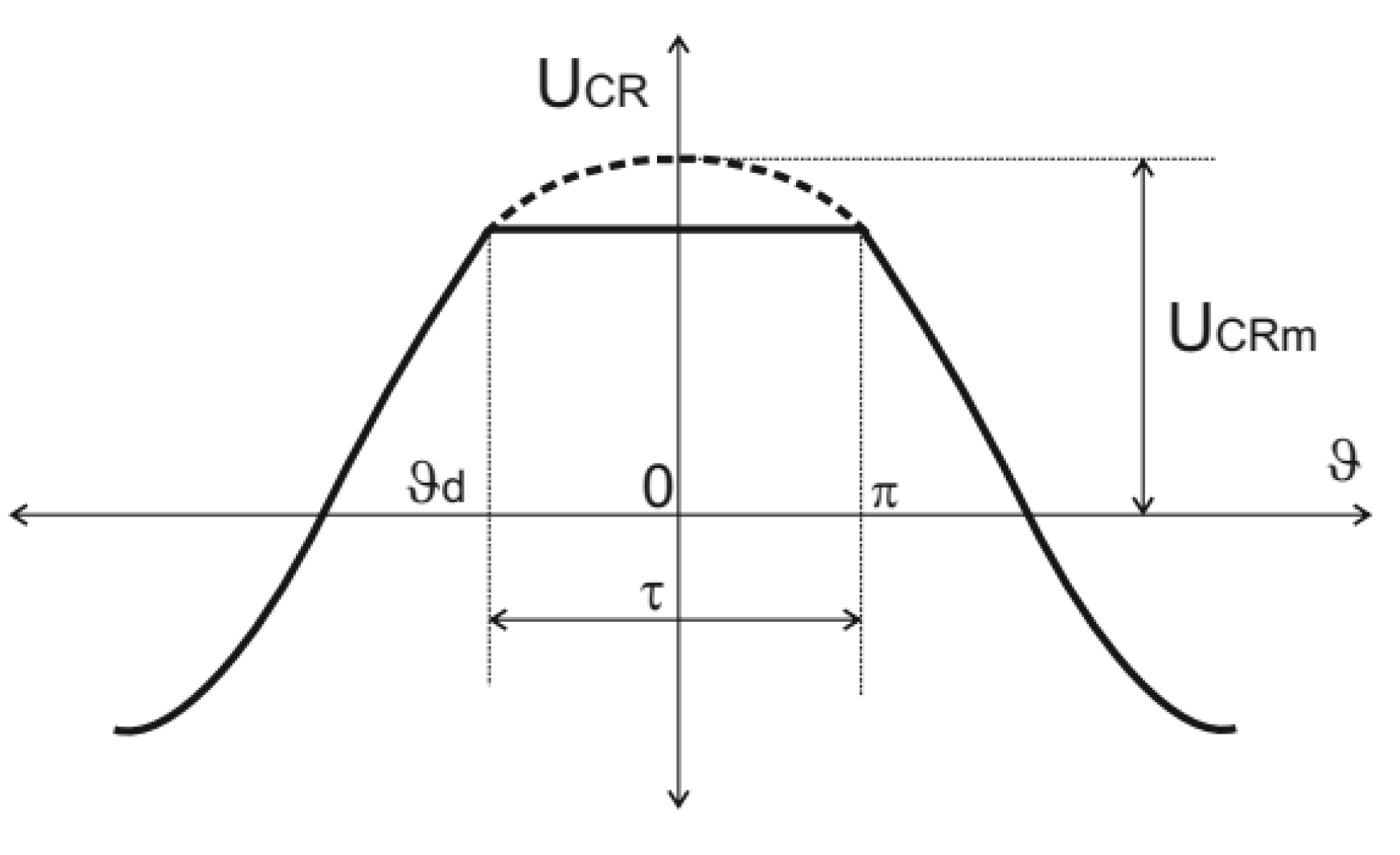
- The voltage of the resonant (dosing) capacitors in the interval ϑd ÷ π can be considered a truncated top and bottom cosine at the level E/2 or E, respectively, for the half-bridge and full-bridge circuit variants;
- (5)
- Regardless of the diversity of the task related to RI operation modes and load change limits, the following initial data for the design are unambiguously defined: (1) power of the converter; (2) operating frequency; (3) load parameters and range of their change; (4) DC power source voltage.
- (1)
- The pause φ0 is initially set. Its size is determined depending on the required operating frequency and catalog switching times of the transistors. For example, a suitable value for this parameter is the following: φ0 = 0.1π.
- (2)
- The ratio value ω0p/ω = 1.2–1.4 is selected. Most often, a value of ω0p/ω = 1.3 is chosen, and this ratio is adjusted during the design process if necessary.
- (3)
- The phase angle δ is determined, according to the fundamental ratio [31] for RI—tgδ > (1.2–1.4) ω0/ω.
- (4)
- Based on the set power and operating frequency, the value of the resonant capacitor CR is calculated:
- (5)
- The detuning at which the voltage and current through the parallel circuit will have a phase—ψ is determined by the expression:
- (6)
- For the selected value of tgδ and the detuning obtained according to (19), the real and relative values of the equivalent resistance of the load circuit are determined:
- (7)
- The value of the parallel capacitor C is found from the expression:
- (8)
- From the load circuit resonance condition, the substitution circuit elements R, L and the load voltage are determined:
- (9)
- A particularly important place in the design methodology is the determination of the moment ϑd, which provides information about the end of the interval of energy consumption from the power source and the beginning of the short circuit through the plus or minus bus of the input power source. For the value of ϑd, it is obtained:
- (10)
- From the expression
- (11)
- By numerically solving equation: wherea check is carried out, and, if necessary, the attitude is specified ω0/ω. The quality factor Q of the equivalent AC replacement circuit of the inverter is also found.
- (12)
- The resonant inductance LR is calculated with the value of the generalized parameter Q obtained according to (11):
- (13)
- The maximum values of the voltages UOUTm and UCRm are, respectively, equal:
- (14)
- The average and maximum values of the current through the transistors and diodes are determined by the following expressions:
- (15)
- The moment ϑm at which the current through the transistor has a maximum value is determined by the expression:
- (16)
- The average current consumed by the power source is equal to the difference between the current of the transistors and the dosing diodes:
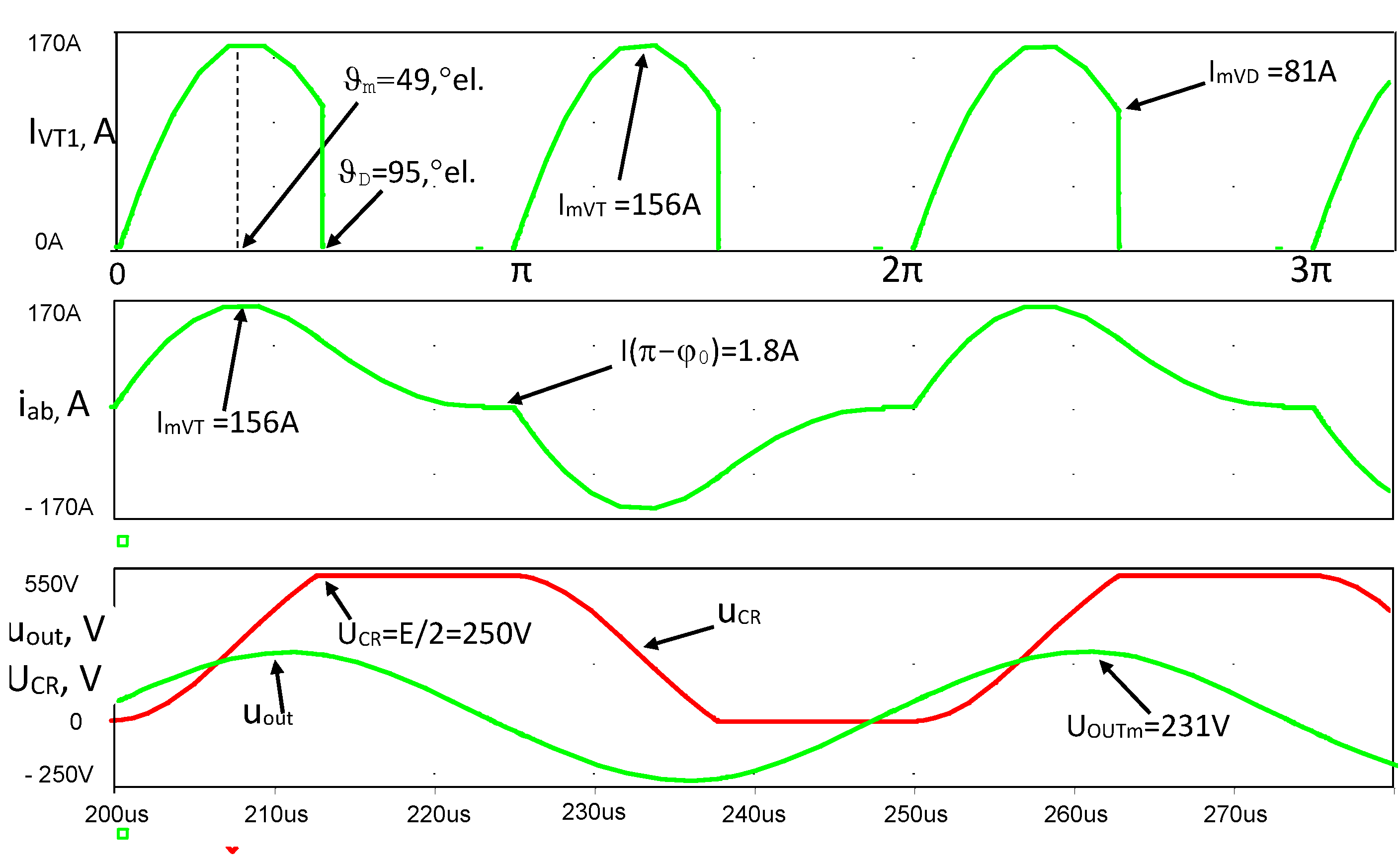
4. Verification of the Design Procedure
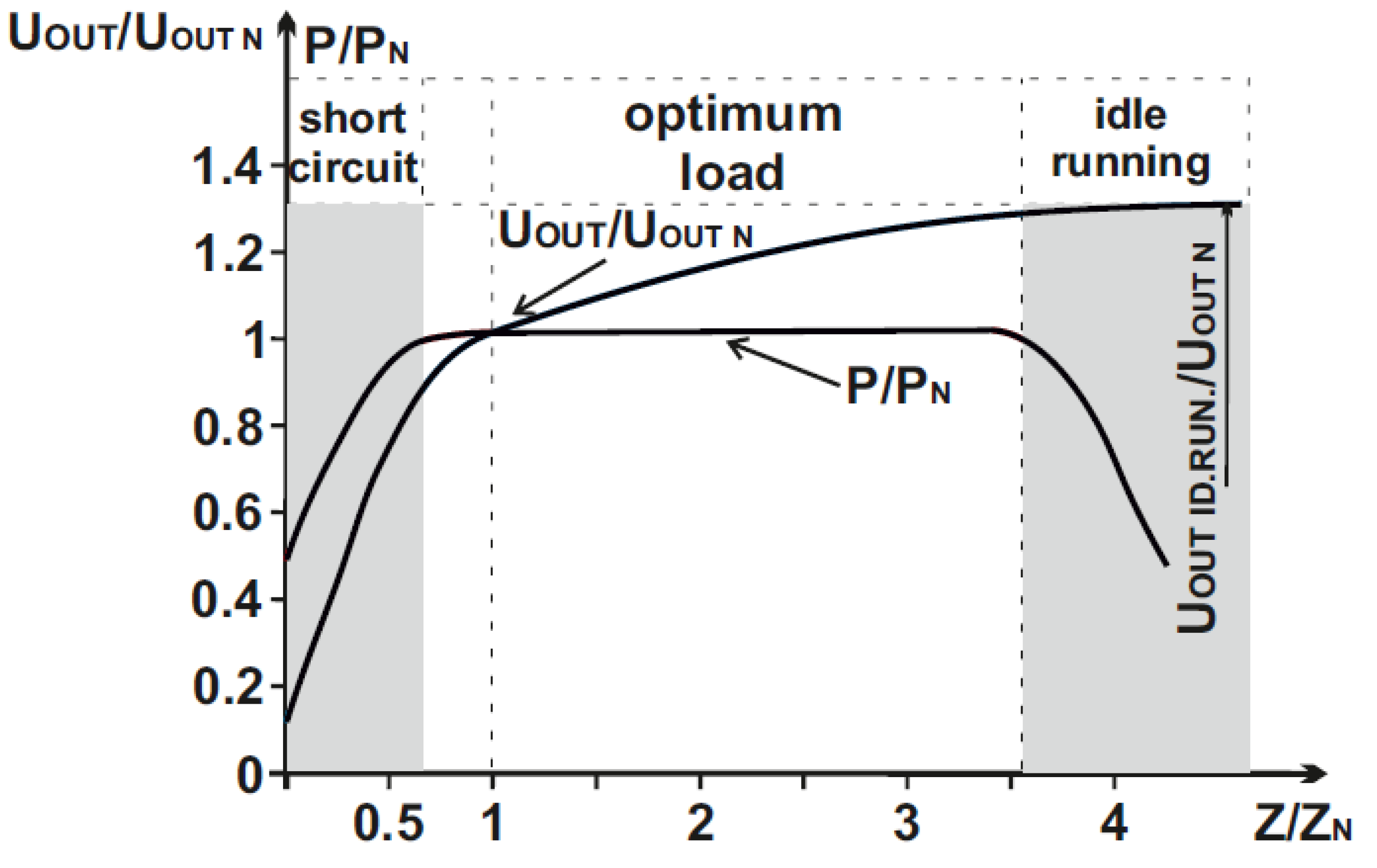
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Desisa, D. Numerical Modeling of Induction Heating Process Control. In Proceedings of the 22nd International Scientific Conference on Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 8–10 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Kovac, D.; Melnykov, V. Simulation and Laboratory Model of Induction Heating in COMSOL Multiphysics. In Proceedings of the IEEE International Conference on Modern Electrical and Energy Systems (MEES), Kremenchuk, Ukraine, 21–24 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Rasheed, F.A.; Abdulbaqi, I.M. Analysis of a Current-Fed Parallel Resonant Inverter for Induction Heating Applications. In Proceedings of the 1st Babylon International Conference on Information Technology and Science (BICITS), Babil, Iraq, 28–29 April 2021; pp. 169–173. [Google Scholar] [CrossRef]
- Vishnuram, P.; Ramachandiran, G.; Babu, T.S.; Nastasi, B. Induction Heating in Domestic Cooking and Industrial Melting Applications: A Systematic Review on Modelling, Converter Topologies and Control Schemes. Energies 2021, 14, 6634. [Google Scholar] [CrossRef]
- Lucia, O.; Maussion, P.; Dede, E.J.; Burdio, J.M. Induction Heating Technology and Its Applications: Past Developments, Current Technology, and Future Challenges. IEEE Trans. Ind. Electron. 2013, 61, 2509–2520. [Google Scholar] [CrossRef]
- Meinert, J.D.; Kjærsgaard, B.F.; Aunsborg, T.S.; Jorgensen, A.B.; Munk-Nielsen, S.; Duun, S.B. Class-E Push-Pull Resonance Converter with Load Variation Robustness for Industrial Induction Heating. In Proceedings of the 2022 24th European Conference on Power Electronics and Applications (EPE’22 ECCE Europe), Hannover, Germany, 5–9 September 2022; pp. 1–8. [Google Scholar]
- Sarnago, H.; Lucia, O.; Burdio, J.M. High-Performance Class-E Quasi-Resonant Inverter for Domestic Induction Heating Applications. In Proceedings of the 2022 IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 19–23 March 2022; pp. 1202–1207. [Google Scholar] [CrossRef]
- Han, W.; Chau, K.T.; Liu, W.; Tian, X.; Wang, H. A Dual-Resonant Topology-Reconfigurable Inverter for All-Metal Induction Heating. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 3818–3829. [Google Scholar] [CrossRef]
- Herasymenko, P.; Yurchenko, O. An Extended Pulse-Density-Modulated Series-Resonant Inverter for Induction Heating Applications. In Proceedings of the 2020 IEEE 61th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 5–7 November 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Ivanov, A.; Bukanin, V.; Zenkov, A.; Vologdin, V.; Vologdin, V. Cyber Physical Systems Integration for Induction Heating Technologies. In Proceedings of the 2020 9th Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 8–11 June 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Panchal, S.; Kulkarni, R.; Raja, M.K.; Nataraj, J. Design, Simulation and Hardware Implementation of Soft Switching based Induction Heating System. In Proceedings of the 2021 6th International Conference for Convergence in Technology (I2CT), Maharashtra, India, 2–4 April 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Salehi, S.; Abbaszadeh, K.; Sani, S.G.; Mohamadi, H.H. A new Domestic Induction Heating Resonant Converter with High Power Conversion Efficiency. In Proceedings of the 2021 12th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tabriz, Iran, 2–4 February 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Hawryluk, M.; Rychlik, M.; Pietrzak, M.; Górski, P.; Marzec, J. Development of Induction Heating System Ensuring Increased Heating Efficiency of the Charge Material in a Forging. Materials 2022, 15, 1516. [Google Scholar] [CrossRef] [PubMed]
- Perevalov, Y.Y.; Demidovich, V.B. Intelligent Design and Control System of Automated Installations for Induction Heating of Products. In Proceedings of the 2022 22nd International Symposium on Electrical Apparatus and Technologies (SIELA), Bourgas, Bulgaria, 1–4 June 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Phankong, N.; Chudjuarjeen, S.; Chakkuchan, P.; Nawong, M. Preheat Welding with Induction Heating Based Control of Phase-Locked Loop Resonant Inverter. In Proceedings of the 2022 International Electrical Engineering Congress (iEECON), Khon Kaen, Thailand, 9–11 March 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Park, N.-J.; Lee, D.-Y.; Hyun, D.-S. A Power-Control Scheme with Constant Switching Frequency in Class-D Inverter for Induction-Heating Jar Application. IEEE Ind. Electron. Mag. 2007, 54, 1252–1260. [Google Scholar] [CrossRef]
- Sankhe, D.N.; Sawant, R.R.; Rao, Y.S. FPGA-Based Hybrid Control Strategy for Resonant Inverter in Induction Heating Applications. IEEE J. Emerg. Sel. Top. Ind. Electron. 2021, 3, 156–165. [Google Scholar] [CrossRef]
- Ngo-Phi, T.; Nguyen-Quang, N. Variable Pulse Density Modulation for Induction Heating. In Proceedings of the 2021 International Symposium on Electrical and Electronics Engineering (ISEE), Ho Chi Minh, Vietnam, 15–16 April 2021; pp. 226–231. [Google Scholar] [CrossRef]
- Lee, Y.-L.; Lin, C.-H.; Liu, H.-D. A Novel MPPT Heating Control Strategy Applied to the Induction Heating System. Processes 2022, 10, 1151. [Google Scholar] [CrossRef]
- Oh, Y.; Yeon, J.; Kang, J.; Galkin, I.; Oh, W.; Cho, K. Sensorless Control of Voltage Peaks in Class-E Single-Ended Resonant Inverter for Induction Heating Rice Cooker. Energies 2021, 14, 4545. [Google Scholar] [CrossRef]
- Artal-Sevil, J.S.; Rivases, F.; Beyza, J.; Evangelista, M.A. Design and Implementation of a High-Power Resonant Converter for an Induction Steel-Melting Furnace. In Proceedings of the 2021 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 10–12 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Villa, J.; Navarro, D.; Dominguez, A.; Artigas, J.I.; Barragan, L.A. Vessel Recognition in Induction Heating Appliances—A Deep-Learning Approach. IEEE Access 2021, 9, 16053–16061. [Google Scholar] [CrossRef]
- Lucia, S.; Navarro, D.; Karg, B.; Sarnago, H.; Lucia, O. Deep Learning-Based Model Predictive Control for Resonant Power Converters. IEEE Trans. Ind. Informat. 2020, 17, 409–420. [Google Scholar] [CrossRef]
- Kouro, S.; Perez, M.A.; Rodriguez, J.; Llor, A.M.; Young, H.A. Model Predictive Control: MPC’s Role in the Evolution of Power Electronics. IEEE Ind. Electron. Mag. 2015, 9, 8–21. [Google Scholar] [CrossRef]
- Bedford, B.D.; Hoft, R.G. Principles of Inverter Circuits; John Wiley & Sons: New York, NY, USA, 1964; ISBN 978-0471061342. [Google Scholar]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics—Converters, Applications, and Design, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Kazimierczuk, M.K.; Czarkowski, D. Resonant Power Converters, 2nd ed.; IEEE Press and John Wiley & Sons: New York, NY, USA, 2011; pp. 1–595. ISBN 978-0-470-90538-8. [Google Scholar]
- Dokić, B.L.; Blanuša, B. Power Electronics Converters and Regulators, 3rd ed.; Springer International Publishing: Cham, Switzerland, 2015; ISBN 978-3-319-09401-4. [Google Scholar]
- Rashid, M.H. Power Electronics Handbook: Devices, Circuits, and Applications; Academic Press: Burlington, MA, USA, 2007. [Google Scholar]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 2nd ed.; Kluwer Academic Publishers Group: Norwell, MA, USA, 2001. [Google Scholar]
- Todorov, T.S.; Madzharov, N.D.; Alexiev, D.T.; Ivanov, P.T. Autonomous Inverters; Technical University of Gabrovo: Gabrovo, Bulgaria, 1996. [Google Scholar]
- Madzharov, N. High-Frequency Power Source with Constant Output Power. J. Eng. Sci. Technol. Rev. 2016, 9, 157–162. [Google Scholar] [CrossRef]
| Interval 0 ÷ ϑd | |||
|---|---|---|---|
| Type of Load | Differential Equation for the Inverter Current i1 | Solution of Differential Equation for i1 | Solution for ϑd |
| R | |||
| L-R | LE, RE—equivalent inductance and active resistance of the load circuit; LAC—equivalent inductance of the AC circuit. | ||
| C-R | ; CAC—equivalent capacity of the AC circuit; CE, RE—equivalent capacitance and active resistance of the load circuit. |
| Interval ϑd ÷ π-φ0 | ||
|---|---|---|
| Type of Load | Differential Equation for the Inverter Current i1 | Solution of Differential Equation for i1 |
| R | ||
| L-R | ||
| C-R | roots of the characteristic equation: | (1) —aperiodic mode (2) —critical-aperiodic mode (3) —resonant mode |
| Schematic Element Values: Load Parameters: R = 0.05 Ω; L = 2.3 μH; LR = 11.1 μH; CR/2 = 1.5 μF | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Dimension | ϑm, ° | ϑD, ° | UOUTm, V | I0, A | ImVT, A | IOVT, A | ImVD, A | IOVD, A | P, kW | I(π-t0), A |
| Calculated | 46 | 93 | 230 | 30 | 151 | 33.2 | 81 | 3.23 | 15 | 2.3 |
| Simulated | 49 | 95 | 231 | 30 | 156 | 33.2 | 88 | 3.8 | 15 | 1.8 |
| Schematic Element Values: P = 5 kW; f = 20 kHz; E = 295 V; R = 0.05 Ω; L = 2.3 μH; LR = 11.1 μH; CR/2 = 1.5 μF | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Dimension | φm,° | φd,° | UOUTm,V | I0, A | IVT1,2m, A | IVT1,2o, A | ID3,4m, A | ID3,4, A | I(π-φ0), A |
| Calculated | 45.5 | 96.3 | 149 | 17 | 85.6 | 18.4 | 47.9 | 1.4 | 0.9 |
| Simulated | 44.8 | 95.1 | 146.8 | 16.9 | 86 | 18.5 | 48.1 | 1.5 | 0.8 |
| Measured | 45 | 96 | 148 | 17 | 85 | 18.4 | 49.5 | 1.4 | 0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madzharov, N.; Hinov, N. Analysis and Design of Resonant DC/AC Converters with Energy Dosing for Induction Heating. Energies 2023, 16, 1462. https://doi.org/10.3390/en16031462
Madzharov N, Hinov N. Analysis and Design of Resonant DC/AC Converters with Energy Dosing for Induction Heating. Energies. 2023; 16(3):1462. https://doi.org/10.3390/en16031462
Chicago/Turabian StyleMadzharov, Nikolay, and Nikolay Hinov. 2023. "Analysis and Design of Resonant DC/AC Converters with Energy Dosing for Induction Heating" Energies 16, no. 3: 1462. https://doi.org/10.3390/en16031462
APA StyleMadzharov, N., & Hinov, N. (2023). Analysis and Design of Resonant DC/AC Converters with Energy Dosing for Induction Heating. Energies, 16(3), 1462. https://doi.org/10.3390/en16031462







