Alternative Current Injection Newton and Fast Decoupled Power Flow
Abstract
:1. Introduction
2. Alternative Newton-Raphson Current Injection Model

|Vpq|v + 1 = |Vpq|v + Δ|Vpq|v
3. BX Version of Current Injection Fast Decoupled Power Flow
4. Test Results
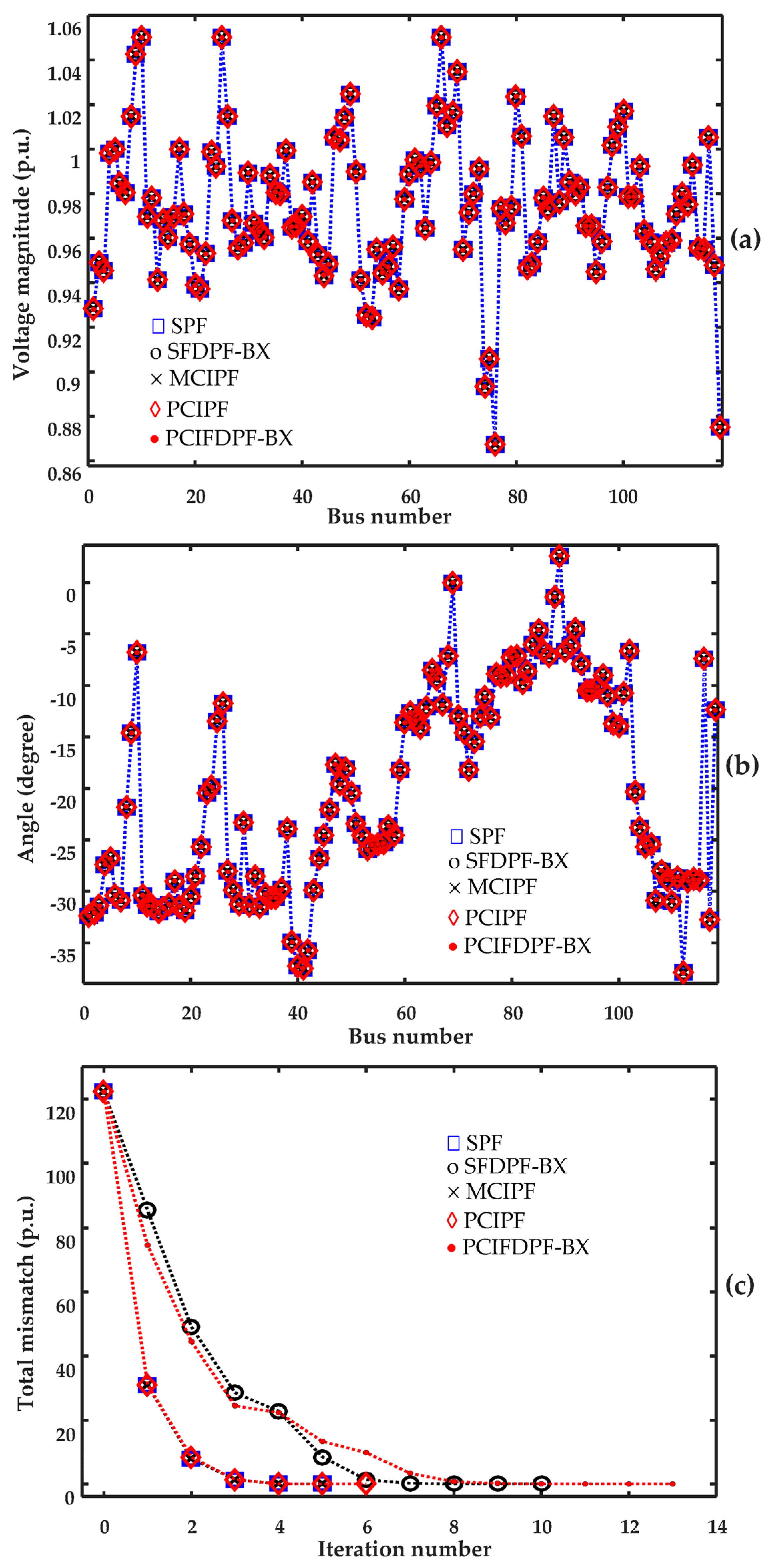
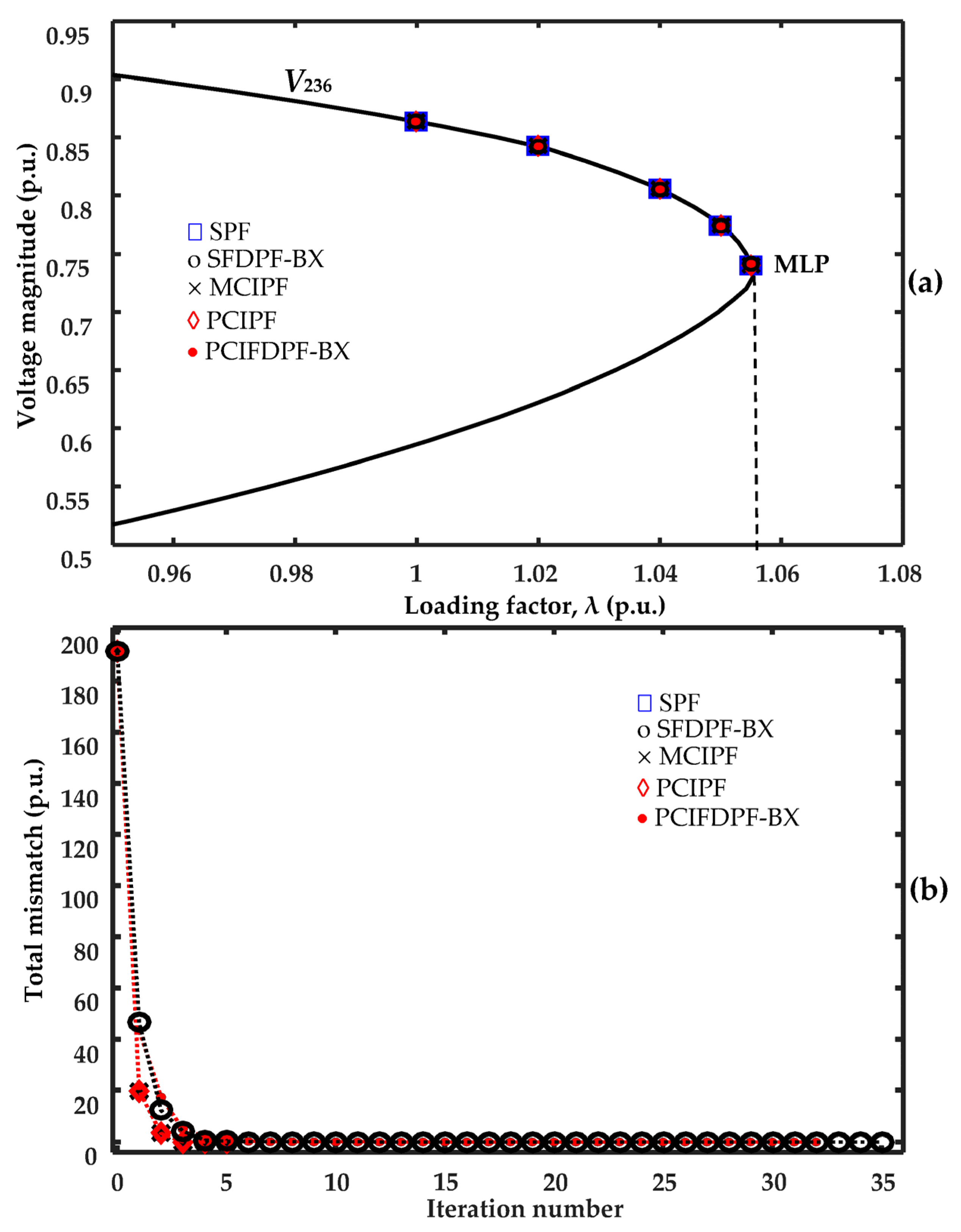
4.1. Performance of the Methods for the IEEE Test Systems
| λ (p.u.) | SPF | MCIPF | PCIPF | SFDPF-BX Pθ/QV | PCIFDPF-BX Pθ/QV |
|---|---|---|---|---|---|
| 1.0 | 4 | 4 | 4 | 8-8 | 8-8 |
| 1.4 | 5 | 5 | 5 | 10-9 | 11-11 |
| 1.5 | 5 | 5 | 5 | 12-11 | 13-13 |
| 1.58 | 6 | 6 | 6 | 21-20 | 23-22 |
| 1.596 | 7 | 7 | 7 | 41-40 | 44-43 |
| 1.6 | NC | NC | NC | NC | NC |
| λ (p.u.) | SPF | MCIPF | PCIPF | SFDPF-BX Pθ/QV | PCIFDPF-BX Pθ/QV |
|---|---|---|---|---|---|
| 1.0 | 4 | 4 | 4 | 8-8 | 9-8 |
| 1.4 | 5 | 5 | 5 | 9-9 | 9-9 |
| 1.7 | 6 | 6 | 6 | 12-12 | 13-13 |
| 1.86 | 8 | 8 | 8 | 51-50 | 41-40 |
| 1.865 | 8 | 8 | 8 | 82-81 | 49-48 |
| 1.9 | NC | NC | NC | NC | NC |
| R/X Ratios | SPF | MCIPF | PCIPF | SFDPF-BX Pθ/QV | PCIFDPF-BX Pθ/QV | λmax (p.u.) |
|---|---|---|---|---|---|---|
| 1.0xR/0.5xX | 3 | 3 | 4 | 11-10 | 13-12 | 2.2296 |
| 1.0xR/1.0xX | 4 | 4 | 4 | 8-8 | 8-8 | 1.5972 |
| 2.0xR/1.0xX | 5 | 5 | 5 | 10-10 | 17-16 | 1.3444 |
| 3.0xR/1.0xX | 8 | 8 | 7 | 13-21 | 44-44 | 1.1104 |
| 4.0xR/1.0xX | NC | NC | NC | NC | NC | 0.9339 |
| R/X Ratios | SPF | MCIPF | PCIPF | SFDPF-BX Pθ/QV | PCIFDPF-BX Pθ/QV | λmax (p.u.) |
|---|---|---|---|---|---|---|
| 1.0xR/0.5xX | 5 | 5 | 5 | 11-10 | 10-10 | 2.5868 |
| 1.0xR/1.0xX | 4 | 4 | 4 | 8-8 | 9-8 | 1.8664 |
| 2.0xR/1.0xX | 5 | 5 | 5 | 10-9 | 10-10 | 1.6228 |
| 3.0xR/1.0xX | 5 | 5 | 6 | 10-10 | 13-13 | 1.2371 |
| 4.0xR/1.0xX | NC | NC | NC | NC | NC | 0.9154 |
| λ (p.u.) | SPF | MCIPF | PCIPF | SFDPF-BX Pθ/QV | PCIFDPF-BX Pθ/QV |
|---|---|---|---|---|---|
| 1.0 | 4 | 4 | 4 | 13-12 | 13-12 |
| 1.02 | 4 | 4 | 4 | 16-15 | 15-14 |
| 1.04 | 5 | 5 | 5 | 24-23 | 22-21 |
| 1.05 | 5 | 5 | 5 | 36-35 | 32-32 |
| 1.055 | 7 | 7 | 7 | 80-80 | 74-73 |
| 1.056 | NC | NC | NC | NC | NC |
| R/X Ratios | SPF | MCIPF | PCIPF | SFDPF-BX Pθ/QV | PCIFDPF-BX Pθ/QV | λmax (p.u.) |
|---|---|---|---|---|---|---|
| 1.0xR/0.5xX | 5 | 6 | 4 | 7-7 | 16-18 | 1.4303 |
| 1.0xR/1.0xX | 4 | 4 | 4 | 13-12 | 12-12 | 1.0553 |
| 1.2xR/1.0xX | 5 | 5 | 4 | 17-16 | 15-15 | 1.0292 |
| 1.4xR/1.0xX | 6 | 5 | 5 | 28-27 | 25-25 | 1.0086 |
| 1.47xR/1.0xX | 7 | 7 | 6 | 79-77 | 70-69 | 1.0002 |
| 1.473xR/1.0xX | NC | NC | NC | NC | NC | 0.9998 |
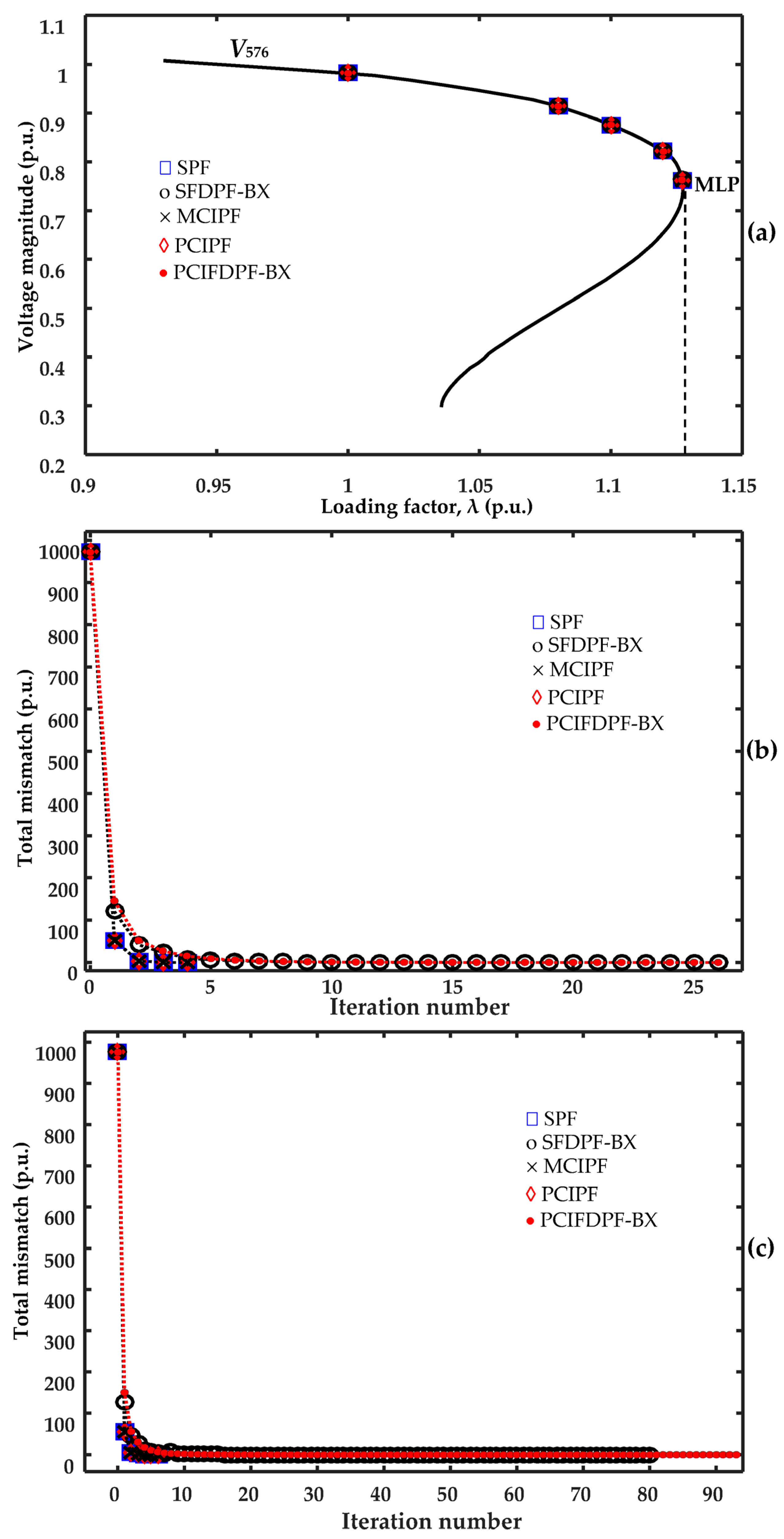
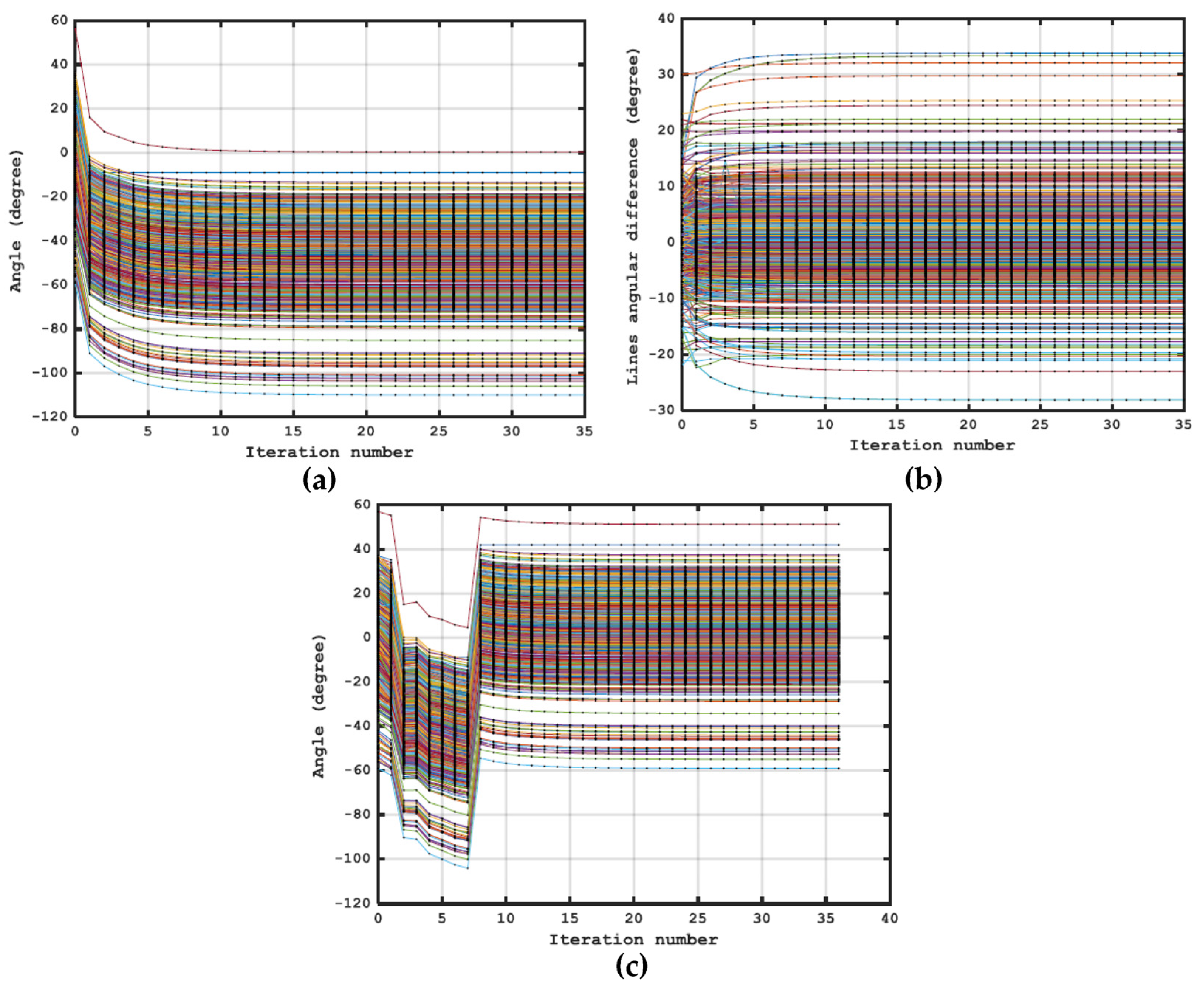
4.2. Performance of the Methods for the Real, Large Systems
| λ (p.u.) | SPF | MCIPF | PCIPF | SFDPF-BX Pθ/QV | PCIFDPF-BX Pθ/QV |
|---|---|---|---|---|---|
| 1.000 | 3 | 3 | 3 | 8-8 | 10-9 |
| 1.080 | 4 | 4 | 4 | 14-15 | 15-15 |
| 1.100 | 5 | 5 | 5 | 18-19 | 18-18 |
| 1.120 | 4 | 4 | 4 | 26-26 | 26-26 |
| 1.127 | 6 | 6 | 6 | 95-94 | 92-93 |
| 1.1274 | NC | NC | NC | NC | NC |
| R/X Ratios | SPF | MCIPF | PCIPF | SFDPF-BX Pθ/QV | PCIFDPF-BX Pθ/QV | MCIFDPF-BX Pθ/QV (α) | λmax (p.u.) |
|---|---|---|---|---|---|---|---|
| 1.0xR/0.5xX | 4 | 4 | 4 | 15-17 | 16-17 | 15-16 (4.535°) | 1.7863 |
| 1.0xR/1.0xX | 3 | 3 | 3 | 8-8 | 10-9 | 10-9 (1.003°) | 1.1272 |
| 2.0xR/1.0xX | 4 | 4 | 4 | 14-17 | 38-34 | 16-15 (31.604°) | 1.0596 |
| 2.2xR/1.0xX | 4 | 4 | 4 | 19-18 | NC | 21-20 (40.280°) | 1.0361 |
| 2.4xR/1.0xX | 5 | 5 | 5 | 35-34 | NC | 36-36 (50.925°) | 1.0113 |
| 2.45xR/1.0xX | 6 | 6 | 6 | 51-51 | NC | 52-52 (54.030°) | 1.0047 |
| 2.48xR/1.0xX | 7 | 7 | 7 | 80-80 | NC | 111-111 (56.02°) | 1.0008 |
| 2.486xR/1.0xX | NC | NC | NC | NC | NC | NC | 0.99996 |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| PF | Power flow |
| SPF | Standard power flow |
| PCIPF | Proposed current injection power flow |
| MCIPF | Modified current injection power flow |
| FDPF | Fast decoupled power flow |
| SFDPF-BX | Standard fast decoupled power flow—BX version |
| PCIFDPF-BX | Proposed current injection fast decoupled power flow—BX version |
| MCIFDPF-BX | Modified current injection fast decoupled power flow—BX version |
| MLP | Maximum loading point |
| P-V | Voltage versus active power curve |
| PV | Generation bus |
| PQ | Load bus |
| λ | Loading factor |
| NC | no convergence considering the maximum number of iterations. |
Appendix A
References
- Bonini Neto, A.; Alves, D.A.; Minussi, C.R. Artificial Neural Networks: Multilayer Perceptron and Radial Basis to Obtain Post-Contingency Loading Margin in Electrical Power Systems. Energies 2022, 15, 7939. [Google Scholar] [CrossRef]
- Huang, Y.; Ju, Y.; Zhu, Z. An Asymptotic Numerical Continuation Power Flow to Cope with Non-Smooth Issue. Energies 2019, 12, 3493. [Google Scholar] [CrossRef] [Green Version]
- Ajjarapu, V. Computational techniques for voltage stability assessment and control. In Power Electronics and Power Systems Series; Springer: New York, NY, USA, 2010. [Google Scholar]
- Kulworawanichpong, T. Simplified Newton–Raphson power-flow solution method. Int. J. Electr. Power Energy Syst. 2010, 32, 551–558. [Google Scholar] [CrossRef]
- Kamel, S.; Abdel-Akher, M.; Jurado, F. Improved NR current injection load flow using power mismatch representation of PV bus. Int. J. Electr. Power Energy Syst. 2013, 53, 64–68. [Google Scholar] [CrossRef]
- Kamel, S.; Jurado, F.; Chen, Z.; Abdel-Akher, M.; Ebeed, M. Developed generalised unified power flow controller model in the Newton–Raphson power-flow analysis using combined mismatches method. IET Gener. Transm. Distrib. 2016, 10, 2177–2184. [Google Scholar] [CrossRef]
- Gómez-Expósito, A.; Romero-Ramos, E.; Dzafic, I. Hybrid real-complex current injection-based load flow formulation. Electr. Power Syst. Res. 2015, 119, 237–246. [Google Scholar] [CrossRef]
- Oliveira, C.C.; Bonini Neto, A.; Minussi, C.R.; Alves, D.A.; Castro, C.A. New Representation of PV Buses in the Current Injection Newton Power Flow. Int. J. Electr. Power Energy Syst. 2016, 90, 237–244. [Google Scholar] [CrossRef] [Green Version]
- Karimi, M.; Shahriari, A.; Aghamohammadi, M.R.; Marzooghi, H.; Terzija, V. Application of Newton-based load flow methods for determining steady state condition of well and ill-conditioned power systems: A review. Int. J. Electr. Power Energy Syst. 2019, 113, 298–309. [Google Scholar] [CrossRef]
- Matarucco, R.R.; Bonini Neto, A.; Alves, D.A. Assessment of branch outage contingencies using the continuation method. Int. J. Electr. Power Energy Syst. 2014, 55, 74–81. [Google Scholar] [CrossRef]
- Yuan, H.; Li, F. Hybrid voltage stability assessment (VSA) for N − 1 contingency. Electr. Power Syst. Res. 2015, 122, 65–75. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; Gao, J.; Wang, Y.; Harley, R.G. A survey of contingency analysis regarding steady state security of a power system. In Proceedings of the 2017 North American Power Symposium (NAPS), Morgantown, WV, USA, 17–19 September 2017; pp. 1–6. [Google Scholar]
- Stott, B. Review of load-flow calculation methods. Proc. IEEE 1974, 62, 916–929. [Google Scholar] [CrossRef]
- El-Hawary, M.E. Electrical Power Systems: Design and Analysis; Revised Printing, v. 2; John Wiley & Sons: Hoboken, NJ, USA, 1995; p. 799. [Google Scholar]
- Monticelli, A.J. Power Flow in Electric Networks; Edgard Blucher: São Paulo, Brazil, 1983. (In Portuguese) [Google Scholar]
- Powell, L. Power System Load Flow Analysis; The McGraw-Hill Education: New York, NY, USA, 2004. [Google Scholar]
- Zhang, Y.; Lu, Y. A novel newton current equation method on power flow analysis in microgrid. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Da Costa, V.M.; Pereira, J.L.R.; Martins, N. An augmented Newton-Raphson power flow formulation based on current injections. Int. J. Electr. Power Energy Syst. 2001, 23, 305–312. [Google Scholar] [CrossRef]
- Da Costa, V.M.; Martins, N.; Pereira, J.L.R. Developments in the Newton-Raphson power flow formulation based on current injections. IEEE Trans. Power Syst. 1999, 14, 1320–1326. [Google Scholar] [CrossRef]
- Garcia, P.A.N.; Pereira, J.L.R.; Carneiro, S., Jr.; Vinagre, M.P.; Gomes, F.V. Improvements in the representation of PV buses on three-phase distribution power flow. IEEE Trans. Power Deliv. 2004, 19, 894–896. [Google Scholar] [CrossRef]
- Dommel, H.W.; Tinney, W.F.; Powell, W.L. Further developments in Newton’s method for power system applications. In Winter Power Meeting; Conference Paper No. 70 CP 161-PWR; IEEE: New York, NY, USA, 1970. [Google Scholar]
- Portelinha, R.K.; Durce, C.C.; Tortelli, O.L.; Lourenço, E.M. Fast-decoupled power flow method for integrated analysis of transmission and distribution systems. Electr. Power Syst. Res. 2021, 196, 107215. [Google Scholar] [CrossRef]
- Stott, B.; Alsac, O. Fast decoupled load Flow. IEEE Trans. Power Appar. Syst. 1974, PAS-93, 859–869. [Google Scholar] [CrossRef]
- Abhyankar, S.; Cui, Q.; Flueck, A.J. Fast power flow analysis using a hybrid current-power balance formulation in rectangular coordinates. In Proceedings of the 2014 IEEE PES T&D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014; pp. 1–5. [Google Scholar]
- Van Amerongen, R.A.M. A general-purpose version of the fast decoupled load flow. IEEE Trans. Power Syst. 1989, 4, 760–770. [Google Scholar] [CrossRef]
- Monticelli, A.; Garcia, A.; Saavedra, O.R. Fast decoupled load flow: Hypothesis, derivations and testing. IEEE Trans. Power Syst. 1990, 5, 1425–1431. [Google Scholar] [CrossRef]
- Tortelli, O.L.; Lourenço, E.M.; Garcia, A.V.; Pal, B.C. Fast decoupled power flow to emerging distribution systems via complex pu normalization. IEEE Trans. Power Syst. 2015, 30, 1351–1358. [Google Scholar] [CrossRef] [Green Version]
- Portelinha, R.K.; Durcel, C.C.; Tortelli, O.L.; Lourenço, E.M.; Pal, B.C. Unified Transmission and Distribution Fast Decoupled Power Flow. J. Control Autom. Electr. Syst. 2019, 30, 1051–1058. [Google Scholar] [CrossRef]
- Bonini Neto, A.; Alves, D.A. Improved geometric parameterisation techniques for continuation power flow. IET Gener. Transm. Distrib. 2010, 4, 1349–1359. [Google Scholar] [CrossRef]
- Singh, S.P.; Raju, G.S.; Rao, V.S.S. A technique to improve the convergence of FDLF for systems with high R/X lines. In Proceedings of the TENCON’91. Region 10 International Conference on EC3-Energy, Computer, Communication and Control Systems, New Delhi, India, 28–30 August 1991; pp. 204–207. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coutinho de Oliveira, C.; Bonini Neto, A.; Alves, D.A.; Minussi, C.R.; Castro, C.A. Alternative Current Injection Newton and Fast Decoupled Power Flow. Energies 2023, 16, 2548. https://doi.org/10.3390/en16062548
Coutinho de Oliveira C, Bonini Neto A, Alves DA, Minussi CR, Castro CA. Alternative Current Injection Newton and Fast Decoupled Power Flow. Energies. 2023; 16(6):2548. https://doi.org/10.3390/en16062548
Chicago/Turabian StyleCoutinho de Oliveira, Cristina, Alfredo Bonini Neto, Dilson Amancio Alves, Carlos Roberto Minussi, and Carlos Alberto Castro. 2023. "Alternative Current Injection Newton and Fast Decoupled Power Flow" Energies 16, no. 6: 2548. https://doi.org/10.3390/en16062548
APA StyleCoutinho de Oliveira, C., Bonini Neto, A., Alves, D. A., Minussi, C. R., & Castro, C. A. (2023). Alternative Current Injection Newton and Fast Decoupled Power Flow. Energies, 16(6), 2548. https://doi.org/10.3390/en16062548







