Stochastic Security-Constrained Economic Dispatch of Load-Following and Contingency Reserves Ancillary Service Using a Grid-Connected Microgrid during Uncertainty
Abstract
:1. Introduction
- Solving multiperiod SSCED by the co-optimization of energy and ramping reserves in both normal and contingency conditions.
- Modeling the uncertainty of wind power output and solving the aforementioned complex problem using “probability-weighted scenarios and transition matrices” [13].
- Modeling probabilistic contingency conditions.
- Demonstrating the management of Fast Ramping (FR) resources, such as wind energy, and using its negative characteristic of power ramping into an advantageous one.
- Validating the impact of change in the flexibility (ramping rate) of generators on active power costs in normal and contingency conditions.
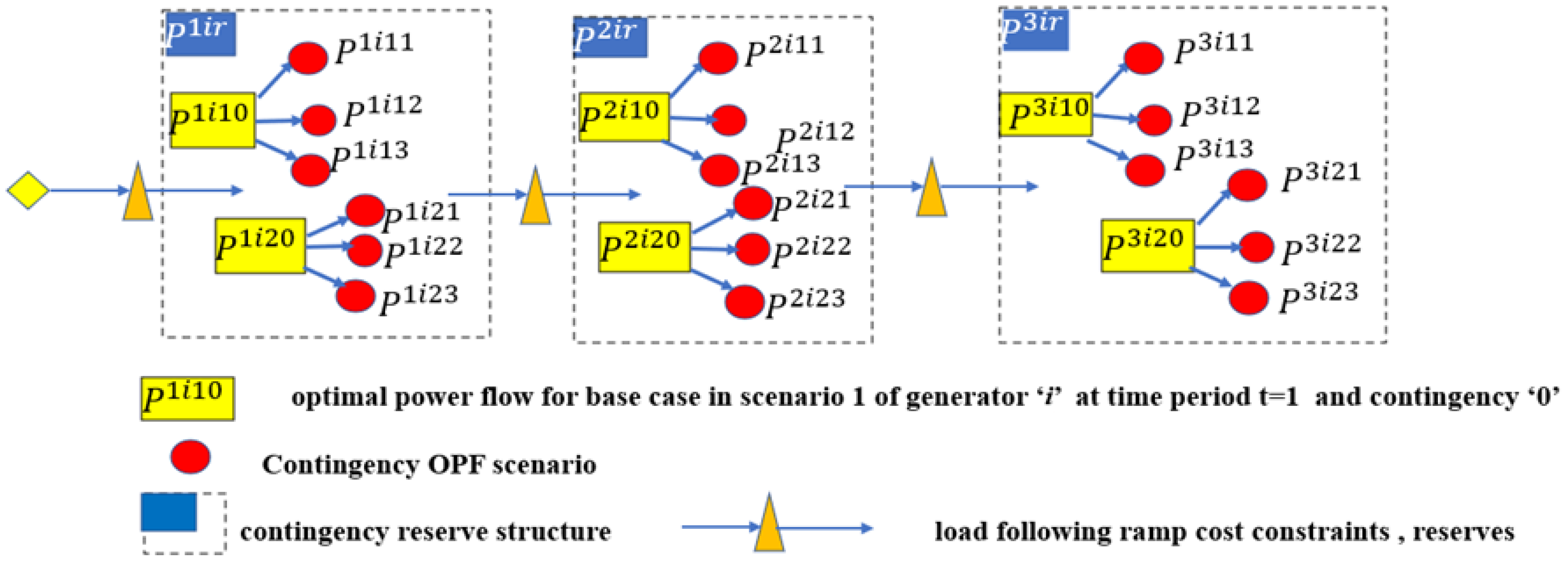
2. Typical Structure of Proposed SSCED Multiperiod Problem Structure
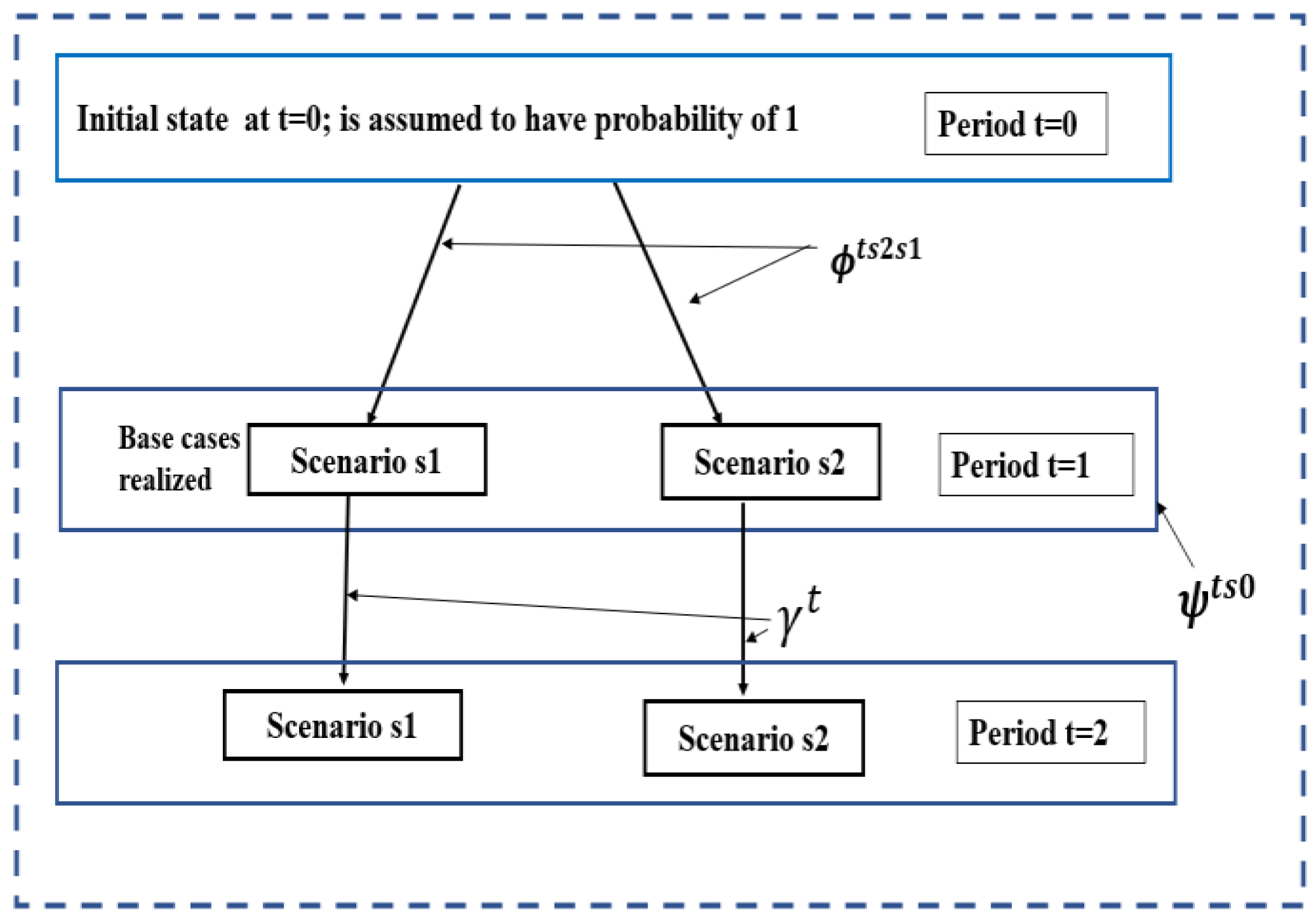
2.1. Single Base Scenario (Single Renewable Generation Profile)
2.2. Multiple Base Scenario (Multiple Renewable Generation Profile)
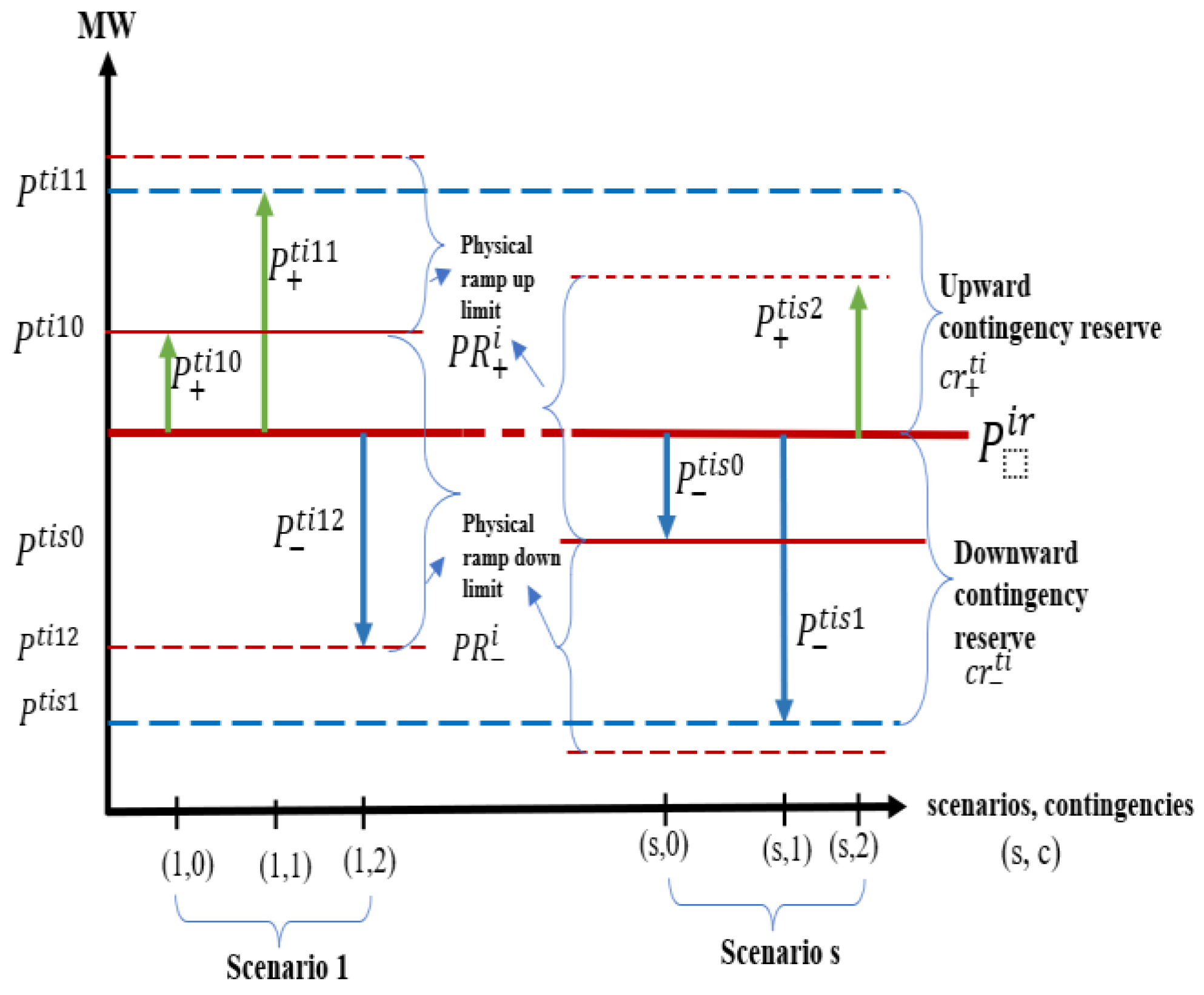
2.3. Load-Following Reserve Ramping under Uncertainty Using ‘Central Path’
2.4. Contingency Condition Reserve Ramping during Uncertainty
3. Proposed Methodology for Solving Multiperiod SSCED Problem
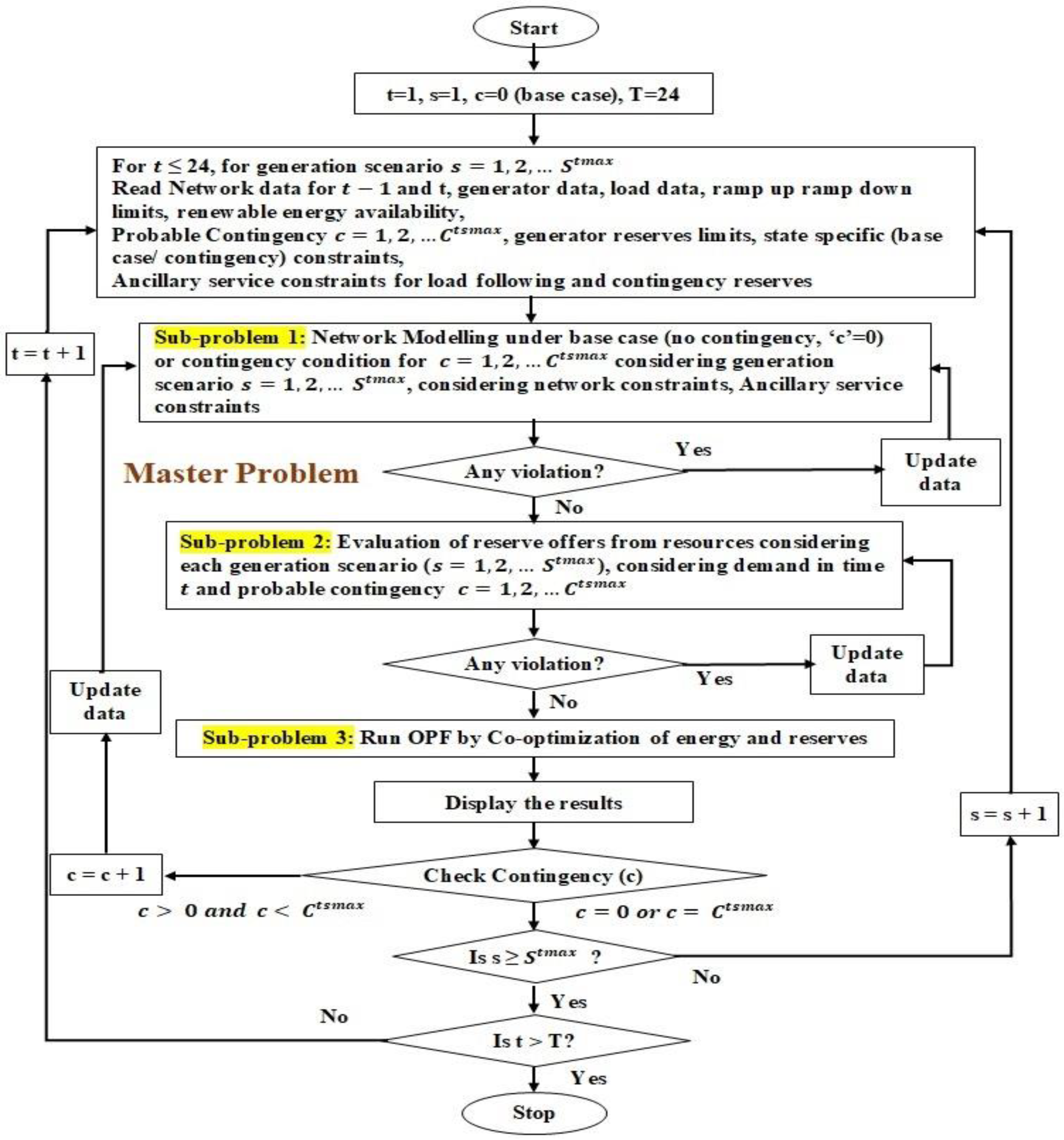
3.1. Proposed Methodology for Solving SSCED considering the Uncertainty of Renewable Generation and the Uncertainty of Contingency Occurrence
- ➢
- Sub-problem 1: Network modeling.
- ➢
- Sub-problem 2: The evaluation of the reserve offer from resources considering the uncertainty of generation scenarios and probable contingency.
- ➢
- Sub-problem 3: Objective function cost minimization by OPF Co-optimization of energy and reserves.
- The optimization of the expected cost of active power dispatch and redispatch.
- The optimization of the expected cost of load-following ramping (wear and tear).
- The optimization of the cost of load-following ramp reserves.
- The cost of endogenous contingency reserves.
- The optimization of no-load, startup, and shutdown costs.
3.2. Subproblem 1: Network Modeling
3.2.1. Cost of Active Power from CHP-Based Generators
3.2.2. Cost of Wind Energy Conversion System (WECS)
3.2.3. Modeling the Uncertainty of Wind Power Output Scenarios Using Probability-Weighted Scenarios
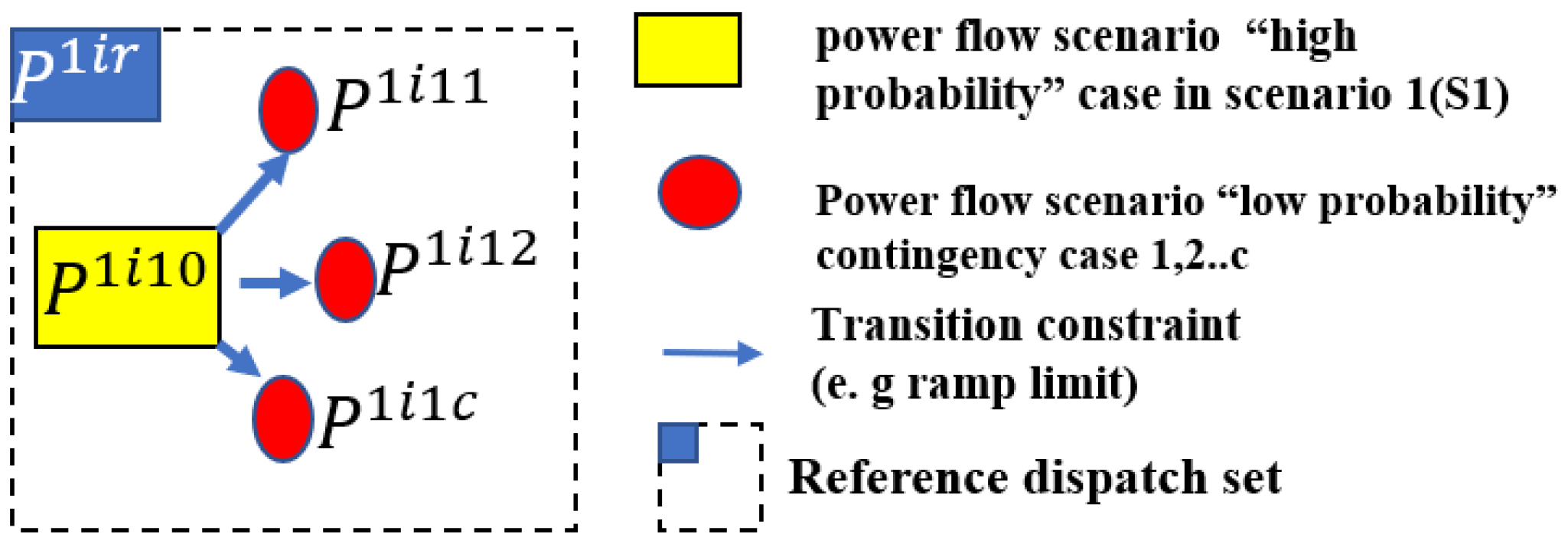
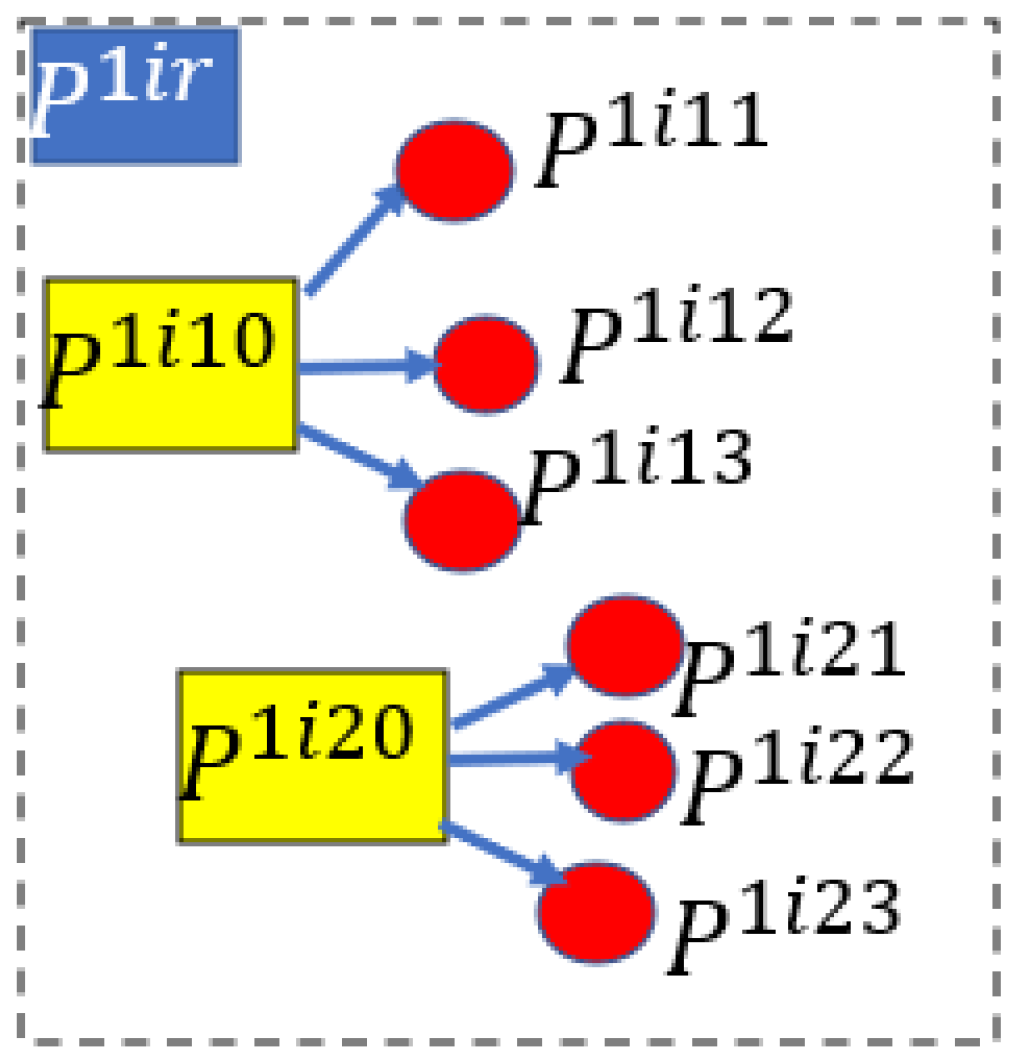
3.2.4. Mathematical Modeling of Probabilistic Transition of States from Base Case to Contingency State [16,20]
3.3. Subproblem 2: Ramping Evaluation
3.3.1. Mathematical Modeling of Load-Following Ramping Reserves in Normal (Base Case-No Contingency) State
3.3.2. Mathematical Modeling of Contingency Reserves Ramping in Contingency
- Reserve, redispatch, and contract variables:
- Ramping limits on transitions from base to contingency cases:
3.4. Subproblem 3: Objective Function Cost Minimization by OPF Co-Optimization of Energy and Reserves
- In the normal state, the objective function becomes:
- In the contingency state, the objective function considered is as follows:
- 1.
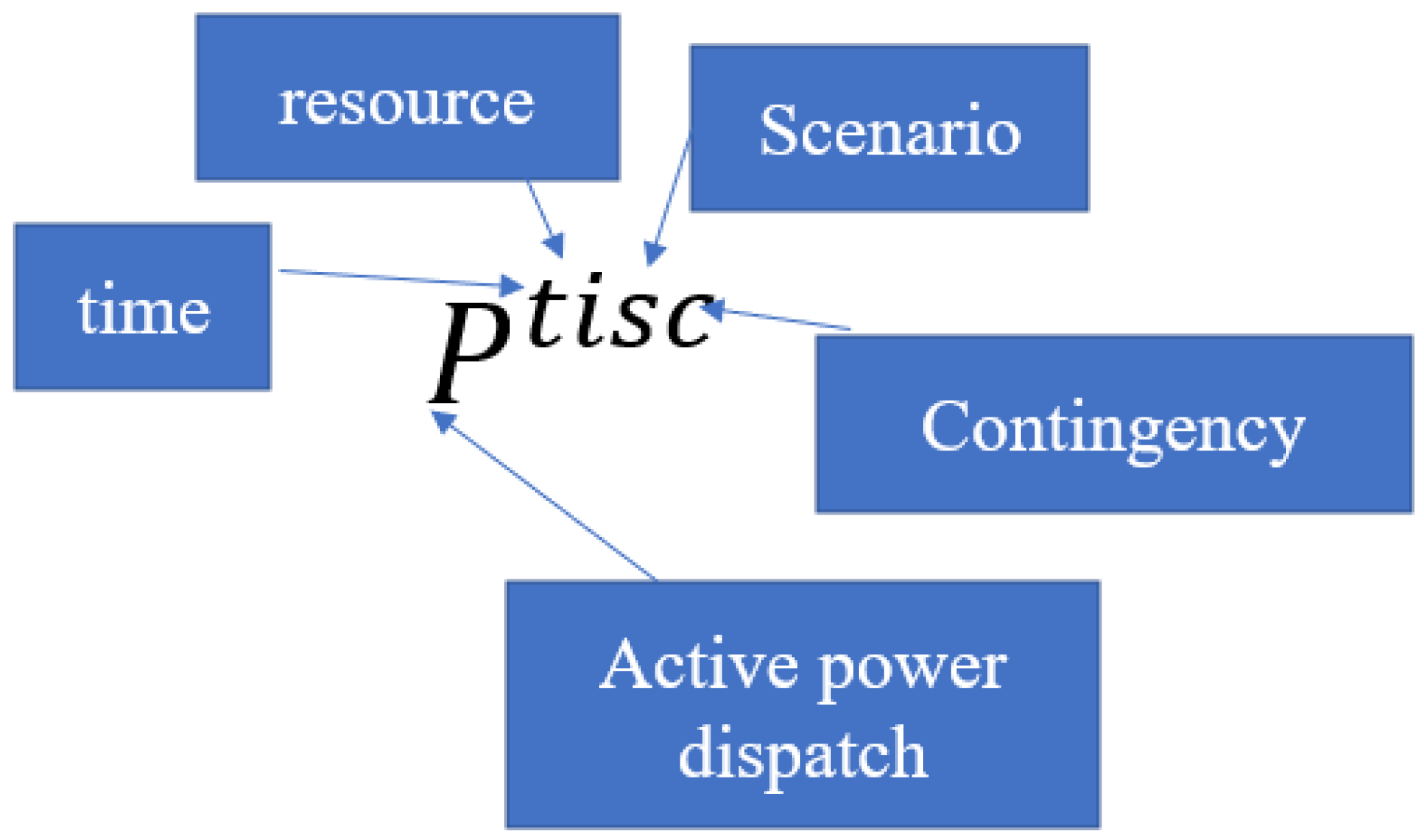
- Optimization of the expected cost of active power dispatch and redispatch ($/h)where is the cost function for active power injected by unit i at time t. is the cost function for upward deviation from the reference active power. is the cost function for downward deviation from the reference active power quantity for unit i at time t for scenario s and contingency c.
- 2.
- Optimization of the expected cost of load-following ramping (wear and tear) ($/h)
- 3.
- Optimization of cost of load-following ramp reserves ($/h)
- 4.
- Cost of endogenous contingency reserves in ($/h)
- 5.
- Optimization of no-load, startup, and shutdown costs in ($/h)
- Network operations Constraints:
- Unit Commitment:
- Generator injection limits and commitments:
- Startup and shutdown events:
- Minimum up and down times:
4. Case Study and Results
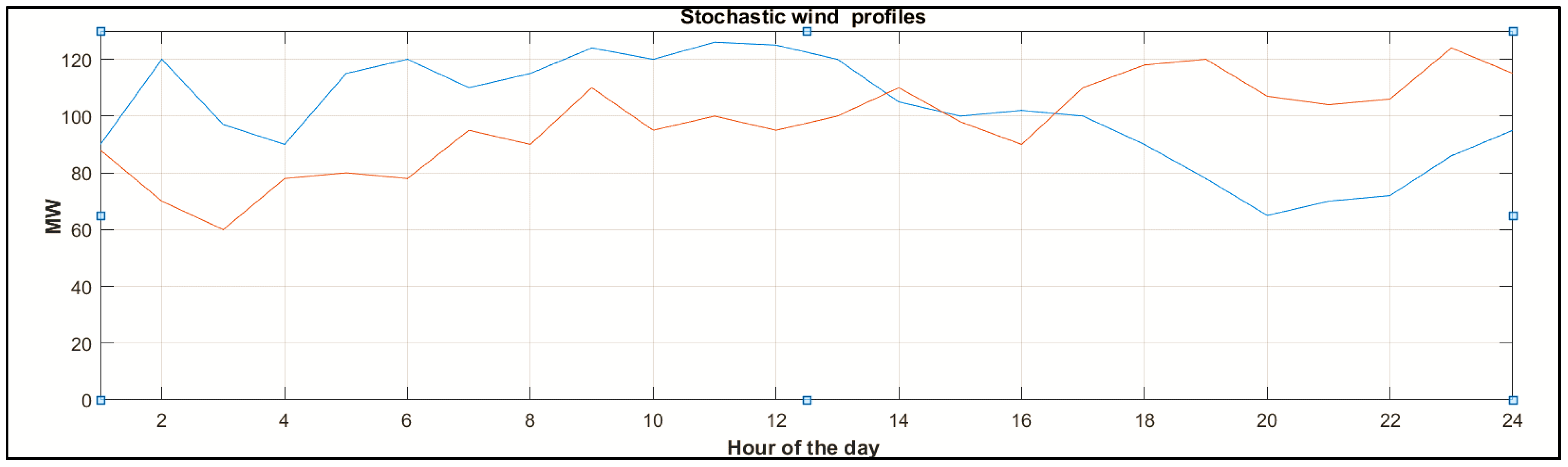
4.1. System Configuration
| Bus Number | Generator Type (Fuel) | Pmax Pmin | $/MW | Ramping Capability [27] | Contingency Reserve Positive and Negative Active Reserve in MW |
|---|---|---|---|---|---|
| 1 | Natural gas | 80 | 90 | ±5 to 8% | ±10 |
| 10 | |||||
| 2 | WECS (Wind 1) | 100 | 30 | ±30–60% | ±30 |
| 20 | |||||
| 27 | Biogas Gen 1 | 55 | 80 | ±8 to 10% | ±10 |
| 10 | |||||
| 22 | Biogas Gen 2 | 50 | 80 | ±8 to 10% | ±10 |
| 10 | |||||
| 23 | Biogas Gen 3 | 30 | 80 | ±8 to 10% | ±10 |
| 10 | |||||
| 13 | Biogas Gen 4 | 40 | 80 | ±8 to 10% | ±10 |
| 10 |
4.2. Case Studies
- Case 1: Base case—Normal State (load-following ramping reserve ancillary service)
- Case 2: Contingency condition—Generator outage occurrence in Case 1, contingency reserve ancillary service
- Case 3: Contingency condition—Underloading for 24 h (load decreased by 20% for all 24 h) of Case 1, contingency reserve ancillary service.These case studies are executed using Matpower Optimal Scheduling Tool (MOST) [16].
- The voltages of DG units and PCC change.
- In the range of (5%), i.e., 95% to 105% of the rated value.
- All conventional and distributed energy sources have P/f droop control capability.
- Well-equipped communication infrastructure is present in grid-connected microgrids.
- The timescale considered for load-following ramp-up and ramp-down services reserves is 1 h for the simplicity of analysis.
- The frequency of the system is maintained at 50 Hz with ±0.5 Hz tolerance.
4.3. Results and Discussion
4.3.1. Case 1: Base Case—Normal State: Load-Following Ramping Reserve Ancillary Service
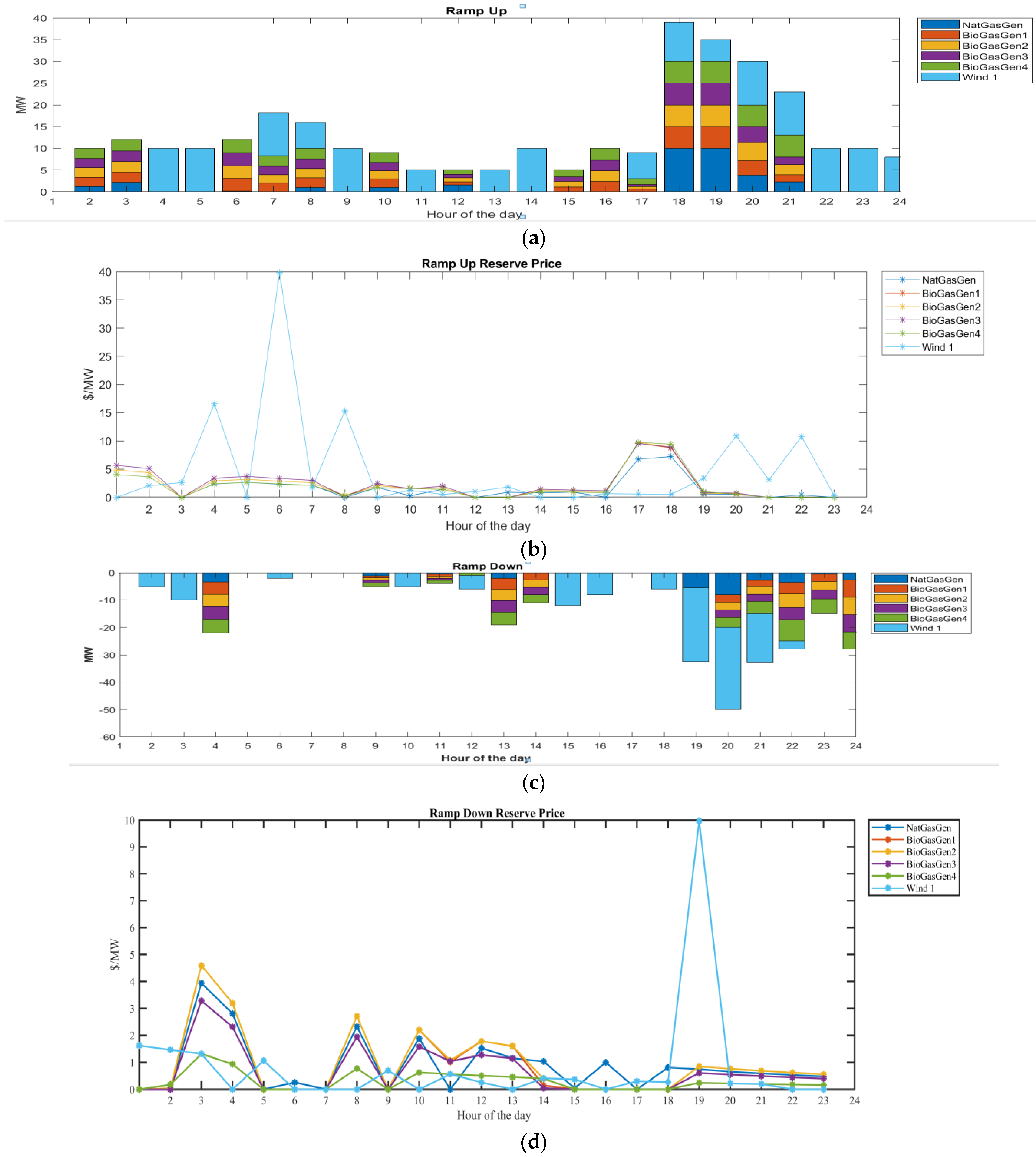
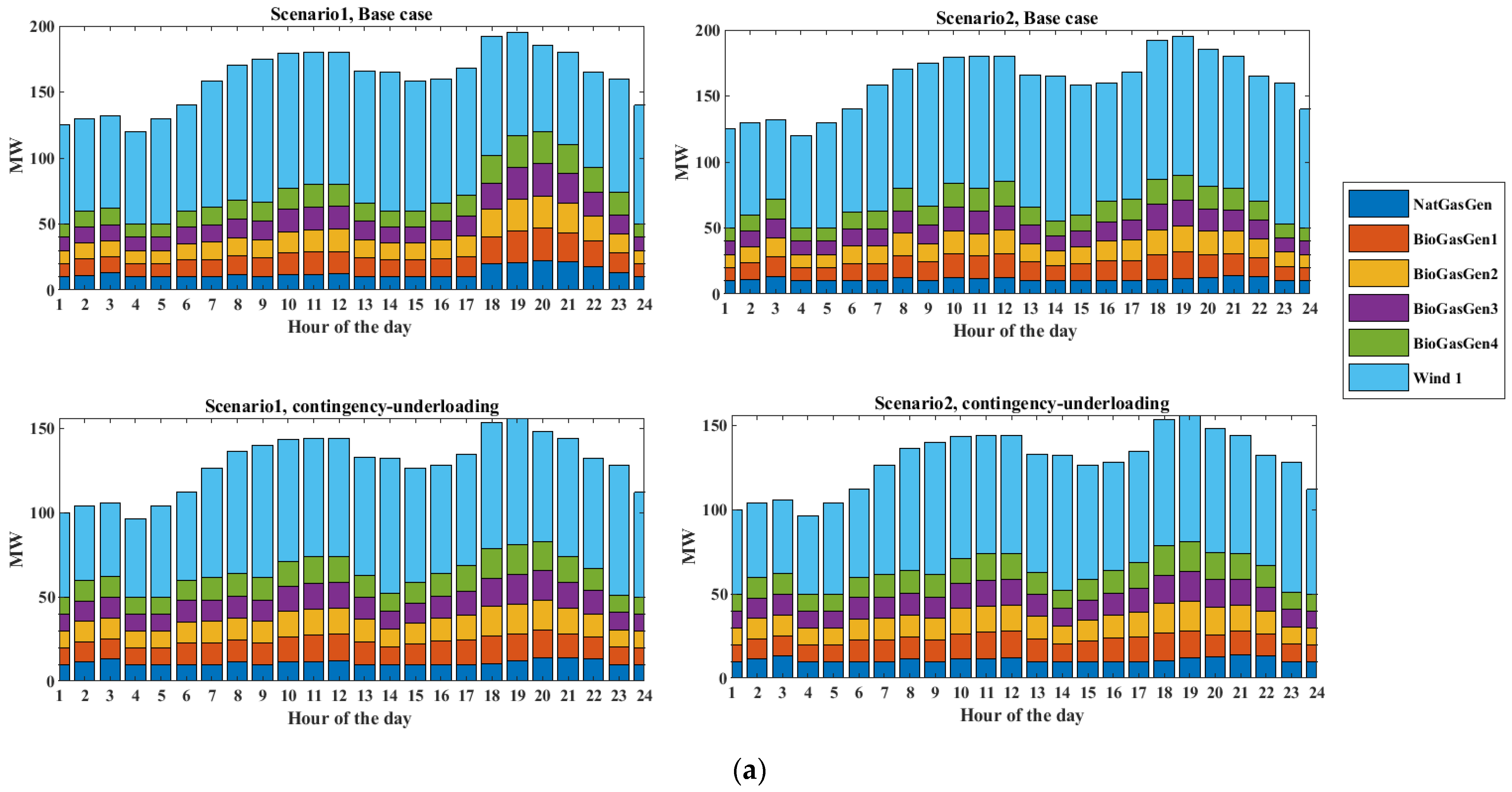
Power Generation in Case 1
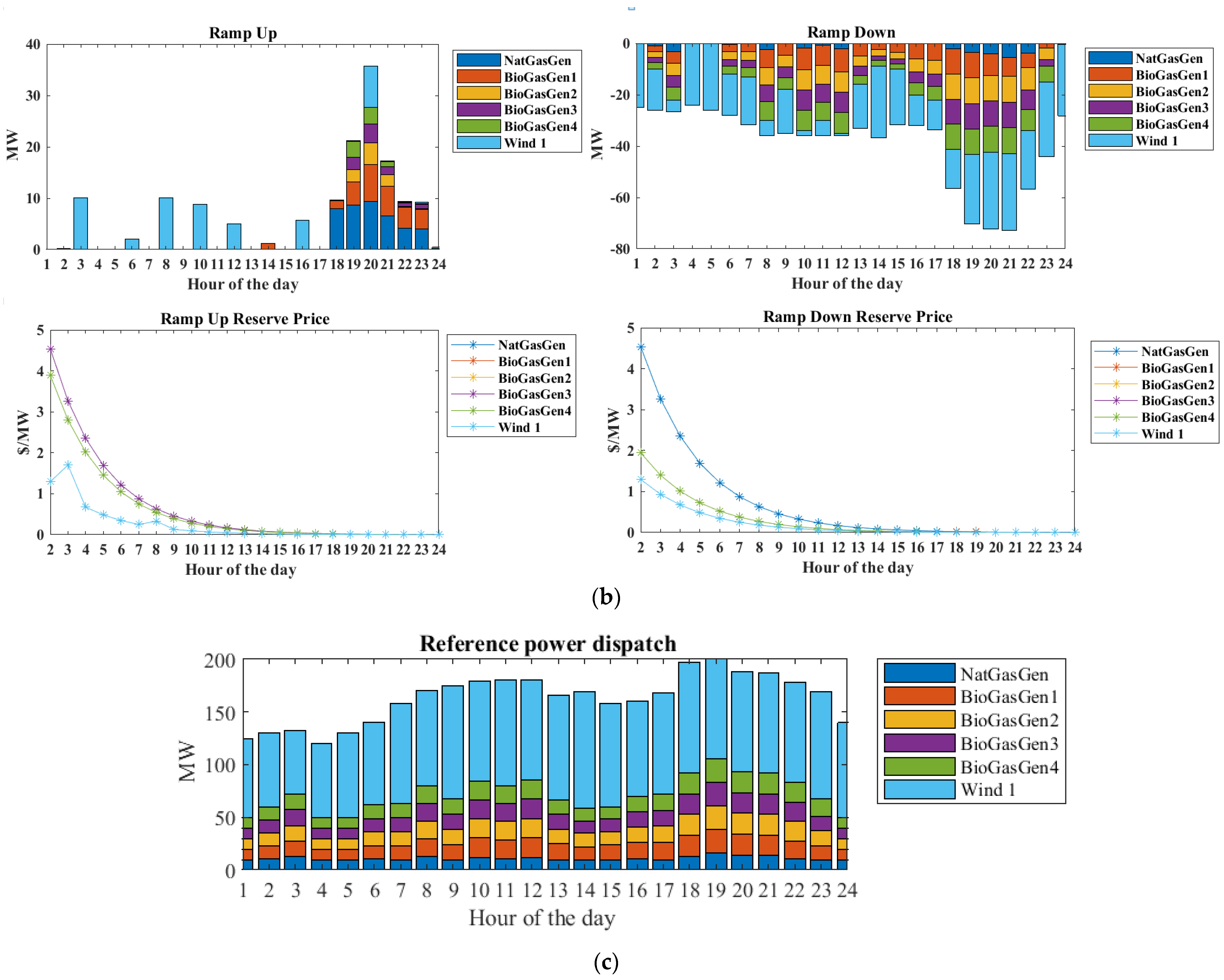
Ramping Process in Case 1: Normal Condition (Base Case)
Operating Cost Minimization in Case 1: Normal Condition (Base Case)
4.3.2. Case 2: Contingency Condition: Generator Outage Occurrence in Case 1, Contingency Reserve Ancillary Service
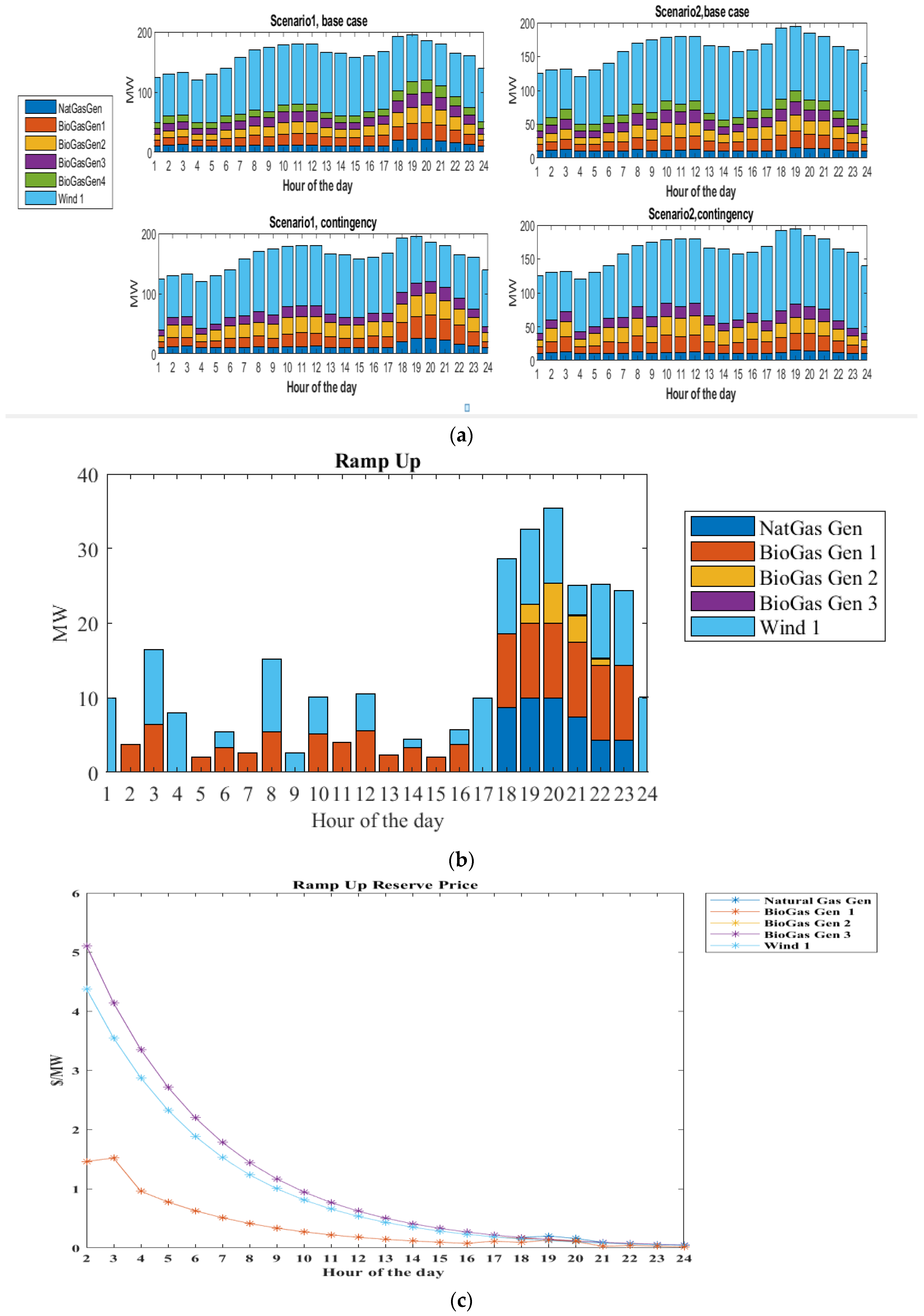
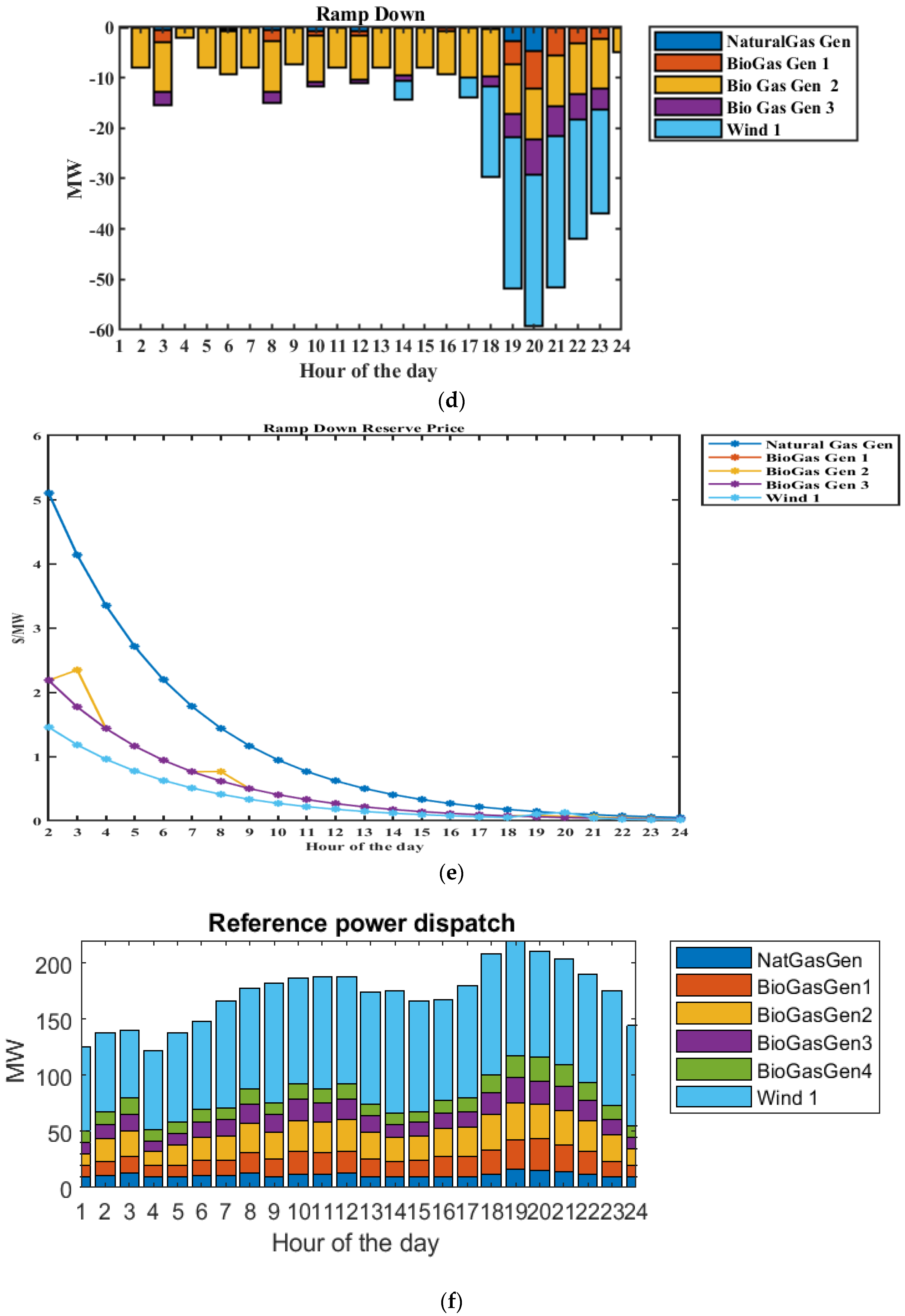
Power Generation in Case 2
Ramping Process in Case 2: Contingency Condition (Generator Outage)
Operating Cost Minimization in Case 2
4.3.3. Case 3: Contingency Condition: Underloading for 24 h (Load Decreased by 20% for All 24 h) of Case 1, Contingency Reserve Ancillary Service
Power Generation in Case 3
Ramping Process in Case 3: Contingency Condition
Operation Cost Minimization in Case 3
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Index of time periods (1 h). | |
| T | Set of indices of periods in the planning horizon, typically |
| s | Index of scenarios. |
| Indexes of every possible scenario taken into consideration at time t. | |
| Maximum number of generation profiles (scenarios) in time period t. | |
| c | Index of post-contingency cases (c = 0 for the base case, meaning that there was no contingency). |
| Maximum number of contingency indices taken into account in scenario s at time period t. | |
| Injections index (generation units). | |
| Indices of all the units (generators, dispatchable, or curtailable loads) that are available for dispatch in any situation at time t. | |
| Quantity/reference of the active power dispatching active power to unit I at time t. | |
| Unit i at time t provides an active contingency reserve quantity that is moving upward or downward. | |
| Maximum capacity restrictions for the unit i at time t can go up or down. | |
| Limits on active injection for unit i at time t in a post-contingency state c of scenario s. | |
| Unit i is required to provide ramping reserves for loads moving up or down for the changeover to time t + 1 at time t. | |
| Angles and magnitudes of the voltage as well as active injections of power for the post-contingency condition (state c) of scenario (s) at time (t). | |
| Limits for unit i upward/downward load-following ramping reserves at time t for the transition to time t + 1. | |
| Probability Contingency k in the scenario s at the time t, adjusted for . | |
| For contingency cases, the fraction of the time slice that is spent in the base case before the contingency occurs. | |
| Length of the time slice for scheduling, usually 1 h. | |
| Binary commitment state: 1 if a unit is online, otherwise 0, for unit i in period t. | |
| Probability conditional on reaching period t without deviating from the main path in a contingency in periods 1…t − 1 and on scenario s being realized in some way of the contingency c in scenario s at period t. (base or contingency). The basic case, or conditional probability of no contingency, is . | |
| Probability of moving from scenario s1 to scenario s2 in period t, given that s1 was completed in period t − 1. | |
| Whether the transition to scenario s2 in Period t, assuming that scenario s1 from period t − 1 should be included in the load-following ramp requirements, is indicated by a binary-valued mask. | |
| Estimated likelihood of contingency c in scenario s at time t using transition probabilities . Conditional probabilities of contingencies . | |
| Physical ramping upper/lower limits. for unit i when moving from base (c = 0) to contingency scenarios. | |
| For unit i in period t, the commitment state is binary: 1 if the unit is online, otherwise 0. | |
| For unit I in period t, there are binary startup and shutdown states: 1 if the unit experiences a startup or shutdown event in period t, otherwise 0. | |
| Cost formula for i at time t for active injection. | |
| Cost for a deviation from the active power reference quantity for unit i at time t in either an upward or downward direction. | |
| Cost formula for a contingency reserve that was bought from unit i at time t. | |
| Cost of the ramp reserve for an upward or downward load for unit i at time t for the transition to time t + 1. | |
| On the difference between the dispatches for unit i in neighboring periods, there is a quadratic, symmetric ramping cost. | |
| With the no-load cost eliminated, the cost function for active power injection has been modified to read as . |
References
- Chowdhury, S.P.; Chowdhury; Crossley, P. Microgrids and Active Distribution Networks; The Institution of Engineering and Technology: London, UK, 2009. [Google Scholar]
- Braun, M. Technological Control Capabilities of Der To Provide Future Ancillary Services. Int. J. Distrib. Energy Resour. 2007, 3, 191–206. [Google Scholar]
- Oureilidis, K.; Malamaki, K.N.; Gallos, K.; Tsitsimelis, A.; Dikaiakos, C.; Gkavanoudis, S.; Cvetkovic, M.; Mauricio, J.M.; Maza Ortega, J.M.; Ramos, J.L.M.; et al. Ancillary Services Market Design in Distribution Networks: Review and Identification of Barriers. Energies 2020, 13, 917. [Google Scholar] [CrossRef] [Green Version]
- Smeers, Y.; Martin, S.; Aguado, J.A. Co-optimization of Energy and Reserve with Incentives to Wind Generation: Case Study. IEEE Trans. Power Syst. 2022, 37, 2063–2074. [Google Scholar] [CrossRef]
- Available online: http://www.forumofregulators.gov.in/data/Reports/SANTULAN-FOR-Report-April2020.pdf (accessed on 2 December 2022).
- Shah, C.; Wies, R. Three-stage Power Flow & Flexibility Reserve Co-Optimization for Converter Dominated Distribution Network Lookahead Model using Blockchain & S-ADMM—I: Method. TechRxiv 2022, TechRxiv.11-08-2022. [Google Scholar] [CrossRef]
- Ozay, C.; Celiktas, M.S. Stochastic optimization energy and reserve scheduling model application for alaçatı, Turkey. Smart Energy 2021, 3, 100045. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, Z.; Jiang, C.; Zhang, Y. Dispatch and bidding strategy of active distribution network in energy and ancillary services market. J. Mod. Power Syst. Clean Energy 2015, 3, 565–572. [Google Scholar] [CrossRef] [Green Version]
- Cong, P.; Tang, W.; Zhang, L.; Zhang, B.; Cai, Y. Day-ahead active power scheduling in active distribution network considering renewable energy generation forecast errors. Energies 2017, 10, 1291. [Google Scholar] [CrossRef] [Green Version]
- Kurundkar, M.K.; Karve, M.G.; Vaidya, M.G. Comparative performance analysis of Firefly algorithm and Particle swarm Optimization for Profit Maximization of Grid connected Microgrid providing energy and ancillary service. Solid State Technol. 2021, 64, 4610–4626. [Google Scholar]
- Ye, H.; Li, Z. Pricing the Ramping Reserve and Capacity Reserve in Real Time Markets. arXiv 2015, arXiv:1512.06050. [Google Scholar]
- Fang, X.; Sedzro, K.S.A.; Hodge, B.S.; Zhang, J.; Li, B.; Cui, M. Providing Ramping Service with Wind to Enhance Power System Operational Flexibility; National Renewable Energy Laboratory, University of Texas at Dallas: Golden, CO, USA, 2020.
- Murillo-Sánchez, C.E.; Zimmerman, R.D.; Anderson, C.L.; Thomas, R.J. Secure Planning and Operations of Systems with Stochastic Sources, Energy Storage and Active Demand. IEEE Trans. Smart Grid 2013, 4, 2220–2229. [Google Scholar] [CrossRef]
- Makarov, Y.V.; Loutan, C.; Ma, J.; de Mello, P. Operational Impacts of Wind Generation on California Power Systems. IEEE Trans. Power Syst. 2009, 24, 1039–1050. [Google Scholar] [CrossRef]
- Ela, E.; O’Malley, M. Probability-Weighted LMP and RCP for Day-Ahead Energy Markets using Stochastic Security-Constrained Unit Commitment. In Proceedings of the 12th International Conference on Probabilistic Methods Applied to Power Systems, Istanbul, Turkey, 10–14 June 2012; National Renewable Energy Laboratory, University College Dublin: Golden, CO, USA, 2012. [Google Scholar]
- Zimmerman, R.D.; Murillo-S, C.E.; Thomas, R.J. MATPOWER: Steady- State Operations, Planning and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef] [Green Version]
- Bär, K.; Wageneder, S.; Solka, F.; Saidi, A.; Zörner, W. Flexibility Potential of Photovoltaic Power Plant and Biogas Plant Hybrid Systems in the Distribution Grid, Katharina Bar. Chem. Eng. Technol. 2020, 43, 1571–1577. [Google Scholar] [CrossRef]
- Akrami, A.; Doostizadeh, M.; Aminifar, F. Power system flexibility: An overview of emergence to evolution. J. Mod. Power Syst. Clean Energy 2019, 7, 987–1007. [Google Scholar] [CrossRef] [Green Version]
- Kaushik, E.; Prakash, V.; Mahela, O.P.; Khan, B.; El-Shahat, A.; Abdelaziz, A.Y. Comprehensive Overview of Power System Flexibility, during the Scenario of High Penetration of Renewable Energy in Utility Grid. Energies 2022, 15, 516. [Google Scholar] [CrossRef]
- Wang, H.; Murillo-Sanchez, C.E.; Zimmerman, R.D.; Thomas, R.J. On Computational Issues of Market-Based Optimal Power Flow. IEEE Trans. Power Syst. 2007, 22, 1185–1193. [Google Scholar] [CrossRef]
- Dvorkin, Y.; Kirschen, D.S.; Ortega-Vazquez, M.A. Assessing flexibility requirements in power systems. IET Gener. Transm. Distrib. 2014, 8, 1820–1830. [Google Scholar] [CrossRef]
- Ethan, D.; Avallone. Market Design Concepts to Prepare for Significant Renewable Generation Flexible Ramping Product: Market Design Concept Proposal; Market Issues Working Group, NYISO: Rensselaer, NY, USA, 26 April 2018. [Google Scholar]
- Alsac, O.; Stott, B. Optimal Load Flow with Steady State Security. IEEE Trans. Power Appar. Syst. 1974, PAS 93, 745–751. [Google Scholar] [CrossRef] [Green Version]
- Ferrero, R.; Shahidehpour, S.; Ramesh, V. Transaction Analysis In Deregulated Power Systems Using Game Theory. IEEE Trans. Power Syst. 1997, 12, 1340–1347. [Google Scholar] [CrossRef]
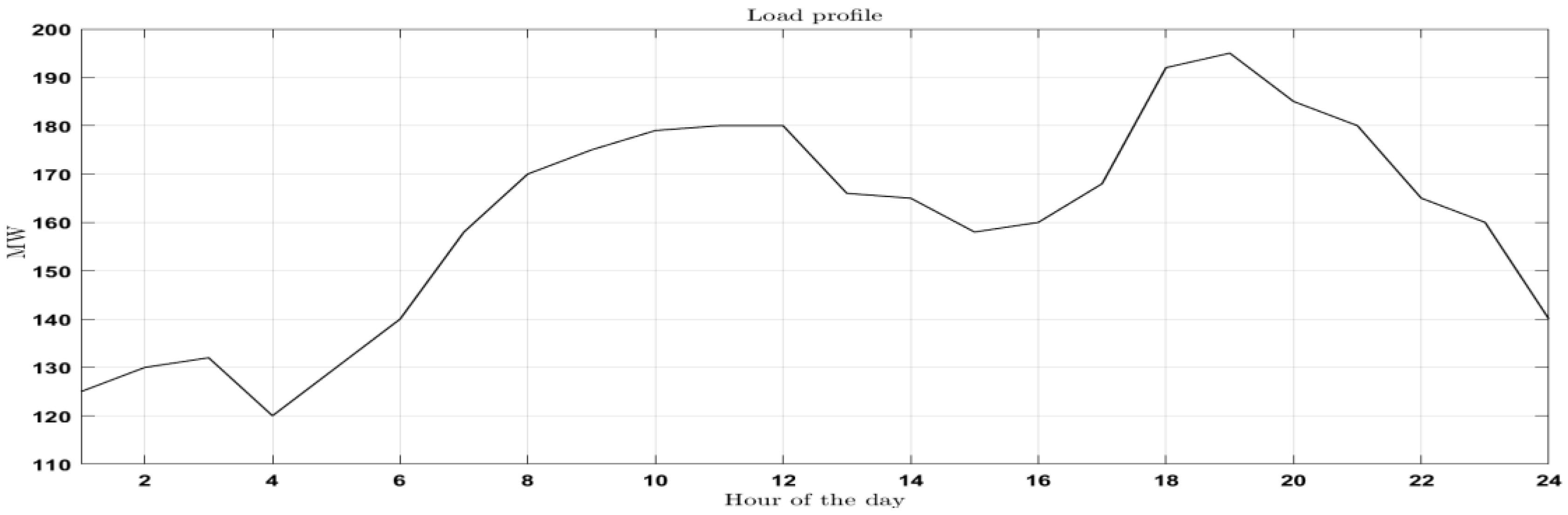
- Available online: https://weather.com/en-IN/weather/today/l/18.52,73.86?par=google (accessed on 30 November 2022).
- Available online: https://prayaspune.org/peg/electricity-load-patterns (accessed on 2 December 2022).
- Joshi, M.; Palchak, J.D.; Rehman, S.; Soonee, S.K.; Saxena, S.C.; Narasimhan, S.R. Ramping Up the Ramping Capability, India’s Power System Transition; National Renewable Energy Laboratory: Golden, CO, USA, 2020.



| Case | WECS Flexibility | Objective Function Cost ($/Day) | Increase in WECS Flexibility | New Objective Function Cost ($/Day) |
|---|---|---|---|---|
| Case 1 | 30% | 9819 | 40% | 9017 |
| Case 2 | 30% | 27,622 | 40% | 27,605 |
| Case 3 | 30% | 18,623 | 40% | 18,598 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurundkar, K.M.; Vaidya, G.A. Stochastic Security-Constrained Economic Dispatch of Load-Following and Contingency Reserves Ancillary Service Using a Grid-Connected Microgrid during Uncertainty. Energies 2023, 16, 2607. https://doi.org/10.3390/en16062607
Kurundkar KM, Vaidya GA. Stochastic Security-Constrained Economic Dispatch of Load-Following and Contingency Reserves Ancillary Service Using a Grid-Connected Microgrid during Uncertainty. Energies. 2023; 16(6):2607. https://doi.org/10.3390/en16062607
Chicago/Turabian StyleKurundkar, Kalyani Makarand, and Geetanjali Abhijit Vaidya. 2023. "Stochastic Security-Constrained Economic Dispatch of Load-Following and Contingency Reserves Ancillary Service Using a Grid-Connected Microgrid during Uncertainty" Energies 16, no. 6: 2607. https://doi.org/10.3390/en16062607




