Frequency Support Studies of a Diesel–Wind Generation System Using Snake Optimizer-Oriented PID with UC and RFB
Abstract
1. Introduction
- Study and present the modeling of a diesel–wind isolated system in an interconnected mode for frequency regularization studies capable enough to provide uninterrupted electrical energy during a change in the load demand.
- Present the new control strategy for a diesel–wind isolated system to reduce or minimize the frequency and power deviations in the event of load change or in case of a change in wind speed. The proposed design is formulated by using PID and the gains of PID, which play an important role and are obtained via the new SO algorithm.
- Study and present the modeling of UC and RFB for diesel–wind generating systems.
- The results are matched for a step change in load, step change in wind speed, load change at the different instances of time, and for continuous load patterns and via calculating gains of the controller and through error values, i.e., integral of time multiplied absolute error (ITAE), integral absolute error (IAE), and integral of time multiplied square error (ITSE).
- The outcome of SO-PID was also compared via plotting frequency and power deviation response for the diesel–wind system.
- In addition, the effect of UC and RFB impact on the output of the diesel–wind system was also investigated and compared to determine the best control design within the system for diverse working conditions.
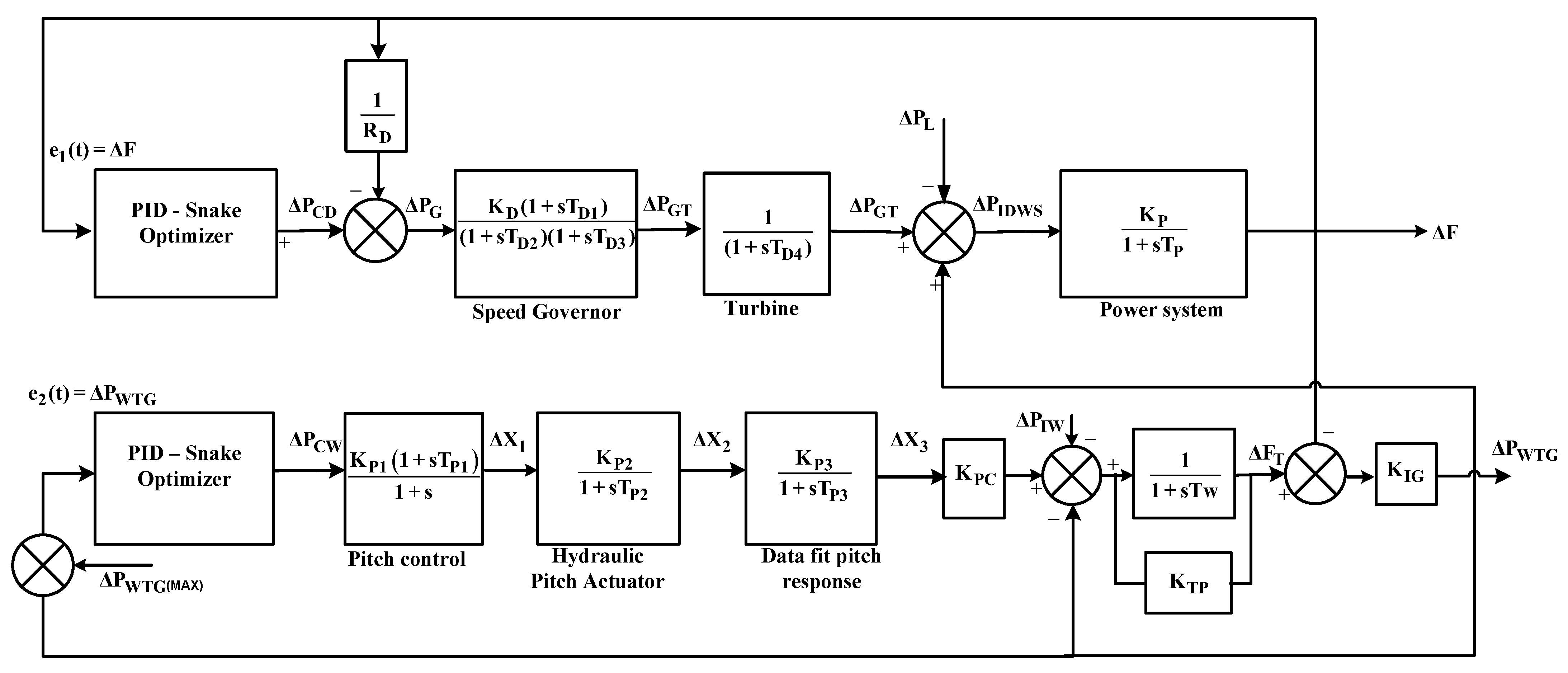
2. The Detailed Modeling of the Isolated Diesel–Wind System
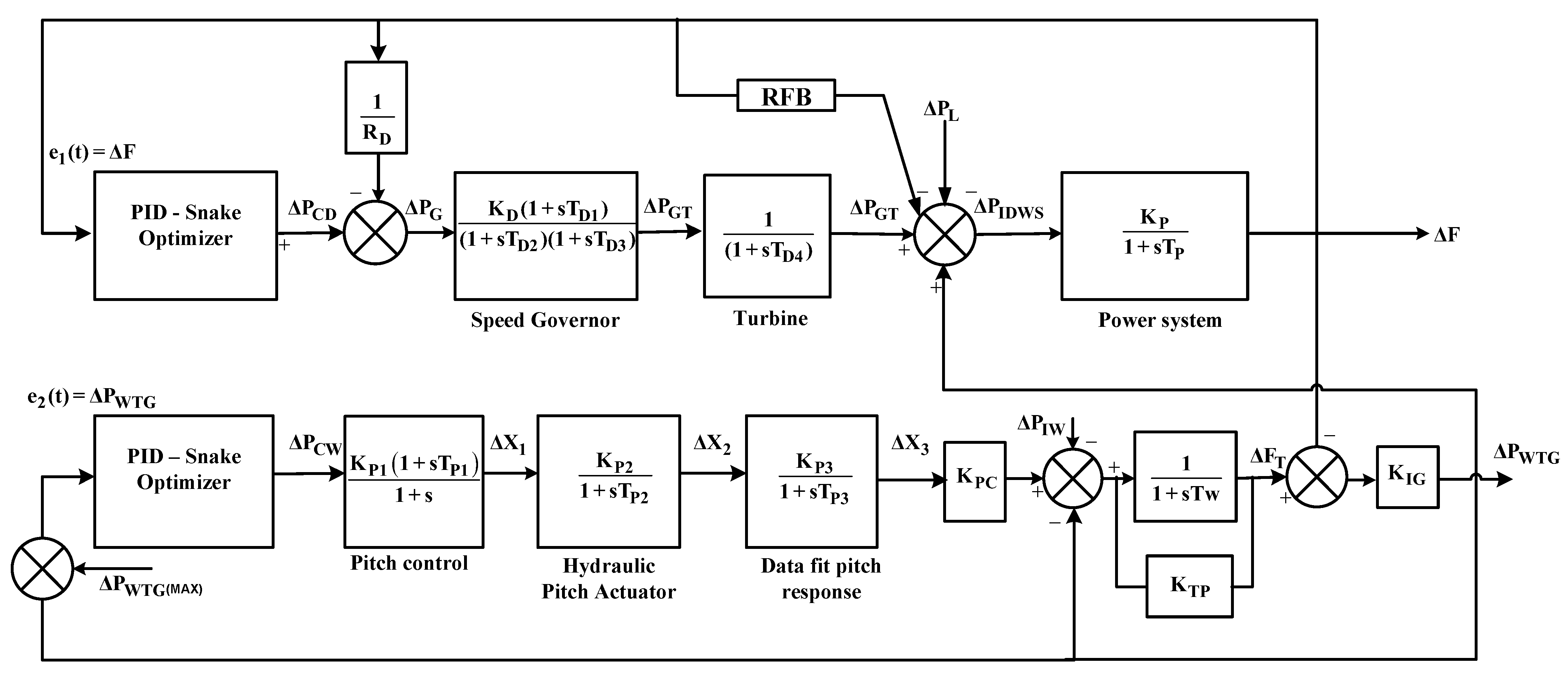
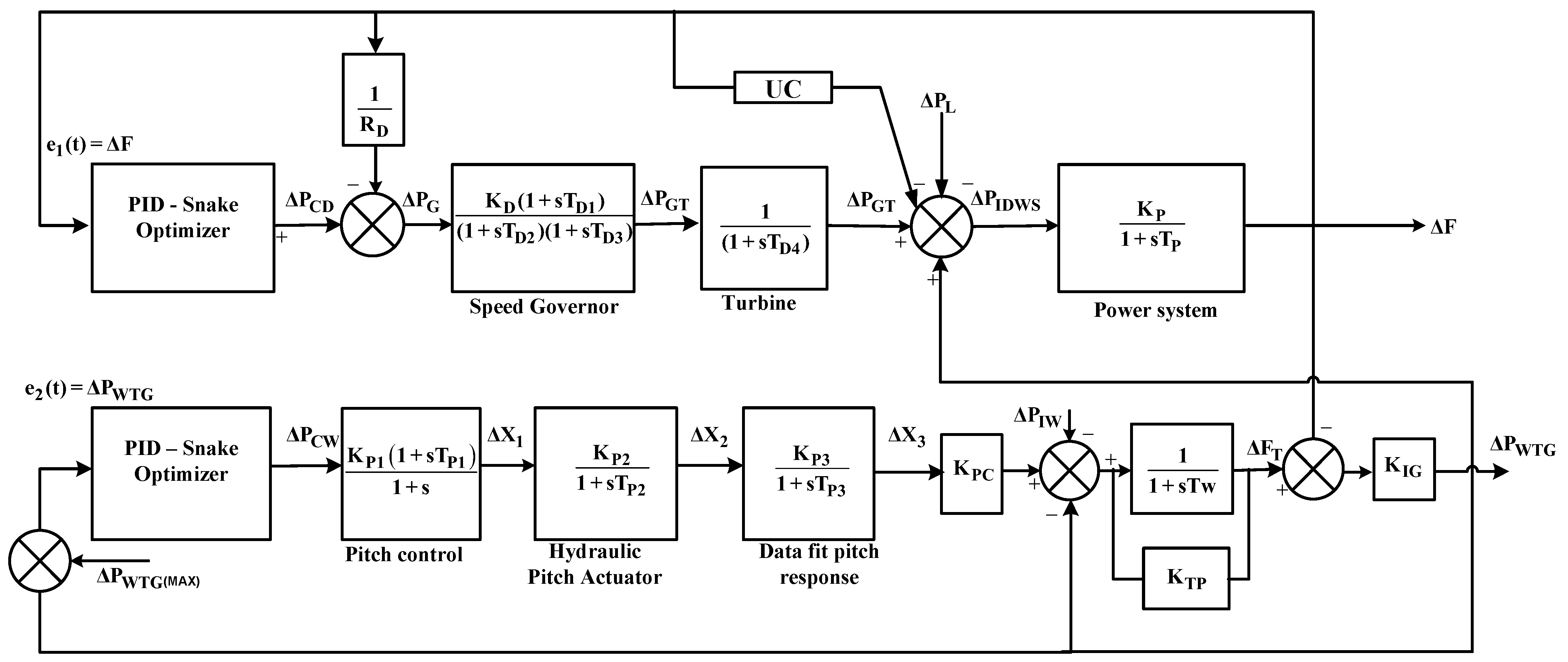
3. Redox Flow Battery (RFB) and Ultracapacitor (UC) Details
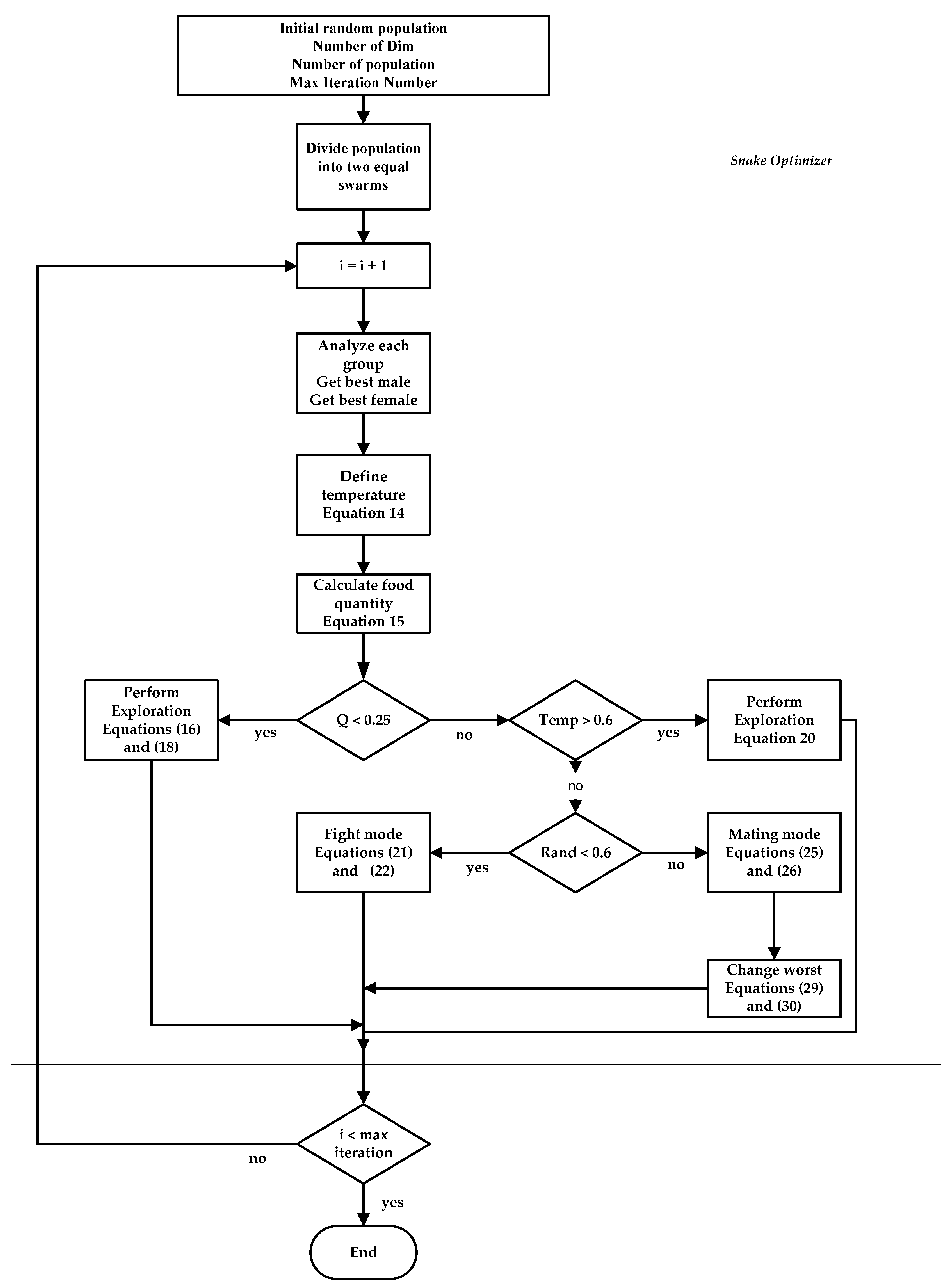
4. Snake Optimizer Details and Execution Steps
4.1. Mating Behavior of Snakes
4.2. Inspiration Source
4.3. Algorithm and Mathematical Model
4.3.1. Initialization
4.3.2. Division of the Swarm into Two Groups: Females and Males
4.3.3. Food Quality and Temperature and Each Group Valuation
4.3.4. Exploration Phase (No Food)
4.3.5. Exploitation Phase (Existing Food)
5. Results and Analysis
6. Conclusions
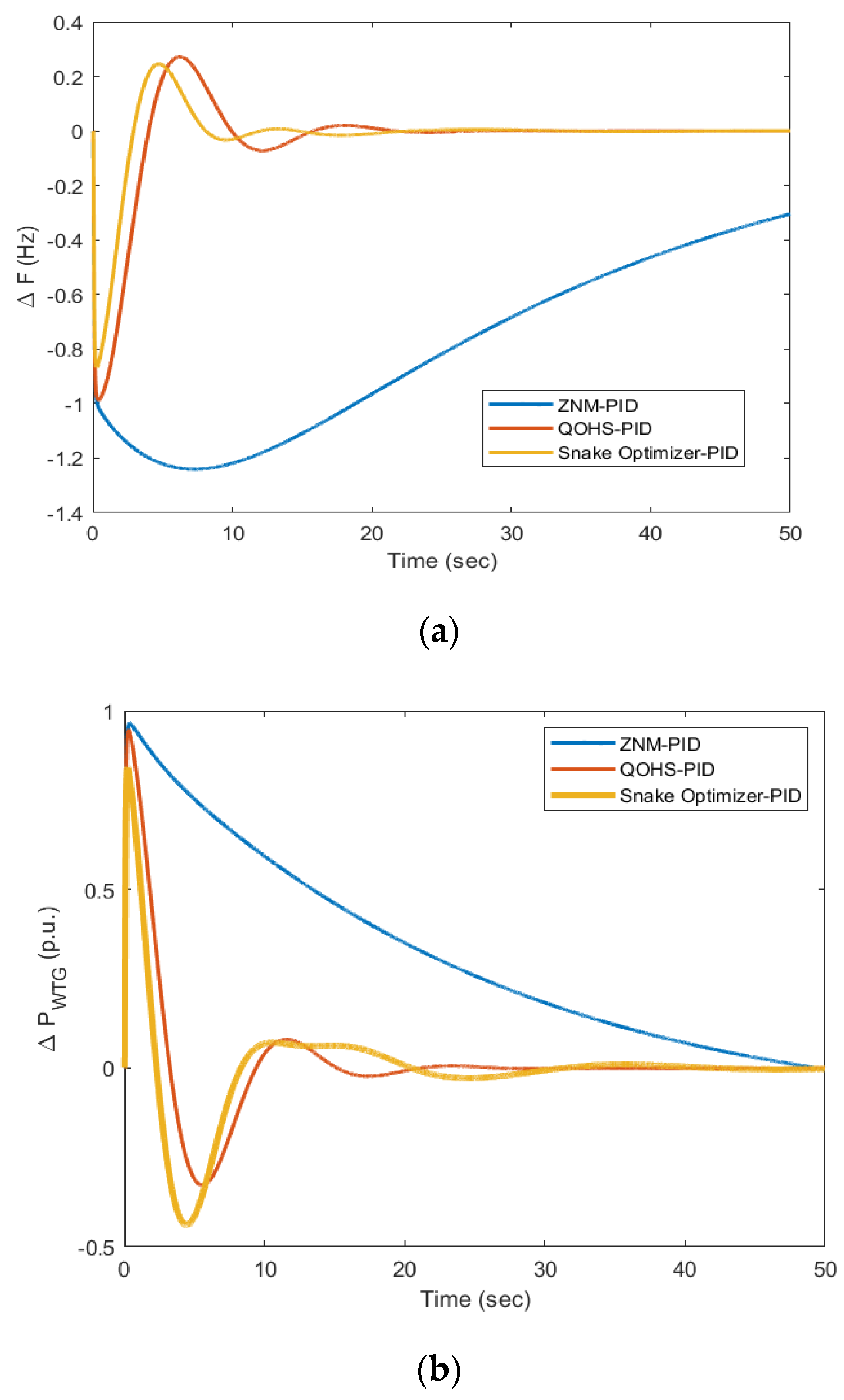
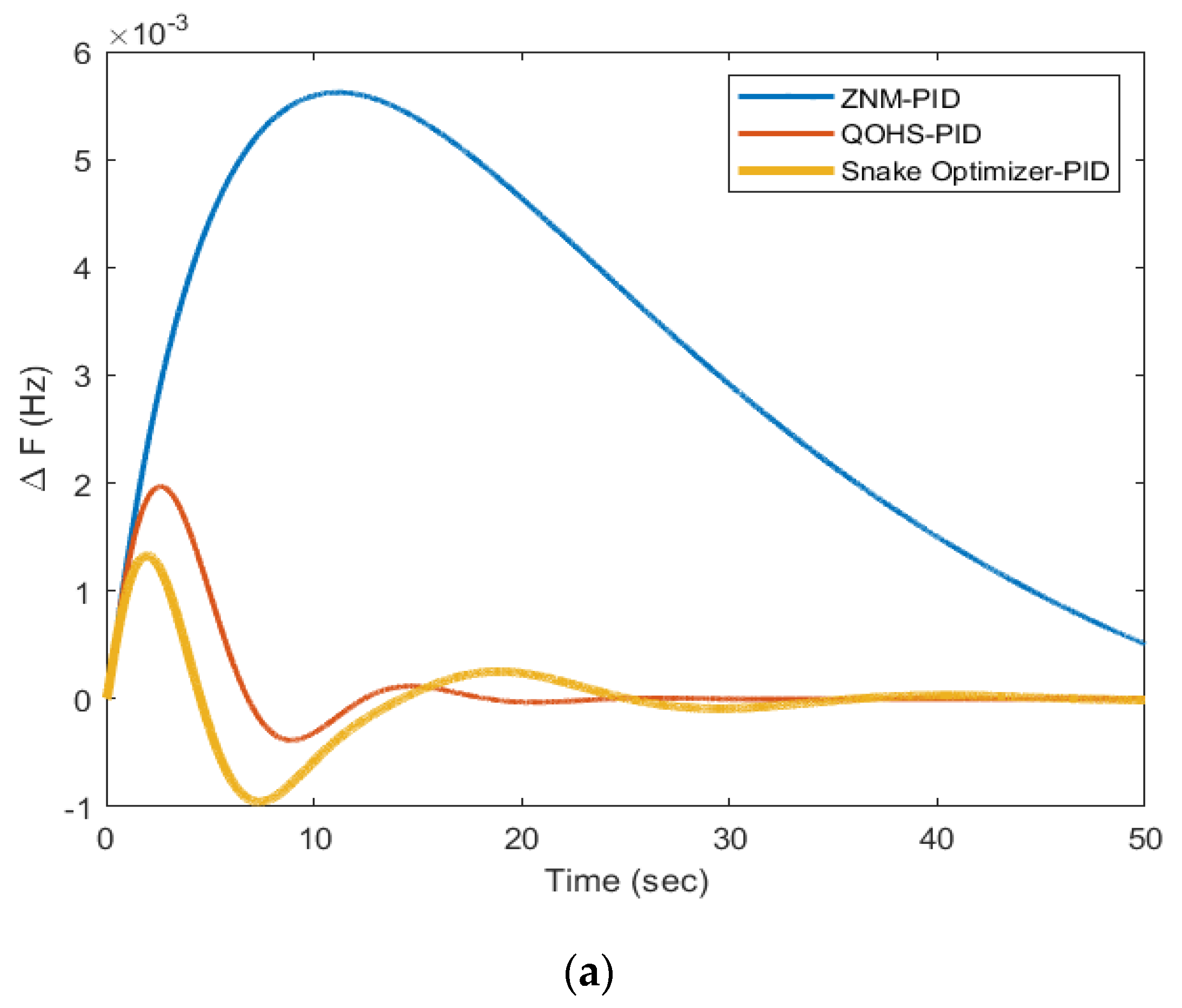
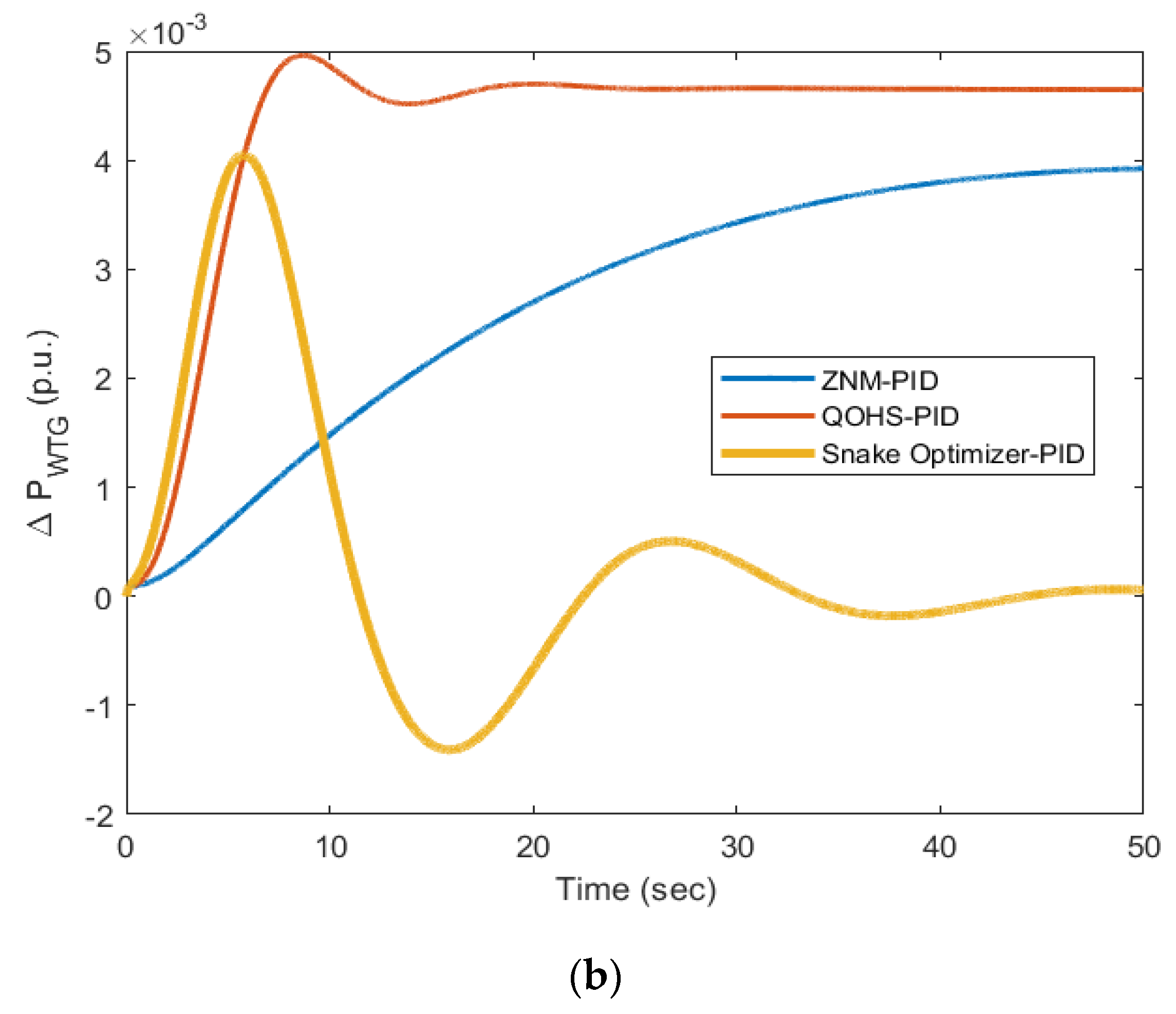
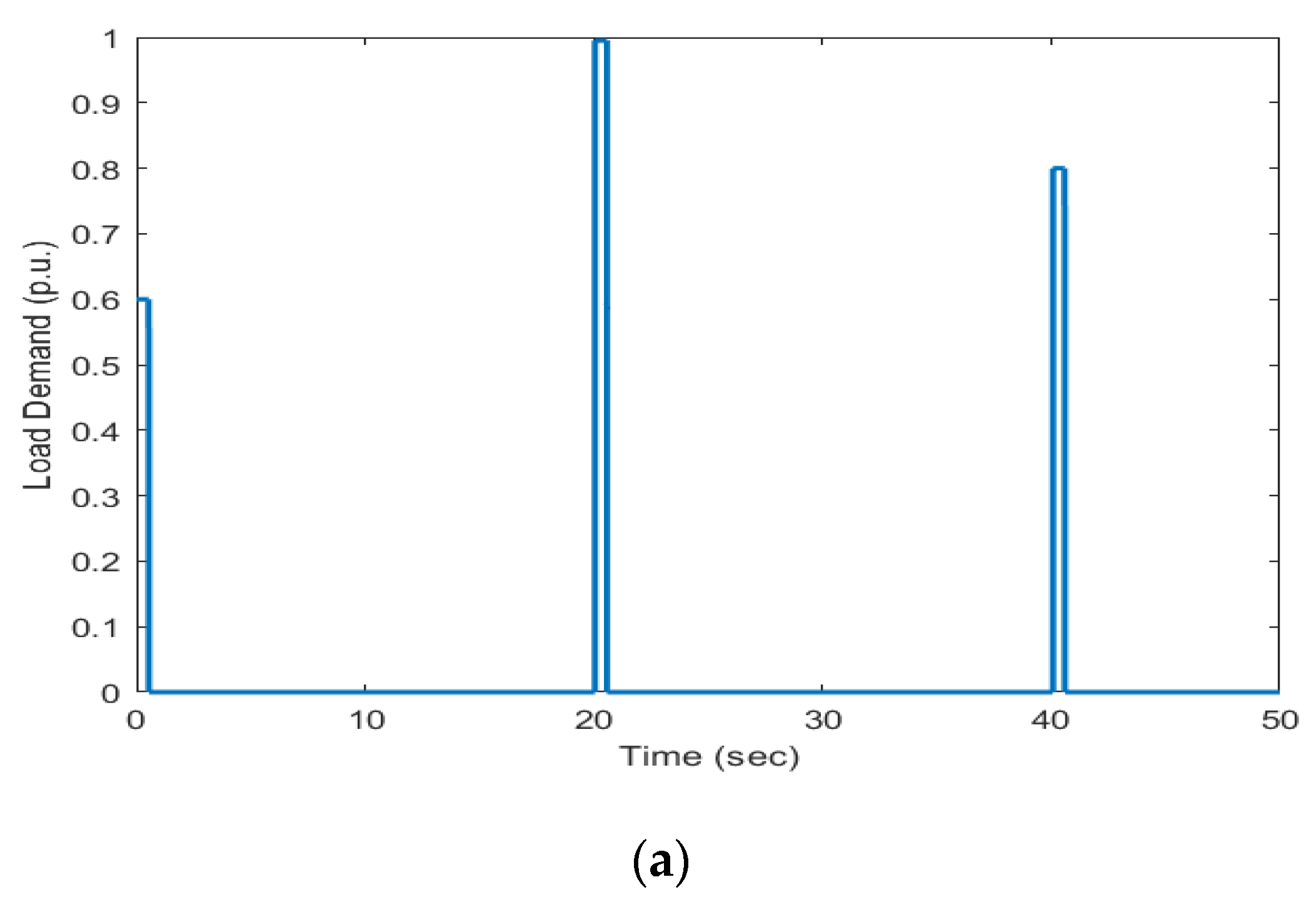
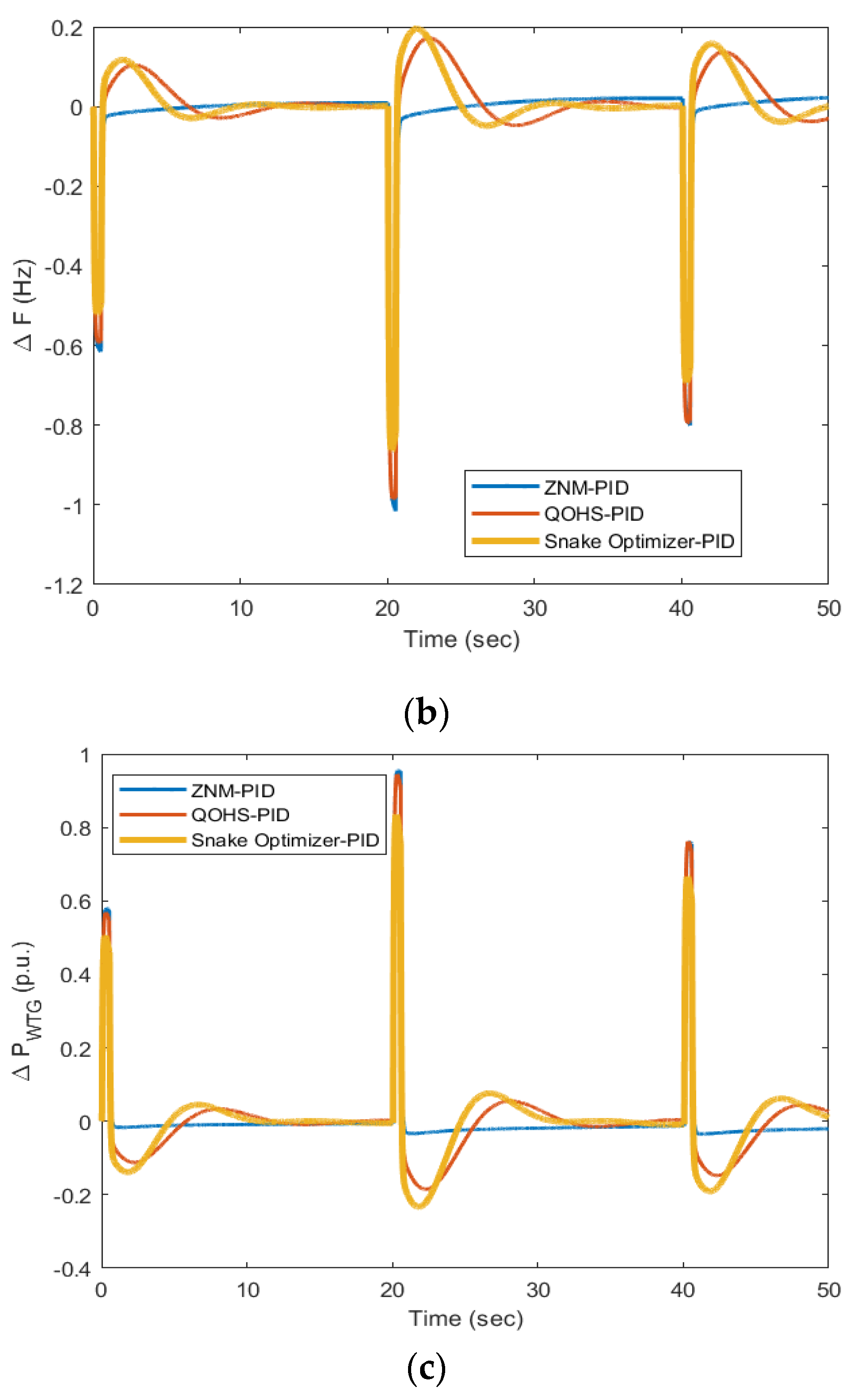
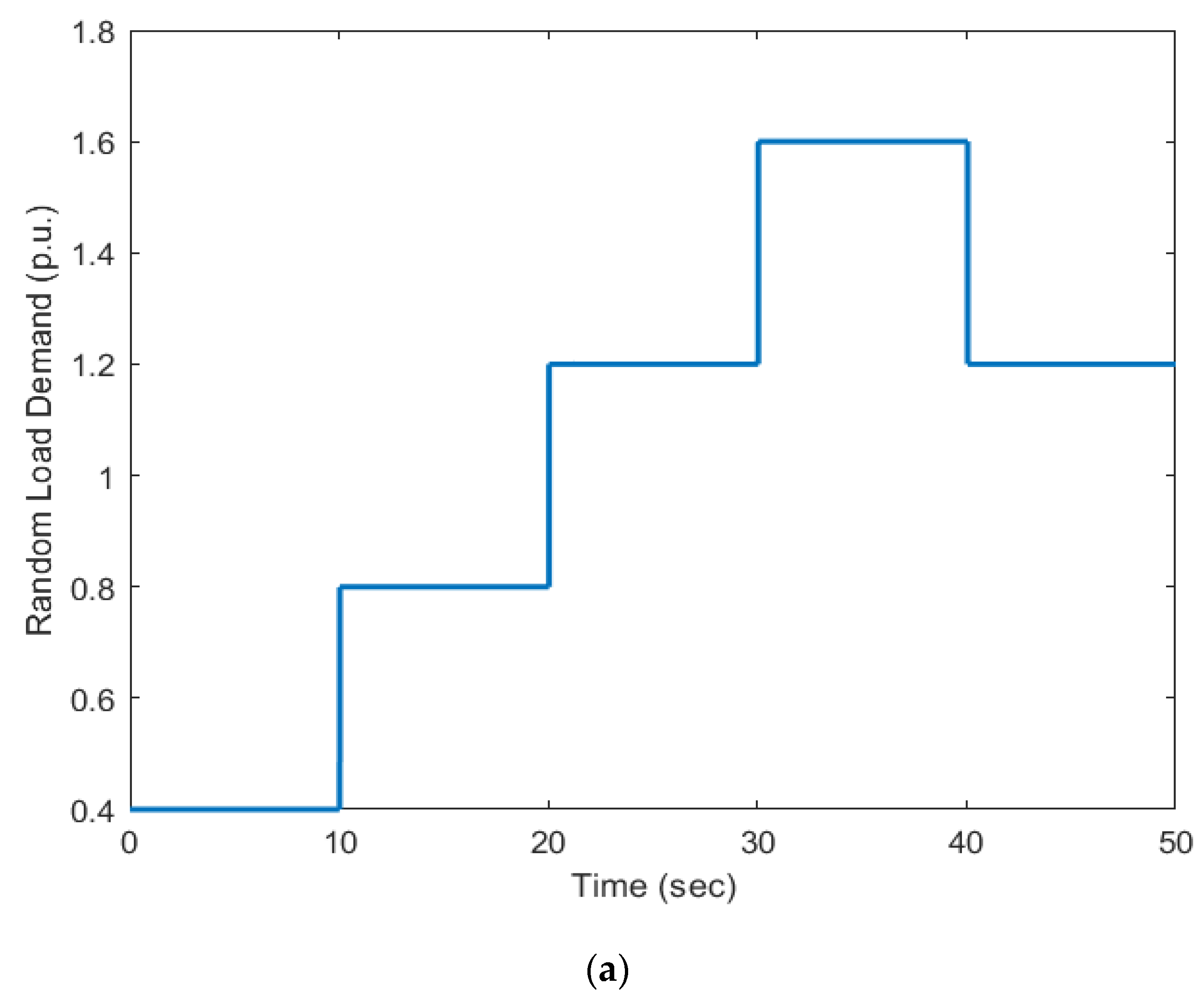
- The SO-PID gave the minimum frequency and wind power deviations for a step change in load, step change in wind speed, load changes at different instances, and for a random load pattern compared to ZNM-PID and QOHS-PID under similar working conditions.
- The output of SO-PID was compared via calculating the gains of PID and through error values such as ITAE, IAE, and ITSE.
- The ITAE achieved through ZNM-PID was 4249, IAE was 89.91, and ITSE was 2590. Further, the ITAE obtained via QOHS-PID was 59.54, IAE was 7.257, and ITSE was 13.97; hence, it can be clearly seen that a remarkable reduction in these values was obtained for the same model with the same disturbance.
- The SO-PID reduced the error value, i.e., ITAE to 37.1 from 59.54, IAE to 4.706 from 7.257, and ITSE to 5.762 from 13.97 and hence, SO-PID outperformed all the other methods in terms of ITAE, IAE, and ITSE. The graphical results supported the numerical results for the various considered cases.
- The research was extended to see the impact of a UC or RFB with SO-PID for a diesel–wind isolated system. The ITAE obtained with SO-PID was 37.1 and was reduced to 32.46 with the integration of a UC and further reduced to 5.336 after linking an RFB into the diesel–wind isolated system under similar disturbances.
- The trend was the same for IAE and ITSE and IAE became 1.411 and ITSE was reduced to 0.453 from 4.706 and 5.762; hence, it was evident that a UC and RFB with SO were able to improve the dynamic performance of the diesel–wind isolated system.
- The RFB and SO-PID combination effectively suppressed frequency and power deviations of the diesel–wind isolated system for a step change in load, load changes at different instances, and random load patterns when compared to SO-PID with UC and with SO-PID only.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FF | Fossil Fuel |
| UC | Ultra Capacitor |
| RES | Renewable Energy Storage |
| ESD | Energy Storage Device |
| RFB | Redox Flow Battery |
| HAE | Hydrogen Generative Aqua Electrolyzer |
| FC | Fuel Cell |
| FL | Fuzzy Logic |
| SO | Snake Optimization |
| DEG | Diesel Engine Generator |
| WTG | Wind Turbine Generator |
| ZNM | Ziegler–Nichols Method |
| DPM | D Partition Method |
| ITAE | Integral Time Absolute Error |
| IAE | Integral Absolute Error |
| ISE | Integral Squared Error |
| Kp | Proportional Gain |
| Ki | Integral Gain |
| Kd | Derivative Gain |
| PID | Proportional Integral Derivative |
| QOHS | Quasi-Opposition Harmony Search |
Appendix A
| Model | Parameters | ||||||
|---|---|---|---|---|---|---|---|
| Diesel Unit | KD = 0.3333 | RD = 3.0 Hz/pu | TD1 = 1.00 s | TD2 = 2.00 s | TD3 = 0.025 s | KP = 120 | TP = 14.4 s |
| Wind Unit | KP1 = 1.25 | KP2 = 1.00 | KP3 = 1.40 | KTP = 0.0033 | KIG = 0.9969 | TW = 13.25 s | KPC = 0.080 |
| TP1 = 0.60 s | TP2 = 0.041 s | TP3 = 1.0 s | |||||
| RFB | KO = 0.45 p.u. MW/Hz | Td = 0 s | Krb = 1 | Trb = 6.7 s | ΔPrbmax = +0.004 p.u. MW | ΔPrbmin = −0.004 p.u. MW | |
References
- Mallesham, G.; Mishra, S.; Jha, A.N. Ziegler-Nichols based controller parameters tuning for load frequency control in a microgrid. In Proceedings of the 2011 International Conference on Energy, Automation and Signal (ICEAS), Bhubaneswar, India, 28–30 December 2011; pp. 1–8. [Google Scholar]
- Veronica, J.; Kumar, N.S.; Longatt, F.G. Design of Load Frequency Control for a Microgrid Using D-partition Method. Int. J. Emerg. Electr. Power Syst. 2020, 21, 1–11. [Google Scholar] [CrossRef]
- Dekaraja, B.; Chandra Saikia, L. Impact of RFB and PLL Dynamic on Combined ALFC-AVR Regulation of Multiarea Multisource System Under Deregulated Environment with AC/Accurate HVDC link. IETE J. Res. 2022, 1–25. [Google Scholar] [CrossRef]
- Bevrani, H.; Ghosh, A.; Ledwich, G. Renewable energy sources and frequency regulation: Survey and new perspectives. IET Renew. Power Gener. 2010, 4, 438. [Google Scholar] [CrossRef]
- Eduardo, M.G.; Manuel, A.M. Evaluating operational risk in a power system with a large amount of wind power. Electr. Power Syst. Res. 2009, 79, 734–739. [Google Scholar]
- Senjyu, T.; Nakaji, T.; Uezato, K.; Funabashi, T. A hybrid power system using alternative energy facilities in isolated island. IEEE Trans. Energy Conver. 2005, 20, 406–414. [Google Scholar] [CrossRef]
- Rekioua, D.; Bensmail, S.; Bettar, N. Development of hybrid photovoltaic-fuel cell system for stand-alone application. Int. J. Hydrogen Energy 2014, 39, 1604–1611. [Google Scholar] [CrossRef]
- Mokrani, Z.; Rekioua, D.; Rekioua, T. Modeling, control and power management of hybrid photovoltaic fuel cells with battery bank supplying electric vehicle. Int. J. Hydrogen Energy 2014, 39, 15178–15187. [Google Scholar] [CrossRef]
- Mezzai, N.; Rekioua, D.; Rekioua, T.; Mohammedi, A.; Idjdarane, K.; Bacha, S. Modeling of hybrid photovoltaic/wind/fuel cells power system. Int. J. Hydrogen Energy 2014, 39, 15158–15168. [Google Scholar] [CrossRef]
- Aissou, S.; Rekioua, D.; Mezzai, N.; Rekioua, T.; Bacha, S. Modeling and control of hybrid photovoltaic wind power system with battery storage. Energy Convers. Manag. 2015, 89, 615–625. [Google Scholar] [CrossRef]
- Tamalouzt, S.; Benyahia, N.; Rekioua, T.; Rekioua, D.; Abdessemed, R. Performances analysis of WT-DFIG with PV and fuel cell hybrid power sources system associated with hydrogen storage hybrid energy system. Int. J. Hydrogen Energy 2016, 41, 21006–21021. [Google Scholar] [CrossRef]
- Wang, L.; Lee, D.; Lee, W.; Chen, Z. Analysis of a novel autonomous marine hybrid power generation/energy storage system with a high-voltage direct current link. J. Power Sources 2008, 185, 1284–1292. [Google Scholar] [CrossRef]
- Ngamroo, I. Robust frequency control of wind-diesel hybrid power system using superconducting magnetic energy storage. Int. J. Emerg. Electr. Power Syst. 2009, 10–18. [Google Scholar] [CrossRef]
- Francis, R.; Chidambaram, I.A. Optimized PI+ load frequency controller using BWNN approach for an interconnected reheat power system with RFB and hydrogen electrolyser units. Int. J. Elect. Power Energy Syst. 2015, 67, 381–392. [Google Scholar] [CrossRef]
- Sahu, R.K.; Gorripotu, T.S.; Panda, S. A hybrid DE-PS algorithm for load frequency control under deregulated power system with UPFC and RFB. Ain Shams Eng. J. 2015, 6, 893–911. [Google Scholar] [CrossRef]
- Sharma, G.; Narayanan, K.; Adefarati, T.; Sharma, S. Frequency regularization of a linked wind–diesel system using dual structure fuzzy with ultra-capacitor. Prot. Control Mod. Power Syst. 2022, 7, 12. [Google Scholar] [CrossRef]
- Ibraheem Kumar, P.; Kothari, D.P. Recent philosophies of automatic generation control strategies in power systems. IEEE Trans. Power Syst. 2005, 20, 346–357. [Google Scholar] [CrossRef]
- Yang, H.; Wei, Z.; Chengzhi, L. Optimal design and techno-economic analysis of a hybrid solar-wind power generation system. Appl. Energy 2009, 86, 163–169. [Google Scholar] [CrossRef]
- Ray, P.; Mohanty, S.; Kishor, N. Proportional-integral controller based small signal analysis of hybrid distributed generation systems. Energy Convers. Manag. 2011, 52, 1943–1954. [Google Scholar] [CrossRef]
- Abou El Ela, A.A.; El-Sehiemy, R.; Shaheen, A.M.; Diab, A.E.G. Optimal Design of PID Controller Based Sampe-Jaya Algorithm for Load Frequency Control of Linear and Nonlinear Multi-Area Thermal Power Systems. Int. J. Eng. Res. Afr. 2020, 50, 79–93. [Google Scholar] [CrossRef]
- Das, D.C.; Roy, A.; Sinha, N. PSO based frequency controller for wind-solar-diesel hybrid energy generation/energy storage system. Proc. ICEAS 2011, 458–463. [Google Scholar] [CrossRef]
- Zhou, T.; Sun, W. Optimization of battery super-capacitor hybrid energy storage station in wind/solar generation system. IEEE Tran. Sustain. Energy 2014, 5, 408–415. [Google Scholar] [CrossRef]
- Maleki, A.; Askarzadeh, A. Artificial bee swarm optimization for optimum sizing of a stand-alone PV/WT/FC hybrid system considering LPSP concept. Sol. Energy 2014, 107, 227–235. [Google Scholar] [CrossRef]
- Das, D.C.; Roy, A.; Sinha, N. GA based frequency controller for solar thermal diesel–wind hybrid energy generation/energy storage system. Electr. Power Energy Syst. 2012, 43, 262–279. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Fractional order fuzzy control of hybrid power system with renewable generation using chaotic PSO. ISA Trans. 2016, 62, 19–29. [Google Scholar] [CrossRef] [PubMed]
- Gangulya, S.; Shivab, C.K.; Mukherjeec, V. Frequency stabilization of isolated and grid connected hybrid power system models. J. Energy Storage 2018, 19, 145–159. [Google Scholar] [CrossRef]
- El-Sehiemy, R.; Shaheen, A.; Ginidi, A.; Al-Gahtani, S.F. Proportional-Integral-Derivative Controller Based-Artificial Rabbits Algorithm for Load Frequency Control in Multi-Area Power Systems. Fractal Fract. 2023, 7, 97. [Google Scholar] [CrossRef]
- Abou El-Ela, A.A.; El-Sehiemy, R.A.; Shaheen, A.M.; Diab, A.E.G. Enhanced coyote optimizer-based cascaded load frequency controllers in multi-area power systems with renewable. Neural Comput. Appl. 2021, 33, 8459–8477. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Çelik, E.; Öztürk, N. Novel fuzzy 1PD-TI controller for AGC of interconnected electric power systems with renewable power generation and energy storage devices. Eng. Sci. Technol. 2022, 35, 101166. [Google Scholar] [CrossRef]
- Çelik, E.; Öztürk, N.; Houssein, E.H. Improved load frequency control of interconnected power systems using energy storage devices and a new cost function. Neural Comput. Appl. 2023, 35, 681–697. [Google Scholar] [CrossRef]
- Çelik, E.; Öztürk, N.; Houssein, E.H. Influence of energy storage device on load frequency control of an interconnected dual-area thermal and solar photovoltaic power system. Neural Comput. Appl. 2022, 34, 20083–20099. [Google Scholar] [CrossRef]
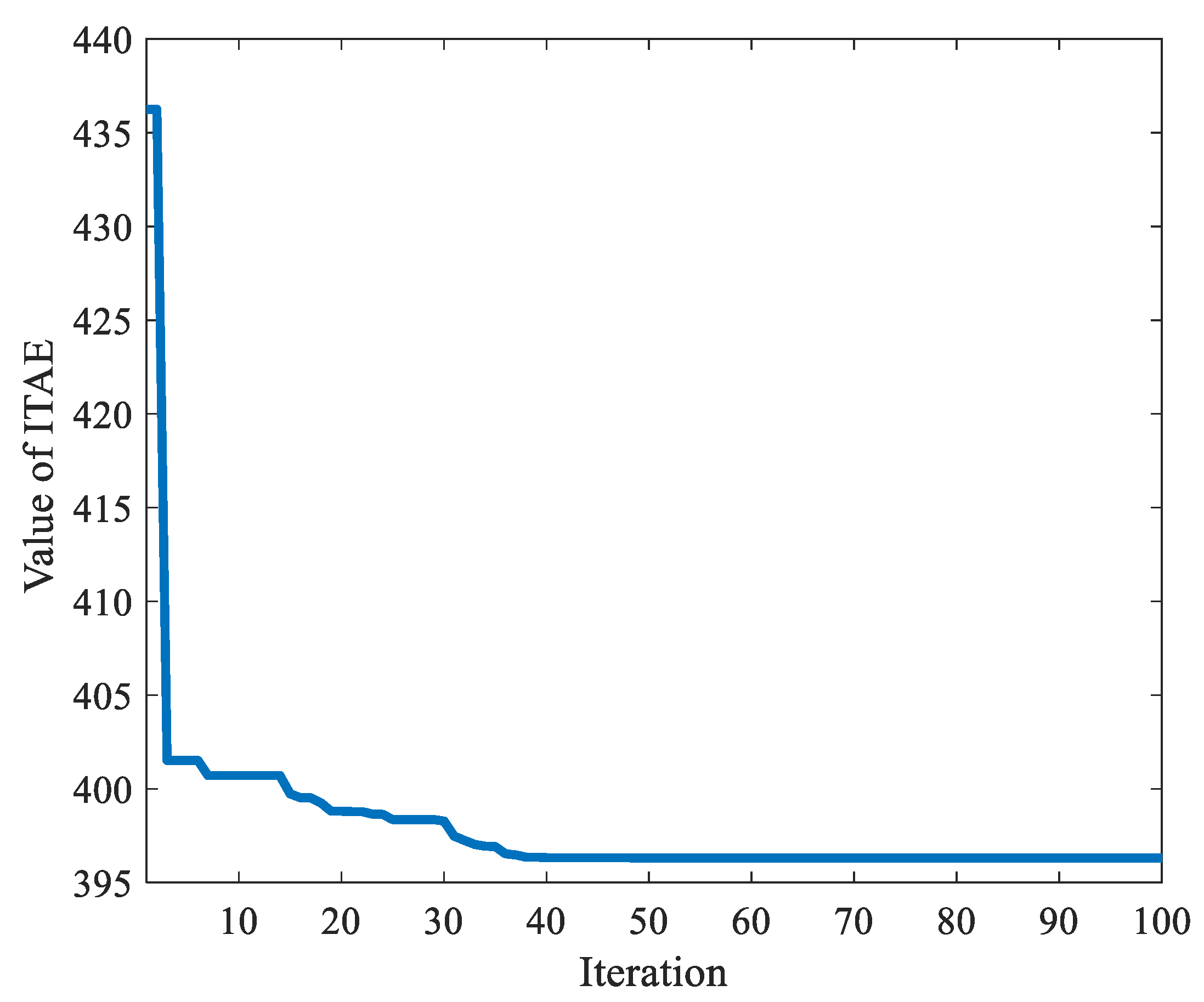
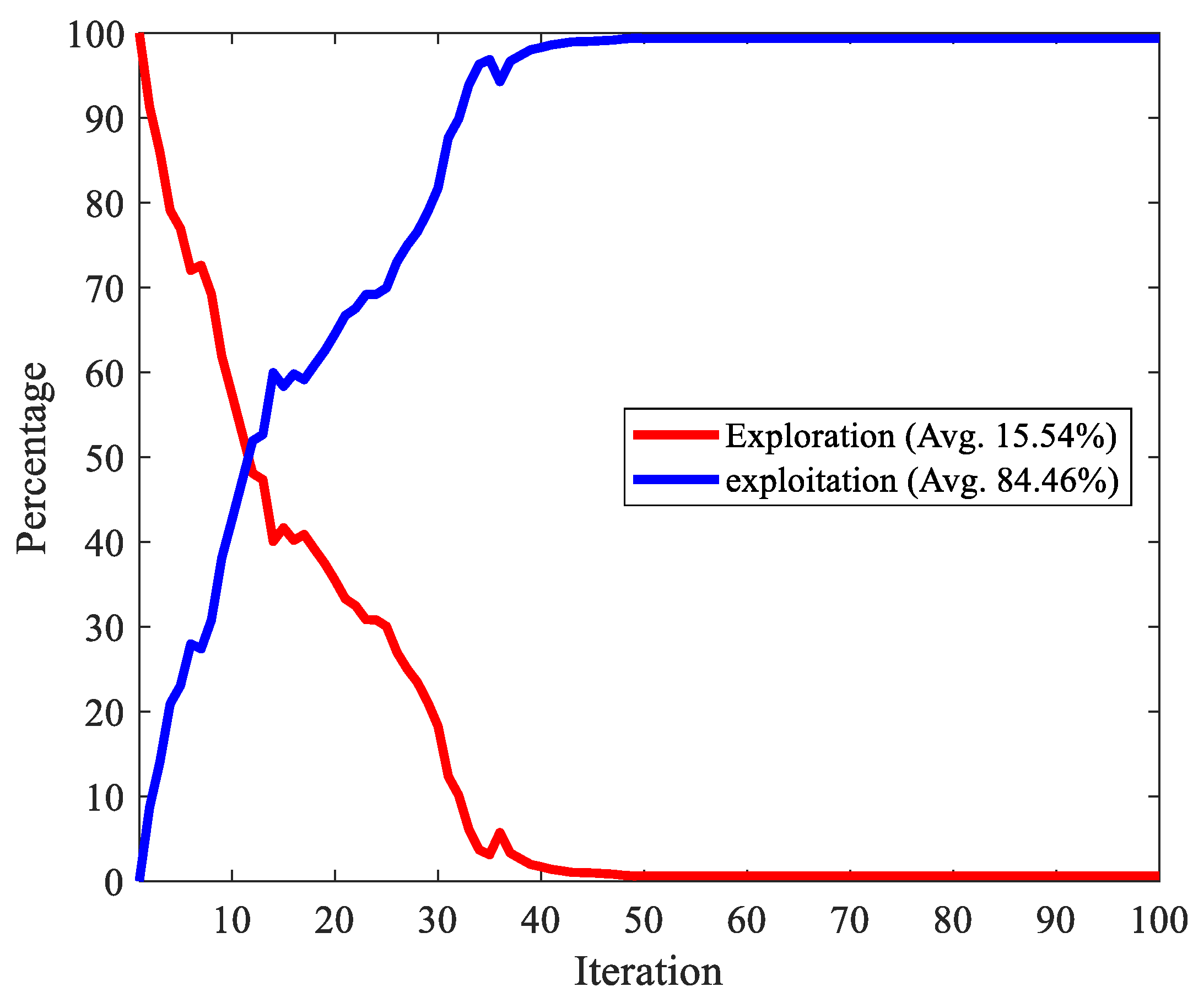
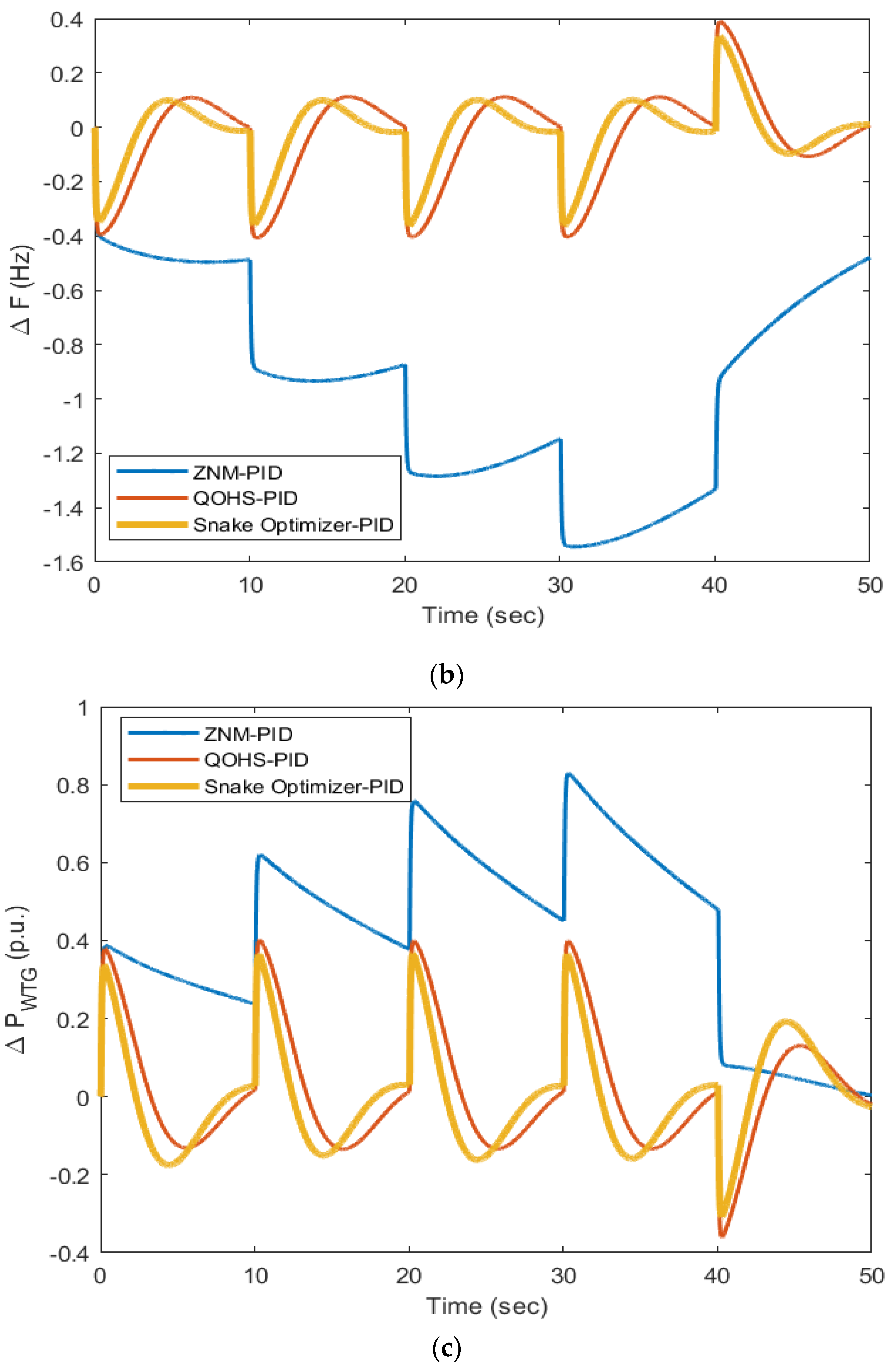
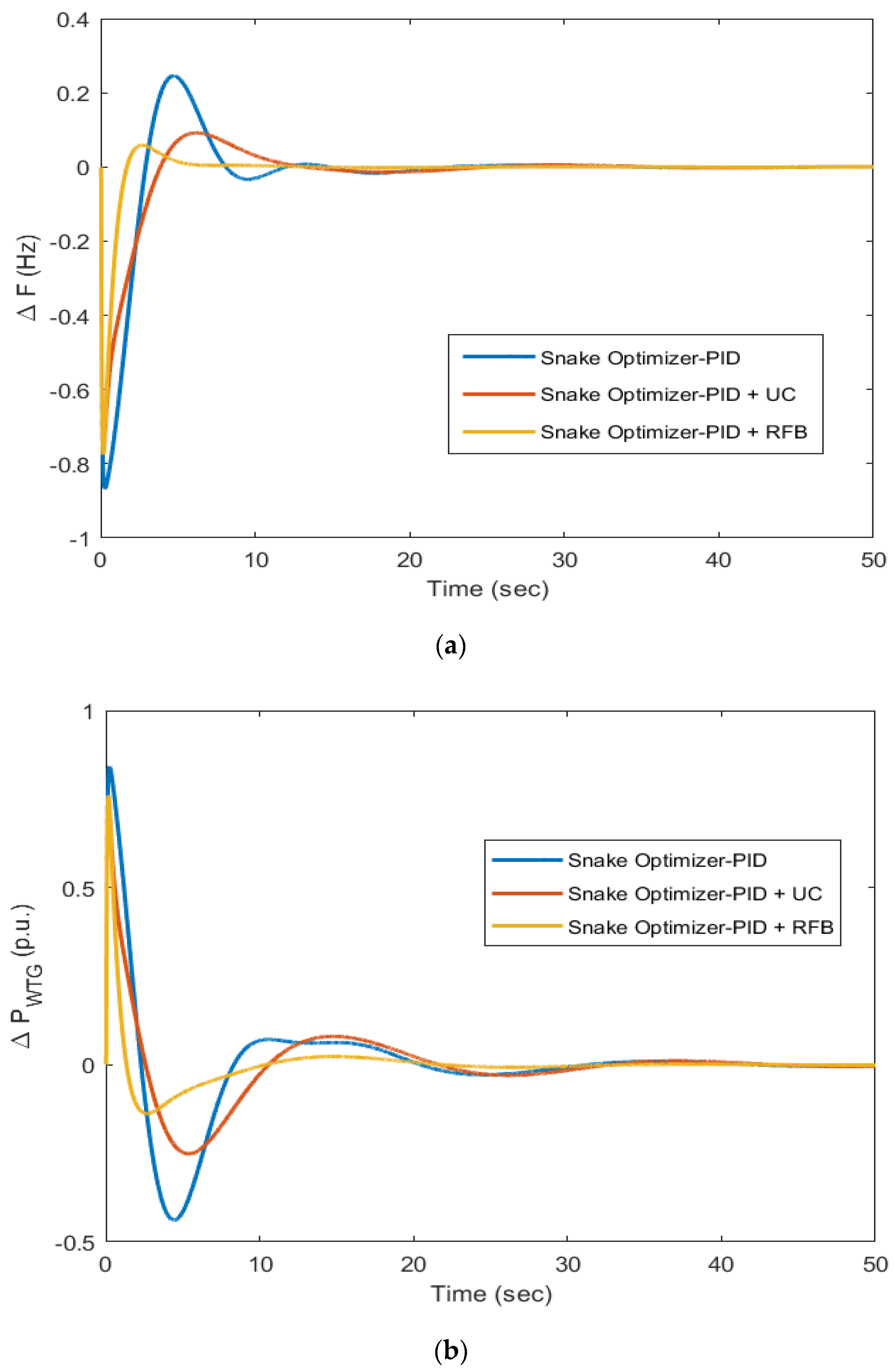

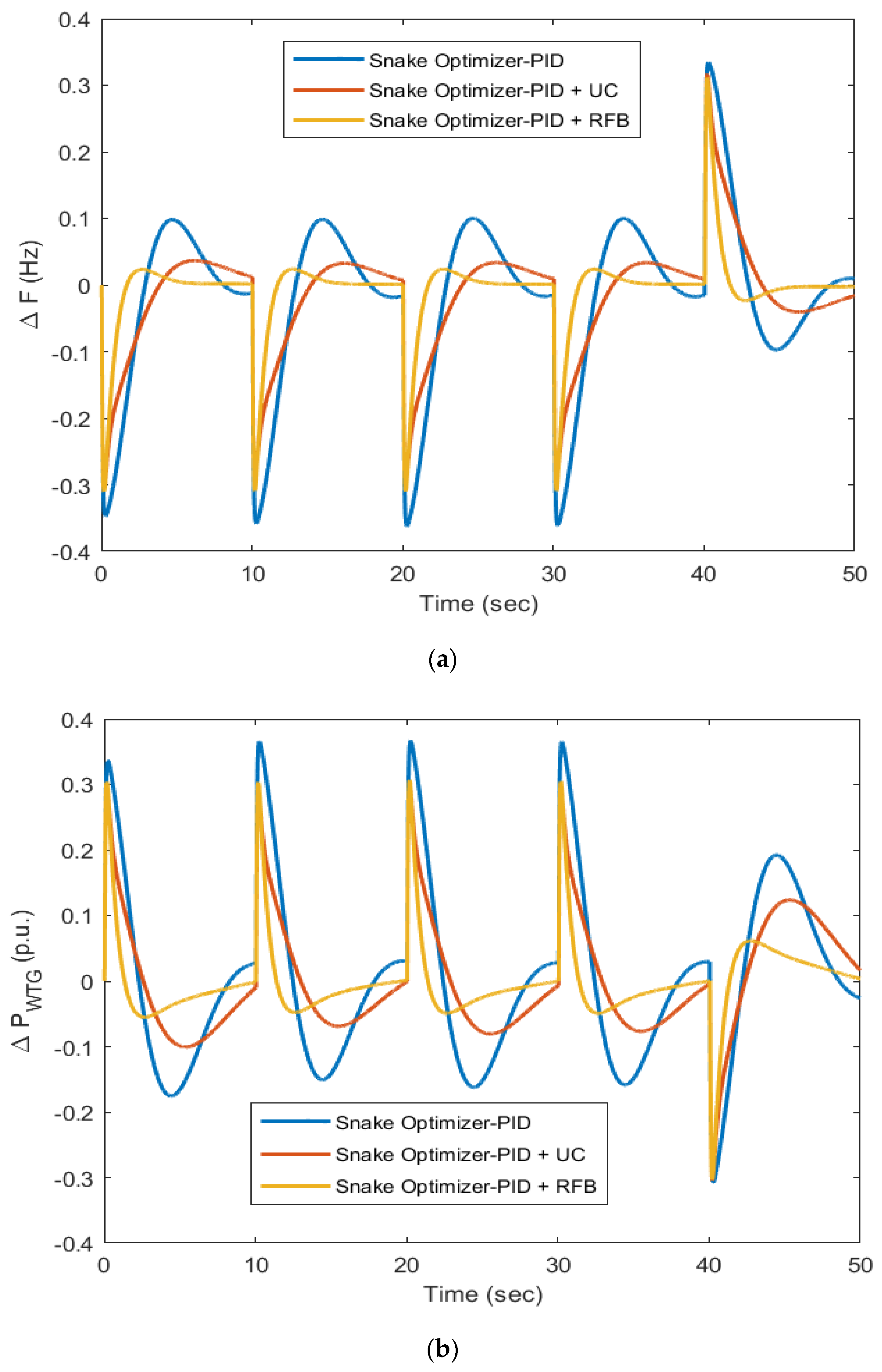
| Statistical Measure | Minimum | Maximum | Average | Standard Deviation |
|---|---|---|---|---|
| SO-PID | 396.3405 | 396.7219 | 396.5133 | 0.1435 |
| Design | Kp (DEG) | Ki (DEG) | Kd (DEG) | Kp (WTG) | Ki (WTG) | Kd (WTG) | ITAE | IAE | ITSE |
|---|---|---|---|---|---|---|---|---|---|
| ZNM-PID [1] | 0.096 | 0.036 | 0.062 | 0.12 | 0.057 | 0.062 | 4249 | 89.91 | 2590 |
| QOHS-PID [26] | 0.9124 | 0.9976 | 0.0349 | 0.9996 | 0.0011 | 0.6519 | 59.54 | 7.257 | 13.97 |
| SO-PID [Proposed] | 2 | 1.99387 | 1.99453 | 0 | 2 | 0 | 37.1 | 4.706 | 5.762 |
| Design | ITAE | IAE | ITSE |
|---|---|---|---|
| ZNM-PID [1] | 12.51 | 0.3219 | 0.04365 |
| QOHS-PID [26] | 0.4405 | 0.02259 | 0.000176 |
| SO-PID [Proposed] | 0.1873 | 0.01979 | 0.000156 |
| Design | ITAE | IAE | ITSE |
|---|---|---|---|
| SO-PID | 37.1 | 4.706 | 5.762 |
| SO-PID + Ultracapacitor | 32.46 | 3.411 | 2.458 |
| SO-PID + Redox Flow Battery | 5.336 | 1.411 | 0.453 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rameshar, V.; Sharma, G.; Bokoro, P.N.; Çelik, E. Frequency Support Studies of a Diesel–Wind Generation System Using Snake Optimizer-Oriented PID with UC and RFB. Energies 2023, 16, 3417. https://doi.org/10.3390/en16083417
Rameshar V, Sharma G, Bokoro PN, Çelik E. Frequency Support Studies of a Diesel–Wind Generation System Using Snake Optimizer-Oriented PID with UC and RFB. Energies. 2023; 16(8):3417. https://doi.org/10.3390/en16083417
Chicago/Turabian StyleRameshar, Vikash, Gulshan Sharma, Pitshou N. Bokoro, and Emre Çelik. 2023. "Frequency Support Studies of a Diesel–Wind Generation System Using Snake Optimizer-Oriented PID with UC and RFB" Energies 16, no. 8: 3417. https://doi.org/10.3390/en16083417
APA StyleRameshar, V., Sharma, G., Bokoro, P. N., & Çelik, E. (2023). Frequency Support Studies of a Diesel–Wind Generation System Using Snake Optimizer-Oriented PID with UC and RFB. Energies, 16(8), 3417. https://doi.org/10.3390/en16083417







