Review on Battery State Estimation and Management Solutions for Next-Generation Connected Vehicles
Abstract
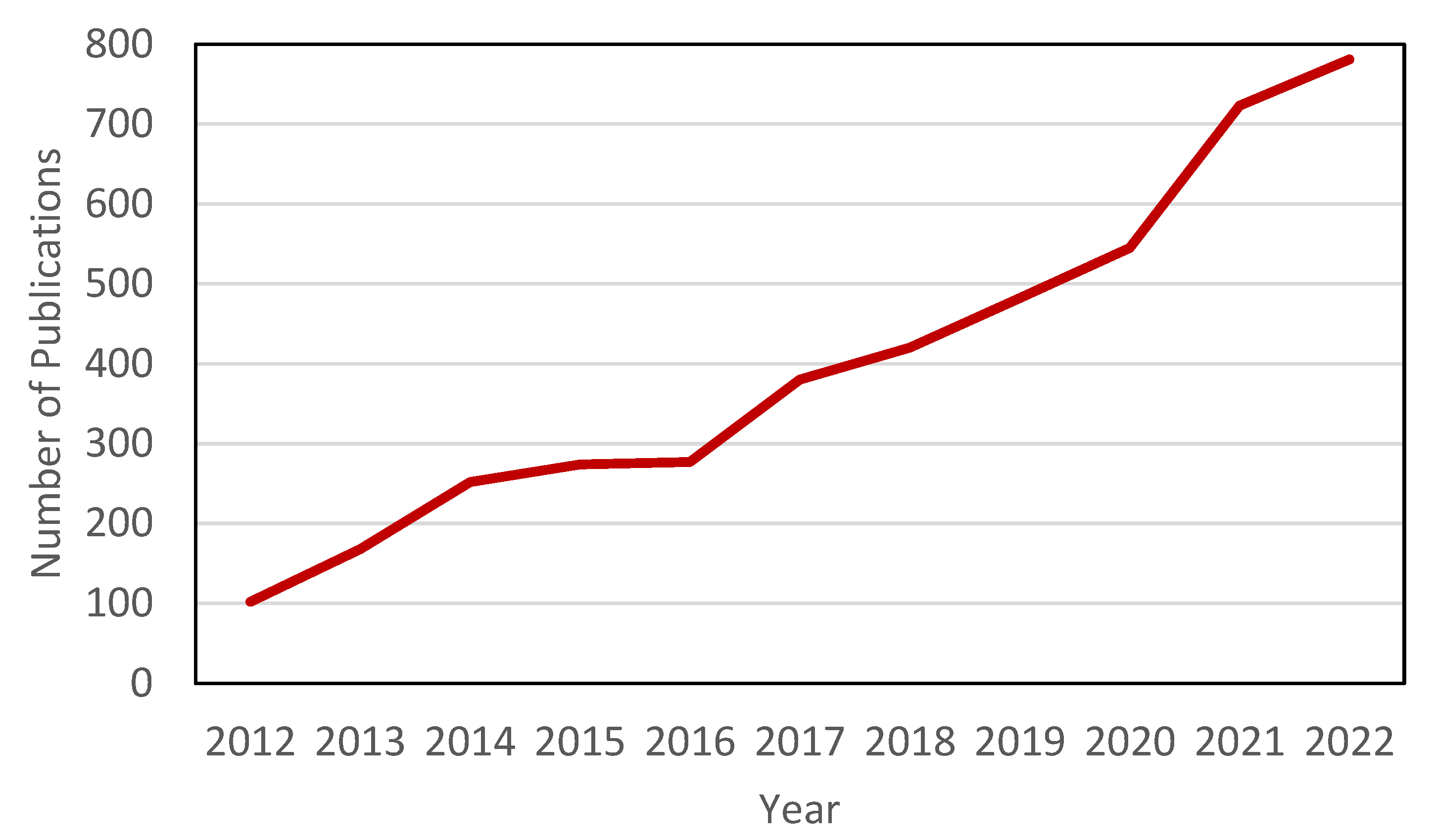
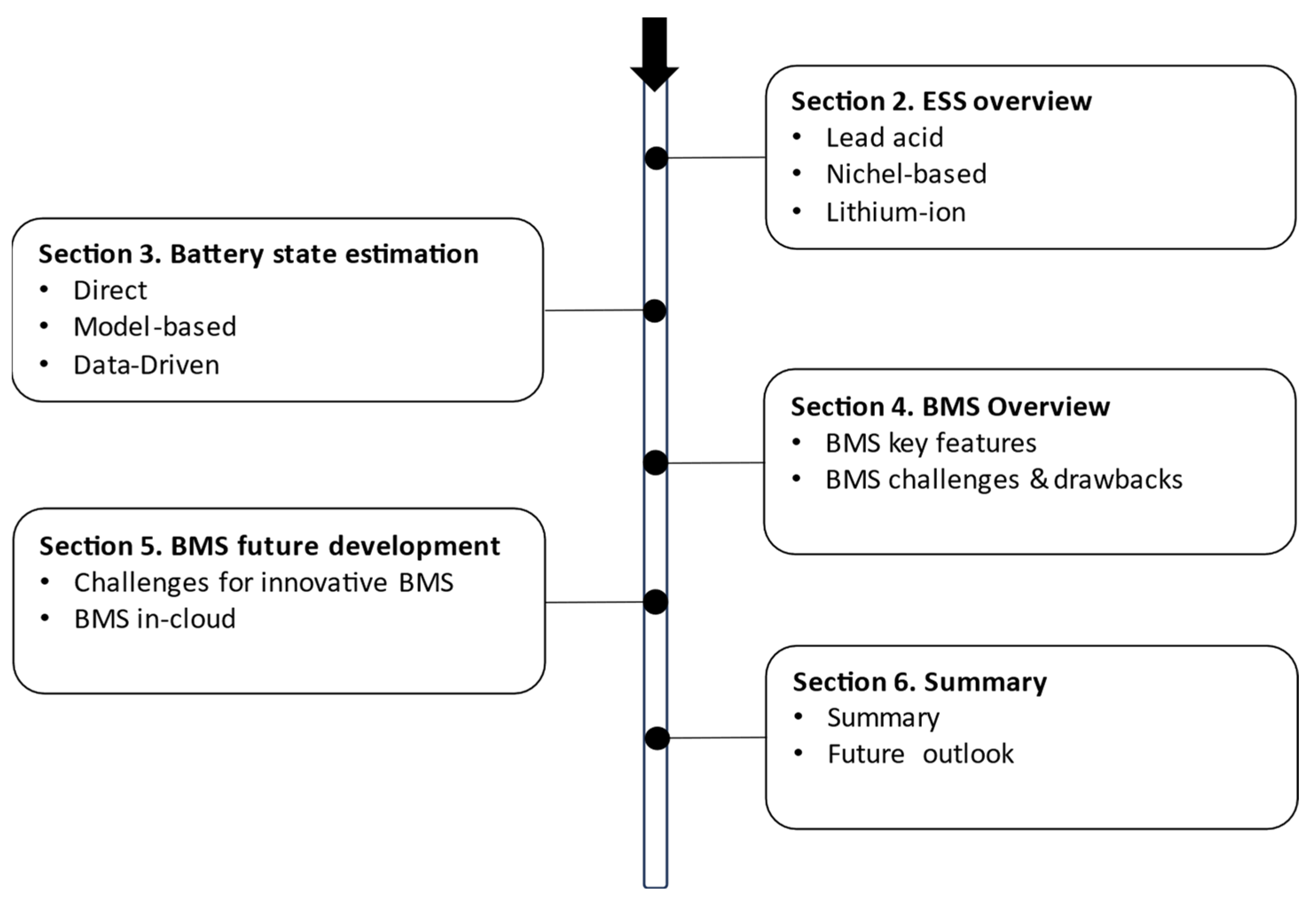
:1. Introduction
2. Energy Storage Systems for Electrified Vehicles
3. Key Battery Parameters Estimation
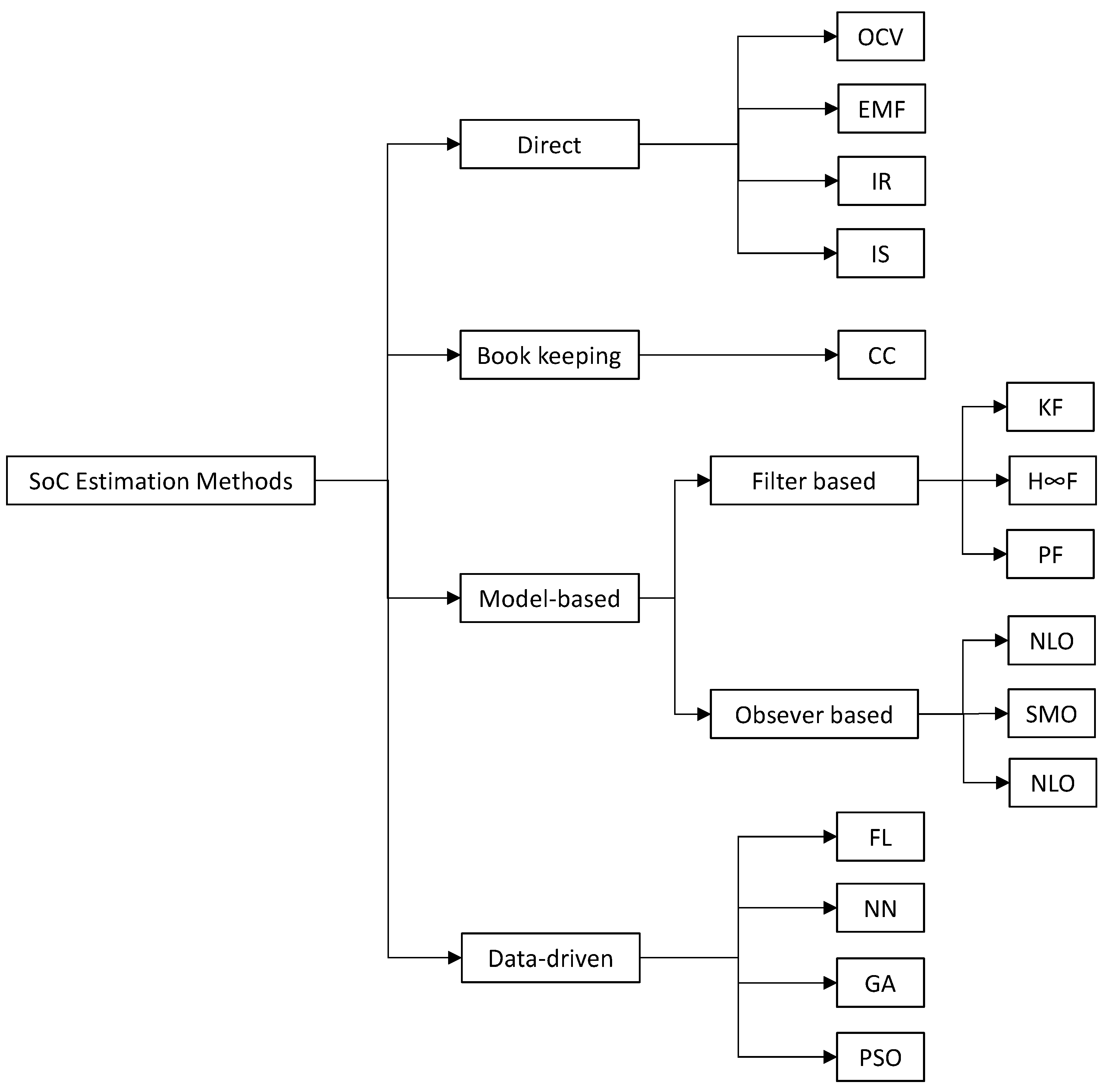
3.1. State of Charge Estimation Methodologies
3.1.1. Direct Estimation Methods
- (1)
- Open Circuit Voltage
- (2)
- Internal Resistance
- (3)
- Impedance spectroscopy
- (4)
- Electromotive force
- (5)
- Coulomb Counting
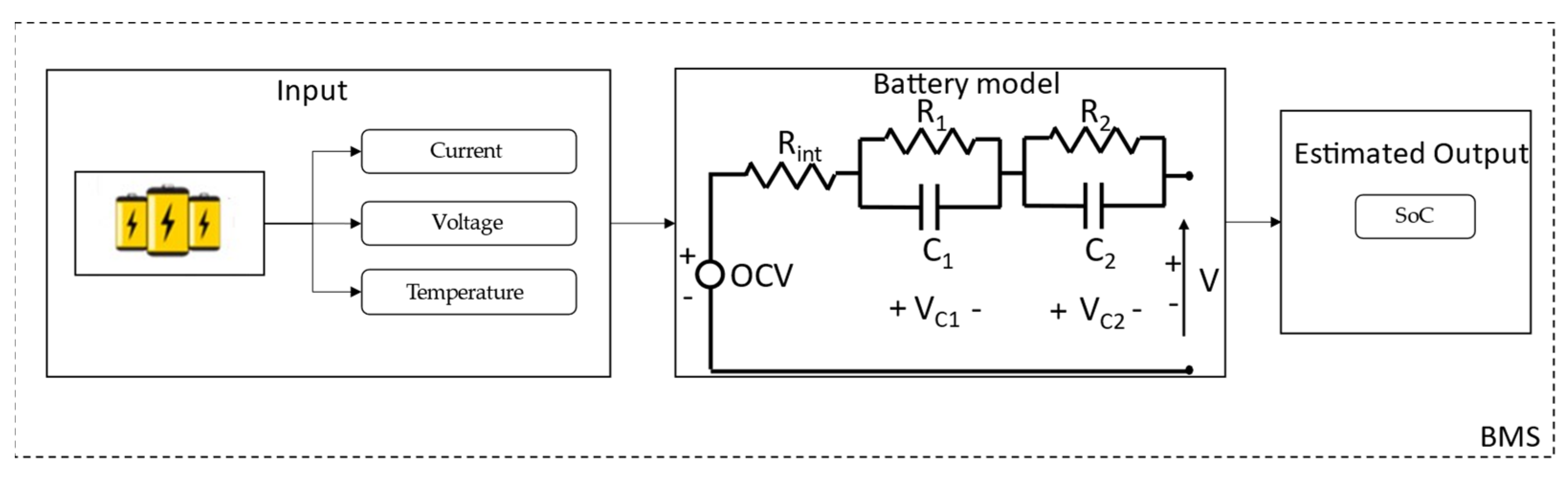
3.1.2. Model-Based Estimation Methods
- (1)
- Kalman Filter-based algorithms
- (2)
- H∞ Filter
- (3)
- Particle Filter
- (4)
- Observer-based methods
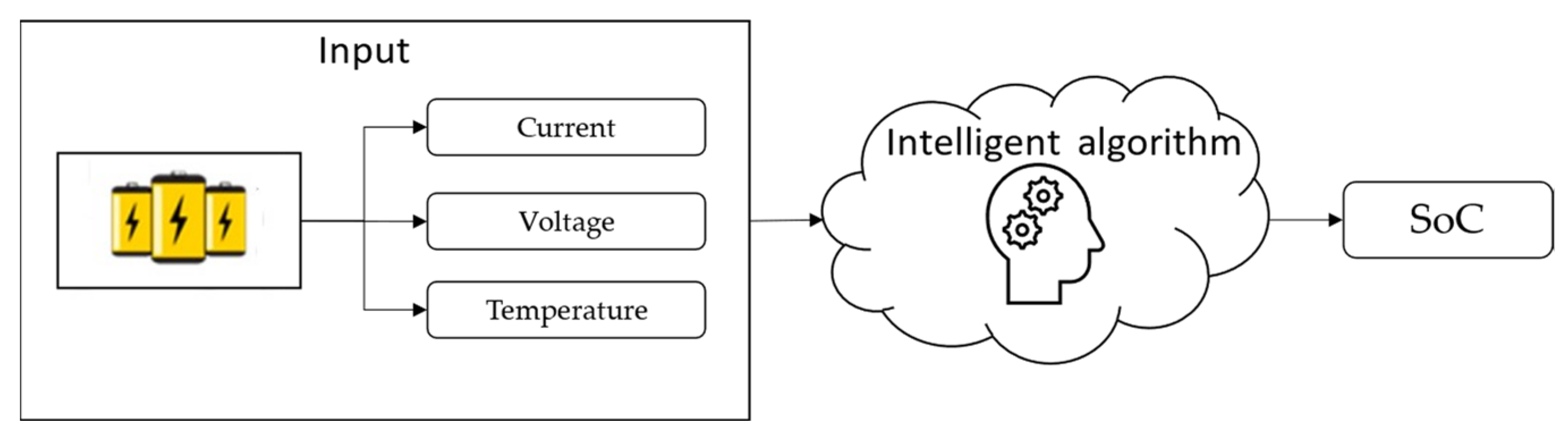
3.1.3. Data-Driven
- (1)
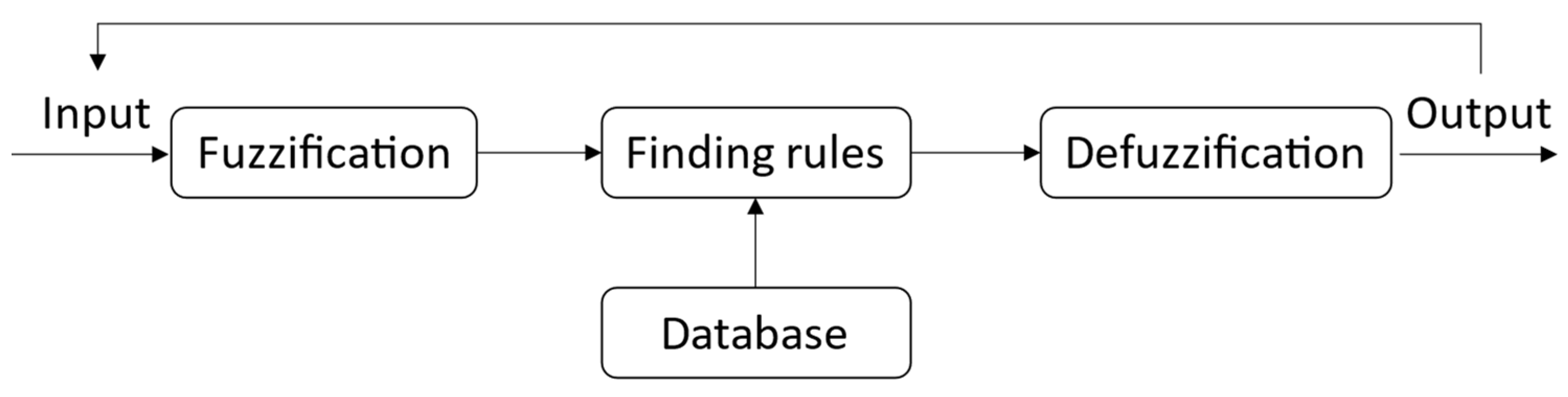
- Fuzzy logic
- (2)
- Neural network
- (3)
- Genetic algorithm
- (4)
- Particle swarm optimization
3.2. State of Health Estimation Methodologies
3.2.1. Direct Estimation Methods
3.2.2. Filter-Based Method
3.2.3. Data-Driven Methods
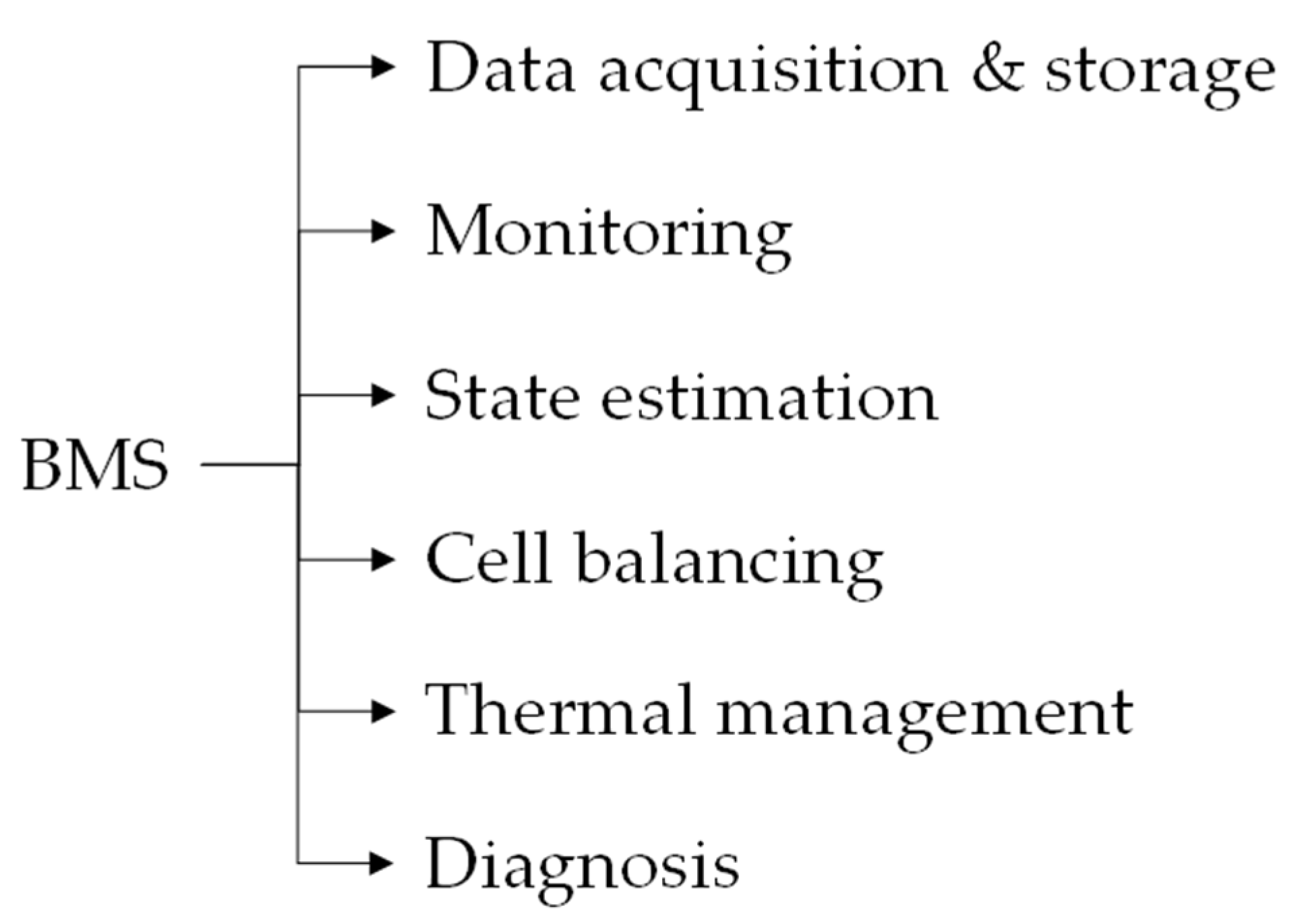
4. Battery Management System Overview
- a.
- Data acquisition and storage
- b.
- Monitoring
- c.
- State estimation
- d.
- Cell balancing
- e.
- Thermal management
- f.
- Diagnosis
5. Towards the Future: BMS in the Cloud Applications
6. Summary and Future Outlook
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AEKF | Adaptive Extended Kalman Filter |
| AC | Alternate Current |
| BEVs | Battery Electric Vehicles |
| BMS | Battery Management System |
| BPNN | Back Propagation Neural Network |
| CC | Coulomb Counting |
| CO2 | Carbon Dioxide |
| DC | Direct Current |
| DD | Data-Driven |
| DEKF | Dual Extended Kalman Filter |
| ECM | Equivalent circuit model |
| EChM | Electrochemical model |
| EMF | Electromotive Force |
| ESS | Energy Storage System |
| EU | European Commission |
| EKF | Extended Kalman Filter |
| FL | Fuzzy Logic |
| FNN | Feedforward Neural Network |
| GA | Genetic Algorithm |
| HIF | H∞(Infinity) Filter |
| IEA | International Energy Agency |
| IR | Internal Resistance |
| IS | Impedance Spectroscopy |
| LKF | Linear Kalman Filter |
| LS | Least Square |
| LSTM | Long Short-Term Memory |
| KF | Kalman Filter |
| ML | Machine Learning |
| NLO | Non Linear Observer |
| NN | Neural Network |
| OCV | Open Circuit Voltage |
| P2D | Pseudo Two Dimension |
| PF | Particle Filter |
| PIO | Proportional Integral Observer |
| PSO | Particle Swarm Optimization |
| PNGV | Partnership for New Generation of Vehicles |
| RC | Resistor–Capacitor |
| SMO | Sliding Mode Observer |
| SoC | State of Charge |
| SoH | State of Health |
| SoP | State of Power |
| TMS | Thermal Management System |
| UKF | Unscented Kalman Filter |
References
- IEA. Transport—Topics. Available online: https://www.iea.org/topics/transport (accessed on 25 April 2023).
- Hjelkrem, O.A.; Arnesen, P.; Bø, T.A.; Sondell, R.S. Estimation of tank-to-wheel efficiency functions based on type approval data. Appl. Energy 2020, 276, 115463. [Google Scholar] [CrossRef]
- European Green Deal. Available online: https://climate.ec.europa.eu/eu-action/european-green-deal_en (accessed on 3 May 2023).
- International Council on Clean Transportation. Fit for 55: A Review and Evaluation of the European Commission Proposal for Amending the CO2 Targets for New Cars and Vans. Available online: https://theicct.org/publication/fit-for-55-a-review-and-evaluation-of-the-european-commission-proposal-for-amending-the-co2-targets-for-new-cars-and-vans/ (accessed on 3 May 2023).
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.-C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Nnikhil, K.N. A Review on Battery Management System for Electric Vehicles. Int. J. Res. Appl. Sci. Eng. Technol. 2022, 10, 3699–3710. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Noura, N.; Boulon, L.; Jemeï, S. A Review of Battery State of Health Estimation Methods: Hybrid Electric Vehicle Challenges. World Electr. Veh. J. 2020, 11, 66. [Google Scholar] [CrossRef]
- Lai, X.; He, L.; Wang, S.; Zhou, L.; Zhang, Y.; Sun, T.; Zheng, Y. Co-estimation of state of charge and state of power for lithium-ion batteries based on fractional variable-order model. J. Clean. Prod. 2020, 255, 120203. [Google Scholar] [CrossRef]
- Zhou, L.; Lai, X.; Li, B.; Yao, Y.; Yuan, M.; Weng, J.; Zheng, Y. State Estimation Models of Lithium-Ion Batteries for Battery Management System: Status, Challenges, and Future Trends. Batteries 2023, 9, 131. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, X. Joint estimation method for maximum available energy and state-of-energy of lithium-ion battery under various temperatures. J. Power Sources 2021, 506, 230132. [Google Scholar] [CrossRef]
- Anselma, P.G.; Kollmeyer, P.; Lempert, J.; Zhao, Z.; Belingardi, G.; Emadi, A. Battery state-of-health sensitive energy management of hybrid electric vehicles: Lifetime prediction and ageing experimental validation. Appl. Energy 2021, 285, 116440. [Google Scholar] [CrossRef]
- da Silva, S.F.; Eckert, J.J.; Silva, F.L.; Silva, L.C.A.; Dedini, F.G. Multi-objective optimization design and control of plug-in hybrid electric vehicle powertrain for minimization of energy consumption, exhaust emissions and battery degradation. Energy Convers. Manag. 2021, 234, 113909. [Google Scholar] [CrossRef]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Zhang, J.; Lee, J. A review on prognostics and health monitoring of Li-ion battery. J. Power Sources 2011, 196, 6007–6014. [Google Scholar] [CrossRef]
- Agarwal, V.; Uthaichana, K.; DeCarlo, R.A.; Tsoukalas, L.H. Development and Validation of a Battery Model Useful for Discharging and Charging Power Control and Lifetime Estimation. IEEE Trans. Energy Convers. 2010, 25, 821–835. [Google Scholar] [CrossRef]
- Yang, H.; Sun, X.; An, Y.; Zhang, X.; Wei, T.; Ma, Y. Online parameters identification and state of charge estimation for lithium-ion capacitor based on improved Cubature Kalman filter. J. Energy Storage 2019, 24, 100810. [Google Scholar] [CrossRef]
- Ren, Z.; Du, C. A review of machine learning state-of-charge and state-of-health estimation algorithms for lithium-ion batteries. Energy Rep. 2023, 9, 2993–3021. [Google Scholar] [CrossRef]
- Hou, J.; Li, T.; Zhou, F.; Zhao, D.; Zhong, Y.; Yao, L.; Zeng, L. A Review of Critical State Joint Estimation Methods of Lithium-Ion Batteries in Electric Vehicles. World Electr. Veh. J. 2022, 13, 159. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.; Cao, J. A new method to estimate the state of charge of lithium-ion batteries based on the battery impedance model. J. Power Sources 2013, 233, 277–284. [Google Scholar] [CrossRef]
- Li, W.; Rentemeister, M.; Badeda, J.; Jöst, D.; Schulte, D.; Sauer, D.U. Digital twin for battery systems: Cloud battery management system with online state-of-charge and state-of-health estimation. J. Energy Storage 2020, 30, 101557. [Google Scholar] [CrossRef]
- Tran, M.-K.; Panchal, S.; Khang, T.D.; Panchal, K.; Fraser, R.; Fowler, M. Concept Review of a Cloud-Based Smart Battery Management System for Lithium-Ion Batteries: Feasibility, Logistics, and Functionality. Batteries 2022, 8, 19. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, Z.; Cao, R.; Wang, M.; Cheng, H.; Zhang, L.; Jiang, Y.; Li, Y.; Chen, B.; Ling, H.; et al. Implementation for a cloud battery management system based on the CHAIN framework. Energy AI 2021, 5, 100088. [Google Scholar] [CrossRef]
- Kumar, P.; Bansal, S.; Sonthalia, A. Chapter 4—Introduction to battery systems. In Handbook of Thermal Management Systems; Aloui, F., Varuvel, E.G., Sonthalia, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2023; pp. 95–118. [Google Scholar] [CrossRef]
- Budde-Meiwes, H.; Drillkens, J.; Lunz, B.; Muennix, J.; Rothgang, S.; Kowal, J.; Sauer, D.U. A review of current automotive battery technology and future prospects. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2013, 227, 761–776. [Google Scholar] [CrossRef]
- Hannan, M.A.; Hoque, M.M.; Mohamed, A.; Ayob, A. Review of energy storage systems for electric vehicle applications: Issues and challenges. Renew. Sustain. Energy Rev. 2017, 69, 771–789. [Google Scholar] [CrossRef]
- Andwari, A.M.; Pesiridis, A.; Rajoo, S.; Martinez-Botas, R.; Esfahanian, V. A review of Battery Electric Vehicle technology and readiness levels. Renew. Sustain. Energy Rev. 2017, 78, 414–430. [Google Scholar] [CrossRef]
- Hasan, M.K.; Mahmud, M.; Habib, A.K.M.A.; Motakabber, S.M.A.; Islam, S. Review of electric vehicle energy storage and management system: Standards, issues, and challenges. J. Energy Storage 2021, 41, 102940. [Google Scholar] [CrossRef]
- Noudeng, V.; Quan, N.V.; Xuan, T.D. A Future Perspective on Waste Management of Lithium-Ion Batteries for Electric Vehicles in Lao PDR: Current Status and Challenges. Int. J. Environ. Res. Public Health 2022, 19, 16169. [Google Scholar] [CrossRef] [PubMed]
- Verma, S.; Mishra, S.; Gaur, A.; Chowdhury, S.; Mohapatra, S.; Dwivedi, G.; Verma, P. A comprehensive review on energy storage in hybrid electric vehicle. J. Traffic Transp. Eng. Engl. Ed. 2021, 8, 621–637. [Google Scholar] [CrossRef]
- Hannan, M.A.; Hoque, M.M.; Hussain, A.; Yusof, Y.; Ker, P.J. State-of-the-Art and Energy Management System of Lithium-Ion Batteries in Electric Vehicle Applications: Issues and Recommendations. IEEE Access 2018, 6, 19362–19378. [Google Scholar] [CrossRef]
- Zhu, J.; Zhu, P.; Yan, C.; Dong, X.; Zhang, X. Recent progress in polymer materials for advanced lithium-sulfur batteries. Prog. Polym. Sci. 2019, 90, 118–163. [Google Scholar] [CrossRef]
- Ali, M.U.; Zafar, A.; Nengroo, S.H.; Hussain, S.; Alvi, M.J.; Kim, H.-J. Towards a Smarter Battery Management System for Electric Vehicle Applications: A Critical Review of Lithium-Ion Battery State of Charge Estimation. Energies 2019, 12, 446. [Google Scholar] [CrossRef]
- Danko, M.; Adamec, J.; Taraba, M.; Drgona, P. Overview of batteries State of Charge estimation methods. Transp. Res. Procedia 2019, 40, 186–192. [Google Scholar] [CrossRef]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W. State of the Art of Lithium-Ion Battery SOC Estimation for Electrical Vehicles. Energies 2018, 11, 1820. [Google Scholar] [CrossRef]
- Tang, X.; Wang, Y.; Chen, Z. A method for state-of-charge estimation of LiFePO4 batteries based on a dual-circuit state observer. J. Power Sources 2015, 296, 23–29. [Google Scholar] [CrossRef]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W.; Wang, M. A Study on the Open Circuit Voltage and State of Charge Characterization of High Capacity Lithium-Ion Battery Under Different Temperature. Energies 2018, 11, 2408. [Google Scholar] [CrossRef]
- Lavigne, L.; Sabatier, J.; Francisco, J.M.; Guillemard, F.; Noury, A. Lithium-ion Open Circuit Voltage (OCV) curve modelling and its ageing adjustment. J. Power Sources 2016, 324, 694–703. [Google Scholar] [CrossRef]
- Bao, Y.; Dong, W.; Wang, D. Online Internal Resistance Measurement Application in Lithium Ion Battery Capacity and State of Charge Estimation. Energies 2018, 11, 1073. [Google Scholar] [CrossRef]
- Shete, S.; Jog, P.; Kumawat, R.K.; Palwalia, D.K. Battery Management System for SOC Estimation of Lithium-Ion Battery in Electric Vehicle: A Review. In Proceedings of the 2021 6th IEEE International Conference on Recent Advances and Innovations in Engineering (ICRAIE), Kedah, Malaysia, 1–3 December 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Zhou, W.; Zheng, Y.; Pan, Z.; Lu, Q. Review on the Battery Model and SOC Estimation Method. Processes 2021, 9, 1685. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Han, X.; Lu, L.; Li, J. Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles. J. Power Sources 2018, 377, 161–188. [Google Scholar] [CrossRef]
- Coleman, M.; Lee, C.K.; Zhu, C.; Hurley, W.G. State-of-Charge Determination From EMF Voltage Estimation: Using Impedance, Terminal Voltage, and Current for Lead-Acid and Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2007, 54, 2550–2557. [Google Scholar] [CrossRef]
- Hoekstra, F.S.J.; Raijmakers, L.H.J.; Donkers, M.C.F.; Bergveld, H.J. Comparison of battery electromotive-force measurement and modelling approaches. J. Energy Storage 2022, 56, 105910. [Google Scholar] [CrossRef]
- Waag, W.; Sauer, D.U. Adaptive estimation of the electromotive force of the lithium-ion battery after current interruption for an accurate state-of-charge and capacity determination. Appl. Energy 2013, 111, 416–427. [Google Scholar] [CrossRef]
- Bergveld, H.J.; Kruijt, W.S.; Notten, P.H.L. Battery State-of-Charge indication. In Battery Management Systems: Design by Modelling; Bergveld, H.J., Kruijt, W.S., Notten, P.H.L., Eds.; Springer: Dordrecht, The Netherlands, 2002; pp. 193–240. [Google Scholar] [CrossRef]
- Chang, W.-Y. The State of Charge Estimating Methods for Battery: A Review. ISRN Appl. Math. 2013, 2013, 953792. [Google Scholar] [CrossRef]
- Zhang, C.; Li, K.; Pei, L.; Zhu, C. An integrated approach for real-time model-based state-of-charge estimation of lithium-ion batteries. J. Power Sources 2015, 283, 24–36. [Google Scholar] [CrossRef]
- Lee, J.; Won, J. Enhanced Coulomb Counting Method for SoC and SoH Estimation Based on Coulombic Efficiency. IEEE Access 2023, 11, 15449–15459. [Google Scholar] [CrossRef]
- Espedal, I.B.; Jinasena, A.; Burheim, O.S.; Lamb, J.J. Current Trends for State-of-Charge (SoC) Estimation in Lithium-Ion Battery Electric Vehicles. Energies 2021, 14, 3284. [Google Scholar] [CrossRef]
- Pop, V.; Bergveld, H.J.; Veld, J.H.G.O.H.; Regtien, P.P.L.; Danilov, D.; Notten, P.H.L. Modeling Battery Behavior for Accurate State-of-Charge Indication. J. Electrochem. Soc. 2006, 153, A2013. [Google Scholar] [CrossRef]
- Wu, S.-L.; Chen, H.-C.; Tsai, M.-Y.; Lin, T.-C.; Chen, L.-R. AC Impedance Based Online State-of-Charge Estimation for Li-ion Battery. In Proceedings of the 2017 International Conference on Information, Communication and Engineering (ICICE), Xiamen, China, 17–20 November 2017; pp. 53–56. [Google Scholar] [CrossRef]
- Wu, T.-H.; Moo, C.-S. State-of-Charge Estimation with State-of-Health Calibration for Lithium-Ion Batteries. Energies 2017, 10, 987. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, W.; Lin, S.; Feng, Z. A novel model of the initial state of charge estimation for LiFePO4 batteries. J. Power Sources 2014, 248, 1028–1033. [Google Scholar] [CrossRef]
- Saqli, K.; Bouchareb, H.; Oudghiri, M.; M’Sirdi, N. An Overview of State of Charge(Soc) and State of Health(Soh) Estimation Methods of Li-Ion Batteries. 2019. Available online: https://www.semanticscholar.org/paper/AN-OVERVIEW-OF-STATE-OF-CHARGE(SOC)-AND-STATE-OF-OF-Saqli-Bouchareb/514e28b47bba0daa287476e81a6349cb8c62daba (accessed on 26 July 2023).
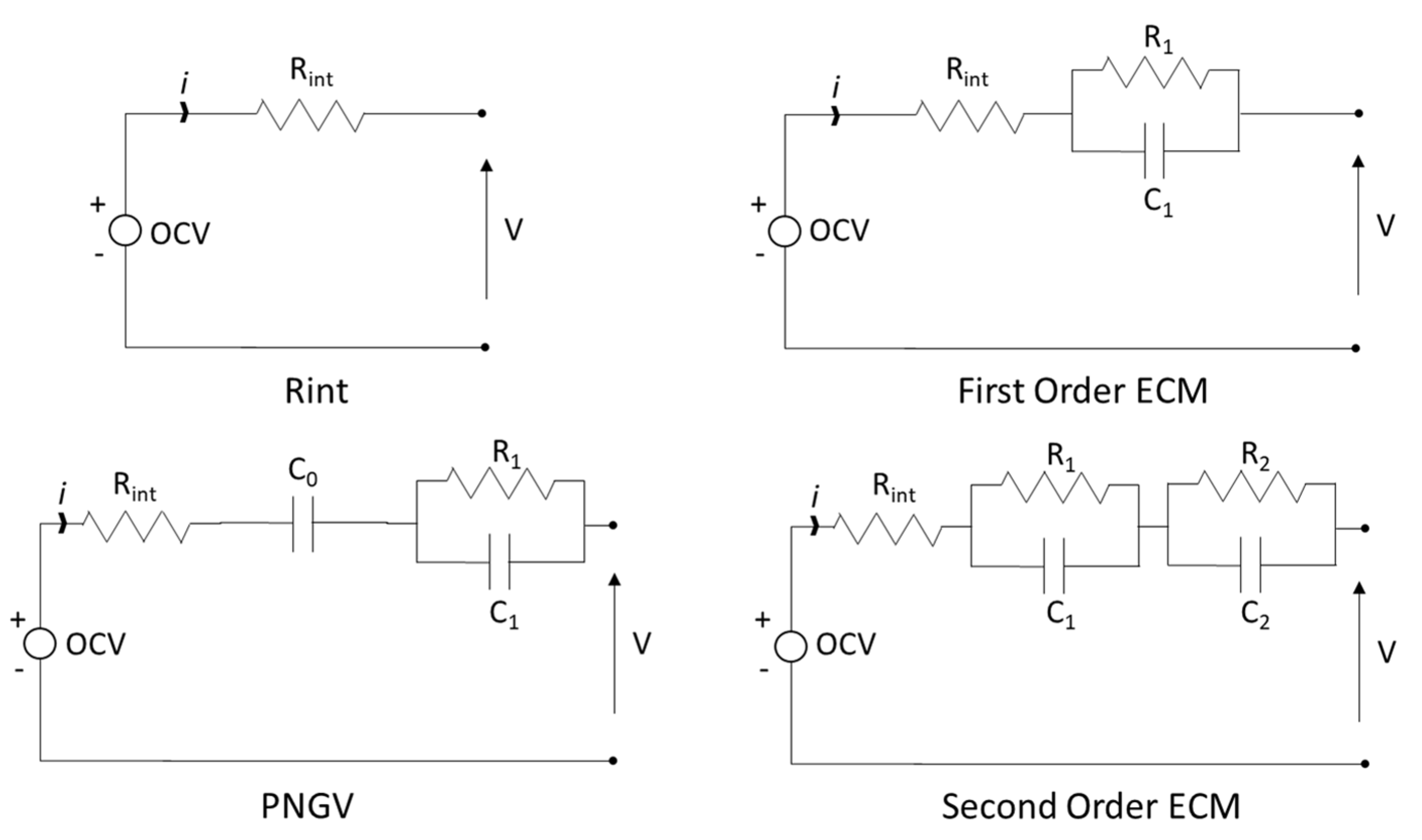
- He, H.; Xiong, R.; Fan, J. Evaluation of Lithium-Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach. Energies 2011, 4, 582. [Google Scholar] [CrossRef]
- Huria, T.; Ludovici, G.; Lutzemberger, G. State of charge estimation of high power lithium iron phosphate cells. J. Power Sources 2014, 249, 92–102. [Google Scholar] [CrossRef]
- Locorotondo, E.; Pugi, L.; Berzi, L.; Pierini, M.; Lutzemberger, G. Online Identification of Thevenin Equivalent Circuit Model Parameters and Estimation State of Charge of Lithium-Ion Batteries. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, W.; Lei, G. A Review of Li-ion Battery Equivalent Circuit Models. Trans. Electr. Electron. Mater. 2016, 17, 311–316. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 113, 109233. [Google Scholar] [CrossRef]
- Mawonou, K.S.R.; Eddahech, A.; Dumur, D.; Beauvois, D.; Godoy, E. Improved state of charge estimation for Li-ion batteries using fractional order extended Kalman filter. J. Power Sources 2019, 435, 226710. [Google Scholar] [CrossRef]
- Rivera-Barrera, J.P.; Muñoz-Galeano, N.; Sarmiento-Maldonado, H.O. SoC Estimation for Lithium-ion Batteries: Review and Future Challenges. Electronics 2017, 6, 102. [Google Scholar] [CrossRef]
- Kemper, P.; Li, S.E.; Kum, D. Simplification of pseudo two dimensional battery model using dynamic profile of lithium concentration. J. Power Sources 2015, 286, 510–525. [Google Scholar] [CrossRef]
- Lee, J.L.; Chemistruck, A.; Plett, G.L. Discrete-time realization of transcendental impedance models, with application to modeling spherical solid diffusion. J. Power Sources 2012, 206, 367–377. [Google Scholar] [CrossRef]
- Stetzel, K.D.; Aldrich, L.L.; Trimboli, M.S.; Plett, G.L. Electrochemical state and internal variables estimation using a reduced-order physics-based model of a lithium-ion cell and an extended Kalman filter. J. Power Sources 2015, 278, 490–505. [Google Scholar] [CrossRef]
- Gould, C.; Wang, J.; Stone, D.; Foster, M. EV/HEV Li-ion battery modelling and State-of-Function determination. In Proceedings of the Automation and Motion International Symposium on Power Electronics Power Electronics, Electrical Drives, Sorrento, Italy, 20–22 June 2012; pp. 353–358. [Google Scholar] [CrossRef]
- Yatsui, M.W.; Bai, H. Kalman filter based state-of-charge estimation for lithium-ion batteries in hybrid electric vehicles using pulse charging. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Mastali, M.; Vazquez-Arenas, J.; Fraser, R.; Fowler, M.; Afshar, S.; Stevens, M. Battery state of the charge estimation using Kalman filtering. J. Power Sources 2013, 239, 294–307. [Google Scholar] [CrossRef]
- Faragher, R. Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation [Lecture Notes]. IEEE Signal Process. Mag. 2012, 29, 128–132. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Dong, G.; Wei, J.; Chen, Z. Kalman filter for onboard state of charge estimation and peak power capability analysis of lithium-ion batteries. J. Power Sources 2016, 328, 615–626. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, L.; Wang, L.; Liao, C. An improved adaptive estimator for state-of-charge estimation of lithium-ion batteries. J. Power Sources 2018, 402, 422–433. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Z.; Zhao, Z.; Wang, L.; Lai, C.S.; Wang, D. Robustness Evaluation of Extended and Unscented Kalman Filter for Battery State of Charge Estimation. IEEE Access 2018, 6, 27617–27628. [Google Scholar] [CrossRef]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. Improved extended Kalman filter for state of charge estimation of battery pack. J. Power Sources 2014, 255, 368–376. [Google Scholar] [CrossRef]
- Jiang, C.; Taylor, A.; Duan, C.; Bai, K. Extended Kalman Filter based battery state of charge(SOC) estimation for electric vehicles. In Proceedings of the 2013 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 16–19 June 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Hu, X.; Sun, F.; Zou, Y. Comparison between two model-based algorithms for Li-ion battery SOC estimation in electric vehicles. Simul. Model. Pract. Theory 2013, 34, 1–11. [Google Scholar] [CrossRef]
- Xu, L.; Wang, J.; Chen, Q. Kalman filtering state of charge estimation for battery management system based on a stochastic fuzzy neural network battery model. Energy Convers. Manag. 2012, 53, 33–39. [Google Scholar] [CrossRef]
- Liu, X.; Li, K.; Wu, J.; He, Y.; Liu, X. An extended Kalman filter based data-driven method for state of charge estimation of Li-ion batteries. J. Energy Storage 2021, 40, 102655. [Google Scholar] [CrossRef]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. A novel on-board state-of-charge estimation method for aged Li-ion batteries based on model adaptive extended Kalman filter. J. Power Sources 2014, 245, 337–344. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Evaluation on State of Charge Estimation of Batteries with Adaptive Extended Kalman Filter by Experiment Approach. IEEE Trans. Veh. Technol. 2013, 62, 108–117. [Google Scholar] [CrossRef]
- Hossain, M.; Haque, M.E.; Arif, M.T. Kalman filtering techniques for the online model parameters and state of charge estimation of the Li-ion batteries: A comparative analysis. J. Energy Storage 2022, 51, 104174. [Google Scholar] [CrossRef]
- Plett, G.L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs. J. Power Sources 2006, 161, 1356–1368. [Google Scholar] [CrossRef]
- Wang, L.; Wang, L.; Liao, C.; Liu, J. Sigma-point Kalman filter application on estimating battery SOC. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 1592–1595. [Google Scholar] [CrossRef]
- Li, L.; Hu, M.; Xu, Y.; Fu, C.; Jin, G.; Li, Z. State of Charge Estimation for Lithium-Ion Power Battery Based on H-Infinity Filter Algorithm. Appl. Sci. 2020, 10, 6371. [Google Scholar] [CrossRef]
- Chen, N.; Zhang, P.; Dai, J.; Gui, W. Estimating the State-of-Charge of Lithium-Ion Battery Using an H-Infinity Observer Based on Electrochemical Impedance Model. IEEE Access 2020, 8, 26872–26884. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, C.; Zhang, X. State-of-charge estimation of the lithium-ion battery system with time-varying parameter for hybrid electric vehicles. IET Control Theory Appl. 2014, 8, 160–167. [Google Scholar] [CrossRef]
- Alfi, A.; Charkhgard, M.; Zarif, M.H. Hybrid state of charge estimation for lithium-ion batteries: Design and implementation. IET Power Electron. 2014, 7, 2758–2764. Available online: https://ietresearch.onlinelibrary.wiley.com/doi/10.1049/iet-pel.2013.0746 (accessed on 18 September 2023). [CrossRef]
- Lin, C.; Mu, H.; Xiong, R.; Shen, W. A novel multi-model probability battery state of charge estimation approach for electric vehicles using H-infinity algorithm. Appl. Energy 2016, 166, 76–83. [Google Scholar] [CrossRef]
- Yu, Q.; Xiong, R.; Lin, C.; Shen, W.; Deng, J. Lithium-Ion Battery Parameters and State-of-Charge Joint Estimation Based on H-Infinity and Unscented Kalman Filters. IEEE Trans. Veh. Technol. 2017, 66, 8693–8701. [Google Scholar] [CrossRef]
- Jiani, D.; Youyi, W.; Changyun, W. Li-ion battery SOC estimation using particle filter based on an equivalent circuit model. In Proceedings of the 2013 10th IEEE International Conference on Control and Automation (ICCA), Hangzhou, China, 12–14 June 2013; pp. 580–585. [Google Scholar] [CrossRef]
- Biazi, V.; Moreira, A.C.; Pinto, J.L.; Nascimento, M.; Marques, C. A particle filter-based virtual sensor for estimating the state of charge and internal temperature of lithium-ion batteries: Implementation in a simulated study case. J. Energy Storage 2023, 61, 106814. [Google Scholar] [CrossRef]
- Gao, M.; Liu, Y.; He, Z. Battery state of charge online estimation based on particle filter. In Proceedings of the 2011 4th International Congress on Image and Signal Processing, Shanghai, China, 15–17 October 2011; pp. 2233–2236. [Google Scholar] [CrossRef]
- Xia, B.; Sun, Z.; Zhang, R.; Lao, Z. A Cubature Particle Filter Algorithm to Estimate the State of the Charge of Lithium-Ion Batteries Based on a Second-Order Equivalent Circuit Model. Energies 2017, 10, 457. [Google Scholar] [CrossRef]
- Li, B.; Peng, K.; Li, G. State-of-charge estimation for lithium-ion battery using the Gauss-Hermite particle filter technique. J. Renew. Sustain. Energy 2018, 10, 014105. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Ning, B.; Xu, J.; Cao, B.; Wang, B.; Xu, G. A Sliding Mode Observer SOC Estimation Method Based on Parameter Adaptive Battery Model. Energy Procedia 2016, 88, 619–626. [Google Scholar] [CrossRef]
- Xia, B.; Zheng, W.; Zhang, R.; Lao, Z.; Sun, Z. A Novel Observer for Lithium-Ion Battery State of Charge Estimation in Electric Vehicles Based on a Second-Order Equivalent Circuit Model. Energies 2017, 10, 1150. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.; Deng, J.; Chen, Z.; Li, S. The State of Charge Estimation of Lithium-Ion Batteries Based on a Proportional-Integral Observer. IEEE Trans. Veh. Technol. 2014, 63, 1614–1621. [Google Scholar] [CrossRef]
- Xia, B.; Chen, C.; Tian, Y.; Sun, W.; Xu, Z.; Zheng, W. A novel method for state of charge estimation of lithium-ion batteries using a nonlinear observer. J. Power Sources 2014, 270, 359–366. [Google Scholar] [CrossRef]
- Ma, Y.; Li, B.; Li, G.; Zhang, J.; Chen, H. A nonlinear observer approach of SOC estimation based on hysteresis model for lithium-ion battery. IEEECAA J. Autom. Sin. 2017, 4, 195–204. [Google Scholar] [CrossRef]
- Hu, X.; Feng, F.; Liu, K.; Zhang, L.; Xie, J.; Liu, B. State estimation for advanced battery management: Key challenges and future trends. Renew. Sustain. Energy Rev. 2019, 114, 109334. [Google Scholar] [CrossRef]
- Khayat, N.; Karami, N. Adaptive techniques used for lifetime estimation of lithium-ion batteries. In Proceedings of the 2016 Third International Conference on Electrical, Electronics, Computer Engineering and their Applications (EECEA), Beirut, Lebanon, 21–23 April 2016; pp. 98–103. [Google Scholar] [CrossRef]
- Schouten, N.J.; Salman, M.A.; Kheir, N.A. Fuzzy logic control for parallel hybrid vehicles. IEEE Trans. Control Syst. Technol. 2002, 10, 460–468. [Google Scholar] [CrossRef]
- Bayindir, K.Ç.; Gözüküçük, M.A.; Teke, A. A comprehensive overview of hybrid electric vehicle: Powertrain configurations, powertrain control techniques and electronic control units. Energy Convers. Manag. 2011, 52, 1305–1313. [Google Scholar] [CrossRef]
- Sheng, H.; Xiao, J. Electric vehicle state of charge estimation: Nonlinear correlation and fuzzy support vector machine. J. Power Sources 2015, 281, 131–137. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Lu, L.; Li, J.; Han, X.; Xu, L. On-line equalization for lithium-ion battery packs based on charging cell voltages: Part 2. Fuzzy logic equalization. J. Power Sources 2014, 247, 460–466. [Google Scholar] [CrossRef]
- Burgos, C.; Sáez, D.; Orchard, M.E.; Cárdenas, R. Fuzzy modelling for the state-of-charge estimation of lead-acid batteries. J. Power Sources 2015, 274, 355–366. [Google Scholar] [CrossRef]
- Salkind, A.J.; Fennie, C.; Singh, P.; Atwater, T.; Reisner, D.E. Determination of state-of-charge and state-of-health of batteries by fuzzy logic methodology. J. Power Sources 1999, 80, 293–300. [Google Scholar] [CrossRef]
- Malkhandi, S. Fuzzy logic-based learning system and estimation of state-of-charge of lead-acid battery. Eng. Appl. Artif. Intell. 2006, 19, 479–485. [Google Scholar] [CrossRef]
- Chen, Z.; Qiu, S.; Masrur, M.A.; Murphey, Y.L. Battery state of charge estimation based on a combined model of Extended Kalman Filter and neural networks. In Proceedings of the The 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 2156–2163. [Google Scholar] [CrossRef]
- Dang, X.; Yan, L.; Xu, K.; Wu, X.; Jiang, H.; Sun, H. Open-Circuit Voltage-Based State of Charge Estimation of Lithium-ion Battery Using Dual Neural Network Fusion Battery Model. Electrochimica Acta 2016, 188, 356–366. [Google Scholar] [CrossRef]
- Zheng, Y.; Lu, L.; Han, X.; Li, J.; Ouyang, M. LiFePO4 battery pack capacity estimation for electric vehicles based on charging cell voltage curve transformation. J. Power Sources 2013, 226, 33–41. [Google Scholar] [CrossRef]
- Costa, M.; Di Blasio, G.; Prati, M.; Costagliola, M.; Cirillo, D.; La Villetta, M.; Caputo, C.; Martoriello, G. Multi-objective optimization of a syngas powered reciprocating engine equipping a combined heat and power unit. Appl. Energy 2020, 275, 115418. [Google Scholar] [CrossRef]
- Beatrice, C.; Capasso, C.; Costa, M.; Di Blasio, G.; Di Luca, G.; Iantorno, F.; Martoriello, G. Model based optimal management of a hybrid propulsion system for leisure boats. J. Energy Storage 2022, 46, 103896. [Google Scholar] [CrossRef]
- Xu, J.; Cao, B.; Chen, Z.; Zou, Z. An online state of charge estimation method with reduced prior battery testing information. Int. J. Electr. Power Energy Syst. 2014, 63, 178–184. [Google Scholar] [CrossRef]
- Castanho, D.; Guerreiro, M.; Silva, L.; Eckert, J.; Alves, T.A.; Tadano, Y.d.S.; Stevan, S.L.; Siqueira, H.V.; Corrêa, F.C. Method for SoC Estimation in Lithium-Ion Batteries Based on Multiple Linear Regression and Particle Swarm Optimization. Energies 2022, 15, 6881. [Google Scholar] [CrossRef]
- Shekar, A.C.; Anwar, S. Real-Time State-of-Charge Estimation via Particle Swarm Optimization on a Lithium-Ion Electrochemical Cell Model. Batteries 2019, 5, 4. [Google Scholar] [CrossRef]
- Mohandes, M.A. Modeling global solar radiation using Particle Swarm Optimization (PSO). Sol. Energy 2012, 86, 3137–3145. [Google Scholar] [CrossRef]
- Daş, M.T.; Dülger, L.C.; Daş, G.S. Robotic applications with Particle Swarm Optimization (PSO). In Proceedings of the 2013 International Conference on Control, Decision and Information Technologies (CoDIT), Hammamet, Tunisia, 6–8 May 2013; pp. 160–165. [Google Scholar] [CrossRef]
- Zhao, F.; Zhu, A.; Yu, D.; Yang, Y. A Hybrid Particle Swarm Optimization(PSO) Algorithm Schemes for Integrated Process Planning and Production Scheduling. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 6772–6776. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Gong, X.; Gao, C. A data-driven based adaptive state of charge estimator of lithium-ion polymer battery used in electric vehicles. Appl. Energy 2014, 113, 1421–1433. [Google Scholar] [CrossRef]
- Cuma, M.U.; Koroglu, T. A comprehensive review on estimation strategies used in hybrid and battery electric vehicles. Renew. Sustain. Energy Rev. 2015, 42, 517–531. [Google Scholar] [CrossRef]
- Sun, Q.; Guo, X.; Lv, H.; Gao, S.; Xu, J.; Wei, K. SOC Estimation Algorithm of Lithium-Ion Batteries Based on Particle Swarm Optimization. In Proceedings of the 2020 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), Tianjin, China, 16–18 October 2020; pp. 1–2. [Google Scholar] [CrossRef]
- Ye, M.; Guo, H.; Cao, B. A model-based adaptive state of charge estimator for a lithium-ion battery using an improved adaptive particle filter. Appl. Energy 2017, 190, 740–748. [Google Scholar] [CrossRef]
- Barcellona, S.; Colnago, S.; Dotelli, G.; Latorrata, S.; Piegari, L. Aging effect on the variation of Li-ion battery resistance as function of temperature and state of charge. J. Energy Storage 2022, 50, 104658. [Google Scholar] [CrossRef]
- You, G.-W.; Park, S.; Oh, D. Real-time state-of-health estimation for electric vehicle batteries: A data-driven approach. Appl. Energy 2016, 176, 92–103. [Google Scholar] [CrossRef]
- Haifeng, D.; Xuezhe, W.; Zechang, S. A new SOH prediction concept for the power lithium-ion battery used on HEVs. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 1649–1653. [Google Scholar] [CrossRef]
- Shu, X.; Shen, S.; Shen, J.; Zhang, Y.; Li, G.; Chen, Z.; Liu, Y. State of health prediction of lithium-ion batteries based on machine learning: Advances and perspectives. iScience 2021, 24, 103265. [Google Scholar] [CrossRef]
- Chen, L.; Lü, Z.; Lin, W.; Li, J.; Pan, H. A new state-of-health estimation method for lithium-ion batteries through the intrinsic relationship between ohmic internal resistance and capacity. Measurement 2018, 116, 586–595. [Google Scholar] [CrossRef]
- Basia, A.; Simeu-Abazi, Z.; Gascard, E.; Zwolinski, P. Review on State of Health estimation methodologies for lithium-ion batteries in the context of circular economy. CIRP J. Manuf. Sci. Technol. 2021, 32, 517–528. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van Den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Eddahech, A.; Briat, O.; Bertrand, N.; Delétage, J.-Y.; Vinassa, J.-M. Behavior and state-of-health monitoring of Li-ion batteries using impedance spectroscopy and recurrent neural networks. Int. J. Electr. Power Energy Syst. 2012, 42, 487–494. [Google Scholar] [CrossRef]
- Guo, F.; Huang, G.; Zhang, W.; Liu, G.; Li, T.; Ouyang, N.; Zhu, S. State of Health estimation method for lithium batteries based on electrochemical impedance spectroscopy and pseudo-image feature extraction. Measurement 2023, 220, 113412. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.; Hussain, A.; Hoque, M.; Ker, P.J.; Saad, M.; Ayob, A. A review of state of health and remaining useful life estimation methods for lithium-ion battery in electric vehicles: Challenges and recommendations. J. Clean. Prod. 2018, 205, 115–133. [Google Scholar] [CrossRef]
- Ng, K.S.; Moo, C.-S.; Chen, Y.-P.; Hsieh, Y.-C. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Guo, Z.; Qiu, X.; Hou, G.; Liaw, B.Y.; Zhang, C. State of health estimation for lithium ion batteries based on charging curves. J. Power Sources 2014, 249, 457–462. [Google Scholar] [CrossRef]
- Weng, C.; Sun, J.; Peng, H. A unified open-circuit-voltage model of lithium-ion batteries for state-of-charge estimation and state-of-health monitoring. J. Power Sources 2014, 258, 228–237. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Cho, B.H. Complementary Cooperation Algorithm Based on DEKF Combined With Pattern Recognition for SOC/Capacity Estimation and SOH Prediction. IEEE Trans. Power Electron. 2012, 27, 436–451. [Google Scholar] [CrossRef]
- Azis, N.A.; Joelianto, E.; Widyotriatmo, A. State of Charge (SoC) and State of Health (SoH) Estimation of Lithium-Ion Battery Using Dual Extended Kalman Filter Based on Polynomial Battery Model. In Proceedings of the 2019 6th International Conference on Instrumentation, Control, and Automation (ICA), Bandung, Indonesia, 31 July–2 August 2019; pp. 88–93. [Google Scholar] [CrossRef]
- Zhu, F.; Fu, J. A Novel State-of-Health Estimation for Lithium-Ion Battery via Unscented Kalman Filter and Improved Unscented Particle Filter. IEEE Sens. J. 2021, 21, 25449–25456. [Google Scholar] [CrossRef]
- Schwunk, S.; Armbruster, N.; Straub, S.; Kehl, J.; Vetter, M. Particle filter for state of charge and state of health estimation for lithium–iron phosphate batteries. J. Power Sources 2013, 239, 705–710. [Google Scholar] [CrossRef]
- Wei, J.; Chen, C. State of Charge and Health Estimation For Lithium-Ion Batteries Using Recursive Least Squares. In Proceedings of the 2020 5th International Conference on Advanced Robotics and Mechatronics (ICARM), Shenzhen, China, 18–21 December 2020; pp. 686–689. [Google Scholar] [CrossRef]
- Wu, M.; Wang, L.; Wu, J. State of health estimation of the LiFePO4 power battery based on the forgetting factor recursive Total Least Squares and the temperature correction. Energy 2023, 282, 128437. [Google Scholar] [CrossRef]
- Elmahallawy, M.; Elfouly, T.; Alouani, A.; Massoud, A.M. A Comprehensive Review of Lithium-Ion Batteries Modeling, and State of Health and Remaining Useful Lifetime Prediction. IEEE Access 2022, 10, 119040–119070. [Google Scholar] [CrossRef]
- Kim, J.; Nikitenkov, D. Fuzzy logic-controlled online state-of-health (SOH) prediction in large format LiMn2O4 cell for energy storage system (ESS) applications. In Proceedings of the 2014 IEEE International Conference on Industrial Technology (ICIT), Busan, Republic of Korea, 26 February–1 March 2014; pp. 474–479. [Google Scholar] [CrossRef]
- Lin, H.-T.; Liang, T.-J.; Chen, S.-M. The state-of-health diagnosis of Li-Co batteries with fuzzy identification. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; pp. 2678–2682. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Fu, Y.; Xu, J.; Gong, X. Online battery state of health estimation based on Genetic Algorithm for electric and hybrid vehicle applications. J. Power Sources 2013, 240, 184–192. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, Z.; Liu, K.; Zhang, Y.; Feng, W. A compact and optimized neural network approach for battery state-of-charge estimation of energy storage system. Energy 2021, 219, 119529. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, G.; Zhen, D.; Gu, F.; Ball, A. A review on online state of charge and state of health estimation for lithium-ion batteries in electric vehicles. Energy Rep. 2021, 7, 5141–5161. [Google Scholar] [CrossRef]
- Song, L.; Zhang, K.; Liang, T.; Han, X.; Zhang, Y. Intelligent state of health estimation for lithium-ion battery pack based on big data analysis. J. Energy Storage 2020, 32, 101836. [Google Scholar] [CrossRef]
- Yang, Q.; Xu, J.; Li, X.; Xu, D.; Cao, B. State-of-health estimation of lithium-ion battery based on fractional impedance model and interval capacity. Int. J. Electr. Power Energy Syst. 2020, 119, 105883. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Chen, W.; Wang, L.; Lin, P.; Qu, C. Online accurate state of health estimation for battery systems on real-world electric vehicles with variable driving conditions considered. J. Clean. Prod. 2021, 294, 125814. [Google Scholar] [CrossRef]
- Falai, A.; Giuliacci, T.A.; Misul, D.A.; Anselma, P.G. Reducing the Computational Cost for Artificial Intelligence-Based Battery State-of-Health Estimation in Charging Events. Batteries 2022, 8, 209. [Google Scholar] [CrossRef]
- Rahimi-Eichi, H.; Ojha, U.; Baronti, F.; Chow, M.-Y. Battery Management System: An Overview of Its Application in the Smart Grid and Electric Vehicles. IEEE Ind. Electron. Mag. 2013, 7, 4–16. [Google Scholar] [CrossRef]
- Hoque, M.M.; Hannan, M.A.; Mohamed, A. Voltage equalization control algorithm for monitoring and balancing of series connected lithium-ion battery. J. Renew. Sustain. Energy 2016, 8, 025703. [Google Scholar] [CrossRef]
- Mishra, S.; Swain, S.C.; Samantaray, R.K. A Review on Battery Management system and its Application in Electric vehicle. In Proceedings of the 2021 International Conference on Advances in Computing and Communications (ICACC), Kochi, Kakkanad, India, 21–23 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Bashir, H.; Yaqoob, A.; Jawaid, I.; Khalid, W.; Javed, M.Y.; Sultan, W. A Review of Battery Management System and Modern State Estimation Approaches in Lithiumion Batteries for Electric Vehicle. In Proceedings of the 2022 5th International Conference on Energy Conservation and Efficiency (ICECE), Lahore, Pakistan, 16–17 March 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Gabbar, H.A.; Othman, A.M.; Abdussami, M.R. Review of Battery Management Systems (BMS) Development and Industrial Standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.M.; Tsui, K.L.; Pecht, M. Battery Management Systems in Electric and Hybrid Vehicles. Energies 2011, 4, 1840. [Google Scholar] [CrossRef]
- Spoorthi, B.; Pradeepa, P. Review on Battery Management System in EV. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power (ICICCSP), Hyderabad, India, 21–23 July 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Sanitha Michail, C.; Chithra, M.; Nithara, P.V.; Eldho, R.P. Overview on Battery Management System and Energy Storage System of Electric Vehicle. In Proceedings of the 2022 International Conference on Automation, Computing and Renewable Systems (ICACRS), Pudukkottai, India, 13–15 December 2022; pp. 143–147. [Google Scholar] [CrossRef]
- Tang, H.; Wu, Y.; Cai, Y.; Wang, F.; Lin, Z.; Pei, Y. Design of power lithium battery management system based on digital twin. J. Energy Storage 2022, 47, 103679. [Google Scholar] [CrossRef]
- Shoukat, M.U.; Yan, L.; Du, C.; Raza, M.U.M.; Adeel, M.; Khan, T. Application of Digital Twin in Smart Battery Electric Vehicle: Industry 4.0. In Proceedings of the 2022 International Conference on IT and Industrial Technologies (ICIT), Chiniot, Pakistan, 3–4 October 2022; pp. 1–7. [Google Scholar] [CrossRef]
- García, E.; Quiles, E.; Correcher, A. Distributed Intelligent Battery Management System Using a Real-World Cloud Computing System. Sensors 2023, 23, 3417. [Google Scholar] [CrossRef] [PubMed]
- Nuroldayeva, G.; Serik, Y.; Adair, D.; Uzakbaiuly, B.; Bakenov, Z. State of Health Estimation Methods for Lithium-Ion Batteries. Int. J. Energy Res. 2023, 2023, e4297545. [Google Scholar] [CrossRef]
- Alamin, K.S.S.; Chen, Y.; Macii, E.; Poncino, M.; Vinco, S. A Machine Learning-based Digital Twin for Electric Vehicle Battery Modeling. In Proceedings of the 2022 IEEE International Conference on Omni-layer Intelligent Systems (COINS), Barcelona, Spain, 1–3 August 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Guo, W.; Yang, L.; Deng, Z. A Cloud-based State of Health Estimation Method for Lithium-ion Batteries Using Sparse Charging Data. J. Phys. Conf. Ser. 2023, 2456, 012026. [Google Scholar] [CrossRef]
- Naseri, F.; Gil, S.; Barbu, C.; Cetkin, E.; Yarimca, G.; Jensen, A.; Larsen, P.; Gomes, C. Digital twin of electric vehicle battery systems: Comprehensive review of the use cases, requirements, and platforms. Renew. Sustain. Energy Rev. 2023, 179, 113280. [Google Scholar] [CrossRef]


| Battery Type | Specific Energy (Wh/kg) | Specific Power (W/kg) | Nominal Voltage (V) | Cycle Life (# of Cycles) | Cost (USD/kWh) | Application |
|---|---|---|---|---|---|---|
| Lead-acid | 180 | 35–40 | 2 | 1500–5000 | 120–200 | Automotive ignition, starting |
| Ni-Cd | 40–60 | 150 | 1.25 | 2000–3000 | 250–350 | Portable devices |
| Ni-MH | 60–120 | 250–1000 | 1.25 | 500–3000 | 150–250 | Electronic Equipment, xEV |
| Li-ion | 120–140 | 200–2000 | 3.6 | 1500–4500 | 150–1300 | Electronic Equipment, xEV |
| SoC Estimation Approach | SoC Estimation Error | Reference |
|---|---|---|
| OCV | ≤±1.2% | [51] |
| IR | ≤±1.4% | [39] |
| EMF | ≤±2% | [45] |
| IS | ≤±1%; ≤±1.6% | [20,52] |
| CC | ≤±1.9%; ≤±4% | [53,54] |
| Modified CC | ±0.019%; ±0.039% 1 | [49] |
| SoC Estimation Approach | Soc Estimation Error (%) | Reference |
|---|---|---|
| LKF | ≤±1.76; ±2 | [67,71] |
| EKF | ≤±1.5; ≤±1; ≤±1; | [74,75,76] |
| ±0.86; ≤±1.5 | [77,78] | |
| AEKF | ≤±2 | [80] |
| UKF | ±0.80; | [73] |
| HIF | ≤±2.49; ≤±1.1; ≤±0.95; | [86,87,88] |
| ≤±0.5 | [89] | |
| PF | ≤±3.0; ≤±0.5; ≤±1.0 | [90,93,94] |
| SoC Estimation Approach | SoC Estimation Error (%) | Reference |
|---|---|---|
| SMO | ≤±2; ±0.86 | [96,97] |
| PIO | ±2; ≤±2.5 | [36,98] |
| NLO | ≤±2.89; ≤±2 | [99,100] |
| SoC Estimation Approach | SoC Estimation Error (%) | Reference |
|---|---|---|
| FL | ±5; ±5 | [108,109] |
| NN | ≤±1; ≤±1.03; | [110,111] |
| ≤±0.75 | [111] | |
| GA | ≤±1; ≤±1 | [112,115] |
| PSO | ≤±1.5; ≤±1; ≤±1 | [121,123,124] |
| SoH Estimation Approach | SoH Estimation Error (%) | Reference |
|---|---|---|
| IR | ≤±4 | [129] |
| EIS | ≤±2; ≤±2 | [132,133] |
| CC | ≤±1 1 | [135] |
| OCV | ≤±3; ≤±1 | [136,137] |
| SoH Estimation Approach | SoH Estimation Error (%) | Reference |
|---|---|---|
| DEKF | ±5 | [138] |
| PF + UKF | <±0.38; <±0.62 * | [140] |
| PF | <±2 | [141] |
| LS | <±0.35 | [143] |
| SoH Estimation Approach | SoH Estimation Error (%) | Reference |
|---|---|---|
| FL | ±1.46–9.2 | [146] |
| GA | Not provided | // |
| FFNN | ±0.45 | [150] |
| BPNN | ±1.5 | [151] |
| LSTM | ±0.13 | [152] |
| In-Cloud Estimation | Estimation Error (%) | Reference |
|---|---|---|
| SoC | ±0.49 | [21] |
| SoH | ±0.74; ±1.74 | |
| SoC | ±0.549 | [166] |
| SoH | ±0.603 | |
| SoH | ≤±2.0 | [167] |
| Estimation Approach | Pro | Cons |
|---|---|---|
| OCV | Simplicity and high accuracy | Not suitable for online implementation due to long rest time. Extensive laboratory tests are necessary to find SoH–OCV correlation |
| IR | Simple and easily implementable | Internal resistance changes slowly and is hard to observe for SoC estimation, thus it is not suitable for online estimation. |
| EMF | Simple and easily implementable | The OCV relaxation process may take up a lengthy time and is not suitable for online applications. |
| IS | Accurate, quick, and non-destructive capturing of dynamic batteries behavior | For lab purposes only; expensive, it requires a dedicated battery model. |
| CC | Simple to be implemented with low computational cost | This method is time-consuming due to the continuous tracking of ampere-hours. |
| KF | Real-time estimation with high accuracy | Non suitable for the non-linear problem. It could not converge for SoH estimation due to non-linear degradation process of the battery. |
| EKF | Real-time estimation for non-linear problems | A linearization error may occur under highly non-linear conditions. |
| UKF | For strong non-linear problem; comparable computational effort with EKF | Its robustness depends on the linearization process. |
| HIF | Overcomes the noise influence on the accuracy of the traditional EKF algorithm | Aging, hysteresis, and temperature effects could influence its accuracy. |
| PF | Suitable for nonlinear systems with non-Gaussian noise | The main difficulty is to select the proper proposal distributions that can approximate the posterior distributions. |
| SMO | Compensates for the modelling errors caused by parameter variations of the circuit model | Difficult to determine the gain. |
| PIO | Good accuracy | Complicated controllers are necessary. |
| NLO | It does not need complicated matrix operations; reduced computation cost | Accuracy may be influenced by gain determination. |
| FL | Suitable for complex and non-linear problems, a precise mathematical model is not a prerequisite | Expensive in terms of storage and computational effort requirements. Not suitable for online SoC and SoH estimation. |
| GA | Precise and robust | Requires high computational effort, generally coupled with another method for SoC and SoH estimation. Furthermore, a proper tuning is necessary. |
| NN | Strong adaptability and self-learning skills; no knowledge of the cell’s internal structure is necessary; ideal for parameter estimation | A large amount of training data and storage is required; non-negligible computational effort; challenging for on-line implementation. |
| PSO | Simpler than the GA approach; fewer parameters to be tuned; lower computational effort; higher degree of convergence | Time-consuming in parameter tuning |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Luca, G.; Di Blasio, G.; Gimelli, A.; Misul, D.A. Review on Battery State Estimation and Management Solutions for Next-Generation Connected Vehicles. Energies 2024, 17, 202. https://doi.org/10.3390/en17010202
Di Luca G, Di Blasio G, Gimelli A, Misul DA. Review on Battery State Estimation and Management Solutions for Next-Generation Connected Vehicles. Energies. 2024; 17(1):202. https://doi.org/10.3390/en17010202
Chicago/Turabian StyleDi Luca, Giuseppe, Gabriele Di Blasio, Alfredo Gimelli, and Daniela Anna Misul. 2024. "Review on Battery State Estimation and Management Solutions for Next-Generation Connected Vehicles" Energies 17, no. 1: 202. https://doi.org/10.3390/en17010202
APA StyleDi Luca, G., Di Blasio, G., Gimelli, A., & Misul, D. A. (2024). Review on Battery State Estimation and Management Solutions for Next-Generation Connected Vehicles. Energies, 17(1), 202. https://doi.org/10.3390/en17010202











