Fault Diagnosis of Hydropower Units Based on Gramian Angular Summation Field and Parallel CNN
Abstract
1. Introduction
2. Materials and Methods
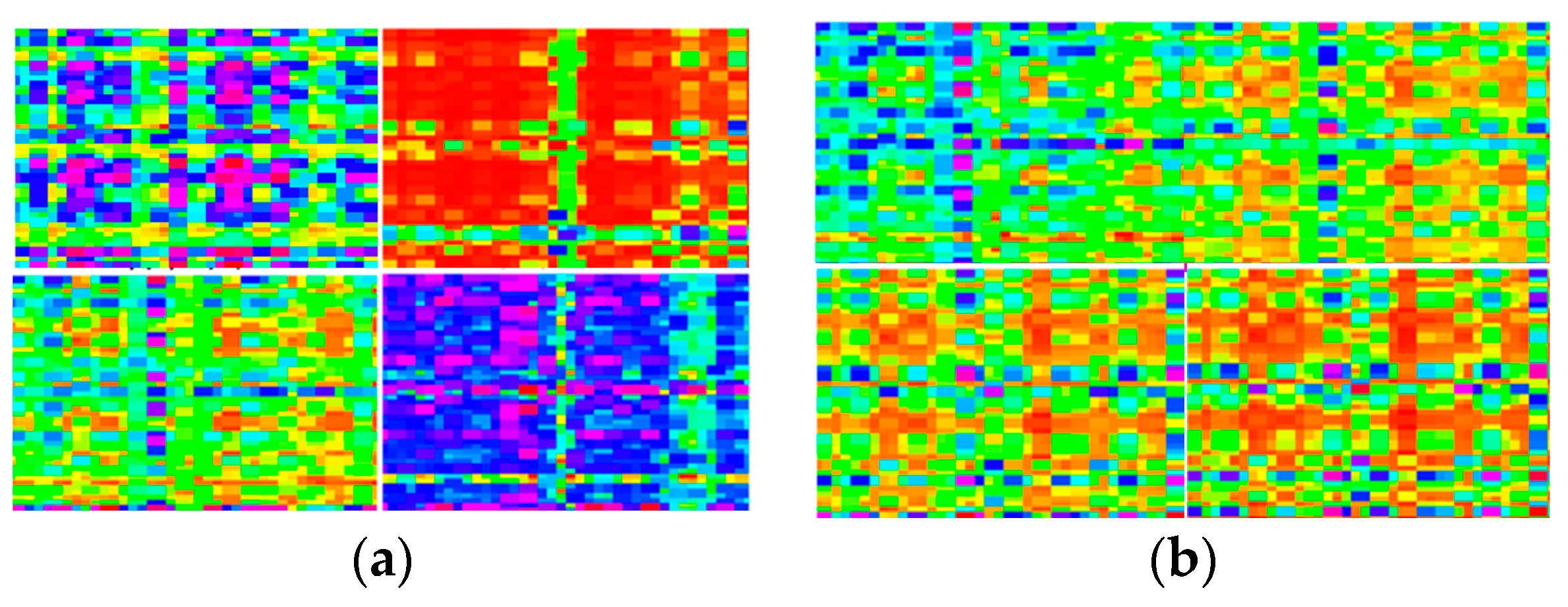
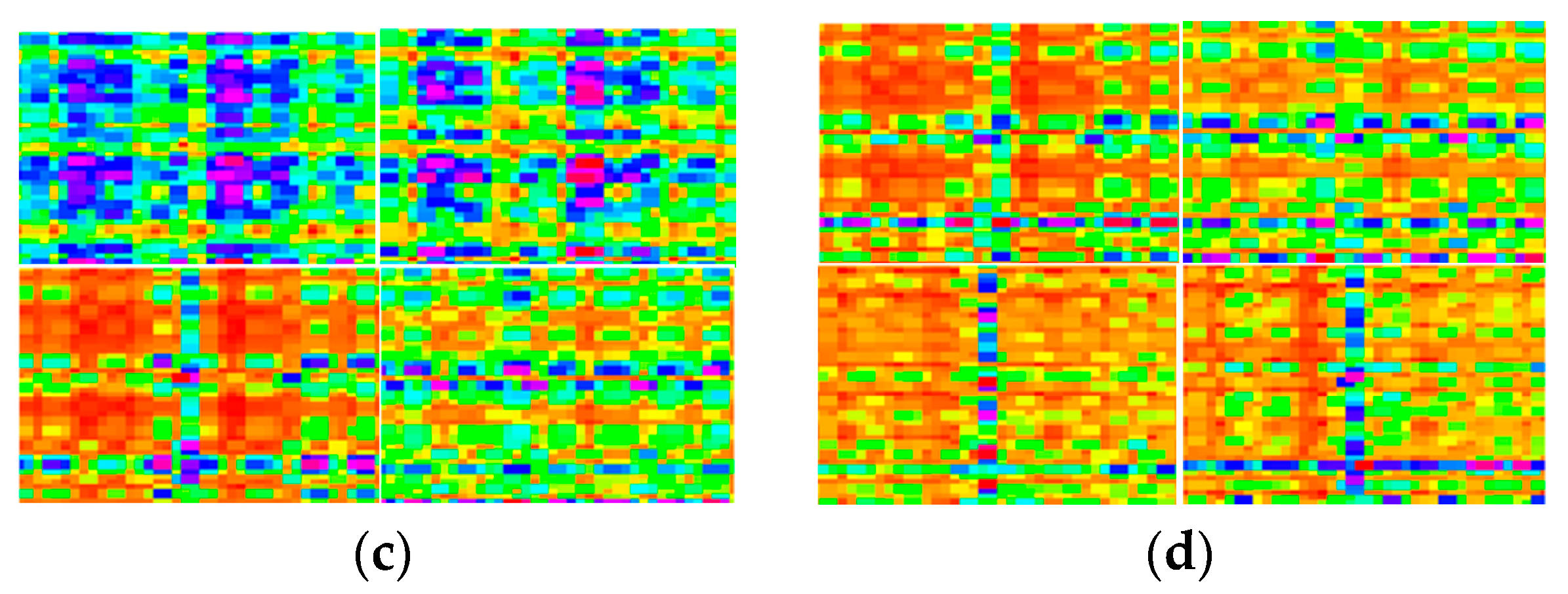
2.1. GASF Algorithm
- I.
- The original time series is normalized:
- II.
- The data obtained in the first step are transformed into a polar co-ordinate system to obtain the radius and angle corresponding to each data point:where is the Gram matrix; is the inner product operation.Time-series vibration data are converted into vectors.where is the radius in polar co-ordinates and is the angle.
- III.
- Using the Gram matrix, a two-dimensional image of the time series is obtained:where GASF is the Gramian angular summation field and GADF is the Gramian angular difference field.
2.2. ICOA Algorithm
2.2.1. Exploration—Co-Operative Iguana Hunting
2.2.2. Development—Decentralized Escape from Predators
2.2.3. ICOA Algorithm Principle
- A.
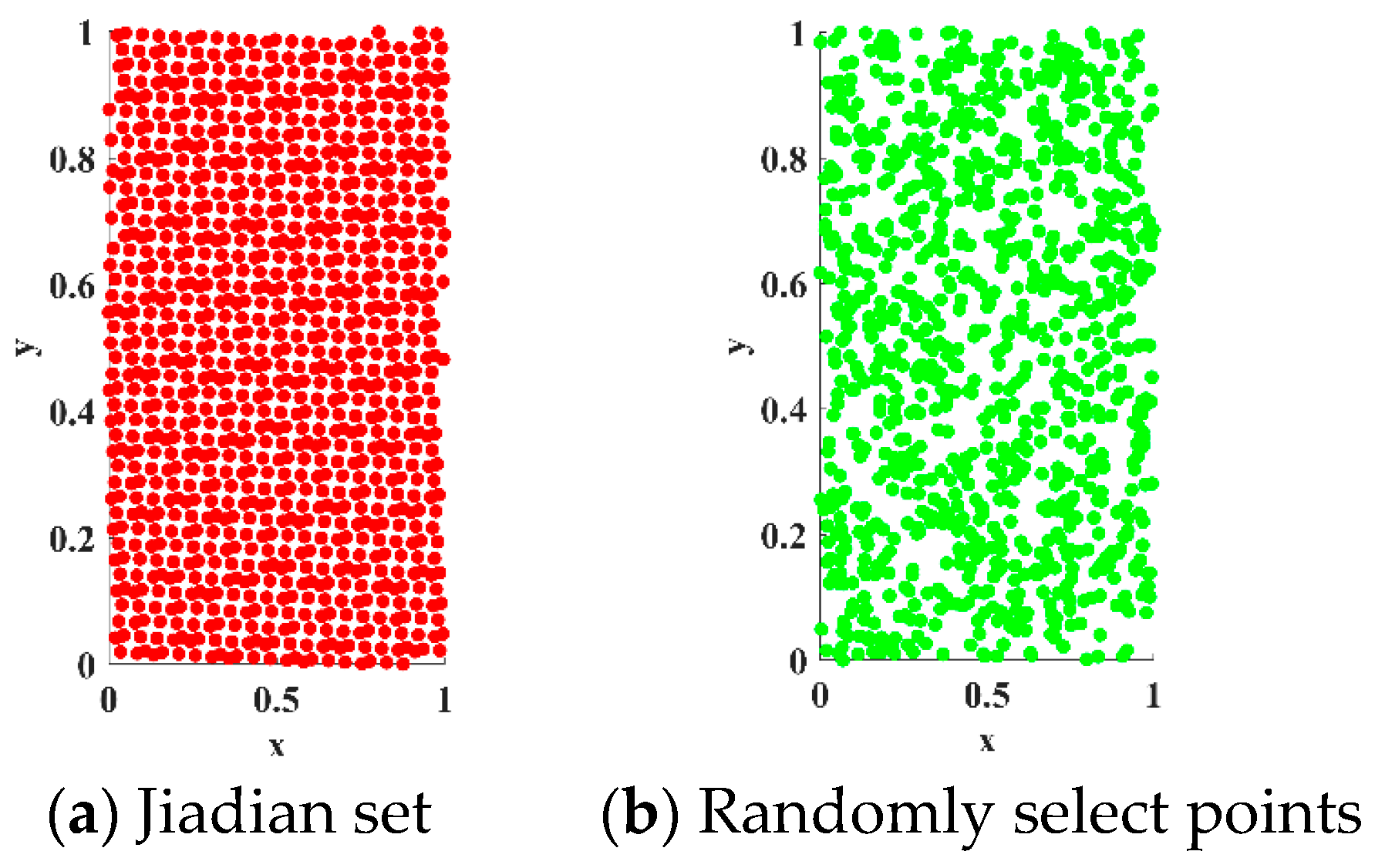
- Improvements in initialized populations.
- B.
- A dynamic reverse learning strategy is introduced to improve the quality of the initial population again:where is the individual after reverse learning, is the current individual, and and are random numbers from 0 to 1.
- C.
- The golden sine strategy is incorporated in the exploration phase of COA to enhance the global search capability of the algorithm; then, the mathematical model of tree-climbing long-nosed raccoon behavior is:
- D.
- In the development stage, four strategies, namely, soft encirclement of Harris Hawk, hard encirclement, soft encirclement of progressive fast dive, and hard encirclement of progressive fast dive, are fused, assuming that is the probability of escape of the prey, , and that it can be escaped if , and a random number E is also introduced:
- , ; at this time, the soft envelope is implemented, and its position update formula is:where is the difference between the prey position and the individual position, (0,2), is the original position, and is the updated position.
- and , at which point hard bracketing is implemented with the position update formula:
- and , at which time the soft envelopment of progressive fast swooping is implemented with the position update equation:
- and ; at this point in the hard envelope of real-time progressive fast swooping, the position update equation is:
- E.
- In the late iteration, in order to avoid the algorithm falling into the local optimum dilemma, this paper utilizes the vertical and horizontal crossover strategy to correct the individuals, the horizontal crossover to cross-search the population to reduce the search blind spots, and the vertical crossover to increase the diversity of the population while reducing the probability of the algorithm falling into the local optimum. However, although the vertical and horizontal crossover strategy has excellent search performance, the full-dimensional crossover operation will significantly increase the computational burden. In the face of high-dimensional problems, its computational cost will increase geometrically. Therefore, this paper adopts an unordered dimensional sampling method, which reduces the computational cost and also prevents the reduction in overall sparsity due to the reduction in the number of dimensions of the near-optimal individuals.
- The sampling rate determines the number of dimensions involved in the longitudinal crossover, and the dimensions involved are selected by the sampling rate, which is defined as follows:
- Horizontal crossover is the process of selecting two individuals from the same dimension of the population and exchanging individual information at a certain randomized rate:where and are the dimension of the offspring individuals and obtained after crossover, and are the dth dimensions of the parent individuals and , and and are random numbers between –1 and 1, where the number of crossover dimensions is determined by the sampling rate.
- Longitudinal crossover refers to the exchange of dimensional information between different dimensions of the best individuals in the population according to a certain longitudinal crossover probability, thus generating a new generation of the best individuals to compete with their parents, which is conducive to the learning of different dimensions from each other and avoids the premature convergence of a certain dimension:where is the child obtained after crossover of the parent; again, the crossover dimension is determined by the sampling rate. is a random number from 0 to 1.
2.3. CNN Algorithm
2.4. MSA Algorithm
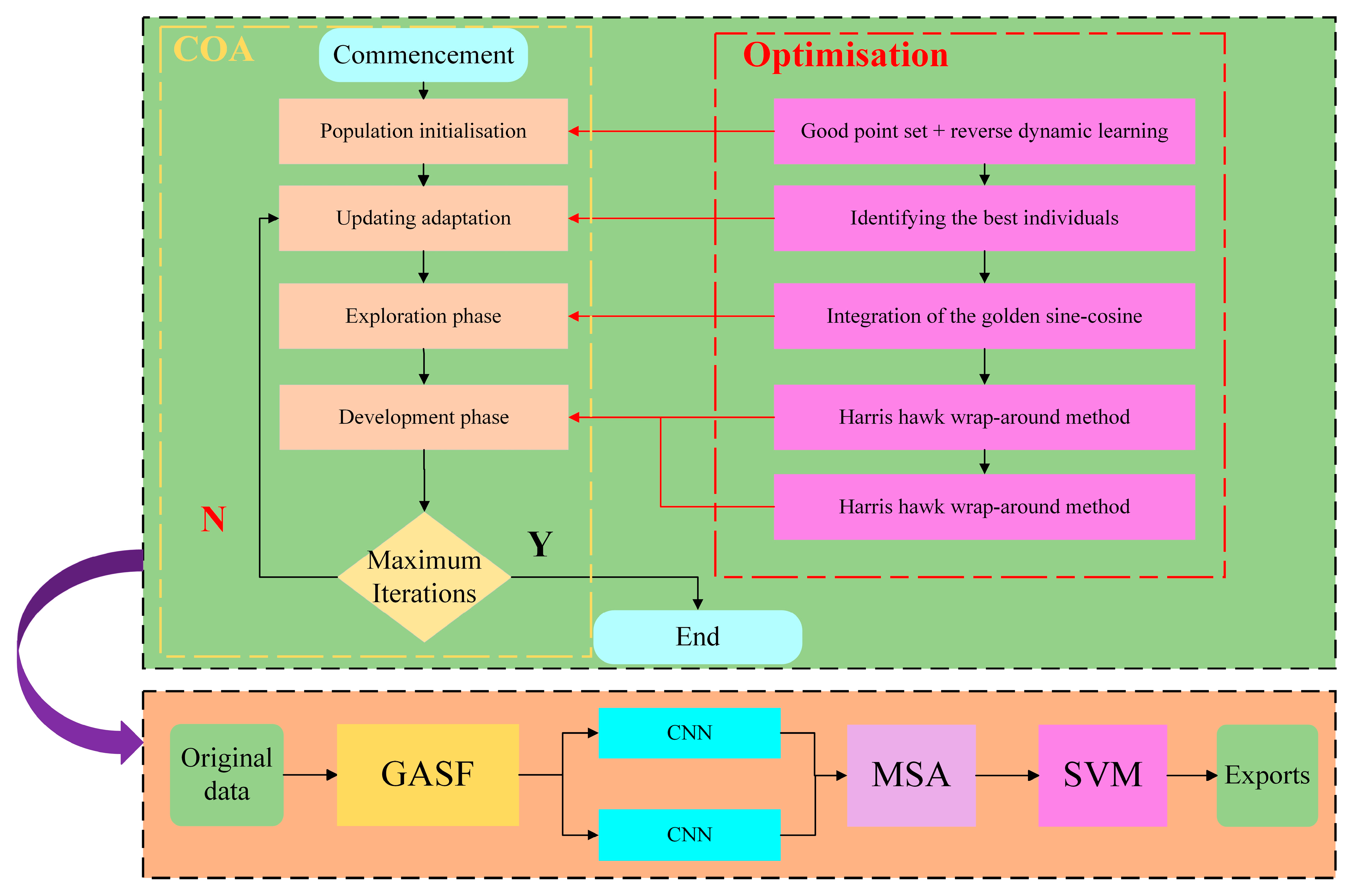
2.5. Rotor Fault Diagnosis Model Based on GASF and ICOA-PCNN-MSA-SVM
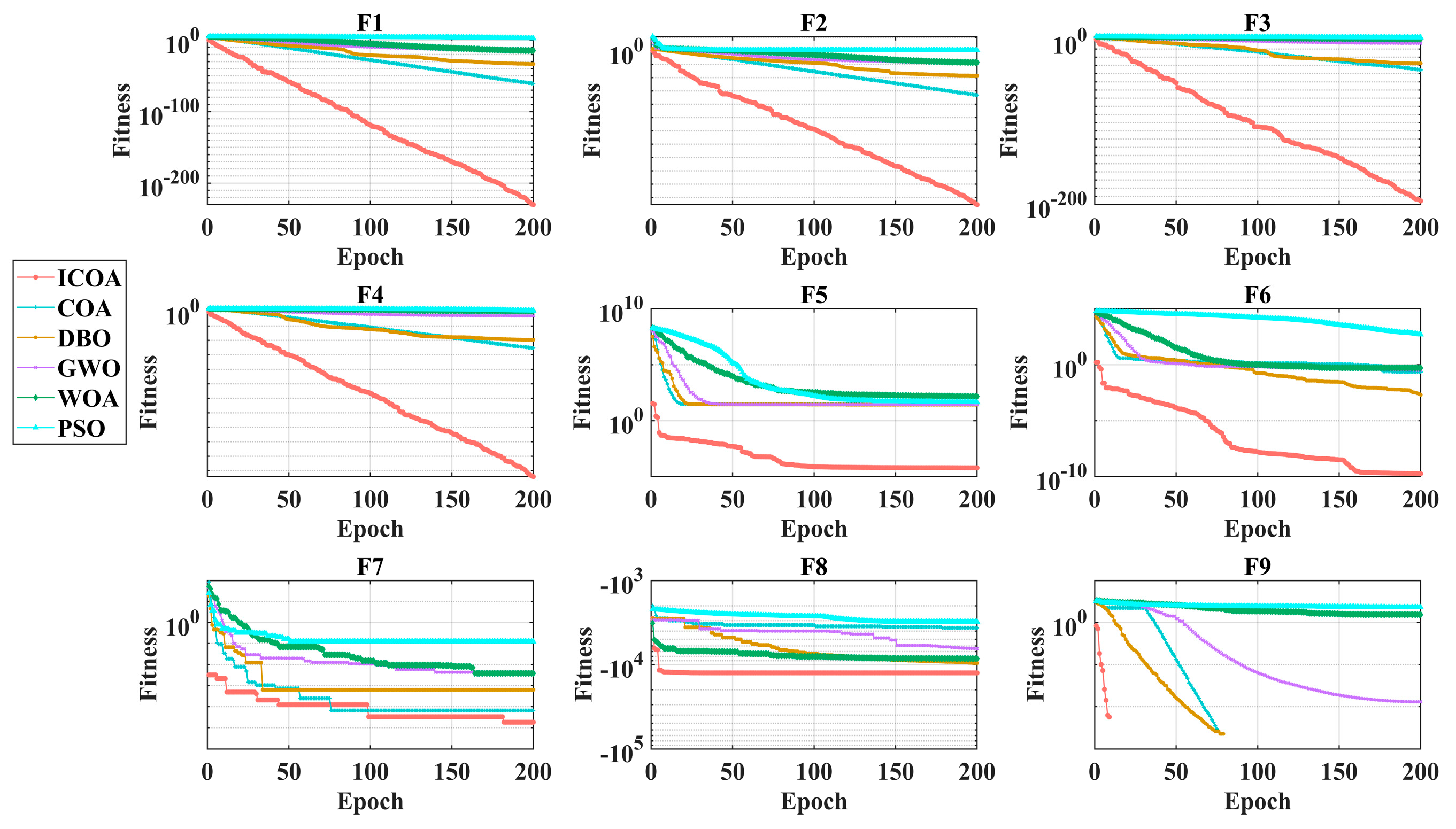
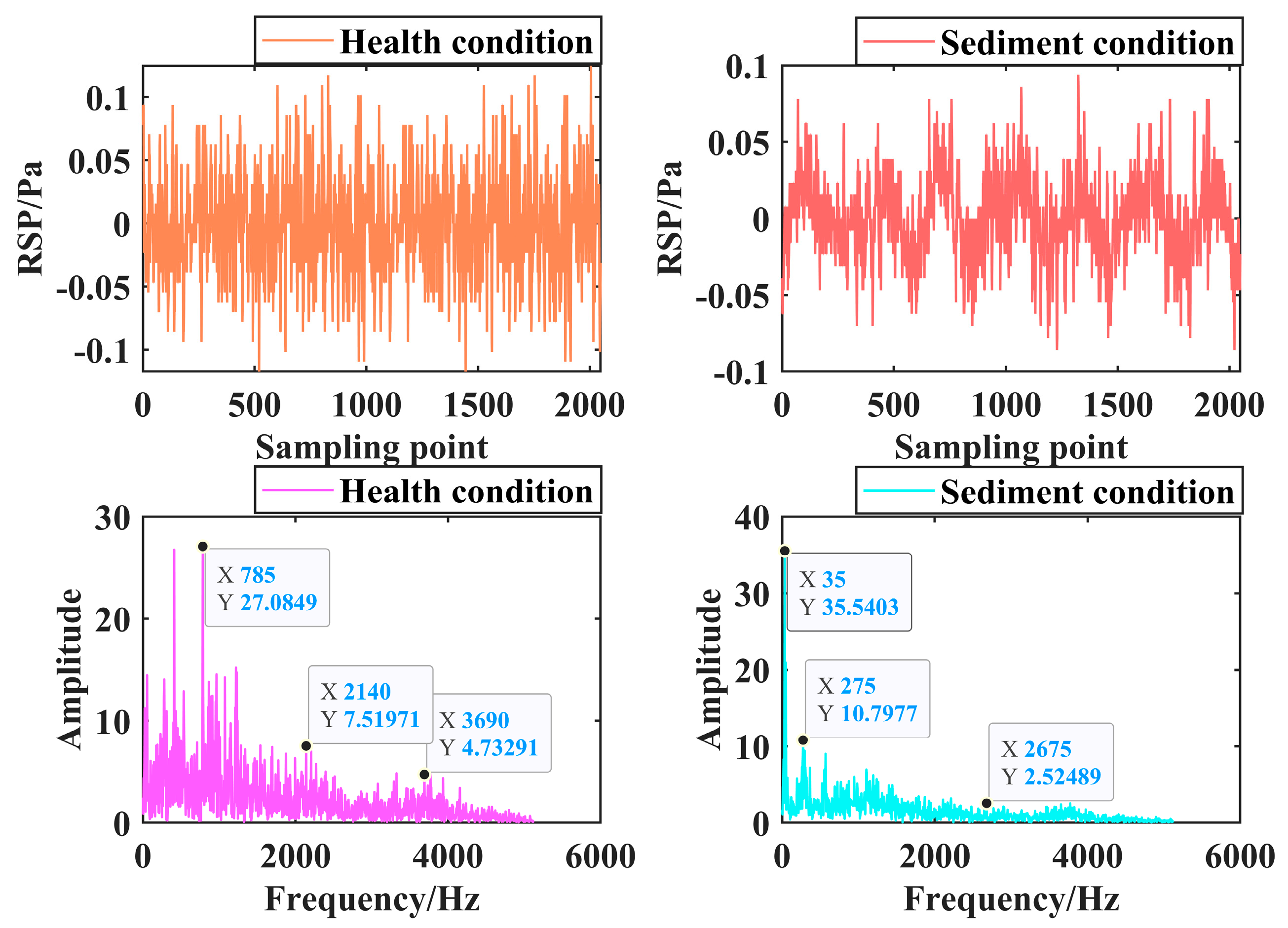
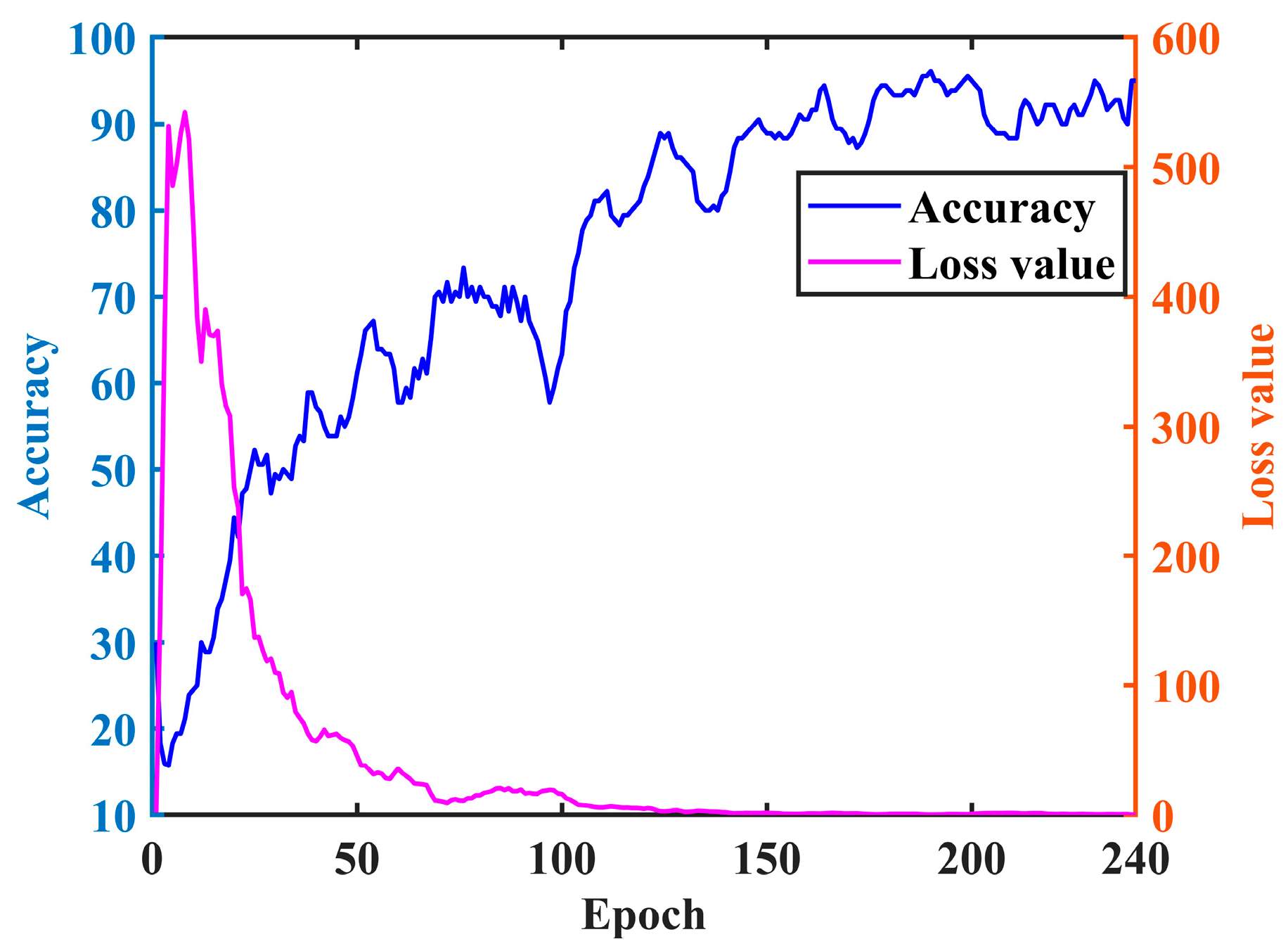
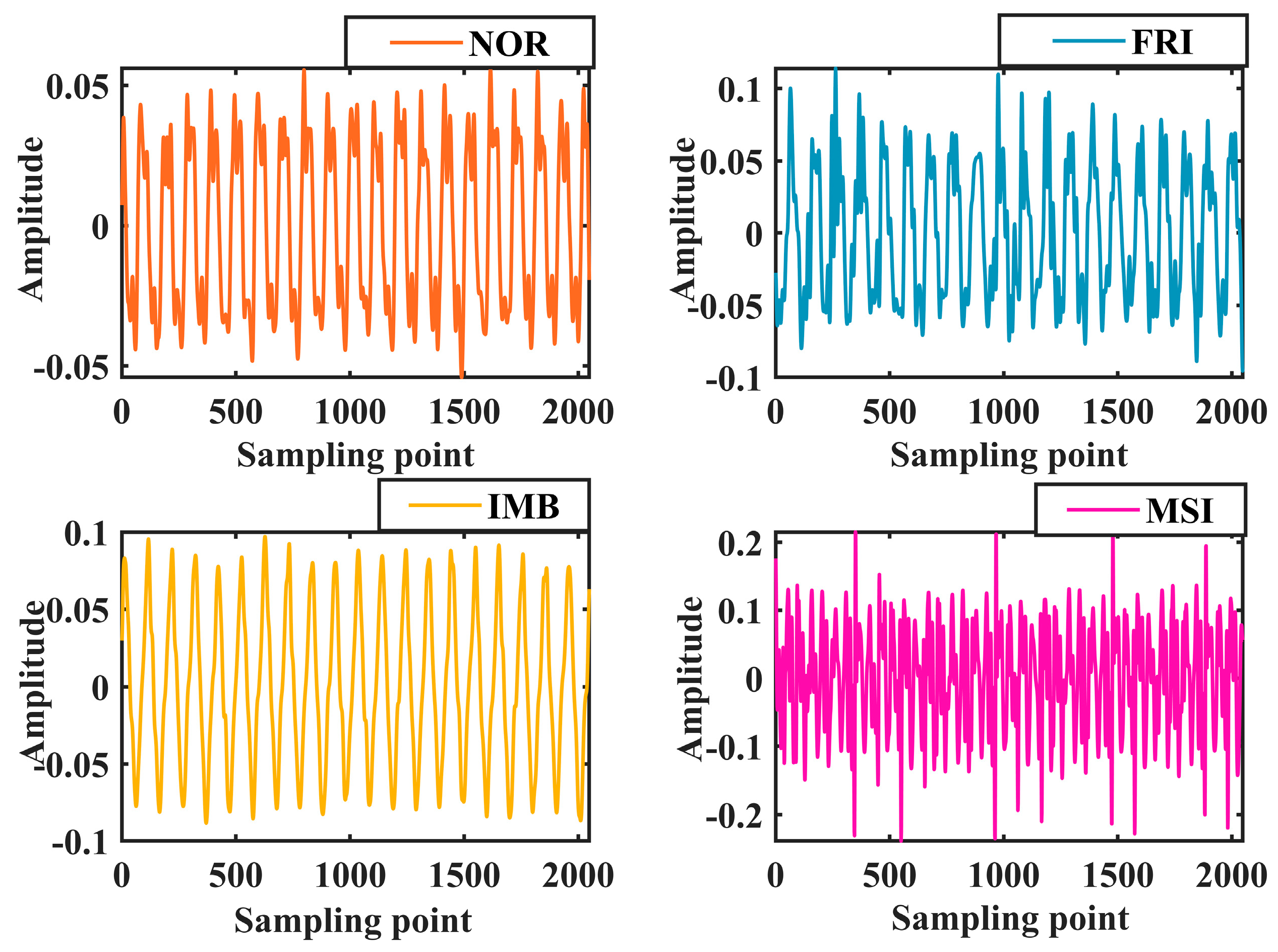
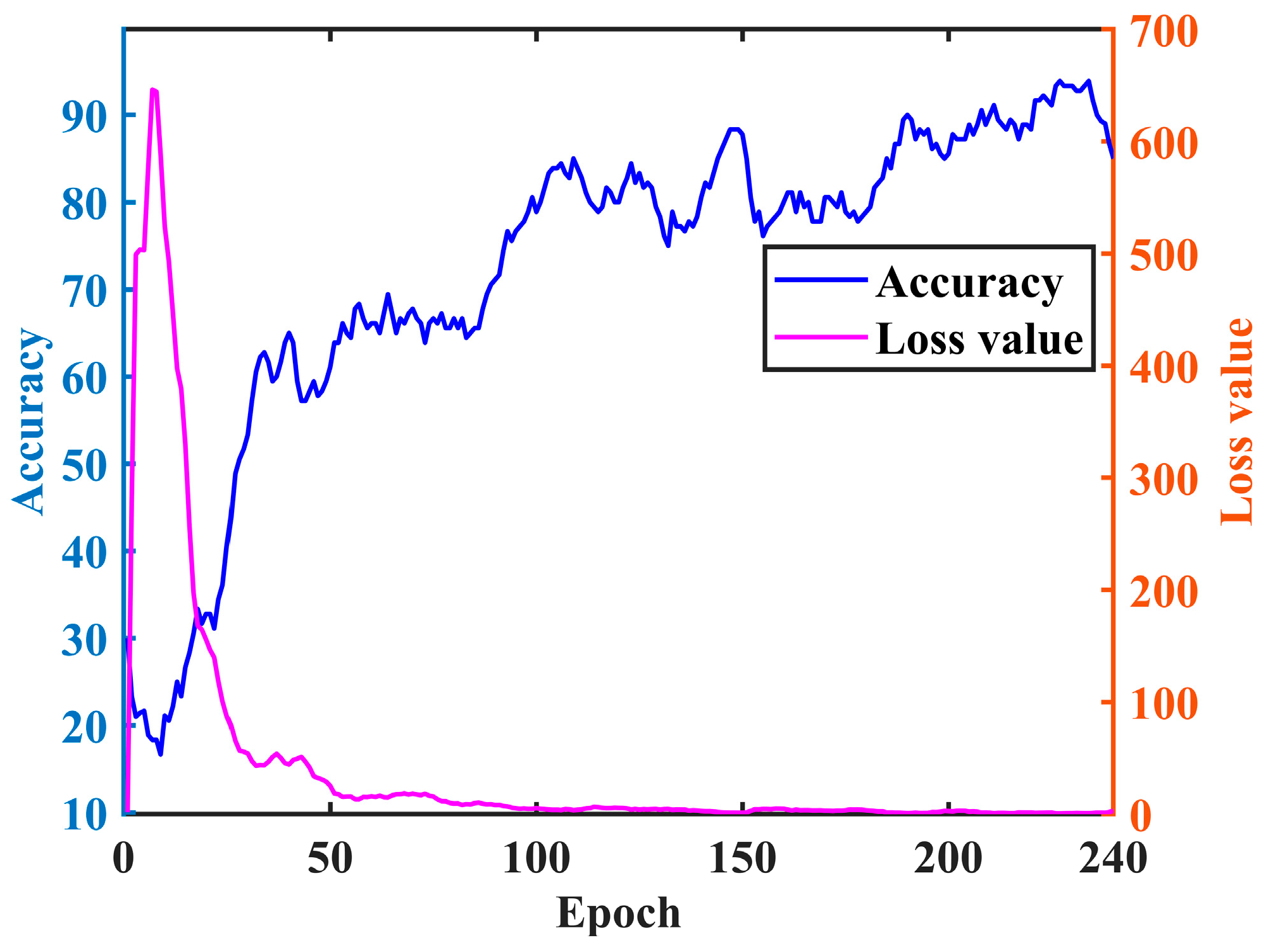
3. Simulation Verification 1
4. Simulation Verification 2
5. Conclusions
- (1)
- Converting one-dimensional time series signals into two-dimensional images helps extract richer and more distinguishable features.
- (2)
- ICOA can optimize the learning rate, convolution kernel size, and other parameters in the model, which makes the model more reasonable and effectively improves the fault recognition accuracy.
- (3)
- A double-branching design can make the CNN learn different weight values. The two branching high-dimensional features complement each other, which significantly enhances the deep spatial features. Replacing the SVM with the Softmax layer in the CNN and introducing the MSA to focus on feature reinforcement makes the model more robust to outliers and improves the accuracy of fault recognition.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Villeneuve, Y.; Séguin, S.; Chehri, A. AI-Based Scheduling Models, Optimization, and Prediction for Hydropower Generation: Opportunities, Issues, and Future Directions. Energies 2023, 16, 3335. [Google Scholar] [CrossRef]
- Piwowar, A.; Dzikuć, M. Water energy in Poland in the context of sustainable development. Energies 2022, 15, 7840. [Google Scholar] [CrossRef]
- Morcillo, J.D.; Angulo, F.; Franco, C.J. Analyzing the hydroelectricity variability on power markets from a system dynamics and dynamic systems perspective: Seasonality and ENSO phenomenon. Energies 2020, 13, 2381. [Google Scholar] [CrossRef]
- Kulpa, J.; Kopacz, M.; Stecuła, K.; Olczak, P. Pumped Storage Hydropower as a Part of Energy Storage Systems in Poland—Młoty Case Study. Energies 2024, 17, 1830. [Google Scholar] [CrossRef]
- Palma, L. Hybrid Approach for Detection and Diagnosis of Short-Circuit Faults in Power Transmission Lines. Energies 2024, 17, 2169. [Google Scholar] [CrossRef]
- Li, X.; Zeng, Y.; Qian, J.; Xiao, B.; Fei, N.; Dao, F.; Zou, Y. Modeling new nature of extraction and state identification of vibration shock signals from hydroelectric generating units using LCGSA optimized RBF combined with CEEMDAN sample entropy. IEEE Access 2024. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, Y.; Hu, W.; Chen, J.; Xiao, Z. Intelligent fault diagnosis of hydroelectric units based on radar maps and improved GoogleNet by depthwise separate convolution. Meas. Sci. Technol. 2023, 35, 025103. [Google Scholar] [CrossRef]
- Dao, F.; Zeng, Y.; Zou, Y.; Li, X.; Qian, J. Acoustic vibration approach for detecting faults in hydroelectric units: A review. Energies 2021, 14, 7840. [Google Scholar] [CrossRef]
- Xu, B.; Li, H.; Pang, W.; Chen, D.; Tian, Y.; Lei, X.; Gao, X.; Wu, C.; Patelli, E. Bayesian network approach to fault diagnosis of a hydroelectric generation system. Energy Sci. Eng. 2019, 7, 1669–1677. [Google Scholar] [CrossRef]
- Zheng, Y.; Pan, T.; Wang, H.; Ge, X.; Zhang, Y. Application Study of Improved EMD-ICA Denoising in Hidden Rubbing Diagnosis of Hydraulic Turbine Units. J. Vib. Shock 2017, 36, 235–240. [Google Scholar]
- Hu, X.; Xiao, Z.; Liu, D.; Jiang, W.; Liu, D. Fault Diagnosis of Hydroelectric Units Based on VMD-CNN. Hydropower Energy Sci. 2020, 38, 137–141. [Google Scholar]
- Fu, Z.; Yin, G.; Zhu, J.; Yuan, Y. Study on Degradation Prediction Method for Hydroelectric Units Based on EEMD and LSTM. J. Sol. Energy 2022, 43, 75–81. [Google Scholar]
- Chen, F.; Wang, B.; Zhou, D.; Zhao, Z.; Ding, C. Fault Diagnosis Method for Hydroelectric Unit Shaft System Integrating Improved Symbolic Dynamic Entropy and Random Configuration Network. J. Hydraul. Eng. 2022, 53, 1127–1139. [Google Scholar]
- Chen, F.; Wang, B.; Liu, T.; Zhang, W.; Gao, Y. Fault Diagnosis of Hydroelectric Units Based on Time-Shifted Multi-scale Attention Entropy and Random Forest. J. Hydraul. Eng. 2022, 53, 358–368+378. [Google Scholar]
- Hu, M.; Yang, X.; Huang, J.; Hu, J.; Wang, C. Fault Diagnosis Method Based on MTF-ResDSCNN Two-Dimensional Images. Mech. Transm. 2024, 48, 170–176. [Google Scholar]
- Li, G.; Ao, J.; Hu, J.; Liu, Y.; Huang, Z. Dual-source gramian angular field method and its application on fault diagnosis of drilling pump fluid end. Expert Syst. Appl. 2024, 237, 121521. [Google Scholar] [CrossRef]
- Cui, J.; Zhong, Q.; Zheng, S.; Peng, L.; Wen, J. A lightweight model for bearing fault diagnosis based on gramian angular field and coordinate attention. Machines 2022, 10, 282. [Google Scholar] [CrossRef]
- Ding, C.; Wang, Z.; Ding, Q.; Yuan, Z. Convolutional neural network based on fast Fourier transform and gramian angle field for fault identification of HVDC transmission line. Sustain. Energy Grids Netw. 2022, 32, 100888. [Google Scholar] [CrossRef]
- Amiri, A.F.; Kichou, S.; Oudira, H.; Silvestre, S. Fault detection and diagnosis of a photovoltaic system based on deep learning using the combination of a convolutional neural network (cnn) and bidirectional gated recurrent unit (Bi-GRU). Sustainability 2024, 16, 1012. [Google Scholar] [CrossRef]
- Hadroug, N.; Iratni, A.; Hafaifa, A.; Alili, B. Implementation of vibrations faults monitoring and detection on gas turbine system based on the support vector machine approach. J. Vib. Eng. Technol. 2024, 12, 2877–2902. [Google Scholar] [CrossRef]
- Li, Y.; Liu, W.; Huang, D. Image Denoising Network Model Integrating Multi-Head Attention Mechanism. Comput. Sci. 2023, 50, 326–333. [Google Scholar]
- Memarian, A.; Damarla, S.K.; Memarian, A.; Huang, B. Detection of poor controller tuning with Gramian Angular Field (GAF) and StackAutoencoder (SAE). Comput. Chem. Eng. 2024, 185, 108652. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovsky, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl. -Based Syst. 2022, 259, 110011. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, T.; Lai, Z. Gold Jackal Optimization Algorithm Improved by Hybrid Strategy. Comput. Eng. Appl. 2024, 60, 99–112. [Google Scholar]
- Goumiri, S.; Benboudjema, D.; Pieczynski, W. A new hybrid model of convolutional neural networks and hidden Markov chains for image classification. Neural Comput. Appl. 2023, 35, 17987–18002. [Google Scholar] [CrossRef] [PubMed]
- Ghazimoghadam, S.; Hosseinzadeh, S.A.A. A novel unsupervised deep learning approach for vibration-based damage diagnosis using a multi-head self-attention LSTM autoencoder. Measurement 2024, 229, 114410. [Google Scholar] [CrossRef]
- Dao, F.; Zeng, Y.; Qian, J. Fault diagnosis of hydro-turbine via the incorporation of bayesian algorithm optimized CNN-LSTM neural network. Energy 2024, 290, 130326. [Google Scholar] [CrossRef]
- Xiao, B.; Zeng, Y.; Dao, F.; Zou, Y.; Li, X. EEMD-CNN Integrated Hydropower Unit Rubbing Fault Acoustic Fingerprint Recognition Model. J. Hydroelectr. Eng. 2024, 43, 59–69. [Google Scholar]




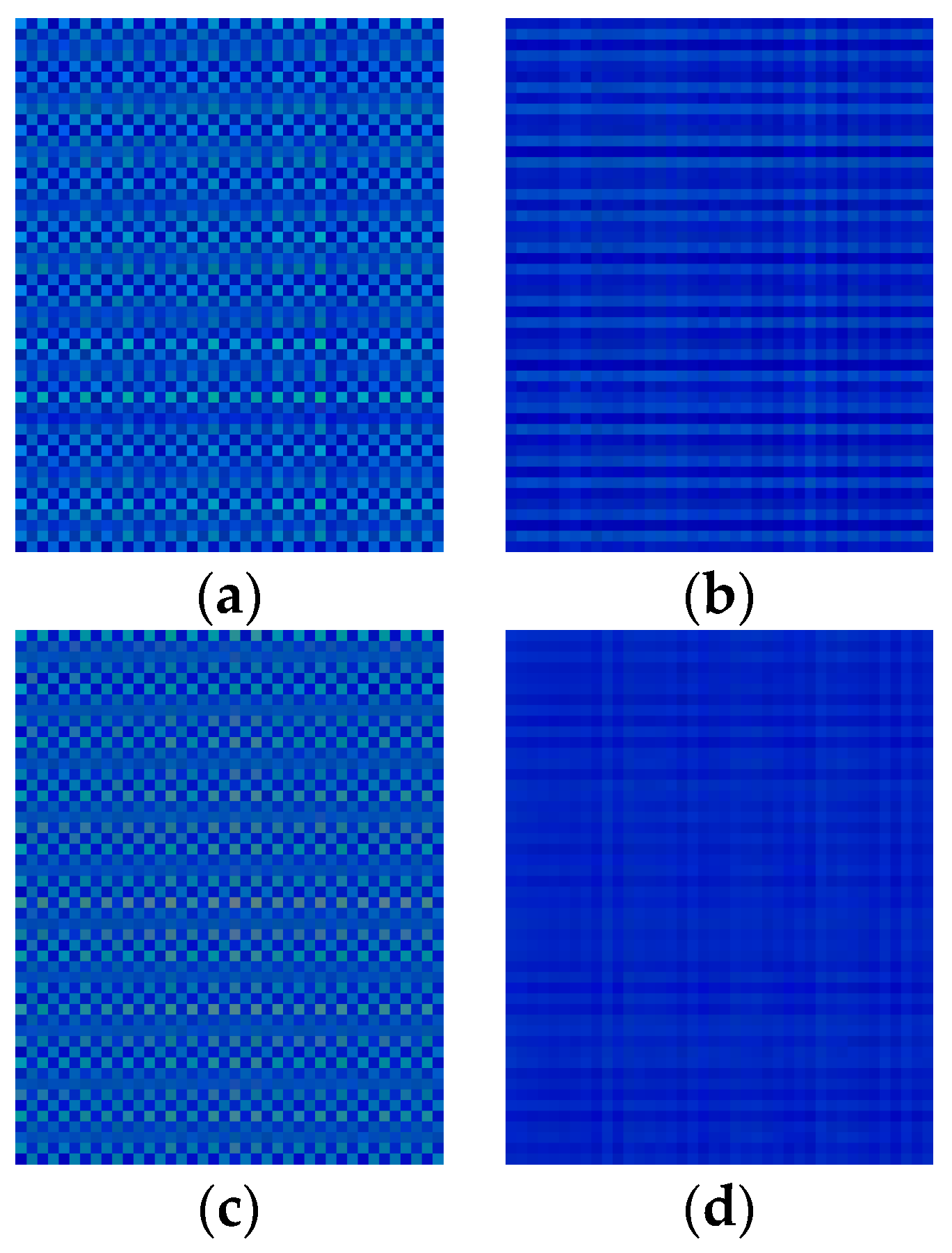


| Parameter Name | Specifications | Unit |
|---|---|---|
| sampling rate | 48 | kHz |
| measurement frequency range | 10–20,000 | Hz |
| standard measurement range | 25–130 | dBA |
| measure dynamic range | ≥110 | dBA |
| communication interface | USB Audio + USB HID | |
| size | 25 × 115 | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhang, J.; Xiao, B.; Zeng, Y.; Lv, S.; Qian, J.; Du, Z. Fault Diagnosis of Hydropower Units Based on Gramian Angular Summation Field and Parallel CNN. Energies 2024, 17, 3084. https://doi.org/10.3390/en17133084
Li X, Zhang J, Xiao B, Zeng Y, Lv S, Qian J, Du Z. Fault Diagnosis of Hydropower Units Based on Gramian Angular Summation Field and Parallel CNN. Energies. 2024; 17(13):3084. https://doi.org/10.3390/en17133084
Chicago/Turabian StyleLi, Xiang, Jianbo Zhang, Boyi Xiao, Yun Zeng, Shunli Lv, Jing Qian, and Zhaorui Du. 2024. "Fault Diagnosis of Hydropower Units Based on Gramian Angular Summation Field and Parallel CNN" Energies 17, no. 13: 3084. https://doi.org/10.3390/en17133084
APA StyleLi, X., Zhang, J., Xiao, B., Zeng, Y., Lv, S., Qian, J., & Du, Z. (2024). Fault Diagnosis of Hydropower Units Based on Gramian Angular Summation Field and Parallel CNN. Energies, 17(13), 3084. https://doi.org/10.3390/en17133084









