Multi-Objective Optimization towards Heat Dissipation Performance of the New Tesla Valve Channels with Partitions in a Liquid-Cooled Plate
Abstract
1. Introduction
2. Physical Model and Numerical Methods
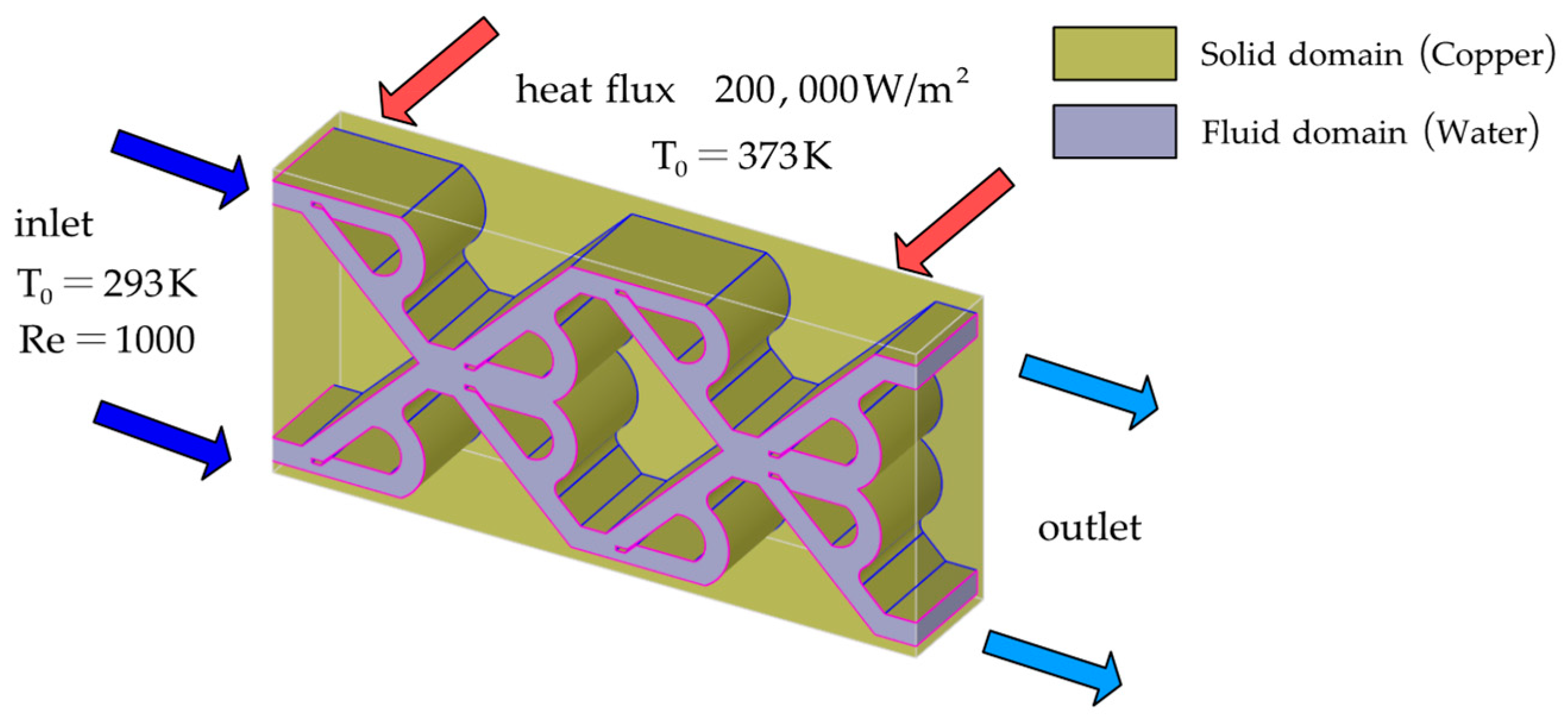
2.1. Physical Model
2.2. Numerical Methods and Data Reduction
2.3. Boundary Conditions and Assumptions
- (a)
- Gravity is negligible;
- (b)
- The working fluids and solids are incompressible;
- (c)
- Radiant heat transfer is negligible;
- (d)
- The material is thermophysically stable;
- (e)
- Heat source surface thickness of 1 mm.
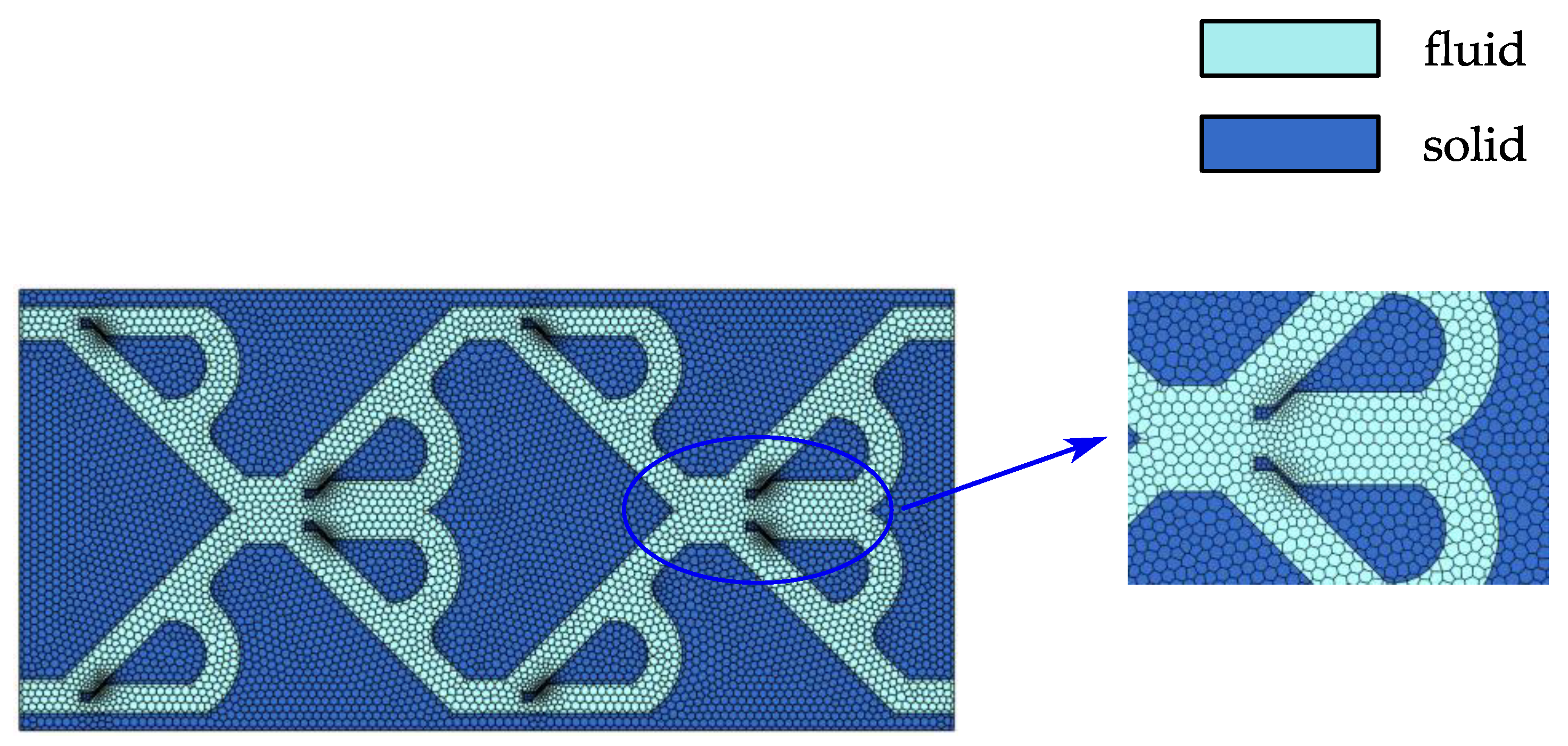
2.4. Grid Independence and Validation of Results
3. Optimization Methods
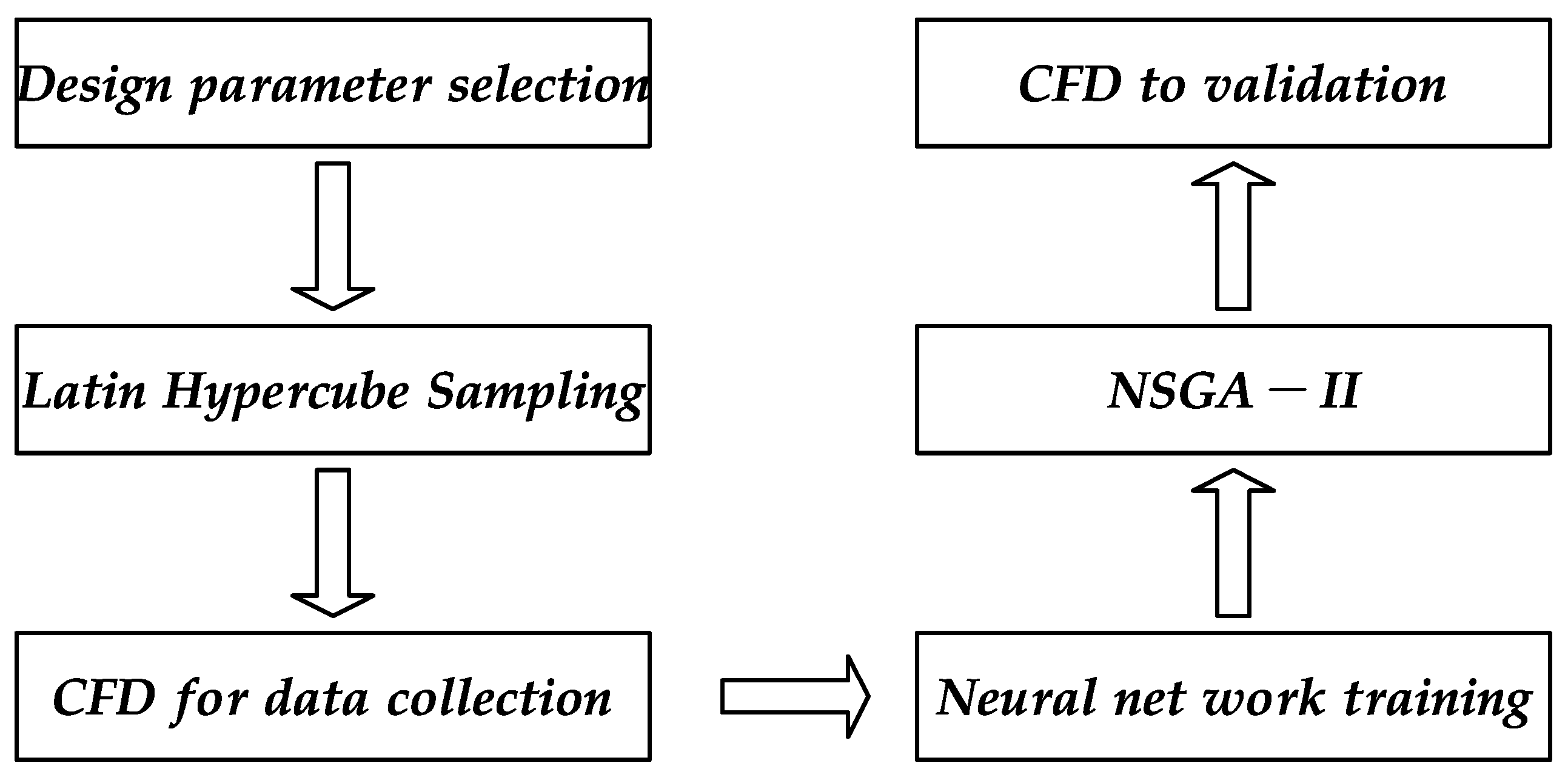
3.1. Design Parameter Selection and Optimization Problem Formulation
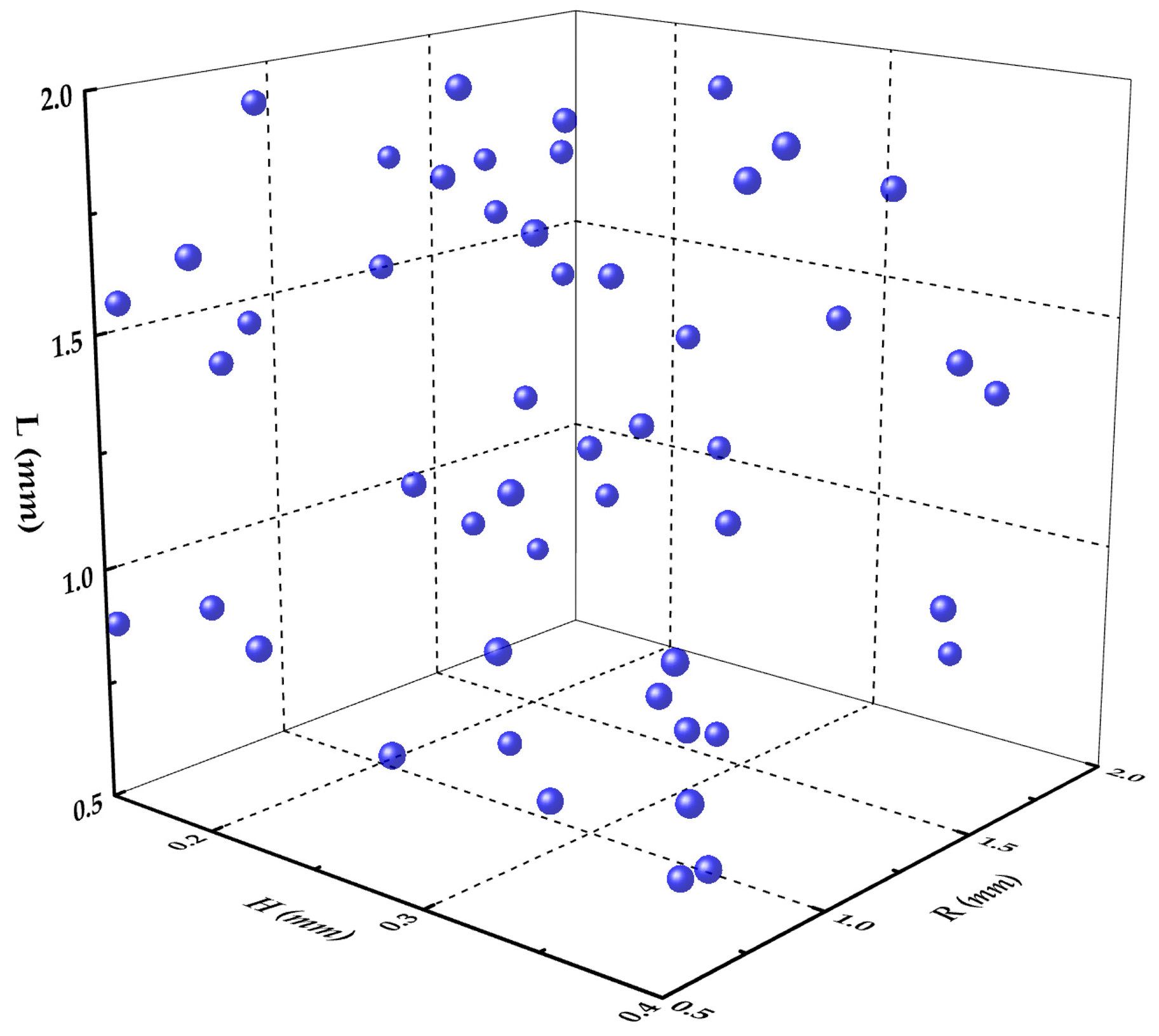
3.2. Design of Experiments
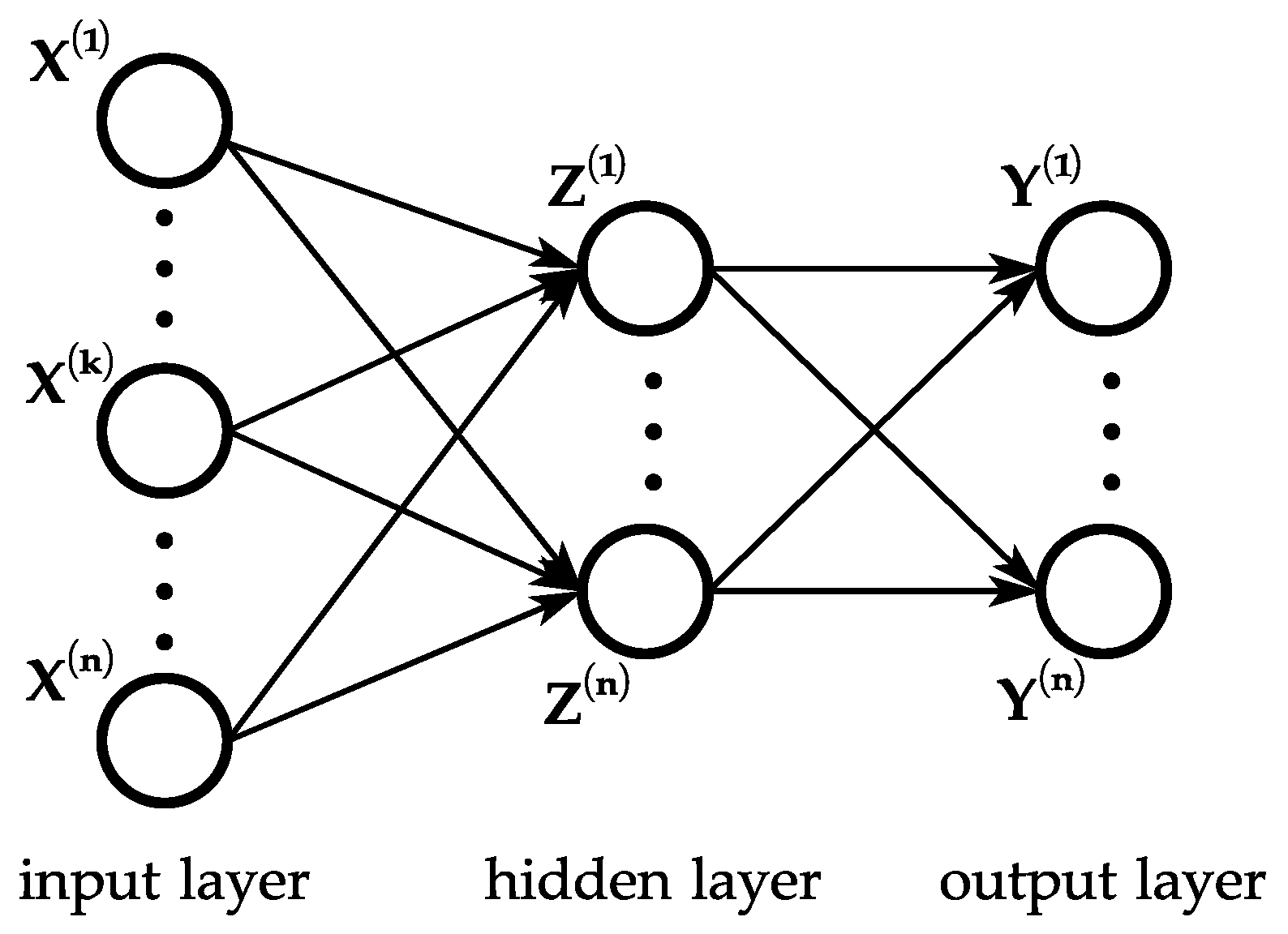
3.3. Neural Network Fitting Model
3.4. Multi-Objective Genetic Algorithm
4. Results and Analysis
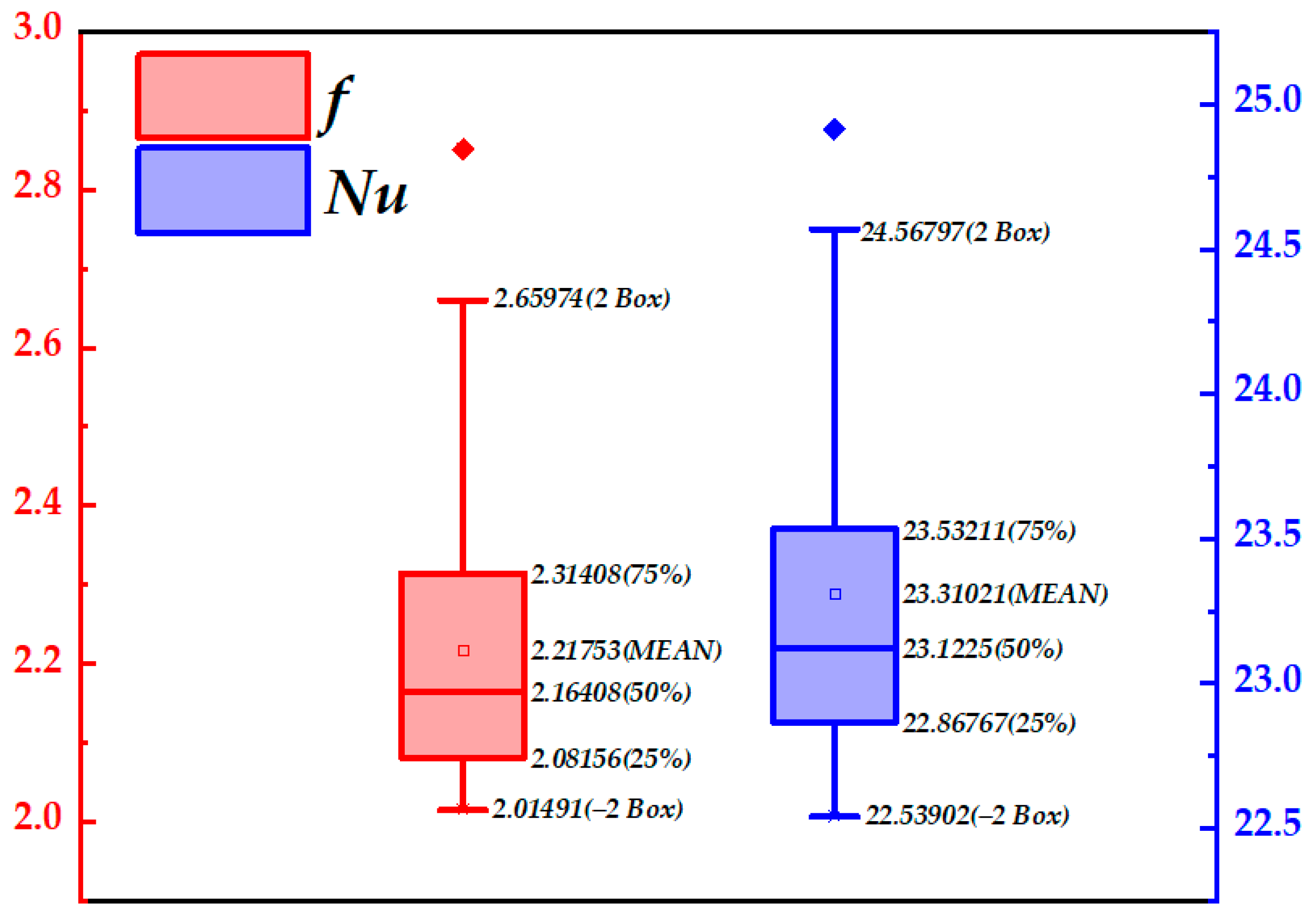
4.1. Dataset Quality Analysis
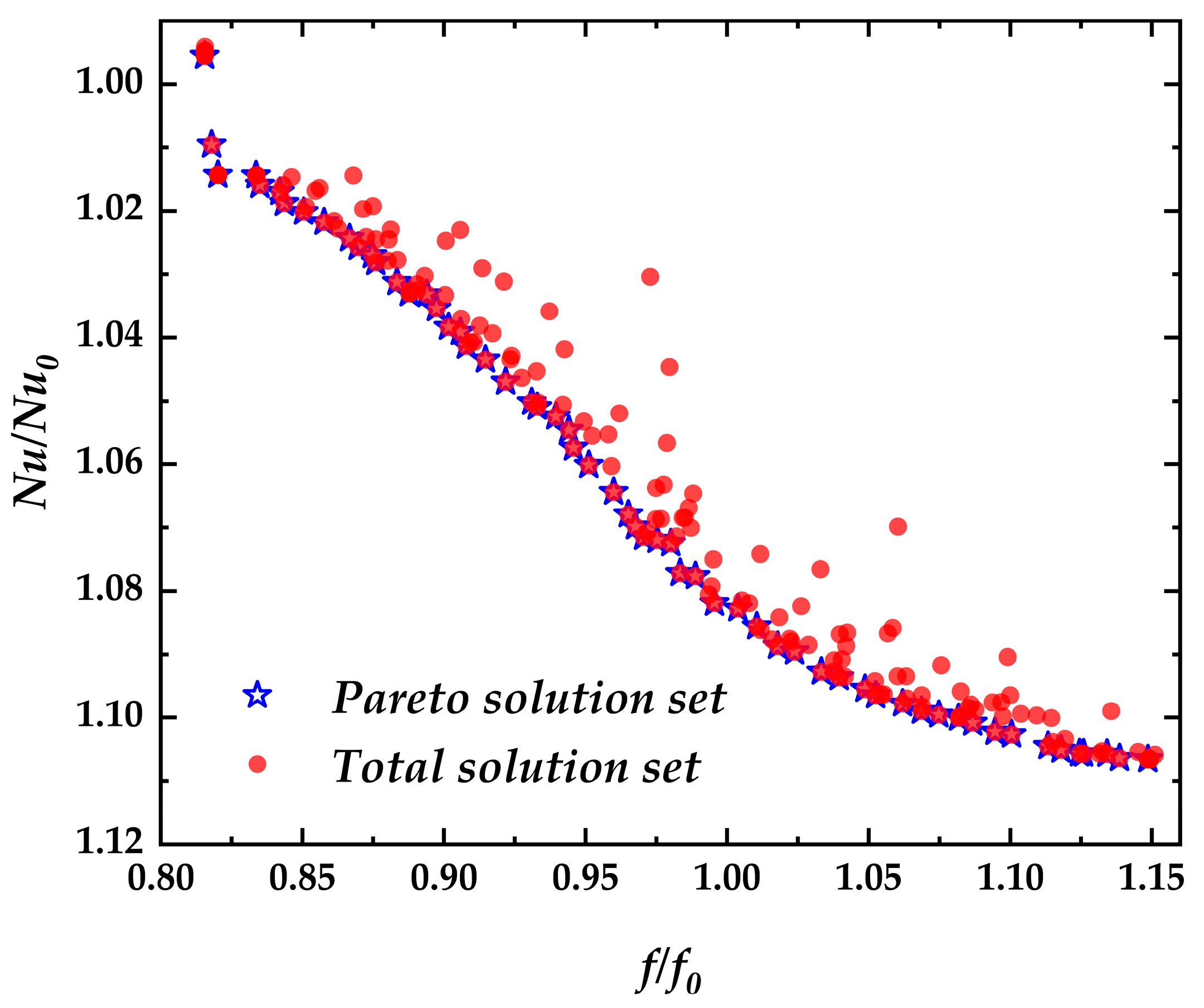
4.2. Optimization Results Analysis
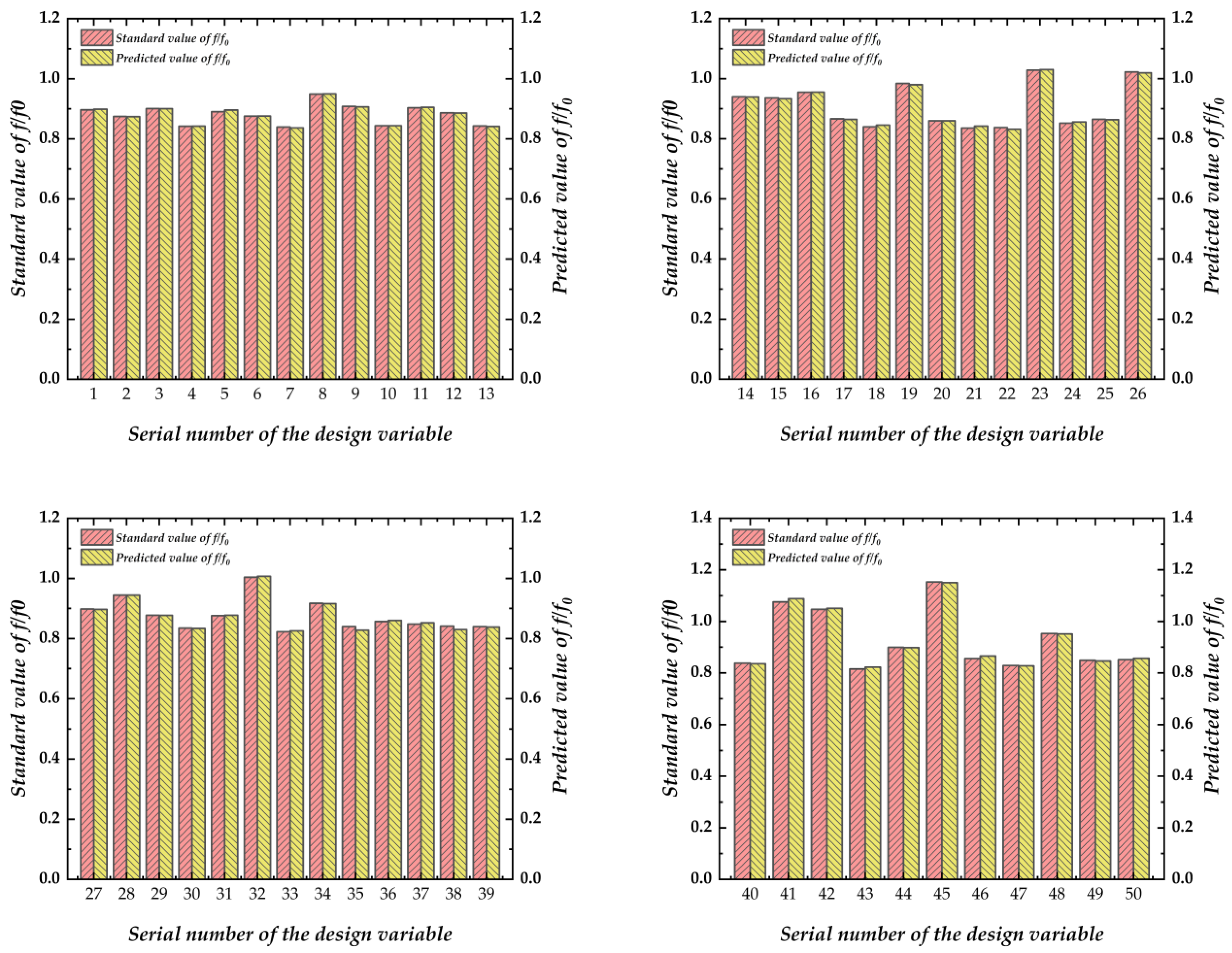
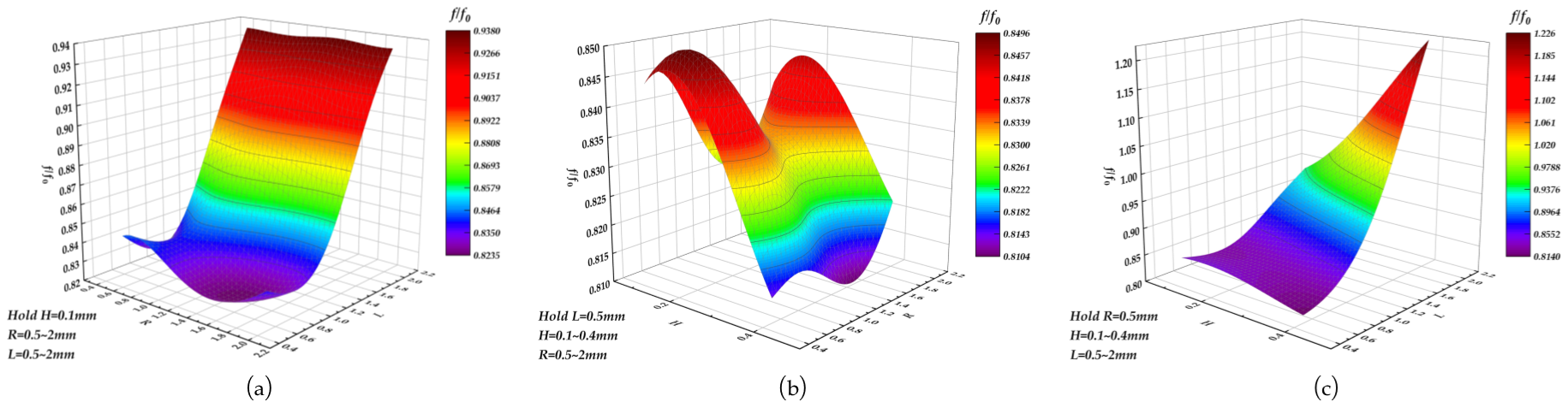
4.3. Parameter Sensitivity Analysis
4.4. Comparative Performance Analysis of the Optimal and Reference Structures
5. Conclusions
- (1)
- The accuracy of the prediction model constructed using the neural network is demonstrably high, with R-squared values of 0.9971 and 0.9966 when the target variable is Nu/Nu0 and f/f0, respectively.
- (2)
- The initial 10 optimal solutions identified by the NSGA-II were found to be highly accurate following simulation validation, with a maximum error of no more than 1% for both objective variables.
- (3)
- After sensitivity analysis, it is found that L is significant for both target variables, followed by H and finally R. For the design of this structure, smaller values of L and H are recommended, and for R, a value near 1.3 is recommended.
- (4)
- Compared with the reference structure, the average temperature of the first two-thirds of the solid domain is reduced by 1.8 K, but the temperature of the last one-third of the solid domain is not much different. The inlet and outlet pressure drop of the optimal structure is only 300 Pa, which is reduced by 160 Pa compared with the reference structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| BTMS | battery thermal management system | |
| PCM | phase change material | |
| RBF | radial basis function | |
| SVR | support vector regression | |
| ANN | artificial neural network | |
| RF | random forest | |
| Nu | Nusselt number | |
| Nu0 | the Nusselt number of the reference structure | |
| f | Fanning’s factor | |
| f0 | the Fanning friction factor of the reference structure | |
| Re | Reynolds number | |
| RNG | renormalization group | |
| k | turbulent kinetic energy equation | |
| ε | diffusion equation | |
| SIMPLEC | semi-implicit method for pressure linked equation | |
| L | the length of the partition | |
| H | the height of the partition | |
| R | the radius of the fillet | |
| LHS | Latin hypercube sampling | |
| MLP | multilayer perceptron | |
| NSGA-II | multi-objective genetic algorithm | |
| R2 | determination coefficients | |
References
- Akbarzadeh, M.; Jaguemont, J.; Kalogiannis, T.; Karimi, D.; He, J.C.; Jin, L.; Xie, P.; Van Mierlo, J.; Berecibar, M. A novel liquid cooling plate concept for thermal management of lithium-ion batteries in electric vehicles. Energ. Convers. Manag. 2021, 231, 113862. [Google Scholar] [CrossRef]
- Zhang, X.H.; Li, Z.; Luo, L.A.; Fan, Y.L.; Du, Z.Y. A review on thermal management of lithium-ion batteries for electric vehicles. Energy 2022, 238, 121652. [Google Scholar] [CrossRef]
- Sheng, L.; Su, L.; Zhang, H.; Li, K.; Fang, Y.D.; Ye, W.; Fang, Y. Numerical investigation on a lithium ion battery thermal management utilizing a serpentine-channel liquid cooling plate exchanger. Int. J. Heat. Mass. Transf. 2019, 141, 658–668. [Google Scholar] [CrossRef]
- Wu, W.X.; Wang, S.F.; Wu, W.; Chen, K.; Hong, S.H.; Lai, Y.X. A critical review of battery thermal performance and liquid based battery thermal management. Energ. Convers. Manag. 2019, 182, 262–281. [Google Scholar] [CrossRef]
- Fayaz, H.; Afzal, A.; Samee, A.D.M.; Soudagar, M.E.M.; Akram, N.; Mujtaba, M.A.; Jilte, R.D.; Islam, M.T.; Agbulut, Ü.; Saleel, C.A. Optimization of Thermal and Structural Design in Lithium-Ion Batteries to Obtain Energy Efficient Battery Thermal Management System (BTMS): A Critical Review. Arch. Comput. Methods Eng. 2022, 29, 129–194. [Google Scholar] [CrossRef] [PubMed]
- Akbarzadeh, M.; Kalogiannis, T.; Jaguemont, J.; Jin, L.; Behi, H.; Karimi, D.; Beheshti, H.; Van Mierlo, J.; Berecibar, M. A comparative study between air cooling and liquid cooling thermal management systems for a high-energy lithium-ion battery module. Appl. Therm. Eng. 2021, 198, 117503. [Google Scholar] [CrossRef]
- Saechan, P.; Dhuchakallaya, I. Numerical study on the air-cooled thermal management of Lithium-ion battery pack for electrical vehicles. Energy Rep. 2022, 8, 1264–1270. [Google Scholar] [CrossRef]
- Luo, J.; Zou, D.Q.; Wang, Y.S.; Wang, S.; Huang, L. Battery thermal management systems (BTMs) based on phase change material (PCM): A comprehensive review. Chem. Eng. J. 2022, 430, 132741. [Google Scholar] [CrossRef]
- Tang, X.W.; Guo, Q.; Li, M.; Wei, C.H.; Pan, Z.Y.; Wang, Y.Q. Performance analysis on liquid-cooled battery thermal management for electric vehicles based on machine learning. J. Power Sources 2021, 494, 229727. [Google Scholar] [CrossRef]
- Farhan, M.; Amjad, M.; Tahir, Z.U.; Anwar, Z.; Arslan, M.; Mujtaba, A.; Riaz, F.; Imran, S.; Razzaq, L.; Ali, M.; et al. Design and Analysis of Liquid Cooling Plates for Different Flow Channel Configurations. Therm. Sci. 2022, 26, 1463–1475. [Google Scholar] [CrossRef]
- Jarrett, A.; Kim, I.Y. Design optimization of electric vehicle battery cooling plates for thermal performance. J. Power Sources 2011, 196, 10359–10368. [Google Scholar] [CrossRef]
- Jarrett, A.; Kim, I.Y. Influence of operating conditions on the optimum design of electric vehicle battery cooling plates. J. Power Sources 2014, 245, 644–655. [Google Scholar] [CrossRef]
- Jin, L.W.; Lee, P.S.; Kong, X.X.; Fan, Y.; Chou, S.K. Ultra-thin minichannel LCP for EV battery thermal management. Appl. Energ. 2014, 113, 1786–1794. [Google Scholar] [CrossRef]
- Guo, R.; Li, L. Heat dissipation analysis and optimization of lithium-ion batteries with a novel parallel-spiral serpentine channel liquid cooling plate. Int. J. Heat. Mass. Transf. 2022, 189, 122706. [Google Scholar] [CrossRef]
- Chen, S.Q.; Peng, X.B.; Bao, N.S.; Garg, A. A comprehensive analysis and optimization process for an integrated liquid cooling plate for a prismatic lithium-ion battery module. Appl. Therm. Eng. 2019, 156, 324–339. [Google Scholar] [CrossRef]
- Mo, X.B.; Zhi, H.; Xiao, Y.Z.; Hua, H.Y.; He, L. Topology optimization of cooling plates for battery thermal management. Int. J. Heat. Mass. Transf. 2021, 178, 121612. [Google Scholar] [CrossRef]
- E, J.Q.; Han, D.D.; Qiu, A.; Zhu, H.; Deng, Y.W.; Chen, J.W.; Zhao, X.H.; Zuo, W.; Wang, H.C.; Chen, J.M.; et al. Orthogonal experimental design of liquid-cooling structure on the cooling effect of a liquid-cooled battery thermal management system. Appl. Therm. Eng. 2018, 132, 508–520. [Google Scholar] [CrossRef]
- Fan, Y.W.; Wang, Z.H.; Fu, T. Multi-objective optimization design of lithium-ion battery liquid cooling plate with double-layered dendritic channels. Appl. Therm. Eng. 2021, 199, 117541. [Google Scholar] [CrossRef]
- Yuan, J.; Gu, Z.; Bao, J.; Yang, T.; Li, H.; Wang, Y.; Pei, L.; Jiang, H.; Chen, L.; Yuan, C. Structure optimization design and performance analysis of liquid cooling plate for power battery. J. Energy Storage 2024, 87, 111517. [Google Scholar] [CrossRef]
- Shang, Z.Z.; Qi, H.Z.; Liu, X.T.; Ouyang, C.Z.; Wang, Y.S. Structural optimization of lithium-ion battery for improving thermal performance based on a liquid cooling system. Int. J. Heat. Mass. Transf. 2019, 130, 33–41. [Google Scholar] [CrossRef]
- Deng, T.; Ran, Y.; Yin, Y.L.; Chen, X.; Liu, P. Multi-objective optimization design of double-layered reverting cooling plate for lithium-ion batteries. Int. J. Heat. Mass. Transf. 2019, 143, 118580. [Google Scholar] [CrossRef]
- Kudela, J.; Matousek, R. Recent advances and applications of surrogate models for finite element method computations: A review. Soft Comput. 2022, 26, 13709–13733. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Kim, K.M.; Hurley, P.; Duarte, J.P. High-resolution prediction of quenching behavior using machine learning based on optical fiber temperature measurement. Int. J. Heat. Mass. Transf. 2022, 184, 122338. [Google Scholar] [CrossRef]
- Mudawar, I.; Darges, S.J.; Devahdhanush, V.S. Prediction technique for flow boiling heat transfer and critical heat flux in both microgravity and Earth gravity via artificial neural networks (ANNs). Int. J. Heat. Mass. Transf. 2024, 220, 124998. [Google Scholar] [CrossRef]
- Mann, G.W.; Eckels, S. Multi-objective heat transfer optimization of 2D helical micro-fins using NSGA-II. Int. J. Heat. Mass. Transf. 2019, 132, 1250–1261. [Google Scholar] [CrossRef]
- Gosselin, L.; Tye-Gingras, M.; Mathieu-Potvin, F. Review of utilization of genetic algorithms in heat transfer problems. Int. J. Heat. Mass. Transf. 2009, 52, 2169–2188. [Google Scholar] [CrossRef]
- Pan, L.S.; Yao, Z.K.; Yao, W.; Wei, X.L. Multi-objective optimization on bionic fractal structure for heat exchanging of two fluids by genetic algorithm. Int. J. Heat. Mass. Transf. 2023, 212, 124298. [Google Scholar] [CrossRef]
- Sun, W.; Wen, P.F.; Zhu, S.J.; Zhai, P.C. Geometrical Optimization of Segmented Thermoelectric Generators (TEGs) Based on Neural Network and Multi-Objective Genetic Algorithm. Energies 2024, 17, 2094. [Google Scholar] [CrossRef]
- Yildizeli, A.; Cadirci, S. Multi objective optimization of a micro-channel heat sink through genetic algorithm. Int. J. Heat. Mass. Transf. 2020, 14, 1188476. [Google Scholar] [CrossRef]
- Nikola, T. Valvular Conduit. U.S. Patent No. 1,329,559, 3 February 1920. [Google Scholar]
- Porwal, P.R.; Thompson, S.M.; Walters, D.K.; Jamal, T. Heat transfer and fluid flow characteristics in multistaged Tesla valves. Numer. Heat. Transf. Part. A Appl. 2018, 73, 347–365. [Google Scholar] [CrossRef]
- Li, K.; Wang, S.; Zong, C.; Liu, Y.; Song, X. Diodicity Optimization of Tesla-Type Check Valve Based on Surrogate Modeling Techniques. In Advances in Mechanical Design; Mechanisms and Machine Science; Springer: Singapore, 2022; pp. 1225–1243. [Google Scholar]
- de Vries, S.F.; Florea, D.; Homburg, F.G.A.; Frijns, A.J.H. Design and operation of a Tesla-type valve for pulsating heat pipes. Int. J. Heat. Mass. Transf. 2017, 105, 1–11. [Google Scholar] [CrossRef]
- Monika, K.; Chakraborty, C.; Roy, S.; Sujith, R.; Datta, S.P. A numerical analysis on multi-stage Tesla valve based cold plate for cooling of pouch type Li-ion batteries. Int. J. Heat. Mass. Transf. 2021, 177, 121560. [Google Scholar] [CrossRef]
- Du, G.; Alsenani, T.R.; Kumar, J.; Alkhalaf, S.; Alkhalifah, T.; Alturise, F.; Almujibah, H.; Znaidia, S.; Deifalla, A. Improving thermal and hydraulic performances through artificial neural networks: An optimization approach for Tesla valve geometrical parameters. Case Stud. Therm. Eng. 2023, 52, 103670. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, L.; Gao, J.; Xi, L.; Ruan, Q.; Li, Y. Multi-Objective Optimization of Parameters of Channels with Staggered Frustum of a Cone Based on Response Surface Methodology. Energies 2022, 15, 1240. [Google Scholar] [CrossRef]
- Zeng, M.; Zhang, G.P.; Li, Y.; Niu, Y.Z.; Ma, Y.; Wang, Q.W. Geometrical Parametric Analysis of Flow and Heat Transfer in the Shell Side of a Spiral-Wound Heat Exchanger. Heat. Transf. Eng. 2015, 36, 790–805. [Google Scholar] [CrossRef]
- Ni, T.; Si, J.; Li, F.; Pan, C.; Li, D.; Pan, M.; Guan, W. Performance analysis on the liquid cooling plate with the new Tesla valve capillary channel based on the fluid solid coupling simulation. Appl. Therm. Eng. 2023, 232, 120977. [Google Scholar] [CrossRef]
- Truong, T.Q.; Nguyen, N.T. Simulation and optimization of Tesla valves. Nanotech 2003, 1, 178–181. [Google Scholar]






| Material | Cp (J/kg·K) | |||
|---|---|---|---|---|
| Copper | 8978 | 381 | 387.6 | |
| Water | 998.2 | 4182 | 0.6 | 0.001003 |
| H | R | L | Predicted f/f0 | Predicted Nu/Nu0 | Standard f/f0 | Standard Nu/Nu0 | Error f/f0 | Error Nu/Nu0 |
|---|---|---|---|---|---|---|---|---|
| 0.250 | 1.253 | 0.768 | 0.836 | 1.016 | 0.836 | 1.009 | 0.00% | 0.69% |
| 0.228 | 1.285 | 0.934 | 0.842 | 1.017 | 0.838 | 1.013 | 0.48% | 0.39% |
| 0.215 | 1.244 | 0.995 | 0.846 | 1.019 | 0.843 | 1.015 | 0.36% | 0.39% |
| 0.222 | 1.517 | 1.717 | 0.957 | 1.061 | 0.963 | 1.061 | 0.62% | 0.00% |
| 0.229 | 1.619 | 1.740 | 0.966 | 1.064 | 0.971 | 1.063 | 0.51% | 0.09% |
| 0.229 | 1.723 | 1.760 | 0.970 | 1.065 | 0.975 | 1.065 | 0.51% | 0.00% |
| 0.236 | 1.725 | 1.611 | 0.940 | 1.054 | 0.945 | 1.052 | 0.53% | 0.19% |
| 0.232 | 1.492 | 1.675 | 0.952 | 1.059 | 0.959 | 1.059 | 0.73% | 0.00% |
| 0.232 | 1.447 | 1.631 | 0.942 | 1.055 | 0.949 | 1.054 | 0.74% | 0.09% |
| 0.234 | 1.773 | 1.572 | 0.930 | 1.050 | 0.933 | 1.048 | 0.32% | 0.19% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Lin, H.; Hu, N.; Xi, L.; Li, Y.; Gao, J. Multi-Objective Optimization towards Heat Dissipation Performance of the New Tesla Valve Channels with Partitions in a Liquid-Cooled Plate. Energies 2024, 17, 3106. https://doi.org/10.3390/en17133106
Xu L, Lin H, Hu N, Xi L, Li Y, Gao J. Multi-Objective Optimization towards Heat Dissipation Performance of the New Tesla Valve Channels with Partitions in a Liquid-Cooled Plate. Energies. 2024; 17(13):3106. https://doi.org/10.3390/en17133106
Chicago/Turabian StyleXu, Liang, Hongwei Lin, Naiyuan Hu, Lei Xi, Yunlong Li, and Jianmin Gao. 2024. "Multi-Objective Optimization towards Heat Dissipation Performance of the New Tesla Valve Channels with Partitions in a Liquid-Cooled Plate" Energies 17, no. 13: 3106. https://doi.org/10.3390/en17133106
APA StyleXu, L., Lin, H., Hu, N., Xi, L., Li, Y., & Gao, J. (2024). Multi-Objective Optimization towards Heat Dissipation Performance of the New Tesla Valve Channels with Partitions in a Liquid-Cooled Plate. Energies, 17(13), 3106. https://doi.org/10.3390/en17133106







