Inverter Multi-Machine Grid Integration Resonance Suppression Strategy by Active Damping
Abstract
:1. Introduction
2. Literature Review
3. Research Methodology
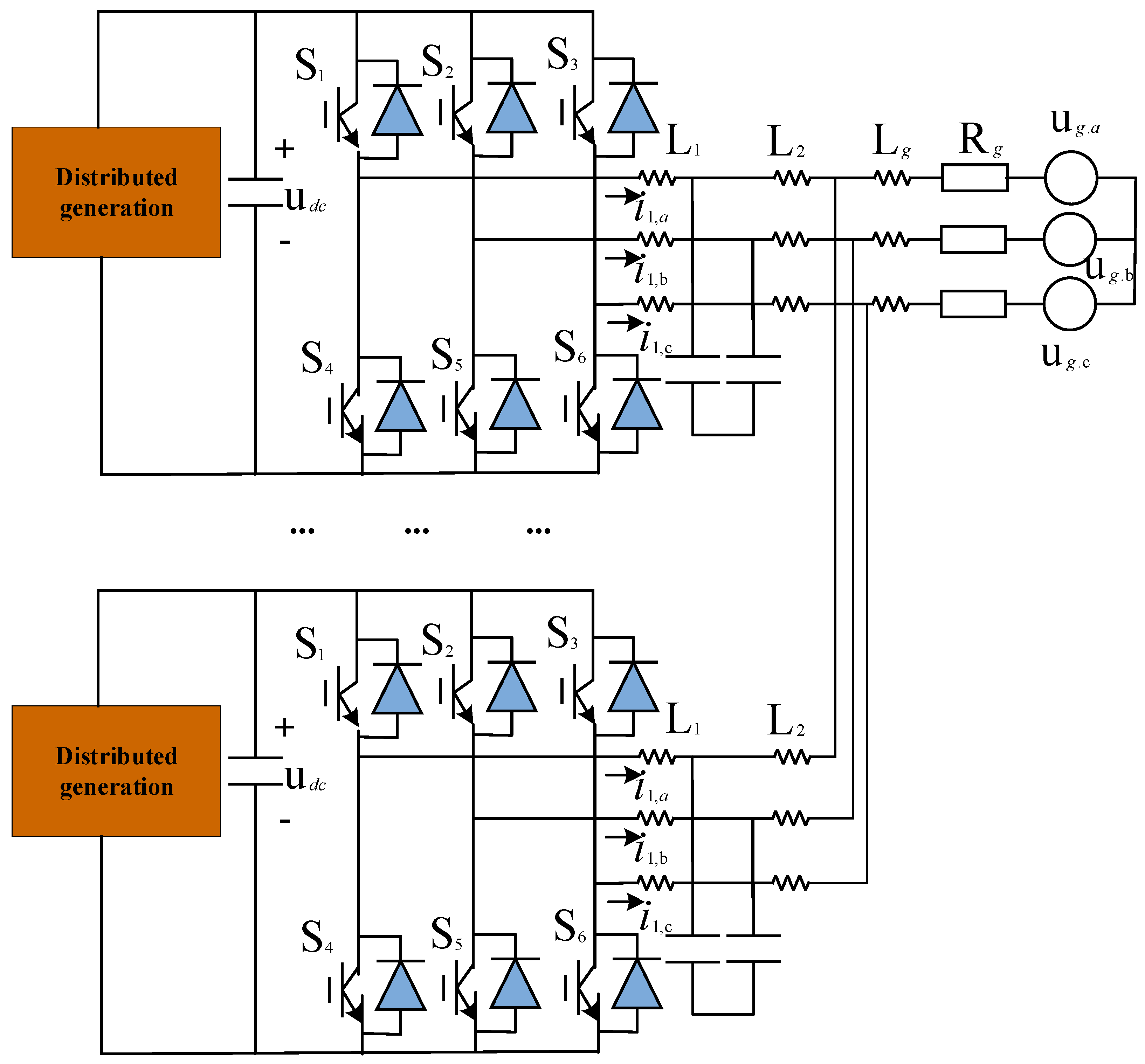
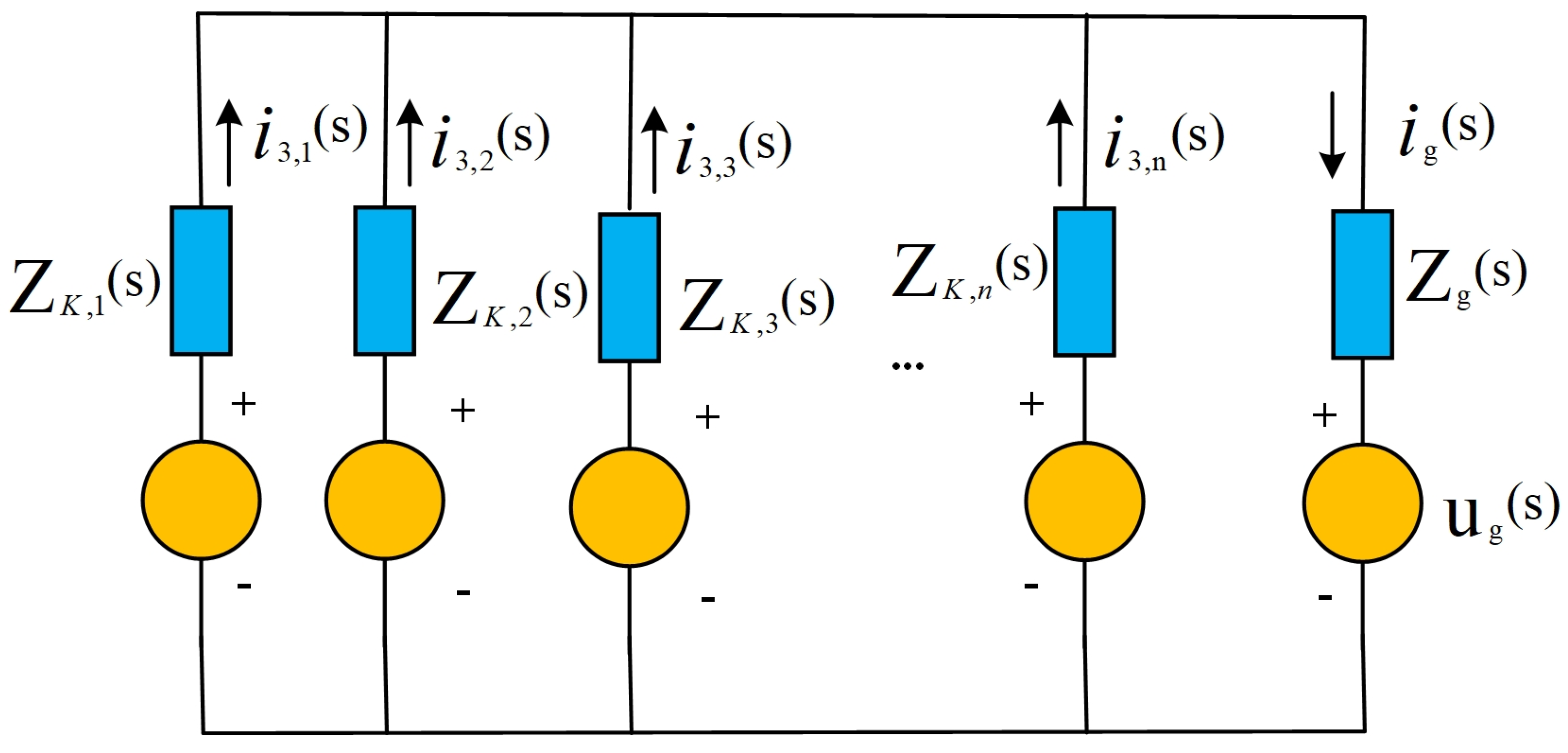
3.1. Establishment of System Model
3.2. Active Damping Strategy Design
3.3. Simulation Environment Construction
4. Results and Discussion
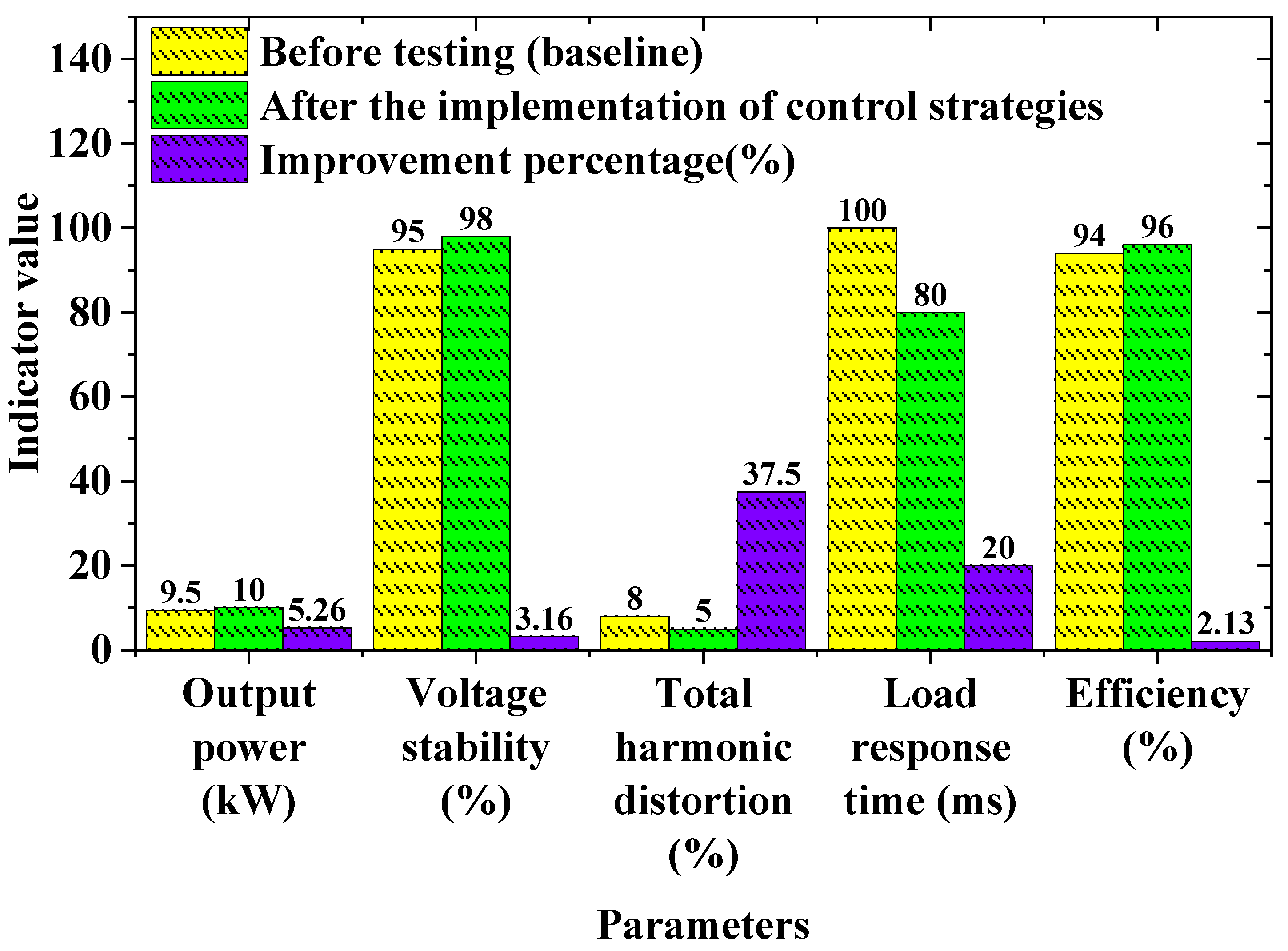
4.1. Basic Performance Evaluation
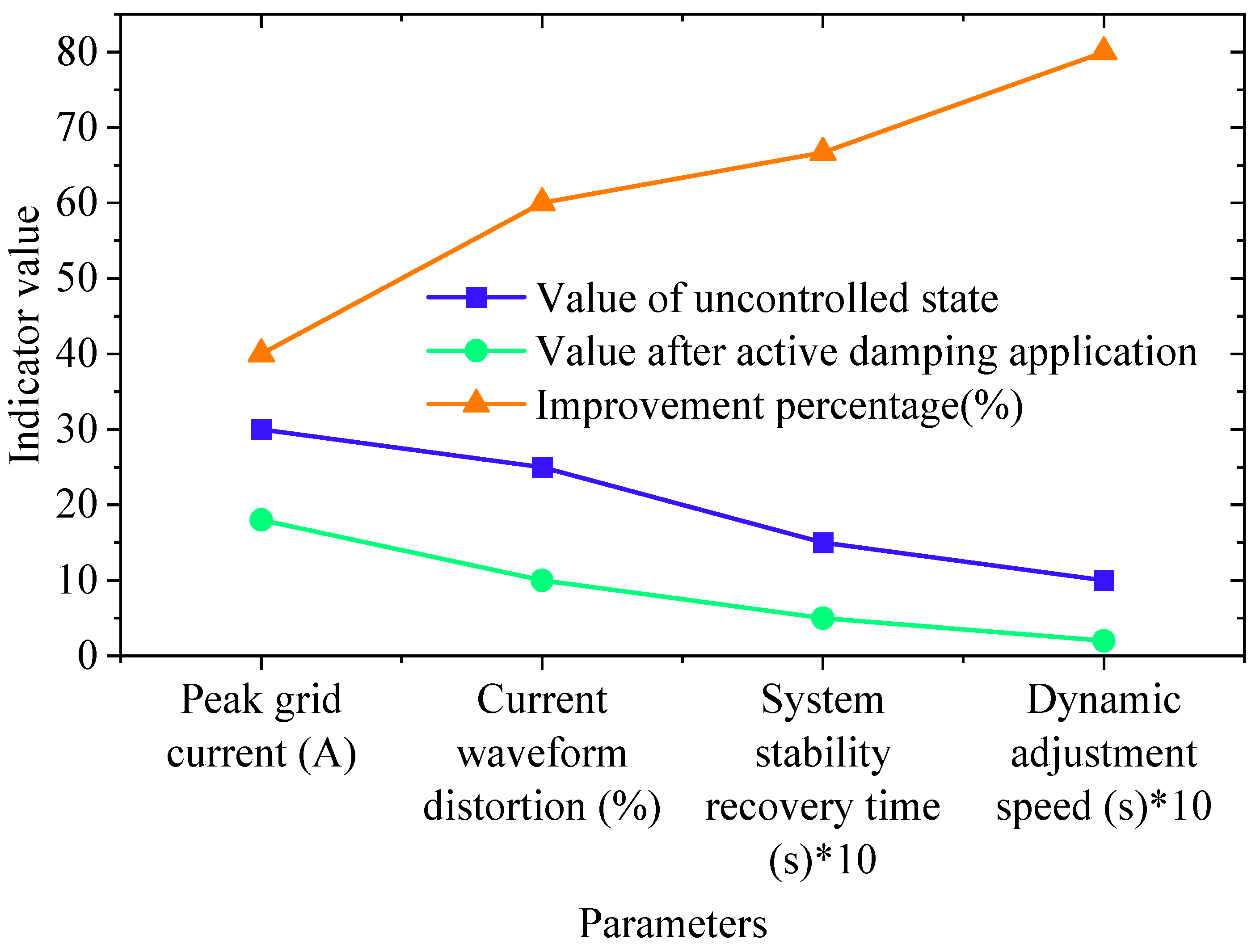
4.2. Resonance Suppression Effect
4.3. System Stability Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Salem, M.; Richelli, A.; Yahya, K.; Hamidi, M.N.; Ang, T.Z.; Alhamrouni, I. A comprehensive review on multilevel inverters for grid-tied system applications. Energies 2022, 15, 6315. [Google Scholar] [CrossRef]
- Easley, M.; Shadmand, M.B.; Abu-Rub, H. Hierarchical model predictive control of grid-connected cascaded multilevel inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 3137–3149. [Google Scholar] [CrossRef]
- Barkat, F.; Cheknane, A.; Guerrero, J.M.; Lashab, A.; Istrate, M.; Viorel Banu, I. Hybrid islanding detection technique for single-phase grid-connected photovoltaic multi-inverter systems. IET Renew. Power Gener. 2020, 14, 3864–3880. [Google Scholar] [CrossRef]
- He, S.; Zhou, D.; Wang, X.; Blaabjerg, F. Line voltage sensorless control of grid-connected inverters using multisampling. IEEE Trans. Power Electron. 2021, 37, 4792–4803. [Google Scholar] [CrossRef]
- Barzegarkhoo, R.; Lee, S.S.; Khan, S.A.; Siwakoti, Y.P.; Lu, D.D.C. A novel generalized common-ground switched-capacitor multilevel inverter suitable for transformerless grid-connected applications. IEEE Trans. Power Electron. 2021, 36, 10293–10306. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, J.; Zhang, S.; Gao, L.; Guo, X.; Chen, L.; Xu, Y. Harmonic Resonance Analysis and Impedance Remodeling Method of Multi-Inverter Grid-Connected System. Electronics 2023, 12, 3684. [Google Scholar] [CrossRef]
- Yang, W.; Wang, D.; Wang, X.; Li, X.; Zhang, P. Resonance Analysis of Medium Voltage Multi-Microgrids Considering the Interaction of Controllable Series Compensator and Grid-Connected Inverters. J. Electr. Eng. Technol. 2024, 19, 1005–1022. [Google Scholar] [CrossRef]
- Liu, J.; Sun, X.; Chen, Z.; Chi, Y.; Song, W.; Zhu, Q.; Wheeler, P. A Hybrid Multiresonances Suppression Method for Nonsynchronous LCL-Type Grid-Connected Inverter Clusters Under Weak Grid. IEEE Trans. Power Electron. 2024, 39, 5386–5399. [Google Scholar] [CrossRef]
- Li, Q.; Sun, P.; Dong, G.; Chen, Y. Resonance coupling analysis of multiple differently parameterized grid-connected inverters in new energy generation. Int. J. Electr. Power Energy Syst. 2024, 156, 109743. [Google Scholar] [CrossRef]
- Chen, L.; Xu, Y.; Tao, S.; Wang, T.; Sun, S. Multi-inverter resonance modal analysis based on decomposed conductance model. Electronics 2023, 12, 1251. [Google Scholar] [CrossRef]
- Zheng, F.; Wu, G.; Lin, X.; Zheng, S.; Wu, X.; Lin, Y.; Deng, C. Research on control strategy for improving stability of multi-inverter parallel system under weak grid condition. Int. J. Electr. Power Energy Syst. 2023, 153, 109121. [Google Scholar] [CrossRef]
- Wang, X.; Rong, X.; Huang, P.; Zhao, X. Stability analysis and resonance suppression of multi-inverter parallel operation. Electr. Power Syst. Res. 2024, 226, 109907. [Google Scholar] [CrossRef]
- Samanes, J.; Urtasun, A.; Gubia, E.; Petri, A. Robust multisampled capacitor voltage active damping for grid-connected power converters. Int. J. Electr. Power Energy Syst. 2019, 105, 741–752. [Google Scholar] [CrossRef]
- Khan, A.; Gastli, A.; Ben-Brahim, L. Modeling and control for new LLCL filter based grid-tied PV inverters with active power decoupling and active resonance damping capabilities. Electr. Power Syst. Res. 2018, 155, 307–319. [Google Scholar] [CrossRef]
- Yuan, C.; Shi, D.; Hu, Q.; Liao, Y.; Yu, J.; Zhou, P. Active damping resonance suppression and optimization of photovoltaic cluster grid connected system. J. Electr. Eng. Technol. 2021, 16, 2509–2521. [Google Scholar] [CrossRef]
- Guo, Y.; Lu, X.; Chen, L.; Zheng, T.; Wang, J.; Mei, S. Functional-rotation-based active dampers in AC microgrids with multiple parallel interface inverters. IEEE Trans. Ind. Appl. 2018, 54, 5206–5215. [Google Scholar] [CrossRef]
- Xu, X.; Yao, W.; Xie, G. A Damping Control Strategy to Improve the Stability of Multi-Parallel Grid-Connected PCSs. Energies 2023, 16, 4633. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, C.; Liu, F.; Li, F.; Xu, H. Overview on resonance characteristics and resonance suppression strategy of multi-parallel photovoltaic inverters. Chin. J. Electr. Eng. 2016, 2, 40–51. [Google Scholar]
- Li, Y.; Zhang, J.; Hao, Z.; Tian, P. Improved PR control strategy for an LCL three-phase grid-connected inverter based on active damping. Appl. Sci. 2021, 11, 3170. [Google Scholar] [CrossRef]
- Petric, I.Z.; Mattavelli, P.; Buso, S. Passivation of grid-following VSCs: A comparison between active damping and multi-sampled PWM. IEEE Trans. Power Electron. 2022, 37, 13205–13216. [Google Scholar] [CrossRef]
- Jurkov, A.S.; Radomski, A.; Perreault, D.J. Tunable matching networks based on phase-switched impedance modulation. IEEE Trans. Power Electron. 2020, 35, 10150–10167. [Google Scholar] [CrossRef]
- Jiang, S.; Konstantinou, G. Generalized impedance model and interaction analysis for multiple grid-forming and grid-following converters. Electr. Power Syst. Res. 2023, 214, 108912. [Google Scholar] [CrossRef]
- Büyük, M.; Tan, A.; Tümay, M. Resonance suppression of LCL filter for shunt active power filter via active damper. Int. J. Electr. Power Energy Syst. 2022, 134, 107389. [Google Scholar] [CrossRef]
- Yang, S.; Liu, K.; Qin, L.; Zhu, S.; Xu, B.; Wang, Q. A broadband active damping method for high-frequency resonance suppression in MMC-HVDC system. Int. J. Electr. Power Energy Syst. 2023, 146, 108791. [Google Scholar] [CrossRef]
- Babu, N.; Guerrero, J.M.; Siano, P.; Peesapati, R.; Panda, G. A novel modified control scheme in grid-tied photovoltaic system for power quality enhancement. IEEE Trans. Ind. Electron. 2020, 68, 11100–11110. [Google Scholar]
- Wang, S.; Li, Y.; Zhang, M.; Peng, Y.; Tian, Y.; Lin, G.; Chang, F. Harmonic resonance suppression with inductive power filtering method: Case study of large-scale photovoltaic plant in China. IEEE Trans. Power Electron. 2023, 38, 6444–6454. [Google Scholar] [CrossRef]
- Meraj, S.T.; Yahaya, N.Z.; Hasan, K.; Lipu, M.H.; Elavarasan, R.M.; Hussain, A.; Hannan, M.A.; Muttaqi, K.M. A filter less improved control scheme for active/reactive energy management in fuel cell integrated grid system with harmonic reduction ability. Appl. Energy 2022, 312, 118784. [Google Scholar] [CrossRef]
- Li, Z.; Wang, M.; Fan, G.; Zeng, X.; Yan, Y.; Ma, F. Effects of rolling motion on flow and heat transfer characteristics in a tube bundle channel. Appl. Therm. Eng. 2023, 220, 119696. [Google Scholar] [CrossRef]
- Xue, R.; Li, G.; Tong, H.; Chen, Y. Adaptive active damping method of grid-connected inverter based on model predictive control in weak grid. J. Power Electron. 2022, 22, 1100–1111. [Google Scholar] [CrossRef]
- Cai, Y.; He, Y.; Zhou, H.; Liu, J. Active-damping disturbance-rejection control strategy of LCL grid-connected inverter based on inverter-side-current feedback. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 7183–7198. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Zhu, X.; Xu, Y.; Tao, S. DC Active Damper Control Strategy Based on Resonance Suppression Effectiveness Evaluation Method. Energies 2024, 17, 480. [Google Scholar] [CrossRef]
- Dash, D.K.; Sadhu, P.K. A Review on the Use of Active Power Filter for Grid-Connected Renewable Energy Conversion Systems. Processes 2023, 11, 1467. [Google Scholar] [CrossRef]
- Yusuf, S.D.; Loko, A.Z.; Abdullahi, J.; Abdulhamid, A.A. Performance Analysis of Three-Phase Shunt Active Power Filter for Harmonic Mitigation. Asian J. Res. Rev. Phys. 2022, 6, 7–24. [Google Scholar] [CrossRef]

| Parameter Category | Parameter Name | Value |
|---|---|---|
| Grid parameters | Power voltage | 400 V |
| Grid frequency | 50 Hz | |
| Grid inductance | 1.2 mH | |
| DC side parameters | DC side voltage | 750 V |
| Inverter parameters | Inverter side inductor 1 | 2.5 mH |
| Inverter side inductor 2 | 1.5 mH | |
| Filter parameters | filter capacitor LCL filter inductor 1 (inverter side) LCL filter inductor 2 (grid side) | 0.35 µF 2.5 mH 1.5 mH |
| Control parameters | On-off level | 16 kHz |
| Sampling frequency | 16 kHz | |
| Performance parameters | Grid-connected rated power | 12 kW |
| Power conversion efficiency parameters | Maximum conversion efficiency | 96% |
| Inverter response parameters | Response time | 30 ms |
| Power Grid Conditions | Resonance Suppression Effect (%) | System Stability Improvement (%) | Frequency Fluctuation (Hz)*100 | Improvement in Voltage Stability (%) | Power Factor Improvement (%) | Peak Current Reduction (%) | THD Reduction (%) |
|---|---|---|---|---|---|---|---|
| High impedance, long line | 55 | 22 | 12 | 6 | 5 | 27 | 32 |
| Low impedance, short line | 42 | 15 | 25 | 4 | 3 | 18 | 22 |
| Medium impedance, standard | 48 | 18 | 18 | 5 | 4 | 23 | 25 |
| High impedance, high temperature | 50 | 20 | 10 | 5 | 6 | 25 | 30 |
| Low impedance, low temperature | 38 | 12 | 28 | 3 | 2 | 16 | 18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, T.; Jiang, Y.; Cai, Z. Inverter Multi-Machine Grid Integration Resonance Suppression Strategy by Active Damping. Energies 2024, 17, 3791. https://doi.org/10.3390/en17153791
Hou T, Jiang Y, Cai Z. Inverter Multi-Machine Grid Integration Resonance Suppression Strategy by Active Damping. Energies. 2024; 17(15):3791. https://doi.org/10.3390/en17153791
Chicago/Turabian StyleHou, Tianhao, Yunhao Jiang, and Zishuo Cai. 2024. "Inverter Multi-Machine Grid Integration Resonance Suppression Strategy by Active Damping" Energies 17, no. 15: 3791. https://doi.org/10.3390/en17153791
APA StyleHou, T., Jiang, Y., & Cai, Z. (2024). Inverter Multi-Machine Grid Integration Resonance Suppression Strategy by Active Damping. Energies, 17(15), 3791. https://doi.org/10.3390/en17153791





