Abstract
The behaviour of bubbles in cavitation and boiling processes is determined by the thermodynamic parameters of the two-phase medium and the intensity of heat and mass transfer, which affect the final dynamic effects. In this review, we analyse the influences of these factors on bubble behaviour, as described in existing mathematical models. In particular, we analyse the physical processes that govern bubble behaviour, the influence of mass transfer, vapor and liquid temperature, vapour, and liquid pressure on the inertial and dynamic stages of development. In conclusion, we summarize the problems associated with modelling, the accuracy of numerical predictions, and propose directions for further research.
1. Introduction
In recent decades, there has been a surge of interest in studying bubble dynamics due to its wide range of practical applications. This seemingly mundane phenomenon, the growth or collapse of a spherical bubble in a liquid, is significant because the behaviour of individual bubbles in dynamically evolving bubble systems determines the nature and characteristics of various processes. These include bulk and surface boiling, bulk condensation, and hydrodynamic and acoustic cavitation, which are fundamental to many modern technologies.
Boiling, in itself, is a distinct branch of thermophysics and a cornerstone of chemical engineering. Consider the methods for intensifying various processes using acoustic treatment, whose effectiveness is attributed to the cavitation collapse of micro-bubbles formed in an ultrasonic field [1,2,3]. Hydrodynamic cavitation devices are successfully employed in various industries [4,5,6]. The phenomenon of explosive boiling of highly superheated liquids has found practical application as a promising and energy-efficient method for mechanical processing of dispersed media [7,8,9,10]. In particular, many works have been published devoted to the homogenization of dispersed media by the explosive boiling method [11,12,13]. Naturally, the demand for enhancing the efficiency of such technological operations and their optimal utilization necessitates a more detailed and thorough examination of the underlying processes and phenomena.
The pioneering work of Lord Rayleigh [14] marked the beginning of theoretical studies on bubble dynamics. He analysed the collapse of a spherical vacuum cavity in an ideal liquid, neglecting the capillary effects. This seminal work introduced the equation for the radial motion of the liquid at the boundary of the spherical cavity, known in hydrodynamics as the Rayleigh equation:
Equation (1) has a simple analytical solution R = f(T), which cannot be used in practice due to the idealization of the initial conditions.
Various modifications of Equation (1) which take into account the contribution of capillary and viscous components to normal stress on the bubble surface (the Rayleigh–Lamb–Plesset equation) can only be solved numerically [15,16,17]. These equations are included in almost all subsequent mathematical models that describe the dynamics of steam and vapour–gas bubbles in cavitation processes.
Without considering heat and mass transfer between the bubble and the liquid, or the kinetics of phase transitions, equations of this type describe the inertial stage of the process when bubble growth or collapse is determined solely by mechanical disequilibrium, that is, the pressure difference in both phases. Since bubble behaviour is determined by the interconnected potentials of non-equilibrium processes (Δp, ΔT, Δµ), using a single equation that only considers mechanical disequilibrium is not sufficient for solving real-world problems.
An alternative approach to bubble dynamics analysis focusses solely on the thermal stage, neglecting the inertial stage. This assumption assumes that bubble formation and vapour phase growth during boiling processes occur exclusively in the thermal stage, where the rate of vapour generation is determined solely by the heat transfer rate from the liquid to the bubble.
Theoretical models that describe the behaviour of steam bubbles in bulk or surface boiling processes, from the earliest works to the present, are based on the fundamental assumption of equal pressures in the vapour and liquid phases, i.e., the absence of mechanical disequilibrium [18,19,20,21,22].
This approach was first used in the works of Plesset and Zwick [23] and Forster and Zuber [24]. The equations derived in these works form the basis of general theoretical models for bubble growth in superheated liquids, which have gained wide acceptance in the study of boiling mechanisms [25,26,27,28,29,30,31,32,33,34,35,36,37].
In these models, instead of Equation (1), a heat balance equation is used to describe the bubble expansion rate, which can be generalised as:
In this equation, it is assumed that the heat supplied from the liquid to the bubble surface is only used for vaporisation, and there is no heat exchange between the bubble and the liquid. Equation (2) is usually supplemented by an equation for convective heat conduction in the liquid phase, as well as an empirical correlation that relates the saturated vapour pressure to temperature.
As highlighted in [38], theoretical studies on bubble dynamics can be broadly categorised into two approaches, where bubble behaviour is governed either by inertial forces or by heat transfer rates in the liquid phase. When discussing the state of bubble dynamics research, the authors of this work note that there are two types of equation system describing growth rates (for inertial and thermal regimes). However, given the specified thermophysical parameters and initial conditions, it is impossible to predict a priori, without experimentation, which system of equations should be used in a particular case.
To date, this concept has persisted, but numerous new studies have emerged with various modelling approaches. Consequently, several groups of models can be identified (Table 1).

Table 1.
Types of models.
In several of these model categories, researchers have compared the calculated bubble growth rates obtained from the “inertial” and “thermal” concepts with experimental results. The findings indicate that the experimentally observed growth rates are often significantly lower than the calculated values.
The first analytical expression for the growth rate of steam bubbles considering both inertial and thermal effects was proposed in [55,56]. This solution in some cases showed good agreement with experimental results, but in other conditions significant discrepancies were observed between theoretical and experimental results.
As demonstrated in [57,58], the satisfactory agreement between the generalised formula [59] and some experimental data [60] is attributed to the mutual compensation of two errors. The first error arises from the assumption ρ(τ) = const, which significantly overestimates the calculated growth rate. The second error results from using a linear approximation of the Clapeyron–Clausius equation to estimate the vapour pressure ρ = ρsat (Ts) in [56]. For relatively high superheats, this leads to a substantial underestimation of the calculated growth rate, and consequently to the compensation of the first error. However, for conditions where these errors do not compensate, the discrepancy between theory and experiment becomes significant [61,62].
An analytical solution for the growth rate of a steam bubble, considering the change in vapour density during growth and using a more accurate linear approximation for the ρsat (Ts) relationship, was presented in [63]. However, satisfactory agreement with experimental data was observed only for very small superheats.
To obtain a simple approximation of the R = f(τ) relationship suitable for practical calculations at extremely high superheats, [64] simultaneously employs Equations (1) and (2). Essentially, the authors exclude the inertial stage of growth a priori by neglecting the d2R/dτ2 term in Rayleigh’s equation and making simplifying assumptions when solving Equation (2): dρ/dτ = 0 and ql = λl∂Tl/∂r∞ΔTl/τ0.5. To represent the ρsat(Ts) relationship, a Taylor series expansion of the Clapeyron–Clausius equation can be used. This approach could reduce the saturation curve approximation error to 40%, which is more accurate than the linear approximation used in [63,64]. These simplifications allow for the derivation of a calculation equation for bubble growth rate that matches experimental data with an accuracy of about 20% within the range of pressures and temperatures where the author’s limitations are acceptable. However, the calculated values still exceed the experimentally obtained data.
In the search for analytical solutions, the authors of [64] made the simplifying assumption that the vapour within the bubble could be treated as an ideal gas. This assumption became a crude approximation at high superheats. The work of [64] exemplifies the limitations of analytical solutions for specific bubble dynamics problems, as authors often neglect the influence of certain factors that could become crucial under different parameter conditions.
Since the seminal works of Rayleigh, Plesset, Zwick, Forster, and Zuber [65,66,67] introduced analytical solutions, the development of bubble dynamics theory has progressed by incorporating an increasing number of governing factors into models. This has necessitated the solution of complex and cumbersome systems of equations. As obtaining exact analytical solutions for these equations in their general form is often impractical, two approaches have emerged:
- -
- approximate analytical solutions. This approach involves simplifying assumptions, often with questionable physical justifications, to derive approximate analytical estimates.
- -
- numerical solutions. This approach involves the numerical solution of the original equations. The advancement of computer technology in recent years has undoubtedly contributed to a more detailed study of steam bubble dynamics, as it enables the numerical solution of even highly complex systems of equations with high accuracy in a relatively short time [68,69,70].
Although early investigations of steam bubble dynamics were driven by pressing issues in boiling physics, since the mid-1970s there has been a surge of interest in bubble behaviour in vapour cavitation and explosive boiling processes, primarily from the perspective of understanding the destructive effects of bubbles in these phenomena [71,72,73,74,75,76,77,78,79,80].
A critical review of bubble dynamics research reveals that accurately representing interphase heat and mass transfer, the thermodynamic state of the vapour phase, and the temperature field around the bubble is crucial for modelling bubble behaviour, regardless of the model’s application. For instance, considering heat transfer in oscillating and collapsing bubbles significantly reduces the thermodynamic parameters within the bubble by almost an order of magnitude compared to adiabatic collapse [52,81]. Recent model advancements have focused on this aspect.
However, model developers often employ simplifying assumptions that substantially limit the ability to accurately describe the processes under investigation. Bubble behaviour during growth or collapse is often considered in a quasi-equilibrium approximation, neglecting the inertial stage of development. The authors of these models believe that their primary advantage, which they claim provides a higher degree of reliability compared to other models, is the consideration of heat transfer in the gas phase, assuming that ∂T/∂r ≠ 0 and ∂ρ/∂r ≠ 0 within the bubble [82,83,84,85,86,87].
These models, which are currently the most detailed and widely used by researchers, provide a reasonably accurate description of interphase heat and mass transfer and the specifics of bubble behaviour in inertial and thermal regimes. However, as shown in [81], despite the fact that almost all authors demonstrate good agreement between their calculated data and experiments, this agreement is only characteristic of specific stages in bubble dynamics development. This is attributed to the complex physical processes both within the bubble itself and in its surroundings, which are not always amenable to experimental investigation.
Consequently, there are no mathematical models that can guarantee equally accurate predictions of individual bubble behaviour, let alone bubble clusters, across the entire range of operating parameters relevant to real-world conditions. We consider that the imperfection of existing models reflects the traditional tendency to treat phenomena such as acoustic and hydrodynamic cavitation, bulk condensation, boiling at low superheats, explosive boiling, and bubble growth in subcooled liquids as fundamentally distinct branches of thermophysics.
From a physical standpoint, however, these phenomena represent the same underlying process of relaxation of the “bubble–liquid” system towards thermodynamic equilibrium. Bubble behaviour in these processes follows the same general principles and should be described by the same equations, albeit with different initial conditions. Therefore, a mathematical model of bubble dynamics that accounts for all the key governing factors should be equally capable of describing any of these phenomena.
Such a model cannot contain specific assumptions that are only valid for one of the phenomena, as there is no objective basis for establishing a clear boundary, and the question of where cavitation ends and boiling begins is physically meaningless. Thus, it is possible to construct a mathematical model of bubble dynamics by combining models that satisfactorily describe only specific stages of bubble development [88]. However, this would require expanding the initial classification of models presented in the article by dividing them into nucleation models [89,90,91,92], growth and oscillation models [93,94,95,96,97], collapse and destruction models [98,99,100,101,102,103], and bubble coalescence or fragmentation models [104,105,106,107,108,109]. The next step would be to analyse the impact of various factors on the development of these processes.
2. Factors Affecting the Behaviour of Cavitation Bubbles
Analysis of the articles cited above shows that in most models, the authors make assumptions about the sphericity of bubbles. The liquid is considered viscous but incompressible and the bubble is filled with vapour and gas, the amount of which is determined by the mass transfer between the bubble and the liquid. The vapour and components of the gas mixture inside the bubble are treated as real gases.
The validity of these assumptions is confirmed by the analysis of known experimental data, which show that the bubble retains its spherical shape at all stages of its development. This assumption would be invalid for the case of bubble growth near solid surfaces.
The factor of liquid compressibility is important in detailing the shape and propagation of the pressure pulse emitted into the liquid by the bubble at the moment of its final collapse. There are many publications in which the liquid is considered compressible [110,111,112,113,114,115]. The consideration of liquid compressibility is compensated for by an inadequate description of heat and mass transfer processes and the kinetics of phase transitions, which, of course, reduces the accuracy of numerical predictions. The factor of liquid compressibility is discussed in detail in [116,117]. It should also be noted that the models do not give an accurate description of the entire cycle of bubble development or destruction, especially when it comes to bubble clusters. What factors affect the accuracy of analytical predictions and to what extent? Let us consider this in more detail.
The primary goal of cavitation bubble dynamics modelling is to determine the kinematical, dynamical, and energetical characteristics of a growing bubble. This encompasses the local values of the velocity w(r,τ), acceleration dw/dτ, pressure p(r,τ), and the kinetic energy Ek (r,τ) at any point within the liquid volume. These parameters are influenced by a combination of factors, including the initial parameters of the liquid: Tl0, Δτ, pl0, R, and m. Additionally, current thermophysical parameters of the vapour (Ts, p, R, and ρ) play a crucial role, as do the heat transfer rate q and the mass transfer rate j across the interphase surface.
Models based on the Rayleigh–Plesset equations are widely employed because of their formulation within the framework of the liquid volume concept. This approach facilitates their straightforward implementation in most computational fluid dynamics (CFD) software packages. Despite their age (many of these models are older than 20 years), they continue to serve as the standard for most cavitation research, providing a foundational starting point for further modelling endeavours.
The Rayleigh equation and its derived Equations (1) and (2) hold immense significance in the modelling of cavitation bubble dynamics. These equations are obtained by solving the Navier–Stokes equation and the continuity equation. Under the assumption of irrotational flow, these equations can be reduced to the Euler equation and the Laplace equation, ultimately leading to the Lagrange–Cauchy integral. It can be demonstrated that Equation (1) essentially expresses the law of conservation of mechanical energy in the liquid during the system’s relaxation to a thermodynamic equilibrium state.
We will examine the motion of an incompressible fluid in the vicinity of a spherical bubble during its expansion or contraction in an infinite volume, employing solely the assumption of spherical symmetry for the velocity field. Consider a thin spherical layer of fluid in a liquid with a thickness dr at a distance r from the bubble’s centre. For the radial motion of the velocity of the bubble surface, the fluid directly at the bubble surface is wr = dR/dτ. Consequently, the velocity of the spherical layer is:
and the kinetic energy of the layer is:
The kinetic energy of the infinite volume of fluid surrounding the bubble is determined by integrating the right-hand side of Equation (4) over the entire volume of the fluid. This yields the following.
Equation (5) reveals that the kinetic energy of the infinite volume of fluid surrounding the bubble assumes a finite value, equal to the product of the effective fluid mass meff, occupying a volume three times that of the bubble, and the velocity of the bubble surface. In other words, from an energetic standpoint, the entire mass of fluid around the bubble is equivalent to the mass of fluid occupying a volume three times that of the bubble.
If the fluid volume is finite and represented by a sphere with radius R2 > R, integration is performed within the limits R and R2, and the kinetic energy of the fluid becomes:
As R2 approaches infinity (R2→∞), Equation (6) converges to Equation (5). This derivation is consistent with the presented equations. However, in real cavitation processes involving numerous bubbles, this fluid mass and its energy should be distributed among the total volume of the bubbles. This implies that the calculated values will be overestimated compared to real-world data, as also confirmed by experiments.
With changes in bubble size, the effective fluid mass meff varies proportionally to R3(τ). Therefore, the radial displacement of the fluid induced by the movement of the bubble boundary can formally be considered as the motion of a body with variable mass meff = f(τ). Even if we assume that the bubble growth or collapse rate dR/dτ ≡ wR = const, the kinetic energy of the fluid will still change due to the variation of meff. During bubble growth at a constant rate, Ek increases, while during bubble collapse at a constant rate, Ek decreases, in accordance with the change in meff.
In the absence of viscous dissipation, the change in kinetic energy is associated with its conversion into potential energy. In the context of fluid motion during bubble expansion or collapse, the change in potential energy is due to the work performed by external forces , where is the total pressure applied to the fluid and dV is the change in bubble volume. The work carried out on the fluid in the time interval from 0 to τ is determined by the expression:
From the law of conservation of energy, it follows that:
Substituting the expressions for Ek and A from Equations (5) and (7), we obtain the energy conservation equation:
or, assuming that , we obtain Rayleigh’s Equation (1).
Thus, Rayleigh’s equation in the form (1) is directly derived from the equation of conservation of mechanical energy and would be valid for a single bubble in an infinite volume of liquid. It also follows from the equation that the main factors influencing bubble behaviour are the temperatures and pressures of the liquid and vapour, the thermophysical parameters of the vapour, and the heat and mass transfer processes at the phase interface.
2.1. Bubble Surface Motion and Rayleigh Equation
The Rayleigh Equation (1), which describes the motion of a spherical bubble in an infinite volume of liquid, involves only the radius of the bubble R(τ) and its radial velocity wR(τ) as variables dependent on time. These variables are independent of spatial coordinates. However, the equation contains two unknowns: R(τ) and wR(τ). To determine the current radius of the bubble, an additional equation is required. As mentioned above, in the absence of phase transitions , the equation for finding R(τ) takes the simple form:
When intense evaporation or condensation of vapour occurs on the inner surface of a bubble, the bubble radius changes not only due to the radial motion of the liquid but also due to the depletion of the liquid phase in the near-surface layer or, conversely, its “buildup” during vapour condensation. To account for this factor, instead of Equation (10), a more accurate equation should be used:
where j represents the mass flux of vapour through the bubble surface per unit of time. This correction, although theoretically important, is often relatively small in magnitude and may not significantly impact bubble behaviour in most cases, as demonstrated in studies such as [46,118,119].
Authors of works [120,121,122,123] have attempted to solve the full Equation (11), incorporating the phase transition term. However, such solutions have limited appeal from a methodological standpoint due to the complexity of the algorithm and the significant computational time required. Moreover, the substantial increase in computational complexity is not offset by the ability to validate models for the entire bubble lifecycle. Although some time intervals of bubble dynamics may exhibit good agreement between numerical results and experimental data, the specific mass flux can increase by several orders of magnitude during the maximum compression stage of an oscillating or collapsing bubble, substantially affecting the process dynamics.
Therefore, in the inertial growth regime, where the bubble growth rate is primarily governed by inertial forces, the simplified Rayleigh–Plesset equation can provide a sufficiently accurate representation of bubble dynamics. This simplified approach offers a balance between computational efficiency and reasonable accuracy for modelling bubble growth under these conditions. Although accounting for phase transitions through the mass flux term provides a more complete theoretical description of bubble dynamics, the computational challenges and limited applicability of this approach across the entire bubble lifecycle often make it impractical. The simplified Rayleigh–Plesset equation remains a valuable tool for modelling bubble growth in the inertial regime, offering a balance between accuracy and computational efficiency.
2.2. Pressure and Density in the Bubble
The gas phase pressure p(τ) is included in Equation (1) as an unknown function of time, which requires independent equations for its determination. During bubble oscillation or collapse, the value of p can vary tens of thousands of times, highlighting the significant influence of this factor on bubble behaviour. The pressure of the gas mixture inside the bubble p = ps + pg depends on both the temperature of the mixture Tb and the densities of each component—ρv and ρg. Therefore, to find the dependence p = f(τ), independent equations should be used to determine the time dependencies ρv(τ), ρg(τ), and Tb(τ).
Many authors [124,125,126,127,128,129], when investigating bubble dynamics in boiling or cavitation processes, have assumed that the components of the mixture inside the bubble at any stage of its development obey the ideal gas laws. This assumption is justified in cases where the pressure and temperature of the gas phase are relatively low. However, during the collapse of cavitation bubbles or explosive boiling processes, the pressure and temperatures of the vapour inside the bubble reach extremely high values, and the assumption of an ideal gas can introduce significant errors into the calculation results.
In models in which the vapour–gas mixture is considered a real gas [130,131,132,133,134], two important assumptions are used, which significantly simplify the overall system of equations and facilitate analysis without introducing significant errors. The first is the condition of homobaricity, or uniformity of gas pressure throughout the bubble volume. The homobaricity condition is satisfied if the radial velocity of the liquid on the bubble wall wR wR is much less than the speed of sound in gas u, and the characteristic time for the change in velocity wR is significantly greater than the time it takes for a sound pulse to travel from the surface to the centre of the bubble. The latter requirement can be expressed in the form of the inequality , where is the magnitude of the radial acceleration of the surface. Thus, the homobaricity condition must be satisfied if both inequalities hold simultaneously:
The homobaricity assumption significantly simplifies the analysis of bubble dynamics by allowing for a uniform gas pressure within the bubble. This assumption is valid under conditions where the radial motion of the liquid is slow compared to the speed of sound in the gas and the characteristic time scales for velocity changes are longer than the sound propagation time across the bubble. However, it is important to assess the validity of this assumption in specific applications, particularly when dealing with high-pressure or high-velocity bubble dynamics.
In [135], an alternative form for the criterion of uniform pressure within a bubble is proposed: , where is the characteristic time of the change in velocity wR. Other studies [136,137,138,139] have demonstrated that the homobaricity condition is generally satisfied in a broad class of problems.
Our analysis indicates that conditions (12) may only be violated during the final stage of bubble collapse, when the bubble compression rate reaches its maximum (first inequality in (12)), and then, upon reaching the minimum bubble size, abruptly decreases to zero (second inequality). However, this stage only lasts for a few nanoseconds, that is, less than 0.01% of the time of one oscillation cycle.
The second assumption concerns the homogeneity of the temperature of the vapour or vapour–gas mixture within the bubble. Compared with the previous one, this is a stricter limitation, since in some cases the intensity of heat transfer between the bubble and the liquid is determined precisely by the thermal resistance in the gas phase. These studies have shown that in the case of a pure vapour bubble, in contrast to a gas bubble, the external heat conduction problem plays a dominant role; therefore, temperature inhomogeneity inside the bubble can be neglected.
A consequence of the assumptions adopted for homogeneity of pb and Tb is the density of the homogeneity of the vapour–gas mixture density ρb in the bubble ρb, which follows from the van der Waals equation (pg = f(ρg,Tb) and pv = f(ρv,Tb)). The density of vapour or gas will also be homogeneous if the second component is absent. However, the density of each component in the vapour–gas mixture cannot be homogeneous if interphase mass transfer occurs (and the latter always occurs, since vapour is necessarily present inside a real bubble). From the density condition of homogeneity of the vapour–gas mixture density dρb = 0, it follows that dρg/dr = −dρv/dr. In the presence of a noncondensable gas in the bubble, the intensity of the bubble’s mass transfer with the liquid is determined by the rate of molecular diffusion of vapour in the second gas component.
Consider a general case where the gas mixture inside the bubble consists of vapour and noncondensable gas, so that mg = const. The vapour content in the bubble changes as a result of condensation on the wall or evaporation of the liquid into the bubble. The total mass of the gas mixture mb = mg + mv(τ), where mg = 4/3πR3ρg and mv = 4/3πR3ρv, and ρg and ρv are the volume-averaged densities of gas and vapour. Taking into account that dmg = 0 and dmv/dτ = 4 πR2j, we obtain equations to determine the functions ρg = f(τ) and ρv = f(τ):
2.3. Heat and Mass Transfer across a Phase Interface
In cavitation simulations, accurately modelling the phase boundaries of bubbles is computationally demanding. Simplified approaches to mass transfer have often neglected the distinction between vapour and noncondensable gas. Earlier approaches to vapour–liquid equilibrium, such as those based on equations of state [140,141,142], did not account for noncondensable gas, considering only the vapour–liquid system.
Subsequent research has considered the released noncondensable gas to form a coherent gas pocket within the cavitation flow [143,144,145,146,147]. These studies employed various algorithms to approximate the interface between vapour and liquid.
Several authors, such as [148], have investigated homogeneous mixtures of liquid and vapour, disregarding the noncondensable gas.
The transfer of heat and mass across the bubble surface is often studied using molecular kinetic theory. This approach provides the most physically accurate description of the phase transition kinetics at the liquid–gas interface [149,150,151,152].
In [52], the authors evaluated the impact of heat and mass transfer processes on bubble behaviour. They assumed that the liquid-side surface temperature of the bubble, Tl(R) = Ts, is different from the gas phase temperature, Tb. Considering this assumption and the homogeneity of Tb(r), the condition Ts ≠ Tb is equivalent to assuming a temperature jump in the bubble wall from the gas phase side. Under these conditions, it is necessary to determine the magnitude of the specific mass flow rate across the phase interface due to vapour condensation on the bubble wall or its evaporation. According to the principles of molecular kinetic theory, the mass of vapour molecules colliding with a unit surface per unit time is given by the following: , where is the average thermal velocity of the vapour molecules at temperature Tb. A portion of these molecules with mass a condenses on the liquid surface, while the remaining part of the molecules with mass is reflected back into the gas phase. Here, αm is the coefficient of evaporation, characterising the fraction of vapour molecules that condense in the liquid upon collision. Consequently, 1 − αm defines the fraction of vapour molecules that undergo elastic reflection. The mass of liquid that evaporates per unit time from a unit surface is given by , where is the saturated vapour density at the liquid surface temperature Ts, and is the average thermal velocity of vapour molecules at temperature Ts.
The mass transfer intensity j at a phase transition is defined as the difference between the amount of liquid evaporating from a unit surface per unit time and the amount of vapour condensing on it. Mathematically, it can be expressed as follows:
where the value of j is positive if the mass flow is directed from the liquid phase to the gas phase.
Let us now determine the value of the specific heat flux q through the interphase surface caused by the energetic interaction of the vapour and neutral gas molecules with the bubble wall. The assumption of the presence of a temperature jump allows us to consider the transfer of heat through the surface of the bubble in terms of molecular kinetic theory. Otherwise, it would be necessary to abandon the condition of temperature uniformity and solve the much more complex problem of thermal conductivity inside a bubble in the presence of radial gas motion. The formulation of a similar problem can be found in [52]. Because of the temperature differences Tb and Ts, vapour and gas molecules in contact with the surface of a liquid completely exchange energy, regardless of whether the molecule condenses on the surface or is reflected back. In other words, the coefficient of thermal accommodation is assumed to be equal to unity, which is a generally accepted assumption and corresponds, with the exception of some special cases, to the real mechanism of heat transfer.
Let us examine the energy balance when vapour and gas molecules interact with a unit liquid surface. We will focus on the heat transfer imparted by vapour molecules colliding with the liquid surface.
The amount of heat transferred per unit time by vapour molecules upon impact with the liquid surface can be expressed as:
The amount of heat carried away per unit time by vapour molecules upon their elastic reflection from the surface can be expressed as:
The amount of heat transferred per unit time by gas molecules upon collision with the surface of a liquid can be expressed as:
The amount of heat carried away per unit time by gas molecules during their elastic reflection from the surface can be expressed as:
The amount of heat carried away per unit of time by vapour molecules during their evaporation from the surface can be expressed as:
The resulting amount of heat transferred to the bubble from the liquid side per unit time can be determined by summing up the flows discussed above:
Substituting the right-hand sides of the equalities given here into this equation, we write the equation for the intensity of heat transfer through the following surface in the form:
Replacing the second term on the right side of (16) with its value from (15), we finally write:
For a vapour bubble in the absence of extraneous gas, the heat transfer equation takes the simple form:
The value q is considered positive if the heat flow is directed from the liquid to the gas.
With the non-equilibrium nature of phase transitions, the temperature at the interface always undergoes a jump, the magnitude of which determines the intensity of the mass flow from the bubble wall into the gas phase during evaporation or condensation of the vapour. In molecular kinetic theory, this temperature jump is described by the well-known Hertz–Knudsen equation [151,153,154]:
In previous studies, the temperature jump at the phase interface in vapour–liquid systems has been neglected due to the small evaporation coefficient (αm ≪ 1) for these systems. However, for substances with maximum values of αm ≈ 1 [155], accounting for the temperature jump is crucial. This commonly accepted assumption becomes invalid when considering bubble dynamics with strict consideration of non-equilibrium processes.
In describing the kinetics of phase transitions in single-component liquid–vapour systems, ΔT and αm are the primary parameters that characterise the intensity of mass transfer [156]. Assuming ΔT = 0 is equivalent to stating that the vapour in the bubble is in equilibrium with the liquid surface and there is no resistance to mass transfer.
Determining the experimental values of αm and ΔT is challenging, although both parameters are closely correlated, as evidenced in Equation (25). Arbitrarily choosing an αm value within the range 0 < αm ≤ 1 automatically establishes a specific ΔT value. While this ΔT may not correspond to the actual temperature jump, it accurately describes the mass transfer rate in conjunction with the chosen αm.
2.4. Heat Transfer in the Liquid Phase
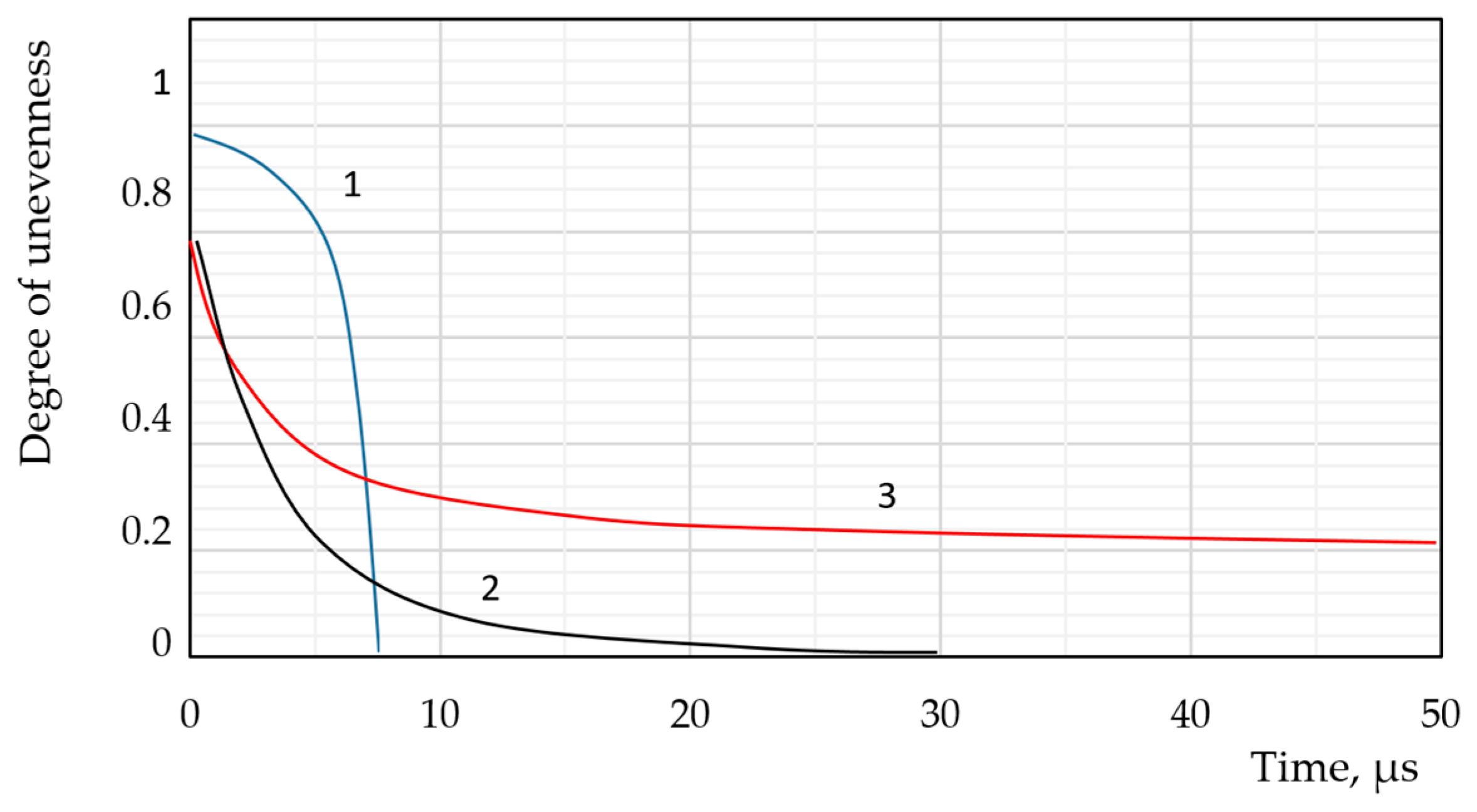
Heat transfer in the liquid phase plays a crucial role in bubble dynamics, significantly influencing bubble growth, collapse, and fragmentation. The rate of heat transfer between the bubble and the surrounding liquid determines the temperature distribution within the bubble and the flow patterns around it. Numerous studies have shown that the time scale for non-stationary heat transfer in the liquid phase is considerably longer than the time scales of other associated processes (Figure 1). This implies that the bubble’s dynamic behaviour is heavily influenced by the rate at which heat is supplied to or removed from the bubble surface.
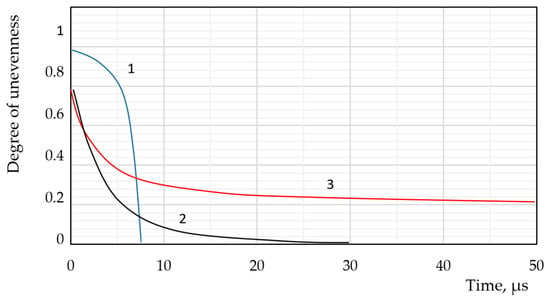
Figure 1.
Comparison of relaxation times of non-equilibrium thermodynamic processes, each of which alternately limits the rate of evolution of a two-phase liquid–vapour bubble system to a stable state according to the data [52]; graph legend: 1—compression of a bubble under the influence of a pressure difference in the absence of phase transitions; dependency presented (pl0 − pv)/(pl0 − pv0) = f(τ), R0 = 80 µm; 2—condensation of superheated vapour on the wall of a bubble of constant radius (R0 = 80 µm) at a constant temperature of the interfacial surface Ts < Tv; dependency presented ; 3—stabilisation of the temperature field near a bubble of constant radius (R0 = 80 µm) with constant surface temperature Ts > <Tl0; dependency is presented .
The dynamics of bubbles have been a subject of extensive research, with particular attention paid to the relaxation times of various non-equilibrium thermodynamic processes that govern the evolution of a two-phase liquid–vapour bubble system towards a stable state [157,158,159,160,161]. Analytical solutions for bubble growth or collapse have been derived under the assumption of monotonic size change [162,163,164]. While this assumption may be valid for analysing boiling processes, it is not justified for investigating cavitation phenomena.
Some researchers have introduced the assumption that the thermal layer is small compared to the size of the bubble, allowing the boundary layer to be treated as flat [165,166,167]. Although this assumption simplifies analysis of boiling processes, it does not hold for collapsing cavitation bubbles and leads to qualitatively inaccurate results.
To assess the heat exchange between the liquid and the bubble, it is necessary to know the temperature of the liquid Ts directly at the interface. This temperature is decisive when calculating the rate of mass and heat transfer using Equations (15)–(25) and is included in these equations as an unknown parameter. A commonly used assumption is Ts = Tb [52,168]. This assumption, while justified for quasi-stationary boiling, is inappropriate for analysing collapsing and oscillating bubbles. Therefore, it is essential to incorporate an independent equation into the system to determine Ts.
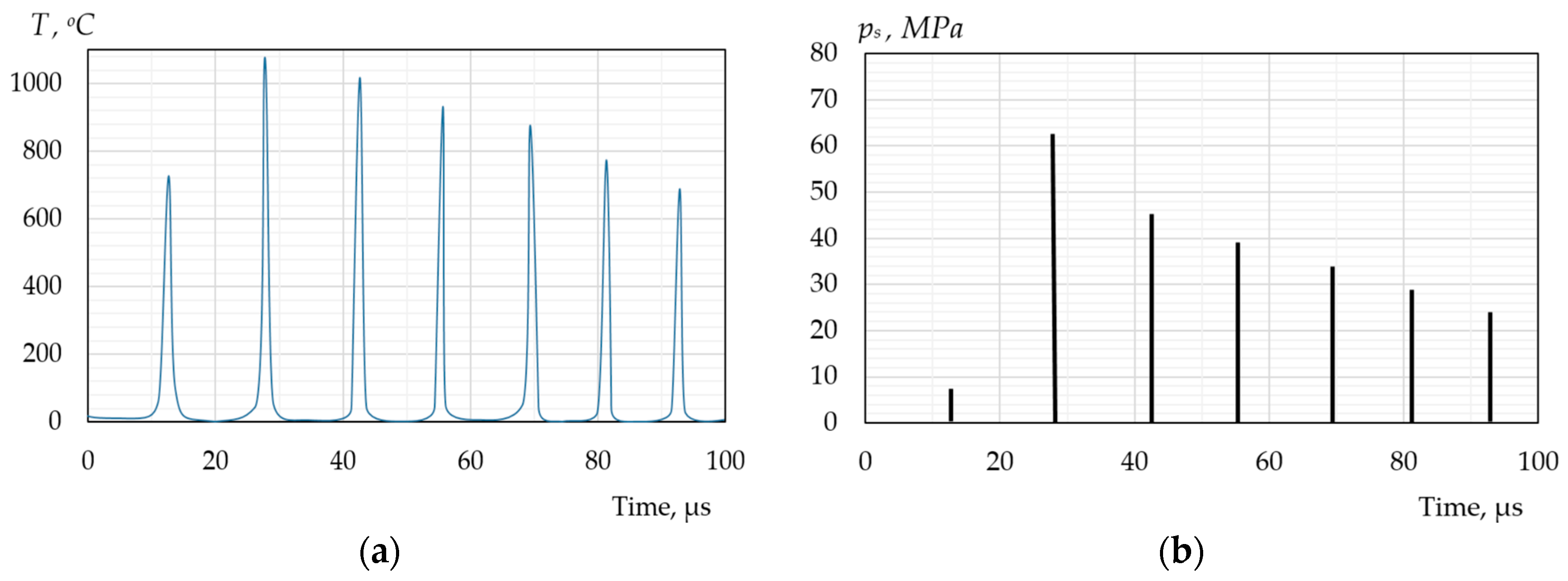
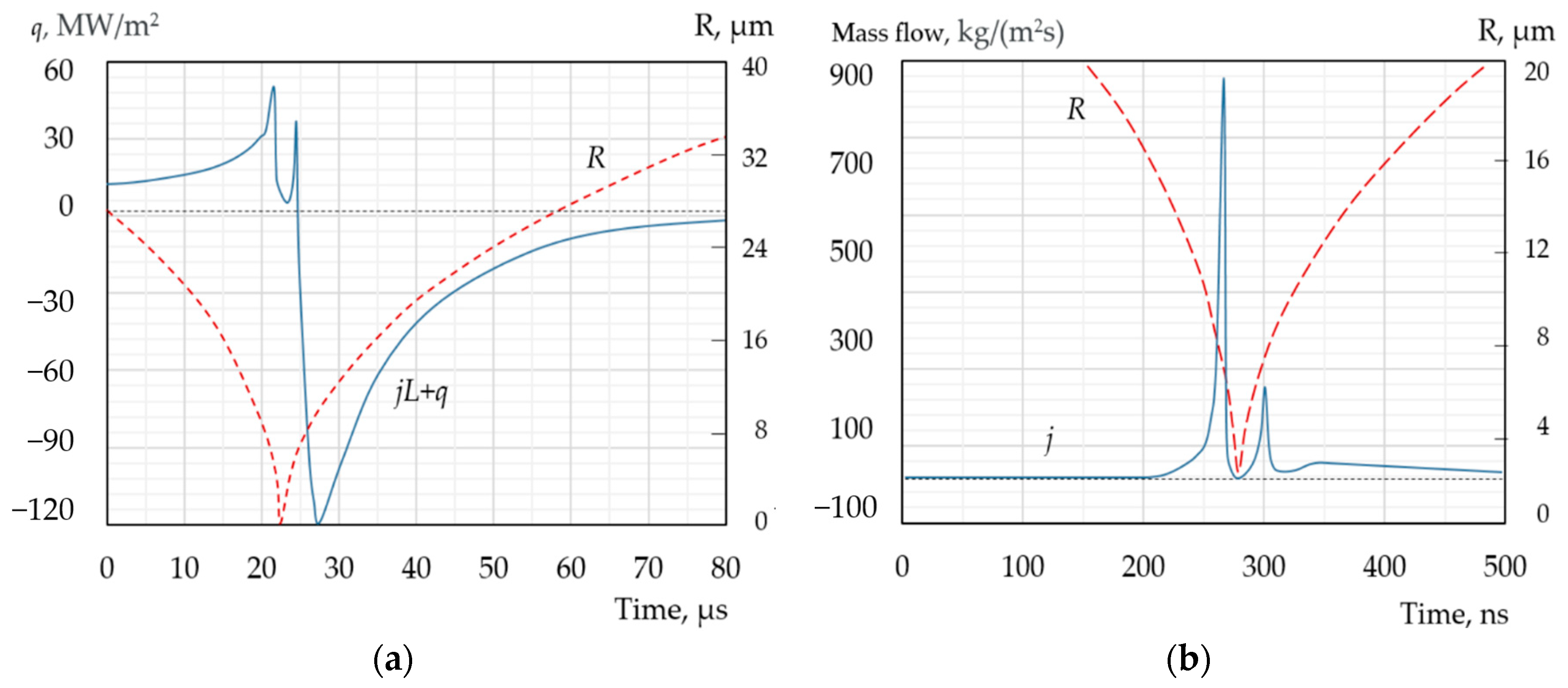
The stage of maximum bubble compression is characterised by the most intense heat and mass transfer across the interface, accompanied by the most vigorous evaporation and condensation processes, as illustrated in Figure 2 and Figure 3. Although the peak values of the heat flux impulse jL + q during this stage reach extreme levels, the actual amount of thermal energy transferred through the bubble wall during this period is surprisingly small. This is attributed to the extremely short duration of the impulse, which limits the contribution of this energy to a negligible fraction of the total thermal energy accumulated in the bubble following the conversion of the kinetic energy into potential energy. These calculations are based on the model presented in [52,169,170,171,172].
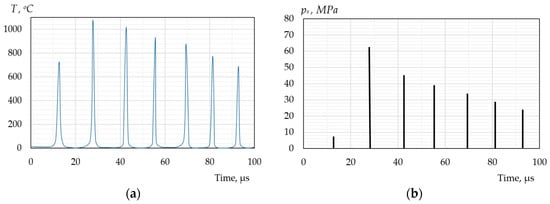
Figure 2.
Variation of vapour temperature (a) and vapour pressure (b) during the collapse of a steam bubble in a subcooled liquid: Tl0 = 20 °C; Ts0 = 130 °C; pl0 = 100 kPa; R0 = 100 µm.
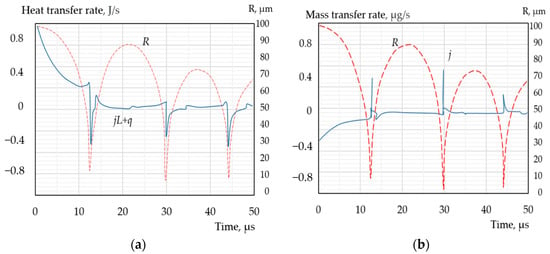
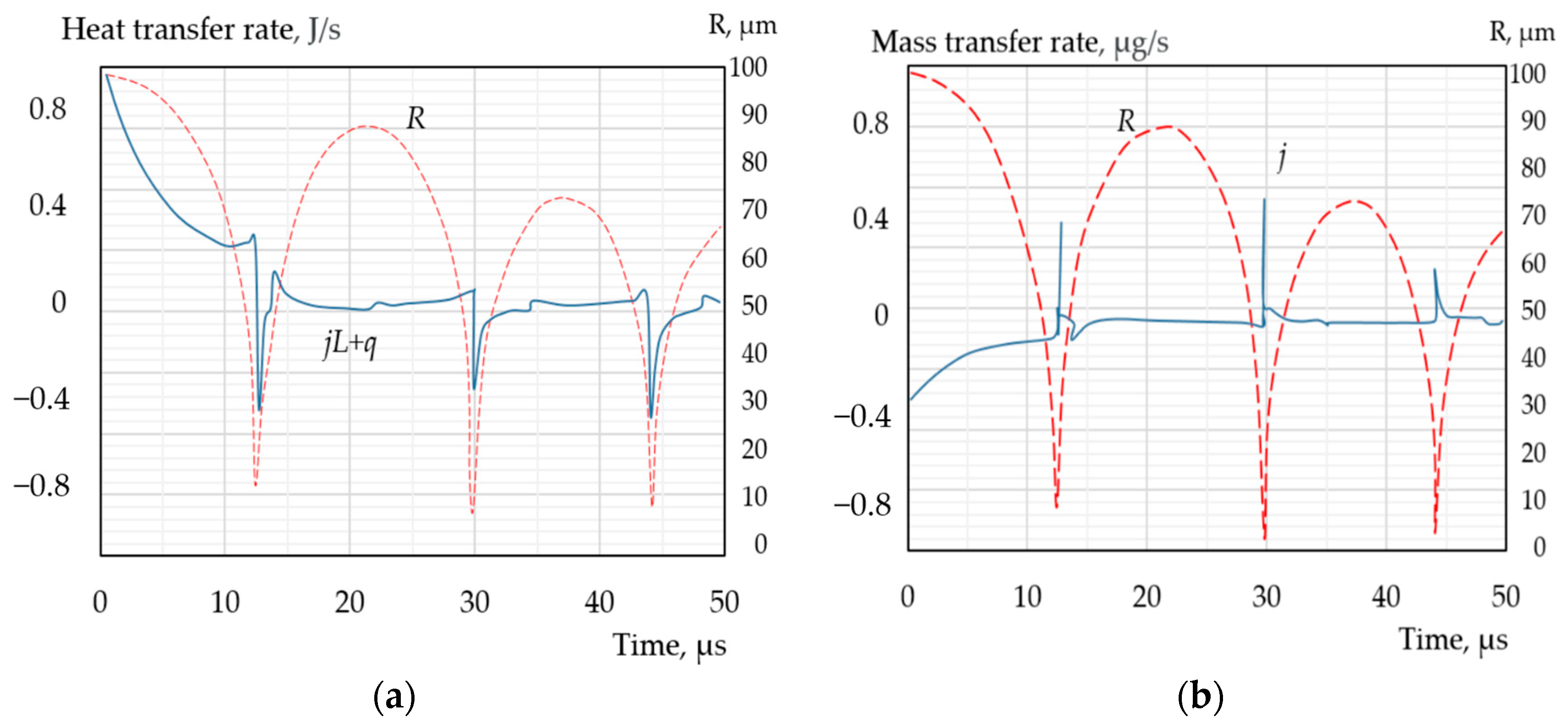
Figure 3.
Variation of heat flux intensity (a) and mass flux (b) across the surface of a steam bubble during its collapse in subcooled liquid: Tl0 = 20 °C; Ts0 = 130 °C; pl0 = 100 kPa; R0 = 100 µm.
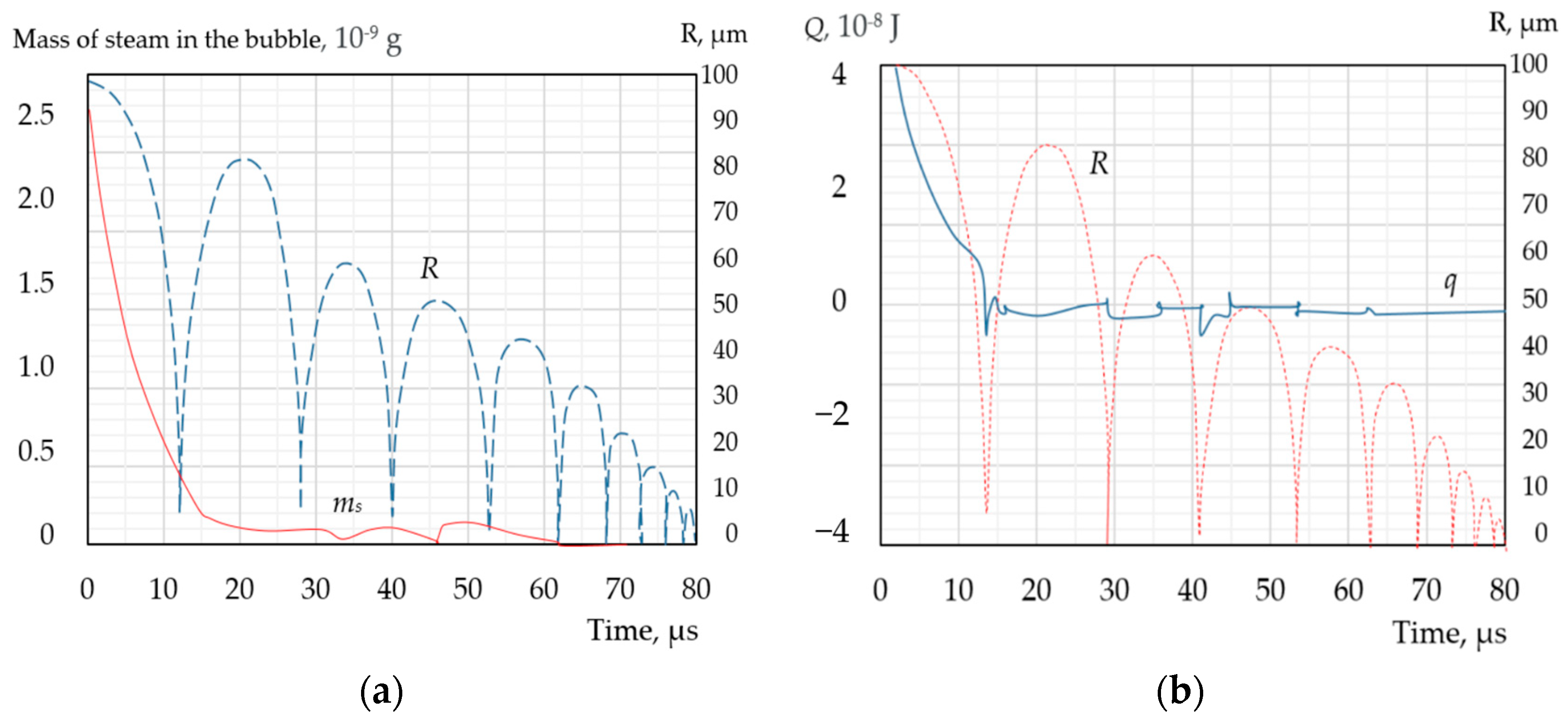
The intensity of mass transfer, j, also exhibits an extreme increase during the stage of maximum compression. However, the proportion of steam mass lost or gained during this period is negligibly small in the overall mass balance. Throughout the rest of the bubble’s development, the relatively low rates of heat and mass transfer can still have a significant impact on the bubble’s dynamics. Figure 4 and Figure 5 illustrate the changes in the bubble steam mass (ms) and the amount of heat (Q = mscs(Ts − Tint)) accumulated in the bubble during its oscillation. Despite the strong fluctuations in bubble size, both ms and Q decrease practically monotonically, with the greatest loss of steam mass and heat energy occurring in the first oscillation period.
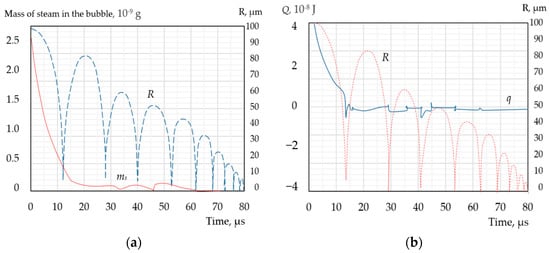
Figure 4.
Dynamic behaviour of the mass of steam (a) and the amount of heat (b) in a steam bubble during its collapse in a subcooled liquid. The dashed line shows the change in bubble radius: Tl0 = 20 °C; Ts0 = 130 °C; pl0 = 100 kPa; R0 = 100 µm.
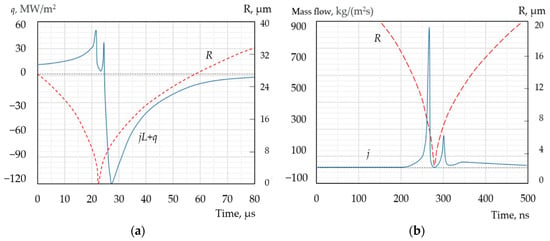
Figure 5.
The intensity of the heat flow jL + q (a) and the mass flow j (b) through the interphase surface at the stage of maximum compression of the bubble during its collapse in a subcooled liquid. The dotted curve shows the change in the radius of the bubble: Tl0 = 20 °C; Ts0 = 130 °C; pl0 = 100 kPa; R0 = 100 µm.
While the absolute amounts of energy and mass transferred across the bubble surface per unit time are not very large, considering the small size of the bubble at the moment of maximum compression, it is possible to estimate the magnitude of the specific mass and heat fluxes per unit surface area. As shown in Figure 5, the magnitude of the specific mass flux of steam condensing into the liquid or evaporating into the bubble is estimated to be in the order of 100 kg/m2s, while the specific energy flux is in the order of 100 MW/m2.
2.5. Impact of External Pressure Changes on Bubble Dynamics
The intensity of bubble growth is determined by the rate of pressure change in the system, pl, from its initial value pl = pb0 − 2σ/R to its final value plf. Here, pl represents the pressure in the liquid at a long distance from the bubble.
In most studies, bubble behaviour is modelled under the assumption of a gradual (sudden) change in liquid pressure [168,169,170,171,172]. Some researchers arbitrarily define the form of the function pl = f(τ), approximating it with a parabola, an exponential, or simply a straight line [173,174].
Analysis of these previous works suggests that regardless of the method of pressure change in the system, the nature of the actual pl = f(τ) curve can be well approximated by a cosine dependence of the form:
The value of plf represents the constant pressure in the liquid far from the bubble, which is established as a result of the change in external pressure. It indicates the final pressure level reached after the pressure change. The parameter Δτ denotes the duration of this external pressure change and characterises the time period over which the pressure transition occurs.
In general, the intensity of heat and mass transfer through the interface has little effect on the behaviour of the bubble in the inertial stage. At the short stage of maximum compression of the bubble, which is difficult to study experimentally, the kinetics of phase transitions have a decisive influence on the dynamics of the bubble.
In terms of the general approach to modelling, the modelling of cavitation processes is performed, as a rule, in relation to the analysis of a specific experiment without considering interphase heat transfer or the kinetics of phase transitions.
3. Discussion
Various modelling approaches have been developed to capture the complex dynamics of bubbles in liquids. These approaches can be broadly categorised into five main strategies.
- Thermophysical property-based approach. This method emphasises the temperature-dependent thermophysical properties of the bubble and surrounding liquid. The energy equation is employed to capture the temperature distribution and its influence on bubble behaviour. This approach provides a detailed representation of heat transfer and temperature effects within the bubble.
- Vapour pressure and temperature approach. In this approach, the focus is on determining the vapour pressure and corresponding temperature within the bubble. The energy equation is not explicitly used, simplifying the model’s equations but potentially affecting the accuracy of numerical predictions. This approach offers computational efficiency, but may compromise the accuracy of heat transfer simulations.
- Rayleigh equation approach. This method utilises the Rayleigh equation to calculate the current bubble radius based on the velocity of the phase boundary interface. It is primarily applied to the inertial stage of bubble dynamics, where inertia and pressure forces dominate the bubble’s motion. This approach is well-suited to capturing the initial growth and collapse of bubbles.
- Modified Rayleigh–Plesset equation approach. This approach employs a modified form of the Rayleigh–Plesset equation to determine the bubble radius during the dynamic stage of bubble dynamics. It accounts for the influence of heat and mass transfer on bubble behaviour. This approach provides a more comprehensive representation of bubble dynamics, including heat and mass transfer effects during the collapse and rebound stages.
- Bubble cluster dynamics approach. This method focusses on modelling the dynamics of bubble clusters, considering the interactions and collective behaviour of multiple bubbles within a cluster. The aim of this is to capture the influence of neighbouring bubbles on the overall dynamics of the cluster. This approach is particularly relevant for applications involving cavitation, where bubble clusters play a significant role.
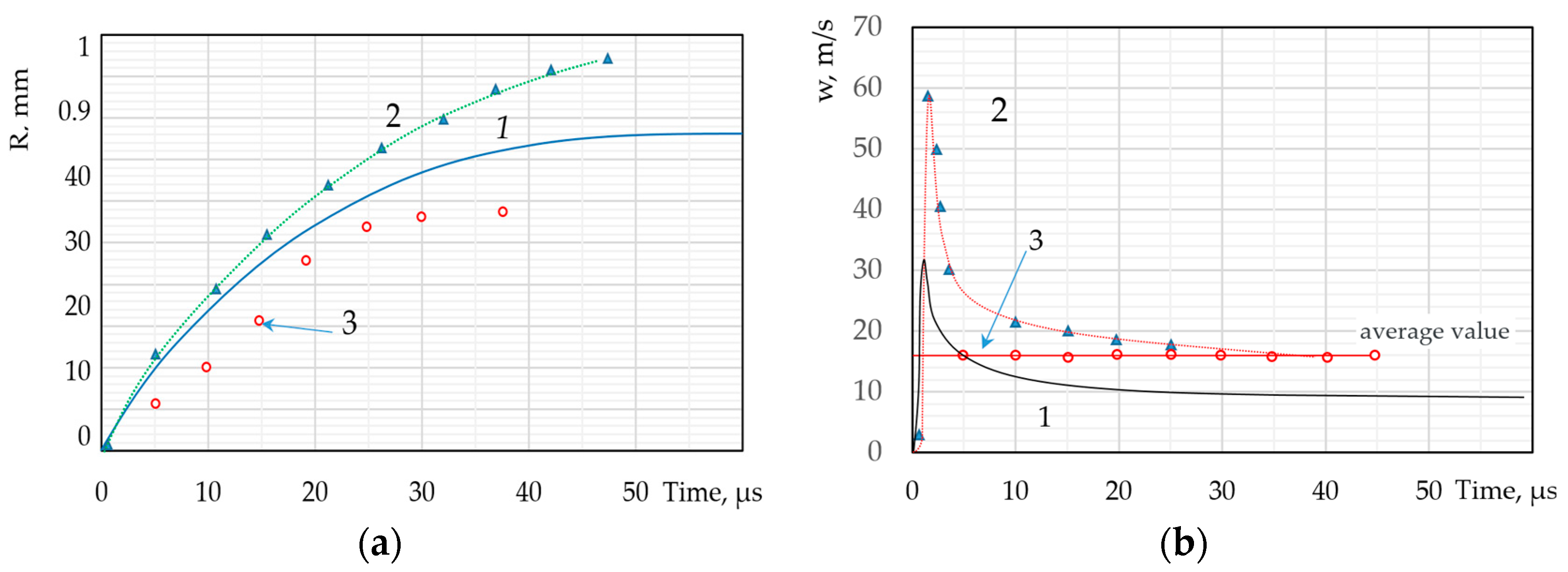
Almost all studies concluded that such an influence exists, but due to the stochastic nature of the appearance and growth of bubbles, this influence could not be generalised. However, in the cited works, a pattern is clearly evident, reflecting overestimated calculated data in comparison with experimental data. Experimental studies of the behaviour of bubbles are associated with certain difficulties, since the most dramatic changes in dynamics can be observed at the stage of maximum compression of the bubble, which lasts about 50 ns, while at the same time the thermophysical characteristics of the bubble change by 6 orders of magnitude. In this case, the use of the first four approaches will obviously not provide the required accuracy of the calculated forecasts. Physical processes in and around bubbles in such a short period of time occur in the nanoscale region. Under such conditions, the difficulties of conducting an experiment are obvious, and thus a direct experimental study of the dynamics of a bubble is beyond the scope of technical capabilities. Therefore, the assessment of effects in clusters, as a rule, is identified with the effects of a single bubble, which excludes the possibility of taking into account the influence of the dynamics of surrounding bubbles. They can reduce these effects, which we can observe in graphs presented by various authors (Figure 6).
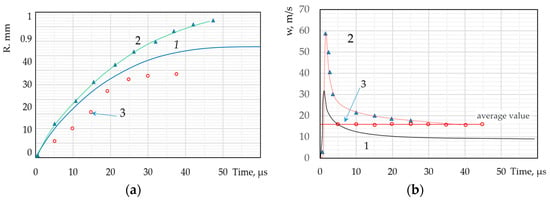
Figure 6.
(a,b)Dynamic properties of bubble clusters: 1—[52], 2—model [175], 3—experiment [176].
The calculated values on the graphs exceed the mean experimental value by an average of 50%, although the experimental estimate likely also has significant errors.
4. Conclusions
Analysis of the data in the literature shows that today, despite the large number of publications concerning theoretical studies of the dynamics of vapour bubbles, there are no mathematical models that provide an equally accurate prediction of the behaviour of an individual bubble and, moreover, bubble media, in any given range of operating parameters corresponding to real conditions.
The prevailing assumption of quasi-equilibrium during bubble formation and growth in boiling processes precludes the analysis of dynamic bubble–liquid interactions and their associated characteristics. In cavitation studies, the kinetics of phase transitions and the thermodynamic states of vapour and liquid are often disregarded or inaccurately represented, hindering the proper description of bubble dynamics in these phenomena. An analysis of works on bubble dynamics shows that when modelling the behaviour of bubbles, regardless of the applied direction of the model, the most important thing is an adequate representation of interfacial heat and mass transfer, the thermodynamic state of the vapour phase, and the temperature field in the vicinity of the bubble. In recent years, models have been improved in this direction.
Interfacial heat and mass transfer and the specific behaviour of a bubble in inertial and thermal modes are quite correctly described in many models for analysing the collapse of cavitation bubbles in a compressible liquid, which is confirmed by experimental data. These models are the most detailed of all and are used by many researchers when analysing experiments. The disadvantages of the model include the assumption of ideal steam, the inadequate approximation of the Clapeyron–Clausius equation, and the need for lengthy and complex calculations for a numerical solution, which is due to the consideration of liquid compressibility.
In the cited studies, heat transfer in the liquid phase surrounding the bubble and the formation of a nonstationary thermal layer were considered under the assumption of monotonic expansion or contraction of the bubble. This implies that the direction of heat flux across the phase interface remains constant throughout the process. This condition is met, for instance, in the growth of bubbles in boiling liquids or in the idealised case of the collapse of a vacuum cavity (Rayleigh’s problem).
However, when an increase in external pressure causes intense compression and subsequent collapse of bubbles, the bubbles can undergo several oscillations before their final disappearance, accompanied by periodic changes in vapour pressure and temperature by 2–3 orders of magnitude over an extremely short period (less than 1 µs). Consequently, within one oscillation period of the bubble, its surface temperature Ts can rise by hundreds of degrees relative to the temperature of the surrounding liquid Tl0 within fractions of a microsecond and then drop equally rapidly to a value Ts ≤ Tl0.
The assumption of a monotonic temperature distribution of the liquid within the thermal layer, which is justified when modelling the bubble growth process, is automatically carried over to mathematical models designed to analyse the collapse of cavitation bubbles. In these cases, this simplification can introduce significant errors, especially when evaluating peak temperature and pressure values in the stage of maximum bubble compression.
Because the oscillation period of the bubble is significantly shorter than the characteristic relaxation time of the temperature field in the liquid, the liquid layers adjacent to the surface do not have time to heat up and cool down so quickly, and the temperature distribution in the vicinity of the oscillating bubble cannot remain monotonic.
Based on evaluation of the dynamic parameters of bubbles in cavitation and critical compression processes, a hypothesis can be put forward about the thermal instability of the interfacial surface due to significant superheating of the vapour inside the bubble and the transition of the surrounding liquid into the supercritical temperature region. Mathematical models for these conditions have not yet been developed.
Numerous approaches and models have been developed that provide good-quality numerical predictions, but only for specific conditions and stages of bubble development. While these remarkable works can be used for numerical studies of bubble dynamics, the creation of a universal model remains a task for further research.
Author Contributions
Conceptualization, A.P.; methodology, A.P.; software, A.P.; validation, H.K.; formal analysis, A.P. and H.K.; investigation, A.P.; resources, A.P.; data curation, H.K.; writing—original draft preparation, A.P.; writing—review and editing, H.K.; visualization, H.K.; supervision, A.P.; project administration, A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| R | radius |
| τ | time |
| c | specific heat |
| λ | surface tension |
| j | mass flow |
| L | latent heat of vaporisation (condensation) |
| m | mass |
| p | pressure |
| q | specific heat flux |
| r | radial coordinate |
| T | temperature |
| wr | radial velocity |
| ρ | density |
| σ | interfacial tension coefficient |
| Indexes | |
| l | liquid |
| 0 | initial value |
| b | boiling |
| c | continuous phase |
| R | value of the parameter at the boundary with the bubble |
| sat | parameter value in saturation condition |
| s | vapour |
References
- Stringer, M.; Zeng, Z.; Zhang, X.; Chai, Y.; Li, W.; Zhang, J.; Ong, H.; Liang, D.; Dong, J.; Li, Y.; et al. Methodologies, technologies, and strategies for acoustic streaming-based acoustofluidics. Appl. Phys. Rev. 2023, 10, 011315. [Google Scholar] [CrossRef]
- Kumar, C.; Hejazian, M.; From, C.; Saha, S.C.; Sauret, E.; Gu, Y.; Nguyen, N.-T. Modeling of mass transfer enhancement in a magnetofluidic micromixer. Phys. Fluids 2019, 31, 063603. [Google Scholar] [CrossRef]
- Alcántara Avila, J.R.; Kong, Z.Y.; Lee, H.-Y.; Sunarso, J. Advancements in Optimization and Control Techniques for Intensifying Processes. Processes 2021, 9, 2150. [Google Scholar] [CrossRef]
- Gawande, G.; Mali, P.; Dhavane, P.; Nahata, Y. Hydrodynamic Cavitation—A Promising Technology for Water Treatment. Mater. Today Proc. 2024, 98. [Google Scholar] [CrossRef]
- Wang, B.; Su, H.; Zhang, B. Hydrodynamic cavitation as a promising route for wastewater treatment—A review. Chem. Eng. J. 2021, 412, 128685. [Google Scholar] [CrossRef]
- Zhang, K.; Zheng, J.; Xu, Y.; Liao, Z.; Huang, Y.; Lu, L. Enhanced fabrication of size-controllable chitosan-genipin nanoparticles using orifice-induced hydrodynamic cavitation: Process optimization and performance evaluation. Ultrason. Sonochemistry 2024, 106, 106899. [Google Scholar] [CrossRef]
- Tian, Z.; Shang, Q.; Pan, X.; Zhang, R.; Hua, M.; Zhao, Y.; Jiang, J. Experimental study on explosive boiling mechanism of superheated liquid containing ethanol impurities under rapid depressurization. Process Saf. Environ. Prot. 2022, 168, 443–453. [Google Scholar] [CrossRef]
- Pan, X.; He, L.; Tian, Z.; Zhang, R.; Hua, M.; Fang, Y.; Jiang, J. Experimental research on the explosion boiling mechanism of superheated liquids containing short chain alcohol impurities with different boiling points. Appl. Therm. Eng. 2024, 238, 121998. [Google Scholar] [CrossRef]
- Gao, W.; Qi, J.; Zhang, J.; Chen, G.; Wu, D. An experimental study on explosive boiling of superheated droplets in vacuum spray flash evaporation. Int. J. Heat Mass Transf. 2019, 144, 118552. [Google Scholar] [CrossRef]
- Pavlenko, A.M.; Koshlak, H. Application of Thermal and Cavitation Effects for Heat and Mass Transfer Process Intensification in Multicomponent Liquid Media. Energies 2021, 14, 7996. [Google Scholar] [CrossRef]
- Pavlenko, A. Energy conversion in heat and mass transfer processes in boiling emulsions. Therm. Sci. Eng. Prog. 2020, 15, 100439. [Google Scholar] [CrossRef]
- Pavlenko, A.M. Dispersed phase breakup in boiling of emulsion. Heat Transf. Res. 2018, 49, 633–641. [Google Scholar] [CrossRef]
- Pavlenko, A.M. Change of emulsion structure during heating and boiling. Int. J. Energy A Clean Environ. 2019, 20, 291–302. [Google Scholar] [CrossRef]
- Plesset, M.S.; Prosperetti, A. Bubble dynamics and cavitation. Annu. Rev. Fluid Mech. 1977, 9, 145–185. [Google Scholar] [CrossRef]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical Basis and Validation of the Full Cavitation Model. ASME J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Zwart, P.; Gerber, A.; Belamr, T. A Two-Phase Flow Model for Predicting Cavitation Dynamics. In Multiphase flow, Proceedings of the ICMF 2004 International Conference on Multiphase Flow, Yokohama, Japan, 30 May–3 June 2004; Yokohama Pacifico Conference Center: Yokohama, Japan; p. 2, Paper No. 152.
- Abu-Nab, A.K.; Hakami, A.M.; Abu-Bakr, A.F. Charged Cavitation Multibubbles Dynamics Model: Growth Process. Mathematics 2024, 12, 569. [Google Scholar] [CrossRef]
- Cogné, C.; Labouret, S.; Peczalski, R.; Louisnard, O.; Baillon, F.; Espitalier, F. Theoretical model of ice nucleation induced by acoustic cavitation. Part 1: Pressure and temperature profiles around a single bubble. Ultrason. Sonochemistry 2016, 29, 447–454. [Google Scholar] [CrossRef]
- Podbevšek, D.; Lokar, Ž.; Podobnikar, J.; Petkovšek, R.; Dular, M. Experimental evaluation of methodologies for single transient cavitation bubble generation in liquids. Exp. Fluids 2021, 62, 167. [Google Scholar] [CrossRef]
- Dular, M.; Coutier-Delgosha, O. Thermodynamic effects during growth and collapse of a single cavitation bubble. J. Fluid Mech. 2013, 736, 44–66. [Google Scholar] [CrossRef]
- Lam, J.; Lombard, J.; Dujardin, C.; Ledoux, G.; Merabia, S.; Amans, D. Dynamical study of bubble expansion following laser ablation in liquids. Appl. Phys. Lett. 2016, 108, 074104. [Google Scholar] [CrossRef]
- Mancas, S.C.; Rosu, H.C. Evolution of spherical cavitation bubbles: Parametric and closed-form solutions. Phys. Fluids 2016, 28, 022009. [Google Scholar] [CrossRef]
- Plesset, M.; Zwick, A. The growth of vapor bubbles in superheated liquids. J. Appl. Phys. 1954, 25, 493–500. [Google Scholar] [CrossRef]
- Prosperetti, A.; Plesset, M.S. Vapour-bubble growth in a superheated liquid. J. Fluid Mech. 1978, 85, 349–368. [Google Scholar] [CrossRef]
- Li, J.; Carrica, P.M. A population balance cavitation model. Int. J. Multiph. Flow 2021, 138, 103617. [Google Scholar] [CrossRef]
- Ghahramani, E.; Ström, H.; Bensow, R. Numerical simulation and analysis of multi-scale cavitating flows. J. Fluid Mech. 2021, 922, A22. [Google Scholar] [CrossRef]
- Dumond, J.J.; Magagnato, F.; Class, A. Stochastic-field cavitation model. Phys. Fluids 2013, 25, 073302. [Google Scholar] [CrossRef]
- Denner, F.; Evrard, F.; van Wachem, B. Modeling Acoustic Cavitation Using a Pressure-Based Algorithm for Polytropic Fluids. Fluids 2020, 5, 69. [Google Scholar] [CrossRef]
- Wang, Z.; Li, L.; Li, X.; Zhu, Z.; Yang, S.; Yang, G. Investigation on multiscale features of cavitating flow in convergent-divergent test section using Eulerian–Lagrangian method. Int. J. Mech. Sci. 2023, 238, 107853. [Google Scholar] [CrossRef]
- Budich, B.; Schmidt, S.J.; Adams, N.A. Numerical simulation and analysis of condensation shocks in cavitating flow. J. Fluid Mech. 2018, 838, 759–813. [Google Scholar] [CrossRef]
- Asnaghi, A.; Svennberg, U.; Bensow, R.E. Numerical and experimental analysis of cavitation inception behaviour for high-skewed low-noise propellers. Appl. Ocean. Res. 2018, 79, 197–214. [Google Scholar] [CrossRef]
- Kinzel, M.P.; Lindau, J.W.; Kunz, R.F. An Evaluation of CFD Cavitation Models using Streamline Data. In Proceedings of the 10th International Symposium on Cavitation (CAV2018); Katz, J., Ed.; ASME Press: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Sun, L.; Guo, P.; Luo, X. Numerical investigation on inter-blade cavitation vortex in a Franics turbine. Renew. Energy 2020, 158, 64–74. [Google Scholar] [CrossRef]
- Yilmaz, N.; Aktas, B.; Atlar, M.; Fitzsimmons, P.A.; Felli, M. An experimental and numerical investigation of propeller-rudder-hull interaction in the presence of tip vortex cavitation (TVC). Ocean Eng. 2020, 216, 108024. [Google Scholar] [CrossRef]
- Grandjean, H.; Jacques, N.; Zaleski, S. Shock propagation in liquids containing bubbly clusters: A continuum approach. J. Fluid Mech. 2012, 701, 304–332. [Google Scholar] [CrossRef]
- Sikirica, A.; Čarija, Z.; Lučin, I.; Grbčić, L.; Kranjčević, L. Cavitation Model Calibration Using Machine Learning Assisted Workflow. Mathematics 2020, 8, 2107. [Google Scholar] [CrossRef]
- Folden, T.S.; Aschmoneit, F.J. A classification and review of cavitation models with an emphasis on physical aspects of cavitation. Phys. Fluids 2023, 35, 081301. [Google Scholar] [CrossRef]
- Mikic, B.B.; Rohsenow, W.M.; Griffith, P. On Bubble Growth Rates. Int. J. Heat Mass Transf. 1970, 13, 657–666. [Google Scholar] [CrossRef]
- Li, W.; Yu, Z. Cavitation models with thermodynamic effect for organic fluid cavitating flows in organic Rankine cycle systems: A review. Therm. Sci. Eng. Prog. 2021, 26, 101079. [Google Scholar] [CrossRef]
- Li, L.; Wang, Z.; Li, X.; Zhu, Z. Multiscale modeling of tip-leakage cavitating flows by a combined volume of fluid and discrete bubble model. Phys. Fluids 2021, 33, 062104. [Google Scholar] [CrossRef]
- Li, L.; Huo, Y.; Wang, Z.; Li, X.; Zhu, Z. Large eddy simulation of tip-leakage cavitating flow using a multiscale cavitation model and investigation on model parameters. Phys. Fluids 2021, 33, 092104. [Google Scholar] [CrossRef]
- Adamkowski, A.; Henke, A.; Lewandowski, M. Resonance of torsional vibrations of centrifugal pump shafts due to cavitation erosion of pump impellers. Eng. Fail. Anal. 2016, 70, 56–72. [Google Scholar] [CrossRef]
- Ghahramani, E.; Jahangir, S.; Neuhauser, M.; Bourgeois, S.; Poelma, C.; Bensow, R.E. Experimental and numerical study of cavitating flow around a surface mounted semi-circular cylinder. Int. J. Multiph. Flow 2020, 124, 103191. [Google Scholar] [CrossRef]
- Reuter, F.; Mettin, R. Mechanisms of Single Bubble Cleaning. Ultrason. Sonochemistry 2016, 29, 550–562. [Google Scholar] [CrossRef] [PubMed]
- Han, W.; Gu, Z.; Li, R.; Mi, J.; Bai, L.; Deng, W. Study on the Dynamic Characteristics of Single Cavitation Bubble Motion near the Wall Based on the Keller–Miksis Model. Processes 2024, 12, 826. [Google Scholar] [CrossRef]
- Li, W.; Li, Z.; Han, W.; Yan, S.; Zhao, Q.; Chen, F. Measured viscosity characteristics of Fe3O4 ferrofluid in magnetic and thermal fields. Phys. Fluids 2023, 35, 012002. [Google Scholar] [CrossRef]
- Li, W.; Li, Z.; Qin, Z.; Yan, S.; Wang, Z.; Peng, S. Influence of the solution pH on the design of a hydro-mechanical magneto-hydraulic sealing device. Eng. Fail. Anal. 2022, 135, 106091. [Google Scholar] [CrossRef]
- Ding, Q.; Li, X.; Cui, Y.; Lv, J.; Shan, Y.; Liu, Y. Study on Non-Spherical Deformation Velocity of a Single Cavitation Bubble. Processes 2024, 12, 553. [Google Scholar] [CrossRef]
- He, X.; Peng, H.; Zhang, J.; Yuan, H. Multiple vapor cavitation bubble interactions with a thermal lattice Boltzmann method. Ocean. Eng. 2022, 266 Pt 4, 113058. [Google Scholar] [CrossRef]
- Gevari, M.T.; Abbasiasl, T.; Niazi, S.; Ghorbani, M.; Koşar, A. Direct and indirect thermal applications of hydrodynamic and acoustic cavitation: A review. Appl. Therm. Eng. 2020, 171, 115065. [Google Scholar] [CrossRef]
- Mulbah, C.; Kang, C.; Mao, N.; Zhang, W.; Shaikh, A.R.; Teng, S. A review of VOF methods for simulating bubble dynamics. Prog. Nucl. Energy 2022, 154, 104478. [Google Scholar] [CrossRef]
- Pavlenko, A. Numerical Modeling of the Behavior of Bubble Clusters in Cavitation Processes. Energies 2024, 17, 1741. [Google Scholar] [CrossRef]
- Zhang, A.-M.; Li, S.-M.; Cui, P.; Li, S.; Liu, Y.-L. A unified theory for bubble dynamics. Phys. Fluids 2023, 35, 033323. [Google Scholar] [CrossRef]
- Van Gorder, R.A. Dynamics of the Rayleigh–Plesset equation modelling a gas-filled bubble immersed in an incompressible fluid. J. Fluid Mech. 2016, 807, 478–508. [Google Scholar] [CrossRef]
- Ghazivini, M.; Hafez, M.; Ratanpara, A.; Kim, M. A review on correlations of bubble growth mechanisms and bubble dynamics parameters in nucleate boiling. J. Therm. Anal. Calorim. 2022, 147, 6035–6071. [Google Scholar] [CrossRef]
- Bhati, J.; Paruya, S. Numerical simulation of bubble dynamics in pool boiling at heated surface. Int. J. Heat Mass Transf. 2020, 152, 119465. [Google Scholar] [CrossRef]
- Chakraborty, B.; Gallo, M.; Marengo, M.; De Coninck, J.; Casciola, C.M.; Miche, N.; Georgoulas, A. Multi-scale modelling of boiling heat transfer: Exploring the applicability of an enhanced volume of fluid method in sub-micron scales. Int. J. Thermofluids 2024, 22, 100683. [Google Scholar] [CrossRef]
- Sullivan, P.; Dockar, D.; Borg, M.K.; Enright, R.; Pillai, R. Inertio-thermal vapour bubble growth. J. Fluid Mech. 2022, 948, A55. [Google Scholar] [CrossRef]
- Saritha, G.; Banerjee, R. Bubble dynamics of a pressure-driven cavitating flow in a micro-scale channel using a high density pseudo-potential Lattice Boltzmann method. Heat Transfer Eng. 2020, 41, 622–636. [Google Scholar] [CrossRef]
- Bardia, R.; Trujillo, M.F. Assessing the physical validity of highly-resolved simulation benchmark tests for flows undergoing phase change. Int. J. Multiph. Flow 2019, 112, 52–62. [Google Scholar] [CrossRef]
- Theofanous, T.G.; Patel, P.D. Universal relations for bubble growth. Int. J. Heat Mass Transf. 1976, 19, 425–429. [Google Scholar] [CrossRef]
- Miyatake, O.; Tanaka, I.; Lior, N. A simple universal equation for bubble growth in pure liquids and binary solutions with a nonvolatile solute. Int. J. Heat Mass Transf. 1997, 40, 1577–1584. [Google Scholar] [CrossRef]
- Li, W.; Yu, Z.; Kadam, S. An improved cavitation model with thermodynamic effect and multiple cavitation regimes. Int. J. Heat Mass Transf. 2023, 205, 123854. [Google Scholar] [CrossRef]
- Wang, Q.; Gu, J.; Li, Z.; Yao, W. Dynamic modeling of bubble growth in vapor-liquid phase change covering a wide range of superheats and pressures. Chem. Eng. Sci. 2017, 172, 169–181. [Google Scholar] [CrossRef]
- Forster, H.K.; Zuber, N. Growth of a Vapor Bubble in a Superheated Liquid. J. Appl. Phys. 1954, 25, 474–478. [Google Scholar] [CrossRef]
- Morlat, T. Bubble growth rate in superheated droplets. Therm. Sci. Eng. Prog. 2022, 36, 101505. [Google Scholar] [CrossRef]
- Lesage, F.J.; Siedel, S.; Cotton, J.S.; Robinson, A.J. A mathematical model for predicting bubble growth for low Bond and Jakob number nucleate boiling. Chem. Eng. Sci. 2014, 112, 35–46. [Google Scholar] [CrossRef]
- Li, J.; Liao, Y.; Bolotnov, I.A.; Zhou, P.; Lucas, D.; Li, Q.; Gong, L. Direct numerical simulation of heat transfer on a deformable vapor bubble rising in superheated liquid. Phys. Fluids 2023, 35, 023319. [Google Scholar] [CrossRef]
- Deike, L. Mass transfer at the ocean-atmosphere interface: The role of wave breaking, droplets, and bubbles. Annu. Rev. Fluid Mech. 2022, 54, 191–224. [Google Scholar] [CrossRef]
- Yi, Q.; Guo, P.; Zuo, Z.; Liu, S. Modeling of vapor bubble dynamics considering the metastable fluid state. Phys. Fluids 2024, 36, 023326. [Google Scholar] [CrossRef]
- Suslick, K.S.; Eddingsaas, N.C.; Flannigan, D.J.; Hopkins, S.D.; Xu, H. The Chemical History of a Bubble. Acc. Chem. Res. 2018, 51, 2169–2178. [Google Scholar] [CrossRef]
- Denner, F.; Schenke, S. Modeling acoustic emissions and shock formation of cavitation bubbles. Phys. Fluids 2023, 35, 012114. [Google Scholar] [CrossRef]
- Ando, K.; Sugawara, M.; Sakota, R. Particle removal in ultrasonic water flow cleaning role of cavitation bubbles as cleaning agents. Solid State Phenom. 2021, 314, 218–221. [Google Scholar] [CrossRef]
- Ando, K.; Sakota, R.; Usui, H.; Ishibashi, T.; Matsuo, H.; Watanabe, K. Optimal injection distance in ultrasonic water flow cleaning. Solid State Phenom. 2023, 346, 258–262. [Google Scholar] [CrossRef]
- Mnich, D.; Reuter, F.; Denner, F.; Ohl, C.-D. Single cavitation bubble dynamics in a stagnation flow. J. Fluid Mech. 2024, 979, A18. [Google Scholar] [CrossRef]
- Shi, H.; Zhang, H.; Geng, L.; Qu, S.; Wang, X.; Nikrityuk, P.A. Dynamic behaviors of cavitation bubbles near biomimetic surfaces: A numerical study. Ocean. Eng. 2024, 292, 116628. [Google Scholar] [CrossRef]
- Pandit, A.V.; Sarvothaman, V.P.; Ranade, V.V. Estimation of chemical and physical effects of cavitation by analysis of cavitating single bubble dynamics. Ultrason. Sonochemistry 2021, 77, 105677. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.-N.; Ding, Z.-L.; Hu, J.-R.; Zheng, X.-X.; Yu, J.-X.; Hu, J.-S. Theoretical investigation on the cavitation bubble dynamics near three spherical particles based on Weiss theorem. J. Hydrodyn. 2023, 35, 1119–1130. [Google Scholar] [CrossRef]
- Chen, J.; Chen, T.; Geng, H.; Huang, B.; Cao, Z. Investigation on dynamic characteristics and thermal effects of single cavitation bubble in liquid nitrogen. Phys. Fluids 2024, 36, 023325. [Google Scholar] [CrossRef]
- Altay, R.; Sadaghiani, A.K.; Sevgen, M.I.; Şişman, A.; Koşar, A. Numerical and Experimental Studies on the Effect of Surface Roughness and Ultrasonic Frequency on Bubble Dynamics in Acoustic Cavitation. Energies 2020, 13, 1126. [Google Scholar] [CrossRef]
- Pavlenko, A.M.; Koshlak, H. Intensification of Gas Hydrate Formation Processes by Renewal of Interfacial Area between Phases. Energies 2021, 14, 5912. [Google Scholar] [CrossRef]
- Qin, Z.; Alehossein, H. Heat transfer during cavitation bubble collapse. Appl. Therm. Eng. 2016, 105, 1067–1075. [Google Scholar] [CrossRef]
- Yang, Y.; Shan, M.; Kan, X.; Duan, K.; Han, Q.; Juan, Y. Thermodynamic effects of gas adiabatic index on cavitation bubble collapse. Heliyon 2023, 9, e20532. [Google Scholar] [CrossRef] [PubMed]
- Choi, K.; Kim, S.; Kim, H.; Kim, C. Computational investigation on the non-isothermal phase change during cavitation bubble pulsations. Ocean. Eng. 2023, 285 Pt 2, 115414. [Google Scholar] [CrossRef]
- Tian, L.; Zhang, Y.; Yin, J.; Lv, L.; Zhang, J.; Zhu, J. Investigation on heat and mass transfer characteristics of a near-wall multi-cycle cavitation bubble and its thermal effects on the wall using an improved compressible multiphase model. Ocean. Eng. 2024, 298, 117118. [Google Scholar] [CrossRef]
- Bermudez-Graterol, J.M.; Nickaeen, M.; Skoda, R. Numerical simulation of spherical bubble collapse by a uniform bubble pressure approximation and detailed description of heat and mass transfer with phase transition. Appl. Math. Model. 2021, 96, 80–110. [Google Scholar] [CrossRef]
- Aganin, A.A.; Khismatullina, N.A. Influence of the phase interface mass transfer characteristics on the cavitation bubble collapse in water. Ocean. Eng. 2023, 283, 115013. [Google Scholar] [CrossRef]
- Wang, J.; Li, H.; Guo, W.; Wang, Z.; Du, T.; Wang, Y.; Abe, A.; Huang, C. Rayleigh-Taylor instability of cylindrical water droplet induced by laser-produced cavitation bubble. J. Fluid Mech. 2021, 919, A42. [Google Scholar] [CrossRef]
- Kim, C.; Choi, W.J.; Kang, W. Cavitation nucleation and its ductile-to-brittle shape transition in soft gels under translational mechanical impact. Acta Biomater. 2022, 142, 160–173. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Liao, Y.; Zhou, P.; Lucas, D.; Li, Q. Numerical study of flashing pipe flow using a TFM-PBM coupled method: Effect of interfacial heat transfer and bubble coalescence and breakup. Int. J. Therm. Sci. 2023, 193, 108504. [Google Scholar] [CrossRef]
- Yu, Z.; Li, J.; Zhang, X. A new hypothesis for cavitation nucleation in gas saturated solutions: Clustering of gas molecules lowers significantly the surface tension. Chin. J. Chem. Eng. 2022, 50, 347–351. [Google Scholar] [CrossRef]
- Khoo, M.T.; Venning, J.A.; Pearce, B.W.; Brandner, P.A. Nucleation and cavitation number effects on tip vortex cavitation dynamics and noise. Exp. Fluids 2021, 62, 216. [Google Scholar] [CrossRef]
- Pavlenko, A.; Koshlak, H.; Usenko, B. Heat and mass transfer in fluidized layer. Metall. Min. Ind. 2014, 6, 96–100. [Google Scholar]
- Dergarabedian, P. The rate of growth of vapor bubbles in superheated water. J Appl. Mech. 2021, 20, 537–545. [Google Scholar] [CrossRef]
- Zhou, G.; Prosperetti, A. Modelling the thermal behaviour of gas bubbles. J. Fluid Mech. 2020, 901, R3. [Google Scholar] [CrossRef]
- Cheng, F.; Ji, W. Numerical and experimental study on dynamic characteristics of cavitation bubbles. Ind. Lubr. Tribol. 2018, 70, 1119–1126. [Google Scholar] [CrossRef]
- Wu, P.; Bai, L.; Lin, W.; Wang, X. Mechanism and dynamics of hydrodynamic-acoustic cavitation (HAC). Ultrason. Sonochemistry 2018, 49, 89–96. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; He, X.; Peng, H.; Lin, Y.; Zhang, J. Mesoscopic modeling of vapor cavitation bubbles collapse and interaction in near-wall region with a pseudopotential lattice Boltzmann method. Phys. Fluids 2022, 34, 092012. [Google Scholar] [CrossRef]
- Orthaber, U.; Zevnik, J.; Petkovšek, R.; Dular, M. Cavitation bubble collapse in a vicinity of a liquid-liquid interface—Basic research into emulsification process. Ultrason. Sonochemistry 2020, 68, 105224. [Google Scholar] [CrossRef]
- Peng, C.; Tian, S.; Li, G.; Sukop, M.C. Single-component multiphase lattice Boltzmann simulation of free bubble and crevice heterogeneous cavitation nucleation. Phys. Rev. E 2018, 98, 023305. [Google Scholar] [CrossRef]
- Liang, X.-X.; Linz, N.; Freidank, S.; Paltauf, G.; Vogel, A. Comprehensive analysis of spherical bubble oscillations and shock wave emission in laser-induced cavitation. J. Fluid Mech. 2022, 940, A5. [Google Scholar] [CrossRef]
- Geng, S.; Yao, Z.; Zhong, Q.; Du, Y.; Xiao, R.; Wang, F. Propagation of Shock Wave at the Cavitation Bubble Expansion Stage Induced by a Nanosecond Laser Pulse. J. Fluids Eng. 2021, 143, 051209. [Google Scholar] [CrossRef]
- Peng, K.; Tian, S.; Zhang, Y.; Li, J.; Qu, W.; Li, C. The violent collapse of vapor bubbles in cryogenic liquids. Ultrason. Sonochemistry 2024, 104, 106845. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Luo, K.; Chen, X.; Li, D.; Jia, L. A new cavitation model considering inter-bubble action. Int. J. Nav. Archit. Ocean. Eng. 2021, 13, 566–574. [Google Scholar] [CrossRef]
- Liang, L.; Xu, L.; Zhang, H.; Bing, C.; Lihai, C. The numerical investigationon bubble interaction dynamics in hydrodynamic cavitation. Mechanics 2021, 27, 115. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, G.; Zhang, J.; Tian, M.; Li, S. The bubble merger in rectangular microchannels during boiling processes based on conjugate heat transfer. Appl. Therm. Eng. 2024, 247, 123093. [Google Scholar] [CrossRef]
- Pavlenko, A.M.; Basok, B.I. Kinetics of water evaporation from emulsions. Heat Transf. Res. 2005, 36, 425–430. [Google Scholar] [CrossRef]
- Pavlenko, A.M.; Basok, B.I.; Avramenko, A.A. Heat conduction of a multi-layer disperse particle of emulsion. Heat Transf. Res. 2005, 36, 55–61. [Google Scholar] [CrossRef]
- Pavlenko, A.M. Thermodynamic Features of the Intensive Formation of Hydrocarbon Hydrates. Energies 2020, 13, 3396. [Google Scholar] [CrossRef]
- Wang, Q. Multi-oscillations of a bubble in a compressible liquid near a rigid boundary. J. Fluid Mech. 2014, 745, 509–536. [Google Scholar] [CrossRef]
- Wang, Q.X.; Blake, J.R. Non-spherical bubble dynamics in a compressible liquid. Part 1. Travelling acoustic wave. J. Fluid Mech. 2010, 659, 191–224. [Google Scholar] [CrossRef]
- Zhang, A.M.; Wang, S.P.; Wu, G.X. Simulation of bubble motion in a compressible liquid based on the three dimensional wave equation. Eng. Anal. Bound. Elem. 2013, 37, 1179–1188. [Google Scholar] [CrossRef]
- Tian, Z.-L.; Liu, Y.-L.; Zhang, A.-M.; Tao, L. Energy dissipation of pulsating bubbles in compressible fluids using the Eulerian finite-element method. Ocean. Eng. 2020, 196, 106714. [Google Scholar] [CrossRef]
- Xiao, W.; Zhang, A.M.; Wang, S.P. Investigation of bubble dynamics of underwater explosion based on improved compressible numerical model. Appl. Ocean. Res. 2016, 59, 472–482. [Google Scholar] [CrossRef]
- Liu, J.; Xiao, W.; Yao, X. Pressure characteristics of a nonspherical underwater explosion bubble in a compressible fluid. Phys. Fluids 2024, 36, 057145. [Google Scholar] [CrossRef]
- Prosperetti, A.; Lezzi, A. Bubble dynamics in a compressible liquid. Part 1. First-order theory. J. Fluid Mech. 1986, 168, 457–478. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, X.; Zhang, Y. A single oscillating bubble in liquids with high Mach number. Ultrason. Sonochemistry 2022, 85, 105985. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Li, Z.; Han, W.; Tan, S.; Yan, S.; Wang, D.; Yang, S. Time-mean equation and multi-field coupling numerical method for low-Reynolds-number turbulent flow in ferrofluid. Phys. Fluids 2023, 35, 125145. [Google Scholar] [CrossRef]
- Fourest, T.; Deletombe, E.; Faucher, V.; Arrigoni, M.; Dupas, J.; Laurens, J.-M. Comparison of Keller–Miksis model and finite element bubble dynamics simulations in a confined medium. Application to the Hydrodynamic Ram. Eur. J. Mech. B/Fluids 2018, 68, 66–75. [Google Scholar] [CrossRef]
- Wang, Q.; Sandberg, M.; Lin, Y.; Yin, S.; Hang, J. Impacts of Urban Layouts and Open Space on Urban Ventilation Evaluated by Concentration Decay Method. Atmosphere 2017, 8, 169. [Google Scholar] [CrossRef]
- Zanje, S.; Iyer, K.; Murallidharan, J.S.; Punekar, H.; Gupta, V.K. Development of generalized bubble growth model for cavitation and flash boiling. Phys. Fluids 2021, 33, 077116. [Google Scholar] [CrossRef]
- Bardia, R.; Trujillo, M.F. An improved categorization of vapor bubble collapse: Explaining the coupled nature of hydrodynamic and thermal mechanisms. Int. J. Heat Mass Transf. 2019, 145, 118754. [Google Scholar] [CrossRef]
- Colombet, D.; Da Silva, E.G.; Fortes-Patella, R. On numerical simulation of cavitating flows under thermal regime. Int. J. Heat Mass Transf. 2017, 105, 411–428. [Google Scholar] [CrossRef]
- Chen, T.; Huang, B.; Wang, G.; Wang, K. Effects of fluid thermophysical properties on cavitating flows. J. Mech. Sci. Technol. 2015, 29, 4239–4246. [Google Scholar] [CrossRef]
- Chen, T.; Huang, B.; Wang, G.; Zhao, X. Numerical study of cavitating flows in a wide range of water temperatures with special emphasis on two typical cavitation dynamics. Int. J. Heat Mass Transf. 2016, 101, 886–900. [Google Scholar] [CrossRef]
- Zhu, J.; Zhao, D.; Xu, L.; Zhang, X. Interactions of vortices, thermal effects and cavitation in liquid hydrogen cavitating flows. Int. J. Hydrog. Energy 2016, 41, 614–631. [Google Scholar] [CrossRef]
- Kinzel, M.P.; Lindau, J.W.; Kunz, R.F. A Unified Homogenous Multiphase CFD Model for Cavitation. In Proceedings of the ASME 2017 Fluids Engineering Division Summer Meeting, Waikoloa, HI, USA, 30 July–3 August 2017; Volume 1B. [Google Scholar] [CrossRef]
- Pavlenko, A.; Koshlak, Y. Heat and Mass Transfer During Phase Transitions in Liquid Mixtures. Rocz. Ochr. Śr. 2019, 21, 234–249. [Google Scholar]
- Cattaneo, M.; Supponen, O. Shell viscosity estimation of lipid-coated microbubbles. Soft Matter 2023, 19, 5925–5941. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Habchi, C. Real-fluid phase transition in cavitation modeling considering dissolved non-condensable gas. Phys. Fluids 2020, 32, 032102. [Google Scholar] [CrossRef]
- Kähler, G.; Bonelli, F.; Gonnella, G.; Lamura, A. Cavitation inception of a van der Waals fluid at a sack-wall obstacle. Phys. Fluids 2015, 27, 123307. [Google Scholar] [CrossRef]
- Bidi, S.; Koukouvinis, P.; Papoutsakis, A.; Shams, A.; Gavaises, M. Numerical study of real gas effects during bubble collapse using a disequilibrium multiphase model. Ultrason. Sonochemistry 2022, 90, 106175. [Google Scholar] [CrossRef]
- Delale, C.F.; Pasinlioğlu, Ş. On the gas pressure inside cavitation bubbles. Phys. Fluids 2023, 35, 023330. [Google Scholar] [CrossRef]
- Peng, K.; Qin, F.G.F.; Jiang, R.; Qu, W.; Wang, Q. Production and dispersion of free radicals from transient cavitation Bubbles: An integrated numerical scheme and applications. Ultrason. Sonochemistry 2022, 88, 106067. [Google Scholar] [CrossRef]
- Nigmatulin, R.I.; Khabeev, N.S.; Nagiev, F.B. Dynamics, heat and mass transfer of vapour-gas bubbles in a liquid. Int. J. Heat Mass Transf. 1981, 24, 1033–1044. [Google Scholar] [CrossRef]
- Li, J.; Carrica, P.M. Numerical study of the cavitating flow over backward facing step with a polydisperse two-phase flow model. Phys. Fluids 2023, 35, 063313. [Google Scholar] [CrossRef]
- Denner, F. The Gilmore-NASG model to predict single-bubble cavitation in compressible liquids. Ultrason. Sonochemistry 2021, 70, 105307. [Google Scholar] [CrossRef]
- Bermudez-Graterol, J.M.; Skoda, R. Numerical simulation of bubble dynamics and segregation in binary heptane/dodecane mixtures. J. Fluid Mech. 2022, 947, A9. [Google Scholar] [CrossRef]
- Joshi, S.; Franc, J.P.; Ghigliotti, G.; Fivel, M. Bubble collapse induced cavitation erosion: Plastic strain and energy dissipation investigations. J. Mech. Phys. Solids 2020, 134, 103749. [Google Scholar] [CrossRef]
- Schmidt, D.; Gopalakrishnan, S.; Jasak, H. Multi-dimensional simulation of thermal non-equilibrium channel flow. Int. J. Multiph. Flow 2010, 36, 284–292. [Google Scholar] [CrossRef]
- Stasheuski, S.; Keskinen, K.; Schmidt, D.P.; Vuorinen, V.; Hyvönen, J.; Kaario, O. Impact of modelling assumptions in cavitating flow of simplified injector. Int. J. Multiph. Flow 2024, 177, 104847. [Google Scholar] [CrossRef]
- Mottyll, S.; Skoda, R. Numerical 3D flow simulation of ultrasonic horns with attached cavitation structures and assessment of flow aggressiveness and cavitation erosion sensitive wall zones. Ultrason. Sonochem 2016, 31, 570–589. [Google Scholar] [CrossRef] [PubMed]
- Magnotti, G.M.; Battistoni, M.; Saha, K.; Som, S. Development and validation of the cavitation-induced erosion risk assessment tool. Transp. Eng. 2020, 2, 100034. [Google Scholar] [CrossRef]
- Trummler, T.; Schmidt, S.J.; Adams, N.A. Effect of stand-off distance and spatial resolution on the pressure impact of near-wall vapor bubble collapses. Int. J. Multiph. Flow 2021, 141, 103618. [Google Scholar] [CrossRef]
- Ahmed, A.; Duret, B.; Reveillon, J.; Demoulin, F.X. Numerical simulation of cavitation for liquid injection in non-condensable gas. Int. J. Multiph. Flow 2020, 127, 103269. [Google Scholar] [CrossRef]
- Santos, E.G.; Shi, J.; Venkatasubramanian, R.; Hoffmann, G.; Gavaises, M.; Bauer, W. Modelling and prediction of cavitation erosion in GDi injectors operated with E100 fuel. Fuel 2021, 289, 119923. [Google Scholar] [CrossRef]
- Trummler, T.; Schmidt, S.J.; Adams, N.A. Numerical investigation of non-condensable gas effect on vapor bubble collapse. Phys. Fluids 2021, 33, 096107. [Google Scholar] [CrossRef]
- Brandao, F.L.; Bhatt, M.; Mahesh, K. Numerical study of cavitation regimes in flow over a circular cylinder. J. Fluid Mech. 2020, 885, A19. [Google Scholar] [CrossRef]
- Pavlenko, A.; Koshlak, H.; Usenko, B. The processes of heat and mass exchange in the vortex devices. Metall. Min. Ind. 2014, 6, 55–59. [Google Scholar]
- Aganin, A.A.; Mustafin, I.N. Cavitation bubble collapse and rebound in water: Influence of phase transitions. Int. J. Multiph. Flow 2022, 157, 104256. [Google Scholar] [CrossRef]
- Ohashi, K.; Kobayashi, K.; Fujii, H.; Watanabe, M. Vapor condensation induced by fast-moving liquid film in the presence of noncondensable gas molecules. Int. Commun. Heat Mass Transf. 2023, 142, 106622. [Google Scholar] [CrossRef]
- Naranmandula, Q. Influence of large bubbles on cavitation effect of small bubbles in cavitation multi-bubbles. Acta Phys. Sin. 2019, 68, 167–175. [Google Scholar]
- Joshi, S.; Franc, J.P.; Ghigliotti, G.; Fivel, M. SPH modelling of a cavitation bubble collapse near an elasto-visco-plastic material. J. Mech. Phys. Solids 2019, 125, 420–439. [Google Scholar] [CrossRef]
- Aliabadi, A.; Taklifi, A. The effect of magnetic field on dynamics of gas bubbles in visco-elastic fluids. Appl. Math. Model. 2012, 36, 2567–2577. [Google Scholar] [CrossRef]
- Veshchunov, M. On the Theory of Two-Dimensional Homogeneous Nucleation on Close-Packed Faces of Crystals Growing from Vapour. J. Exp. Theor. Phys. 2021, 133, 449–454. [Google Scholar] [CrossRef]
- Ljung, A.L.; Lundström, T. Heat and mass transfer boundary conditions at the surface of a heated sessile droplet. Heat Mass Transf. 2017, 53, 3581–3591. [Google Scholar] [CrossRef]
- Hao, Y.; Zhang, Y.; Prosperetti, A. Mechanics of gas-vapor bubbles. Phys. Rev. Fluids 2017, 2, 034303. [Google Scholar] [CrossRef]
- Chen, T.; Wang, G.; Huang, B.; Wang, K. Numerical study of thermodynamic effects on liquid nitrogen cavitating flows. Cryogenics 2015, 70, 21–27. [Google Scholar] [CrossRef]
- Bhatt, M.; Mahesh, K. Numerical investigation of partial cavitation regimes over a wedge using large eddy simulation. Int. J. Multiph. Flow 2020, 122, 103155. [Google Scholar] [CrossRef]
- Yu, A.; Tang, Q.; Zhou, D.; Liu, J. Entropy production analysis in two-phase cavitation flows with thermodynamic cavitation model. Appl. Therm. Eng. 2020, 171, 115099. [Google Scholar] [CrossRef]
- Yu, A.; Tang, Q.; Zhou, D. Daqing Entropy production analysis in thermodynamic cavitating flow with the consideration of local compressibility. Int. J. Heat Mass Transf. 2020, 153, 119604. [Google Scholar] [CrossRef]
- Hong, F.; Yuan, J.; Zhou, B. Application of a new cavitation model for computations of unsteady turbulent cavitating flows around a hydrofoil. J. Mech. Sci. Technol. 2017, 31, 249–260. [Google Scholar] [CrossRef]
- Feng, H.; Wan, Y.; Fan, Z. Numerical investigation of turbulent cavitating flow in an axial flow pump using a new transport-based model. J. Mech. Sci. Technol. 2020, 34, 745–756. [Google Scholar] [CrossRef]
- Yuan, W.; Sauer, J.; Schnerr, G.H. Modeling and Computation of Unsteady Cavitation Flows in Injection Nozzles. Mécanique Ind. 2001, 2, 383–394. Available online: https://www.sciencedirect.com/science/article/pii/S1296213901011204 (accessed on 30 October 2001). [CrossRef]
- Priy, A.; Ahmad, I.; Khan, M.K.; Pathak, M. Bubble Interaction and Heat Transfer Characteristics of Microchannel Flow Boiling With Single and Multiple Cavities. ASME J. Thermal Sci. Eng. Appl. 2024, 16, 061010. [Google Scholar] [CrossRef]
- Vaca-Revelo, D.; Gnanaskandan, A. Numerical assessment of the condensation shock mechanism in sheet to cloud cavitation transition. Int. J. Multiph. Flow 2023, 169, 104616. [Google Scholar] [CrossRef]
- Long, X.; Liu, Q.; Ji, B.; Lu, Y. Numerical investigation of two typical cavitation shedding dynamics flow in liquid hydrogen with thermodynamic effects. Int. J. Heat Mass Transf. 2017, 109, 879–893. [Google Scholar] [CrossRef]
- Li, W.; Yu, Z. Cavitating flows of organic fluid with thermodynamic effect in a diaphragm pump for organic Rankine cycle systems. Energy 2021, 237, 121495. [Google Scholar] [CrossRef]
- Xue, R.; Ruan, Y.; Liu, X.; Cao, F.; Hou, Y. The influence of cavitation on the flow characteristics of liquid nitrogen through spray nozzles: A CFD study. Cryogenics 2017, 86, 42–56. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Hou, H.; Zhang, J.; Xu, C. Entropy production diagnostic analysis of energy consumption for cavitation flow in a two-stage LNG cryogenic submerged pump. Int. J. Heat Mass Transf. 2019, 129, 342–356. [Google Scholar] [CrossRef]
- Song, P.; Sun, J. Cryogenic cavitation mitigation in a liquid turbine expander of an air-separation unit through collaborative fine-tuned optimization of impeller and fairing cone geometries. Energies 2020, 13, 50. [Google Scholar] [CrossRef]
- Xu, B.; Feng, J.; Wan, F.; Zhang, D.; Shen, X.; Zhang, W. Numerical investigation of modified cavitation model with thermodynamic effect in water and liquid nitrogen. Cryogenics 2020, 106, 103049. [Google Scholar] [CrossRef]
- Li, W.; Yang, Y.; Shi, W.; Zhao, X.; Li, W. The correction and evaluation of cavitation model considering the thermodynamic effect. Math. Probl. Eng. 2018, 2018, 7217513. [Google Scholar] [CrossRef]
- Kim, H.; Kim, C. A physics-based cavitation model ranging from inertial to thermal regimes. Int. J. Heat Mass Transf. 2021, 181, 121991. [Google Scholar] [CrossRef]
- Shepherd, J.E.; Sturtevant, B. Rapid evaporation at the superheat limit. J. Fluid Mech. 1982, 121, 379–402. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Furzeland, R.M.; Ijpelaar, M.J.M. Rapid evaporation at the superheat limit. Int. J. Heat Mass Transf. 1988, 31, 1687–1700. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).