Power Semiconductor Junction Temperature and Lifetime Estimations: A Review

Abstract

The lifetime of power electronic systems is the focus of both the academic and industrial worlds. Today, compact systems present high switching frequency and power dissipation density, causing high junction temperatures and strong thermal fluctuations that affect their performance and lifetime. This paper is a review of the existing techniques for the electro-thermal modelling of Mosfet and IGBT devices regarding lifetime estimation. The advantages and disadvantages of the methodologies used to achieve lifetime prediction are discussed, and their benefits are highlighted. All the factors required to predict power electronic device lifetime, including Mosfet and IGBT electrical models, the computation of power losses, thermal models, temperature measurement and management, lifetime models, mission profiles, cycle counting, and damage accumulation, are described and compared.

1. Introduction

Power semiconductors, which are a key part of power converters, integrated power electronics modules, and inverters, are the most fragile components in such systems. Today, power-switching semiconductors, such as Mosfet and IGBT, are widely used in industrial applications that require more compact systems, thus reducing the physical size and weight of products. This power densification imposes increasing operational constraints in terms of voltage, current, electromagnetic interference, and temperature. Each device is characterized by a maximum admissible junction temperature, $T_j$. This modifies the device characteristics. When exceeding this maximum, the catalog exploitive parameters will not be maintained. Indeed, when taking all the factors into account, it is crucial to maintain the performance of the functional components in their new environment but, above all, to ensure their operational safety to avoid any failures.

This paper presents a detailed methodology to build up a thermal model for power devices. The lifetime evaluation procedure is shown in Figure 1, with the example of a boost converter. The datasheet information is interpolated with a lookup table in order to extrapolate the switching energy losses and approximate conduction losses. The Mosfet thermal analysis is studied using the Foster network; it provides a Mosfet thermal profile by respecting a mission profile. The rainflow-counting algorithm is then applied to predict the number of failure cycles in the functioning of swing temperature, mean junction temperature, and heating time. Then, a lifetime model is used to obtain the Mosfet failure cycle. Finally, Miner’s rule is employed to determine the accumulated damage of the power device.

A stepwise procedure is compulsory; it offers an overview of recent references in that direction.

The Mosfet and IGBT models, as well as the diode devices, are available to view in Section 2. The current–voltage characteristics [1] of Mosfet [2], IGBT [3], and the diodes are modeled in different ways with the help of transconductance [4], as polynomial fitting functions [3,5], with an additional square-root term [6] or as a function of junction temperature [2]. This section proposes several exponential degradation models of the drain-source resistance as in [4,7,8,9]. After the coefficient identification of the second or third-order polynomial fitting function, the current–voltage characteristics datasheet is compared with the fitting curve. Then, a voltage–current function is generated if necessary.

In Section 3, the power loss estimation is presented mainly for Mosfet, IGBT, and the diode. Both conduction and switching losses are calculated from [10,11], measuring $U_{ds}$ and $I_{ds}$ and integrating a current sensor installed in each leg of a Z-source inverter [12]. The generally applicable algorithm, introduced in [13], is based on an inverter’s instantaneous voltage and current values. In [3,4], the various time intervals of the commutation process are determined for Mosfet and IGBT. The conduction power loss is determined using the lookup table method in [2]. The same method generates the switching energy losses for the switching losses calculation, where the fitting functions of the datasheet points are necessary [5]. The switching energy estimated by [14] takes into account the dependence on the DC link voltage and the junction temperature; meanwhile, the authors of [6] developed an empirical switching loss model with a linear current dependency and an offset term by also using two exponential terms [15]. The linear relation between switching energies and the semiconductor current pointed out in [16] is proposed in the current-fed [17] and the voltage-fed [11] qZ-source inverter. The derived switching loss model for diode turn-on losses is developed in [15]. In [7], the diode conduction loss depends on the root mean square forward saturation current and the diode resistance. The switching power loss of a diode is defined as the product of the switching frequency and of the switching energy as a result of reverse recovery charge $Q_{rr}$ (calculated with the models of [3,18]).

Section 4 points out several approaches to using the thermal model as a simple conventional thermal network; the Cauer [19,20] and Foster models [21,22] do not describe the temperature distributions inside the device. Other models with a mathematical treatment, such as the Fourier series [23], Green’s function [24], or particle swarm optimization method [25], are considered complex analytical models due to various influence factors. One can quote numerical methods such as the finite element method (FEM) [26] and finite difference method (FDM) [27] for the simulation and thermal analysis of complex layout geometries, identifying hot spots and temperature distribution within the module. Ref. [28] studies the thermal coupling between neighboring devices, defining the thermal coupling model as a thermal impedance matrix [29]. By taking into consideration the material and layers, the determination of the temperature distribution within the module is the result of numerical methods such as FEM [26] and FDM [27]. These analyses take a very long time to compile. This is why the authors of [30] use Kirchhoff transformation to avoid extra memory storage. This is the case for Simulink piecewise linear electrical circuit simulation (PLECS) with less computational storage and less computational burden during simulation [31]. Yet, a high-accuracy temperature prediction device needs [32] FDM, an electro-thermal modeling method considering nonlinear thermal conductivity, requiring a high thermal impedance matrix order [33]. The thermal behavior in a multichip power module was observed using finite element analysis (FEA) in [34,35], extracting the thermal-impedance matrix by using 3D thermal simulation. Ref. [36] proposes a distributed thermal model that takes the cross-coupling effects among multiple heat sources into account, assisted by FEM. In the same section, several degradations affecting the semiconductor thermal impedance are reviewed: the physical degradation mechanism [37,38,39,40], wire bond degradation [41], plastic stress [41], and the degradation of the semiconductor’s solder joints [42].

Section 5 describes thermal measurement and management approaches in order to extend the power module lifetime and improve its reliability. In this paper, different direct contact methods to measure power device junction temperature are investigated, utilizing an infrared camera [43] or a temperature sensor integrated into the power semiconductor chip die area [44]. As an indirect method [45], the resistance is also used as an indicator of the temperature of the junction. With the turn-on drain-source voltage and current measurements, the drain-source resistance is derived, giving information about temperature [46]. The junction temperature is estimated in [6,47,48,49,50,51,52] by measuring temperature-sensitive electrical parameters. Because the temperature swing, $\Delta$$T_j$, has a significant impact on device reliability [53], many thermal management solutions are implemented to reduce $\Delta$$T_j$ [5,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68].

The empirical values and the physics of lifetime failure models are described in Section 6. In the Coffin-Mason model [69], only junction temperature variation, $\Delta T_j$, is taken into account, while the Arrhenius-Coffin-Manson model [70] takes into account the mean junction temperature. Then, [71] proposes the Norris-Landzberg model, which depends on frequency f. The Bayerer lifetime model [72] is related to load pulse duration, current per wire, voltage, wire diameter, $T_{jm}$, and $\Delta T_j$. Scheuermann and Schmidt [73] proposed a model similar to Bayerer, which uses curve fitting parameters and includes the influence of bond wire aspect ratio for lifetime evaluation. In [74,75,76,77], the strain-based model, the Basquin form, the Paris law, and the strain-stress energy model are defined. Then, in the same section, the accelerated power cycling test notion is addressed [78,79]. In [80], many Mosfets were tested experimentally until failure, i.e., the occurrence of an instantaneous increase in $\Delta T_j$. The authors of [7] point out that a variation in $\Delta R_{ds}$ up to 0.5 Ω of its initial value brings the device to failure. In [81], the authors confirm IGBT lifetime reduces with mean junction temperature increase. In [5], the Coffin-Manson-Arrhenius model coefficients are calculated; otherwise, three exponential accelerated power cycling tests are used.

Section 7 begins with identifying an appropriate mission profile to obtain a reliable assessment of device lifetime. Power semiconductors are the most fragile components and are heavily affected by mission profiles [82]. In [21], a 30-min automotive drive cycle was translated into a frequency and current mission profile for a 30 kW three-phase voltage source inverter. The authors of [2] used the input reference speed of an electric vehicle as the new European driving cycle speed profile. Ref. [83] investigates the reliability solutions of multichip module-based power converters embedded in rolling mill applications, considering vertical hoist acceleration as the mission profile. In an electric traction application [29], many speed and torque mission profiles are presented. For an installation in Denmark [84], daytime solar irradiance variation is considered as a mission profile. Ref. [84] demonstrates the impact of time resolution on the mission profile during clear-day and cloudy-day conditions. Wind speed fluctuations over time were recorded in a wind power generation system as a mission profile in [85]. Finally, the authors of [5] point out an important degradation factor of the Mosfet’s lifetime for chaotic compared to periodic current behavior, reducing it by half [86].

Various counting approaches are listed in Section 8. The maximum edge method is discussed in [87]. Comparative discussions between the rising edge and the rainflow-counting methods are presented in [88]. Temperature swing, $\Delta$$T_j$, minimum temperature, $T_{jmin}$, heating time, $t_{on}$, and current density per the wire parameters are used in [42,89] to predict the number of cycles to failure. The authors of [90] highlight that almost 90% of damage is caused by 10% of the total cycles having the largest temperature amplitudes. The Moshrefifar and Azamfar method [91] leads to more reasonable estimations of the fatigue life than that of the peak-counting method. Three-point rainflow counting was developed in [92] and standardized in [93]. Ref. [94] shows the equivalence of four-point and three-point rainflow-cycle-counting algorithms. In order to avoid data storage limitations, the “maximum range” and the “maximum time window” [95] criteria are added to the original rainflow-counting method. A conventional rainflow-counting method [96] that expanded upon three-parameter rainflow counting is used in [97] to predict solder joint fatigue. Ref. [98] develops a modified rainflow-counting algorithm based on [96,99] to extract temperature cycles. Ref. [100] reports rainflow counting as having the lowest relative error compared to other counting approaches. Because the offline counting method requests a complete loading profile, the authors of [53,101] propose an online rainflow-counting method.

Section 9 points out device thermal stress and reliability performance. The feedback model in [19] leads to more than 60% for the lifetime of an IGBT module based on low-frequency thermal loading. The two different aging models proposed in [7] induce an aging of 9.67 years and 13 years, respectively. If the number of electric vehicle charging times increases from 5 to 40 per day, the power module’s lifetime will be reduced by more than 85% [102]. In photovoltaic inverter semiconductors [22], the accumulated fatigue is 10 to 25% less for the averaged thermal profile than for the reduced profile. In the same application, a modular H-bridge lifetime is estimated at 13 years and 30 years for a single IGBT [103]. If the resolution of the mission profile increases from 1 s to 5 min, the estimated damage of a photovoltaic inverter power device is divided by two [84]. In a Buck converter [5], the accumulated fatigue of the chaotic mission profile is 10 to 65% higher than for the reduced profile. An IGBT power module lifetime is 15,000 years in a directly driven wind turbine [104] due to the average wind speed of 7 m/s.

Finally, Section 10 summarizes all the steps required for power electronic device lifetime prediction and discusses future research demands, opportunities, and perspectives.

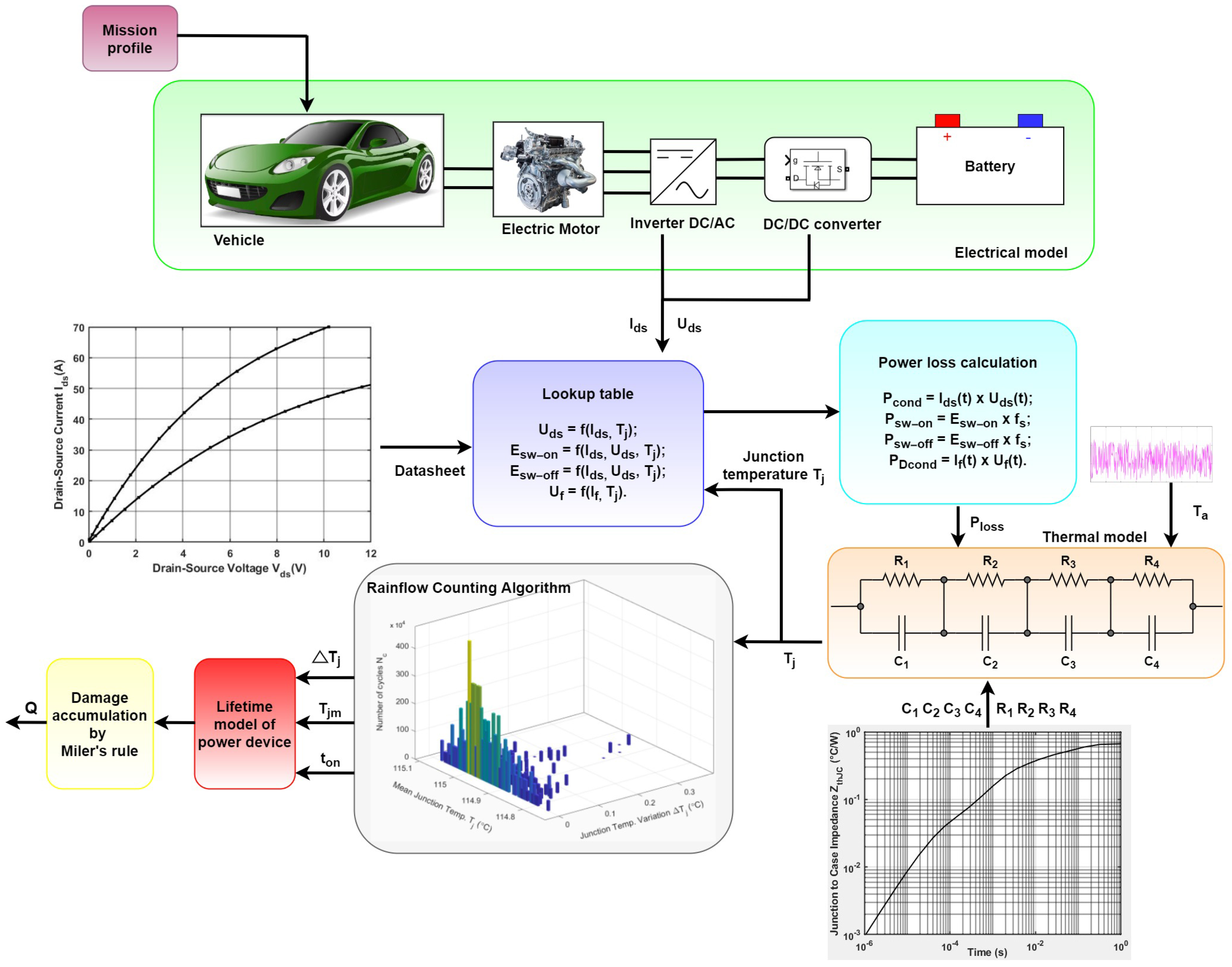
2. Electrical Model

Power semiconductor components are a part of power converters, integrated power electronics modules, and inverters. Based on the physical structures, the small-signal models of a Mosfet and an IGBT are shown in Figure 2. The drain-source current (Mosfet—Figure 2a) or the collector-emitter current (IGBT—Figure 2b) are modeled as a current source. These power devices are non-ideal transistors because of their parasitic elements of bone wires and/or the electric terminals, as well as the intrinsic nature of the device itself, which experiences Mosfet inductances (source inductance $L_s$, drain inductance $L_d$, and gate inductance $L_g$) and the Mosfet parasitic capacitances ($C_{gs}$, $C_{gd}$, and $C_{ds}$). The realistic electric model takes into consideration the source $R_s$, drain $R_d$, gate $R_g$, and drain-source $R_{ds}$ resistances. In the same way, the parasitic elements of the IGBT can be defined as inductances (collector inductance $L_c$, emitter inductance $L_e$, gate inductance $L_g$), capacitances ($C_{gc}$, $C_{ge}$, and $C_{ce}$) and gate, collector, and emitter resistances ($R_g$, $R_c$, and $R_e$, respectively). These parameters are compulsory to run the SimScape Mosfet model.

The parasitic elements have an influence on the dynamic characteristics of a power switch Mosfet or IGBT. The Mosfet model describes the three operational regions (off, linear, and saturation) according to the following equations, taking these parasitic elements into consideration:

$$\left\{\begin{array}{c}{I}_{ds}=0,\mathrm{if}{U}_{gs}<U_{th}\hfill \\ I_{ds}=k·\left[\left(U_{gs}-U_{th}\right)U_{ds}-{\displaystyle \frac{U_{ds}^2}{2}}\right](1+\lambda |U_{ds}\left|\right),\mathrm{if}0<U_{ds}<U_{gs}-U_{th}\hfill \\ I_{ds}={\displaystyle \frac{k}{2}}·{\left(U_{gs}-U_{th}\right)}^2(1+\lambda |U_{ds}\left|\right),\mathrm{if}{U}_{gs}-U_{th}<U_{ds}\hfill \end{array}\right.$$

(1)

where $U_{th}$ is the threshold voltage, k is the transistor gain, and $\lambda$ is the channel length modulation. For an IGBT [3], the collector-emitter current, $I_{ce}$, is described by

$$\left\{\begin{array}{c}{I}_{ce}=0,\mathrm{if}{U}_{ge}<U_{th}\hfill \\ I_{ce}=k·\left(U_{ge}-U_{th}-{\displaystyle \frac{U_{ce}}{2}}\right),\mathrm{if}{U}_{ce}<U_{ge}-U_{th}\hfill \\ I_{ce}={\displaystyle \frac{k}{2}}·{\left(U_{ge}-U_{th}\right)}^2,\mathrm{if}{U}_{ce}>U_{ge}-U_{th}\hfill \end{array}\right.$$

(2)

where $U_{ge}$ is the gate-emitter voltage, and $U_{ce}$ is the collector-emitter voltage.

In [105], an accurate temperature-dependent static model of a power Mosfet is presented. The model is composed of two equations related to linear and saturation operating regions, as per Equation (1); they ensure continuity and smooth transition in pinch-off regions with high precision. The peculiar features of Mosfet characteristics can be observed via a new formalism: (a) low gate voltages or moderate inversion regions and (b) quasi-saturation regions of high gate voltages, for which the drain current becomes less sensitive to gate voltage increase. In order to establish a Mosfet model, ref. [106] uses a continuous function to describe the Mosfet static characteristics, a parasitic parameter extraction method, and the nonlinear characteristics of inter-stage capacitances [107]. Ref. [108] develops an electrical equivalent circuit model of IRF740 10 A/400 V Mosfet, including linear and nonlinear electrical elements (resistors, capacitances, and controlled current source). The authors of [109] investigate different compact Mosfet models by employing capacitance models of $C_{gd}$, $C_{gs}$, and Cds dependent on $U_{gs}$ and $U_{ds}$ voltages. In [110], a new approach is presented for Mosfet electrical modeling. Inspired by the Curtice model, this model uses a mathematical function reflecting Mosfet output characteristics. Ref. [111] presents an IGBT model with dynamic and static collector current based on gate charge (obtained by measuring the voltage across the gate mirror circuit capacitance). This model does not require device structure parameters such as doping concentration, length, and thickness. The experimental results achieved a collector current error of less than 5.6%.

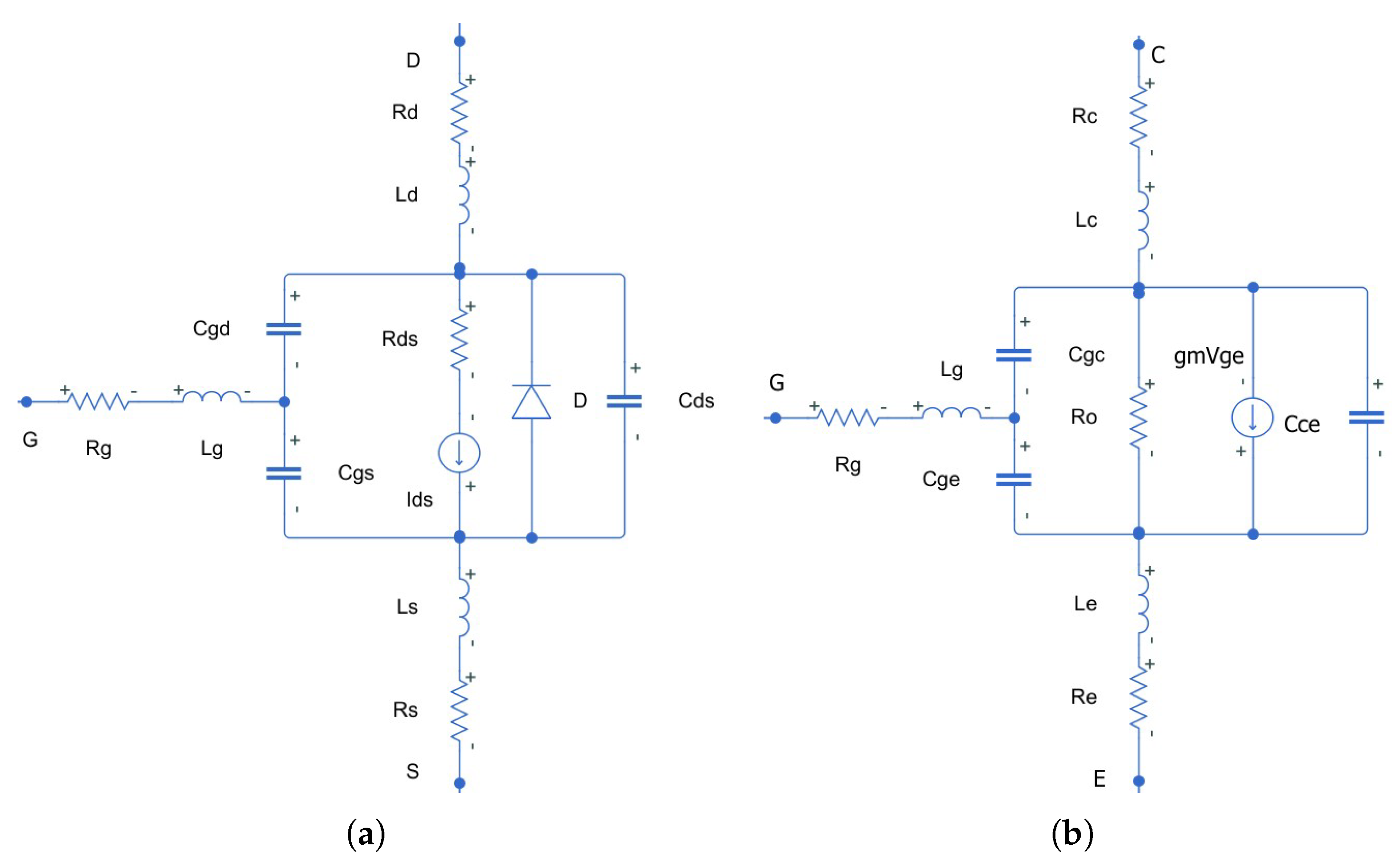
2.1. Mosfet Characteristic

Some elements are given by the datasheet, for example, from the static current–voltage characteristic $I_{ds}-U_{ds}$ (the dots in Figure 3a curve) and reverse diode of the Mosfet datasheet (the dots in Figure 3b curve). In [2], $U_{ds}$ and $I_{ds}$ are functions of junction temperature, $T_j$, as $U_{ds}\left(t\right)$ = f ($I_{ds}$(t), $T_j$). Based on [5], the following polynomial fitting functions are used to obtain fitting simulation curves of $I_{ds}-U_{ds}$ at two different junction temperatures, $T_j$ (here, at 25 °C and 150 °C):

$$I_{ds}\left(U_{ds}\right)=a_3·{U_{ds}}^3+a_2·{U_{ds}}^2+a_1·U_{ds}+a_0,$$

(3)

The coefficients $a_0$, $a_1$, $a_2$, and $a_3$ of the $I_{ds}-U_{ds}$ curves were fitted by using a Matlab R2020b curve fitting tool. Equation (3) can also be represented under the following form: $U_{ds}$ = $f\left(I_{ds}\right)$. During the saturation region, ref. [4] models the channel current with the transconductance $g_m$ and the gate-source voltage $U_{gs}$. It underlines a further dependence channel current and threshold voltage $U_{th}$ on the junction temperatures, $T_j$, as

$$i_{ch}=k_1·{\left[U_{gs}-U_{th}\left(T_j\right)\right]}^x+k_2,$$

(4)

$$U_{th}\left(T_j\right)=a{T}_j^2+b{T}_j+c,$$

(5)

$$g_m(i_{ch},T_j)=\sqrt[x]{k_1{i}_{ch}^x/(i_{ch}-k_2)}.$$

(6)

where a, b, c, $k_1$, $k_2$ and x are the curbe fitting parameters.

For the conduction loss estimation, $R_{ds}$ is required. For an IRFP340, ref. [7] proposed:

$$R_{ds}=\left(R_{ds-{25}^{°}\mathrm{C}}+\Delta R_{ds}\right)·{\left(1+{\displaystyle \frac{{\alpha }_M}{100}}\right)}^{T_j-{25}^{°}\mathrm{C}}$$

(7)

where ${\alpha }_M$ is a fitting coefficient, and $\Delta R_{ds}$ is an increment of $R_{ds}$ resistance caused by degradation. Based on the experimental results, the authors of [8] proposed an exponential degradation model as

$$R_{ds}\left(t\right)=R_{ds-{25}^{°}\mathrm{C}}+\alpha ·e^{\beta ·t}$$

(8)

where $\alpha$ and $\beta$ are coefficients of the fitting curve.

The authors of [4] show the dependence of this C2M0080120D Mosfet resistance on $I_{ds}$ and $T_j$:

$$R_{ds}=R_{ds-{25}^{°}\mathrm{C}}·{\left({\displaystyle \frac{I_{ds}}{I_{ds-ref}}}\right)}^{b_1}·{\left({\displaystyle \frac{T_j}{T_{j-ref}}}\right)}^{b_2}$$

(9)

where $I_{ds-ref}$ is the reference current, $T_{j-ref}$ is the reference temperature, and $b_1$ and $b_2$ are the fitting coefficients. The authors of [9] consider the temperature dependence of the drain-source resistance (for an IRFP4232) in the following form:

$$R_{ds}=R_{ds-{25}^{°}\mathrm{C}}·\left(T_j·{\displaystyle \frac{1.024·U_{ds}^{0.1124}}{100}}+{\displaystyle \frac{5-1.024·U_{ds}^{0.1124}}{4}}\right).$$

(10)

2.2. IGBT Characteristic

The collector–emitter characteristic can be presented as a linear function as

$$U_{ce}\left(I_{ce}\right)=U_{ce,0}+R_{ce}·I_{ce}.$$

(11)

In [3], the collector-emitter voltage, $U_{ce}$, is determined as a function of the collector–emitter current, $I_{ce}$, for an IGBT:

$$U_{ce}\left(I_{ce}\right)=c_3·{I_{ce}}^3+c_2·{I_{ce}}^2+c_1·I_{ce}+c_0.$$

(12)

$U_{ce}$ depends on device current, $I_{ce}$, and device junction temperature, $T_j$. However, the characteristic in the datasheet has a strong square root shape. This is why the authors of [6] proposed an additional square root term scaled by the factor $S_{ce}$ (providing a more faithful approach to the IGBT characteristic shape). In this case, the forward voltage equation of the IGBT is the following:

$$U_{ce}(I_{ce},T_{jIGBT})=U_{ce,0}+R_{ce}\left(T_{jIGBT}\right)·I_{ce}+S_{ce}\left(T_{jIGBT}\right)·\sqrt{I_{ce}},$$

(13)

2.3. Diode Characteristic

In [2], $U_f$ and $I_f$ are functions of junction temperature, $T_j$, as $U_f\left(t\right)$ = f($I_f$(t), $T_j$). The forward voltage, $U_f$, of a diode can be written as

$$U_f\left(I_f\right)=U_{thD}+R_f·I_f.$$

(14)

where $I_f$, $R_f$, and $U_{thD}$ are the diode forward current and resistance and the diode threshold voltage, respectively. The $I_f$ and $U_f$ variables are provided by the datasheet and are noted as datasheet points in Figure 3b. In [5], the authors compare the datasheet dots and fitted curves obtained using the following third-order polynomial fitting function:

$$I_f\left(U_f\right)=d_3·{U_f}^3+d_2·{U_f}^2+d_1·U_f+d_0,$$

(15)

where $U_f$ and $I_f$ represent a forward saturation voltage and the diode’s current, rspectively, and the coefficients $d_0$, $d_1$, $d_2$, and $d_3$ have been fitted using a Matlab curve fitting tool. In order to check model accuracy, these characteristics obtained via simulation were compared with the datasheet (at different temperatures). The forward voltage, $U_f$, depends on $I_f$ and device junction temperature, $T_j$. However, the authors of [6] developed a forward voltage, $U_f$, for the IGBT diode, similar to Equation (13):

$$U_f(I_f,T_{jD})=U_{thD}+R_f\left(T_{jD}\right)·I_f+S_f\left(T_{jD}\right)·\sqrt{I_f}.$$

(16)

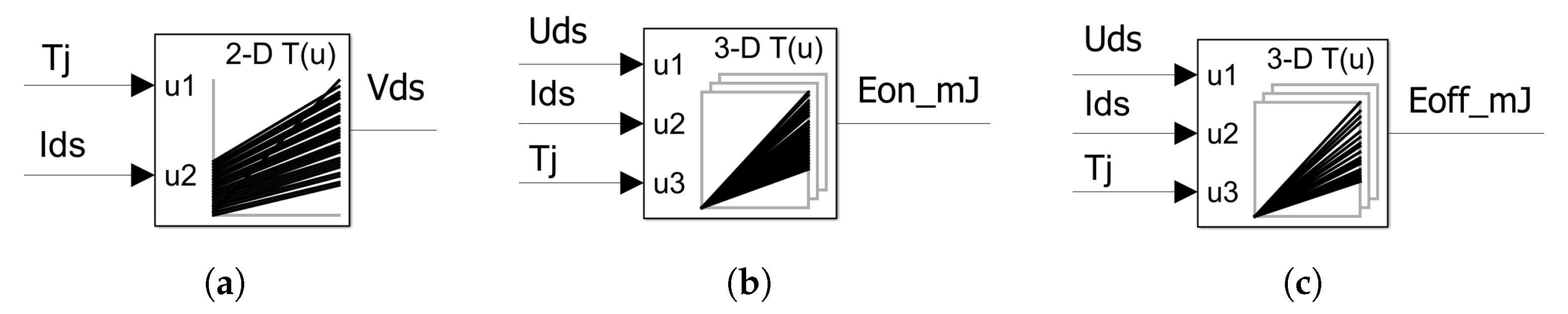
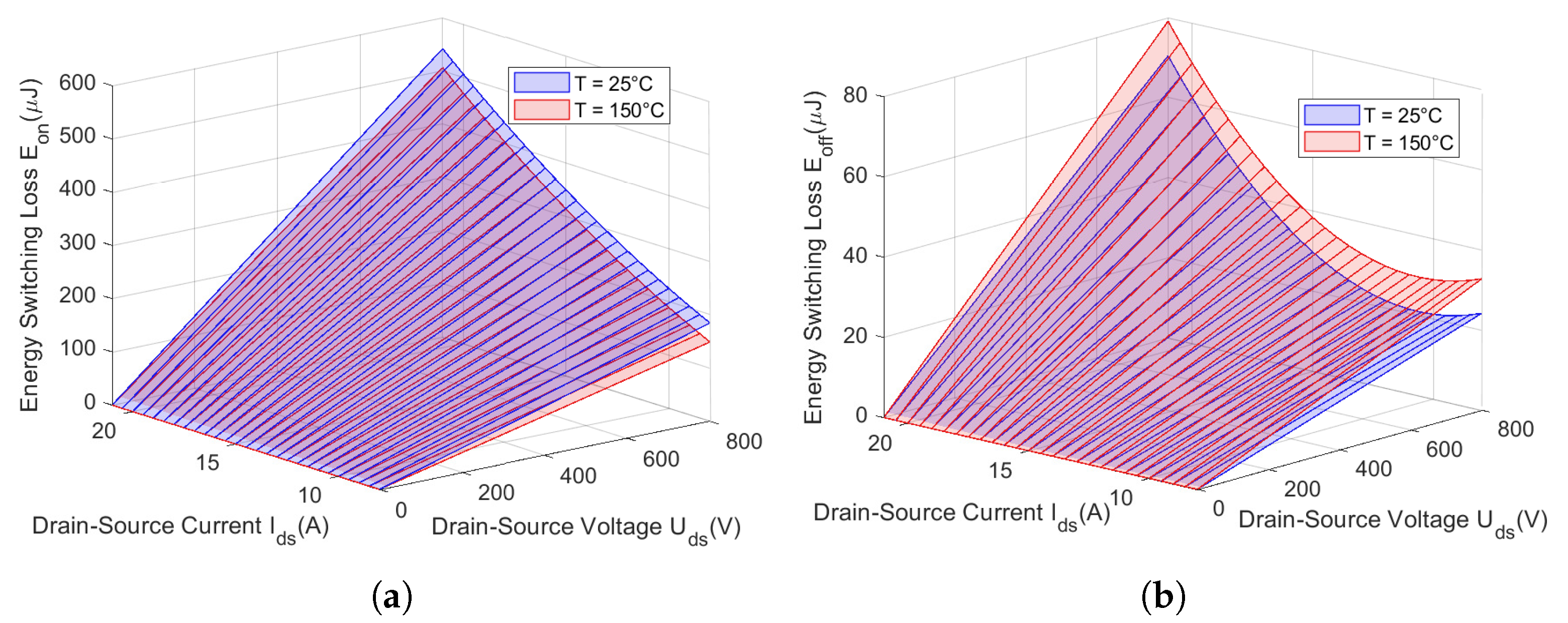
3. Power Losses Computation

Inverter or converter power losses are a key factor in their analysis. They consist of device losses, i.e., semiconductors and passive components. Numerous methods have been proposed to evaluate them. Ref. [12] calculates the Mosfet losses of a Z-source inverter based on measured $U_{ds}$ and $I_{ds}$, with a current sensor in each leg of the inverter. On the other hand, the loss-calculation algorithm proposed in [11] requires the mean and the RMS values of voltages and currents; it is only applicable to one or a few similar topologies and for a specific strategy for switching modulation.

A more generally applicable algorithm presented in [13] is based on an inverter currents and voltages instantaneous values, which are highly dependent on the output current–voltage characteristics. The algorithms of [10] calculate both the switching and conduction losses of a Z-source inverter. A linear relation between switching energies and semiconductor current is considered in [16]. The same linear relationship is proposed in the current-fed qZ-source inverter in [17], whereas in [11], the same was carried out for the voltage-fed qZ-source inverter.

For a more accurate power loss estimation, one approach uses power loss as a cubic function of current, voltage, and temperature by using a lookup table and fitting curves. However, the accuracy of power loss estimation depends on the waveforms of voltages and currents, which vary under different operation conditions. In [4], energy loss in a Mosfet is determined by the channel current, $I_{ch}$, and the drain-source voltage $U_{ds}$. The various time intervals of the commutation process are determined for two Mosfets, such as $Q_1$ and $Q_2$, in a half-bridge. Considering the voltage and current dynamics, the analytical energy loss expressions for $Q_1$ and $Q_2$ at each time interval are shown in [4]. The authors of [3] developed time intervals during the switching transitions of one Infineon IKW40T120 IGBT (600 V, 40 A). In [7], diode conduction loss was determined by using a formula with a root mean square current, the active resistance of the element, and the switching losses with turn-on and turn-off switching.

Finally, ref. [10] considers the impact of the phase angle between fundamental output phase voltage and current on switching losses, and refs. [11,16,17] calculates the losses without this consideration.

3.1. Mosfet Power Losses

Power devices produce power loss in terms of conduction loss and switching loss. Instantaneous conduction power loss can be determined as the product of $I_{ds}$ and of $U_{ds}$ when the Mosfet is under conduction:

$$P_{Mcond}\left(t\right)=U_{ds}\left(t\right)·I_{ds}\left(t\right).$$

(17)

In [7], losses are calculated by using the following formula with a known value for the RMS current and the active resistance of the element:

$$P_{Mcond}\left(t\right)=R_{ds}\left(T_j\right)·i_{Mrms}^2·D.$$

(18)

The same author shows that the power losses for turn-on and turn-off switching can be added into

$$P_{Msw}\left(t\right)={\displaystyle \frac{f·(T_r+T_f)·U_{ds}·I_{ds}}{2}}.$$

(19)

where $T_r$ and $T_f$ are the Mosfet turn-on rise and turn-off fall times, respectively. Many datasheets present the influence of some temperature, current, or voltage values on switching energy losses. For example, C2M0080120D energy switching loss is provided via its datasheet for only two values of $U_{ds}$ (600 V and 800 V) at 20 °C for a large variation in $I_{ds}$ [112]. The energy switching loss is also given for a large variation in $T_j$ for $I_{ds}$ = 20 A and $U_{ds}$ = 800 V. These known values are interpolated using a lookup table, extrapolating the switching energy losses and approximating conduction losses. A 2D lookup table (Figure 4a) with vectors of $T_j$ and $I_{ds}$ as breakpoint inputs interpolates $U_{ds}$ for any $I_{ds}$ and $T_j$, as in [2]. Then, the instantaneous conduction power loss of Mosfet, $P_{Mcond}$, is calculated as the product of $I_{ds}$ and $U_{ds}$.

Two switching loss energies [112]—the turn-on $E_{sw-on}$ and turn-off $E_{sw-off}$— for $U_{ds}$ = 800 V and $T_j$ = 25 °C are presented in the C2M0080120D Mosfet datasheet, as in Figure 5a. The rise and fall times of drain-source voltage and current are used to calculate them.

The functions that fit the datasheet points are represented in these figures; they are determined as per [5]; first, the switching loss energies as a function of the drain-source current, $I_{ds}$, i.e., $E_{sw-on}$ ($I_{ds}$) and $E_{sw-off}$ ($I_{ds}$) are presented, as in Figure 5a; then, the switching loss energies as a function of the junction temperature $T_j$, i.e., $E_{sw-on}$ ($T_j$) and $E_{sw-off}$ ($T_j$) are given, as in Figure 5b. $E_{sw-on}$ and $E_{sw-off}$ depend on the $U_{ds}$, $I_{ds}$, and $T_j$ variables. A 3D lookup table with $U_{ds}$, $I_{ds}$, and $T_j$ inputs (3D lookup table using Matlab breakpoints) interpolates the $E_{sw-on}$ for any $U_{ds}$, $I_{ds}$, and $T_j$ when the Mosfet turns on (Figure 6a). Another 3D lookup table (Figure 6b) is used to determine the $E_{sw-off}$ with $U_{ds}$, $I_{ds}$, and $T_j$ as inputs. Then, the product of the loss energies and the switching frequency gives the instantaneous switching power loss, $P_{Msw}$.

3.2. IGBT Power Loss

Instantaneous conduction power loss can be calculated as $P_{IGBTcond}\left(t\right)$ = $i_{ce}$·$u_{ce}$$(i_{ce}$, $T_{jIGBT}$). In [14], the averaged conduction power loss model is obtained by integrating the load current over one period according to

$$P_{IGBTcond}\left(t\right)={\displaystyle \frac{1}{T}}{\int }_0^T{i}_{ce}·u_{ce}(i_{ce},T_j)dt={\displaystyle \frac{1}{T}}{\int }_0^T\left(u_{ce}\left(t\right)+r·i_{ce}^{\beta }\right)·I_{ce}\left(t\right)dt.$$

(20)

where $\beta$ is a curve-fitting constant. However, in the literature, the typical value of $\beta$ is 2. Conduction losses with temperature dependency are

$$P_{IGBTcond}\left(t\right)={\displaystyle \frac{1}{T}}{\int }_0^T\left(C_1·T_j+U_0+(C_2·T_j+r_{ce})·I_{ce}^{\beta }\right)·I_{ce}\left(t\right)dt.$$

(21)

where $C_1$ and $C_2$ are the temperature coefficients and $r_{ce}$ is the collector–emitter resistance. The switching loss only occurs for a short time; the average switching loss, $P_{IGBTsw}$, depends on the switching frequency, $f_{sw}$. The switching energy, $E_{IGBTsw}$, is converted to heat during the switching, as $P_{IGBTsw}$ = $E_{IGBTsw}$·$f_{sw}$, where

$$E_{IGBTsw}\left(t\right)={\displaystyle \frac{1}{t}}{\int }_0^T{i}_{ce}\left(t\right)·u_{ce}\left(t\right)dt.$$

(22)

The switching energy estimated in [14] takes into account its dependence on $T_j$ and on the DC link voltage:

$$E_{IGBTsw}\left(t\right)=A·i_{ce}{\left(t\right)}^{\beta }·{\left({\displaystyle \frac{U_{DC}}{U_{base}}}\right)}^C·{\left({\displaystyle \frac{T_j}{T_{jref}}}\right)}^D.$$

(23)

where A depends on the gate resistance, $R_g$, and the chip characteristics ($\beta$, C, and D) are curve-fitting constants. $U_{base}$ is the link voltage base value, and $T_{jref}$ is the junction temperature base value. The author of [6] developed an empirical switching loss model with a linear current dependency and an offset term. $E_{IGBTsw}$ depends on gate resistance, the dc-link voltage with exponential terms, and an additional linear temperature-dependent term:

$$E_{IGBTsw}\left(t\right)=\left(E_0+K_0·i_{ce}\left(t\right)·{\left({\displaystyle \frac{U_{DC}}{U_{base}}}\right)}^{\alpha }·{\left({\displaystyle \frac{R_g}{R_{gbase}}}\right)}^{\beta }\right)·\left(1+(T_j-T_{jref})·K_T\right).$$

(24)

where $E_0$, $K_0$, $\alpha$, $\beta$, and $K_T$ are obtained as fitting coefficients; $U_{base}$ and $R_{gbase}$ are the operation point dc-link voltage and resistance, respectively. The power losses are calculated in the IGBT and the inverter bridge free-wheeling diodes [15] as follows:

$$E_{IGBTsw}\left(i_{ce}\right)={\left({\displaystyle \frac{U_{pn}}{U_{base}}}\right)}^{k_T}·\left(e_3·{i_{ce}}^3+e_2·{i_{ce}}^2+e_1·i_{ce}+e_0,\right)$$

(25)

where the coefficients $e_0$, $e_1$, $e_2$, and $e_3$ are the average of those determined for the two provided temperatures, and $k_T$ represents the IGBT switching loss voltage dependence.

3.3. Diode Power Loss

The calculation of conduction loss is similar for a Mosfet and for a body diode. In [7], diode conduction loss is presented as

$$P_{Dcond}\left(T_j\right)=R_f\left(T_{jD}\right)·i_{Drms}^2+U_f\left(T_{jD}\right)·i_{Drms}.$$

(26)

where

$$R_f\left(T_{jD}\right)=R_{f-{25}^{°}\mathrm{C}}·(1+{\alpha }_{DR}·(T_{jD}-T_a)),U_f\left(T_{jD}\right)=U_{f-{25}^{°}\mathrm{C}}+{\alpha }_{DU}·(T_{jD}-T_a).$$

(27)

The temperature coefficients of the change in resistance, ${\alpha }_{DR}$, and of the diode voltage, ${\alpha }_{DU}$, are identified according to [113]. The product of $I_f$ and $U_f$ can also be used:

$$P_{Dcond}\left(t\right)=U_f\left(t\right)·I_f\left(t\right),$$

(28)

where $I_f$ and $U_f$ are the forward saturation current and voltage, respectively. Similar to Equation (25), the authors of [15] derived a switching loss model for diode turn-on losses. In order to estimate the $P_{Dcond}$, a 2D lookup table that has $T_j$ and $I_f$ as the breakpoint inputs and outputs, $U_f$, was used, as it interpolates $U_f$ for any $I_f$ and $T_j$. During Mosfet turn-off, the diode contributes to the loss of energy, $E_{rr}$, as a result of reverse recovery charge, $Q_{rr}$, as represented in Figure 7.

The analytical switching energy mode depends on the peak reverse recovery current, $I_{rr}$, [18], $T_j$, and the diode forward saturation voltage, $U_f$. Furthermore, $I_{rr}$ is a function of the turn-off switching rate ($d{i}_f/dt$) and $Q_{rr}$:

$$I_{rr}=\sqrt{{\displaystyle \frac{2}{S+1}}·Q_{rr}·{\displaystyle \frac{d{i}_f}{dt}}}.$$

(29)

where S is the snappiness factor determined using datasheet-specific information. Ref. [3] uses a simplified version:

$$I_{rr}=\sqrt{Q_{rr}·{\displaystyle \frac{d{i}_f}{dt}}}.$$

(30)

Diode switching power loss, $P_{rr}$, is then calculated as the product of the switching frequency and of the loss energy $E_{rr}$, defined as the product of $U_f$ and $Q_{rr}$ (calculated from Equations (30) or (29)). Finally, the total power losses, $P_{out}$, are calculated via the addition of all power losses.

4. Thermal Model

Several approaches can be used to perform thermal analysis. The early evaluation of electro-thermal simulation is necessary to avoid expensive prototype designs. Thermal models are used to estimate temperature profiles describing a device’s thermal behavior during operation. Thermal behavior can be predicted by using a classical electro-thermal model (a thermal network of resistors and capacitors) that is deduced from the device datasheet’s thermal impedance value, $Z_{th-jc}$. The total power losses, $P_{out}$, are passed through the resistors and capacitors’ thermal network, resulting in $T_j$; it is estimated using the following equation:

$$T_j\left(t\right)=Z_{th-jc}\left(t\right)·P_{out}\left(t\right)+T_a\left(t\right).$$

(31)

where $T_a\left(t\right)$ is the ambient temperature. $Z_{th-jc}\left(t\right)$ can be calculated as

$$Z_{th-jc}\left(t\right)=\sum _{i=1}^n{R}_i·\left(1-ex{p}^{-t/{\tau }_i}\right).$$

(32)

where ${\tau }_i=R_i·C_i$. According to Equation (31), the computation of $T_j$ requires the knowledge of $Z_{th-jc}\left(t\right)$, a graph of which is provided in the device datasheet, as in Figure 8. The implementation of a curve-fitting identification obtains the $RC$ of the thermal network.

Several degradations affect semiconductor device thermal impedance. The physical mechanism of degradation [37] is related to the thermal stress created between two materials [38,39,40] (e.g., between silicium and aluminum, as in Figure 9a), with different thermal expansion coefficients that characterize the expansion ability of a material under temperature variations. The authors of [41] found out that wire bond degradation (Figure 9b) is propagated in an aluminum wire. Ref. [114] shows that the thermo-mechanical stresses can exceed the elastic limits of the aluminum layer in the metallization layer. The plastic behavior of aluminum increases the serie resistance [41] due to this stress. In [42], the mismatch between the silicon die and the copper tab leads to solder joint degradation with possibilities of creep fatigue or cohesion fracture.

There are two conventional thermal networks: Cauer (Figure 10a) and Foster (Figure 10b). The Cauer model [19,20] directly results from the heat transfer equation and is made up of an $RC$ network corresponding to selected points on the device. The voltage at each node has physical significance; it represents the temperature at a physical location of the device. The dimensions and the materials involved in the device (the device structure) will generate the $RC$ values. The Foster network [21,22] is even simpler; no design structure consideration is required. On the other hand, the temperature distribution inside the device is not available.

Unfortunately, in many studies, the thermal cross-coupling effect is not taken into account. Nevertheless, each heat source contributes to an increase in the temperature of its neighboring devices [28]. Consequently, the thermal coupling model is defined as a thermal impedance matrix [29]. However, these conventional thermal networks are oversimplified without a physical module layout representation, therefore generating thermal behavior inaccuracy.

The compact thermal model is derived from the analytical models with a mathematical treatment of the 1D or 2D heat condition diffusion equation that often results in a short simulation duration. In [23], the Fourier series-based method with variable separation is compared to the finite element method, providing excellent matching; the temperature error found in the centers of dies is approximately 0.27% by simulation and 3.5% experimentally. The thermal model can also be derived from a complex nonlinear behavior model that can be accompanied by numerical divergence. In [24], the heat equation is solved by another analytical model based on Green’s function, bringing flexibility and improving simulation speed to avoid costly chip space discretization. In [25], the parameters of the Foster network were extracted from the datasheet data using the particle swarm optimization method (population size: 10; inertia weight: between 0.5 and 1; acceleration factors: between 2 to 2.05; maximum iteration: 1000). However, the complexity of an analytical model depends on many influencing factors, such as chip-to-chip thermal coupling, the geometric layout of modules, the cooling system, and module-to-module heat spreading. Such a method maintains the advantage of low computation cost when compared to numerical methods.

Numerical methods such as FEM [26] and FDM [27] have attracted attention in the thermal analysis of complex layout geometries. They identify the hot spots and temperature distribution within a module and take into consideration material properties and layers. The FEM provides an exact temperature distribution of any device geometry, and the boundary conditions for thermal analysis are included. Unfortunately, such an analysis takes a very long time to compile when several components are present. In [30], by considering nonlinear thermal conductivity, an electro-thermal modeling method is proposed, using Kirchhoff transformation to avoid extra memory storage. Temperature package material dependence (using the FDM thermal solvers) is presented in [33] using a high-order system matrix approach. The electro-thermal modeling approach in [32] is based on the FDM and a circuit simulator providing high-accuracy device temperature prediction.

Multiphysics tools, such as COMSOL [115] and ANSYS [116] take nonlinear temperature-dependent material properties into account. Only temperature-invariant thermal models can be used with ANSYS Icepak. The nonlinear thermal model can not be extracted in a straightforward way; it is imported as a Cauer or Foster network (typically obtained by performing FEM simulations) or reduced-order equivalent circuit models [30,117].

FEA was introduced to study the thermal behavior of multichip modules. Ref. [34] presents a methodology to study module-to-module thermal crosstalk, heat propagation within a chip, the under layers, and the impact of cooling. For an IGBT power module included in a traction inverter, power loss estimation is performed by an analytical model and is then used as input by the FEA model. Initially, a 3D geometry model representing an IGBT module mounted on a liquid-cooled plate was built in SolidWorks, and later, FEA thermal analysis was conducted using COMSOL. Eight different meshes have been used (“extremely fine, extra fine, finer, fine, normal, coarser, extra coarse, and extremely coarse”) to investigate mesh sensitivity. Then, COMSOL is used to create the FEA model. Electro-thermal modeling using FEA focuses on the transient and steady-state thermal analyses of multichip devices [35], extracting thermal-impedance matrices using 3D thermal simulations.

Thermal modeling can also be carried out in piecewise linear electrical circuit simulation (PLECS) Simulink environment with some advantages, such as easy user interface, less computational storage, and less computational burden during simulation. A 3D model and meshing of the IXFN50N120SiC in the SOT-227 package was created in [31] using SolidWorks. The $RC$ parameters of a Cauer network and thermal analysis were carried out using PLECS for an electro-thermal inverter model operating at 100 kHz.

5. Temperature Measurement and Management

Several methods can be used to directly measure chip temperature, such as physical contact and optical measurement. The physical contact method requires a thermo-sensitive material to be in direct contact with the die of the device with a thermistor or thermo-couple. With an infrared thermal camera, a thermo-coupler is attached to the die and an integrated semiconductor temperature sensor, with the advantage of measuring thermal distribution over the entire surface of the device. In [43], IGBT surface temperature was observed utilizing an infrared camera to determine the exact location of hot spots. Embedded temperature sensors are preferred by some companies, such as Toyota and Tesla, for electric vehicle applications. Another option is the integration of temperature sensors onto the power semiconductor chip die area as a diode-on-die temperature sensor [44]. In order to create this diode, a portion of the chip area is doped.

Indirect temperature measurement methods investigate the relationship between typical thermal-dependent parameters (such as current and voltage signals) and the $T_j$ of the IGBT on-state, $U_{ce}$, or Mosfet on-state drain-source resistance [118]. In [45], this resistance can be derived by measuring the on-state drain-source voltage [46] and current. Due to the location of internal gate resistance in the center of the die, this resistance is also used as an indicator of the $T_j$.

Other numerous temperature-sensitive electrical parameter methods include the measurement of threshold voltage $U_{th}$, peak gate current [47], turn-on collector current transient dIc/dt [48], plateau voltage [6], turn-off collector–emitter voltage transient dVce/dt [49], voltage across source/emitter parasitic inductances [50], turn-on delay time [51], and turn-off delay time [52]. Furthermore, the use of temperature-sensitive electrical parameters-based sensors increases overall circuit complexity.

The junction temperature of the power module rises and falls, therefore creating a thermal cycle. The number of cycles needed for a power module to fail depends on the difference between the maximum and minimum junction temperatures in a thermal cycle (temperature swing, $\Delta$$T_j$) and the medium temperature, $T_{jm}$. $\Delta$$T_j$ has a significant impact on module reliability [53]; the number of cycles to failure decreases with the increase in $\Delta$$T_j$. Therefore, reducing the thermal cycle ripple improves power module lifetime. Thermal management is an effective means of reducing $\Delta$$T_j$ [54].

There are many ways to reduce thermal cycle amplitude. The use of new materials can help to regulate $\Delta$$T_j$ significantly, such as “moisture sorption–desorption process” materials [55], “phase-change materials” [56] (metallic [57] or flexible [58]) and “thick cvd-grown graphene nano-materials” [59]. The use of new materials implies production process changes. Therefore, many methods concentrate on the regulation of heat dissipation. Some adjust the speed of a cooling fan [60] or the flow rate of a liquid [61] to mitigate thermal stress. Others control the power loss-related parameters, such as the active power command [62], load and reactive currents [63,68], gate drivers [64], modulation strategies [65], switching frequencies [5,66], or neutral points [67].

6. Lifetime Modeling

The calculation of the consumed lifetime is the next step. The simplest empirical lifetime model is based on the Coffin-Mason law, for which only junction temperature variation $\Delta T_j$ is taken into account:

$$N_f=A·\Delta {T_j}^{\alpha },$$

(33)

where $N_f$ is the number of cycles to failure for a given thermal stress, and coefficient A relates to the device technology. The Coffin-Mason-Arrhenius law, with the influence of $T_{jm}$, can be expressed as

$$N_f=A·\Delta {T_j}^{\alpha }·e^{E_a/\left(k{T}_{jm}\right)},$$

(34)

where k is the Boltzmann constant. In [71], the Norris-Landzberg model for the lifetime estimation of power modules is proposed:

$$N_f=A·\Delta {T_j}^{\alpha }·f^{\beta }·e^{E_a/\left(k{T}_{jm}\right)},$$

(35)

which depends on frequency f. The Bayerer lifetime model [72], which can be chosen for lifetime estimation, is related to load pulse duration, $t_{on}$, current per wire, I, blocking voltage, V and $T_{jm}$, wire diameter, D, and $\Delta T_j$ as

$$N_f=A·\Delta {T_j}^{{\beta }_1}·e^{{\beta }_2/T_{jm}}·t_{on}^{{\beta }_3}·I^{{\beta }_4}·V^{{\beta }_5}·D^{{\beta }_6},$$

(36)

Scheuermann and Schmidt [73] proposed a model that is similar to the Bayerer model, which evaluates both IGBT and diode lifetimes using

$$N_f=A·\Delta {T_j}^{\alpha }·e^{E_a/\left(k{T}_{jm}\right)}·a{r}^{{\beta }_1+{\beta }_2·\Delta T_j}·\left({\displaystyle \frac{C_d+t_{on}^{\gamma }}{C_d+1}}\right)·f_d,$$

(37)

where ${\beta }_1$, ${\beta }_2$, $\gamma$, and $C_d$ are the curve-fitting parameters [73]. Additionally, this model includes the influence of bond wire aspect ratio, $ar$.

Accelerated power cycling tests collect failure data. The $\Delta$$T_j$ jumps and $T_{jm}$ are the main stress factors in a power device. In order to find out device failure, many devices are exposed to power cycles under the same conditions. Device performance degradations differ because of the small discrepancies in the manufacturing parameters of devices, as shown in Figure 11. The datasheet characteristics, $I_{ds}-U_{ds}$, present the variations between several devices of the same type. Therefore, variability exists between $T_{jm}$ and $\Delta$$T_j$ regarding tested devices.

Some researchers take the physical structures of semiconductors into account in failure models. The bond wire lift-off due to the plastic strain is based on the strain-based model [74] as follows:

$$N_f=c_1·{\Delta {ϵ}_p}^{-c_2},$$

(38)

where $c_1$ and $c_2$ are specific parameter materials, and $\Delta {ϵ}_p$ is the average accumulated plastic strain (per cycle). The solder fatigue effect can be taken into account as

$$N_f={\displaystyle \frac{L}{c_1·{\Delta {ϵ}_p}^{-c_2}}},$$

(39)

where L is solder length. The Basquin form [75] is based on the stress range instead of the average accumulated plastic strain. Instead of using the same term, ref. [76] uses the integrated accumulated creep strain mean value to define the Paris laws: the number of cycles until crack initiation and the crack propagation rate. Based on the total energy to failure and the energy per cycle, ref. [77] defines the strain-stress energy model.

The number of cycles to failure can also significantly vary between devices. In [80], many C2M0080120D Mosfets were experimentally tested under a long cycle time, where they were turned on for 5 s and turned off for 12 s. The three sample devices did not fail until the test was stopped, showing the high number of cycles and an increased $R_{ds}$, whereas samples 4, 5, and 6 exhibited significant, instantaneous increases in the $\Delta T_j$ curves when failures occurred. These three experimental tests record device failure after $N_{f1}$ = 12,267 cycles, $N_{f2}$ = 8638 cycles, and $N_{f3}$ = 25,399 cycles. The authors of [78] introduced an online condition for monitoring and detecting early signs of failure in package thermal performance degradation. In [79], a data-driven convolutional neural network-based method is proposed for the quad-classification of IGBT failure modes.

$R_{ds}$ contains the information (such as temperature, $T_j$) involved in device degradation just before device failure. The authors of [7] point out that a variation in $\Delta R_{ds}$ of up to 0.5 $\Omega$ of its initial value will bring the device to failure. Figure 12 shows the experimental results of $\Delta R_{ds}$ for four cases during thermal cycling; multiple groups of Mosfets were tested under several conditions (such as $\Delta T_j$ and $T_{max}$). A voltage source in a series with an IRFP340 Mosfet, $R_{ds}$, and a pulsating load was adopted to achieve the thermal cycles.

In [81], eight different IGBTs were tested under the same test conditions ($V_{GE}$ = 15 V; $\Delta T_j$ = 90 °C; mean junction temperature $T_{jm}$ = 105 °C; load pulse duration $t_{on}$ = 2 s; $t_{off}$ = 4 s). After the identification of the Coffin-Manson coefficients, the authors experimentally confirm a lifetime reduction when the mean junction temperature increases with different temperature swings. For bond wire failure, the Coffin-Manson exponent $\alpha$ is similar to the value given in the Vishay semiconductors datasheet, as in Figure 13a.

Based on the test results, Figure 13b shows the activation energy, $E_a$, derived for the IGBT. The experimental coefficients A and $\delta$ and the activation energy $E_a$ are then deduced. The expected lifetime is calculated based on the lifetime model as

$$N_f=A·\Delta {T_j}^{\alpha }·e^{E_a/\left(k{T}_{jm}\right)}·I^{\beta }.$$

(40)

Then, ref. [81] made a comparison between the expected lifetime (calculated using the model in (40)) and the original test results in order to check lifetime modeling accuracy.

In order to estimate the device failure cycles, the coefficients A, $\alpha$, and $E_a$ can be calculated using the Coffin-Manson-Arrhenius Equation (34), as in [5]. In Figure 12, there are three tests of Mosfets under different failure cycles; first, $\Delta T_{j1}$, $T_{jm1}$, and $N_{f1}$; then, $\Delta T_{j2}$, $T_{jm2}$, and $N_{f2}$, and finally, $\Delta T_{j3}$, $T_{jm3}$, and $N_{f3}$. The three exponential functions (34) can be expressed in linear forms with the help of the natural logarithm. Once the unknown constants A and $E_a$ are eliminated, the development $\alpha$ can be represented by

$$\alpha ={\displaystyle \frac{\left(\frac{1}{T_{jm1}}-\frac{1}{T_{jm2}}\right)·log\frac{N_{f2}}{N_{f3}}-\left(\frac{1}{T_{jm2}}-\frac{1}{T_{jm3}}\right)·log\frac{N_{f1}}{N_{f2}}}{\left(\frac{1}{T_{jm1}}-\frac{1}{T_{jm2}}\right)·log\frac{\Delta T_{j2}}{\Delta T_{j3}}-\left(\frac{1}{T_{jm2}}-\frac{1}{T_{jm3}}\right)·log\frac{\Delta T_{j1}}{\Delta T_{j2}}}}.$$

(41)

Consequently, the thermal activation energy has the following form:

$$E_a=k·{\displaystyle \frac{log\frac{N_{f1}}{N_{f2}}-\alpha ·log\frac{\Delta T_{j1}}{\Delta T_{j2}}}{\frac{1}{T_{jm1}}-\frac{1}{T_{jm2}}}}.$$

(42)

Hence, the last coefficient can be written as

$$A={\displaystyle \frac{N_{f1}}{\Delta {T_{j1}}^{\alpha }·e^{E_a/\left(k{T}_{jm1}\right)}}}.$$

(43)

The following numerical values were obtained: $\alpha$ = −4.4887, $E_a$ = 0.0667, and A = 2.8823 ×${10}^8$, according to relations (41)–(43) and using the three experimental test data in [5].

7. Mission Profiles

Power semiconductors are the most fragile components in converters and inverters; furthermore, they are very affected by mission profiles [82]. Therefore, the adoption of a realistic mission profile can help to obtain a more reliable Mosfet or IGBT lifetime assessment. For example, photovoltaic systems may have daily solar irradiance profiles [22,84], and motor drive applications may have reference speed [2,29] and reference torque profiles [29], whereas electric bus applications may have reference voltage [119] and load mission profiles [7].

The thermal cycling behavior of power devices can be either long-cycle or short-cycle. The long cycles are specific to dc–dc converter semiconductor devices; the mission profile variation imposes long thermal cycles. Dc–ac-stage semiconductor grid applications are concerned with short and long cycles because of grid frequency oscillations [82].

The power device lifetime model inputs involve thermal cycling information: heating time, $t_{on}$, mean junction temperature, $T_{jm}$, and junction temperature fluctuations, $\Delta T_j$, which can be determined for long and short-cycle analysis. In a long-cycle analysis, the mission profile dynamics cause irregular behavior in thermal cycling. A rainflow-counting algorithm is then employed to find regular cycles for $T_{jm}$, $t_{on}$, and $\Delta T_j$ [82]. On the other hand, in short-cycle analysis, the cycles are already well-defined due to the grid frequency. Therefore, in this case, $T_{jm}$ is considered equal to the $T_j$ obtained from the thermal model, $t_{on}$ is equal to half of the grid period, and $\Delta T_j$ is analytically defined according to the model presented in [82].

In [21], a 30-minute drive cycle for automotive application (

Table 1. Mission profile.

Application	Mission Profile 1	Mission Profile 2
(a) Automotive application: inverter’s frequency mission profile.
(b) Electrical motor: the new European driving cycle speed and city profiles.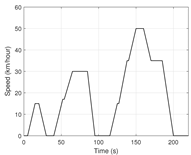
(c) Wound Rotor Synchronous Machine: speed and torque profiles.
(d) Photovoltaic application: solar irradiance mission profiles with two minutes resolution during clear and cloudy days.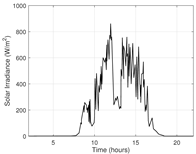
(e) Wind power system: wind speed and ambiant temperature profiles.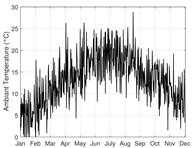
(f) Power boost converter: periodic and chaotic Mosfet current profiles with a constant load.

(part a), mission profiles 1) was translated into a frequency and current mission profile for a 30 kW three-phase voltage source inverter. Subsequently, the mission profile is transformed into a sin pulse width modulation switching pattern for a Mosfet using the converter model.

In [2], the authors establish an accurate electro-thermal model of an inverter using an IRFS4115PbF. In an electric vehicle, the inverter drives the vehicle’s electric motor by controlling battery power flow. In this application, the new European driving cycle speed profile is applied as an input reference speed (Table 1 (part b), mission profile 1), where the urban and highway phases are included. In Table 1 (part b), the urban profile is presented as mission profile 2. The authors of [83] investigated reliability solutions for the design and thermal management of multichip module-based power converters embedded in critical industry applications (rolling mills). The mill is part of a system driven by an induction machine with field-oriented control and is responsible for the precise control of the strip speed. The bidirectional rolling process and the vertical hoist acceleration with material thickness variation result in mission profiles. Thereby, the torque and velocity dynamics result in highly dynamic power variations (also critical thermal cycling for power semiconductors). The authors of [83] used speed and torque mission profiles that are simpler than the usual profile used for wound rotor synchronous machines, as in Table 1 (part c).

The work in [21,29] presents a lifetime prediction method of a three-phase inverter supplying an electric drive machine. Lifetime prediction is performed under the conditions provided by the application mission profile (650 V; 45 A SiC power Mosfet). Different operating scenarios are considered: high torque and low speed, low torque with medium or high speed, and mixed operation. For each scenario, two hours of daily drive use is considered, although working hours can vary greatly depending on the application. For the low-speed and high-torque mission profiles, the rotor speed frequency is higher (in the range of 0–700 rpm). The lifetime of the Mosfet of the electric drive inverter is estimated to be 12 years because of the numerous standing starts usually occurring in an urban cycle case. In the low-torque with medium- or high-speed scenario, a higher lifetime is expected: low torques imply low currents, which lead to lower SiC power device degradation. For low electromagnetic torques (kept quite low in this working profile) with medium or high speed, the SiC lifetime is about 28 years. The authors also present a mixed-use case of an intermediate profile between the two previous scenarios.

For photovoltaic systems, solar irradiance and ambient temperature are considered as mission profiles. For example, the solar irradiance considerably varies during the day for a Denmark installation site [84]. During a clear day, the solar irradiance varies smoothly, but considerable solar irradiance fluctuation is induced by passing clouds. Ref. [84] demonstrates the impact of time resolution (1 min, 10 min, and 1 h) on the mission profiles. The figures from Table 1 (part d) present clear- and cloudy-day mission profiles with only one time resolution (2 min). During a clear day, small differences are noticed in the mission profile with different resolutions. In contrast, the fast variations in solar irradiance are not totally captured by the 1-h cloudy-day mission profile.

The figure from Table 1 (part e) presents a wind power system speed mission profile (1). As an example, the bridge arm of a two-level, back-to-back voltage source converter [85] is composed of two parallel Infineon FF1000R17IE4 IGBT modules with a maximum current rating of 1000 A and a maximum voltage rating of 1700 V. Ref. [85] depicts the mission profile, i.e., the wind speed fluctuations during a whole year (for 2017 near Lauswersoog, Netherlands). Moreover, a constant ambient temperature is considered for many simulation applications. In Table 1 (part e) (mission profile 2), the authors of [84] present annual information on ambient temperature for a realistic study.

The mission profile is translated into a power semiconductor temperature profile using the system’s electric and thermal models. In a Boost converter [5], a mission profile constant load generates a stable period-1T operation regarding the inductance current, $i_L$ (Table 1 (part f) mission profile 1), and junction temperature, $T_j$. With a further load increase (particularly for large values of load), repeated period-doubling bifurcations and chaos in the inductance and Mosfet currents (Table 1 (part f) mission profile 2) are generated, leading to large thermal stress (impacting the overall magnitude of the junction temperature). Finally, chaotic behavior leads to a very important degradation of the Mosfet’s lifetime, which is reduced by half.

8. Rainflow Algorithms

The rainflow algorithm can be adopted to evaluate the frequency and amplitude of temperature cycles. Each cycle applies different stresses. Lifetime models are used to predict the number of cycles to failure as a function of relevant parameters: temperature swing, $\Delta$$T_j$, minimum temperature, $T_{jmin}$, and heating time, $t_{on}$ [42,89].

Various counting approaches such as “range counting”, “peak counting”, “level crossing counting”, and “rainflow counting” have been developed in recent years to count maximum amplitude cycles in random conditions. Each time the positive (or negative) sloped portion exceeds a preset level above (or below) a temperature reference, one count is recorded in the level crossing counting technique, as in Figure 14a. Peak counting (Figure 14b) identifies the maximum (resp. minimum) temperature profile value; peaks above (resp. valleys under) a reference level are then counted. A variant of this method can be to count all peaks and valleys. Figure 14c presents the range-counting method, which considers the difference between two successive reversals as a range. The range is positive when a valley is followed by a peak and negative when a peak is followed by a valley. In the half-cycle method, the different slopes are counted as a half-cycle.

In [87], the maximum edge method (the bigger slope pair of the rising and falling edge for amplitude) is one cycle (i.e., the maximum swing). For the rising edge method, every subsequent rising edge is counted as a cycle, while falling edges are ignored. Comparative discussions of these counting algorithms and rainflow counting are given in [88]. A conventional method, such as Shadow, finds the cycles with the maximum stress amplitude. One difference between the Shadow method and the peak-counting method is that it considers the highest peak and the lowest valley in addition to counting the highest amplitudes. Indeed, almost 90% of damage is usually caused by 10% of the total cycles having the largest amplitude; hence, the necessity to collect the cycles with maximum amplitude [90]. Yet, the mean stress of each counted cycle is also determinative of lifetime; indeed, the effect of mean stress is not considered by the peak-counting and simple range-counting methods. The Moshrefifar and Azamfar method [91] has been evaluated experimentally and shows lower errors compared to the peak-counting method.

Rainflow-counting methods have been developed to analyze complex time series. According to [100], rainflow counting has the lowest relative error (11%), while the other counting approaches are between 19% and 27% for a certain mission profile. Consequently, rainflow counting is the most widely adopted. The three-point version of rainflow counting was developed by Downing and Socie [92] and later standardized by ASTM [93]. Ref. [94] demonstrates that the estimated fatigue damage calculated using the standard four-point version is equivalent to the three-point algorithm criteria; both identify the same hysteresis loops but are listed in a different order. The authors of [95] add two criteria to the original rainflow-counting method: the maximum range and the maximum time window, with the aim of avoiding data storage limitations. Cluff [96] developed the rainflow-counting method into three-parameter rainflow counting (the range, mean, and dwell time of temperature cycle time data) and assigned 50% of the half-cycle period to dwell time. This method has been used for an IGBT to predict solder joint fatigue life [97]. A similar three-parameter rainflow algorithm was implemented, which records the elapsed half-cycle time but does not estimate dwell time. Based on [96,98,99], an enhanced rainflow-counting algorithm was developed to extract temperature cycles from temperature data. The rainflow-counting function in [101] is an offline counting method that provides convenient implementation but requires a complete loading profile. Online-rainflow-counting methods are proposed in [53]. The first step in the rainflow-counting method is to extract the junction temperature peaks and valleys, followed by a rotation of 90° to get the shape of the pagodas, as in Figure 15. When imagining rain flow, a half cycle is defined by allowing the rain to flow to a larger maximum point or a smaller minimum point. Cycles can then be identified. In the flow-counting approach, the large amount of data required is a great constraint on real-time implementation.

9. Damage Accumulation

In order to determine the accumulated damage of a power device, Miner’s rule is employed:

$$Q=\sum _{i=1}^n{\displaystyle \frac{N_c}{N_f}},$$

(44)

where $N_c$ is the number of cycles calculated using the rainflow-counting algorithm, and $N_f$ is the number of cycles to failure for a particular stress condition. The end-of-life of the power device, represented by $L_c$ (year), can then be calculated: $L_c$ = 1/Q. Miner’s rule is the simplest cumulative damage model and is most widely used to identify accumulated stress. This linear accumulation law is commonly used and assumes that the material is damage-interaction free. Nonlinear accumulative damage was introduced by Corten and Dolan; it provides the load interaction effects during fatigue cycling [120]. The damage accumulation of the Corten–Dolan model is nonlinearly expressed by

$$Q=\sum _{i=1}^n{\displaystyle \frac{n_i}{N_1}}·{\left({\displaystyle \frac{{\sigma }_i}{{\sigma }_1}}\right)}^d,$$

(45)

where ${\sigma }_i$ is the stress amplitude, with ${\sigma }_1$ being the highest value, $N_1$ is the fatigue life at ${\sigma }_1$, $n_i$ is the number of cycles at ${\sigma }_i$, and d is the material constant. For the ideal case, the material constant, d, should be constant. However, the results indicate that d is smaller at a higher maximal stress than at a lower stress [121]. In order to improve the accuracy of the Corten-Dolan model, the authors of [121] proposed a dynamic Corten-Dolan equation, where d decreases with the increase in loading stress amplitude. Ref. [122] combined the linear and nonlinear damage rules and proposed a modification of Miner’s rule as

$$Q=\sum _{i=1}^{n}f\left(i\right)·{\displaystyle \frac{n_{ai}}{N_a}}+{\displaystyle \frac{n_{bi}}{N_b}},$$

(46)

where $n_{ai}$ is the number of cycles at low amplitude, $n_{bi}$ is the number of cycles at high amplitude, $N_a$ and $N_b$ are the life at low and high amplitudes, respectively, and $f\left(i\right)$ is the hysteresis energy amplitude factor [123]. Ref. [124] proposes a novel nonlinear accumulation rule based on the damage curve and the fatigue crack propagation theories. The parameters of this rule are deduced experimentally. This rule is extended to more general cases for applications by using FEM. Compared to Miner’s linear accumulation rule, the prediction of solder joint thermal fatigue life via this rule is closer to the accelerated life test results of real-world electronic solder joints under a combined temperature profile.

The feedback effect model in [19] greatly affects the lifetime of an IGBT module; a low frequency in an IGBT module leads to a reduction to more than 60% for lifetime compared to fundamental the frequency. Ref. [7] proposes two different aging models, both adopting a feedback method; the estimated lifetime with included aging effects is 9.67 years and 13 years without. The results of [102] demonstrate that, in electrical vehicle applications, the power module’s lifetime is severely affected and reduced by more than 85% when the number of charging times per day increases from 5 to 40 for $\Delta$$T_j$ = 60 °C. For a photovoltaic inverter semiconductor [22], the accumulated IGBT fatigue is 0.4890% from the complete thermal profile, whereas it is 0.4882% from the reduced thermal profile and 0.3543% from the averaged thermal profile. The diode accumulated fatigue is 0.3228% for both the complete and reduced thermal profiles and 0.2849% for the averaged thermal profile. The lifetime of the modular cascaded H-bridge multilevel photovoltaic inverters (about 13 years), as observed in [103], is about 57% less compared to the lifetime of a single IGBT (about 30 years). A chaotic mission profile in a Buck converter significantly modifies the Mosfet’s thermal stress and reliability performance; the accumulated fatigue is increased to between 10% and 65% [5].

Another example is described in [104], where an IGBT power module in a direct-driven wind turbine located in south-eastern Finland was studied. The estimated lifetime is 15,000 years, whereas the traditional lifetime is 20 years. This huge difference is due to the average wind speed of 7 m/s on the site, which is far inferior to the turbine nominal power wind speed of 12 m/s. The annual global lifetime consumption is 6.48 ×${10}^{-3}$%; the power modules cycling lifetime is not a limitation on the wind turbine’s lifetime. Another study (1-year mission profile from Denmark) [84] indicates that mission profile resolution strongly impacts damage accumulation during fluctuating solar irradiance. Indeed, when the mission profile resolution decreases from 1 s to 5 min, the estimated damage of a photovoltaic inverter power device is divided by two. Ref. [125] covers the lifetime of one Si-IGBT and two SiC Mosfet power modules in a three-phase propulsion inverter for two driving cycles: the worldwide harmonized light vehicles test cycle (WLTC) and the city mission profile. The latter appears to cause much less accumulated damage in the devices compared to the WLTC. Moreover, the WLTC has a higher impact on the SiC Mosfet than on the Si IGBT. However, SiC modules have a substantially higher lifetime than Si-IGBTs at greater than 80% for the WLTC and greater than 90% for the city mission profile. In addition, a limited range for fluid flow rate in the heatsink can considerably improve or reduce power device lifetime. SiC MOSFETs showed higher performance than Si IGBTs, regardless of the motor type and test vehicles. For these two different driving cycles, ref. [125] analyses the influence of thermal feedback on inverter power losses. Mosfet conduction losses (up to 1.5%) and IGBT switching losses (up to 3%) for the city profile (without thermal feedback) are considerably underestimated. Similarly, power losses increase Mosfet conduction losses (up to 3.5%) and IGBT switching losses (up to 6%) for the WLTC drive cycle (with thermal feedback).

The authors of [126] estimate energy savings when implementing SiC Mosfet rather than Si IGBT technology in a railway inverter. The analysis of the usage phase in a typical driving cycle shows that SiC Mosfet can save up to 40% of the energy losses of the Si IGBT module. Finally, about 24 MWh can be saved per module with the implementation of SiC Mosfet, considering the entire 30 years lifecycle of the power module. In the photovoltaic application, the results in [127] showed that SiC MOSFET could fail before the packaged version, which leads to thoughts that IGBTs are more reliable than SiC MOSFETs.

10. Conclusions

This article reviews the latest research on junction temperature estimation and the lifetime of power electronic devices. The advantages and disadvantages of the existing techniques to achieve lifetime prediction are described, compared, and discussed, highlighting their benefits.

Because power semiconductor devices are strongly affected by their mission profiles, a realistic mission profile must be adopted for a reliable assessment of device lifetime. The mission profiles are displayed with their industrial applications: daily and 1-year solar irradiance profiles for photovoltaic systems; reference torque and reference speed profiles for motor vehicles; reference voltage and load mission profiles for an electric bus; a wind speed mission profile for a wind power generation system; a frequency–current mission profile for a three-phase voltage source inverter; junction temperature with a stable period-1T operation and chaotic behavior for a constant load profile. Then, several electrical models of Mosfets, IGBTs, and diodes, derived from current–voltage datasheet characteristics, are presented, together with their power loss computations for conduction and switching power loss calculations. In addition to power loss computing, thermal impedance is necessary for junction temperature estimation. Several thermal approaches are listed as Foster and/or Cauer networks or analytical models with a mathematical treatment, such as Fourier series, Green’s function, or the particle swarm optimization method. For a visualization of the temperature distributions inside the component, numerical methods such as FEM, FDM, and FEA can be used with Matlab-Simulink, COMSOL, PLECS, SolidWorks, and ANSYS tools. Several degradations (power module aging failures, heel cracks, and bond wire metallurgic damage, fractures, and lift-off) that change semiconductor thermal impedance are included. The discussions on temperature measurement and management have focused on the direct and indirect Mosfet and IGBT temperature measurement methods. The Coffin-Mason, Coffin-Mason-Arrhenius, Norris-Landzberg, Bayerer and Scheuermann, and Schmidt lifetime models are proposed to identify the number of cycles to failure for the occurrence of thermal stress. When a failure occurs, much device-degradation information from the experimental test can be acquired as the lifetime model experimental coefficients. For each mission profile, the number of cycles to failure is extracted by using the level crossing-counting, peak-counting, range-counting, and rainflow-counting algorithms or modified versions.

Finally, future research demands, opportunities, and perspectives are identified here: the fast dynamics of mission profiles; the inclusion of the impact of other device lifetimes; the integration of nonconstant operating conditions, such as ambient temperature; and new indicator modeling, such as vibration and humidity. For further background information on these aspects and other relevant research topics, we refer the reader to the references.