Optimization of Operation Strategy of Multi-Islanding Microgrid Based on Double-Layer Objective

Abstract

The shared energy storage device acts as an energy hub between multiple microgrids to better play the complementary characteristics of the microgrid power cycle. In this paper, the cooperative operation process of shared energy storage participating in multiple island microgrid systems is researched, and the two-stage research on multi-microgrid operation mode and shared energy storage optimization service cost is focused on. In the first stage, the output of each subject is determined with the goal of profit optimization and optimal energy storage capacity, and the modified grey wolf algorithm is used to solve the problem. In the second stage, the income distribution problem is transformed into a negotiation bargaining process. The island microgrid and the shared energy storage are the two sides of the game. Combined with the non-cooperative game theory, the alternating direction multiplier method is used to reduce the shared energy storage service cost. The simulation results show that shared energy storage can optimize the allocation of multi-party resources by flexibly adjusting the control mode, improving the efficiency of resource utilization while improving the consumption of renewable energy, meeting the power demand of all parties, and realizing the sharing of energy storage resources. Simulation results show that compared with the traditional PSO algorithm, the iterative times of the GWO algorithm proposed in this paper are reduced by 35.62%, and the calculation time is shortened by 34.34%. Compared with the common GWO algorithm, the number of iterations is reduced by 18.97%, and the calculation time is shortened by 22.31%.

1. Introduction

Currently, China is building a clean and efficient new power system around the form of new energy power generation. As various distributed power generation units continue to integrate into the grid, the generation of electricity from these units exhibits inherent fluctuations and unpredictability, posing challenges to the safety and stability of the overall system operation. The generation of electric energy by distributed generation equipment has the problem of fluctuation and randomness, which will also reduce the safety and stability of system operation, and the diversification of power supply demand is difficult to meet [1]. To enhance the dependability of electricity provision and address the challenge of electricity accessibility in remote or isolated regions, the concept of a microgrid is proposed [2,3] using the Stackelberg game to solve the indeterminacy of renewable energy power generation, energy storage devices, and load. Electric vehicles are introduced into the power system as mobile energy storage to participate in regulation. Literature [4] focuses on a general two-population n-strategy evolutionary game (2PnS-EG) and applies it to investigate the evolutionary equilibrium properties of long-term strategic bidding issues in deregulated homogeneous and heterogeneous power generation-side markets (PGMs) under different market clearing mechanisms. In order to obtain an optimal joint planning and cost allocation strategy for multiple park-level integrated energy systems with shared energy storage. Literature [5] proposes a joint planning and cost allocation method for multiple park-level integrated energy systems with shared energy storage. Literature [6] focuses on the general N-population multi-strategy evolutionary games and uses them to investigate the generation-side long-term bidding issues in the electricity market. Literature [7] refers to the current situation; the indeterminacy on both sides of the signal source will cause large power imbalances and serious frequency fluctuations, threatening the stability and reliability of the operating load. Based on Nash bargaining theory and robust interval optimization, a point-to-point economic operation model is established for several microgrids. Literature [8] implemented four scheduling strategies for a microgrid system comprising solar-diesel hybrid generators, photovoltaic arrays, battery energy storage systems, and wind turbines: load tracking, generator orders, combined scheduling, and cyclic charging strategies. From the perspective of economy and reliability, a risk-based multi-grid for networked microgrids under the indeterminacy of load consumption and renewable energy generation is proposed [9].

Islanded microgrids often appear in remote areas, or when the microgrid is disconnected from the power grid due to faults, it is necessary to coordinate the output of each main body and maintain the balance of supply and demand. Its characteristic is to preferentially consume renewable energy locally and ensure equilibrium between electricity supply and demand. At present, new energy power generation still has problems, such as low utilization efficiency and weak coordination ability. The emergence of shared energy storage has solved these problems to some extent. Literature [10,11] put forward a microgrid risk-constrained scheduling strategy considering single-load demand response, introduced a bidirectional demand response mechanism and used power flexible load as a dispatchable resource to adjust the system net load curve. Literature [12] proposed a metaheuristic optimization algorithm based on fuzzy logic for the energy management of an islanded microgrid. In literature [13], a stochastic optimal scheduling strategy considering dependency relationship is proposed, and a stochastic optimal scheduling strategy is constructed by using improved scenario deep reinforcement learning. Literature [14] combined the comprehensive evaluation criteria of the economy and environmental protection to establish the optimal scheduling model of microgrid systems, including wind turbines, micro gas turbines, diesel generators, fuel cells, and batteries.

In 2018, China’s Qinghai Province first proposed the concept of “shared energy storage”. It is to point to being independent of the grid-centralized large independent energy storage power station. While meeting the needs of its power station, it can also provide charge and discharge services for other new energy power stations [15]. In literature [16], the Stackelberg game is employed to augment the financial returns of the shared energy storage power station. In this scenario, the user takes on the role of a follower, while the shared energy storage system acts as the leader, with the user’s electricity expenditure being a key consideration in the process. The energy storage formulates the strategy according to the historical data and finally decides the transaction price. Literature [17] proposed the “shared energy storage-demand” model to track the output curve of renewable energy so that users have more choices, establish a model to optimize the net income of users and enhance the use efficiency of resources and energy storage equipment. Literature [5] specifically established a comprehensive evaluation system and gradually approached the ideal ranking by changing the weights of different indicators. An evaluation of investment costs, power distribution, and capacity sharing between centralized and distributed energy storage systems was conducted alongside the development of a multi-scenario model tailored to variations in the context of renewable energy production and user-side energy consumption [18]. The findings indicate that the centralized energy storage sharing mode is more economical.

As technology improves by leaps and bounds for the island operation scenario, considering the new scenario of shared energy storage participating in scheduling optimization, this paper establishes a typical multi-microgrid system composed of wind-solar-storage-load gas turbines. This article is mainly divided into the following contents.

(1)

In terms of optimal scheduling, shared energy storage devices are introduced between islanded microgrids to integrate power resources and realize resource sharing. The improved grey wolf algorithm (GWO) is used to optimize the scheduling model. It demonstrates that incorporating shared energy storage capabilities could greatly decrease the extent of wasted wind and solar power generation and enhance the efficiency of resource utilization.

(2)

From an economic point of view, a more reasonable use of shared energy storage is formulated by alternating quotations and compared with the disposition of off-grid storage. The results demonstrate a significant reduction in the capacity requirements for shared energy storage, the maximum charging and discharging capabilities of the storage system, and the overall investment costs associated with energy storage power stations.

(3)

In this paper, the improved GWO is used, and the scheduling is optimized. Simulation results from typical scenarios reveal that in comparison to stand-alone off-grid energy storage configurations for individual microgrids, a shared energy storage power station enables the optimization of power flows, leading to a mutually advantageous scenario where both energy storage providers and users reap benefits.

The main structure of this paper is as follows: Section 2 builds the topology of the islanded microgrid system. Section 3 introduces the modeling process of each subject of the islanded microgrid. The optimization solution model is established in Section 4. In Section 5, it is verified that the proposed method is effective by taking the islanded multi-microgrid as the research object. Section 6 is the conclusion.

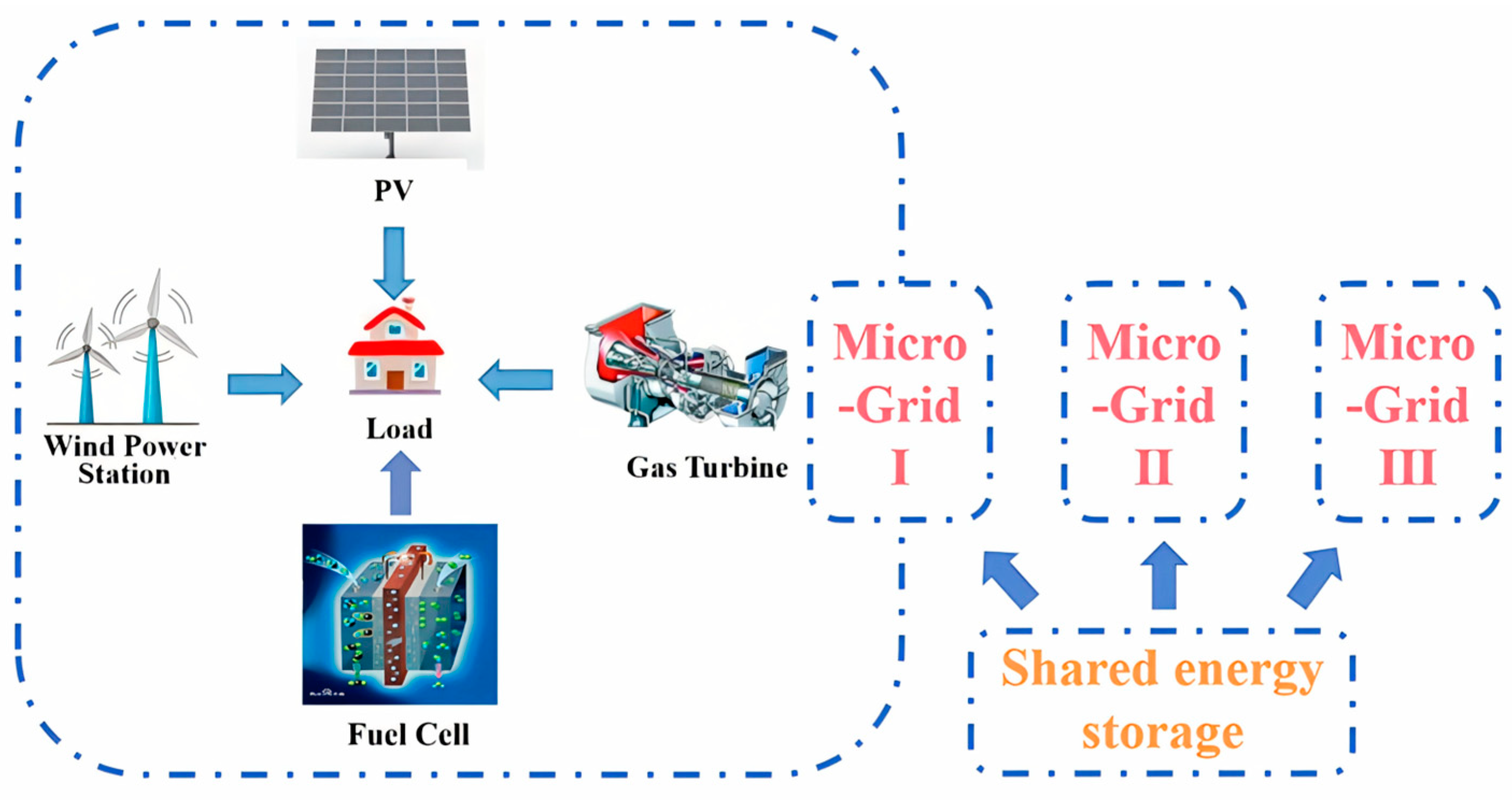
2. Modeling of Islanded Microgrid System

To enrich the application scenarios of microgrids, the microgrid model established mainly includes wind power generation equipment, PV equipment, micro-turbines, fuel cells, and load, as shown in Figure 1. Positioned as the central hub interconnecting multiple island microgrids, the shared energy storage power station effectively fulfills the specific charging and discharging requirements of each microgrid in an efficient manner. The shared energy storage can improve the user’s satisfaction with electricity while reducing the rate of solar and wind abandonment and further reducing the cost of the user group [19]. Large-capacity shared energy storage could achieve coordination between regions and different periods, utilize energy storage capacity to its fullest potential, enhance the utilization of renewable energy, and alleviate grid supply pressure. The shared energy storage power station, in the case of a system emergency, can swiftly activate turbines for immediate operation, thereby sustaining the system’s normal functionality [20].

The schematic diagram of the two-layer optimization decision model of an is-landed microgrid equipped with shared energy storage is shown in Figure 2. In order to describe the joint operation of new energy stations under the condition of multiple islands, a multi-island microgrid is proposed in this paper. The multi-microgrid grid-connected optimization model is mainly decomposed into the following two-stage problems for research.

(1)

Optimized scheduling module

The objective of maximizing the microgrid operational economy guides the determination of each component’s output literature [21]. When shared energy storage participates in the operation of multiple microgrids, the resource allocation and power flow are optimized, and the improved GWO is used to obtain the optimal scheduling results.

(2)

Transaction bargaining module

To achieve a more equitable distribution of benefits between microgrids and shared energy storage, the income distribution problem is transformed into a game problem of negotiated bargaining. In the context of this game-theoretic framework, the microgrid and shared energy storage represent the two opposing sides or players, and the alternating direction multiplier method (ADMM) is used to formulate the transaction price so as to optimize the shared energy storage service fee [22].

3. Mathematical Model of Each Subject

This section, segmented by subheadings, offers a succinct and exact portrayal of experimental outcomes, their interpretations, and the definitive conclusions that can be deduced from the experiments conducted.

3.1. Distributed Power Station Model

The radial basis neural network model [23] is used to predict the power generation of photovoltaic stations at time t is $P_{\mathrm{pv}}^t$ and the power generation of wind is $P_{\mathrm{wt}}^t$. Satisfying the power balance constraint conditions are as follows:

$$P_{\mathrm{pv}}^t=P_{\mathrm{pv}2\mathrm{b}}^t+P_{\mathrm{pv}2\mathrm{L}}^t$$

(1)

$$P_{\mathrm{wt}}^t=P_{\mathrm{wt}2\mathrm{b}}^t+P_{\mathrm{wt}2\mathrm{L}}^t$$

(2)

$$0\le P_{\mathrm{pv}2\mathrm{b}}^t,0\le P_{\mathrm{pv}2\mathrm{L}}^t,0\le P_{\mathrm{wt}2\mathrm{b}}^t,0\le P_{\mathrm{wt}2\mathrm{L}}^t$$

(3)

where $P_{\mathrm{pv}2\mathrm{b}}^t$ and $P_{\mathrm{wt}2\mathrm{b}}^t$ are the electricity sold by photovoltaic and wind power to shared energy storage, $P_{\mathrm{pv}2\mathrm{L}}^t$ and $P_{\mathrm{wt}2\mathrm{L}}^t$ are the electricity sold by photovoltaic and wind power to users.

The operational expenses of photovoltaic and wind power stations primarily consist of maintenance costs and the financial penalties associated with the reduction or limitation of wind and solar power generation output. The maintenance cost of the photovoltaic power station is $C_{\mathrm{pvm}}$, and the maintenance cost of the wind power station is $C_{\mathrm{wtm}}$:

$$C_{\mathrm{pvm}}={\displaystyle \sum {\tau }_{\mathrm{pv}}{\displaystyle \sum _{t=1}^T{\kappa }_{\mathrm{pv}}\cdot P_{\mathrm{pv}}^t}}$$

(4)

$$C_{\mathrm{wtm}}={\displaystyle \sum {\tau }_{wt}{\displaystyle \sum _{t=1}^T{\kappa }_{\mathrm{wt}}\cdot P_{\mathrm{wt}}^t}}$$

(5)

The expression for the penalty cost incurred due to the abandonment of wind and solar energy generation is presented as follows [24]:

$$C_{\mathrm{q}}=\{\begin{array}{c}{\gamma }_1\cdot P_{\mathrm{q}},P_{\mathrm{q}}\le P_1\\ {\gamma }_1\cdot P_1+{\gamma }_2\cdot \left(P_{\mathrm{q}}-P_1\right),P_1<P_{\mathrm{q}}\le P_2\\ {\gamma }_1\cdot P_1+{\gamma }_2\cdot \left(P_2-P_1\right)+{\gamma }_3\cdot \left(P_{\mathrm{q}}-P_2\right),P_2<P_{\mathrm{q}}\le P_3\end{array}$$

(6)

where ${\tau }_{\mathrm{pv}}$ and ${\tau }_{\mathrm{wt}}$ are the scene probability. The scene probability ${\tau }_{\mathrm{pv}}$ refers to the probability that photovoltaic power generation is $P_{\mathrm{pv}}^t$. The scene probability ${\tau }_{\mathrm{wt}}$ in the paper refers to the probability that wind power generation is $P_{\mathrm{wt}}^t$. ${\kappa }_{\mathrm{pv}}$ and ${\kappa }_{\mathrm{wt}}$ are maintenance cost coefficients, ${\gamma }_1$, ${\gamma }_2$, ${\gamma }_3$ and are the penalty coefficients of each stage, $P_1$, $P_2$, and $P_3$ are the power standard values of the three penalty stages. $P_{\mathrm{q}}$ is the power of wind and light abandonment.

The overall operating expenditure of the new energy power station is recorded as follows:

$$C_{\mathrm{new}}=C_{\mathrm{pvm}}+C_{\mathrm{wtm}}+C_{\mathrm{q}}$$

(7)

3.2. Model of Gas Turbine

The variability and randomness of renewable energy will pose a serious hidden danger to the security and stability of microgrids. Especially in the case that energy storage technology has not been widely used, gas turbines can form complementary advantages with energy storage batteries by their good power climbing ability to achieve an ‘incremental energy storage’ effect. The power constraint and climbing constraints are in Equation (8).

$$\{\begin{array}{c}{P}_{\mathrm{mt}\_\min }\le P_{\mathrm{mt}}^t\le P_{\mathrm{mt}\_\max }\\ R_{i,down}\Delta t\le P_{\mathrm{mt}}^t-P_{\mathrm{mt}}^{t-1}\le R_{i,up}\Delta t\end{array}$$

(8)

where, $P_{\mathrm{mt}}^t$ is the output of the gas turbine at time t, $P_{\mathrm{mt}\_\min }$ and $P_{\mathrm{mt}\_\max }$ are the minimum and maximum gas turbine output, $R_{i,up}$ and $R_{i,down}$ are the maximum and minimum output of the gas turbine at time $\Delta t$.

When renewable energy power generation cannot provide users with normal operation, the gas turbine can be used as one of the reserve forces [25]. The operational cost of gas turbines encompasses three primary components: fuel expenses, maintenance costs, and environmental pollution control fees. The fuel cost is related to its output power, which is shown in Expression (9)–(11) [26].

$$C_{\mathrm{MT}}={\displaystyle \sum _{t=1}^T\frac{C_{\mathrm{NG}}}{\mathrm{LHV}}\cdot \frac{P_{\mathrm{MT}}^t}{{\eta }_{\mathrm{MT}}}}$$

(9)

$${\eta }_{\mathrm{MT}}=0.0753{\left({\displaystyle \frac{P_{\mathrm{MT}}^t}{65}}\right)}^3-0.3095{\left({\displaystyle \frac{P_{\mathrm{MT}}^t}{65}}\right)}^2+0.4174\left({\displaystyle \frac{P_{\mathrm{MT}}^t}{65}}\right)+0.1068$$

(10)

where $C_{\mathrm{MT}}$ is the fuel expenditure of gas turbine, $C_{\mathrm{NG}}$ is the unit price of fuel, LHV is the energy content or heating value of fuel, $P_{\mathrm{MT}}^t$ is the output power of a gas turbine in t period, ${\eta }_{\mathrm{MT}}$ is the power generation efficiency of gas turbines. The expression of gas turbine maintenance expenditure and environmental treatment expenditure is as follows:

$$C_{\mathrm{mtc}}={\displaystyle \sum _{t=1}^T{K}_{\mathrm{mtc}}\cdot P_{\mathrm{mt}}^t}+{\displaystyle \sum _{t=1}^T\left({\displaystyle \sum _{j=1}^W{\mu }_j}{\displaystyle \sum _{i=1}^N{K}_{ij}{P}_i^t}\right)}$$

(11)

where $K_{\mathrm{mtc}}$ is the maintenance expenditure coefficient of microgas turbine, ${\mu }_j$ is the unit treatment expenditure of the jth pollutant, $K_{ij}$ is the jth pollutant emission coefficient of the ith equipment, $P_i^t$ is the output power of the i equipment in t period.

3.3. Fuel Cell Model

In theory, the fuel cell has high power generation efficiency. At present, the energy conversion efficiency can reach 40% to 60%, and it has often been used in microgrids because of its advantages of small environmental pollution, simple structure, and low power generation cost to remedy the volatility and uncertainty of new energy power generation and ensure that the power system can operate stably. The expression of fuel cell output power is:

$$P_{\mathrm{FC}}=V_{\mathrm{FC}}\cdot {\eta }_{\mathrm{FC}}\cdot {\mathrm{LHV}}_f$$

(12)

where $V_{\mathrm{FC}}$ is the fuel consumption, ${\eta }_{\mathrm{FC}}$ is the fuel cell power generation efficiency, ${\mathrm{LHV}}_f$ is the low calorific value of the fuel.

3.4. Shared Energy Storage Model

Within a system comprising multiple microgrids, the shared energy storage acts as a central hub, seamlessly connecting and dynamically managing the power flow among individual microgrids. It formulates charging and discharging schedules tailored to the operational status of each microgrid, ensuring optimal energy utilization. Compared with the independent configuration energy storage station, large-scale shared energy storage exhibits characteristics of standardized energy storage protocols and a relatively smaller aggregate capacity compared to individual installations [27]. The operation of the shared energy storage power station should meet the continuous dynamic constraints. The corresponding expression is as follows:

$$C_{\mathrm{FC}}={\displaystyle \frac{{\mathrm{c}}_{\mathrm{gas}}}{{\mathrm{LHV}}_f}}{\displaystyle \sum \frac{P_{\mathrm{FC}}}{{\eta }_{\mathrm{FC}}}}$$

(13)

$$\{\begin{array}{c}{P}_{\mathrm{b}\_\mathrm{c}}^{\min }\le P_{\mathrm{b}\_\mathrm{c}}^t\le P_{\mathrm{b}\_\mathrm{c}}^{\max }{U}_{\mathrm{b}\_\mathrm{c}},\Delta {\mathrm{E}}_{\mathrm{bat}}\left(t\right)>0\\ \begin{array}{l}{P}_{\mathrm{b}\_\mathrm{d}}^{\min }\le P_{\mathrm{b}\_\mathrm{d}}^t\le P_{\mathrm{b}\_\mathrm{d}}^{\max }{U}_{\mathrm{b}\_\mathrm{d}},\Delta {\mathrm{E}}_{\mathrm{bat}}\left(t\right)<0\\ U_{\mathrm{b}\_\mathrm{c}}+U_{\mathrm{b}\_\mathrm{d}}\le 1\\ U_{\mathrm{b}\_\mathrm{c}}\in \left\{0,1\right\}\\ U_{\mathrm{b}\_\mathrm{d}}\in \left\{0,1\right\}\end{array}\end{array}$$

(14)

where ${\mathrm{c}}_{\mathrm{gas}}$ is the fuel price, $E_{\mathrm{bat}}^t$ is the electrical power stored in the t period, $E_{\min }$ and $E_{\max }$ are the minimum and maximum energy storage, ${\xi }_{\mathrm{b}\_\mathrm{c}}$ and ${\xi }_{\mathrm{b}\_\mathrm{d}}$ are efficiency of charging and discharging processes of the t period. $P_{\mathrm{b}\_\mathrm{c}}^{\min }$ and $P_{\mathrm{b}\_\mathrm{c}}^{\max }$ are the minimum and maximum power capacity for charging. $\Delta E_{\mathrm{bat}}\left(t\right)<0$ indicates that the shared energy storage is in the discharge state, $U_{\mathrm{b}\_\mathrm{d}}$ and $U_{\mathrm{b}\_\mathrm{c}}$ indicates the state of discharge and charge for the shared energy storage system. $P_{\mathrm{b}\_\mathrm{d}}^{\min }$ and $P_{\mathrm{b}\_\mathrm{d}}^{\max }$ are the minimum and maximum discharge power.

In order to ensure the continuity and sustainability of the charging and discharging, the storage capacity of the energy storage power station should return to the initial state value after a running cycle. The constraint formula is:

$$E_{\mathrm{bat}}^{\mathrm{T}}=E_{\mathrm{bat}}^0$$

(15)

where $E_{\mathrm{bat}}^0$ and $E_{\mathrm{bat}}^{\mathrm{T}}$ denote the starting and ending points of the energy storage cycle, respectively.

Leveraging the disparity in generation and consumption timings across diverse microgrids, the shared energy storage system harmoniously integrates and dispatches power flows within a unified regional microgrid framework. This approach enhances the satisfaction of microgrid charging and discharging requirements while also reducing overall investment costs. The constraints pertaining to the charging and discharging power of the energy storage system are linearized using the large M approach. The revenue for the shared energy storage power station arises from the 28 service charges levied on microgrids for the utilization of its charging and discharging capabilities. The service expenses incurred by the microgrid are settled on a daily basis.

$$C_{\mathrm{b}}={\displaystyle \sum _{t=1}^{\mathrm{T}}{\lambda }_{\mathrm{b}}\left(P_{\mathrm{b}\_\mathrm{c}}^t+P_{\mathrm{b}\_\mathrm{d}}^t\right)}$$

(16)

where ${\lambda }_{\mathrm{b}}$ is the service expenditure paid when the shared energy storage provides unit charging power or discharging power.

The average annual cost $C_{\mathrm{bat}}$ of energy storage batteries is mainly composed of installation expenditure and operation and maintenance expenditure, which is proportional to the capacity of the energy storage configuration [28].

$$C_{\mathrm{bat}}=C_{\mathrm{sys}}{\displaystyle \frac{i{\left(1+i\right)}^m}{{\left(1+i\right)}^m-1}}+C_{\mathrm{FOM}}$$

(17)

where m represents the investment return period, which is mainly inversely proportional to the installation cost $C_{\mathrm{sys}}$, and the expression is as follows:

$$m={\log }_{i+1}{\displaystyle \frac{1}{1+\frac{i{C}_{\mathrm{sys}}}{C_{\mathrm{FOM}}}}}$$

(18)

where i is the discount rate and $C_{\mathrm{FOM}}$ is operational and maintenance expenses.

3.5. Microgrid Operation Model

The user’s electricity consumption in each period is $P_{\mathrm{L}}^t$ calculated using the prediction model. For the users in the island microgrid, the energy comes from PV, wind power, gas turbines, and shared energy storage. The trading power is recorded as $P_{\mathrm{pv}2\mathrm{L}}^t$, $P_{\mathrm{wt}2\mathrm{L}}^t$, $P_{\mathrm{mt}2\mathrm{L}}^t$, and $P_{\mathrm{b}2\mathrm{L}}^t$. The power balance relationship to be satisfied is as follows:

$$P_{\mathrm{pv}2\mathrm{L}}^t+P_{\mathrm{wt}2\mathrm{L}}^t+P_{\mathrm{mt}2\mathrm{L}}^t+P_{\mathrm{b}2\mathrm{L}}^t=P_{\mathrm{L}}^t$$

(19)

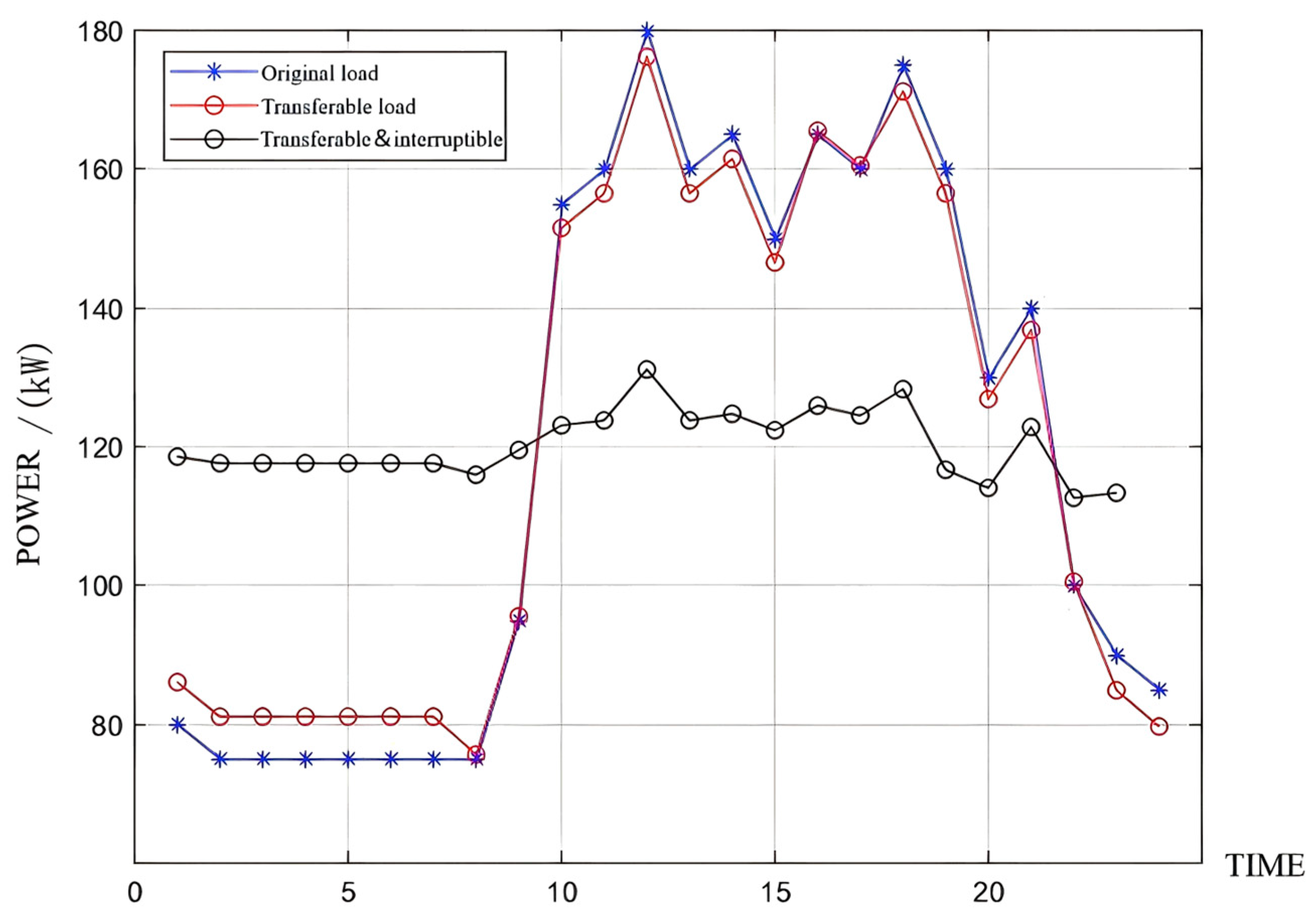
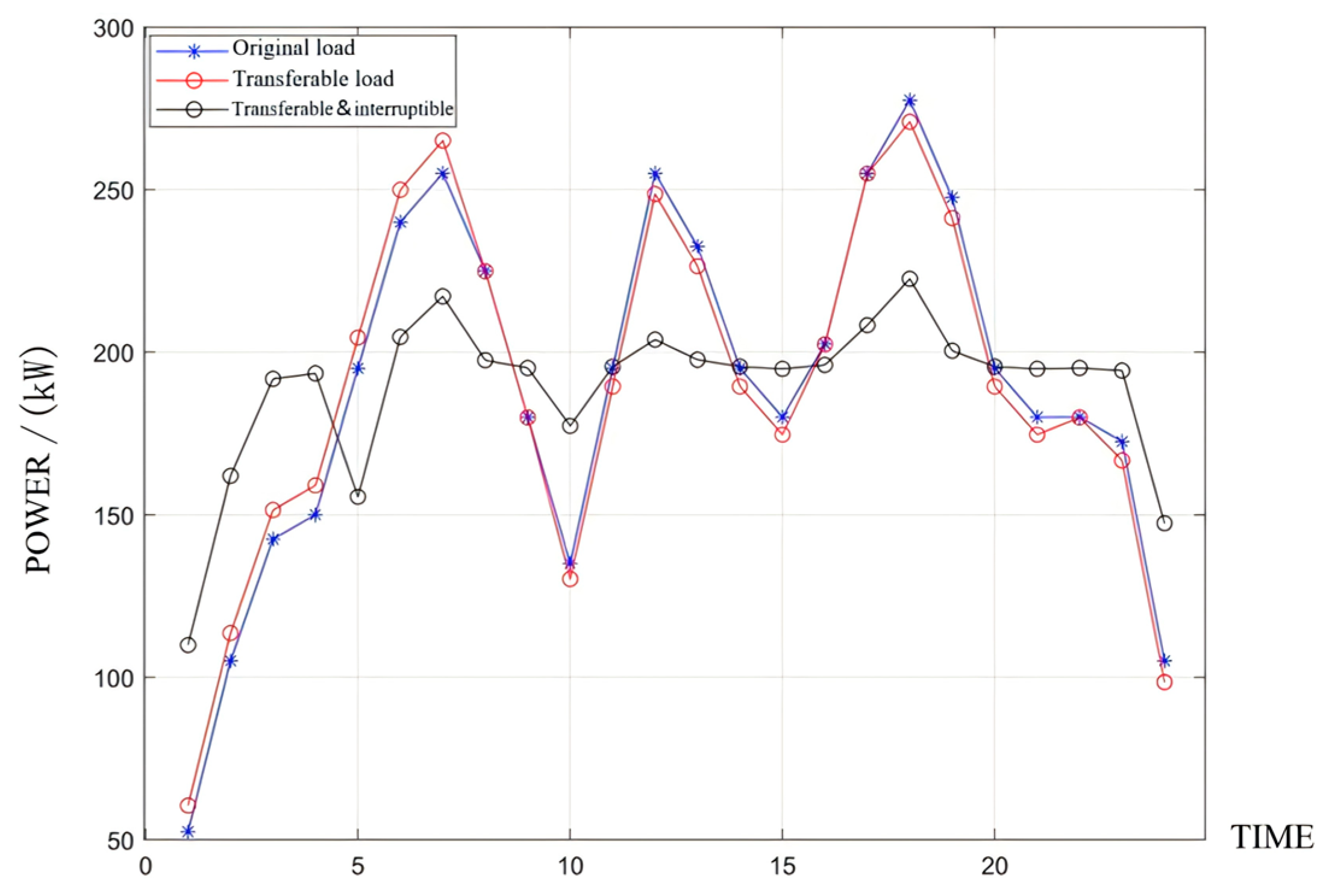
(1)

Transferable load

The transferable load’s primary objective is to mitigate the adverse effects of load fluctuations, peak-valley differences, voltage fluctuations, and flicker, all of which are induced by the frequent operation of power electronic devices. For the power generation side, the increase of power generation output during the trough period avoids low-load fuel operation and can reduce operating costs.

$$\{\begin{array}{c}\min {\Vert P_{\mathrm{L}}^t+P_{\mathrm{TL}}^t-P_{\mathrm{L}\_\mathrm{ave}}\Vert }_2\\ {\displaystyle \sum _{t=1}^T{P}_{\mathrm{TL}}^t}=0\\ P_{\mathrm{L}\_\mathrm{ave}}={\displaystyle \frac{{\displaystyle \sum _{t=1}^{\mathrm{T}}{P}_{\mathrm{L}}^t}}{T}}\\ P_{\mathrm{TL}\_\min }^t\le P_{\mathrm{TL}}^t\le P_{\mathrm{TL}\_\max }^t\end{array}$$

(20)

where $P_{\mathrm{TL}}^t$ is the user transferable load, $P_{\mathrm{L}\_\mathrm{ave}}$ is the mean load in one day, ${\displaystyle \sum _{t=1}^{\mathrm{T}}{P}_{\mathrm{TL}}^t}$ represents the total amount of transferable load in a day, $P_{\mathrm{TL}\_\min }^t$ and $P_{\mathrm{TL}\_\max }^t$ are the minimum and maximum values of transferable load. The adjusted load is:

$$P_{\mathrm{L}\prime }^t=P_{\mathrm{L}}^t+P_{\mathrm{TL}}^t$$

(21)

(2)

Interruptible load considering demand response

To enhance the operational stability of island microgrids, the flexibility offered by interruptible loads is harnessed to mitigate electricity shortages. Its adjustment ability largely depends on the proportion of interruptible load and compensation cost. The mathematical conditions of load constraints are as follows:

$$\{\begin{array}{c}{\displaystyle \sum _{t\in H_{IL}}{P}_{\mathrm{L}}^t}\le {\displaystyle \sum _{j\in A}\Delta P_{\mathrm{L}}^t{U}^t}+{\displaystyle \sum _{t\in H_{IL}}{P}_{\mathrm{NCL}}^t}\\ P_{\mathrm{NCL}}^t\le P_{\mathrm{L}}^t,t\in \mathrm{T}\\ P_{\mathrm{NCL}}^t=P_{\mathrm{L}}^t,t\notin H_{\mathrm{IL}}\end{array}$$

(22)

where $H_{\mathrm{IL}}$ is the interruptible time period, $\Delta P_{\mathrm{L}}^t$ is the active power of load interruption in the t period, $U^t$ denotes the decision variable in the t period, $P_{\mathrm{NCL}}^t$ is uncontrollable load power. The expression of the adjusted load $P_{\mathrm{L}\_\mathrm{new}}^t$ is:

$$P_{\mathrm{L}\_\mathrm{new}}^t=P_{\mathrm{L}\prime }^t-\Delta P_{\mathrm{L}}^t$$

(23)

The penalty function for the interrupted load is expressed as follows:

$$C_{\mathrm{pen}}=K_{\mathrm{pen}}{\displaystyle \sum _{t=1}^{\mathrm{T}}\Delta }{P}_{\mathrm{L}}^t$$

(24)

where $K_{\mathrm{pen}}$ is the penalty coefficient of the interruption load.

Combined with the above model, the total cost expression of microgrid operation is:

$$\min C_{\mathrm{mg}}=C_{\mathrm{new}}+C_{\mathrm{MT}}+C_{\mathrm{mtc}}+C_{\mathrm{FC}}+C_{\mathrm{bat}}-C_{\mathrm{b}}+C_{\mathrm{pen}}$$

(25)

4. An Improved GWO Optimization Model Based on BAS

The GWO has the characteristics of strong global search ability but a low convergence rate. The Beetle Antennae Search Algorithm (BAS) has the characteristics of a fast search but easily falls under the local optimal solutions. Combining the advantages and disadvantages of the two, an improved GWO based on BAS is proposed. In the first stage, the purpose of the improved GWO calculation is to minimize the overall operation expenditure of the microgrid so as to plan the output of each main body. Combined with the constraints of each subject and the shared energy storage service expenditure. The second phase involves equilibrating the interests of both the microgrid and the shared energy storage power station. The non-cooperative game theory is introduced, and the ADMM is used to optimize the service expenditure.

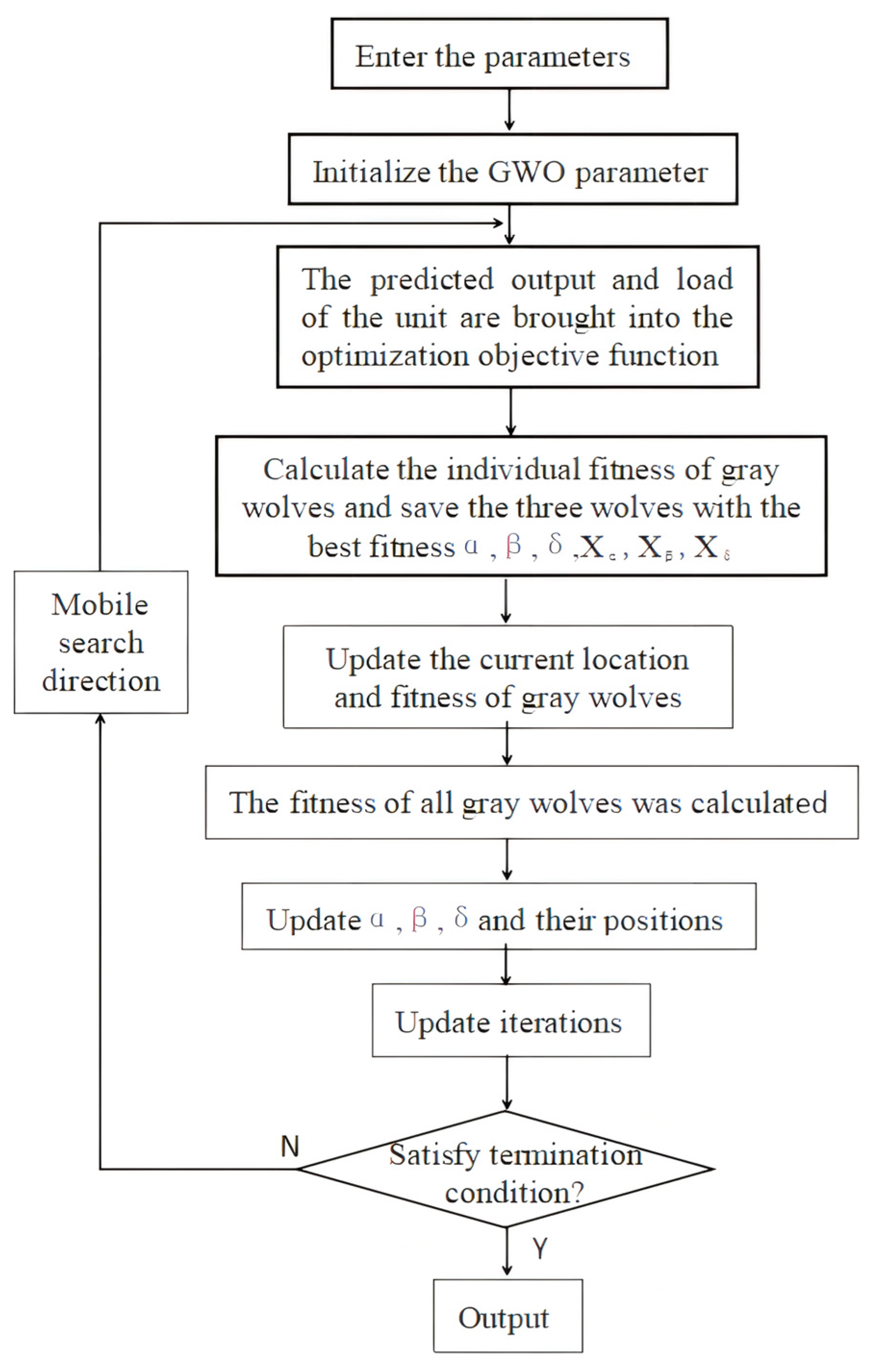
4.1. Optimal Scheduling Model Based on Improved GWO

The GWO has the characteristics of a simple overall structure, easy programming, fast convergence speed, and high search efficiency. However, its problem of falling into local optimal solution limits its application in engineering. This paper solves this problem by adding the beetle antennae search algorithm. The process is shown in Figure 3.

(1)

Input the microgrid load prediction value $P_{\mathrm{L}}^t$, photovoltaic output prediction value $P_{\mathrm{pv}}^t$, wind power output prediction value $P_{\mathrm{wt}}^t$, abandoned wind and abandoned light penalty coefficient ${\gamma }_1$, ${\gamma }_2$, ${\gamma }_3$, and the maintenance cost coefficient of each piece of equipment, upper and lower limits of output values, and record the number of iterations as $k=1$;

(2)

With the goal of optimizing the power generation expenditure of the microgrid, the output of each subject is calculated as the Wolf individual fitness value;

(3)

The calculated fitness value of each gray Wolf is ranked. The first three are recorded as $\alpha$, $\beta$, and $\delta$ respectively. The corresponding location information is $X_{\alpha }$, $X_{\beta }$, and $X_{\delta }$ respectively;

(4)

If the $k>K_{\max }$ iteration ends, this value is the optimal result and outputs this value; otherwise, continue to perform step 5;

(5)

Updated the location of the Gray Wolf to re-elect new wolves $\alpha$, $\beta$, and $\delta$;

(6)

Update iterations, $k=k+1$;

(7)

Verify whether the termination condition is met, and if so, verify whether it falls into the local optimal solution; if it is satisfied, jump out of the loop and output the final result; if it is not satisfied, use the BAS to gain a new search direction, and Revert back to step (2) and proceed with the solution.

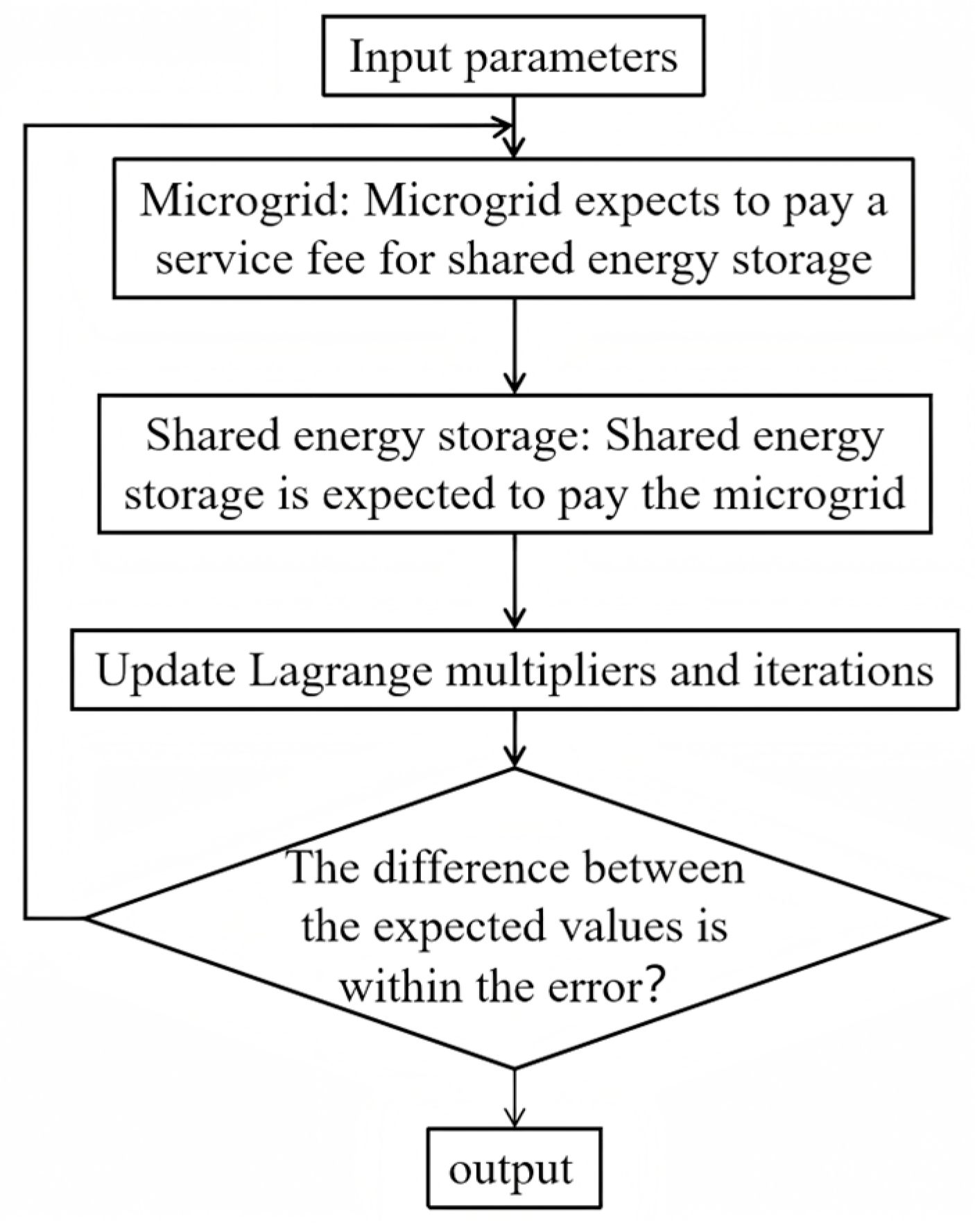
4.2. Service Fee Optimization Formulation Model Based on ADMM

During the formulation of service fees, the user charges vary depending on the microgrid’s operational state. Given the higher initial investment cost of shared energy storage, these costs are amortized on a daily basis to ensure fairness [29]. To ensure equitable benefits for all parties, the analysis initially employs Nash equilibrium to explore the influence of transaction prices on transactional modes. Subsequently, a non-cooperative game-theoretic framework is employed to determine the optimal pricing approach for shared energy storage [30].

With the intention of minimizing the costs of the shared energy storage and the operating expenditure of the microgrid [31], the optimal scheduling results obtained in the first stage are input into the service expenditure optimization model for the solution. The process is shown in Figure 4.

(1)

Input the original data variables of various parameters, such as the prediction data of the PV station, wind power station, load forecast value, Lagrange penalty factor $\rho$, the maximum number of iterations, and convergence accuracy.

(2)

For the main body of the microgrid, the mathematical model of the PV station, wind power station, gas turbine, and load is used to calculate the expected service fee $r_{\mathrm{g}2\mathrm{b}}$ of the microgrid to share energy storage under the maximization of microgrid revenue.

(3)

For the core entity of the microgrid, the mathematical model of the PV station, wind power station, gas turbine, and load is calculated, and the expected service fee of the microgrid to share energy storage is $r_{\mathrm{g}2\mathrm{b}}$ under the maximization of microgrid revenue.

(4)

Update the Lagrange multiplier and iterations.

(5)

Determine whether the deviation value of $r_{\mathrm{g}2\mathrm{b}}$ and ${\tilde{r}}_{\mathrm{g}2\mathrm{b}}$ is within the allowable convergence accuracy range, and if it is greater than the convergence accuracy requirement, return step 2 to continue the iteration; if it is less than the convergence accuracy requirement, the iteration ends, and the optimized electricity price is output as the result.

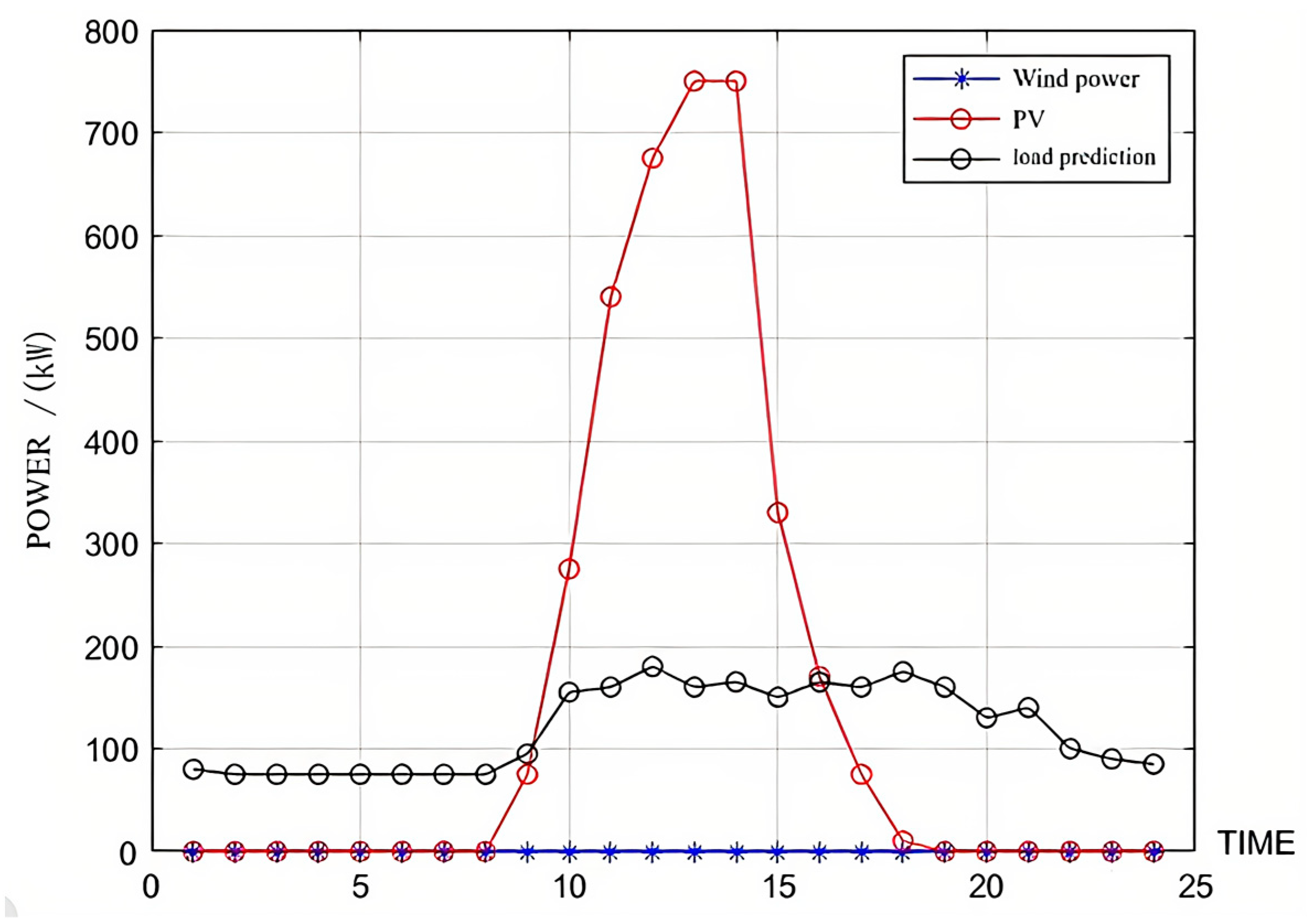
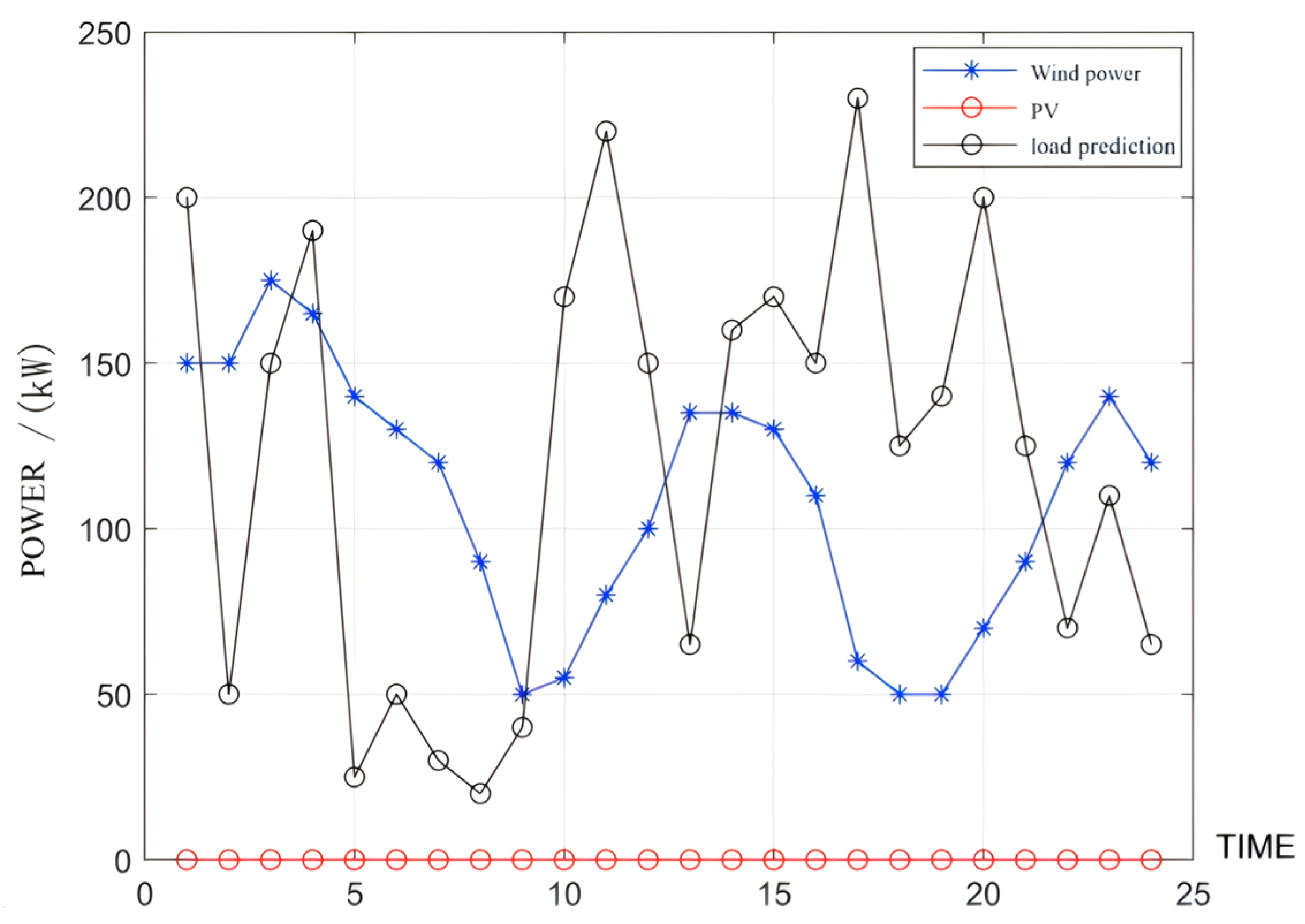
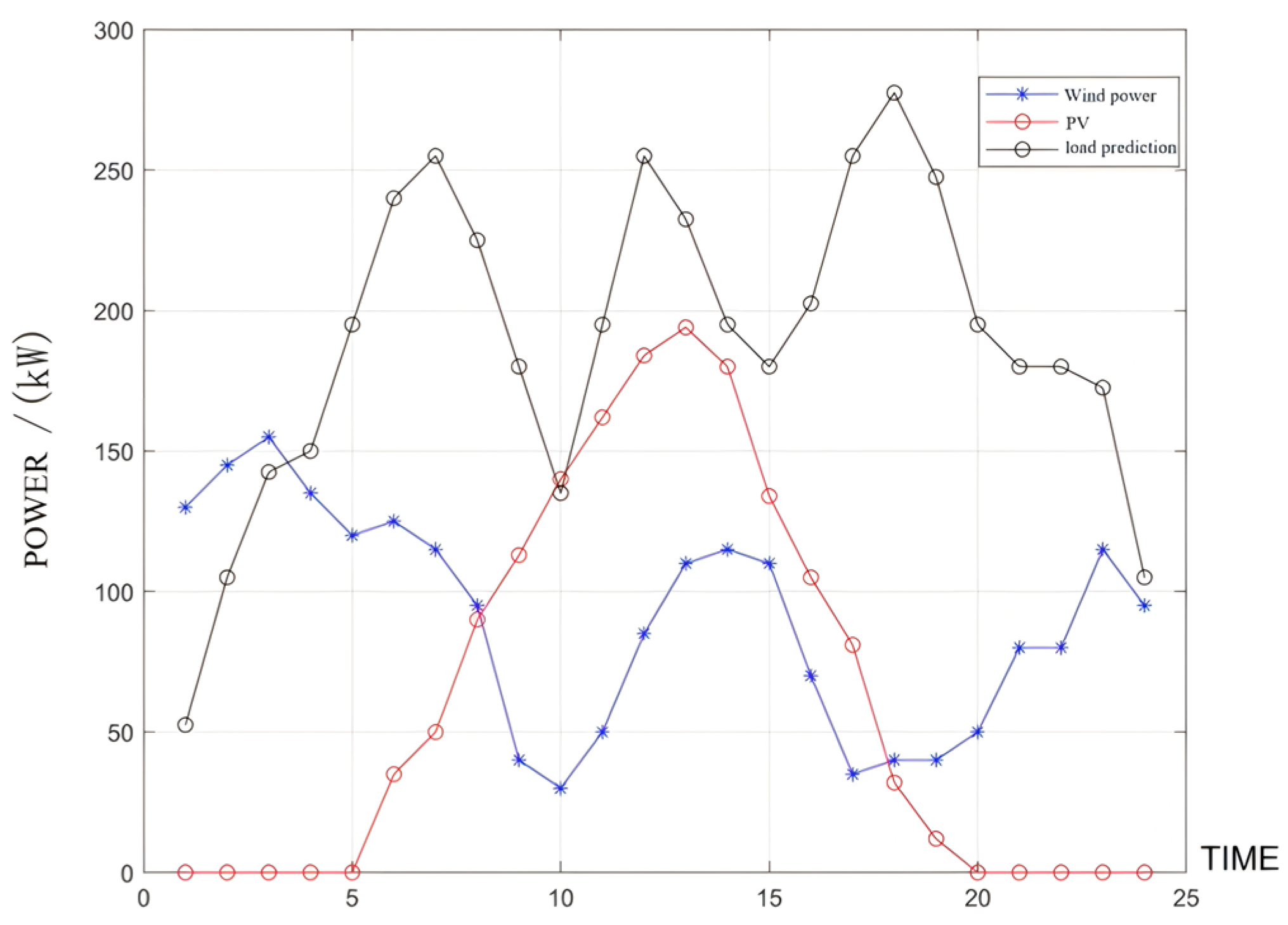
5. Case Study

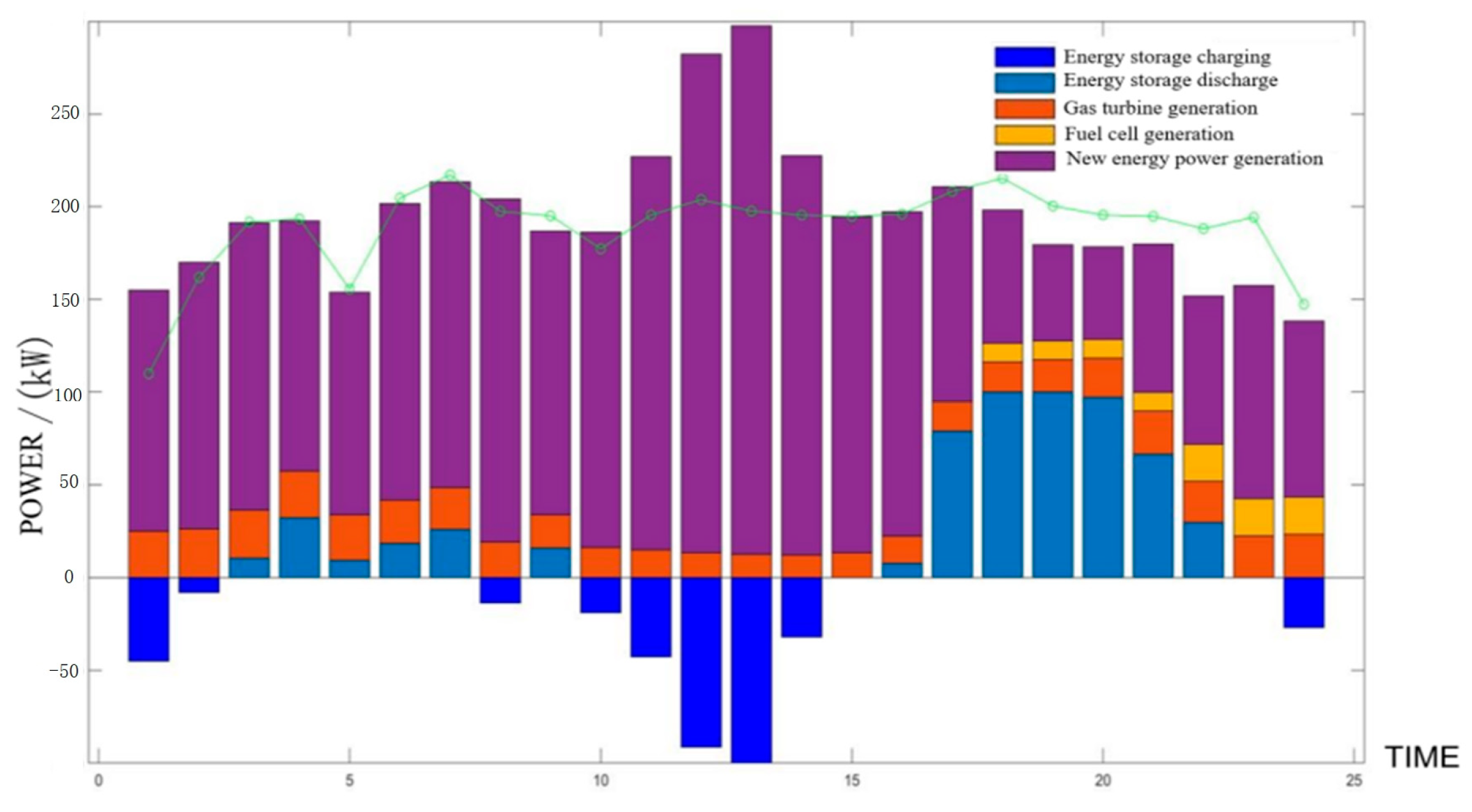
5.1. Island Multi-Microgrid Is Equipped with Independent Energy Storage

To assess the operational characteristics of diverse microgrid types and validate the model’s practicality, three illustrative scenarios have been selected for analysis. Through a comparative analysis of the economic and energy flow performance between independent and shared energy storage systems across three microgrid scenarios, the superiority of multi-microgrid operation in island mode is clearly demonstrated. The three microgrids are as follows.

• Microgrid I: PV + load;
• Microgrid II: Wind power + load;
• Microgrid III: PV + Wind power + load.

(1)

Microgrid I is configured with independent energy storage

The output of each main subject of microgrid I is shown in Figure 5. Only the participation of PV generation in microgrid operation is considered, and the PV generation is much larger than the load power consumption during the peak period.

Figure 6 shows the curve after load optimization and adjustment. As can be seen from the figure, compared with the original load, the load curve, after taking interruptible load and transferable load into account, is more stable, which is conducive to system stability while promoting the consumption of new energy.

Figure 7 shows the energy transaction diagram of microgrid I. It can be seen that the microgrid preferentially consumes new energy power generation, and the power storage is charged when the PV generation is excess at 9:00–12:00. Due to the finite energy storage capacity, the storage system tends to reach its full capacity by 12:00. During 12:00–13:00, the energy storage is no longer charged or discharged, and the electricity for users is supplied by new energy generation and gas turbine. Resulting in the discarding and wastage of excess PV generation during the period from 13:00 to 15:00.

(2)

Microgrid II is configured with independent energy storage

The output of each main body of microgrid II is shown in Figure 8, which only considers the participation of wind power generation in microgrid operation. Figure 9 shows the curve after load optimization and adjustment.

Figure 10 shows the microgrid II energy transaction diagram. It shows that the new energy power generation is preferentially consumed.

(3)

Microgrid III is configured with independent energy storage

The output of each main body of microgrid III is shown in Figure 11. Figure 12 shows the curve after load optimization and adjustment. The microgrid III energy transaction result is shown in Figure 13. The green curve represents the optimized load curve.

According to the specific situation of each microgrid, the three microgrids are equipped with independent energy storage of corresponding capacity, respectively. On the basis of the original operation expenditure, the average daily investment expenditure, operation expenditure, and maintenance expenditure of independent energy storage is increased [32] as follows:

$$C_{\mathrm{inv}}={\displaystyle \frac{{\eta }_{\mathrm{P}}\cdot P_{\max }+{\eta }_{\mathrm{s}}{E}_{\max }}{T_{\mathrm{s}}}}+M$$

(26)

where ${\eta }_{\mathrm{P}}$ and ${\eta }_{\mathrm{s}}$ represent the power expenditure and capacity expenditure, respectively. $P_{\max }$ is the maximum charge and discharge power, $E_{\max }$ is the maximum capacity of energy storage, $T_{\mathrm{s}}$ is the expected service life of energy storage, days, m is the average daily maintenance expenditure. The improved GWO is used to calculate the optimization results when the three microgrids are configured with independent energy storage, which is shown in

Table 1. Optimization Results for Each Microgrid.

	Energy Storage Capacity/(kWh)	Energy Storage Maximum Charge and Discharge Power/kW	Cost of Operation/Yuan
Microgrid I	2796.5625	590	1625.48
Microgrid II	739.2434	130	561.79
Microgrid III	836.8421	195.5	754.38
Total	4372.648	915.5	2941.65

.

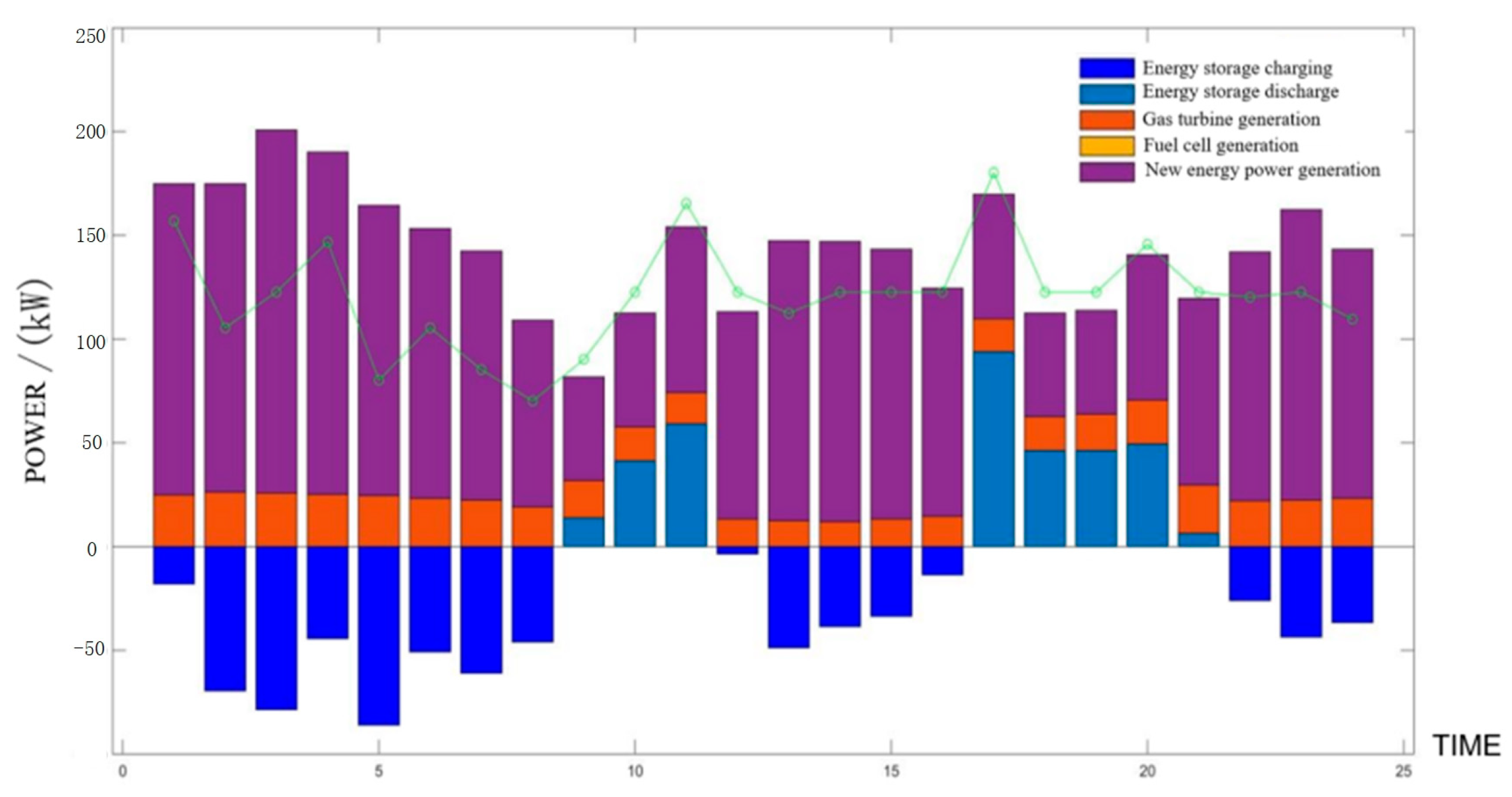
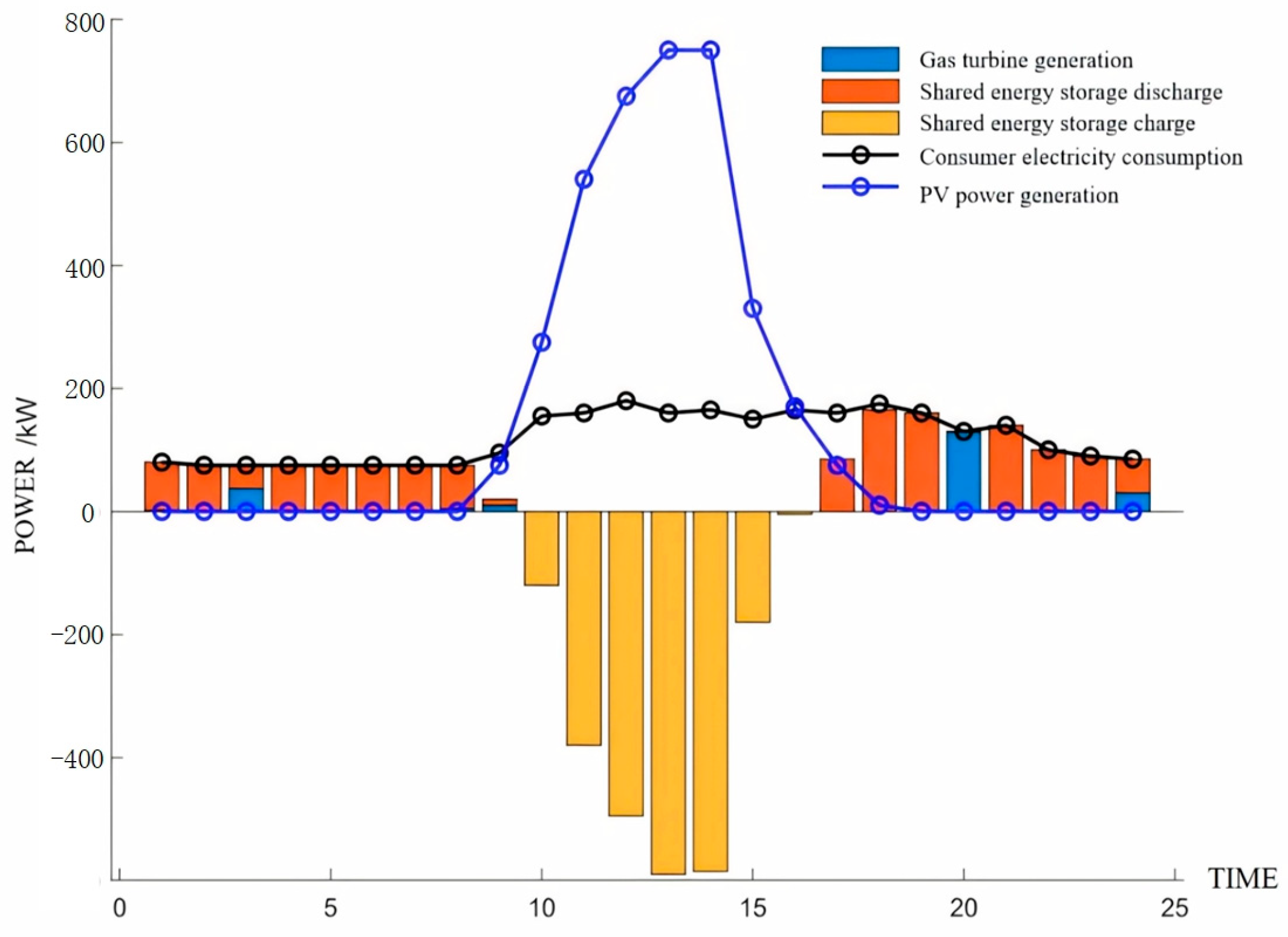
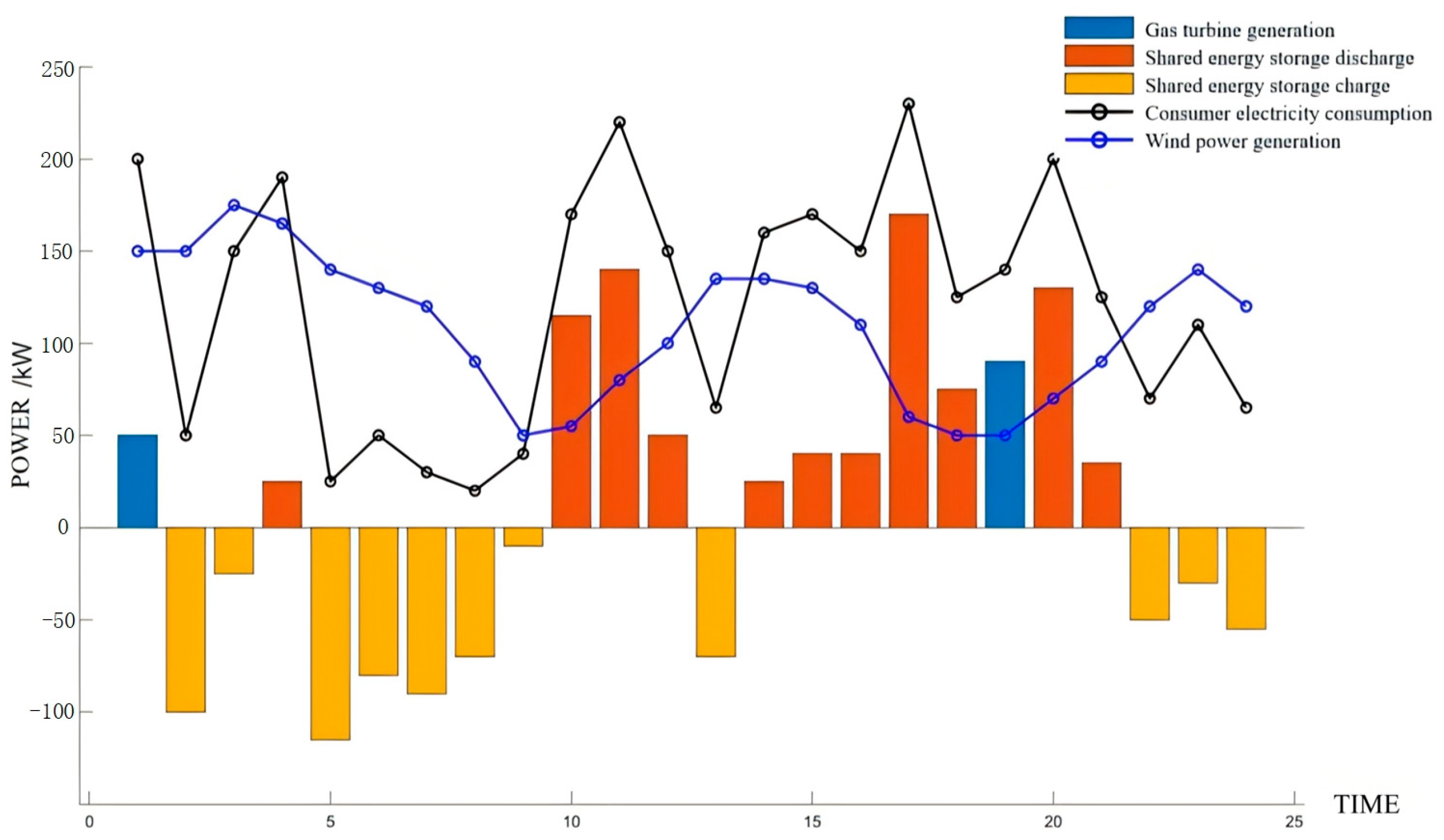
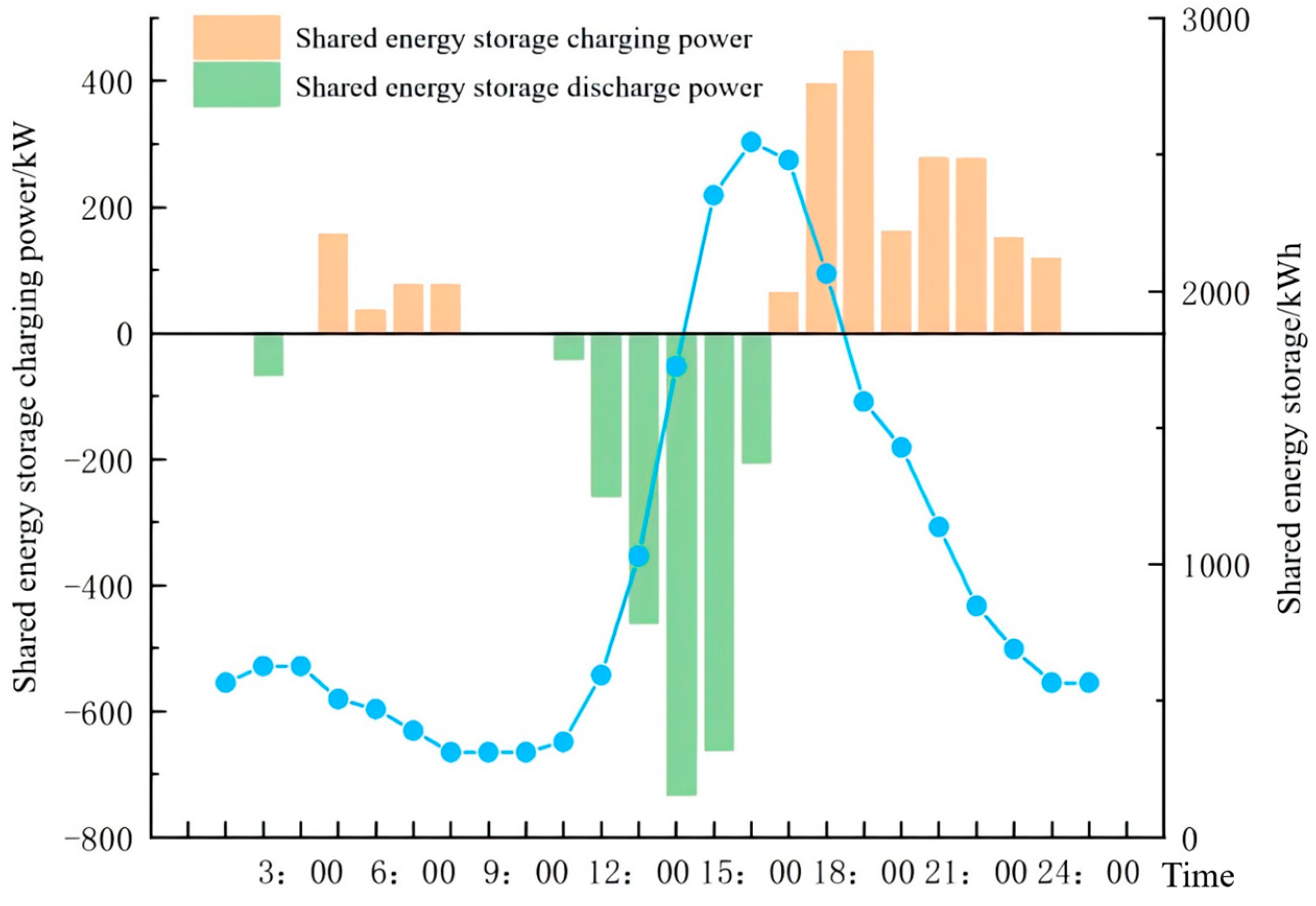
5.2. Islanded Multi-Mcrogrid Is Equipped with Shared Energy Storage

A multi-microgrid system comprising three distinct microgrids in the above summary is equipped with shared energy storage as an example for analysis, and the charge and discharge service fee for the shared energy storage system has been established as 1.4 yuan/kWh. Figure 14, Figure 15 and Figure 16 illustrate the optimal power allocation outcomes for the three microgrids. Figure 17 shows the energy state of the shared energy storage station, where the blue curve represents the energy of the energy storage station.

After the shared energy storage involved in the optimal scheduling among the three microgrids, the optimal capacity planning value of the shared energy storage power station is 2828.4079 kWh by using the GWO, which is about 35.316% lower than that of the independent energy storage capacity of 4372.648 kWh. The maximum charging and discharging capacity of the shared energy storage station is 732 kw, which is about 20% lower than the maximum charging and discharging power of 915.5 kW with independent energy storage. The overall payment expenditure of the three microgrids is 2487.7 yuan, which is about 15.43% lower than that of 2941.65 yuan equipped with independent energy storage. Shared energy storage greatly improves the utilization rate of new energy power generation; on the other hand, it also greatly reduces the investment expenditure of energy storage power stations and realizes multi-regional energy complementary circulation.

Based on the optimized trading electricity results obtained in the previous summary, the non-cooperative game model is used to further optimize the trading price by alternating quotations. In the initial calculation of the example, the shared energy storage is set as the price increaser, and the user is the decision maker. Taking into account the rental expenses, the ADMM is employed to address the problem, and the iterative process eventually converges to a solution. Finally, the optimal transaction price is 1.53 yuan/(kWh), which includes the average daily expenditure and maintenance expenditure of the shared energy storage investment.

In Figure 14, the two curves represent user demand and photovoltaic power generation, and the bar graph represents gas turbine power generation, energy storage discharge, and energy storage charge. The superposition of each main output is user demand. As can be seen from the figure, when the photovoltaic power generation from 1:00 to 8:00, 17:00 to 19:00, and 21:00 to 24:00 does not meet the needs of users, energy storage and discharge are shared to supply users. When there is a surplus of photovoltaic power generation from 10:00 to 15:00, the remaining power is stored by a shared energy storage power station in order to reduce the light abandonment rate and improve the level of new energy consumption. At 13:00, the photovoltaic output reaches a maximum of 753.2 kW, and the shared energy storage also reaches a maximum charging power of 590 kW. When the rest of the shared energy storage is insufficient, the gas turbine power generation supplies the load. It can be seen that more photovoltaic surplus power is stored, and the gas turbine output is significantly reduced, which greatly improves the level of new energy consumption.

As can be seen from Figure 15, when there is a surplus of wind power generation from 2:00 to 3:00, 5:00 to 9:00, and 22:00 to 24:00, shared energy storage stores the excess power to reduce the curtailment rate. When the wind power generation is insufficient from 10:00 to 12:00, 14:00 to 18:00, and 20:00 to 21:00, the shared energy storage discharge is provided to the user. At 5:00, the remaining power of wind power generation is the largest, and the wind power generation is 142.1 kW, and the shared energy storage also reaches the maximum charging power of 115.9 kW. When the rest of the shared energy storage is insufficient, the gas turbine power generation supplies the load. It can be seen that the use frequency of gas turbines decreases, and shared energy storage increases the utilization rate of new energy power generation.

As can be seen from Figure 16, when there is a surplus of new energy generation at 1:00–3:00 and 10:00–15:00, the shared energy storage starts to charge and stores the excess electricity. When the new energy generation is insufficient from 4:00 to 7:00, 16:00 to 18:00, and 20:00 to 23:00, the shared energy storage discharge supplies energy to the user. The maximum shared energy storage charging power at 14:00 is 98.76 kW. At 8:00–9:00 and 24:00, shared energy storage is not enough to support the user and the gas turbine power generation. It can be seen that shared energy storage improves the utilization rate of new energy generation, and the use frequency of gas turbines is also greatly reduced.

The improvement of the algorithm in this paper is mainly reflected in the first stage, which is to optimize the output of each body. The improved GWO algorithm combines the fast search characteristics of BAS and the strong global search ability of GWO. Compared with the traditional particle swarm optimization algorithm and GWO algorithm, the improved GWO algorithm has faster convergence speed and shorter calculation times. The comparison of algorithms is shown in

Table 2. Comparison of calculation results of different algorithms.

Algorithm	Number of Iterations	Calculation Time/s
PSO	73	8.59
GWO	58	7.26
improved GWO	47	5.64

.

6. Conclusions and Prospects

6.1. Conclusions

Within the power system that incorporates renewable energy generation, energy storage is the best way to solve the time-space mismatch between new energy generation and load power consumption. In this paper, the optimal scheduling module and the transaction bargaining are studied in two stages, considering that the shared energy storage participates in the optimal scheduling. The improved GWO and ADMM are used to figure out the multi-microgrid example, which consists of three typical microgrids successively. Through case verification and result analysis, the subsequent conclusions can be deduced from the analysis:

(1)

Formulate the optimal scheduling model under the multi-microgrid island operation mode. Shared energy storage gives full play to the complementarity of power consumption among microgrids to reduce wind and light abandonment rates and adopts an improved gray Wolf algorithm to optimize scheduling. According to the simulation results of the example, compared with the independent energy storage configuration of each microgrid, the shared energy storage power station can optimize the power flow and achieve a win-win situation between energy storage and users.

(2)

Optimize the transaction price model under the multi-microgrid island operation mode. Using ADMM to negotiate the price, the results show that compared with the configuration of independent energy storage, the shared energy storage capacity and investment costs are greatly reduced, and the utilization rate of energy storage capacity is greatly improved.

6.2. Prospects

(1)

The microgrid mathematical model established in this paper is relatively simple. In the future, it is necessary to consider the actual scenario state, consider the addition of more types of agents, and establish more abundant application scenarios.

(2)

This paper only analyzes the operation status of shared energy storage participation in isolated island operation mode. In fact, shared energy storage also plays a great role in peak regulation and frequency regulation in grid-connected operation modes. In the future, it is necessary to continue to explore the study of shared energy storage participation in peak regulation and frequency regulation operation mode in grid-connected mode.