Comprehensive Comparison of Physical and Behavioral Approaches for Virtual Prototyping and Accurate Modeling of Three-Phase EMI Filters
Abstract
1. Introduction
- (a)
- The filter model relies on an analytical formulation in terms of chain-parameter matrices, which allows us to easily evaluate its attenuation characteristics. Furthermore, the model is designed to effectively predict filter behavior by including only a limited number of parasitic elements that can be easily estimated before any prototype is actually constructed (unlike previously discussed literature contributions).
- (b)
- The filter model is tailored for high-power filters, built with thick wires, while most physical model available in the literature are targeted toward small filters built on PCBs.
- (c)
- The physical model is validated step by step, discussing the accuracy of each component model and its impact on the overall filter model accuracy, and compared to measurements after the filter assembly.
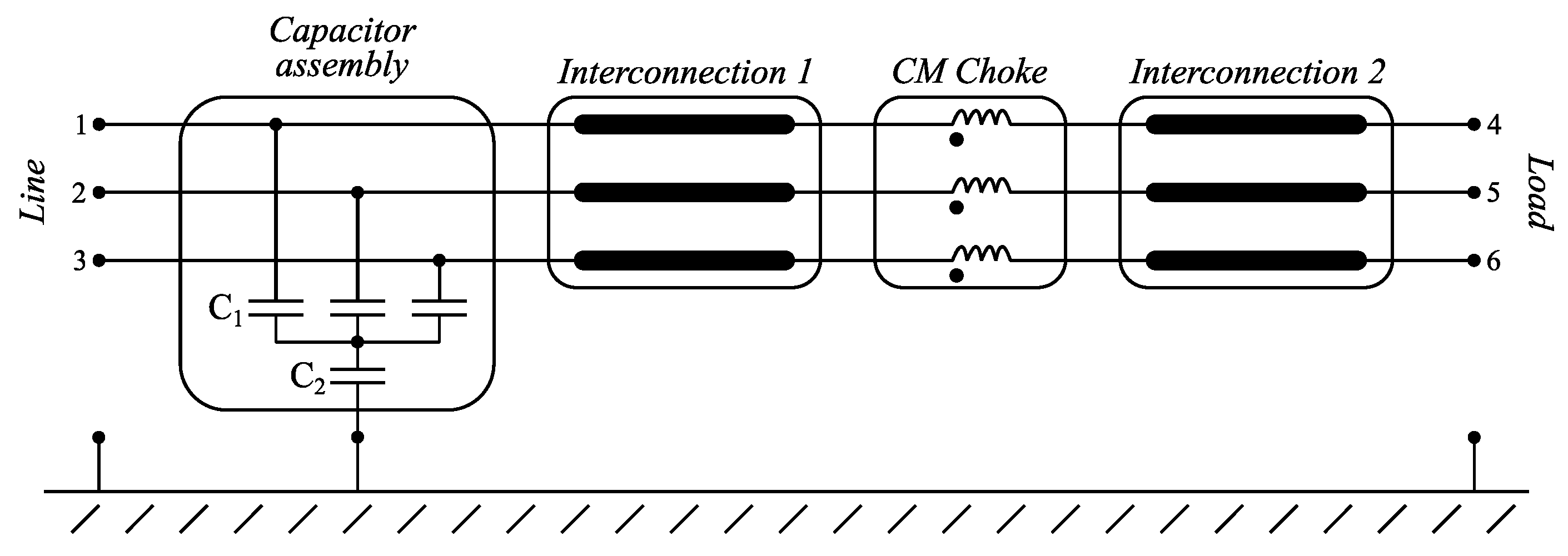
2. EMI Filter Example
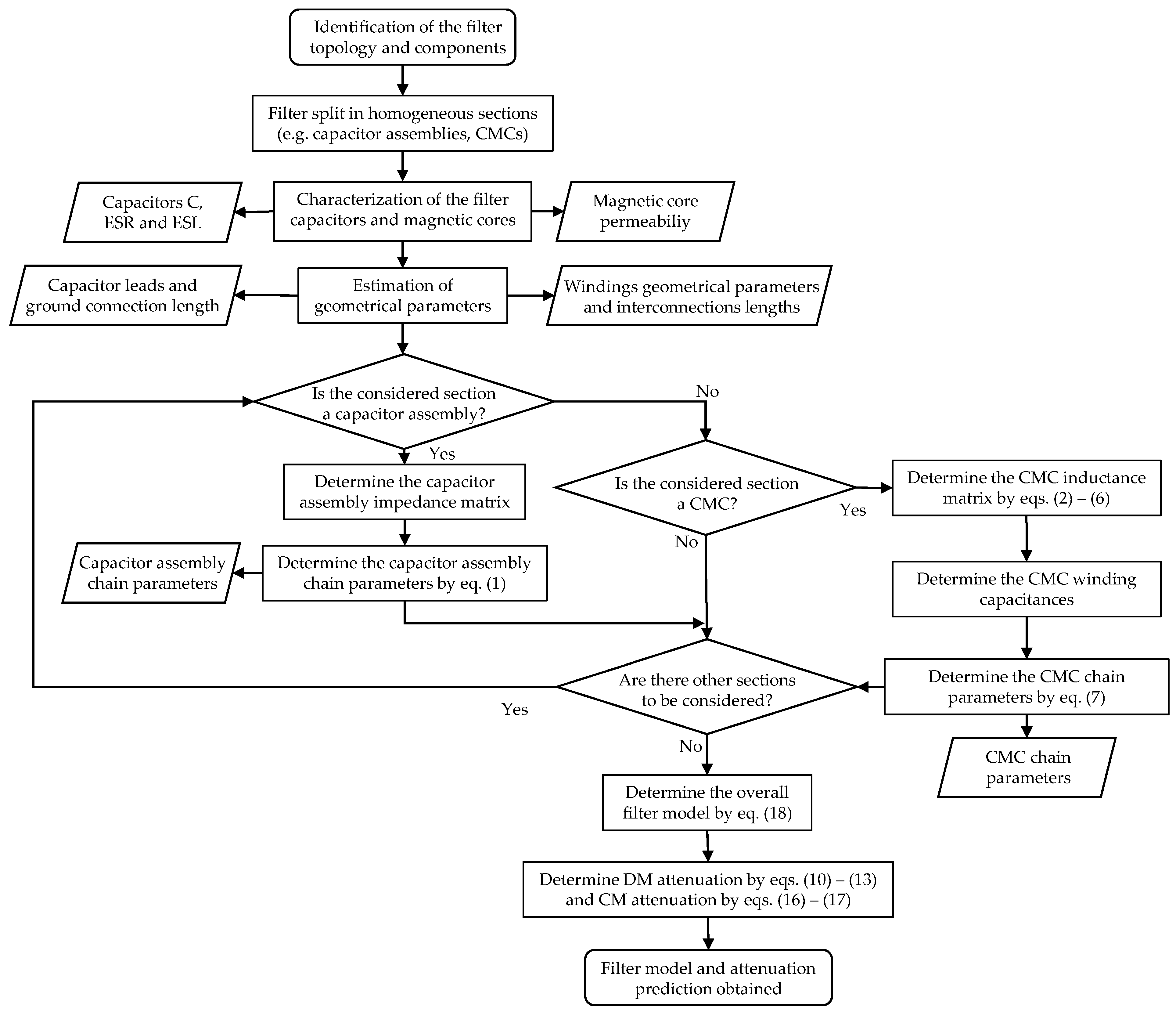
3. Physical Modeling Procedure for Three-Phase EMI Filters
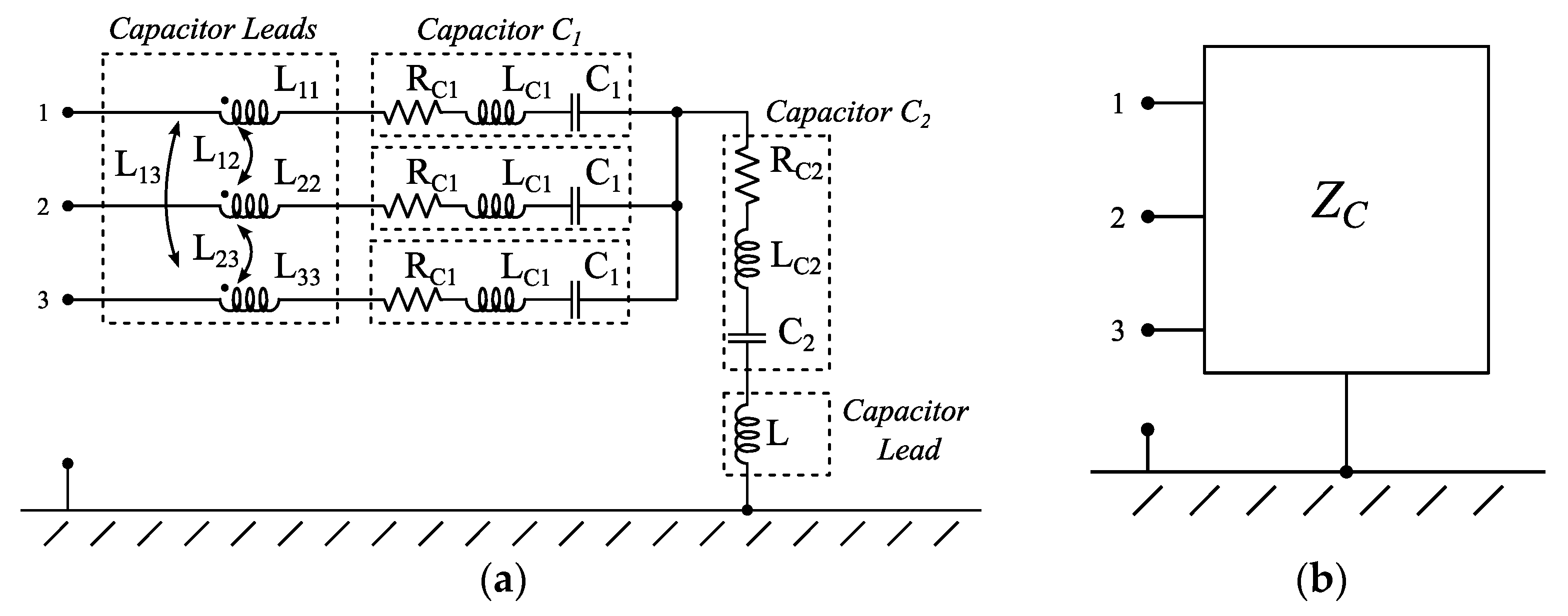
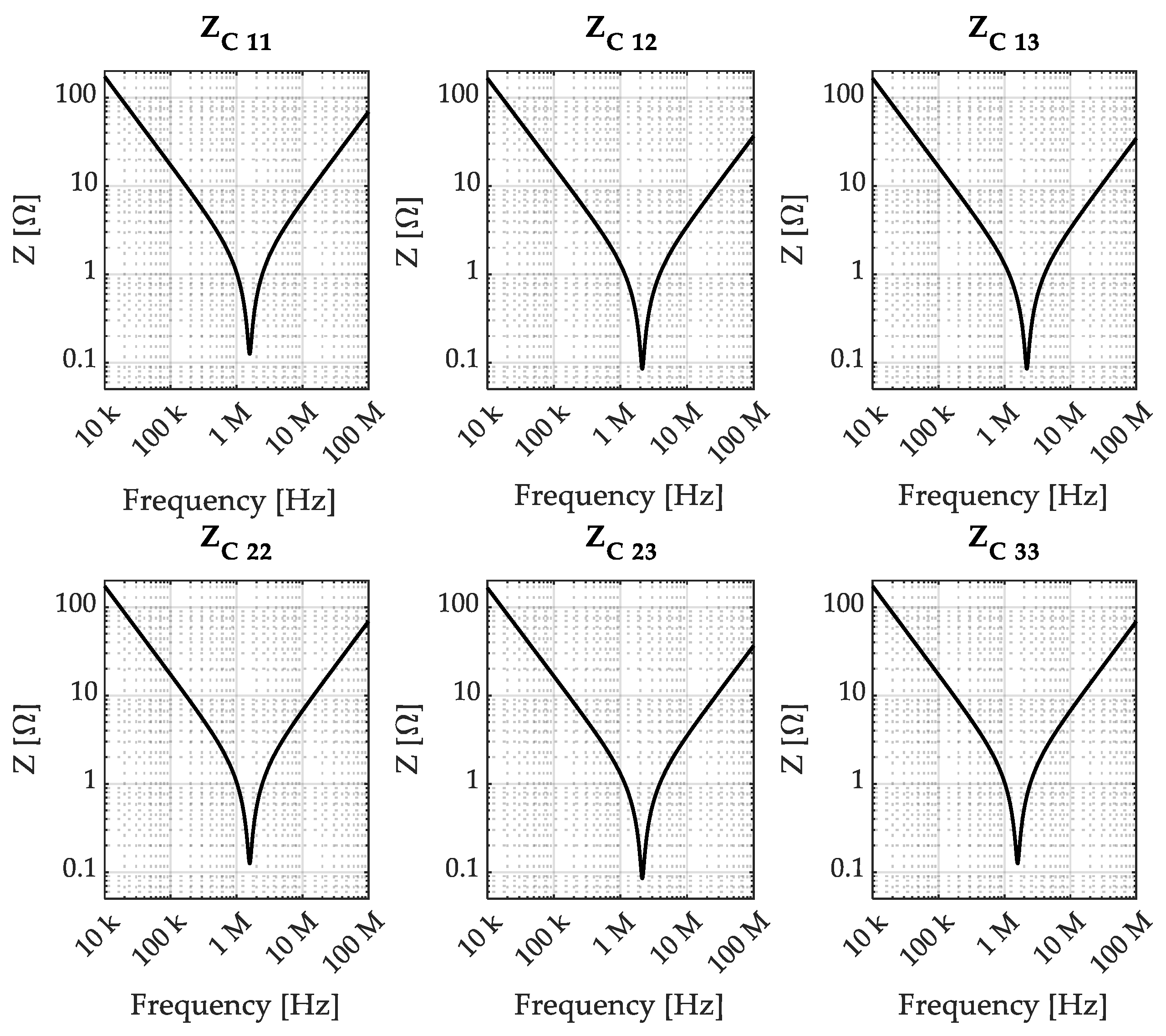
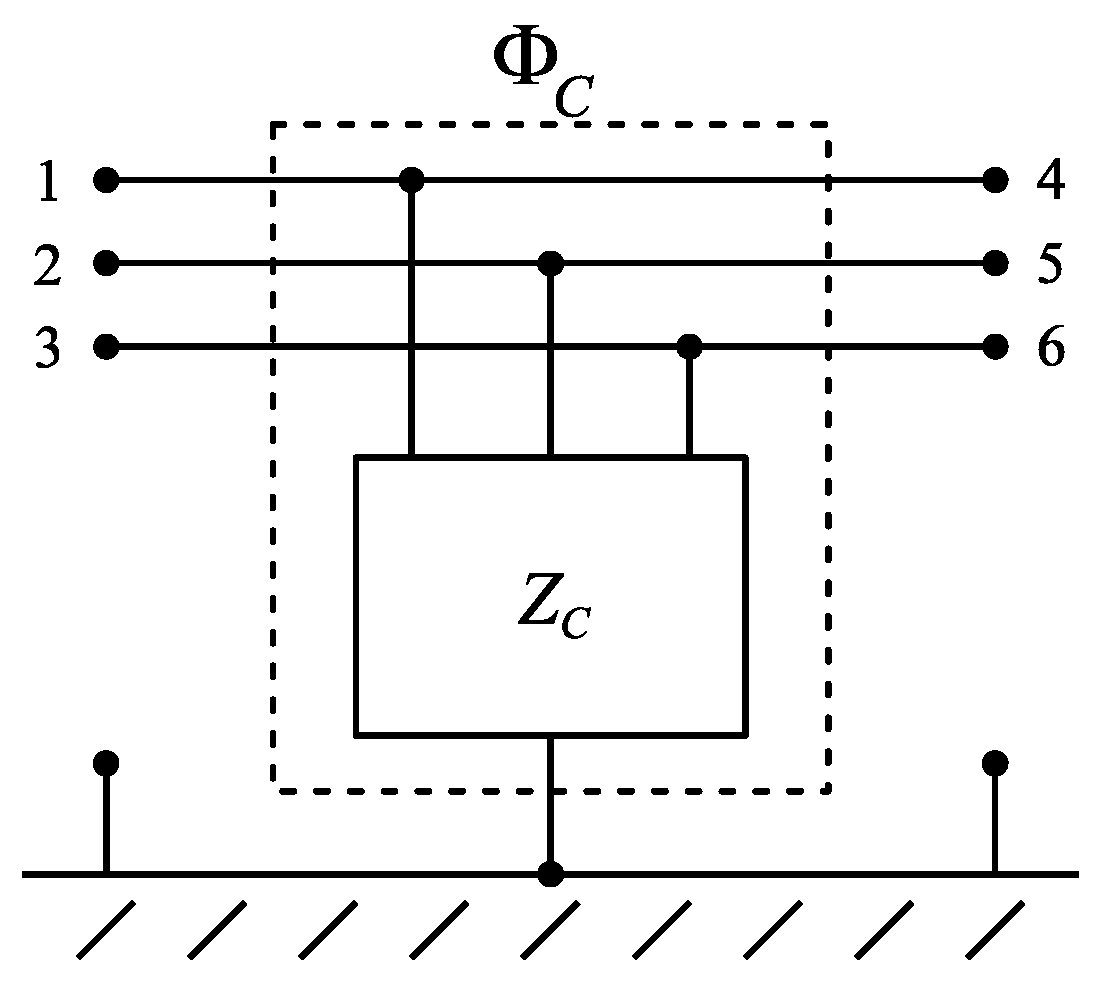
3.1. Capacitor Assembly Model
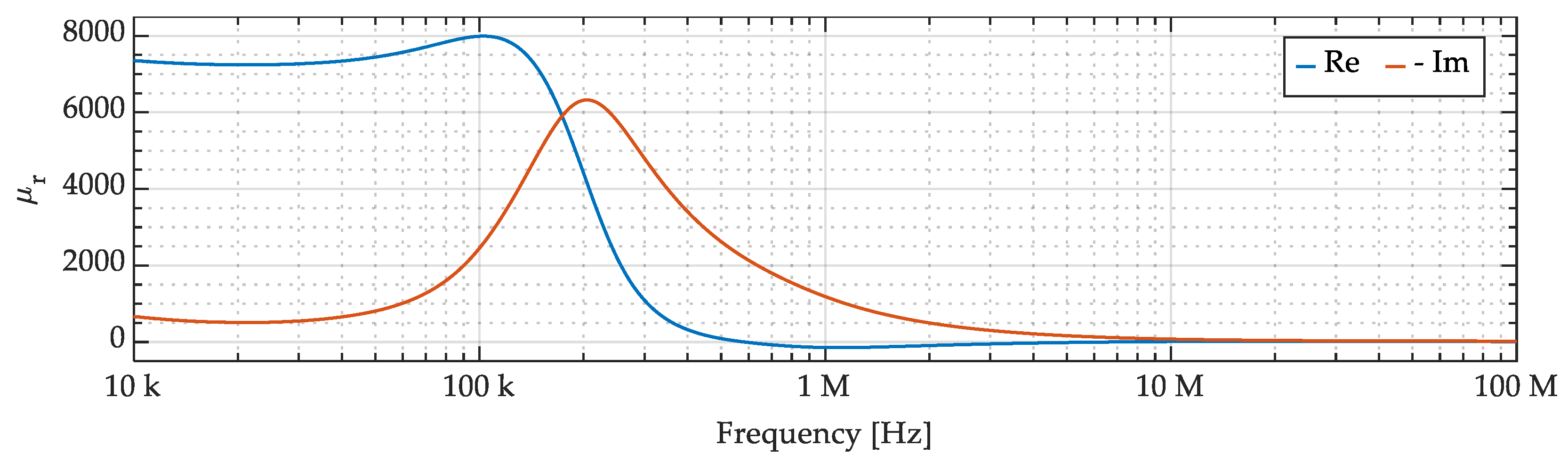
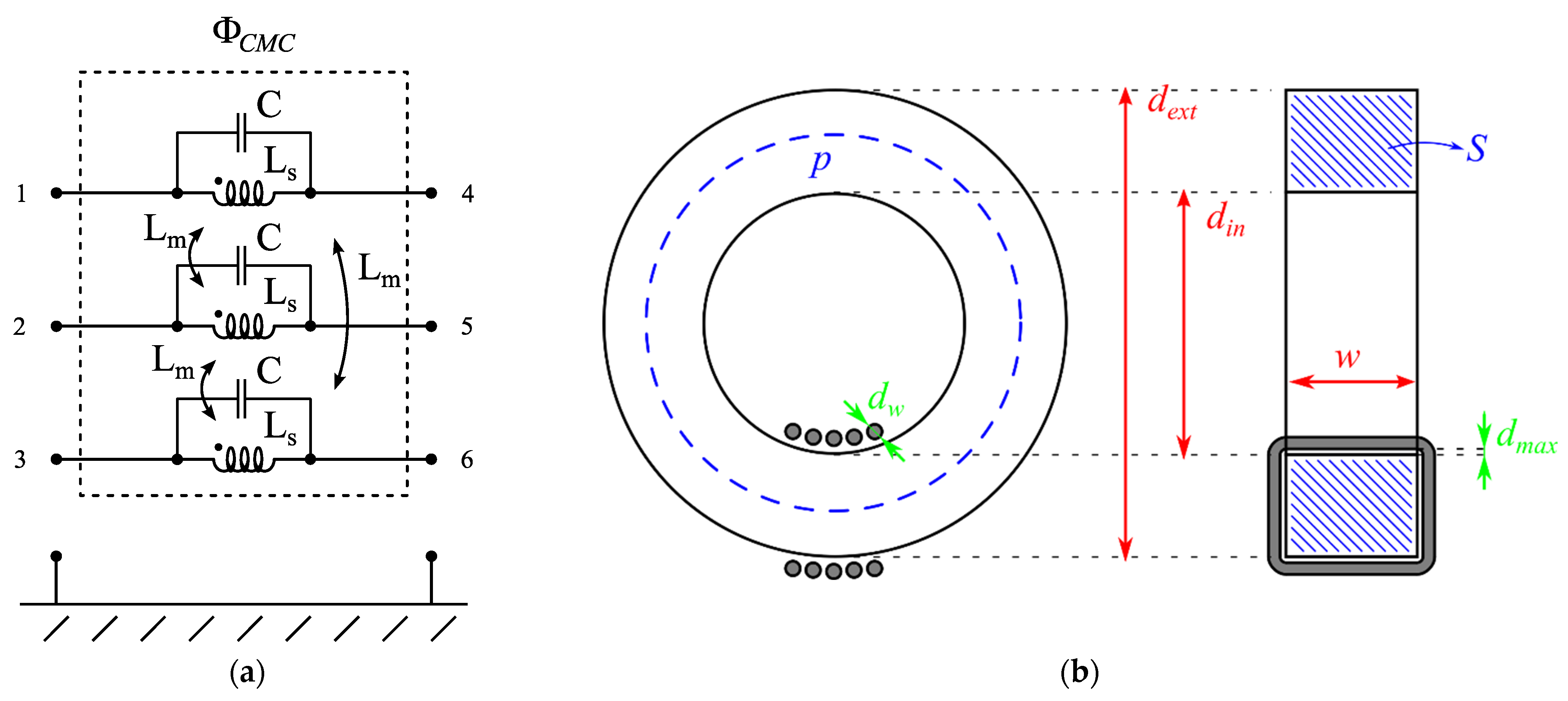
3.2. Common-Mode Choke and Interconnections Model
- Core permeability and geometrical dimensions
- Number of turns of each winding (equal for each phase)
- Wire thickness, distance between wire turns and core, and distance between turns of the same winding
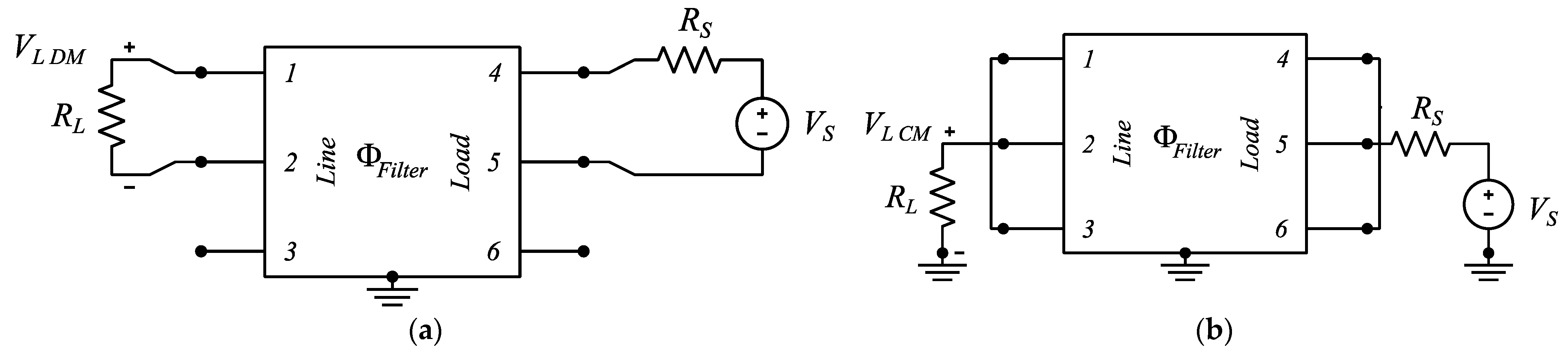
3.3. Complete EMI Filter Model
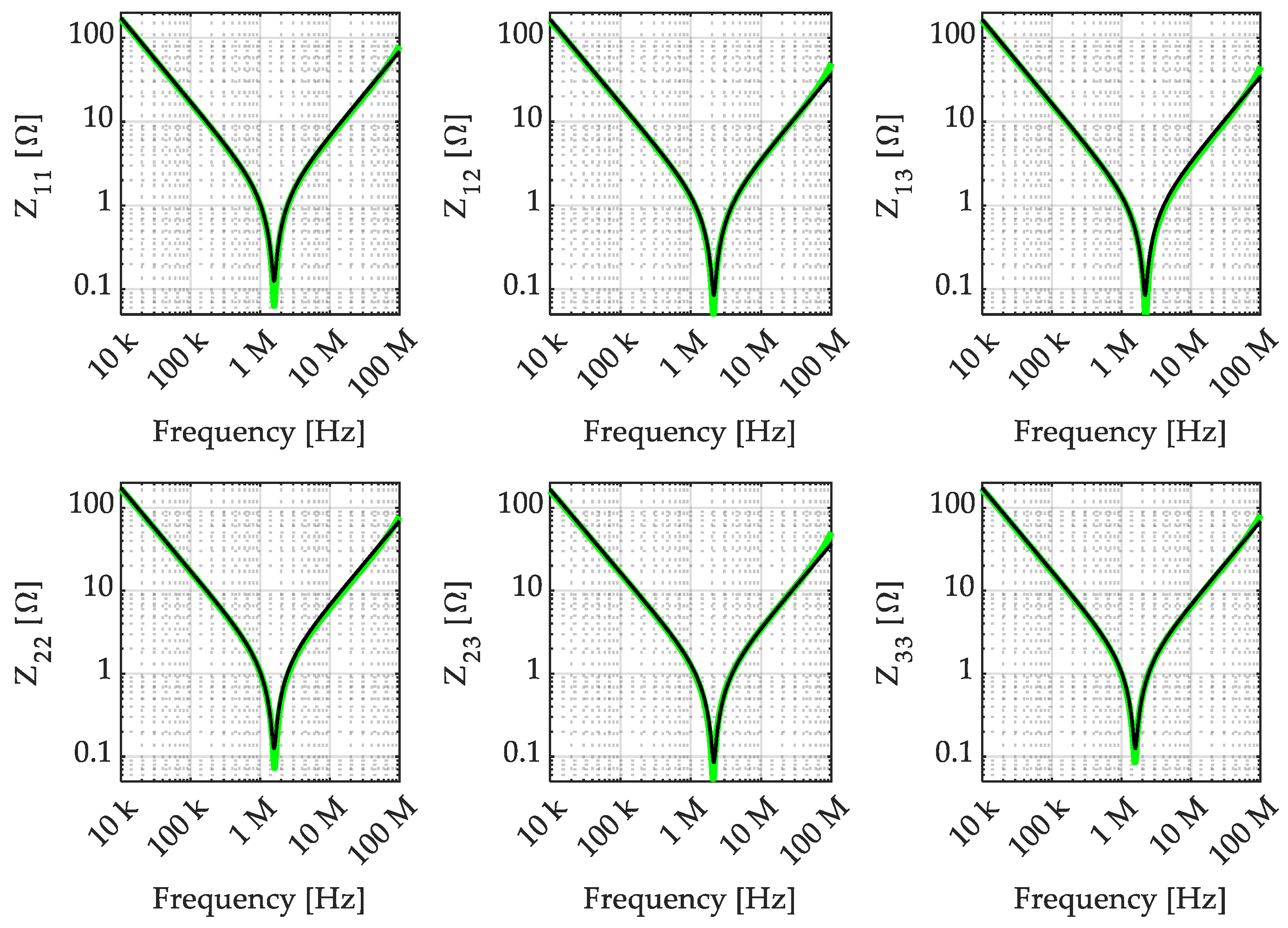
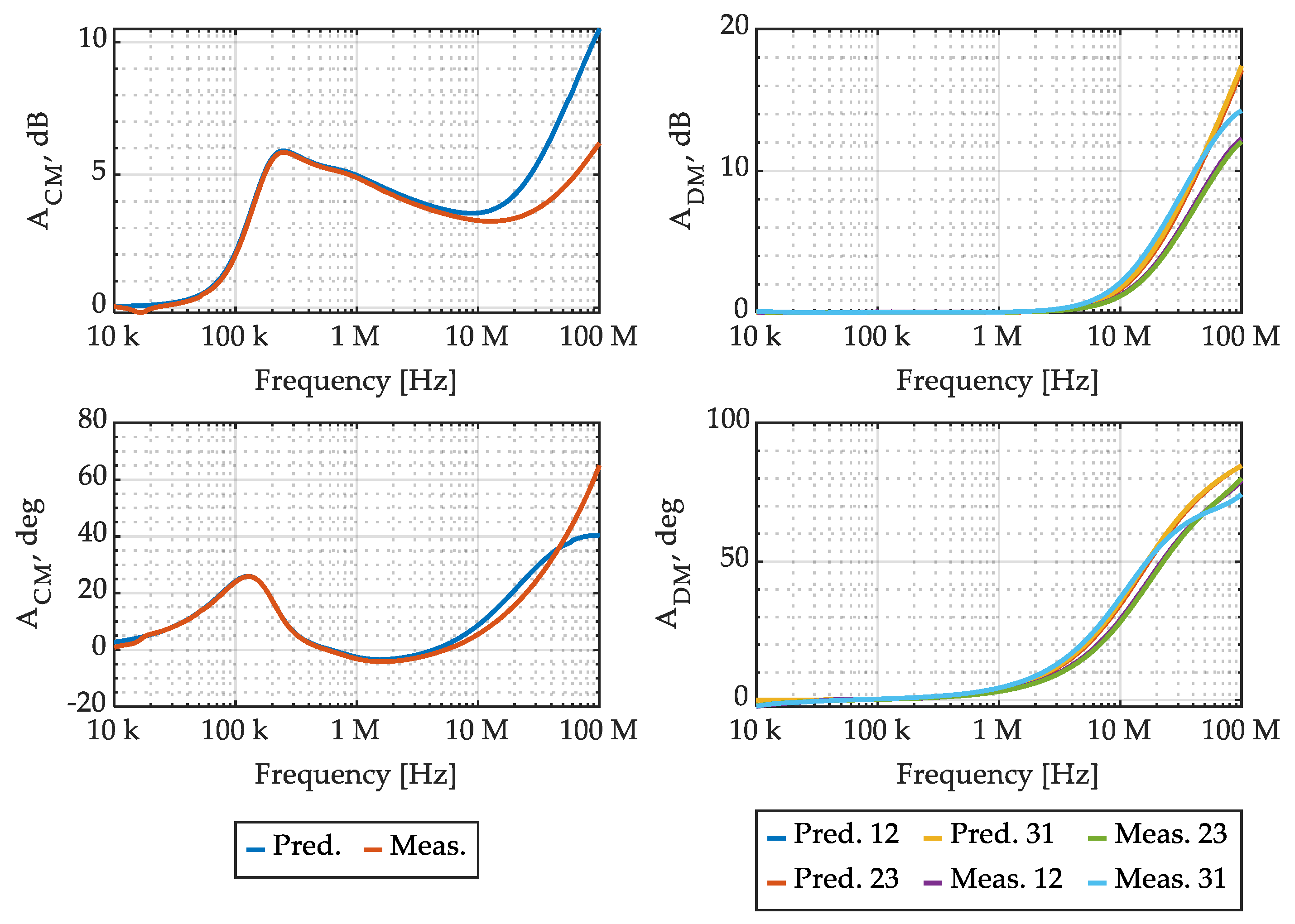
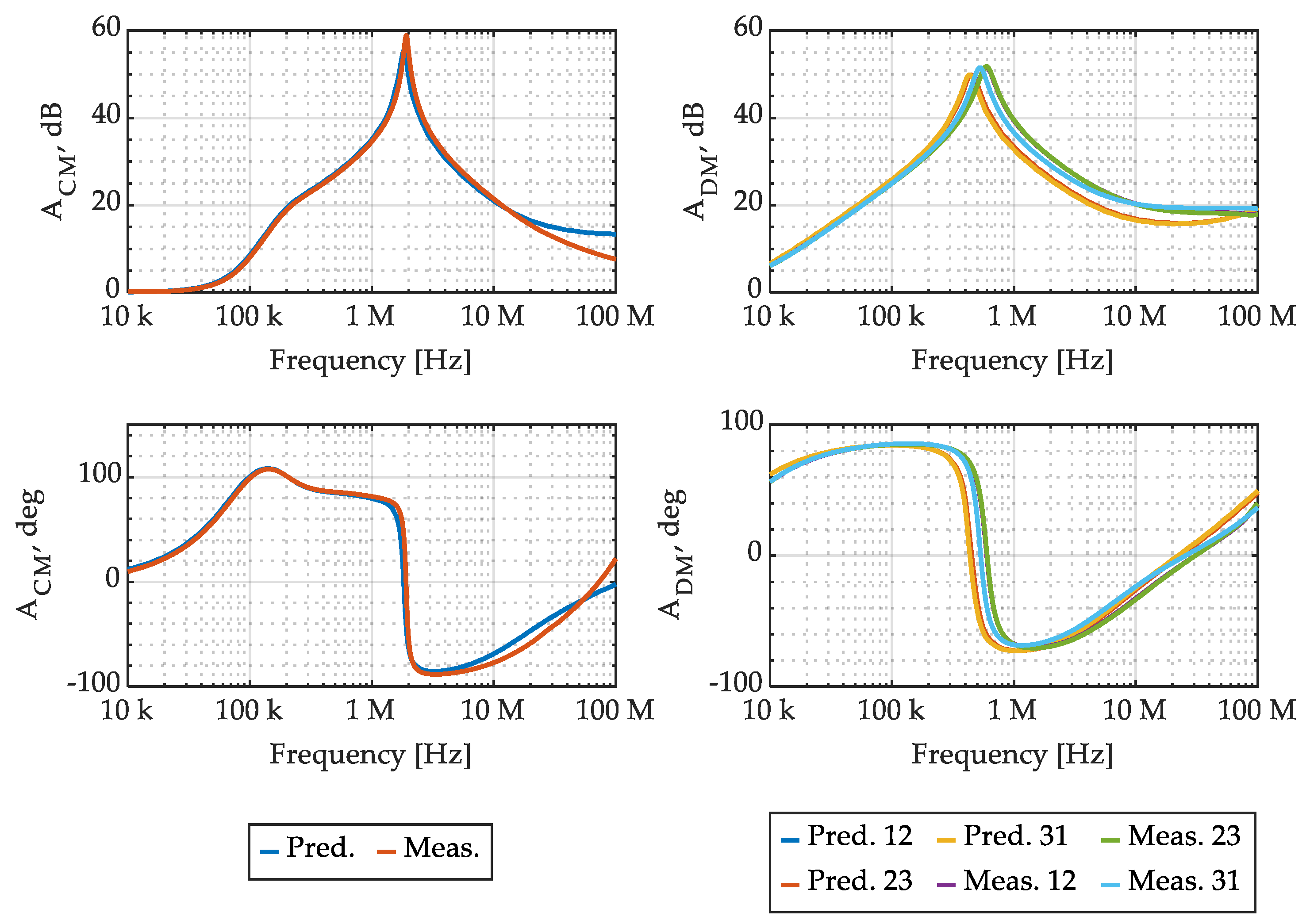
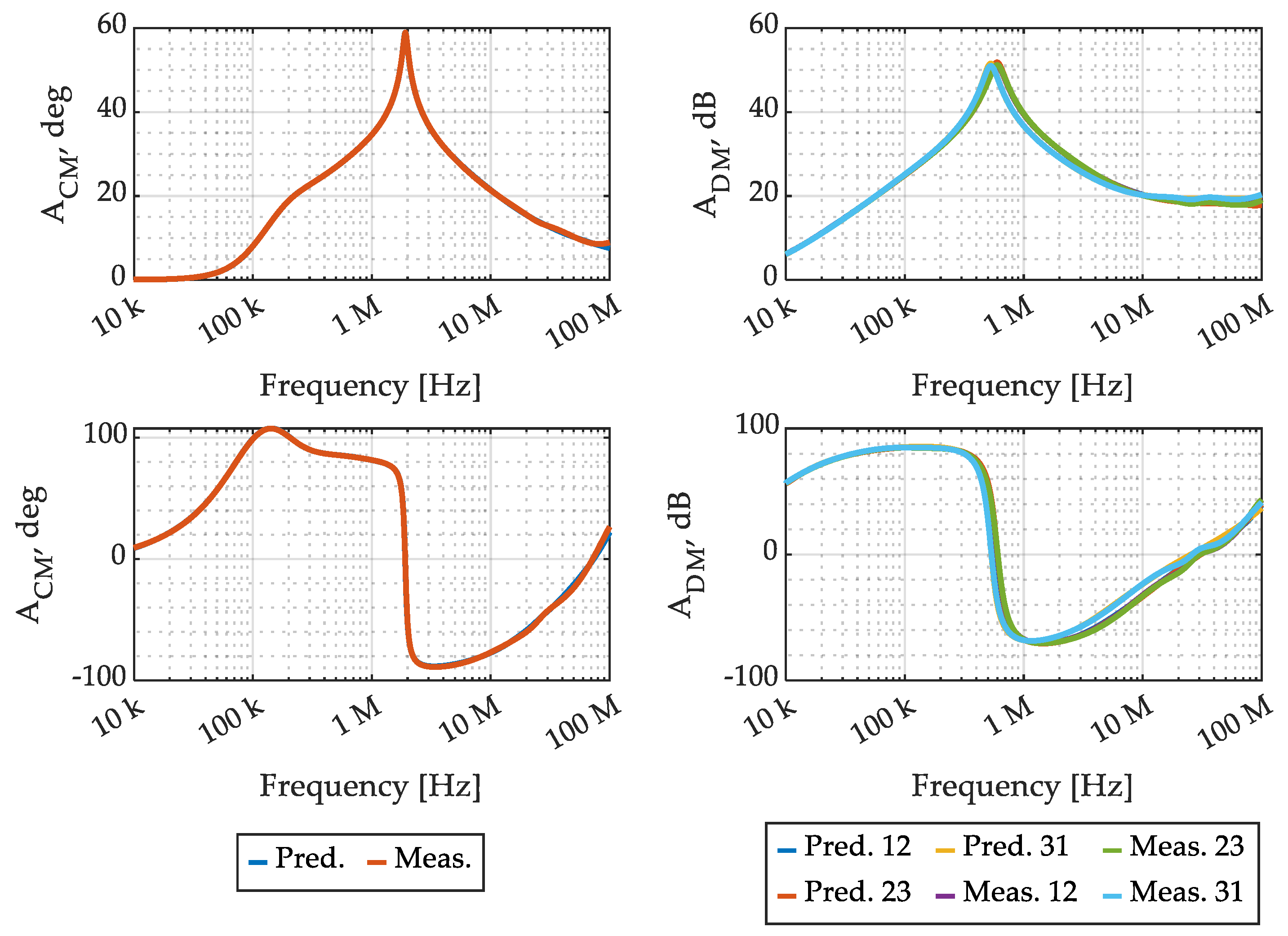
3.4. Experimental Verification
4. Behavioral Modeling Procedure for Three-Phase EMI Filters
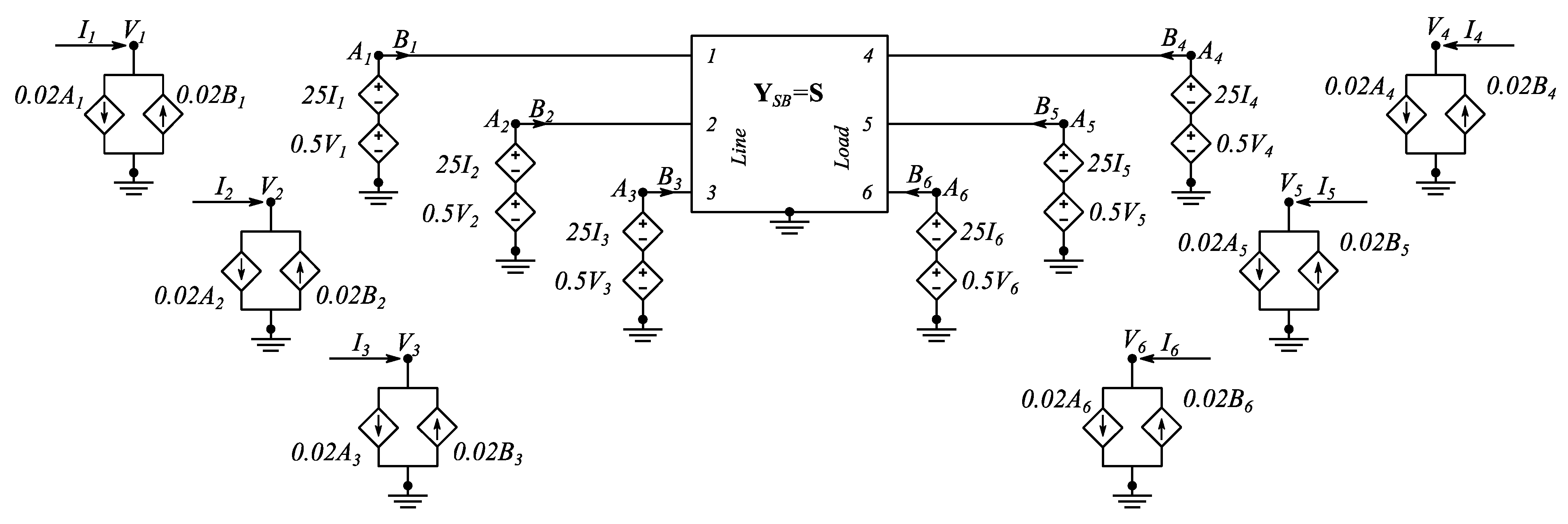
4.1. EMI Filter Characterization and Rational Approximation of Its Frequency Response
4.2. Equivalent Circuit Synthesis
4.3. Experimental Verification
5. Comparison of Physical and Behavioral Approaches for Virtual Prototyping and Accurate Modeling of Three-Phase EMI Filters
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ran, L.; Gokani, S.; Clare, J.; Bradley, K.J.; Christopoulos, C. Conducted electromagnetic emissions in induction motor drive systems part I: Time domain analysis and identification of dominant modes. IEEE Trans. Electromagn. Compat. 1998, 13, 757–767. [Google Scholar]
- Ran, L.; Gokani, S.; Clare, J.; Bradley, K.; Christopoulos, C. Correction to “Conducted Electromagnetic Emissions in Induction Motor Drive Systems Part II: Frequency Domain Models”. IEEE Trans. Power Electron. 1998, 13, 1229. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, F.; Boroyevich, D. Modular-Terminal-Behavioral (MTB) Model for Characterizing Switching Module Conducted EMI Generation in Converter Systems. IEEE Trans. Power Electron. 2006, 21, 1804–1814. [Google Scholar] [CrossRef]
- Pérez, A.; Sánchez, A.-M.; Regué, J.-R.; Ribó, M.; Rodríguez-Cepeda, P.; Pajares, F.-J. Characterization of Power-Line Filters and Electronic Equipment for Prediction of Conducted Emissions. IEEE Trans. Electromagn. Compat. 2008, 50, 577–585. [Google Scholar] [CrossRef]
- Laour, M.; Tahmi, R.; Vollaire, C. Modeling and Analysis of Conducted and Radiated Emissions Due to Common Mode Current of a Buck Converter. IEEE Trans. Electromagn. Compat. 2017, 59, 1260–1267. [Google Scholar] [CrossRef]
- Liu, Y.; See, K.Y.; Yin, S.; Simanjorang, R.; Gupta, A.K.; Lai, J.-S. Equivalent circuit model of high power density SiC converter for common-mode conducted emission prediction and analysis. IEEE Electromagn. Compat. Mag. 2019, 8, 67–74. [Google Scholar] [CrossRef]
- Rondon-Pinilla, E.; Morel, F.; Vollaire, C.; Schanen, J.-L. Modeling of a Buck Converter With a SiC JFET to Predict EMC Conducted Emissions. IEEE Trans. Power Electron. 2013, 29, 2246–2260. [Google Scholar] [CrossRef]
- Rahman, M.A.; Sozer, Y.; De Abreu-Garcia, J.A. Reduction of Electromagnetic Interference (EMI) in Interleaved DC-DC Converters. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 3552–3557. [Google Scholar]
- Harasis, S.K.; Haque, M.E.; Chowdhury, A.; Sozer, Y. SiC Based Interleaved VSI Fed Transverse Flux Machine Drive for High Efficiency, Low EMI Noise and High Power Density Applications. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 30 October 2020; pp. 4943–4948. [Google Scholar]
- Loschi, H.; Lezynski, P.; Smolenski, R.; Nascimento, D.; Sleszynski, W. FPGA-Based System for Electromagnetic Interference Evaluation in Random Modulated DC/DC Converters. Energies 2020, 13, 2389. [Google Scholar] [CrossRef]
- Dey, S.; Mallik, A. A Comprehensive Review of EMI Filter Network Architectures: Synthesis, Optimization and Comparison. Electronics 2021, 10, 1919. [Google Scholar] [CrossRef]
- Rebholz, H.M.; Tenbohlen, S.; Köhler, W. Time-Domain Characterization of RF Sources for the Design of Noise Suppression Filters. IEEE Trans. Electromagn. Compat. 2009, 51, 945–952. [Google Scholar] [CrossRef]
- Bosi, M.; Sánchez, A.M.; Pajares, F.J.; Peretto, L. Three-Phase Modal Noise Analysis and Optimal Three-Phase Power Line Filter Design. Energies 2023, 16, 5461. [Google Scholar] [CrossRef]
- CISPR 17, Methods of Measurement of the Suppression Characteristics of Passive EMC Filtering Devices; IEC: Geneva, Switzerland, 2011.
- Dominguez-Palacios, C.; Gonzalez-Vizuete, P.; Martin-Prats, M.A.; Mendez, J.B. Smart Shielding Techniques for Common Mode Chokes in EMI Filters. IEEE Trans. Electromagn. Compat. 2019, 61, 1329–1336. [Google Scholar] [CrossRef]
- Wang, S.; Lee, F.; Odendaal, W. Characterization and Parasitic Extraction of EMI Filters Using Scattering Parameters. IEEE Trans. Power Electron. 2005, 20, 502–510. [Google Scholar] [CrossRef]
- He, R.; Xu, Y.; Walunj, S.; Yong, S.; Khilkevich, V.; Pommerenke, D.; Aichele, H.L.; Boettcher, M.; Hillenbrand, P.; Klaedtke, A. Modeling Strategy for EMI Filters. IEEE Trans. Electromagn. Compat. 2020, 62, 1572–1581. [Google Scholar] [CrossRef]
- Kovacevic, I.F.; Friedli, T.; Musing, A.M.; Kolar, J.W. 3-D Electromagnetic Modeling of Parasitics and Mutual Coupling in EMI Filters. IEEE Trans. Power Electron. 2013, 29, 135–149. [Google Scholar] [CrossRef]
- Kumar, M.; Jayaraman, K. Design of a Modified Single-Stage and Multistage EMI Filter to Attenuate Common-Mode and Differential-Mode Noises in SiC Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 4290–4302. [Google Scholar] [CrossRef]
- Zhai, L.; Hu, G.; Lv, M.; Zhang, T.; Hou, R. Comparison of Two Design Methods of EMI Filter for High Voltage Power Supply in DC-DC Converter of Electric Vehicle. IEEE Access 2020, 8, 66564–66577. [Google Scholar] [CrossRef]
- Mallik, A.; Ding, W.; Khaligh, A. A Comprehensive Design Approach to an EMI Filter for a 6-kW Three-Phase Boost Power Factor Correction Rectifier in Avionics Vehicular Systems. IEEE Trans. Veh. Technol. 2016, 66, 2942–2951. [Google Scholar] [CrossRef]
- Zhai, L.; Yang, S.; Hu, G.; Lv, M. Optimal Design Method of High Voltage DC Power Supply EMI Filter Considering Source Impedance of Motor Controller for Electric Vehicle. IEEE Trans. Veh. Technol. 2023, 72, 367–381. [Google Scholar] [CrossRef]
- Zhang, X.; Khodabandeh, M.; Amirabadi, M.; Lehman, B. A Simulation-Based Multifunctional Differential Mode and Common Mode Filter Design Method for Universal Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 658–672. [Google Scholar] [CrossRef]
- Negri, S.; Spadacini, G.; Grassi, F.; Pignari, S.A. Prediction of EMI Filter Attenuation in Power-Electronic Converters via Circuit Simulation. IEEE Trans. Electromagn. Compat. 2022, 64, 1086–1096. [Google Scholar] [CrossRef]
- Negri, S.; Spadacini, G.; Grassi, F.; Pignari, S.A. Black-Box Modeling of EMI Filters for Frequency and Time-Domain Simulations. IEEE Trans. Electromagn. Compat. 2021, 64, 119–128. [Google Scholar] [CrossRef]
- Haase, M.; Hoffmann, K.; Hudec, P. General Method for Characterization of Power-Line EMI/RFI Filters Based on S-Parameter Evaluation. IEEE Trans. Electromagn. Compat. 2016, 58, 1465–1474. [Google Scholar] [CrossRef]
- Gustavsen, B.; Semlyen, A. Rational approximation of frequency domain responses by vector fitting. IEEE Trans. Power Deliv. 1999, 14, 1052–1061. [Google Scholar] [CrossRef]
- Gustavsen, B. Improving the pole relocating properties of vector fitting. IEEE Trans. Power Deliv. 2006, 21, 1587–1592. [Google Scholar] [CrossRef]
- Deschrijver, D.; Mrozowski, M.; Dhaene, T.; De Zutter, D. Macromodeling of multiport systems using a fast implemen-tation of the Vector Fitting method. IEEE Microw. Wireless Compon. Lett. 2008, 18, 383–385. [Google Scholar] [CrossRef]
- Gustavsen, B.; Semlyen, A. Fast Passivity Assessment for $S$-Parameter Rational Models Via a Half-Size Test Matrix. IEEE Trans. Microw. Theory Tech. 2008, 56, 2701–2708. [Google Scholar] [CrossRef]
- Gustavsen, B. Fast Passivity Enforcement for S-Parameter Models by Perturbation of Residue Matrix Eigenvalues. IEEE Trans. Adv. Packag. 2009, 33, 257–265. [Google Scholar] [CrossRef]
- Negri, S.; Spadacini, G.; Grassi, F.; Pignari, S. Measurement-Based Equivalent Circuit Model for Time-Domain Simulation of EMI Filters. In Proceedings of the 2022 International Symposium on Electromagnetic Compatibility–EMC Europe, Gothenburg, Sweden, 5–8 September 2022; pp. 793–798. [Google Scholar]
- Clayton, R.P. The TransmissionLine Equations for Multiconductor Lines. In Analysis of Multiconductor Transmission Lines; IEEE: Piscataway, NJ, USA, 2008; pp. 89–109. [Google Scholar]
- Kotny, J.-L.; Margueron, X.; Idir, N. High-Frequency Model of the Coupled Inductors Used in EMI Filters. IEEE Trans. Power Electron. 2012, 27, 2805–2812. [Google Scholar] [CrossRef]
- De Leo, A.; Cerri, G. A Charge Distribution Based Model for the Evaluation of an Air-Coil Stray Capacitance. IEEE Trans. Electromagn. Compat. 2019, 61, 1673–1677. [Google Scholar] [CrossRef]
- Pasko, S.W.; Kazimierczuk, M.K.; Grzesik, B. Self-Capacitance of Coupled Toroidal Inductors for EMI Filters. IEEE Trans. Electromagn. Compat. 2015, 57, 216–223. [Google Scholar] [CrossRef]
- Gustavsen, B. User’s Guide for Vectfit3. Available online: https://www.sintef.no/projectweb/vectorfitting/ (accessed on 17 July 2024).
- Grivet-Talocia, S.; Gustavsen, B. Passive Macromodeling Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- de Almeida, I.C. Frequency Domain Equivalent Circuit Modeling of Electromagnetic-Interference Filters through Scattering Parameters and Rational Approximation. Master’s Thesis, Department of Electronics, Information and Bioengineering, Politecnico di Milano, Milan, 2019. Available online: https://www.politesi.polimi.it/handle/10589/148940 (accessed on 17 July 2024).
- Antonini, G. Spice equivalent circuits of frequency-domain responses. IEEE Trans. Electromagn. Compat. 2003, 45, 502–512. [Google Scholar] [CrossRef]
- Linear Technology Inc. LTspice IV Getting Started Guide. 2011. Available online: https://www.analog.com/en/design-center/design-tools-and-calculators/ltspice-simulator.html (accessed on 17 July 2024).









| Rated C [nF] | Measured C [nF] | ESR [mΩ] | ESL [nH] | |
|---|---|---|---|---|
| C1 | 2200 | 2208 | 40.42 | 33.89 |
| C2 | 100 | 96.11 | 85.12 | 17.78 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Core Thickness | 25.5 mm | Turns number | 2 |
| Core external diameter | 63 mm | Wire-to-core distance | 0.7 mm |
| Core internal diameter | 37.5 mm | Wire thickness | 1.6 mm |
| γ | 2.5 |
| Interconnection 1 | Interconnection 2 | |
|---|---|---|
| Length | 10 cm | 5 cm |
| Separation | 1.5 cm | 1.5 cm |
| Wire diameter | 1.6 mm | 1.6 mm |
| Distance from ground | 9 cm | 9 cm |
| Physical Model | Behavioral Model | |
|---|---|---|
| Required input | Capacitors frequency response and CMC ferrite cores magnetic permeability, estimated filter size | External measurement of the complete filter |
| Accuracy | Good up to 10 MHz, limited from 10 MHz to 100 MHz | Good over the whole frequency range of interest |
| Relation between single components and filter performance | Clear | Unclear |
| Suitable for virtual prototyping | Yes, allows fast comparison of many filter designs with no need for prototypes | No, requires one prototype to be built for each design of interest |
| Suitable for frequency-domain simulations | Yes | Yes |
| Suitable for time-domain simulations | Yes, but requires a behavioral CMC model to include the magnetic permeability frequency dependency in the model. | Yes |
| Suitable as a commercial model | No, requires to disclose details on the internal filter structure, limited accuracy | Yes, no proprietary information on filter realization is disclosed, high accuracy |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Negri, S.; Spadacini, G.; Grassi, F.; Lezynski, P.; Smolenski, R.; Pignari, S.A. Comprehensive Comparison of Physical and Behavioral Approaches for Virtual Prototyping and Accurate Modeling of Three-Phase EMI Filters. Energies 2024, 17, 4974. https://doi.org/10.3390/en17194974
Negri S, Spadacini G, Grassi F, Lezynski P, Smolenski R, Pignari SA. Comprehensive Comparison of Physical and Behavioral Approaches for Virtual Prototyping and Accurate Modeling of Three-Phase EMI Filters. Energies. 2024; 17(19):4974. https://doi.org/10.3390/en17194974
Chicago/Turabian StyleNegri, Simone, Giordano Spadacini, Flavia Grassi, Piotr Lezynski, Robert Smolenski, and Sergio Amedeo Pignari. 2024. "Comprehensive Comparison of Physical and Behavioral Approaches for Virtual Prototyping and Accurate Modeling of Three-Phase EMI Filters" Energies 17, no. 19: 4974. https://doi.org/10.3390/en17194974
APA StyleNegri, S., Spadacini, G., Grassi, F., Lezynski, P., Smolenski, R., & Pignari, S. A. (2024). Comprehensive Comparison of Physical and Behavioral Approaches for Virtual Prototyping and Accurate Modeling of Three-Phase EMI Filters. Energies, 17(19), 4974. https://doi.org/10.3390/en17194974










