A Control-Oriented Model for Predicting Variations in Membrane Water Content of an Open-Cathode Proton Exchange Membrane Fuel Cell
Abstract
1. Introduction
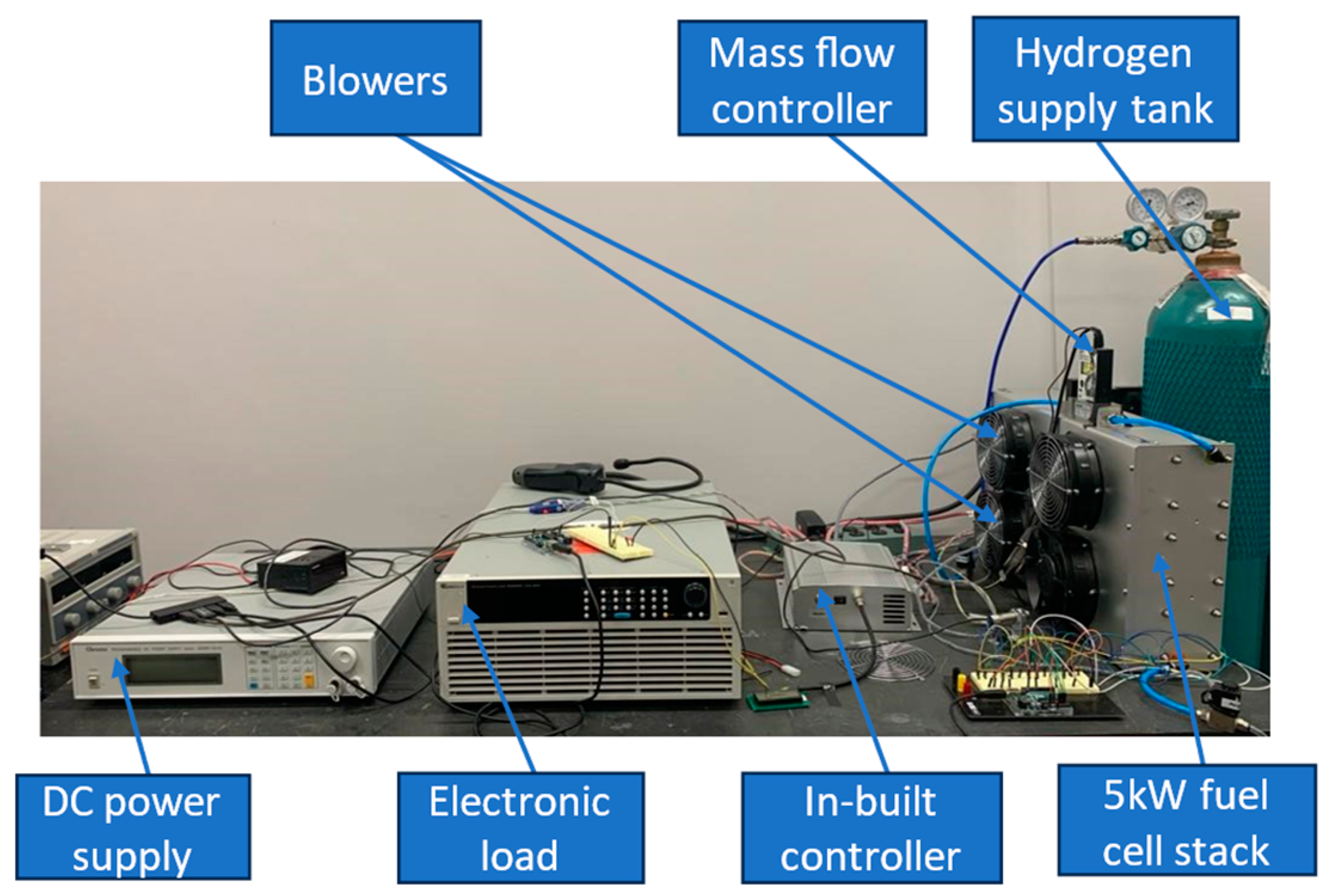
2. Experimental Setup
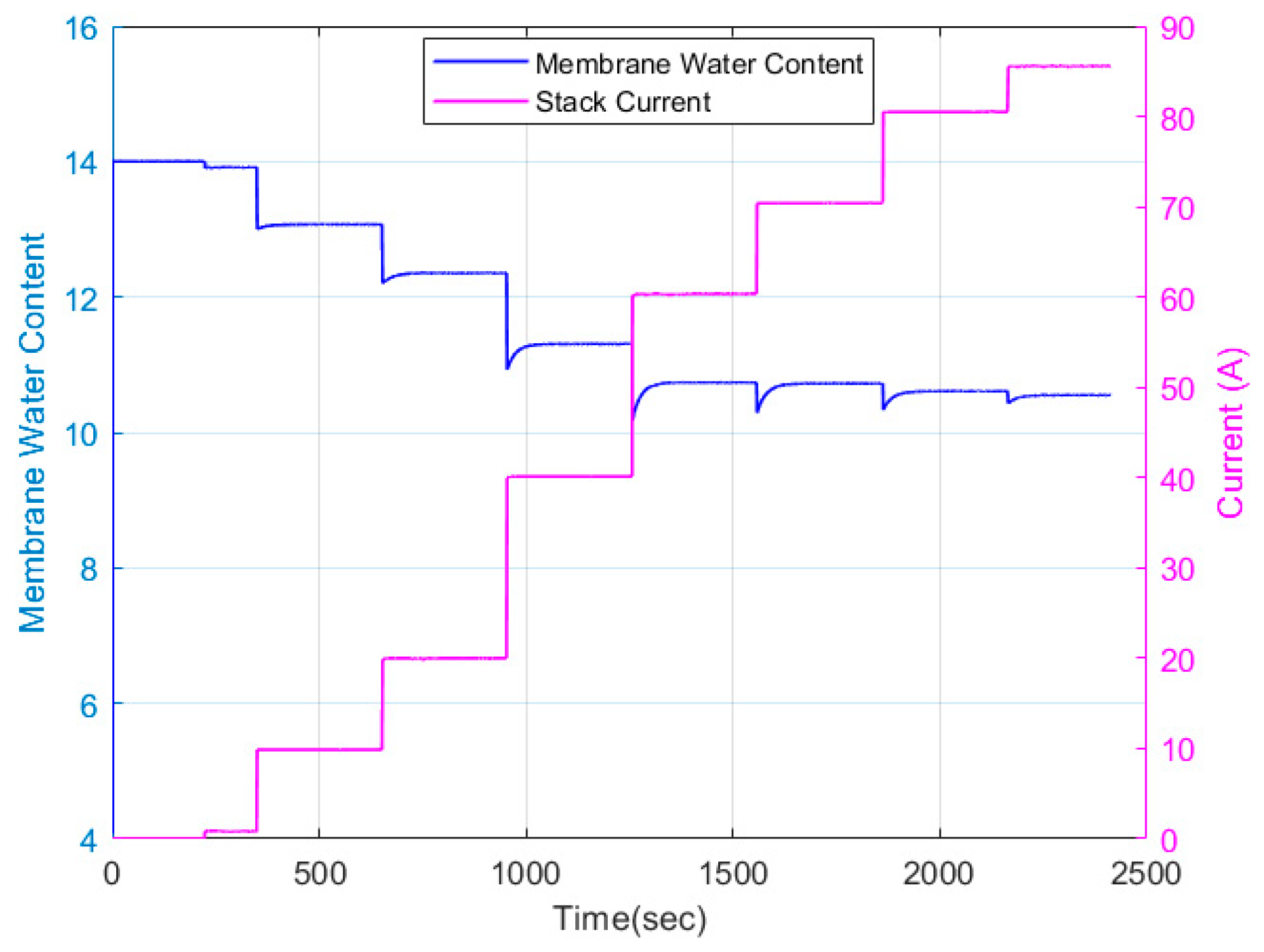
Experimental Procedure
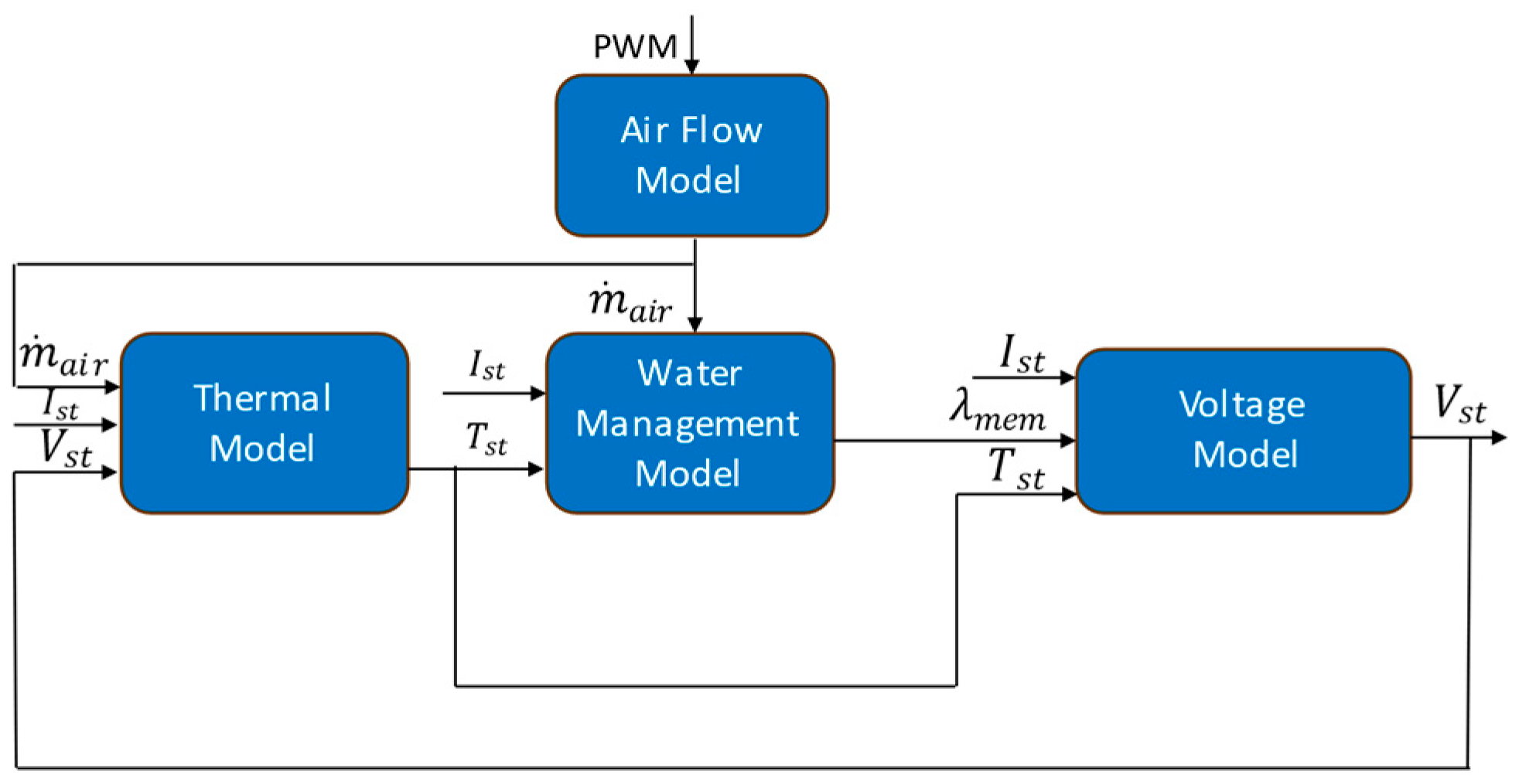
3. Model Development
3.1. Physics-Based Model
3.1.1. Stack Voltage Model
3.1.2. Air Flow Model
3.1.3. Thermal Model
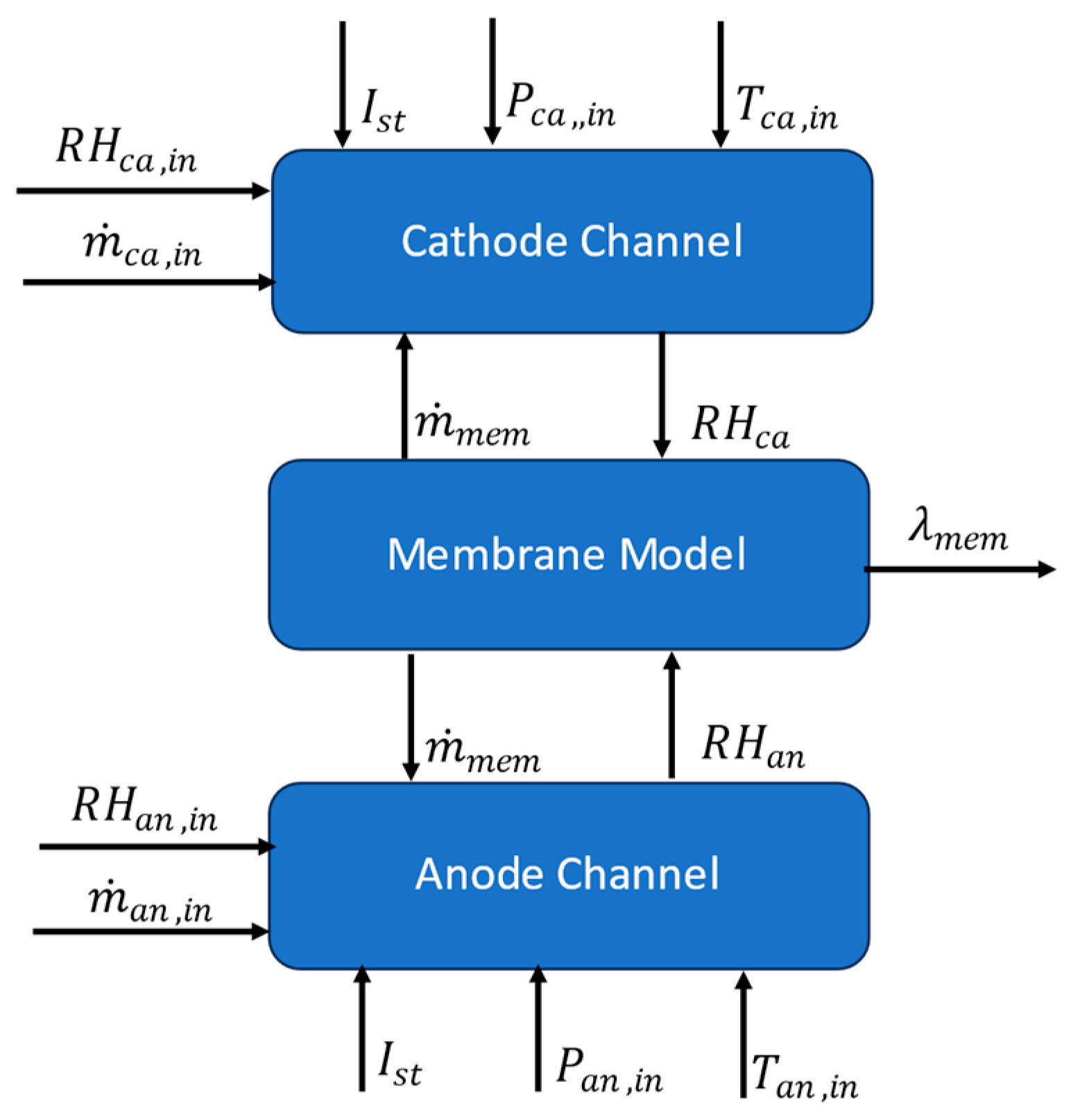
3.1.4. Water Management Model
Cathode Channel
Anode Channel
Proton Exchange Membrane
3.2. GT-Suite Model
4. Model Discretization
4.1. Physics-Based Model
4.2. GT-Suite Model
5. Results and Discussion
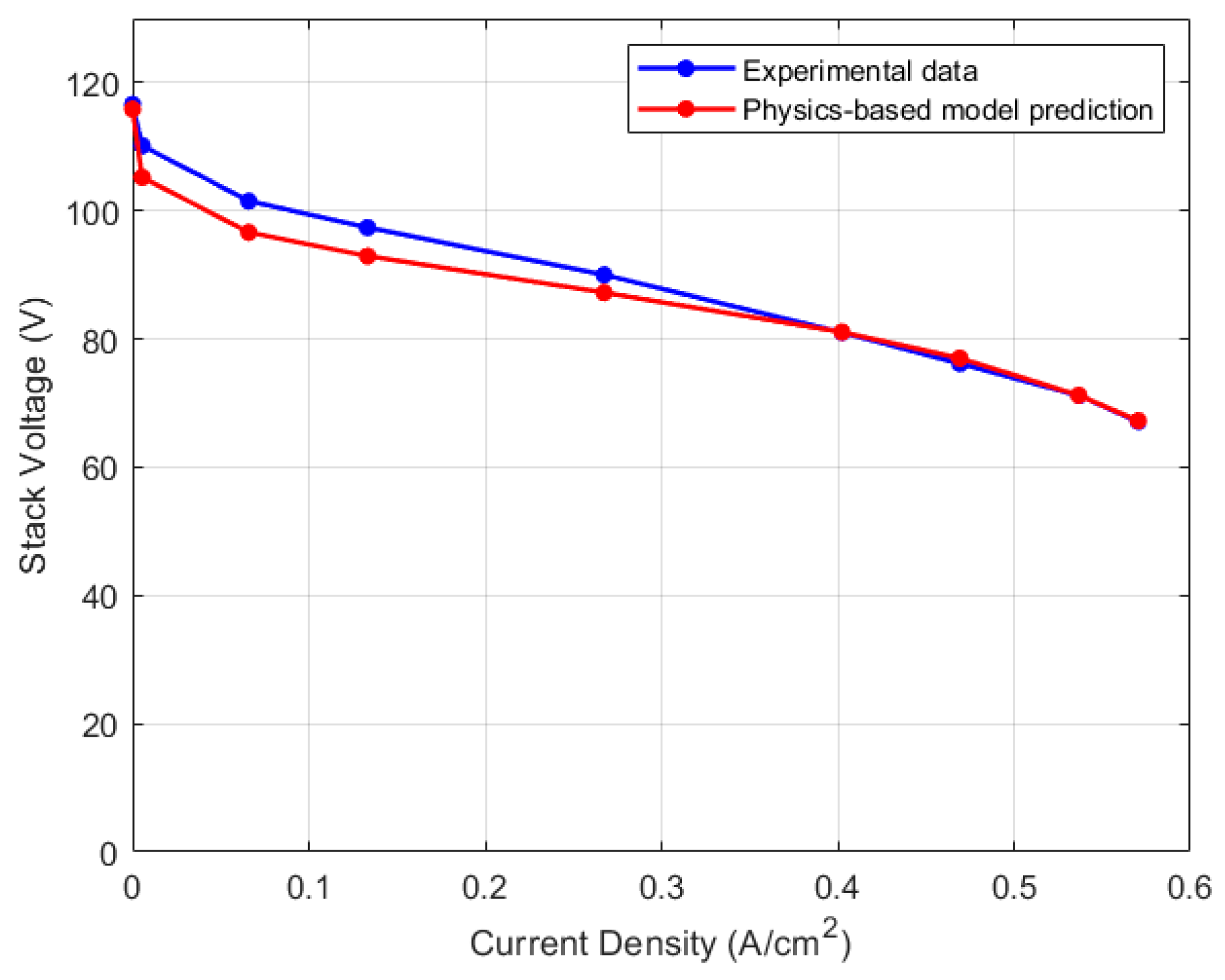
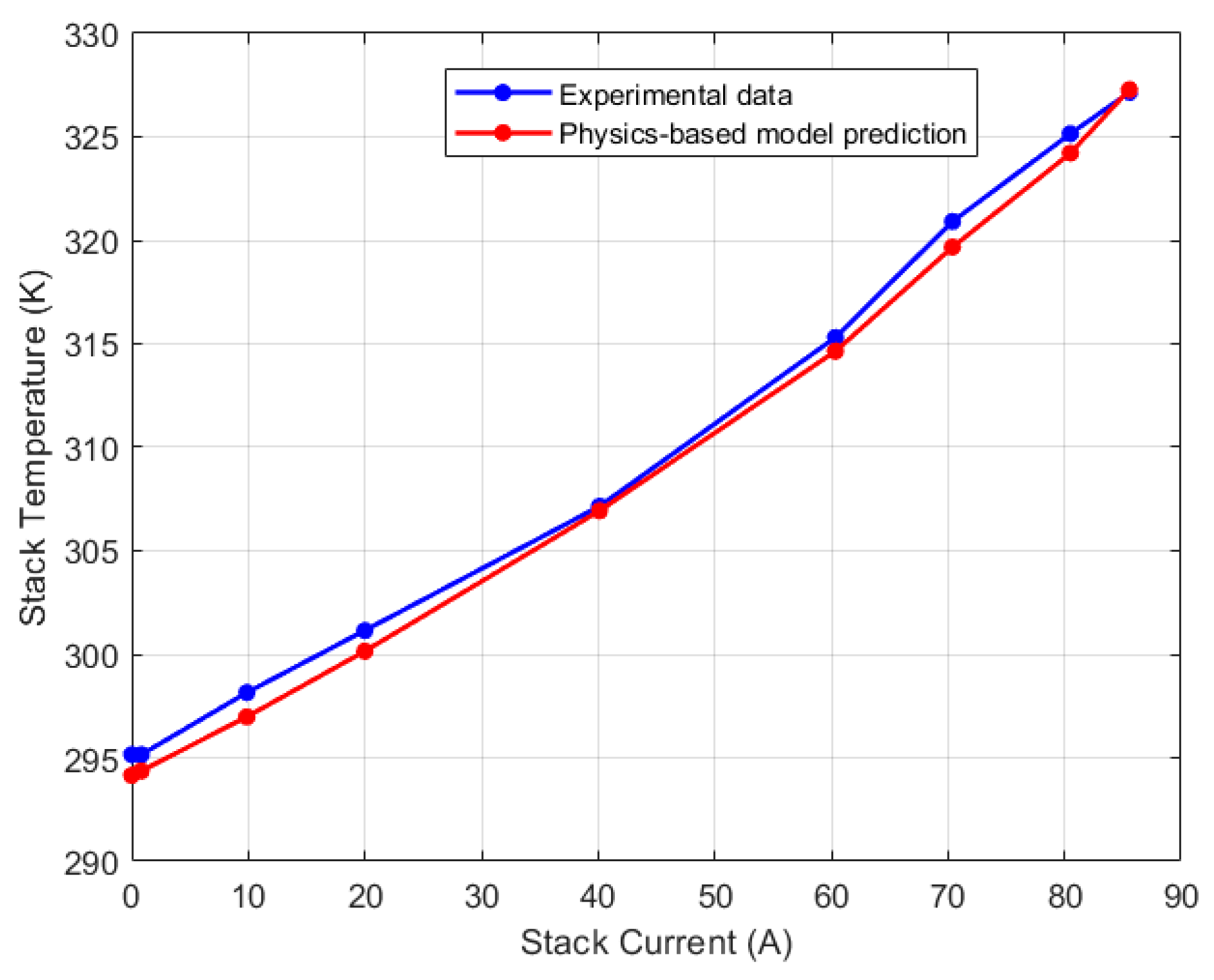
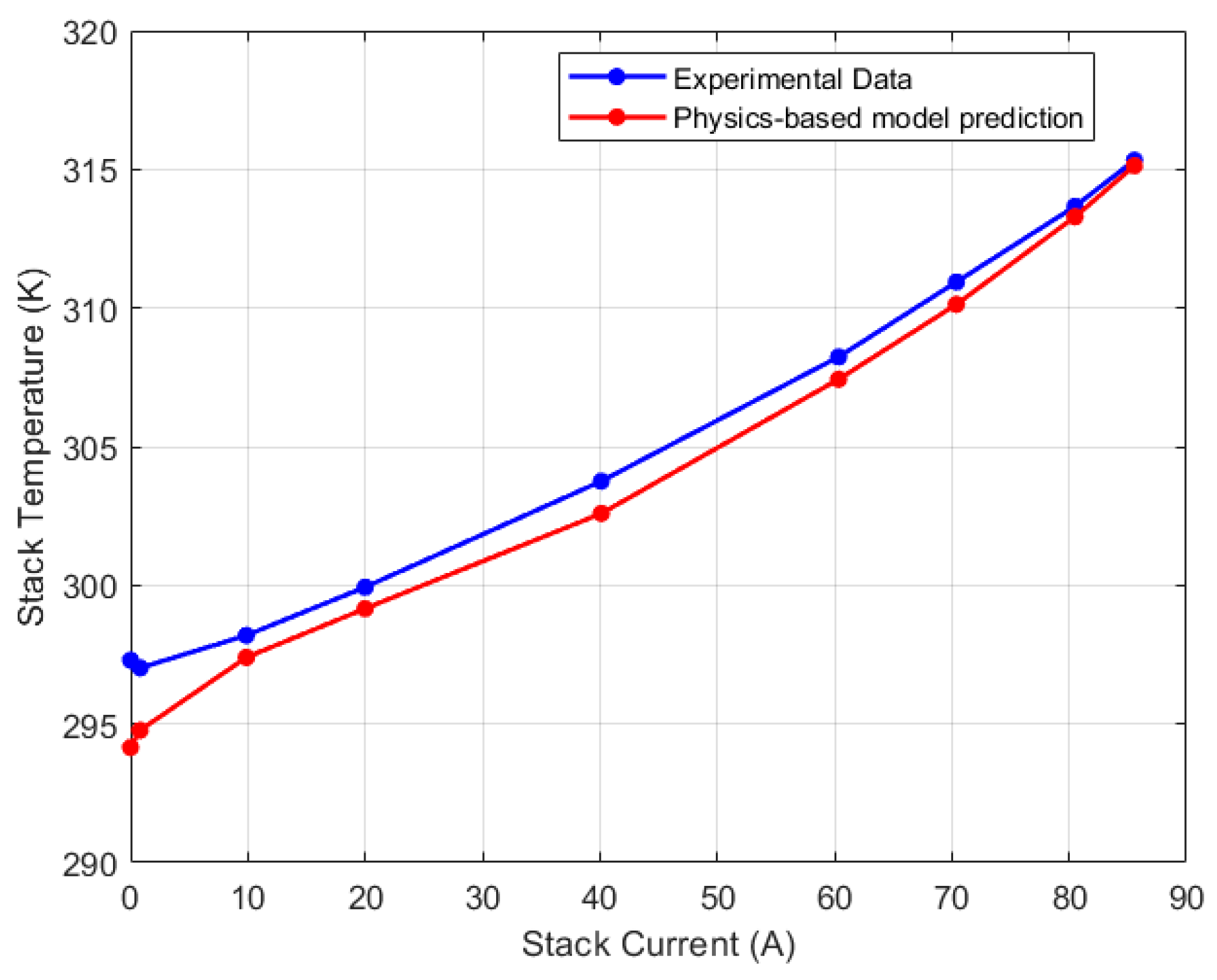
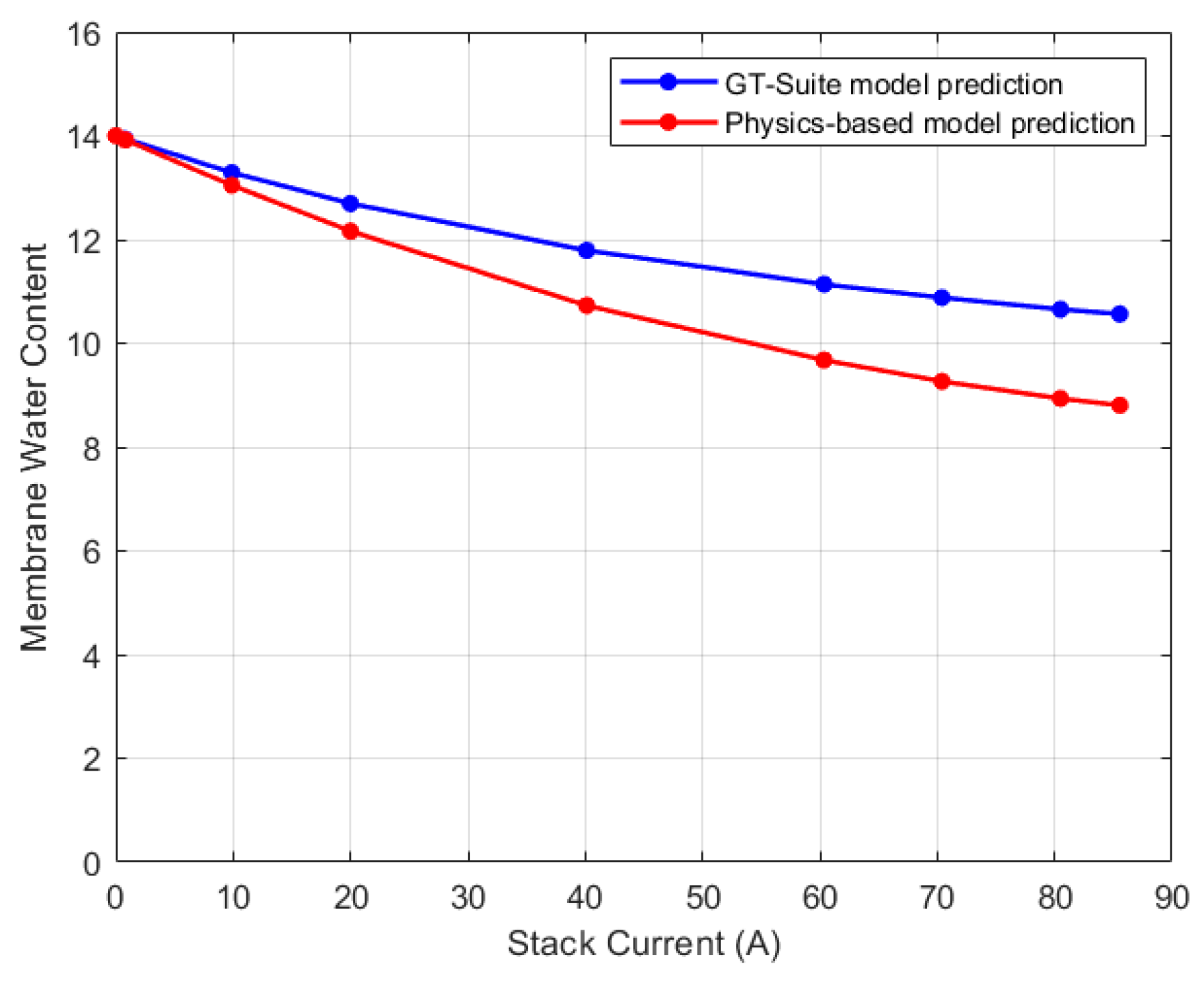
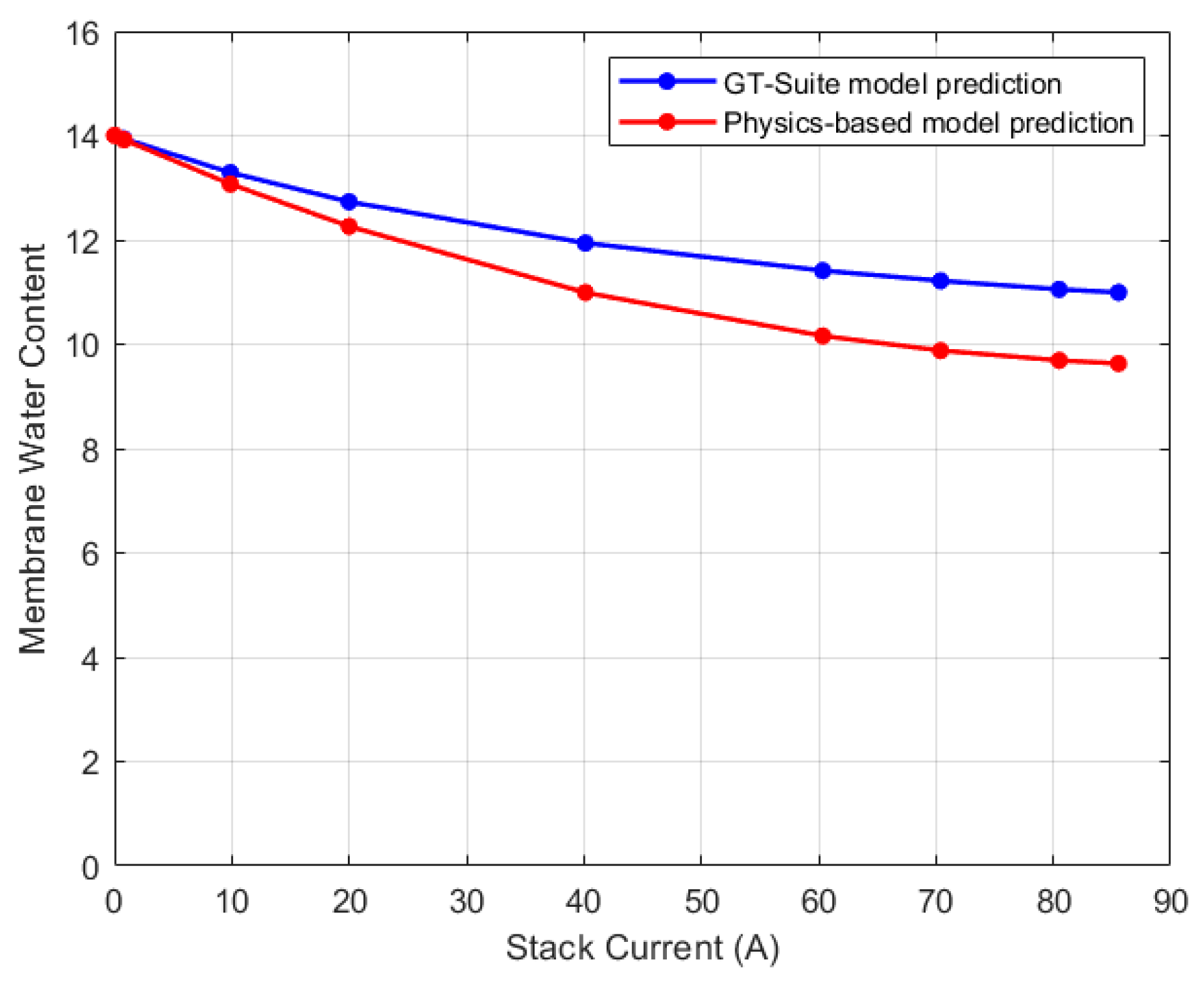
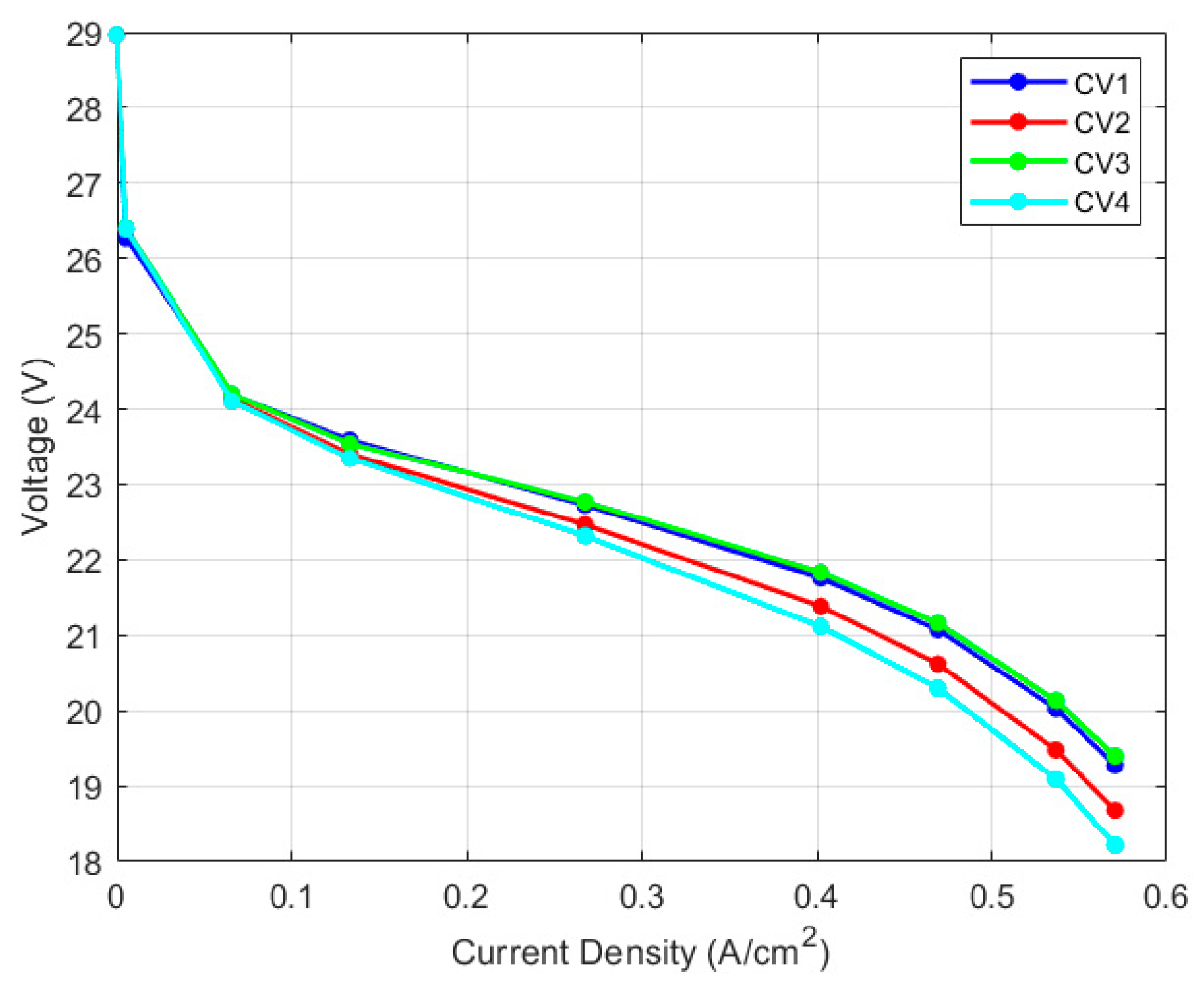
5.1. Lumped Model Validation
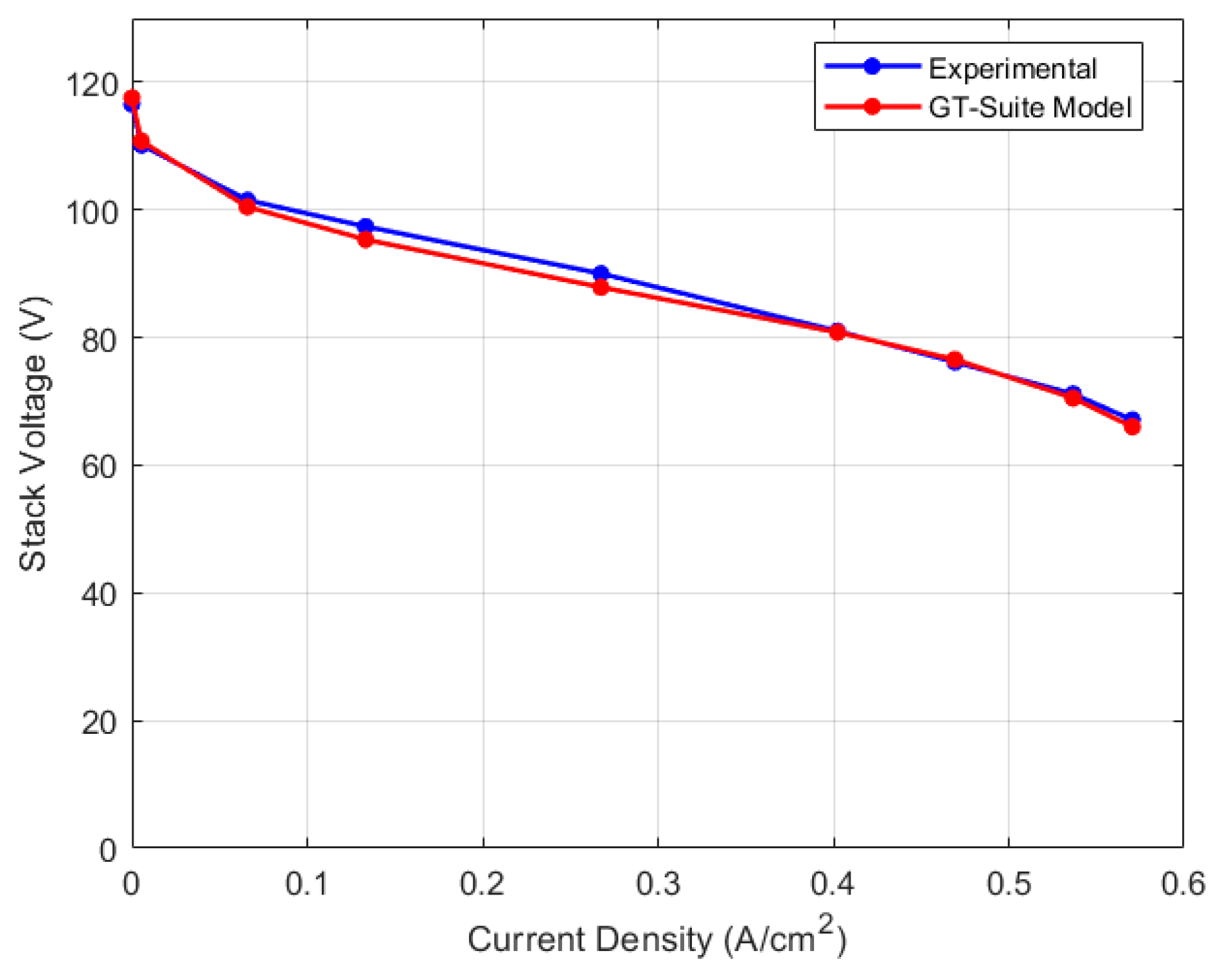
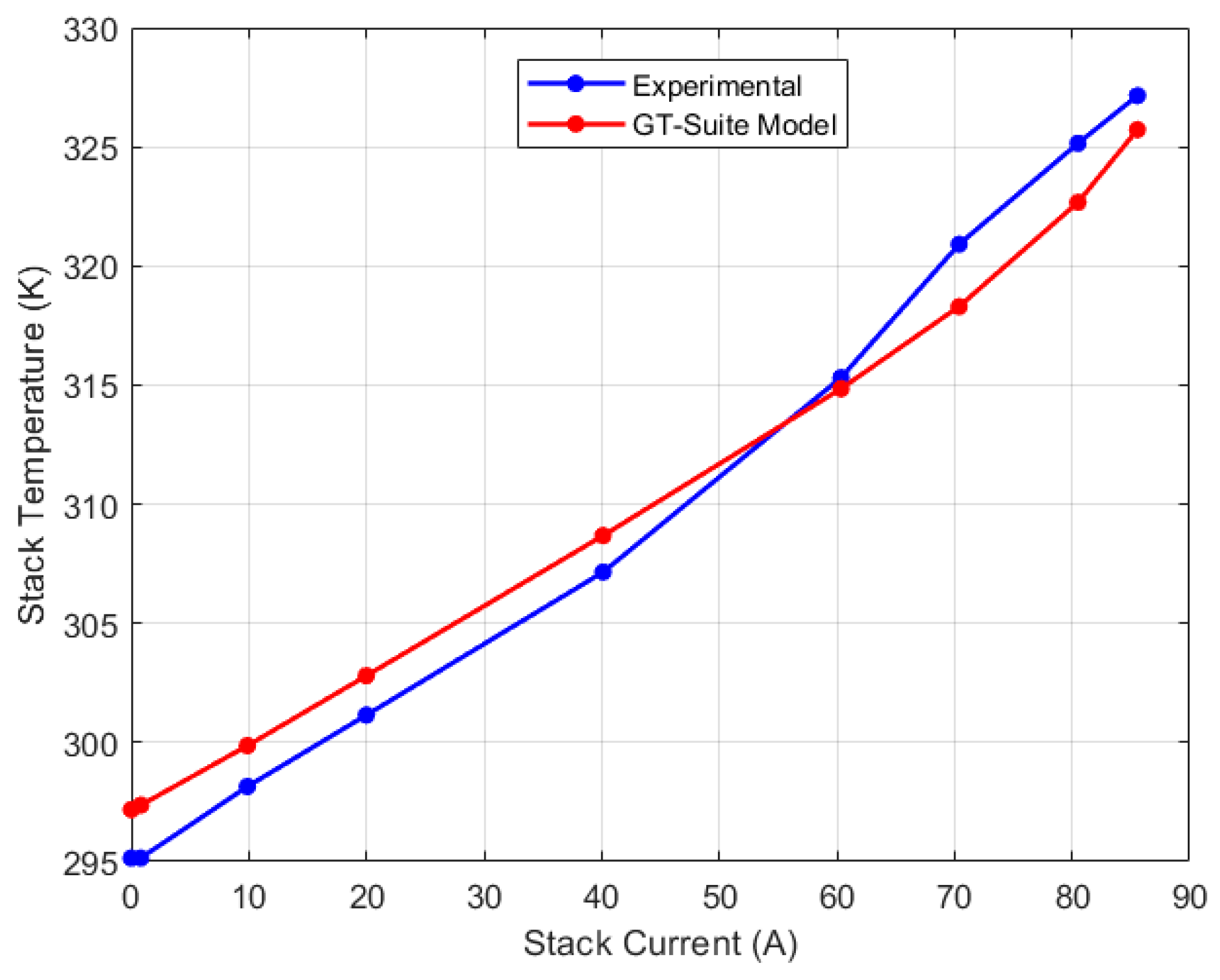
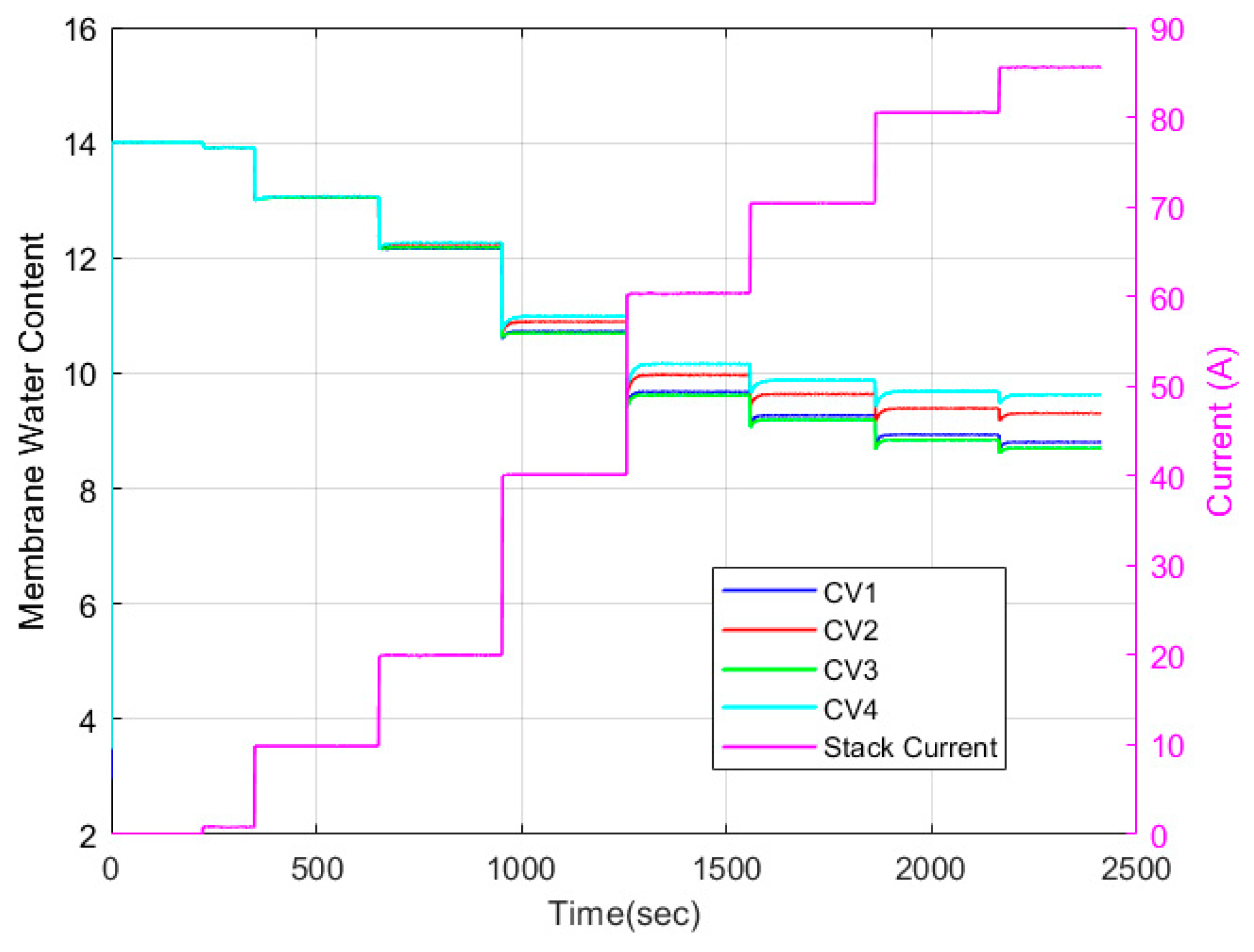
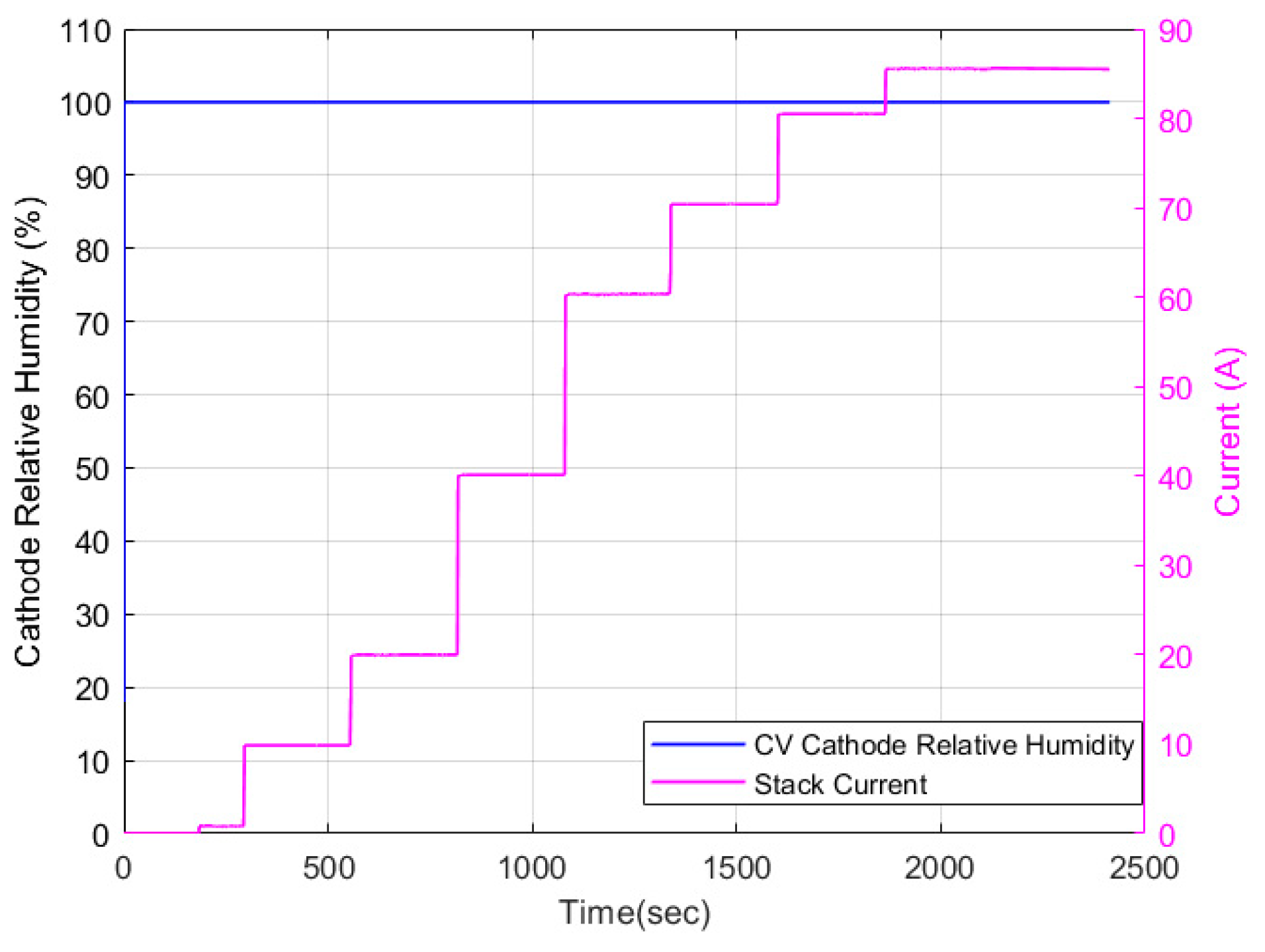
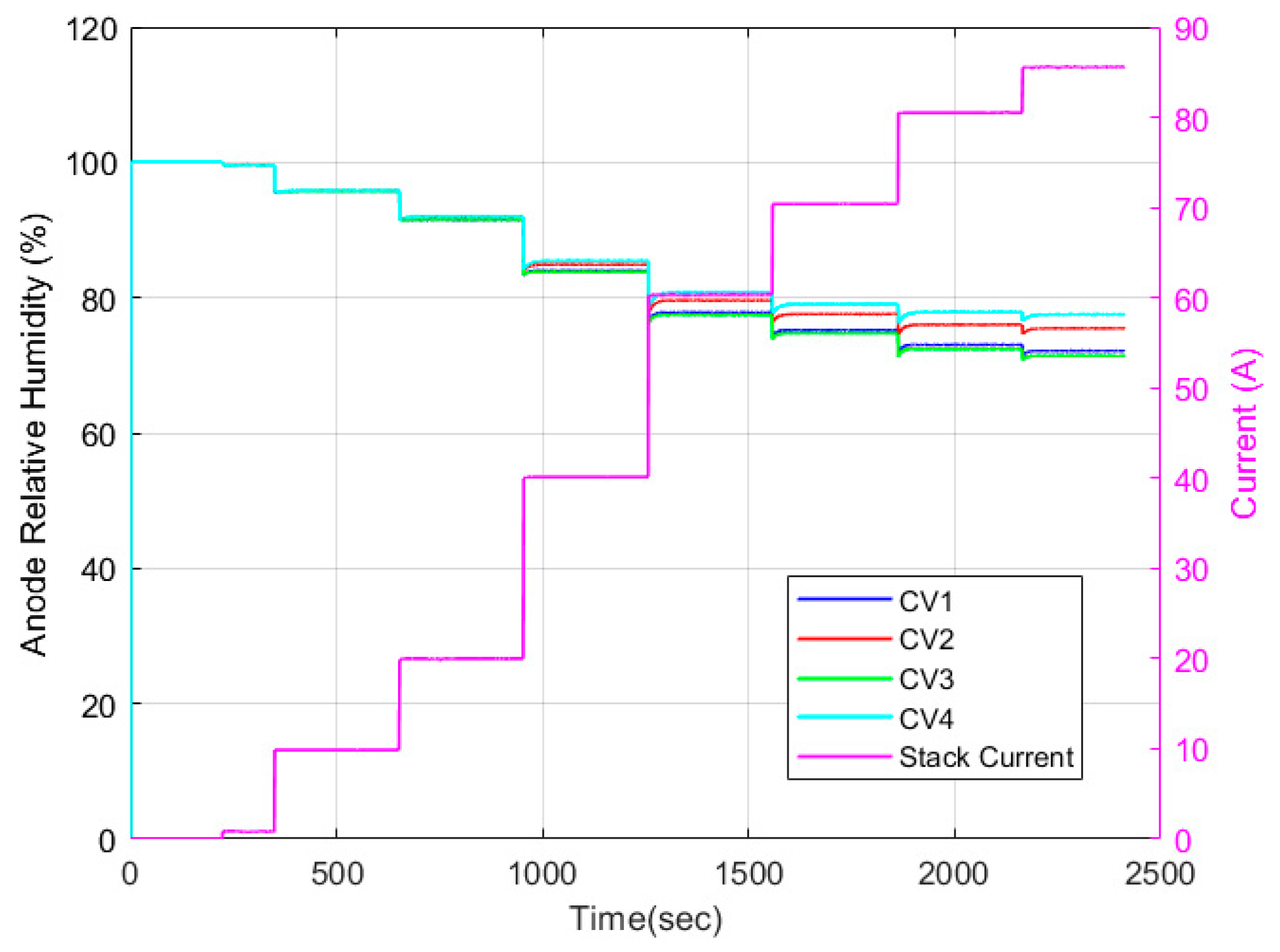
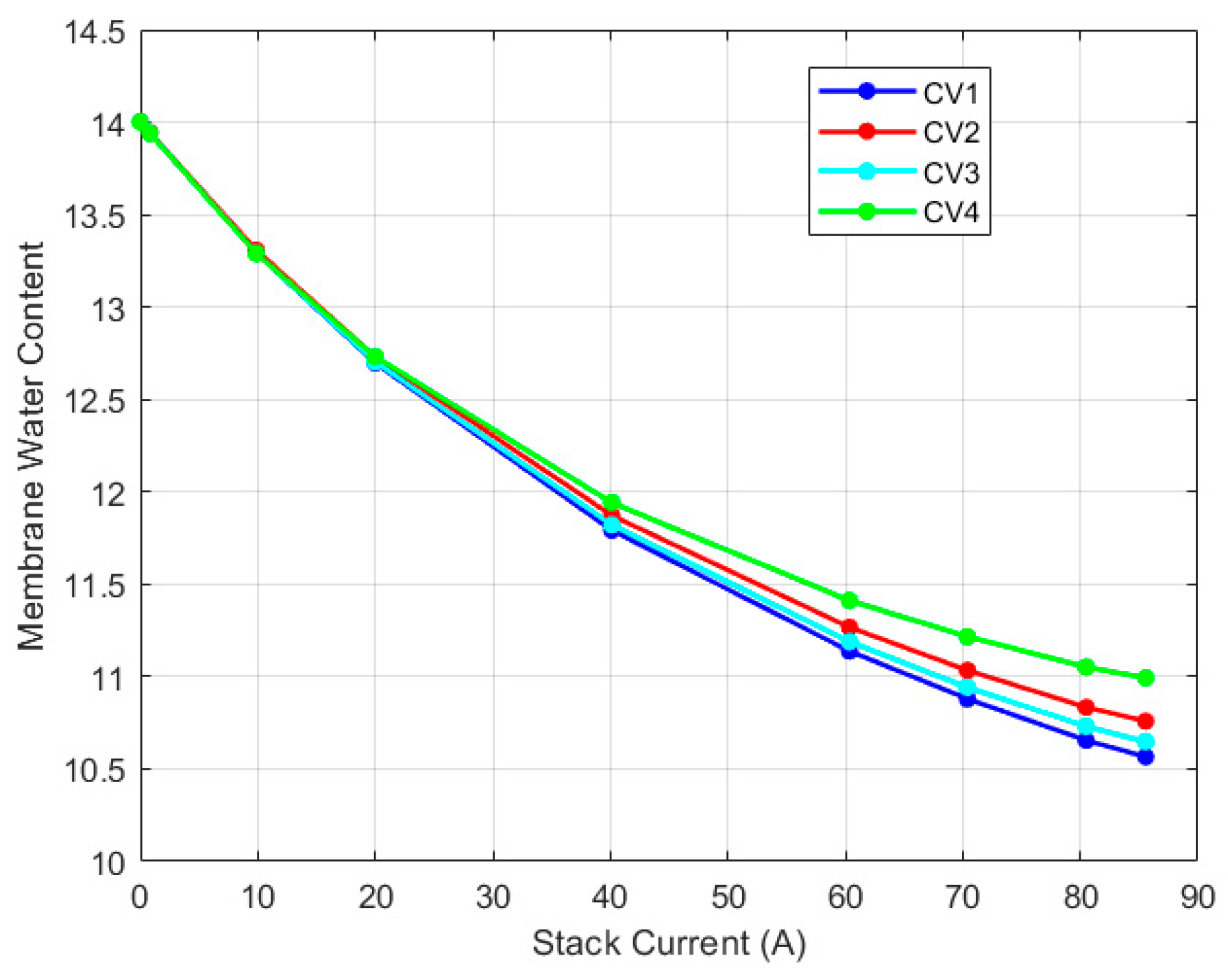
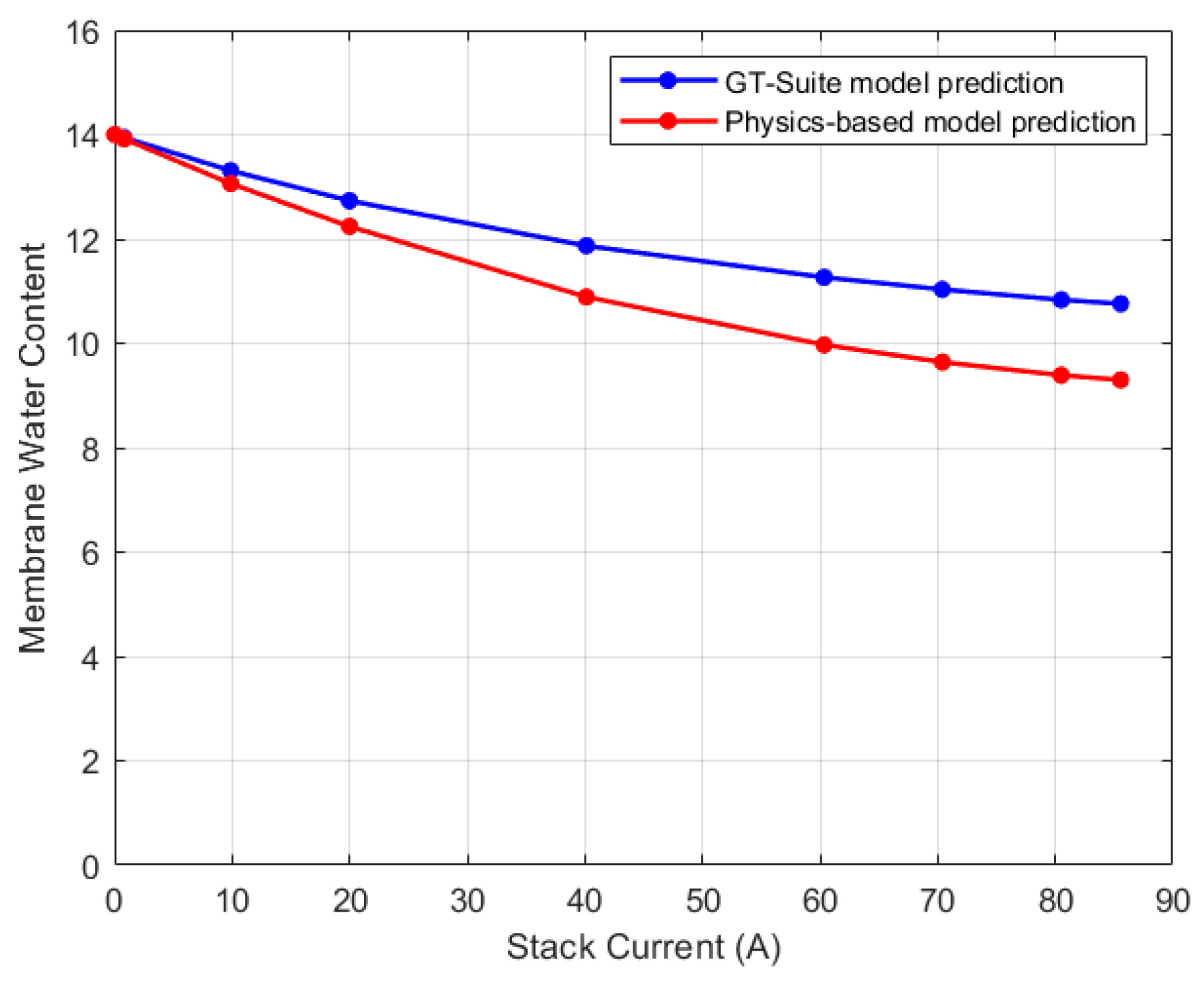
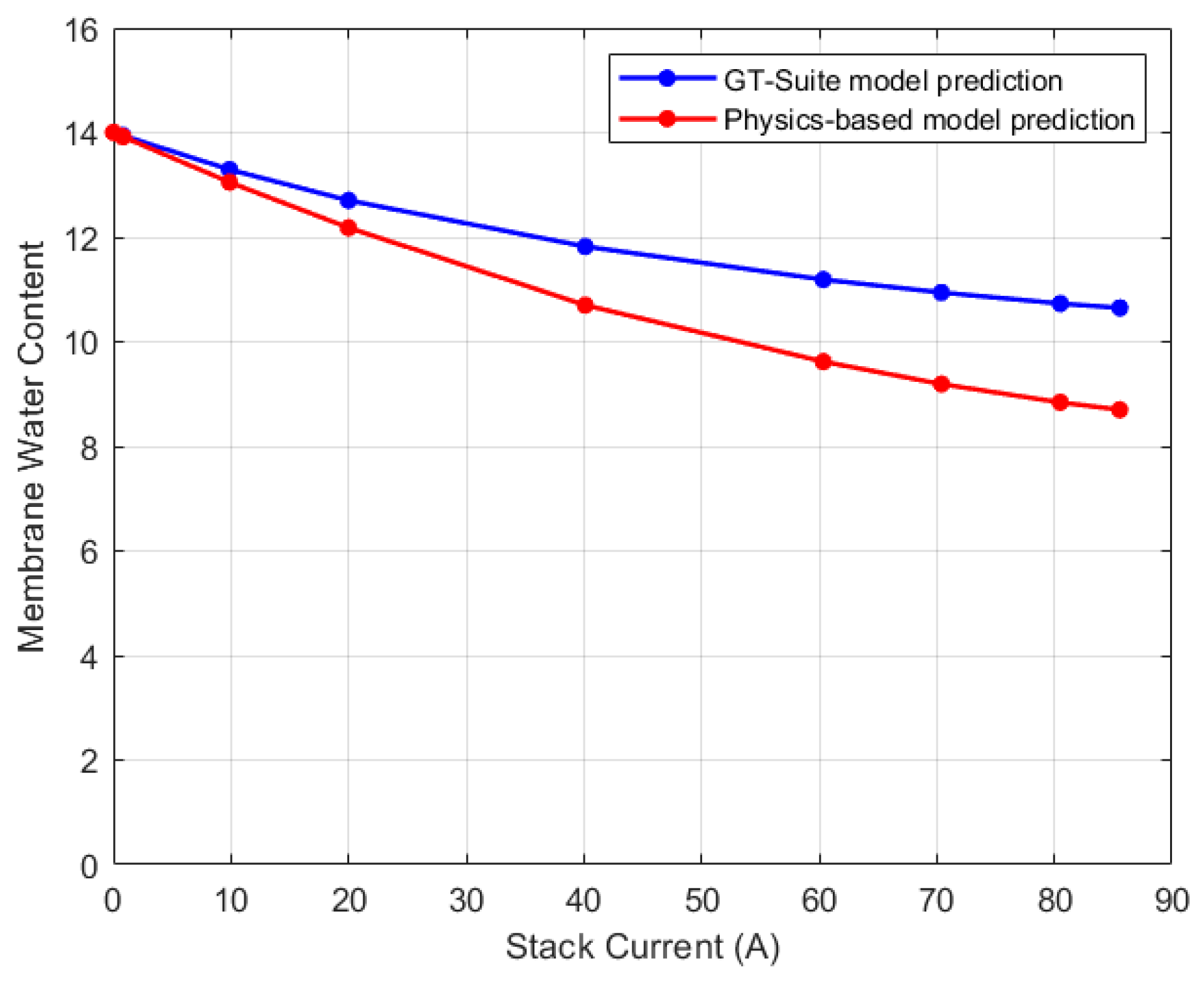
5.2. Discretized Model
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| CV | control volume |
| EOD | electro osmotic drag |
| GT | gamma technologies |
| HTM | heat transfer multiplier |
| MEA | membrane electrode assembly |
| PEM | proton exchange membrane |
| PWM | pulse width modulation |
| RH | relative humidity |
| RMSE | root mean square error |
| rpm | revolutions per minute |
| Subscripts | |
| act | activation |
| amb | ambient |
| an | anode |
| ca | cathode |
| conc | concentration |
| ds | downstream |
| elec | electronic |
| fc | fuel cell |
| g | gas |
| gen | generated |
| hydrogen | |
| water vapor | |
| in | inlet |
| mem | membrane |
| nitrogen | |
| nom | nominal |
| oc | open circuit |
| out | outlet |
| ref | reference |
| rxn | electrochemical reaction |
| sat | saturation |
| st | stack |
| Parameters and variables | |
| A | area of fuel cell (m2) |
| i | current density (A/m2) |
| exchange current density (A/m2) | |
| I | current (A) |
| k | nozzle constant (kg/(s·Pa)) |
| M | molar mass (kg/mol) |
| mass flow rate (kg/s) | |
| P | power (W) or pressure (Pa) |
| V | voltage (V) or volume (m3) |
| R | ideal gas constant (J/(mol·K)) or resistance (W) |
| t | time (s) or thickness (m) |
| T | temperature (K) |
| mass fraction | |
| y | mole fraction |
| λ | water content |
| ρ | density (kg/m3) |
| η | efficiency |
References
- Tellez-Cruz, M.M.; Escorihuela, J.; Solorza-Feria, O.; Compañ, V. Proton exchange membrane fuel cells (Pemfcs): Advances and challenges. Polymers 2021, 13, 3064. [Google Scholar] [CrossRef]
- Zeng, T.; Zhang, C.; Huang, Z.; Li, M.; Chan, S.H.; Li, Q.; Wu, X. Experimental investigation on the mechanism of variable fan speed control in Open cathode PEM fuel cell. Int. J. Hydrogen Energy 2019, 44, 24017–24027. [Google Scholar] [CrossRef]
- Morner, S.O.; Klein, S.A. Experimental evaluation of the dynamic behavior of an air-breathing fuel cell stack. J. Sol. Energy Eng. Trans. ASME 2001, 123, 225–253. [Google Scholar] [CrossRef]
- Jeon, D.; Nam, K.; Man, S.; Hyun, J. The effect of relative humidity of the cathode on the performance and the uniformity of PEM fuel cells. Int. J. Hydrogen Energy 2011, 36, 12499–12511. [Google Scholar] [CrossRef]
- Chen, Z.; Ingham, D.; Ismail, M.; Ma, L.; Hughes, K.J.; Pourkashanian, M. Effects of hydrogen relative humidity on the performance of an air-breathing PEM fuel cell: A numerical study. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 2077–2097. [Google Scholar] [CrossRef]
- Ozen, D.; Timurkutluk, B.; Altinisik, K. Effects of operation temperature and reactant gas humidity levels on performance of PEM fuel cells. Renew. Sustain. Energy Rev. 2016, 59, 1298–1306. [Google Scholar] [CrossRef]
- Watanabe, M.; Igarashi, H.; Uchida, H.; Hirasawa, J. Experimental analysis of water behavior in Nafion electrolyte under fuel cell operation. J. Electroanal. Chem. 1995, 399, 239–241. [Google Scholar] [CrossRef]
- Zhang, Z.; Martin, J.; Wu, J.; Wang, H.; Promislow, K.; Balcom, B.J. Magnetic Resonance Imaging of Water Content across the Nafion Membrane in an Operational PEM Fuel Cell. J. Magn. Reson. 2005, 193, 259–266. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Jiao, K. Three-dimensional multi-phase simulation of PEMFC at high current density utilizing Eulerian-Eulerian model and two-fluid model. Energy Convers. Manag. 2018, 176, 409–421. [Google Scholar] [CrossRef]
- Dutta, S.; Shimpalee, S.; Van Zee, J.W. Numerical prediction of mass-exchange between cathode and anode channels in a PEM fuel cell. Int. J. Heat Mass Transf. 2001, 44, 2029–2042. [Google Scholar] [CrossRef]
- Sagar, A.; Chugh, S.; Sonkar, K.; Sharma, A.; Kjeang, E. A computational analysis on the operational behaviour of open-cathode polymer electrolyte membrane fuel cells. Int. J. Hydrogen Energy 2020, 45, 34125–34138. [Google Scholar] [CrossRef]
- Pukrushpan, J.T.; Peng, H.; Stefanopoulou, A.G. Control-oriented modeling and analysis for automotive fuel cell systems. J. Dyn. Syst. Meas. Control Trans. ASME 2004, 126, 14–25. [Google Scholar] [CrossRef]
- Meyer, R.T.; Yao, B. Modeling and Simulation of a Modern Pem Fuel Cell System. In Proceedings of the ASME 2006 4th International Conference on Fuel Cell Science, Engineering and Technology, Irvine, CA, USA, 19–21 June 2006; pp. 133–150. [Google Scholar]
- Chen, X.; Xu, J.; Fang, Y.; Li, W.; Ding, Y.; Wan, Z.; Wang, X.; Tu, Z. Temperature and humidity management of PEM fuel cell power system using multi-input and multi-output fuzzy method. Appl. Therm. Eng. 2022, 203, 117865. [Google Scholar] [CrossRef]
- Chen, X.; Xu, J.; Liu, Q.; Chen, Y.; Wang, X.; Li, W.; Ding, Y.; Wan, Z. Active disturbance rejection control strategy applied to cathode humidity control in PEMFC system. Energy Convers. Manag. 2020, 224, 113389. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, L.; Jiao, J. Modelling of humidity dynamics for open-cathode proton exchange membrane fuel cell. World Electr. Veh. J. 2021, 12, 106. [Google Scholar] [CrossRef]
- Headley, A.; Yu, V.; Borduin, R.; Chen, D.; Li, W. Development and Experimental Validation of a Physics-Based PEM Fuel Cell Model for Cathode Humidity Control Design. IEEE/ASME Trans. Mechatron. 2016, 21, 1775–1782. [Google Scholar] [CrossRef]
- Nguyen, T.V.; White, R.E. A Water and Heat Management Model for Proton-Exchange-Membrane Fuel Cells. J. Electrochem. Soc. 1993, 140, 2178–2186. [Google Scholar] [CrossRef]
- O’hayre, R.; Cha, S.-W.; Colella, W.; Prinz, F.B. Fuel Cell Fundamentals; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Wang, Y.; Yu, D.; Chen, S.; Kim, Y. Robust DC/DC converter control for polymer electrolyte membrane fuel cell application. J. Power Sources 2014, 261, 292–305. [Google Scholar] [CrossRef]
- Huo, D.; Hall, C.M. Data-driven prediction of temperature variations in an open cathode proton exchange membrane fuel cell stack using Koopman operator. Energy AI 2023, 14, 100289. [Google Scholar] [CrossRef]
- Ishaku, J.; Lotfi, N.; Zomorodi, H.; Landers, R.G. Control-oriented modeling for open-cathode fuel cell systems. In Proceedings of the American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 268–273. [Google Scholar]
- Karnik, A.Y.; Stefanopoulou, A.G.; Sun, J. Water equilibria and management using a two-volume model of a polymer electrolyte fuel cell. J. Power Sources 2007, 164, 590–605. [Google Scholar] [CrossRef]
- Pukrushpan, J.T.; Stefanopoulou, A.G.; Peng, H. Modeling and control for PEM fuel cell stack system. Proc. Am. Control Conf. 2002, 4, 3117–3122. [Google Scholar]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer electrolyte fuel cell model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- Karthik, M.; Vijayachitra, S. An integrated exploration of thermal and water management dynamics on the performance of a stand-alone 5-kW Ballard fuel-cell system for its scale-up design. Proc. Inst. Mech. Eng. Part A J. Power Energy 2014, 228, 836–852. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, B. Modeling and control of a portable proton exchange membrane fuel cell-battery power system. J. Power Sources 2011, 196, 8413–8423. [Google Scholar] [CrossRef]
- Falcão, D.S.; Pinho, C.; Pinto, A.M.F.R. Water management in PEMFC: 1-D model simulations. Cienc. e Tecnol. Dos Mater. 2016, 28, 81–87. [Google Scholar] [CrossRef]



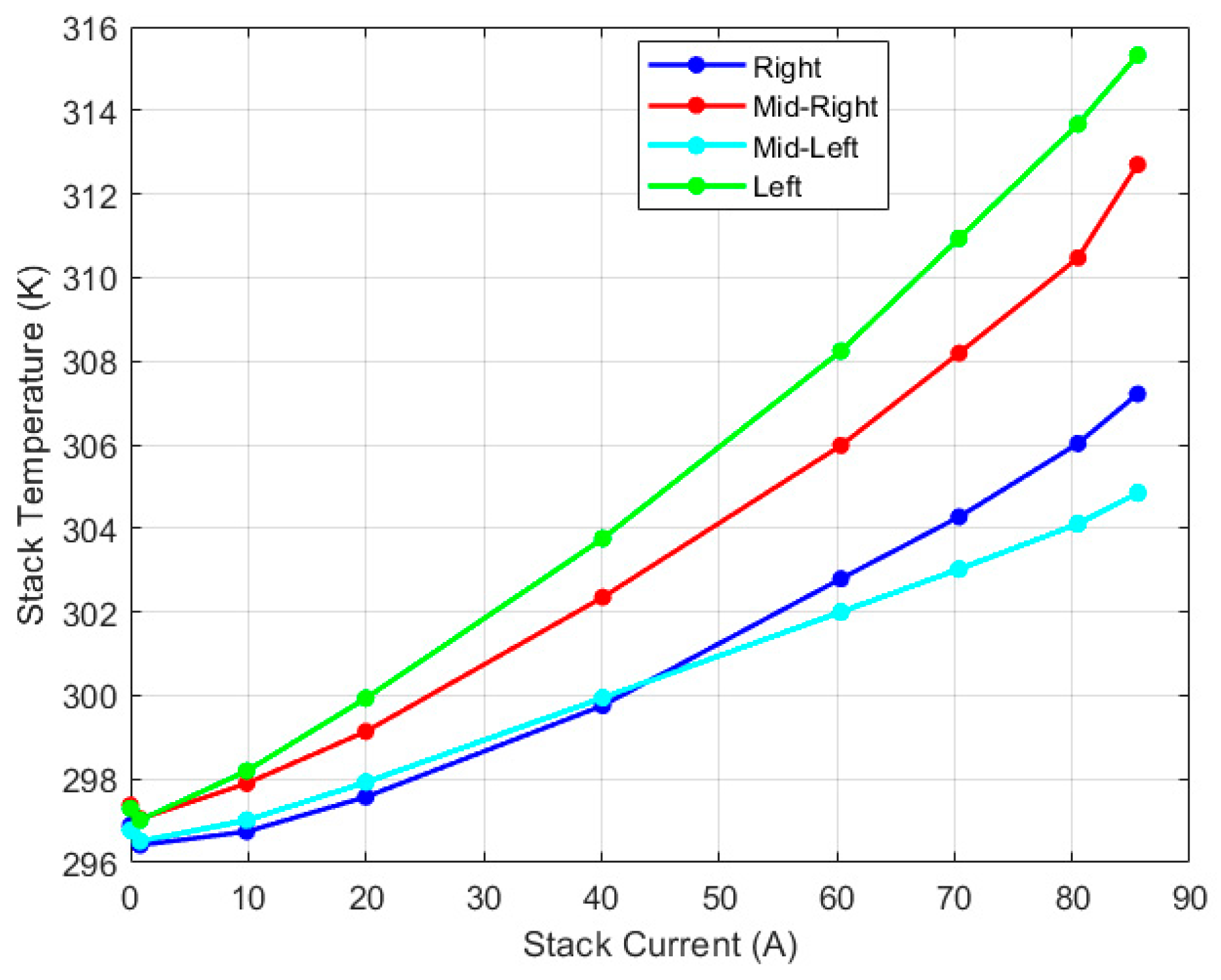
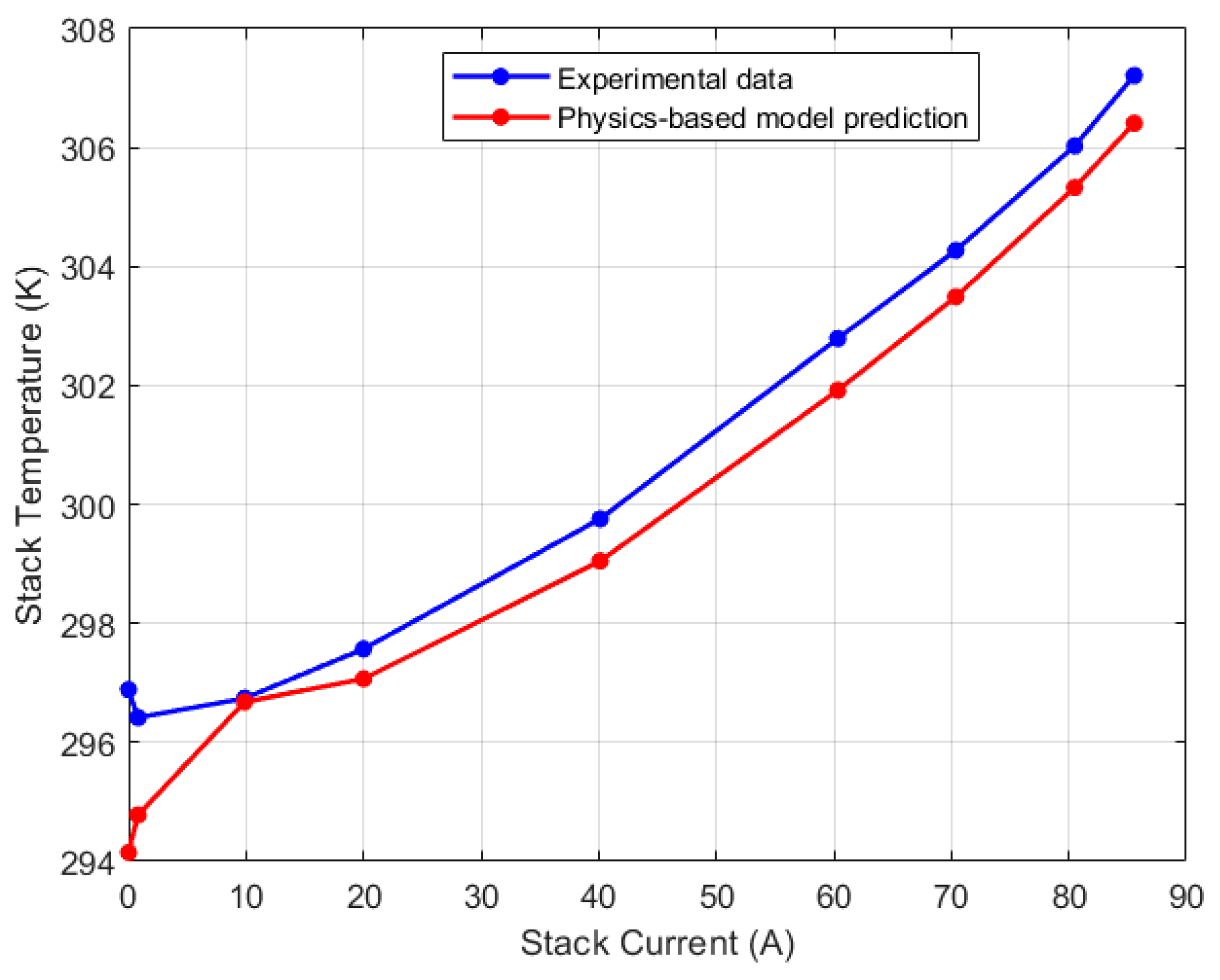
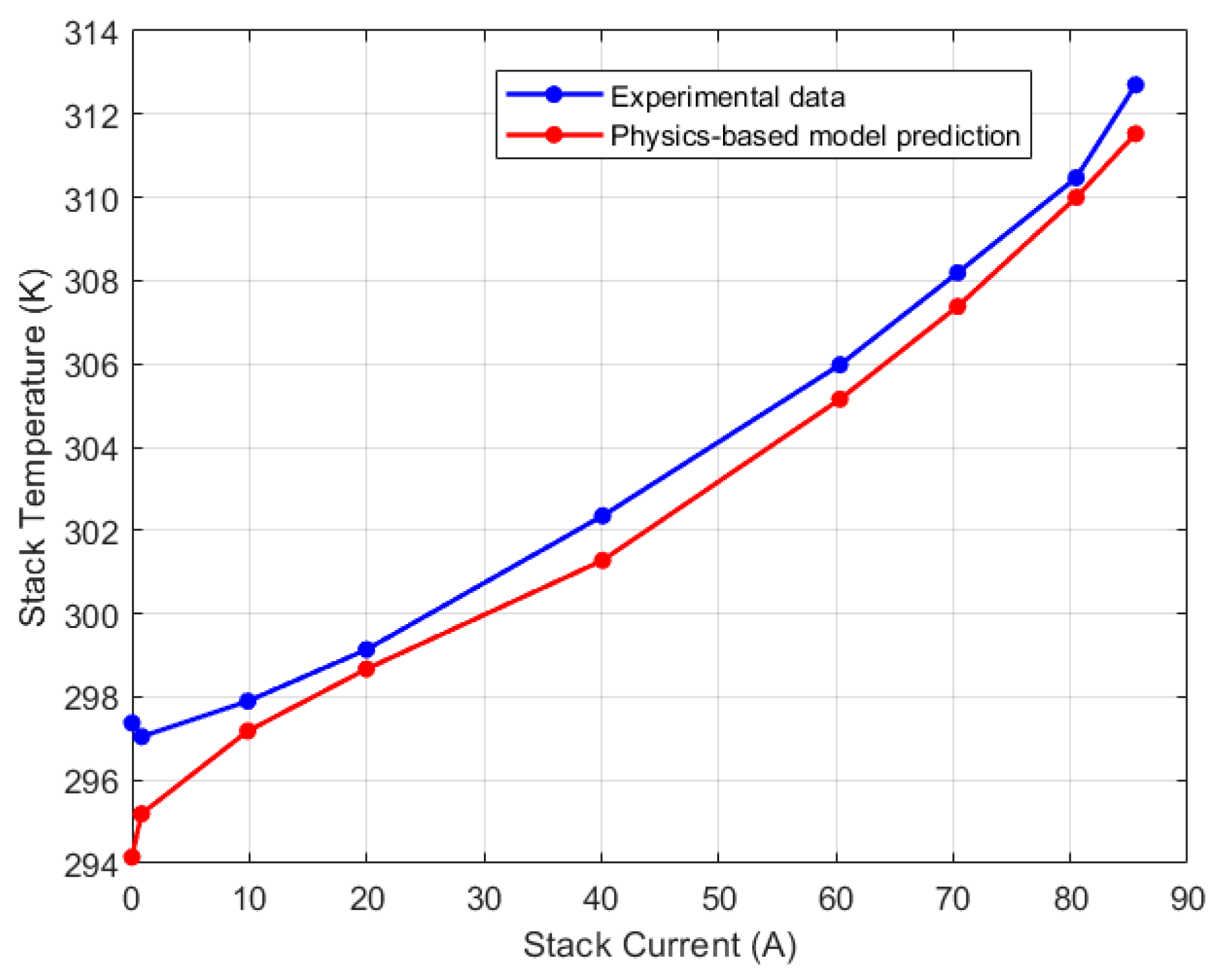
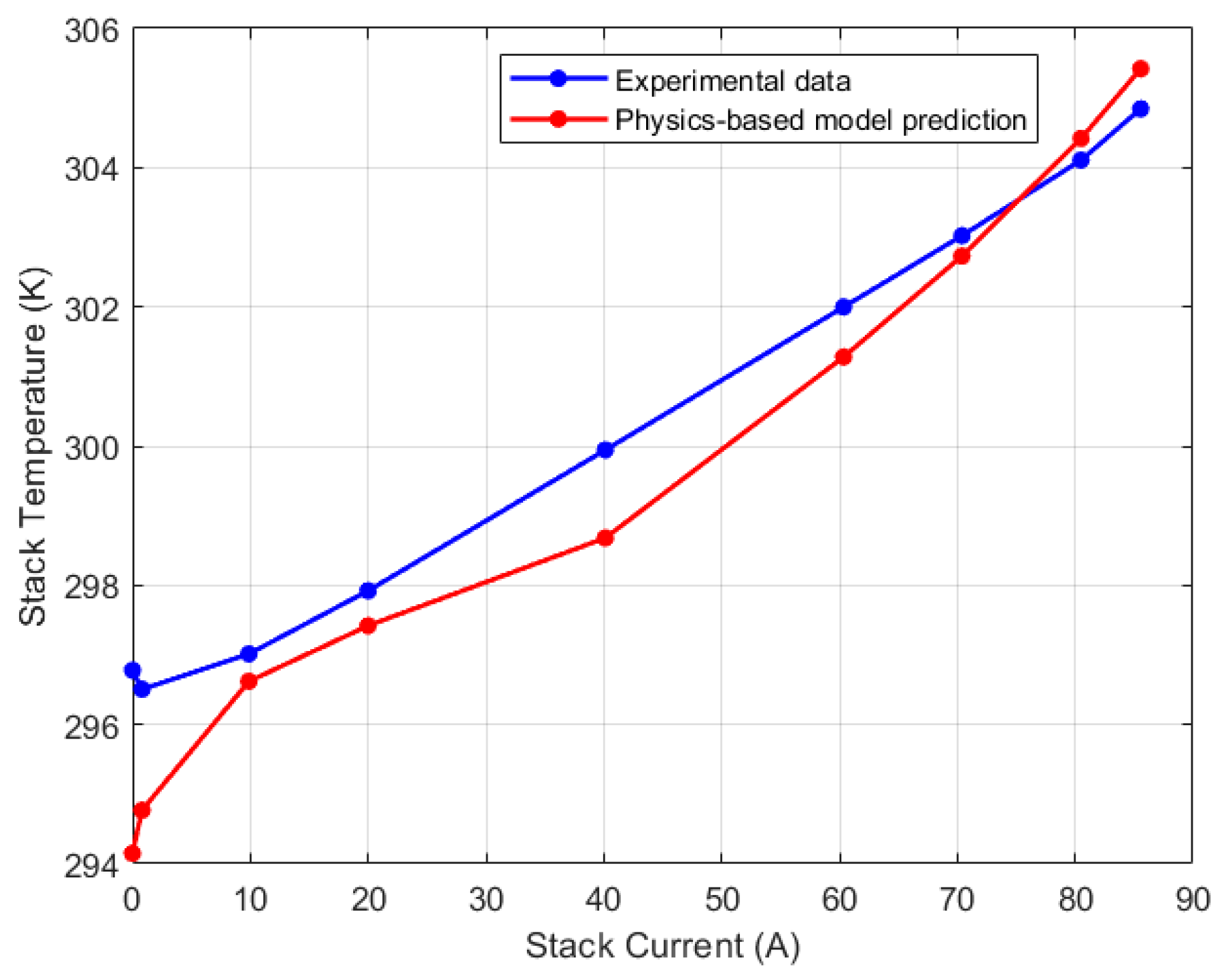
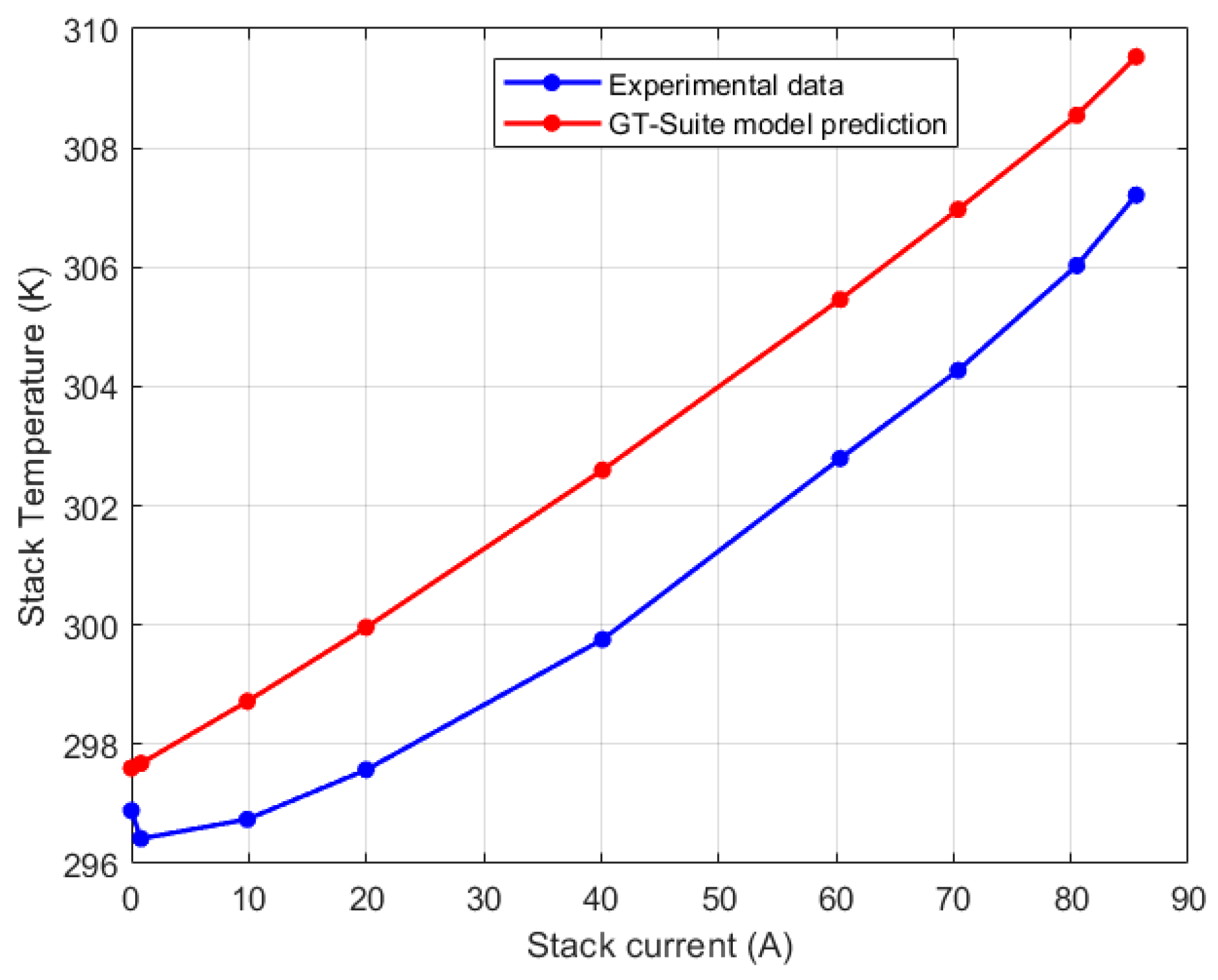
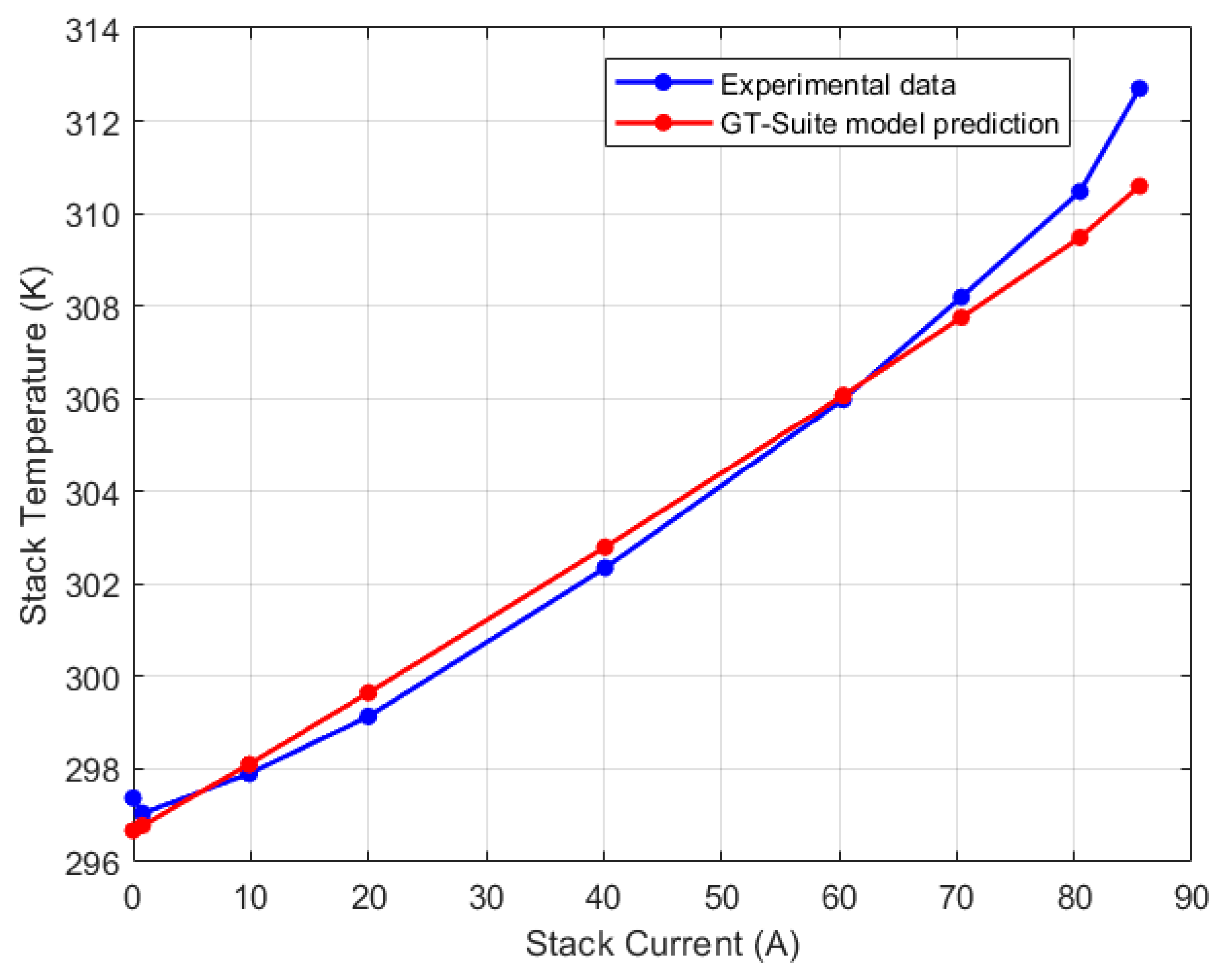
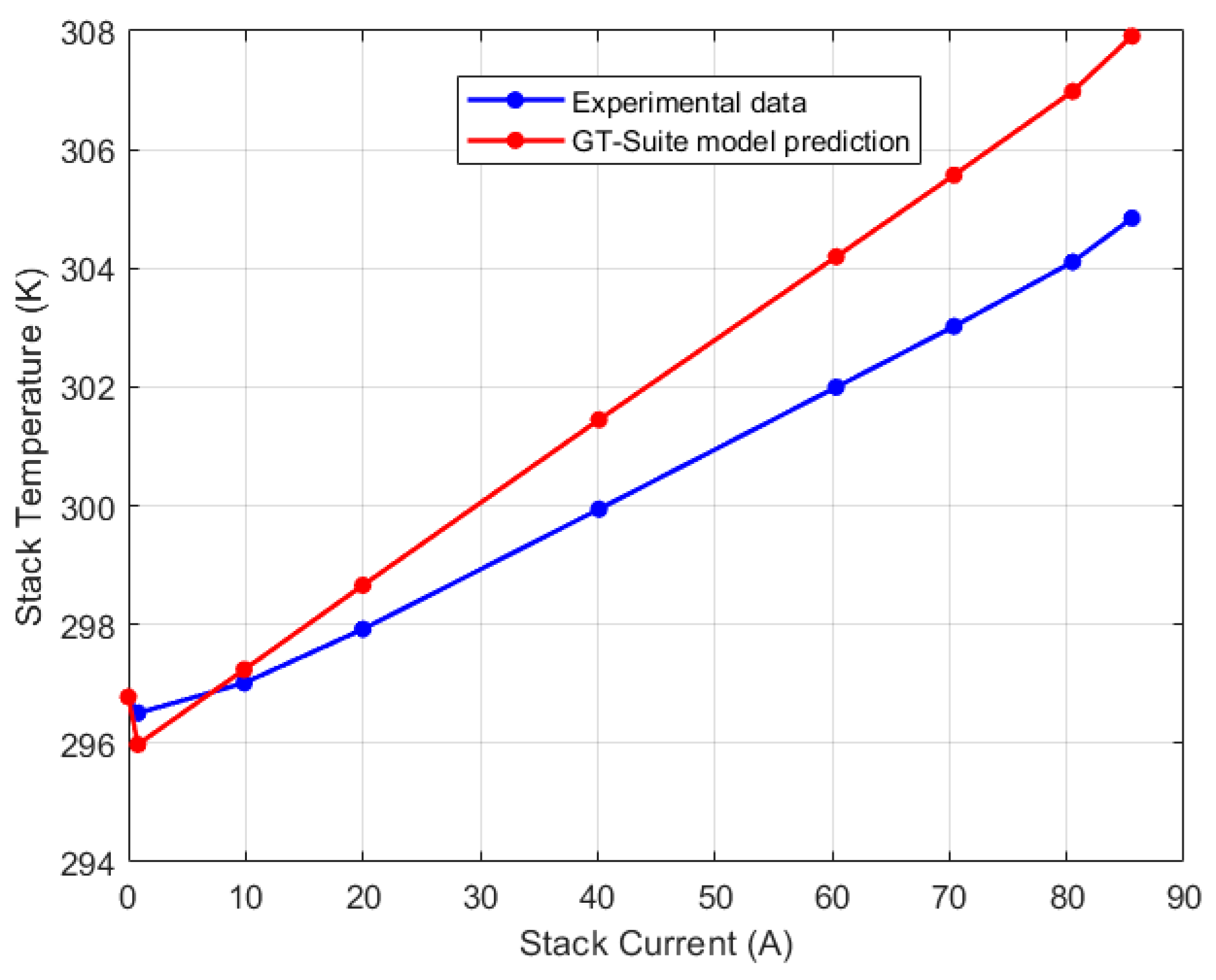
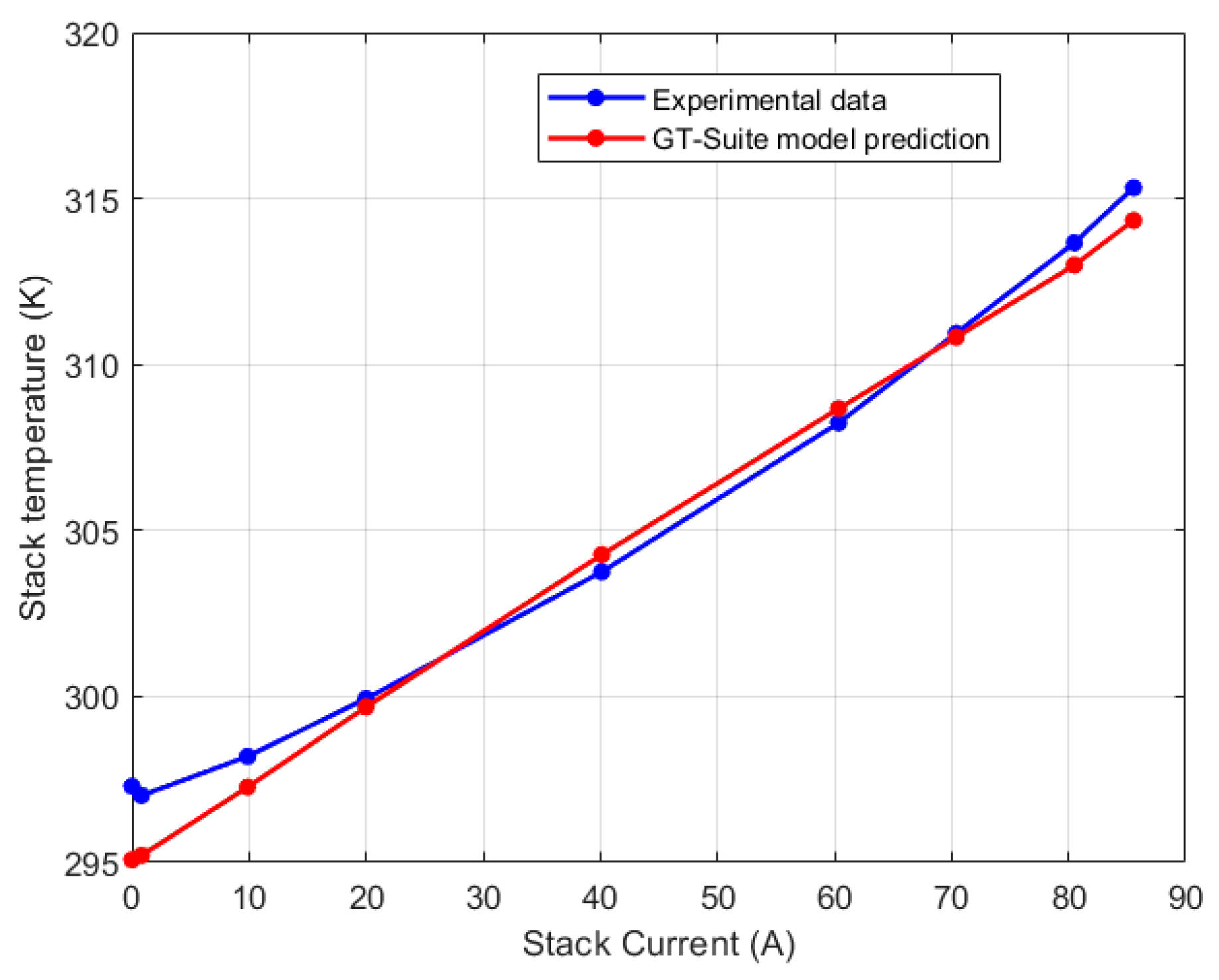
| Test Parameters | Minimum | Maximum |
|---|---|---|
| Gas mass flow rate (kg/s) | 0.000111 | |
| Gas pressure (Pa) | 129,863 | 163,974 |
| Gas temperature (K) | 303.49 | 305 |
| Right thermocouple (K) | 296.42 | 307.21 |
| Mid-right thermocouple (K) | 297.04 | 312.70 |
| Mid-left thermocouple (K) | 296.51 | 305.85 |
| Left thermocouple (K) | 297.02 | 315.32 |
| In-Stack Temperature (K) | 295.15 | 327.15 |
| Voltage (V) | 67.10 | 116.60 |
| Symbol | Variable | Value |
|---|---|---|
| Active area of fuel cell | 150 cm2 | |
| Number of cells in stack | 120 | |
| Faraday constant | 96,485 Coulombs | |
| Membrane thickness | 0.0035 cm | |
| Ideal gas constant | 8.314 J/(mol·K) | |
| Water vapor gas constant | 461.5 J/(kg·K) | |
| Oxygen gas constant | 259.8 J/(kg·K) | |
| Nitrogen gas constant | 296.9 J/(kg·K) | |
| Hydrogen gas constant | 4124.3 J/(kg·K) | |
| Water vapor molar mass | 0.018 kg/mol | |
| Oxygen molar mass | 0.032 kg/mol | |
| Nitrogen molar mass | 0.028 kg/mol | |
| Hydrogen molar mass | 0.002 kg/mol | |
| No. of electrons transferred | 2 | |
| Cathode outlet flow coefficient | kg/(s·Pa) | |
| Anode volume per cell | m3 | |
| Cathode volume per cell | m3 | |
| Membrane dry density | 0.002 kg/cm3 | |
| Membrane equivalent weight | 1.1 kg/mol | |
| Specific heat capacity of air | 1006 J/(kg·K) | |
| Electronic resistance | 0.00007 W |
| Thermocouple/CV | Max. Relative Error | |
|---|---|---|
| Physics-Based | GT-Suite | |
| Right/CV1 | 0.92% | 0.95% |
| Mid-right/CV2 | 1.08% | 0.68% |
| Mid-left/CV3 | 0.89% | 1.00% |
| Left/CV4 | 1.06% | 0.75% |
| Control Volume (CV) | RMSE |
|---|---|
| CV1 | 1.17 |
| CV2 | 1.00 |
| CV3 | 1.27 |
| CV4 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adunyah, A.S.; Gawli, H.A.; Hall, C.M. A Control-Oriented Model for Predicting Variations in Membrane Water Content of an Open-Cathode Proton Exchange Membrane Fuel Cell. Energies 2024, 17, 831. https://doi.org/10.3390/en17040831
Adunyah AS, Gawli HA, Hall CM. A Control-Oriented Model for Predicting Variations in Membrane Water Content of an Open-Cathode Proton Exchange Membrane Fuel Cell. Energies. 2024; 17(4):831. https://doi.org/10.3390/en17040831
Chicago/Turabian StyleAdunyah, Adwoa S., Harshal A. Gawli, and Carrie M. Hall. 2024. "A Control-Oriented Model for Predicting Variations in Membrane Water Content of an Open-Cathode Proton Exchange Membrane Fuel Cell" Energies 17, no. 4: 831. https://doi.org/10.3390/en17040831
APA StyleAdunyah, A. S., Gawli, H. A., & Hall, C. M. (2024). A Control-Oriented Model for Predicting Variations in Membrane Water Content of an Open-Cathode Proton Exchange Membrane Fuel Cell. Energies, 17(4), 831. https://doi.org/10.3390/en17040831







