Simplified Current-Equivalent Circuit Models of Synchronous Reluctance Machines and Salient Pole Synchronous Machines Considering the Reluctance Torque
Abstract
:1. Introduction
2. Two-Reaction Theory
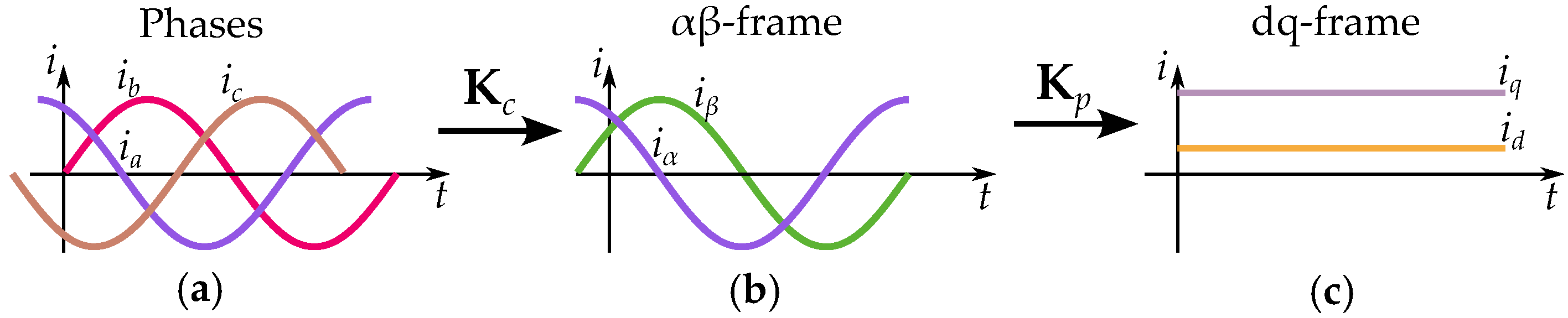
2.1. Clark and Park Transform
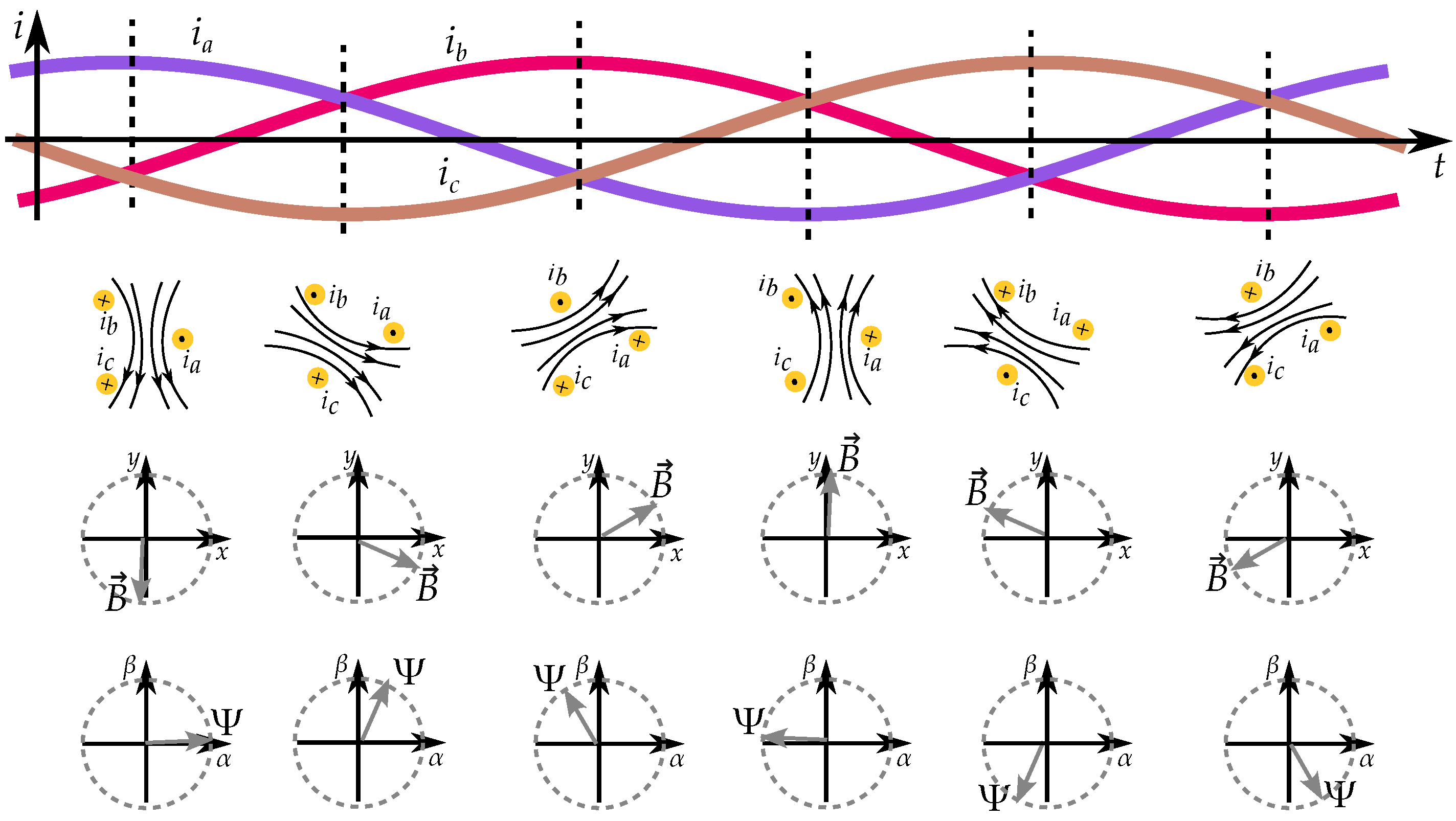
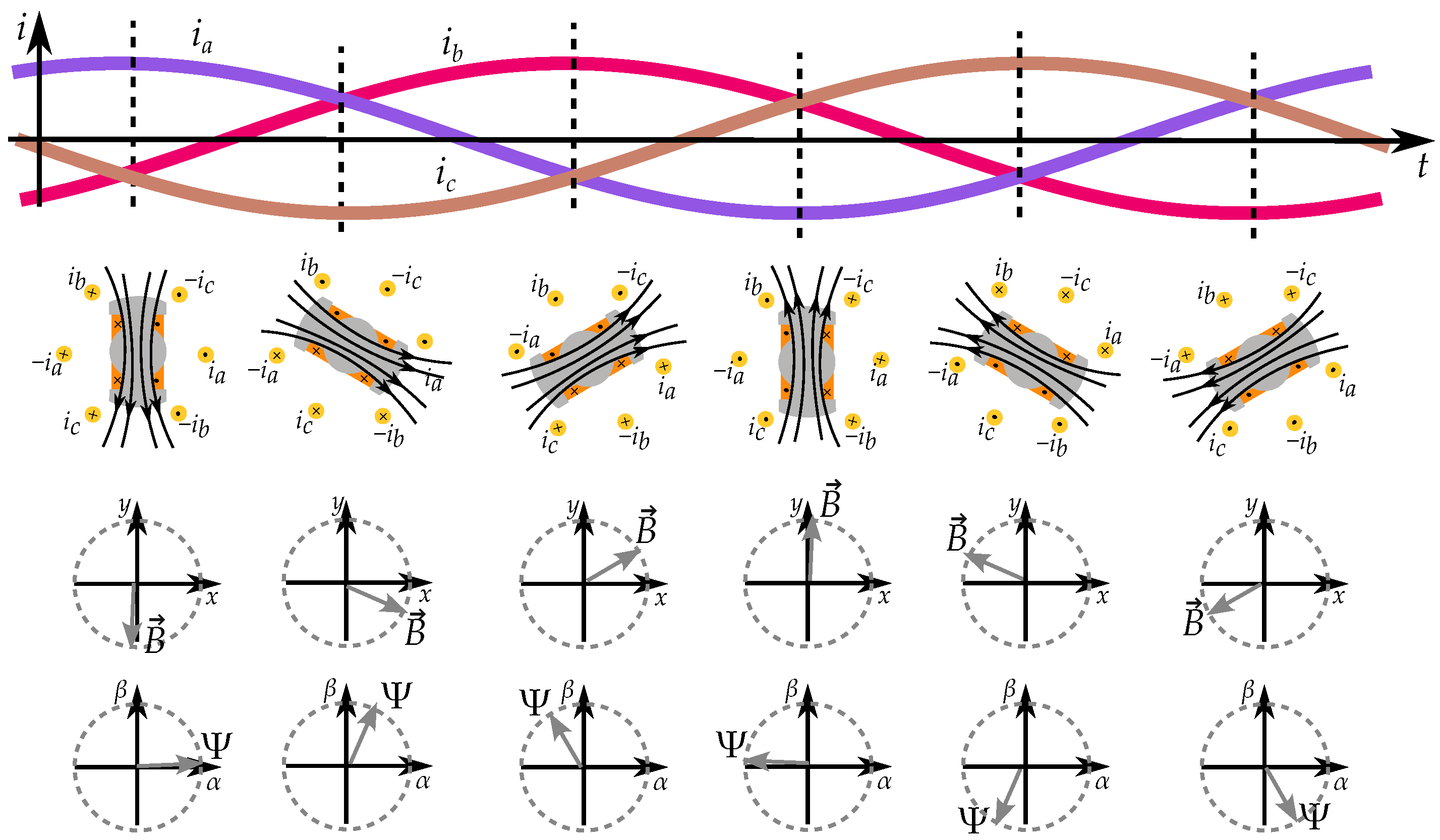
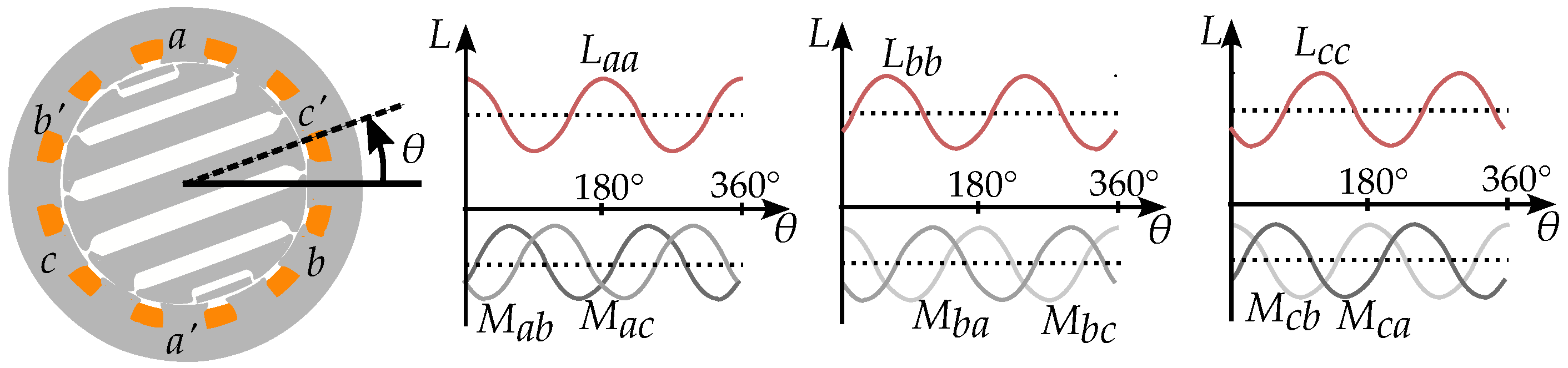
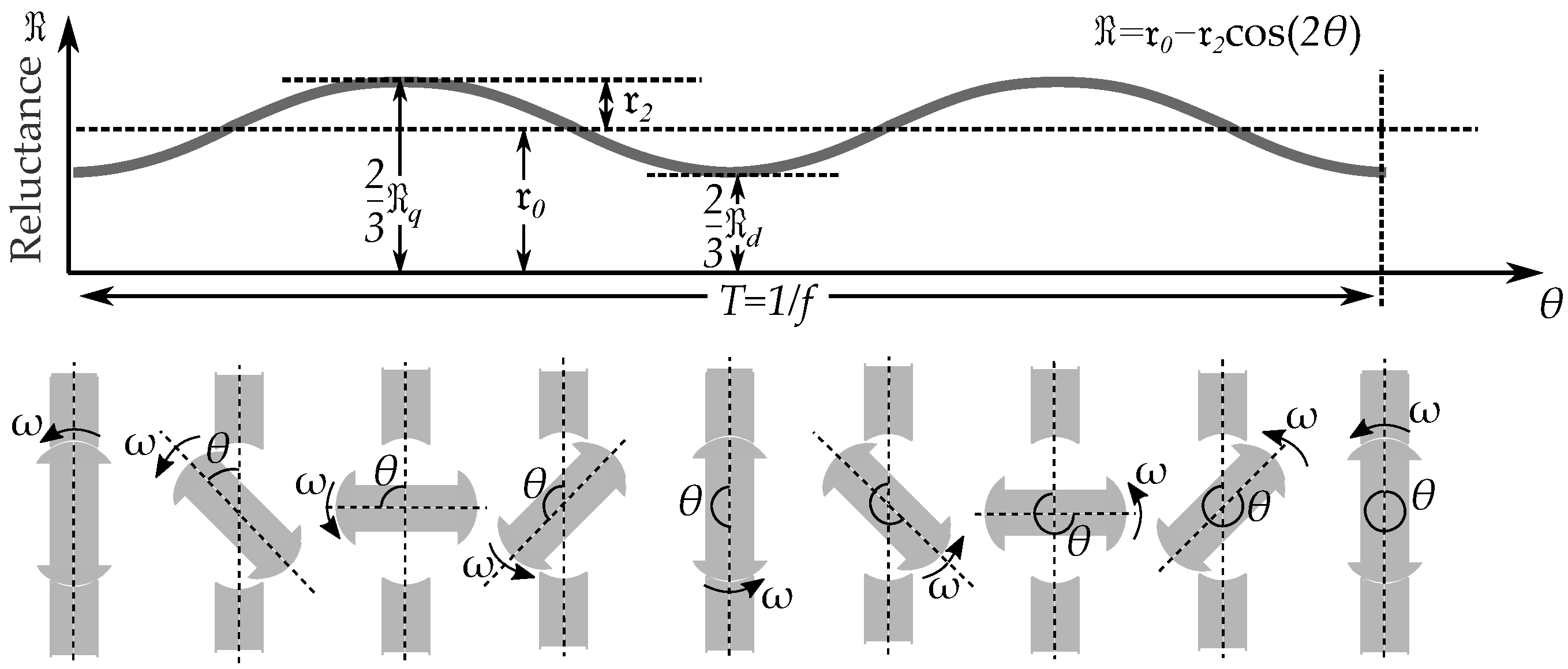
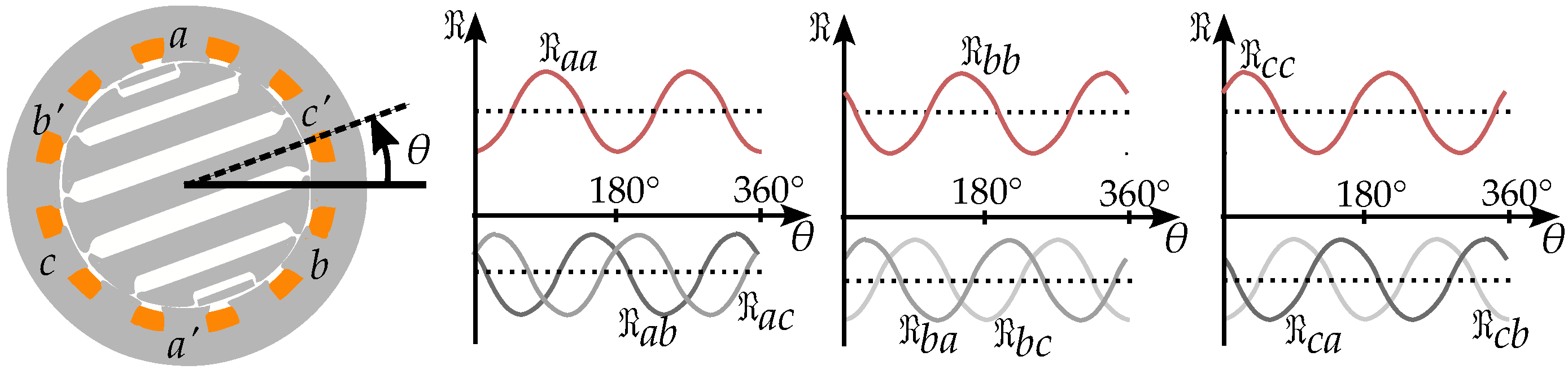
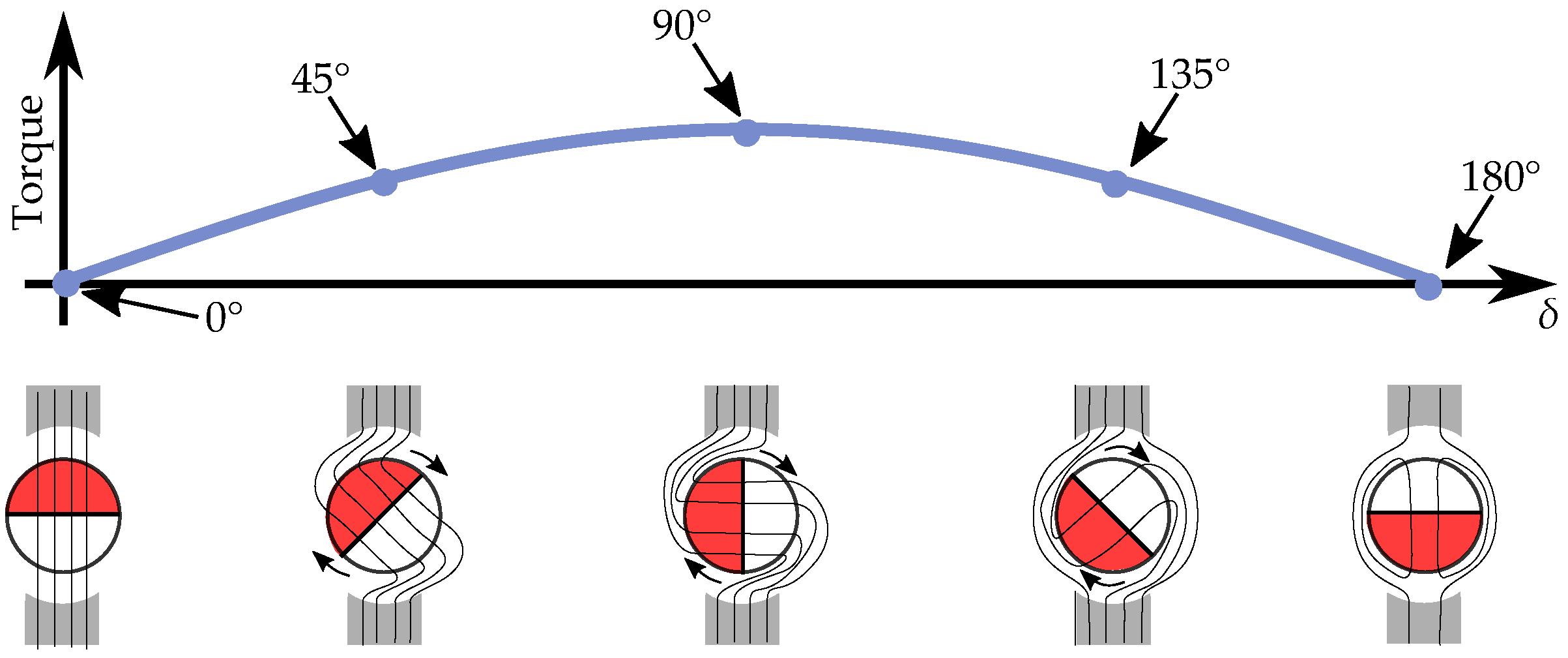
2.2. Pole Saliency in a Three-Phase Machine
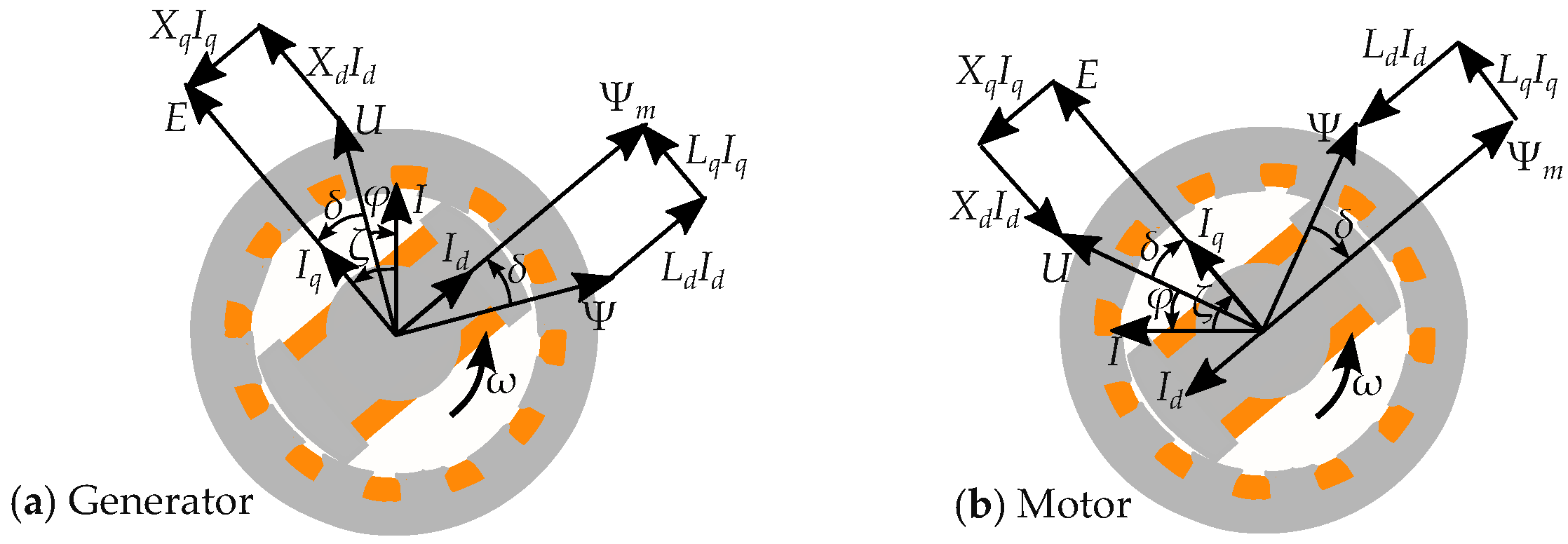
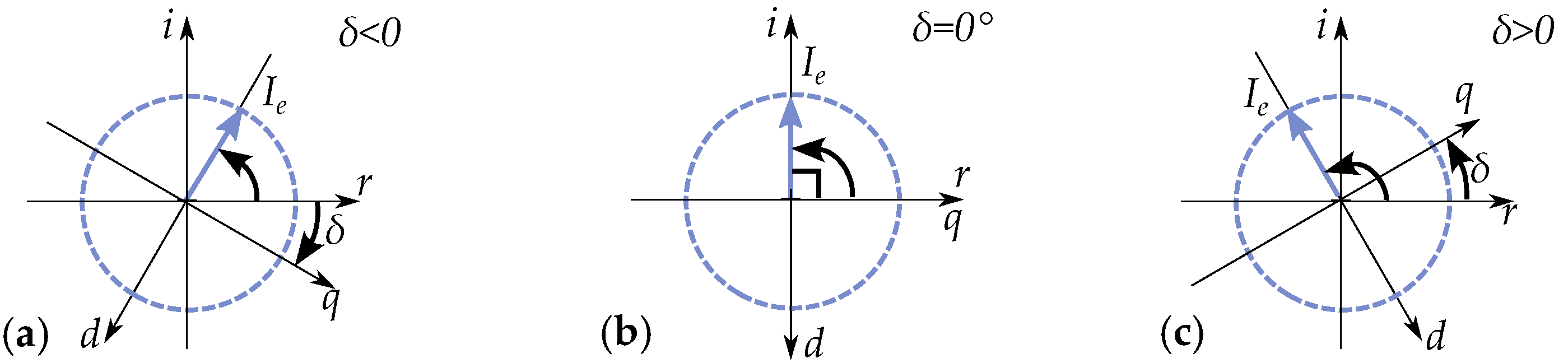
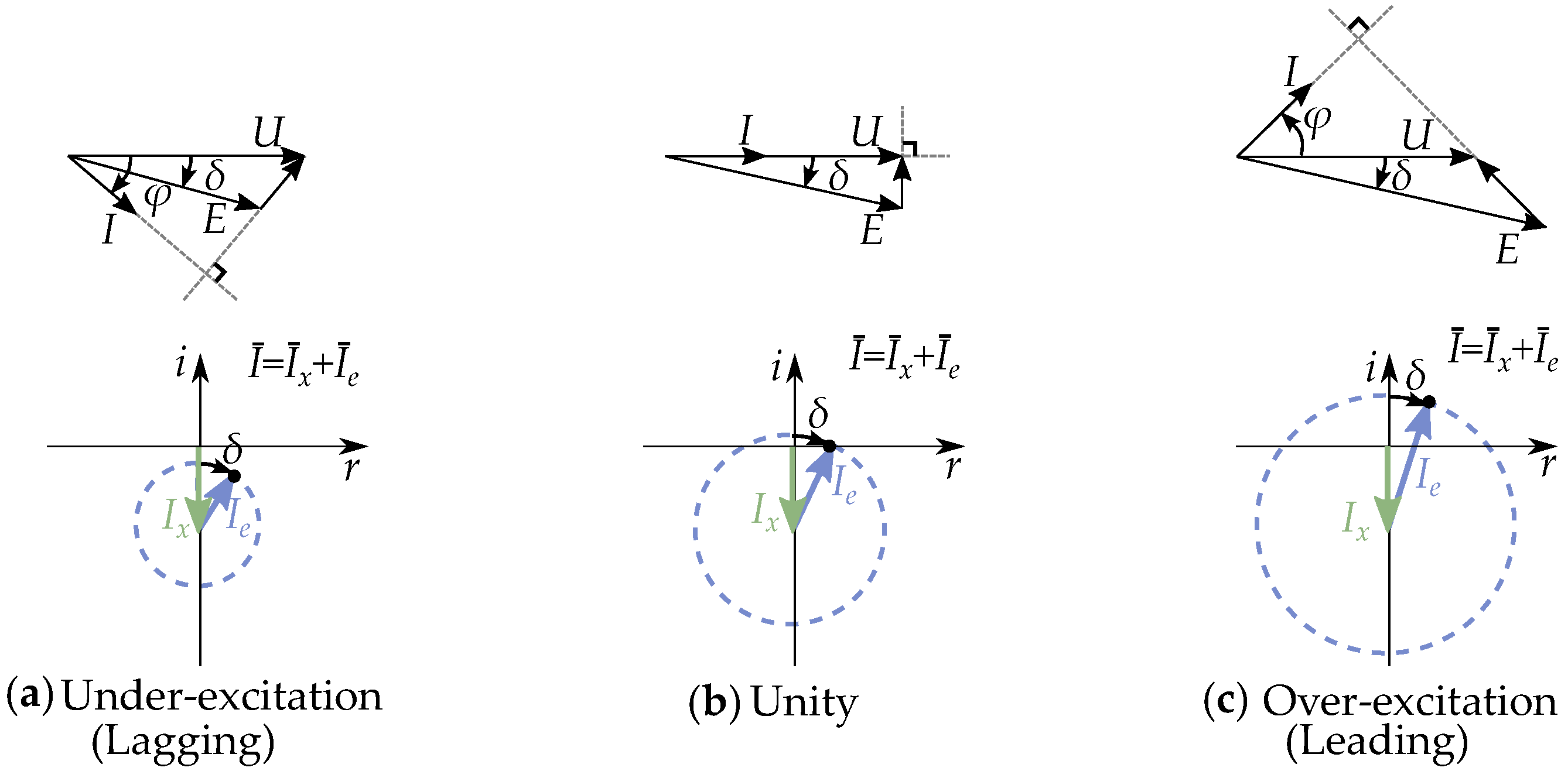
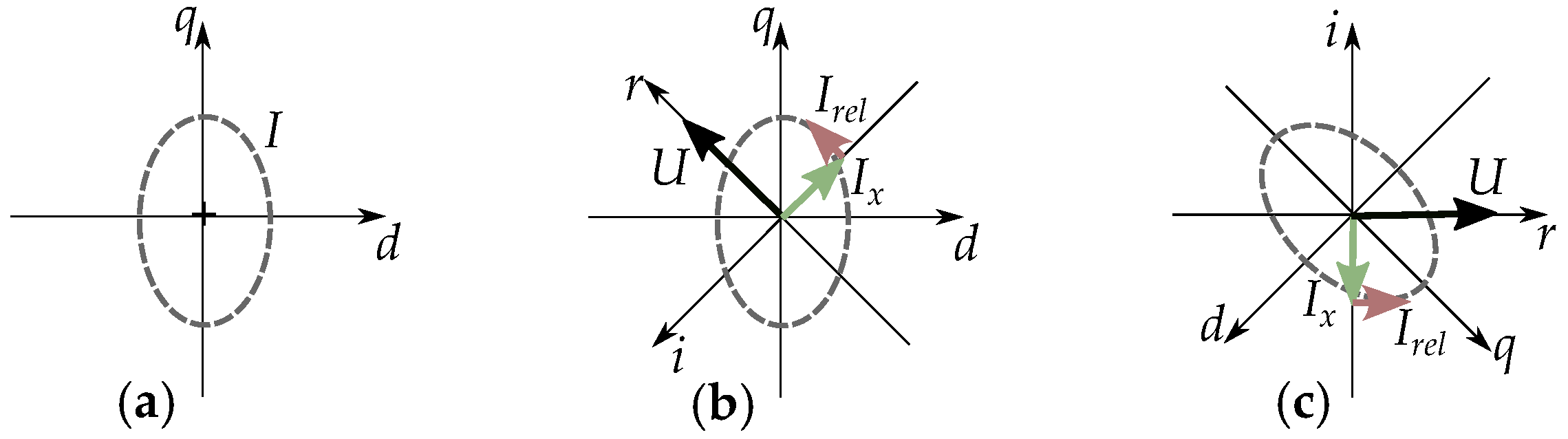
2.3. Phasor Interpretation of Vector Model
2.4. Power Flow in -Frame
2.5. Matrix Representation of Phasor Models
2.6. Voltage Reference Frame
3. Reactance Written in Two Parts
Alternative Adoption for Salient Pole Synchronous Machines
4. Reluctance Models
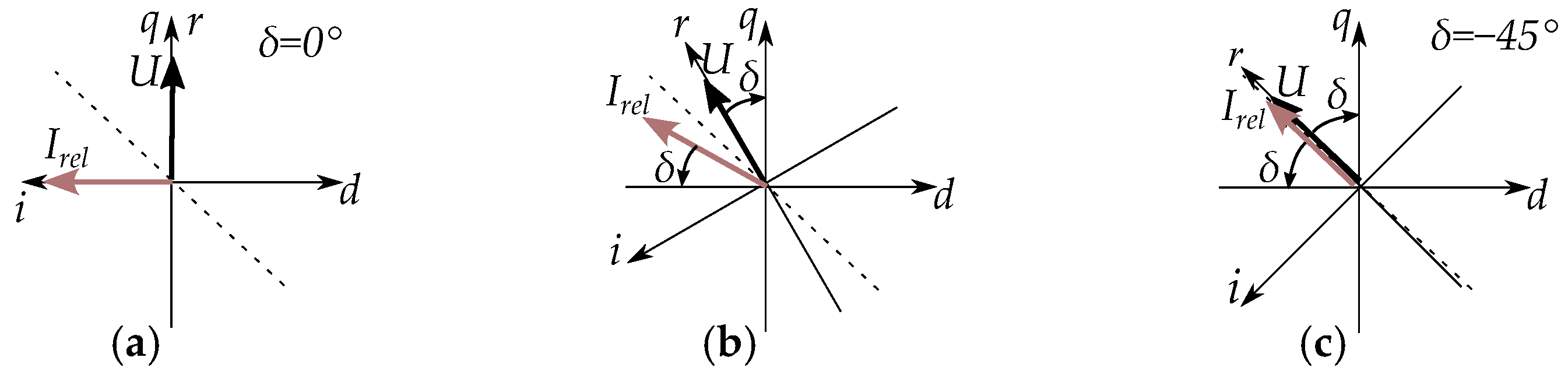
4.1. Three-Phase Reluctance Model
4.2. Inverse Expression of Reactances
4.3. Simplified One-Phase Equivalent
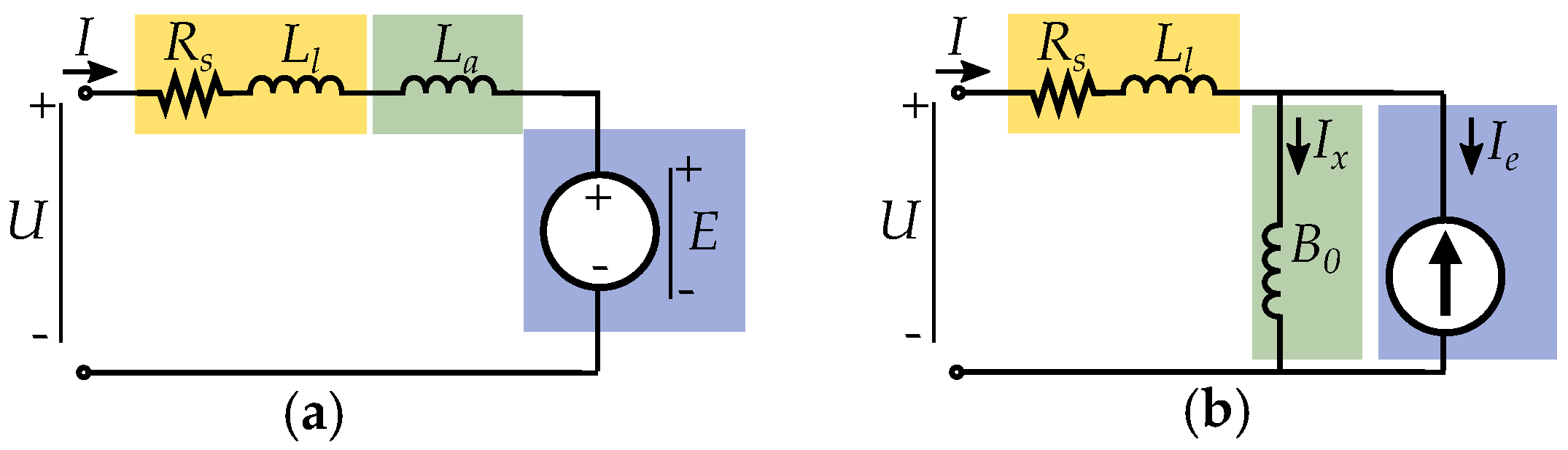
5. Current Equivalent Models
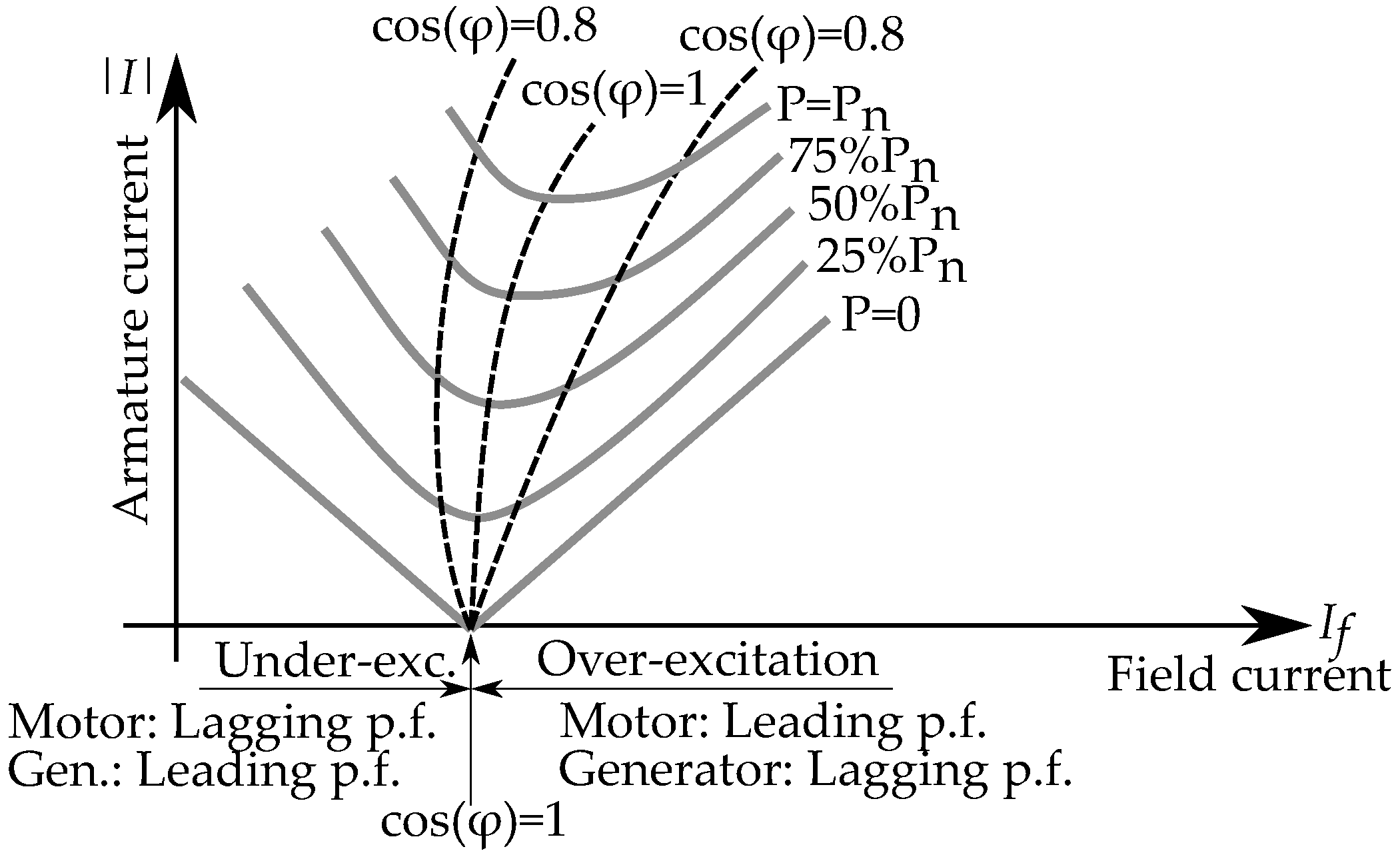
5.1. Field Weakening
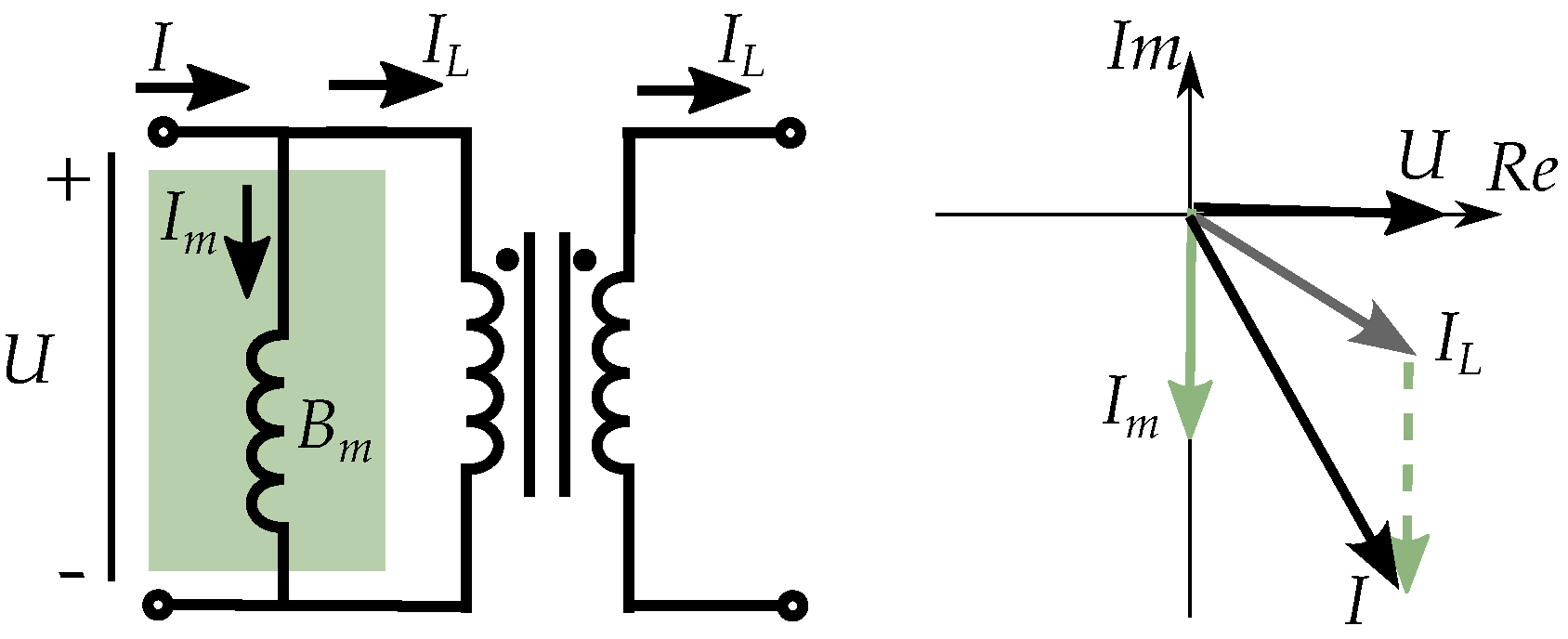
5.2. Comparison to Transformer Models
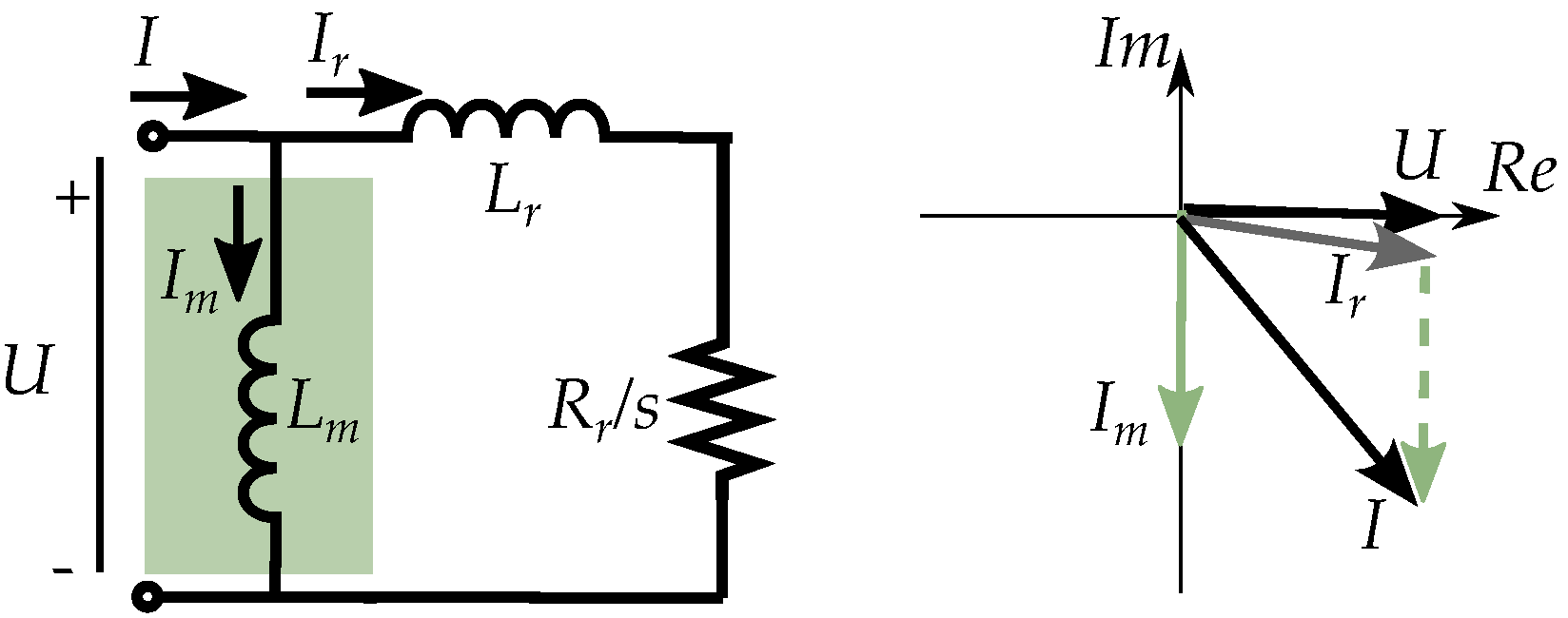
5.3. Comparison to Induction Motor Models
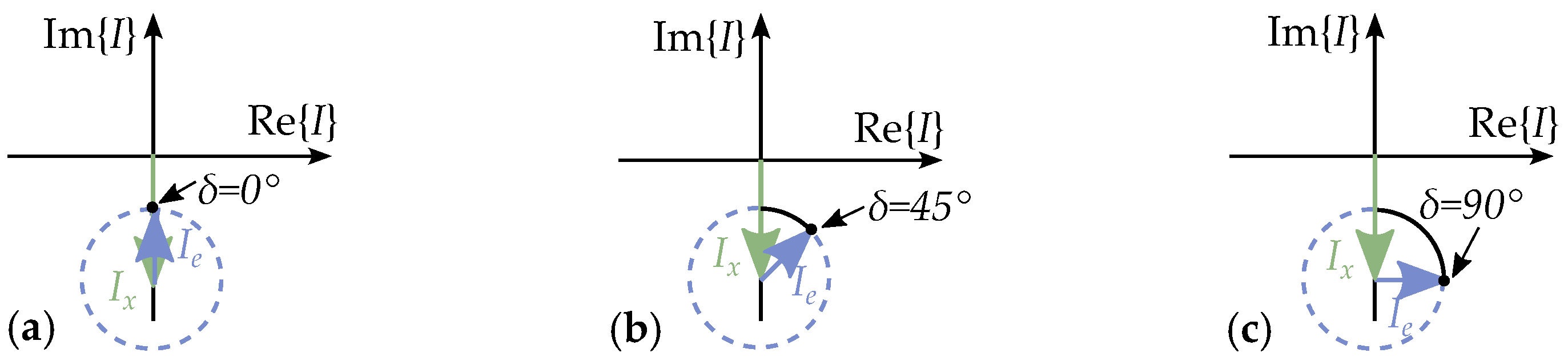
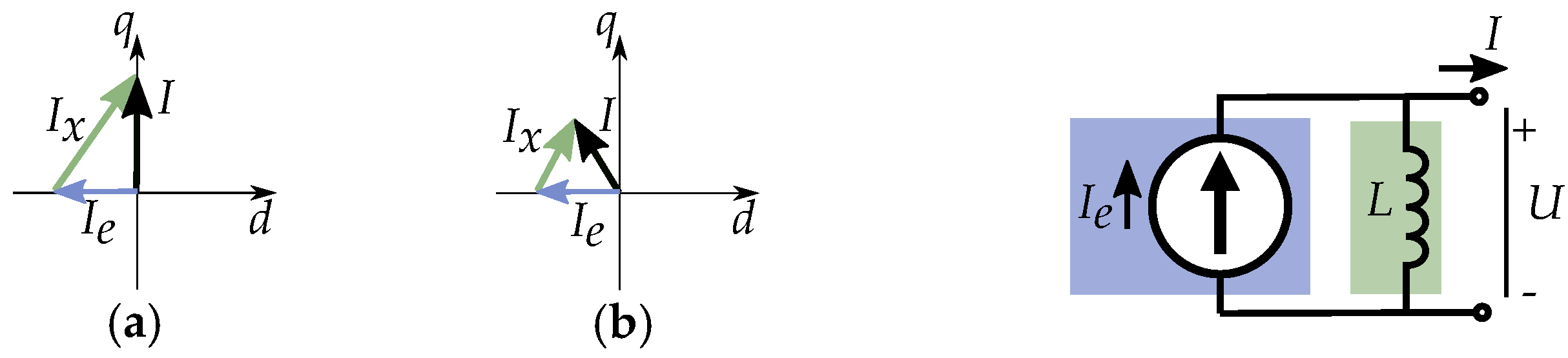
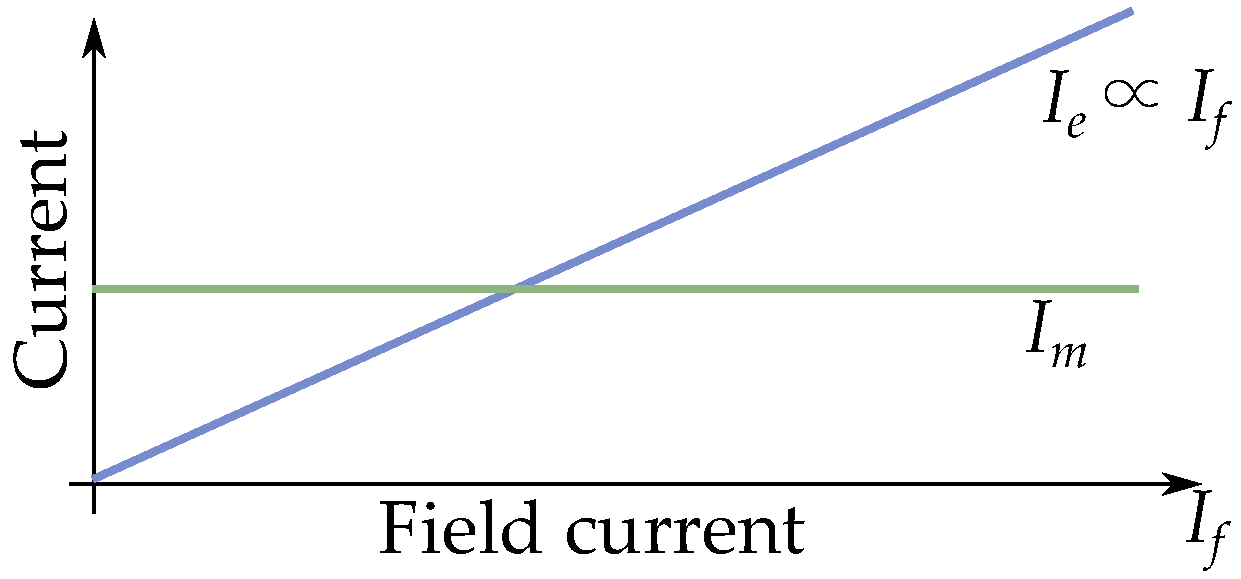
5.4. Equivalent Excitation Current
5.5. Current Equivalent of Permanent Magnets
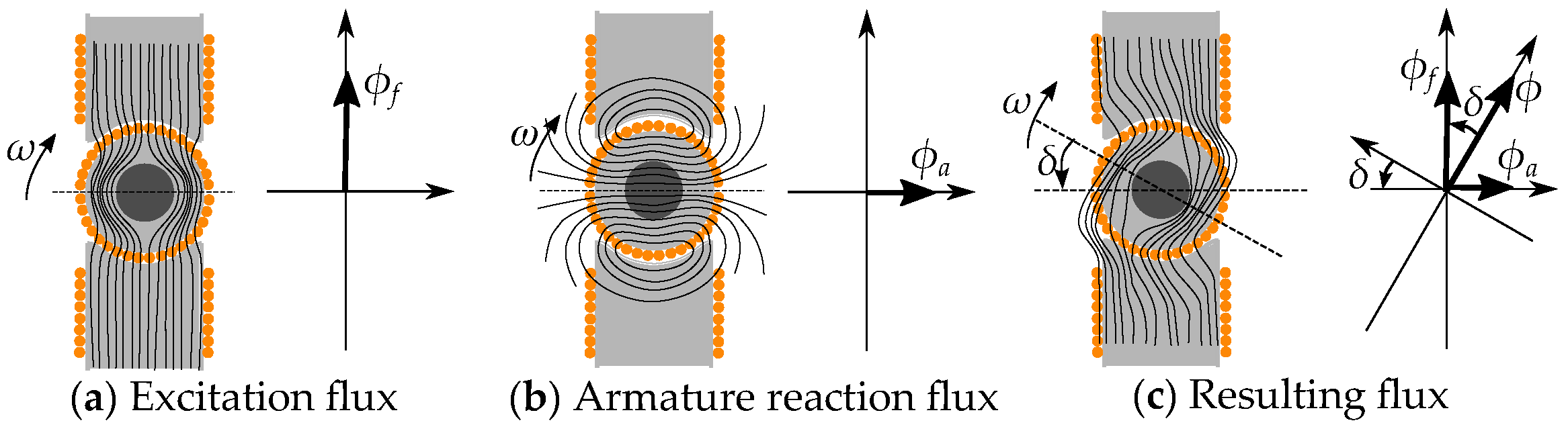
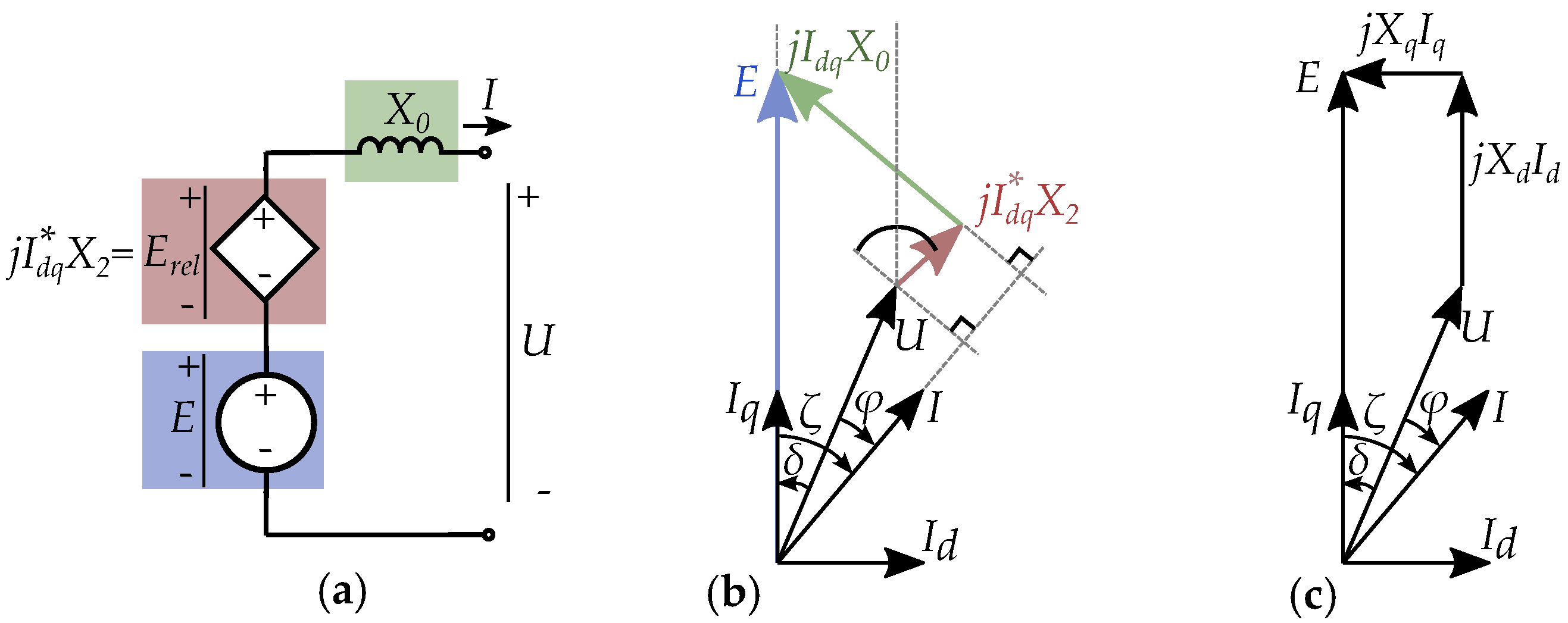
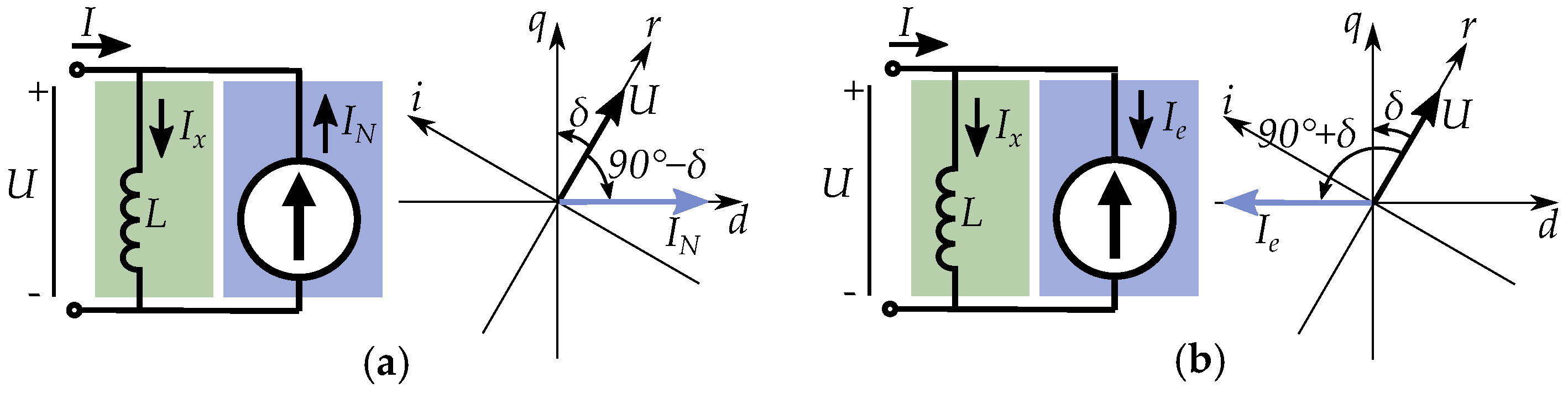
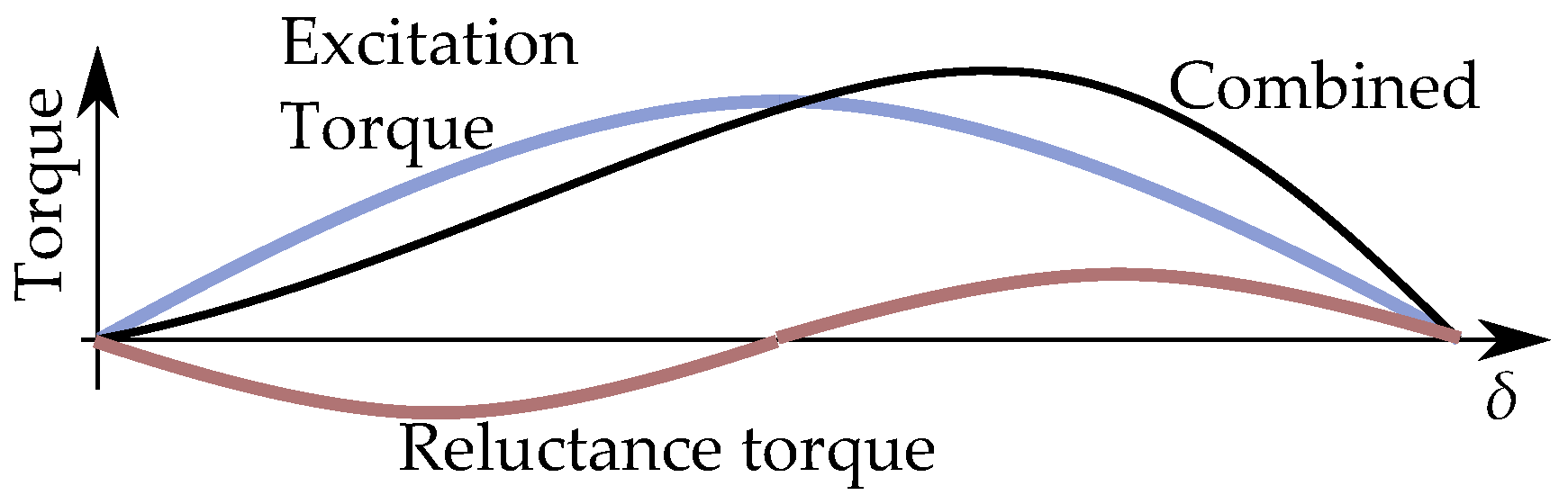
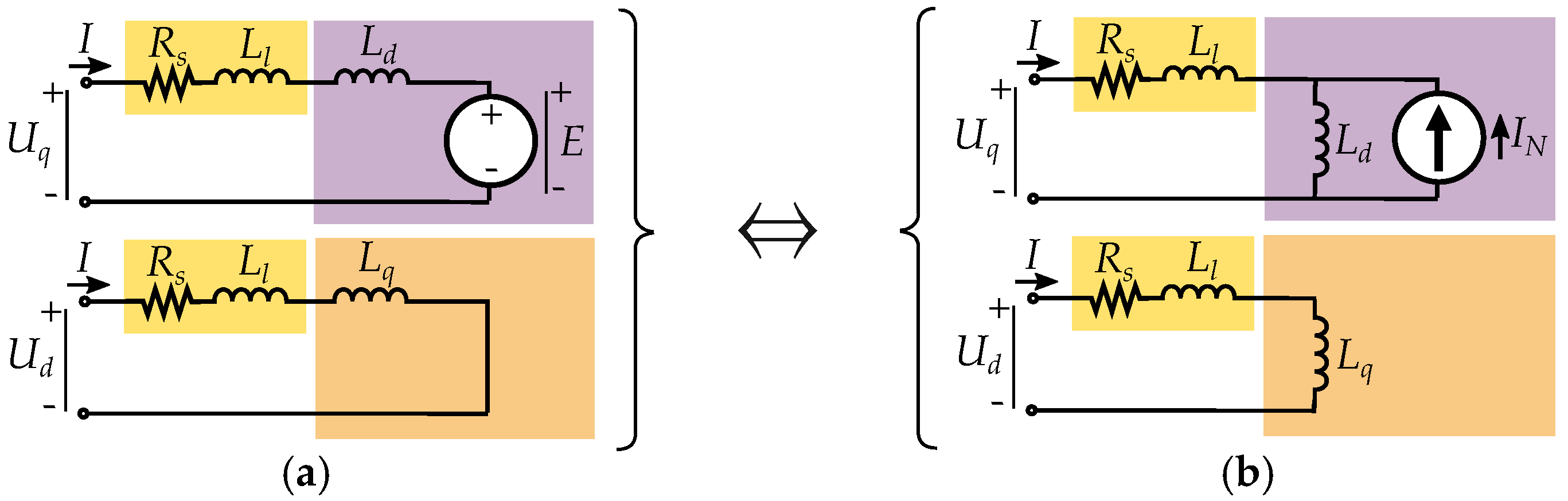
6. Salient Pole Machine Modeling
Current-Equivalent Model for Salient Pole Machines
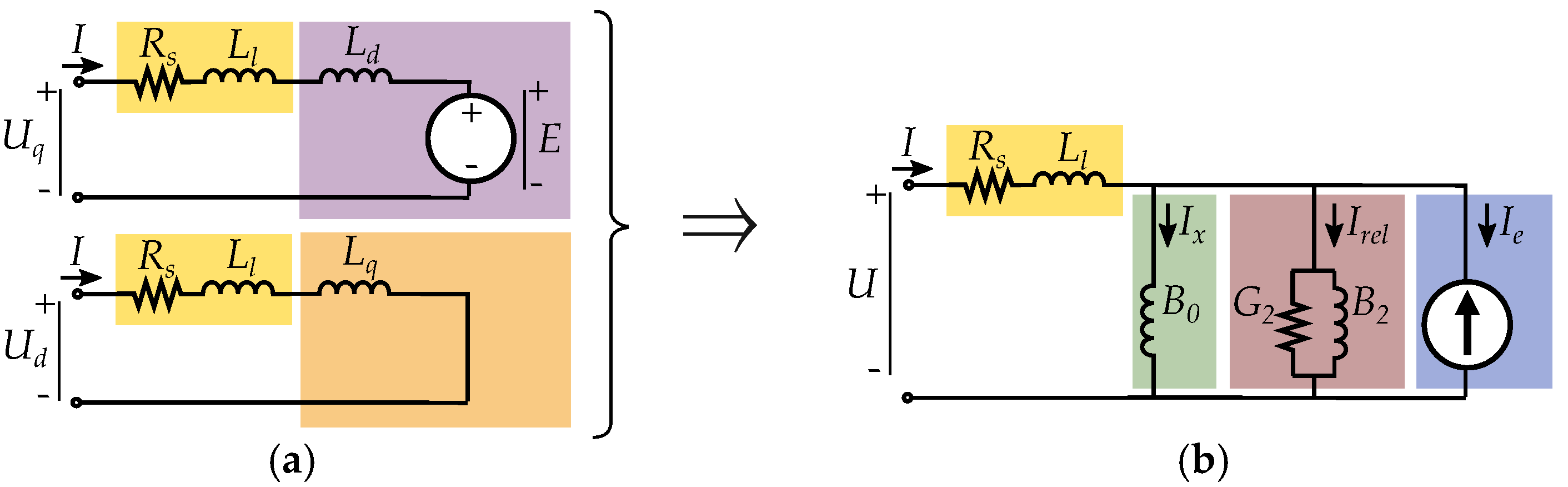
7. Reluctance Machine Model
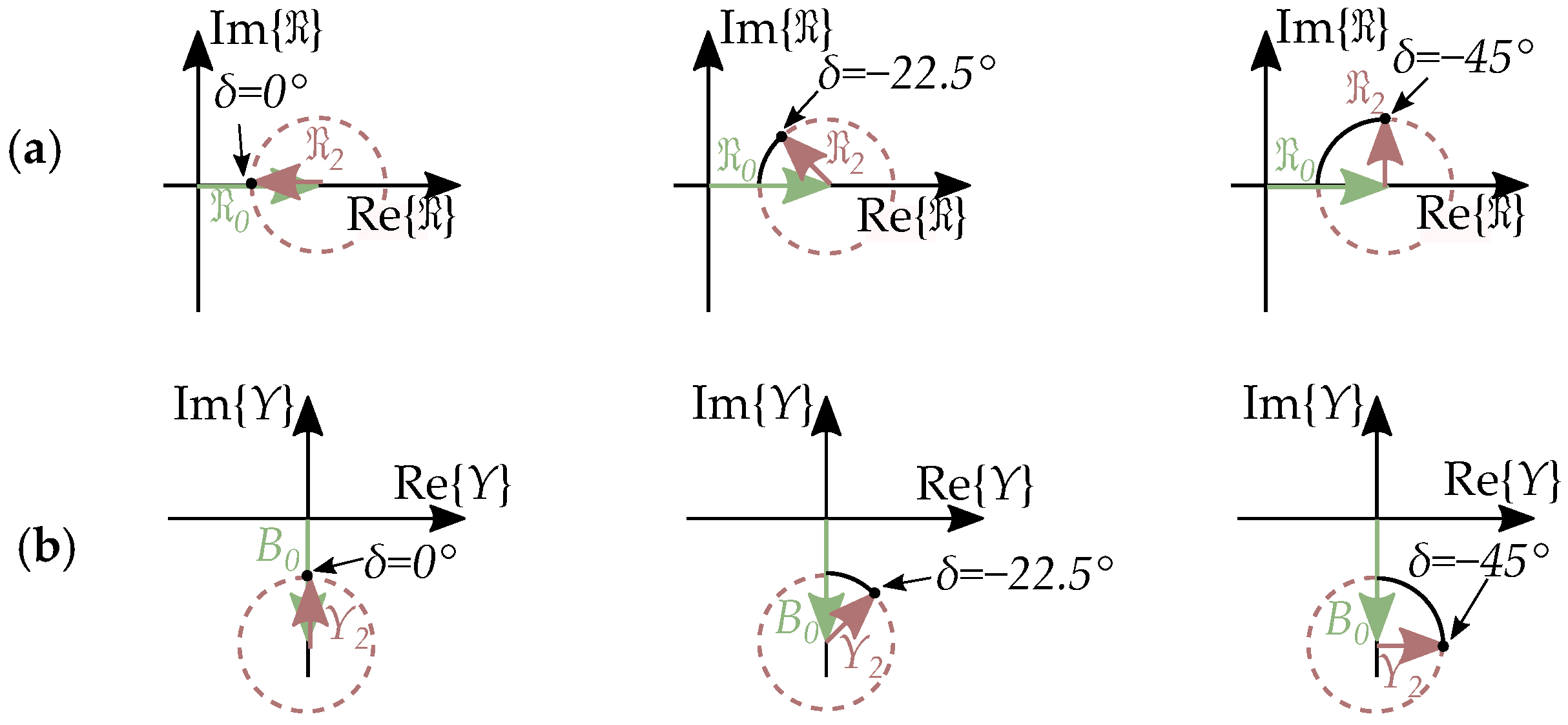
7.1. The Complex Saliency Susceptance Model
7.2. Imaginary Reluctance Compared to Resistance
7.3. Comparison to Hysteresis Models
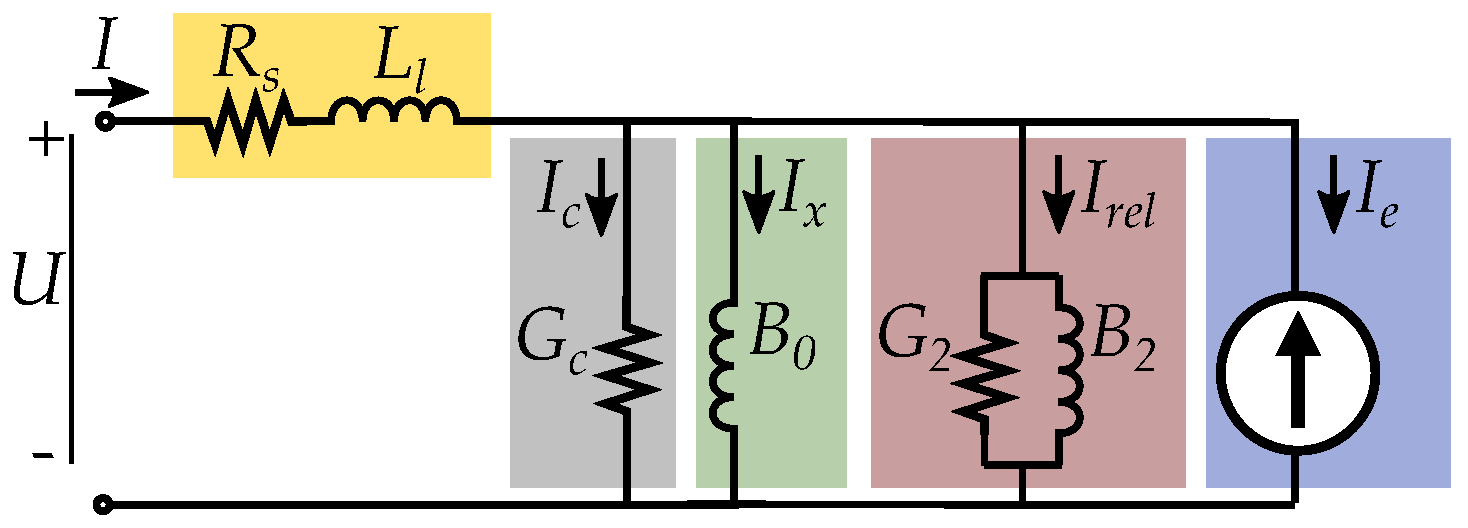
8. Extended Circuit Model
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blondel, A.E. Synchronous Motors and Converters: Theory and Methods of Calculation and Testing; McGraw-Hill: New York, NY, USA, 1913. [Google Scholar]
- Park, R.H.; Robertson, B.L. The Reactances of Synchronous Machines. Trans. Am. Inst. Electr. Eng. 1928, 47, 514–535. [Google Scholar] [CrossRef]
- Park, R.H. Two-reaction theory of synchronous machines generalized method of analysis-part I. Trans. Am. Inst. Electr. Eng. 1929, 48, 716–727. [Google Scholar] [CrossRef]
- Park, R.H. Two-reaction theory of synchronous machines-II. Trans. Am. Inst. Electr. Eng. 1933, 52, 352–354. [Google Scholar] [CrossRef]
- Ahmed-Zaid, S.; Mohammadi, D.; Oteafy, A.M.A. A new equivalent circuit of a salient-pole synchronous machine and its phasor interpretation. In Proceedings of the 2015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Ahmed-Zaid, S.; Oteafy, A.M.A. A New Interpretation of the Steady-State Two-Reaction Theory of a Salient-Pole Synchronous Machine. IEEE Access 2022, 10, 128187–128194. [Google Scholar] [CrossRef]
- Ibrahim, M.; Pillay, P. Aligning the Reluctance and Magnet Torque in Permanent Magnet Synchronous Motors for Improved Performance. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 2286–2291. [Google Scholar] [CrossRef]
- Zhao, X.; Kou, B.; Huang, C.; Zhang, L. Optimization Design and Performance Analysis of a Reverse-Salient Permanent Magnet Synchronous Motor. Machines 2022, 10, 204. [Google Scholar] [CrossRef]
- Liu, F.; Quan, L.; Zhu, X.; Ge, L.; Wu, W. Reverse Saliency Optimization of Flux-Intensifying Hybrid Permanent Magnet Machine for Variable Speed Applications. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Kashif, M.; Singh, B.; Modi, M.; Dudharejiya, D.; Jain, C. Analysis of Reverse-Saliency PMSM with Multiple Flux-Barriers for SWPS. In Proceedings of the 2020 International Conference on Power, Instrumentation, Control and Computing (PICC), Thrissur, India, 17–19 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Morimoto, S. Trend of permanent magnet synchronous machines. IEEJ Trans. Electr. Electron. Eng. 2007, 2, 101–108. [Google Scholar] [CrossRef]
- Tawfiq, K.B.; Ibrahim, M.N.; El-Kholy, E.E.; Sergeant, P. Performance Improvement of Synchronous Reluctance Machines—A Review Research. IEEE Trans. Magn. 2021, 57, 1–11. [Google Scholar] [CrossRef]
- Boglietti, A.; Pastorelli, M. Induction and synchronous reluctance motors comparison. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; pp. 2041–2044. [Google Scholar] [CrossRef]
- de Pancorbo, S.M.; Ugalde, G.; Poza, J.; Egea, A. Comparative study between induction motor and Synchronous Reluctance Motor for electrical railway traction applications. In Proceedings of the 2015 5th International Electric Drives Production Conference (EDPC), Nuremberg, Germany, 15–16 September 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Ban, B.; Stipetić, S.; Klanac, M. Synchronous Reluctance Machines: Theory, Design and the Potential Use in Traction Applications. In Proceedings of the 2019 International Conference on Electrical Drives & Power Electronics (EDPE), The High Tatras, Slovakia, 24–26 September 2019; pp. 177–188. [Google Scholar] [CrossRef]
- Murataliyev, M.; Degano, M.; Di Nardo, M.; Bianchi, N.; Gerada, C. Synchronous Reluctance Machines: A Comprehensive Review and Technology Comparison. Proc. IEEE 2022, 110, 382–399. [Google Scholar] [CrossRef]
- Hoffer, A.E.; Moncada, R.H.; Pavez, B.J.; Tapia, J.A.; Laurila, L. A high efficiency control strategy for synchronous reluctance generator including saturation. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 39–45. [Google Scholar] [CrossRef]
- Huynh, T.A.; Hsieh, M.F. Comparative Study of PM-Assisted SynRM and IPMSM on Constant Power Speed Range for EV Applications. IEEE Trans. Magn. 2017, 53, 1–6. [Google Scholar] [CrossRef]
- Ngo, D.K.; Hsieh, M.F.; Huynh, T.A. Torque Enhancement for a Novel Flux Intensifying PMa-SynRM Using Surface-Inset Permanent Magnet. IEEE Trans. Magn. 2019, 55, 1–8. [Google Scholar] [CrossRef]
- Hsieh, M.F.; Ngo, D.K.; Thao, N.G.M. Flux Intensifying Feature of Permanent Magnet Assisted Synchronous Reluctance Motor with High Torque Density. Electronics 2022, 11, 397. [Google Scholar] [CrossRef]
- Wang, Y.; Bianchi, N.; Qu, R. Comparative Study of Non-Rare-Earth and Rare-Earth PM Motors for EV Applications. Energies 2022, 15, 2711. [Google Scholar] [CrossRef]
- Xie, Y.; Shao, J.; He, S.; Ye, B.; Yang, F.; Wang, L. Novel PM-Assisted Synchronous Reluctance Machines Using Asymmetrical Rotor Configuration. IEEE Access 2022, 10, 79564–79573. [Google Scholar] [CrossRef]
- Bianchi, N. Synchronous reluctance and interior permanent magnet motors. In Proceedings of the 2013 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Paris, France, 11–12 March 2013; pp. 75–84. [Google Scholar] [CrossRef]
- Johnson, D. Origins of the equivalent circuit concept: The current-source equivalent. Proc. IEEE 2003, 91, 817–821. [Google Scholar] [CrossRef]
- Johnson, D. Origins of the equivalent circuit concept: The voltage-source equivalent. Proc. IEEE 2003, 91, 636–640. [Google Scholar] [CrossRef]
- Brittain, J. Thevenin’s theorem. IEEE Spectr. 1990, 27, 42. [Google Scholar] [CrossRef]
- Anttila, S.; Döhler, J.S.; Oliveira, J.G.; Boström, C. Grid Forming Inverters: A Review of the State of the Art of Key Elements for Microgrid Operation. Energies 2022, 15, 5517. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Doherty, R.E.; Shirley, O.E. Reactance of Synchronous Machines and its Applications. Trans. Am. Inst. Electr. Eng. 1918, XXXVII, 1209–1340. [Google Scholar] [CrossRef]
- Doherty, R.E.; Nickle, C.A. Synchronous machines I-an extension of blondel’s two-reaction theory. Trans. Am. Inst. Electr. Eng. 1926, XLV, 912–947. [Google Scholar] [CrossRef]
- Doherty, R.E.; Nickle, C.A. Synchronous Machines-III Torque-Angle Characteristics Under Transient Conditions. Trans. Am. Inst. Electr. Eng. 1927, XLVI, 1–18. [Google Scholar] [CrossRef]
- Doherty, R.E.; Nickle, C.A. Synchronous Machines-IV. Trans. Am. Inst. Electr. Eng. 1928, 47, 457–487. [Google Scholar] [CrossRef]
- Clarke, E.; Weygandt, C.N.; Concordia, C. Overvoltages caused by unbalanced short circuits: Effect of amortisseur windings. Electr. Eng. 1938, 57, 453–468. [Google Scholar] [CrossRef]
- Park, R.H.; Skeats, W.F. Circuit Breaker Recovery Voltages Magnitudes and Rates of Rise. Trans. Am. Inst. Electr. Eng. 1931, 50, 204–238. [Google Scholar] [CrossRef]
- Kimbark, E.W. Two-phase co-ordinates of a three-phase circuit. Electr. Eng. 1939, 58, 894–910. [Google Scholar] [CrossRef]
- Duesterhoeft, W.C.; Schulz, M.W.; Clarke, E. Determination of Instantaneous Currents and Voltages by Means of Alpha, Beta, and Zero Components. Trans. Am. Inst. Electr. Eng. 1951, 70, 1248–1255. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Mitra, M.; Sengupta, S. Clarke and Park Transform. In Electric Power Quality; Springer: Dordrecht, The Netherlands, 2011; pp. 89–96. [Google Scholar] [CrossRef]
- O’Rourke, C.J.; Qasim, M.M.; Overlin, M.R.; Kirtley, J.L. A Geometric Interpretation of Reference Frames and Transformations: dq0, Clarke, and Park. IEEE Trans. Energy Convers. 2019, 34, 2070–2083. [Google Scholar] [CrossRef]
- Ilyasov, R.I. The Phasor Diagram of a Superconducting Synchronous Electrical Machine. Inventions 2023, 8, 68. [Google Scholar] [CrossRef]
- Madnani, R.; Mishra, M.K. A visual understanding of electrical transformations and generalized abc to αβ0 and dq0 transformation. Int. J. Circuit Theory Appl. 2023, 51, 963–978. [Google Scholar] [CrossRef]
- Fortescue, C.L. Method of Symmetrical Co-Ordinates Applied to the Solution of Polyphase Networks. Trans. Am. Inst. Electr. Eng. 1918, XXXVII, 1027–1140. [Google Scholar] [CrossRef]
- Fortescue, C.L. Method of symmetrical co-ordinates applied to the solution of polyphase networks. Proc. Am. Inst. Electr. Eng. 1918, 37, 629–716. [Google Scholar] [CrossRef]
- Nee, H.P.; Lefevre, L.; Thelin, P.; Soulard, J. Determination of d and q reactances of permanent-magnet synchronous motors without measurements of the rotor position. IEEE Trans. Ind. Appl. 2000, 36, 1330–1335. [Google Scholar] [CrossRef]
- Rallabandi, V.; Taran, N.; Ionel, D.M.; Zhou, P. Inductance Testing for IPM Synchronous Machines According to the New IEEE Std 1812 and Typical Laboratory Practices. IEEE Trans. Ind. Appl. 2019, 55, 2649–2659. [Google Scholar] [CrossRef]
- IEEE Std 115-2019 (Revision of IEEE Std 115-2009); IEEE Guide for Test Procedures for Synchronous Machines Including Acceptance and Performance Testing and Parameter Determination for Dynamic Analysis. IEEE: Piscataway, NJ, USA, 2020; pp. 1–246. [CrossRef]
- Gao, Y.; Qu, R.; Li, D. Improved hybrid method to calculate inductances of permanent magnet synchronous machines with skewed stators based on winding function theory. Chin. J. Electr. Eng. 2016, 2, 52–61. [Google Scholar] [CrossRef]
- Kim, S.H. Chapter 3—Alternating current motors: Synchronous motor and induction motor. In Electric Motor Control: DC, AC and BLDC Motors; Kim, S.H., Ed.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 95–152. [Google Scholar] [CrossRef]
- Ichikawa, O. 12—Synchronous reluctance bearingless motors. In Magnetic Bearings and Bearingless Drives; Chiba, A., Fukao, T., Ichikawa, O., Oshima, M., Takemoto, M., Dorrell, D.G., Eds.; Newnes: Oxford, UK, 2005; pp. 238–250. [Google Scholar] [CrossRef]
- Vo-Duy, T.; Ta, M.C. Fundamental design of electric motor control systems. In Encyclopedia of Electrical and Electronic Power Engineering; García, J., Ed.; Elsevier: Oxford, UK, 2023; pp. 428–453. [Google Scholar] [CrossRef]
- Hughes, A.; Drury, B. Chapter 9—Synchronous, permanent magnet and reluctance motors and drives. In Electric Motors and Drives, 5th ed.; Hughes, A., Drury, B., Eds.; Newnes: London, UK, 2019; pp. 307–373. [Google Scholar] [CrossRef]
- Murty, P. Chapter 8—Synchronous Machine. In Power Systems Analysis, 2nd ed.; Murty, P., Ed.; Butterworth-Heinemann: Boston, MA, USA, 2017; pp. 149–174. [Google Scholar] [CrossRef]
- Hayes, J.G.; Goodarzi, G.A. Electric Powertrain: Energy Systems, Power Electronics and Drives for Hybrid, Electric and Fuel Cell Vehicles; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Hamill, D. Lumped equivalent circuits of magnetic components: The gyrator-capacitor approach. IEEE Trans. Power Electron. 1993, 8, 97–103. [Google Scholar] [CrossRef]
- Lambert, M.; Mahseredjian, J.; Martínez-Duró, M.; Sirois, F. Magnetic Circuits Within Electric Circuits: Critical Review of Existing Methods and New Mutator Implementations. IEEE Trans. Power Deliv. 2015, 30, 2427–2434. [Google Scholar] [CrossRef]
- Hamilton, N. Ferrites: Magnetic and electric equivalent circuits and the complex permeability spectra. In Proceedings of the Active and Passive RF Devices Seminar, London, UK, 17 February 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Rahman, M.; Little, T.; Slemon, G. Analytical models for interior-type permanent magnet synchronous motors. IEEE Trans. Magn. 1985, 21, 1741–1743. [Google Scholar] [CrossRef]
- Sebastian, T.; Slemon, G.; Rahman, M. Modelling of permanent magnet synchronous motors. IEEE Trans. Magn. 1986, 22, 1069–1071. [Google Scholar] [CrossRef]
- Rahman, M. Analytical models for exterior-type permanent magnet synchronous motors. IEEE Trans. Magn. 1987, 23, 3625–3627. [Google Scholar] [CrossRef]
- Slemon, G.R. Analytical Models for Saturated Synchronous Machines. IEEE Trans. Power Appar. Syst. 1971, PAS-90, 409–417. [Google Scholar] [CrossRef]
- Fasil, M.; Antaloae, C.; Mijatovic, N.; Jensen, B.B.; Holboll, J. Improved dq-Axes Model of PMSM Considering Airgap Flux Harmonics and Saturation. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Nakamura, K.; Saito, K.; Watanabe, T.; Ichinokura, O. A new nonlinear magnetic circuit model for dynamic analysis of interior permanent magnet synchronous motor. J. Magn. Magn. Mater. 2005, 290–291, 1313–1317. [Google Scholar] [CrossRef]
- Chiba, A. 7—Analysis in rotational coordinates and magnetic suspension strategy for bearingless drives with 2-pole and 4-pole windings. In Magnetic Bearings and Bearingless Drives; Chiba, A., Fukao, T., Ichikawa, O., Oshima, M., Takemoto, M., Dorrell, D.G., Eds.; Newnes: Oxford, UK, 2005; pp. 159–183. [Google Scholar] [CrossRef]
- Gabriel, F.; De Belie, F.; Druyts, P.; Neyt, X.; Melkebeek, J.; Acheroy, M. Compensating the influence of the stator resistor and inverter nonlinearities in signal-injection based sensorless strategies. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 283–290. [Google Scholar] [CrossRef]
- Eilenberger, A.; Schroedl, M.; Heissenberger, J. Comparison of outer rotor PMSM with single- and double-layer windings at same machine geometry with respect to the sensorless control capability. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–7. [Google Scholar]
- Schroedl, M. Sensorless control of AC machines at low speed and standstill based on the "INFORM" method. In Proceedings of the IAS ’96. Conference Record of the 1996 IEEE Industry Applications Conference Thirty-First IAS Annual Meeting, San Diego, CA, USA, 6–10 October 1996; Volume 1, pp. 270–277. [Google Scholar] [CrossRef]
- De Belie, F.; Melkebeek, J.; Vandevelde, L.; Boel, R.; Geldhof, K.; Vyncke, T. A nonlinear model for synchronous machines to describe high-frequency signal based position estimators. In Proceedings of the IEEE International Conference on Electric Machines and Drives, San Antonio, TX, USA, 15 May 2005; pp. 696–703. [Google Scholar] [CrossRef]
- Mohanarajah, T.; Hellany, A.; Rizk, J.; Nagrial, M. Analysis and design of high-performance synchronous reluctance machine. In Proceedings of the 2018 IEEE 12th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG 2018), Doha, Qatar, 10–12 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Heidari, H.; Rassõlkin, A.; Kallaste, A.; Vaimann, T.; Andriushchenko, E.; Belahcen, A.; Lukichev, D.V. A Review of Synchronous Reluctance Motor-Drive Advancements. Sustainability 2021, 13, 729. [Google Scholar] [CrossRef]
- Vartanian, R.; Toliyat, H.A.; Akin, B.; Poley, R. Power factor improvement of synchronous reluctance motors (SynRM) using permanent magnets for drive size reduction. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 628–633. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the Law of Hysteresis. Trans. Am. Inst. Electr. Eng. 1892, IX, 1–64. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the Law of Hysteresis (Part II.) and Other Phenomena of the Magnetic Circuit. Trans. Am. Inst. Electr. Eng. 1892, IX, 619–758. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the Law of Hysteresis (Part III.), and the Theory of Ferric Inductances. Trans. Am. Inst. Electr. Eng. 1894, XI, 570–616. [Google Scholar] [CrossRef]
- O’Kelly, D. Flux penetration in a ferromagnetic material including hysteresis and eddy-current effects. J. Phys. D Appl. Phys. 1972, 5, 203. [Google Scholar] [CrossRef]
- Zaher, F. An analytical solution for the field of a hysteresis motor based on complex permeability. IEEE Trans. Energy Convers. 1990, 5, 156–163. [Google Scholar] [CrossRef]
- Tavakoli, H.; Bormann, D.; Ribbenfjärd, D.; Engdahl, G. Comparison of a simple and a detailed model of magnetic hysteresis with measurements on electrical steel. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2009, 28, 700–710. [Google Scholar] [CrossRef]
- Glover, J.D.; Overbye, T.J.; Sarma, M.S. Power System Analysis & Design, 6th ed.; Cengage Learning: Boston, MA, USA, 2017. [Google Scholar]
- Li, S.; Haskew, T.A.; Hong, Y.K. Characteristic study of vector-controlled permanent magnet synchronous motor in electric drive vehicles. In Proceedings of the PES T&D 2012, Orlando, FL, USA, 7–10 May 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Li, Q.; Fan, T.; Wen, X. Characterization of Iron Loss for Integral-Slot Interior Permanent Magnet Synchronous Machine During Flux Weakening. IEEE Trans. Magn. 2017, 53, 1–8. [Google Scholar] [CrossRef]
- Asef, P.; Bargallo, R.; Lapthorn, A. Iron Loss Prediction Using Modified IEM-Formula during the Field Weakening for Permanent Magnet Synchronous Machines. Machines 2017, 5, 30. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Xue, S.; Chu, W.; Feng, J.; Guo, S.; Chen, Z.; Peng, J. Evaluation of Iron Loss Models in Electrical Machines. IEEE Trans. Ind. Appl. 2019, 55, 1461–1472. [Google Scholar] [CrossRef]
- Shutta, Y.; Takahashi, Y.; Fujiwara, K. Behavioral modeling of permanent magnet synchronous motor fed by PWM inverters considering iron losses due to carrier harmonics. Electr. Eng. Jpn. 2020, 210, 37–46. [Google Scholar] [CrossRef]
- Chen, W.; Ma, J.; Huang, X.; Fang, Y. Predicting Iron Losses in Laminated Steel with Given Non-Sinusoidal Waveforms of Flux Density. Energies 2015, 8, 13726–13740. [Google Scholar] [CrossRef]
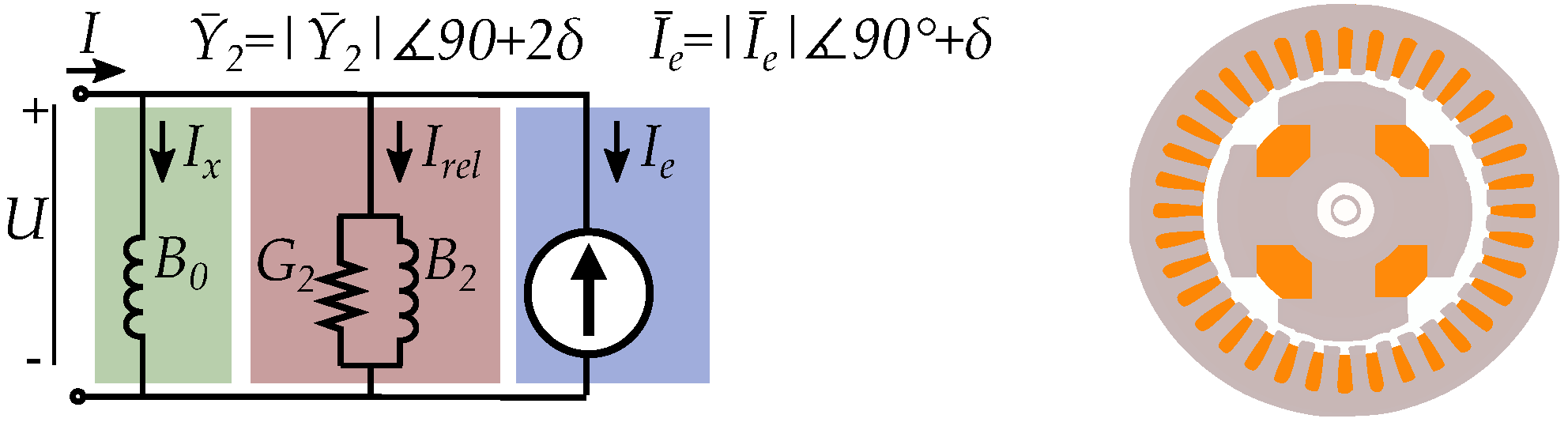

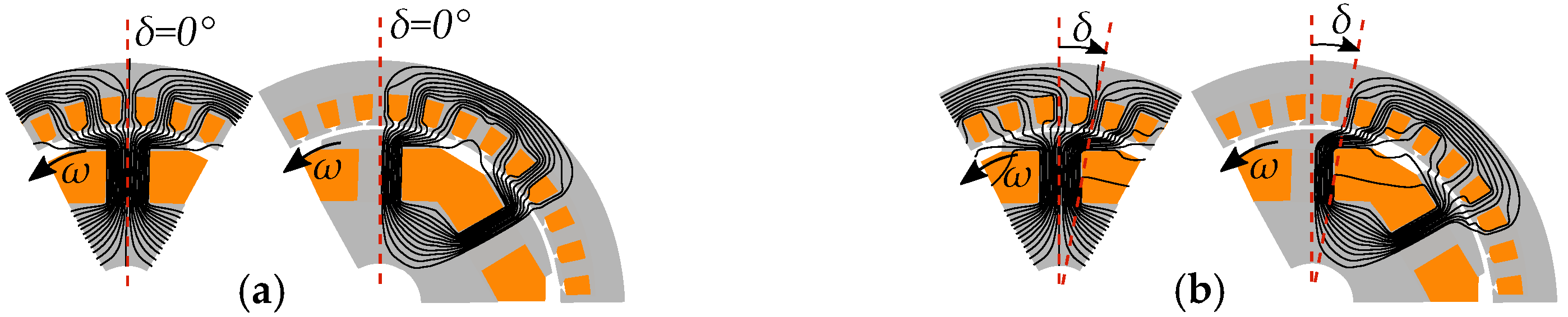



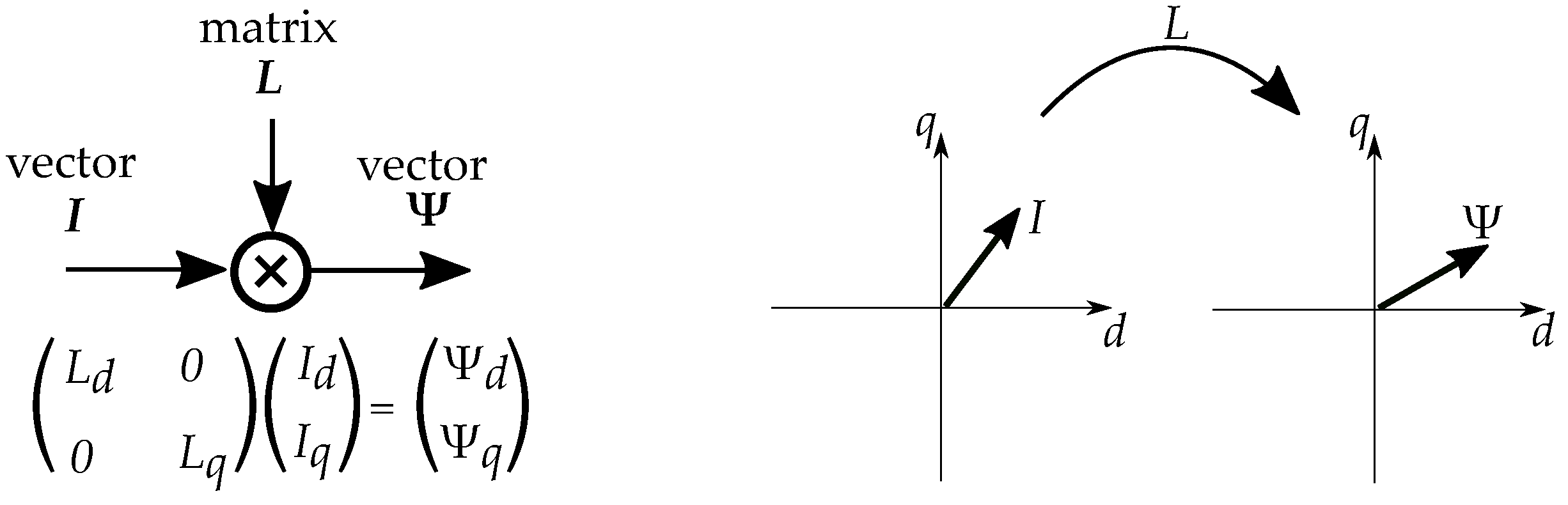

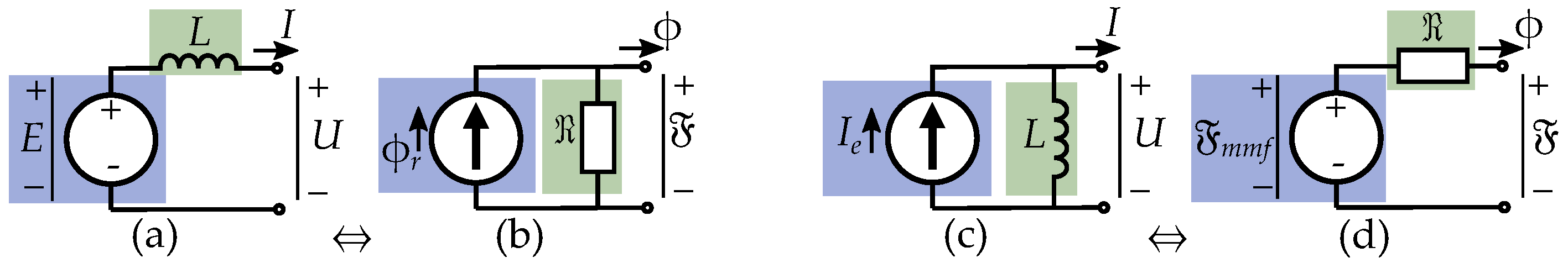
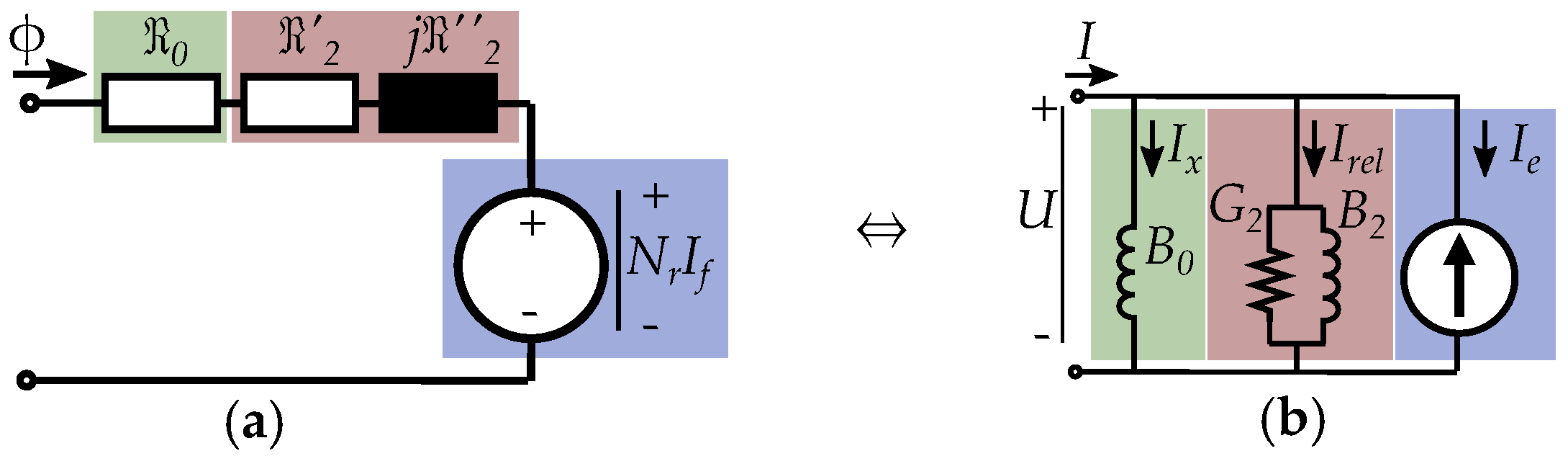
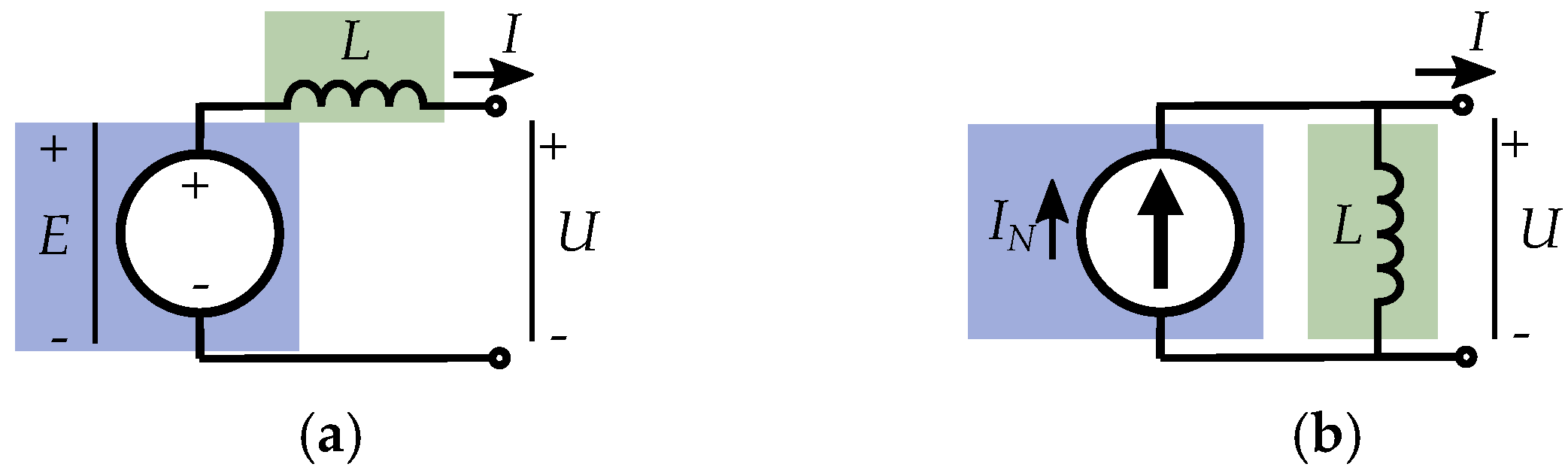


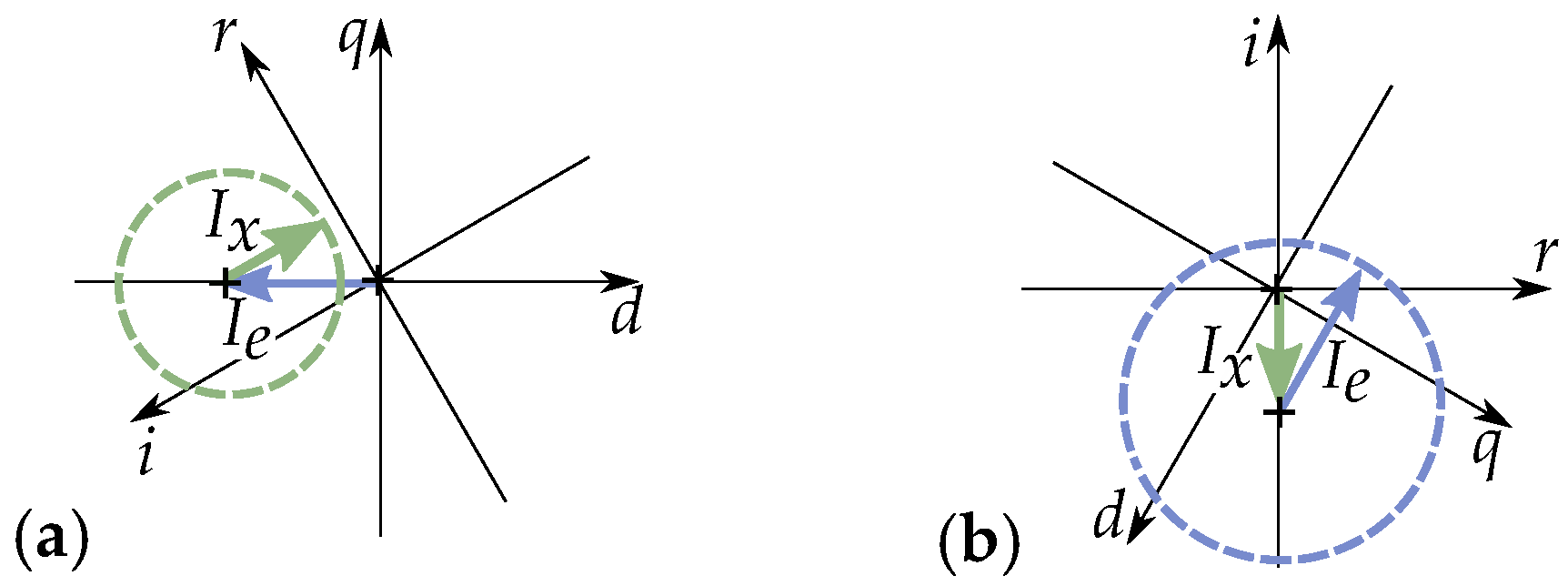
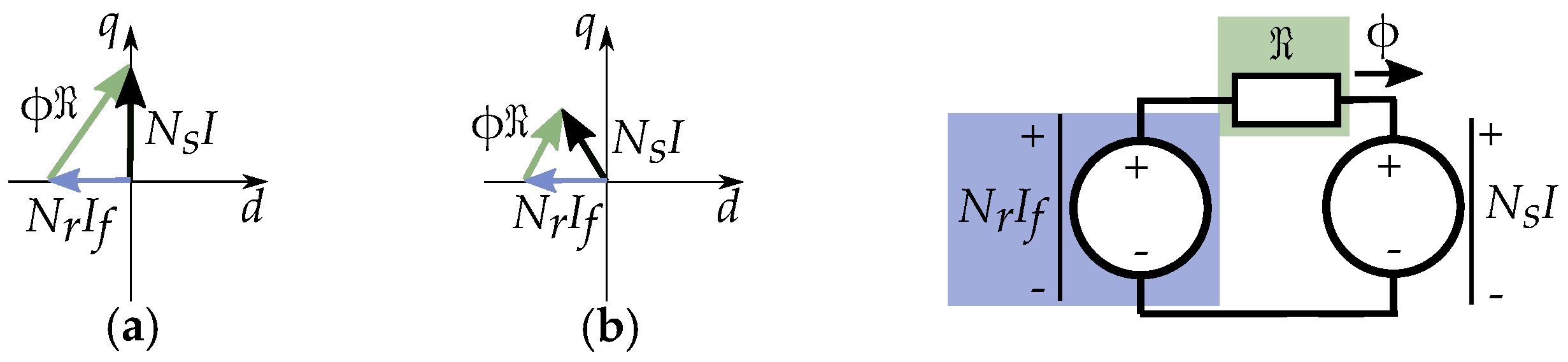
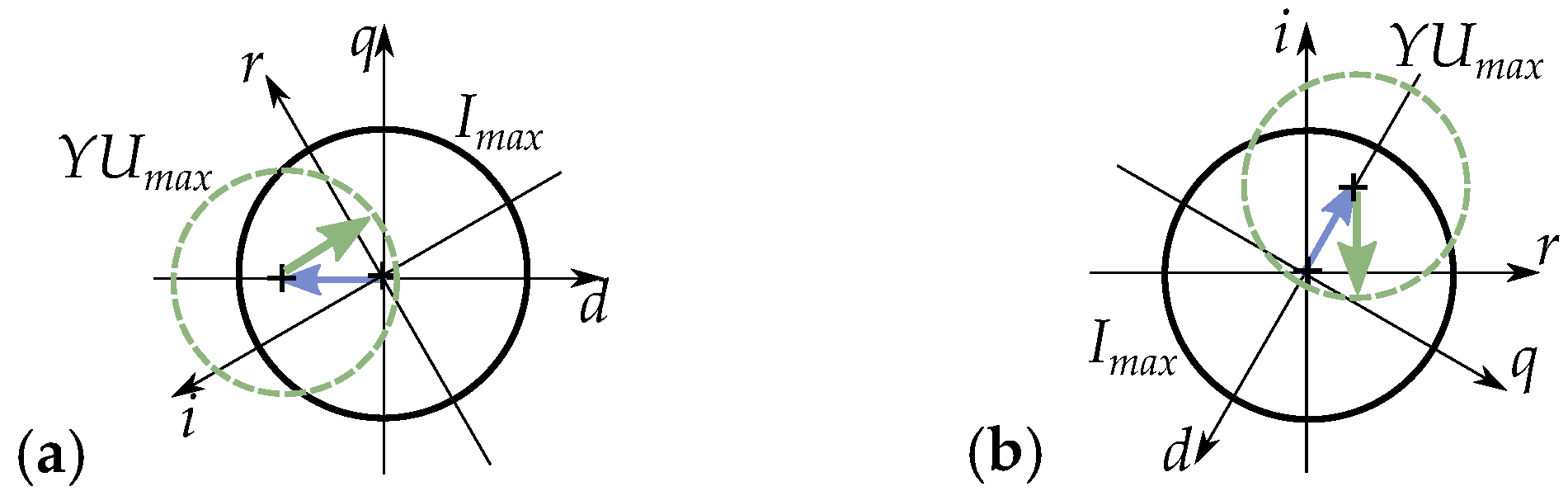




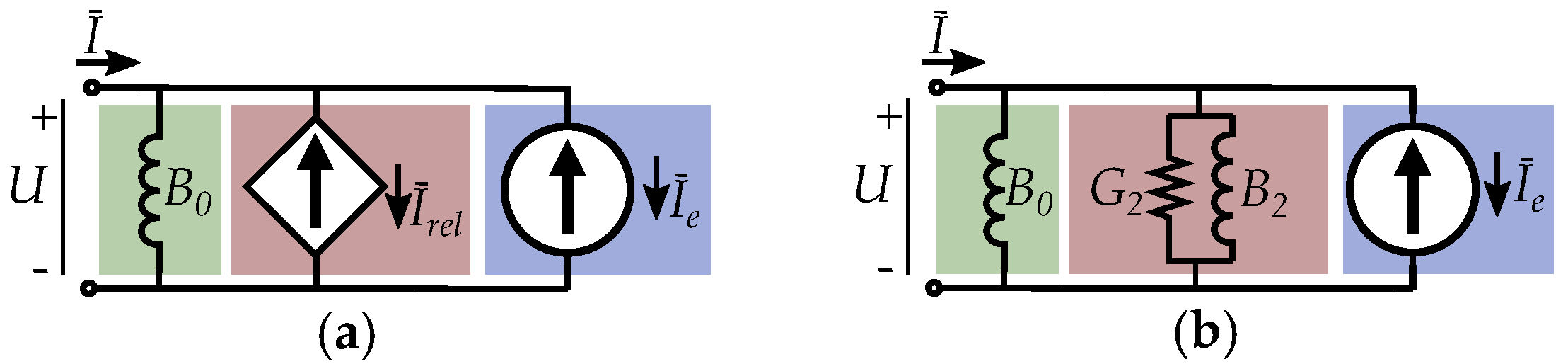
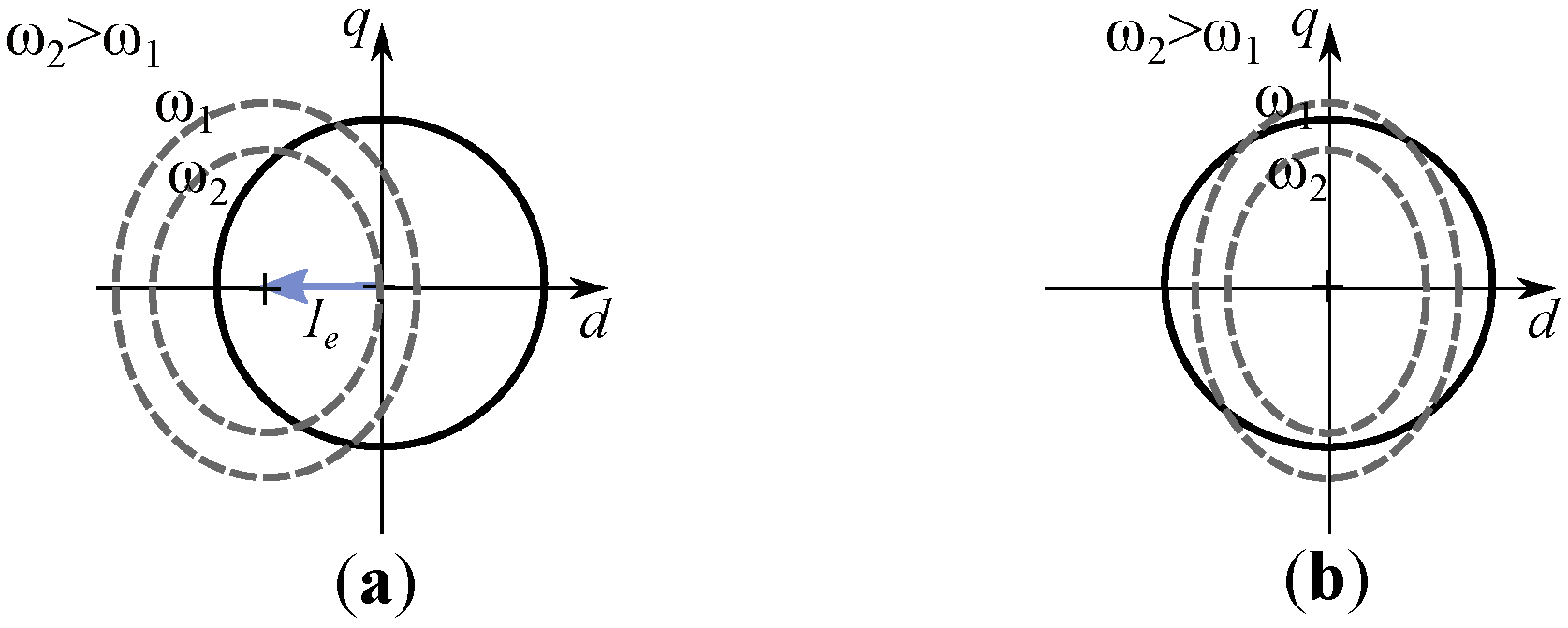


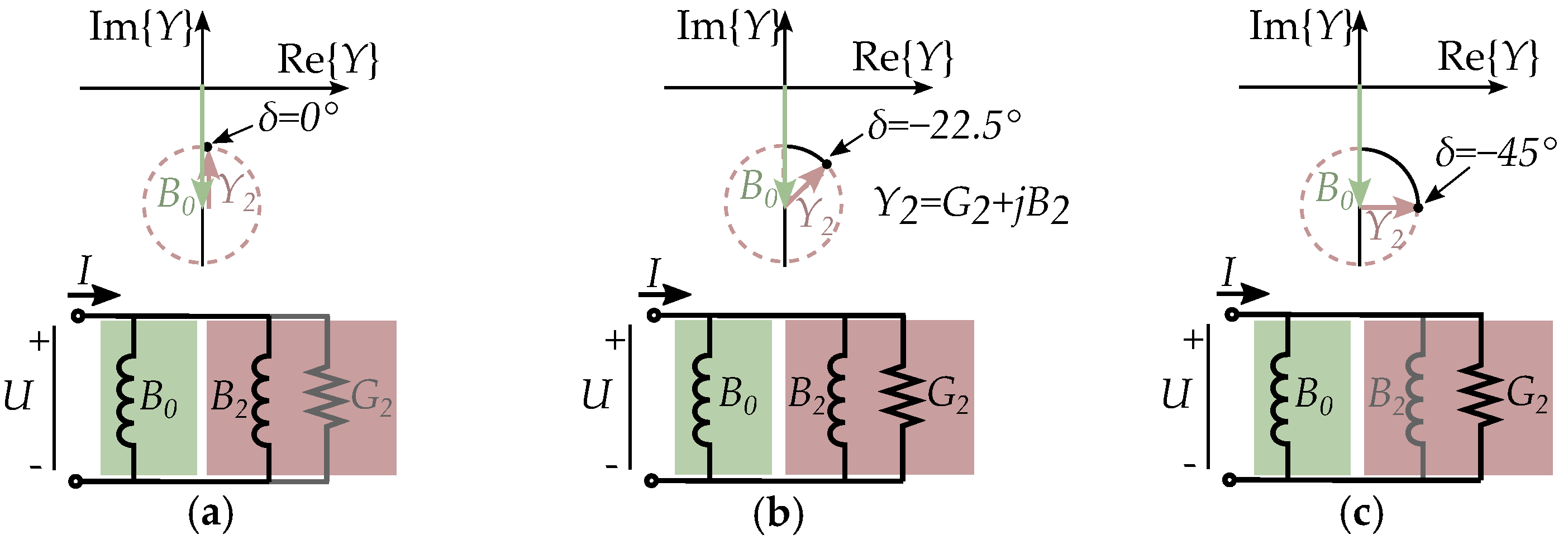

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mörée, G.; Leijon, M. Simplified Current-Equivalent Circuit Models of Synchronous Reluctance Machines and Salient Pole Synchronous Machines Considering the Reluctance Torque. Energies 2024, 17, 1015. https://doi.org/10.3390/en17051015
Mörée G, Leijon M. Simplified Current-Equivalent Circuit Models of Synchronous Reluctance Machines and Salient Pole Synchronous Machines Considering the Reluctance Torque. Energies. 2024; 17(5):1015. https://doi.org/10.3390/en17051015
Chicago/Turabian StyleMörée, Gustav, and Mats Leijon. 2024. "Simplified Current-Equivalent Circuit Models of Synchronous Reluctance Machines and Salient Pole Synchronous Machines Considering the Reluctance Torque" Energies 17, no. 5: 1015. https://doi.org/10.3390/en17051015





