Static-Voltage-Stability Analysis of Renewable Energy-Integrated Distribution Power System Based on Impedance Model Index
Abstract
1. Introduction
- (1)
- We apply the traditional impedance model index of single-infeed power systems to a general power system, making it more applicable for analyzing static-voltage stability with the large-scale integration of renewable energy.
- (2)
- The method of calculating the impedance model index is proposed, addressing the time-consuming nature of traditional methods in dealing with complex power systems.
- (3)
- Based on the proposed method, the selection of network topologies and connection nodes is presented using the impedance model index in different scenarios. This presents new inspiration for the grid connection of renewable energy considering stability limitations.
2. Introduction to Tradition Static-Voltage-Stability Analysis Methods
2.1. Singular Value Decomposition Method
2.2. Sensitivity Analysis Method
2.3. Continuation Power Flow Method
2.4. Voltage Collapse Point Method
2.5. Bifurcation Theory Method
3. Static-Voltage-Stability Analysis Method Based on Impedance Model Index
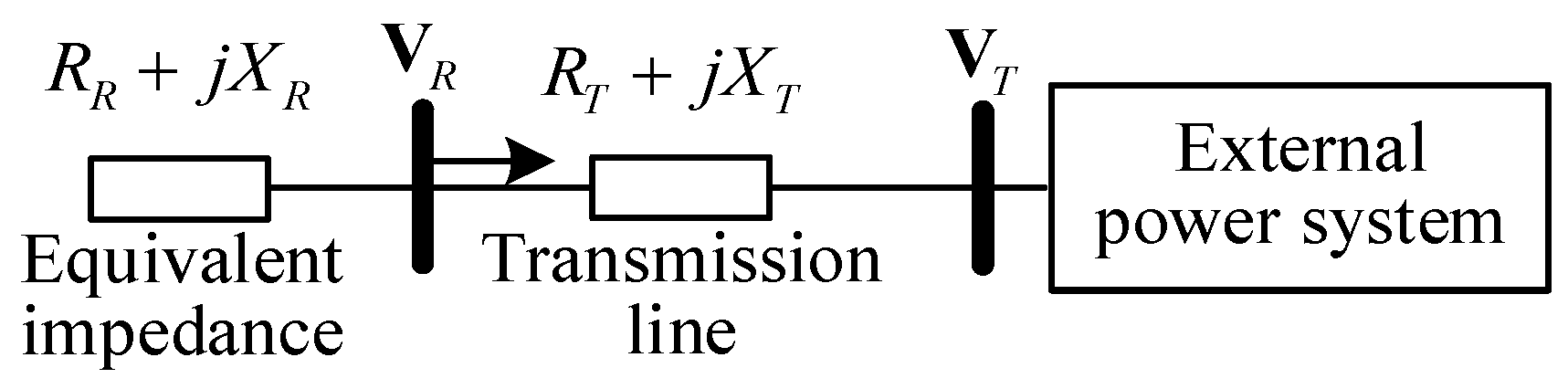
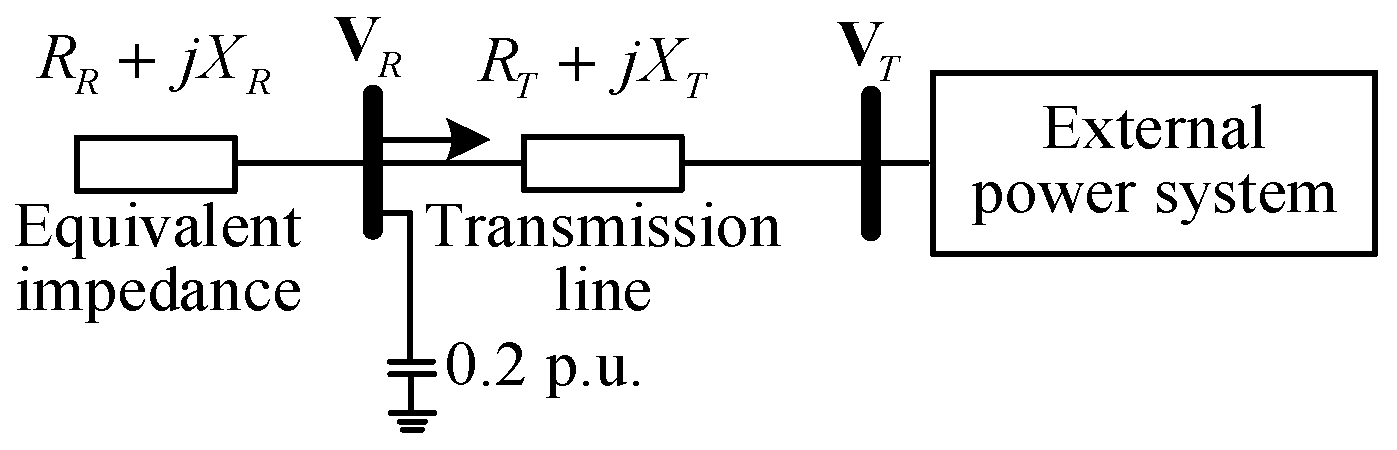
3.1. Review of Impedance Model Index
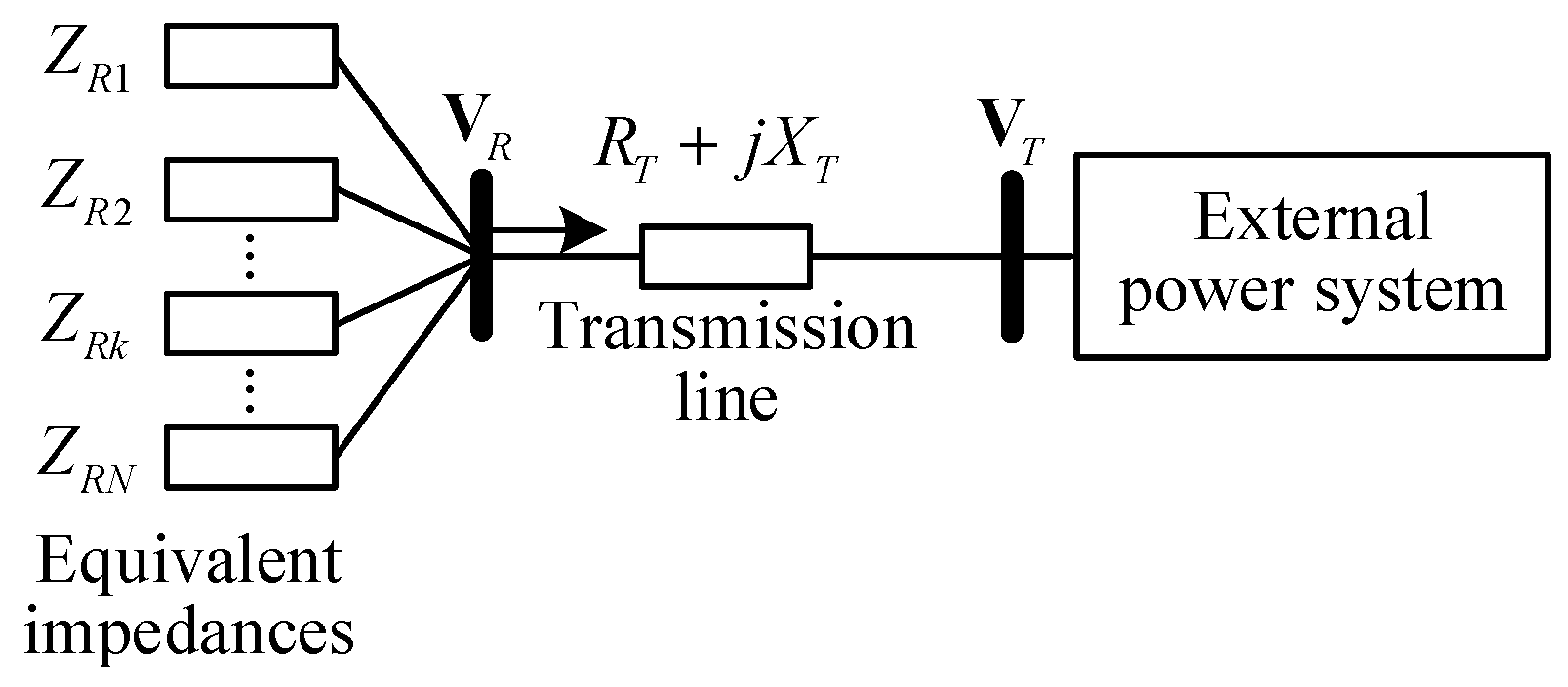
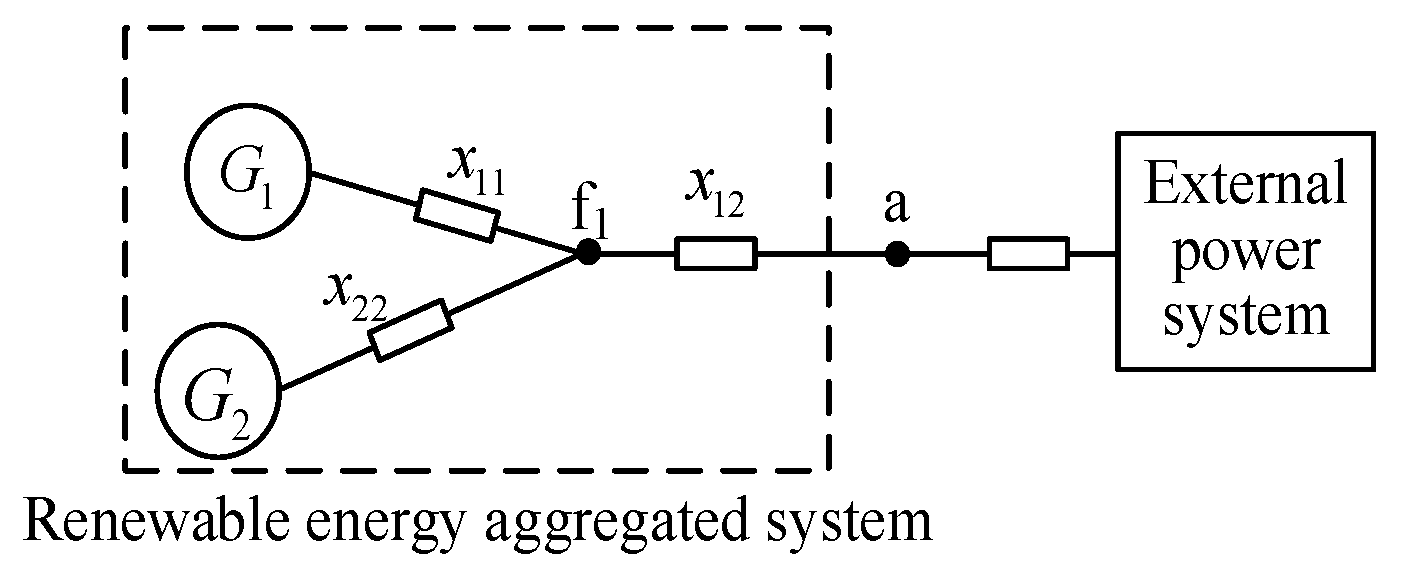
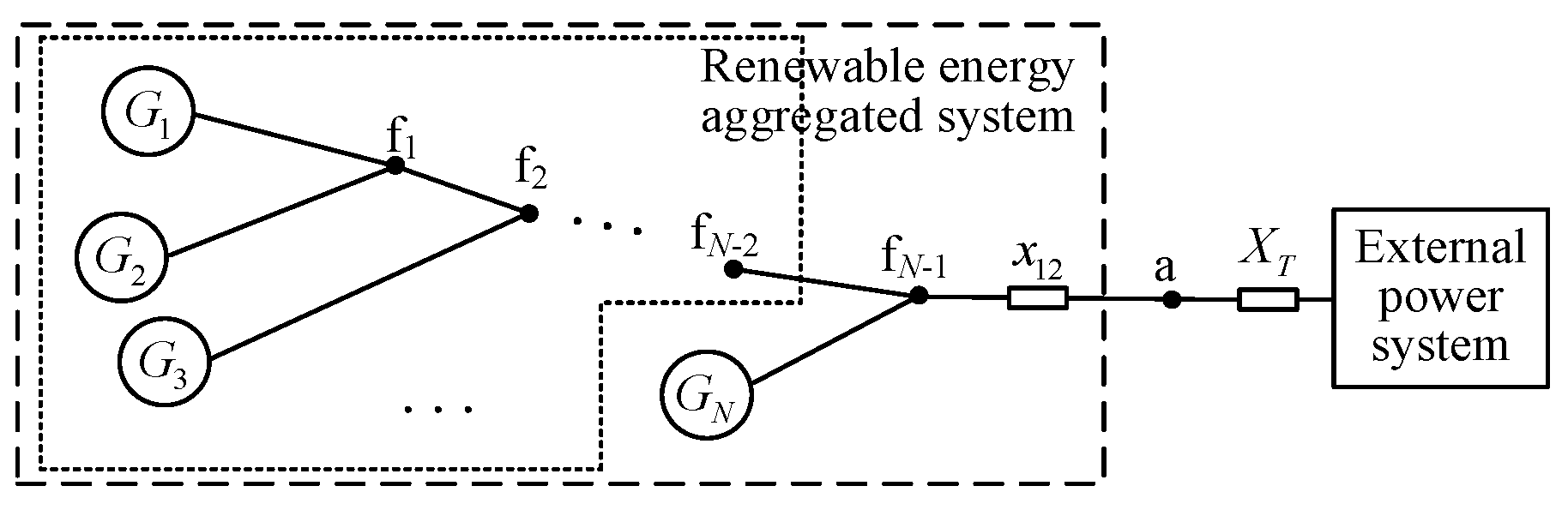
3.2. Simple Application of Impedance Model Index for Renewable Energy Aggregated Distribution Power Systems
3.3. Proposed Static-Voltage-Stability Analysis Method Based on Impedance Model Index
3.4. Impact of Parameter Errors on Calculated Results of Static-Voltage Stability
4. Analysis of Factors Affecting Static-Voltage Stability
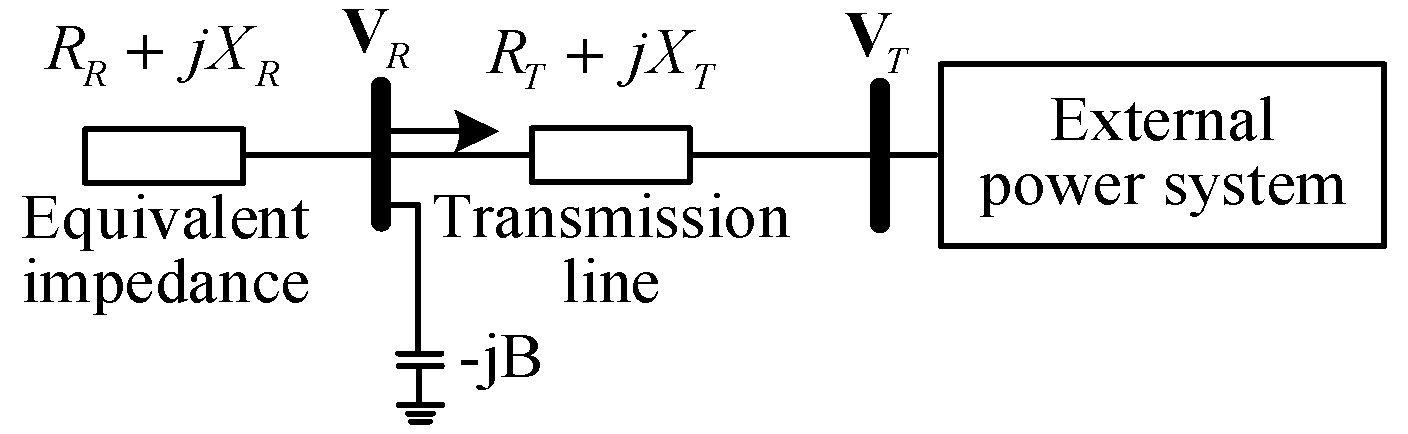
4.1. Impact of Reactive Power Compensation on Impedance Model Index
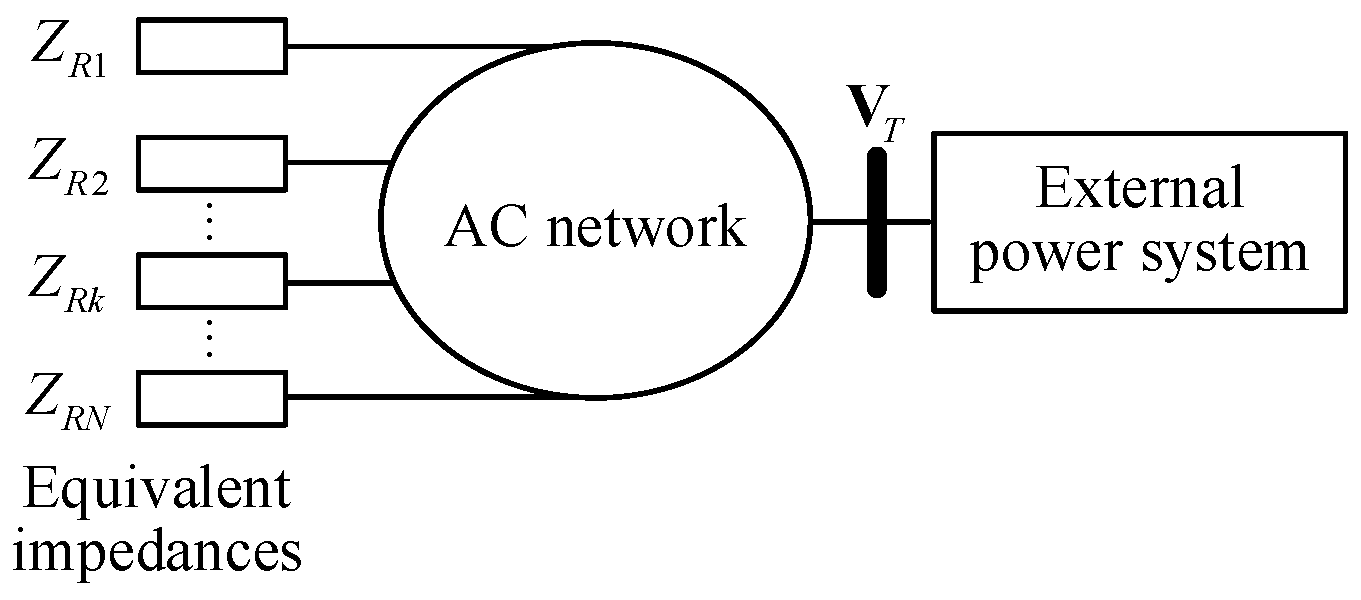
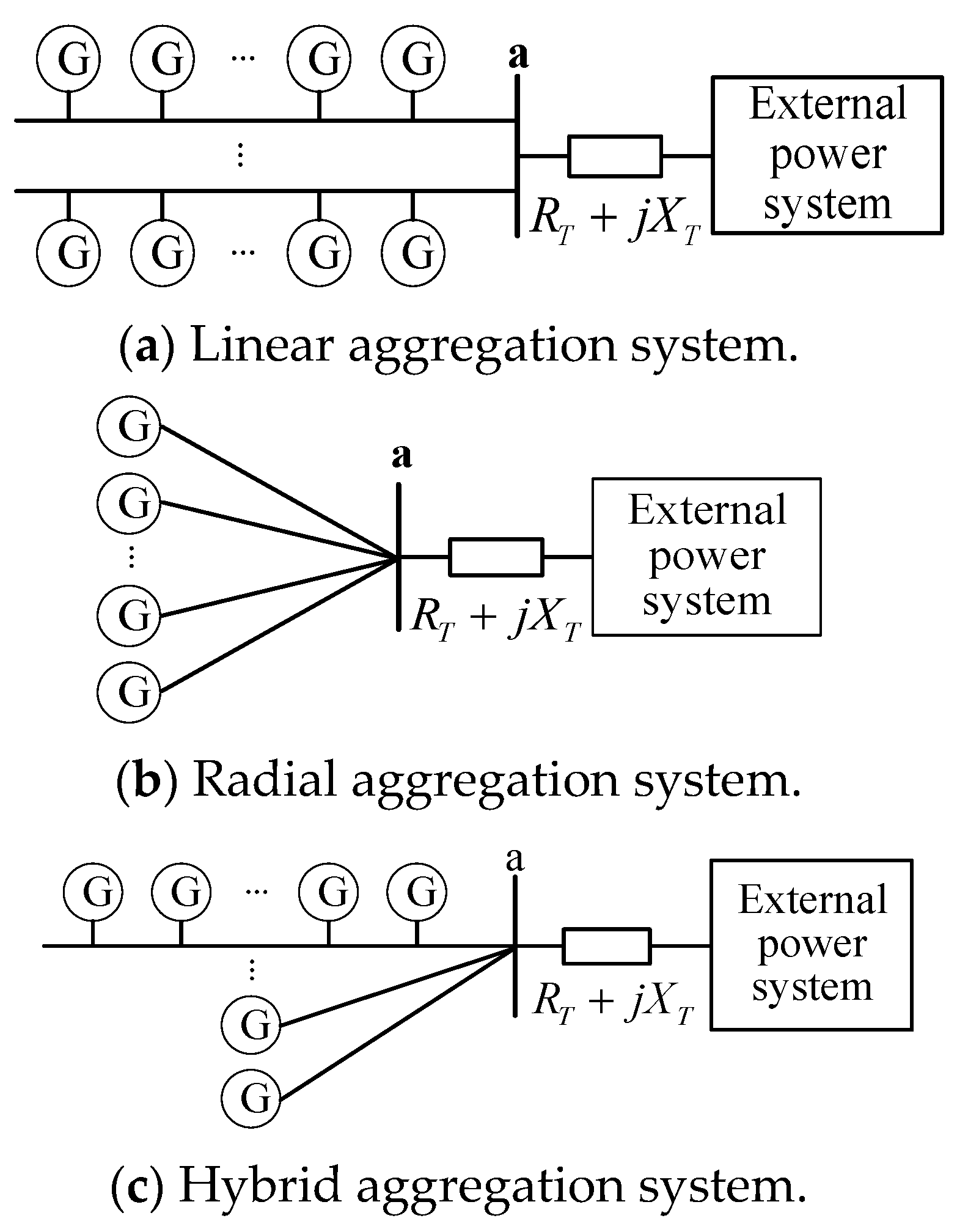
4.2. Influence of Renewable Energy Aggregation Topology on Static-Voltage Stability
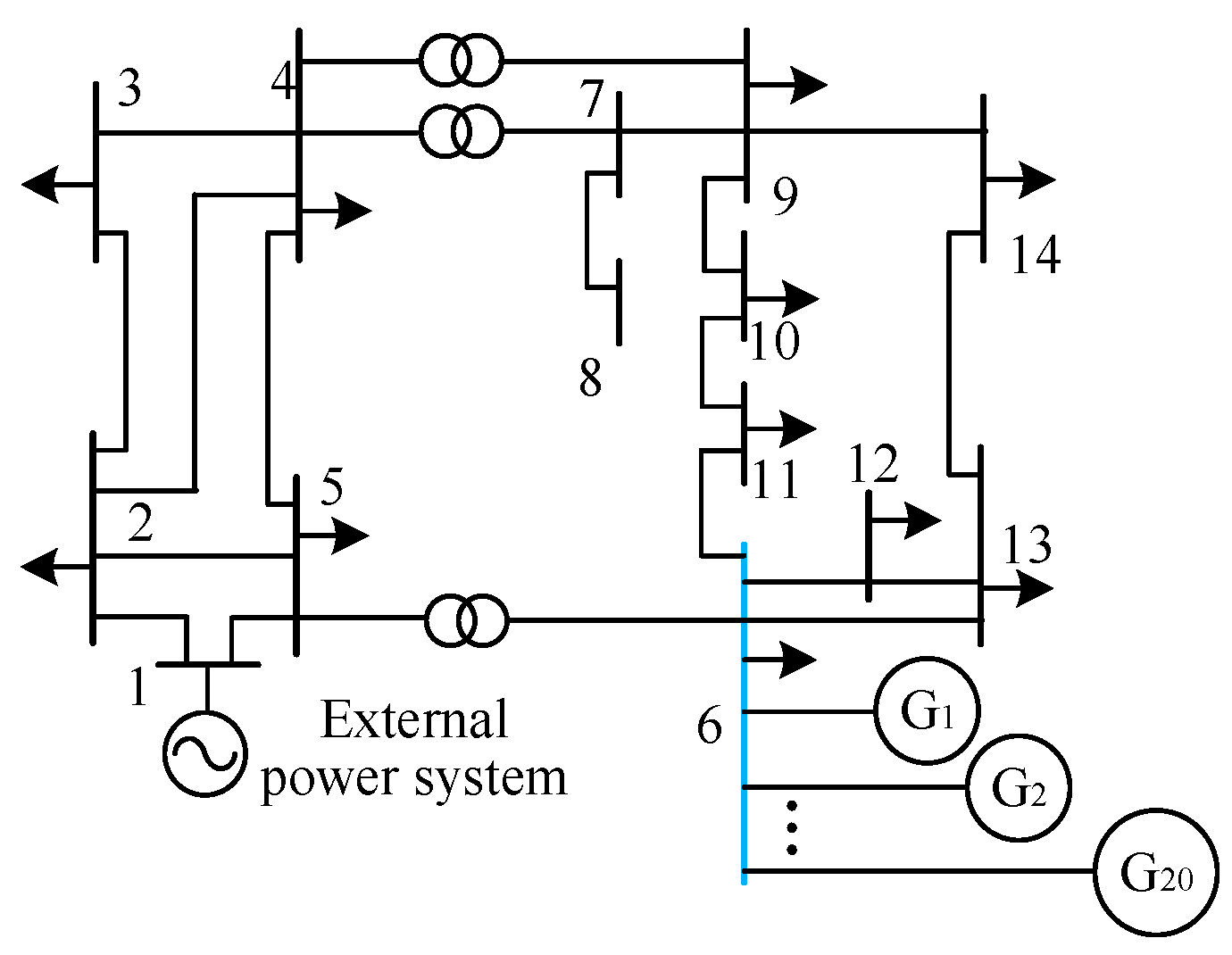
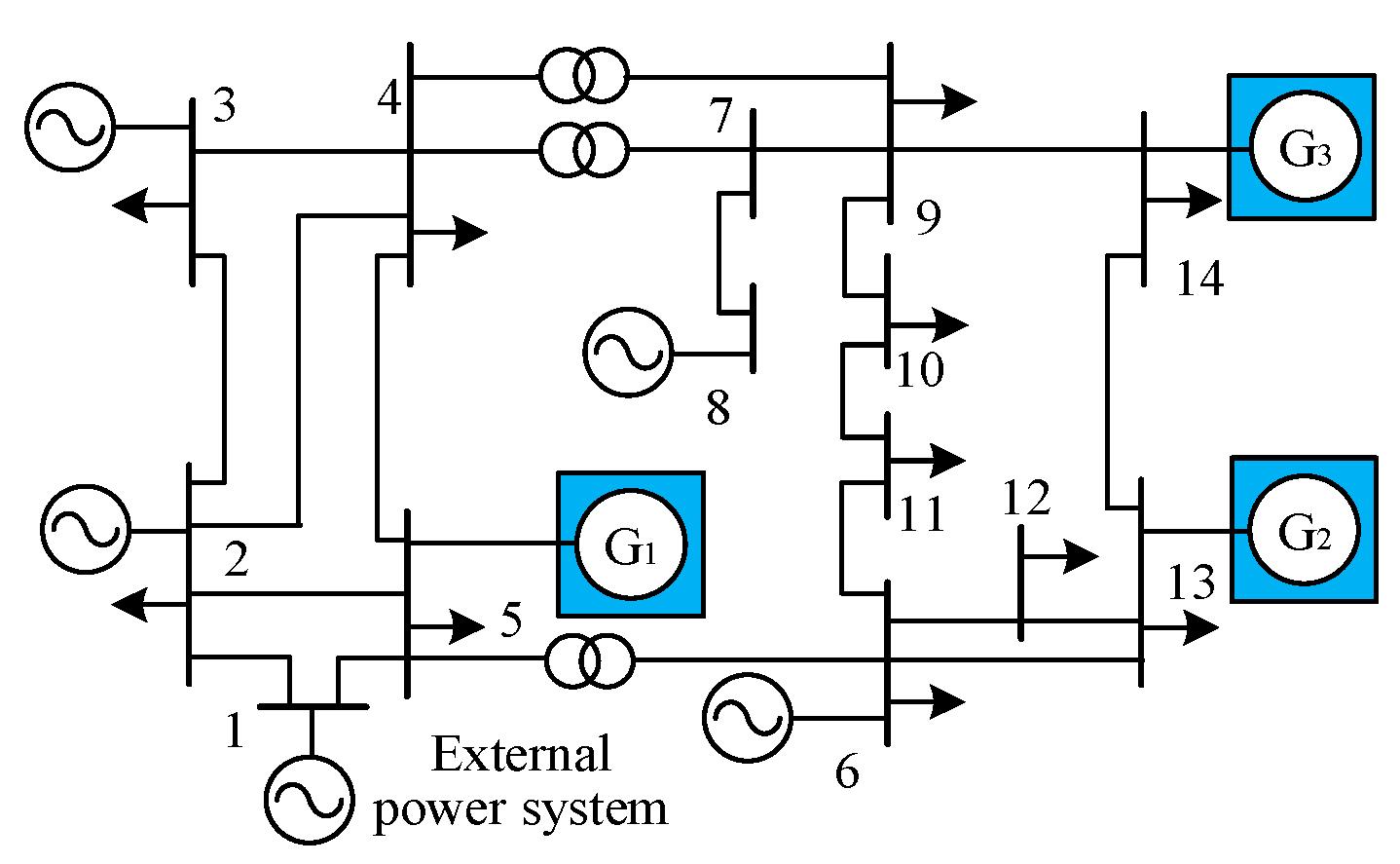
5. Case Study Analysis
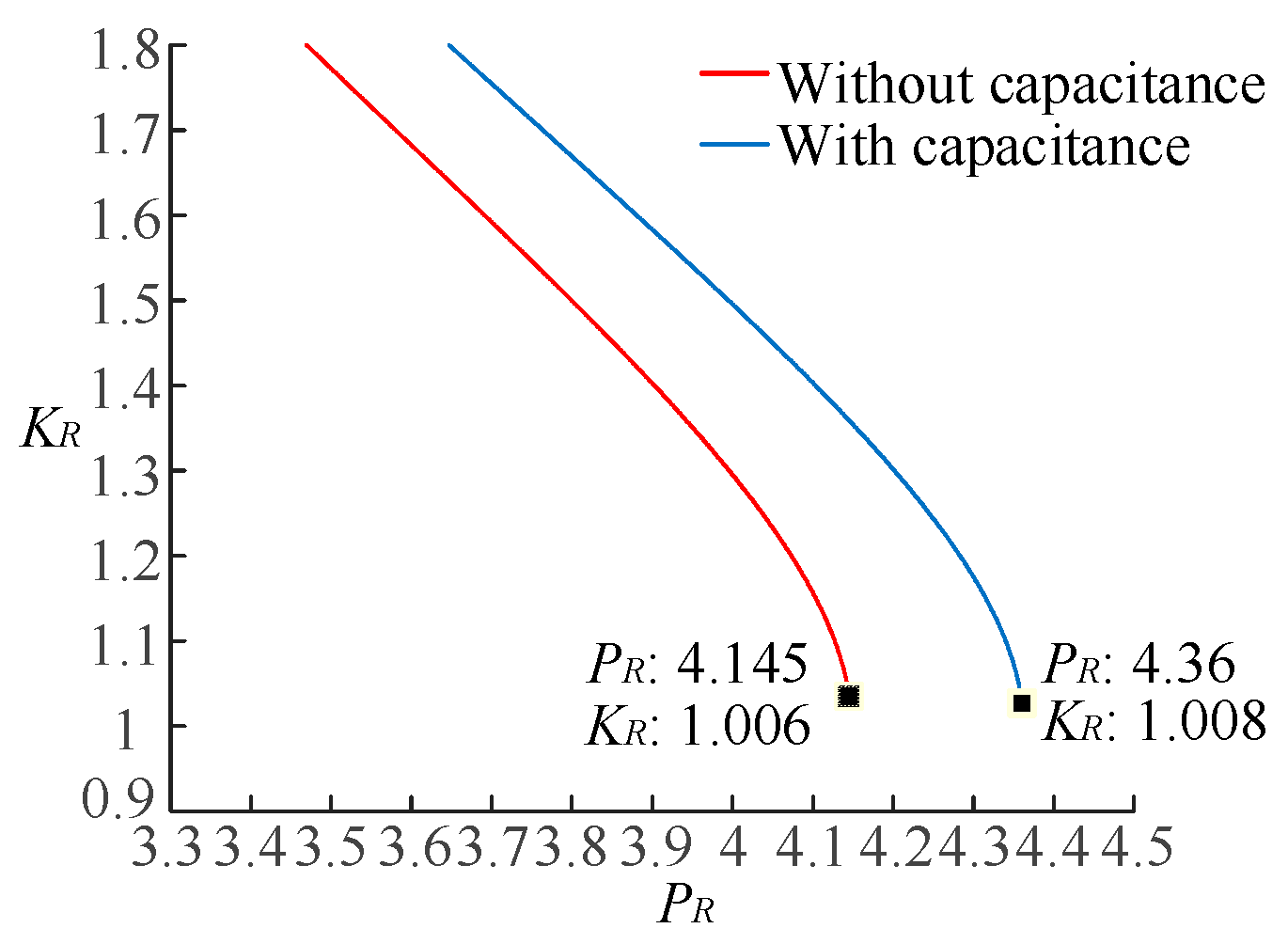
5.1. Impact of Reactive Power Compensation on Static-Voltage Stability
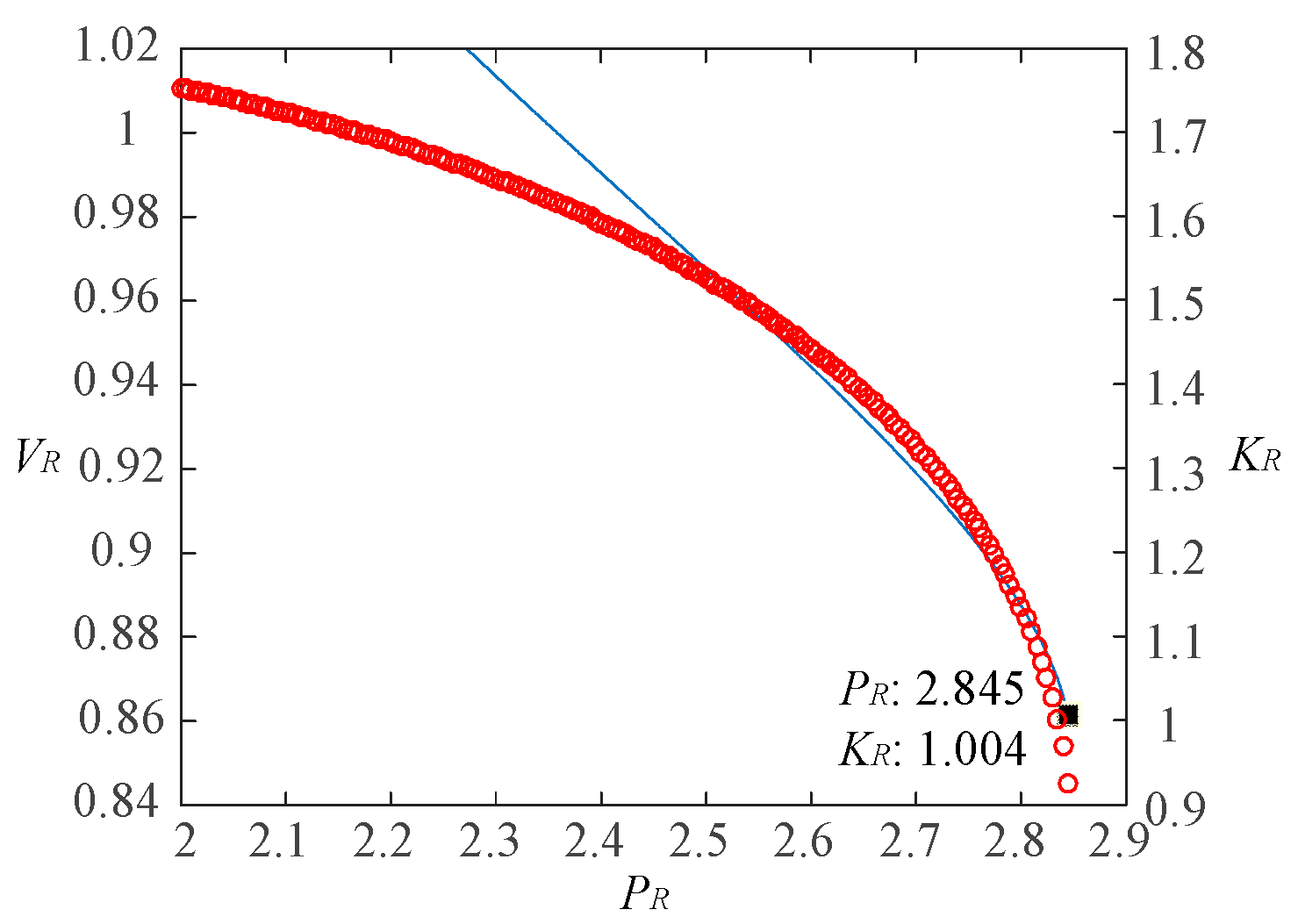
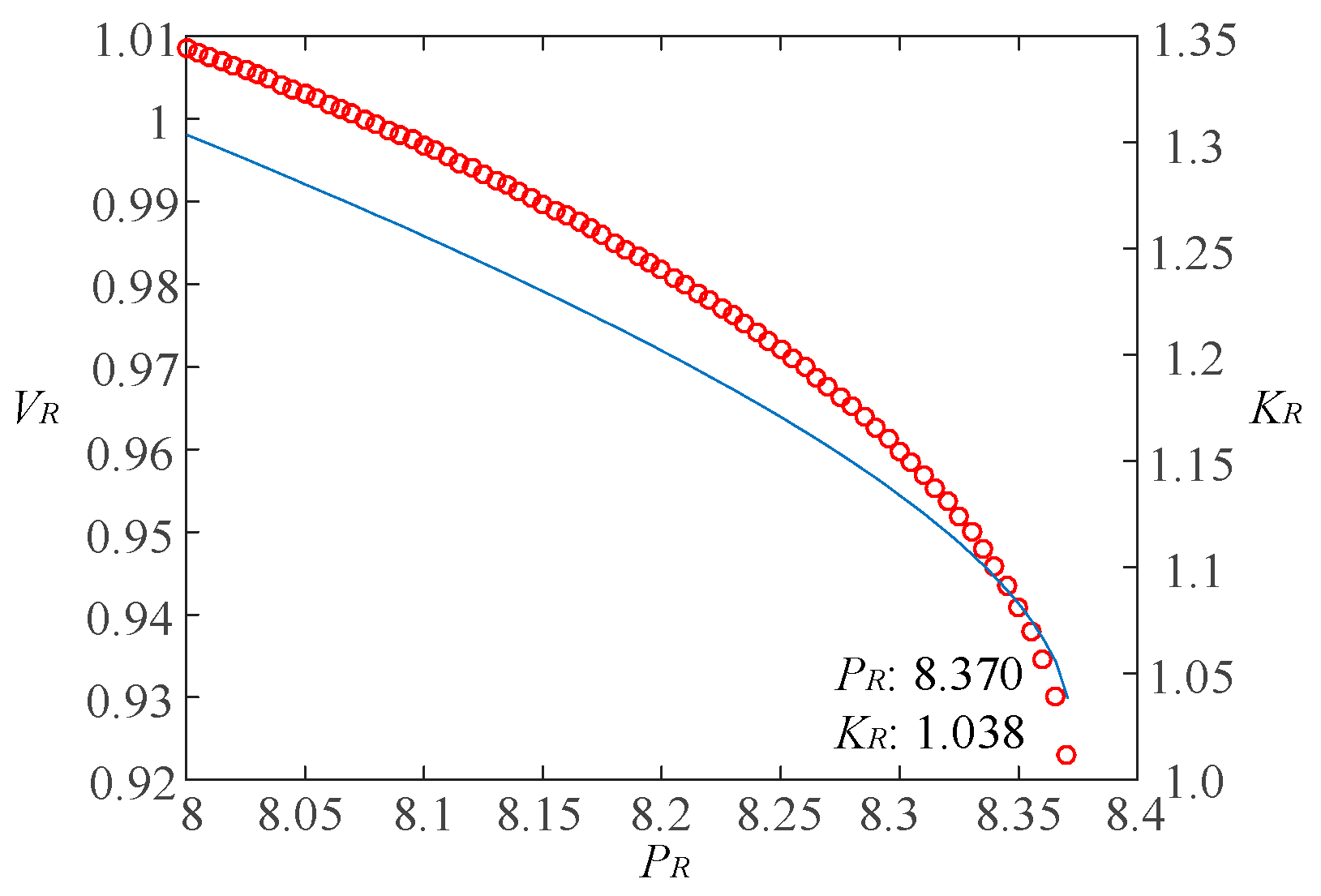
5.2. Calculation of Impedance Model Index for Renewable Energy Aggregated Distribution Power Systems
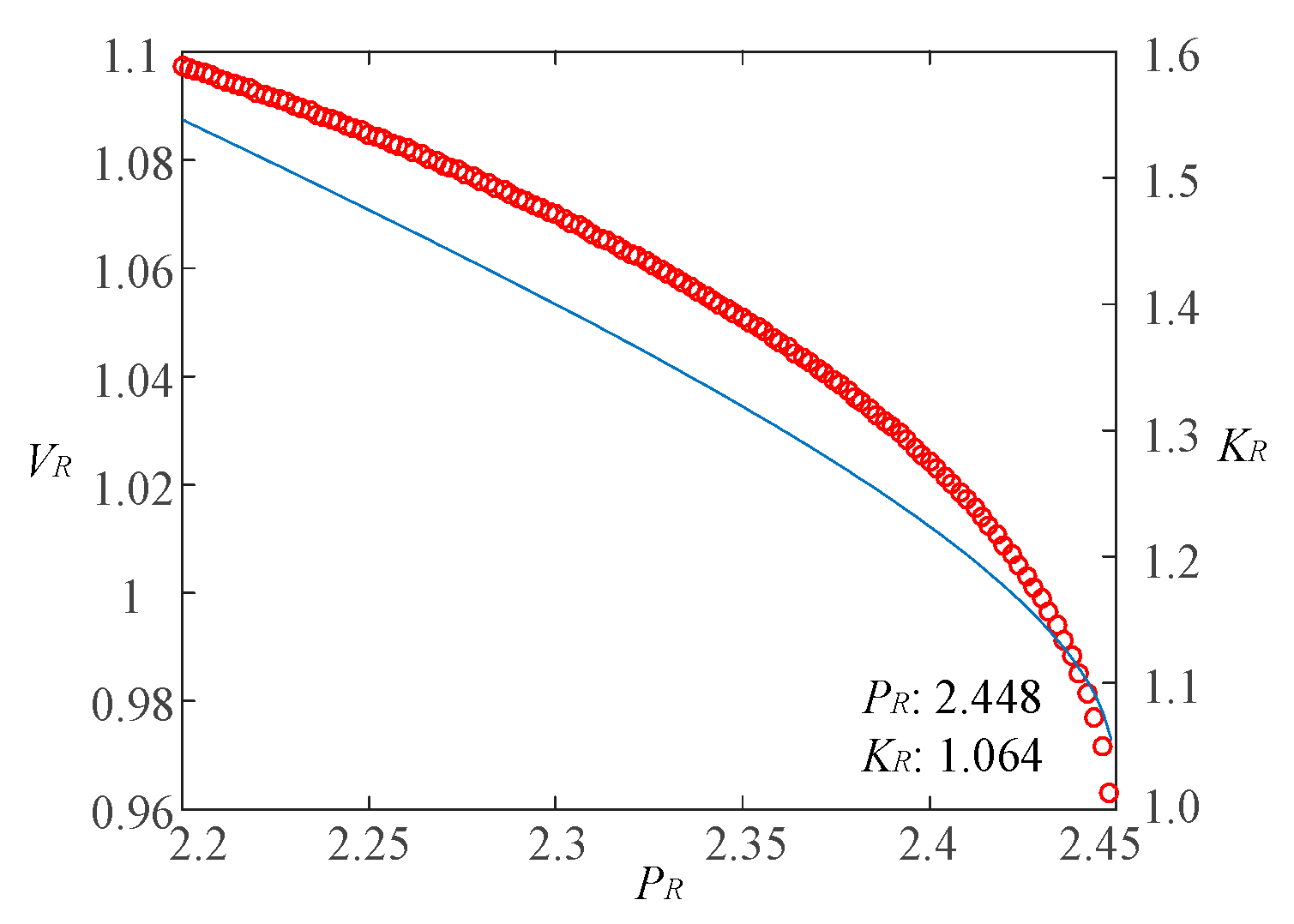
5.3. Calculation of Impedance Model Index for Renewable Energy Multi-Infeed Distribution Power Systems
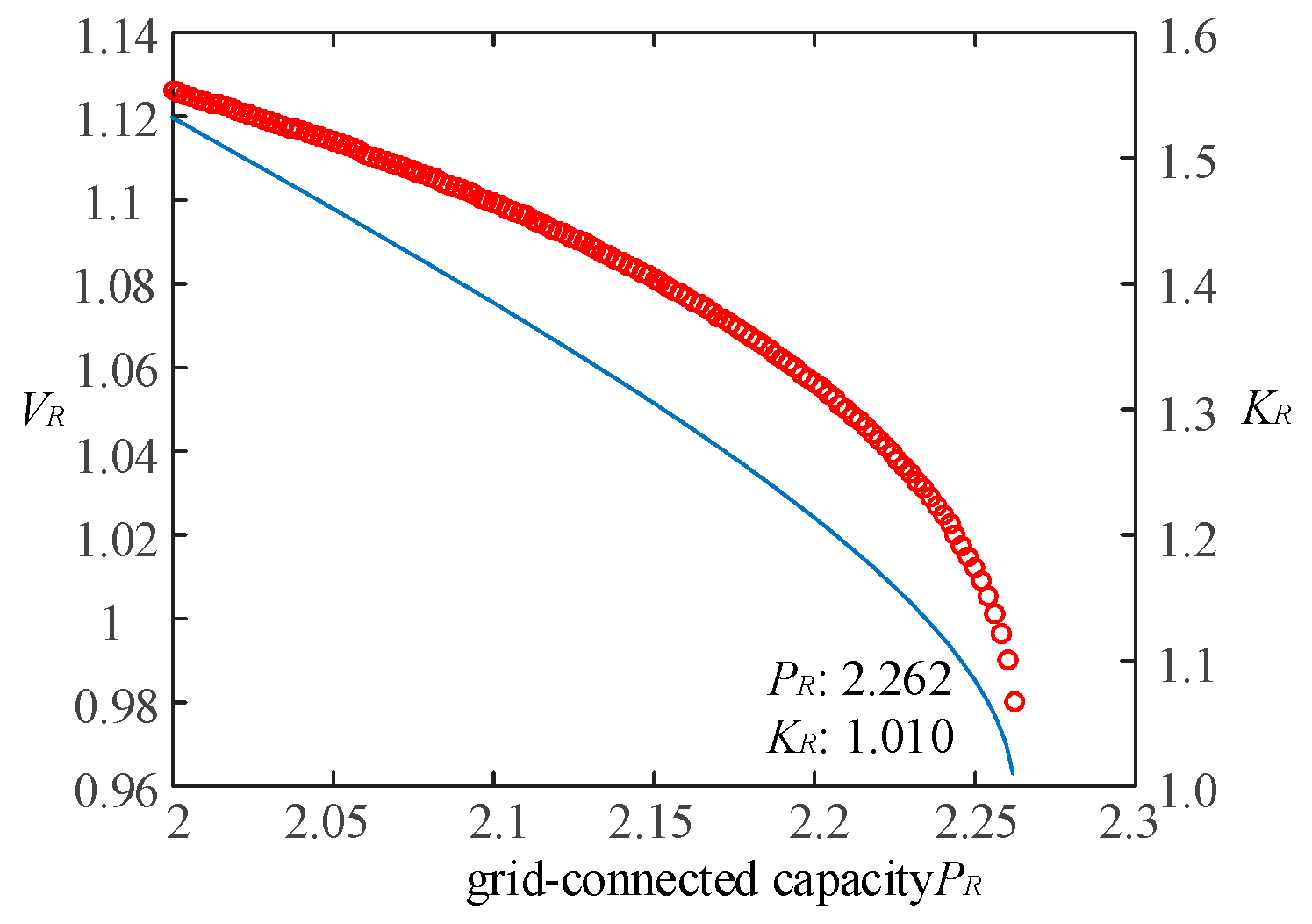
5.4. Impact of Network Topology on Impedance Model Index
6. Conclusions
- The impedance model index proposed in this study is not only applicable to renewable energy single-infeed distribution power systems but also suitable for renewable energy multi-infeed distribution power systems. It effectively reflects the static-voltage-stability margin of the renewable energy-integration nodes.
- The network topology of renewable energy aggregated systems can affect the static-voltage stability of the distribution power system. This study demonstrated that the radiation-type network topology for renewable energy offers the best static-voltage stability of the distribution power system.
- The addition of AC and DC lines can increase the impedance model index, thereby improving the system’s static-voltage stability. When planning the integration of renewable energy, selecting the node with the highest impedance model index can enhance the stability of the distribution power system.
- This study offers valuable insights into the static-voltage stability of renewable energy-integrated distribution power systems, and considering the fast development of EVs, this proposed method also has huge application scope in the future in similar scenarios, enhancing decision-making in renewable energy planning and operation. Future studies will consider the intermittency of active power generation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tielens, P.; Van Hertem, D. The relevance of inertia in power systems. New Sustain. Energy Rev. 2016, 55, 999–1009. [Google Scholar] [CrossRef]
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; et al. Definition and classification of power system stability. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C.; Ajjarapu, V.; Canizares, C.; Erlich, I.; Hill, D.; Hiskens, I.; Kamwa, I.; Pal, B.; et al. Definition and classification of power system stability–Revisited & extended. IEEE Trans. Power Syst. 2021, 36, 3271–3281. [Google Scholar]
- Xie, X.; He, J.; Mao, H.; Li, H. New Issues and Classification of Power System Stability with High Shares of News and Power Electronics. Proc. CSEE 2021, 41, 461–473. [Google Scholar]
- Ge, P.; Xiao, F.; Tu, C.; Guo, Q.; Gao, J.; Song, Y. Comprehensive transient stability enhancement control of a VSG considering power angle stability and fault current limitation. CSEE J. Power Energy Syst. 2022, 1–10. [Google Scholar] [CrossRef]
- Laiva Roca, D.A.; Mercado, P.; Suvire, G. System Frequency Response Model Considering the Influence of Power System Stabilizers. IEEE Lat. Am. Trans. 2022, 20, 912–920. [Google Scholar] [CrossRef]
- Ranjan, S.; Das, D.C.; Latif, A.; Sinha, N.; Hussain, S.M.S.; Ustun, T.S. Maiden Voltage Control Analysis of Hybrid Power System with Dynamic Voltage Restorer. IEEE Access 2021, 9, 60531–60542. [Google Scholar] [CrossRef]
- Song, Y.; Hill, D.J.; Liu, T. Static Voltage Stability Analysis of Distribution Systems Based on Network-Load Admittance Ratio. IEEE Trans. Power Syst. 2019, 34, 2270–2280. [Google Scholar] [CrossRef]
- US-Canada Power Outage Task Force. Final Report on the August 14th 2003 Blackout in the United States and Canada. Available online: http://www.ferc.gov/ (accessed on 1 October 2023).
- Australian Energy Market Operator. Black System South Australia 28 September 2016–Third Preliminary Report; Australian Energy Market Operator Limited: Melbourne, Australia, 2016. [Google Scholar]
- Xue, Y.; Xu, T.; Liu, B.; Li, Y. Quantitative assessments for transient voltage security. IEEE Trans. Power Syst. 2000, 15, 1077–1083. [Google Scholar] [CrossRef]
- Ellithy, K.; Shaheen, M.; Al-Athba, M.; Al-Subaie, A.; Al-Mohannadi, S.; Al-Okkah, S.; Abu-Eidah, S. Voltage stability evaluation of real power transmission system using singular value decomposition technique. In Proceedings of the IEEE 2nd International Power and Energy Conference, Johor Bahru, Malaysia, 1–3 December 2008; pp. 1691–1695. [Google Scholar] [CrossRef]
- Alzaareer, K.; Saad, M.; Mehrjerdi, H.; Salem, Q.; Harasis, S.; Aldaoudeyeh, A.-M.I.; Al-Masri, H.M.K. Sensitivity Analysis for Voltage Stability Considering Voltage Dependent Characteristics of Loads and DGs. IEEE Access 2021, 9, 156437–156450. [Google Scholar] [CrossRef]
- Nirbhavane, P.S.; Corson, L.; Rizvi, S.M.H.; Srivastava, A.K. TPCPF: Three-Phase Continuation Power Flow Tool for Voltage Stability Assessment of Distribution Networks with Distributed Energy Resources. IEEE Trans. Ind. Appl. 2021, 57, 5425–5436. [Google Scholar] [CrossRef]
- Flueck, A.J.; Gonella, R.; Dondeti, J.R. A new power sensitivity method of ranking branch outage contingencies for voltage collapse. IEEE Trans. Power Syst. 2002, 17, 265–270. [Google Scholar] [CrossRef]
- Pierrou, G.; Wang, X. Analytical Study of the Impacts of Stochastic Load Fluctuation on the Dynamic Voltage Stability Margin Using Bifurcation Theory. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 1286–1295. [Google Scholar] [CrossRef]
- Lim, J.M.; DeMarco, C.L. SVD-Based Voltage Stability Assessment from Phasor Measurement Unit Data. IEEE Trans. Power Syst. 2016, 31, 2557–2565. [Google Scholar] [CrossRef]
- Gao, B.; Morison, G.K.; Kundur, P. Voltage stability evaluation using modal analysis. IEEE Trans. Power Syst. 1992, 7, 1529–1542. [Google Scholar] [CrossRef]
- Pan, X.; Li, L.; Huang, H.; Yan, J.; Yang, L. Method for evaluating voltage weak area of AC power system at DC receiving end considering sensitivity and static voltage stability margin. Electr. Power Autom. Equip. 2019, 39, 1–8. [Google Scholar]
- Cui, X.; Yun, Z.; Liu, D.; Yang, H.; Li, Z.; Gao, D.; Jin, X. A New Method of Sensitivity Analysis for Static Voltage Stability Online Prevention and Control of Large Power Grids. Power Syst. Technol. 2020, 44, 246–254. [Google Scholar]
- Zhou, J.; He, Y.; He, H.; Li, C.; Li, P. Calculation Method for Continuation Power Flow Based on Line Voltage Stability Index. Proc. CSU EPSA 2018, 30, 140–144. [Google Scholar]
- Chen, G.; Zhou, Y.; Zhao, J.; Huang, G.; Bao, Y.; Lin, Q. A Three-Stage Progressive Voltage Stability Contingency Screening and Ranking Method for Large Power Grids. South. Power Syst. Technol. 2018, 12, 70–75. [Google Scholar]
- Chen, C.; Jiang, T.; Wan, K.; Feng, Z. Improved point of collapse method for direct calculation of static voltage stability margin. Electr. Power Autom. Equip. 2020, 40, 150–155. [Google Scholar]
- Tang, X.; Gao, L. Analysis on Static Voltage Stability Considering Restriction of Branch Power. Power Syst. Technol. 2011, 35, 99–102. [Google Scholar]
- Kwatny, H.G. Static bifurcati on in electric power networks: Loss of steady-state stability and voltage collapse. IEEE Trans CAS 1986, 33, 981–991. [Google Scholar] [CrossRef]
- Chiang, H.D.; Ju Meau, R.J. A more efficient formulation for computation of the maximum loading in electric power system. IEEE Trans Power Syst. 1995, 10, 635–646. [Google Scholar] [CrossRef]
- Kamaruzzaman, Z.A.; Mohamed, A. Impact of grid-connected photovoltaic generator using P-V curve and improved voltage stability index. In Proceedings of the IEEE International Conference on Power and Energy (PECon), Kuching, Malaysia, 1–3 December 2014; pp. 196–200. [Google Scholar]


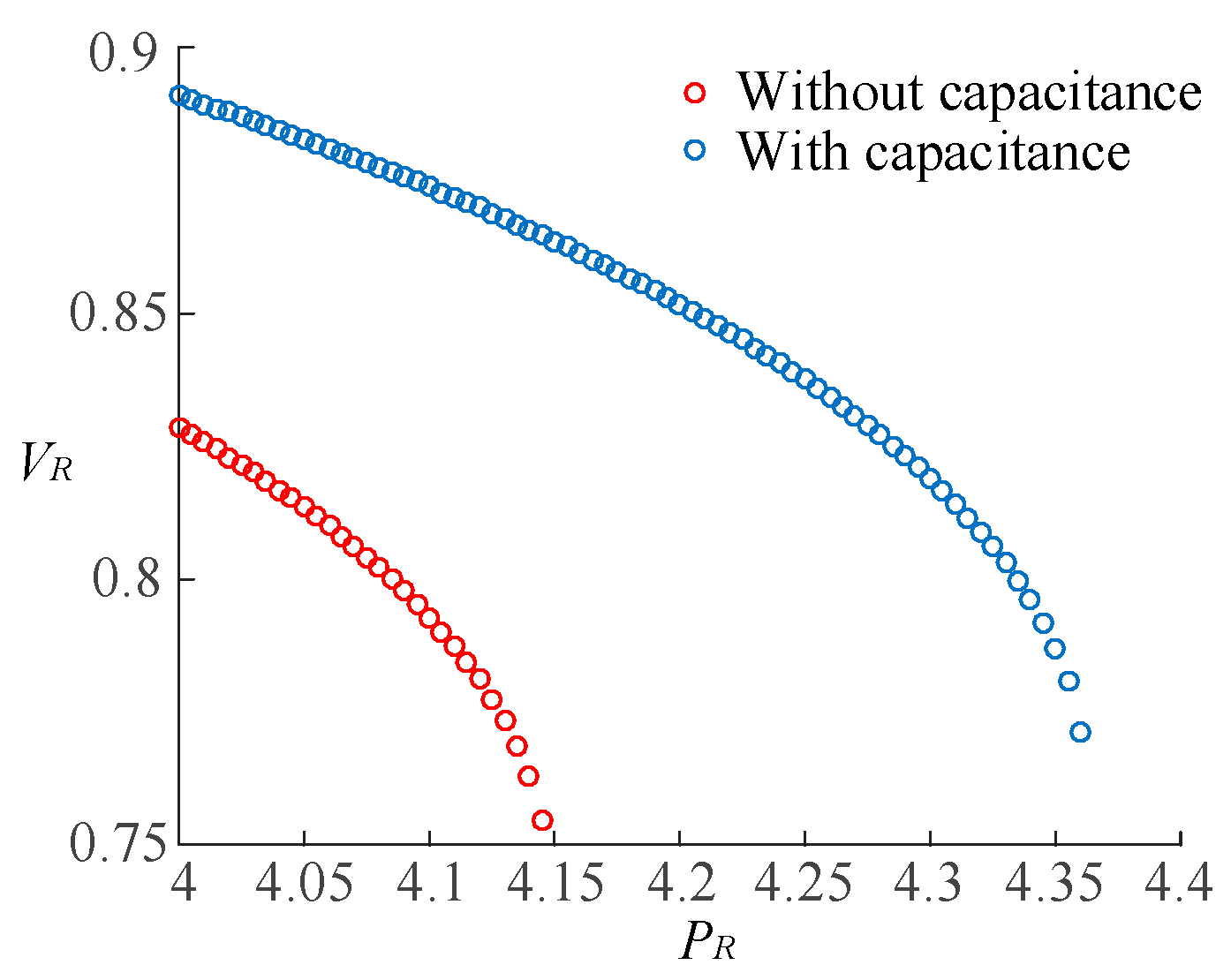
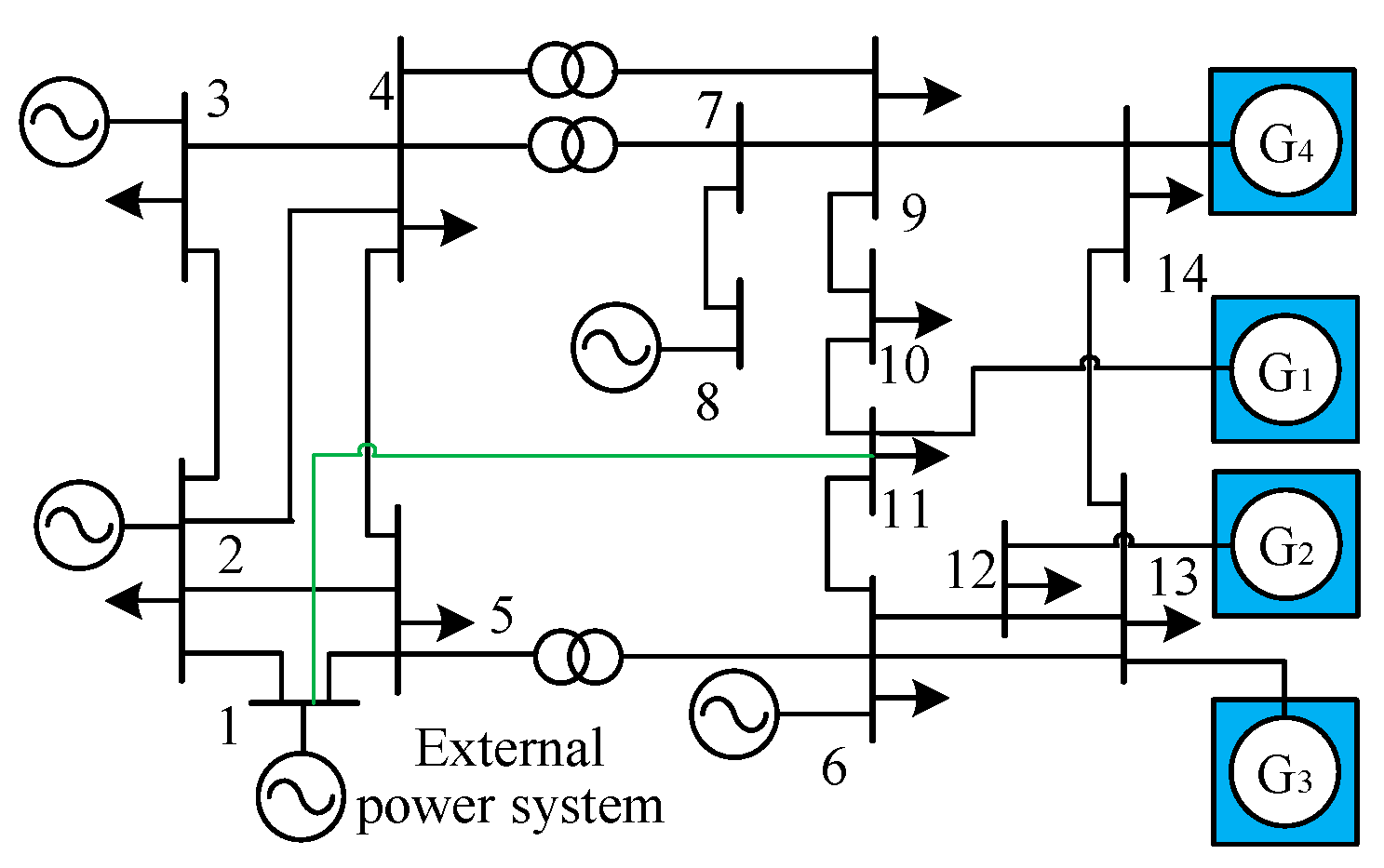
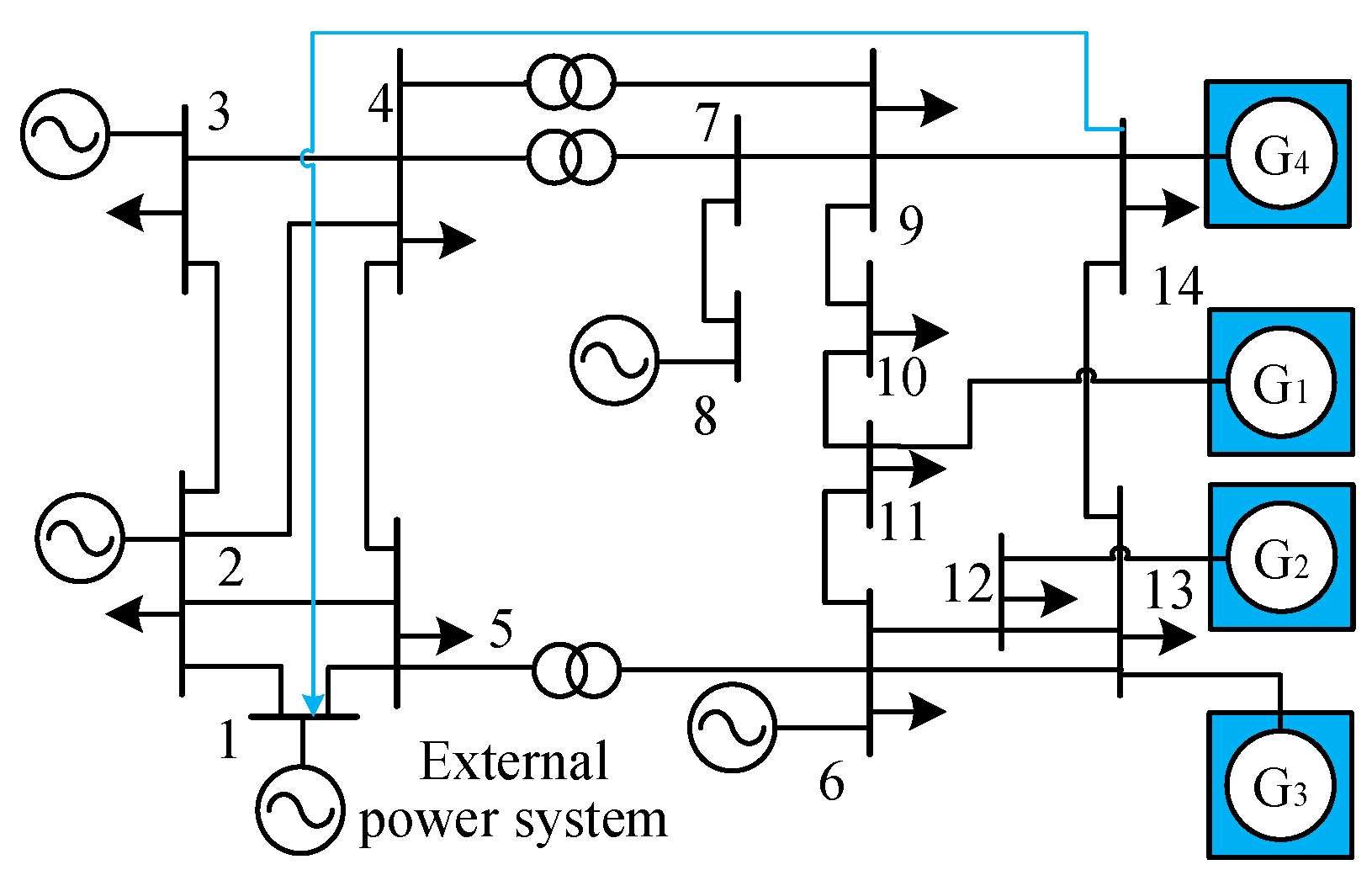
| Method | Advantages | Disadvantages | Applicability |
|---|---|---|---|
| Singular Value Decomposition Method | Rapid assessment of voltage stability margin | Computation dependent on eigenvalue decomposition of the Jacobian matrix | Suitable for fast evaluation of voltage stability in large-scale power systems |
| Sensitivity Analysis Method | Identification of regions of voltage relative instability | Requires solving and maintaining the sensitivity matrix | Used to analyze the impact of control variables on system stability |
| Continuation Power Flow Method | Iterative calculation of power flow distribution at critical states | High computational complexity in iterative calculations | Applied to compute voltage stability margin near critical states |
| Voltage Collapse Point Method | Direct computation of system voltage limit points | Increased complexity in augmented Jacobian matrix calculation | Used to determine voltage limit points and stability margins |
| Bifurcation Theory Method | Analysis of sudden qualitative changes near critical points | Sensitivity to system parameter variations | Utilized to predict stability changes near critical states |
| Methods | The Method Proposed in This Paper |
|---|---|
| Continuation Power Flow Method in [24] | By calculating the impedance model index, static-voltage stability can be determined in a single computation, with the maximum dimension in calculations being equivalent to the node number. In contrast, the Continuation Power Flow Method requires multiple calculations of the voltage at each node, leading to time inefficiencies, particularly for large-scale power systems. |
| Impedance model index method in [8] | The impedance model index introduced in this paper facilitates the selection of network topology based on the impedance matrix of the network. Conversely, the impedance model index proposed in [8] necessitates the calculation of results for all nodes to make decisions about network selection, resulting in a time-consuming process. |
| Capacities of Each Group of Renewable Energy Sources | Aggregation Bus Maximum Grid-Connected Capacity | |
|---|---|---|
| 0.115, 0.145, 0.165 | 2.842 | 1.008 |
| 0.165, 0.130, 0.135 | 2.841 | 1.010 |
| 0.135, 0.150, 0.140 | 2.838 | 1.012 |
| Before Adding AC Branches | 1.5412 | 1.3155 | 1.4870 | 1.2717 |
| After Adding AC Branches | 5.0474 | 1.6547 | 2.1329 | 1.6498 |
| Improvement Margin of the Index (%) | 227.50 | 25.78 | 43.44 | 29.73 |
| Before DC Line Connection | 1.5412 | 1.3155 | 1.4870 | 1.2717 |
| After DC Line Connection | 1.5462 | 1.3351 | 1.5062 | 1.3297 |
| Improvement Margin of the Index (%) | 0.32 | 1.49 | 1.29 | 4.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Cai, Y.; Li, W.; Tan, Z.; Song, Z.; Li, Y.; Bai, H.; Liu, T. Static-Voltage-Stability Analysis of Renewable Energy-Integrated Distribution Power System Based on Impedance Model Index. Energies 2024, 17, 1028. https://doi.org/10.3390/en17051028
Wang Y, Cai Y, Li W, Tan Z, Song Z, Li Y, Bai H, Liu T. Static-Voltage-Stability Analysis of Renewable Energy-Integrated Distribution Power System Based on Impedance Model Index. Energies. 2024; 17(5):1028. https://doi.org/10.3390/en17051028
Chicago/Turabian StyleWang, Yang, Yongxiang Cai, Wei Li, Zhukui Tan, Zihong Song, Yue Li, Hao Bai, and Tong Liu. 2024. "Static-Voltage-Stability Analysis of Renewable Energy-Integrated Distribution Power System Based on Impedance Model Index" Energies 17, no. 5: 1028. https://doi.org/10.3390/en17051028
APA StyleWang, Y., Cai, Y., Li, W., Tan, Z., Song, Z., Li, Y., Bai, H., & Liu, T. (2024). Static-Voltage-Stability Analysis of Renewable Energy-Integrated Distribution Power System Based on Impedance Model Index. Energies, 17(5), 1028. https://doi.org/10.3390/en17051028







